Assessing pulsatile waveforms of paravascular cerebrospinal fluid dynamics using dynamic diffusion-weighted imaging (dDWI)

Abstract

Cerebrospinal fluid (CSF) in the paravascular spaces of the surface arteries (sPVS) is a vital pathway in brain waste clearance. Arterial pulsations may be the driving force of the paravascular flow, but its pulsatile pattern remains poorly characterized, and no clinically practical method for measuring its dynamics in the human brain is available. In this work, we introduce an imaging and quantification framework for in-vivo non-invasive assessment of pulsatile fluid dynamics in the sPVS. It used dynamic Diffusion-Weighted Imaging (dDWI) at a lower b-values of 150s/mm² and retrospective gating to detect the slow flow of CSF while suppressing the fast flow of adjacent arterial blood. The waveform of CSF flow over a cardiac cycle was revealed by synchronizing the measurements with the heartbeat. A data-driven approach was developed to identify sPVS and allow automatic quantification of the whole-brain fluid waveforms. We applied dDWI to twenty-five participants aged 18–82 y/o. Results demonstrated that the fluid waveforms across the brain showed an explicit cardiac-cycle dependency, in good agreement with the vascular pumping hypothesis. Furthermore, the shape of the CSF waveforms closely resembled the pressure waveforms of the artery wall, suggesting that CSF dynamics is tightly related to artery wall mechanics. Finally, the CSF waveforms in aging participants revealed a strong age effect, with a significantly wider systolic peak observed in the older relative to younger participants. The peak widening may be associated with compromised vascular compliance and vessel wall stiffening in the older brain. Overall, the results demonstrate the feasibility, reproducibility, and sensitivity of dDWI for detecting sPVS fluid dynamics of the human brain. Our preliminary data suggest age-related alterations of the paravascular pumping. With an acquisition time of under six minutes, dDWI can be readily applied to study fluid dynamics in normal physiological conditions and cerebrovascular/neurodegenerative diseases.

1. Introduction

Cerebrospinal fluid (CSF) aids in the removal of metabolic waste from the brain (Iliff et al., 2012). In vivo experiments in rodents that track tracer particles injected into the cisterna magna have shown the flow of CSF through the paravascular spaces surrounding major and pial arteries, with a bulk flow in the same direction as blood flow (Iliff et al., 2012; Iliff et al., 2013a). These paravascular spaces, sometimes referred to as surface paravascular spaces (sPVS), are found near the surface of the brain and are continuous with the subarachnoid space (Bacyinski et al., 2017; Bedussi et al., 2017). The artery pulsation is deemed a major factor for the CSF in the sPVS to move into and through the brain, facilitating the exchange with brain interstitial fluid (ISF) and the clearance of interstitial solutes (e.g., amyloid-β) (Bilston et al., 2003; Iliff et al., 2013b; Bedussi et al., 2018; Mestre et al., 2018). The disrupted fluid movement has been found to impede the clearance of brain waste proteins and is an emerging risk factor for poor brain aging and dementia (Gaberel et al., 2014; Iliff et al., 2014; Kress et al., 2014; Mestre et al., 2018; Nedergaard and Goldman, 2020). Therefore, in vivo assessment of the pulsatile fluid dynamics in the sPVS is of high clinical significance.

Although 3D MRI acquisition can anatomically locate the sPVS (e.g., T2-weighted imaging), as yet, no method for noninvasively measuring its dynamics is available clinically (Naganawa and Taoka, 2020; Taoka and Naganawa, 2020). Two-photon microscopy imaging has made ground-breaking discoveries of the CSF pathways by tracking down fluorescent tracer dissipation but is limited to rodent studies and restricted to the brain surface. MRI has been used to evaluate whole-brain glymphatic function primarily with ex vivo tracers (e.g., gadolinium-based contrast agents) (Iliff et al., 2013a; Gaberel et al., 2014; Ratner et al., 2017; Benveniste et al., 2021). However, intrathecal gadolinium contrast agent injection may be considered too invasive and risky for routine clinical study of the human brain. It also requires a long time (4–8hrs) for tracer to dissipate to the PVS. A non-invasive method for directly measuring CSF dynamics is highly desirable. Phase-contrast MRI (PC-MRI) is such a technique, which uses velocity encoding and cardiac synchronization to measure CSF flow along the cardiac cycle. However, PC-MRI requires majority of spins within a voxel to have a coherent motion to produce a measurable phase shift. As a result, it can only quantify CSF flow in larger structures, such as ventricles, cerebral aqueduct, cervical subarachnoid space, and foramen magnum; but not in the sPVS (Battal et al., 2011; Hirayama et al., 2015; Korbecki et al., 2019; Abderezaei et al., 2021). Furthermore, velocities measured in typical clinical PC-MRI scans range from 30–200cm/s (Markl et al., 2012) and can go as low as 1–5cm/s (Lee et al., 1995), appropriate for fast CSF and blood flows. The use of PC-MRI to encode slower flows, such as creeping flow in the paravascular space (e.g., in the order of μm/s), is hampered by diffusion weighting (Walker-Samuel et al., 2018; Magdoom et al., 2019; Williamson et al., 2020).

A major challenge of measuring fluid in the sPVS is its delicate structure. The diameter of paravascular space has a scale similar to the adjacent major and pial arteries, ranging from sub-1mm to 4mm, with the majority being 1–2mm (Kwee and Kwee, 2007; Mestre et al., 2018). Partial volume effects with adjacent tissue, such as blood and parenchyma, are inevitable even with state-of-the-art MRI techniques. Despite this challenge, the fluid in the sPVS is still detectable due to its unique dynamics. Driven by arterial pulsation, CSF flow is pulsatile (Iliff et al., 2013b; Mestre et al., 2018); also, the flow velocity is much slower than adjacent intravascular arterial blood by 3 orders of magnitude (Mestre et al., 2018). Among non-invasive MRI techniques to assess such flow, diffusion MRI represents a prime candidate owing to its established sensitivity to water displacement. By appropriately tuning the diffusion gradient, the technique can pick up spins that move in both diffusion (i.e., random motion) and slow flow (i.e., coherent motion) (Dixon, 1988; Taoka et al., 2019; Bito et al., 2021). The fast-moving blood spins, on the other hand, will dephase and be nulled prior to image readout at the presence of diffusion gradient due to the time-of-flight effect (where spins move out of the imaged slice before the EPI echo); as well as intravoxel dephasing, where spins move with different velocities due to turbulent/laminar flow and acquire different phases. Diffusion gradient at a b-value of 5–10s/mm² (i.e., also known as velocity encoding) has been widely utilized to spoil vascular signals in many applications, including black blood imaging (Ye et al., 1997; Nguyen et al., 2008), perfusion imaging (Wang et al., 2003; Wang et al., 2007) and functional MRI (Song and Li, 2003; Song et al., 2004).

Recently, the feasibility of using diffusion MRI to measure glymphatic fluid transport has been demonstrated in a phantom study (Komlosh et al., 2019). Diffusion-encoding gradient has been successfully applied in the preclinical setting to capture the fluid motion within paravascular channels surrounding the middle cerebral artery of the rat brain (Harrison et al., 2018; Phoebe Evans, 2019) and the human brain at 7T (Hirschler et al., 2022). However, due to a relatively long repetitation time (TR) (e.g., turbo spin-echo readout), the temporal fluid movement is only partially captured at two-to-six delay times over a cardiac cycle. The prolonged acquisition time prohibits its translation to humans.

To capture the fluid dynamics along an entire cardiac cycle within a clinically feasible time, we proposed a diffusion imaging and analytical framework called dynamic Diffusion-Weighted Imaging (dDWI). Using a b-value of 150s/mm² and a retrospective cardiac gating, dDWI can detect paravascular CSF fluctuations along a cardiac cycle, revealing its pulsatile waveform. We test the reproducibility of the CSF waveforms and investigate their dependency on surrounding artery sizes. Lastly, we compare waveforms collected on a group of participants aged 18–82 y/o and discuss our preliminary findings.

2. Material and methods

In this manuscript, we use “paravascular CSF (pCSF)” to refer to the CSF in the surface paravascular spaces of the major and pial arteries.

2.1. Selection of b-value

The b-value used to spoil arterial signals in most studies is 1–10 s/mm², and the common b-value used for detecting brain-tissue diffusion property is 1000 s/mm². A smaller b-value is sensitive to flow, and a larger b-value is sensitive to diffusion. Our signal of interest, the pCSF, may have a varying status along a cardiac cycle —during the systole, the mechanical force of the vessel wall moves the fluid in slow flow, while during the diastole period, the flow slows down and may transit into a diffusion-dominant status, with a flow velocity close to zero (Mestre et al., 2018; Thomas, 2019). Thus, we chose an intermediate b-value of 150 s/mm² in the current study to ensure sufficient blood signal suppression while maintaining sensitivity to the fluid movement over a cardiac cycle. An experiment with a range of b-values (50, 100, 150, 200, 300s/mm²) was conducted to compare pCSF waveform dependency on b-values in one volunteer (32 y/o male).

2.2. Data acquisition and processing

A single-shot echo-planar imaging sequence with Stejskal-Tanner pulsed gradient spin echo was used for diffusion weighting. Retrospective gating was applied, such that the sequence was continuously repeated temporally to randomly sample different phases of the heartbeat. A pulse oximeter was used to synchronize the acquired data with the heartbeat, and a respiratory belt was used to record the respiratory cycle. By retrospectively aligning temporal image volumes to the cardiac cycle, the sequence produced a set of diffusion-weighted images (DWIs) over one cardiac cycle. The data were acquired using the following imaging parameters: 134×134 acquisition matrix with 50 phase encodes (GRAPPA factor=2, partial Fourier=75%), 240mm×240mm field of view, repetition time/echo time=1999ms/48.6ms, diffusion time (Δ=22.6ms), pixel bandwidth of 2072 Hz per pixel, and 24 slices with a 1.8×1.8×4mm³ voxel size. DWIs were collected at three cardinal diffusion encoding directions (x/y/z) using b-value of 150s/mm², with each diffusion direction repeated 50 times. Ten b=0 s/mm² were collected to calculate the apparent diffusion coefficient (ADC). The total acquisition time was 5 minutes and 40 seconds.

After aligning acquired DWIs to the pulse cycle by matching slice acquisition time with the phase of the pulse cycle, a 4D dataset was generated with 50 randomly spaced temporal data points for each diffusion direction. The 50 data points were then linearly interpolated (Matlab: interp1) to produce 50 temporally evenly-spaced data points. The three diffusion directions were averaged to produce one temporal curve in each voxel. ADC was used to depict the pCSF waveforms, calculated from DWIs and b=0 s/mm² images. Compared to DWIs, ADC removes signal dependencies on proton density and T2 and better reflects the pCSF movement.

In addition to dDWI, T1-weighted (T1W) anatomical imaging data were collected using a 3D magnetization rapid gradient echo (MPRAGE) with 1.1×1.1×1.2mm³ voxels. Anatomical regions of interest (ROIs) were segmented on T1W, including gray matter, white matter, CSF (FLS: fsl_anat). The ROI masks were brought to the diffusion space through T1W using linear registration (FSL: epi_reg).

2.3. Human participants

Twenty-five healthy participants aged 18–82 (14 male and 11 female; 13 younger (<50y/o) and 12 older (≥50y/o) (Table 1) were imaged on a Siemens Prisma 3T scanner with a 64-channel RF receiver head-neck coil. All participants provided written informed consent according to procedures approved by the Institutional Committee for the Protection of Human Subjects at Indiana University.

Table 1.

Demographics of all participants. BMI: body mass index. HR: Mean heart rate during dDWI acquisition. BPM: beats per minute.

ID	Age (year)	Sex	Height (inch)	Weight (lb)	BMI	HR (BPM)
S1	18	F	62	130	23.8	58
S2	20	M	73	185	24.4	80
S3	22	F	61	155	29.3	114
S4	23	F	62	175	32.0	87
S5	23	M	71	180	25.1	81
S6	23	F	64	144	24.7	80
S7	25	M	74	190	24.4	77
S8	31	M	66	170	27.4	95
S9	32	M	69	141	20.8	104
S10	34	F	63	130	23.0	86
S11	39	M	70	170	24.4	89
S12	42	M	67	165	25.8	85
S13	49	M	69	160	23.6	69
S14	60	F	65	145	24.1	97
S15	68	F	63	167	29.6	89
S16	68	M	67	190	29.8	84
S17	68	F	64	163	28.0	78
S18	74	M	72	192	26.0	85
S19	75	F	69	172	25.4	79
S20	75	F	67	165	25.8	64
S21	77	F	63	144	25.5	76
S22	78	M	72	234	31.7	88
S23	79	M	72	153	20.7	75
S24	80	M	73	156	20.6	85
S25	82	M	68	192	29.2	91

2.4. Reproducibility assessment

We repeated the same imaging protocol four times on one volunteer (23 y/o, female) over six months between 12pm-3pm with 1–2 months apart (8/27/2020, 11/11/2020, 1/05/2021, 2/18/2021). dDWI was collected at the beginning of the imaging session to ensure the wake-fulness of the volunteer. pCSF waveforms of the four datasets were extracted using the pipeline as described in 2.3 and 2.5. The shapes of the waveforms were examined for reproducibility.

2.5. A data-driven approach for automatic identification of sPVS

To facilitate data quantification, we developed a data-driven approach to automatically identify sPVS regions by taking advantage of the pulsatile pCSF signals (Fig. 1). Three masks were used to produce the initial sPVS mask, including a CSF mask segmented on T1W (FSL: first) (Fig. 1A); An artery probability map with value > 0.5 (Fig. 1B); and a mask presenting voxels with Systole ADC - Diastole ADC > 200×10⁻⁶mm²/s (Fig. 1C). The artery probability map was used to guide the general artery locations (Mouches and Forkert, 2019), which was brought to the subject’s dDWI space through T1W using non-linear registration (ANTS: antsRegistration). The atlas also includes a radius map, which was used to categorize artery sizes in the subsequent analyses. Systole-Diastole ADC difference was used to constrain the selected voxels to have a pulsatile pattern. The threshold of 200×10⁻⁶mm²/s was determined to achieve the best agreement between the final sPVS mask and the subject-specific time-of-flight (TOF) angiography in the validation (section 2.6). After obtaining the initial sPVS mask (Fig. 1D), an iterative approach was performed to refine the mask by only including voxels whose temporal signals were correlated with the global mean of the sPVS (Fig. 1E, blue voxels). Specifically, voxel-wise temporal correlations were performed to generate a correlation map (Fig. 1F). A correlation coefficient > 0.6 was used to constrain the initial sPVS mask. The updated sPVS mask would trigger the next iteration. The iterative procedure continued until the volume of sPVS converged (i.e., percent of sPVS volume change <1%) (Fig. 1G), and a final sPVS mask was produced (Fig. 1H blue; red indicates arteries as determined by the subject-specific TOF angiography).

Fig. 1.

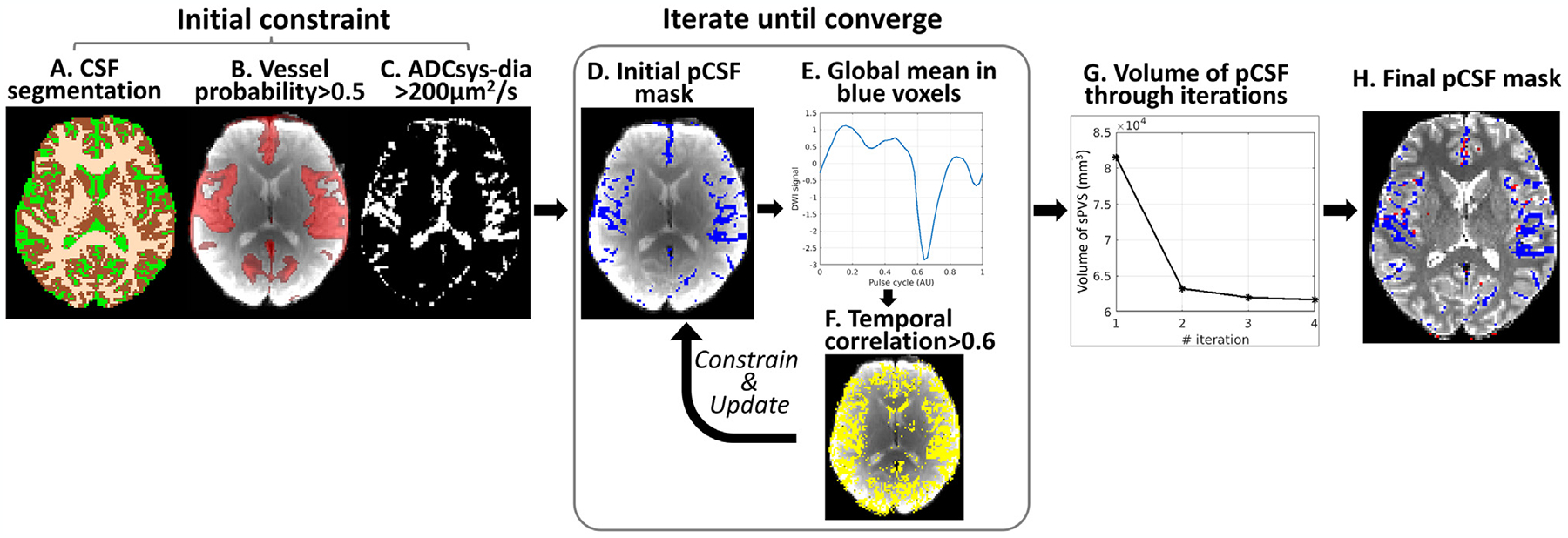
A data-driven approach for automatic identification of sPVS. CSF (A), Vessel probability (B), and ADC_sys-dia (C) masks were used to determine the initial sPVS mask (D). An iterative process was followed to constrain the sPVS mask to only include voxels that showed pulsatile pattern (E). A temporal correlation coefficient >0.6 was applied to constrain and update the sPVS mask for the next iteration. The iteration continued until the volume of sPVS converged (G), and a final sPVS mask was generated (H).

2.6. sPVS mask validation

To validate the sPVS masks described above, we collected time-of-flight (TOF) angiography (0.3×0.3×0.6mm³ voxel size) to localize arteries and 3D-SPACE (0.8×0.8×0.8mm³ voxel size), a turbo spin-echo sequence with heavy T2-weighting (T2W), to localize paravascular spaces in a subset of six participants.

2.7. Experiments testing blood contributions to CSF waveforms

To determine if dDWI signal is free of arterial blood contributions, we performed two experiments in volunteers. In the first one, we reduced slice thickness from 4mm to 2mm with a multiband factor of two to keep TR unchanged. If the 4mm-slice acquisition included arterial blood contribution, thinner slices would reduce it due to a more substantial time-of-flight effect. In the second experiment, we placed one wide saturation band (150mm thickness) over the neck and right below the lowest slices to saturate the incoming arterial blood from the carotid arteries and executed it right before every slice excitation (every 100ms). To address imperfect saturation pulses and ensure complete blood saturation, we further placed two saturation bands overlaid on top of each other (Fig. 7B in 3.6 section). If there was blood signal contamination in the acquisition without saturation bands, the waveforms obtained when using one and two saturation band acquisitions would differ.

Fig. 7.

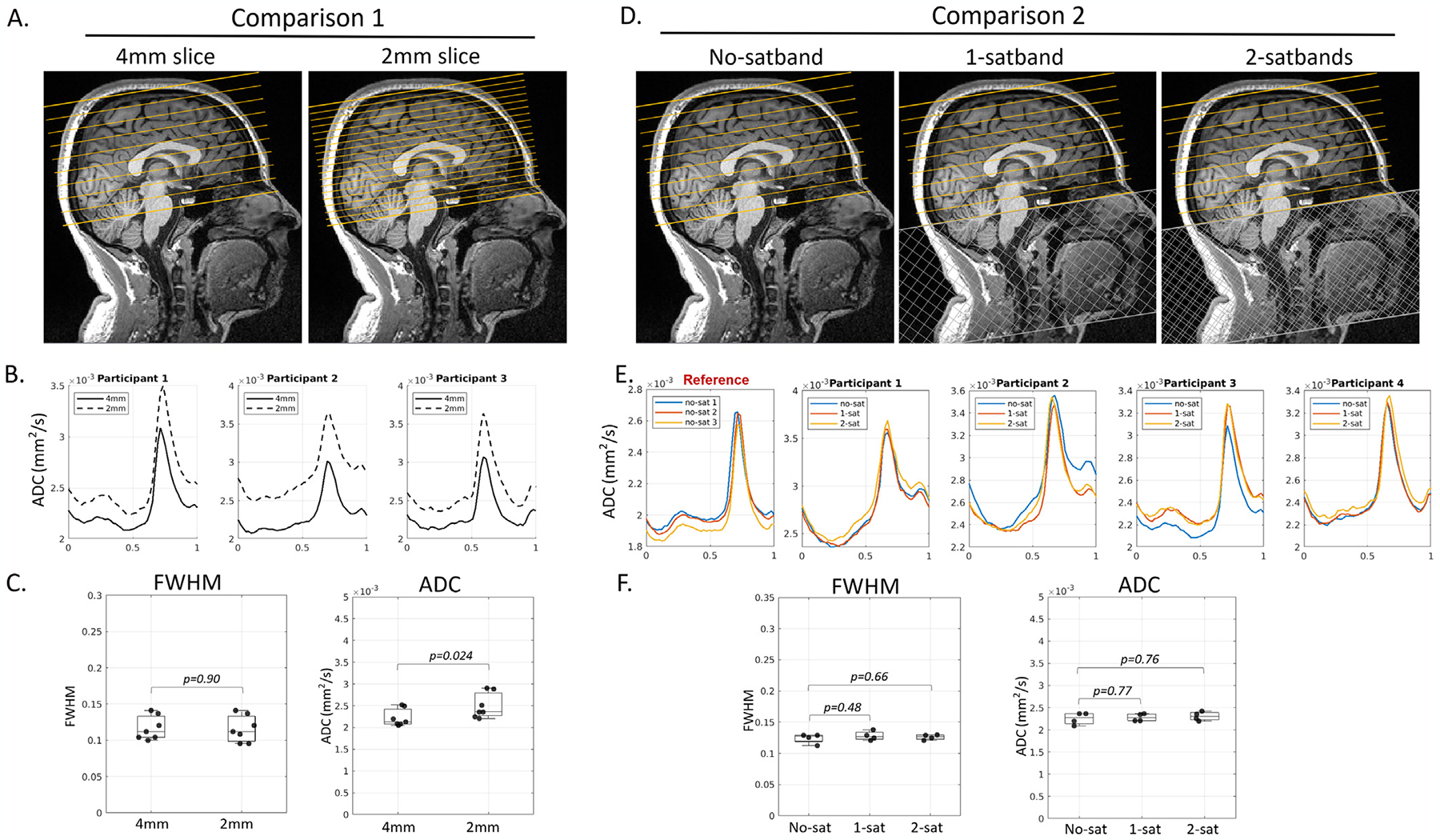
Experimental results supported that pCSF waveforms were free from arterial blood contribution. (Panels A-C): No differences in FWHM were observed between 4mm and 2mm slice thickness (seven participants, paired t-test, p=0.90). As expected, trough ADC was higher at 2mm due to less partial voluming with adjacent parenchyma. (Panels D-F): No differences were observed between an acquisition without a saturation band (no-satband), and those with one or two saturation bands (1-satband and 2-satband).

2.8. Experiments testing parenchyma contributions to CSF waveforms

Cardiac-synchronized brain tissue motion has been reported previously (Zhong et al., 2009; Terem et al., 2021). To estimate the level of parenchyma movement detected by dDWI and whether it can significantly affect the adjacent pCSF signal, we quantified the ADC waveforms in the brainstem – a region with the most apparent pulsatile motion across the brain (Zhong et al., 2009; Terem et al., 2021). The ADC fluctuations within this region can inform us of the level of ADC changes in the parenchymal tissue adjacent to the pCSF.

2.9. CSF waveforms in the ventricular system

Ventricles and sPVS are in the CSF circulation pathways but may show distinct flow dynamics (i.e., waveforms) due to their specific driving forces. Heartbeat and respiration are known drivers for ventricle wall movements. Chroid plexus shape change (chroid plexus pulsation) also drives CSF movement (Bering, 1955). Thus, a more complex waveform might be expected in the ventricles. Ventricle ROIs were delineated on T1W using Freesurfer v6.0 segmentation (freesurfer: recon-all), including lateral ventricles, inferior lateral ventricles (temporal lobe), the third ventricle, and the fourth ventricle. Mean ADC waveforms were extracted in each ventricular subregion.

2.10. CSF waveforms along respiratory cycles

Respiration has also been suggested as a driver for CSF flow (Hadaczek et al., 2006; Vinje et al., 2019). We applied the same analytical approach to examine respiratory dependency by aligning the temporal dDWI signal with the respiratory cycle.

2.11. Statistical analyses

Student’s t-test was used to assess group differences between males and females, as well as young (<50yo) and old (≥50yo) participants on body mass index (BMI), heart rate (HR), and imaging metrics. Pearson correlation coefficient was used to test associations between age and imaging metrics within the young, old, and all participants. Shapiro-Wilk normality test was performed for each variable, and those that did not follow normal distributions (p < 0.05) were log-transformed prior to the correlation coefficient calculation.

3. Results

3.1. pCSF dynamics captured by dDWI

Fig. 2 shows the temporal diffusion-weighted (DW) signal of three representative voxels. The black voxel (Fig. 2A) was sampled from pCSF in the Sylvian fissure (bright on the T2W image). A purple voxel was selected from the white matter (WM) (i.e., corpus callosum), and a green voxel was chosen from gray matter (GM) (Fig. 2A). The raw temporal DWI signals of pCSF fluctuated much more than the white matter and gray matter voxels in all diffusion directions (Fig. 2B, D). After aligning to the pulse cycle, the voxel in the pCSF demonstrated an explicit cardiac-cycle dependency (Fig. 2C), which was not seen in white matter or gray matter voxels (Fig. 2E). The DW signal minimum in Fig. 2C was right in the systole phase, corresponding to a faster CSF movement during systole. The pulsatile signal in the pCSF was observed across the cerebrum (Supplementary Movie).

Fig. 2.

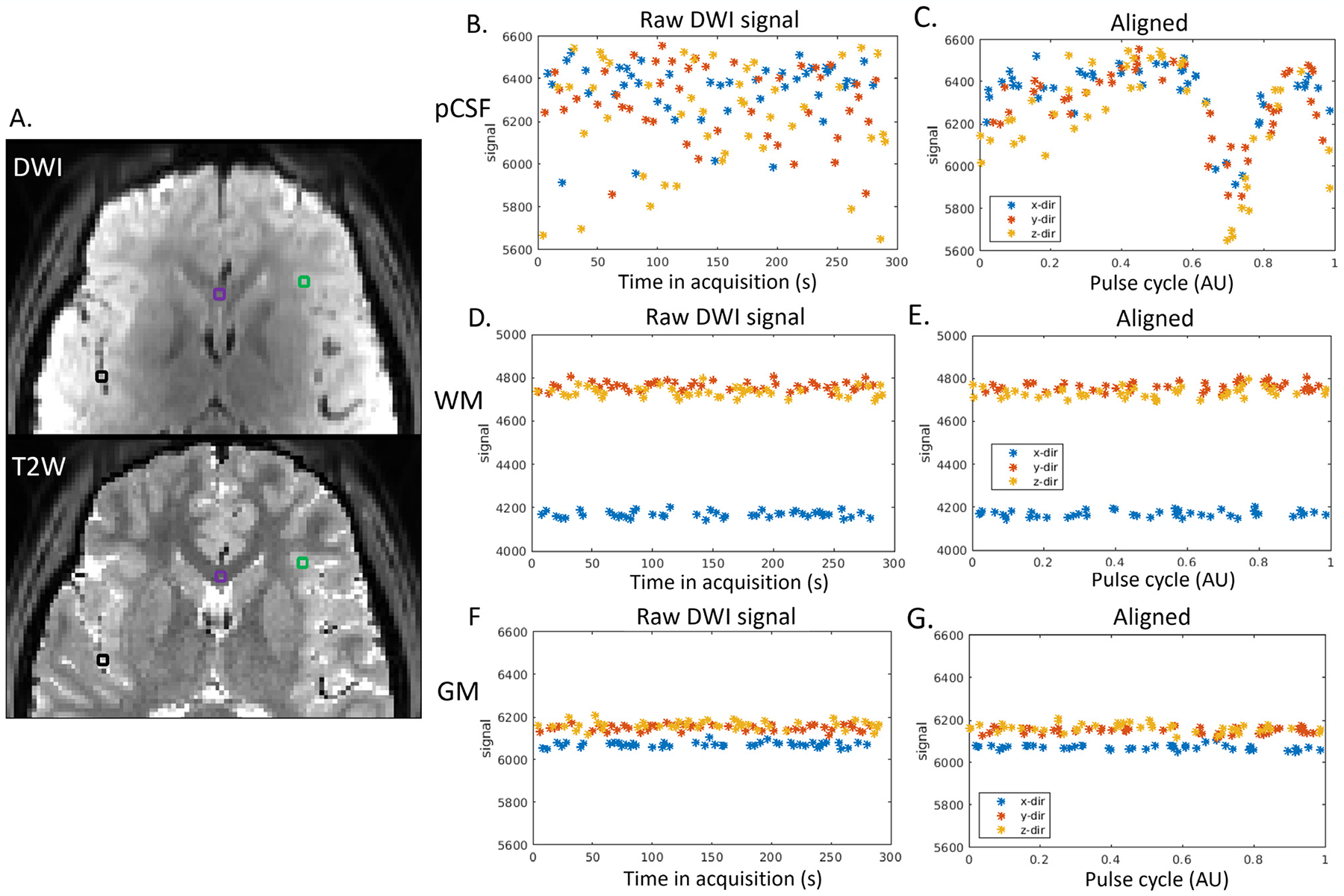
Cardiac-cycle dependency of pCSF dynamics captured by dDWI. (A). Three representative voxels were selected in: the pCSF (black voxel), the white matter (WM, purple voxel), and the gray matter (GM, green voxel). The top panel shows one DWI acquired during diastole. The bottom panel is T2W of the same slice, where pCSF shows a bright signal; (Panels B,D,F). The raw temporal DWI signal. (Panels C,E,G). The DWI signal after aligning to the pulse cycle. (x/y/z-dir: diffusion weighting along x/y/z direction.)

3.2. sPVS mask validation

The sPVS mask generated using the automatic identification pipeline was overlaid on the T2W image for visual inspections. Fig. 3 shows all participants who had T2W and TOF data available. The pipeline took 4–6 iterations to converge. The automatically delineated sPVS (blue voxels) matched well with the TOF artery locations (red voxels) and T2W paravascular spaces (bright signals). Some blue voxelsdid not have adjacent TOF-detected arteries, especially in the higher slices (neocortex). These sPVS regions were likely adjacent to smaller pial arteries with a diameter <0.3mm, which were not visible on TOF acquired with 0.3×0.3×0.6mm³ voxels.

Fig. 3.

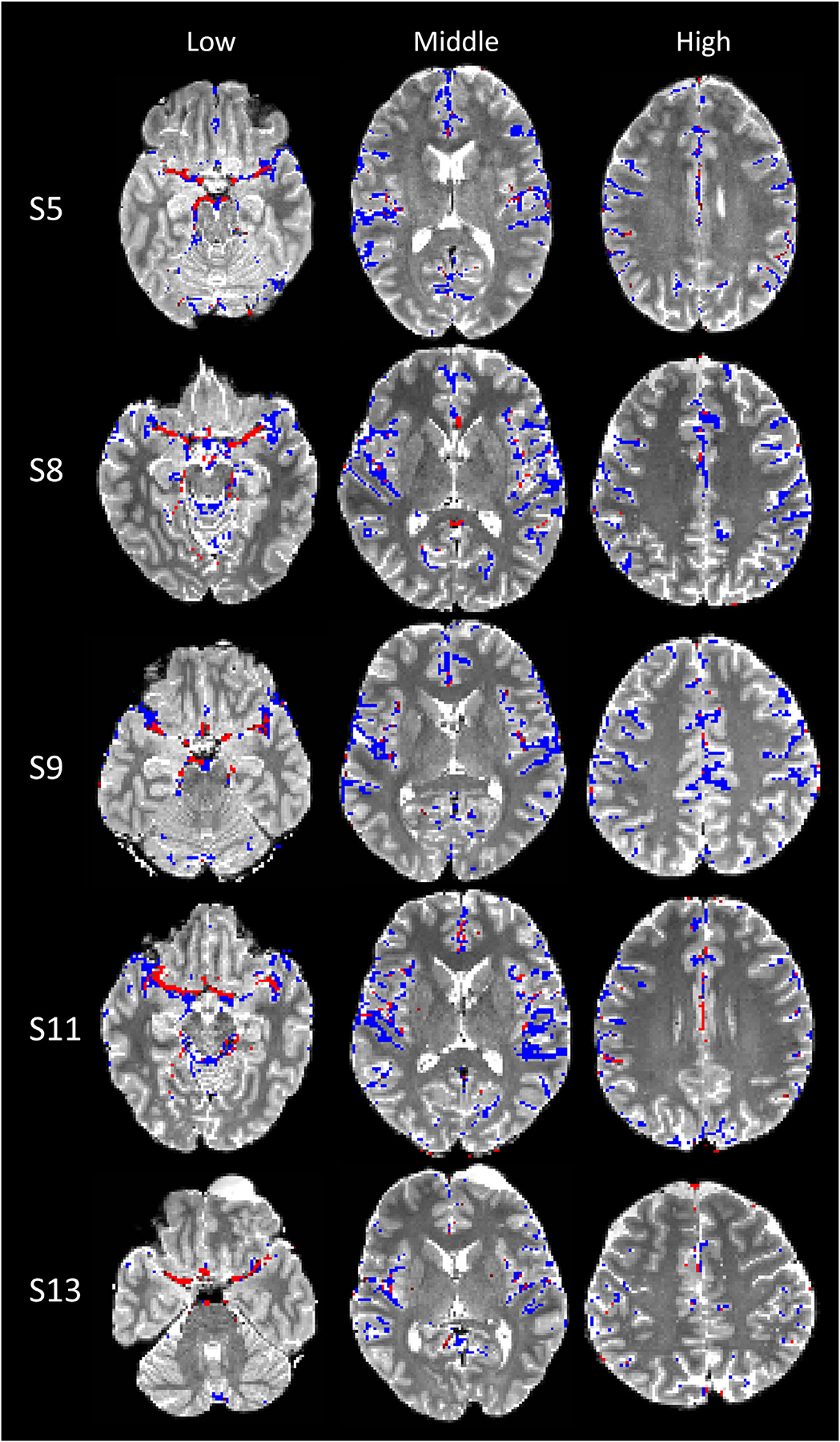
sPVS mask (blue) and TOF (red) overlaid on T2W images of six participants. The subject number (e.g., S5) corresponds to the ID in Table 1.

3.3. Waveform characteristics and its dependency on artery sizes

Fig. 4 (panels A, B) shows the averaged sPVS waveform across the whole brain in one representative participant (S6). A clean and smooth pulsatile pattern was seen, indicating the strong cardiac-cycle dependency of the waveforms (Fig. 4 B). sPVS mask was further divided according to adjacent artery dimensions based on the radius map of the artery atlas: Small (artery diameter<1.2mm, dark blue), Medium (1.2mm≤diameter<1.8mm, green), and Large (diameter≥1.8mm, light blue) (Fig. 4C). The Small, Medium and Large took up approximately 53%, 41%, and 6% of the total sPVS volume. The averaged waveforms of the three groups are shown in Fig. 4D.

Fig. 4.

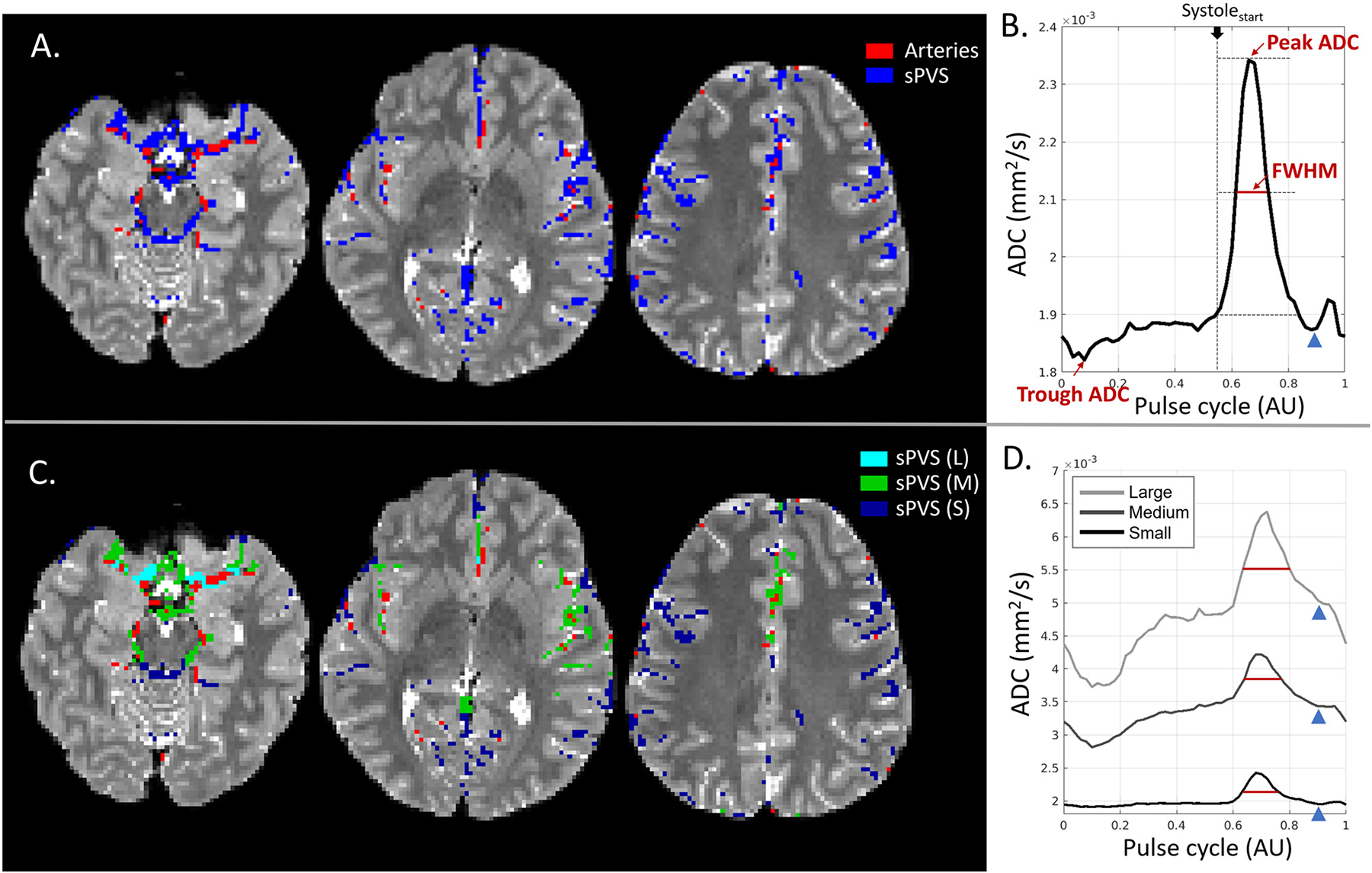
CSF waveform and its dependency on adjacent artery sizes. (A). Surface paravascular space (sPVS) (blue) and artery mask (red) overlaid on T2W from three slices. (B). Averaged ADC waveform in the whole-brain sPVS. The full width at half max (FWHM) was used to quantify the systolic peak width. (C). sPVS was divided into Small (dark blue), Medium (green), and Large (light blue) based on adjacent artery diameters using the radius map of the artery atlas. (D). Averaged ADC waveforms calculated in the Small, Medium, and Large sPVS. The blue arrowheads indicate the “dicrotic notch” toward the end of the systolic phase. L: Large; M: Medium; S: Small.

The pulsatile pattern was seen in all three waveforms, indicating the fluid near major and pial arteries of all sizes pulses in synchrony with the heart. Another common feature in all waveforms was the notch toward the end of the systolic decline (Fig. 4D, blue arrowhead), which was more evident in the whole-brain average curves (Fig. 4B, blue arrowhead). This notch corresponded nicely to the “dicrotic notch” in the arterial pressure waveform.

A few distinctions were observed among the three waveforms. Firstly, the systolic peak width was different. We used full width at half max (FWHM) to quantify the width of the systolic peak (Fig. 4B, red line). The start of the peak lobe overlapped with the start of the systole phase (Fig. 4B, vertical dash line). FWHM of the whole-brain waveform was 0.104. FWHM increased with artery size (Fig. 4C, red line), being 0.096, 0.113, and 0.130 for Small, Medium, and Large, respectively. Secondly, the ADC dynamic range was larger in Large compared to Small. ΔADC, calculated as the peak-trough ADC difference of the waveform (Fig. 4 B), was 600, 1200, and 3100×10⁻⁶mm²/s for Small, Medium, and Large, respectively. Lastly, the Large had a higher trough ADC than the Small, with ADC being 1700, 2100, 2800×10⁻⁶mm²/s for Small, Medium, and Large, respectively. The higher trough ADC might be attributed to the larger sPVS near larger arteries, causing a higher CSF flow/diffusion and a less partial voluming with adjacent brain tissue.

3.4. dDWI Reproducibility

Four repeated experiments on the same participant showed good reproducibility of the waveforms (Fig. 5A–D). Boxplots of the FWHM also revealed good consistency (Fig. 5E). Overall, the jitter of the FWHM was small, with a mean±standard deviation of 0.097±0.007 for All, 0.094±0.002, 0.110±0.004, and 0.138±0.014 for Small, Medium, and Large, respectively. The trend of a higher FWHM in the Larger sPVS was consistent (t-test: p < 0.001 for Small vs. Medium and Medium vs. Large). Both trough ADC and ΔADC were higher in the Larger sPVS (p < 0.001 for Small vs. Medium and Medium vs. Large). A baseline shift of the pCSF waveforms were observed among the four scans. This baseline ADC shift might be related to the changes in sPVS volume due to varying physiological conditions (e.g., changes in blood pressure and/or drowsiness conditions).

Fig. 5.

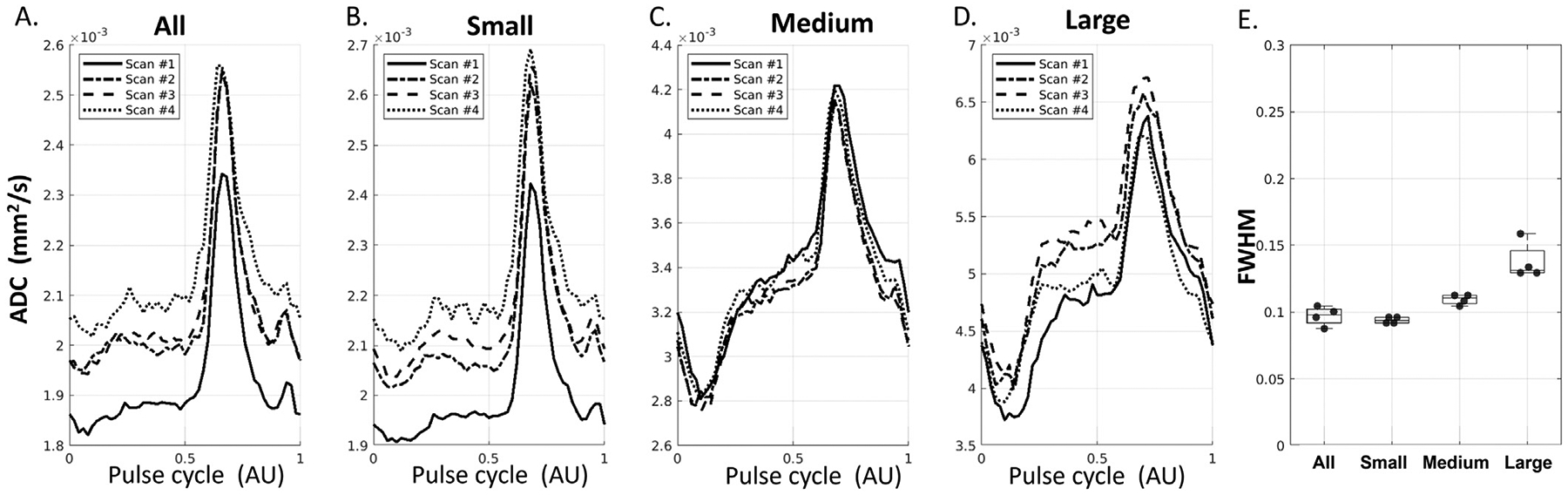
Reproducibility of sPVS waveforms in All (A), Small (B), Medium (C), and Large (D) computed from four scans of the same participant. E. Boxplots of FWHM from four scans.

3.5. pCSF waveform dependence on b-values

Fig. 6 shows the waveforms at five b-values from 50 to 300 s/mm². Greater ADC at smaller b-values was observed for all vessel sizes across the waveforms (Fig. 6A–D). The FWHM, Trough ADC, and ΔADC increased with the vessel sizes for all b-values (Fig. 6E–G).

Fig. 6.

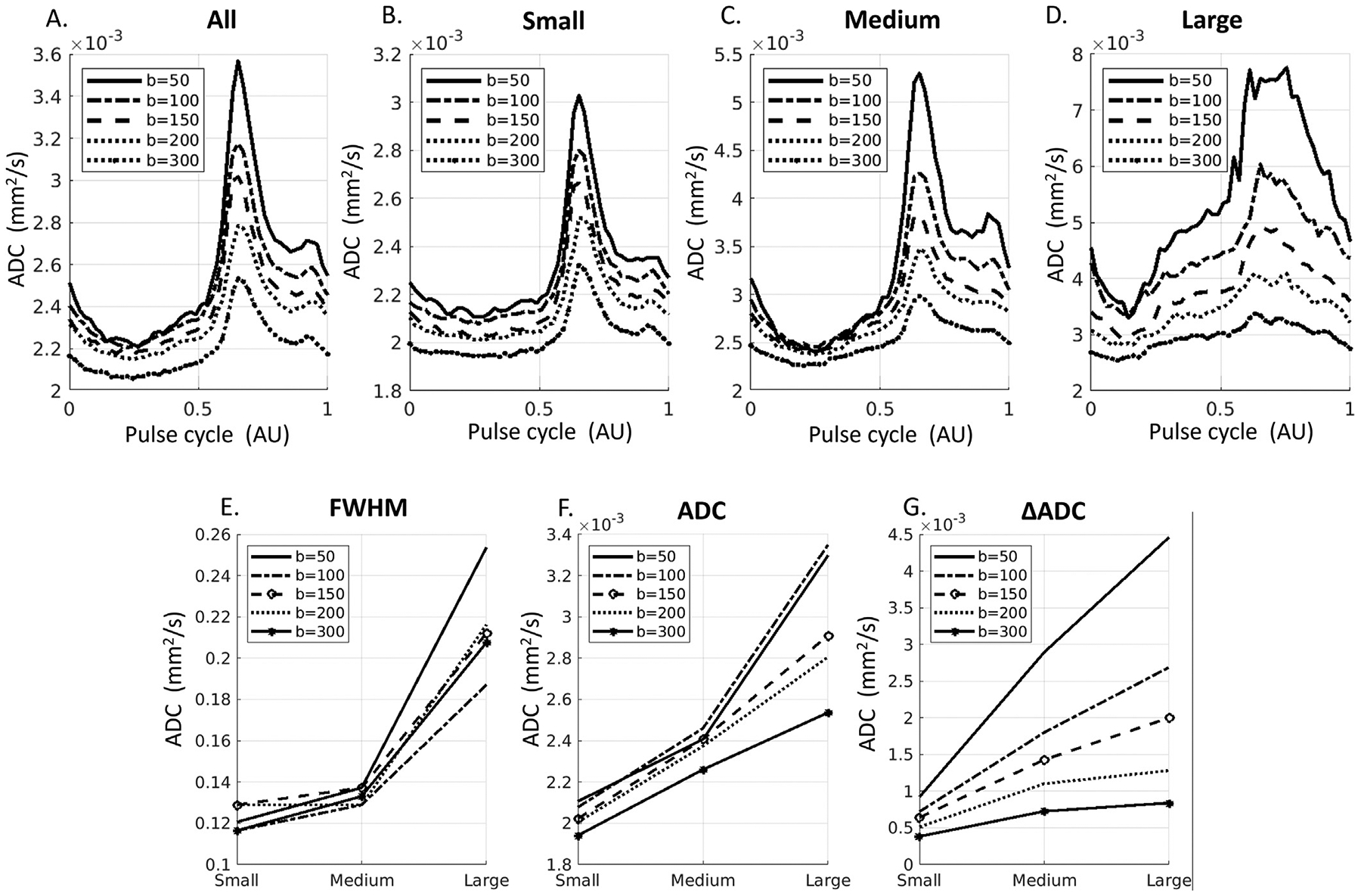
pCSF waveforms at fives b-values (50, 100, 150, 200, 300 s/mm²). A-D: Waveforms from All, Small, Medium, and Large sPVS regions. E-G: Comparison of waveforms metrics for Small, Medium and Large sPVS spaces. FWHM: Full-width at half maximum of the diastolic peak. ADC: baseline/trough ADC values. ΔADC: Peak-Trough ADC differences.

3.6. Assessment of arterial blood contribution to the waveforms

Fig. 7A–C illustrates the placement and results for 4mm and 2mm slice thickness in seven participants. FWHMs for the 4mm and 2mm slice thickness acquisitions did not differ (paired t-test, p = 0.90, Fig. 7A), and no difference was found for ΔADC (results not shown). As expected, trough ADC was higher at 2mm than at 4mm due to less partial volume with adjacent parenchyma. Fig. 7D–F illustrates placement of acquisitions without (no-satband), and with one and two saturation bands (1-satband and 2-satbands) and the results in four participants. Note that the pCSF waveforms of three consecutive scans were not completely overlapping, with baselines shifting up and down. Such shift was also observed when repeating the same experiments without saturation bands (Fig. 7E reference), which may be related to the changes in sPVS volume due to physiological changes (e.g., participants were entering drowsier conditions). Despite minor baseline shifts, no differences were found in FWHM, trough ADC, or ΔADC when saturation bands were applied (t-test, p > 0.1 for no- vs. 1-satband, no- vs. 2-satband, Fig. 7F; ΔADC results not shown).

3.7. Pulsatile parenchyma movement is negligible

Mean ADC waveforms in the brainstem (Fig. 8A) showed pulsatile patterns in four randomly selected participants (Fig. 8B). However, the pulsatile patterns were barely noticeable when displayed on the same scale as the pCSF waveforms (Fig. 8C). The dynamic range of ADC (quantified in temporal standard deviation [t-std]) was 10–30 folds larger (240, 191, 192, and 219 ×10⁻⁶mm²/s) in the sPVS than in the brainstem (19, 10, 3, 6 ×10⁻⁶mm²/s).

Fig. 8.

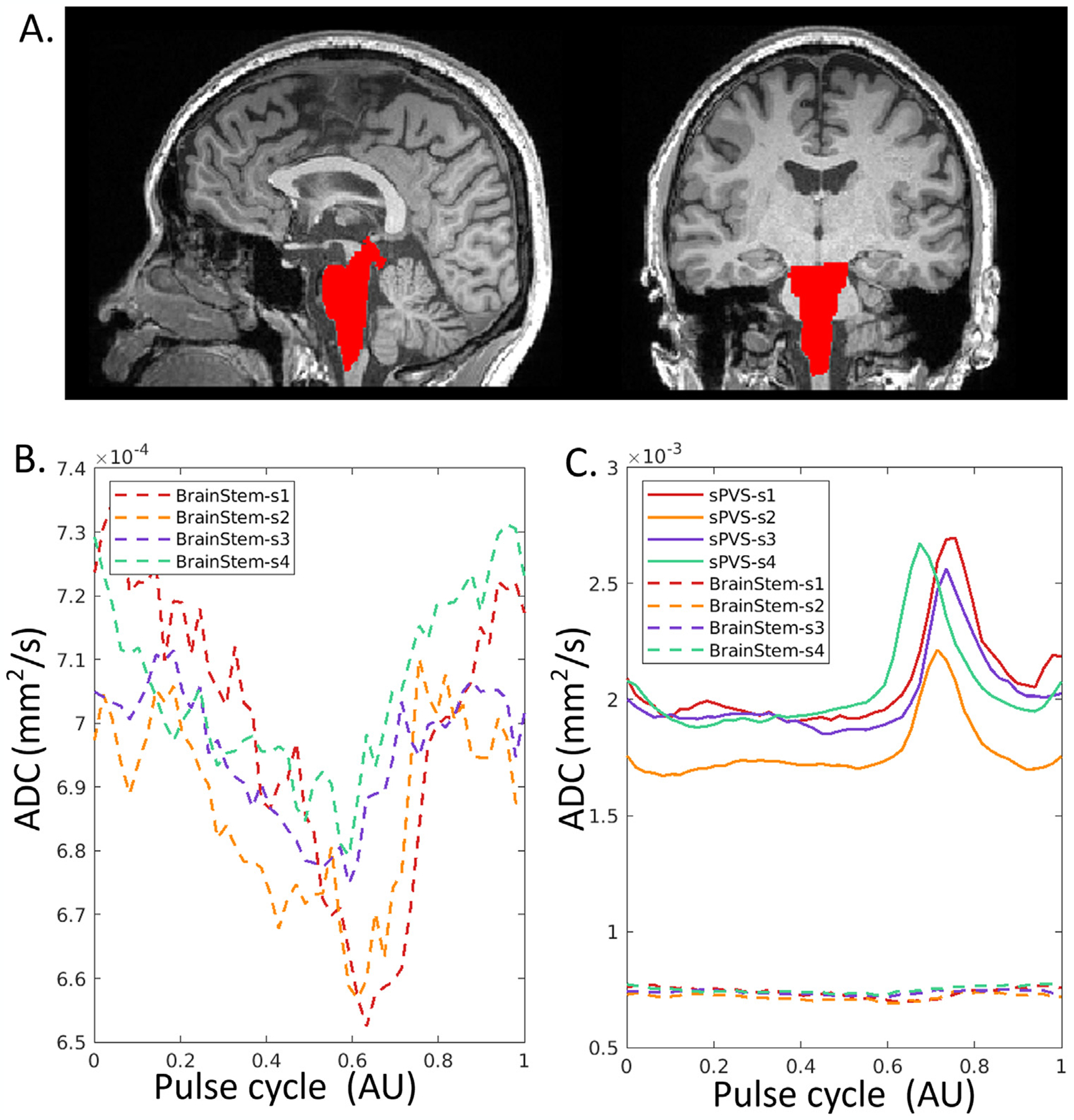
ADC waveforms in the brainstem of four participants. (A). T1W with brainstem highlighted in red. (B). Mean ADC waveforms in the brainstem demonstrate a pulsatile pattern, with temporal standard deviation of 19, 10, 3, 6 ×10⁻⁶mm²/s for the four individuals. (C). The dynamic range of ADC in the sCSF (solid line) is 10–30 folds larger than in the brainstem, with a temporal standard deviation of 240, 191, 192, and 219 ×10⁻⁶mm²/s, respectively.

3.8. CSF waveforms in the ventricular system

Fig. 9 shows the waveforms in the ventricular system from the same four repeated experiments as in Fig. 5. Compared with sPVS, the waveforms in ventricles demonstrated a more sinusoidal shape in the lateral, third and fourth ventricles. In the fourth ventricle, the positive peak appeared at different delay times than in the lateral and third ventricles.

Fig. 9.

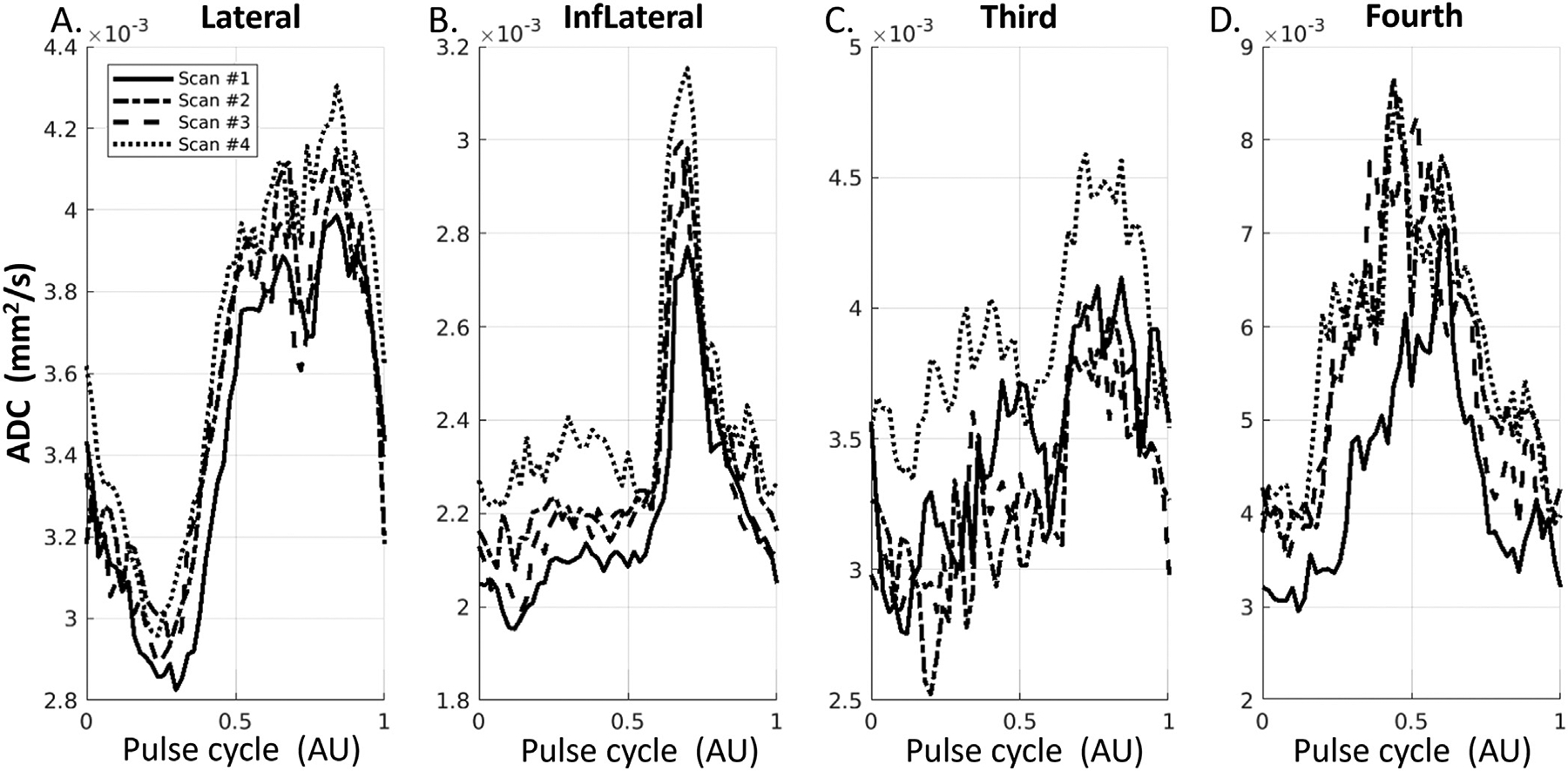
Waveforms in the ventricle regions, including Lateral ventricles (A), Inferior Lateral ventricles (B), the third ventricle (C), and the fourth ventricle (D).

3.9. CSF waveforms along respiratory cycles

Fig. 10 shows the waveforms when aligned with the respiratory cycle from four repeated scans on one volunteer. We observed a less clear pattern of signal changes along the respiratory cycle compared to the cardiac cycle in sPVS (Fig. 10A–D) and in ventricles (Fig. 10E–H).

Fig. 10.

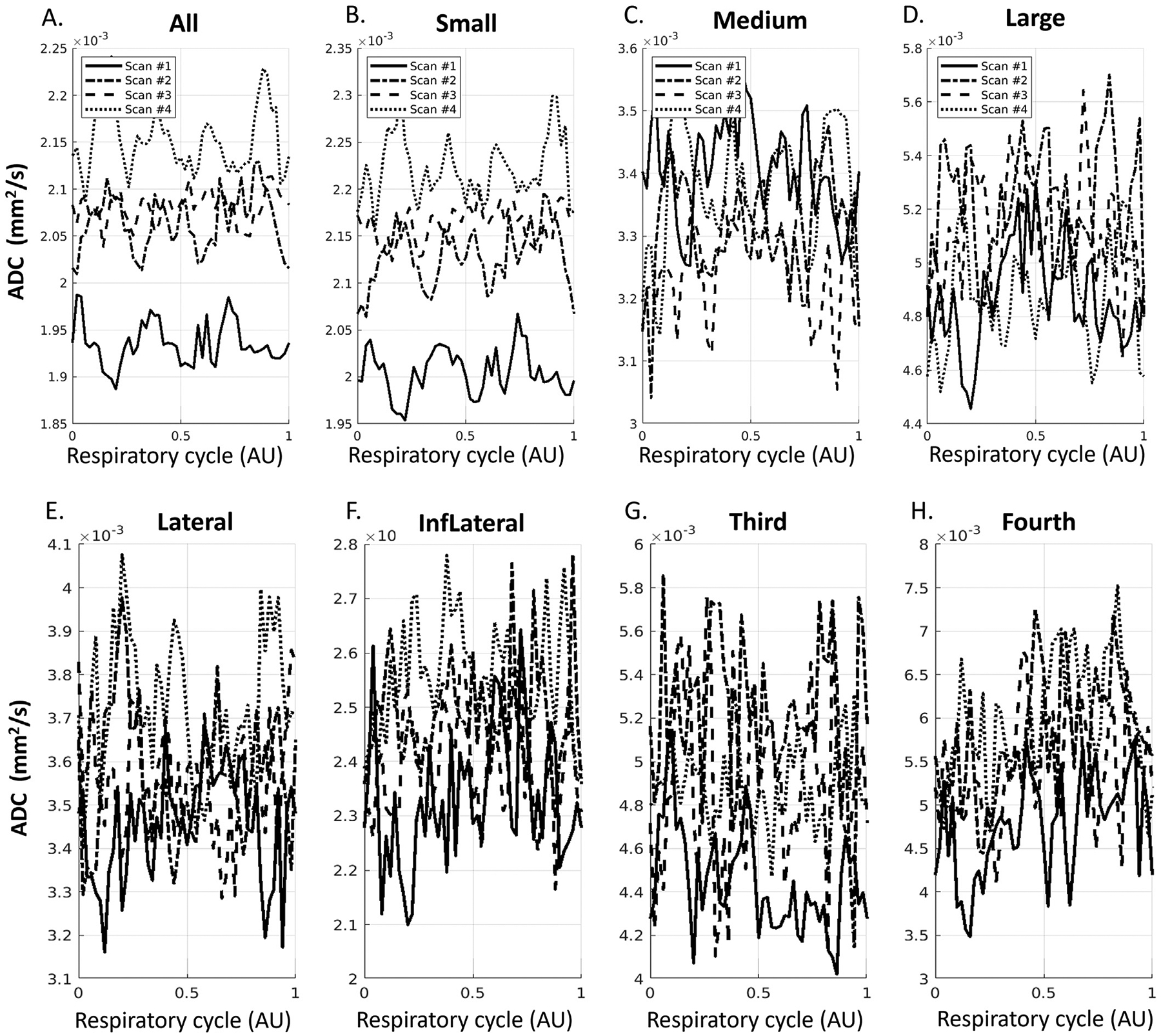
ADC waveforms after aligning to respiratory cycle in sPVS (A-D) and in ventricles (E-H) from four repeated scans on one volunteer. (A). All sPVS regions. (B-D). sPVS of Small, Medium, and Large pial arteries. (E-I): Lateral ventricles, Inferior Lateral ventricles, the third ventricle, and the fourth ventricle.

3.10. Age effect on fluid waveforms

Summary statistics of group differences and aging are shown in Table 2. Males and females did not show differences in any physiological or waveform metrics except for the volume of sPVS (vol_sPVS) (Table 2, left panel). Comparing Young with Old (Table 2, middle panel), no differences were found for BMI and HR. Most of the waveform metrics showed group differences, with Old showing higher FWHM, trough ADC, ΔADC in sPVS, and higher ADC in ventricles. Pearson correlation revealed the most substantial age effect in FWHM (Table 2, right panel). FWHM was not normally distributed (Shapiro-Wilks normality test p < 0.05) and was log-transformed before Pearson correlation analysis. There was no association between HR and waveform metrics (e.g., FWHM or ADC) (Pearson correlation p > 0.1, results not shown in table).

Table 2.

Summary statistics for group differences between males and females, Young and Old (t-test); and age effect within the Young, Old, and All participants as assessed by Pearson correlation.

	Male vs. Female (t-test)					Young vs. Old (t-test)					Age Effect (Pearson Correlation)
	Male (N=14)	Female (N=11)				Young (N=13)	Old (N=12)				Young (N=13)		Old (N=12)		All (N=25)
	mean (std)	mean (std)	t-value	p-value		mean (std)	mean (std)	t-value	p-value		r	p-value	r	p-value	r	p-value
Age (years)	52 (24)	49 (25)	0.21	0.83	Age (years)	NA	NA	NA	NA	Age (years)	NA	NA	NA	NA	NA	NA
BMI	25 (3.4)	26 (2.8)	−0.96	0.35	BMI	25 (2.9)	26 (3.5)	−0.85	0.41	BMI	−0.3	0.32	−0.17	0.61	0.09	0.67
HR (BPM)	85 (8.7)	83 (15)	0.45	0.66	HR (BPM)	85 (14)	83 (8.8)	0.52	0.61	HR (BPM)	0.0031	0.99	−0.32	0.31	−0.13	0.54
FWHM_All	0.19 (0.1)	0.17 (0.092)	0.58	0.57	FWHM_All	0.11 (0.0096)	0.26 (0.084)	−6.3	<0.001	FWHM_All	0.81	<0.001	0.61	0.034	0.94	<0.001
FWHM_Small	0.18 (0.11)	0.17 (0.091)	0.37	0.72	FWHM_Small	0.1 (0.0089)	0.26 (0.083)	−6.5	<0.001	FWHM_Small	0.59	0.035	0.79	0.0022	0.92	<0.001
FWHM_Medium	0.2 (0.1)	0.17 (0.091)	0.72	0.48	FWHM_Medium	0.12 (0.011)	0.26 (0.086)	−5.8	<0.001	FWHM_Medium	0.72	0.0056	0.61	0.034	0.94	<0.001
FWHM_Large	0.2 (0.1)	0.17 (0.075)	1	0.31	FWHM_Large	0.13 (0.026)	0.25 (0.087)	−4.9	<0.001	FWHM_Large	0.74	0.004	0.81	0.0013	0.8	<0.001
ADC_All	0.0026 (0.00041)	0.0026 (0.00048)	−0.12	0.91	ADC_All	0.0022 (0.00021)	0.0029 (0.00032)	−6.2	<0.001	ADC_All	0.1	0.74	0.24	0.46	0.78	<0.001
ADC_Small	0.0022 (0.00024)	0.0021 (0.00025)	1.1	0.29	ADC_Small	0.002 (0.00019)	0.0024 (0.00019)	−4.3	<0.001	ADC_Small	0.18	0.56	0.17	0.59	0.67	<0.001
ADC_Medium	0.0029 (0.00052)	0.0029 (0.00063)	−0.32	0.75	ADC_Medium	0.0025 (0.00026)	0.0033 (0.00047)	−5.3	<0.001	ADC_Medium	0.017	0.96	0.38	0.22	0.74	<0.001
ADC_Large	0.0035 (0.00066)	0.0034 (0.00057)	0.64	0.53	ADC_Large	0.0032 (4e-04)	0.0037 (7e-04)	−2.3	0.032	ADC_Large	−0.12	0.7	0.56	0.06	0.47	0.018
ΔADC_All	0.0014 (0.00039)	0.0014 (0.00044)	−0.41	0.69	ΔADC_All	0.0012 (0.00026)	0.0017 (0.00038)	−3.8	0.0013	ΔADC_All	0.29	0.34	−0.48	0.12	0.57	0.003
ΔADC_Small	0.00092 (3e-04)	0.00088 (0.00028)	0.34	0.74	ΔADC_Small	0.00081 (0.00021)	0.001 (0.00034)	−1.6	0.12	ΔADC_Small	0.083	0.79	−0.25	0.43	0.29	0.16
ΔADC_Medium	0.0019 (0.00039)	0.002 (0.00049)	−0.3	0.77	ΔADC_Medium	0.0017 (0.00037)	0.0022 (0.00033)	−3.5	0.002	ΔADC_Medium	0.37	0.21	−0.45	0.14	0.58	0.0026
ΔADC_Large	0.0022 (0.00048)	0.0021 (5e-04)	0.73	0.48	ΔADC_Large	0.0023 (0.00042)	0.0021 (0.00054)	1	0.31	ΔADC_Large	−0.097	0.75	0.097	0.76	−0.21	0.32
ADC_LatVent	0.0029 (2e-04)	0.0028 (0.00013)	1.4	0.17	ADC_LatVent	0.0029 (0.00024)	0.0029 (5.9e-05)	0.082	0.94	ADC_LatVent	−0.17	0.58	0.84	0.0006	−0.033	0.87
ADC_InfLatVent	0.0023 (0.00024)	0.0022 (0.00015)	1.2	0.26	ADC_InfLatVent	0.0021 (0.00017)	0.0024 (0.00017)	−3.8	0.001	ADC_InfLatVent	−0.2	0.51	0.65	0.023	0.62	0.001
ADC_3rdVent	0.0059 (0.0014)	0.0056 (0.0011)	0.66	0.52	ADC_3rdVent	0.0051 (0.00092)	0.0064 (0.0013)	−3	0.0063	ADC_3rdVent	0.0033	0.99	0.39	0.21	0.56	0.0035
ADC_4thVent	0.0049 (0.0017)	0.0041 (0.00076)	1.6	0.13	ADC_4thVent	0.0039 (0.00094)	0.0051 (0.0016)	−2.2	0.041	ADC_4thVent	−0.084	0.79	0.84	0.0006	0.52	0.008
Vol_sPVS (mm3	48000 (14000)	35000 (11000)	2.6	0.015	Vol_sPVS (mm3)	46000 (14000)	38000 (15000)	1.4	0.19	Vol_sPVS (mm3)	−0.21	0.49	0.51	0.092	−0.23	0.26

Abbreviations: BMI: Body mass index; HR: Heart rate; BMP: Beats per minute; FWHM: Full-width at half maximum; ADC (mm²/s): Apparent diffusion coefficient at the trough of the waveform; ΔADC: peak-trough ADC difference of the waveform; Vol_sPVS (mm³): volume of sPVS ROI; LatVent: Lateral ventricle; InfLatVent: Inferior lateral ventricle; 3rdVent: Thrid ventricle; 4thVent: Fourth ventricle

Representative pCSF waveforms of two younger (both 22y/o male) and two older participants (74 y/o male and 78 y/o male) are shown in Fig. 11, panels A–D. The curves were repeated to cover two pulse cycles to show the end-of-cycle waveforms. The younger and older participants showed distinct waveforms, with the older brains showed higher baseline ADC due to enlarged paravascular spaces. Notably, the systolic peak was much wider in the Old, evident for all artery sizes (Fig. 11, panels B–D). It can be further noted that while the curves in the two younger brains were more alike, the curves of the older brains, despite a similar FWHM, contained distinct features, e.g., near the systolic peak.

Fig. 11.

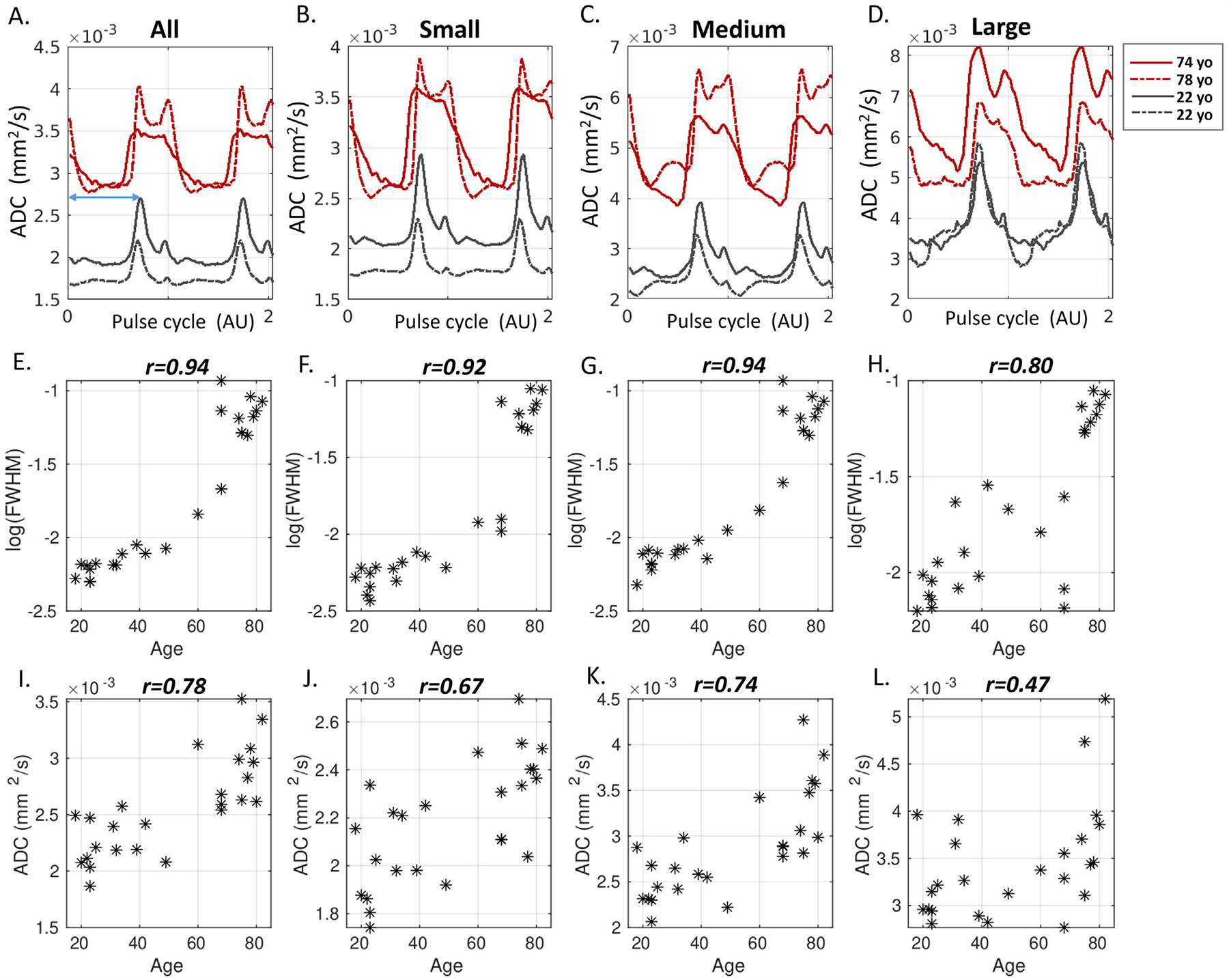
Age-dependency of pCSF waveforms. A-D: Representative pCSF waveforms of two younger and two older participants. E-H: Scatter plots of FWHM (log-transformed) as a function of age in all 25 participants. A high correlation between FWHM and age is found, with the Pearson correlation r-value displayed on top. I-L: Scatter plot of trough ADC against age. Older age showed a higher trough ADC.

The scatter plots of FWHM as a function of age in all 25 participants revealed a strong age effect in all artery sizes, with Pearson correlation r = 0.94, 0.92, 0.94, 0.80 for All, Small, Medium, and Large, respectively (p < 0.001) (Fig. 11, panels E–H). Furthermore, the age effect of FWHM was also present within the Young and Old subgroups, respectively (p < 0.05) (Table 2, right panel). In comparison, trough ADC was associated with age in all but was not associated with age when examining the Young and Old subgroups (p > 0.1).

To further investigate which part of the peak (e.g., systolic upstroke or systolic decline) contributed to the FWHM widening in the older brain, Peak time was calculated from the start of the pulse cycle (time 0) to the systolic peak (Fig. 11 A, blue line arrow). Results showed that Peak time was not age dependent (Pearson correlation p > 0.1). This indicated that the systolic upstroke was similar at all ages, and the prolonged systolic decline contributed to the peak widening in the older brain. The voxel-wise FWHM maps in one young and one older participant (Fig. 12) showed a brain-wide larger FWHM in the older brain.

Fig. 12.

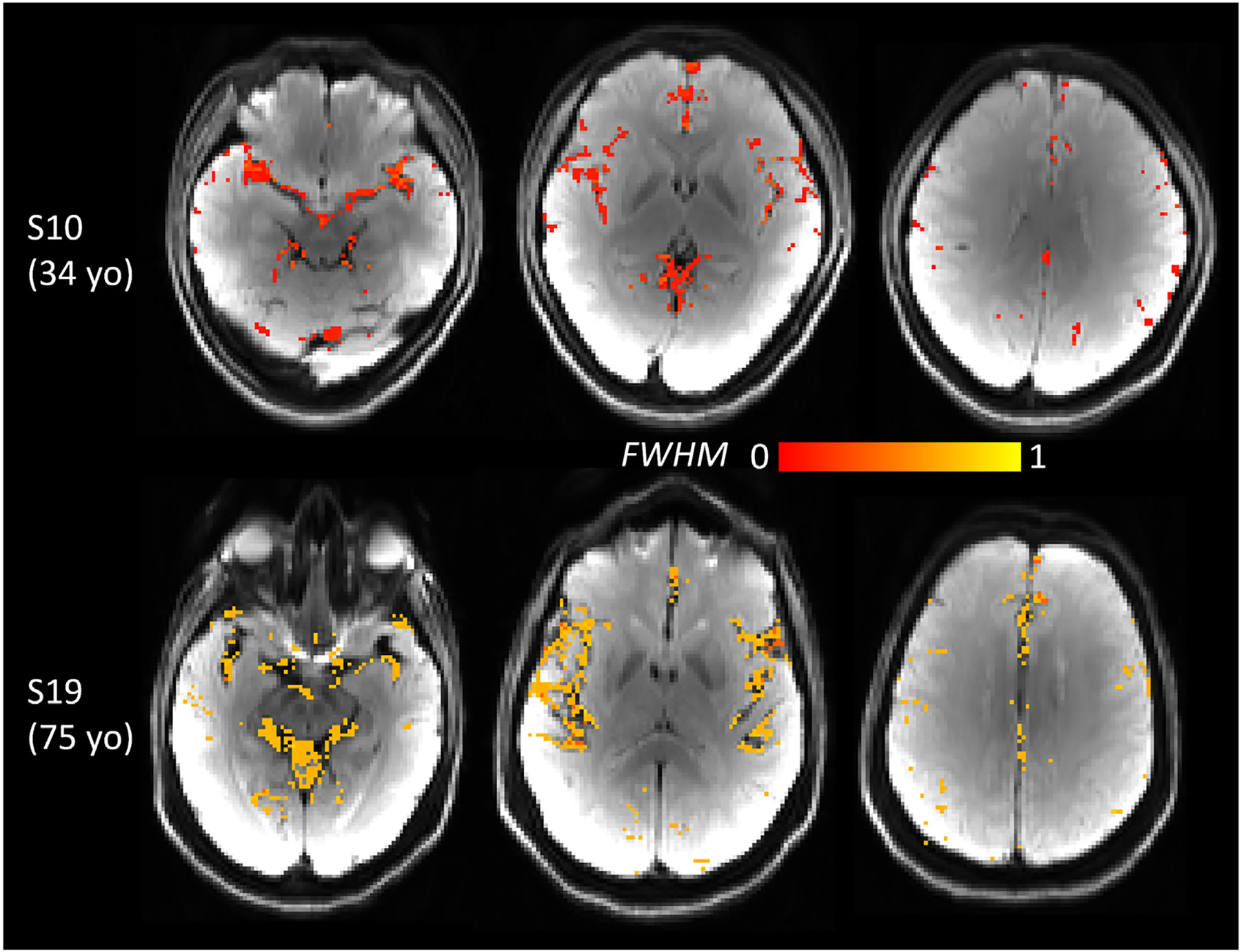
Voxel-wise FWHM maps of one younger (34 yo) and one older (75 yo) participant revealed brain-wide larger FWHM in the older brain. FWHM map was overlaid on DWI.

4. Discussion

While the pulsatile properties of blood and brain tissue have been respectively studied using phase-contrast MRI (Enzmann et al., 1993), transcranial doppler ultrasound (Aaslid et al., 1982), and gated diffusion-weighted imaging (Skare and Andersson, 2001; Habib et al., 2010; Bopp et al., 2018), little is known about the paravascular CSF dynamics of the human brain. Our study provides the preliminary results of pCSF waveforms of the human brain measured using dynamic DWI. We note that our signal of interest comes from the CSF surrounding major and pial arteries at the surface of the cortex, which does not include the CSF surrounding the penetrating arterioles. The penetrating arterioles that dive down through the brain parenchyma are very small (much less than 1mm), and the CSF in its paravascular space may not be reliably detected with the current imaging resolution. Anatomically, pial arteries transit into penetrating arterioles as they enter the parenchyma, and their paravascular spaces are continuous fluid compartments based on evidence from rodent model (Bedussi et al., 2017). While the continuity of these two compartments remains unclear in humans (Brinker et al., 2014), it is reasonable to expect that the fluid dynamics of these two compartments would be tightly connected.

4.1. pCSF dynamics depicted by ADC and its b-value dependency

Our results revealed pCSF waveforms measured in ADC. Conventionally, ADC is used to measure water diffusivity in tissue where water moves in diffusion. pCSF movement may alternate between advection and diffusion along a cardiac cycle, with flow-dominant movement during the systole and slowdown to a zero flow speed (diffusion-dominant movement) during the diastole (Mestre et al., 2018). Péclet (Pé) number can be used to describe the relative transport status between flow and diffusion, defined as the ratio of the rate of advection to the rate of diffusion. When flow transport outweighs diffusion, i.e., Pé >> 1, the theoretical framework shows that ADC = f(ν) is monotone increasing in ν (Bito et al., 2021). When Pé nears 1, ADC becomes insensitive to flow (Williamson et al., 2020). Our results agree well with the Pé>> 1 scenario in the systole period, as the waveforms nicely follow the expected velocity change in this phase, suggesting a flow-dominant movement during systole. This flow-dominant phase is in good agreement with animal studies. Using particle tracking velocimetry of fluorescent microspheres by two-photon spectroscopy, the measured pCSF flow in mice has a mean velocity between 17 – 19 μm/s and a Pé near 1000 (Bedussi et al., 2018; Mestre et al., 2018). In diastole, the flow/diffusion ratio may have reached Pé=1 or Pé<1, especially for smaller pial arteries, as the measured ADC does not show much variation, suggesting a transitioning into a diffusion-dominant status.

The dependency of ADC waveforms on b-values was also observed, with higher ADC at lower b-values. Such a trend is more evident in the systole period. This agrees with the theoretical work showing ADC is inversely related to the b-value in measuring the pseudorandom flow of pCSF (Bito et al., 2021)(equation 2). While the optimal b-value for measuring pCSF is yet to be determined, the waveforms acquired at b-values of 50–300s/mm² revealed similar shapes. While a lower b-value (e.g., b=50 s/mm²) was more sensitive to fluid dynamics (i.e., higher ΔADC), it is close to the limit for sufficient blood suppression (i.e., b-value=39s/mm²) (Nguyen et al., 2008). As a result, we chose an intermediate b-value of 150 s/mm² as a trade-off between pCSF sensitivity and blood insensitivity.

4.2. pCSF waveforms closely resemble arterial pressure waveforms

Our study revealed a tight relationship between the pCSF dynamics and vessel wall kinetics, evidenced in three aspects. Firstly, the waveforms confirmed that pCSF flow is pulsatile, at the same frequency as the cardiac cycle (Iliff et al., 2013b; Bedussi et al., 2018; Mestre et al., 2018). While previous fluid dynamics findings were made by examining PVS near larger arteries in rodents (Harrison et al., 2018; Mestre et al., 2018), our study showed that such pulsatile feature is present for all artery sizes. These results are highly consistent with a fluid transport mechanism – perivascular pumping, wherein vascular wall kinetics directly drive pulsatile CSF bulk flow in the paravascular spaces (Hadaczek et al., 2006). Secondly, the systole peak of the waveform is broader in large PVS and becomes narrower in small PVS. This trend corresponds well to a known characteristic of the pressure waveform of the vessel wall. The pressure waveforms are wider in larger arteries due to its rich elastin and high compliance (ability to distend in response to an increase in the blood pressure), and become narrower as being transferred to its dismal branches (i.e., smaller arteries) that are more resistant with less compliance, a phenomenon known as the “Windkessel effect” (Belz, 1995; O’Rourke et al., 2011). Thirdly, the dicrotic notch, a prominent and distinctive feature of the pressure waveform of the vessel wall, was also observed in the pCSF waveform in arteries of all sizes. Collectively, our results support the “vascular pulsation” as a major mechanism by which pCSF moves. That is, the cardiac cycle drives pCSF flow through the pressure change of the artery wall.

4.3. Age effect

The close correspondence between the pCSF waveforms and vessel wall kinetics suggests that pCSF waveforms may, in turn, reflect vessel wall integrity. This idea is supported by the strong age effect observed in the results. Aging is accompanied by loss of elastin and increased collagen deposition in vessel wall, which causes vessel wall to stiffen and lose vascular compliance (Van Bortel and Spek, 1998; Lee and Oh, 2010; Kohn et al., 2015). The compromised artery wall would distend less with a higher wall pressure than a healthy artery. These changes would affect the pCSF movement, resulting in a shape change of its waveform. We observed that the pCSF movement during systolic upstroke was not significantly affected, with the peak time being similar at all ages. Instead, the systolic decline and the diastolic runoff (after the dicrotic notch) slowed down with age. Two possibilities may explain the prolonged systolic decline. One is the altered pressure pulse waves in the elderly. Studies investigating arterial pulse wave properties have shown an increase in late systolic pressure augmentation with age due to increased arterial stiffness (i.e., higher pulse wave velocity), leading to a wider systolic peak in the pressure waveforms (Charlton et al., 2019). Another possibility is increased backflow of pCSF. A recent animal study observed increased backflow of pCSF under hypertension by tracking the movement of tracer in the paravascular space (Mestre et al., 2018). While the vessel wall moves pCSF flows forward under normal pressure, acute hypertension causes a greater negative wall velocity and a subsequent “forward-backward” pCSF movement, leading to slower net flow and a less effective perivascular pumping. As diffusion signals cannot differentiate forward or backward flow, increased backflow would also have a high ADC, resulting in a prolonged level of high ADC and a broader peak.

Disrupted pCSF flow in the aging brain can impede waste clearance. Animal studies have reported that advancing age was associated with a dramatic decline in the efficiency of exchange between the subarachnoid CSF and the brain parenchyma, with a significant concomitant reduction in vessel wall pulsatility and widespread loss of astrocytic water channel aquaporin-4 (AQP4) polarization. Multiple studies have demonstrated hypertension and arterial stiffness are correlated with amyloid-β accumulation (Gentile et al., 2009; Carnevale et al., 2012; Shah et al., 2012; Hughes et al., 2014). A recent mouse study showed that vascular disease caused a marked reduction of glympahtic drainage through reduced vascular pulsation and altered pCSF dynamics (Li et al., 2021). Our study offers preliminary human evidence for altered fluid dynamics in the older brain. Its relevance to glymphatic function in human awaits to be explored in future studies.

4.4. Minimal contributions from adjacent blood and parenchyma movement

Our experiments with saturation bands and varying slice thickness indicate that the fluid waveforms are free from blood contribution. A piece of additional evidence is that the shape change of the pCSF waveforms between large and small arteries is very different from the velocity waveforms of the blood flow. Specifically, the flow waveforms have a broader peak in smaller arteries compared to large ones due to diminished flow velocity (O’Rourke et al., 2011)(Chapter 10). In contrast, pCSF waveforms agree well with the pressure waveforms and are opposite to the blood flow.

Our results also showed the shape of the waveform had minimal contribution from adjacent parenchymal tissue. This big difference in ADC fluctuations between the tissue and pCSF likely reflects that the tissue water is much more restricted with a higher viscosity. In contrast, pCSF is a free water pool. Collectively, our results indicate that the waveform is dominated by pCSF, with minimal contribution from blood or parenchyma. We note that parenchyma still contributes to the absolute ADC values at the current imaging resolution. In other words, the shape of the waveform carries meaningful information about pCSF dynamics.

4.5. Ventricular system vs. sPVS

The waveforms in the ventricular system showed a more complex pattern than sPVS. The observed sinusoidal shapes agree with the velocity waves measured with PC-MRI (Zhu et al., 2006). Compared to sPVS, the ventricle waveforms are less smooth, likely due to the multiple drivers other than the heartbeat (e.g., respiration, ventricular wall, and choroid plexus pulsation). It is also less coherent between ventricular subregions, reflecting a more complex CSF movement. The complex CSF movement in the ventricles has been reported in previous studies. PC and balanced steady-state free precession techniques have revealed irregular CSF motion in the ventricular space, e.g., stagnant in the lateral ventricle, mixing and swirling in the third ventricles, and bi-directional movement in the aqueduct (Matsumae et al., 2014; Horie et al., 2017). In contrast, a markedly diminished pressure gradient and a less irregular motion were observed in the convexity of the cerebrum (e.g., sPVS) in both studies. Together, our results and others support that CSF motion in the ventricular system is very different from the sPVS spaces.

4.6. Image parameters

In the present study, data were acquired using relatively conservative spatial and temporal resolutions to ensure good signal-to-noise (SNR) ratio and reproducibility. Higher spatial and temporal resolutions can be achieved using the multiband technique. However, a higher temporal resolution at TR<2s will cause signal loss due to the incomplete recovery of longitudinal magnetization. Thus, its trade-off with SNR needs to be considered. Another critical parameter that needs to be considered and controlled is the diffusion time (i.e., Δ). Diffusion time determines the average distance that the spins travel within the imaging time, which affects the measured ADC values when the displacement profile (q-space propagator) is not Gaussian (Basser et al., 1994). In the case of flow, ADC is monotonically increasing in Δ (Bito et al., 2021). Caution needs to be taken when comparing waveforms acquired at different diffusion times.

4.7. Limitations and future work

The altered waveforms observed in the older brain could be attributed to the enlarged paravascular spaces. We could not quantify its volume and perform sensitivity analysis as T2 SPACE was not available for all participants. However, the volume of sPVS as quantified by the automatic identification pipeline was not associated with age (Table 2). This finding suggests that while paravascular space of the older brain is anatomically enlarged, the volume that shows physiological pulsatility may not increase. The effect of enlarged PVS on the fluid dynamics will be systematically evaluated in future studies when a larger cohort becomes available. Another limitation is that we could not quantify the signal contributions from the para-venous CSF. Like parenchyma, the pulsatility in cerebral veins is a passive process in response to intracranial pressure changes. Therefore, we speculate that para-venous CSF pulsatility may be much smaller than para-arterial CSF. Future studies for evaluating para-venous CSF dynamics and its drivers are warranted. Lastly, while respiration has also been shown as a driver of CSF flow (Yamada et al., 2013; Dreha-Kulaczewski et al., 2015; Vinje et al., 2019), we did not observe an explicit respiratory dependency in either sPVS or ventricles. This may be because free breathing is less periodic compared to pulsation. Future studies with paced breathing may better reveal respiratory dependency.

5. Conclusion

We introduced a diffusion-imaging-based acquisition and quantification framework, named dynamic DWI (dDWI), for noninvasively assessing human CSF dynamics in the surface paravascular space surrounding the arteries. Our results showed dDWI detected pulsatile CSF waveforms in the sPVS near both large and small arteries. The shape of the waveforms revealed a close relationship between the fluid dynamics and the vessel wall mechanics. Our measurements provided the preliminary results of the age effect on the paravascular pumping in humans. dDWI may be a valuable tool for assessing paravascular fluid dynamics and may provide relevant biomarkers for waste clearance function. The short acquisition time makes it readily applicable to studying cerebrovascular/neurodegenerative diseases.

Abbreviations:

dDWI

dynamic Diffusion-Weighted Imaging

pCSF

paravascular cerebrospinal fluid

sPVS

surface paravascular space

FSL

FMRIB software library

ANTs

advanced normalization tools

Data and code availability statement

Due to the ethics and privacy issues of clinical data, the original imaging data will not be made openly available to the public.

A demo code is available through reasonable requests.