Synergy between Protein Positioning and DNA Elasticity: Energy Minimization of Protein-Decorated DNA Minicircles

Abstract

The binding of proteins onto DNA contributes to the shaping and packaging of the genome as well as to the expression of specific genetic messages. With a view to understanding the interplay between the presence of proteins and the deformation of DNA involved in such processes, we developed a new method to minimize the elastic energy of DNA fragments at the mesoscale level. Our method makes it possible to obtain the optimal pathways of protein-decorated DNA molecules for which the terminal base pairs are spatially constrained. We focus in this work on the deformations induced by selected architectural proteins on circular DNA. We report the energy landscapes of DNA minicircles subjected to different levels of torsional stress and containing one or two proteins as functions of the chain length and spacing between the proteins. Our results reveal cooperation between the elasticity of the double helix and the structural distortions of DNA induced by bound proteins. We find that the imposed mechanical stress influences the placement of proteins on DNA and that the proteins, in turn, modulate the mechanical stress and thereby broadcast their presence along DNA.

Graphical Abstract

INTRODUCTION

The organization of long genomes in the confined spaces of a cell requires special facilitating mechanisms. A variety of architectural proteins play key roles in these processes. Some of these proteins help to compact the DNA by introducing sharp turns along its pathway while others bring distant parts of the chain molecule into close proximity. The histone-like HU protein from Escherichia coli strain U93 and the structurally related Hbb protein from Borrelia burgdorferi induce some of the largest known deformations of the DNA double-helical structure, including global bends in excess of 160°, appreciable untwisting, and accompanying dislocations of the helical axis.^1–5 The degree of DNA deformation reflects both the phasing of the protein-induced structural distortions and the number of nucleotides wrapped on the protein surface. Changes in the spacing between deformation sites on DNA, with one such deformation associated with each half of these two dimeric protein assemblies, contribute to chiral bends, while variation in the electrostatic surface of the proteins perturbs the degree of association with DNA and the extent of duplex bending.

By contrast, recent studies have highlighted the important role played by proteins which bridge and scaffold distant DNA sites and induce the formation of loops. For example, the Escherichia coli H-NS (histone-like nucleoid structuring) protein forms a superhelical scaffold to compact DNA,⁶ and the Escherichia coli terminus-containing factor MatP can bridge two DNA sites to form a loop.⁷ The MatP protein is responsible for the compaction of a specific macrodomain (Ter) in Escherichia coli and is believed to be able to bind sites located either on separate chromosomes or within one chromosome.⁸ The detailed influence of MatP on chromosome segregation and cellular division is yet to be unraveled,⁸ but it is expected that the presence of MatP proteins could significantly alter the organization and the dynamics of the whole Ter macrodomain.⁷

The composite kinking and wrapping of DNA on the surface of HU resembles, albeit on a much smaller scale, the packaging of DNA around the histone octamer of the nucleosome core particle,⁹ while MatP might serve as a bacterial analogue of the insulator-binding proteins that divide chromatin into independent functional domains.¹⁰ Deciphering how these two very different bacterial proteins influence the structure and properties of DNA provides a first step in understanding how architectural proteins contribute to the spatial organization of genomes.

With this goal in mind, we have developed a new method for the optimization of DNA structure at the base-pair level. Our method takes account of the sequence-dependent elasticity of DNA and can be applied to chain fragments in which the first and last base pairs are spatially constrained. Moreover, our approach allows for constraints in intervening parts of the DNA and thus makes it possible to model the presence of bound proteins on DNA. We can accordingly compute the energy landscape for a wide variety of protein–DNA systems and herein illustrate the effects of HU and Hbb on the configurations of circular DNA and provide examples of the bridging of distant sites on circular DNA by MatP.

The advantage of our method resides in the direct control of the positions and orientations of the base pairs at the ends of a DNA chain and in the capability of accounting for the presence of bound proteins. In addition, the different constraints due to the boundary conditions and the presence of proteins are directly integrated in the minimization process, which makes it possible to rely on unconstrained numerical optimization methods. Others have derived methods to optimize the energy of elastic deformation for DNA fragments. For example, Coleman et al.¹¹ developed a method similar to ours, but their approach requires explicit specification of the forces and moments acting on the terminal base pairs (i.e., there is no direct control on the positions and orientations of the terminal base pairs). Zhang and Crothers also presented an optimization method,¹² albeit limited to circular DNA, which only considers angular deformations within the double helix and takes the boundary conditions into account through Lagrange multipliers.

MATERIALS AND METHODS

We present in this section our new method for minimizing the elastic energy of a collection of DNA base pairs. The method accounts for the sequence-dependent elasticity of DNA and can be applied to a DNA fragment in which the first and last base pairs are spatially constrained. Moreover, our approach makes it possible to constrain parts of the DNA in order to model the presence of bound proteins. We describe the method in symbolic fashion for readability and present full details of the calculations and optimization procedure in the Supporting Information.

Geometry of a Collection of Base Pairs.

We consider a collection of N rigid base pairs, and for the ith base pair, we denote ${\underset{\_}{x}}^i$ its origin and dⁱ the matrix containing the axes of the base-pair frame organized as column vectors. The segmented curve defined by the base-pair origins ${\underset{\_}{x}}^i$ is referred to as the collection centerline and can be interpreted as a discrete double-helical axis. Here and in the rest of this paper, vector symbols are underlined and matrices are represented with bold symbols. Superscripted italic letters (i, j, …) are used to index base pairs and base-pair steps.

Base-Pair Step Parameters.

The geometry of a collection of base pairs is traditionally described in terms of the base-pair step parameters (or step parameters for short).¹³ These parameters describe the relative arrangement of successive base pairs and are denoted for the ith step, following Coleman et al.,¹¹ as ${\underset{\_}{p}}^i=\left({\theta }_1^i,{\theta }_2^i,{\theta }_3^i,{\rho }_1^i,{\rho }_2^i,{\rho }_3^i\right)$ and referred to, respectively, as tilt, roll, twist, shift, slide, and rise. The first three parameters correspond to three angles describing the relative orientation of base-pair frames dⁱ and dⁱ⁺¹, and the last three parameters are the components of the step-joining vector ${\underset{\_}{r}}^i={\underset{\_}{x}}^{i+1}-{\underset{\_}{x}}^i$ expressed in a particular frame referred to as the step frame (see Section 2 in the Supporting Information for more details and the papers of Lu and Olson,¹⁴ El Hassan and Calladine,¹⁵ and Coleman et al.¹¹ for pictorial definitions and explicit equations). The set of step parameters for the base-pair collection is a 6(N – 1) vector and is denoted P.

We shall see later that the energy of elastic deformation for a base-pair step can be written as a quadratic form with respect to the step parameters. The step parameters, however, are not a convenient representation to express constraints on the positions and orientations of base pairs within the collection. This is due to the fact that the components of the step-joining vector rⁱ depend on the relative orientation of the two base pairs forming the step. In order to circumvent this issue, we introduce a different representation of the geometry of a base-pair collection.

Base-Pair Step Degrees of Freedom.

We now define a new set of variables for each step of the base-pair collection. These variables are denoted ${\underset{\_}{\varphi }}^i=\left({\psi }_1^i,{\psi }_2^i,{\psi }_3^i,r_1^i,r_2^i,r_3^i\right)$ for the ith step and referred to as the step degrees of freedom or step dofs for short. Although the variables ψⁱ are identical to the angular step parameters θⁱ, we use a different symbol for clarity. The variables rⁱ are the components of the step-joining vector ${\underset{\_}{r}}^i={\underset{\_}{x}}^{i+1}-{\underset{\_}{x}}^i$ expressed with respect to the global reference frame (a convenient choice for the global reference frame is the first base-pair frame). The set of step dofs for the base-pair collection is a 6(N − 1) vector and is denoted Φ.

The main advantage of this choice of variables is to separate the representation of the centerline of the base-pair collection from the orientation of the base-pair frames. This is somewhat similar to the centerline/spin representation of Langer and Singer¹⁶ for continuous elastic rods. This representation is particularly convenient to deal with the end conditions applied to a collection of base pairs.

Energy of Elastic Deformation.

The energy of elastic deformation for a DNA base-pair collection is defined as the sum of the energy of elastic deformation for each step. For the ith step, this energy is given by the following quadratic form:

$$E^i=\frac{1}{2}{\left({\underset{\_}{p}}^i-{\underset{\_}{p}}_0^i\right)}^T{F}^i\left({\underset{\_}{p}}^i-{\underset{\_}{p}}_0^i\right)$$ (1)

where ${\underset{\_}{p}}_0^i$ contains the intrinsic step parameters, i.e., the zero-energy configuration of the step, also called the rest state), and Fⁱ is a 6 × 6 matrix containing the elastic moduli associated with the different modes of deformation. Both the intrinsic step parameters and the force constant matrix can differ for each step depending on the DNA sequence. The elastic energy for the base-pair collection is then given by

$$E=\sum _{i=1}^{N-1}{E}^i$$ (2)

The purpose of our method is to minimize the elastic energy of a base-pair collection given by eq 2 under the constraints detailed below. In other words, we need to calculate the derivatives of the elastic energy. The difficulty stems from the fact that this gradient has to be calculated with respect to a set of independent variables. This set of independent variables depends on the end conditions applied to the collection of base pairs and also on the presence of bound proteins. As mentioned above, the step parameters are not convenient for dealing with the end conditions. We therefore calculate the gradient with respect to the step dofs. We first consider the trivial case of an unconstrained collection (i.e., a collection with no imposed end conditions and no bound proteins), and we then show how to account for specific end conditions and the presence of bound proteins. These constraints are explicitly solved (see Supporting Information for the details of the calculations), which makes it possible to reduce the number of step dofs used as independent variables in the minimization process.

The minimization of the elastic energy given by eq 2 can be carried out using any traditional gradient-based methods (our results are obtained using a L-BFGS algorithm, but other methods would lead to similar results).

Note that our method does not require the elastic energy of a step to be a quadratic form with respect to the step parameters.¹⁷ The expression for the elastic energy of a step can also include contributions arising from the coupling between neighboring base-pair steps.

Elastic Energy Gradient for a Free Base-Pair Collection.

The case of a base-pair collection free of any end conditions and without bound proteins is trivial in the sense that the optimization leads to the reference configuration. We will use this gradient for a free collection as the starting point of our method.

The gradient of the elastic energy for a single step is obtained directly from eq 1:

$$\frac{\partial E^i}{\partial {\underset{\_}{p}}^i}=F_{\text{s}}^i\left({\underset{\_}{p}}^i-{\underset{\_}{p}}_0^i\right)$$ (3)

where we introduce the symmetrized force constant matrix $F_{\text{s}}^i$ defined as $F_{\text{s}}^i=(F^i+F^{i^T})/2$. It follows that the variation of the elastic energy for the complete collection is given by

$$\delta E={\frac{\partial E}{\partial \underset{\_}{P}}}^T\delta \underset{\_}{P}={\sum _{i=1}^{N-1}\frac{\partial E^i}{\partial {\underset{\_}{p}}^i}}^T\delta {\underset{\_}{p}}^i=\sum _{i=1}^{N-1}{\left(F_{\text{s}}^i\left({\underset{\_}{p}}^i-{\underset{\_}{p}}_0^i\right)\right)}^T\delta {\underset{\_}{p}}^i$$ (4)

In order to obtain the gradient with respect to the step dofs, we introduce the Jacobian matrix ${\mathbf{\text{J}}}_{\underset{\_}{\text{Φ}}}$, defined as

$$\delta \underset{\_}{P}=\frac{\partial \underset{\_}{P}}{\partial \underset{\_}{\mathbf{\Phi }}}\delta \underset{\_}{\mathbf{\Phi }}=J_{\underset{\_}{\mathbf{\Phi }}}\delta \underset{\_}{\mathbf{\Phi }}$$ (5)

It follows that

$$\delta E={\left({J_{\underset{\_}{\mathbf{\Phi }}}}^{\text{T}}\frac{\partial E}{\partial \underset{\_}{P}}\right)}^{\text{T}}\delta \underset{\_}{\mathbf{\Phi }}$$ (6)

which leads to the following expression for the free-collection gradient with respect to the step dofs:

$$\frac{\partial E}{\partial \underset{\_}{\mathbf{\Phi }}}={J_{\underset{\_}{\mathbf{\Phi }}}}^{\text{T}}\frac{\partial E}{\partial \underset{\_}{P}}$$ (7)

The details of the calculation for the matrix J_Φ, are given in Section 3.2 of the Supporting Information.

End Conditions.

We now consider the case of a base-pair collection with end conditions; i.e., both the end-to-end vector and the orientation between the first and last base pairs are fixed. Our results can easily be generalized to other types of end conditions.

The end-to-end vector for the collection of base pairs is given by

$${\underset{\_}{x}}^{\text{N}}-{\underset{\_}{x}}^1=\sum _{i=1}^{N-1}{\underset{\_}{r}}^i$$ (8)

If the end-to-end vector is imposed, it follows that

$$\sum _{i=1}^{N-1}\delta {\underset{\_}{r}}^i=\underset{\_}{0}$$ (9)

The end-to-end rotation corresponds to the orientation between the first and last base pairs and is given by

$$d^{1^{\text{T}}}{d}^N=D^{\left(1,N\right)}=\prod _{i=1}^{N-1}{D}^i\left({\psi }^i\right)$$ (10)

where D^(i,j) denotes the rotation matrix between the ith and jth base pairs, and Dⁱ is the rotation matrix for the ith step which is completely parametrized by the angular step dofs ${\underset{\_}{\psi }}^i=\left({\psi }_1^i,{\psi }_2^i,{\psi }_3^i\right)$ (see Sections 2.1 and 3.1 of the Supporting Information and the work of Coleman et al.¹¹ for further details). If the end-to-end rotation is imposed, we have the following constraint:

$$\delta D^{\left(1,N\right)}=\delta \left(\prod _{i=1}^{N-1}{D}^i\left({\underset{\_}{\psi }}^i\right)\right)=\mathbf{0}$$ (11)

We show in Section 4 of the Supporting Information that these two constraints imply that the step dofs ${\underset{\_}{\varphi }}^{N-1}$ are not independent variables. In other words, the end conditions reduce the number of independent step dofs. Note that we choose to express the last step dofs as the nonindependent variables, but any other step could have been chosen. We now denote $\underset{\_}{\hat{\mathbf{\Phi }}}$ as the set of independent step dofs, and we have the relation $\underset{\_}{\hat{\mathbf{\Phi }}}\subset \underset{\_}{\mathbf{\Phi }}$. We then define the Jacobian matrix $\widehat{J}$ such that

$$\delta \underset{\_}{\mathbf{\Phi }}=\widehat{J}\delta \underset{\_}{\hat{\mathbf{\Phi }}}$$ (12)

The dimensions of this matrix depend on the precise details of the end conditions (although the number of rows is always 6(N − 1) and the details of its expression are given in Section 4 of the Supporting Information).

It follows that the gradient of the elastic energy for a collection of base pairs subjected to imposed end-to-end conditions is

$$\frac{\partial E}{\partial \underset{\_}{\widehat{\mathbf{\Phi }}}}={\left(J_{\underset{\_}{\text{Φ}}}\widehat{J}\right)}^{\text{T}}\frac{\partial E}{\partial \underset{\_}{P}}$$ (13)

Note that this gradient corresponds to the gradient with respect to the independent step dofs and accounts for the end conditions. This is one advantage of our method: the end conditions are directly accounted for. Hence, we transform a constrained optimization problem into an unconstrained one, which makes the numerical implementation simpler and more robust.

Bound-Protein Constraint.

In order to study protein-decorated DNA, we need to account for the presence of bound proteins on the double helix. We model the binding of proteins on the DNA by considering the step parameters of the binding domain as frozen; i.e., these step parameters are imposed and cannot change. For example, the frozen step parameters can be extracted from high-resolution crystal structures of protein–DNA complexes with the help of the 3DNA software.¹⁴ The choice of frozen steps can, of course, be varied in different rounds of minimization to allow for deformations in the protein–DNA complex.

We first consider that the kth step in the base-pair collection is frozen; i.e., the step parameters p^k are imposed (the following results can be easily generalized to an arbitrary number of frozen steps). It follows directly that the angular step dofs are constant, and we therefore have $\delta {\underset{\_}{\psi }}^k=\underset{\_}{0}$. The translational step dofs, however, are not constant: any changes in the angular steps dofs ψ^j with j < k will change the orientation of the joining vector ${\underset{\_}{r}}^k$ of the frozen step. Indeed, we show in Section 5 of the Supporting Information how to relate the variations in the joining vector to the variations in the angular step dofs of the preceding steps.

Similar to the set of independent step dofs $\underset{\_}{\hat{\mathbf{\Phi }}}$ introduced for the treatment of the end conditions, we introduce a new set of independent step dofs $\underset{\_}{\hat{\mathbf{\Phi }}}$, which corresponds to the set of nonfrozen step dofs among the set $\underset{\_}{\hat{\mathbf{\Phi }}}$; i.e., we have $\underset{\_}{\hat{\mathbf{\Phi }}}\subset \underset{\_}{\hat{\mathbf{\Phi }}}\subset \underset{\_}{\mathbf{\Phi }}$. We define the matrix $\widetilde{\mathbf{\text{J}}}$ as the Jacobian (see Section 5 of the Supporting Information for details):

$$\delta \underset{\_}{\hat{\mathbf{\Phi }}}=\widetilde{\mathbf{\text{J}}}\delta \underset{\_}{\tilde{\mathbf{\Phi }}}$$ (14)

We obtain for the gradient

$$\frac{\partial E}{\partial \underset{\_}{\tilde{\mathbf{\Phi }}}}={\left({\widetilde{\mathbf{\text{J}}}}_{\underset{\_}{\mathbf{\Phi }}}\widehat{\mathbf{\text{J}}}\widetilde{\mathbf{\text{J}}}\right)}^T\frac{\partial E}{\partial \underset{\_}{\tilde{P}}}$$ (15)

Here, $\underset{\_}{\tilde{P}}$ denotes the set of nonfrozen step parameters, and ${\widetilde{\mathbf{\text{J}}}}_{\underset{\_}{\mathbf{\Phi }}}$ is the Jacobian matrix defined as

$${\tilde{\mathbf{J}}}_{\underset{\_}{\mathbf{\Phi }}}=\frac{\partial \underset{\_}{\tilde{P}}}{\partial \underset{\_}{\mathbf{\Phi }}}$$ (16)

This matrix is directly obtained from ${\mathbf{\text{J}}}_{\underset{\_}{\mathbf{\Phi }}}$ by removing the rows associated with the frozen step parameters.

The gradient obtained with eq 15 corresponds to the gradient of the elastic energy of the base-pair collection (eq 2) with respect to the set of nonfrozen independent step dofs.

Force Field.

The expression for the elastic energy of a base-pair step (eq 1) depends on two sequence-dependent quantities: the intrinsic step parameters ${\underset{\_}{p}}_0^i$ and the force constant matrix Fⁱ. These quantities constitute the force field of our theory. The intrinsic step parameters describe the rest states of the base-pair steps, while the force constants are the stiffnesses of the steps.

In this work, we use a uniform ideal force field, i.e., not depending on the details of the DNA sequence. The intrinsic step parameters for this force field are given by p₀ = (0°, 0°, 34.2857°, 0 Å, 0 Å, 3.4 Å), which correspond to a B-DNA-like straight rest state and a helical repeat of 10.5 bp. We do not consider coupling between the different modes of deformation, and hence, the force constants matrix is diagonal and reads

$$\text{diag}\left(F^{\text{ideal}}\right)=\left(0.0427,0.0427,0.0597,20,20,20\right)$$ (17)

The units for the first three diagonal entries are k_BT deg⁻² and k_BT Å⁻² for the last three entries. This force field can be considered quasi-inextensible due to the high force constants associated with the translational step parameters. In the limit of an infinitely long base-pair collection, we can calculate the persistence lengths corresponding to the force field, and we find that the bending and twisting persistence lengths are 47.7 and 66.6 nm, respectively.

Protein-Binding Procedure.

As explained earlier, we model the presence of proteins on DNA by setting the base-pair step parameters of the binding domain to imposed values. These imposed values can be extracted from high-resolution crystal structures of protein–DNA complexes or can be chosen to represent an ideal protein–DNA binding system.

In this study, we use an iterative procedure to bind a protein onto DNA. For example, we consider a protein with a binding domain of n_p steps to be bound starting at the kth step; i.e., steps k to k + n_p − 1 are bound (and, hence, frozen). The iterative procedure consists of adjusting the step parameters of the binding domain using the following linear ramp function:

$$\begin{array}{cc}{\underset{\_}{p}}^j\left(\lambda \right)=\left(1-\lambda \right){\underset{\_}{p}}_{\text{free}}^j+\lambda {\underset{\_}{p}}_{\text{protein}}^j& \forall j\in \lfloor k,k+n_{\text{p}}-1\rfloor \end{array}$$ (18)

where the ${\underset{\_}{p}}_{\text{free}}^j$ term denotes the step parameters of the protein-free DNA (in our case, they will correspond to the step parameters of a portion of a naked-DNA minicircle) and the ${\underset{\_}{p}}_{\text{protein}}^j$ terms are the step parameters of the DNA found in the protein–DNA complex. The parameter λ ∈ [0, 1] is the ramp parameter. Our procedure starts with λ = 0, and we minimize the DNA base-pair collection while gradually increasing the value of the ramp parameter until λ = 1. The outcome is an optimized DNA base-pair collection in which a part of DNA is shaped as if the protein were bound to it. This numerical procedure is not meant to convey the physical process of protein binding to DNA. It is designed to set regions of DNA to the states found in protein–DNA complexes. The binding ramp can also be tuned in order to improve the robustness of the method. For example, the linear terms can be replaced by quadratic expressions. Such modifications might be needed to avoid instabilities or to control changes in the total twist while ramping the step parameters in the case of binding domains with large deformations.

Minicircle Topology.

The topology of a DNA minicircle is characterized by its linking number Lk,¹⁸ writhing number Wr,^19,20 and total twist Tw.²⁰ The linking number of a minicircle, an integer, describes the entanglement of the minicircle centerline and the curve traced out by one of the edges of the base-pair frames (see our earlier work²¹ for detailed explanations and computational methods). In particular, for a planar minicircle the linking number corresponds to the number of turns the double helix makes. For a minicircle of N bp, the relaxed linking number Lk⁰ is given by the integer nearest to N/10.5, where 10.5 is the assumed helical repeat of DNA We introduce the difference between the actual and relaxed linking numbers of a minicircle as ΔLk = Lk − Lk⁰. Because a DNA minicircle is covalently closed, its linking number, and hence ΔLk, is constant and not altered by the deformation of the double helix.

The linking number of a minicircle is always equal to the sum of its writhing number and total twist, Lk = Tw + Wr. The writhing number characterizes the global folding and nonchiral distortions of the minicircle centerline, while the total twist measures the twisting or twist density of the base pairs around the centerline. Like the linking number, the writhing number and total twist can be directly obtained from the minicircle base-pair frames as explained previously.²¹ The invariance of the linking number implies that when the minicircle is deformed, the total twist and the writhing number are redistributed. The total twist is directly related to the torsional stress within the double helix, while the writhing number depends on the curvature of the centerline, albeit in a nontrivial way.

Protein-Free DNA Minicircles.

In order to study protein-decorated DNA minicircles, we first need to generate protein-free minicircles. For a minicircle of N bp, we first build a set of step parameters using the following formula for the ith step:

$${\underset{\_}{p}}^i=\left(\text{Δ}\sin \left({\theta }_3^{\ast }i\right),\text{Δ}\cos \left({\theta }_3^{\ast }i\right),{\theta }_3^{\ast },0,0,{\rho }_3^0\right)$$ (19)

where Δ = 2π/N is the bending angle between the planes of successive base pairs and ${\rho }_3^0$ denotes the intrinsic value of the rise step parameter within our force field. The parameter ${\theta }_3^{\ast }$ corresponds to the local twist density in the minicircle and can be adjusted to generate over- or undertwisted configurations. In order to enforce the covalent closure of the minicircle, we add at the end of the base-pair collection an additional base-pair identical to the first one. We then minimize the energy of the base-pair collection under the imposed end-to-end vector and rotation (which are both null in the present case). The outcome of the minimization is an optimized DNA minicircle with an imposed ΔLk.

We initially focus on planar, protein-free minicircles of lengths ranging from 63 to 105 bp, i.e., from 6 to 10 helical repeats. Planar minicircles always have a writhing number equal to zero, which means that the total twist is equal to the linking number. Because we require the naked minicircles to be planar, there is an upper bound on the value of |Tw| (and, hence, of |ΔLk|). This limiting value is related to the Michell–Zajac instability,^22,23 and for larger values of |Tw|, planar circular configurations are no longer stable. With our ideal force field, for a given chain length, we can always generate optimized minicircles with ΔLk = 0 and, depending on the chain length, ΔLk = −1 or ΔLk = +1 (for a few specific chain lengths, all three values are possible; see Section 6 of the Supporting Information for more details). In other words, we always compute optimized protein-free minicircles with ΔLk = 0, and in addition, we also generate optimized minicircles with ΔLk= −1 and/or ΔLk= +1. These different minicircles are then used with the binding ramp (eq 18) to model the presence of bound proteins.

RESULTS AND DISCUSSION

We first apply our minimization method to the optimization of DNA minicircles on which one or two proteins are bound. We focus on two distinct proteins: the abundant histone-like HU protein and the structurally related Hbb protein. These two proteins have a common fold and share some structural similarities, such as the fact that they both associate as dimers and both introduce significant localized bends in the double helix. The Hbb dimer, however, binds a longer stretch of DNA and induces a sharper turn of double helix than the HU dimer. We used the 3DNA software¹⁴ to extract the step parameters of the DNA found in known crystal complexes^1,5 (Protein Data Bank files 1P71 and 2NP2 for HU and Hbb, respectively). The length of the extracted binding domains of HU is 17 bp, and that of Hbb is 35 bp. The net bending angle introduced by the HU dimer, roughly 135°, is also less than that induced by Hbb (about 160°), where the measured values correspond to the angles between the normals of the first and last base pairs of the two protein–DNA complexes. Both proteins also slightly underwind the double helix. That is, the total twist across the DNA bound to each protein is less than the total twist of an undeformed B-DNA fragment of same length (for HU ΔTw ≃ −0.18 turn and for Hbb ΔTw ≃ −0.1 turn).

Minicircles with a Single Bound Protein.

We first performed a series of optimizations to study how the addition of an HU or Hbb dimer affects the configurations of a DNA minicircle. We considered minicircles of 63–105 bp in both relaxed ΔLk = 0) and supercoiled ΔLk = ±1) states. The known uniformity of closed protein-bound DNA structures generated through earlier Monte Carlo treatments of chains of comparable length,²⁴ combined with the success of others in mirroring the observed and simulated cyclization properties of even longer (150–160 bp) DNA chains through the minimization of DNA elastic energy,²⁵ lends support to our approach, allowing us to omit consideration of thermal fluctuations and focus instead on the lowest-energy states.

In order to characterize the optimized configurations, we define a relative step energy ε as

$$\epsilon =\frac{N}{N_{\text{free}}}\frac{E}{E^0}$$ (20)

where E is the energy of the optimized minicircle with the bound dimer, E⁰ is the energy of the optimized protein-free minicircle, N denotes the minicircle chain length, and N_free the protein-free chain length. In other words, ε is the ratio of the energy per base-pair step for the minicircle bearing a single protein versus that for the naked minicircle. Recall that our elastic energy for a minicircle accounts for protein-free steps only and ignores the contributions of protein–DNA binding.

The results for both proteins are presented in Figure 1. The relaxed minicircles include configurations from two competing families of structures, which exhibit similar ~21 bp periodic dependencies on chain length.^26–29 The oscillations of energy with chain length differ in phase by about a helical turn such that the valleys in the energy profile of one family of closed configurations coincide with the peaks in the other and vice versa. The breaks in the plotted data correspond to jumps between the configurational families. The reported supercoiled states are natural extensions of these families that arise as the DNA ends fall out of register. The underwound states build up with an increase in chain length and the overwound states with a decrease.

Figure 1.

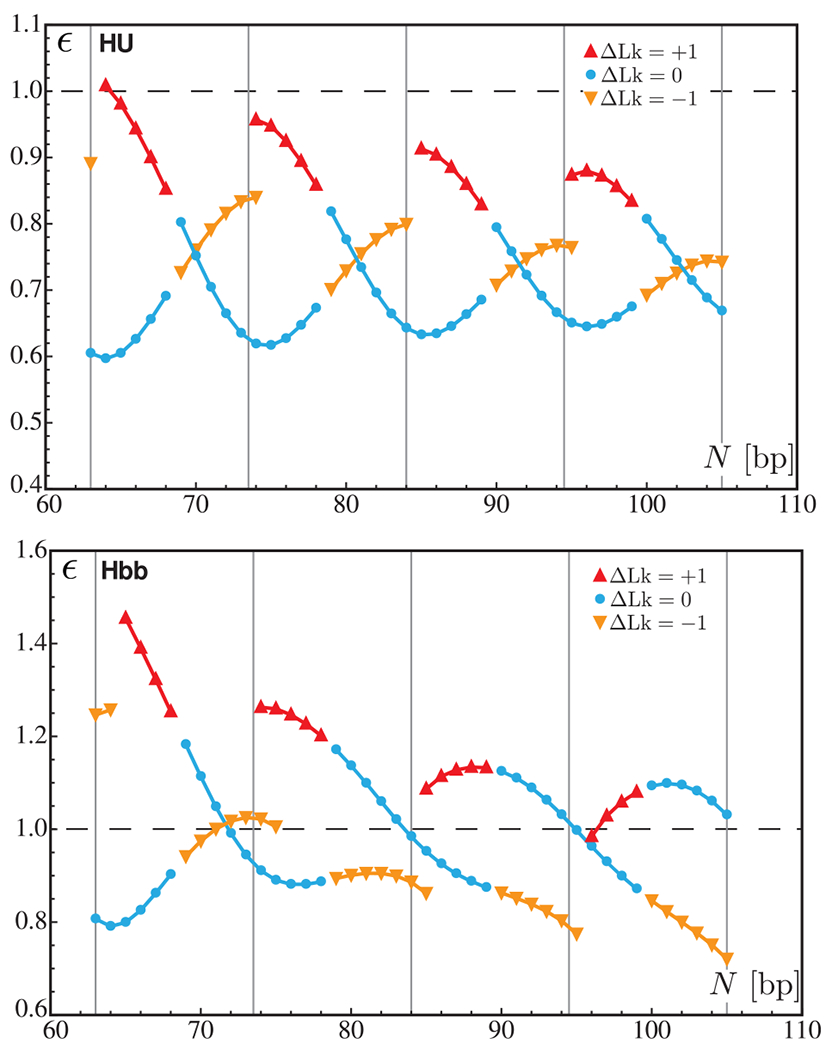
Chain-length dependence of the relative step energy per base pair ε for minicircles bearing a single HU (top) and Hbb (bottom) dimer. The blue circles correspond to the energies of relaxed minicircles over the complete range of chain lengths. The red and orange triangles represent the energies of over- and underwound minicircles, respectively. The horizontal dashed line (ε = 1) corresponds to the energy of a base-pair step in a naked minicircle of the same length. The vertical lines indicate the chain lengths equal to integral numbers of helical repeats.

The presence of an HU dimer almost always reduces the energy of the protein-free DNA compared to that of the naked minicircle (as shown by the values of the relative step energy ε less than 1 in the upper panel in Figure 1). On the other hand, the addition of an Hbb protein has a mixed effect on the relative step energy depending on the chain length and the value of ΔLk (lower panel in Figure 1). A possible explanation lies in the fact that the binding domain of the Hbb dimer is twice as long as that of the HU dimer. Thus, the number of protein-free DNA steps on an Hbb-bound minicircle is lower than that on a minicircle of the same size bearing an Hbb protein. In other words, the deformation required to satisfy the boundary conditions is more localized in minicircles with an Hbb dimer, and hence, the energy is higher. This argument also accounts for the differences in the chain-length dependence of the relative step energy for minicircles containing an HU dimer versus those with an Hbb dimer. As noted above, the chain-length dependence of the relative step energy dimer follows a damped oscillatory pattern. The periodicity in the Hbb pattern is not as clear as that for HU, suggesting that, within the present range of chain lengths, a minicircle with a single Hbb dimer is more constrained than one with an HU protein.

The other interesting feature found in these results is the influence of the linking number and the total twist on the relative step energy. In the case of the HU dimer, relaxed minicircles have, in most cases, a lower energy than under- or overwound minicircles. It is only for chain lengths close to half-integral numbers of helical repeats that the energy is lower for underwound minicircles. On the other hand, underwound minicircles of 79 bp or greater bearing an Hbb dimer are consistently lower in energy than relaxed or overwound minicircles. As mentioned above, both dimers slightly underwind the double helix, which means that their presence on a minicircle induces a redistribution of the torsional stress. Note that this redistribution may entail the conversion of part of the torsional stress into bending deformations as a consequence of the changes in the total twist and the writhing number. This also explains why overwound minicircles lead to higher energies: the large difference in the torsional stress between the naked DNA (prior to the addition of a protein) and the bound DNA causes higher deformations in the remaining part of the minicircle. In addition, the torsional stress in naked DNA depends on the chain length: for chain lengths close to integral numbers of helical repeats, the torsional stress is lower in relaxed minicircles than in underwound minicircles, but for chain lengths near half-integral numbers of helical repeats, the situation is reversed.

Our results further suggest that the torsional stress in DNA may influence the recruitment of HU and Hbb dimers and might act as a control mechanism for the presence of such proteins. For example, a relaxed minicircle of 94 bp might be more likely to associate with an HU than an Hbb dimer (assuming that the binding affinities of the two dimers are comparable), whereas an underwound minicircle of the same length might be more likely to take up an Hbb dimer. Although our results are obtained on covalently closed DNA minicircles (and, hence, under a topological constraint), it is reasonable to think that similar effects will take place on torsionally constrained linear DNA fragments (e.g., where the anchoring conditions could be set by large protein assemblies or magnetic/optical tweezers).

Minicircles with Two Bound Proteins.

Our second series of optimizations focuses on minicircles of 100 and 105 bp containing two HU or two Hbb dimers. In addition, for minicircles of 100 bp we consider relaxed (ΔLk = 0) and underwound (ΔLk = −1) molecules. This choice is motivated by the fact that the difference in energy between a naked-DNA minicircle of 100 bp with ΔLk = 0 and ΔLk = −1 is only 1.8 k_BT (the relaxed minicircle corresponds to the lower energy). Our computations provide energy landscapes of the protein-bound minicircles as functions of the spacing s between the two binding sites. These landscapes are directly related to the relative likelihoods of forming minicircles with two dimers at specific locations. In other words, the landscapes reveal which dimer positions along the minicircle are more apt to be occupied, e.g., in cyclization experiments. We report in Figures 2 and 3 the energy landscapes as well as the associated changes in the total twist ΔTw (with respect to the planar, naked minicircles).

Figure 2.

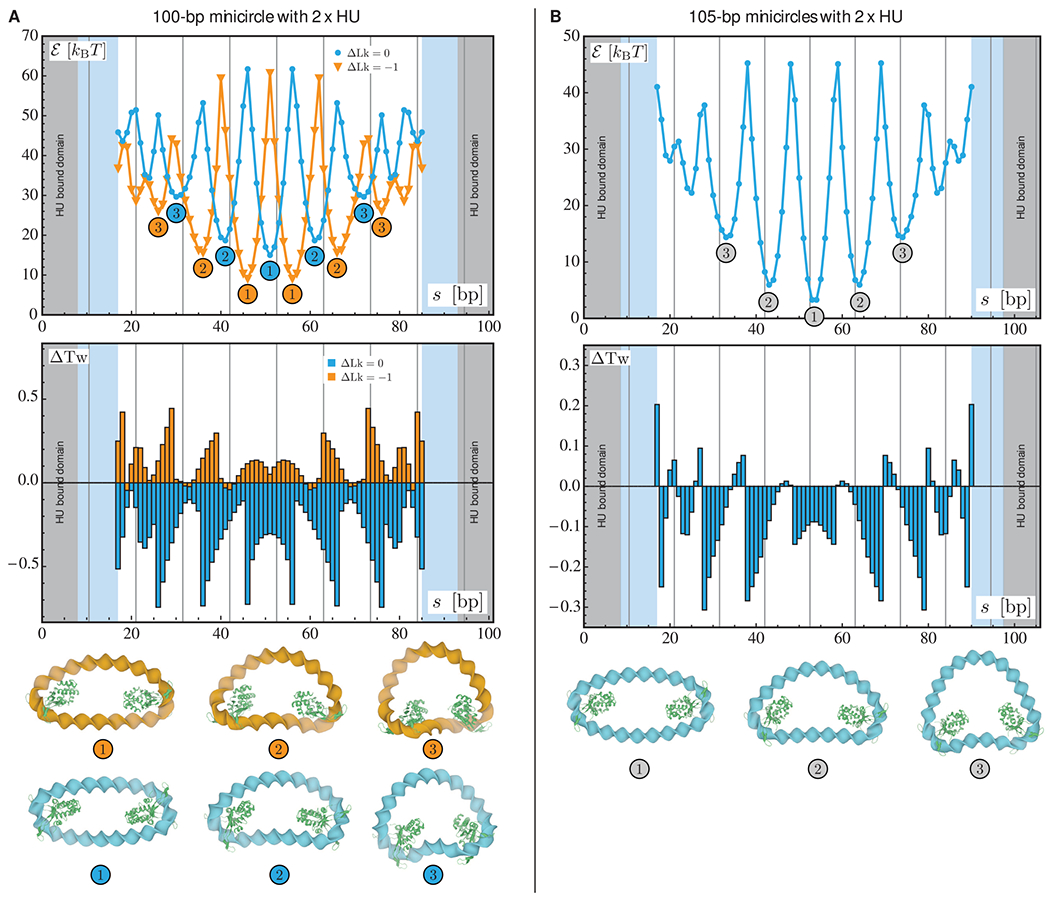
Optimization results for relaxed and underwound minicircles of 100 bp (A) and relaxed minicircles of 105 bp (B) bearing two HU dimers. For each chain length, the two plots represent the optimized energy (top) and the changes in the total twist (bottom) as functions of the center-to-center spacing s between the two proteins. The results for the relaxed (ΔLk = 0) and underwound (ΔLk = −1) minicircles of 100 bp are represented in blue and orange, respectively. In all plots, the gray areas denote the length of DNA in contact with the first HU dimer and the light blue areas the length in contact with the second dimer. The vertical lines indicate chain lengths equal to integral numbers of helical repeats. The numbers in the energy plot refer to the structures depicted at the bottom of the figure in which the HU proteins are represented in green.

Figure 3.

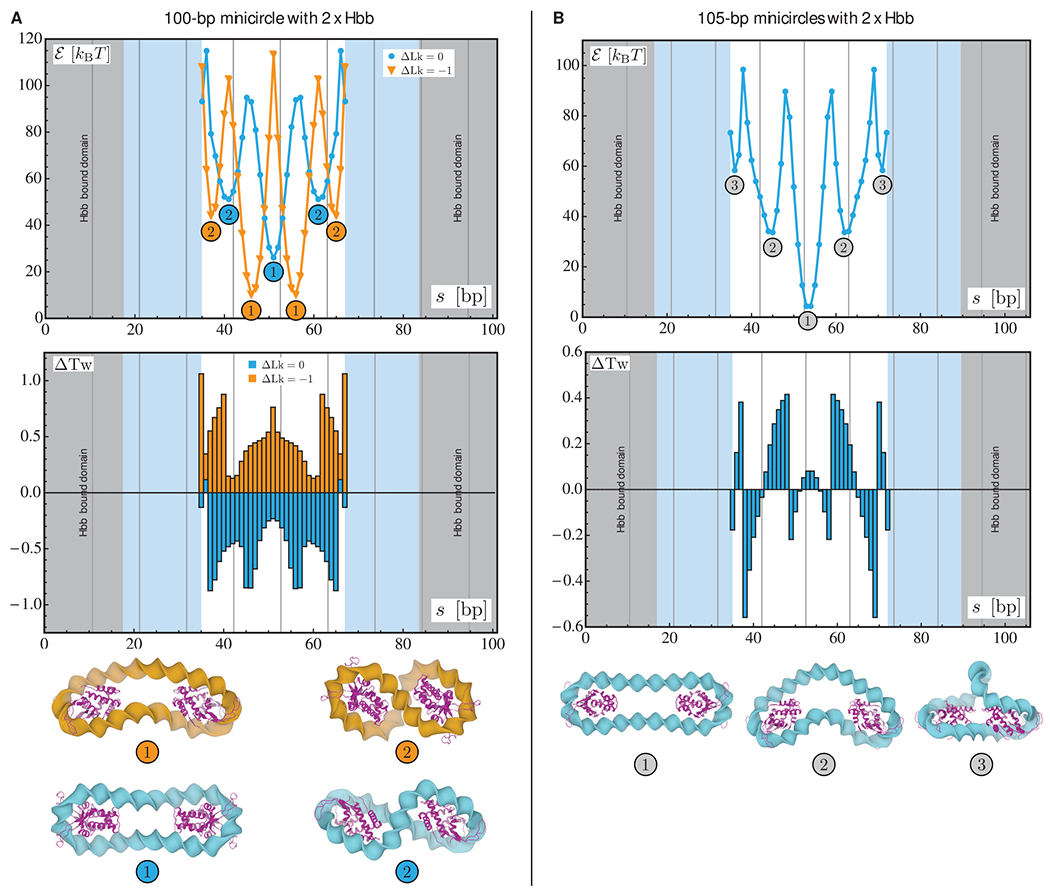
Optimization results for relaxed and underwound minicircles of 100 bp (A) and relaxed minicircles of 105 bp (B) bearing two Hbb dimers. For each chain length, the two plots represent the optimized energy (top) and the changes in the total twist (bottom) as functions of the center-to-center spacing s between the two proteins. The results for the relaxed (ΔLk = 0) and underwound (ΔLk = 1) minicircles of 100 bp are represented in blue and orange, respectively. In all plots, the gray areas denote the length of DNA in contact with the first Hbb dimer and the light blue areas the length in contact with the second dimer. The vertical lines indicate chain lengths equal to integral numbers of helical repeats. The numbers in the energy plot refer to the structures depicted at the bottom of the figure in which the Hbb proteins are represented in magenta.

The energy landscapes consist of several local minima separated by high-energy states. In other words, there are well-defined locations for optimal placements of two HU or Hbb proteins along the DNA minicircles. Note that, only the minima with the lowest energies and, hence, with the highest Boltzmann weights, are likely to be relevant to the statistical physics of protein-decorated minicircles. These minima appear periodically in the landscapes, and as expected, the period is roughly equal to the assumed DNA helical repeat (10.5 bp). In addition, the relative locations of the two proteins along the minicircle appear to affect the torsional stress significantly as evidenced by the variations in the total twist. Moreover, the lowest energy configurations are all similar from a geometric point of view. That is, for both HU and Hbb proteins, the globally optimal configurations are obtained when the two dimers are located at antipodal or near antipodal sites (as shown by the configurations labeled “1” in Figures 2 and 3). We note that the minima for the minicircles with two HU dimers are of lower energy than those for minicircles with two Hbb dimers. As noted above, the length of protein-free DNA for Hbb-bound minicircles is shorter than that for HU. Indeed, for two Hbb dimers, the length of naked DNA is comparable in size to the Hbb binding domain. The Hbb system is therefore highly constrained and leads to larger values in the illustrated energy landscapes and greater changes in the total twist.

The results for the minicircles of 100 bp containing two HU or two Hbb dimers (see data on left in Figures 2 and 3) show that the energy minima are lower for the underwound minicircle (ΔLk = −1) than for the relaxed minicircle (ΔLk = 0). This is consistent with the results obtained for minicircles of 100 bp with a single dimer (see Figure 1). The variations in the energy landscapes of the relaxed and underwound minicircles of 100 bp are out of phase. That is, the minima for the relaxed minicircles correspond to the maxima of the underwound minicircles and vice versa. This phase shift between the energy landscapes of relaxed and underwound minicircles is roughly equal to half the assumed helical repeat (~5–6 bp). The changes in the total twist for these minicircles are also similar, although the magnitude of the change is larger for the minicircles with two Hbb proteins. For the relaxed minicircles of 100 bp, the changes in the total twist are negative (with respect to the planar, protein-free minicircles), while for underwound minicircles the changes are positive. This implies, because of the conservation of the linking number, that the changes in the writhing number are of opposite sign for relaxed versus underwound minicircles. Indeed, as shown in Figure 3 (configurations labeled “2”), the minicircles are of different handedness. Also, notice that the pattern in the changes in the total twist for minicircles of 100 bp bearing two dimers is similar regardless of the associated protein: the local maxima in the energy correspond to the highest changes in the total twist, while the local minima correlate with those of moderate values of ΔTw.

For minicircles of 105 bp containing two HU or Hbb dimers, the energy landscapes resemble those obtained for 100 bp minicircles. In particular, the minima appear periodically (every ~10.5 bp) and are separated by high-energy configurations. The minima for the 105 bp chains are lower than those on the minicircles of 100 bp. This difference is due to the fact that the torsional stress in the 105 bp minicircle is lower than that in the 100 bp minicircle prior to the addition of the proteins. The main difference between minicircles of 100 and 105 bp resides in the changes in the total twist. Whereas the changes in the total twist are comparable for 100 bp minicircles bearing two HU or two Hbb dimers, the values of ΔTw at the local minima are of different signs for the corresponding 105 bp HU and Hbb minicircles. That is, for the lower energy configurations, the presence of two HU dimers reduces the torsional stress in the minicircle (see Figure 2), while two Hbb dimers increase the torsional stress (see Figure 3). Notice, however, that the magnitudes of the changes in the total twist for these local minima are comparable.

Our findings for minicircles with two dimers reveal an interplay between the elastic properties of DNA and the positioning of proteins on the double helix. It appears that this result is neither about the proteins shaping the double helix nor about the DNA stiffnesses controlling the positioning of proteins. Rather, there is cooperation between the presence of proteins and the elasticity of the double helix, particularly in the distribution of the torsional stress. The high degree of contrast in the energy landscapes suggests that once a protein is bound to a topologically constrained DNA fragment, the stress in the double helix will favor specific binding sites for other proteins. Such an interpretation echoes the results about DNA–protein allosteric effects found in single-molecule studies.³⁰ It is also interesting to note that the local minima found in the energy landscapes are always flanked by configurations of comparable energy (up to a few k_BT). This suggests that there should be fluctuations in experimental measurements of the most likely binding sites of HU and Hbb dimers on DNA minicircles. Also note that these results have been obtained with a minimal model, i.e., DNA is modeled as an isotropic material with standard bending and twisting stiffnesses and is focused on a special class of protein geometry, which includes specific deformations of the double helix. Nevertheless, the approach serves as a proof of concept and paves the way for more detailed studies about the synergy between DNA deformation and protein positioning.

CONCLUSIONS

The minimization procedure introduced in this work facilitates the investigation of how architectural proteins may contribute to the spatial organization and genetic processing of DNA. This new approach gives direct control of the positions and orientations of the base pairs at the ends of a DNA chain and makes it possible to specify the precise sites of protein uptake and the detailed changes in double-helical structure brought about by the binding of protein. Here we illustrate the utility of the method in a study of the elastic energy landscapes of DNA minicircles decorated by the nonspecific architectural protein HU and the similarly folded, albeit site-specific,³¹ Hbb protein. Both proteins associate as dimers and introduce severe bends and untwist their DNA targets. We consider the Hbb-bound DNA as an extreme example of HU-induced DNA distortion and thus treat both proteins as nonspecific. We focus on covalently closed molecules comparable in length to the loops that are formed by various regulatory proteins and enzymes that bind to sequentially distant sites on DNA^32,33 and allow for the uptake of one or two HU or Hbb dimers on the DNA. We also consider underwound and overwound minicircles in order to study the added effects of torsional stress within the double helix on the protein-binding landscapes. We find that the presence of protein has a significant effect on the bending and twisting deformations in the minicircles and, conversely, that the torsional stress within DNA prior to the addition of proteins has a strong effect on the optimal placement of proteins along the minicircles. For example, we show that a single HU dimer is more likely to bind relaxed rather than under- or overwound minicircles of most chain lengths between 63 and 105 bp and that an Hbb dimer binds preferentially to underwound minicircles of the same lengths.

Our results reveal cooperation between the deformability of the double helix and the structural distortions of DNA induced by bound proteins. In the case of minicircles with two HU or two Hbb dimers, the presence of a first protein strongly influences the locations of the optimal binding sites of a second protein. That is, the DNA, through its elastic deformation, acts as a communication medium between the proteins. In particular, the torsional stress and the twisting stiffness appear to play a major role in this action at a distance. The mechanical signaling also provides a rationale for the DNA allostery reported in single-molecule studies of the dissociation of proteins on DNA chains constrained to full extension by the flow of solvent.³⁰ In particular, the binding of one protein on the extended DNA stabilizes or destabilizes the binding of another protein, even when not in direct contact. Indeed, this sort of long-range communication, in which the binding of a ligand in one part of the DNA helix influences (positively or negatively) the recognition of a different ligand at a remote site, also termed telestability,³⁴ has puzzled DNA scientists for decades. Although our results concern a special class of proteins bound to covalently closed rather than straightened DNA, we observe an interplay between the elasticity of the double helix and the placement of proteins along DNA that may hold for extended as well as cyclic chains. Indeed, constraints on the twist of the intervening DNA give rise to a decaying oscillatory pattern of protein uptake on linear chains of the type observed experimentally,³⁵ as does the interplay between DNA double-helical geometry and the deformations of base pairs considered in recent analytical work³⁶ and the many interatomic interactions incorporated in detailed molecular simulations of protein-bound DNA chain fragments.^37–41 In our case, the most likely placement of a second DNA-bending protein on a minicircle is antipodal to the first, i.e., as sequentially far apart as possible. Our studies provide examples of how the mechanical stress in DNA can control the placement of proteins and how proteins can alter the mechanical stress to broadcast their presence along DNA. Our findings further suggest that local modifications of the mechanical properties of DNA, such as methylation or the occurrence of kinks, could modulate and possibly repress this type of mechanical signaling. The very different responses of the minicircles to the degree of DNA uptake on HU vs Hbb also lend support to ideas suggesting how the unwrapping of nucleosomal DNA in chromatin might contribute to the binding of other molecules on the intervening protein-free DNA linkers and the deformability of chromatin as a whole.⁴² Note, for example, the greater accessibility and lower energy of the DNA connecting proteins at sites labeled “2” on 100-bp minicircles in Figures 2 and 3. The DNA connecting the HUs adopts a smooth bend with a locally accessible groove structure compared to the tightly folded supercoiled configuration that accompanies the uptake of nearly a turn of DNA (9 bp) on the termini of each Hbb.

Although the minimal elastic energy configurations of long DNA chains are not necessarily relevant from a statistical physics point of view, our method can be used to study larger systems, such as long DNA molecules decorated by multiple proteins. For example, we show in Figure 4 two examples of multiple loops on circular DNA induced by the Ter-specific protein MatP,⁷ which is thought to be involved in the condensation of chromosomes in Escherichia coli. We also show in Figure 5 a long DNA plasmid decorated by 64 closely spaced Hbb proteins. The software can be used in combination with other tools (e.g., 3DNA¹⁴) to optimize DNA fragments anchored by proteins. An interesting application of our approach resides in the development of software for biomolecular sculpting,⁴³ which would make it possible to study how proteins can bundle and organize DNA. Our methodology could also be used to investigate the effects of DNA “melting” within a closed double-helical pathway, e.g., introducing noncanonical, opened states of the type captured in molecular-dynamics simulations⁴⁴ or observed in high-resolution structures⁴⁵ at selected sites and studying the “dynamic” response of the DNA as a whole. We are currently working on improving our method to account for additional types of constraints, such as the treatment of DNA excluded volume via electrostatic interactions.⁴⁶ The software does not currently check for collisions between DNA and proteins. Although the proteins collide on some of the minicircles presented here (see Figures 2 and 3), the collisions only occur in high-energy configurations, in which pairs of proteins lie immediately next to one another. We also plan to include more realistic force fields to account, for example, for the higher deformability of pyrimidine–purine compared to other base-pair steps or for the flexibility of protein–DNA assemblies. This task is facilitated by the fact that the method already takes into account the sequence-dependent elasticity of DNA. It is thus also possible to use our approach to examine the effects of different force fields, e.g., knowledge-based⁴⁷ vs computer-simulated⁴⁸ elastic potentials, on large-scale chain properties, such as protein-mediated DNA looping.²⁹ Note that the software makes it possible for the user to define and use custom force fields, thus facilitating investigations on the sensitivity of optimized structures with respect to the details of the force constants and intrinsic parameters. Finally, we have begun to study other biomolecular systems, including the short loops mediated by the Lac and Gal repressor proteins, nucleosome-decorated minicircles, and the relative contributions of protein and DNA flexibility in these systems.

Figure 4.

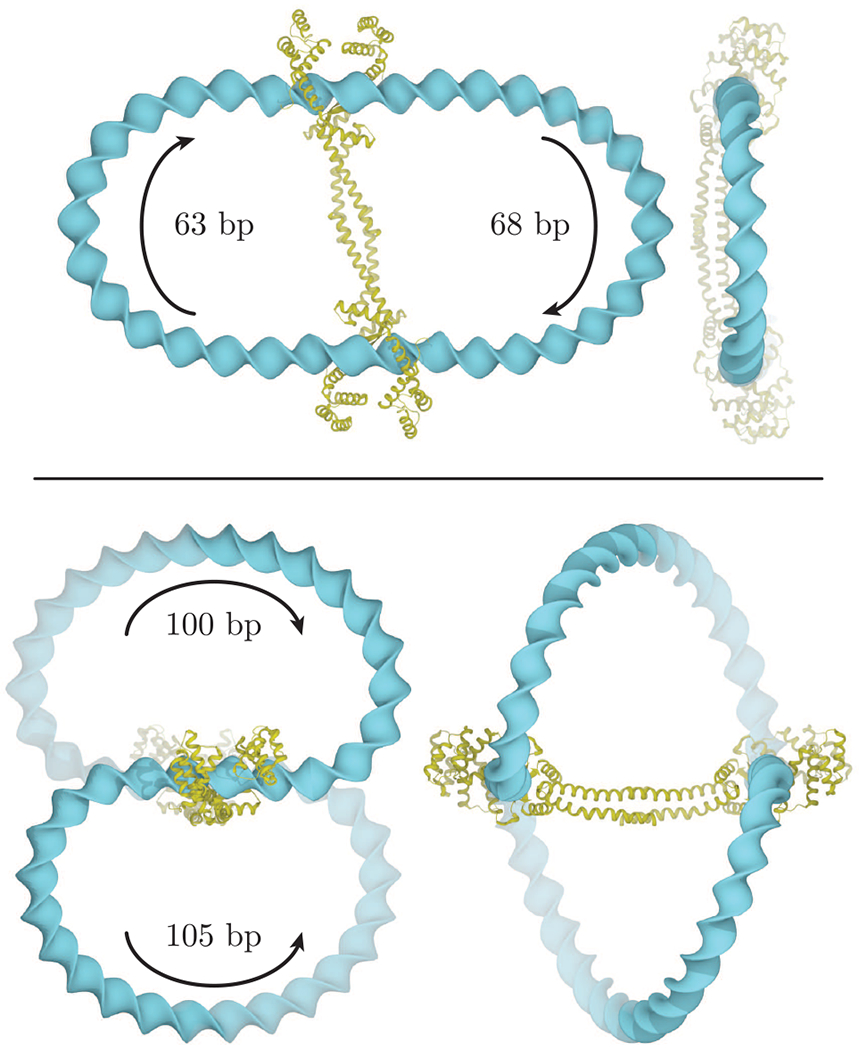
Orthogonal views of optimized loops induced by the DNA-bridging protein MatP⁷ on circular DNA molecules of 177 bp (top) and 251 bp (bottom). The loops depicted on the former minicircle run in antiparallel directions, and those on the latter run in parallel directions (note the arrows and chain lengths in the images). The MatP dimeric protein is represented in gold. The step parameters of the two bound DNA domains have been extracted from Protein Data Bank file 3VEA.

Figure 5.

Perspective (top) and orthographic (bottom) views of an optimized DNA plasmid of 1280 bp containing 64 Hbb proteins regularly spaced by 5 bp protein-free linkers. The presence of the Hbb proteins (represented in magenta) greatly condenses the DNA into a helical fiber-like structure that folds into a circular configuration. The circular radius of the resulting superstructure is 31.5 nm, and the fiber radius is 3 nm (the same DNA plasmid without any proteins has a circular radius of 69.2 nm and a cross-sectional radius of 1 nm). The elastic energy stored in each naked-DNA linker is 0.19 k_BT, suggesting that the linkers are only slightly deformed. In contrast to the zigzag superhelical structure found in the crystal lattice in which the proteins lie on opposite sides of the superhelical axis,⁵ the proteins form a central core in the optimized structure. Notice that this structure has been generated with a reduced Hbb model with only the 15 central base pairs of the full crystallographic model, i.e., with 10 bp peeled off each end of the protein-bound DNA fragment used in earlier figures. As a consequence, the spacing between the proteins is smaller in the optimized structure than in the pseudocontinuous helix found in the crystal lattice.

The methods described in this paper are implemented as a set of documented C++ tools available at https://nicocvn.github.io/emDNA/.