Predicting time‐resolved electrophysiological brain networks from structural eigenmodes

Abstract

How temporal modulations in functional interactions are shaped by the underlying anatomical connections remains an open question. Here, we analyse the role of structural eigenmodes, in the formation and dissolution of temporally evolving functional brain networks using resting‐state magnetoencephalography and diffusion magnetic resonance imaging data at the individual subject level. Our results show that even at short timescales, phase and amplitude connectivity can partly be expressed by structural eigenmodes, but hardly by direct structural connections. Albeit a stronger relationship was found between structural eigenmodes and time‐resolved amplitude connectivity. Time‐resolved connectivity for both phase and amplitude was mostly characterised by a stationary process, superimposed with very brief periods that showed deviations from this stationary process. For these brief periods, dynamic network states were extracted that showed different expressions of eigenmodes. Furthermore, the eigenmode expression was related to overall cognitive performance and co‐occurred with fluctuations in community structure of functional networks. These results implicate that ongoing time‐resolved resting‐state networks, even at short timescales, can to some extent be understood in terms of activation and deactivation of structural eigenmodes and that these eigenmodes play a role in the dynamic integration and segregation of information across the cortex, subserving cognitive functions.

We study time‐resolved amplitude and phase connectivity in resting‐state agnetoencephalography data. We show that there is hardly signature of structural connections in time‐resolved connectivity. Time‐resolved connectivity can be expressed in terms of structural eigenmodes. This relationship was stronger for amplitude connectivity than for phase connectivity.

1. INTRODUCTION

During the last decades, a wealth of network neuroscience studies have contributed to the understanding of how large‐scale neuronal interactions are shaped and constrained by the underlying anatomical wiring (Bassett & Sporns, 2017). The anatomical wiring forms the structural network and whole‐brain functional networks are formed by large‐scale neuronal interactions, that is, so‐called functional connections (FC) (Friston, 1994). It is widely assumed that the structural network, or connectome, supports a diversity of functional network patterns that emerge and dissolve over time (Park & Friston, 2013), which in turn are responsible for information transfer across the cortex, subserving cognition and behaviour (Bassett & Sporns, 2017). The relationship between large‐scale structural and functional networks has so far mainly been addressed in the domain of ‘static’ functional connectivity and at the group level rather than for individual subjects (Avena‐Koenigsberger et al., 2018; Honey et al., 2007). In other words, functional connectivity is usually estimated over the entire duration of a recording and is subsequently averaged across subjects. In this way, information about the temporal evolution of functional connectivity (i.e., dynamic functional connectivity or time‐resolved connectivity) and its variance across individuals is neglected. Assessment of the structure–function relationship at the individual level may reveal biologically meaningful and useful relationships, for example, in the context of individualised trajectories of functional network alterations in neurological diseases (Douw et al., 2019).

Functional connectivity studies at the static group‐averaged level reveal clear relationships between structural and functional brain networks (Avena‐Koenigsberger et al., 2018; Suárez et al., 2020). However, FC fluctuate on the millisecond timescale in relation to the current cognitive demands and, therefore, an assumed static or fixed relationship between structural and static functional networks may not provide an accurate description (O'Neill et al., 2017). Rather, a weak coupling between structural and functional networks is required, allowing for flexibility of the functional network so that it can change according to variations in cognitive demand (Deco & Kringelbach, 2016). At the same time, modelling studies predict that, especially at shorter timescales, a decoupling between structural and functional networks could occur, that is, a structure–function discrepancy (Honey et al., 2007; Ton et al., 2014), due to rapid transitions between functional network states. It therefore remains an open question how strong structural networks could be related to a repertoire of functional networks when the time‐varying aspect of functional connectivity is considered at the individual subject level.

A few previous studies have addressed the relationship between structural and temporally evolving functional networks using functional MRI (fMRI) (Glomb et al., 2020; Hansen et al., 2015; Preti & Van De Ville, 2019; Rué‐Queralt et al., 2021; Shen et al., 2015). A recent and successful approach to disentangle the relationship between structural and functional brain networks is the so‐called eigenmode approach (Abdelnour et al., 2018; Aqil et al., 2021; Atasoy et al., 2016, 2018; Robinson, 2021; Robinson et al., 2016). These eigenmodes correspond to eigenvectors of the Laplacian of the structural network and they can be interpreted as spatial connection patterns in the structural network that can become activated at the level of FC. Eigenmodes belonging to higher Laplacian eigenvalues tend to spatially oscillate stronger over the end nodes of a link in any undirected network. Combinations of structural eigenmodes have been related to resting‐state functional networks (Atasoy et al., 2016, 2018). Recent studies have demonstrated that fluctuations in neuronal activity across the brain, as reconstructed from electroencephalography or indirectly from fMRI, can be expressed in terms of a set of eigenmodes of the connectome (Glomb et al., 2020; Preti & Van De Ville, 2019; Raj et al., 2020; Rué‐Queralt et al., 2021).

However, the role of these structural eigenmodes in relation to temporal fluctuations in electrophysiological connectivity and the functional relevance of this potential relationship for cognition remains to be elucidated. Electrophysiological connectivity can be reconstructed from magnetoencephalography (MEG) data. MEG has good spatial resolution and high temporal resolution (in the order of milliseconds). The latter is important given the observation that cognitive relevant modulations of neuronal activity and communication also occur in this timescale (Fries, 2015). More specifically, it is assumed that normal cognitive functioning strongly relies on time‐varying, locally segregated communities (Park & Friston, 2013). Until now, it is unclear if communities at the functional level in electrophysiological data relate to structural eigenmodes.

It is widely assumed that there are two dominant intrinsic modes of large‐scale functional connectivity in electrophysiological data, namely amplitude coupling and phase coupling (Siegel et al., 2012). Connectivity patterns from both modes show considerable similarities (Colclough et al., 2016), yet contain nonredundant and complementary information (Siems & Siegel, 2020). Recent work found power‐law scaling for both amplitude and phase dynamics, albeit with the difference that phase dynamics showed faster decay of temporal auto‐correlations, suggesting a more flexible way of information‐coding in the brain for phase coupling (Daffertshofer et al., 2018). Hence, in the light of these findings we argue that such divergent temporal dynamics could entail distinct coupling between structural and time‐varying functional networks for amplitude and phase coupling. Recently developed approaches and methods allow us to capture temporally evolving functional connectivity without the need for sliding windows with arbitrary widths, for example, using Hidden Markov modelling or measures of functional connectivity with high temporal resolution (Baker et al., 2014; O'Neill et al., 2017; Vidaurre et al., 2018). In this work, we therefore used metrics with high temporal resolution that capture amplitude coupling, the recently introduced instantaneous amplitude correlation (IAC) metric (Tewarie et al., 2019b), and phase coupling, the phase difference derivative (PDD) metric (Breakspear et al., 2004).

The novelty and contribution of the current work is the application of the eigenmode approach to time‐resolved functional connectivity estimated from MEG data. We first aimed to analyse whether temporal fluctuations in phase and amplitude connectivity could be explained by modulations in expression of structural eigenmodes in individual subjects using their own structural connectivity data. This potential relationship was examined using both an analytical and numerical (i.e., statistical) approach for individual data. We analytically derived the conditions for which the relationship between eigenmodes and time‐resolved functional connectivity for both phase and amplitude holds, and whether these conditions were met in empirical data. The first step in the numerical approach was to test the structure–function discrepancy hypothesis for dynamic functional connectivity. We expected to see little resemblance of the structural network in ongoing fluctuations in functional connectivity for both phase and amplitude. Hence, we tested the null hypothesis that time‐resolved functional connectivity could equally well be explained by direct structural connections or structural eigenmodes (Tewarie et al., 2020). If the null hypothesis could be rejected, we further tested whether a relationship between structural eigenmodes and time‐varying connectivity could be obtained by chance (using surrogate data with equal degrees of freedom). To support the use of individual structural connectivity, we analysed and compared the relationship between structural eigenmodes and time‐varying functional connectivity based on individual and group average structural connectivity. We lastly extended our analysis to detect how eigenmodes map onto time‐varying functional connectivity when the null hypothesis of stationary connectivity was rejected.

The second aim was to explore the functional relevance of a potential relationship between structural eigenmodes and time‐varying functional connectivity (for both phase and amplitude). This was done by analysing (1) whether modulations in expression of structural eigenmodes co‐varied with communities at the functional level; (2) whether expression of structural eigenmodes related to overall cognitive test scores.

2. METHODS

2.1. Diffusion MRI: Estimation of structural networks

We included diffusion MRI data from 88 healthy controls (who also underwent MEG recordings) of the Human Connectome project (Larson‐Prior et al., 2013), (range of the age 22–35 years, mean age 29 years, 41 females, 47 males). Diffusion MRI data were obtained from the Human Connectome Project (Van Essen et al., 2013). Full acquisition protocol details are described in Sotiropoulos et al. (2013). Briefly, a monopolar Stejskal‐Tanner echo planar imaging sequence was used in a 3 T Siemens Connectom Skyra to acquire data at (1.25 mm)³ isotropic resolution. Diffusion‐sensitization was applied with three b‐values (b = 1000, 2000 and 3000 s/mm²) and along 90 directions per b‐shell. Two repeats were obtained with blip‐reversed phase encoding. The minimally processed data were used (Glasser et al., 2013), where susceptibility‐induced distortions, eddy currents and subject motion were all corrected simultaneously using a nonparametric framework (Andersson & Sotiropoulos, 2016) based on Gaussian processes (Andersson & Sotiropoulos, 2015). We refer the reader to Tewarie et al. (2019a) for a full description of the estimation of the structural connectivity. In short, diffusion data was fed into probabilistic tractography in FMRIB Software Library to estimate structural networks (Behrens et al., 2007). Streamlines were seeded from 60,000 standard‐space vertices on the white/grey matter boundary surface (5000 streamlines per seed). Connectivity was quantified as the number of streamlines reaching each vertex normalised by the total number of valid streamlines propagated. Using the automated anatomical labelling (AAL) cortical parcellation, this connectivity was reduced to a 78 × 78 parcellated connectome (denoted as $A$), by computing for each pair of regions the mean structural connectivity between all pairs of vertices that they were comprised of.

2.2. MEG: Participants, data acquisition and source reconstruction

We included resting‐state MEG data from 89 healthy controls of the Human Connectome project (Larson‐Prior et al., 2013). One subject was excluded due to a lack of diffusion data (hence 88 subjects in total). Human connectome project (HCP) provides resting‐state MEG data where participants were in supine position with their eyes open and fixated on a central cross. For the main analysis, we used the first recording session (out of three repeated recordings) in the same subject. The second recording session was used as validation data set. The data have been provided pre‐processed (Larson‐Prior et al., 2013), after passing through a pipeline to remove any artefactual segments of time from the recordings, identify any recording channels that were faulty, and to regress out artefacts that appear as independent components with clear artefactual temporal signatures (such as eye‐blinks or cardiac interference) in an independent component analysis decomposition. An atlas‐based beamforming approach (Hillebrand et al., 2012) was adopted to project MEG sensor level data into source‐space as outlined by Tewarie et al. (2019a). To this end, the cortex was parcellated into 78 cortical regions according to the AAL atlas (Tzourio‐Mazoyer et al., 2002) and source localised data was only reconstructed for the centroid voxels of the parcels. Source localised data was frequency filtered into five frequency bands: delta (1–4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (13–30 Hz) and low gamma (30–48 Hz).

2.3. Behavioural data

We used the ‘cognition total composite’ as obtained from the provided cognitive test battery (NIH toolbox Cognitive Function Battery) as a proxy measure for cognitive performance (Barch et al., 2013). We omitted other separate test scores that were based on measures of cognitive domains that were not fully covered by the NIH toolbox. The ‘cognition total composite’ score was used as score of global cognition based on the following tests in the NIH toolbox: dimensional card sort test (executive function), flanker inhibitory control and attention test (executive function), list sorting working memory test (working memory), oral reading recognition test (language/reading decoding), pattern comparison processing speed test (information processing speed), picture sequence memory test (episodic memory), picture vocabulary test (language/vocabulary comprehension). Three subjects had missing behavioural data. The mean and SD of the ‘cognition total composite’ score was 122.6 ± 15.2 (scores are normalised to population averages of 100). Cognitive performance scores were correlated to the goodness‐of‐fit of time‐varying functional connectivity from the spatial eigenmodes (see Section 2.8). We used the Bonferroni method to correct for multiple testing (five frequency bands × two statistical outcome measures × two connectivity metrics).

2.4. MEG: Time‐varying functional connectivity

We used two high temporal resolution metrics of functional connectivity, the IAC (Tewarie et al., 2019b) for amplitude coupling and the PDD for phase coupling (Breakspear et al., 2004), as implemented in Tewarie et al. (2019b). For both measures, we extract the phases and the amplitude envelopes from the analytic signal using the Hilbert transform of bandpass filtered data. Since both metrics are sensitive to the effects of signal leakage, we used pairwise orthogonalisation as a method to reduce leakage effects prior to the calculation of functional connectivity (Hipp et al., 2012).

The IAC metric captures simultaneous increases in amplitude envelopes between two time‐series, and can be regarded as a time‐resolved version of the amplitude envelope correlation metric (Brookes et al., 2011; Hipp et al., 2012). If two regions show simultaneously high amplitudes, the correlation between the two amplitude envelopes is driven up. The IAC is computed by taking the Hadamard product (element wise product) between the amplitude envelope vector of two band‐filtered time‐series. This product provides a high temporal resolution measure of functional connectivity

$${\mathrm{IAC}}_{\mathit{ij}}\left(t\right)={\widehat{E}}_i\left(t\right)\circ {\widehat{E}}_j\left(t\right),$$ (1)

where $\circ$ represents the Hadamard product. The hat symbol in Equation 1 indicates that the time‐series (not the amplitude envelopes) were normalised using the z‐scores.

The PDD is a measure that captures the stability of phase relationships between two time‐series. For each pair of signals i and j, it is assumed that there is phase‐locking, that is, a functional interaction, when the phase difference $∆{\phi }_{\mathit{ij}}$ remains approximately constant over time. Hence, the derivative of the phase difference is assumed to be approximately zero. A representation of dynamic phase connectivity for each pair of time‐series can be computed using the following expression

$${\mathrm{PDD}}_{\mathit{ij}}\left(t\right)=\exp \left(-{\left(\frac{d∆{\phi }_{\mathit{ij}}\left(t\right)}{\mathit{dt}}\right)}^2\right),$$ (2)

where the use of the decaying exponential ensures that the outcome is bounded between one and zero, and where ${\left(\frac{d∆{\phi }_{\mathit{ij}}\left(t\right)}{\mathit{dt}}\right)}^2\approx 0$ corresponds to a PDD value of 1, and a PDD value approaching 0 corresponds to no coupling. Here, we used a slightly different implementation of the PDD compared to Tewarie et al. (2019b), where we used $\left|\frac{d∆{\phi }_{\mathit{ij}}\left(t\right)}{\mathit{dt}}\right|$ instead of ${\left(\frac{d∆{\phi }_{\mathit{ij}}\left(t\right)}{\mathit{dt}}\right)}^2$. Here, we had to avoid the use of the absolute value $\left|\dots \right|$ in our analytical derivation on the relationship between phase connectivity and the structural network (see section analytical approach).

2.5. The relationship between structural eigenmodes and time‐varying functional connectivity

We followed the same approach as in Tewarie et al. (2020) to map structural eigenmodes onto time‐varying functional connectivity, with the difference that our method is now applied to time‐resolved functional connectivity rather than static functional connectivity. An in‐depth explanation of the method can be found in Tewarie et al. (2020), but the main proposition is that there is a relationship between the eigenvectors of the graph Laplacian of the structural network and the graph Laplacian of the functional network. The rationale for using structural eigenmodes of the normalised graph Laplacian instead of the weighted adjacency matrix is that the eigenmodes of the graph Laplacian relate to spatial configurations with ascending spatial frequencies (Preti & Van De Ville, 2019).

We extracted the structural eigenmodes from the graph Laplacian of the $N\times N$ structural connectivity matrix $A$. The graph Laplacian of the structural connectivity matrix is denoted by $Q_A=K_A-A$. Here $K_A$ refers to the diagonal node strength matrix. We further applied symmetric normalisation to the graph Laplacian with

$$Q_{\mathit{As}}={K_A}^{-1/2}{Q}_A{K_A}^{-1/2},$$ (3)

followed by diagonalisation of the Laplacian as $Q_{\mathit{As}}=Z\mathrm{diag}\left({\mu }_1,\dots ,{\mu }_N\right)Z^T$, where $Z$ corresponds to the matrix in which the columns refer to the eigenvectors belonging to the eigenvalues ${\mu }_i$ ($1\le i\le N$, where N is the number of nodes in the network) of the normalised Laplacian Q _AS . Since the $N\times 1$ vector $u={\left(1,\dots ,1\right)}^T$ is an eigenvector of the Laplacian matrix $Q_A$, it holds that

$$Q_{\mathit{AS}}\left(K_A^{-\frac{1}{2}}u\right)=K_A^{-\frac{1}{2}}{Q}_{A}u=0.$$

Hence, the $N\times 1$ eigenvector of the normalised Laplacian $Q_{\mathit{AS}}$ corresponding to the eigenvalue ${\mu }_N=0$ is given by

$$z_N=\frac{1}{{‖K_A^{\frac{1}{2}}u‖}_2}{K}_A^{\frac{1}{2}}u.$$

Since $K_A$ refers to the diagonal node strength matrix, we can rewrite the eigenvector $z_N$ in terms of node strength $d_i={\sum }_{j=1}^N{a}_{\mathit{ij}}$ (weighted degree for node i)

$$z_N=\frac{1}{\sqrt{{\sum }_{i=1}^N{d}_i}}\left(\begin{array}{c}\sqrt{d_1}\\ ⋮\\ \sqrt{d_N}\end{array}\right).$$

The $N\times N$ Laplacian of the functional connectivity matrix $W\left(t\right)$ at time $t$ equals $Q_W\left(t\right)=K_W\left(t\right)-W\left(t\right)$. $W\left(t\right)$ refers to either the $\mathrm{PDD}\left(t\right)$ or $\mathrm{IAC}\left(t\right)$ functional connectivity matrices and $K_W\left(t\right)$ is the diagonal node strength matrix of the functional connectivity matrix $W\left(t\right)$. We apply the same symmetric normalisation as for the structural case, hence the normalised Laplacian of the functional connectivity matrix is given by

$$Q_{\mathit{Ws}}={K_W}^{-1/2}\left(t\right)Q_W\left(t\right){{\mathrm{K}}_W}^{-1/2}\left(t\right).$$ (4)

If we assume a linear relationship between structural and functional networks, then we can approximate $W\left(t\right)\approx W_{\mathrm{apx}}\left(t\right)$ using a well understood relationship between the eigenvectors $Z$ of the graph Laplacian of the structural connectivity matrix and $W_{\mathrm{apx}}\left(t\right)$ (Tewarie et al., 2020), encoded in the diagonal matrix $P\left(t\right)$ with weighting coefficients. In Tewarie et al. (2020) we show that the relationship between eigenvectors $Z$ and $W_{\mathit{apx}}\left(t\right)$ can be formulated as

$$W_{\mathrm{apx}}\left(t\right)=K_W\left(t\right)-{K_W}^{\frac{1}{2}}\left(t\right)\left(\mathit{ZP}\left(t\right)Z^T\right){K_W}^{\frac{1}{2}}\left(t\right).$$ (5)

The estimation of the weighting coefficients $P\left(t\right)$ is an optimisation problem. The analytical solution to optimisation problem was derived in Tewarie et al. (2020) and given by

$$P\left(t\right)=\mathrm{diag}\left(z_1^T{Q}_{\mathit{Ws}}\left(t\right)z_1,\dots ,z_N^T{Q}_{\mathit{Ws}}\left(t\right)z_N\right).$$ (6)

Note that the current notation differs from Tewarie et al. (2020) in the sense that some state variables are time‐dependent.

2.6. Analytical approach: Amplitude connectivity

The relationship between structural eigenmodes and functional connectivity as outlined in Equation 5 and derived in Tewarie et al. (2020) is naïve to the connectivity metric of interest. In contrast to our previous work (Tewarie et al., 2020), we analytically derive conditions for which the relationship between eigenmodes and time‐resolved phase and amplitude connectivity holds.

We first consider time‐varying amplitude connectivity in the absence of leakage correction followed by the case where there is leakage correction. At every time $t$ we can define the $N\times 1$ amplitude envelope vector

$$\widehat{E}\left(\mathrm{t}\right)=\left(\begin{array}{c}{\widehat{E}}_1\left(t\right)\\ ⋮\\ {\widehat{E}}_N\left(t\right)\end{array}\right).$$

The symmetric $N\times N$ instantenous amplitude correlation matrix $\mathrm{IAC}\left(t\right)$ equals to the outer product

$$\mathrm{IAC}\left(t\right)=\widehat{E}\left(t\right){\widehat{E}}^T\left(t\right).$$ (7)

Proposition 1

Suppose that the functional connectivity matrix $W\left(t\right)$ is given by the instantaneous amplitude correlation matrix, that is, $W\left(t\right)=\mathrm{IAC}\left(t\right)$. Furthermore, consider that ${\widehat{\mathrm{E}}}_{\mathrm{i}}\left(t\right)\ne \mathsf{0}$ for at least one region i. Then, the approximation $W_{\mathsf{apx}}\left(t\right)=W\left(t\right)$ if and only if there is a scalar $\gamma \left(t\right)>0$ such that the amplitude envelope vector $\widehat{\mathrm{E}}\left(\mathrm{t}\right)$ equals to

$$\widehat{E}\left(t\right)=\gamma \left(t\right)d$$ (8)

Here, $d={\left(d_1,\dots ,d_N\right)}^T$ dennotes the node strength vector of the structural connectome $A$. The proof of this proposition can be found in Data S1.

In other words, Proposition 1 states that the eigenmode approach Equation 5 is exact if and only if the envelope vector $\widehat{E}\left(t\right)$ is parallel to the degree vector $d$.

So far we have not considered leakage correction, but if we consider pairwise leakage correction, than the $\mathrm{IAC}\left(t\right)$ matrix will not exactly equal to the outer product in Equation 7. For almost all amplitude envelope vectors $\widehat{E}\left(t\right)$, condition of Equation 8 is not strictly satisfied, which implies that the eigenmode approach is not exact, that is, $W_{\mathit{apx}}\left(t\right)\ne W\left(t\right)$. We would like to know if relaxing condition of Equation 8 to

$$\widehat{E}\left(t\right)\approx \gamma \left(t\right)d$$ (9)

implies that $W_{\mathit{apx}}\left(t\right)\approx W\left(t\right)$. The formulation of Equation 9 is imprecise. Hence, instead of Equation 9, we consider the angle $\alpha$ between the two vectors $\widehat{E}\left(t\right)$ and $d$, which is defined by

$$\cos \left(\alpha \right)=\frac{{\widehat{E}}^T\left(t\right)d}{{‖{\widehat{E}}^T\left(t\right)‖}_2{‖d‖}_2}$$

$$=\frac{1}{{‖{\widehat{E}}^T\left(t\right)‖}_2{‖d‖}_2}\sum _{i=1}^N{d}_i{\widehat{E}}_{\mathrm{i}}\left(t\right).$$

Since the components of both vectors $\widehat{E}\left(t\right)$ and $d$ are nonnegative, it holds that $\cos \left(\alpha \right)\in \left[0,1\right]$. The closer $\cos \left(\alpha \right)$ is to 1, the larger the alignment of the envelope vector $\widehat{E}\left(t\right)$ and the structural degree vector $d$.

To quantify the goodness of the approximation $W_{\mathit{apx}}\left(t\right)$, we consider the relative two‐norm error

$$\mathrm{err}\left(W\left(t\right),W_{\mathit{apx}}\left(t\right)\right)=\frac{{‖W\left(t\right)-W_{\mathit{apx}}\left(t\right)‖}_2}{{‖W\left(t\right)‖}_2}$$ (10)

If the approximation $W_{\mathit{apx}}\left(t\right)$ is exact, then it holds that $\mathrm{err}\left(W\left(t\right),W_{\mathit{apx}}\left(t\right)\right)=0$. Further evaluation of $\mathrm{err}\left(W\left(t\right),W_{\mathit{apx}}\left(t\right)\right)$ will be demonstrated in the result section, which would hence answer whether $\widehat{E}\left(t\right)\approx \gamma \left(t\right)d$ indeed implies that $W_{\mathit{apx}}\left(t\right)\approx W\left(t\right)$.

2.7. Analytical approach: Phase connectivity

Likewise for amplitude connectivity, we are interested in the conditions for which eigenmodes of the graph Laplacian of the structural connectivity matrix form an accurate basis set for time‐varying phase connectivity. Unlike for amplitude connectivity (see Equation 7), the matrix $\mathit{PDD}\left(t\right)$ cannot be easily obtained by the outer product of the phase vector by itself. To obtain a simpler, approximate expression for the matrix $\mathit{PDD}\left(t\right)$, we define the $N\times 1$ phase derivative vector $\omega \left(t\right)$ with components

$${\omega }_i\left(t\right)=\frac{d{\phi }_i\left(t\right)}{\mathit{dt}}-\frac{1}{N}{\sum }_{j=1}^N\frac{d{\phi }_j\left(t\right)}{\mathit{dt}},\text{with}i=1,\dots ,N.$$ (11)

Thus, the vector $\omega \left(t\right)$ equals the derivative of the phase vector $\phi \left(t\right)$ plus offset, such that $u^T\omega \left(t\right)=0$. If the phases ${\phi }_j\left(t\right)$ change not too erratically, then the derivative $d{\phi }_i\left(t\right)/\mathit{dt}$ is small, which implies that the phase derivative vector $\omega \left(t\right)$ is small. For a small vector $\omega \left(t\right)$, we can approximate the phase difference derivative matrix $\mathrm{PDD}\left(t\right)$ by a simpler expression than Equation 2:

Lemma 2

For small phase derivatives $\omega \left(t\right)$ , the phase difference derivative matrix $\mathit{PDD}\left(t\right)$ in Equation 2 can be approximated by

$$\mathit{PDD}\left(t\right)\approx v\left(t\right)v^T\left(t\right).$$ (12)

Here, the $N\times 1$ vector $v\left(t\right)$ is given by

$$v\left(t\right)=\left(\begin{array}{c}{e}^{-{\omega }_1^2\left(t\right)}\\ ⋮\\ e^{-{\omega }_N^2\left(t\right)}\end{array}\right).$$ (13)

The proof can be found in Data S1.

In other words, Lemma 2 states that, for small phase derivatives ${\omega }_i\left(t\right)$, the matrix $\mathrm{PDD}\left(t\right)$ approximately equals the outer product $v\left(t\right)v^T\left(t\right)$. If the approximation of Equation 12 is exact, then we obtain the analogue of Proposition 1 for phase connectivity:

Proposition 3

Suppose that the functional connectivity matrix $\mathrm{W}\left(\mathrm{t}\right)$ equals the approximation of Equation (12) of the phase difference derivative matrix $\mathrm{PDD}\left(t\right)$, that is, $W\left(t\right)=v\left(t\right)v^T\left(t\right)$. Then, the approximation $W_{\mathrm{apx}}\left(t\right)$ equals $W\left(t\right)$ if and only if there is a scalar $\gamma \left(t\right)>0$ such that the vector $v\left(t\right)$ equals to

$$v\left(t\right)=\gamma \left(t\right)d.$$

Proof. By definition of Equation 13, all components of the vector $v\left(t\right)$ are positive. Hence, we can prove Proposition 3 analogously to Proposition 1, by formally replacing the amplitude envelope vector $\widehat{E}\left(t\right)$ by the vector $v\left(t\right)$.

Thus, Proposition 3 indicates that if the phase derivatives ${\omega }_i\left(t\right)$ satisfy $e^{-{\omega }_i^2\left(t\right)}=\gamma \left(t\right)d_i$ for some scalar $\gamma \left(t\right)$, then the approximation $W_{\mathrm{apx}}\left(t\right)$ of the phase connectivity matrix $\mathrm{PDD}\left(t\right)$ is accurate. Similar to the angle $\alpha$ in the previous section, we introduce the angle $\beta$ for phase connectivity as

$$\cos \left(\beta \right)=\frac{v^T\left(t\right)d}{{‖v\left(t\right)‖}_2{‖d‖}_2}$$ (14)

$$=\frac{1}{{‖v\left(t\right)‖}_2{‖d‖}_2}\sum _{i=1}^N{d}_i{e}^{-{\omega }_i^2\left(t\right)}.$$

Similar as for the amplitude, we will evaluate $\mathrm{err}\left(W\left(t\right),W_{\mathit{apx}}\left(t\right)\right)$ according to Equation 10 for phase connectivity in the result section as well. This again will imply that if $v\left(t\right)\approx \gamma \left(t\right)d$ it indeed implies that $W_{\mathit{apx}}\left(t\right)\approx W\left(t\right)$.

Propositions 1 and 3 show that the accuracy of the method is theoretically justified if the functional connectivity is proportional to the structural degree vector. Hence, the approximation is not meant to gain computation time, but to gain insight into the theoretical accuracy of our approach.

2.8. Numerical approach

The analysis pipeline is shown in Figure 1. In addition to the error metric formulated in the analytical approach (Equation 10), we used a goodness‐of‐fit metric that is more straightforward to interpret in the context of the current literature, namely the linear correlation expressed in the amount of explained variance, R ². Below, we outline the analysis steps that were carried out for both time‐varying amplitude and phase connectivity and for the canonical frequency bands (delta [1–4 Hz], theta [4–8 Hz], alpha [8–13 Hz], beta [13–30 Hz] and low gamma [30–48 Hz]).

1. We first analysed the extent to which the individual structural network, described by the matrix $A$, was mirrored in ongoing fluctuations of $W\left(t\right)$ of individual subjects. We computed the correlation for every $W\left(t\right)$ with $A$ for every subject, resulting in a time‐series of R ² with a size equal to $T$ (in seconds) × sampling frequency ($t=1,\dots .,T$).

2. We further evaluated whether the explained variance of $W\left(t\right)$ would remarkably increase if $W\left(t\right)$ was approximated by individual structural eigenmodes in terms of $W_{\mathrm{apx}}\left(t\right)$ (Equation 5). That is, the linear correlation between the observed $W\left(t\right)$ and the predicted $W_{\mathrm{apx}}\left(t\right)$ was computed for every point in time, and R ² was estimated. This procedure (again) resulted in a time‐series for the goodness‐of‐fit R ². Subsequent analysis steps all yield such a time‐series of goodness‐of‐fit R ².

FIGURE 1.

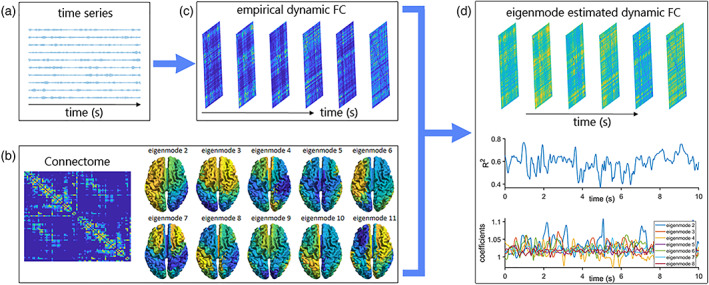
Analysis pipeline. Panel (a) shows an example of bandpass‐filtered timeseries. Panel (b) shows the group‐averaged connectome and the structural eigenmodes obtained from the symmetric normalised Laplacian of this connectome. The Laplacian is defined as ${\mathrm{Q}}_{\mathrm{A}}={\mathrm{K}}_{\mathrm{A}}-\mathrm{A}$, where the ${\mathrm{K}}_{\mathrm{A}}$ refers to the diagonal node strength matrix and $\mathrm{A}$ to the structural connectivity matrix. Normalisation is computed by ${\mathrm{Q}}_{\mathrm{As}}={{\mathrm{K}}_{\mathrm{A}}}^{-1/2}{\mathrm{Q}}_{\mathrm{A}}{{\mathrm{K}}_{\mathrm{A}}}^{-1/2}$. There is an increase in spatial frequency for increasing eigenmode numbers. Panel (c) shows the empirical dynamic functional connectivity (FC). Panel (d) shows the eigenmode‐estimated dynamic FC, along with the goodness‐of‐fit fluctuations over time and the fluctuations of eigenmode expression (coefficients) over time for an arbitrarily selected number of eigenmodes

To test the null hypothesis that relationships between structural eigenmodes and functional connectivity could be obtained by chance in a system with the same degrees of freedom, we created surrogate data by adding random Gaussian noise to the mapping coefficients on the diagonal of $P\left(t\right)$.

We evaluated whether the use of individual structural eigenmodes should be preferred over group‐averaged structural eigenmodes. We averaged the $A$ matrices across subjects to obtain a group‐averaged $A_{\text{group}}$ structural connectivity matrix. The Laplacian matrix of $A_{\text{group}}$ was computed and the eigenvectors of this Laplacian matrix were used for predictions for all individual $W\left(t\right)$.

• 3We repeated step 2. using MEG data from the same HCP subjects, but from a different recording session, with the purpose to validate the results of step 2 in a different data set.

Comparisons of R ² distributions between conditions (i.e., R ² [obtained from step 1] versus R ² [obtained from step 2, 3 or 4]) were performed using the Mann–Whitney U test.

To test the functional relevance of the a relationship between structural eigenmodes and time‐varying functional connectivity we extracted measures acknowledged to be important for ongoing cognitive functioning (Bassett et al., 2011; Bassett & Sporns, 2017), average functional connectivity and community structure. Global time‐dependent functional connectivity is described as $⟨W⟩\left(t\right)=\frac{1}{N\left(N-1\right)/2}\sum _{i,j=1,\dots ,N;j<i}{w}_{\mathit{ij}}\left(t\right)$. We also estimated for every time point t the community structure $Q\left(t\right)$, which describes the extent to which connectivity could be partitioned into communities. Community detection was evaluated using the Louvain algorithm with default parameters (Blondel et al., 2008). Hence, for both $⟨W⟩\left(t\right)$ and $Q\left(t\right)$ we obtained time‐series with the same dimensions as R ². We computed correlations between $Q\left(t\right)$ with R ² (obtained from step 1). We also computed the power spectral densities of $⟨W⟩\left(t\right)$, $Q\left(t\right)$, and R ² by taking the square of the absolute value of the Fourier coefficients of the respective time‐series in order to get some insight into the temporal dynamics of these state variables.

2.9. Stationary versus dynamic connectivity

We constructed surrogate data with preserved stationary (or static) connectivity to test the null‐hypothesis that eigenmodes map onto dynamic functional connectivity in a similar way as for surrogate data with static functional connectivity. A uniform phase randomisation method was used, that is, the same random numbers were added to the Fourier phases of all time time‐series (Prichard & Theiler, 1994). For every subject 10 surrogates were constructed. Both the PDD and IAC were computed from these surrogate data sets. Connectivity estimation from these surrogates are henceforth referred to as static or stationary connectivity. For both metrics we computed global functional connectivity in surrogate data $⟨W_{\mathit{\text{surr}}}⟩\left(t\right)$, which was compared to global functional connectivity $⟨W⟩\left(t\right)$ from genuine data. Time points corresponding to values of $⟨W⟩\left(t\right)$ from genuine data that lie in or outside the 1% tail of the distribution of $⟨W_{\mathit{\text{surr}}}⟩\left(t\right)$, were considered to be genuinely ‘dynamic’. For all these ‘dynamic’ time points we compared the eigenmode coefficients and R ² with the corresponding values obtained from surrogate data using the Mann–Whitney U test. In addition, we extracted dynamic network states using nonnegative tensor factorisation (Andersson & Bro, 2000; Gauvin et al., 2014) as in Tewarie et al. (2019b). The input for the nonnegative tensor factorisation were the connectivity matrices $W\left(t^{\prime }\right)$ for $t^{\prime }$ that were labelled as ‘dynamic’. The number of network states or components was determined based on the plateau of the goodness‐of‐fit as outlined in Andersson and Bro (2000) and Tomasi and Bro (2006). We approximated every network state using the eigenmode approach.

3. RESULTS

For illustration purposes, we show the first 11 eigenmodes of the Laplacian of the group‐averaged connectome in Figure 1, but all eigenmodes were used in the predictions of functional connectivity. The first eigenmode of the Laplacian is not shown as it could be considered as an offset with the same magnitude for all regions (see also Wang et al., 2017). The explained variance of the Laplacian of the group‐averaged connectome, for increasing numbers of incorporated eigenmodes, is shown in Figure S1.

3.1. Amplitude connectivity: An analytical approach

We analytically showed that the eigenmode prediction of amplitude‐based time‐resolved functional networks is accurate if and only if the vector $E\left(t\right)={\left[E_1\left(t\right),E_2\left(t\right),\dots ,E_N\left(t\right)\right]}^T$ containing the amplitude envelopes $E_i\left(t\right)$ across regions $i\in \left\{1,\dots ,N\right\}$ at a single time point is aligned (albeit with some angle $\alpha$) with the node strength vector of the structural network. This alignment can be verified by assessing the relationship between the goodness‐of‐fit of the eigenmode approach and the angle $\alpha$, that is, by the projection of the node strength vector onto the amplitude envelopes vector. Figure 2i shows the alignment in terms of a distribution of correlation values (between R ² and cos($\alpha$)) for all frequency bands, which indeed showed strong correlations for all bands (p < 0.001), indicating that predictions in the current work can be considered accurate.

FIGURE 2.

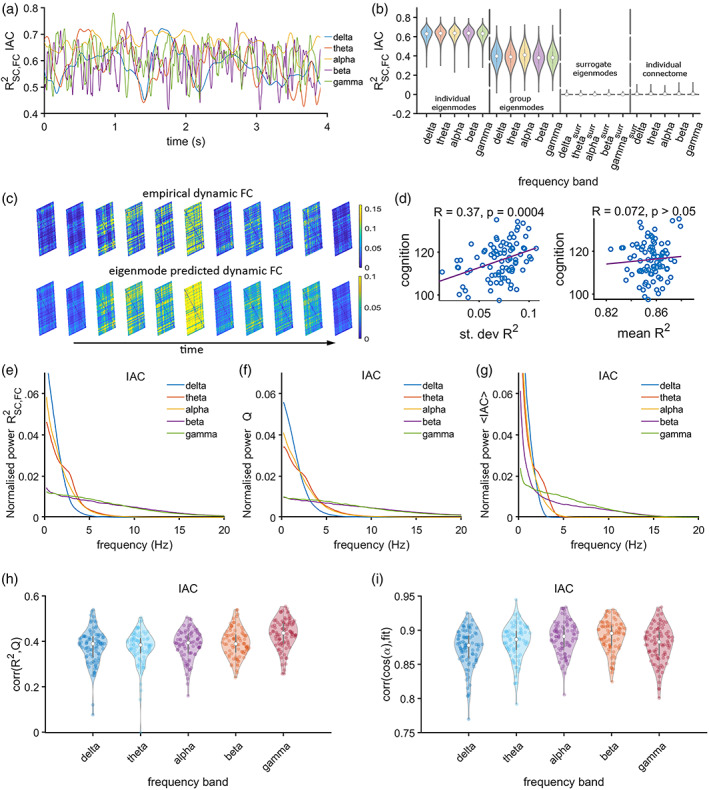
Expression of structural eigenmodes during time‐resolved amplitude coupling. Panel (a) shows a short segment of the fluctuation of the explained variance R ² of time‐resolved functional connectivity by the linear combination of structural eigenmodes for the different frequency bands (colours as in b). Panel (b) shows violin plots for R ² values across all participants for the entire recording, together with the R ² values for surrogate data and R ² values obtained from the prediction of time‐resolved functional connectivity based on direct structural connections (individual connectome). The eigenmode results are illustrated based on individual eigenmodes (first quadrant) and eigenmodes obtained from the group‐averaged connectome (second quadrant). Panel (c) shows examples of empirical and predicted time‐varying functional connectivity matrices. Panel (d) shows the correlation between mean and SD of the R ² and cognitive performance. Panels (e, f, g) show the power spectral densities of the time‐series of the goodness‐of‐fit R ² for experimental data, community structure Q and average functional connectivity, all averaged over subjects. Panel (h) shows a distribution of moderate correlations between the expression of the eigenmodes and fluctuations of community structure over time, across all frequency bands. Panel (i) shows subject‐wise correlations for the goodness‐of‐fit and the cosine of the angle between the degree vector and the amplitude envelope across all regions. A dot in panels (h, i) corresponds to a correlation for a single subject

3.2. Amplitude connectivity: A numerical approach

The goodness‐of‐fit, R ², expressed as the proportion of the variance of functional connectivity explained by the linear combination of individual structural eigenmodes (Figure 1), is illustrated for a short segment of the data of one representative subject (Figure 2a). This time‐series for R ² reflects the extent to which the eigenmodes are expressed in the functional connectivity patterns over time. The goodness‐of‐fit R ² fluctuates slower for the lower frequencies (delta, gamma) and faster for the higher frequencies (alpha, beta, gamma, see Figure 2a). The differences between frequency bands in terms of fluctuation‐frequency of R ² can also be observed from their respective power spectral densities (Figure 2e). A few examples of empirical and predicted time‐varying functional networks are illustrated in Figure 2c. The distributions of R ² across frequency bands and subjects are displayed in Figure 2b. We showed that there is a poor representation of direct structural connections (i.e., the connectome itself, instead of its eigenmodes) in time‐varying FC, as we observed very low correlations between the structural and functional connectivity at each time point, resulting in an average R ² close to zero (Figure 2b, fourth quadrant of the plot). Results show that predictions of time‐varying functional connectivity based on individual connectomes (R ² for the IAC modulates at around 0.6) outperformed predictions based on a group‐averaged connectome (R ² for the IAC modulates at around 0.4; Mann–Whitney U test, p < 0.001 for all frequency bands; Figure 2b). In order to verify that the obtained R ² could not have been obtained by chance, we tested the null hypothesis that a randomly weighted linear combination of the eigenmodes could explain functional connectivity patterns at each time point. The analysis revealed that the R ² based on the genuine mapping between structural eigenmodes and functional connectivity clearly outperformed the R ² for the surrogate data (Figure 2b, third quadrant); for all frequency bands a nonparametric test (Mann–Whitney U test) was performed, which revealed that the results for genuine data were significantly different from those obtained for surrogate data (p < 0.001). In other words, fluctuations in amplitude coupling across all frequency bands can partly be expressed by eigenmodes of the structural network. The R ² based on individual eigenmodes was replicated in the validation dataset (see Figure S2).

3.3. Amplitude connectivity: Functional relevance

Since structural eigenmodes may support functional subnetworks or communities (Atasoy et al., 2016), we tracked whether the time‐series of R ², such as shown in Figure 2a, co‐occurred with fluctuations in community patterns of time‐varying functional networks. Figure 2f,g shows the power spectral densities of community structure and global functional connectivity across regions for the different frequency bands for amplitude coupling. As was found for R ², community and global functional connectivity fluctuated slower in the lower than in the higher frequency bands. For all frequency bands and subjects, fluctuations in the expression of eigenmodes showed a significant moderate positive correlation with the fluctuations of community structure Q (Figure 2h).

The functional relevance of the fluctuations in R ² was further assessed by correlating the mean and SD of the time‐series of R ² to the overall cognitive performance across subject, where cognitive performance was quantified by the ‘cognition total composite’ score as obtained using the NIH toolbox (see Section 2). There was a moderate and positive statistically significant correlation between SD of R ² in the alpha band and cognitive performance across subjects (Figure 2d). Mean of R ² in the alpha band did not show a significant correlation (Figure 2d, right panel), nor SD or mean of R ² in any other frequency bands after correcting for multiple testing (Figure S3).

3.4. Amplitude connectivity: Stationary versus dynamic connectivity

To further pin down the dynamics of connectivity and corresponding eigenmode predictions, we compared static versus dynamic connectivity. This analysis shows that there are brief periods when time‐varying connectivity exceeds the level of static connectivity. This observation is illustrated for a single subject in the beta band in Figure 3a, which shows an example of whole brain connectivity fluctuations for the dynamic (blue curve) and static connectivity case (red curve), and when the dynamic connectivity exceeds the static connectivity (black). Time‐varying connectivity was again approximated by the eigenmode approach. For time points when dynamic connectivity did not exceed the magnitude of stationary connectivity, there was no significant difference in explained variance R ² or mapping coefficients $P\left(t\right)$ (Mann–Whitney U, p > 0.05). However, for the brief periods when dynamic connectivity exceeded the magnitude of stationary connectivity (time points t′), the first five eigenmodes were more dominant compared to those obtained for stationary connectivity (Figure 3c). However, the amount of explained variance was the same for the dynamic and stationary connectivity case (Figure 3b). We further estimated dynamic network states (or components) for time points t′, revealing a sensorimotor network, a lateralised hemispheric network, a right temporal network, a visual network and an occipitoparietal (visual)/frontal network (Figure 3e). Eigenmode predicted brain maps and mapping coefficients for these network states are shown in Figure 3f and d, which show that these states recruit eigenmodes with different weighting coefficients. For illustrational purposes, we showed results for the beta band, see Figure S9 and S11–S14 for results for the other frequency bands.

FIGURE 3.

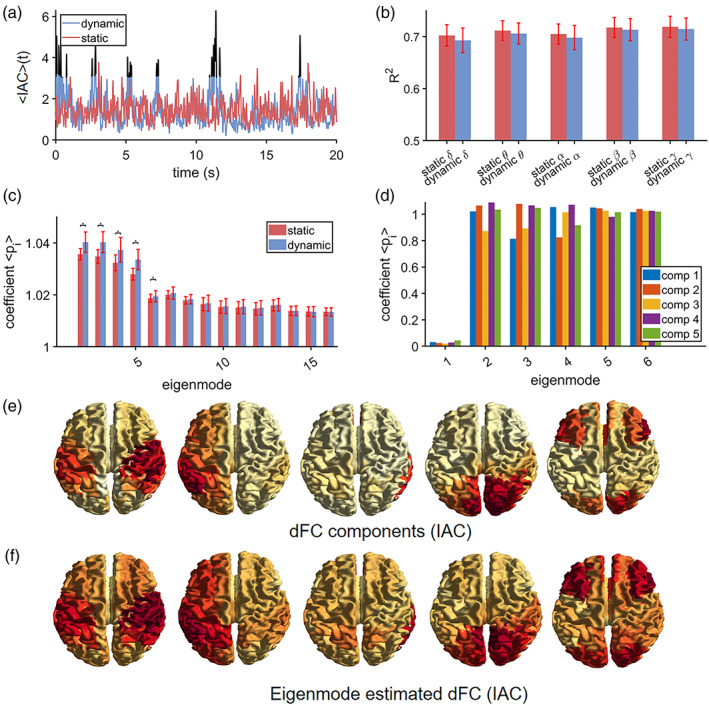
Stationary (static) versus dynamic connectivity (IAC). Results are, apart from panel (b), shown for the beta band. Panel (a) shows a short segment from a single subject of whole brain connectivity fluctuation for genuine data (dynamic connectivity, depicted in blue) and surrogate data with preserved static connectivity (depicted in red). There are brief periods when dynamic connectivity exceeds stationary connectivity (depicted in black). Panel (b) shows the goodness‐of‐fit (R ²) of the eigenmode approach for the stationary connectivity (red) and for the genuine data at time‐points when dynamic connectivity exceeded stationary connectivity (blue). For all frequency bands there is no difference in goodness‐of‐fit between stationary and dynamic connectivity. Panel (c) shows the estimated mapping coefficients for the same conditions as in (b). An asterisk refers to a significant difference (p < 0.001). Dynamic network states for time‐points when dynamic connectivity exceeded stationary connectivity are shown in (e), which shows a sensorimotor network, a lateralised hemispheric network, a right temporal network, a visual network and an occipitoparietal (visual)/frontal network. Eigenmode predicted brain maps and mapping coefficients are depicted in (f) and (d), respectively. $⟨{\mathrm{p}}_{\mathrm{i}}⟩$, average eigenmode coefficients; dFC, dynamic functional connectivity, comp., component, PDD, phase difference derivative, R ², explained variance

3.5. Phase connectivity: An analytical approach

We analytically showed that the eigenmode prediction of phase‐based dynamic functional networks is accurate only if a specific condition is met. This condition is based on similar reasoning as for the IAC (see Section 2.7). In this case, the eigenmode prediction of phase connectivity is accurate if the node strength vector of the structural network is aligned (albeit with some angle $\beta$) with a vector $v\left(t\right)=\left[v_1\left(t\right),v_2\left(t\right),\dots ,v_N\left(t\right)\right]$ containing PDD information $v\left(t\right)$ across regions $i\in \left\{1,\dots ,N\right\}$ at a single time point. Distributions of the strong correlations between the goodness‐of‐fit of the eigenmode approach and the alignment between the node strength vector and the PDD information are illustrated in Figure 4i. The high correlations (R > 0.7, p < 0.001) implicate that the condition for which the eigenmode approach is accurate was met. However, the correlations were lower than was the case for the instantaneous amplitude envelope correlation (compare Figures 2i and 4i).

FIGURE 4.

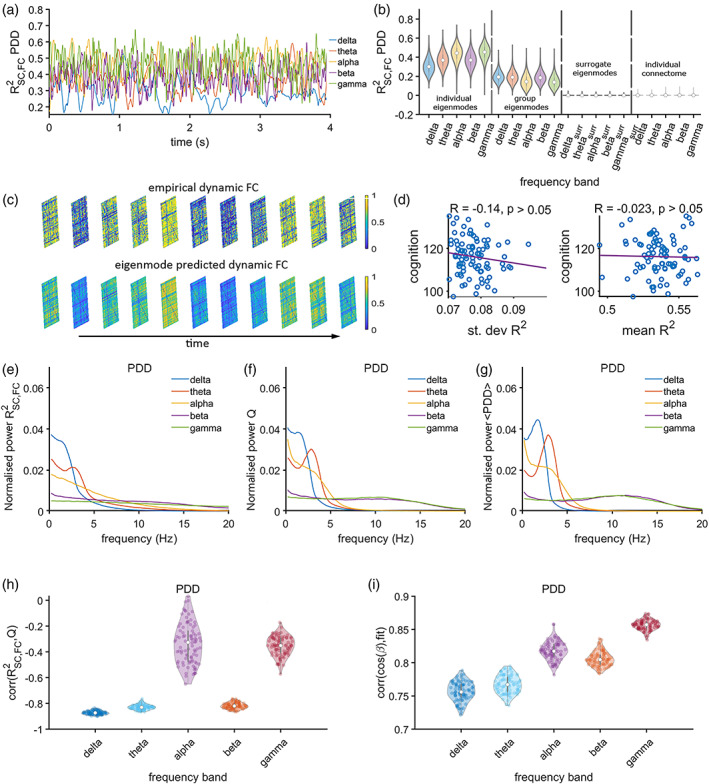
Expression of structural eigenmodes during time‐resolved phase coupling. Panel (a) shows a short epoch of the fluctuating proportion of the explained variance R ² of dynamic functional by the linear combination of structural eigenmodes for the different frequency bands (colours as in b). Panel (b) shows violin plots for R ² values across all participants and recording, together with the R ² values for surrogate data and R ² values obtained from the prediction of dynamic functional connectivity based on direct structural connections (individual connectome). The eigenmode results are illustrated based on individual eigenmodes and group average obtained eigenmodes. Panel (c) shows some examples of empirical and predicted time‐varying functional connectivity matrices. Panel (d) shows the correlation between mean and SD of the R ² and cognitive performance. Panels (e, f, g) show the power spectral densities of the time‐series of eigenmodes R ² for genuine data, community structure Q and average functional connectivity, all averaged over subjects. Panel (h) shows a distribution of moderate correlations between the expression of the eigenmodes over time and fluctuations of community structure across all frequency bands. Panel (i) shows subject wise correlations for the goodness‐of‐fit and the cosine of the angle between the degree vector and the vector encompassing the exponential of the phase derivative across all regions. A dot in (h, i) corresponds to a correlation for a single subject.

3.6. Phase connectivity: A numerical approach

Akin to the results for amplitude coupling, direct structural connectivity was hardly reflected in the fluctuations of phase connectivity (Figure 4b, fourth quadrant). A few examples of time‐varying functional networks and their predictions are illustrated in Figure 4c. Similarly, as for the IAC, temporal fluctuations of phase connectivity could partly be explained by fluctuations in the expression of structural eigenmodes (see Figure 4a for an example of a time‐series for R ²). This finding was strengthened by the demonstration that there was far a better prediction of varying functional connectivity when using genuine data instead of surrogate data (Figure 4b): for all frequency bands a nonparametric test (Mann–Whitney U test) showed that results with genuine data were significantly different from those obtained with surrogate data (p < 0.001). Again, predictions based on individual eigenmodes outperformed predictions based on group‐average‐based eigenmodes (Mann–Whitney U, p < 0.001 for all frequency bands). The R ² based on individual eigenmodes was replicated in the validation data set (Figure S4). However, the extent to which phase‐based connectivity modulations could be explained by the eigenmodes was smaller than for amplitude‐based connectivity (compare Figures 2b and 4b, Mann–Whitney U, p < 0.001). Modulations of the eigenmode expression for the phase coupling were faster than for amplitude coupling, as can be observed for an exemplar short epoch from a single subject (Figure 4a), and from the power spectral density of the fluctuations of R ² (compare Figures 4e and 2e). The main difference with amplitude coupling is the much smaller contribution of the very slow fluctuations of R ² for the phase coupling. The same is true for fluctuations of community structure Q and average connectivity, denoted as $⟨\mathit{PDD}⟩$ (compare Figures 4f and 2f, and Figures 4g and 2g, respectively).

3.7. Phase connectivity: Functional relevance

Unlike for amplitude coupling, there was no correlation between SD or mean of R ² and cognitive performance for the alpha band (Figure 4d), or any other frequency band (Figure S5). In contrast to amplitude coupling, there was a negative and strong correlation between fluctuations in community structure and eigenmode expressions, except for the alpha and gamma band, which showed significant but moderate to weak negative correlations. Consecutive eigenmodes correspond to spatial configurations with increasing spatial frequency. Given the opposite sign of the correlations between eigenmode expressions and community structure (for some frequency bands) for amplitude and phase coupling, we investigated whether this discrepancy could be related to a different weighting of eigenmodes for the two different intrinsic modes of coupling. Figure S6 shows that eigenmode mappings of dynamic amplitude connectivity are indeed more strongly weighted by the first 10 to 15 eigenmodes (for all frequency bands) than is the case for phase coupling, that is, eigenmodes with lower spatial frequency are more expressed in amplitude coupling compared to phase coupling. This difference in eigenmode weighting could potentially explain the positive correlation with community structure for amplitude coupling and negative correlation for phase coupling.

3.8. Phase connectivity: Stationary versus dynamic connectivity

Stationary versus dynamic connectivity for PDD also shows brief periods when time‐varying connectivity exceeded the level of stationary connectivity. This is illustrated for the beta band in a single subject in Figure 5a. This figure demonstrates how whole brain connectivity fluctuates for the dynamic (blue curve) and stationary connectivity case (surrogate data; red curve). Time points when dynamic connectivity exceeded the stationary connectivity are depicted in black. For the set of time points when the null hypothesis of stationary connectivity could not be rejected, there was no significant difference in eigenmode prediction, both in terms of explained variance R ² and estimated mapping coefficients $\mathrm{P}\left(\mathrm{t}\right)$ (Mann–Whitney U, p > 0.05). For the time points when there was a significant increase in dynamic connectivity relative to stationary connectivity, there was a significant difference in both explained variance R ² and estimated parameters (Figure 5b,c). Results for the beta band are illustrated in Figure 5a,c,d–f, results for the other frequency bands can be found in Figure S10–S14. For the PDD, the explained variance was higher whenever dynamic connectivity exceeded stationary connectivity (Figure 5b). In the same way as for IAC, during these times, there was more dominance of the first five eigenmodes for the dynamic connectivity case compared to the stationary connectivity case. Estimation of dynamic network states (or components) revealed a sensorimotor network, a right temporal network, a visual network and a frontal network (Figure 3e). Eigenmode predicted brain maps and mapping coefficients for these network states are shown in Figure 3f and d, which show that also for PDD these states recruit eigenmodes with different weighting coefficients.

FIGURE 5.

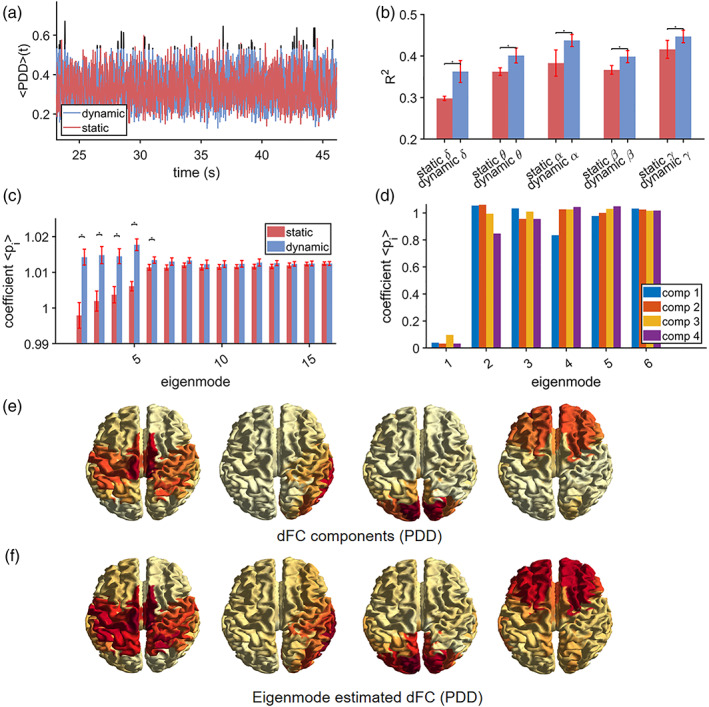
Stationary versus dynamic connectivity (PDD). Results are, apart from (b), shown for the beta band. Panel (a) shows a short segment from a single subject of whole brain connectivity fluctuation for genuine data (called dynamic connectivity depicted in blue) and surrogate data with preserved stationary connectivity (depicted in red). There were brief periods when dynamic connectivity exceeds stationary connectivity (depicted in black). Panel (b) shows the goodness‐of‐fit (R ²) of the eigenmode approach for the stationary connectivity case (red) and for the case whenever dynamic connectivity exceeded stationary connectivity (blue). For all frequency bands predictions are better for dynamic connectivity. Panel (c) shows the estimated parameters for the same conditions as in (b). An asterisk refers to a significant difference (p < 0.001). Dynamic network for time‐points when dynamic connectivity exceeded stationary connectivity are shown in (e), which shows a sensorimotor network, a right temporal network, a visual and frontal network. Eigenmode predicted brain maps and mapping coefficients are depicted in (f) and (d), respectively. $⟨{\mathrm{p}}_{\mathrm{i}}⟩$, average eigenmode coefficients; dFC, dynamic functional connectivity; comp., component, PDD, phase difference derivative, R ², explained variance

4. DISCUSSION

How fluctuations in functional connectivity are shaped by the underlying structural network remains an open research question. On the one hand, it is widely argued that hierarchical organisation captured in structural networks gives rise to a diversity of functional connectivity patterns across multiple timescales. On the other hand, modelling studies claim that for shorter timescales a decoupling between structural and functional connectivity would occur, the so‐called structure–function discrepancy (Ton et al., 2014). The current work demonstrates that there is hardly any signature of direct structural connections present within time‐varying functional connectivity patterns. However, there is clear expression of the various structural eigenmodes in the dynamics of functional connectivity, for both amplitude and phase coupling, but to a higher extent in amplitude than in phase connectivity fluctuations. There were brief periods when time‐varying functional connectivity deviated significantly from stationary connectivity. For amplitude connectivity, dynamic and stationary functional connectivity during these brief periods could equally well expressed in terms of eigenmodes. While for phase connectivity, dynamic functional connectivity could be better explained by a weighted combination of eigenmodes than stationary functional connectivity. For both modes of coupling, eigenmodes were differentially during deviations from stationary connectivity. In addition, predictions based on individual connectomes clearly outperformed predictions based on a group‐averaged connectome. Our results further show that fluctuations in the expression of the eigenmodes relate to cognitive performance and fluctuate to some extent in synchrony with fluctuations of community structure, further underlining the functional relevance of time‐varying expressions of the structural eigenmodes.

Despite the observation that the structural network itself was hardly expressed during time‐varying functional connectivity, to some extent structural eigenmodes were always expressed in dynamic functional connectivity, which ranged from low expressions to moderate expressions. Since the pattern of structural connectivity is fixed, this description of the structural connectome seems to be insufficient to describe fluctuations in functional connectivity. It is probably rather the case that a set of structural connections are being used at the functional level at some point in time while others are unused. Clustering approaches would potentially be able to capture such sets of structural connections that subserve function and it is an open question whether there would be a clear relationship between eigenmodes and sets of structural connections activated at different time points. At least, the eigenmode approach is a data‐driven and relatively assumption‐free way to capture such information. We used surrogate data to show that the extent to which the variance of functional connectivity could be explained by the eigenmodes was not merely the result of high degrees of freedom in the prediction.

Stationary versus dynamic connectivity analysis revealed that ongoing functional connectivity can mostly be described by a stationary process, but that there are brief periods when ongoing connectivity deviates from this stationary process. This was the case for both amplitude and phase connectivity. These findings seem in line with previous work on time‐resolved functional connectivity in MEG (De Pasquale et al., 2010), showing that dynamic network states reminiscent of the well‐known resting state networks usually occur during brief periods of time. During these periods of deviation from the stationary state we observed that especially the first five eigenmodes were more dominantly represented in the predictions compared to the stationary connectivity case. These five eigenmodes also differed in their expression for different dynamic network states. Hence, we can state that the evolution and dissolution of dynamic network states are characterised by differential recruitment of eigenmodes over time.

It remains an open question as to what the mechanism is that underlies the relationship between the temporally evolving functional connectivity and structural eigenmodes and why that differs between stationary and dynamic connectivity. Numerous previous studies have suggested that empirical functional connectivity emerges if the system operates near a phase transition for synchronisation, in a so‐called metastable state (Cabral et al., 2017a; Deco et al., 2017). From previous MEG modelling work, we know that in a network of neuronal oscillators the spatial pattern of functional connectivity is dominated by the first eigenmode (of the structural connectivity matrix) if the system operates at this phase transition (Tewarie et al., 2019a). In other words, the first eigenmode is the first pattern that gets activated or expressed when neuronal oscillators start to synchronise. However, if there are no conduction delays, this first eigenmode remains dominant and hence functional connectivity can be considered as a stationary process. However, once conduction delays are taken into account in the system, the first eigenmode can lose its stability and at the same time, other eigenmodes can become activated (Tewarie et al., 2019a). Hence, metastability and a system with conduction delays may be sufficient to explain the mechanism for eigenmodes to get activated and deactivated over time at the level of time‐varying functional connectivity.

Amplitude connectivity modulations were better predicted by the structural eigenmodes than fluctuations in phase connectivity (compare R ² values in Figure 3b and b). This was also verified from our analytical results for the accuracy of the eigenmode approach for the two intrinsic modes of functional connectivity (compare Figure 2j with 3j). There is no straightforward explanation for this difference. The reason can either be related to an intrinsic property of the brain, or due to extrinsic factors such as noise‐related issues, for example, phase slips or other noise factors in phase data can lead to noisy estimates of phase connectivity, especially when computing the derivative of the phase difference. In order to evaluate whether less noisy phase connectivity could better be predicted by individual structural eigenmodes, we reanalysed the structure–function mappings by denoising time‐varying phase connectivity by using only the first 10 eigenmodes of the time‐varying functional networks instead of the complete FC connectivity matrix, similarly as in Cabral et al. (2017b). The results remained qualitatively the same as those obtained without denoising (Figure S7), indicating that noise may not be the sole factor driving a weaker correlation between structural eigenmodes and time‐varying phase connectivity. The overlapping and complementary nature of phase‐ and amplitude‐based connectivity remains complex. Some previous work suggest that amplitude connectivity is more dominant in resting‐state data and task independent (Hipp et al., 2012), while phase connectivity seem to be highly task dependent (Helfrich et al., 2016). It remains an open question whether this could relate more decoupling between structure and function for phase connectivity.

Some methodological issues warrant further discussion. Our eigenmode approach is based on a few main assumptions: firstly, we assume that functional connectivity on top of the structural network behaves linearly, which allows for a well understood analytical relationship between functional connectivity and the eigenmodes of the structural network (Tewarie et al., 2020). There is previous work suggesting that time‐varying functional connectivity (based on fMRI BOLD) requires nonlinear dynamics (Hansen et al., 2015), however, there is also evidence that linear models already explain a significant part of the variance of functional connectivity (Messé et al., 2015; Raj et al., 2020; Tewarie et al., 2019a). Hence, although linear models may not capture all information, they do provide good approximations. Secondly, this approach assumes separation of timescales, that is, dynamics of functional networks are sufficiently fast compared to the evolution of the structural network such that the latter can be considered to be static. Thirdly, we have assumed symmetric matrices for functional and structural networks. Taking into account directed functional connectivity would violate this assumption and would require handling of complex eigenvectors. Fourthly, we have assumed the same dimension for structural and functional networks, which given the spatial resolution of different imaging modalities may not necessary be the case. Besides the eigenmode approach, several approaches have also been successful in explaining the emergence of resting‐state functional networks from the underlying structural network (Suárez et al., 2020; Avena‐Koenigsberger et al., 2018), including approaches that use coupled neural mass models (Cabral et al., 2017a; Deco & Kringelbach, 2016). The advantage of the current approach is that it is not dependent on the choice of the model for the neurophysiology (Breakspear, 2017). Another promising approach is the analytical and linear graph spectral model of brain activity, which predicts both spatial and spectral features of neural activity based on a superposition of eigenmodes (Raj et al., 2020). In addition, a dominant view is that functional connectivity can be represented in terms of the sum of all possible walks on the underlying structural network, that is, the so‐called series expansion or communicability approach (Gilson et al., 2018; Robinson, 2012). However, recent work has proven that the eigenmode and series expansion approaches are equivalent (Robinson, 2019), but that due to numerical errors, the eigenmode approach should be preferred over the series expansion approach (Tewarie et al., 2020). Further, previous work has demonstrated that a limited set of eigenmodes could already explain a large proportion of the explained variance of the structural connectome (Figure S1), indicating that it may not be necessary to take all eigenmodes into account when predicting functional connectivity (Glomb et al., 2020; Tewarie et al., 2019a). However, since our analytical expression for the mapping between structure and function was based on the use of all eigenmodes (Tewarie et al., 2020), we also included all eigenmodes in the predictions in the current work. In our previous work, using a system with known ground truth, we have shown that current high‐temporal‐resolution‐metrics outperform metrics based on sliding windows, although it remains an open question whether the time‐varying network states obtained using the current method are generalizable and comparable to, for example, stated obtained using Hidden Markov modelling. A future study on the comparison of these methods could shed light on this. Lastly, we applied pairwise orthogonalisation (Hipp et al., 2012) rather than symmetric orthogonalisation (Colclough et al., 2015). Pairwise orthogonalisation may come with spurious connectivity especially if sources are densely sampled over the cortex (Palva et al., 2018). However, the use of symmetric orthogonalisation changes the signal‐to‐noise in the data in such a way that the underlying modulations in functional connectivity are much harder to capture (see Figure S8).

In summary, we have demonstrated that structural connectomes are hardly reflected directly in time‐varying functional networks at the individual level. Our findings provide compelling evidence in support of the structure–function decoupling hypothesis at faster timescales. Moreover, we show for the first time in empirical data and analytically that the formation and dissolution of temporally evolving network states can be understood in terms of differential recruitment of eigenmodes over time. This could play a role in the dynamic integration and segregation of information across the cortex, subserving cognitive functions.

CONFLICT OF INTEREST

There were no competing or conflicting interests for any of the authors.

Supporting information

Figure S1 Explained variance of connectome by structural eigenmodes. The explained variance of the graph Laplacian is shown based on the first n number of eigenmodes. In other words, we analyse if an approximation ${\tilde{Q}}_{\mathit{AS}}={\sum }_{n=1}^K{\mu }_n{u}_n{u}_n^T$ is accurate for increasing K. Here, K is ranged from 1 to N (N is number of nodes), u _n and μ _n correspond to the eigenvectors and eigenvalues of the Laplacian Q _AS . The approximation ${\tilde{Q}}_{\mathit{AS}}$ is also known as truncated singular value decomposition of Q _A S of rank K, since the Laplacian is symmetric. Out of all possible matrices B with rank K, the matrix ${\tilde{Q}}_{\mathit{AS}}$ minimises the 2‐norm error: ${‖Q_{\mathit{AS}}-{\tilde{Q}}_{\mathit{AS}}‖}_2={\min }_B{‖B-Q_{\mathit{AS}}‖}_2$.

Figure S2: Validation of findings on expression of structural eigenmodes during modulation of amplitude connectivity. A different recording session from the same HCP subjects was used as a validation set for findings in the main article. Panel (a) shows a short epoch of the modulation of the proportion of the variance R ² of dynamic functional connectivity by the linear combination of structural eigenmodes for the different frequency bands (colours as in b). Panel (b) shows R ² values across all participants and recordings. Note that the eigenmode results were based on predictions from individual eigenmodes (i.e., not group‐averaged eigenmodes). Panels (c, d, e) show the power spectral densities of the timecourses of R ², community strength Q and average functional connectivity, all averaged over subjects.

Figure S3: Correlations of R ² for amplitude connectivity and overall cognition. Results show scatterplots between overall cognition and SD and mean of the R ² (time series of the explained variance of time varying amplitude connectivity based on the structural eigenmodes) for all frequency bands. Only SD of R ² for the alpha band remained significant after Bonferroni correction (five frequency bands × two statistical measures × two intrinsic modes of connectivity = 20, yielding a threshold of p < 0.0025). Single stars denote significant correlations (p < 0.05) before corrections for multiple testing, and double stars denote significant correlations after correction for multiple testing.

Figure S4: Validation of findings on expression of structural eigenmodes during modulation of phase connectivity. A different recording session from the same HCP subjects was used as a validation set for findings in the main article. Panel (a) shows a short epoch of the modulation of the proportion of the variance R ² of dynamic functional connectivity by the linear combination of structural eigenmodes for the different frequency bands (colours as in b). Panel (b) shows R ² values across all participants and recordings. Note that the eigenmode results were based on predictions from individual eigenmodes (i.e., not group‐averaged eigenmodes). Panels (c, d, e) show the power spectral densities of the timecourses of R ², community strength Q and average functional connectivity, all averaged over subjects.

Figure S5: Correlations of R ² for phase connectivity and overall cognition. Results show scatterplots between overall cognition and SD and mean of the R ² (time series of the explained variance of time varying phase connectivity based on the structural eigenmodes) for all frequency bands. There were no significant correlations.

Figure S6: weighting coefficients of the eigenmodes for dynamic connectivity. Results show the distribution of weighting coefficients over subjects for the different eigenmodes and frequency bands for both dynamic amplitude connectivity (IAC) and dynamic phase connectivity (PDD). A divergent pattern for especially the first 10–15 eigenmodes can be observed for phase versus amplitude connectivity, but also for the eigenmodes 35 and higher.

Figure S7: Re‐analysis of findings on expression of structural eigenmodes during modulation of phase connectivity using denoised functional connectivity matrices. Here, we analysed exactly the same data as in the main manuscript shown in Figure 4. However, since phase connectivity data can be noisy, we denoised the time varying connectivity as follows: For every t, we assumed that $\tilde{W}\left(t\right)$ is an approximation of the functional connectivity matrix W(t), where $\tilde{W}\left(t\right)={\sum }_{n=1}^{10}{\lambda }_n{v}_n{v}_n^T$, where v _n and λ _n are the eigenvectors and eigenvalues of W(t). Hence, we assume that only taking into account the first 10 eigenmodes of the functional connectivity matrix is a good approximation of W(t), as in Cabral et al. (2017) and Tewarie et al. (2016). By doing so, results are not qualitatively different to results in main manuscript Figure 3 though. Panel (a) shows a short epoch of the modulation of the proportion of the variance R ² of dynamic functional by the linear combination of structural eigenmodes for the different frequency bands (colours as in b). Panel (b) shows R ² values across all participants and recordings. Note that the eigenmode results were based on predictions from individual eigenmodes. Panel (c) shows a distribution of moderate correlations between the expression of the eigenmodes over time and modulations of modularity across all frequency bands. Panel (d) shows low and negative correlations between the expression of the eigenmodes and average phase connectivity (average across regions). Lastly, Panel (e) shows subject wise correlations for the goodness‐of‐fit and the cosine of the angle between the degree vector and the vector encompassing the exponential of the phase derivative across all regions. Note that a dot in panels (c,d, e) corresponds to a correlation from a single subject.

Figure S8: pairwise versus symmetric orthogonalisation for time‐varying connectivity. We performed simulations to demonstrate the amount of loss of genuine information on dynamic connectivity after pairwise versus symmetric orthogonalisation for different levels of SNR. To isolate the problem of effects of SNR on the dynamic connectivity estimation, we analysed this in the ideal situation in a neural mass model in the absence of leakage. Exactly as in Liuzzi et al. (2019) we used coupled Jansen‐Rit neural mass models (Jansen and Rit 1995) using the same parcellation as the empirical data (Tzourio‐Mazoyer et al., 2002). We included conduction delays to allow for nonzero phase coupling (see Liuzzi et al., 2019). The neural mass model was fed with a structural connectivity tensor (Network size × Network size × Time), where time refers to the duration of the simulation. At every point in time, the structural connectivity tensor was characterised by a resting‐state network pattern (default mode, sensorimotor network frontoparietal network and visual network, see figure 2 in Liuzzi et al., 2019). We added noise to the data to simulate different levels of SNR in exactly the same way as (Lobier et al., 2014; Tewarie et al., 2019). SNR was defined as $\mathrm{SNR}=20{\log }_{10}{y}_s/y_n$, where y _s is the mean amplitude of the neural mass signal and y _n the mean amplitude of the noise. Noise signals S _n (t) were obtained by a uniform phase randomisation of the original neural mass signal S _j (t). These noise signals are subsequently added to the original signal as S _jn (t) = Sj(t) + cS _n (t), where c = 10^−SNR/20. For every simulation we computed the IAC on the simulated neural mass signals (i.e., ground truth IAC). We then computed the IAC after pairwise and symmetric orthogonalisation (Colclough et al., 2015). The IAC tensors for all three conditions (no correction, pairwise and symmetric correction) were vectorised. Pearson correlations were computed between (1) IAC from the simulated signal and IAC after pairwise correction; (2) IAC from the simulated signal and IAC after symmetric correction. The correlation with original simulated signal was much lower for multivariate symmetric orthogonalisation than for pairwise orthogonalization (see figure below). This result shows that you require much higher SNR to obtain the same correlation with the ground truth as pairwise correction. Hence, for timevarying connectivity, it is a challenge to balance between correcting for spurious connectivity and retaining enough data with high‐enough SNR to enable estimation of time‐varying connectivity that captures the underlying ground truth.

Figure S9: Eigenmode coefficients for IAC. We show the eigenmode coefficients for all frequency computed for time points when time‐varying IAC exceeded stationary connectivity. Stars refer to a significant different expression of that eigenmode compared to the stationary case.

Figure S10: Eigenmode coefficients for PDD. We show the eigenmode coefficients for all frequency computed for time points when time‐varying PDD exceeded stationary connectivity. Stars refer to a significant different expression of that eigenmode compared to the stationary case.

Figure S11: Dynamic network states delta. Dynamic network states are shown for both the IAC and PDD and eigenmode predictions for both connectivity measures. Results for both PDD and IAC show dominant frontal, central, parieto‐temporal and occipital networks.

Figure S12: Dynamic network states theta. Dynamic network states are shown for both the IAC and PDD and eigenmode predictions for both connectivity measures. Results for both PDD and IAC show dominant frontal, occipitoparietal, hemispheric and occipital networks.

Figure S13: Dynamic network states alpha. Dynamic network states are shown for both the IAC and PDD and eigenmode predictions for both connectivity measures. Results for both PDD and IAC show dominant frontal, sensorimotor, fronto‐parietal, hemispheric and occipital networks.

Figure S14: Dynamic network states gamma. Dynamic network states are shown for both the IAC and PDD and eigenmode predictions for both connectivity measures. Results for both PDD and IAC show dominant frontal, parieto‐temporal and occipital networks.

Figure S15: Consistency of eigenmode mappings between sessions. For both sessions of HCP data we report the mean, minimum and maximum of the explained variance across subjects. No differences were found between sessions.

Data S1. Supporting Information

Tewarie, P. , Prasse, B. , Meier, J. , Mandke, K. , Warrington, S. , Stam, C. J. , Brookes, M. J. , Van Mieghem, P. , Sotiropoulos, S. N. , & Hillebrand, A. (2022). Predicting time‐resolved electrophysiological brain networks from structural eigenmodes. Human Brain Mapping, 43(14), 4475–4491. 10.1002/hbm.25967

DATA AVAILABILITY STATEMENT

Data that was included in this paper was obtained from the human connectome database, and included all subjects with resting‐state MEG data.