Abstract
Individual differences among human brains exist at many scales, spanning gene expression, white matter tissue properties, and the size and shape of cortical areas. One notable example is an approximately 3-fold range in the size of human primary visual cortex (V1), a much larger range than is found in overall brain size. A previous study (Andrews et al., 1997) reported a correlation between optic tract (OT) cross-section area and V1 size in postmortem human brains, suggesting that there may be a common developmental mechanism for multiple components of the visual pathways. We evaluated the relationship between properties of the OT and V1 in a much larger sample of living human brains by analyzing the Human Connectome Project (HCP) 7 Tesla Retinotopy Dataset (including 107 females and 71 males). This dataset includes retinotopic maps measured with functional MRI (fMRI) and fiber tract data measured with diffusion MRI (dMRI). We found a negative correlation between OT fractional anisotropy (FA) and V1 surface area (r = −0.19). This correlation, although small, was consistent across multiple dMRI datasets differing in acquisition parameters. Further, we found that both V1 surface area and OT properties were correlated among twins, with higher correlations for monozygotic (MZ) than dizygotic (DZ) twins, indicating a high degree of heritability for both properties. Together, these results demonstrate covariation across individuals in properties of the retina (OT) and cortex (V1) and show that each is influenced by genetic factors.
SIGNIFICANCE STATEMENT The size of human primary visual cortex (V1) has large interindividual differences. These differences do not scale with overall brain size. A previous postmortem study reported a correlation between the size of the human optic tract (OT) and V1. In this study, we evaluated the relationship between the OT and V1 in living humans by analyzing a neuroimaging dataset that included functional MRI (fMRI) and diffusion MRI (dMRI) data. We found a small, but robust correlation between OT tissue properties and V1 size, supporting the existence of structural covariance between the OT and V1 in living humans. The results suggest that characteristics of retinal ganglion cells (RGCs), reflected in OT measurements, are correlated with individual differences in human V1.
Keywords: diffusion MRI, functional MRI, optic tract, primary visual cortex, structural covariance, white matter
Introduction
Human brains differ on many levels, including gene expression, morphology of macroscale anatomical landmarks, tissue properties of cortical areas and white matter tracts, size of cortical areas, and perceptual performance. One notable example at the cm scale is primary visual cortex (V1), which varies in size between human brains by up to a factor of 3–4 (Stensaas et al., 1974; Andrews et al., 1997; Amunts et al., 2000; Dougherty et al., 2003; Schwarzkopf et al., 2011; Benson et al., 2021). These individual differences are not explained by variation in whole brain size (Andrews et al., 1997; Benson et al., 2020). Moreover, some studies have found that individual differences in V1 size can be related to properties of visual perception (Duncan and Boynton, 2003; Schwarzkopf et al., 2011; Song et al., 2013, 2015; Genç et al., 2015; Bergmann et al., 2016; Himmelberg et al., 2022). Understanding what factors influence individual differences in V1 size is likely to clarify our understanding of how human visual processing and perception vary across people.
One approach to improve understanding of individual differences is to measure covariance across brain regions (Dougherty et al., 2003; Mechelli et al., 2005). The logic is that if properties of two related structures covary, then these structures may mature by common mechanisms. Andrews and colleagues (1997) analyzed postmortem human brains to investigate the relationship between V1 and the optic tract (OT), a white matter tract composed of axons from retinal ganglion cells (RGCs). They found that V1 size was significantly correlated with OT size, suggesting that there are common factors determining individual variability in this fiber tract and V1. This study measured a relatively small number of postmortem brains. Here, we investigated similar questions in a much larger sample of living brains.
Recent progress in noninvasive neuroimaging methods have opened an avenue to quantify the structural properties of cortical areas and white matter tracts in living humans. Specifically, functional MRI (fMRI) enables the identification of visual field maps including V1 (Wandell and Winawer, 2011), whereas diffusion MRI (dMRI) and tractography enable one to measure properties of white matter tracts including the OT (Rokem et al., 2017). dMRI provides both macroscopic (tract volume) and microstructural measurements [such as fractional anisotropy (FA)], each of which provide complementary information about anatomical variability of white matter (Thiebaut de Schotten et al., 2011; Amemiya et al., 2021). By taking advantages of these two methods, it is possible to build a large neuroimaging dataset including both fMRI and dMRI data, thus enabling comparisons between them in a large sample (Van Essen et al., 2012). One such dataset is the Human Connectome Project (HCP) 7 Tesla Retinotopy dataset, which includes fMRI data on retinotopic mapping acquired at 7T and structural MRI and dMRI data acquired at 3T in 178 healthy young adults (Benson et al., 2018). In addition, this dataset includes data acquired from monozygotic (MZ) and dizygotic (DZ) twin pairs, enabling the assessment of heritability. Heritability is complementary to variability: heritability measures the contribution of genetics to individual differences, and hence addresses the question of where variability in neuroimaging measures arise (Benson et al., 2021).
In this study, we analyzed the HCP 7T Retinotopy dataset to investigate the structural covariance of V1 and OT in living humans to understand how much individual variability in human V1 size is related to properties of the OT. We identified V1 by combining fMRI with structural MRI data (Benson and Winawer, 2018) and the OT by analyzing dMRI data (Sherbondy et al., 2008). We then evaluated structural covariance between V1 size and macrostructural and microstructural measures of OT properties. Finally, we examined the heritability of each structure by analyzing twin data. This study has implications for the biological origin of individual differences in human V1 size, a key cortical area for distributing visual information to the rest of the brain.
Materials and Methods
Subjects
We analyzed data from 178 subjects (aged 22–35; 107 females, 71 males) whose structural MRI and dMRI data, as well as their retinotopic mapping fMRI data, were collected as part of the Young Adult HCP (Van Essen et al., 2013). Population receptive field models from the retinotopic mapping experiment were solved and published as a separate dataset (Van Essen et al., 2013; Benson et al., 2018). This dataset includes 53 MZ pairs and 31 DZ pairs. All subjects in the HCP dataset provided written informed consent. Further details of the dataset are described in previous publications (Van Essen et al., 2013; Benson et al., 2018).
MRI data acquisition and preprocessing methods
Structural MRI data acquisition and preprocessing
T1-weighted (T1w) structural MR images with an isotropic voxel size of 0.7 mm were acquired from a 3T MRI scanner and used for surface-based analysis of fMRI data as well as for identifying V1 in individual subjects. The dataset was preprocessed by the HCP consortium. This preprocessing included automated tissue segmentation implemented in FreeSurfer (Fischl, 2012) and reconstructing the white and pial cortical surfaces (Glasser et al., 2013).
dMRI data acquisition and preprocessing
We analyzed the dMRI dataset acquired by the HCP consortium. In brief, whole-brain dMRI data were corrected at an isotropic voxel size of 1.25 mm using 3T MRI. The dMRI data were preprocessed by the HCP consortium to correct eddy-current artifacts and susceptibility-induced image distortions (Andersson et al., 2003; Glasser et al., 2013; Andersson and Sotiropoulos, 2016). The dMRI data consists of three types of diffusion-weighted images (b = 1000, 2000, 3000 s/mm2) as well as nondiffusion weighted images (b = 0 s/mm2).
Tensor-based analysis
We divided the dMRI data into three datasets acquired with different b-values. We used b = 2000 s/mm2 as the test dataset. This choice of b-value reflects a trade-off between signal-to-noise ratio (SNR) and specificity: dMRI data acquired with lower b-value has higher SNR but weaker image contrast and less specific to the intracellular diffusion signal (Raffelt et al., 2012). The data acquired with other b-values were used as validation datasets to assess generalizability. We fit a tensor model to each voxel in the dMRI data using a least-squares algorithm implemented in mrDiffusion of vistasoft software (https://github.com/vistalab/vistasoft/). The tensor fits were then used to derive FA (Basser and Pierpaoli, 1996).
Neurite density and orientation dispersion imaging (NODDI) analysis
We used NODDI (Zhang et al., 2012) to evaluate tissue properties of the OT. NODDI is a model assuming multiple types of microstructural environment and aims to provide biologically meaningful parameters from dMRI signals. We fit NODDI to the whole dMRI dataset including all b-values using the NODDI MATLAB toolbox (http://mig.cs.ucl.ac.uk/index.php?n=Tutorial.NODDImatlab). From these fits, we obtained intracellular volume fractions (ICVF) and the orientation dispersion index (ODI).
fMRI image acquisition and preprocessing
We used the fMRI data already preprocessed by the HCP Consortium with the HCP pipelines (Glasser et al., 2013; Vu et al., 2017; Benson et al., 2018). In brief, whole-brain fMRI data were collected at an isotropic voxel size of 1.6 mm using 7T MRI. During the fMRI data acquisition, subjects were instructed to perform a fixation task that required them to maintain gaze at the center of the screen; simultaneously, they were presented with retinotopic mapping stimuli. These stimuli were constructed from slowly moving apertures that contained dynamic colorful textures (Dumoulin and Wandell, 2008; Benson et al., 2018).
MRI data analysis methods
dMRI data analysis
Defining regions of interest (ROIs) for tractography
We identified ROIs for tractography based on T1w images in each individual subject. The optic chiasm was defined based on FreeSurfer's automated segmentation (Fischl, 2012). We then defined the lateral geniculate nucleus (LGN) ROIs manually by following streamlines found using deterministic tractography from a seed-region in the optic chiasm to their termination points. The LGN ROI is defined as a 4 mm radius sphere covering these endpoints (Takemura et al., 2019). We also identified the V1 ROI for tractography using the Brodmann area atlas implemented in FreeSurfer. We used this atlas, rather than V1 boundaries identified using fMRI data because, for the purpose of tractography, the larger Brodmann V1 ROI may improve the sensitivity of tractography for the purposes of identifying the optic radiation (OR). The V1 ROIs were redefined using functional data for the purpose of quantifying V1 size (see below; fMRI data analysis).
Tractography
We performed tractography on the dMRI data (with b = 2000 s/mm2) to identify the OT using ConTrack (Sherbondy et al., 2008). ConTrack is a probabilistic tractography method specifically designed for identifying visual white matter tracts by selecting the most probable path of the white matter tract connecting two ROIs. Specifically, we sampled 5000 candidate streamlines connecting the optic chiasm and the LGN ROIs in both hemispheres (angle threshold, 90°; step size, 1 mm; maximum streamline length, 80 mm). We then refined OT streamlines using the following criteria. First, we selected 100 streamlines with the highest scores in the ConTrack scoring process (Sherbondy et al., 2008). Second, we removed outlier streamlines with (1) length >3 SD longer than the median streamline length in the tract, or (2) position >3 SD away from the median position of the tract using AFQ MATLAB toolbox (Yeatman et al., 2012).
In addition to the OT, we also identified the OR. For the OR, we used ConTrack to generate streamlines connecting the LGN and V1 ROIs and to reject outlier streamlines (Takemura et al., 2019).
Estimating the cross-section area of the OT
We quantified the cross-section area of the OT to match the dependent measures from previous anatomical work (Andrews et al., 1997). To do this, we first identified voxels that intersected the OT streamlines in each coronal section of the dMRI data. We then multiplied the voxel size in the section (1.25 × 1.25 mm2) by the voxel count to calculate the cross-section area in each coronal section. Finally, we averaged the cross-section area across coronal sections to obtain the mean cross-section area of the OT in each individual subject. When averaging, we excluded the 10% of sections nearest the optic chiasm ROI and the 10% of sections nearest the LGN ROI. This reduces the possibility of including the optic chiasm or the LGN in our estimate of OT cross-section area. For comparisons with V1 data, we averaged the data from the left and right hemisphere of each individual subject.
Estimating the cross-section area of the OT adjusted for angle between the coronal section and OT
In addition, we also estimated OT cross-section area adjusted for the angle between the coronal section and OT based on the geometry of tilted cylinder (Kapitány et al., 2013):
where α is an angle between the coronal section and OT.
Evaluating tissue properties of the OT
We evaluated tissue properties of the OT using the AFQ MATLAB toolbox (Yeatman et al., 2012; Duan et al., 2015; Takemura et al., 2019). Briefly, we resampled each streamline to 100 equidistant nodes. Tissue properties (FA, ICVF, and ODI) were calculated at each node of each streamline. The properties at each node were summarized by taking a weighted average of the tissue measurements of each streamline within that node. The weight of each streamline was based on the Mahalanobis distance from the tract core to minimize partial voluming effects with tissue or cerebrospinal fluid outside the OT. We excluded the first and last 10 nodes from the calculation of the tissue property of the tract core to further reduce any partial voluming effects with neighboring structures, which often occur near the endpoints of the tract. We averaged data from the remaining 80 nodes to obtain a single-number summary of each tissue property (FA, ICVF, and ODI) for each subject. In the main analysis, the data from the left and right hemisphere were averaged to reduce noise for comparisons with V1. We performed the same analysis for the OR.
fMRI data analysis
Bayesian retinotopy analysis for identifying the V1 surface area
We measured the surface area of V1 in each subject by analyzing fMRI and structural MRI data. To do so, we first performed Bayesian analysis of retinotopic maps (Benson and Winawer, 2018), which combines traditional fMRI-based retinotopic mapping (Dumoulin and Wandell, 2008) with a retinotopic template (Benson et al., 2012, 2014). Specifically, this method identifies the retinotopic parameters of each surface vertex in visual cortex, as well as the boundaries between maps, using Bayesian inference in which structural MRI acts as a prior constraint and fMRI data as an observation. This analysis procedure has been demonstrated to reliably identify properties of the early retinotopic areas (V1/V2/V3) and is implemented in the publicly available neuropythy library (https://github.com/noahbenson/neuropythy).
The V1 ROIs were projected onto the mid-gray cortical surface mesh for measuring surface area. Surface area for each subject's V1 was calculated by summing the area of the mesh triangles and partial subtriangles they contained. In the main analysis, we averaged the surface areas of V1 across hemispheres to reduce noise for a comparison with the OT data.
Experimental design and statistical analyses
Statistical evaluation
Correlation between the OT and V1
We quantified the correlation between the OT measurements (cross-section area, FA, ICVF, and ODI) and V1 surface area by calculating the Pearson correlation coefficient between them. We report the P-value of the Pearson correlation and define the statistical significance as p = 0.0125, which is equivalent to p = 0.05 after Bonferroni correction for four comparisons. We note that this threshold might be too stringent for considering a correlation between FA and ODI (Zhang et al., 2012). While the main analysis was performed on the OT and V1 data averaged across hemispheres, we also separately analyzed the left and right hemisphere.
Correlation between OT measurements and SNR of MRI images
We performed a supplementary analysis to evaluate how much the OT measurements (cross-section area, FA, ICVF, and ODI) correlate with the SNR of MRI images. An accurate estimation of SNR for diffusion-weighted images is difficult because in these images, a loss of image signal intensity is associated with more diffusion, and the signal depends on the orientation of the motion probing gradient. Instead, we estimated the SNR of b = 0 images within the OT using the following equation comparing two b = 0 images (Reeder et al., 2005; Kida et al., 2016):
where SI (first image) is the mean signal intensity of the first b = 0 image within the OT. SD (subtracted image) is the standard deviation of signal intensity difference between first and second b = 0 images within the OT. We estimated the SNR of b = 0 image using this method by pooling the OT voxels in left and right hemispheres and calculated the Pearson correlation between SNR and OT measurements (cross-section area, FA, ICVF, and ODI) across subjects.
Evaluating interhemispheric correlation
We also tested the interhemispheric correlation of the OT measurements for evaluating the reliability of the measurement. To this end, we calculated the Pearson coefficient across hemispheres. We test interhemispheric correlations as a proxy for test-retest reliability on the assumption that the true values (without measurement noise) are highly correlated between hemispheres.
Evaluating test-retest reliability
We also analyzed the retest dMRI dataset acquired from 19 subjects who also participated in the retest scan. We then evaluated the test-retest reliability of OT measurements (cross-section area and FA) by calculating the intraclass correlation coefficient (ICC; Shrout and Fleiss, 1979) between the test and retest dataset.
Evaluating the influence of the inclusion of twin pairs on the correlation
We evaluated how much the inclusion of twin pairs, which may not be fully independent samples, affects the correlation between OT and V1. To perform this analysis, we generated a subsample of subjects in which we removed one member of each twin pair from the whole dataset and reassessed the OT-V1 correlation, leaving 94 subjects. Because either of the members of each twin pair could be removed, there are many to select the subset of subjects. Hence, we generated subsamples of 94 subjects 10,000 times, and each time calculated the OT-V1 correlation to obtain a distribution of the correlation coefficient after the removal of twin pairs. This distribution was compared with the null distribution of the correlation coefficient, which was obtained by randomly choosing 94 subjects 10,000 times (without regard to twin status) and shuffling the association between OT and V1 data.
Evaluating heritability
We evaluated the heritability, i.e., the fraction of the variance for a given trait that is attributable to genetics, of the OT FA and of the surface area of V1 by comparing the correlations of these measurements between MZ twin-pairs to the correlations between DZ twin-pairs. We used the ICC when examining twin-pairs. We then employed Falconer's formula (Falconer and Mackay, 1996) to estimate OT FA and V1 surface area heritabilities:
where h2 is the heritability index and rMZ and rDZ are the ICCs between MZ pairs and DZ pairs, respectively.
Code accessibility
Code for reproducing figures and statistical analyses of this work is publicly available at a public repository (https://osf.io/t2kh3/). Codes were written in MATLAB 2015a and tested on Ubuntu 14.04 LTS. However, we cannot release data for reproducing the twin analyses because the family structure data belongs to the HCP's restricted dataset and thus cannot be shared without consent of the HCP Consortium. To reproduce analysis requiring family structure, researchers must apply for access to “Restricted Data” on ConnectomeDB (see https://www.humanconnectome.org/study/hcp-young-adult/document/wu-minn-hcp-consortium-restricted-data-use-terms).
Results
We identified V1 and the OT by analyzing fMRI, structural MRI, and dMRI datasets in the HCP Young Adult and the HCP 7T Retinotopy datasets (Fig. 1A,B), in 178 subjects. Similar to previous works (Stensaas et al., 1974; Andrews et al., 1997; Amunts et al., 2000; Dougherty et al., 2003; Schwarzkopf et al., 2011), and as reported recently for this dataset (Benson et al., 2020), there is a considerable degree of interindividual difference in V1 surface area, spanning a 2-fold range (Fig. 1C). Cross-section area and FA of the OT also exhibited considerable interindividual differences (Fig. 1D,E). In subsequent analyses, we focused on the relationship between individual differences of V1 and the OT in the HCP dataset.
Figure 1.
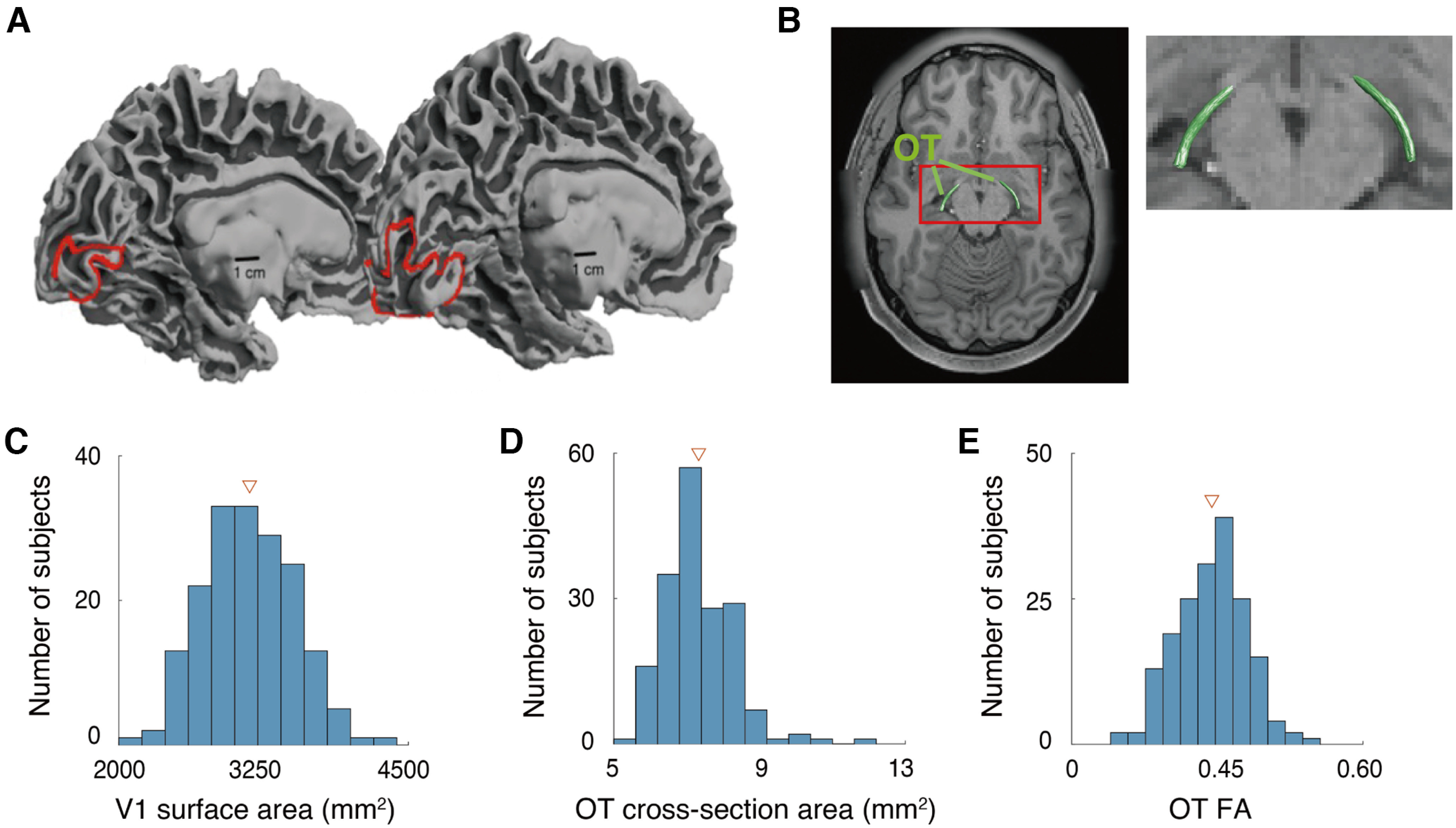
Individual variability of structural properties of the early visual system in human brains. A, Human V1 identified by fMRI-based retinotopy measurements. The locations of V1 in the left hemisphere of two subjects are shown as red lines on the mid-gray surface. The V1 surface area of these two hemispheres differs by a factor of 3.5 (left, subject 958976, 620 mm2; right, subject 100610, 2180 mm2). This image is adapted from Benson et al. (2020). B, Human OT of a representative subject (subject 100610), identified by dMRI-based tractography, overlaid on an axial slice of the subject's T1w image. The red rectangle on the left panel indicates the region that is magnified on the right. C–E, Histograms of the V1 surface area (C), OT cross-section area (D), and OT FA (E) of individual subjects (N = 178) averaged across the left and right hemispheres. Triangles in each plot depict mean across subjects.
Correlation between V1 surface area and OT cross-section area
We first examined the correlation between V1 surface area and OT cross-section area, because such a correlation was reported in postmortem anatomical work (Andrews et al., 1997). Figure 2 depicts a scatter plot comparing the V1 surface area and the OT cross-section area. We did not find a statistically significant correlation between these measurements (r = −0.05; p = 0.5). We also did not find evidence of correlation when we separately analyzed the data from left and right hemispheres (r = 0.09 and 0.01 for left and right hemispheres, respectively) and treating data of each hemisphere as independent samples (r = −0.02; as done by Andrews et al., 1997). Therefore, we failed to replicate the previous anatomical finding in an in vivo neuroimaging dataset. The correlation coefficient remained almost the same even after adjusting the OT cross-section area for the angle between the coronal section and the OT (r = −0.05).
Figure 2.
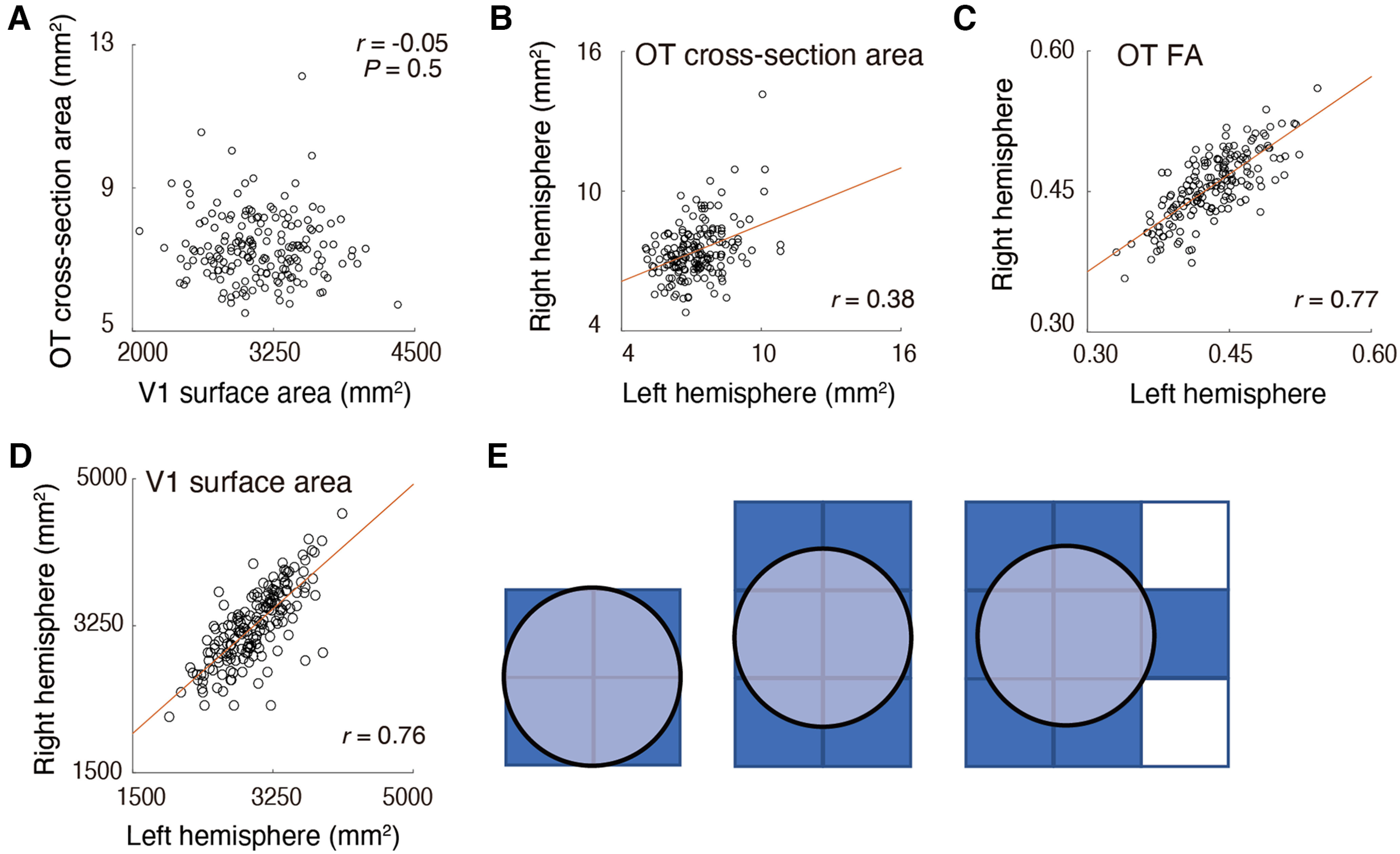
A, No significant correlation between V1 surface area (horizontal axis) and OT cross-section area (vertical axis). B–D, Interhemispheric correlation of OT cross-section area (B), OT FA (C), and V1 surface area (D). The OT cross-section area showed smaller interhemispheric correlation (r = 0.38) than OT FA (r = 0.77), presumably because of instability of dMRI-based measurements on the OT size. Red lines indicate linear regression lines. E, A schematic figure explaining how the spatial arrangement of voxels impacts the estimate of OT cross-section area when the spatial resolution of the measurements is limited. In all panels, the true cross-section area of the OT (light blue circle) is identical. However, the voxel count (dark blue) significantly differs across these three cases because of differences in the placement of the voxels (squares).
This result differs from Andrews et al. (1997)'s postmortem findings. It is unlikely that this mismatch occurs simply by chance, because when we randomly subsampled the HCP data into 29 samples (as used by Andrews et al., 1997), the probability of obtaining a correlation coefficient at least as high as Andrew and colleagues (1997; r = 0.48) is very low (p = 0.0006). The correlation obtained in this study (r = −0.06) is also outside of the 95% confidence interval of the correlation coefficient in Andrews et al. (1997) estimated by bootstrapping their data (r = 0.19–0.68).
One possible interpretation of this mismatch is that there is a high degree of measurement noise in our OT cross-section area estimates because of low spatial resolution. The voxel size of the dMRI dataset in the 3T HCP Young Adult dataset is 1.25 mm, isotropic. The cross-section area of the OT ranges from 5.1 to 11.3 mm2, according to Andrews et al. (1997). If we aim to estimate the volume of such a small tract with 1.25 mm voxel size, a large proportion of the OT voxels will be located on the border between the OT and neighboring tissue, and thus the estimates of OT size will depend on the placement of voxels (Fig. 2E). This will cause additional noise in the measurements and will mask true interindividual differences in OT size. In contrast, measurements of diffusivity properties, such as FA, are likely to be less prone to this issue because one can calculate a weighted summary of tract FA by minimizing the weight of voxels located far from the tract core (Yeatman et al., 2012).
One metric of reliability is interhemispheric correlations. We computed this for the OT cross-section area and FA. A key assumption in this analysis is that measurements of the left and right OT in the same subject should be similar. While this assumption is only likely to be approximately correct, it provides a reasonable estimate of reliability because interhemispheric correlation was very high in a previous postmortem study (r = 0.84, in data presented by Andrews et al., 1997). We found that the correlation between left and right OT cross-section areas was much smaller (r = 0.38) than that between left and right OT FA (r = 0.77). This difference in correlation coefficient was statistically significant (p < 0.001). In addition, we also evaluated reliability of OT measurements by analyzing retest dMRI data acquired from a subset of subjects (n = 19) who also participated in the retest scan. We also found that test-retest reliability (ICC) of OT cross-section area was much smaller (ICC = 0.60) than that of OT FA (ICC = 0.89). These results suggest that the OT cross-section area measurements based on dMRI are noisier than the FA measurements. We note that we obtained a high correlation between the left and right V1 surface area (Fig. 2D; r = 0.76). This result motivated us to investigate the correlation between V1 surface area and OT FA, because FA is a more robust measurement for characterizing individual differences in OT structural properties.
Correlation between V1 surface area and OT tissue properties
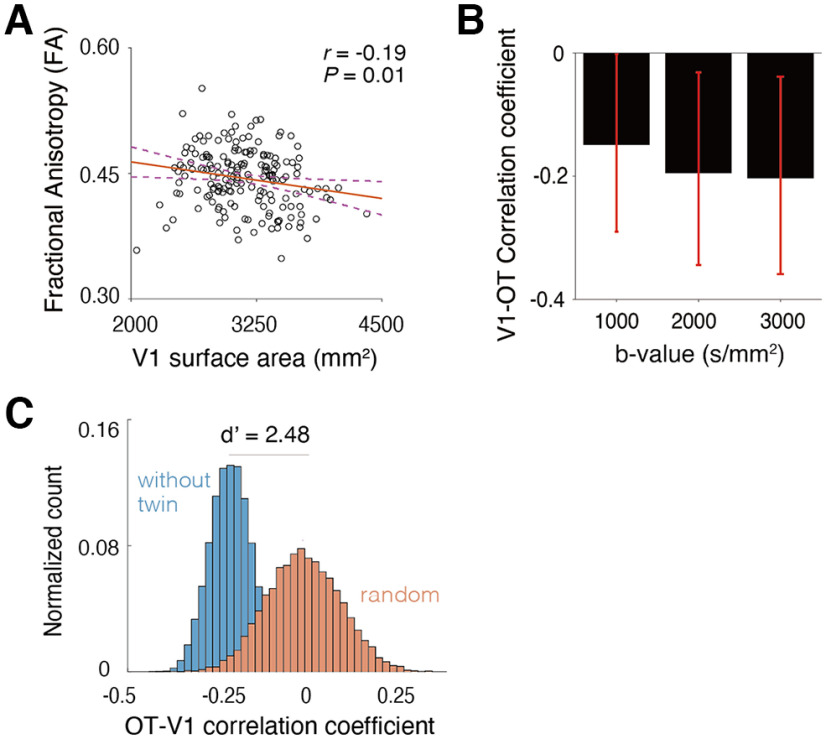
We investigated the correlation between V1 surface area and OT FA. Figure 3A depicts a scatter plot between these two quantities. We found a small, but statistically significant negative correlation between them (Fig. 3A; r = −0.19, p = 0.01), suggesting the existence of structural covariance between the surface area of V1 and tissue properties of the OT. The negative correlation was also observed when we performed a supplementary analysis separately analyzing data from the left and right hemisphere (r = −0.15 and −0.19 for left and right hemispheres, respectively).
Figure 3.
The correlation between V1 surface area and OT tissue property. A, A scatter plot of the V1 surface area (horizontal axis) and OT FA (vertical axis). The correlation between V1 surface area and OT FA was small, but statistically significant (r = −0.19, p = 0.009, N = 178). A red line indicates a linear regression line. The purple dotted curves indicate 95% confidence interval of a linear regression estimated by the bootstrapping. B, The correlation between V1 surface area and OT FA was replicated in dMRI data acquired with different b-values (b = 1000 s/mm2, weaker diffusion weighting; b = 3000 s/mm2, stronger diffusion weighting). The vertical axis depicts the correlation coefficient between V1 surface area and OT FA. We performed the bootstrap 10,000 times for each b-value to compute the 95% confidence interval of this probability. Error bars indicate this interval. C, Assessment of OT-V1 correlation when excluding twin subjects. The blue histogram indicates the probability density of the correlation coefficient between V1 surface area and OT FA when subsampling 94 subjects' data by avoiding the inclusion of both members of any twin pair. The red histogram shows the correlation coefficient when subsampling 178 subjects and shuffling the association between V1 surface area and OT FA. This histogram indicates that even if we exclude the effect of twin pairs (blue), the median correlation coefficient is almost equal to that of the main analysis (r = −0.21), and the distribution is clearly separate from that of random shuffling (d' = 2.48). The vertical axis of the histogram depicts the normalized count of correlation coefficient (from all shuffles) and the horizontal axis depicts the correlation coefficient between OT FA and V1 surface area.
We then asked whether this observed correlation in the main analysis, which used dMRI data acquired with b = 2000 s/mm2, generalizes. To this end, we performed the same analyses across different b-values (Lerma-Usabiaga et al., 2019). We found that the negative correlation between V1 surface area and OT FA is similar in other dMRI datasets with different acquisition parameters (Fig. 3B; b = 1000 s/mm2, r = −0.15; b = 3000 s/mm2, r = −0.20). This result suggests that the observed structural covariance between V1 and OT FA is unlikely to be because of measurement noise.
The HCP 7T Retinotopy dataset includes many twin subjects (see Materials and Methods) and twin pair subjects may show similar properties in OT and V1. We evaluated how much the inclusion of twin pairs in the dataset impacted the correlation between OT FA and V1 surface area. First, we randomly sampled 94 subjects from the whole dataset while avoiding the inclusion of twin pairs (for both MZ and DZ twins). We repeated this sampling procedure to generate many subsamples (see Materials and Methods). Then for each subsample we calculated the correlation coefficient between OT FA and V1 surface area (Fig. 3C, blue). The median correlation coefficient among subsamples was −0.21, which is comparable to that obtained in the main analysis of data from all subjects (Fig. 3A). The distribution of correlation coefficients among subsamples avoiding twin pairs (Fig. 3C, blue) significantly differs from the distribution of correlation coefficients when randomly shuffling the association between OT FA and V1 surface area (Fig. 3C, orange). This result suggests that a negative correlation in OT FA and V1 surface area (Fig. 3A) is preserved after excluding the impact of twin pairs.
We also investigated whether V1's observed structural covariance with OT generalized to the other visual white matter tract. To this end, we identified the OR, which is a geniculo-cortical pathway connecting the LGN and V1, from the dMRI dataset. We did not find a significant correlation between OR FA and V1 surface area, unlike with the OT (r = 0.04, p = 0.61). We also did not find a significant correlation between OR FA and V1 surface area when we separately analyzed each hemisphere (r = 0.002 and 0.07 for left and right hemisphere, respectively).
Possible microstructural basis of OT-V1 correlation evaluated by NODDI
While FA is a widely used metric with high reproducibility, it is based on a simplistic diffusion tensor model, and the interpretation of its microstructural origin is inherently ambiguous. To better understand the microstructural basis of the OT-V1 correlation, we used NODDI (Zhang et al., 2012), which is a multi-compartment model of dMRI data. NODDI enables one to estimate ICVF and ODI, which are thought to be correlated with neurite density and the orientation dispersion of fibers, respectively. Similar to FA, these metrics are strongly correlated between hemispheres (ICVF, r = 0.80; ODI, r = 0.85), suggesting high measurement reliability.
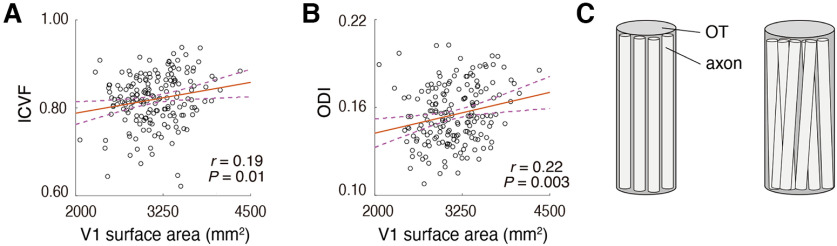
Figure 4 depicts scatter plots comparing V1 surface area and OT ICVF and ODI. We found a small, but statistically significant positive correlation with V1 surface area in both ICVF (Fig. 4A; r = 0.19, p = 0.01) and ODI (Fig. 4B; r = 0.22, p = 0.003). This result suggests that a negative correlation between FA and V1 surface area can be explained by greater axonal density and orientation dispersion in subjects with a larger V1 (Fig. 4C; see Discussion, Microstructural origin of OT-V1 correlation).
Figure 4.
The correlation between V1 surface area and microstructural properties of the OT as quantified by NODDI (A, ICVF; B, ODI). Other conventions are identical to those used in Figure 3A. C, A schematic figure explaining how the number and the spatial configuration of axons correlates with V1 surface area. The pattern of OT-V1 correlation raises the hypothesis that individuals with smaller V1 surface areas have fewer axons and reduced orientation dispersion (left panel) relative to individuals with larger V1 surface areas (right panel).
Evaluating the impact of SNR of the MRI image
We further investigated how the SNR of the MRI image may contribute to the observed correlation between V1 surface area and OT measurements. To this end, we quantified SNR of b = 0 image within the OT in each individual subject and quantified the correlation between SNR and each OT measurement (cross-section area, FA, ICVF, and ODI). Three of the metrics do not show significant correlation with SNR (r = 0.13, −0.02, and −0.07; p = 0.08, 0.81, and 0.33 for cross-section area, FA, and ODI); therefore, it is not very likely that SNR variability across individuals explains correlations related to these metrics. In contrast, OT ICVF showed significant correlation with SNR (r = −0.24; p = 0.0001).
To control the influence of SNR on OT ICVF, we calculated a partial correlation between V1 surface area and OT ICVF with the effect of SNR removed. We still observe a positive correlation similar to the main analysis (r = 0.16). Therefore, we think that an interindividual variability of SNR will not fully explain a positive correlation between V1 surface area and OT ICVF.
Heritability of human OT and V1 structural properties
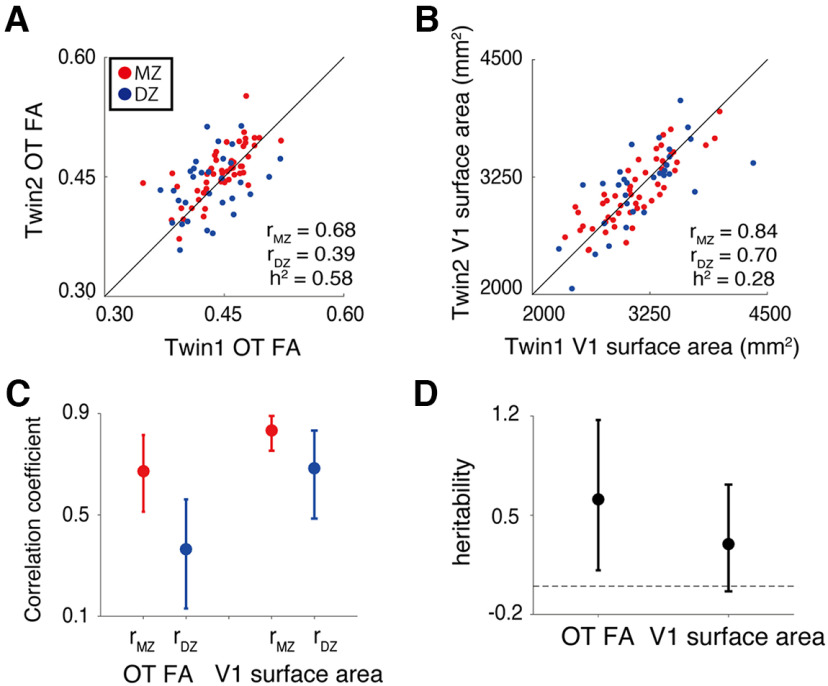
Finally, we evaluated the heritability of OT FA and V1 surface area to understand whether individual variability of these measurements derives from genetic factors. To this end, we evaluated the correlation of OT FA and V1 surface areas between MZ and DZ twin pairs and calculated the heritability index (Falconer and Mackay, 1996). For both V1 surface area and OT FA, correlations between MZ twins were higher than correlations between DZ twins, suggesting a considerable degree of heritability (Fig. 5A, Falconer's h2 = 0.58 for OT FA; Fig. 5B, Falconer's h2 = 0.28 for V1 surface area; for confidence intervals, see Fig. 5C,D).
Figure 5.
Heritability of structural properties of OT and V1 evaluated by analysis of twin data. The scatter plot depicts a comparison of twin pair data for OT FA (A) and V1 surface area (B). Red dots depict data from MZ twins whereas blue dots depict data from DZ twins. The black lines depict the line of equality (x = y). The heritability index (h2) was calculated by Falconer's formula of heritability based on ICC in MZ and DZ data (rMZ and rDZ). C. ICC of OT FA and V1 surface area across MZ (red) and DZ (blue) twin pairs. D, Falconer's heritability index (vertical axis) of OT FA and V1 surface area. In both panels C, D, error bars depict the 95% confidence interval estimated using 10,000 bootstraps.
Discussion
We evaluated the structural covariance between V1 and OT in living humans, which was hypothesized based on previous anatomical work (Andrews et al., 1997), by analyzing fMRI and dMRI data in the HCP Young Adult and the HCP 7T Retinotopy dataset. We did not find a significant correlation between OT size and V1 surface area, presumably because of the instability of the OT size measurements from the dMRI data (Fig. 2). In contrast, we found a significant negative correlation between V1 surface area and OT FA, and this correlation generalized across acquisition parameters (Fig. 3). Moreover, we found that a negative correlation between OT FA and V1 could be explained by individual differences in intracellular diffusivity and orientation dispersion along the OT (Fig. 4). Finally, we found that there is a considerable degree of heritability in both OT FA and V1 surface area (Fig. 5), suggesting that genetic factors influence both measurements.
Structural covariance between OT and V1 in living humans
In contrast to previous work (Andrews et al., 1997), we did not find a statistically significant correlation between OT cross-section area and V1 surface area (Fig. 2A). This is likely because the spatial resolution of dMRI data (voxel size; 1.25 mm isotropic) is not sufficient to robustly identify the cross-section area of the OT, which ranges from 5.1 to 11.3 mm2 in postmortem living brains (Andrews et al., 1997). If we assume that the OT cross-section area is comparable in the living human brain, the number of voxels covering OT in each coronal section should range from 3 to 7. Because the estimation of OT cross-section area significantly depends on the spatial arrangement of voxels and partial voluming with neighboring tissues (Fig. 2E), it is likely that measurements of the OT cross-section area are unstable at this spatial resolution. In fact, we also found the interhemispheric correlation of the OT cross-section area measurements from dMRI data to be low (r = 0.37; Fig. 2B), confirming that this measurement is unstable.
In contrast, OT FA can be reliably measured from this dataset because in the AFQ analysis pipelines, as used by Yeatman et al. (2012), the tract profile of FA was calculated by taking a weighted average where the weights were defined based on distance from the tract core (see Materials and Methods). This procedure is known to be highly reliable in terms of test-retest reliability (Kruper et al., 2021) and has successfully identified OT tissue abnormalities in retinal disease patients (Ogawa et al., 2014; Takemura et al., 2019). In fact, our results show that the interhemispheric correlation of OT FA is higher than that of OT cross-section area, suggesting that this is a more reliable dMRI-based metric for OT structural properties (Fig. 2C). Because OT FA is a reliable measurement and because the significant negative correlation between OT FA and V1 surface area (Fig. 3A) has been generalized across acquisition parameters (Fig. 3B), our results support the existence of structural covariance between the OT and V1 in living human brains.
Microstructural origin of OT-V1 correlation
FA is a fairly reproducible dMRI-based metric of white matter microstructure (Kruper et al., 2021), but it does not have a direct correlation with specific microstructural properties, such as the properties of axons and myelin (Wandell and Le, 2017; Assaf et al., 2019). Therefore, it is challenging to interpret the microstructural origin of the OT-V1 correlation solely from FA results (Fig. 3). One plausible hypothesis is that individuals with larger V1s have more RGCs, and therefore, those individuals will have more neurons in V1, which will result in greater V1 surface area. In fact, this hypothesis is supported by a correspondence of radial field asymmetries between retina and cortex at the population level (Kupers et al., 2022). If this is the case, the OT-V1 correlation may suggest that OT microstructural properties measured by dMRI are related to the number of RGCs. This interpretation remains speculative at this point, because the HCP 7T Retinotopy dataset does not have a direct measurement of RGCs.
One might wonder why the correlation between OT FA and V1 is negative, rather than positive, if the basis of individual differences are derived from differences in numbers of RGCs. To clarify this point, we used NODDI (Zhang et al., 2012), which is a multicompartment model providing ICVF and ODI, two properties that are hypothesized to be correlated with neurite density and orientation dispersion, respectively (Mollink et al., 2017; Schilling et al., 2018). We found that both ICVF and ODI along the OT showed a positive correlation with V1 surface area (Fig. 4A,B). This result is consistent with the interpretation that individuals with larger V1 have larger neurite density with more dispersed fiber orientations along the OT. This suggests that individuals with more RGCs are likely to have a larger number of axons (which might result in larger neurite density/ICVF), but the configuration of axonal orientation in such individuals may also be more dispersed than that of individuals with fewer RGCs (Fig. 4C). Regardless, this hypothesis requires further evaluation by anatomical studies, because the microstructural interpretation of NODDI has some degree of uncertainty (Jelescu et al., 2016). It is also known that there is substantial individual variation in acuity at the fovea and in cone density at the fovea (Curcio et al., 1987). An important open question is whether differences in OT properties and V1 surface area can be traced all the way back to the photoreceptor mosaic.
No evidence of correlation between or and V1
We did not find a significant correlation between OR FA and V1 surface area. This is counter-intuitive, because the OR includes axons that directly project to V1. We speculate that this lack of significance can be explained by the fact that the OR comprises heterogenous fiber populations. For example, it is known that the OR includes feedback axons from V1 to LGN (Ichida and Casagrande, 2002; Angelucci and Sainsbury, 2006). In addition, a recent anatomical study reported that axons from the pulvinar merge into the OR and follow a path similar to that of axons from the LGN (Takemura et al., 2020). Therefore, unlike the OT, in which all axons are feedforward axons from RGCs, feedforward axons can only explain a part of the variance in dMRI measurements along the OR. Resolving this uncertainty requires further anatomical investigations into how different axonal populations are spatially organized within the OR.
Possible underlying mechanism of structural covariance between OT and V1
While it is difficult to identify the underlying mechanisms of the structural covariance between OT and V1, there are, at minimum, several possible interpretations. First, because the OT does not contain feedback axons from V1, it is natural to infer that the OT influences V1, but that V1 would not conversely influence the OT. Accordingly, one hypothesis is that the development of the OT affects the maturation of V1, resulting in a correlation between them. The second possibility is that a common genetic factor affects the development of both OT and V1, resulting in structural covariance, without a direct relationship between the OT and V1.
Although these two possibilities are not mutually exclusive, we investigated the twin data included in the HCP 7T Retinotopy dataset to better interpret the structural covariance of the OT and V1. We found that MZ twin pairs had higher correlations than DZ twins (Fig. 5) for both the OT FA and V1 surface area, suggesting a considerable degree of heritability in these measurements. While the specific genetic factors contributing to the structural covariance between the OT and V1 remain uncertain, these results suggest that one plausible source of that covariance is common genetic factors. An extension of this study, by combining developmental neuroimaging and transcriptomics (Natu et al., 2021), may provide a more precise understanding of the developmental and genetic mechanisms of the structural covariance between the OT and V1.
In conclusion, we found a small, but statistically significant correlation between OT microstructural properties and V1 surface area. This correlation generalized across datasets acquired with different parameters. These results support the existence of structural covariance between the OT and V1, as hypothesized from previous anatomical work (Andrews et al., 1997). Because both the OT and V1 have a considerable degree of heritability, one plausible source of the structural covariance might be common genetic factors.
Footnotes
This work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers JP17H04684 and JP21H03789 (H.T.), the National Institute of Information and Communications Technology Project for Collaborative Research in Computational Neuroscience (CRCNS): Innovative Approaches to Science and Engineering Research on Brain Function (H.T.), and National Eye Institute CRCNS: Innovative Approaches to Science and Engineering Research on Brain Function (N.C.B. and J.W.). We thank Yusuke Sakai in support of data curation and analysis.
The authors declare no competing financial interests.
References
- Amemiya K, Naito E, Takemura H (2021) Age dependency and lateralization in the three branches of the human superior longitudinal fasciculus. Cortex 139:116–133. 10.1016/j.cortex.2021.02.027 [DOI] [PubMed] [Google Scholar]
- Amunts K, Malikovic A, Mohlberg H, Schormann T, Zilles K (2000) Brodmann's areas 17 and 18 brought into stereotaxic space—where and how variable? Neuroimage 11:66–84. 10.1006/nimg.1999.0516 [DOI] [PubMed] [Google Scholar]
- Andersson JLR, Sotiropoulos SN (2016) An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125:1063–1078. 10.1016/j.neuroimage.2015.10.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JLR, Skare S, Ashburner J (2003) How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 20:870–888. 10.1016/S1053-8119(03)00336-7 [DOI] [PubMed] [Google Scholar]
- Andrews TJ, Halpern SD, Purves D (1997) Correlated size variations in human visual cortex, lateral geniculate nucleus, and optic tract. J Neurosci 17:2859–2868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelucci A, Sainsbury K (2006) Contribution of feedforward thalamic afferents and corticogeniculate feedback to the spatial summation area of macaque V1 and LGN. J Comp Neurol 498:330–351. 10.1002/cne.21060 [DOI] [PubMed] [Google Scholar]
- Assaf Y, Johansen-Berg H, Thiebaut de Schotten M (2019) The role of diffusion MRI in neuroscience. NMR Biomed 32:e3762. 10.1002/nbm.3762 [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C (1996) Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B 111:209–219. 10.1006/jmrb.1996.0086 [DOI] [PubMed] [Google Scholar]
- Benson NC, Winawer J (2018) Bayesian analysis of retinotopic maps. Elife 7:e40224. 10.7554/eLife.40224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Butt OH, Datta R, Radoeva PD, Brainard DH, Aguirre GK (2012) The retinotopic organization of striate cortex is well predicted by surface topology. Curr Biol 22:2081–2085. 10.1016/j.cub.2012.09.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Butt OH, Brainard DH, Aguirre GK (2014) Correction of distortion in flattened representations of the cortical surface allows prediction of V1-V3 functional organization from anatomy. PLoS Comput Biol 10:e1003538. 10.1371/journal.pcbi.1003538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson N, Jamison K, Vu A, Winawer J, Kay K (2018) The HCP 7T retinotopy dataset: a new resource for investigating the organization of human visual cortex. J Vis 18:215. 10.1167/18.10.215 [DOI] [Google Scholar]
- Benson NC, Yoon JMD, Forenzo D, Engel SA, Kay KN, Winawer J (2020) Variability of the surface area of the V1, V2, and V3 maps in a large sample of human observers. bioRxiv. doi: 10.1101/2020.12.30.424856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Kupers ER, Barbot A, Carrasco M, Winawer J (2021) Cortical magnification in human visual cortex parallels task performance around the visual field. Elife 10:e67685. 10.7554/eLife.67685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergmann J, Genç E, Kohler A, Singer W, Pearson J (2016) Smaller primary visual cortex is associated with stronger, but less precise mental imagery. Cereb Cortex 26:3838–3850. 10.1093/cercor/bhv186 [DOI] [PubMed] [Google Scholar]
- Curcio CA, Sloan KR, Packer O, Hendrickson AE, Kalina RE (1987) Distribution of cones in human and monkey retina: individual variability and radial asymmetry. Science 236:579–582. 10.1126/science.3576186 [DOI] [PubMed] [Google Scholar]
- Dougherty RF, Koch VM, Brewer AA, Fischer B, Modersitzki J, Wandell BA (2003) Visual field representations and locations of visual areas V1/2/3 in human visual cortex. J Vis 3:586–598. 10.1167/3.10.1 [DOI] [PubMed] [Google Scholar]
- Duan Y, Norcia AM, Yeatman JD, Mezer A (2015) The structural properties of major white matter tracts in strabismic amblyopia. Invest Ophthalmol Vis Sci 56:5152–5160. 10.1167/iovs.15-17097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin SO, Wandell BA (2008) Population receptive field estimates in human visual cortex. Neuroimage 39:647–660. 10.1016/j.neuroimage.2007.09.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan RO, Boynton GM (2003) Cortical magnification within human primary visual cortex correlates with acuity thresholds. Neuron 38:659–671. 10.1016/s0896-6273(03)00265-4 [DOI] [PubMed] [Google Scholar]
- Falconer DS, Mackay TFC (1996) Introduction to quantitative genetics, Ed 4. Harlow: Longmans Green. [Google Scholar]
- Fischl B (2012) FreeSurfer. Neuroimage 62:774–781. 10.1016/j.neuroimage.2012.01.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genç E, Bergmann J, Singer W, Kohler A (2015) Surface area of early visual cortex predicts individual speed of traveling waves during binocular rivalry. Cereb Cortex 25:1499–1508. 10.1093/cercor/bht342 [DOI] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M; WU-Minn HCP Consortium (2013) The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80:105–124. 10.1016/j.neuroimage.2013.04.127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himmelberg MM, Winawer J, Carrasco M (2022) Linking individual differences in human primary visual cortex to contrast sensitivity around the visual field. Nat Comm 13:3309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ichida JM, Casagrande VA (2002) Organization of the feedback pathway from striate cortex (V1) to the lateral geniculate nucleus (LGN) in the owl monkey (Aotus trivirgatus). J Comp Neurol 454:272–283. 10.1002/cne.10441 [DOI] [PubMed] [Google Scholar]
- Jelescu IO, Veraart J, Fieremans E, Novikov DS (2016) Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed 29:33–47. 10.1002/nbm.3450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapitány K, Négyessy L, Barsi Á (2013) Tomographic reconstruction of micro-vascular network in cerebral cortical samples. Biomech Hung 6:1–12. 10.17489/biohun/2013/1/01 [DOI] [Google Scholar]
- Kida I, Ueguchi T, Matsuoka Y, Zhou K, Stemmer A, Porter D (2016) Comparison of diffusion-weighted imaging in the human brain using readout-segmented EPI and PROPELLER turbo spin echo with single-shot EPI at 7 T MRI. Invest Radiol 51:435–439. 10.1097/RLI.0000000000000248 [DOI] [PubMed] [Google Scholar]
- Kruper J, Yeatman JD, Richie-Halford A, Bloom D, Grotheer M, Caffarra S, Kiar G, Karipidis II, Roy E, Chandio BQ, Garyfallidis E, Rokem A (2021) Evaluating the reliability of human brain white matter tractometry. Apert Neuro. doi: 10.52294/e6198273-b8e3-4b63-babb-6e6b0da10669. 10.52294/e6198273-b8e3-4b63-babb-6e6b0da10669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kupers ER, Benson NC, Carrasco M, Winawer J (2022) Asymmetries around the visual field: From retina to cortex to behavior. PLoS Comput Biol 18:e1009771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerma-Usabiaga G, Mukherjee P, Ren Z, Perry ML, Wandell BA (2019) Replication and generalization in applied neuroimaging. Neuroimage 202:116048. 10.1016/j.neuroimage.2019.116048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mechelli A, Friston KJ, Frackowiak RS, Price CJ (2005) Structural covariance in the human cortex. J Neurosci 25:8303–8310. 10.1523/JNEUROSCI.0357-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollink J, Kleinnijenhuis M, van Cappellen van Walsum A-M, Sotiropoulos SN, Cottaar M, Mirfin C, Heinrich MP, Jenkinson M, Pallebage-Gamarallage M, Ansorge O, Jbabdi S, Miller KL (2017) Evaluating fibre orientation dispersion in white matter: comparison of diffusion MRI, histology and polarized light imaging. Neuroimage 157:561–574. 10.1016/j.neuroimage.2017.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natu VS, Rosenke M, Wu H, Querdasi FR, Kular H, Lopez-Alvarez N, Grotheer M, Berman S, Mezer AA, Grill-Spector K (2021) Infants' cortex undergoes microstructural growth coupled with myelination. Commun Biol 4:1191. 10.1038/s42003-021-02706-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Takemura H, Horiguchi H, Terao M, Haji T, Pestilli F, Yeatman JD, Tsuneoka H, Wandell BA, Masuda Y (2014) White matter consequences of retinal receptor and ganglion cell damage. Invest Ophthalmol Vis Sci 55:6976–6986. 10.1167/iovs.14-14737 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raffelt D, Tournier JD, Rose S, Ridgway GR, Henderson R, Crozier S, Salvado O, Connelly A (2012) Apparent Fibre Density: a novel measure for the analysis of diffusion-weighted magnetic resonance images. Neuroimage 59:3976–3994. 10.1016/j.neuroimage.2011.10.045 [DOI] [PubMed] [Google Scholar]
- Reeder SB, Wintersperger BJ, Dietrich O, Lanz T, Greiser A, Reiser MF, Glazer GM, Schoenberg SO (2005) Practical approaches to the evaluation of signal-to-noise ratio performance with parallel imaging: application with cardiac imaging and a 32-channel cardiac coil. Magn Reson Med 54:748–754. 10.1002/mrm.20636 [DOI] [PubMed] [Google Scholar]
- Rokem A, Takemura H, Bock AS, Scherf KS, Behrmann M, Wandell BA, Fine I, Bridge H, Pestilli F (2017) The visual white matter: the application of diffusion MRI and fiber tractography to vision science. J Vis 17:4. 10.1167/17.2.4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling KG, Janve V, Gao Y, Stepniewska I, Landman BA, Anderson AW (2018) Histological validation of diffusion MRI fiber orientation distributions and dispersion. Neuroimage 165:200–221. 10.1016/j.neuroimage.2017.10.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarzkopf DS, Song C, Rees G (2011) The surface area of human V1 predicts the subjective experience of object size. Nat Neurosci 14:28–30. 10.1038/nn.2706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherbondy AJ, Dougherty RF, Ben-Shachar M, Napel S, Wandell BA (2008) ConTrack: finding the most likely pathways between brain regions using diffusion tractography. J Vis 8:15–15. 10.1167/8.9.15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrout PE, Fleiss JL (1979) Intraclass correlations: uses in assessing rater reliability. Psychol Bull 86:420–428. 10.1037/0033-2909.86.2.420 [DOI] [PubMed] [Google Scholar]
- Song C, Schwarzkopf DS, Rees G (2013) Variability in visual cortex size reflects tradeoff between local orientation sensitivity and global orientation modulation. Nat Commun 4:2201. 10.1038/ncomms3201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song C, Schwarzkopf DS, Kanai R, Rees G (2015) Neural population tuning links visual cortical anatomy to human visual perception. Neuron 85:641–656. 10.1016/j.neuron.2014.12.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stensaas SS, Eddington DK, Dobelle WH (1974) The topography and variability of the primary visual cortex in man. J Neurosurg 40:747–755. 10.3171/jns.1974.40.6.0747 [DOI] [PubMed] [Google Scholar]
- Takemura H, Ogawa S, Mezer AA, Horiguchi H, Miyazaki A, Matsumoto K, Shikishima K, Nakano T, Masuda Y (2019) Diffusivity and quantitative T1 profile of human visual white matter tracts after retinal ganglion cell damage. Neuroimage Clin 23:101826. 10.1016/j.nicl.2019.101826 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takemura H, Palomero-Gallagher N, Axer M, Gräßel D, Jorgensen MJ, Woods R, Zilles K (2020) Anatomy of nerve fiber bundles at micrometer-resolution in the vervet monkey visual system. Elife 9:e55444. 10.7554/eLife.55444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiebaut de Schotten M, Dell'Acqua F, Forkel SJ, Simmons A, Vergani F, Murphy DG, Catani M (2011) A lateralized brain network for visuospatial attention. Nat Neurosci 14:1245–1246. 10.1038/nn.2905 [DOI] [PubMed] [Google Scholar]
- Vu AT, Jamison K, Glasser MF, Smith SM, Coalson T, Moeller S, Auerbach EJ, Uğurbil K, Yacoub E (2017) Tradeoffs in pushing the spatial resolution of fMRI for the 7T Human Connectome Project. Neuroimage 154:23–32. 10.1016/j.neuroimage.2016.11.049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, et al. (2012) The Human Connectome Project: a data acquisition perspective. Neuroimage 62:2222–2231. 10.1016/j.neuroimage.2012.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K; WU-Minn HCP Consortium (2013) The WU-Minn Human Connectome Project: an overview. Neuroimage 80:62–79. 10.1016/j.neuroimage.2013.05.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Winawer J (2011) Imaging retinotopic maps in the human brain. Vision Res 51:718–737. 10.1016/j.visres.2010.08.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Le RK (2017) Diagnosing the neural circuitry of reading. Neuron 96:298–311. 10.1016/j.neuron.2017.08.007 [DOI] [PubMed] [Google Scholar]
- Yeatman JD, Dougherty RF, Myall NJ, Wandell BA, Feldman HM (2012) Tract profiles of white matter properties: automating fiber-tract quantification. PLoS One 7:e49790. 10.1371/journal.pone.0049790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC (2012) NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61:1000–1016. 10.1016/j.neuroimage.2012.03.072 [DOI] [PubMed] [Google Scholar]