Semi-automated ventilation defect quantification in exercise-induced bronchoconstriction using hyperpolarized helium-3 magnetic resonance imaging: a repeatability study

Abstract

Rationale and Objectives:

To compare the performance of a semi-automated ventilation defect segmentation approach, adaptive K-means, with manual segmentation of hyperpolarized helium-3 magnetic resonance imaging (HP ³He MRI) in subjects with exercise-induced bronchoconstriction (EIB).

Materials and Methods:

Six EIB subjects underwent HP ³He MRI and spirometry tests at baseline, post-exercise, and recovery over two separate visits. Ventilation defects were analyzed by two methods. First, two independent readers manually segmented ventilation defects. Second, defects were quantified by an adaptive K-means method that corrected for coil sensitivity, applied a vesselness filter to estimate pulmonary vasculature and segmented defects adaptively based on the overall low-intensity signals in the lungs. These two methods were then compared in four aspects: 1) ventilation defect percent (VDP) measurements, 2) correlation between spirometric measures and measured VDP, 3) regional VDP variations pre- and post-exercise challenge and 4) Dice coefficient for spatial agreement.

Results:

The adaptive K-means method was ~ 5 times faster and the measured VDP bias was under 2%. The correlation between predicted forced expiratory volume in 1 second over forced vital capacity and VDP measured by adaptive K-means (ρ = −0.64, p < 0.0001) and by the manual method (ρ = −0.63, p < 0.0001) yielded almost identical 95% confidence intervals. Neither method of measuring VDP indicated apical/basal or anterior dependence in this small study cohort.

Conclusion:

Compared to the manual method, the adaptive K-means method provided faster, reproducible, comparable measures of VDP in EIB and may be applied to a variety of lung diseases.

Introduction

Over the past decade, hyperpolarized helium-3 magnetic resonance imaging (HP ³He MRI) has been used extensively in research for evaluating ventilation and defect in asthma (1–4), cystic fibrosis (CF) (5–7), and chronic obstructive pulmonary disease (COPD) (8–10). Quantitative assessment of ventilation and its regional distribution are critical to the application and advance of HP gas MRI in clinical research. The ventilation defect quantification from HP gas MRI has been advanced from subjective defect scores (11,12) to semi-quantitative measures (1) and quantitative defect volume measures (2,10,13–16). The commonly used quantitative metric is ventilation defect percent (VDP) (8,17). The defect quantification from gas images contains two main steps: 1) lung cavity segmentation and 2) defect measurements within the lung cavity. Although the manual defect segmentation demonstrated good interreader agreement (2), it is tedious, time consuming, and subjective. For automated lung cavity segmentation, Ray et al. (18) proposed merging active contours using the properties of fluid flow to segment the lung in each slice to obtain the total lung cavity volume. Tustison et al. (13) proposed a shape model based lung segmentation, which requires offline preprocessing to obtain the unbiased shape template. Guo et al (16) proposed to co-segment the lung cavity jointly from three-dimensional (3D) proton and ³He MRI pairs. For quantitative measures of defect from ³He MRI within the lung cavity, Tustian et al (13) used Atropos, to partition the lungs into ventilated and unventilated regions with optimal parameter settings. The hierarchical K-means method (10) showed good spatial agreement relative to manual segmentation on COPD and CF subjects and low spatial agreement on asthmatic subjects. Moreover, the histogram-based linear binning method (14) proposed for defect quantification on ¹²⁹Xe images has not been assessed for ³He images. Therefore, there is still a demand for a reliable, automated defect quantification method that is generally applicable for various lung conditions.

Three major confounding factors have made the defect quantification a difficult problem, especially in less-defected lungs. First, due to the inherent low-intensity presence on ³He image, pulmonary vasculature regions are likely to be misclassified as ventilation defects in computer-aided detection. Second, the intensity inhomogeneity due to the non-uniform coil sensitivities can jeopardize the accuracy of intensity-based segmentation algorithms. Third, highly defected lungs tend to have smaller signal-intensity variations, whereas less defected lungs tend to have more subtle signal heterogeneity requiring refined sub-classification. In particular, asthmatic lungs are known to have spatially heterogeneous patterns of ventilation (1). This makes quantitative defect measurement, especially in mild asthma, a more challenging problem than in cystic fibrosis (CF) or chronic obstructive pulmonary disease (COPD), where the ventilation defect is often persistent and focal. Therefore, a robust and reproducible defect quantification method for evaluating longitudinal progression and treatment response is of particular importance in asthma.

The most recent developments for an automated defect segmentation pipeline (13,14) include the exclusion of pulmonary vascular structure using the vesselness filter (19) and intensity correction of the gas images using retrospective bias correction (20). Therefore, we proposed an integrated adaptive K-means approach that improved on the hierarchical method by correcting for coil sensitivity, estimating pulmonary vasculature and detecting defects adaptively based on the percentage of overall low-intensity signals in the lungs.

Exercise-induced bronchoconstriction (EIB) describes airway narrowing that occurs after strenuous exercise. It occurs in a substantial proportion of patients with asthma (21). Previously, the reproducibility of HP ³He MRI was quantitatively evaluated by examining the interday and interreader agreement of manually assessed lung volume and ventilation defect volume in subjects with EIB (2). The objective of the present study was to evaluate the quantitative agreement in whole-lung and regional VDP for manual segmentation and the proposed adaptive K-means clustering, and to examine the effectiveness of the adaptive K-means method with respect to correlation with spirometric measures, VDP change before and after exercise-challenge, and repeatability of the exercise-induced variations at two separate visits.

Materials and Methods

Human Subjects

The study was conducted in accordance with Health Insurance Portability and Accountability Act regulations and was approved by our institutional review board. Six subjects (one male, mean ± age standard deviation for all subjects, 20.8 ± 1.3 years) with EIB were enrolled with written informed consent. Inclusion criteria were a prior diagnosis of EIB and a measured post-exercise forced expiratory volume in one second (FEV1) decrease that was greater than 15% on two separate days. At each of two visits, spirometry and HP ³He MRI were performed 3.5 hours before exercise (baseline), immediately after exercise (post-challenge) and 35 min after exercise (recovery). The 10-min exercise challenge was conducted in the room adjacent to the MRI scanner on a series 2000 TRUE treadmill (TRUE Fitness Technology, St. Louis, MO) with the subject’s heart rate maintained at 80%−90% of their age predicted maximum.

Spirometry

Spirometry was performed with an ndd EasyOne (ndd Medical Technologies, Andover, MA) spirometer. Measurements were taken with the subject seated in a chair directly adjacent to the treadmill. FEV1 and FEV1 over forced vital capacity (FEV1/FVC) were normalized to predicted values for sex, race, age and height from the Hankinson standard tables (22).

³He Polarization and Image Acquisition

All subjects underwent HP ³He MRI at 1.5T (SignaHDx, GE Healthcare, Milwaukee WI) on each visit. ³He was hyperpolarized by a Heli-Spin prototype commercial polarizer (Polarean, Inc., Durham, NC) using the spin-exchange optical pumping method described by Möller et al. (23). A 4.5 mmol per liter dose of HP ³He mixed with N₂ to 1 liter total volume was prepared in a Tedlar^® bag purged of oxygen to slow T₁ relaxation. The mean polarization level per dose was 10.5 ± 2.8%. While supine in the scanner, subjects inhaled the gas from functional residual capacity through a plastic tube with inner diameter of 3.2 mm attached to the bag. Images were acquired during a 16–20 second breath hold. Blood oxygen saturation was monitored by means of pulse oximetry, and 100% oxygen was delivered through a nasal cannula between imaging sequences to assist respiratory recovery.

A flexible wrap single channel volume coil (IGC Medical Advances, Milwaukee, WI) was used. HP ³He MRI used a fast two-dimensional (2D) gradient-echo sequence with the following parameters: echo time (TE) / repetition time (TR) = 1.1/3.6 msec; flip angle = 7º; field of view (FOV) = 40 × 40 cm; acquisition matrix = 128 × 128; slice thickness = 1.5 cm; 12–16 coronal slices. The images were reconstructed to a 256 square matrix with a voxel size of 1.56 × 1.56 × 15 mm.

Prior to the ³He MRI, proton MRI was acquired using a 2D single-shot multislice fast spin echo (SS-FSE) sequence under equivalent breath-hold conditions (functional residual capacity + ~1L) with the following parameters: TE/TR= 34/698 msec, echo train length = 128, percent sampling = 55%, percent FOV = 100%, and acquisition matrix, FOV, slice thickness, and position parameters all matching those of the ³He MRI.

Overview of the Defect Segmentation Pipeline

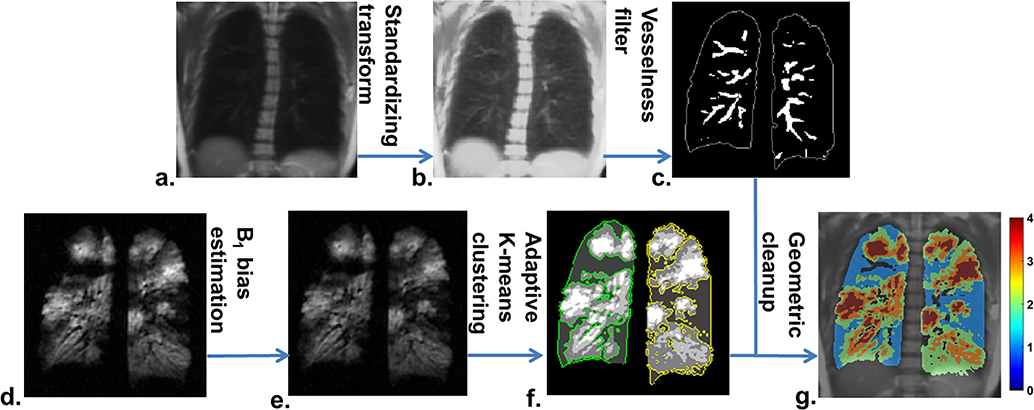
The proposed defect quantification using adaptive K-means is a multistep approach as illustrated in Figure 1. The segmentation pipeline is summarized here, with each step subsequently described in detail below. 1) The total lung volume was segmented using a region-growing algorithm from in-house software written in MATLAB (Mathworks, Natick, MA). 2) The proton image was registered to ³He using image registration based on manually selected landmarks similar to the hierarchical K-means method (10). 3) An intensity transform for standardizing the proton signal was followed by application of a vesselness filter to the registered proton image to obtain a binary pulmonary vasculature mask. 4) ³He image intensities were corrected using retrospective coil sensitivity estimation. 5) ³He images encompassing the lung volume were classified into 4–5 clusters by an adaptive K-means clustering algorithm. 6) The final defect mask was determined by excluding vascular pixels using the vasculature mask described in step 3 and removing low-signal bias along the lung periphery due to partial volume effect. The whole lung VDP is then calculated as the ventilation defect volume over total lung volume.

Figure 1.

The workflow of the adaptive K-means defect quantification: the registered proton image (a) was transformed to obtain a vessel-enhanced proton image (b). The vesselness filter was then applied to estimate the pulmonary vasculature (c). A retrospective coil sensitivity map was estimated from the raw ³He image (d) to obtain the intensity-corrected ³He image (e). The adaptive K-means clustering was applied for the initial ventilation defect segmentation (f) with the defects contoured in green and yellow for the right and left lungs. A morphometric correction step was used to correct the vessels and partial volume effect for the final ventilation map (g). Clusters 1 and 4 represent ventilation defects (blue) and highly ventilated regions (red).

Landmark-based Image Registration

Proton images were registered to ³He images using a landmark-based affine registration approach (24). The best available slice with the most anatomical detail from the ³He image stack and its corresponding proton image were displayed side-by-side. Six to ten landmarks were selected on the ³He image based on the trachea, primary bronchi, and boundaries of the diaphragm as well as other distinguishing features located inside or on the periphery of the lungs. The same landmarks were selected sequentially in the proton image. The resulting transformation matrix was computed and applied to the remaining proton slices.

Vasculature Estimation

The pulmonary vascular structure has low contrast relative to the lung cavities as shown in raw proton images (Figure 2a and e). Therefore, prior to application of the vesselness filter, a two-step standardizing transformation (25) was applied to enhance the tissue contrast in the lungs.

Figure 2.

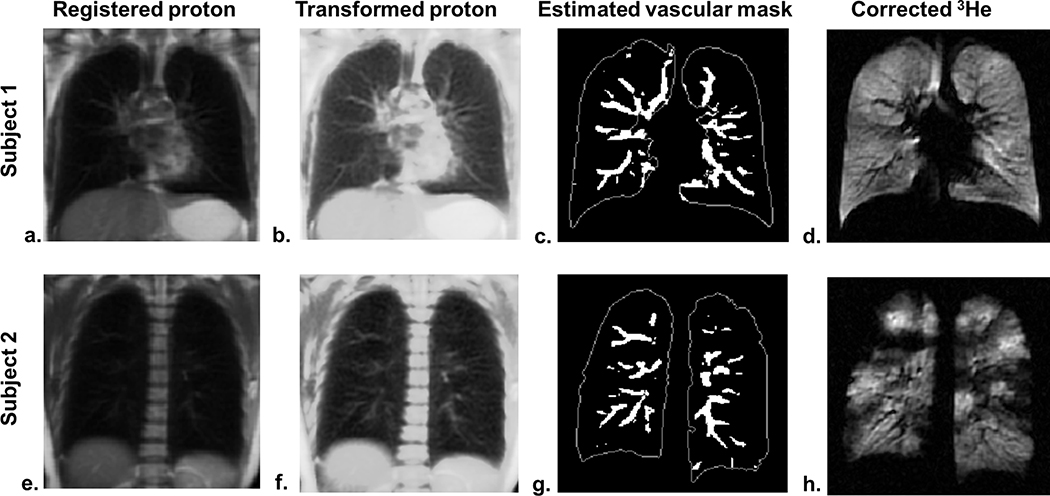
Estimation of the vascular mask. The pulmonary vasculature is not conspicuous in the registered proton images (a and e) and became more distinct on the contrast-enhanced proton images (b and f). The vessel-like object map estimated by the vesselness filter was thresholded to obtain the binary vascular mask (c and g) with the edge of the lung outlined in white solid lines. The vessels present as low-intensity pixels on the sensitivity-corrected ³He image in subject 1 (d) and a vessel is seen to merge into a large defect in subject 2 (h).

The first step is a training step. In a training set of 10 randomly selected EIB scans, the histogram of the proton image within the lungs was computed, and the intensity value μ_s corresponding to the histogram landmark (75% of maximum intensity) was calculated. The μ_s values from the 10 EIB scans were averaged to obtain the mean intensity value ${\overline{\mu }}_s$. The next step was a histogram transformation which mapped the intensity value μ_i corresponding to the 25% of the maximum intensity to ${\overline{\mu }}_s$. For a given proton image stack, the intensity value of every pixel, x, was then linearly mapped to the standard scale [s₁, s₂] using the expression,

$$T(x)=\{\begin{array}{ll}⌈{\overline{\mu }}_s+\left(x-{\mu }_i\right)\frac{s_1-{\overline{\mu }}_s}{p_1-{\mu }_i}⌉,\hfill & \mathrm{if}{p}_1\le x\le {\mu }_i\hfill \\ ⌈{\overline{\mu }}_s+\left(x-{\mu }_i\right)\frac{s_2-{\overline{\mu }}_s}{p_2-{\mu }_i}⌉,\hfill & \mathrm{if}{\mu }_i\le x\le p_2\hfill \end{array}$$

where ⌈∙⌉ denotes the ceiling operation that rounds up to the nearest integer, p₁ and p₂ denote the minimum and maximum intensity values in the lungs, and s₁ and s₂ were chosen as 1 and 512 respectively. This transformation highlights those relatively low-intensity pixels below the μ_i value. Consequently, the vascular structures on the contrast-enhanced proton images (Figure 2b and f) were more distinct relative to the raw proton images (Figure 2a and e).

After the intensity transformation, the vesselness filter was applied. First, the Hessian matrix was computed by the convolution of the 2D transformed proton image and the second order derivative of a Gaussian kernel with σ = 2.5 pixels. Second, the eigenvalues (λ₁ < λ₂) and vectors of the Hessian matrix were computed. The discriminant function (19) that enhances tubular structures while reducing the effect of other morphologies can be expressed as

$$V\left(R_A,R_B\right)=\exp \left(-R_A/\left(2{\alpha }^2\right)\right)\cdot \left(1-\exp \left(-R_B/\left(2{\beta }^2\right)\right)\right),$$

where $R_A={\left({\lambda }_2/{\lambda }_1\right)}^2$ and $R_B={\lambda }_1^2+{\lambda }_2^2$ Parameters α and β were selected as 0.5 and 15 respectively. A threshold < 0.15 was applied on V(R_A, R_B) to obtain the binary vasculature mask. The estimated vasculature masks (Figure 2c and g) were aligned with low-intensity vascular pixels in the corresponding ³He (Figure 2 d and h).

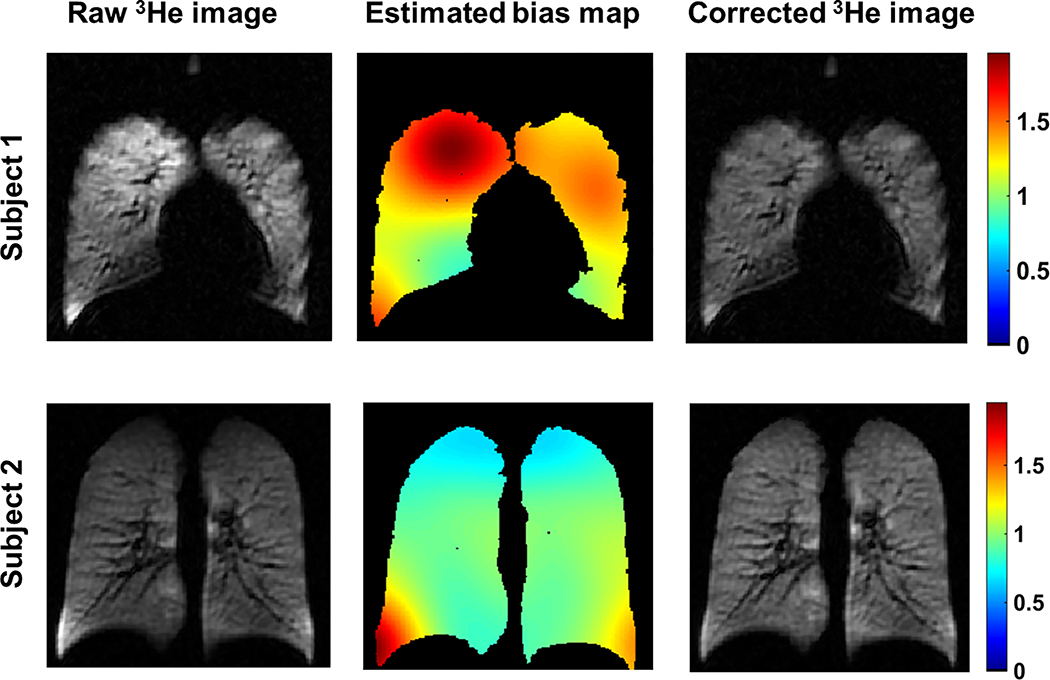
Coil Sensitivity Correction

The non-uniformity of the coil sensitivity was estimated solely using ³He image with the N4ITK bias field correction (20). This method uses an iterative optimization scheme that seeks the smooth multiplicative field in a B-spline approximation that maximizes the high frequency content of the distribution of tissue intensity. The N4ITK software was acquired as part of the Advanced Normalization Tools (ANTs) package (https://github.com/stnava/ANTs). The corrected ³He image was calculated by pixel-wise division of the raw ³He image by the estimated bias map (Figure 3).

Figure 3.

Coil sensitivity estimation. The first column displays the raw ³He image. The middle column shows the estimated sensitivity map within the lungs, and the third column shows the intensity-corrected ³He image. All images are plotted with the same grayscale window/level.

Adaptive K-means clustering

An adaptive decision criterion was used to identify defects in order to improve measurements for a broader range of disease severity as well as for healthy lungs. In order to guide the defect clustering, the low-intensity-signal percentage P_L in the lungs was computed and used to guide the identification of defect clusters. The histogram of all lung voxels was categorized into 10 bins from low- to high-intensity values, and then P_L is given by

$$P_L=\frac{\text{Voxel}\text{count}\text{in}\text{the}\text{first}\text{bin}}{\text{Sum}\text{of}\text{all}\text{lung}\text{voxels}}\times 100\%\text{.}$$

Similar to the hierarchical K-means algorithm, two rounds of K-means clustering with initial cluster centroids uniformly spaced were performed for cases with P_L < 10%. The first round of K-means classified all lung voxels into K clusters (C₁ to C_K) with C₁ containing low-intensity voxels. For cases with P_L < 4%, the first round selected five clusters (K = 5), while for other cases (P_L ≥ 4%) K = 4 was used in the first round. The second round of K-means refined the first cluster C₁ into four subclusters (S₁ to S₄). The defect labeling is illustrated in Figure 4. Based on the P_L value, three options (A, B, and C) for defining the defect clusters are,

$$\text{Defect}\text{cluster}=\{\begin{array}{ll}\text{A}.\text{First}\text{two}\text{subclusters}\text{with}K=5,\hfill & P_L<4\%\hfill \\ \text{B}.\text{First}\text{three}\text{subclusters}\text{with}K=4,\hfill & 4\%\le P_L<10\%\hfill \\ \text{C}.\text{First}\text{cluster}\text{with}K=4,\hfill & P_L\ge 10\%\hfill \end{array}$$

Figure 4.

The adaptive clustering on ventilation defect based on the percent low-intensity signal P_L. The P_L value was calculated from the histogram of all lung voxels and used to adaptively determine the defect cluster with three options based on the extent of ventilation defect volume after two rounds of K-means clustering.

These three options nominally reflect non-, mild- and severe-diseased lungs. The option B is equivalent to the defect cluster defined by hierarchical K-means. With the lung cavity masks for all studies, a spectrum of the P_L values was calculated and analyzed for the cutoff thresholds. The 10% upper limit for P_L was determined using Otsu’s method (26). The histogram plot of P_L suggested that 2 thirds of the studies have P_L values less than 4%. With the assumption that all baseline and recovery scans are lightly-diseased, the lower threshold was therefore set to 4%.

Morphometric Correction of Partial Volume Effect

After the K-means classification, there are three morphometric constraints used to refine the defect segmentation and obtain the final defect mask. First, the vascular mask was applied to prevent classification of the pulmonary vessels as ventilation defects. Second, low-intensity pixels aligned entirely along the lung periphery as a result of partial volume effect were removed by eroding the lung masks by 2 pixels. However, if the candidate peripheral defects remained contiguous with the lung boundary after erosion, the eroded boundary pixels were added back by dilation to preserve the volume of “true” peripheral defects. Finally, in order to remove scattered small peripheral signal voids likely due to noise, a defect was removed if it disappeared after the erosion of two pixels.

Manual Segmentation

The manual lung and defect segmentation were obtained from the previous reproducibility study (2). It was performed once independently and blinded to patient identity and time point by two readers (with 5 and 10 years of experience respectively) on the raw ³He images using customized, in-house software written in MATLAB. Lung volume was segmented by a combination of thresholding and manual correction, with tracing of the revised lung boundary by visual inspection. Ventilation defects were also manually traced based on visual inspection while blinded to patient identity, day of imaging, and time point.

Statistical Analysis

The inter-reader agreement was assessed for VDP values measured by manual and adaptive K-means methods and compared using Bland-Altman plots with repeated measures (27). Correlation between a spirometric reference standard and VDP as measured by semi-automated and manual analysis was assessed using Spearman correlation. In order to address repeated measures and further compare the semi-automated and manual methods via correlation with spirometry, the 95% confidence interval (CI) was computed by bootstrapping (28). Bootstrapping resampled the data with replacement 1000 times and the Spearman correlation was computed for each of these replicates to calculate a CI.

To assess regional VDP variations, 3D lung volumes were reformatted into a stack of axial slices and divided along the superior/inferior axis into 3 equal-volume regions with the upper, middle, and lower thirds being apical, mid and basal regions. Similarly, 3D lung volumes in the coronal view were divided along anterior/posterior into 3 equal volumes: anterior, middle, and posterior regions. For each subject, two visits were averaged at baseline, post-challenge and recovery. A linear mixed-effects model was used to compare the pairwise differences among apical/basal regions as well as anterior/posterior regions.

The Dice coefficient (D) was used to assess spatial agreement between semi-automated (S) and manual (M) analysis of ventilation defect volumes:

$$D=\frac{2\cdot |S\cap M|}{\left|S\right|+\left|M\right|}.$$

D has a range of [0, 1] with 1 indicating perfect spatial agreement. The pairwise comparison of the Dice coefficient among the three defect masks (two by manual and one by adaptive K-means) was assessed using a linear mixed-effects model. A p value less than 0.05 was considered significant. All statistical tests were performed in R v3.1.2 (29).

Results

Manual vs. Semi-automated Measurements

The manual defect segmentation took 27 min on average, whereas the adaptive K-means method took only 5 min, about 5 times faster.

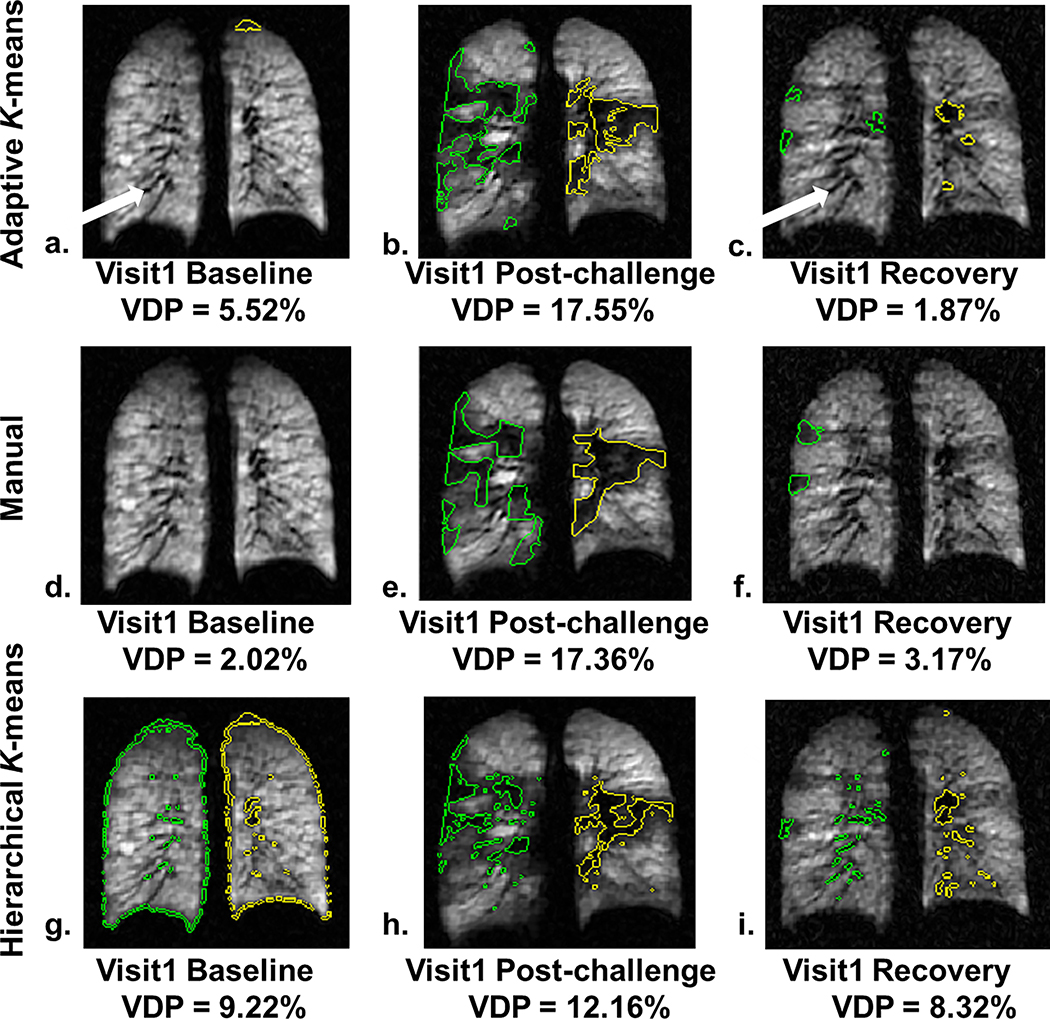
The typical performance of manual, adaptive K-means and hierarchical K-means is shown in Figure 5. The distribution of measured defects within a central slice of the right (green) and left (yellow) lungs is shown at baseline, post-challenge and recovery at visit 1 for the same subject. The low-intensity vessels (white arrows in Figure 5a and 5c) were effectively masked out by the adaptive K-means and were identified as defects using the hierarchical K-means (Figure 5g and 5i). Additionally at the baseline scan, the peripheral voxels along the lung boundaries were detected as defects due to partial volume effect with hierarchical K-means (Figure 5g) and were eliminated using adaptive K-means (Figure 5a). The spatial agreement between the semi-automated and the manual method was most marked at the post-challenge time point where large defects emerged due to exercise. The defects detected by the adaptive K-means (Figure 5b) were better aligned with manually segmented defects (Figure 5e) relative to the defects by the hierarchical K-means (Figure 5h), likely due to the ³He intensity correction. Although the adaptive K-means performed better than the hierarchical K-means overall, the spatial agreement between adaptive K-means and manual segmentation was more varied when the whole lung VDP was less than 3%. It should be noted that the vascular voxels, consistently removed in the adaptive K-means method, are partially included on manual segmentation. In addition small differences may be attributable to the intensity correction from coil sensitivity estimation because manual segmentation was performed directly on the uncorrected raw ³He images.

Figure 5.

The segmented defects overlaid on the ³He images obtained by the adaptive K-means, manual segmentation, and hierarchical K-means methods in the same subject at visit 1. The adaptive K-means results (defects shown as green and yellow contoured regions in the right and left lung respectively) on Row 1 effectively masked out the low-intensity, tubular-shaped vessels (white arrows) at baseline (a), post-challenge (b) and recovery (c) similar to the manually segmented defects on Row 2 (d, e, and f). However, the adaptive K-means showed discrepancies on the size and location of small defects. The hierarchical K-means included low-intensity voxels along the lung periphery due to partial volume effect at baseline (g) and vessels (g and i). The large defects (h) detected by the hierarchical K-means appeared in a more scatter pattern and smaller compared to the manual (e) and adaptive K-means methods (b) likely due to the lack of intensity correction.

The Bland-Altman plots indicate good agreement of VDP measured by adaptive K-means compared to manual measurements performed by both readers, with biases of less than 2% (both p > 0.46) and nearly identical limits of agreement (95% CI) less than 10% (Figure 6a and 6b). The two sets of manual VDP measurements (Figure 6c) agreed well. Therefore, only one set of manual measurements (reader 1) was used for additional comparisons to the adaptive K-means method unless specified otherwise. Without vessel exclusion, the adaptive K-means (Figure 6e) had a bias of 2.2% (p = 0.27) relative to manual segmentation. The hierarchical K-means yielded a significant bias of 6.1% (p = 0.0029) compared to the manual measurements (Figure 6d).

Figure 6.

Bland-Altman plots for pairwise comparison between manual readers, adaptive K-means, and hierarchical K-means. The biases in VDP between adaptive K-means and 2 readers (a and b) were 1.12% and 1.34% respectively. The bias between the 2 manual readers (c) was 0.22%. The hierarchical K-means yielded a significant bias 6.1% (d) compared to Reader1, which was mainly due to the over-segmentation at baseline and recovery. When vasculature was not removed in the adaptive K-means (e), the bias of 2.2% was still insignificant. The VDP measurements are plotted separately at baseline (black circle), post-challenge (dark-gray square) and recovery (light-gray diamond). The upper and lower bounds (dashed lines) were adjusted for repeated measures.

Table 1 summarizes post-challenge VDP changes for all subjects measured by the manual and adaptive K-means methods. Similar to the manual assessment, the adaptive K-means showed a large increase of VDP from baseline to post-challenge. The manual segmentation found the mean VDP increased by 8.43 ± 7.18% (p = 0.13) from baseline to post-challenge. With adaptive K-means, this mean VDP increase was 8.13 ± 9.55% (p = 0.31). For spirometry, the mean FEV1 %P of 85.64 ± 8.84% for the two visits decreased by 18.32% (p = 0.0087), while the mean baseline FEV1/FVC %P of 93.01 ± 5.74% for the two visits decreased by 9.38% (p = 0.041).

Table 1.

Percent change in ventilation defect percent (ΔVDP) from baseline to post-challenge at two separate visits measured by manual and adaptive K-means methods

Subject	Manual		Adaptive K-means
	ΔVDP Visit1 (%)	ΔVDP Visit2 (%)	ΔVDP Visit1 (%)	ΔVDP Visit2 (%)
1	14.27	19.98	19.52	19.60
2	7.66	4.15	4.47	3.33
3	0.23	0.80	0.40	−0.61
4	8.57	15.34	3.58	13.20
5	0	1.02	−2.32	−2.49
6	14.69	14.45	16.85	22.06

The VDP measurements at baseline, post-challenge, and recovery at visit1 were quantitatively all very similar to the corresponding measurements at visit 2 (Table 2) using both manual and adaptive K-means. The increase in VDP from baseline to post-challenge were significantly correlated for the 2 visits using both the manual (ρ = 0.89, p = 0.017) and adaptive K-means (ρ = 0.91, p = 0.011) methods. This is in contrast to the decreases in FEV1 %P and FEV1/FVC %P from baseline to post-challenge, which were not correlated (p > 0.89) between the two visits.

Table 2.

Average ventilation defect percent for exercise challenge protocol in subjects with EIB at each of two visits

Visit	Manual			Adaptive K-means
	Baseline	Post-challenge	Recovery	Baseline	Post-challenge	Recovery
Visit1	1.11±1.12%	8.68±7.41%	1.94±1.47%	2.78±1.63%	9.86±8.21%	2.94±2.67%
Visit2	0.70±0.81%	9.99±8.97%	1.82±1.36%	1.84±1.50%	11.02±9.77%	2.48±2.90%

Values are mean ± standard deviation. Ventilation defect percent (%) was calculated as 100% × defect volumes/total lung volumes.

Correlation to Spirometric Measures

Table 3 shows comparable Spearman correlation coefficients and 95% confidence intervals between VDP and FEV1/FVC %P for both manual and adaptive K-means, suggesting comparable performance of the two methods with respect to this measure. The correlation results between VDP and FEV1 %P were also similar using the two quantification methods. However, the 95% CI for adaptive K-means was somewhat wider than the CI resulting from the manual method.

Table 3.

Spearman correlation between whole lung VDP and spirometric measures

	FEV1/FVC %P			FEV1%P
	ρ	p value	95% CI	ρ	p value	95% CI
Manual	−0.63	<0.0001	[−0.80, −0.38]	−0.54	0.00071	[−0.75, −0.25]
Adaptive K-means	−0.64	<0.0001	[−0.83, −0.38]	−0.40	0.016	[−0.66, −0.049]

FEV1 %P: percent predicted forced expiratory volume in 1 second; FEV1/FVC %P: percent predicted FEV1 over forced vital capacity; CI: confidence interval. A p <0.05 was considered significantly correlated.

Regional Variations in Ventilation Defect Percent

Figure 7 compares VDP for manual and adaptive K-means from baseline to post-challenge in apical, mid and basal regions as well as anterior, middle and posterior regions. The VDP measured by manual segmentation (Figure 7a and c) showed similar qualitative trends compared to the values reported by adaptive K-means (Figure 7b and d). There were no statistically significant differences for anterior/posterior or apical/basal regional dependence of VDP for either manual (all p > 0.17) or adaptive K-means (all p > 0.13) methods. However, the VDP in the posterior region qualitatively appeared higher relative to the anterior region at the post-challenge time point, a phenomenon that was more pronounced with manual measurements. The regional dependence along superior/inferior axis was marginally insignificant measured by either manual segmentation (all p > 0.061) or adaptive K-means (all p > 0.078). Both methods found that the basal region tended to be more defected than the mid region at baseline.

Figure 7.

Boxplots of the regional VDP at baseline, post-challenge and recovery using the two measurement methods. Despite qualitative trends, no significant differences in apical/basal regional dependence were observed by manual (a) and adaptive K-means (b). Similarly, no significant differences in anterior/posterior dependence were observed by manual (c) and adaptive K-means (d).

Dice Coefficient

Table 4 shows the Dice coefficients for manual and adaptive K-means segmentation. The Dice coefficient for repeated adaptive K-means runs was 0.99, suggesting reproducible defect segmentation for repeated measurements. The inter-reader Dice coefficient for manual segmentation showed a moderate agreement. The pairwise comparison among these five pairs of the Dice coefficients for ventilation defects suggested that the two repeated adaptive K-means runs had the best spatial agreement (all p < 0.0002), while the inter-reader spatial agreement (Reader 1 vs. Reader 2 = 0.56) was significantly higher than the agreement between a reader and one of the semi-automated methods (all p < 0.0097). The spatial agreement on ventilation defects between adaptive K-means and reader 1 was similar to the agreement between adaptive K-means and reader 2 (p = 0.75). The relatively low agreement for defect locations using semi-automated approaches are likely due to the small size and number of ventilation defects for the majority of studies in this study cohort. The Dice coefficients of the ventilated regions showed excellent spatial overlap between semi-automated and manual segmentation.

Table 4.

Dice coefficients (Mean ± standard deviation) for manual and semi-automated segmentation

Methods	Ventilation volume	Defect volume
Reader 2 – Reader 1	0.99 ± 0.015	0.56 ± 0.31
Adaptive K-means –Reader 1	0.98 ± 0.027	0.28 ± 0.24
Adaptive K-means –Reader 2	0.97 ± 0.033	0.25 ± 0.21
Hierarchical K-means – Reader 1	0.95 ± 0.013	0.16 ± 0.18
Adaptive K-means 2 – Adaptive K-means 1	1.00 ± 0.00033	0.99 ± 0.022

Discussion

The strong correlation (both ρ ≥ 0.89, p ≤ 0.017) of the post-challenge VDP increase across two visits as reported by both manual and adaptive K-means methods indicates a good repeatability of severity evaluation using HP ³He MRI. Conversely, the lack of correlation across visits of the change in FEV1 %P and FEV1/FVC %P from baseline to post-challenge suggests larger variation in spirometric measures. Therefore, HP ³He MRI may be more suitable for the evaluation of exercise-induced changes in lung function, and the adaptive K-means method may be used to evaluate those changes.

Researchers using several semi-automated defect segmentation algorithms (10,13,14,30) all reported different degrees of systematic bias compared to the manual segmentation of HP gas MR images. In our work there is good overall agreement, even for estimates by subregion of the lungs. Upper, middle, and lower thirds of the lungs showed similar patterns for adaptive K-means vs. manual segmentation. Importantly, VDP measured by both manual and adaptive K-means were strongly correlated across repeated visits, suggesting semi-automated techniques that account for coil sensitivity and vessel volume are robust enough for tracking longitudinal VDP variations.

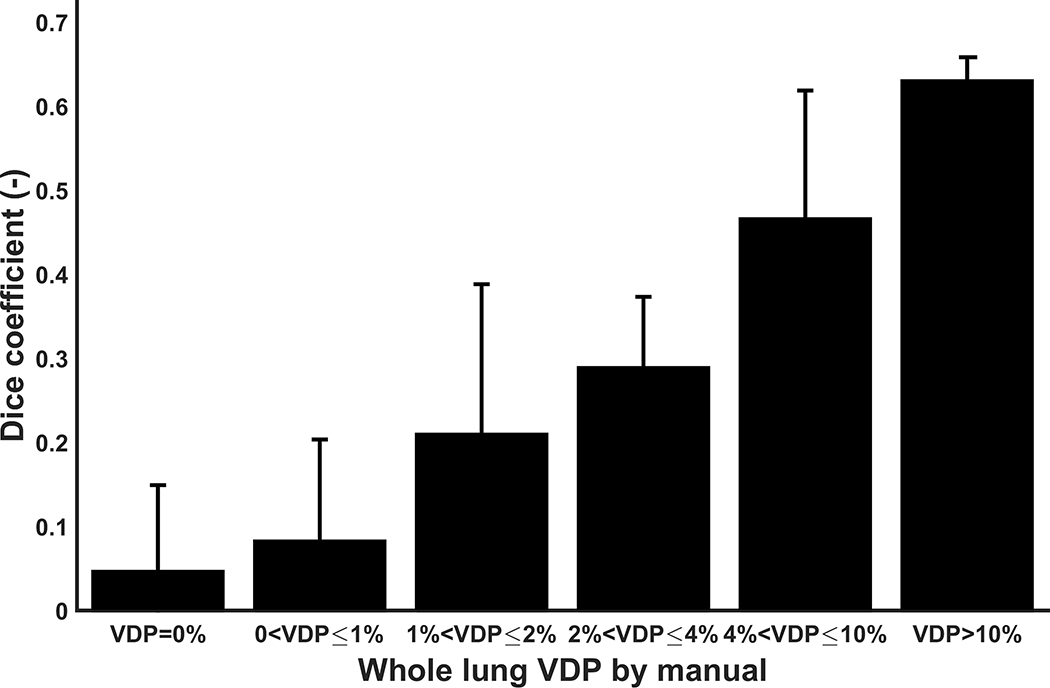
Despite good qualitative and quantitative agreement of the VDP measurements between manual and adaptive K-means, the Dice coefficients reflected a poorer spatial agreement, or absolute overlap, between the manual and adaptive K-means segmentations for defect locations. Conversely, the Dice coefficients on the ventilated regions showed exceptional spatial agreement between the two methods. The average whole lung VDP of this EIB study cohort is 4.0%, suggesting the number and size of ventilation defects in the majority of studies are small. This led to a pattern of multiple smaller regions of defect being segmented by adaptive K-means that were not detected or traced by either manual reader. It should be noted that the vascular pixels, consistently removed in the adaptive K-means method, are included in part by manual segmentation. In addition, small differences may be attributable to the intensity correction from coil sensitivity estimation because manual segmentation was performed directly on the uncorrected ³He images (2). Both of these factors may contribute to the lower overall Dice coefficient for defect locations. In more defected lungs, VDP results were more consistently overlapped as illustrated in Figure 8. Nonetheless, the adaptive K-means showed high repeatability of the Dice coefficient across multiple runs, and exceeded that of manual segmentation performed by two independent readers.

Figure 8.

Bar graph of the mean Dice coefficient between Reader 1 and adaptive K-means at various whole lung VDP values by manual segmentation. The measured VDP was categorized into six bins with values from 0% to over 10%. The error bars represent the standard deviation of the Dice coefficient within each measured VDP bin. The spatial agreement between the two methods improved in more diseased lungs, where the whole lung VDP is higher.

Although the bias for VDP calculated using adaptive k-means was overall positive relative to manual segmentation, when large defects are present as in Figure 5e, the reader tended to ignore the possible pulmonary vessels that are inherently blended into the defect in favor of tracing a single large defect to save time and effort. On the other hand, in less-diseased cases where defects tended to be more peripherally located, a reader would easily identify and clearly exclude these vessels as illustrated in Figure 5d and 5f. This implies that readers tend to make an accurate judgment on the tubular vessels in the lightly-diseased cases, while the semi-automated algorithm may yield a more accurate delineation of large, readily apparent defects. A prior study (30) reported that readers tend to ignore defects that comprise less than 2% of the total volume. However this may reflect an intrinsic difficulty for semi-automated algorithms to accurately identify ventilation defects in slightly-diseased or healthy lungs. In these circumstances it may be useful to have a radiologist check and correct the segmentation results generated by adaptive K-means and then further investigate the discrepancy between corrected and uncorrected defect masks to refine the method.

Although the method here is developed in subjects with EIB, adaptive K-means using HP ³He MRI is expected to be more generally applicable to a variety of lung diseases such as severe asthma, CF, and COPD. Compared to EIB, patients with severe asthma, CF or COPD are likely to have more defected lungs with generally less heterogeneity. Prior work showed the hierarchical K-means demonstrated excellent performance on COPD patients (10). Due to the similarity to the hierarchical K-means and the fact that better agreement to manual segmentation was achieved in more defected lungs (Figure 8), adaptive K-means is expected to perform well in various disease conditions. The good quantitative agreement and reproducibility of the adaptive K-means may potentially be extended to quantify ¹²⁹Xe MRI and is left for future work.

Several limitations of our study are acknowledged. First, the present study is limited by small sample size, although this is mitigated by repeated measures and data acquired before and after challenge. The separation of different levels of defected lungs using K-means methods that are based on P_L histogram analysis needs further investigation over a broader variety of lung conditions, both healthy and diseased. Specifically, the cutoff thresholds for P_L corresponding to 3 levels of lung disease conditions need to be validated in a larger sample size with various obstructive lung diseases and disease severities.

Second, the landmark-based registration method used here requires user interaction and the knowledge of lung anatomy, which opens up the possibility of subjective errors that could add variation for the adaptive K-means algorithm presented in this work. Recent studies (13,14) demonstrated that a symmetric diffeomorphic registration algorithm (31) and the non-rigid registration using Image Registration Toolkit (Visual Information Processing Group, London, UK) (32) can effectively register proton and ³He in a more automated fashion mitigating this potential source of error.

Additionally, the vessel-contrast enhancement that was performed before the vesselness filter can be optional depending on the scanning protocol. The anatomic proton images acquired using a SS-FSE sequence in this study showed limited contrast in the lungs. However, it was reported that a steady-state free precession sequence highlights the pulmonary vasculature and thus the vasculature can be estimated directly from the raw proton images (14). In conclusion, we developed a semi-automated adaptive K-means approach to segment ventilation defects in HP ³He MR images. The algorithm corrected for coil sensitivity, estimated pulmonary vasculature and determined defect cluster adaptively based on the overall low-intensity signal in ³He MR images of the lungs. Moderate to strong significant correlation was found between FEV1/FEV %P and VDP as measured by adaptive K-means, and was comparable to that found for manual segmentation. The time savings when using adaptive K-means is approximately a factor of 5 compared to manual segmentation. The regional VDP variations measured by adaptive K-means also compared well to manual measurements qualitatively and quantitatively for cases of greater extent of defected lung volume. The adaptive K-means may be applied to assess ventilation defect in a variety of lung diseases.