Abstract
Metaheuristic algorithms have a wide range of applications in handling optimization problems. In this study, a new metaheuristic algorithm, called the chef-based optimization algorithm (CBOA), is developed. The fundamental inspiration employed in CBOA design is the process of learning cooking skills in training courses. The stages of the cooking training process in various phases are mathematically modeled with the aim of increasing the ability of global search in exploration and the ability of local search in exploitation. A collection of 52 standard objective functions is utilized to assess the CBOA’s performance in addressing optimization issues. The optimization results show that the CBOA is capable of providing acceptable solutions by creating a balance between exploration and exploitation and is highly efficient in the treatment of optimization problems. In addition, the CBOA’s effectiveness in dealing with real-world applications is tested on four engineering problems. Twelve well-known metaheuristic algorithms have been selected for comparison with the CBOA. The simulation results show that CBOA performs much better than competing algorithms and is more effective in solving optimization problems.
Subject terms: Electrical and electronic engineering, Mechanical engineering, Applied mathematics, Computer science
Introduction
The technique of finding the best feasible solution among all existing ones is known as optimization. Optimization is used in designing and maintaining many engineering, economic, and even social systems to minimize the necessary costs or maximize profits. Due to the wide application of optimization in different sciences, this topic has grown a lot, so it is studied in management, mathematics, industry, and many branches of science1. If we want to solve a real optimization problem, we must first build the corresponding mathematical model. Setting up a model, of course, means creating a complete description of the problem with variables and mathematical relationships so that all the details of the optimization problem are simulated2.
Deterministic optimization methods can be divided into gradient-based and non-gradient methods, which effectively solve linear, convex, and derivable optimization problems and have a continuous search space. On the other hand, many real-world optimization problems have features such as nonlinear, non-convex objective functions, discrete search spaces, non-differentiable, high dimensions, and high complexity3.
The inability of deterministic methods to address such optimization challenges has led to the emergence of effective stochastic approaches in such cases. Metaheuristic algorithms, as the most prominent stochastic method, are capable of tackling optimization problems based on a random search, random operators, and trial-and-error processes4. The simplicity of concepts, easy implementation, efficiency in nonlinear and non-convex environments, and independence of the type of problem are the features that have led to the widespread use and popularity of metaheuristic algorithms5.
The primary source in the design of metaheuristic algorithms is inspiration from various natural phenomena, swarm intelligence, animal life, biological sciences, physical laws, rules of the game, and so on. Among the most famous metaheuristic algorithms are the genetic algorithm (GA)6, inspired by biology, the particle swarm optimization (PSO)7, the ant colony optimization (ACO)8, the Artificial bee colony (ABC)9, and the Northern Goshawk optimization8, inspired by animal life.
The critical issue with metaheuristic algorithms is that these methods do not guarantee that they will be able to find the optimal global solution. However, the solutions obtained from metaheuristic algorithms are close to the global optimal. The desire to achieve better solutions has led to the development of numerous metaheuristic algorithms.
Given the development of numerous metaheuristic algorithms, the main research question is, is there still a need to design newer algorithms? In answer to this question, the No Free Lunch (NFL) theorem10 states that the success of an algorithm in handling a set of optimization problems cannot be a reason for the successful performance of this algorithm in dealing with other optimization problems. There is no presumption of the success or failure of a method in optimizing a problem. The NFL theorem explains that no particular algorithm can be introduced as the best optimizer in all optimization applications. The NFL theorem is a source of motivation for researchers come up with better solutions to optimization problems by designing newer metaheuristic algorithms.
The innovation and novelty of the proposed chef-based optimization algorithm (CBOA) are:
This paper introduces a new metaheuristic algorithm based on the description of a training process.
Every educational process in different types of schools has certain usual properties, forms and stages. In this paper, we were concretely motivated by all specifics of the process of learning the cooking skills of a new chief.
The paper provides a mathematical model of two-phase description of the preparation of a new chef, according to the principles of a real cooking school.
Both phases are typical of all art schools (including cooking courses) because every student wants to learn from the best chef, but on the other hand, the greatest chefs will not want to prepare weak students. So, in the first phase, the chefs compete with each other so that a table of their quality ranking can be created. Similarly, in the second phase, students compete with each other so that their qualitative ranking can be created according to their cooking abilities.
In the mathematical modeling of the first phase, we implemented two master chef strategies. These strategies model the fact that even chefs learn new cooking recipes by observing the teaching of other chefs (Strategy 1), and then they try to improve these observed recipes even more through their autonomous experimentation (Strategy 2).
In the mathematical modeling of the first phase, we implemented three student strategies. The first strategy of each student is to choose a chef and learn all of his/her skills. The second strategy of each student is to choose another chef and learn from him/her one skill (one concrete recipe). In the third strategy, students try to improve all their skills by self-experimentation.
CBOA ability to handle optimization problems is tested on fifty-two standard benchmark functions and compared with twelve well-known meta-heuristic algorithms. In doing so, CBOA achieves much better results than these competing programs.
The rest of the structure of the paper is as follows; the literature review is presented in the “Lecture review’’ section. The proposed CBOA is introduced and modeled in the “Chef-based optimization algorithm’’ section. The simulation studies and results are presented in the “Simulation studies and results’’ section. A discussion of results and performance of the proposed CBOA is presented in the “Discussion’’ section. CBOA implementation on CEC 2017 test suite is presented in “Evaluation CEC 2017 test suite” section. The efficiency of CBOA in handling real-world applications is evaluated in “CBOA for real world applications” section. Conclusions and several suggestions for future research are provided in the “Conclusions and future works’’ section.
Lecture review
Metaheuristic algorithms, according to the primary source of design inspiration, are classified into five groups: (i) swarm-based, (ii) evolutionary-based, (iii) physics-based, (iv) game-based, and (v) human-based methods.
Theorizing on swarming activities and behaviors in the lives of birds, animals, aquatic animals, insects, and other living things in nature has been the main source of inspiration in the development of swarm-based algorithms. PSO, ACO, and ABC are among the most widely used and popular swarm-based algorithms. The natural behavior of the crowds of birds or fish in search of food have been the main idea of the PSO. Discovering the shortest path between the nest and the food source based on the collective intelligence of ants has been main idea of ACO. Hierarchical efforts and activities of bee colonies in search of food has been the main idea of the ABC. The idea of the ability of living organisms to find food sources in nature has led to the design of several swarm-based metaheuristic algorithms, such as: the tunicate swarm algorithm (TSA)11, the African vultures optimization algorithm (AVOA)12, and the snake optimizer (SO)13. The strategy of living things in nature when hunting and trapping prey has been the main idea in designing algorithms such as the grey wolf optimizer (GWO)14, the Golden Jackal optimization (GJO)15, the whale optimization algorithm (WOA)16, the reptile search algorithm (RSA)17, the marine predator algorithm (MPA)18.
The concepts of natural selection, Darwin’s theory of evolution, and stochastic operators such as selection, crossover, and mutation have been used in the design of evolutionary algorithms. GA and differential evolution (DE)19 are among the most famous evolutionary algorithms whose main design idea is the reproduction process and its concepts.
The laws, concepts, and phenomena of physics have been a source of inspiration in designing of numerous methods that fall into the category of physics-based algorithms. Simulated annealing (SA) is the most significant physics-based algorithm produced based on the physical phenomenon of metal annealing20. Physical forces and Newton’s laws of motion have been the main idea behind the design of methods such as the gravitational search algorithm (GSA) based on gravity force21 and the spring search algorithm (SSA) based on spring force22. Mathematical modeling of the natural water cycle in nature has led to the design of the water cycle algorithm (WCA)23. Cosmological studies and space holes have been the inspiration in designing the multi-verse optimizer (MVO)24. Archimedes principle concepts have been the main idea in the design of the archimedes optimization algorithm (AOA)24.
The rules of the game, the behavior of the players, the coaches, and the referees have been a source of inspiration for designing game-based algorithms. Football game based optimization (FGBO)24 and the volleyball premier league (VPL)25 are two game-based approaches designed based on the modeling of football and volleyball league, respectively. The strategy of the players to put the pieces together has been the design idea of the puzzle optimization algorithm (POA)26.
Human activities and behaviors in individual and social life have become the idea of designing approaches that fall into the category of human-based algorithms. Teaching–learning-based optimization (TLBO) is one of the most famous human-based algorithms that has been developed based on the simulation of interactions between a teacher and students in the classroom27. The treatment process that the doctor performs to treat patients has been the main idea in the design of the doctor and patient optimization (DPO)28. The cooperation of the members of a team to achieve success and the common goal of that team has been the main idea in the design of the teamwork optimization algorithm (TOA)29. The City Councils Evolution (CCE) is a human-based approach that is produced based on modeling the evolution of city councils30. The strategic movement of army troops during the war has been the idea employed in the design of the war strategy optimization (WSO)31.
Based on the best knowledge gained from the literature review, no metaheuristic algorithm inspired by the culinary education process has been designed. However, teaching cooking to people who attend training courses is an intelligent process that can be a motivation to design a new metaheuristic algorithm. Consequently, in this study, a new optimization approach has been developed by mathematical modeling the cooking education process, which is discussed in the next section.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was not required as no human or animals were involved.
Chef-based optimization algorithm
This part is devoted to the introduction and mathematical modeling of the proposed algorithm called the Chef-based optimization algorithm (CBOA).
Inspiration of CBOA
Cooking students and young cooks participate in training courses to improve their cooking skills and become chefs. This concept is analogous to metaheuristic algorithms, where several candidate solutions are initialized and then improved through an iterative process to determine the best candidate solution as the solution to the problem at the end of the algorithm implementation. Thus, the process of transforming a cooking student into a chef in a culinary school is a source of inspiration for the design of the proposed CBOA.
It is assumed that a certain number of chef instructors are present in a culinary school. Each chef instructor is responsible for teaching a class. Each cooking student can choose which of these classes to attend. The chef instructor teaches students cooking skills and techniques. However, chef instructors also try to improve their skills based on the instructions of the best chef instructor in the school and individual exercises. Cooking students try to learn and imitate the skills of the chef instructor. In addition, cooking students try to improve the skills they have learned through practice. At the end of the course, cooking students become skilled chefs under the training they have received.
Mathematical modeling of the above concepts is used in designing the CBOA, which is discussed in the following subsections.
Algorithm initialization
The proposed CBOA approach is a population-based algorithm whose members consist of two groups of people, namely cooking students and chef instructors. Each CBOA member is a candidate solution that contains information about the problem variables. From a mathematical point of view, each member of the CBOA is a vector, and the set of CBOA members can be modeled using a matrix according to Eq. (1).
| 1 |
where is the CBOA population matrix, is the th CBOA member (candidate solution), is its th coordinate (i.e., the value of the th problem variable for the th CBOA member), is the population size, and is the number of problem variables of the objective function (dimension of the problem).
The position of the CBOA members at the beginning of the algorithm implementation is randomly initialized for using Eq. (2).
| 2 |
where is a random number in the interval , and are the lower and the upper bounds of the th problem variable, respectively.
By inserting the suggested values of each CBOA member into the variables, a corresponding objective function value is evaluated. As a result, the objective function is evaluated in turns (where is the number of CBOA members) and values are calculated for the objective function. These values can be represented using a vector corresponding to Eq. (3).
| 3 |
where is the vector of values of the objective function and is the value of the objective function obtained for the th member of CBOA, where
The values of the objective functions provide essential information about the quality of the candidate solutions. The value of the objective function is the decision criterion for selecting the best candidate solution. Among CBOA members, the member with the best value for the objective function is recognized as the best member of the population and the best candidate solution. During the running of the algorithm, in each iteration, the members of the CBOA are updated, and the corresponding values of the objective function are calculated. It is, therefore, necessary to update the best member in each iteration based on comparing the values of the objective function.
Mathematical modeling of CBOA
After the algorithm is initialized, the CBOA steps are gradually applied to the candidate solutions to improve them. CBOA members consist of a group of instructing chefs and a group of cooking students. The update process for each of these groups is different. Based on comparing the values of the objective function, some CBOA members with better values of the objective function are selected as the chef instructor. Therefore, if the rows of the CBOA population matrix are sorted in ascending order according to the value of the objective function (thus, the member in the first row is the best member), then the group of the first members is selected as the group of chef instructors and the rest group of members is chosen as the group of cooking students. The CBOA sorted population matrix and the sorted objective function vector are specified in Eqs. (4) and (5).
| 4 |
| 5 |
where is the number of chef instructors, is the sorted population matrix of CBOA, and is a vector of ascending objective function values. In the matrix , members from to represent the group of chef instructors, and members from to represent the group of cooking students. The vector i includes successively the values of the objective functions corresponding to to .
Phase 1: the updating process for group of chef instructors (update of to )
In a culinary school, it is assumed that several chef instructors are responsible for teaching cooking skills to students. Chef instructors follow two strategies to improve their cooking skills. In the first strategy, they emulate the best chef instructor and try to learn the chef instructor techniques. This strategy demonstrates the global search and CBOA exploration capabilities.
The advantage of updating the chef instructors based on this strategy is that the top chefs (top population members) improve their skills based on the best chef (best population member) before they start teaching students. Hence, there is no direct dependence on updating the students’ position only on the base of the best member of the population in CBOA design. Furthermore, this approach prevents the algorithm from getting stuck in local optima and causes different areas of the search space to be scanned more accurately and effectively. Based on this strategy, a new position for each chef instructor is first calculated for using the following equation
| 6 |
where is the new calculated status for the th sorted member of CBOA (that is ) based on the first strategy () of updating the chef instructor, is its th coordinate, is the best chef instructor (denoted as in the matrix ), is the th coordinate of the best chef instructor, is a random number from the interval , and is a number that is selected randomly during execution from the set . This new position is acceptable to the CBOA if it improves the value of the objective function. This condition is modeled using Eq. (7).
| 7 |
where is the value of the objective function of the member
In the second strategy, each chef instructor tries to improve his cooking skills based on individual activities and exercises. This strategy represents the local search and the CBOA’s exploitation ability. If each problem variable is considered a cooking skill, a chef instructor will try to improve all of those skills to achieve a better objective function value.
The advantage of updating based on individual activities and exercises is that each member, regardless of the position of other population members, seeks to discover better solutions near the position where it is located. There is a possibility that better solutions can be obtained based on local search and exploitation, with minor changes in the position of population members in the search space. According to this concept, around each chef instructor in the search space, a random position is generated for using Eqs. (8) to (10). If this random position improves the value of the objective function, it is acceptable for updating, which this condition is modeled using Eq. (11).
| 8 |
| 9 |
where and are the lower and upper local bound of the th problem variable, respectively, and the variable represents the iteration counter.
| 10 |
| 11 |
where is the new calculated status for the th CBOA sorted member (i.e., ) based on the second strategy () of chef instructors updating, is its th coordinate, and is its value of the objective function.
Phase 2: the updating process for the group of cooking students (update of to )
Cooking students attend culinary school to learn cooking skills and become a chef. In the design of CBOA, it is assumed that cooking students follow three strategies to learn cooking skills. According to the first strategy, each cooking student randomly chooses a class taught by one of the chefs, and then he is taught cooking skills by this chef instructor. The advantage of updating cooking students based on this strategy is that there are different chef instructors available to lead them, resulting in cooking students learning different skills (i.e., population members moving to other areas of the search space) based on the guidance of the chosen chef instructor. On the other hand, if all cooking students learn only from the best chef-instructor (all members of the population moved towards the best member), then an efficient global search in the problem-solving space would not be possible. This strategy is simulated in the CBOA in such a way that first for each cooking student, a new position is calculated based on the training and guidance of the chef instructor, for using Eq. (12).
| 12 |
where is the new calculated status for the th sorted member of CBOA (i.e., ) based on the first strategy () of the updating of cooking students, is its th coordinate, and is the selected chef instructor by the th cooking student, where is randomly selected from the set (where denotes the value ).
This new position replaces the previous position for each CBOA member, if it improves the value of the objective function. This concept is modeled for by Eq. (13).
| 13 |
where is the value of the objective function of
In the second strategy, since each problem variable in the CBOA is assumed to be a cooking skill, each cooking student tries to learn one of the skills of the chef instructor completely and fully imitate the chef instructor (therefore, by “skill’’, we mean a recipe for one great meal). This strategy enhances the global search and exploration capabilities of the CBOA. The advantage of this strategy is that instead of updating all candidate solution variables (i.e., all cooking student skills), only one variable (one skill, i.e., one recipe) changes. It may not be necessary to update all member position coordinates to achieve better solutions.
In the design of CBOA, this “skill’’ represents a certain component of a vector of cooking skills of a randomly selected chef instructor (). Hence, the second strategy is mathematically simulated in such a way that for each cooking student (members of CBOA with ), first one chief instructor, which is represented by the vector is randomly selected (a member of CBOA with the index , which is randomly selected from the set ), then it is randomly selected his th coordinate (thus a number from the set which represents a “skill’’ of this selected chief instructor) and by this value we replace the th coordinate of the vector of the th cooking student (thus, ).
According to this concept, a new position is calculated for each CBOA cooking student member using Eq. (14).
| 14 |
where is a randomly selected number from the set Then, it is replaced with the previous position based on Eq. (15) if it improves the target value of the objective function.
| 15 |
where is the new calculated status for the th sorted member of CBOA (i.e., ) based on the second strategy () of updating cooking students, is its th coordinate, is its objective function value.
In the third strategy, each cooking student tries to improve his cooking skills based on his individual activities and exercises. In fact, this strategy represents the local search and the CBOA’s exploitation ability. The advantage of updating cooking students based on the strategy of individual activities and exercises is that it increases the power of local search and exploitation of the algorithm in achieving better possible solutions near the discovered solutions. In this strategy, similar to the local search strategy of chef instructors, cooking students try to converge to better solutions with small and precise steps. If each problem variable is considered a cooking skill, a cooking student will try to improve all of those skills to achieve a better objective function value.
According to this concept, around each cooking student in the search space, a random position is generated by Eqs. (8), and (9) and a new position is calculated using Eq. (16).
| 16 |
where is the new calculated status for the th sorted member of CBOA (that is ) based on the third strategy () of updating cooking students, is its th coordinate, and is randomly selected number from the set , , and If this new random position improves the value of the objective function, it is acceptable for updating of , which is modeled by Eq. (17).
| 17 |
where is the value of the objective function of
Repetition process, pseudocode, and flowchart of CBOA
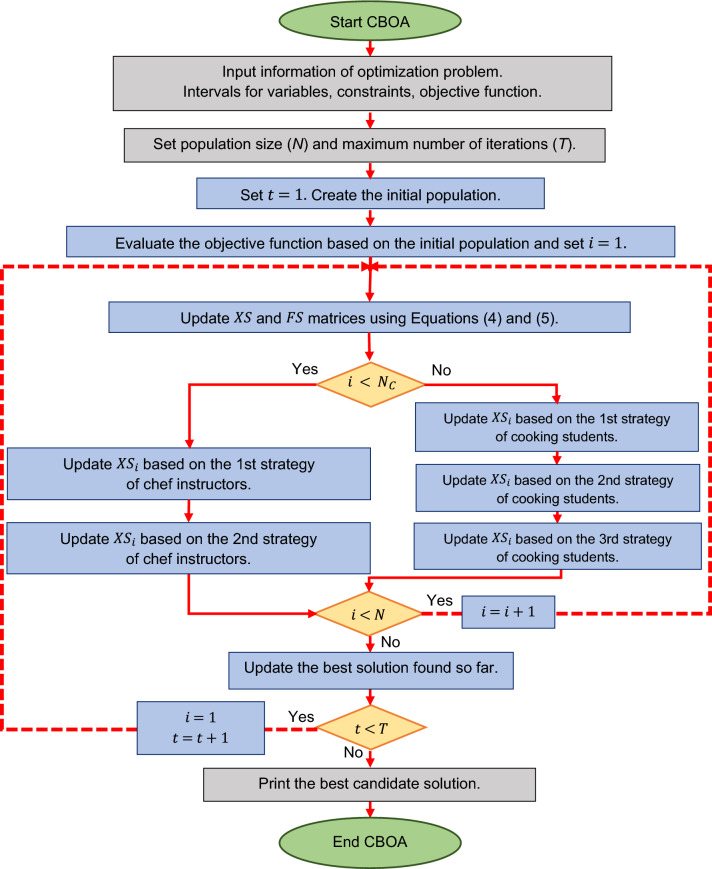
A CBOA iteration is completed by updating all members of the population. The CBOA enters the next iteration with these new statuses, and the groups of chef instructors and cooking students are respecified. The population members are updated based on the implementation of the CBOA steps according to Eqs. (4) to (17) until the last iteration of the algorithm. After reaching the maximum value of the iteration variable CBOA, the best candidate solution obtained during the implementation process is presented as the solution to the problem. Various steps of CBOA implementation are presented in the form of a flowchart in Fig. 1 and its pseudocode in Algorithm 1.
Figure 1.
Flowchart of CBOA.
Computational complexity of CBOA
In this subsection, the computational complexity of the CBOA is analyzed. Preparing and initializing the CBOA for an optimization problem, with the number of decision variables , has a computational complexity of , where is the number of CBOA members. Updating the group of chef instructors in two strategies has a computational complexity equal to , where T is the maximum number of CBOA iterations and is the number of chef instructors. Updating the student cooking group in three strategies has a computational complexity equal to . Thus, the total computational complexity of CBOA is equal to .
Simulation studies and results
This section presents simulation studies and an evaluation of the ability of CBOA to solve optimization problems and real practice tasks. For this purpose, a set of 23 standard benchmark objective functions has been employed. For this purpose, a set of 23 standard benchmark objective functions has been employed. The reason for choosing this collection is as follows. Seven unimodal functions to , which have only one main extremum and lack local optimal solutions, have been selected. Therefore, unimodal functions are employed to challenge the exploitation and local search ability of the proposed CBOA algorithm in convergence to global optimal. The six functions in this set, to , are the high-dimensional multimodal type, which, in addition to the main extremum, has several local extremums and local optimal solutions. Thus, high-dimensional multimodal functions are employed to test the CBOA’s exploration and global search capability in accurately scanning the search space, passing local optimal areas, and discovering the main optimal area. The ten functions in this set, to , are selected from the fixed-dimensional multimodal type, whose dimensions and the number of local extremes are less than those of the high-dimensional multimodal functions. These functions are employed to analyze the ability of the proposed CBOA algorithm to strike a balance between exploration and exploitation. The information on this set of benchmark functions is specified in Tables 1, 2 and 3.
Table 1.
Information about unimodal objective functions.
| Objective function | Range | Dimensions () | ||
|---|---|---|---|---|
| 1. | 30 | 0 | ||
| 2. | 30 | 0 | ||
| 3. | 30 | 0 | ||
| 4. | 30 | 0 | ||
| 5. | 30 | 0 | ||
| 6. | 30 | 0 | ||
| 7. | 30 | 0 | ||
Table 2.
Information about high-dimensional multimodal objective functions.
| Objective function | Range | Dimensions () | ||
|---|---|---|---|---|
| 8. | 30 | |||
| 9. | 30 | 0 | ||
| 10. | 30 | 0 | ||
| 11. | 30 | 0 | ||
| 12. | where , | 30 | 0 | |
| 13. | 30 | 0 | ||
Table 3.
Information about fixed-dimensional multimodal objective functions.
| Objective function | Range | Dimensions () | ||
|---|---|---|---|---|
| 14. | ||||
| 15. | ||||
| 16. | ||||
| 17. |
|
[− 5, 10][0, 15] | ||
| 18. | ||||
| 19. | ||||
| 20. | ||||
| 21. | ||||
| 22. | ||||
| 23. | ||||
The performance of the proposed CBOA approach in optimization is compared with the results of 12 well-known metaheuristic algorithms. The criterion for selecting these 12 competitor algorithms is as follows. PSO, GA, and DE are three prevalent algorithms that have been employed in many optimization applications. CMA, GSA, TLBO, GWO, MVO, and WOA are the six most cited algorithms that always have interested researchers. Finally, the three algorithms, MPA, TSA, and HBO, are the algorithms that have been released recently and have received a lot of attention and application in this short period. The values adopted for the control parameters of the competitor algorithms are specified in Table 4.
Table 4.
Adopted values for control parameters of competitor metaheuristic algorithms.
| Algorithm | Parameter | Value |
|---|---|---|
| GA | Population size | 100 |
| Type | Real coded | |
| Selection | Roulette wheel (Proportionate) | |
| Crossover | Whole arithmetic (, ) | |
| Mutation | Gaussian (Probability = 0.05) | |
| PSO | Population size | 50 |
| Topology | Fully connected | |
| Cognitive and social constant | ||
| Inertia weight | Linear reduction from 0.9 to 0.1 | |
| Velocity limit | 10% of the dimension range | |
| GSA | Population size | 50 |
| Alpha, G0, Rnorm, Rpower | 20, 100, 2, 1 | |
| TLBO | Population size | 50 |
| : teaching factor | where | |
| random number | rand is a random number in | |
| GWO | Population size | 30 |
| Convergence parameter (a) | a: Linear reduction from 2 to 0 | |
| MVO | Population size | 30 |
| Wormhole existence probability (WEP) | and | |
| Exploitation accuracy over iterations (p) | ||
| WOA | Population size | 30 |
| Convergence parameter (a) | a: Linear reduction from 2 to 0 | |
| r is a random vector in the interval | ||
| l is a random number in | ||
| TSA | Population size | 30 |
| and | 1, 4 | |
| Random numbers from the interval | ||
| MPA | Population size | 30 |
| Constant number | ||
| Random vector | is a vector of uniform random numbers from the interval | |
| Fish aggregating devices (FADs) | ||
| Binary vector | or 1 | |
| HBA | Population size | 30 |
| The ability of a honey badger to get food | ||
| Constant number | ||
| DE | Population size | 100 |
| Scaling factor | 0.5 | |
| Crossover probability | 0.5 | |
| CMA | Num taps | 5 |
| Step size | 0.05 | |
| Leakage factor | 1 | |
| CBOA | Population size | 30 |
The CBOA and each of the competing algorithms are tested on benchmark functions in twenty independent implementations while each execution contains 1000 iterations. Optimization results are reported using six indicators: mean, best, standard deviation (std), median, execution time (ET), and rank.
The CBOA and each competing algorithm are tested on benchmark functions in twenty independent implementations, while each execution contains 1000 iterations. Optimization results are reported using six indicators: mean, best, standard deviation (std), median, execution time (ET), and rank.
Evaluation unimodal objective function
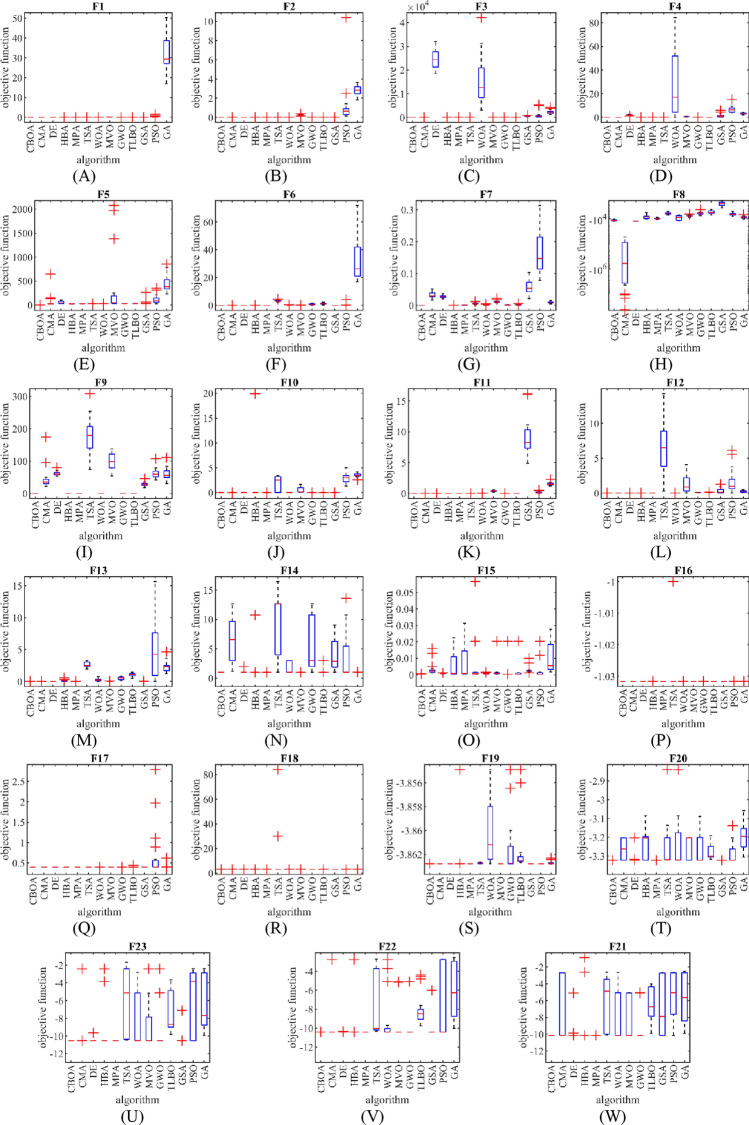
The optimization results of the unimodal functions to using CBOA and competitor algorithms are given in Table 5. The optimization results show that the CBOA has performed very well in optimizing , , , , and and has been able to converge to the global optimal of these functions. In optimizing the functions and , the CBOA has been able to deliver good results and rank the best optimizer among the compared algorithms. The simulation results show that CBOA has a self-evident superiority over competitor algorithms and, with high exploitation ability, has converged to very suitable solutions.
Table 5.
Results of optimization of CBOA and competitor metaheuristics on the unimodal function.
| CBOA | CMA | DE | HBA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0 | 3.87E−12 | 2.65E−12 | 4.4E−277 | 2.95E−50 | 1.41E−46 | 2.5E−154 | 0.165132 | 8.49E−59 | 9.24E−74 | 1.06E−16 | 0.168284 | 32.30955 | |
| Best | 0 | 1.08E−12 | 1.09E−12 | 2.4E−287 | 1.55E−52 | 2.63E−51 | 1E−164 | 0.098704 | 3.66E−61 | 6.41E−77 | 4.4E−17 | 2.32E−06 | 17.01188 | |
| Std | 0 | 1.8E−12 | 1.13E−12 | 0 | 4.89E−50 | 4.47E−46 | 1E−153 | 0.044016 | 1.53E−58 | 3.28E−73 | 5.98E−17 | 0.377572 | 9.537409 | |
| Median | 0 | 3.55E−12 | 2.25E−12 | 1.8E−279 | 6.52E−51 | 5E−48 | 2.1E−157 | 0.157209 | 2.47E−59 | 8.67E−75 | 8.71E−17 | 0.002097 | 29.40147 | |
| ET | 2.172735 | 6.092415 | 5.748222 | 0.553321 | 3.445383 | 1.148152 | 0.568891 | 3.074551 | 1.93628 | 1.905436 | 3.862345 | 0.537751 | 0.815548 | |
| Rank | 1 | 10 | 9 | 2 | 6 | 7 | 3 | 11 | 5 | 4 | 8 | 12 | 13 | |
| Mean | 0 | 7E−06 | 3.25E−08 | 4.4E−146 | 8.73E−28 | 6.93E−29 | 7.1E−106 | 0.267917 | 1.08E−34 | 6.48E−39 | 8.26E−08 | 1.186001 | 2.812708 | |
| Best | 0 | 3.82E−06 | 1.65E−08 | 5E−150 | 3.2E−30 | 7.49E−30 | 7.4E−115 | 0.137216 | 1.36E−35 | 8.26E−40 | 4.05E−08 | 0.141104 | 1.815701 | |
| Std | 0 | 2.94E−06 | 8.52E−09 | 1.5E−145 | 1.65E−27 | 8.97E−29 | 1.8E−105 | 0.057929 | 8.92E−35 | 8.58E−39 | 1.18E−07 | 2.235033 | 0.477151 | |
| Median | 0 | 5.8E−06 | 3.11E−08 | 7.1E−148 | 1.95E−28 | 3.51E−29 | 6.1E−108 | 0.261335 | 8.56E−35 | 3.94E−39 | 5.22E−08 | 0.664504 | 2.832172 | |
| ET | 2.219213 | 6.066346 | 5.848163 | 0.564548 | 3.160192 | 1.175819 | 0.597698 | 2.799057 | 2.012479 | 2.011396 | 3.873261 | 0.531398 | 0.779758 | |
| Rank | 1 | 10 | 8 | 2 | 7 | 6 | 3 | 11 | 5 | 4 | 9 | 12 | 13 | |
| Mean | 0 | 6.83E−05 | 24,716.62 | 7.9E−204 | 9.31E−13 | 1.9E−11 | 15,520.85 | 13.69663 | 8.79E−16 | 3.76E−25 | 479.0439 | 898.3863 | 2271.434 | |
| Best | 0 | 1.15E−05 | 18,432.73 | 9.2E−220 | 4.38E−17 | 1.83E−19 | 3015.781 | 7.076154 | 3.09E−19 | 4.18E−29 | 214.1529 | 46.09636 | 1199.627 | |
| Std | 0 | 5.08E−05 | 3946.206 | 0 | 1.73E−12 | 7.11E−11 | 9780.884 | 5.317871 | 1.73E−−15 | 7.87E−25 | 140.3307 | 1516.41 | 827.2212 | |
| Median | 0 | 5.93E−05 | 24,419.55 | 1.6E−208 | 2.79E−14 | 2.97E−14 | 12,635.08 | 12.11916 | 1.09E−16 | 1.98E−26 | 463.5805 | 502.566 | 2112.874 | |
| ET | 6.621329 | 7.408674 | 7.488921 | 2.055253 | 7.210372 | 2.876052 | 2.174281 | 6.278508 | 3.558108 | 6.204809 | 5.127676 | 1.936225 | 2.226537 | |
| Rank | 1 | 7 | 13 | 2 | 5 | 6 | 12 | 8 | 4 | 3 | 9 | 10 | 11 | |
| Mean | 0 | 0.000159 | 1.983901 | 9.5E−120 | 3.17E−19 | 0.009342 | 28.50847 | 0.500893 | 1.71E−14 | 3E−30 | 1.345517 | 6.592888 | 3.143331 | |
| Best | 0 | 8.69E−05 | 1.316701 | 3.5E−124 | 4.5E−20 | 0.000147 | 0.001866 | 0.247351 | 1.28E−15 | 6.86E−32 | 1.54E−08 | 4.131017 | 1.999125 | |
| Std | 0 | 5.52E−05 | 0.343872 | 1.9E−119 | 2.31E−19 | 0.012302 | 31.87155 | 0.135805 | 2.66E−14 | 3.42E−30 | 1.598979 | 2.599888 | 0.582495 | |
| Med | 0 | 0.000151 | 2.000134 | 3.7E−121 | 2.92E−19 | 0.002038 | 16.99128 | 0.51331 | 8.78E−15 | 1.55E−30 | 0.805803 | 6.449158 | 3.157808 | |
| ET | 2.134919 | 6.048563 | 5.446143 | 0.553277 | 3.030702 | 1.113022 | 0.564871 | 2.946676 | 1.425534 | 1.915917 | 3.81435 | 0.541684 | 0.748298 | |
| Rank | 1 | 6 | 10 | 2 | 4 | 7 | 13 | 8 | 5 | 3 | 9 | 12 | 11 | |
| Mean | 0.000306 | 62.99214 | 52.93904 | 21.83121 | 23.47877 | 28.18633 | 27.05095 | 336.8397 | 26.69749 | 27.00714 | 40.06591 | 113.1056 | 445.1666 | |
| Best | 7.21E−05 | 17.59206 | 26.21261 | 20.89173 | 22.33217 | 26.36048 | 26.42674 | 27.57318 | 25.25594 | 25.76632 | 25.87646 | 22.77282 | 231.7436 | |
| Std | 0.00023 | 142.2852 | 27.60379 | 0.511057 | 0.472798 | 0.82398 | 0.363525 | 649.711 | 0.669329 | 0.992995 | 53.68502 | 90.0744 | 177.5128 | |
| Median | 0.000232 | 19.38299 | 39.00547 | 21.94289 | 23.49991 | 28.63377 | 27.05451 | 45.72737 | 27.09079 | 26.51047 | 26.16945 | 86.01345 | 380.1141 | |
| ET | 2.910138 | 6.151182 | 5.975958 | 0.820889 | 3.802344 | 1.386446 | 0.876656 | 3.45164 | 1.849231 | 2.616349 | 544.2818 | 0.765122 | 0.998529 | |
| Rank | 1 | 10 | 9 | 2 | 3 | 7 | 6 | 12 | 4 | 5 | 8 | 11 | 13 | |
| Mean | 0 | 4.49E−12 | 2.65E−12 | 9.74E−08 | 1.6E−09 | 3.225523 | 0.094859 | 0.155856 | 0.65113 | 1.170598 | 1.04E−16 | 0.230787 | 31.80092 | |
| Best | 0 | 1.55E−12 | 5.64E−13 | 5.49E−09 | 8.41E−10 | 2.295798 | 0.003153 | 0.058846 | 2.06E−05 | 0.243967 | 4.72E−17 | 6.24E−05 | 17.06432 | |
| Std | 0 | 1.99E−12 | 1.2E−12 | 1.27E−07 | 7.43E−10 | 0.530484 | 0.118184 | 0.047567 | 0.436312 | 0.46836 | 3.05E−17 | 0.969372 | 14.38352 | |
| Median | 0 | 4.18E−12 | 2.88E−12 | 4.64E−08 | 1.48E−09 | 3.069241 | 0.050352 | 0.152637 | 0.621537 | 1.1358 | 1E−16 | 0.004883 | 26.29787 | |
| ET | 2.213583 | 6.045107 | 5.258846 | 0.629315 | 3.078155 | 1.132735 | 0.691941 | 2.934654 | 2.037816 | 2.064517 | 1555.628 | 0.566689 | 0.766043 | |
| Rank | 1 | 4 | 3 | 6 | 5 | 12 | 7 | 8 | 10 | 11 | 2 | 9 | 13 | |
| Mean | 4.26E−05 | 0.032899 | 0.027278 | 5.31E−05 | 0.000759 | 0.00571 | 0.001145 | 0.011238 | 0.000888 | 0.002197 | 0.058194 | 0.168787 | 0.008934 | |
| Best | 5.39E−06 | 0.017076 | 0.019679 | 3.7E−05 | 0.000128 | 0.001473 | 9.36E−06 | 0.007012 | 0.000149 | 0.000448 | 0.021831 | 0.078608 | 0.004354 | |
| Std | 2.38E−05 | 0.009295 | 0.004461 | 2.78E−05 | 0.000428 | 0.003007 | 0.001365 | 0.00353 | 0.000638 | 0.001353 | 0.021042 | 0.068875 | 0.002685 | |
| Median | 3.84E−05 | 0.029407 | 0.027521 | 4.44E−05 | 0.000718 | 0.004762 | 0.00054 | 0.010196 | 0.000704 | 0.002016 | 0.053531 | 0.14742 | 0.008549 | |
| ET | 4.444716 | 6.626775 | 5.918818 | 1.427673 | 4.863401 | 1.857502 | 1.622592 | 4.414998 | 2.362614 | 4.26488 | 4.553437 | 1.232753 | 1.46431 | |
| Rank | 1 | 11 | 10 | 2 | 3 | 7 | 5 | 9 | 4 | 6 | 12 | 13 | 8 | |
| Sum rank | 7 | 58 | 62 | 18 | 33 | 52 | 49 | 67 | 37 | 36 | 57 | 79 | 82 | |
| Mean rank | 1 | 8.285714 | 8.857143 | 2.5714285 | 4.714286 | 7.428571 | 7 | 9.571429 | 5.285714 | 5.142857 | 8.142857 | 11.28571 | 11.71429 | |
| Total rank | 1 | 9 | 10 | 2 | 3 | 7 | 6 | 11 | 5 | 4 | 8 | 12 | 13 | |
Evaluation high-dimensional multimodal objective function
Results of CBOA and all competitor algorithms on high-dimensional multimodal functions of to are reported in Table 6. CBOA has achieved precisely the global optimal solution for and , which shows us the high exploration power of CBOA. In optimizing the function , the proposed CBOA has performed well, and for this function is ranked as the first best optimizer in competition with the compared algorithms. The simulation results indicate the high exploration power of CBOA in identifying the best optimal region and the superiority of CBOA compared to competitor algorithms.
Table 6.
Results of optimization of CBOA and competitor metaheuristics on the high-dimensional multimodal function.
| CBOA | CMA | DE | HBA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | − 11,416.7 | − 4,801,045 | − 12,454.5 | − 8544.1 | − 9692.45 | − 6130.76 | − 9160.03 | − 7682.93 | − 6049.79 | − 5508.84 | − 2618.05 | − 6579.01 | − 8661.75 | |
| Best | − 12,332.6 | − 4.4E+07 | − 12,569.5 | − 10,097.4 | − 10,570.1 | − 7089.62 | − 11,847.1 | − 8717.73 | − 7464.67 | − 6946.93 | − 3587.57 | − 8062.67 | − 9997.91 | |
| Std | 608.3322 | 10,233,996 | 124.9645 | 1197.938 | 453.6502 | 540.5303 | 1934.878 | 518.1982 | 718.0628 | 860.7038 | 541.5419 | 813.4314 | 727.7971 | |
| Median | − 11,572.6 | − 608,750 | − 12,451 | − 8477.34 | − 9710.72 | − 6223.05 | − 8800.53 | − 7736.1 | − 5876.46 | − 5527.42 | − 2448.32 | − 6554.02 | − 8708.15 | |
| ET | 3.32474 | 6.272527 | 5.682899 | 0.9268 | 3.733725 | 1.363383 | 1.03715 | 2.590324 | 1.651692 | 3.011316 | 4.237375 | 0.816449 | 1.100977 | |
| Rank | 3 | 1 | 2 | 7 | 4 | 10 | 5 | 8 | 11 | 12 | 13 | 9 | 6 | |
| Mean | 0 | 44.71531 | 61.37856 | 0 | 0 | 176.2674 | 0 | 97.68891 | 1.42E−14 | 0 | 27.46085 | 60.91495 | 59.92033 | |
| Best | 0 | 21.88908 | 53.01217 | 0 | 0 | 73.64015 | 0 | 53.80054 | 0 | 0 | 17.90926 | 41.78905 | 29.99069 | |
| Std | 0 | 34.17988 | 6.678404 | 0 | 0 | 54.01573 | 0 | 26.56134 | 2.53E−14 | 0 | 6.328985 | 15.30696 | 19.0714 | |
| Median | 0 | 34.82353 | 59.66433 | 0 | 0 | 179.0786 | 0 | 98.10387 | 0 | 0 | 26.86388 | 59.20266 | 56.10198 | |
| ET | 2.538358 | 6.205782 | 5.169585 | 0.716117 | 3.369601 | 1.28455 | 0.76484 | 3.217982 | 1.464147 | 2.281739 | 3.880075 | 0.667393 | 0.898574 | |
| Rank | 1 | 4 | 7 | 1 | 1 | 9 | 1 | 8 | 2 | 1 | 3 | 6 | 5 | |
| Mean | 8.88E−16 | 7.25E−07 | 4.66E−07 | 3.983745 | 4.09E−15 | 1.701773 | 3.73E−15 | 0.501389 | 1.62E−14 | 4.26E−15 | 7.76E−09 | 3.003923 | 3.519331 | |
| Best | 8.88E−16 | 4.64E−07 | 2.39E−07 | 8.88E−16 | 8.88E−16 | 1.51E−14 | 8.88E−16 | 0.082022 | 1.51E−14 | 8.88E−16 | 5.52E−09 | 1.340457 | 2.591243 | |
| Std | 0 | 2.12E−07 | 1.26E−07 | 8.174475 | 1.09E−15 | 1.597276 | 2.47E−15 | 0.532278 | 2.33E−15 | 7.94E−16 | 1.64E−09 | 1.002929 | 0.345136 | |
| Median | 8.88E−16 | 6.94E−07 | 4.57E−07 | 8.88E−16 | 4.44E−15 | 2.542805 | 4.44E−15 | 0.150768 | 1.51E−14 | 4.44E−15 | 7.64E−09 | 2.997188 | 3.461528 | |
| ET | 2.493472 | 6.140622 | 6.096217 | 0.74041 | 3.261045 | 1.263234 | 0.810686 | 3.316977 | 1.495081 | 2.358528 | 3.971348 | 0.670133 | 0.930872 | |
| Rank | 1 | 8 | 7 | 13 | 3 | 10 | 2 | 9 | 5 | 4 | 6 | 11 | 12 | |
| Mean | 0 | 0.001108 | 2.13E−10 | 0 | 0 | 0.005297 | 0.003099 | 0.393366 | 0.002687 | 0 | 8.937934 | 0.155581 | 1.52779 | |
| Best | 0 | 5.91E−11 | 3.33E−12 | 0 | 0 | 0 | 0 | 0.201826 | 0 | 0 | 4.884369 | 0.012736 | 1.217033 | |
| Std | 0 | 0.003615 | 6.53E−10 | 0 | 0 | 0.007265 | 0.013861 | 0.087275 | 0.006679 | 0 | 3.012101 | 0.147889 | 0.242677 | |
| Median | 0 | 1.8E−10 | 3.01E−11 | 0 | 0 | 0 | 0 | 0.398108 | 0 | 0 | 8.251011 | 0.116847 | 1.468467 | |
| ET | 3.256439 | 6.444046 | 7.498936 | 1.002643 | 3.606022 | 1.436769 | 1.091555 | 3.741729 | 1.735395 | 3.150524 | 4.587756 | 0.913732 | 1.177281 | |
| Rank | 1 | 3 | 2 | 1 | 1 | 6 | 5 | 8 | 4 | 1 | 10 | 7 | 9 | |
| Mean | 1.96E−09 | 2.18E−12 | 3.95E−13 | 8.45E−09 | 1.99E−10 | 6.305474 | 0.005405 | 1.231756 | 0.035924 | 0.079774 | 0.28432 | 1.662913 | 0.201968 | |
| Best | 3.96E−10 | 6.95E−13 | 1.16E−13 | 3.34E−10 | 5.48E−10 | 0.264734 | 0.001423 | 0.000924 | 0.013184 | 0.056662 | 6.02E−19 | 0.000169 | 0.058181 | |
| Std | 1.23E−09 | 8.82E−13 | 2.71E−13 | 1.47E−08 | 7.9E−09 | 3.766997 | 0.004457 | 1.21416 | 0.013328 | 0.020464 | 0.363627 | 1.723156 | 0.125589 | |
| Median | 1.73E−09 | 2.14E−12 | 3.19E−13 | 4.05E−09 | 1.98E−09 | 6.493901 | 0.00338 | 0.8514 | 0.037334 | 0.075443 | 0.103669 | 0.960977 | 0.175433 | |
| ET | 9.718521 | 7.946868 | 8.937058 | 3.303009 | 7.479572 | 3.532742 | 3.727992 | 7.699429 | 4.874407 | 9.291213 | 6.513698 | 2.878026 | 3.056695 | |
| Rank | 3 | 2 | 1 | 5 | 4 | 13 | 6 | 11 | 7 | 8 | 10 | 12 | 9 | |
| Mean | 5.05E−08 | 5.11E−11 | 2.27E−12 | 0.114684 | 0.002561 | 2.648762 | 0.246551 | 0.02783 | 0.487249 | 1.052281 | 0.006549 | 4.893821 | 2.342733 | |
| Best | 6.18E−09 | 1.42E−11 | 5.44E−13 | 1.57E−08 | 1.42E−09 | 1.949438 | 0.031826 | 0.009919 | 0.100058 | 0.500205 | 5.54E−18 | 0.012249 | 1.205092 | |
| Std | 7.54E−08 | 2.68E−11 | 1.16E−12 | 0.134062 | 0.004919 | 0.381937 | 0.207692 | 0.012327 | 0.220038 | 0.253877 | 0.010866 | 4.946219 | 0.868383 | |
| Median | 2.26E−08 | 4.68E−11 | 2.35E−12 | 0.097372 | 3.66E−09 | 2.494033 | 0.221514 | 0.027171 | 0.583629 | 1.087803 | 1.83E−17 | 4.264547 | 2.307728 | |
| ET | 9.253492 | 7.923011 | 8.270599 | 3.27416 | 7.552763 | 3.531932 | 3.678267 | 7.733775 | 4.754169 | 8.792697 | 6.567627 | 2.870053 | 3.094304 | |
| Rank | 3 | 2 | 1 | 7 | 4 | 12 | 8 | 6 | 9 | 10 | 5 | 13 | 11 | |
| Sum rank | 12 | 20 | 20 | 34 | 17 | 60 | 27 | 50 | 38 | 36 | 47 | 58 | 52 | |
| Mean rank | 2 | 3.333333 | 3.333333 | 5.666667 | 2.833333 | 10 | 4.5 | 8.333333 | 6.333333 | 6 | 7.833333 | 9.666667 | 8.666667 | |
| Total rank | 1 | 3 | 3 | 5 | 2 | 12 | 4 | 9 | 7 | 6 | 8 | 11 | 10 | |
Evaluation fixed-dimensional multimodal objective function
The results of the CBOA and competitor algorithms for the fixed-dimensional multimodal functions to are presented in Table 7. The optimization results show that the CBOA, based on the “mean index’’, alone is the best optimizer to tackle the functions , , and .
Table 7.
Results of optimization of the CBOA and competitor metaheuristics on fixed-dimensional multimodal function.
| CBOA | CMA | DE | HBA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.998004 | 6.468644 | 1.097407 | 1.974522 | 0.998004 | 9.754139 | 1.692637 | 0.998004 | 5.011135 | 1.29562 | 3.977845 | 3.596373 | 1.001145 | |
| Best | 0.998004 | 1.149956 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | |
| Std | 6.62E−17 | 3.807911 | 0.305955 | 3.005658 | 7.2E−17 | 5.084877 | 0.916108 | 5.7E−12 | 4.396499 | 0.72687 | 2.839185 | 3.748318 | 0.010488 | |
| Median | 0.998004 | 6.574582 | 0.998004 | 0.998004 | 0.998004 | 12.67051 | 0.998004 | 0.998004 | 2.982105 | 0.998004 | 2.890313 | 0.998004 | 0.998004 | |
| ET | 8.263481 | 7.439983 | 11.49533 | 5.927204 | 12.84467 | 5.237797 | 6.893766 | 9.8159 | 5.559464 | 15.56081 | 6.505227 | 4.960642 | 5.409746 | |
| Rank | 1 | 12 | 5 | 8 | 2 | 13 | 7 | 3 | 11 | 6 | 10 | 9 | 4 | |
| Mean | 0.000344 | 0.0034 | 0.000686 | 0.005788 | 0.006988 | 0.006334 | 0.000594 | 0.002723 | 0.002313 | 0.002482 | 0.002868 | 0.002183 | 0.010056 | |
| Best | 0.000308 | 0.001084 | 0.000451 | 0.000307 | 0.00032 | 0.000308 | 0.000309 | 0.000308 | 0.000307 | 0.000309 | 0.001183 | 0.000307 | 0.001759 | |
| Std | 6.05E−16 | 3.94E−14 | 1.43E−15 | 9.18E−14 | 1.03E−13 | 1.39E−13 | 3.77E−15 | 6.04E−14 | 6.17E−14 | 6.12E−14 | 2.03E−14 | 4.98E−14 | 9.09E−14 | |
| Median | 0.00032 | 0.002026 | 0.000678 | 0.000765 | 0.000772 | 0.000487 | 0.000459 | 0.000724 | 0.000307 | 0.000316 | 0.002326 | 0.000307 | 0.005585 | |
| ET | 1.021564 | 4.023251 | 5.574032 | 0.536539 | 1.728231 | 0.564211 | 0.637955 | 1.323245 | 0.60876 | 1.95416 | 1.90813 | 0.435123 | 0.717282 | |
| Rank | 1 | 9 | 3 | 10 | 12 | 11 | 2 | 7 | 5 | 6 | 8 | 4 | 13 | |
| Mean | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.02847 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | |
| Best | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | |
| Std | 1.41E−16 | 2.28E−15 | 2.28E−15 | 2.04E−15 | 1.84E−15 | 9.74E−14 | 8.92E−12 | 3.45E−11 | 4.44E−14 | 1.32E−10 | 1.44E−10 | 1.14E−10 | 1.62E−10 | |
| Median | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | |
| ET | 1.341562 | 3.836853 | 5.448002 | 0.452356 | 1.663918 | 0.497087 | 0.576034 | 1.14112 | 0.489379 | 1.733055 | 1.756584 | 0.328678 | 0.632265 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 7 | 2 | 4 | 3 | 6 | 1 | 1 | 5 | |
| Mean | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397904 | 0.397888 | 0.397887 | 0.397888 | 0.400341 | 0.397887 | 0.672818 | 0.409121 | |
| Best | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397888 | 0.397887 | 0.397887 | 0.397887 | 0.397899 | 0.397887 | 0.397887 | 0.397887 | |
| Std | 0 | 0 | 0 | 0 | 0 | 1.88E−16 | 1.68E−17 | 7.31E−19 | 4.57E−18 | 1.03E−13 | 0 | 6.27E−12 | 4.94E−13 | |
| Median | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397897 | 0.397888 | 0.397887 | 0.397888 | 0.397956 | 0.397887 | 0.397887 | 0.397891 | |
| ET | 2.015974 | 3.879041 | 5.777031 | 0.42436 | 1.65395 | 0.482376 | 0.567438 | 1.066481 | 0.479291 | 1.579686 | 2.054971 | 0.281283 | 0.577906 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 5 | 4 | 2 | 3 | 6 | 1 | 8 | 7 | |
| Mean | 3 | 3 | 3 | 3 | 3 | 8.400016 | 3.000012 | 3 | 3.000008 | 3.000002 | 3 | 3 | 3.001894 | |
| Best | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| Std | 1.19E−17 | 7.96E−27 | 4.2E−27 | 6.98E−27 | 1.07E−26 | 1.88E−10 | 1.72E−16 | 6.04E−18 | 6.08E−17 | 2.99E−17 | 1.92E−26 | 2.82E−26 | 3.37E−14 | |
| Median | 3 | 3 | 3 | 3 | 3 | 3.000008 | 3.000006 | 3 | 3.000006 | 3 | 3 | 3 | 3.00035 | |
| ET | 2.652104 | 3.793405 | 5.677689 | 0.379509 | 1.501908 | 0.467816 | 0.494053 | 1.017728 | 0.412652 | 1.523375 | 1.922881 | 0.264965 | 0.567245 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 9 | 7 | 4 | 6 | 5 | 3 | 2 | 8 | |
| Mean | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86121 | − 3.86278 | − 3.86273 | − 3.86002 | − 3.86278 | − 3.86112 | − 3.86175 | − 3.86278 | − 3.86278 | − 3.86272 | |
| Best | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86277 | − 3.86278 | − 3.86278 | − 3.86269 | − 3.86278 | − 3.86278 | − 3.86278 | |
| Std | 1.86E−16 | 2.28E−26 | 2.28E−26 | 3.23E−14 | 2.28E−26 | 3.95E−16 | 2.86E−14 | 9.56E−19 | 3.07E−14 | 2.17E−14 | 1.95E−26 | 2.03E−26 | 1.23E−15 | |
| Median | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86274 | − 3.86119 | − 3.86278 | − 3.86275 | − 3.86252 | − 3.86278 | − 3.86278 | − 3.86277 | |
| ET | 3.1452930 | 4.084194 | 5.110906 | 0.562827 | 1.844683 | 0.61375 | 0.691191 | 1.336033 | 0.618499 | 2.048364 | 2.215913 | 0.434463 | 0.743604 | |
| Rank | 1 | 1 | 1 | 6 | 1 | 3 | 8 | 2 | 7 | 5 | 1 | 1 | 4 | |
| Mean | − 3.322 | − 3.26255 | − 3.3099 | − 3.24296 | − 3.322 | − 3.25141 | − 3.24583 | − 3.23852 | − 3.26038 | − 3.27726 | − 3.322 | − 3.28245 | − 3.19973 | |
| Best | − 3.322 | − 3.322 | − 3.322 | − 3.322 | − 3.322 | − 3.32129 | − 3.32194 | − 3.322 | − 3.32199 | − 3.31657 | − 3.322 | − 3.322 | − 3.30608 | |
| Std | 1.78E−16 | 6.1E−13 | 3.65E−13 | 7.89E−13 | 4.08E−27 | 1.16E−12 | 1.26E−12 | 5.61E−13 | 8.32E−13 | 4.92E−13 | 4.2E−27 | 7.22E−13 | 7.02E−13 | |
| Median | − 3.32199 | − 3.26255 | − 3.322 | − 3.2031 | − 3.322 | − 3.31986 | − 3.32047 | − 3.2029 | − 3.32199 | − 3.30137 | − 3.322 | − 3.322 | − 3.19502 | |
| ET | 2.546312 | 4.168919 | 5.611372 | 0.591109 | 1.961109 | 0.666685 | 0.717402 | 1.586025 | 0.719107 | 2.123327 | 2.376263 | 0.464815 | 0.75444 | |
| Rank | 1 | 5 | 2 | 9 | 1 | 7 | 8 | 10 | 6 | 4 | 1 | 3 | 11 | |
| Mean | − 10.1532 | − 6.79155 | − 9.88592 | − 9.31345 | − 10.1532 | − 6.3241 | − 8.49107 | − 7.87273 | − 9.13554 | − 6.28747 | − 6.70335 | − 5.2634 | − 5.65214 | |
| Best | − 10.1532 | − 10.1532 | − 10.1532 | − 10.1532 | − 10.1532 | − 10.1049 | − 10.1531 | − 10.1532 | − 10.1531 | − 9.91428 | − 10.1532 | − 10.1532 | − 9.91577 | |
| Std | 1.52E−16 | 3.81E−11 | 1.13E−11 | 2.6E−11 | 2.19E−15 | 3.21E−11 | 2.65E−11 | 2.59E−11 | 2.09E−11 | 1.83E−11 | 3.6E−11 | 3.08E−11 | 2.71E−11 | |
| Median | − − 10.1532 | − 10.1532 | − 10.1532 | − 10.1532 | − 10.1532 | − 4.86615 | − 10.1479 | − 10.1531 | − 10.1528 | − 6.73438 | − 7.90835 | − 5.0552 | − 5.63103 | |
| ET | 2.146528 | 4.163368 | 5.270078 | 0.74175 | 2.364909 | 0.742612 | 0.896988 | 1.823964 | 0.775067 | 2.447205 | 2.386266 | 0.586512 | 0.87221 | |
| Rank | 1 | 8 | 3 | 4 | 2 | 10 | 6 | 7 | 5 | 11 | 9 | 13 | 12 | |
| Mean | − 10.4029 | − 10.0211 | − 10.4006 | − 9.25738 | − 10.4029 | − 7.26663 | − 9.11739 | − 9.60765 | − 10.1367 | − 8.07294 | − 10.1831 | − 7.0107 | − 6.10828 | |
| Best | − 10.4029 | − 10.4029 | − 10.4029 | − 10.4029 | − 10.4029 | − 10.3162 | − 10.4029 | − 10.4029 | − 10.4029 | − 9.75254 | − 10.4029 | − 10.4029 | − 10.017 | |
| Std | 1.12E−16 | 1.71E−11 | 9.58E−14 | 2.8E−11 | 3.65E−15 | 3.38E−11 | 2.58E−11 | 1.94E−11 | 1.19E−11 | 1.59E−11 | 9.83E−12 | 3.85E−11 | 2.61E−11 | |
| Median | − 10.4029 | − 10.4029 | − 10.4029 | − 10.4029 | − 10.4029 | − 10.0266 | − 10.3988 | − 10.4029 | − 10.4025 | − 8.49275 | − 10.4029 | − 10.4029 | − 6.26211 | |
| ET | 2.165974 | 4.267036 | 5.149368 | 0.828738 | 2.47023 | 0.830113 | 0.991285 | 2.111943 | 0.881028 | 2.686496 | 2.167587 | 0.666191 | 0.974745 | |
| rank | 1 | 6 | 3 | 8 | 2 | 11 | 9 | 7 | 5 | 10 | 4 | 12 | 13 | |
| Mean | − 10.5364 | − 9.72522 | − 10.4914 | − 9.79563 | − 10.5364 | − 6.27469 | − 8.13732 | − 9.05875 | − 9.58937 | − 7.44495 | − 10.3652 | − 6.10808 | − 6.58071 | |
| Best | − 10.5364 | − 10.5364 | − 10.5364 | − 10.5364 | − 10.5364 | − 10.4786 | − − 10.5357 | − 10.5364 | − 10.5363 | − 9.81289 | − 10.5364 | − 10.5364 | − 9.95588 | |
| Std | 1.63E−16 | 2.5E−11 | 2.01E−12 | 2.29E−11 | 2.7E−16 | 3.9E−11 | 3.08E−11 | 2.69E−11 | 2.37E−11 | 2.11E−11 | 7.66E−12 | 3.77E−11 | 2.75E−11 | |
| Median | − 10.5364 | − 10.5364 | − 10.5364 | − 10.5364 | − 10.5364 | − 5.12692 | − 10.5292 | − 10.5363 | − 10.5357 | − 8.67305 | − 10.5364 | − 3.83543 | − 7.68126 | |
| ET | 2.314952 | 4.380511 | 5.227086 | 0.966058 | 2.820167 | 0.956041 | 1.130458 | 2.209019 | 1.011938 | 3.055197 | 2.329461 | 0.801659 | 1.083483 | |
| Rank | 1 | 6 | 3 | 5 | 2 | 12 | 9 | 8 | 7 | 10 | 4 | 13 | 11 | |
| Sum rank | 10 | 50 | 23 | 53 | 25 | 88 | 62 | 54 | 58 | 69 | 42 | 66 | 88 | |
| Mean rank | 1 | 5 | 2.3 | 5.3 | 2.5 | 8.8 | 6.2 | 5.4 | 5.8 | 6.9 | 4.2 | 6.6 | 8.8 | |
| Total rank | 1 | 5 | 2 | 6 | 3 | 12 | 9 | 7 | 8 | 11 | 4 | 10 | 12 | |
In the other cases where the CBOA has the same conditions in terms of the “mean index’’, it performs more efficiently than the alternative algorithms due to better values for the “std index’’. Analysis of the simulation results shows that the CBOA performs better than competitor algorithms and has a remarkable ability to strike a balance between exploration and exploitation.
In other cases where the CBOA has the same conditions in terms of the “mean index’’, it has more efficient performance than the alternative algorithms due to better values for the “std index’’. Analysis of the simulation results shows that the CBOA performs better than competitor algorithms and has a remarkable ability to strike a balance between exploration and exploitation.
The performance of CBOA and competitor algorithms in evaluating the benchmark functions to is shown in Fig. 2 using the box plot diagrams.
Figure 2.
The boxplot diagram of CBOA and competitor algorithms performances on to .
Statistical analysis
In this subsection, a statistical analysis of the performance of the CBOA compared to competitor algorithms is provided to determine whether the superiority of the CBOA is statistically significant. To provide this analysis, the Wilcoxon test of rank sums32 with the significance level has been used. In this test, the values of the “-value’’ indicate whether there is a significant difference between the means of the two data samples (thus, if the “-value’’ is less than 0.05, then between two data samples is significant difference). The results of the Wilcoxon test of rank sums for the CBOA and competitor algorithms are released in Table 8. Consequently, since all values obtained for the -value are less than 0.05, the CBOA has a significant statistical superiority over all twelve compared algorithms.
Table 8.
Results of Wilcoxon test of rank sums.
| Compared algorithm | Objective function type | ||
|---|---|---|---|
| Unimodal | High-dimensional multimodal | Fixed-dimensional multimodal | |
| CBOA vs. CMA | 1.01E−24 | 7.53E−03 | 5.75E−03 |
| CBOA vs. DE | 1.01E−24 | 8.25E−03 | 2.75E−07 |
| CBOA vs. HBA | 1.21E−11 | 3.91E−11 | 4.14E−06 |
| CBOA vs. MPA | 1.01E−24 | 0.170913 | 1.63E−14 |
| CBOA vs. TSA | 1.01E−24 | 1.28E−19 | 1.88E−32 |
| CBOA vs. WOA | 2.49E−24 | 5.46E−10 | 2.36E−31 |
| CBOA vs. MVO | 1.01E−24 | 1.97E−21 | 9.13E−25 |
| CBOA vs. GWO | 1.01E−24 | 3.55E−16 | 5.16E−25 |
| CBOA vs. TLBO | 1.01E−24 | 1.04E−14 | 1.96E−30 |
| CBOA vs. GSA | 1.01E−24 | 3.61E−17 | 0.0169847 |
| CBOA vs. PSO | 1.01E−24 | 1.97E−21 | 0.0201922 |
| CBOA vs. GA | 1.01E−24 | 1.97E−21 | 1.2E−33 |
Sensitivity analysis
The proposed CBOA is a stochastic optimizer that can achieve the optimal solution by using its members’ search power in an iteration-based process. Therefore, the values of the parameters and , which represent the number of CBOA members and the total number of iterations of the algorithm, respectively, affect the performance of the CBOA. To study this effect, we analyze the sensitivity of CBOA to changes in values of the and parameters in this subsection.
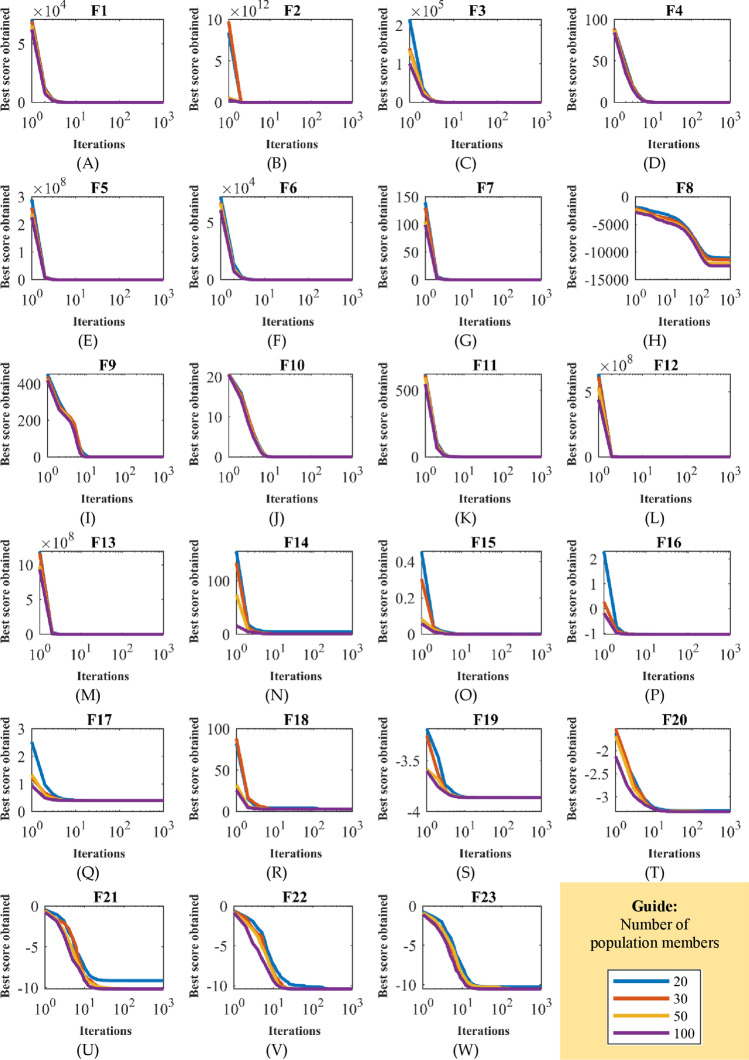
In the first study, to analyze the sensitivity of CBOA to the parameter , the proposed algorithm in independent performance for different values of the parameter equal to 20, 30, 50, and 100 is used to optimize the functions of to . Results of this analysis are presented in Table 9, and CBOA convergence curves to optimize these objective functions under the influence of the changes of the parameter are shown in Fig. 3. Based on simulation results obtained from the sensitivity analysis of the parameter , it is clear that CBOA presents similar results in most objective functions when the parameter is changed, indicating that the CBOA is less affected by the parameter . In other cases of the objective functions, it can be seen that when the value of the parameter increases, then the values of objective functions decrease.
Table 9.
Results of CBOA sensitivity analysis to parameter .
| Objective functions | Number of population members | |||
|---|---|---|---|---|
| 20 | 30 | 50 | 100 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0.000378 | 0.000306 | 0.000144 | 4.23E−05 | |
| 0 | 0 | 0 | 0 | |
| 7.06E−05 | 4.26E−05 | 2.97E−05 | 1.60E−05 | |
| − 11,071 | − 11,416.7 | − 12,119.4 | − 12,504.3 | |
| 0 | 0 | 0 | 0 | |
| 2.84E−15 | 8.88E−16 | 8.88E−16 | 8.88E−16 | |
| 0 | 0 | 0 | 0 | |
| 5.62E−09 | 1.96E−09 | 4.14E−10 | 1.16E−10 | |
| 7.12E−08 | 5.05E−08 | 6.46E−09 | 1.49E−09 | |
| 4.194612 | 0.998004 | 0.998004 | 0.998004 | |
| 0.001348 | 0.000344 | 0.000332 | 0.000321 | |
| − 1.03163 | − 1.03163 | − 1.031630 | − 1.031630 | |
| 0.397892 | 0.397887 | 0.397887 | 0.397887 | |
| 3 | 3 | 3 | 3 | |
| − 3.86235 | − 3.86278 | − 3.86278 | − 3.8628 | |
| − 3.30339 | − 3.3220 | − 3.3220 | − 3.3220 | |
| − 9.13349 | − 10.1532 | − 10.1532 | − 10.1532 | |
| − 10.4027 | − 10.4029 | − 10.4029 | − 10.4029 | |
| − 10.2659 | − 10.5364 | − 10.5364 | − 10.5364 | |
Figure 3.
CBOA convergence curves in the study of sensitivity analysis to parameter .
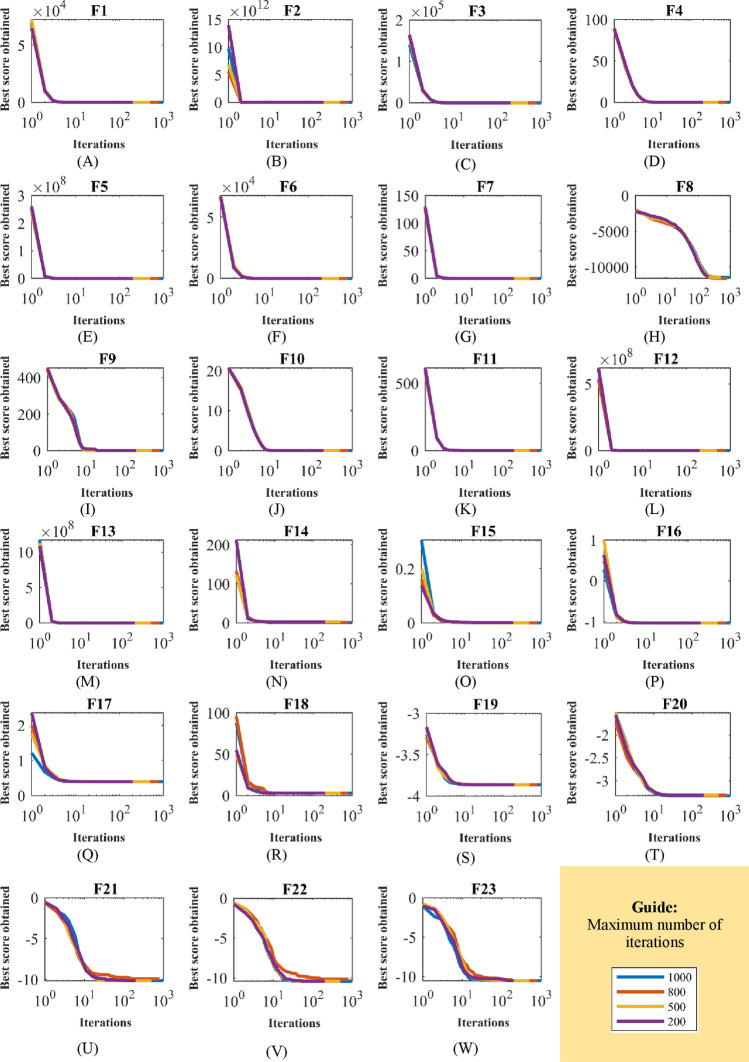
In the second study, to analyze the sensitivity of CBOA to the parameter , the proposed method is implemented in independent performances for different values of the parameter equal to 200, 500, 800, and 1000 on the objective functions to . The results of this analysis are reported in Table 10, and the CBOA convergence curves affected by this study are plotted in Fig. 4. What is clear from the results of the CBOA sensitivity analysis to changes in the parameter is that by increasing the values of the parameter , the performance of CBOA is improved and as a result, the values of objective functions are decreased.
Table 10.
Results of the CBOA sensitivity analysis to parameter .
| Objective functions | Maximum number of iterations | |||
|---|---|---|---|---|
| 200 | 500 | 800 | 1000 | |
| 1.30E−146 | 0 | 0 | 0 | |
| 5.04E−76 | 8.40E−192 | 0 | 0 | |
| 1.10E−127 | 0 | 0 | 0 | |
| 2.46E−72 | 6.60E−184 | 4.20E−294 | 0 | |
| 0.081809 | 0.003117 | 0.000586 | 0.000306 | |
| 0 | 0 | 0 | 0 | |
| 0.00019 | 7.75E−05 | 5.91E−05 | 4.26E−05 | |
| − 11,338.3 | − 11,357.2 | − 11,406.8 | − 11,416.7 | |
| 0 | 0 | 0 | 0 | |
| 2.31E−15 | 1.42E−15 | 1.15E−15 | 8.88E−16 | |
| 0 | 0 | 0 | 0 | |
| 3.84E−05 | 3.66E−08 | 3.81E−09 | 1.96E−09 | |
| 0.000369 | 3.68E−07 | 6.48E−08 | 5.05E−08 | |
| 2.480011 | 2.130218 | 1.542754 | 0.998004 | |
| 0.001379 | 0.000377 | 0.000376 | 0.000344 | |
| − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | |
| 0.39789 | 0.397888 | 0.397889 | 0.397887 | |
| 3 | 3 | 3 | 3 | |
| − 3.86235 | − 3.86243 | − 3.86267 | − 3.86278 | |
| − 3.31573 | − 3.31604 | − 3.31603 | − 3.3220 | |
| − 10.1531 | − 10.1531 | − 10.1532 | − 10.1532 | |
| − 10.4027 | − 10.4028 | − 10.4029 | − 10.4029 | |
| − 10.5361 | − 10.5363 | − 10.5364 | − 10.5364 | |
Figure 4.
CBOA convergence curves in the study of sensitivity analysis to parameter .
Discussion
Metaheuristic algorithms are random approaches with which their main idea employed in the optimization process is random search in the problem-solving space. This random search at both local and global levels is the key to the success of metaheuristic algorithms. In optimization studies, the local search power, which indicates the potential for exploitation, causes the algorithm to look for better solutions around promising candidate solutions and move closer to the optimal global solution. The capability of the “exploitation phase’’ in metaheuristic algorithms is best tested when implemented on functions that have only one main solution. Unimodal functions with this feature are good options for evaluating the exploitation ability. The optimization results of unimodal functions to indicate the high exploitation capability of CBOA, especially in handling to , and . Therefore, the simulation finding from the results of the unimodal functions is that the CBOA has high efficiency in local search and a high potential for exploitation.
The power of global search, which demonstrates the exploration potential of metaheuristic algorithms, allows the algorithm to scan different areas of the search space to discover the optimal global area. The capability of the “exploration phase’’ in metaheuristic algorithms designed for optimization can best be evaluated using optimization problems with several local optimal solutions. Therefore, high-dimensional multimodal functions are a good choice for evaluating exploration ability. The implementation results of CBOA and competitor algorithms on functions to show the high exploration ability of CBOA to global search in various areas of the problem-solving space. This CBOA capability is especially evident in the optimization results of the functions and . The finding from simulations of the CBOA and competitor algorithms on the fixed-dimensional multimodal functions to is that the CBOA, with its high power in global search and exploration, can avoid getting stuck in locally optimal solutions and identify the main optimal region.
The critical point in the capability of metaheuristic algorithms is that in addition to having the desired ability in exploitation and exploration, there must be a balance between these two capabilities so that the algorithm can find the main optimal region and converge towards the global optimal. Fixed-dimensional multimodal functions are good options for testing the ability of metaheuristic algorithms to strike a balance between exploitation and exploration. Optimizing the to functions shows that the CBOA has a high potential to strike a balance between exploitation and exploration. Based on the fixed-dimension multimodal function optimization results, CBOA, with its ability to balance exploitation and exploration, can first discover the main optimal region by global search without getting entangled in locally optimal solutions, then converge to the global optimum by local search. The execution time of CBOA and competing algorithms in optimizing each objective function shows that CBOA is faster than some competing algorithms. But some other competing algorithms, although faster, did not converge to the desired results. Therefore, CBOA has an acceptable execution time when optimizing the objective functions.
The simulation findings show that CBOA has a high quality in exploitation, exploration, and balance between them, which has led to its superior performance compared to similar competing algorithms.
Evaluation CEC 2017 test suite
To analyze the capability of the proposed CBOA approach in complex optimization problems, the proposed algorithm is implemented on the CEC 2017 test suite. This set includes three unimodal objective functions to , seven multimodal objective functions to , ten hybrid objective functions to , and ten composition objective functions to . Complete information and details of the CEC 2017 test suite are described in Ref.33. The function has been removed from the CEC 2017 set due to its unstable behavior. The implementation results of CBOA and competitor algorithms on the CEC 2017 test suite are published in Table 11. Based on the analysis of simulation results, it is clear that the proposed CBOA approach is the first best optimizer for , , , to , to , , , , , and functions compared to competitor algorithms.
Table 11.
Assessment results of the IEEE CEC 2017 objective functions.
| CBOA | CMA | DE | HBA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | Mean | 101.2 | 3108.912 | 3.25E+09 | 1.1E+10 | 110.9548 | 1.88E+09 | 6,961,876 | 8111.161 | 95,212,633 | 1.59E+08 | 799.093 | 3387.4 | 12,792,740 |
| Std | 1.35E−05 | 3271.819 | 7.25E+08 | 1.63E+09 | 4.824002 | 1.64E+09 | 1,733,856 | 3184.727 | 1.68E+08 | 1.51E+08 | 789.2879 | 4480.944 | 4,907,280 | |
| ET | 2.669477 | 1.060814 | 2.741406 | 6.984978 | 3.742614 | 1.420908 | 1.267498 | 2.243143 | 1.496543 | 5.170083 | 3.504213 | 1.654582 | 2.221838 | |
| Rank | 1 | 4 | 12 | 13 | 2 | 11 | 7 | 6 | 9 | 10 | 3 | 5 | 8 | |
| Mean | 101.2 | 247,961.2 | 3.87E+09 | 1.06E+10 | 112.0599 | 4.74E+09 | 5,042,647 | 6350.138 | 92,201,634 | 85,680,111 | 606.3214 | 1660.034 | 13,171,473 | |
| Std | 9.42E-06 | 456,774.1 | 1.01E+09 | 2.25E+09 | 2.827652 | 3.07E+09 | 2,196,191 | 2081.009 | 1.82E+08 | 30,546,657 | 817.5146 | 1234.834 | 12,142,481 | |
| ET | 2.513491 | 1.052585 | 2.633707 | 6.744735 | 3.241847 | 1.349695 | 1.157729 | 1.744399 | 1.384935 | 5.078677 | 3.00369 | 1.505888 | 1.589703 | |
| Rank | 1 | 6 | 11 | 13 | 2 | 12 | 7 | 5 | 10 | 9 | 3 | 4 | 8 | |
| Mean | 303.6 | 470.0877 | 6557.026 | 10,391.17 | 303.6 | 12,068.64 | 1846.57 | 303.6589 | 3291.494 | 763.5923 | 11,049.4 | 334.5206 | 15,922.03 | |
| Std | 4.64E-14 | 257.8634 | 1675.101 | 3802.403 | 4.61E-11 | 5302.915 | 1378.411 | 0.052941 | 2170.273 | 199.4561 | 3332.523 | 7.473065 | 10,711.33 | |
| ET | 2.607193 | 1.044459 | 2.636024 | 6.724772 | 3.308203 | 1.369852 | 1.187209 | 1.660072 | 1.4016 | 5.100191 | 2.948115 | 1.373677 | 1.653028 | |
| Rank | 1 | 5 | 9 | 10 | 2 | 12 | 7 | 3 | 8 | 6 | 11 | 4 | 13 | |
| Mean | 414.3606 | 412.1832 | 714.3499 | 1431.825 | 404.8017 | 595.334 | 431.9613 | 408.4013 | 417.4771 | 414.7045 | 409.7174 | 426.738 | 420.6968 | |
| Std | 1.926314 | 0.618212 | 105.8268 | 461.7888 | 0.003466 | 113.116 | 34.96135 | 1.853898 | 11.96904 | 0.592914 | 1.245504 | 36.41708 | 3.195525 | |
| ET | 2.622783 | 1.029484 | 2.639928 | 6.76956 | 3.440196 | 1.349224 | 1.182745 | 1.778327 | 1.407783 | 5.035687 | 2.897966 | 1.447792 | 1.605425 | |
| Rank | 5 | 4 | 12 | 13 | 1 | 11 | 10 | 2 | 7 | 6 | 3 | 9 | 8 | |
| Mean | 513.8433 | 524.1366 | 551.5381 | 585.3227 | 558.7895 | 576.1053 | 550.596 | 531.7634 | 536.8321 | 543.0554 | 564.6515 | 536.3466 | 536.4685 | |
| Std | 1.321151 | 2.951072 | 7.033816 | 17.97259 | 32.28185 | 25.69122 | 27.24099 | 12.61261 | 30.47843 | 4.324143 | 8.676174 | 20.46161 | 5.170309 | |
| ET | 2.752942 | 1.049288 | 2.710091 | 6.841018 | 3.405888 | 1.443739 | 1.256369 | 1.835352 | 1.504136 | 5.302203 | 3.010028 | 1.466968 | 1.725688 | |
| Rank | 1 | 2 | 9 | 13 | 10 | 12 | 8 | 3 | 6 | 7 | 11 | 4 | 5 | |
| Mean | 607.2005 | 608.0567 | 625.7126 | 651.7765 | 667.2729 | 634.3909 | 632.5699 | 609.5542 | 608.4342 | 614.7151 | 626.0413 | 615.3363 | 618.4357 | |
| Std | 0.000362 | 0.92784 | 2.462733 | 3.674113 | 23.00177 | 11.97368 | 17.37205 | 1.890297 | 0.509057 | 2.688245 | 16.833 | 8.893649 | 3.689074 | |
| ET | 3.280764 | 1.266268 | 2.926952 | 7.050865 | 3.8106 | 1.644312 | 1.449149 | 2.069021 | 1.741808 | 5.997119 | 3.147501 | 1.675329 | 1.895828 | |
| Rank | 1 | 2 | 8 | 12 | 13 | 11 | 10 | 4 | 3 | 5 | 9 | 6 | 7 | |
| Mean | 724.5491 | 747.7368 | 784.9913 | 821.7705 | 751.0584 | 848.1839 | 775.4688 | 741.2936 | 735.9656 | 764.4844 | 750.7485 | 743.3355 | 747.8592 | |
| Std | 1.089227 | 23.78253 | 9.986853 | 13.32549 | 41.61996 | 38.82131 | 21.52091 | 15.21458 | 13.1403 | 6.219753 | 27.77594 | 9.382105 | 7.716694 | |
| ET | 2.998274 | 1.138406 | 2.809196 | 7.021971 | 3.545909 | 1.495996 | 1.323537 | 1.910198 | 1.575269 | 5.486644 | 3.073433 | 1.453913 | 1.751502 | |
| Rank | 1 | 5 | 11 | 12 | 8 | 13 | 10 | 3 | 2 | 9 | 7 | 4 | 6 | |
| Mean | 832.4164 | 818.4122 | 844.1283 | 868.3161 | 820.6759 | 862.389 | 849.3245 | 822.4432 | 826.8465 | 850.8005 | 831.2483 | 834.4307 | 827.8797 | |
| Std | 5.688899 | 5.288314 | 6.336957 | 8.355853 | 3.767465 | 17.32405 | 14.07283 | 4.143453 | 4.726786 | 8.355722 | 7.284064 | 7.299423 | 5.822149 | |
| ET | 2.763709 | 1.115557 | 2.733269 | 6.851644 | 3.439406 | 1.436942 | 1.277088 | 1.851924 | 1.524415 | 5.569266 | 2.968746 | 1.437815 | 1.79004 | |
| Rank | 7 | 1 | 9 | 13 | 2 | 12 | 10 | 3 | 4 | 11 | 6 | 8 | 5 | |
| Mean | 910.8 | 940.4649 | 1208.774 | 1532.356 | 910.8 | 1437.488 | 1431.553 | 911.6781 | 923.8767 | 923.7591 | 982.0398 | 915.4483 | 916.4008 | |
| Std | 0 | 35.31109 | 75.87706 | 108.8322 | 2.37E-08 | 237.4952 | 268.5616 | 1.690314 | 16.73681 | 6.150759 | 25.37577 | 5.975467 | 3.11235 | |
| ET | 3.05801 | 1.160071 | 2.777339 | 6.882568 | 3.556943 | 1.515257 | 1.347831 | 2.134891 | 1.548243 | 5.434826 | 3.089326 | 1.443124 | 1.820621 | |
| Rank | 1 | 8 | 10 | 13 | 2 | 12 | 11 | 3 | 7 | 6 | 9 | 4 | 5 | |
| Mean | 1286.22 | 1626.486 | 2049.993 | 2724.324 | 1453.429 | 2131.957 | 2123.707 | 1858.522 | 1798.419 | 2283.273 | 2398.428 | 2037.753 | 1787.846 | |
| Std | 114.1865 | 402.2849 | 117.5223 | 268.4464 | 61.60307 | 302.0841 | 577.3136 | 434.7159 | 209.3108 | 313.6769 | 203.0563 | 353.1798 | 324.2988 | |
| ET | 2.94732 | 1.080666 | 2.743516 | 6.831648 | 3.497469 | 1.500188 | 1.270246 | 2.487187 | 1.559109 | 5.573976 | 3.039886 | 1.479923 | 1.764071 | |
| Rank | 1 | 3 | 8 | 13 | 2 | 10 | 9 | 6 | 5 | 11 | 12 | 7 | 4 | |
| Mean | 1115.37 | 1137.514 | 3098.063 | 4239.627 | 1249.513 | 5838.905 | 1168.437 | 1143.017 | 1173.114 | 1168.387 | 1155.684 | 1160.384 | 2503.703 | |
| Std | 0.588853 | 6.537338 | 592.0687 | 2445.697 | 38.35352 | 110.5968 | 30.10533 | 23.48768 | 53.94393 | 16.13176 | 22.65592 | 15.99788 | 2599.637 | |
| ET | 2.732119 | 1.070258 | 2.737073 | 6.951227 | 3.429757 | 1.440446 | 1.239599 | 1.850855 | 1.484072 | 5.379859 | 2.98204 | 1.487207 | 1.780409 | |
| Rank | 1 | 2 | 11 | 12 | 9 | 13 | 7 | 3 | 8 | 6 | 4 | 5 | 10 | |
| Mean | 1242.671 | 2371.454 | 1.92E+08 | 7.67E+08 | 1376.876 | 1,129,898 | 2,558,443 | 1,118,413 | 1,538,184 | 5,491,479 | 1,108,928 | 8691.271 | 657,472.1 | |
| Std | 34.81118 | 1339.775 | 1.48E+08 | 5.92E+08 | 22.58375 | 377,867.2 | 1,886,333 | 1,618,529 | 1,039,514 | 4,371,092 | 575,601.5 | 5641.408 | 398,429.3 | |
| ET | 2.750974 | 1.159016 | 2.719459 | 6.770772 | 3.412868 | 1.434666 | 1.227595 | 1.963578 | 1.51061 | 5.446068 | 2.996924 | 1.515922 | 1.768249 | |
| Rank | 1 | 3 | 12 | 13 | 2 | 8 | 10 | 7 | 9 | 11 | 6 | 4 | 5 | |
| Mean | 1321.672 | 1345.379 | 9,353,580 | 37,362,843 | 1452.289 | 13,745.31 | 8138.937 | 7214.729 | 11,095.13 | 18,079.89 | 10,847.64 | 7098.111 | 59,078.95 | |
| Std | 0.905728 | 23.47823 | 14,486,856 | 57,908,805 | 53.42611 | 5906.827 | 5881.728 | 6188.384 | 3509.635 | 1665.486 | 4197.729 | 7394.17 | 91,052.23 | |
| ET | 2.987458 | 1.140728 | 2.762242 | 6.849603 | 3.566721 | 1.508286 | 1.301149 | 2.112364 | 1.546674 | 5.534626 | 3.041972 | 1.531272 | 1.76199 | |
| Rank | 1 | 2 | 12 | 13 | 3 | 9 | 6 | 5 | 8 | 10 | 7 | 4 | 11 | |
| Mean | 1420.829 | 1440.266 | 3294.843 | 5710.918 | 1569.994 | 3578.13 | 1546.269 | 1603.793 | 2446.452 | 1624.394 | 5948.724 | 3152.854 | 13,995.64 | |
| Std | 2.599676 | 12.39114 | 687.4668 | 1133.047 | 51.76615 | 2370.315 | 42.81284 | 305.9188 | 1898.234 | 54.4611 | 1504.696 | 2813.783 | 10,186.7 | |
| ET | 2.845627 | 1.206945 | 2.785167 | 6.874761 | 3.576565 | 1.517747 | 1.305058 | 2.015353 | 1.537448 | 5.567527 | 3.05451 | 1.553163 | 1.859887 | |
| Rank | 1 | 2 | 9 | 11 | 4 | 10 | 3 | 5 | 7 | 6 | 12 | 8 | 13 | |
| Mean | 1518.303 | 1540.237 | 7560.294 | 14,980.49 | 1659.677 | 7504.47 | 6651.267 | 1563.504 | 6211.694 | 1745.582 | 25,866.69 | 9674.444 | 4836.23 | |
| Std | 0.18902 | 7.627427 | 3842.977 | 13,122.67 | 17.88227 | 4781.062 | 5421.678 | 13.28443 | 1664.527 | 114.6471 | 12,793.27 | 5421.193 | 3312.171 | |
| ET | 2.761322 | 1.084223 | 2.716524 | 6.880903 | 3.401858 | 1.432233 | 1.260428 | 2.404585 | 1.466779 | 5.319318 | 3.003796 | 1.475542 | 1.672515 | |
| Rank | 1 | 2 | 10 | 12 | 4 | 9 | 8 | 3 | 7 | 5 | 13 | 11 | 6 | |
| Mean | 1620.33 | 1651.546 | 1897.385 | 2072.1 | 1794.952 | 2105.687 | 2000.377 | 1854.36 | 1758.913 | 1702.789 | 2133.828 | 1971.181 | 1839.25 | |
| Std | 0.413013 | 59.12325 | 88.70904 | 216.3476 | 42.53324 | 182.3609 | 162.1172 | 69.66636 | 94.10053 | 40.68201 | 158.7172 | 131.4634 | 60.70065 | |
| ET | 2.922317 | 1.104349 | 2.750624 | 6.929148 | 3.46053 | 1.466667 | 1.256555 | 2.35024 | 1.499318 | 5.430021 | 3.026472 | 1.504192 | 1.723349 | |
| Rank | 1 | 2 | 8 | 11 | 5 | 12 | 10 | 7 | 4 | 3 | 13 | 9 | 6 | |
| Mean | 1739.769 | 1759.38 | 1809.104 | 1849.202 | 1940.462 | 1831.594 | 1874.797 | 1875.756 | 1794.966 | 1783.928 | 1880.1 | 1777.377 | 1781.317 | |
| Std | 9.390864 | 19.15441 | 17.27001 | 12.63976 | 69.12122 | 12.20181 | 54.70165 | 88.60647 | 75.1563 | 10.82718 | 124.9458 | 6.216098 | 2.739942 | |
| ET | 3.422864 | 1.373381 | 2.961349 | 7.028175 | 3.942321 | 1.707681 | 1.543518 | 2.528669 | 1.731379 | 6.260958 | 3.26785 | 1.687528 | 1.957027 | |
| Rank | 1 | 2 | 7 | 9 | 13 | 8 | 10 | 11 | 6 | 5 | 12 | 3 | 4 | |
| Mean | 1822.393 | 1843.219 | 1,555,684 | 6,182,483 | 1980.379 | 12,953.85 | 25,158.44 | 22,596.97 | 21,467.39 | 31,882.7 | 10,407.72 | 23,605.32 | 13,773.29 | |
| Std | 0.654604 | 10.52135 | 2,046,315 | 8,174,037 | 64.62466 | 3980.99 | 15,769.55 | 12,776.37 | 15,003.12 | 6443.527 | 2530.639 | 21,206.51 | 7131.201 | |
| ET | 2.914595 | 1.113373 | 2.765405 | 6.883858 | 3.491219 | 1.497679 | 1.288268 | 2.305685 | 1.562607 | 5.506185 | 3.025709 | 1.527084 | 1.736712 | |
| Rank | 1 | 2 | 12 | 13 | 3 | 5 | 10 | 8 | 7 | 11 | 4 | 9 | 6 | |
| Mean | 1923.272 | 1928.873 | 226,966.5 | 763,650 | 2131.778 | 136,058.9 | 37,628.15 | 1938.779 | 5703.18 | 4957.527 | 43,724.1 | 26,929.86 | 6569.977 | |
| Std | 0.369818 | 4.100448 | 196,422.4 | 717,757.5 | 29.81473 | 154,801.6 | 24,971.29 | 7.622458 | 6158.53 | 5637.36 | 23,097.21 | 37,993.29 | 3433.467 | |
| ET | 5.681011 | 2.198231 | 3.872663 | 7.996336 | 5.715268 | 2.626269 | 2.383587 | 3.433651 | 2.66522 | 8.937754 | 4.250877 | 2.666788 | 2.843785 | |
| Rank | 1 | 2 | 12 | 13 | 4 | 11 | 9 | 3 | 6 | 5 | 10 | 8 | 7 | |
| Mean | 2067.076 | 2067.046 | 2197.937 | 2265.97 | 2031.928 | 2248.994 | 2248.143 | 2175.404 | 2208.342 | 2102.103 | 2299.254 | 2207.326 | 2078.461 | |
| Std | 12.47033 | 23.77396 | 41.12687 | 60.83282 | 9.028956 | 98.45771 | 98.31852 | 89.32691 | 56.29458 | 9.756751 | 83.94788 | 30.1848 | 11.08937 | |
| ET | 3.495783 | 1.364452 | 3.013562 | 7.143803 | 3.98272 | 1.719226 | 1.574374 | 2.453979 | 1.822637 | 6.275645 | 3.285749 | 1.73905 | 1.986589 | |
| Rank | 3 | 2 | 7 | 12 | 1 | 11 | 10 | 6 | 9 | 5 | 13 | 8 | 4 | |
| Mean | 2226.4 | 2284.466 | 2324.208 | 2299.285 | 2458.014 | 2362.314 | 2345.687 | 2284.106 | 2349.418 | 2334.645 | 2409.16 | 2355.396 | 2332.995 | |
| Std | 1.12E-05 | 64.10826 | 16.92359 | 32.51713 | 90.23298 | 76.53896 | 67.04678 | 66.63367 | 4.098373 | 69.9699 | 15.79384 | 8.338653 | 52.5004 | |
| ET | 3.450832 | 1.401169 | 2.995836 | 7.09781 | 3.970771 | 1.713638 | 1.508972 | 2.28657 | 1.765494 | 6.173443 | 3.298679 | 1.661932 | 1.972283 | |
| Rank | 1 | 3 | 5 | 4 | 13 | 11 | 8 | 2 | 9 | 7 | 12 | 10 | 6 | |
| Mean | 2347.789 | 2331.702 | 2611.25 | 2996.763 | 2327.955 | 2777.291 | 2353.455 | 2312.14 | 2336.94 | 2348.862 | 2327.6 | 2342.014 | 2347.076 | |
| Std | 32.62054 | 1.802696 | 88.39054 | 165.7393 | 0.319001 | 229.1817 | 5.979814 | 40.81921 | 10.56695 | 8.954942 | 4.84E-11 | 23.3774 | 3.410703 | |
| ET | 3.98756 | 1.527526 | 3.143476 | 7.226233 | 4.214015 | 1.932928 | 1.632912 | 2.323814 | 1.882882 | 6.522159 | 3.433647 | 1.846398 | 2.072976 | |
| Rank | 8 | 4 | 11 | 13 | 3 | 12 | 10 | 1 | 5 | 9 | 2 | 6 | 7 | |
| Mean | 2640.107 | 2660.734 | 2703.659 | 2740.655 | 2696.217 | 2765.507 | 2684.208 | 2697.026 | 2776.933 | 2677.491 | 2839.94 | 2679.387 | 2692.296 | |
| Std | 1.129135 | 10.68091 | 22.13161 | 35.48547 | 107.6211 | 65.64839 | 22.30794 | 78.50251 | 174.1397 | 9.670808 | 104.13 | 9.485398 | 14.66617 | |
| ET | 4.261043 | 1.473416 | 3.139665 | 7.218091 | 4.388387 | 1.931915 | 1.671435 | 2.36283 | 1.931631 | 6.710749 | 3.452823 | 1.886706 | 2.105212 | |
| Rank | 1 | 2 | 9 | 10 | 7 | 11 | 5 | 8 | 12 | 3 | 13 | 4 | 6 | |
| Mean | 2530 | 2659.97 | 2764.229 | 2900.871 | 2743.203 | 2703.2 | 2803.692 | 2719.557 | 2790.813 | 2798.492 | 2832.176 | 2809.082 | 2762.881 | |
| Std | 6.57E-05 | 149.894 | 59.07219 | 41.23084 | 152.7406 | 166.5024 | 19.6523 | 126.547 | 18.09781 | 3.569194 | 100.1059 | 14.21019 | 140.1599 | |
| ET | 4.214127 | 1.531454 | 3.208993 | 7.275993 | 4.411459 | 1.908476 | 1.737936 | 2.390203 | 2.116833 | 6.843712 | 3.484969 | 1.996938 | 2.187695 | |
| Rank | 1 | 2 | 7 | 13 | 5 | 3 | 10 | 4 | 8 | 9 | 12 | 11 | 6 | |
| Mean | 2939.972 | 2957.344 | 3115.494 | 3342.127 | 2932.516 | 3186.417 | 2940.533 | 2956.37 | 2974.419 | 2968.799 | 2956.556 | 2957.712 | 2989.152 | |
| Std | 77.54716 | 27.48258 | 116.453 | 66.54141 | 1.89E-08 | 385.9018 | 104.3606 | 27.47506 | 13.34528 | 20.98996 | 25.60616 | 27.44166 | 9.921065 | |
| ET | 3.678597 | 1.413734 | 3.093918 | 7.17875 | 4.198947 | 1.909976 | 1.591243 | 2.284097 | 1.870087 | 6.480475 | 3.367676 | 1.786583 | 2.05537 | |
| Rank | 2 | 6 | 11 | 13 | 1 | 12 | 3 | 4 | 9 | 8 | 5 | 7 | 10 | |
| Mean | 2862.955 | 2948.384 | 3467.513 | 3866.638 | 2909.502 | 3719.161 | 3242.777 | 2934.961 | 3332.336 | 3268.472 | 3981.274 | 2939.218 | 2931.771 | |
| Std | 96.9765 | 91.33146 | 162.0792 | 310.1073 | 50.59636 | 598.8449 | 317.2958 | 0.038934 | 469.9391 | 488.6216 | 777.5515 | 89.98807 | 221.6715 | |
| ET | 4.780488 | 1.621275 | 3.294333 | 7.413718 | 4.558512 | 2.093386 | 1.800535 | 2.440357 | 2.04527 | 7.057821 | 3.533837 | 1.97621 | 2.317277 | |
| Rank | 1 | 6 | 10 | 12 | 2 | 11 | 7 | 4 | 9 | 8 | 13 | 5 | 3 | |
| Mean | 3126.15 | 3145.346 | 3202.102 | 3280.69 | 3375.87 | 3224.543 | 3241.297 | 3128.888 | 3155.531 | 3154.422 | 3275.144 | 3177.256 | 3203.298 | |
| Std | 0.15309 | 10.0279 | 25.45743 | 142.6992 | 96.13972 | 58.84485 | 12.56083 | 2.689293 | 44.05881 | 40.76261 | 16.32711 | 39.49311 | 45.82105 | |
| ET | 4.966231 | 1.564901 | 3.300359 | 7.489424 | 4.652527 | 2.036375 | 1.848247 | 2.489605 | 2.105183 | 7.322945 | 3.630412 | 2.008709 | 2.266859 | |
| Rank | 1 | 3 | 7 | 12 | 13 | 9 | 10 | 2 | 5 | 4 | 11 | 6 | 8 | |
| Mean | 3199.763 | 3244.848 | 3547.719 | 3875.438 | 3137.2 | 3665.733 | 3340.237 | 3287.983 | 3403.426 | 3381.846 | 3518.427 | 3360.736 | 3296.269 | |
| Std | 20.83825 | 126.6863 | 76.36163 | 71.49689 | 7.51E-05 | 215.8928 | 133.0303 | 174.2557 | 109.7254 | 91.61967 | 15.96006 | 105.1771 | 194.2335 | |
| ET | 4.246133 | 1.48251 | 3.205908 | 7.422436 | 4.429292 | 1.928158 | 1.74264 | 2.408991 | 1.988376 | 6.931333 | 3.541678 | 1.885937 | 2.195382 | |
| Rank | 2 | 3 | 11 | 13 | 1 | 12 | 6 | 4 | 9 | 8 | 10 | 7 | 5 | |
| Mean | 3242.31 | 3218.034 | 3313.113 | 3434.28 | 3175.212 | 3283.043 | 3405.644 | 3246.523 | 3314.547 | 3257.359 | 3402.368 | 3315.496 | 3284.129 | |
| Std | 13.50853 | 18.88143 | 44.05249 | 77.70265 | 3.260145 | 62.57449 | 118.6531 | 66.40669 | 98.04684 | 35.42945 | 210.7321 | 89.40796 | 44.90439 | |
| ET | 4.240703 | 1.678074 | 3.287334 | 7.449646 | 4.542081 | 2.003263 | 1.783916 | 2.439172 | 2.014811 | 7.115835 | 3.578222 | 1.984954 | 2.229906 | |
| Rank | 3 | 2 | 8 | 13 | 1 | 6 | 12 | 4 | 9 | 5 | 11 | 10 | 7 | |
| Sum rank | 52 | 89 | 278 | 347 | 138 | 294 | 246 | 129 | 206 | 203 | 262 | 192 | 203 | |
| Mean rank | 1.793103 | 3.068966 | 9.586207 | 11.96552 | 4.758621 | 10.13793 | 8.482759 | 4.448276 | 7.103448 | 7 | 9.034483 | 6.62069 | 7 | |
| Total rank | 1 | 2 | 10 | 12 | 4 | 11 | 8 | 3 | 7 | 6 | 9 | 5 | 6 | |
CBOA for real world applications
In this section, we will show the effectiveness of CBOA in solving real-world problems. To this end, CBOA and competing algorithms are used in the optimization of four engineering applications: (i) pressure vessel design (PVD), (ii) speed reducer design (SRD), (iii) welded beam design (WBD), and (iv) structural tension/compression springs (TCSD). Mathematical models, details, and information about these technical challenges are expressed for PVD in Ref.34, for SRD in Refs.35,36, and for WBD and TCSD in Ref.16. The optimization results of these four engineering optimization problems are published in Table 12. Based on the analysis of the results, it is clear that the CBOA approach is the first best optimizer in solving all four studied problems compared to competing algorithms.
Table 12.
Assessment results of engineering optimization applications.
| CBOA | CMA | DE | HBA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PVD | Mean | 5882.405 | 5884.773 | 6041.266 | 6120.411 | 5891.389 | 5895.471 | 6069.081 | 6481.645 | 6331 | 6845.126 | 6268.202 | 6648.439 | 6429.323 |
| Best | 5883.117 | 5884.772 | 6033.975 | 6112.525 | 5916.011 | 5919.822 | 5921.851 | 6042.598 | 6169.107 | 11,610.02 | 5920.786 | 6583.892 | 6392.769 | |
| Std | 23.71331 | 31.13375 | 31.20048 | 38.25817 | 28.94939 | 13.91933 | 66.66323 | 327.2262 | 126.6938 | 5794.505 | 496.4605 | 657.9637 | 351.4736 | |
| Median | 5886.142 | 5887.641 | 6039.357 | 6118.226 | 5890.172 | 5894.597 | 6420.413 | 6401.767 | 6322.551 | 6842.214 | 6116.786 | 7591.092 | 6904.266 | |
| ET | 1.123067 | 1.741255 | 1.602954 | 3.711218 | 2.214646 | 0.964079 | 0.87132 | 1.204496 | 0.994188 | 3.465667 | 1.770839 | 0.942969 | 1.097691 | |
| Rank | 1 | 2 | 5 | 7 | 3 | 4 | 6 | 11 | 9 | 13 | 8 | 12 | 10 | |
| SRD | Mean | 2999.639 | 3000.889 | 3000.081 | 3001.774 | 3011.639 | 3003.451 | 3009.664 | 3109.197 | 3032.689 | 3069.812 | 3174.361 | 3190.57 | 3299.515 |
| Best | 2996.001 | 2996.084 | 2996.082 | 2996.126 | 3004.747 | 3001.46 | 3004.2 | 3008.679 | 3005.841 | 3033.503 | 3054.081 | 3070.537 | 3031.941 | |
| Std | 1.623508 | 4.163184 | 2.014972 | 5.218941 | 10.36777 | 1.934384 | 5.845356 | 79.73926 | 13.03514 | 18.09716 | 92.6902 | 17.14034 | 57.09594 | |
| Median | 2998.672 | 3000.33 | 2999.746 | 3000.341 | 3010.25 | 3002.997 | 3008.336 | 3109.197 | 3030.877 | 3069.503 | 3160.762 | 3202.25 | 3292.835 | |
| ET | 1.090244 | 0.810638 | 1.647167 | 3.706859 | 2.279256 | 1.046693 | 0.900268 | 1.220179 | 1.022635 | 3.528911 | 1.766919 | 0.988105 | 1.158639 | |
| Rank | 1 | 3 | 2 | 4 | 7 | 5 | 6 | 10 | 8 | 9 | 11 | 12 | 13 | |
| WBD | Mean | 1.696107 | 1.726626 | 1.726898 | 1.703194 | 1.891812 | 1.728636 | 1.729938 | 2.233938 | 1.732494 | 1.820613 | 2.548378 | 2.122687 | 1.765745 |
| Best | 1.724628 | 1.724686 | 1.724629 | 1.672383 | 1.865877 | 1.727431 | 1.728767 | 1.822263 | 1.727242 | 1.760978 | 2.175088 | 1.875894 | 1.838134 | |
| Std | 0.004327 | 0.007131 | 0.005122 | 0.017423 | 0.007959 | 0.000287 | 0.001159 | 0.325054 | 0.004874 | 0.027587 | 0.256276 | 0.034876 | 0.139712 | |
| Median | 1.725382 | 1.72563 | 1.7256 | 1.726194 | 1.883295 | 1.728595 | 1.729897 | 2.248315 | 1.73023 | 1.823089 | 2.499173 | 2.10046 | 1.938897 | |
| ET | 1.125416 | 0.700585 | 1.497918 | 3.548905 | 1.985386 | 0.856819 | 0.754486 | 1.143285 | 0.882747 | 3.086722 | 1.64934 | 0.830966 | 0.986142 | |
| Rank | 1 | 3 | 4 | 2 | 10 | 5 | 6 | 12 | 7 | 9 | 13 | 11 | 8 | |
| TCSD | Mean | 0.012685 | 0.012715 | 0.012696 | 0.01279 | 0.013888 | 0.012793 | 0.012806 | 0.014945 | 0.014588 | 0.01295 | 0.013554 | 0.014156 | 0.013182 |
| Best | 0.012663 | 0.012705 | 0.012664 | 0.012758 | 0.013208 | 0.012776 | 0.01278 | 0.013299 | 0.01292 | 0.012812 | 0.012977 | 0.013141 | 0.012879 | |
| Std | 0.001022 | 0.006146 | 0.001566 | 0.007412 | 0.006136 | 0.005667 | 0.004189 | 0.002292 | 0.001636 | 0.007825 | 0.000289 | 0.002091 | 0.000378 | |
| Med | 0.012682 | 0.01271 | 0.01269 | 0.01278 | 0.013766 | 0.012796 | 0.012809 | 0.013306 | 0.014141 | 0.012955 | 0.013482 | 0.013113 | 0.013063 | |
| ET | 1.191738 | 0.828262 | 2.062968 | 5.196861 | 2.595398 | 1.102364 | 0.942416 | 1.76268 | 1.124489 | 4.072516 | 2.269854 | 1.128144 | 1.292512 | |
| Rank | 1 | 3 | 2 | 4 | 10 | 5 | 6 | 13 | 12 | 7 | 9 | 11 | 8 | |
Conclusions and future works
This paper introduced a new human-based metaheuristic algorithm called the chef-based optimization algorithm (CBOA) and designed it to address optimization issues. The process of learning cooking skills by people who attend training cooking courses inspired the implementation of the proposed CBOA. Different phases of the cooking training process were mathematically modeled to design the CBOA implementation. The CBOA’s performance was evaluated on fifty-two benchmark functions, including seven unimodal functions, six high-dimensional multimodal functions, ten fixed-dimensional multimodal functions, and 29 functions of the CEC 2017 test suite The optimization results showed that CBOA could be used effectively in solving optimization problems due to its ability to maintain a balance between exploration and exploitation. Moreover, the simulation results showed that CBOA is more efficient and competitive than the twelve compared algorithms because it usually provides better solutions.
In addition, the employment of the CBOA on four engineering optimization issues demonstrated the high ability of the proposed approach to address real-world applications.
The proposed CBOA algorithm is a stochastic approach and therefore has some shortages and limitations. As with all metaheuristic algorithms, there is no guarantee that the solutions obtained from the CBOA for optimization problems are equal to the global optima of those problems. Although the CBOA has provided reasonable solutions to most of the objective functions studied in this paper, according to the NFL theorem, there are no preconditions for its successful implementation in all optimization applications Therefore, of course, there is a shortage and limitation of the proposed CBOA that its application may fail in some optimization problems. Also, it is always possible that researchers will design newer metaheuristic algorithms to provide better solutions to real optimization problems than existing algorithms, such as the proposed CBOA method.
The introduction of the CBOA opens research directions and tasks for future work. The most specific research potential for the CBOA is the development of binary and multi-objective versions of this proposed approach. The employment of CBOA in optimization applications in various sciences and real-world challenges are other proposals in this paper.
Author contributions
Conceptualization, E.T.; methodology, E.T.; software, M.D.; validation, E.T. and M.D.; formal analysis, M.D.; investigation, E.T.; resources, E.T.; data curation, E.T. and M.D.; writing—original draft preparation, E.T. and M.D.; writing—review and editing, E.T. and M.D.; visualization, E.T.; supervision, E.T.; project administration, M.D.; funding acquisition, E.T.
Funding
This work was supported by the Project of Specific Research, Faculty of Science, University of Hradec Králové, No. 2104/2022.
Data availability
All data generated or analyzed during this study are included directly in the text of this submitted manuscript. There are no additional external files with datasets.
Code availability
The source code of the CBOA is available at: https://uk.mathworks.com/matlabcentral/fileexchange/114480-chef-based-optimization-algorithm-cboa.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Dhiman G. SSC: A hybrid nature-inspired meta-heuristic optimization algorithm for engineering applications. Knowl. Based Syst. 2021;222:106926. doi: 10.1016/j.knosys.2021.106926. [DOI] [Google Scholar]
- 2.Zeidabadi F-A, et al. SSABA: Search step adjustment based algorithm. Comput. Mater. Continua. 2022;71:4237–4256. doi: 10.32604/cmc.2022.023682. [DOI] [Google Scholar]
- 3.Mohammadi-Balani A, Nayeri MD, Azar A, Taghizadeh-Yazdi M. Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Comput. Ind. Eng. 2021;152:107050. doi: 10.1016/j.cie.2020.107050. [DOI] [Google Scholar]
- 4.Cavazzuti M. Optimization Methods: From Theory to Design Scientific and Technological Aspects in Mechanics, Chap. Deterministic Optimization. Springer; 2013. pp. 77–102. [Google Scholar]
- 5.Gonzalez M, López-Espín JJ, Aparicio J, Talbi E-G. A hyper-matheuristic approach for solving mixed integer linear optimization models in the context of data envelopment analysis. PeerJ Comput. Sci. 2022;8:e828. doi: 10.7717/peerj-cs.828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goldberg DE, Holland JH. Genetic algorithms and machine learning. Mach. Learn. 1988;3:95–99. doi: 10.1023/A:1022602019183. [DOI] [Google Scholar]
- 7.Kennedy, J. & Eberhart, R. Particle swarm optimization. In Proc. ICNN’95—International Conference on Neural Networks, 1942–1948 (IEEE, 1995).
- 8.Dorigo M, Maniezzo V, Colorni A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. B (Cybern.) 1996;26:29–41. doi: 10.1109/3477.484436. [DOI] [PubMed] [Google Scholar]
- 9.Karaboga, D. & Basturk, B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In Foundations of Fuzzy Logic and Soft Computing. IFSA 2007. Lecture Notes in Computer Science, 789–798 (Springer, 2007).
- 10.Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1:67–82. doi: 10.1109/4235.585893. [DOI] [Google Scholar]
- 11.Kaur S, Awasthi LK, Sangal AL, Dhiman G. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020;90:103541. doi: 10.1016/j.engappai.2020.103541. [DOI] [Google Scholar]
- 12.Abdollahzadeh B, Gharehchopogh FS, Mirjalili S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021;158:107408. doi: 10.1016/j.cie.2021.107408. [DOI] [Google Scholar]
- 13.Hashim FA, Hussien AG. Snake optimizer: A novel meta-heuristic optimization algorithm. Knowl. Based Syst. 2022;242:108320. doi: 10.1016/j.knosys.2022.108320. [DOI] [Google Scholar]
- 14.Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
- 15.Chopra N, Ansari MM. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022;198:116924. doi: 10.1016/j.eswa.2022.116924. [DOI] [Google Scholar]
- 16.Mirjalili S, Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- 17.Abualigah L, Elaziz MA, Sumari P, Geem ZW, Gandomi AH. Reptile search algorithm (rsa): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022;191:116158. doi: 10.1016/j.eswa.2021.116158. [DOI] [Google Scholar]
- 18.Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH. Marine predators algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020;152:113377. doi: 10.1016/j.eswa.2020.113377. [DOI] [Google Scholar]
- 19.Storn R, Price K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997;11:341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
- 20.Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 21.Rashedi E, Nezamabadi-Pour H, Saryazdi SGSA. A gravitational search algorithm. Inf. Sci. 2009;179:2232–2248. doi: 10.1016/j.ins.2009.03.004. [DOI] [Google Scholar]
- 22.Dehghani M, et al. A spring search algorithm applied to engineering optimization problems. Appl. Sci. 2020;10:6173. doi: 10.3390/app10186173. [DOI] [Google Scholar]
- 23.Eskandar H, Sadollah A, Bahreininejad A, Hamdi M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012;110:151–166. doi: 10.1016/j.compstruc.2012.07.010. [DOI] [Google Scholar]
- 24.Ray T, Liew KM. Society and civilization: An optimization algorithm based on the simulation of social behavior. IEEE Trans. Evol. Comput. 2003;7:386–396. doi: 10.1109/TEVC.2003.814902. [DOI] [Google Scholar]
- 25.Moghdani R, Salimifard K. Volleyball premier league algorithm. Appl. Soft Comput. 2018;64:161–185. doi: 10.1016/j.asoc.2017.11.043. [DOI] [Google Scholar]
- 26.Zeidabadi FA, Dehghani M. POA: Puzzle optimization algorithm. Int. J. Intell. Eng. Syst. 2022;15:273–281. [Google Scholar]
- 27.Rao RV, Savsani VJ, Vakharia D. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011;43:469–492. doi: 10.1016/j.cad.2010.12.015. [DOI] [Google Scholar]
- 28.Dehghani M, et al. A new doctor and patient optimization algorithm: An application to energy commitment problem. Appl. Sci. 2020;10:5791. doi: 10.3390/app10175791. [DOI] [Google Scholar]
- 29.Dehghani M, Trojovský P. Teamwork optimization algorithm: A new optimization approach for function minimization/maximization. Sensors. 2021;21:4567. doi: 10.3390/s21134567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pira E. City councils evolution: A socio-inspired metaheuristic optimization algorithm. J. Ambient Intell. Hum. Comput. 2022 doi: 10.1007/s12652-022-03765-5. [DOI] [Google Scholar]
- 31.Ayyarao TL, et al. War strategy optimization algorithm: A new effective metaheuristic algorithm for global optimization. IEEE Access. 2022;10:25073–25105. doi: 10.1109/ACCESS.2022.3153493. [DOI] [Google Scholar]
- 32.Wilcoxon F. Individual comparisons by ranking methods. Biometr. Bull. 1945;1:80–83. doi: 10.2307/3001968. [DOI] [Google Scholar]
- 33.Awad N, Ali M, Liang J, Qu B, Suganthan P. Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization. Kyungpook National University; 2016. [Google Scholar]
- 34.Kannan B, Kramer SN. An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J. Mech. Des. 1994;116:405–411. doi: 10.1115/1.2919393. [DOI] [Google Scholar]
- 35.Gandomi AH, Yang X-S. Computational Optimization, Methods and Algorithms. Studies in Computational Intelligence, Chap. Benchmark Problems in Structural Optimization. Springer; 2011. pp. 259–281. [Google Scholar]
- 36.Mezura-Montes, E. & Coello, C.A.C. Useful infeasible solutions in engineering optimization with evolutionary algorithms. In Advances in Artificial Intelligence (MICAI 2005). Lecture Notes in Computer Science, 652–662 (Springer, 2005).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analyzed during this study are included directly in the text of this submitted manuscript. There are no additional external files with datasets.
The source code of the CBOA is available at: https://uk.mathworks.com/matlabcentral/fileexchange/114480-chef-based-optimization-algorithm-cboa.