Kilohertz two-photon brain imaging in awake mice

Abstract

Two-photon microscopy is a mainstay technique for imaging in scattering media and normally provides frame-acquisition rates of ~10–30 Hz. To track high-speed phenomena, we created a two-photon microscope with 400 illumination beams that collectively sample 95,000–211,000 μm² areas at rates up to 1 kHz. Using this microscope, we visualized microcirculatory flow, fast venous constrictions, and neuronal Ca²⁺ spiking with millisecond-scale timing resolution in the brains of awake mice.

Two-photon fluorescence microscopy is widely used for imaging in turbid media, but its conventional laser-scanning form has limited speed ill-suited for tracking 1-ms-scale events. Several past efforts explored fast laser-scanning mechanisms^1-3, but 1-kHz-imaging via rapidly scanning one laser focus often yields poor fluorescence counts, as illumination intensity is limited by sample heating, photobleaching and phototoxicity.

To boost fluorescence for fast two-photon imaging, one can reduce the number of pixels sampled, such as via sculpted illumination⁴ or random-access sampling^3,5. However, these approaches sacrifice micron-scale, full-frame imaging and impede imaging of particle trajectories or tissues requiring motion artifact corrections. Other approaches concurrently illuminate multiple pixels, such as with a line of illumination, which speeds imaging but degrades optical sectioning⁶, or through widefield two-photon excitation and temporal focusing, which maintains sectioning but degrades excitation efficiency⁷. Another strategy involves multiple laser beams and multi-pixel detectors for concurrent sampling from multiple foci^8-10. With this approach, background fluorescence, from fluorescence scattering and interference between beams that excites fluorescence outside the focal plane, is a key design challenge. Overall, no prior study attained full-frame, in vivo two-photon imaging with millisecond-scale resolution of biological events.

Here we report fast two-photon imaging in awake mice up to 300 μm into tissue. Using a unique mechanism for scanning multiple beams, our microscope provided 1-kHz-videos in live animals, for tracking microcirculation and ~10-ms-resolution of neural Ca²⁺-transients. Key features are an ultrafast laser (pulses of 1030 nm, 10–100 μJ energy, ~280 fs duration, 0.2–2 MHz rate), an extra-cavity pulse-picker, a microlens array creating a grid of laser beamlets, a scanning mirror, and an sCMOS camera (100–1000 fps) (Fig. 1a; Supplementary Figs. 1,2). To increase fluorescence, we used 50–200 kHz pulse-picking and 10–19 μJ pulses, which enhanced excitation over conventional two-photon imaging while maintaining cell health (0.3–2.9 mW per focus).

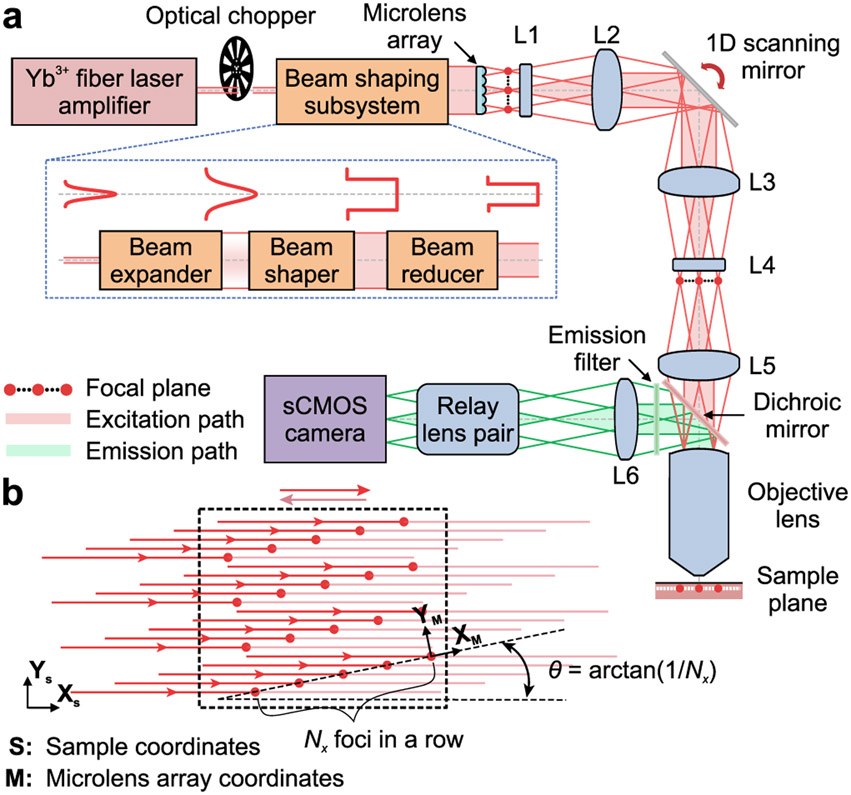
Figure 1 ∣. Microscope design.

(a) A laser amplifier beam (1030 nm; ~280 fs pulse duration) passes through a chopper synchronized to the triangle-wave laser-scanning pattern (Supplementary Figs. 1,2) and is given uniform intensity across a microlens array (lenslet spacing: 100 μm), which creates N_x × N_y beamlets of equal intensity. N_x·N_y is the number of lines scanned in the specimen. Compound (L1 and L4) and aspherical lenses (L2, L3 and L5) establish intermediate and specimen focal planes (red dots: beamlet foci) as Fourier-conjugates to the plane of the scanning mirror. Fluorescence returns through the objective lens, reflects off a dichroic mirror, and is focused by a tube lens (L6) and a relay lens pair onto a sCMOS camera synchronized to the scanning mirror. Excitation and emission pathways for 3 example foci are shown in red and green, respectively. Inset: Bottom, The beam-shaper comprises an expander, a flattop shaper, and a reducer. Top, Beam intensity profiles at each stage.

(b) To scan images at rates ≤1 kHz, the N_x × N_y beamlet array is projected onto the specimen at an angle, θ = tan⁻¹(1/N_x), between the (X_S, Y_S) camera-frame coordinate system (dashed rectangle) and the (X_M, Y_M) microlens array coordinate system. We generally used ≤20 × 20 laser foci (15 μm spacing between beams) oriented 2.9° to the scanning direction, yielding 0.75 μm between scanned lines. We cropped the illumination to match the area projected onto the camera.

We shaped the laser beam to a spatially uniform intensity at the microlens array, yielding an N × N array of beamlets of equal power (Supplementary Fig. 3). We generally used 20 × 20 arrays, tilted 2.9° = tan⁻¹(1/N) relative to the scanning axis and camera image frame, with each beamlet sampling one image row (Fig. 1b). Adjacent laser foci were 15 μm apart in the specimen, yielding 0.75 μm between adjacent scanning lines. The point spread function at each focus had lateral and axial FWHM values of 1.4 ± 0.1 (s.d.) μm and 9.6 ± 2.1 μm, respectively, suitable to the spacing of adjacent image lines. The camera acquired fluorescence images of 1024 × 196 pixels (~95,000 μm² specimen area) at 1 kHz, or 1024 × 512 pixels (~248,000 μm²) at ≤400 Hz, whereas the beamlets covered ~705 × 300 μm² for scanning rates ≤1 kHz. A fast camera with a larger sensor would allow 1-kHz-imaging across the entire illuminated area.

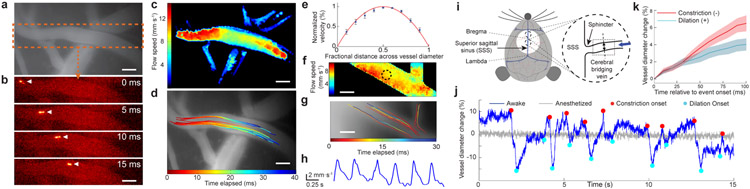
To assess imaging in live mice, we studied cerebral arterioles with flow speeds up to ~12 mm·s⁻¹. Past two-photon imaging studies of microcirculation used laser line-scanning¹¹ but have not tracked individual cells via high-speed full-frame imaging. We intravascularly injected fluorescently labeled HEK cells, followed cells with millisecond-scale resolution (100–1000 Hz imaging; 8 mice; Supplementary Videos 1, 2), and mapped cells’ speeds (Fig. 2a-c; Online Methods). Different cells in the same vessel had distinct kinematics, especially in larger arterioles (Fig. 2d). Speeds rose quadratically with distance from vessel walls, as fluid mechanics predicts (Fig. 2e). With 1-kHz-imaging, we observed the heartbeat’s influence (~150 ± 20 beats · min⁻¹) on flow (Fig. 2f-h; Supplementary Video 2). In individual arterioles, flow speed declined in vessel portions with larger diameters (r = −0.61 ± 0.27 (s.d.); 9 vessels in 6 mice), though larger vessels generally exhibited faster speeds than small ones (r = 0.60 ± 0.07).

Figure 2 ∣. Microcirculation and fast contractions of cerebral bridging veins.

(a) Conventional epi-fluorescence image in motor cortex of an anesthetized mouse after intravenous administration of rhodamine-B. Dashed box encloses the artery in b.

(b) Image time series (2.5 ms per frame; 200 kHz laser pulse rate; 2.2 mW per beamlet) taken by high-speed two-photon imaging reveals flow of injected, fluorescent HEK-293 cells. Arrowheads mark a cell’s progress.

(c) Flow speed map for the vessel in b.

(d) Trajectories of individual HEK-293 cells. Each trajectory is encoded in color and superposed on an epi-fluorescence image of the vasculature.

(e) Flow speeds in neocortical arteries had a parabolic cross-sectional profile. For 15 different cross-sections chosen within 3 different arteries (>50 μm in diameter; N = 3 mice), we computed flow speeds, V(r), as a function of the radial deviation, r, from the vessel’s longitudinal axis. We fit (red curve) the data (blue points) to V/V_max = 1 – (r/R)ⁿ , where V_max is each vessel’s peak flow speed and R is its radius. The fitting parameter, n = 2.0 ± 0.3 (95% C.I.), revealed the flow speed’s quadratic profile. Error bars: s.e.m. (N = 15 cross-sections).

(f) Flow speed map determined by 1-kHz-two-photon imaging (200 kHz laser repetition rate; 2.9 mW per beamlet; 450 × 110 μm² field of view).

(g) Trajectories of individual HEK-293 cells, determined from the same dataset used for f.

(h) Periodic fluctuations in blood flow, as computed within the encircled area in f. The heart rate of ~150 beats·min⁻¹ determined by high-speed imaging matches conventional measurements in ketamine-xylazine-anesthetized mice¹⁷.

(i) Sketch of the mouse superior sagittal sinus (SSS). Inset: We targeted areas near bregma for imaging (dotted rectangle).

(j) Example time traces of bridging vein diameter determined by 200-Hz-imaging (450 × 300 μm² field of view; 200 kHz laser pulse rate; 2.2 mW per beamlet) after intravenous injection of rhodamine-B. During wakefulness, the vein diameter (blue trace) exhibited fast constriction (red dots) and dilation (cyan dots), which anesthesia abolished (gray trace).

(k) Negative- and positive-going changes in vein diameter, relative to each vessel’s mean diameter, during constriction (red curve) and dilation (blue curve) in 4 awake mice. Constriction and dilation rates were, respectively, −6.5 ± 0.9% and +4.0 ± 0.7% per 100 ms (mean ± s.e.m; 36 events of each type). Shading: s.e.m.

Scale bars: 50 μm in a–d, f, g.

Next, we studied bridging veins near the superior sagittal sinus (SSS). The cerebral venous system was thought to be primarily a passive drain, but smooth muscles at the SSS junction with bridging veins (Fig. 2i) suggest active mechanisms¹². To explore, we intravascularly injected a fluorescent dye and performed high-speed imaging in awake mice (Fig. 2i-k). At onsets of vessel constriction, bridging veins decreased in diameter (−6.5 ± 0.9% (s.e.m.) per 100 ms; 36 constriction events) faster than diameter increases at dilation onsets (+4.0 ± 0.7% per 100 ms; 36 dilations). Anesthetized mice lacked these high-speed vessel dynamics.

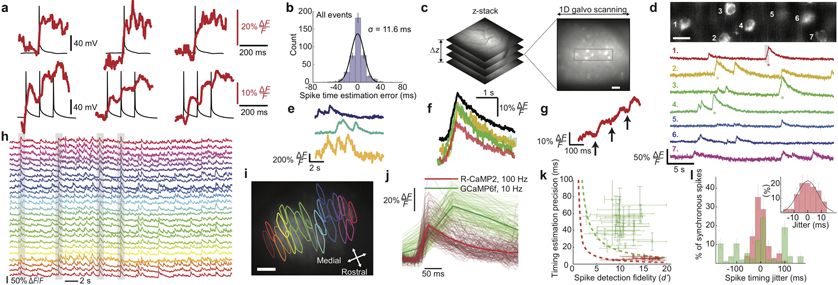
Next, we examined neural activity. We combined 1-kHz-two-photon Ca²⁺-imaging in live cortical tissue slices with electrical measurements of neural membrane impedance and spike duration, and identified imaging conditions with minimal impact on membrane integrity, an indicator of neural health (Supplementary Fig. 4). During dual Ca²⁺-imaging and patch clamp recordings, we electrically evoked single or trains of neural spikes to elicit Ca²⁺-transients. 10-Hz-spike trains induced stepwise increments in fluorescence intensity (Fig. 3a; Supplementary Fig. 5). By comparing electrical and optical traces, we found spike or spike burst initiation times can be estimated from the optical traces to ±11.6 ms (s.d.) (Fig. 3b). Computational studies verified 1-kHz-imaging yields millisecond-scale accuracy (Supplementary Fig. 6).

Figure 3 ∣. High-speed Ca²⁺-imaging in neocortical and Purkinje neurons of awake mice.

(a) To assess the spike-timing accuracy of 1-kHz-two-photon Ca²⁺-imaging, we monitored neocortical pyramidal cells in live tissue slices via whole-cell electrical recordings (black traces) and concurrent Ca²⁺-imaging (red traces; 100 kHz laser pulse rate; 0.7 mW per beamlet) using the Ca²⁺-indicator Calbryte-590. Using one or more electrical pulses (each 2 ms and 0.5–1.7 nA), we evoked individual or ≤5 successive spikes, eliciting Ca²⁺ transients. Examples of single, Top, or bursts of 3 spikes, Bottom. Stepwise increments in Ca²⁺ signals often accompanied individual spikes in a burst.

(b) We estimated occurrence times of spikes and spike bursts via matched filtering of the Ca²⁺ transient waveforms, compared these to the actual times recorded electrically, and made a histogram of timing errors, aggregated across spikes and spike bursts. RMS timing error: 11.6 ms.

(c) In awake mice expressing GCaMP6f in layer 2/3 cortical pyramidal cells, we first sampled a tissue volume to identify a plane suitable for 1-kHz-Ca²⁺-imaging. Boxed area (48 × 192 μm²) is magnified in d.

(d) Top, We recorded the concurrent Ca²⁺ dynamics of 7 layer 2/3 neurons in an awake mouse (1-kHz-imaging; 50 kHz laser pulse rate; ~0.36 mW per beamlet). We bandpass-filtered the image with a difference of Gaussians (cutoffs: 0.42 μm and 12 μm). Scale bar: 20 μm. Bottom, Activity traces of individual cells, shown down-sampled to 500 Hz and median-filtered (time-constant: 16 ms). Asterisks mark individual Ca²⁺ transients shown in color-corresponding traces in f, g.

(e) Ca²⁺ activity traces of layer 2/3 neurons in an awake mouse, acquired by 100-Hz-Ca²⁺-imaging 296 μm beneath the cortical surface (100 kHz pulse rate; 2.15 mW per beamlet). Traces were median-filtered (time constant: 200 ms).

(f) Individual (colored traces) and mean (black trace) waveforms of 4 Ca²⁺ transients with asterisks in d, aligned within 4.2 ± 2.4 ms (mean ± s.d; N = 4 transients) to the onset of excitation.

(g) Gray-shaded portion of the marked Ca²⁺ transient in cell 1 in d reveals a staircase-like waveform in the transient’s rising phase, similar to those seen in vitro, a, suggesting the Ca²⁺ transient accompanied a burst of spikes.

(h, i) We used 100-Hz-Ca²⁺-imaging (200 kHz laser pulse rate; 2.9 mW per beamlet) to observe dendritic Ca²⁺-spiking activity of cerebellar Purkinje neurons expressing R-CaMP2 in awake mice. Example ΔF/F traces, h, of 25 neurons whose contours are shown in i superposed on a mean (0.5-min-average) two-photon image. Gray shading in h marks 4 example events when ≥80% of the visible neurons spiked synchronously. Scale bar in i: 50 μm. Field of view: 450 × 300 μm².

(j) Waveforms of 492 individual Ca²⁺ spikes, after alignment of baseline fluorescence levels and spike occurrence times. Red traces: 177 randomly chosen spikes from 23 neurons imaged as in h. Green traces: 315 randomly chosen spikes from 43 Purkinje neurons imaged using GCaMP6f and conventional two-photon microscopy (10-Hz-imaging; 920 nm illumination; 30 mW).

(k). By fitting a parameterized waveform to each trace in j, we found that the mean s.d. rise time to half-maximum amplitude was 13 ± 5 ms for 177 R-CaMP2 spikes imaged at 100 Hz and 50 ± 15 ms for 315 GCaMP6f spikes imaged at 10 Hz. To quantify the spike-timing estimation accuracy, we used the 95% C.I. for the model parameter setting the spike occurrence time, yielding timing accuracies of 6.8 ± 3.4 ms (mean ± s.d; 177 R-CaMP2 spikes; 100-Hz-imaging) and 48 ± 30 ms (315 GCaMP6f spikes; 10-Hz-imaging). For each Purkinje neuron, we also determined d’, the spike detection fidelity¹³. We plotted for each cell the spike-timing accuracy versus d’ (red data points for cells studied by 100-Hz-imaging; green points for cells studied by conventional two-photon imaging). Dashed curves denote theoretical limits on spike-timing accuracy for 100-Hz-imaging (red curve) and 10-Hz-imaging on the conventional two-photon microscope (green curve), based on the Chapman-Robbins lower bound on the variance of an unbiased estimator¹³ and by approximating the 95% C.I. as twice the s.d. To calculate these limits, we used a 150 ms decay time-constant for both Ca²⁺-indicators and values from j of 30% ΔF/F for R-CaMP2 and 50% ΔF/F for GCaMP6f. Horizontal error bars: s.e.m. of each cell’s d’ value across all its spikes. Vertical error bars: s.e.m. of the 95% C.I. values across all spike occurrence times for each cell. High-speed Ca²⁺-imaging allows higher d’ values and timing accuracies within several milliseconds of the physical limitations.

(l) Histogram of empirically determined timing jitters for individual spikes in synchronous spiking events, defined as instances when ≥80% of the visible Purkinje neurons spiked concurrently. We visually identified candidate events and used the methods of j to estimate spike occurrence times. We determined each spike’s jitter as the difference between its occurrence time and the mean time for all spikes in the synchronous event. The mean absolute jitter using 100-Hz-imaging and R-CaMP2 was 7.8 ± 5.5 ms (mean ± s.d.; N = 77 spikes), versus 61 ± 53 ms (N = 116 spikes) with conventional (10 Hz) two-photon imaging and GCaMP6f. Inset: Expanded view of the histogram for synchronous spikes recorded by high-speed imaging. Error bars: s.d. estimated as counting errors.

We next studied awake mice expressing the Ca²⁺-indicator GCaMP6f in layer 2/3 cortical neurons. Fast two-photon imaging (100–1000 Hz) yielded single cell Ca²⁺ activity traces up to ~300 μm into tissue (Fig. 3c-g; Supplementary Video 3). With 1-kHz-imaging, rising phases of large-amplitude Ca²⁺-transients exhibited stepwise increments, consistent with fluorescence waveforms evoked in vitro by brief spike trains (Fig. 3g). By fitting the mean Ca²⁺-transient waveform to the activity traces, we estimated Ca²⁺-transient occurrence times to within ±12.8 ms (95% C.I.).

To further study spike timing, we examined complex spiking by cerebellar Purkinje neurons in awake mice. To visualize the spike’s dendritic component, we used R-CaMP2, a red Ca²⁺-indicator suited to 1030-nm-illumination. Using 100-Hz-imaging, we tracked tens of cells concurrently and focused on dendrites ~100–200 μm below the brain surface (227 cells; 4 mice; Fig. 3h, i). We acquired 30-s Ca²⁺ videos spaced ~2 min apart over ~25–30 min, computationally extracted individual cells and their Ca²⁺-spiking activity, and evaluated the spike-timing precision against that of conventional two-photon microscopy.

For stringent comparisons, our conventional two-photon imaging (10 Hz) used the Ca²⁺-indicator GCaMP6f, which has comparable kinetics and greater dynamic range (ΔF/F) than R-CaMP2. To optimize GCaMP6f emission we used 920-nm-illumination (20–35 mW). Ca²⁺-spiking rates under conventional (0.5 ± 0.1 (s.d). s⁻¹) and high-speed (0.6 ± 0.1 s⁻¹) microscopy were indistinguishable (227 cells). But, even with the superiority of GCaMP6f, high-speed-imaging with R-CaMP2 better revealed the fluorescence waveforms (Fig. 3j).

For each cell we computed the spike-timing accuracy and detection fidelity, using the metric d’ from signal detection theory¹³ (Fig. 3k). Even with the ~40% smaller amplitude of R-CaMP2 spike waveforms versus those of GCaMP6f, the greater fluorescence flux of the high-speed microscope yielded ~50% greater d’ values. We compared empirically determined spike-timing accuracies to the theoretical limits on timing accuracy (Fig. 3k). High-speed microscopy yielded 6.8 ± 3.4 ms (s.d.) accuracy (177 R-CaMP2 spikes), versus 48 ± 30 ms (315 GCaMP6f spikes) by conventional two-photon imaging. As nearby Purkinje cells often fire synchronized complex spikes¹⁴, we analyzed the timing jitter between synchronized spikes. The jitter observed by 100 Hz-imaging was 7.8 ± 5.5 ms (s.d.), versus 61 ± 53 ms by conventional imaging, which thus inflated the jitter by ~800% (Fig. 3l).

Overall, our microscope allows ~30–100× faster imaging than conventional two-photon microscopy. We thereby revealed microcirculation, rapid vessel constrictions, and the fine timing of neural activity. The high-power illumination was mitigated by its long-wavelength (1030 nm), the low power (≤3 mW) and 15-μm-spacing of adjacent foci, and pulse-picking to minimize tissue exposure. ~30-s-imaging bouts were spaced ~2 min apart, allowing time for cells to recover and new fluorophores to reach the focal plane. In neuroscience research, animals often perform ~100 or more behavioral trials across a 1-h-session, with each trial lasting seconds¹⁵. With this design, ~3 s of high-speed imaging per trial would keep brain temperatures within physiological ranges, even at the maximum powers used here (Supplementary Fig. 7).

Faster scientific cameras, larger illumination arrays, and faster scanners could further improve imaging speeds and fields-of-view. We imaged ≲300 μm into the brain, beyond the ~75–100 μm attained with planar illumination microscopy¹⁶. Camera frame-rates >1 kHz, combined with image sub-sampling and computational un-mixing of fluorescence scattering, could potentially improve imaging depths. To illustrate, we studied scattering patterns in fixed tissue and used this information to visualize cells up to ~500 μm deep (Supplementary Figs. 8,9). Further reduction of background fluorescence, excited outside the focal plane due to interference between beamlets, is also feasible (Supplementary Fig. 10). Thus, we expect multi-focal, high-speed two-photon imaging will continue to improve for visualizing millisecond-scale biological events.

Online Methods

Mice.

The Stanford University Administrative Panel on Laboratory Animal Care approved all procedures using animals. For studies of neocortical hemodynamics, we used male mice (10-12 weeks old) that were either of the C57BL/6J strain (Jackson Laboratory) or PV-Cre/Ai14 mice, which express the red fluorophore tdTomato in parvalbumin interneurons. For imaging studies of layer 2/3 cortical pyramidal neurons in live mice, we used triple transgenic GCaMP6f-tTA-dCre (Rasgrf2-2A-dCre; Camk2a-tTA; Ai93) mice from the Allen Institute (10–16 weeks old at the time of surgery). For studies of cerebellar Purkinje neurons we used male and female PCP2-Cre driver mice (8–16 weeks old), which express Cre recombinase in Purkinje cells. Studies in fixed brain slices of neurons expressing YFP or tdTomato were triple transgenic crosses of Thy1-YFP-H¹⁸, Rasgrf2–2A-dCre, and Ai14 mice. For dual optical and electrical recordings of neocortical neuronal dynamics, we used C57BL/6J male mice from Jackson Laboratories (2–6 weeks old).

Microscope design.

We performed optical design studies using Zemax software (Zemax Development Corporation) and mechanical design studies using Solidworks 2012 (Dassault Systèmes). A diode-pumped Yb³⁺ ion ultrashort-pulsed fiber laser amplifier (Tangerine, Amplitude Systèmes, ~280 fs pulses, variable repetition rate, 1030 nm center wavelength) served as the illumination source. We adjusted the illumination power delivered to the microscope by rotating a half-wave plate (AHWP05M-980, Thorlabs), used in combination with a polarizing beam splitter cube (PBS103, Thorlabs). We remotely controlled the rotation of the half-wave plate using a motorized precision rotation stage (PRM1Z8E, Thorlabs). We made fine adjustments in laser illumination power by changing the modulation efficiency of the pulse picker within the laser.

We used a custom beam-shaping subsystem (Fig. 1a, Inset) that comprised a variable beam expander (68-481, Edmund Optics), a flattop beam shaper (piShaper 6_6_xTIS, AdlOptica), and a custom Keplerian beam reducer made of two infrared-coated achromatic lenses (47-317 and 45-801, Edmund Optics). This subsystem transformed the laser beam’s Gaussian cross-sectional intensity profile to a flattop form that was approximately matched in area to the portion of a microlens array (100 μm square grid of lenslets each with a 0.401 mm radius of curvature and 0.055 numerical aperture, SUSS MicroOptics) used to create a 20 × 20 or similarly sized array of laser beamlets of uniform intensity. We mounted the microlens array in a precision rotation mount (CRM1P, Thorlabs) that allowed us to control the angle between the square grid of beamlets and the rectangular area of the specimen sampled by the camera (Fig. 1b).

To scan a rectangular field of view at rates up to 1 kHz, the square grid of 20 × 20 laser beamlets was projected onto the specimen plane at an angle, θ = tan⁻¹(1/20) = 2.9°, between the rectangular field of view of the camera and the square grid of the microlens array (Fig. 1b). By driving a galvanometer scanning mirror (6230H, Cambridge Technology) with a triangular waveform, we swept the 400 beamlets at a uniform speed across the specimen, with 400 scanned lines per image frame. The efficiency of illumination delivery through the microscope was ~30%.

To block the laser beam during the turnaround portions of its triangular scanning pattern, we used an optical chopper system (MC2000, Thorlabs) and a custom 1-mm-thick steel chopper wheel with 10 uniform blades that blocked the laser beam with a 20% duty cycle. The chopper resided upstream of the beam shaping subsystem in the illumination pathway (Fig. 1a). The rotation of the chopper wheel was synchronized to that of the laser-scanning mirror (Supplementary Fig. 2). Alternatively, we also used an acousto-optic modulator, built-in to the laser source, as a pulse-picker that allowed us to set the repetition rate of the emitted laser pulses.

We generally configured the optical pathway in one of two different ways, termed Configurations 1 and 2. Both configurations yielded a 15-μm-separation between the foci of adjacent beamlets in the specimen plane. We performed nearly all imaging with Configuration 1 (Figs. 1, 2, 3c-l; Supplementary Figs. 3, 4) but later switched to Configuration 2, which exhibited greater stability (Fig. 3a,b; Supplementary Fig. 5). In Configuration 1, the scanning mirror and a set of aspheric, polymer-coated achromatic lenses (49-665, 49-665 and 49-664, all Edmund Optics for lenses L2, L3 and L5, respectively, in Fig. 1a) were positioned such that the scanning mirror and the back aperture of a water-immersion microscope objective lens (either a Olympus XLUMPLFLN-W 0.95 NA 20× lens, a Olympus XLUMPLFLN-W 1.0 NA 20× lens, or a Nikon NIR Apo 40× 0.8 NA, 3.5-mm-working distance, used for all in vitro patch clamp experiments) were located in optical planes that were Fourier-conjugate to the specimen plane. A pair of custom, compound meniscus lenses (L1 and L4 in Fig. 1a, each composed of two singlet lenses (48-710 and 49-516, Edmund Optics)) were held with opposing orientations in the optical pathway and thereby alleviated the field curvature of the laser focal plane in the specimen.

In Configuration 2, we placed the following achromatic lenses between the microlens array and the objective lens. A lens with a 4-cm-focal length (AC254-040-B-ML, Thorlabs) resided between the microlens array and the scanning mirror. A lens with a 3-cm-focal length (AC254-030-B-ML, Thorlabs) and a lens with 5-cm-focal length (AC254-050-B-ML, Thorlabs) resided between the scanning mirror and the objective lens.

We often used a slit in the intermediate image plane lying after the microlens array, as well as an iris in an intermediate plane after the scanning mirror, to restrict the illumination beam pattern to the region imaged on the sCMOS camera and such that each image line sampled by the camera received laser illumination across its full horizontal extent. Thus (Fig. 1b), the fraction of the scanning cycle during which each image line was illuminated was less than the 80% of the scanning cycle during which laser illumination passed through the chopper wheel or pulse picker.

A dichroic mirror (FF705-Di01-25x36 in Configuration 1 or Di03-R785-t3-25x36 in Configurations 2; both from Semrock) reflected fluorescence emissions from the specimen to the microscope’s collection pathway. A fluorescence emission filter (FF01-609/57-25 or FF495-Di03-25x36, Semrock) blocked light of wavelengths outside the emission pass band. After passing through the emission filter, in Configuration 1 the fluorescence photons passed through a tube lens (L6 in Fig. 1a; 32-884, Edmund Optics) and an achromatic relay lens pair (MAP1075150-A, Thorlabs). In Configuration 2, we used a variable focal length (55–200 mm) photography lens (Nikon; f/4–f/5.6) in the fluorescence collection pathway that allowed us to vary the magnification of the fluorescence image on the sCMOS camera (Fig. 1). A high-speed sCMOS camera (ORCA Flash4.0, Hamamatsu or Zyla 4.2 PLUS, Andor; ~1–2 electrons r.m.s. read noise per pixel) captured the fluorescence images. The camera’s maximum data throughput was a bottleneck limiting the sizes of images that could be acquired at high speeds.

We used a digital signal output from the laser that was synchronized with pulse emission as an external clock for a multifunction data acquisition card (PCI-6110, National Instruments). This card sent synchronized timing signals to the laser-scanning mirror, sCMOS camera, and optical chopper system (Supplementary Fig. 2). To control the microscope, we created a custom software interface using the LabVIEW programming environment (National Instruments). During data acquisition, the data streamed right to disk. Beforehand, the user could preview the high-speed videos, but these preview data were not saved.

When imaging at frame acquisition rates of 100–400 Hz (Fig. 2b, j and Fig. 3e, h-l), we set the frequency of the scanning mirror to equal the frame acquisition rate of the sCMOS camera, enabling uniform illumination across successive image frames. The field-of-view for images acquired at ≤ 400 Hz frame rate was ≤ 705 × 300 μm², corresponding to 1024 × 436 camera pixels. When the imaging frame rate was 1 kHz, we set the frequency of the scanning mirror to 500 Hz and acquired separate images on the forward and backward portions of the scanning motion. Due to the limitations on data throughput set by the camera, the field-of-view when imaging at a 1 kHz frame rate was ≤ 705 × 135 μm², corresponding to 1024 × 196 camera pixels. In all cases, the laser pulse repetition rate was 200 kHz, with a pulse-picking frequency between 50–200 kHz.

The above frequencies of laser pulse emission and image frame acquisition were chosen such that every pixel in the acquired image was illuminated by at least one laser pulse per frame. However, pulse emission was not synchronized to the passage of the laser beamlets across areas in the specimen sampled by individual pixels on the camera. Thus, to account for the residual spatial non-uniformities of illumination, for each imaging configuration we performed a calibration in which we imaged a uniform, red fluorescent reference slide. The image of the slide provided a map of illumination intensity, which we used to correct all subsequent images by normalizing each pixel’s emission intensity value by its level of illumination.

In vitro whole-cell patch-clamp electrophysiological recordings.

To verify that the laser illumination protocols used for high-speed two-photon imaging did not impair cell health, we performed whole-cell patch-clamp recordings in live neocortical tissue slices from PV-Cre/Td-Tomato mice (4–8 weeks old) simultaneous with high-speed two-photon imaging.

We perfused the mice with artificial cerebrospinal fluid (ACSF: 92 mM NaCl, 2.5 mM KCl, 1.2 mM NaH₂PO₄, 30 mM NaHCO₃, 20 mM HEPES, 25 mM Glucose, 5 mM Sodium-Ascorbate, 2 mM Thiourea, 3 mM Sodium-Pyruvate, 10 mM MgSO₄, 0.5 mM CaCl₂). After perfusion, we excised the brain and made tissue slices (300 μm thick) using a tissue slicer (Leica VT-1200S) while the brain was immersed in ACSF. After making 6 coronal slices, we incubated the slices at 34° C for 10 min and then transferred them to a room temperature ACSF of identical composition as above except with 2 mM MgSO₄ and 2 mM CaCl₂.

We performed whole-cell patch recordings of tdTomato-positive neurons while the tissue slices were immersed in recording solution (124 mM NaCl, 2.5 mM KCl, 1.2 mM NaH₂PO₄, 24 mM NaHCO₃, 5 mM HEPES, 12.5 mM Glucose, 2 mM MgSO₄ and 2 mM CaCl₂). We used glass recording pipettes [pulled to 4-7 MOhm impedance with a laser puller (Sutter P-2000)], filled with intracellular solution (125 mM Potassium-Gluconate, 10 mM KCl, 10 mM HEPES, 4 mM Mg₃ATP, 0.3 mM Na₂GTP, 10 mM Na₂Phosphocreatine, 1 mM EGTA).

We tested the health of the patched pyramidal neurons by measuring their membrane impedance values and action potential durations across imaging sessions of 30-min duration that alternated between 30-s-periods of two-photon imaging and 2-min-periods of rest (Supplementary Fig. 4). We examined two different regimes, which typified the conditions we generally used for high-speed brain imaging in live mice. In the first regime, we used illumination pulses of high peak intensity (100 kHz pulse repetition rate, 0.53 mW mean beamlet power, 400 Hz imaging frame rate). In the second regime, we studied a higher mean illumination power but with individual pulses of lower peak intensity (1 MHz pulse repetition rate, 2.3 mW average power, 100 Hz frame rate).

To assess the accuracy of spike timing estimation based on neuronal Ca²⁺ activity traces obtained by high-speed two-photon Ca²⁺ imaging, we performed in vitro whole-cell patch-clamp recordings in live cortical slices with concurrent high-speed two-photon microscopy. Following the procedures described above, we made cortical slices from male C57BL/6J wild type mice (2–6 weeks of age). In these experiments, we filled neurons with an intracellular solution containing 50 mM of the Ca²⁺ indicator Calbryte-590 (AAT Bioquest). We patched single neurons and evoked either single spikes or bursts of action potentials using one or a train of 2-ms-current pulses delivered at either 150 Hz or 10 Hz (Supplementary Fig. 5a).

Surgical procedures.

To prepare mice for in vivo imaging sessions, we performed surgeries using isoflurane anesthesia (1.5–2% isoflurane in O₂) while mice were mounted in a stereotaxic frame. To reduce post-operative inflammation and pain, we administered a pre-operative dose of carprofen (5 mg/kg; subcutaneous injection into the mouse’s lower back), which we repeated once a day for 3 days following the surgery.

For studies of neocortical microcirculation (Fig. 2a-h), we created a cranial window by removing a 5-mm-diameter skull flap (centered at AP −2.5, ML 3.0) or a 7-mm-diameter skull flap (centered at AP −1.0, ML 0.0). We covered the exposed cortical surface with a glass cover slip (thickness: #1), which we secured to the cranium using an ultraviolet-light curable cyanoacrylate glue (Loctite 4305). We cemented a metal head plate to the skull using dental acrylic for head fixation during imaging. For imaging of subdural bridging vein constriction near the superior sagittal sinus (Fig. 2i, j), we created a thinned skull window (centered at AP −1.5, ML 0.0) by polishing the skull to its bottom compact layer over a 6 mm (AP) × 3 mm (ML) area. We applied the cyanoacrylate glue to cover the thinned skull surface, gently pressed a head-plate module (#1.5 cover slip cemented to the metal head plate) into the glue and then cured it. In both cases we monitored the mouse’s breathing rate and body temperature and the skin color of its paws during the surgery. We performed all hemodynamic imaging studies 3–7 d after surgery.

For studies of cerebellar Purkinje neurons using R-CaMP2¹⁹, we injected PCP2-Cre mice with 500 nL of AAV2/1-CAG-DIO-R-CaMP2 virus (~1.5 · 10¹³ genome copies·mL⁻¹, produced¹⁹ and purified²⁰ as previously) at the midline of cerebellar lobules V and VI. We allowed 2 weeks for the virus to incubate before attempting two-photon imaging. For studies using GCaMP6f²¹, we injected PCP2-Cre mice in cerebellar lobule V with 500–700 nL of AAV1-CAG-Flex-GCaMP6f (purchased from University of Pennsylvania viral vector core), and waited 2–3 weeks for viral expression before starting imaging.

For studies of layer 2/3 necortical pyramidal neurons in triple transgenic mice expressing GCaMP6f in these cells, we installed curved glass cranial windows following our detailed, published procedures²². We waited at least 2 weeks after surgery before starting brain imaging.

Fluorescence labeling of HEK cells.

We labeled HEK-293T cells (TriBioScience Inc.) with fluorescent quantum dots using the Qtracker 605 cell labeling kit (Life Technologies), with a slight modification of the standard labeling procedures. We dissociated cultured HEK-293T cells by trypsinization and diluted them to a concentration of ~10⁷ cells/mL in a solution of 90% Dulbecco's modified Eagle’s medium (10596-044, Invitrogen) and 10% fetal bovine serum (SH3007103HI, Fisher). We prepared the labeling solution by mixing 1 μL each of Qtracker components A and B, incubating at room temperature for 5 min, and then adding 0.25 mL of the HEK-293T cell suspension into the labeling solution. We incubated the samples at 37°C for 1–2 h and washed the quantum-dot-labeled HEK-293T cells twice with phosphate buffered saline (PBS); after each wash we collected the cells by centrifugation at 200 G-force for 5 min. We re-suspended the final cell pellet in PBS at a concentration of ~2.5 · 10⁷ cells/mL.

Imaging sessions.

For hemodynamic studies, we anesthetized mice with ketamine (100 mg/kg) and xylazine (10 mg/kg), both administered intraperitoneally, until the mice no longer responded to a squeeze of the rear paw. We then injected rhodamine B isothiocyanate dextran dye (Sigma, R9379) into the lateral tail vein (either 100 μL solution of 1 mg or 50 μL solution of 20 mg rhodamine, for studies of microcirculation and bridging vein constriction, respectively). After mounting the mouse’s head in a frame under the microscope objective, we found and focused upon the largest artery in the field, 50–150 μm deep into neocortical tissue. We injected 200 μL of a solution of fluorescently labeled HEK-293T cells into the left cardiac ventricle using a 27-gauge hypodermic needle and concurrently began high-speed two-photon imaging.

For studies of Purkinje neurons expressing R-CaMP2, on the day of the imaging session we implanted the mice with a metal head plate and opened a cranial window (~3.5 mm diameter) over cerebellar lobules V and VI along the midline, and sealed the window with a 3-mm-diameter cover glass. Once the mice awoke from anesthesia, we afforded them 30–60 min recovery time, then restrained the mouse’s head using two stainless steel bars affixed to the front and back of the head plate, and placed the mouse on a running wheel under the objective lens of the two-photon microscope. Two-photon brain imaging sessions lasted 10–30 min. The mouse was free to walk or run in place during brain imaging.

To image neocortical pyramidal cells expressing GCaMP6f, we head-restrained mice with curved glass cranial replacements by using two stainless steel bars that were affixed to the left and right sides of the head plate. The mice were placed on a running wheel under the microscope objective lens and allowed to run or walk in place. Imaging sessions alternated between imaging intervals (<30 s duration) and recovery intervals (2 min duration).

To image cerebellar Purkinje neurons expressing GCaMP6f, we used a custom-built two-photon microscope of a conventional design. A Ti:sapphire laser (SpectraPhysics, MaiTai) provided ultrashort-pulsed illumination (920 nm wavelength). Power at the sample was 20–35 mW. We used a 0.95 numerical aperture (NA) 20× microscope objective lens (Olympus XLUMPlanFl). We acquired raw images across a field of view of 110 μm × 270 μm (130 × 280 pixels) at 20 Hz and down-sampled them to 10 Hz.

Measurements of brain temperature during high-speed two-photon imaging.

To perform temperature measurements in the brains of awake mice (GCaMP6f-tTA-dCre) during high-speed two-photon imaging, we surgically prepared mice by performing a 5-mm-diameter craniotomy following the same surgical procedures as for imaging studies of microcirculation (see above). However, before placement of the cranial window, we inserted a flexible 200-μm-diameter thermocouple probe²³ (IT24P; Physitemp) into the brain, 100–200 μm beneath the dura, near the edge of the craniotomy (Supplementary Fig. 7a). The thermocouple resided within a 5-mm-long plastic micropipette and extended ~2.5 mm beyond the tip of the micropipette.

Using ultraviolet-light curable glue (Loctite, 4305) and dental cement, we affixed the micropipette to the cranium at a shallow angle of 5 degrees relative to the surface of the cranium. We then placed the glass cranial window onto the craniotomy and fixed the window in place with dental cement. The thermocouple probe was connected to a two-channel digital thermometer (CL3515R; Omega), which conveyed digitized temperature data (10 Hz sampling rate) to a computer via a USB port. We protected the wires of the thermocouple connecting to the digital thermometer using a 5-cm-long piece of flexible plastic tubing. We then commenced concurrent high-speed two-photon imaging and temperature recordings. Due to the cranial window, in the absence of laser illumination the brain temperature was ≥10 °C below normal body temperature in mice, as previously reported²⁴. After the onset of imaging, the time-courses of the temperature measurements, normalized by the illumination power, all had similar time-dependencies²⁵ and were predictable in advance (Supplementary Fig. 7c,d).

Blood flow speeds.

To determine the average speed of fluorescent HEK-293T cells through a chosen reference pixel in a fluorescence video, we computed the temporal cross-correlation between the fluorescence intensities at that pixel and at neighboring pixels, for relative temporal delays, τ, of −1, 0 and +1 image frames²⁶. After setting to zero the values of all pixels lying outside blood vessels or exhibiting cross-correlations with the reference pixel below a minimum threshold value, we computed the centroid of each of the three cross-correlograms. We determined the mean speed of the cells passing through the reference pixel as the average of the two distances between the cross-correlation centroids from successive image frames, divided by the time between successive image frames. To create maps of mean flow speed, we computed the mean flow speeds for all pixels in a vessel. To create a time series of mean flow speed, we repeated the procedures above for a given region-of-interest in the video across time windows of a uniform duration.

To calculate the streamlines of individual cells’ trajectories, we computed a movie that equaled the difference of successive image frames in the raw movie data. To highlight the motion of individual cells, we applied both positive and negative binary thresholds to the difference movie. To remove noise from the resultant, we applied the ‘open” then ‘close’ morphological steps in image processing²⁷. We used the spatial average of the centroids of the positive and negative blobs as an interpolation of the cell’s position between successive image frames. After requiring that all candidate cells should flow at a minimum threshold speed between frames and within the plausible range of directions given the vessel’s size and orientation, we connected the centroids from successive frames to create estimated streamlines.

Analysis of blood vessel diameter.

To determine the width of a blood vessel in an individual image frame, we visually identified the region of interest and fit a Gaussian function to the fluorescence intensity values along a cross-section of the vessel. We used the full-width at half-maximum (FWHM) of the Gaussian fit as a measure of the vessel’s diameter. To examine vessel dynamics, we plotted the vessel diameter values as a function of a time (Fig. 2j). We visually scored the onset times of constrictions and dilations by identifying local maxima and minima in the time traces of vessel diameter.

Extraction of Ca²⁺ activity traces.

To extract the somatic Ca²⁺ activity of neocortical layer 2/3 pyramidal cells expressing GCaMP6f (Fig. 3d-g, Supplementary Video 3), we first filtered each movie frame using a band-pass Gaussian spatial filter (typical spatial cutoffs: 0.42–1.2 μm and 12–24 μm). To extract Ca²⁺ activity traces, we manually encircled regions-of-interest that were ~12 μm in diameter and plotted the mean fluorescence within these regions as a function of time.

To extract dendritic trees of individual Purkinje cells from in vivo two-photon Ca²⁺ imaging videos, we used an established cell-sorting algorithm based on the successive application of principal component analysis (PCA) and independent component analysis (ICA)²⁸. We selected spatial filters provided by ICA that corresponded to individual Purkinje cells, smoothed the filters by applying one round of spatial erosion and dilation²⁷, and applied a threshold to obtain a final set of spatial masks that we applied to the fluorescence videos to obtain the Ca²⁺ activity-related traces from individual cells, ΔF(t)/F₀ = (F(t)−F₀) /F₀ , where F₀ is the mean value of the time series.

Identification of Ca²⁺ spikes.

To identify Ca²⁺ spikes in the Purkinje cells’ activity traces, we first temporally deconvolved each cell’s ΔF(t)/F₀ trace with a decaying exponential function (150 ms time constant) to account for the signal decay kinetics of the Ca²⁺ indicator^19,28. We then applied a threshold function to identify all positive-going signal deflections. We retained as spikes all such deflections that reached a peak value at least twice the standard deviation of the cell’s baseline fluorescence fluctuations.

Fidelity of spike detection.

To estimate the fidelity of spike detection¹³, we calculated d’ for each neuron as d’ ≈ (ΔF/F₀)⋅ (F₀ τ/2)^½ , where ΔF/F₀ is the fluorescence amplitude of the Ca²⁺ spike, F₀ is the baseline fluorescence, and τ is the time constant governing a spike’s exponential decay of fluorescence. We calculated the mean and s.e.m. of these d’ estimates across all the spikes fired by each cell, while approximating τ H 150 ms for both Ca²⁺ indicators.

Spike timing estimation.

In the in vitro studies of cortical neurons using dual high-speed two-photon and electrophysiological recordings, we estimated the occurrence times of individual neuronal spikes or spike bursts based on the Ca²⁺ activity traces. We first averaged 80 neuronal Ca²⁺ responses (10 traces from each of 8 cells) to both single action potentials and 150-Hz-bursts of action potentials, and we then fit a parametric trace of the form $f(t)=\frac{A{e}^{-(t-t_0)∕{\tau }_1}}{1+e^{-(t-t_0)∕{\tau }_2}}$ to the mean Ca²⁺ transient waveform, where A, t₀, τ₁, τ₂, are, respectively, the waveform’s amplitude, time of half-rise, decay-time constant and the logistic-growth-rate constant. The fit parameters were A = 12 ± 1.2%, t₀ = 11 ± 2.0 ms, τ₁ = 766 ± 80 ms, and τ₂ = 5.6 ± 1.9 ms, where the uncertainties are 95% confidence intervals (Supplementary Fig. 5b). We then used the waveform of this parametric fit as a matched filter for estimating the occurrence times of individual spikes or spike bursts. To do this, we convolved the matched filter with individual Ca²⁺ transient waveforms and determined the spike or spike burst occurrence time as the time bin at which the output of the matched filter attained a local maximum. To assess the accuracy of these estimated occurrence times, we compared their values to the spike occurrence times in the concurrently acquired electrophysiological recordings, which we took as the ground truth.

To estimate the times of spikes from the Ca²⁺ activity traces of neocortical neurons imaged in live mice, we first created a template model using the same parametric form, f (t), and parameter values identified in vitro through the fit to the mean Ca²⁺ transient waveform. To estimate the occurrence time of an individual neural spike based on its Ca²⁺ transient waveform, we fit the template model to the Ca²⁺ transient and took the fit value of t₀ as the occurrence time and its 95% confidence interval as the uncertainty in the occurrence time.

To estimate the occurrence time of each Purkinje neuron Ca²⁺ spike imaged in live mice, we performed a parametric fit of the fluorescence trace for each spike to a template model of the form F(t) = F₀ + A ⊕ (1−e^−k1^(t−t0⁾ )⊕ e^−k2^(t−t0⁾ , where F₀ denotes the baseline fluorescence, and A, t₀, k₁ and k₂ represent the spike waveform’s amplitude, occurrence time, and kinetic rate-constants of rise and decay, respectively. We used the fit parameters and their 95% confidence intervals to compute the 95% confidence interval of the estimated rise time to half-maximum amplitude, which we used as a metric for the precision of spike timing determination (Fig. 3k).

Chapman-Robbins bounds on spike-timing accuracy.

We compared our empirical determinations of the accuracy of spike timing estimation for Purkinje cells to the theoretical limit provided by the Chapman-Robbins lower bound on the variance of an unbiased estimator¹³. To calculate the curves expressing the theoretical limits (Fig. 3k), for each frame acquisition rate (10 Hz and 100 Hz) we varied d’ between 2–20 while leaving unchanged the indicator’s decay time constant (150 ms for both the R-CaMP2 and GCaMP6f Ca²⁺ indicators) and the empirical values from Fig. 3j of 30% ΔF/F for R-CaMP2 and 50% ΔF/F for GCaMP6f.

Detection of synchronous Purkinje cell Ca²⁺ spikes and computation of spiking jitter.

We visually identified candidate occurrences of synchronous spiking, examined the occurrence times for all the constituent spikes, and required that ≥ 80% of the cells must have spiked within ≤1 time bin from the candidate event’s mean spike time. For each event and its constituent spikes that passed this criterion, we determined the timing jitter of each spike as the difference between its occurrence time and the mean time for all spikes in the synchronous event.

Studies of fluorescence scattering.

We used fixed coronal brain slices from the GCaMP6f-tTA-dCre mice to assess the extent of fluorescence scattering for different imaging depths in tissue. Using a stationary laser beam to induce localized two-photon excited fluorescence at different depths in tissue, and the resulting fluorescence images captured by the sCMOS camera, we measured the lateral spatial distributions of fluorescence, P_s(x,y), relative to the position of the laser focus at x = y = 0. We averaged these spatial distributions over all polar angles and 50 different individual locations of the laser beam for each of 51 different depths in tissue and 7 different cortical regions. We normalized P_s(x,y) so that its integral over all space was unity, allowing one to interpret P_s(x,y) as a probability density (Supplementary Fig. 8a-c).

To compute the probability that a fluorescence photon emitted from the focus of one laser beamlet would scatter in tissue into to a nearby image tile (Supplementary Fig. 8d), we used the x-y coordinate system aligned with the grid of laser beamlets and applied the formula

$${\mathit{p}}_{\mathit{i},\mathit{j}}={\iint }_{}{}_{\begin{array}{c}\mathit{x}\in {\mathit{x}}_{\mathit{i}}\hfill \\ \mathit{y}\in {\mathit{y}}_{\mathit{j}}\hfill \end{array}}{\mathit{P}}_{\mathit{S}}(\mathit{x},\mathit{y})\mathit{d}\mathit{x}\mathit{d}\mathit{y},$$

where p_i,j is the probability that a photon excited by the (n, m)-th beamlet will be detected in the (n+i, m+j)-th tile, and the domain of integration is given by x_i ∈ [(n + i) d − d/2, (n + i) d + d/2] and y_j ∈ [(m + j) d − d/2,(m + j) d + d/2]. Using this approach, we empirically determined P_s(x,y) and P_s(x,y) and p_i,j for the protein fluorophore GCaMP6f (Supplementary Fig. 8a-d).

We also estimated the depth-dependent decline in fluorescence Ca²⁺ signals that would occur in a neural Ca²⁺ imaging study using GCaMP6f (Supplementary Fig. 8e). For each depth in tissue, we convolved the corresponding P_S (x, y) distribution with a uniform, circularly symmetric source of fluorescence that was 12 μm in diameter, about the size of a neocortical neural cell body. From the results of this convolution, we computed the proportion of fluorescence signals that remained inside the cell body perimeter. We fit these determinations of signal decline with imaging depth to an exponentially decaying function, e^−z/z_S, with a characteristic decay length of z_S = 142 ± 30 μm (s.d.; N = 7 different locations in tissue).

Image reconstructions using sub-sampling.

For these proof-of-concept studies (Supplementary Fig. 9), we used an optical layout that was a re-arrangement of Configuration 2 (see above) with a 24-μm-separation between the foci of adjacent laser beamlets in the specimen plane. Specifically, the 3-cm-focal length (AC254-030-B-ML, Thorlabs) lens resided between the microlens array and the scanning mirror. The 4-cm-focal length (AC254-040-B-ML, Thorlabs) and the 5-cm-focal length (AC254-050-B-ML, Thorlabs) lenses resided between the scanning mirror and the objective lens. In the fluorescence collection pathway, we used a 8.5-cm-focal length photography lens (Canon; f/1.8) as the tube lens. We explored two alternative image processing approaches based on image sub-sampling, as a means of counteracting the effects of fluorescence scattering in tissue.

In both cases, the image sub-sampling involves acquiring multiple camera frames at regular time intervals within a single scanning period of the galvanometer mirror. One can then computationally correct each image sub-frame for the effects of fluorescence scattering before reconstructing the final image. The first approach, termed ‘Reconstruction Method 1’ involves a spatial deconvolution of the image sub-samples prior to assembling the final reconstructed image. The second approach, termed ‘Reconstruction Method 2’, involves a re-assignment of fluorescence signals to the nearest laser beamlet focus, followed by a spatial un-mixing of these signals to account for fluorescence scattering, and then reconstruction of the final image.

For our studies of both reconstruction methods, we acquired 2048 image sub-samples per scanning cycle (800 × 1024 pixels; 256 Hz camera frame acquisition rate). We denote I(x,y) as the fluorescence image in the absence of any fluorescence scattering. We then approximate the image in the presence of fluorescence scattering, I_S(x,y), as a convolution (denoted by the operator, G):

$$I_S(x,y)\simeq G(I,P_S)(x,y)\equiv (I\ast P_S)(x,y)\equiv {\iint }_{}I(x,y)P_S(x-x^{\prime },y-y^{\prime })d{x}^{\prime }d{y}^{\prime }.$$

The set of points at which the laser beamlets are focused is described by the function

$$B_t(x,y)=T_{vt}\left[Q_{\theta }\left[{\sum }_{i,j}\delta (x-id-x_0,y-jd-y_0)\right]\right],$$

where d is the spatial separation between adjacent beamlets, i and j are horizontal and vertical (integer) indices, respectively, x₀ and y₀ are spatial offsets, t is the time elapsed since the start of the scanning cycle, v is a speed at which the beamlets are swept across the specimen, Q_θ denotes the operator that rotates the image frame by an angle, θ, and T_a denotes the operation that horizontally translates the image by a distance a. In the case that fluorescence scattering is a more important constraint on the resolution of the image sub-frames than their finite integration times, we can approximate the n’th image subframe as

$$I_n(x,y)=(I\ast B_{t_n}\ast P_S)(x,y),$$

where t_n is the time at which the n’th image subframe is acquired relative to the start of the scanning cycle. Normally, when the camera acquires a single image per scanning cycle,

$$I_S(x,y)\simeq {\sum }_n{I}_n(x,y).$$

Although in principle I(x,y) can be found via the deconvolution, G⁻¹(I_S, P_S)(x,y), it is well known that in practice this operation yields unsatisfactory results due to the severity and non-uniformity of fluorescence scattering deep in tissue. However, as shown in Supplementary Fig. 9, fluorescence scattering can be effectively counteracted if a deconvolution or un-mixing operation is applied to the individual sub-frames, I_n, before image reconstruction.

Reconstruction Method 1

We reconstructed the final image by deconvolving the effects of scattering from every sub-frame, and then forming the maximum projection image across all the deconvolved sub-frames:

$$I(x,y)\simeq \underset{n}{max}{G}^{-1}(I_n,P_S)(x,y)$$

The maximum projection operation reduced the impact of background fluorescence, which arises from both fluorescence scattering and fluorescence excitation outside the focal plane (Supplementary Fig. 10). To perform the deconvolution, we used the MATLAB function deconvblind, with the kernel initialized as the function P_S(x,y), as measured for the relevant tissue depth. Reconstruction Method 1 is schematized in Supplementary Fig. 9b.

Reconstruction Method 2

We first identified the orientation and focal spot locations of the grid of illumination beamlets in each image sub-frame, I_n . To estimate θ, the angle of the grid relative to the camera frame, we first performed a Radon transform

$$R[I_n](\phi ,\zeta )=\int I_n(\xi sin(\phi )+\zeta cos(\phi ),-\xi cos(\phi )+\zeta sin(\phi ))d\xi ,$$

and then estimated θ as argmax_φ ∀ζR[I_n](φ,ζ). After rotating the image by −θ to yield a grid aligned with the x- and y-axes, we next estimated d, x₀, y₀ and vt, defined as above. To do this, we integrated the sub-frame over all x values and then identified the y-coordinates with intensity values that were local maxima. This provided the y-coordinates of the laser foci. We used analogous procedures to find their x-coordinates. We estimated d as the median separation between adjacent laser foci.

Having determined these parameters for each image sub-frame, we then corrected computationally for the effects of fluorescence scattering, first by re-assigning fluorescence signals to the center of the image tile in which they were located,

$$L_{i,j}={\int }_{x_0+id-\gamma ∕2}^{x_0+id+\gamma ∕2}{\int }_{y_0+jd-\gamma ∕2}^{y_0+jd+\gamma ∕2}{I}_n(x,y)dxdy,$$

where 0 < γ ≤ d defines a square region within each image tile containing the fluorescence signals used for the re-assignment procedure, and L is the resulting matrix of re-assigned intensity values. Fluorescence photons outside these square regions are treated as background fluorescence, rather than signals, and hence are discarded. We generally used γ = 4 pixels as a reasonable tradeoff between the mitigation of scattering effects and fluorescence generated outside the focal plane, and the need to preserve sufficient fluorescence signals across the image.

We corrected for scattering by using the MATLAB function deconvblind to perform a blind un-mixing operation, L ⋅ p⁻¹, where p⁻¹ is the un-mixing matrix, which accounted for the probability that a fluorescence photon had scattered from one image tile to another. We initialized the mixing matrix, p, with empirically determined values for p_i,j (Supplementary Fig. 8), calculated using the same domain of integration as for the computation of L_i,j, for the relevant fluorophore and tissue depth. We transformed the resulting image sub-frame back into the coordinate system of the camera, accounting for the orientation and locations of the image tiles, and mapping the fluorescence from each tile to a Gaussian spatial distribution with sigma σ = 1.2 pixels (i.e. rather than to a single point). Lastly, we reconstructed the final image by summing all of the reconstructed sub-frames. Reconstruction Method 2 is schematized in Supplementary Fig. 9c.

We assessed the performance of the image reconstruction methods by quantifying the resulting image contrast values. Both reconstruction methods based on sub-sampling markedly improved image contrast values over those of the raw images. Reconstruction Methods 1 and 2 improved image contrast by 310 ± 130% (s.d.) and 310 ± 190%, respectively, as determined on a set of 59 different images acquired in fixed brain tissue slices with neurons expressing tdTomato, YFP or GCaMP6f, across a range of tissue depths from 0–615 μm beneath the tissue surface.

Suppressing optical interference between laser beamlets.

The studies of Supplementary Fig. 10 demonstrate that the image contrast in high-speed two-photon microscopy can be enhanced by suppressing the homogeneous background fluorescence that arises from optical interference between the different beamlets and is consequently excited at out-of-focus Talbot planes and fractional Talbot planes²⁹. As in prior work^8,9, we sought to minimize such interference by desynchronizing the optical pulses within the different beamlets. However, we used a distinct strategy for achieving this desynchronization, in which we imposed a spatially pseudo-randomized set of temporal delays on the different beamlets (Supplementary Fig. 10a), rather than a spatially periodic set of delays as used in past work⁸.

We designed custom delay masks and had them commercially fabricated (Fluence Sp. z o.o.) by laser micromachining of glass plates (Supplementary Fig. 10c). Each mask comprised a stack of multiple glass plates, each of which was a 170-μm-thick coverslip. Each plate contained a set of square holes, pseudo-randomly arranged in space. The sides of adjacent holes were separated by no less than one row or column of beamlets. The relative temporal delay between a beamlet traversing 170 μm of glass and a beamlet traversing an air hole was 280 fs. Thus, by stacking 6 glass plates in series, we achieved an assortment of different temporal delays ranging from 0–1680 fs in 7 equal increments. Notably, our approach to desynchronization is scalable to larger arrays of beams and delay masks conferring a wide range of different delays.

To assess the benefits of this form of desynchronization, we imaged fixed neocortical tissue from TTA-dCre-GCaMP6f mice with and without insertion of the delay mask in front of the microlens array. The delay mask indeed reduced background fluorescence, to an extent comparable to that achievable by low-pass spatial filtering of the images (Supplementary Fig. 10e).

We quantified the reduction in background fluorescence excitation that was attainable via laser pulse desynchronization. To do this, we placed a slide with a 1–2 μm thick, uniform fluorescent layer (FluorCal FC-OCS-EC, Valley Scientific) into the path of laser beamlets, and we characterized the resulting patterns of fluorescence as a function of the axial displacement between the slide and the focal plane of the beamlet array, with and without insertion of the delay mask in front of the microlens array (Supplementary Fig. 10f). We also assessed how these measurements were affected by unlabeled brain tissue slices lying atop the fluorescent slide (Supplementary Fig. 10g). With brain slices of increasing thickness, the ability of the temporal delay mask to reduce background fluorescence declined in efficacy, suggesting that forward scattering in tissue of the excitation beams increases the extent of optical interference outside the focal plane.

Statistical and image analyses .

We performed all analyses using custom software written in MATLAB (Mathworks). The Life Sciences Reporting Summary provides additional details.

Data and software code availability.

Readers interested in either the experimental data or the software code used for analyses should please contact the corresponding author.