Abstract
Accurately predicting the spread of the SARS-CoV-2, the cause of the COVID-19 pandemic, is of great value for global regulatory authorities to overcome a number of challenges including medication shortage, outcome of vaccination, and control strategies planning. Modeling methods that are used to simulate and predict the spread of COVID-19 include compartmental model, structured metapopulations, agent-based networks, deep learning, and complex network, with compartmental modeling as one of the most widely used methods. Compartmental model has two noteworthy features, a flexible framework that allows users to easily customize the model structure and its high adaptivity that allows well-matured approaches (e.g., Bayesian inference and mixed-effects modeling) to improve parameter estimation. We retrospectively evaluated the prediction performances of the compartmental models on the CDC COVID-19 Mathematical Modeling webpage based on data collected between August 2020 and February 2021, and subsequently discussed in detail their corresponding model enhancement. Finally, we presented examples using the compartmental models to assist policymaking. By evaluating all models in parallel, we systemically evaluated the performance and evolution of using compartmental models for COVID-19 pandemic prediction. In summary, as a 100-year-old epidemic approach, the compartmental model presents a powerful tool that is extremely adaptive and can be readily customized and implemented to address new data or emerging needs during a pandemic.
Graphical Abstract
Keywords: compartmental model, COVID-19, epidemiology modeling
Introduction
Accurately predicting the spread of the severe acute respiratory syndrome-associated coronavirus-2 (SARS-CoV-2), the cause of the COVID-19 pandemic, is of great value to global regulatory authorities, including the US Food and Drug Administration (FDA). According to a 2020 viewpoint report by the Center for Infectious Disease Research and Policy at the University of Minnesota, several COVID-19 medications (73%, 29 out of 40) and critical acute care drugs (43%, 67 out of 156) were in shortage status in the early stages of the COVID-19 pandemic (1). Accuracy in COVID-19 forecasting would help provide early preparation and mitigation strategies to counter the negative impact of the pandemic on the healthcare system. Such strategies may help resolve drug shortage issues in a timely manner, set regulatory review priorities, and facilitate resource allocations during regulatory policymaking.
The outbreak of SARS-CoV-2 was first reported in early 2020 (2). Shortly thereafter, the World Health Organization (WHO) declared COVID-19 a pandemic (3). While a peak of over 70,000 daily new infections occurred in the USA in July 2020 (4), improved intervention policies and medication strategies resulted in a reduced number of cases in the following months. However, the number of daily new infections sharply increased again with the arrival of wintry weather in the northern hemisphere. A peak of over 250,000 daily new infections was reported in the USA in January 2021 (4). In December 2020, Israel was one of the countries to start a national vaccination campaign against COVID-19 early and observed a reduction of severe cases of COVID-19 at the national level (5). A similar decline in both infection and hospitalization rates was observed in the USA (4), following the FDA’s Emergency Use Authorization (EUA) of several vaccines against COVID-19 (e.g., Pfizer-BioNTech, Moderna, Janssen) (6–8). However, while vaccination is widely available, the pandemic cannot be yet considered totally suppressed. In early May 2021, India became a new COVID-19 epicenter, as a second peak of reported daily new infections surpassed over 400,000 cases (9). In late July 2021, the Delta variant, a more infectious SARS-CoV-2 strain, first reported in late 2020, became the predominant strain in the USA (10). The 7-day moving average of cases reached over 60,000 in the USA, similar to the rate of new cases observed before the availability and wide usage of vaccines. At the beginning of 2022, WHO designated variant B.1.1.529 as a new variant of concern, named Omicron (11). Omicron subvariants BA.2, BA2.12.1, BA.4, and BA.5 widely spread in the USA, with BA.5 becoming the new predominant strain in the USA as of July 2022 (12). The Omicron variant has been reported to be more transmissible and able to infect previously vaccinated people (13, 14).
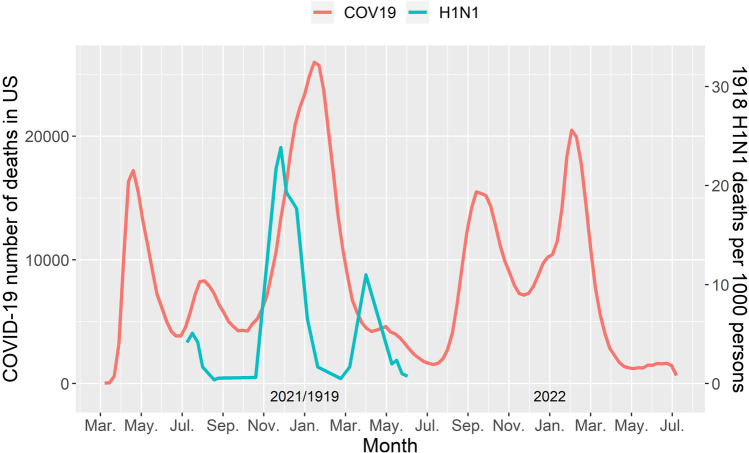
Prior to COVID-19, the 1918 H1N1 influenza was the most severe pandemic in recent history, causing an estimated 50 million casualties worldwide (15). Comparing the 1918 influenza and the COVID-19 outbreaks in terms of the number of daily deaths, similarities can be observed regarding the timeline and trend of the first two peaks. In the 1918 influenza pandemic, three peaks of daily deaths were observed in the UK (Fig. 1) (15). The peaks occurred in July of 1918 (first peak), winter of 1918 (second peak, which reached the highest number of cases), and spring of 1919 (third peak). Similarly, the first and second peaks of COVID-19 cases in the USA were observed in July and November 2020, respectively. At the time of writing (July 2022), five waves have been observed in the USA, even after vaccines became widely available (16).
Fig. 1.
Trend of the daily death of COVID-19 in the USA (June 2020 to July 2022) vs. trend of the death rate of 1918 influenza in United Kingdom (H1N1 virus)
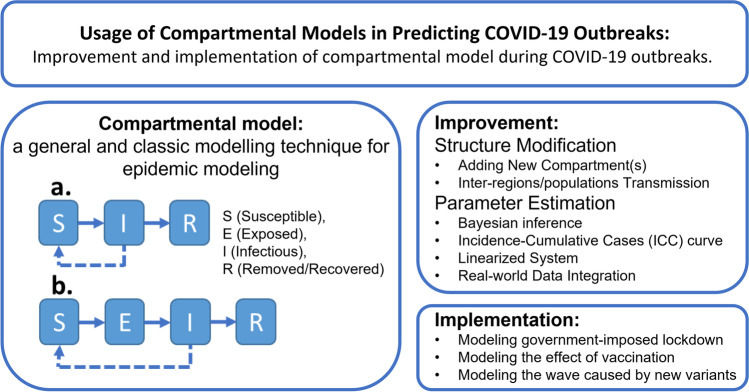
Forecasting the virus spread from an epidemiological standpoint is important to plan control strategies and assess their impacts. Modeling methods that are used to simulate and predict the spread of COVID-19 include compartmental model, structured metapopulations, agent-based networks, deep learning, and complex networks (17–23). The compartmental model is a general and classic modelling approach that can be traced back about 100 years ago (24). The structured metapopulation model, derived from the compartmental model, is mainly designed for capturing the heterogeneity across subpopulations within a compartment, e.g., subpopulations based on age groups and small geographical regions (20). The agent-based network model further extends the metapopulation model and is able to model the epidemic dynamics at a single individual level (20). The deep learning technology, popular in recent years, has the potential to process various types of noisy heterogeneous data and capture the hidden information in the observed data pattern (19). The complex network, a new methodology inspired by observations from real-world networks, models the epidemic dynamics using non-trivial topology (21, 22, 25). Among all modeling methods, the compartmental model is one of the most widely used methods in COVID-19 pandemic predictions (26, 27).
In a compartmental model, the population is separated into multiple sub-population based on specific features (e.g., whether a person is susceptible, infectious, or has recovered). These sub-populations are referred to as compartments and are assigned different labels. The compartments are then connected using predefined transit rules, so individuals can transit between the compartments.
There are two noteworthy features of compartmental modeling that make this 100-year-old technique still applicable and relevant nowadays. First, the flexible framework of a compartment model allows users to easily modify the model structure and enhance its performance. Such flexibility aids in adding any new compartment(s) or splitting an existing compartment into multiple ones, thus allowing the model to better fit the observed pandemic data (28, 29). For instance, adding an undetected or asymptomatic compartment by splitting it from the exposed or infectious compartment may provide information for asymptomatic infection cases, which are important to accurately predict infections. Second, the adaptivity of a compartmental model allows well-matured approaches such as Bayesian inference, mixed-effects modeling, stochastic walk, and others, to improve the parameter estimation (30–38).
The Centers for Disease Control and Prevention (CDC) created a webpage (39) listing prediction models collected by the COVID-19 Forecast Hub (40). The COVID-19 Forecast Hub acts as the data source and central repository of forecasts for over 50 research groups worldwide (https://covid19forecasthub.org). The models from the Hub are submitted weekly to the CDC COVID-19 Mathematical Modeling page (39) to assist public health decision-making. All models are required to periodically report their predictions, which are subsequently compared to the ground truth data when new data are available. At the time of data analysis (September 2021), over 50 models were available. Around 40% of the models from the CDC COVID-19 Mathematical Modeling webpage used the compartmental model method.
In this review, we described the concepts and applications of the compartmental model for the forecast of the COVID-19 pandemic. The models were taken from those forecasting models listed on the CDC COVID-19 Mathematical Modeling page (39). The prediction performance of all these listed models was evaluated using a score function based on the residual error between model prediction and real data. Then, five well-performed compartmental models were selected for further discussion as they included features of interest expanding the concepts of compartmental models. In addition, we investigated the effects and impact of possible government-imposed policies and vaccination strategies on compartmental modeling.
Performance of Compartmental Model Prediction
The measurement of the performance of compartmental model prediction can be described using a score function developed by Gu et al. (41). As the epidemiological data is updated weekly, every model had a set of weekly-updated forecast scores representing its prediction performance. The forecast score was calculated using the historical “ground truth” data (i.e., Johns Hopkins University CSSE Time Series Summary). The number of deaths has been used as an indicator of the burden of COVID-19 on health care systems and the effectiveness of intervention policy (42). The forecast score is a function of error between the forecast and the actual number of deaths in the USA (41), which can be written as follows:
| 1 |
where N(t) is the number of reported cumulative deaths on day t, is the number of predicted cumulative deaths and T is the number of weeks-ahead forecast e.g., T = 2 represents 2 weeks-ahead forecast (i.e., 14 days’ forecast). Weeks-ahead forecasts normally range from 1 week to 4 weeks to represent short-term and long-term forecast performance, respectively. In our analysis, the 1-week ahead forecast score was selected as the indicator of the forecast performance.
A baseline model is established based on the mean of the previous week’s daily deaths which has a forecast score that can be written in a similar formulation without the prediction , as follows:
| 2 |
It is noted that the forecast score of this baseline model is calculated from the reported cumulative deaths of the previous period week’s daily deaths. The T is the same as described in the forecast score calculation in Eq. 1. Similar to the prediction models, the 1-week ahead forecast score was used in the analysis.
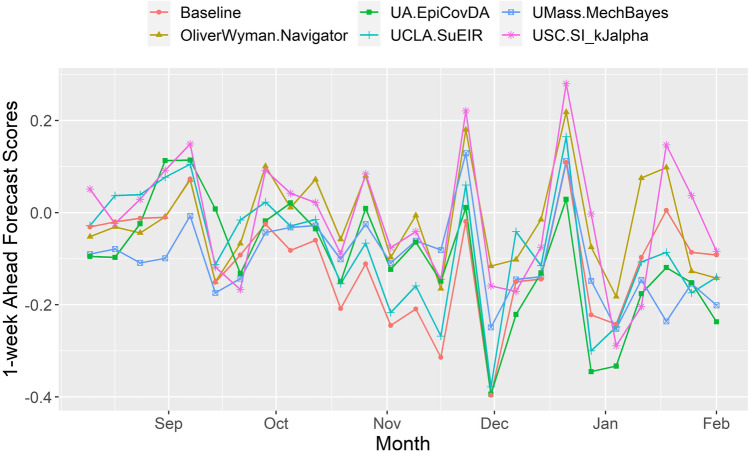
The 1-week ahead forecast scores were obtained for each model as well as the baseline model (41) from a total of 25 weeks starting from the week of August 10, 2020, to the week of February 1, 2021. The considered time frame (i.e. 25-week period) started during the decreasing phase of the second wave and covered the peak of the third wave, the highest wave observed in the USA to date (16). The absolute values of these forecast scores were used to evaluate the deviation of the model prediction from the ground truth data. Therefore, the mean absolute values of these forecast scores were subsequently used as the performance indicator. A lower mean absolute score indicates a better prediction. Overall, we calculated the mean absolute score for all 22 compartmental models and 1 baseline model. Table I lists the mean absolute scores for the five compartmental models with the lowest mean absolute scores. The five selected models had lower or comparable mean absolute scores when compared to the baseline model, indicating good forecasting performance. Figure 2 shows the 1-week ahead forecast scores for these five well-performed compartmental models.
Table I.
The Five Well-Performed Compartmental Prediction Models among the 22 Compartmental Models Listed on CDC COVID-19 Mathematical Modeling webpage
| Mean absolute score (baseline model: 0.123 ) | Model Name on the CDC webpage | Author/organization | Reference |
|---|---|---|---|
| 0.09 | OliverWyman-Navigator | Oliver Wyman | (35) |
| 0.111 | USC-SI_kJα | Data Science Lab, University of Southern California | (43, 44) |
| 0.119 | Umass-MechBayes | University of Massachusetts Amherst | (30) |
| 0.122 | UCLA-SuEIR | Statistical Machine Learning Lab, University of California, Los Angeles | (33) |
| 0.127 | UA-EpiCovDA | University of Arizona | (32, 45) |
Fig. 2.
Performance of the five well-performed compartmental models listed in CDC COVID-19 Mathematical Modeling webpage. (Scores from the week of August 10,2020 to the week of February 1, 2021 were used). Scores = 0: perfect prediction
Strategies for Compartmental Model-Based Forecast Performance Improvement
By reviewing these five well-performed compartmental models, we identified two categories for modeling enhancement such as (i) structure modification of the compartmental model, and (ii) parameter estimation enhancement. Table II summarizes the observed enhancement strategies.
Table II.
Modeling Enhancement Strategies Summarized from the Five Selected Compartmental Model-Based Forecasts
| Categories | Model name on CDC webpage | Strategies |
|---|---|---|
| Model structure modification | SuEIR | Adding compartment for unreported infectious cases |
| SI_kJα | Incorporating multiple infectious sub-states and considering spreading due to inter-region mobility | |
| Parameter estimation enhancement | MechBayes | Estimating parameters using Bayesian inference |
| EpiCovDA | Estimating parameters using Incidence-Cumulative Cases (ICC) curve. | |
| SI_kJα | Estimating parameters using a linearized system | |
| OliverWyman-Navigator | Incorporating real-world datasets to predict the values of parameters used in forecast |
Structure Modifications of the Compartment model
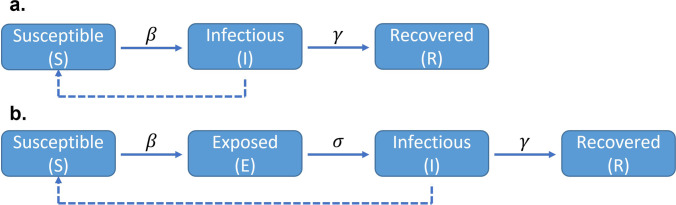
In the basic compartmental model in epidemiology, the total population can be assigned to compartments labeled such as S (susceptible), E (exposed), I (infectious), or R (removed/recovered). The susceptible compartment includes the population susceptible to the disease. The exposed compartment comprises the population infected by the disease but not yet infectious to others. The infectious compartment consists of the population that can infect those in the susceptible compartment. Finally, the removed compartment includes the population removed from the system either because of recovering or death. Notably, the death/deceased compartment (labeled as D) is another commonly used compartment when the disease can be fatal for the population. Thus, the R compartment can also be interpreted as a recovered compartment, especially in case a separated death compartment is included, or the immunity is not lifelong. Under this framework, the number of deaths can be predicted using the death compartment (if existing) or by multiplying the population in each of the compartments with their corresponding death rates. The latter can be inferred by multiple methods, for example by using data from clinical reports or by dividing the reported number of deaths by the reported number of infection cases. Population assigned to different compartments can be updated dynamically with inter-compartmental transitions. Depending on the disease, different combinations of the above-mentioned compartments or even additional ones can be included in compartmental models.
A basic susceptible-infectious-removed (SIR) model (Fig. 3a) can be formulated as follows (Eqs. 3–5):
| 3 |
| 4 |
| 5 |
where N is the total number of populations which equals S + I + R, β is the transmission rate and γ is the inverse of recovering time.
Fig. 3.
Graphical representation of the basic SIR (Susceptible-Infectious-Removed, panel a) and SEIR (Susceptible-Exposed-Infectious-Recovered, panel b) compartmental models. β: the transmission rate; γ: the inverse of recovering time; σ: the inverse of incubation period. Dotted lines represent transmission
Similarly, a susceptible-exposed-infectious-recovered (SEIR) model (Fig. 3b) can be formulated by adding an exposed compartment to account for the incubation period (Eqs. 6–9)
| 6 |
| 7 |
| 8 |
| 9 |
where σ is the inverse of the incubation period.
SuEIR Model: a Modified SEIR Model with Unreported Compartment
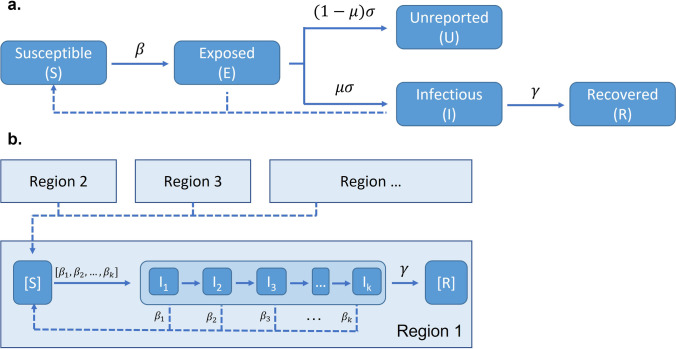
In classic SIR and SEIR models, only the number of reported infectious cases is used for model estimation. While asymptomatic infections have been reported during the COVID-19 pandemic (46), their exact number is hard to determine. The performance of the classic SIR/SEIR model may be weakened by a mismatch between the reported cases and the actual number of infectious cases defined in the model, due to the missing asymptomatic cases. To address this problem, Zou et al. proposed a susceptible-unreported-exposed-infectious-recovered (SuEIR) model (Fig. 4a) (33). The equations for the SuEIR model are listed as follows:
| 10 |
| 11 |
| 12 |
| 13 |
where β is the transmission rate between the susceptible and “infected” groups (the latter including both exposed and infectious compartments), σ is the rate of exposed cases that are either confirmed as infectious or dead/recovered without confirmation, μ is the discovery rate (a parameter between 0 and 1) which reflects unreported and undiscovered cases, and γ represents the transition rate between the I and R compartments. This model addresses the mismatch between the reported cases and the actual number of infections. The estimation of the discovery rate (μ) can provide predictions on cases of asymptomatic infections.
Fig. 4.
Graphical representation of the SuEIR model (Zou et al., 2020) with unreported state (panel a), and SI-kJα model (Prasanna, 2020a; Prasanna, 2020b) with infection caused by infectious individuals from other regions (panel b). μ: the discovery rate
SI-kJα Model: Heterogeneous Susceptible-Infected Model with Human Mobility
Since classic SIR or SEIR models assume a closed population without contact with other populations, Srivastava et al. proposed a heterogeneous susceptible-infectious (SI) model with human mobility, named SI-kJα model (43, 44) (Fig. 4b). The SI-kJα model can simulate disease transmission between regions. In the SI-kJα model, an individual in a specific region (i.e., hospital/city/state/country) can be in either a susceptible or an infectious compartment. A susceptible individual can be infected by others from the same region or from other regions (known as a “moving state”). Due to the complexity caused by the sub-states design of the infectious state, this model uses a new fitting method differing from the traditional approach, as discussed later in the section “Estimating Parameters Using the Linearized System.”
Improving Parameter Estimation
Researchers have used the following four approaches to improve parameter estimation (Table II): (i) Bayesian inference, (ii) fitting with incidence-cumulative cases (ICC) curve, (iii) using the linearized system, and (iv) incorporating real-world data in the model estimation.
Bayesian Inference
Bayesian inference is a well-known data-driven method that uses Bayes’ theorem to update the parameter values when new data is available. The Bayesian inference model estimates the values of the parameters using previous knowledge and observation data. In Bayesian theory, the posterior distribution is proportional to prior distribution and likelihood distribution which can be formulated as Eq. 14.
| 14 |
where P(θ| Y) is the posterior distribution, L(Y| θ) is the likelihood distribution, and P(θ) is the prior distribution.
When estimating an interested parameter θ in the epidemic model, knowledge about the epidemic can be used and translated into the prior distribution while the likelihood distribution can be inferred from the observed data. Therefore, the posterior distribution can be estimated using approaches such as the Markov chain Monte Carlo (MCMC) method or the Hamiltonian Monte Carlo (HMC) method. This estimated posterior distribution can be used to provide the estimate of θ given the available data. When a new observation becomes available, the previously estimated posterior distribution can be used as a new prior distribution. Then, this new prior distribution along with the new likelihood distribution derived from the newly observed data can be used to estimate a new posterior distribution, which will then provide the updated estimate for θ. A strong prior can originate from known information and previous experience, thus leading to better control over parameters estimation. However, a relatively weak prior can still be implemented if a parameter is believed to be highly relevant to random or indescribable factors.
Depending on the situation, both strong and weak prior information in Bayesian inference can be used in parameter estimation for modeling the COVID-19 pandemic. Most of the essential parameters (e.g., length of the incubation period and days of recovery) in the compartment model can be assigned with strong priors obtained from clinical research. In contrast, the value of the transmission coefficient in SIR and SEIR models can be highly affected by external situations such as evolving public health guidance, and social or weather events, and as such can be assigned as a weak prior. The Umass-MechBayes model (30) implemented both strong and weak Bayesian priors and, as a result, gained a high level of accuracy for model prediction in the complex pandemic situation.
Fitting with Incidence-Cumulative Cases Curve
Normally, when modeling a disease outbreak, the epidemic models aim to characterize and fit the curve of the observed daily infectious cases. In 2016, a novel approach was developed in the compartmental model by fitting the incidence of cumulative cases (ICC), in addition to the observed daily infectious cases (32). The EpiGro tool was developed based on this concept for disease outbreak forecasting (45).
This method first smooths and interpolates the epidemiological time curve. Then, an ICC curve is generated from this converted smooth curve. Next, an inverted parabola is fitted by minimizing the root mean square error to the ICC curve. Finally, the parameters in the fitted parabola can then identify the corresponding epidemic model. This approach was mainly designed to model a single peak of an outbreak, especially when available data is limited. Nonetheless, its performance is reported to be robust over multiple systems and noisy datasets (32).
Estimating Parameters Using the Linearized System
In the SI-kJα model, the states in the compartmental model are further divided into multiple sub-states by different time points with varying transmission rates (Fig. 4b). The model assumes that the infection occurring at time point t can only be caused by the infectious population between t and an earlier time point (t − k), indicating that a patient is infectious to others only for a certain period of time after being infected. In addition, following a similar dynamic, the local population can also be infected by the moving population from adjacent areas.
Developed from the basic compartmental model of SI components, a model for region p can be written as Eqs. 15–16.
| 15 |
| 16 |
where p is the target region, q represents regions connected to the target region p, F(q, p) is the moving population from q to p, and are the transmission coefficients in infectious sub-states (t − i) in the corresponding region p or q, δ is the transmission rate between the local and moving population, and k is the total number of infectious sub-states related to the infections occurring at time t.
To train the model, the system can be linearized by setting equal to a new variable and fitting it as an independent parameter. This modification enables the model to use different infection rates for the moving population in different sub-states, which can capture the rapidly changing trends of the epidemic. When using βp to represent the vector containing ’s and ’s, the increasing cases in each sub-state can be simplified to Eq. 17.
| 17 |
where contains the local and moving population in the corresponding sub-states. This linearized equation can then be solved using a constrained linear solver.
To train the interested parameters in βp, the following weighted least square function is used as an objective function for data fitting.
| 18 |
where is the actual reported number of cases and α is the forgetting factor with a value less or equal to 1, which gives more weight to more recently reported data.
By modifying the model structure and linearizing the system, the SI-kJα model can be used to forecast the spread of the virus while accounting for human mobility at the state- and country-levels. Since there are no assumptions on transmission coefficients, the model can adapt to real-life situations in a rapidly changing environment. However, adding these sub-states/transit compartments increases the number of parameters to be estimated and may potentially lead to over-parameterization.
Incorporating Real-World Data for Parameter Estimation (e.g., Social Mobility and Distancing)
Since the spreading of an infectious disease is highly related to the extent of social interaction between people, multiple real-world datasets, such as social mobility, age structure, and number of tests versus population, have the potential to be useful in parameter estimation.
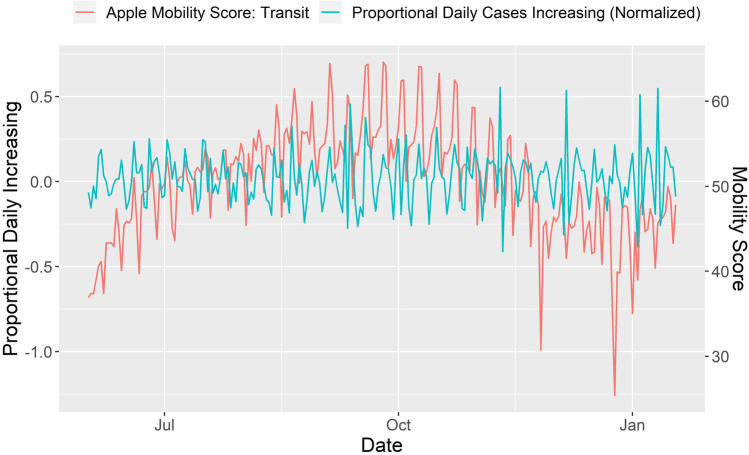
Mobility data is an example of a useful dataset to estimate the transmission coefficient (35, 47). Companies such as Apple (https://covid19.apple.com/mobility) and Google (https://www.google.com/covid19/mobility), publicly shared mobility data collected by cell phone GPS, thus providing high-quality mobility datasets for model building. Figure 5 shows the Apple mobility score versus the proportional daily increasing positive cases (https://covidtracking.com) from June 1, 2020, to January 18, 2021. We calculated the proportional daily increasing positive cases with the following equation:
| 19 |
where D(t) is the proportional daily increasing positive cases on day t and N(t) is the reported positive cases on day t. To account for the incubation period, we aligned the mobility scores from a specific day to the proportional daily increasing positive cases with an 8-day delay, i.e. D(t) was aligned to the mobility scores for day t − 8. For example, the mobility score for June 2 was aligned to the proportional daily increasing positive cases for June 10.
Fig. 5.
Mobility scores from Apple Transit (https://covid19.apple.com/mobility) aligned to proportional daily increasing positive cases (https://covidtracking.com). Mobility from day 1 is aligned to the number of cases from day 8 to account for the SARS-CoV-2 incubation period
Mobility data is a good resource for modeling as indicated by the similar trends between the two curves (i.e., mobility and the delayed proportional daily increasing positive cases) (Fig. 5). In addition to the mobility data, other datasets (such as social distancing, weather information, and turnaround time of COVID-19 testing) can also be applied to compartmental modeling (35, 47, 48).
Another example of using real-world data can be found in the OliverWyman-Navigator model, in which time-dependent transmission coefficients are deduced from the existing datasets. The predicted transmission coefficient values for forecasting are then estimated by fitting a function to the historical transmission coefficient value in their modified SIR-based model. The function can be written as:
| 20 |
which includes the information of an initial value (β0), the moving average of a mobility index from 8 days prior (T(t − 8)), number of tests per 1K of population (Et), speed of testing vs. recent new cases (F(t − 1)), and three fitted function parameters (x, y, and z) (35).
Although not included in the five well-performed models, the IHME model notably uses another interesting approach to handle real-world datasets. The model established by the IHME COVID-19 Forecasting Team incorporates real-world datasets as the covariates in a mixed effect model, instead of using a self-defined function (49). The mixed-effect model can be described as follows:
| 21 |
where X is a matrix containing all the covariates, α is the corresponding coefficients, and α0 is the random intercept. The covariates used in the model include both time-related features (such as social distance and mobility) and time-invariant features (such as population density and adult age-standardized tobacco smoking prevalence). After training the model, with the fitted α and predicted/given covariates, the future transmission coefficient values can be estimated and then used for case forecasting.
Assisting Policymaking using Compartmental Modelling
Modeling Government-Imposed Lockdown
Generally, lockdown is a potential measure to be implemented in severe cases to eliminate contact between people and thus prevent the spreading of the infectious disease. Since lockdown is a costly measure, evaluating the overall outcome of lockdown is necessary. The outcome of lockdown directly reflects on the basic reproduction number (R0) in the epidemic model. Thus, manipulating R0 to simulate the overall outcome of a lockdown is the most straightforward method. Chinyoka proposed a modified compartmental model built with states of susceptible (S), exposed (E), un-quarantined (U), quarantined (Q), hospitalized (H), recovered (R), and deaths (D) (50). In the model, the transition between compartments can represent the rate of (i) infection (S to E and S to U); (ii) asymptomatic individuals developing symptoms (E to U and E to Q); (iii) hospitalization (U to H and Q to H); and (iv) recovery or death (U, Q, H to either R or D). Given the transition rate between the states, the model can be written into a set of deterministic equations subjected to an initial condition. Stochastic variations are then introduced into the model, thus making it into a stochastic model containing the basic reproduction number R0. The simulation of the lockdown outcome can then be conducted by implementing different values of R0.
Mellone and colleagues considered that absolute lockdown is not possible since people must contact others for basic life needs, and thus developed a Free-to-Lockdown Hybrid model (FL-Hybrid model) (51). This model simulates the free and lockdown phases by switching between its two sub-models. During the free phase, a relatively simply compartmental model is used, such as susceptible, undetected, detected, extinct, and recovered (SUDER) model. The susceptible population can only be infected by undetected patients. Undetected patients will become either detected or recovered, and the detected patients will transfer to either the recovered or extinct states in the model. Upon entering the lockdown phase, the population is separated into two groups: free and lockdown. The free population, subject to the same SUDER model described in the free phase, comprises people who must interact with others (e.g., essential workers). The lockdown population represents people staying at home and only going outside for essential needs. The unit of the lockdown population is a household composed of three individuals. A household can be in one of the following four situations: no infected individuals (i.e., infection-free), one infected individual, two infected individuals, and three infected individuals. An infection-free household can only become infected after contact with the free population. In an infected household, the disease can spread because of contact with one or more infected household member(s) as well as with the free population. Using this model, lockdowns of varying lengths can be simulated by adjusting the switching time points of the two sub-models. The different levels of lockdown enforcement can also be simulated by adjusting the percentage of the free population over the whole population.
Modeling the Effect of Vaccination
Once vaccination campaigns are implemented, a larger portion of the general public is expected to be vaccinated, which should result in a reduction in the number of new cases. Thus, including vaccination in the model is useful to evaluate the effect of vaccination on the epidemic and to guide future policy.
As the vaccinated population is expected to have a significantly reduced risk of getting infected by the virus, adding a vaccinated state is the most straightforward method. In the model proposed by Lu and Ishwaran (52), two vaccinated compartments (i.e. vaccinated susceptible and vaccinated infected population) are added to a classic SIR model. Populations of vaccinated and unvaccinated susceptible states will transfer into their corresponding vaccinated and unvaccinated infected states at different rates. This model successfully fitted to the real data, indicating the effectiveness of the model design (52).
Considering that vaccination efficiency may differ at the individual level, a more sophisticated model can be used to model the outcome of vaccination. In the model proposed by Lee et al., a modified SEIR model is used as the basic epidemic model (53). The infectious and recovered state (I and R) are further divided into symptomatic/asymptomatic and recovered with/without immunity states, respectively. A hospitalized state (H) is added between the symptomatic state and the recovered/death states to represent the patients who are hospitalized after being diagnosed. To simulate the differences in vaccination efficiency, the population is categorized into five groups: unvaccinated, vaccinated, full immunity, partial immunity, and vaccinated not immunized. Except for the full immunity group which exits the system, the remaining groups are subject to the modified SEIR model with different parameter settings. Specifically, four compartmental models are running simultaneously for the four population groups. An individual can transfer from one group to another under a given rule. This modeling framework can be used to simulate the outcome of a mass vaccination event. The model can assist intervention decision-making and can be especially useful to plan for the optimal outcome when the vaccine supply is limited.
Discussion
We analyzed the forecasting models from the CDC COVID-19 Mathematical Modeling/COVID-19 Forecast Hub by evaluating the average score calculated from the error between the model prediction and “ground truth” data.
Based on our analysis, compartmental models can be implemented to include novel approaches and efficiently modified to fit the need of researchers. A basic compartmental model was used to predict the outbreak at the beginning of the epidemic. As the epidemic progressed, asymptomatic infections were reported (54). As a result, asymptomatic and undetected infectious states were widely used in the models to predict asymptomatic infections. Subsequently, multiple locations reported a second peak of the infection, showing high variability in terms of shape and timing. Thus, dynamic parameters were introduced to replace fixed value parameters to correctly predict the change of the infection trends. At the same time, more complicated models were built to assist policymaking by estimating the outcome of interventions. When vaccines became available to the public, models with vaccinated states were proposed to estimate the outcome of vaccination and guide resource allocation. When the Delta variant became the predominant variant of the virus in the USA, researchers used the compartmental model to analyze its spread (55). In 2022, the Omicron variant, shown to be more transmissible and able to infect people with immunization, caused a new wave of infection in the USA (11, 13, 14). Considering the features of the Omicron variant, an adapted compartment model was developed and used to analyze the outbreak caused by such variant (56). As highlighted above, the compartmental model is extremely adaptive and can quickly be modified and implemented to address new data or issues. It represents a powerful tool to help fight pandemic(s).
However, compartmental modelling also shows some limitations. Firstly, as the compartmental model naturally requires many parameters to be estimated, over-parameterization can potentially pose a challenge for model fitting. Secondly, when used by itself, compartmental modelling can only perform a single peak prediction. To improve the prediction performance in complicated scenarios, compartmental modelling must be used in combination with other methods or techniques.
Finally, there are a few limitations in our review. It does not cover the entire field of the compartmental model as it is based on the models listed on the CDC webpage for COVID-19 outbreak prediction. We focused on country-level data in the prediction performance assessment, as the local region might be defined differently by different models, and not every model included local prediction results. In addition, to assess model performance, we selected a 25-week time interval when most of the modeling teams had been actively reporting their predictions.
Conclusion
The 100-year-old epidemic compartmental model (24) is still the most popular method for modeling and forecasting the ongoing COVID-19 pandemic. Among the over 50 forecasting models collected by the CDC COVID-19 Mathematical Modeling page, around 40% are using the compartmental model-based method. The compartmental model is powerful (i.e., able to analyze real-world, multi-peak outbreaks) when used in conjunction with performance-enhancing methods. Compartmental model-based methods have similar accuracy as other novel methods that emerged in recent years (e.g., deep learning), but are less computationally intensive. The flexibility of compartmental models can provide accurate short-term COVID-19 predictions and be helpful for long-term pandemic projection, accounting for situations such as vaccination. COVID-19 model predictions can help inform decision-making for pandemic intervention, resource allocation, and drug shortage mitigations. Our study identified several well-performing models that can be potentially employed during a future pandemic like COVID-19.
Abbreviations
- SARS-CoV-2
severe acute respiratory syndrome-associated coronavirus-2
- FDA
United States Food and Drug Administration
- WHO
World Health Organization
- EUA
emergency use authorization
- CDC
Centers for Disease Control and Prevention
- SI Model
susceptible-infectious model
- SIR Model
susceptible-infectious-removed model
- SEIR Model
susceptible-exposed-infectious-recovered model
- SuEIR Model
susceptible-unreported-exposed-infectious-recovered model
- ICC Curve
incidence-cumulative cases curve
- R_0
basic reproduction number
- FL-Hybrid Model
free-to-lockdown hybrid model
- SUDER Model
susceptible, undetected, detected, extinct and recovered model
Author Contribution
P.Z., L.Z., and K.F. conceptualized the study. P.Z. collected and analyzed the data. P.Z., L.Z., K.F., Y.G., and J.L. contributed to the interpretation of the results. P.Z. wrote the first draft and P.Z., S.L. and L.Z. took the lead in the revision of the manuscript. All authors had full access to all the data in the study and critically reviewed, edited, and approved the final manuscript.
Declarations
Conflict of Interest
All authors declare no competing interests.
Disclaimer
The opinions expressed in this manuscript are those of the authors and should not be interpreted as the position of the US Food and Drug Administration.
Footnotes
The work was conducted as outside activities from the authors’ official duties.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Schondelmeyer SW, Dickson C, Dasararaju D, Margraf DJ, Caschetta C, Mueller M, et al. Part 6: Ensuring a resilient us prescription drug supply. COVID-19: the CIDRAP viewpoint. 2020.
- 2.Huang C, Wang Y, Li X, Ren L, Zhao J, Hu Y, et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395(10223):497-506. 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed]
- 3.Cucinotta D, Vanelli M. WHO declares COVID-19 a pandemic. Acta Biomed. 2020;91(1):157-60. 10.23750/abm.v91i1.9397. [DOI] [PMC free article] [PubMed]
- 4.Brown M, Bryant K, Curiskis A, French A, Glickhouse R, Goldfarb A, et al. The COVID tracking project. https://covidtracking.com/ (2021). Accessed 02 Aug 2022.
- 5.Rinott E, Youngster I, Lewis YE. Reduction in COVID-19 patients requiring mechanical ventilation following implementation of a national COVID-19 vaccination program — Israel, December 2020–February 2021. MMWR Morb Mortal Wkly Rep 20212021. p. 70:326–8. [DOI] [PMC free article] [PubMed]
- 6.The United States Food and Drug Administration. Pfizer-BioNTech COVID-19 Vaccine. https://www.fda.gov/emergency-preparedness-and-response/coronavirus-disease-2019-covid-19/pfizer-biontech-covid-19-vaccine (2020). Accessed 2 Aug 2022.
- 7.The United States Food and Drug Administration. Moderna COVID-19 Vaccine. https://www.fda.gov/emergency-preparedness-and-response/coronavirus-disease-2019-covid-19/moderna-covid-19-vaccine (2020). Accessed 2 Aug 2022.
- 8.The United States Food and Drug Administration. Janssen COVID-19 Vaccine. https://www.fda.gov/emergency-preparedness-and-response/coronavirus-disease-2019-covid-19/janssen-covid-19-vaccine (2021). Accessed 2 Aug 2022.
- 9.World Health Organization. WHO Coronavirus (COVID-19) Dashboard. https://covid19.who.int/region/searo/country/in Accessed 2 Aug 2022.
- 10.Centers for Disease Control and Prevention. Delta variant: what we know about the science. https://www.cdc.gov/coronavirus/2019-ncov/variants/delta-variant.html (2021). Accessed 2 Aug 2022.
- 11.World Health Organization. Update on Omicron. https://www.who.int/news/item/28-11-2021-update-on-omicron (2021). Accessed 2 Aug 2022.
- 12.Centers for Disease Control and Prevention. COVID data tracker: variant proportions. https://covid.cdc.gov/covid-data-tracker/#variant-proportions (2022). Accessed 2 Aug 2022.
- 13.Ren SY, Wang WB, Gao RD, Zhou AM. Omicron Variant (B.1.1.529) of SARS-CoV-2: mutation, infectivity, transmission, and vaccine resistance. World J Clin Cases. 2022;10(1):1-11. 10.12998/wjcc.v10.i1.1. [DOI] [PMC free article] [PubMed]
- 14.Araf Y, Akter F, Tang YD, Fatemi R, Parvez MSA, Zheng C, et al. Omicron variant of SARS-CoV-2: genomics, transmissibility, and responses to current COVID-19 vaccines. J Med Virol. 2022;94(5):1825-1832. 10.1002/jmv.27588. [DOI] [PMC free article] [PubMed]
- 15.Taubenberger JK, Morens DM. 1918 Influenza: the mother of all pandemics. Emerg Infect Dis. 2006;12(1):15–22. doi: 10.3201/eid1201.050979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.National Center for Health Statistics. Provisional COVID-19 death counts by week ending date and state. https://data.cdc.gov/NCHS/Provisional-COVID-19-Death-Counts-by-Week-Ending-D/r8kw-7aab (2022). Accessed 2 Aug 2022.
- 17.Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-ncov outbreak originating in wuhan, china: a modelling study. Lancet. 2020;395(10225):689–697. doi: 10.1016/s0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou T, Liu Q, Yang Z, Liao J, Yang K, Bai W, et al. Preliminary prediction of the basic reproduction number of the wuhan novel coronavirus 2019-nCoV. J Evid-Based Med. 2020;13(1):3-7. 10.1111/jebm.12376. [DOI] [PMC free article] [PubMed]
- 19.Rodríguez A, Tabassum A, Cui J, Xie J, Ho J, Agarwal P, et al. DeepCOVID: an operational deep learning-driven framework for explainable real-time COVID-19 forecasting. Proc AAAI Conf Artif Intell. 2021;35(17):15393-15400.
- 20.Adiga A, Dubhashi D, Lewis B, Marathe M, Venkatramanan S, Vullikanti A. Mathematical models for COVID-19 pandemic: a comparative analysis. J Indian Inst Sci. 2020:1–15. 10.1007/s41745-020-00200-6. [DOI] [PMC free article] [PubMed]
- 21.Della Morte M, Orlando D, Sannino F. Renormalization group approach to pandemics: the COVID-19 case. Front Phys. 2020;8. 10.3389/fphy.2020.00144.
- 22.Della Morte M, Sannino F. Renormalization group approach to pandemics as a time-dependent SIR model. Front Phys. 2021;8. 10.3389/fphy.2020.591876.
- 23.Cacciapaglia G, Cot C, Sannino F. Second wave COVID-19 pandemics in Europe: a temporal playbook. Sci Rep. 2020;10(1):15514. 10.1038/s41598-020-72611-5. [DOI] [PMC free article] [PubMed]
- 24.Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A . 1927;115(772):700–721. doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
- 25.Albert R, Barabási A-L. Statistical mechanics of complex networks. Rev Mod Phys. 2002;74(1):47–97. doi: 10.1103/RevModPhys.74.47. [DOI] [Google Scholar]
- 26.Lin YF, Duan Q, Zhou Y, Yuan T, Li P, Fitzpatrick T, et al. Spread and impact of COVID-19 in China: a systematic review and synthesis of predictions from transmission-dynamic models. Front Med (Lausanne). 2020;7:321. 10.3389/fmed.2020.00321. [DOI] [PMC free article] [PubMed]
- 27.Guan J, Wei Y, Zhao Y, Chen F. Modeling the transmission dynamics of COVID-19 epidemic: a systematic review. J Biomed Res. 2020;34(6):422–430. doi: 10.7555/JBR.34.20200119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mohamadou Y, Halidou A, Kapen PT. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of COVID-19. Appl Intell. 2020;50(11):3913–3925. doi: 10.1007/s10489-020-01770-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ansumali S, Kaushal S, Kumar A, Prakash MK, Vidyasagar M. Modelling a pandemic with asymptomatic patients, impact of lockdown and herd immunity, with applications to SARS-CoV-2. Annu Rev Control. 2020;50:432–447. doi: 10.1016/j.arcontrol.2020.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sheldon DRG, Graham C; Reich, Nicholas. Bayesian compartmental models for COVID-19. https://github.com/dsheldon/covid Accessed 02 Aug 2022.
- 31.Burant J. COVID19 Political Realities Model. https://viz.covid19forecasthub.org/ (2020). Accessed 2 Aug 2022.
- 32.Lega J, Brown HE. Data-driven outbreak forecasting with a simple nonlinear growth model. Epidemics. 2016;17:19–26. doi: 10.1016/j.epidem.2016.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zou D, Wang L, Xu P, Chen J, Zhang W, Gu Q. Epidemic model guided machine learning for COVID-19 forecasts in the United States. medRxiv [Preprint]. 2020:2020.05.24.20111989. 10.1101/2020.05.24.20111989.
- 34.LockNQuay. Model: LockNQuay - LNQ-ens1. https://www.kaggle.com/sasrdw/locknquay (2021). Accessed 2 Aug 2022.
- 35.Wyman O. Oliver Wyman COVID-19 Pandemic Navigator. https://pandemicnavigator.oliverwyman.com/ Accessed 2 Aug 2022.
- 36.Hong Q-J. QJHong COVID Model. https://qjhong.github.io/ (2021). Accessed 2 Aug 2022.
- 37.Wang Q, Xie S, Wang Y, Zeng D. Survival-convolution models for predicting COVID-19 cases and assessing effects of mitigation strategies. Front Public Health. 2020;8(325). 10.3389/fpubh.2020.00325. [DOI] [PMC free article] [PubMed]
- 38.Arik SO, Li CL, Yoon J, Sinha R, Epshteyn A, Le L, Menon V, Singh S, Zhang L, Yoder N, Nikoltchev M, Sonthalia Y, Nakhost H, Kanal E, Pfister T. Interpretable sequence learning for COVID-19 forecasting. ArXiv [Preprint]. 2021. 10.48550/arXiv.2008.00646.
- 39.Centers for Disease Control and Prevention. COVID-19 Mathematical Modeling. https://www.cdc.gov/coronavirus/2019-ncov/science/forecasting/mathematical-modeling.html Accessed 2 Aug 2022.
- 40.Cramer EY, Huang Y, Wang Y, Ray EL, Cornell M, Bracher J, et al. The United States COVID-19 Forecast Hub Dataset. Sci Data. 2022;9(1):462. doi: 10.1038/s41597-022-01517-w. [DOI] [PMC free article] [PubMed]
- 41.Gu Y. Evaluation of COVID-19 Models. https://github.com/youyanggu/covid19-forecast-hub-evaluation Accessed 02 Aug 2022.
- 42.Ray EL, Wattanachit N, Niemi J, Kanji AH, House K, Cramer EY, et al. Ensemble forecasts of coronavirus disease 2019 (COVID-19) in the U.S. medRxiv [Preprint]. 2020:2020.08.19.20177493. 10.1101/2020.08.19.20177493.
- 43.Srivastava A, Xu T, Prasanna VK. Fast and Accurate Forecasting of COVID-19 Deaths Using the SIkJalpha Model. ArXiv [Preprint]. 2020. 10.48550/arXiv.2007.05180.
- 44.Srivastava A, Prasanna VK. Learning to forecast and forecasting to learn from the COVID-19 pandemic. ArXiv [Preprint]. 2020. 10.48550/arXiv.2004.11372.
- 45.Lega J. Parameter Estimation From ICC Curves. J Biol Dyn. 2021;15(1):195–212. doi: 10.1080/17513758.2021.1912419. [DOI] [PubMed] [Google Scholar]
- 46.Bai Y, Yao L, Wei T, Tian F, Jin D-Y, Chen L, et al. Presumed asymptomatic carrier transmission of COVID-19. JAMA. 2020;323(14):1406-1407. 10.1001/jama.2020.2565. [DOI] [PMC free article] [PubMed]
- 47.Shao W, Xie J, Zhu Y. Mediation by human mobility of the association between temperature and COVID-19 transmission rate. Environ Res. 2021;194:110608. doi: 10.1016/j.envres.2020.110608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Liu M, Thomadsen R, Yao S. Forecasting the spread of COVID-19 under different reopening strategies. Sci Rep. 2020;10(1):20367. doi: 10.1038/s41598-020-77292-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Reiner RC, Barber RM, Collins JK, Zheng P, Adolph C, Albright J, et al. Modeling COVID-19 scenarios for the United States. Nat Med. 2021;27(1):94-105. 10.1038/s41591-020-1132-9. [DOI] [PMC free article] [PubMed]
- 50.Chinyoka T. Stochastic modelling of the dynamics of infections caused by the SARS-CoV-2 and COVID-19 under various conditions of lockdown, quarantine, and testing. Results Phys. 2021;28:104573. doi: 10.1016/j.rinp.2021.104573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mellone A, Gong Z, Scarciotti G. Modelling, prediction and design of COVID-19 lockdowns by stringency and duration. scientific reports. 2021;11(1):15708. 10.1038/s41598-021-95163-8. [DOI] [PMC free article] [PubMed]
- 52.Lu M, Ishwaran H. Cure and death play a role in understanding dynamics for COVID-19: data-driven competing risk compartmental models, with and without vaccination. PLoS ONE. 2021;16(7):e0254397. doi: 10.1371/journal.pone.0254397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lee EK, Li ZL, Liu YK, LeDuc J. Strategies for vaccine prioritization and mass dispensing. vaccines (Basel). 2021;9(5). 10.3390/vaccines9050506. [DOI] [PMC free article] [PubMed]
- 54.Sah P, Fitzpatrick MC, Zimmer CF, Abdollahi E, Juden-Kelly L, Moghadas SM, et al. Asymptomatic SARS-CoV-2 infection: a systematic review and meta-analysis. Proc Natl Acad Sci. 2021;118(34):e2109229118. 10.1073/pnas.2109229118. [DOI] [PMC free article] [PubMed]
- 55.Head JR, Andrejko KL, Remais JV. Model-based assessment of SARS-CoV-2 Delta variant transmission dynamics within partially vaccinated K-12 school populations. Lancet Reg Health Am. . 2022;5:100133. doi: 10.1016/j.lana.2021.100133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zuo C, Meng Z, Zhu F, Zheng Y, Ling Y. Assessing vaccination prioritization strategies for COVID-19 in south africa based on age-specific compartment model. Front Public Health. 2022;10:876551. doi: 10.3389/fpubh.2022.876551. [DOI] [PMC free article] [PubMed] [Google Scholar]