Social Distancing, Vaccination and Evolution of COVID-19 Transmission Rates in Europe

Abstract

This paper provides estimates of COVID-19 transmission rates and explains their evolution for selected European countries since the start of the pandemic taking account of changes in voluntary and government mandated social distancing, incentives to comply, vaccination and the emergence of new variants. Evidence based on panel data modeling indicates that the diversity of outcomes that we document may have resulted from the nonlinear interaction of mandated and voluntary social distancing and the economic incentives that governments provided to support isolation. The importance of these factors declined over time, with vaccine uptake driving heterogeneity in country experiences in 2021. Our approach also allows us to identify the basic reproduction number, ${\mathcal{R}}_0$, which is precisely estimated around 5, which is much larger than the values in the range of 2.4–3.9 assumed in the extant literature.

Supplementary Information

The online version contains supplementary material available at 10.1057/s41308-022-00181-9.

Introduction

The COVID-19 pandemic has claimed millions of lives and brought about very costly government interventions to contain it, with unprecedented and widespread economic disruption worldwide. China responded to the outbreak with strict policies, including binding and mandatory social distancing. These policies have initially proved successful in containing the epidemic in China, but later became much harder to sustain. At the other end of the spectrum, for example, Sweden initially attempted to let its epidemic run its course with only minimal interventions from the government. Other countries responded by adopting a mixture of policies, either by deliberate choice or due to popular opposition to the implementation of lock-downs or even milder forms of social distancing. What drives heterogeneity across countries in outcomes? As the COVID-19 pandemic evolved into a an endemic infectious disease in the midst of heated debates on the pros and cons of social distancing, what lessons do we learn for the management of future epidemics?

In this paper, we contribute toward answering these questions by providing estimates of COVID-19 effective reproduction numbers and explain their evolution for selected European countries since the start of the pandemic in early 2020, taking account of changes in voluntary and government mandated social distancing, economic support to comply with isolation, vaccination, and the emergence of new mutations.1 Although the European countries we focus on had similar patterns of transmissions at the beginning of the pandemic, they end up with quite different outcomes. We show that familiar factors such as social distancing, incentives to comply, or people’s voluntary responses to the epidemic on their own cannot account for the heterogeneity of outcomes that we document across selected European countries over the period 2020-2021. Vaccine uptake, however, clearly becomes the dominant factor accounting for country differences in outcomes in 2021.

Reproduction numbers are epidemiological metrics to measure the spread of an infectious disease. The basic reproduction number, denoted by ${\mathcal{R}}_0$, is the number of new infections expected to result from one infected individual at the start of the epidemic, assuming no interventions. Computation of the reproduction number is inherently model specific. Within a classical susceptible-infectious-removed (SIR) model, the basic reproduction number is given by ${\mathcal{R}}_0={\beta }_0/\gamma$, where ${\beta }_0$ is the initial (biological) transmission rate, and $\gamma$ is the recovery rate. Since the transmissibility of a disease will vary over time due to changes in immunity, mitigation policies, or voluntary precautionary behavior, the effective reproduction number, which we denote by ${\mathcal{R}}_{\mathit{et}}$, measures the $\mathcal{R}$ number t periods after the initial outbreak. As we show in the paper, in the classical SIR model, we have ${\mathcal{R}}_{\mathit{et}}=\left(1,-,c_t\right){\beta }_t/\gamma$, where $c_t$ is the per capita number of infected cases at time t. As a result, conditional on this particular epidemiological model, one can separate changes in ${\mathcal{R}}_{\mathit{et}}$ due the extent to which the susceptible population is shrinking, $1-c_t$ (which we call herding), or due to changes in the transmission rate, ${\beta }_t$. Social distancing, either voluntary due to precautionary behavior or mandatory due to non-pharmaceutical interventions (which we also call mitigation or containment policies for brevity), compliance with mandated measures, and immunity changes due to virus mutations or vaccination all lead to time-variation in the transmission rate.

We obtain estimates of time-varying transmission rates, ${\beta }_t$, using a moment condition recently derived by Pesaran and Yang (2021), henceforth PY from an agent-based stochastic network model of the epidemic diffusion. We extend the PY model to allow for time variations in underlying drivers of the aggregate transmission rate ${\beta }_t$, which in this model can approximately be written as ${\tau }_t{k}_t/{\mu }_t$, where $k_t$ is the mean number of contacts during day t among the population, ${\tau }_t$ is the mean exposure intensity to the virus given contact, and ${\mu }_t\ge 1$ captures the mean immunity level in the population.

Our estimation method only requires data on infected cases, thus complementing estimation methods that make use of death statistics. Both the reported number of infected cases and deaths are subject to important measurement issues, with different countries adopting different concepts and standards. In a number of countries, COVID-19 death statistics have undergone major revisions on several occasions. For example, the UK death toll was revised downward by 5377 on August 12, 2020, after a review concluded that daily death figures should only include deaths which had occurred within 28 days of a positive COVID-19 test. We follow the medical evidence in Gibbons et al. (2014), and introduce a multiplication factor (MF) to allow for under-reporting of infected cases, and investigate the robustness of our results to different choices of MF.

To understand the potential factors behind the heterogeneous evolution of effective reproduction numbers in Europe, we separate the herding component (given by shrinking share of the susceptible individuals in the population) from the transmission rate, and empirically model the latter conditional on our chosen epidemiological model. In our set up, the transmission rate depends on the average number of contacts, individual-specific susceptibility to becoming infected, and the average exposure intensity given contacts, which in turn depends on wearing of face masks, and other recommended precautions, as well as the average degree of immunity in the population. Accordingly, in our empirical analysis we assume that a country’s time-varying transmission rate potentially depends on five factors: mandatory and voluntary social distancing, economic support to comply with mandatory polices, vaccine uptake and virus mutations.

Consistent with a simple decision theoretic model of voluntary social distancing presented in the paper and a large body of empirical evidence, we consider both government-mandated social distancing policies and voluntary self-isolation. We also control for government economic support that affects the incentive to comply as reported in survey data (e.g., Papageorge et al. 2021; Hamermesh 2020). To proxy mandated-social distancing and incentives to comply with these policies we use the stringency and support indices compiled by Oxford COVID-19 Government Response Tracker project.2 To assess the potential impact of voluntary social distancing, we allow for threshold effects capturing the impact of fear of becoming infected arising from news of rising cases on individual precautionary behavior.3 The importance of these factors in controlling the effective rate of transmission is jointly estimated within the context of the epidemic model. In 2021, virus mutations and vaccine availability and uptake became more prominent. Thus, we add to the baseline model the population share of vaccinated people and the Delta share of the confirmed sequenced cases, and we re-estimate the model through November 2021.

We focus on nine European countries with similar starts to the epidemic outbreak in March 2020, but with differing outcomes subsequently. In a pre-vaccine sample, we find that all determinants of the transmission rate considered in the paper are statistically highly significant and have the expected signs, and have been important in bring downing the effective production number, ${\mathcal{R}}_{\mathit{et}}$, below unity over sustained periods. However, in the post-vaccine sample ending in November 2021, we find that vaccine uptake is the most important contributor to the decline in the effective transmission rate. In both samples, we estimate model-consistent basic reproduction numbers to lie between 5 and 6 for all the European countries that we consider, somewhat higher than the early estimates of around 3 reported in the literature and documented below.

In conclusion, our empirical analysis shows that mandatory and voluntary social distancing and incentives to comply were critical in bringing the reproduction number below one. Similarly, vaccine uptake in 2021 is estimated to be the most important factor contributing to the reduction in effective transmission rates, but the other factors continued to be salient.

Related Literature A very large body of research investigates the COVID-19 outbreak and the policies to contain its spread.4 For example, Fang et al. (2020) analyze efforts to contain the COVID-19 outbreak in China, measuring the effectiveness of the lock-down of Wuhan and showing that these policies also contributed significantly to reducing the total number of infections also outside of Wuhan. Similarly, there is ample reduced form evidence on the impact of mandatory social distancing using state and county level data in the case of the USA and for a few other countries. However, there are not many studies on the relative importance of mandatory and voluntary social distancing, especially comparative across countries.

Caselli et al. (2020) find that both lock-downs and voluntary social distancing helped contain the first wave of COVID-19, but mandatory interventions have been critical. Jinjarak et al. (2020) find that more stringent policies are associated with lower mortality growth rates in a large cross section of countries but with some heterogeneity depending on demographics, the degree of urbanization and political freedom, as well as the international travel flows. In general, however, countries with more stringent policies at the onset of the epidemic realized lower peak mortality rates and exhibited lower duration during the first epidemic wave. We distinguish not only between mandatory and voluntary social distancing, but also consider the incentives to comply and herd immunity in lowering the reproduction number, as well as vaccine uptake and mutations. To our knowledge, no study which considers voluntary or government-mandated social distancing also controls for the possibility of herd immunity and distinguishes its impacts on effective reproduction numbers from the influence of policy and/or behavioral factors.

A number of studies consider the effects of different intervention strategies—such as isolating the elderly, closing schools and/or workplaces, and alternating work/school schedules—which should lower the average number of contacts of specific age groups, contact locations, or time windows relative to normal (pre-COVID) patterns using calibrated behavioral SIR or compartmental models.5 We take an empirical/econometrics approach calibrating only the recovery rate, $\gamma$; a parameter on which we have much more precise clinical information.

Various methods are available in the epidemiological literature to estimate the reproduction numbers at the beginning and/or in real time during epidemics. Estimation of reproduction numbers based on different models is reviewed by Chowell and Nishiura (2008), Obadia et al. (2012), and Nikbakht et al. (2019). More recent contributions, focusing on estimation of reproduction numbers for the COVID-19 pandemic based on death statistics includes Atkeson et al. (2020b), Baqaee et al. (2020), Korolev (2020) and Toda (2020). As we noted earlier both death and case statistics are problematic, and we provide complementary evidence relying only on case statistics correcting for measurement errors and under-reporting. Other closely related papers are Fernández-Villaverde and Jones (2020), Atkeson et al. (2020a) , and Cakmakli and Simsek (2020).

The rest of the paper is organized as follows. Section 2 discusses SIR model with time-varying transmission rates. Section 3 presents the method and estimation results for the transmission rates and reproduction numbers for selected European countries. Section 4 sets up the panel data model to assess the relative importance of the key factors driving the effective transmission rate over time and across countries and reports the estimation results. Section 5 concludes. “Appendix” presents an extension of PY model to allow for time variations in key parameters affecting the transmission of the virus.

A SIR Model with Time-Varying Transmission Rate

There are many approaches to modeling the spread of epidemics. The basic mathematical model widely used by researchers is the susceptible-infected-removed (SIR) model advanced by Kermack and McKendrick (1927). This model and its various extensions have been the subject of a vast number of studies and have been applied extensively to investigate the spread of COVID-19.6

The basic SIR model considers a given population of fixed size n, composed of three distinct groups, those individuals in period t who have not yet contracted the disease and are therefore susceptible, denoted by $S_t$; the ‘removed’ individuals who can no longer contract the disease, consisting of recovered and deceased, denoted by $R_t$; and those who remain infected at time t and denoted by $I_t$. Thus,

$$\begin{array}{c}\hfill n=S_t+I_t+R_t.\end{array}$$ 1

As it stands, this is an accounting identity, and it is therefore sufficient to model two of the three variables ($S_t$, $I_t$, and $R_t$) to obtain the third as the remainder.

The classic SIR model is deterministic. It is cast in the following set of difference equations (for $t=1,2,\dots ,T$)

$$\begin{array}{cc}\hfill S_{t+1}-S_t=& -S_t\beta I_t,\hfill \end{array}$$ 2

$$\begin{array}{cc}\hfill I_{t+1}-I_t=& S_t\beta I_t-\gamma I_t,\hfill \end{array}$$ 3

$$\begin{array}{cc}\hfill R_{t+1}-R_t=& \gamma I_t.\hfill \end{array}$$ 4

The parameter $\beta$ is the rate of transmission, while $\gamma$ is the recovery rate. The evolution of the epidemic crucially depends on these two key parameters. It is easy to see from Eqs. (2)–(4) that, without any mitigating intervention, the epidemic will spread if $\beta /\gamma ={\mathcal{R}}_0>1$ and will stops spreading only once $({\mathcal{R}}_0-1)/{\mathcal{R}}_0$ proportion of the population are infected. The parameter ${\mathcal{R}}_0$ is known as the basic reproduction number, defined as “the average number of secondary cases produced by one infected individual during the infected individual’s entire infectious period assuming a fully susceptible population” (Del Valle et al. 2013). The ratio $({\mathcal{R}}_0-1)/{\mathcal{R}}_0$ is also known as the herd immunity threshold.

In the case of COVID-19, a number of different estimates have been suggested in the literature, initially placing ${\mathcal{R}}_0$ somewhere in the range of 2.4 to 3.9, with even larger numbers for more recent variants of concern such as Delta and Omicorn.7 So, the classical SIR model predicts that in the absence of intervention as much as 2/3-3/4 of the population could eventually become infected before herd immunity is reached. Inevitably, the estimation of ${\mathcal{R}}_0$ is model-dependent and different epidemiological models will imply different estimates of ${\mathcal{R}}_0$. Our panel estimates reported below suggest ${\mathcal{R}}_0$ is in excess of 5 in Europe, requiring as much as 4/5 of the population to achieve immunity before COVID-19 stops from spreading.

This well-understood possibility triggered unparalleled mitigation and containment interventions, first by China and South Korea, then Europe, the USA and all other countries around the world. Such interventions, which broadly speaking we refer to as “mandated social distancing” include case isolation, mask mandates, banning of gatherings, closures of schools and universities, and even local and national lock-downs; all aimed at slowing down the transmission rate of the virus. It is clear that these policies, together with voluntary changes in behavior in response to the epidemic, make it harder for the virus to transmit between individuals.

The standard SIR model (2)–(4) takes the transmission rate as given. In this paper, to isolate and estimate the effects of different factors on the spread of the virus we treat the transmission rate as time-varying, i.e., ${\beta }_t$, and relate its evolution to changes in voluntary and mandatory social distancing, the provision of economic incentives to isolate, as well as to vaccination uptake and the emergence of new variants. However, given the clinical evidence discussed below, we assume the recovery rate $\gamma$ to be fixed over time. We will refer to ${\beta }_t/\gamma$ as the “effective transmission rate.”

Specifically, we adopt and extend the agent-based stochastic network model proposed by Pesaran and Yang (2021), henceforth PY where infection of individual i from a population of n susceptible individuals is modeled using an unobserved variable $x_{i,t+1}^{\ast }$, as $I\left(x_{i,t+1}^{\ast },>,0\right)$, where $I\left(\mathcal{A}\right)$ is the indicator function that takes the value of unity if $\mathcal{A}$ holds and zero otherwise. The latent variable, $x_{i,t+1}^{\ast },$ is modeled as

$$\begin{array}{c}\hfill x_{i,t+1}^{\ast }={\tau }_{\mathit{it}}\left(\sum _{j=1}^n,d_{\mathit{ij}},\left(t\right),z_{\mathit{jt}}\right)-{\mu }_{\mathit{it}}{\xi }_{i,t+1},\end{array}$$ 5

where the $\left({\sum }_{j=1}^n,d_{\mathit{ij}},\left(t\right),z_{\mathit{jt}}\right)$ component captures the contact pattern of individual i with actively infected (contagious) individuals, denoted by the 0/1 variable $z_{\mathit{jt}}$, using the stochastic contact matrix, $\mathbf{D}(t)=\left(d_{\mathit{ij}},\left(t\right)\right)$ and $d_{\mathit{ij}}(t)=1$ with probability $k_{\mathit{it}}/n$, and 0, otherwise, and $k_{\mathit{it}}$ is the average number of contacts of individual i in day t. The ${\tau }_{\mathit{it}}>0$ term captures the degree (or intensity) of the exposure of individual i in day t to the virus upon contacts. For example, two individuals with the same contact patterns have different infection probability in day $t+1$, if they follow different types of precautions as to their mask wearing and hygiene habits. Finally, the term ${\mu }_{\mathit{it}}{\xi }_{i,t+1}>0$ represents individual $i$th immunity to becoming infected, which could depend on whether the individual is vaccinated. Two individuals with the same contact patters and mask wearing habits could have different infection probabilities due to having different levels of immunity, either natural or vaccine induced. Overall, the latent variable $x_{i,t+1}^{\ast }$ captures the contact pattern of individuals, allows for varying exposure intensities and allows for individual heterogeneity in natural or vaccine-induced immunity.

Social distancing, be it mandated and/or voluntary, mask wearing, frequent hand washing, and other mitigating policies will decrease the transmission rate by decreasing the mean contacts per day, $k_t$, and/or reducing the mean exposure intensity parameter, ${\tau }_t$, in (6). Vaccinations, on the other hand, are expected to decrease transmission rate, by increasing individual-specific resistance to the virus, which manifests in an increase in ${\mu }_t$. Virus mutations can increase the transmission rate by affecting both ${\mu }_t$ and ${\tau }_t$.

Using an aggregated version of the above model, ${\beta }_t$ can be approximated by8

$$\begin{array}{c}\hfill {\beta }_t\approx \frac{k_t{\tau }_t}{{\mu }_t},\end{array}$$ 6

where $k_t$ is the average number of contacts during day t, ${\tau }_t$ is the average exposure intensity of the susceptible population to the virus, and ${\mu }_t\ge 1$ is the mean immunity level in the population of susceptible individuals. We exploit time series and cross section variations in factors that influence $k_t$, ${\tau }_t$ and ${\mu }_t$, across countries and over time. We also relate ${\beta }_t$ to the average effective reproduction number, ${\mathcal{R}}_{\mathit{et}}$, defined as the expected number of secondary cases produced by one infected individual in a population that includes both susceptible and non-susceptible individuals at time t. ${\mathcal{R}}_{\mathit{et}}$ depends on the effective transmission rate (${\beta }_t/\gamma$), and the share of susceptible population ($s_t=S_t/n=1-c_t$), and is given by

$$\begin{array}{c}\hfill {\mathcal{R}}_{\mathit{et}}=\left(\frac{{\beta }_t}{\gamma }\right)s_t=\left(\frac{{\beta }_t}{\gamma }\right)\left(1,-,c_t\right),\end{array}$$ 7

where $c_t=1-s_t$ is the fraction of population that has been infected (cumulation of new infected cases) and $1-c_t$ is the herd-immunity component of ${\mathcal{R}}_{\mathit{et}}$. It is also worth bearing in mind that at the outset of epidemic outbreak, assuming a fully susceptible population, we have $s_0=1$ ($c_0=0$),  which in turn ensures that ${\mathcal{R}}_{e0}={\beta }_0/\gamma ={\mathcal{R}}_0$.

In our empirical analysis, we will first provide country-specific estimates of the effective transmission rate, ${\beta }_t/\gamma$. We then model their evolution for a selected number of European countries with similar initial epidemic trajectories. By focusing on the ${\beta }_t/\gamma$ component of ${\mathcal{R}}_{\mathit{et}}$, we avoid changes in ${\mathcal{R}}_{\mathit{et}}$ that arise endogenously due to the rising number of total infections, $c_t$.

Estimating Time-Varying Transmission rates

PY show that the classic aggregate SIR model (2)–(4) with time-invariant transmission rate can be obtained as an approximation (for a large population n) to the individual-based stochastic network model of epidemic that we spell out in “Appendix”, where individuals randomly interact with each other.9 In order to estimate country-specific time-varying transmission rates, ${\beta }_t$, we utilize the following moment condition, modified to allow for time-variations in the transmission rate (see Eq. (48) of PY, or Eq. (A.9) in “Appendix”):

$$\begin{array}{c}\hfill E_t\left(\frac{1-c_{t+1}}{1-c_t},|,i_t\right)=e^{-{\beta }_t{i}_t}+O(n^{-1}),\end{array}$$ 8

where $i_t=I_t/n$ is the per capita number of infected individuals in day t. Since ${\beta }_t{i}_t$ is typically close to zero and n quite large (in millions) we have (noting that $ln(1+x)\approx x$ for a sufficiently small x):

$$\begin{array}{c}\hfill \frac{\mathrm{\Delta }{c}_{t+1}}{\gamma \left(1,-,c_t\right)}\approx \left({\beta }_t,/,\gamma \right)i_t+v_{t+1},\end{array}$$ 9

where $E\left(v_{t+1},\left|i_t\right)\right)=0$, which corresponds to (2) in the standard SIR model. The evolution of $i_t$ and $r_t=R_t/n$, as in the standard SIR model, are governed by (1) and (4), namely $i_t=(1-s_t)-r_t=c_t-r_t$ and $r_t=r_{t-1}+\gamma i_{t-1}=r_{t-1}+\gamma \left(c_{t-1},-,r_{t-1}\right)$, and since $0<\gamma <1$,

$$\begin{array}{c}\hfill i_t=c_t-\gamma \sum _{\ell =0}^{\infty }{(1-\gamma )}^{\ell }{c}_{t-1-\ell },\end{array}$$ 10

which can be approximated well using current and past values of $c_t$, since $c_t=0$ for dates before the start of the epidemic.

In principle, $\gamma$ can be estimated using time series data on $r_t$ and $i_t$. However, data on recoveries, $R_t$, either do not exist or are unreliable due to considerable measurement difficulties. For example, in Europe, the recorded data on recoveries are unavailable for Spain and UK; they are of poor quality for France and Italy; and they are relatively close to our estimated recovery for Austria and Germany. To overcome this problem, we use (10) to impute data on $i_t$ assuming $\gamma =1/14$. We obtain very similar results if we use $\gamma =1/21$.10 The choice of $\gamma =1/14$ is consistent with the assumptions made in designing quarantine policies based on clinical evidence and also used in calibrated behavioral epidemic models.11

Addressing COVID-19 Case Under-Reporting

Another critical data issue surrounds the measurement of confirmed cases, which are likely to be under-reported, in part due to the fact that a non-negligible portion (perhaps about a half) of the cases is asymptomatic and therefore unlikely to be detected without large-scale testing. To mitigate the problem of under-reporting, we follow the epidemiological literature (see, for example, Gibbons et al. 2014) and assume that the magnitude of under-reporting is measured by the multiplication factor (MF—the ratio of true to reported cases). Denoting the observed values of $c_t$ and $i_t$ by ${\tilde{c}}_t$ and ${\tilde{ı}}_t$, we have

$$\begin{array}{c}\hfill c_t=\text{MF}{\tilde{c}}_t\text{and}{i}_t=\text{MF}{\tilde{ı}}_t.\end{array}$$

Then, the moment condition in terms of observed values (${\tilde{c}}_t$ and ${\tilde{ı}}_t$) can be written as

$$\begin{array}{c}\hfill E_t\left(\frac{1-\text{MF}{\tilde{c}}_{t+1}}{1-\text{MF}{\tilde{c}}_t},|,{\tilde{ı}}_t,,,{\tilde{c}}_t\right)=e^{-{\beta }_t\text{MF}{\tilde{ı}}_t}.\end{array}$$ 11

Using condition (11), we then compute rolling-window estimates of the transmission rate as

$$\begin{array}{c}\hfill {\widehat{\beta }}_t\left(W,,,\text{MF}\right)={\text{Argmin}}_{\beta }\sum _{\tau =t-W+1}^t{\left(\frac{1-\text{MF}{\tilde{c}}_{\tau }}{1-\text{MF}{\tilde{c}}_{\tau -1}},-,e^{-\beta \text{MF}{\tilde{ı}}_{\tau -1}}\right)}^2,\end{array}$$ 12

where W is the rolling window size, which we set to 14 days.12 It is plausible to assume that MF and $\beta$ are reasonably stable over a short window used in our empirical analysis, so that MF${\tilde{c}}_{\tau -1}<1$.

Note here that while in principle it is possible to estimate MF and $\beta$ jointly by assuming that both are fixed over a given window, in practice such estimates are likely to be very imprecise. To see why this is the case, note that the minimand in (12) can also be written, approximately, as

$$\begin{array}{cc}& \sum _{\tau =t-W+1}^t{\left(\frac{-\text{MF}\mathrm{\Delta }{\tilde{c}}_{\tau }}{1-\text{MF}{\tilde{c}}_{\tau -1}},+,1,-,e^{-\beta \text{MF}{\tilde{ı}}_{\tau -1}}\right)}^2\hfill \\ \hfill & \approx \sum _{\tau =t-W+1}^t{\left(\frac{-\text{MF}\mathrm{\Delta }{\tilde{c}}_{\tau }}{1-\text{MF}{\tilde{c}}_{\tau -1}},+,\beta ,\text{MF},,{\tilde{ı}}_{\tau -1},-,{\beta }^2,{\text{MF}}^2,,{\tilde{ı}}_{\tau -1}^2,+,.,.,.\right)}^2\hfill \\ \hfill & =\text{MF}\sum _{\tau =t-W+1}^t{\left(\frac{-\mathrm{\Delta }{\tilde{c}}_{\tau }}{1-\text{MF}{\tilde{c}}_{\tau -1}},+,\beta ,,{\tilde{ı}}_{\tau -1},-,{\beta }^2,\text{MF},,{\tilde{ı}}_{\tau -1}^2,+,.,.,.\right)}^2.\hfill \end{array}$$

Identification of MF will be weak when ${\tilde{ı}}_{\tau -1}^2$ is close to zero, which is likely to be the case both at initial and final stages of the epidemic. This is also why estimates of $\beta$ are reasonably robust to the choice of MF at the early stages of the epidemics, where both ${\tilde{ı}}_{\tau -1}$ and ${\tilde{c}}_{\tau }$ are close to zero. In fact, ignoring $\mathrm{\Delta }{\tilde{c}}_{\tau }{\tilde{c}}_{\tau -1}$ and ${\tilde{ı}}_{\tau -1}^2$ and their higher-order terms, the minimand will become a linear function of MF and estimates of $\beta$ no longer will depend on MF. In this case, we have

$$\begin{array}{c}\hfill {\widehat{\beta }}_t\left(W,,,\text{MF}\right)\approx \text{MF}{\text{Argmin}}_{\beta }\sum _{\tau =t-W+1}^t{\left(-,\mathrm{\Delta },{\tilde{c}}_{\tau },+,\beta ,,{\tilde{ı}}_{\tau -1}\right)}^2.\end{array}$$

For this reason, we calibrate the MF but consider several alternative scenarios. Given calibrated values for the MF and $\gamma$, the model is fully identified.

The Choice of the Multiplication Factor

We do not know the true MF. It is likely that confirmed cases were significantly under-reported at the initial stages of the pandemic, when testing was not yet widely available. Among the selected European countries considered in the next section, the number of tests have gradually increased over time from less than 0.5 test per 1000 people conducted daily in March 2020 to about 7 tests per 1000 people at the end of 2021 (Chart 1). We can safely assume that the MF ratio is certainly greater than one, and likely to have declined over time from its initial value in March 2020. Estimates of MF in the literature—see Jagodnik et al. (2020), Li et al. (2020), Havers et al. (2020), Kalish et al. (2021), Rahmandad et al. (2021), and Pesaran and Yang (2021) (Fig. 1) – all suggest significant under-reporting.

Fig. 1.

Daily COVID-19 tests per thousand population in selected European countries. Notes: The figure plots seven-day moving average of the number of daily COVID-19 tests per 1000 population in Belgium, Germany, France, Italy and Poland (in aggregate). These countries were chosen to maximize the available time coverage. There are no testing data available for Spain, and availability of testing data for UK, Netherlands and Portugal start at a later date. Data are from Google’s COVID-19 Open-Data available at: https://github.com/GoogleCloudPlatform/covid-19-open-data

In this section, for the panel estimation in Sect. 4, we report estimates assuming MF linearly declining from 5 at the beginning of the pandemic to 2 at the end of the sample, when testing was widely available. We also show that our estimates are robust to alternative specifications of a path for the $M{F}_t$ values over the sample period.13 Specifically, we explore the possibility for a higher $M{F}_t$ path with values starting at 8 and declining to 2.5. Both MF scenarios yield similar results (Fig. 1).14

One additional challenge is that the reported daily data that we use are subject to weekly within weak seasonality: the reported number of cases on Sundays is usually lower compared with the infected cases reported for other days. To deal with this problem, as it is common practice, we take seven-day moving averages of the reported data used in estimation. But again our results are robust if we use reported daily cases without averaging.

Estimates of Transmission Rates and Reproduction Numbers in Europe

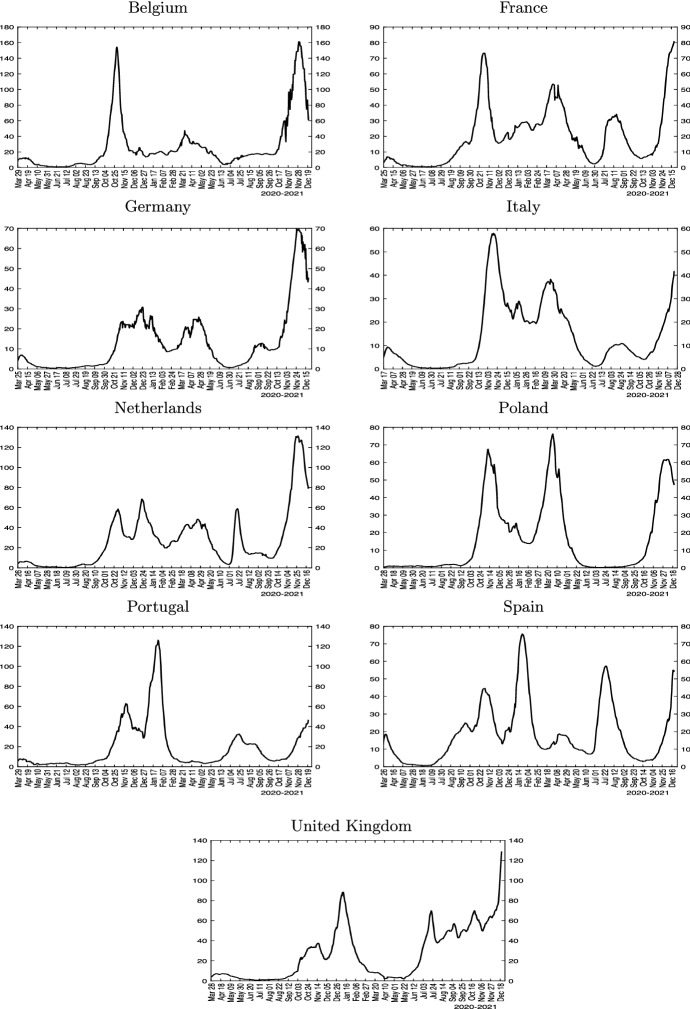
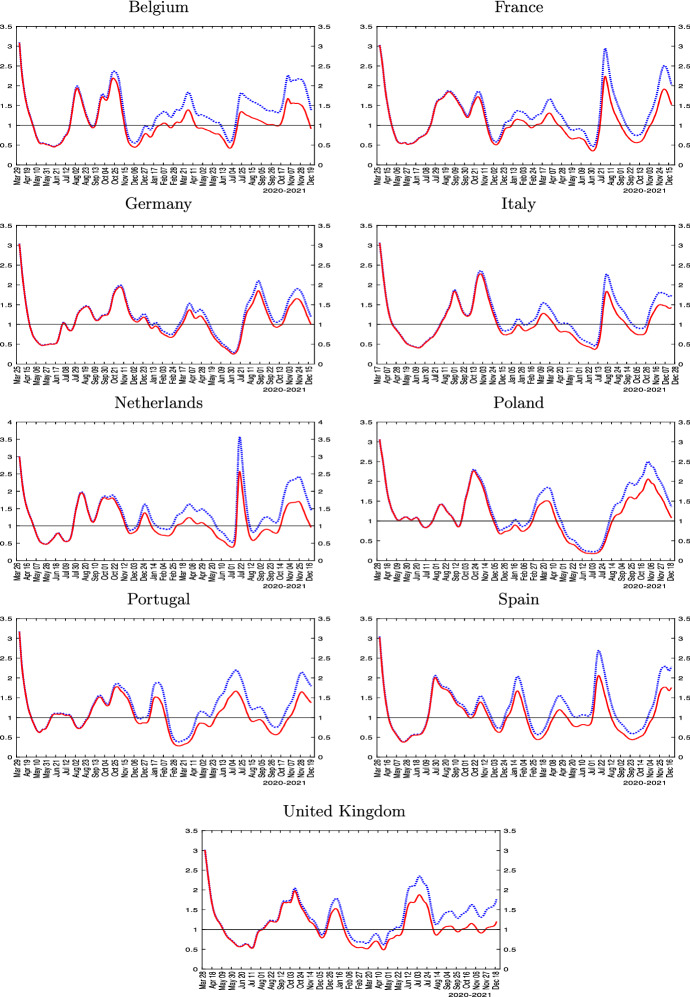
Daily data in case numbers and rolling estimates of scaled effective transmission rates (${\beta }_t/\gamma$) and effective reproduction numbers (${\mathcal{R}}_{\mathit{et}}$) for selected European countries (Belgium, France, Germany, Italy, Netherlands, Poland, Portugal, Spain, and the UK) are displayed in Figs. 2 and 3. We plot the scaled transmission rate ${\beta }_t/\gamma$ in place of ${\beta }_t$ to make it easily comparable with the $\mathcal{R}$ numbers on the same scale. The virus outbreak in continental Europe began with Italy in early 2020, with the recorded number of infections accelerating rapidly from February 21, 2020 onward. Infections start to rise rapidly in Spain, Germany and France one week later.

Fig. 2.

New cases for selected European countries. Note: The figure plots seven-day moving average of the number of reported daily new confirmed cases per 100k population

Fig. 3.

Estimated transmission rates and reproduction numbers for selected European countries. Notes: The figure plots the reproduction number, ${\widehat{\mathcal{R}}}_{\mathit{et}}$ (solid red line), and the effective transmission rate, ${\widehat{\beta }}_t/\gamma ={\widehat{\beta }}_t\times 14$ (dotted blue line). ${\widehat{\mathcal{R}}}_{\mathit{et}}=\left(1,-,{\text{MF}}_t,{\tilde{c}}_t\right){\widehat{\beta }}_t/\gamma$, where $\gamma =1/14$, and $M{F}_t$ linearly declines from 5 at the beginning of the sample to 2 at the end of the sample. ${\widehat{\beta }}_t$ is estimated using (12), where the number of active infections is computed using the data on confirmed cases minus imputed removed cases. The number of removed (recoveries + deaths) is imputed recursively using $R_t=\left(1,-,\gamma \right)R_{t-1}+\gamma C_{t-1}$

The rolling estimates show that the $\mathcal{R}$ number fell below one in mid- to late-April 2020 in all these countries. As lock-downs were eased during the summer of 2020, however, the $\mathcal{R}$ numbers started to rise again. Importantly, by the end of the 2020, the $\mathcal{R}$ numbers were much more dispersed, with some countries doing better than others. All large European countries show a second wave much larger than the first one. The UK, Spain, Portugal and Netherlands exhibit distinct third waves, with larger case counts compared with their second waves. The distinction between the (scaled) transmission rate and the reproduction numbers in Fig. 3 permits assessing the influence of herding, which become more salient toward the end of the sample period.15

In summary, the reported estimates show that European countries display very similar patterns during the first wave, but diverged significantly toward the end of 2020 both in terms of level of effective reproduction numbers, epidemic peaks, and the importance of herd immunity in slowing down the spread of the virus. In the next section, we exploit variation in outcomes across countries and over time to shed light on the likely drivers of the heterogeneity documented. As with all empirical analyses, the estimates we report are conditional on the chosen econometric model.

Modeling Time-Varying Effective Transmission Rates in Europe

It is important to recall here that, in large populations as in our data, the transmission rate, ${\beta }_t$, can change only if the biology of virus changes (mutations), a vaccine is introduced, people change their behaviors either voluntarily or due to policy mandates. We now provide empirical evidence on the likely drivers of ${\beta }_t$ using a panel data approach including the nine European countries, estimated over sub-samples to control for vaccination and variants. We consider five likely drivers. The first three are mandatory and voluntary social distancing and policy support that affects compliance with mandatory distancing policies. These drivers are likely to be of importance throughout the pandemic. They are also consistent with a simple decision-theoretic model of voluntary social distancing presented in “Appendix”, as well as the large literature on behavioral epidemic modeling. In the latter stage of the pandemic in 2021, two additional factors are important, which we also consider: progress on vaccinations and virus mutations.

Mandatory social distancing directly reduces the number of contacts as well as the exposure intensity, the structural parameters of our SIR model. A strong rationale for imposition of mandated social distancing is the presence of externalities, i.e., the fact that agents do not internalize in their cost–benefit analysis that their individual behavior contributes to the aggregate diffusion of the epidemic.16

However, mandated social distancing imposes economic costs and infringes on individual liberty leading to personal inconveniences (Hamermesh 2020). Economic support to workers, households and small businesses during the pandemic can shape incentives of individuals to comply with mandatory social distancing, as it weakens the economic need to interact in work activities. Consider an individual who has a non-teleworkable job and is fired or furloughed. While this leads to an immediate loss of income, if economic support is adequate, individuals can weather the pandemic without needing to seek paid employment in exposed occupations. Lack of compliance with social distancing has been documented empirically by Wright et al. (2020). Based on survey evidence, Papageorge et al. (2021) find that higher income is associated with larger changes in self-protective behavior, particularly for individuals who cannot telework. They conclude that, both in the USA and elsewhere, policies that mandate universal compliance with self-protective measures are unlikely to be effective or sustainable.

It is also well understood that infection risk induces precautionary behavior. Behavioral models of COVID-19 diffusion show that as the probability of getting infected rises, individuals lower consumption and leisure activities to avoid infection (see Eichenbaum et al. 2020; Toxvaerd 2020; Atkeson 2021, and Gupta et al. 2020). In particular, Battiston and Gamba (2020) provide cross section evidence that the $\mathcal{R}$ number during a COVID-19 outbreak is lower the larger the size of the initial wave.

To capture voluntary as well as mandatory social distancing policies empirically, in our statistical analyses we make use of data compiled by the Oxford COVID-19 Government Response Tracker (OxCGRT) project, which is a standard source of comparable indices measuring social distancing and other COVID-19-related policies across countries.17 In particular, we use two aggregate indices: the ‘policy stringency index’ (capturing the containment and lock-down policies) and the ‘economic support index’ (as a proxy variable for support to comply with the containment policies).

We also considered using Google mobility index as an additional regressor but obtained mixed results, largely due to the fact that mobility and lock downs are strongly correlated, but this is not the case for other forms of mitigation measures such as keeping one’s distance, meeting in open spaces, using sanitization, and wearing of face masks. In fact, we find the coefficient of the mobility index is negative once we also allow for other drivers of the transmission rates, suggesting reduced mobility could be associated with a higher rate of transmission! This perverse result is most likely due to the positive relationship that exists with mobility and mitigation measures and vaccination uptakes. It is reasonable to expect that vaccinated individuals and those that are taking precautionary mitigating measures are more likely to increase their mobility without the fear of contracting the virus. For further details, see Section S.7 of the online supplement.

We model precautionary behavior leading to voluntary social distancing using a threshold variable that switches on when the number of infected cases start to rise very rapidly. The idea for a threshold effect, defined in terms of the number of new cases, is to capture possible nonlinearity and changes in people’s willingness to isolate consistent with surveys on the role of information diffusion under COVID-19 (Bursztyn et al. 2020).

Econometric Model

We base our econometric analysis on the moment condition given by (8), but allow the transmission rate to vary with the key drivers identified above. Since n is quite large (in millions), and ${\beta }_t{i}_t$ sufficiently small, then taking logarithms of both sides of Eq. (8) for country j we have

$$\begin{array}{c}\hfill ln\left[(1-c_{j,t+1}),/,(1-c_{\mathit{jt}})\right]=-{\beta }_{\mathit{jt}}{i}_{\mathit{jt}}+e_{j,t+1},\end{array}$$ 13

where $j=1,2,\dots ,N$, and $e_{j,t+1}$ is an error term introduced to allow for approximation errors involved in moving from (8) to (13). We further model the time evolution of the transmission rates, ${\beta }_{\mathit{jt}}$ , as

$$\begin{array}{c}\hfill {\beta }_{\mathit{jt}}/\gamma ={\alpha }_j+{\mathit{\psi }}^{\prime }{\mathbf{x}}_{j,t-p}+\kappa I(f_{j,t-p}>{\tau }_f)+v_{\mathit{jt}},\end{array}$$ 14

where ${\mathbf{x}}_{j,t-p}$ is a vector of regressors, lagged p periods, $I(f_{j,t-p}>{\tau }_f)$ is an indicator variable which takes the value of unity if the threshold variable, $f_{\mathit{jt}}$, also lagged p periods, goes above the threshold parameter ${\tau }_f$, which as a first-order approximation is assumed to be the same across countries. Alternative specifications for the threshold effects are discussed in Sect. 4.3 below.

As a threshold variable, we use the 7-day moving average of the reported number of new cases (per 100,000 people), denoted by $f_{\mathit{jt}}$, as this is the most commonly watched variable used in the media when reporting on the spread of COVID-19 worldwide.18 In addition to estimating the panel regressions with a common constant term, a , we also allow for country-specific constant terms by replacing a in (14) with $a_j$, for $j=1,2,\dots ,N$. The parameters $a_j$ are of particular interest as they can be viewed as an estimate of the basic reproduction number, ${\mathcal{R}}_0$, which relates to the spread of the virus right at the start of the epidemic when ${\mathbf{x}}_{j,t-p}=0$, and $I(f_{j,t-p}>{\tau }_f)=0$. Note at the start of the epidemic $c_t$ is very close to zero, and voluntary and mandatory social distancing are not yet in place. Therefore, the constant terms a, or $a_j$ can be interpreted as measures of ${\mathcal{R}}_0$ which we expect to be the same across all countries. We acknowledge that ${\mathcal{R}}_0$ is the only structural parameter that we can estimate in (14) and that the remaining parameters in (14) cannot be interpreted as causal without further assumptions regarding the nature of regressors.

Substituting (14) in (13), we obtain the following panel data model in the unknown parameters, $a_i$ for $i=1,2,..,N$, $\mathit{\psi }$ and $\kappa$ (recall that $\gamma =1/14$)

$$\begin{array}{c}\hfill y_{j,t+1}=-\frac{ln\left[(1-c_{j,t+1}),/,(1-c_{\mathit{jt}})\right]}{\gamma i_{\mathit{jt}}}=a_j+{\mathit{\psi }}^{\prime }{\mathbf{x}}_{j,t-p}+\kappa I(f_{j,t-p}>{\tau }_f)+u_{j,t+1},\end{array}$$ 15

where the error term $u_{j,t+1}=v_{\mathit{jt}}-{\left(\gamma ,i_{\mathit{jt}}\right)}^{-1}{e}_{t+1}$ is now composed of the country-specific errors in specification of ${\beta }_{\mathit{jt}}$ (namely $v_{\mathit{jt}}$) and the approximating error, $e_{t+1}$, which is common across countries, thus inducing possible error cross-sectional dependence. For estimation, we estimate the panel regressions with common intercepts as well as allowing for fixed effects.

Our sample contains a small number of countries ($N=9$) relative to the much larger time dimension (with the time series dimension varying between $T=321$ and 646). An advantage of our small-N and large-T panel is that the specification in Eq. (15) can be estimated by least squares assuming only that the regressors are weakly exogenous.19

The parameters of interest are the country-specific intercepts, ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N$, that measure the basic reproduction number, ${\mathcal{R}}_0$, and the coefficients $\mathit{\psi }$, $\kappa$ and ${\tau }_f$ that measure the relative importance of the five factors considered in the empirical analysis as we discussed above. We estimate the parameters of interest jointly using (15). This is to be contrasted with a two-step procedure whereby ${\beta }_{\mathit{jt}}$ is first estimated by running country-specific regressions in (13), and the resultant estimates, ${\widehat{\beta }}_{\mathit{jt}}$, are then used in a second stage panel regression where ${\widehat{\beta }}_{\mathit{jt}}$ are regressed on our five drivers of transmission rates. The joint estimation approach is likely to provide more robust inference as compared to a two-step method that does not allow for the estimation uncertainty associated with using ${\widehat{\beta }}_{\mathit{jt}}$ .

We report standard errors of the estimated parameters under three scenarios. As a baseline and for comparison, we compute the standard errors assuming that $u_{j,t+1}$ is cross-sectionally as well as serially uncorrelated. These assumptions are undoubtedly restrictive, and therefore we also consider more robust alternatives. Our second approach to computing the standard errors, labeled as “robust1” in the tables below, allows for serial correlation and heteroskedasticity. Our third choice, denoted as “robust2” in the tables below, and allows $u_{j,t+1}$ to be correlated both over time as well as across countries (i.e., over both the t and j dimensions). Corrections for time series follow the standard Newey and West (1987) formulae, while corrections for cross-country correlations is similar to the standard errors proposed by Driscoll and Kraay (1998). Estimation with the robust standard errors is described in the online supplement.

An additional concern with our specification could be omitted variables and the presence of other confounding factors. The proposed specification (15) is parsimonious and encompasses the main factors considered in the literature. As contacts and susceptibility are not separately identified in our (or any other) SIR model, we use policy stringency and economic support indices, and we do not attempt to disentangle the effects of reducing/increasing the number of contacts from other measures that affect the number of infected cases, such as mask wearing, hand washing and individual’s inherent susceptibility to becoming infected. For example, increased mobility and hence contacts on its own does not imply a higher rate of infections if individuals are more diligent in following other mitigating measures.

We focus on the nine European countries: Belgium, France, Germany, Italy, Netherlands, Poland, Portugal, Spain, and the UK. As we noted already, the reason for focusing on these nine countries is the fact that they experienced a similar trajectory at the start of the COVID-19 outbreak, but had quite differing outcomes subsequently. In this way, we are able to exploit the cross country, as well as time series variations in the number of infected cases to quantify the effects of social distancing, vaccine uptake, and mutations on the effective transmission rates, ${\beta }_{\mathit{jt}}/\gamma$. Recall here that ${\beta }_{\mathit{jt}}/\gamma$ differs from the effective reproduction number, ${\mathcal{R}}_{j,et}$, given by ${\mathcal{R}}_{j,et}=(1-c_{\mathit{jt}})\left({\beta }_{\mathit{jt}},/,\gamma \right)$. As we noted earlier, ${\mathcal{R}}_{j,et}$ can fall below unity not because of the effectiveness of the mitigating policies or voluntary isolation, but simply because an increasingly larger fraction of the population is getting infected, the so-called herd-immunity effect. To avoid the confounding effect of herding on the outcome variable that we want to explain, we focus on modeling of ${\beta }_{\mathit{jt}}/\gamma$ and not ${\mathcal{R}}_{j,et}$.

Empirical Results

Consider first the panel regression (15) estimated with an unbalanced panel over the period February 23, 2020, to January 30, 2021. We allow for differences in the start dates of the outbreaks across the countries. We initially choose the sample end date of January 31, 2021, prior to the uptake of vaccination programs.20 We consequently refer to this period as the pre-vaccination sample. Table 1 reports panel estimation results for two alternative specifications of multiplication factors used to correct for under-reporting—MF declining linearly from 5 to 2, and from 8 to 2.5—and the lag order $p=10$ days.21

Table 1.

Panel regressions of effective transmission rates across selected European countries over the sample ending January 31, 2021

Multiplication factor	Pooled estimates		Fixed effects estimates
	5 to 2	8 to 2.5	5 to 2	8 to 2.5
Stringency Index	− 2.08	− 2.07	− 2.19	− 2.17
standard s.e. (t-ratio)	0.11 (− 19.3)	0.11 (− 18.8)	0.11 (− 19.7)	0.11 (− 19.1)
robust1 s.e. (t-ratio)	0.18 (− 11.5)	0.18 (− 11.3)	0.18 (− 12.4)	0.18 (− 12.2)
robust2 s.e. (t-ratio)	0.26 (− 8.1)	0.26 (− 7.8)	0.34 (− 6.4)	0.35 (− 6.2)
Economic support	− 0.42	− 0.38	− 1.01	− 0.99
standard s.e. (t-ratio)	0.07 (− 6.1)	0.07 (− 5.4)	0.09 (− 11.2)	0.09 (− 10.8)
robust1 s.e. (t-ratio)	0.14 (− 3.0)	0.14 (− 2.7)	0.17 (− 5.9)	0.17 (− 5.9)
robust2 s.e. (t-ratio)	0.23 (− 1.9)	0.22 (− 1.7)	0.23 (− 4.4)	0.22 (− 4.5)
Threshold variable	− 2.46	− 2.45	− 2.01	− 1.99
standard s.e. (t-ratio)	0.09 (− 26.5)	0.09 (− 25.9)	0.10 (− 20.6)	0.10 (− 20.0)
robust1 s.e. (t-ratio)	0.25 (− 9.7)	0.26 (− 9.6)	0.24 (− 8.3)	0.24 (− 8.3)
robust2 s.e. (t-ratio)	0.43 (− 5.8)	0.43 (− 5.7)	0.60 (− 3.4)	0.60 (− 3.3)
threshold value	0.20	0.20	0.20	0.20
${\mathcal{R}}_0$ numbers (Constant Terms)
common [robust2 s.e.]	5.36 [0.23]	5.36 [0.23]
specific [robust2 s.e.]:
Belgium			5.40 [0.62]	5.41 [0.63]
France			5.40 [0.64]	5.39 [0.64]
Germany			5.04 [0.66]	5.02 [0.66]
Italy			5.52 [0.66]	5.50 [0.67]
Netherlands			5.37 [0.63]	5.37 [0.63]
Poland			5.02 [0.65]	5.01 [0.65]
Portugal			5.51 [0.64]	5.52 [0.65]
Spain			5.65 [0.64]	5.66 [0.65]
UK			5.73 [0.62]	5.72 [0.63]
R-squared	0.51	0.50	0.54	0.52

Number of observations is 2989 with $N=9$ countries, $T_{min}=321$ and $T_{max}=343$ days. The estimation sample is unbalanced at the beginning. Starting dates of individual country samples are: 7-March-2020 (Belgium), 3-March-2020 (France), 2-March-2020 (Germany), 24-February-2020 (Italy), 7-March-2020 (Netherlands), 17-March-2020 (Poland), 15-March-2020 (Portugal), 4-March-2020 (Spain), and 3-March-2020 (UK). The last period is 31-January-2021 for all countries. “Robust1” standard errors are robust to serial correlation only (Newey-West type correction), whereas “robust2” standard errors are robust to serial correlation as well as any cross-sectional correlation. See online appendix for a description of the estimation of standard errors. Figures in parentheses are t-ratios. The figures in square brackets of the common intercept or the country-specific fixed effects are the standard errors robust to serial correlation as well as cross-sectional correlation (robust2). Oxford stringency and economic support indices are divided by 100 so that they take values between zero and one. Lag order is set to $p=10$ days in all regressions

As we can see from Table 1, both the policy stringency index and the policy support index have the expected negative signs and are both highly statistically significant. This result confirms that both factors help contain the epidemic diffusion. Their estimated coefficients are robust to alternative MF corrections. The threshold effects also are highly statistically significant. Allowing for country-specific intercepts slightly increases the coefficients on the policy stringency and the economic support indices, and slightly lowers the estimates of the threshold effect, which, however, all estimates remain sizeable and highly significant. Allowing for error correlations (over time and across countries) increases the estimated standard errors, as to be expected, but do not alter the overall inference that all variables considered remain statistically significant.

Regarding the magnitude of the estimated coefficients, it is first useful to note that the intercept is the model-implied estimate of the ${\mathcal{R}}_0$ number, which is the only structural parameter that we can estimate. As discussed before, the definition of the basic reproduction number assumes no changes in behavior in response to the pandemic. The estimated value of the common intercept, $\alpha$, in Table 1, is 5.36, identical for both choices of MF, with a tight robust2 standard error (0.23). The country-specific estimates of ${\mathcal{R}}_0$ are also all in a surprisingly tight range of 5.01 to 5.73.

The estimated threshold value is rather small, below 1 daily new confirmed case per 100,000 people, representing about 4-percent quantile of the daily new cases per 100,000 people in the pre-vaccination sample. This result suggests that the threshold effect kicks in very soon after the onset of the pandemic. In other words, people’s behavior changes soon after the onset of the pandemic, which makes the estimation of the ${\mathcal{R}}_0$ number from case numbers without a conditional statistical models difficult (if not impossible). Threshold effects alone significantly reduce the effective reproduction number (by more than 2), but on its own is not enough to bring the effective $\mathcal{R}$ number below one. Both economic support and stringency indices further reduce the transmission significantly, with the stringency index being associated with a much larger contribution to the decline in $\mathcal{R}$.

Next, we extend the sample to November 30, 2021, prior to the arrival of Omicron variant in December of 2021. Throughout 2021, there was a significant progress with vaccine uptake, which is expected to mitigate the virus transmission. We therefore include an additional variable measuring the share of population fully vaccinated. We expect the coefficient on this variable to be negative. Another factor in 2021 is the Delta mutation, which is considered to be more contagious and became dominant in Europe during the summer of 2021. Therefore, we also include a variable measuring the country-specific share of the Delta variant among the sequenced confirmed cases. A positive coefficient is expected on this additional control variable.

Table 2 presents estimates for the sample ending November 30, 2021. The table shows very similar findings for the estimates of the policy stringency index, the economic support index, the threshold effect, as well as the ${\mathcal{R}}_0$ numbers, as reported in Table 1 for the pre-vaccination sample. The coefficients on the share of population fully vaccinated are all negative (as expected), with magnitude in the range -1.2 to -1.8 and highly statistically significant. Coefficient estimates on the Delta variant share are all positive, in line with our prior, suggesting the basic reproduction number of the Delta variant is about 0.9 to 1.1 larger compared with the earlier strains.

Table 2.

Panel regressions of effective transmission rates across selected European countries over the sample ending November 30, 2021

Multiplication factor	Pooled estimates		Fixed effects estimates
	5 to 2	8 to 2.5	5 to 2	8 to 2.5
Stringency Index	− 1.97	− 1.98	− 2.11	− 2.06
standard s.e. (t-ratio)	0.09 (− 23.0)	0.09 (− 21.5)	0.09 (− 23.1)	0.10 (− 21.0)
robust1 s.e. (t-ratio)	0.18 (− 10.9)	0.19 (− 10.2)	0.18 (− 11.6)	0.19 (− 10.6)
robust2 s.e. (t-ratio)	0.28 (− 7.1)	0.29 (− 6.8)	0.31 (− 6.8)	0.33 (− 6.3)
Economic Support	− 0.26	− 0.20	− 0.54	− 0.54
standard s.e. (t-ratio)	0.05 (− 5.3)	0.05 (− 3.8)	0.07 (− 8.2)	0.07 (− 7.7)
robust1 s.e. (t-ratio)	0.11 (− 2.5)	0.11 (− 1.9)	0.15 (− 3.5)	0.15 (− 3.6)
robust2 s.e. (t-ratio)	0.17 (− 1.6)	0.17 (− 1.2)	0.21 (− 2.5)	0.20 (− 2.7)
Vaccinated Share	− 1.52	− 1.23	− 1.74	− 1.46
standard s.e. (t-ratio)	0.16 (− 9.6)	0.17 (− 7.2)	0.16 (− 10.8)	0.17 (− 8.5)
robust1 s.e. (t-ratio)	0.35 (− 4.3)	0.40 (− 3.1)	0.35 (− 5.0)	0.39 (− 3.8)
robust2 s.e. (t-ratio)	0.55 (− 2.8)	0.60 (− 2.1)	0.53 (− 3.3)	0.58 (− 2.5)
Delta Variant Share	1.00	0.93	1.09	1.04
standard s.e. (t-ratio)	0.10 (9.7)	0.11 (8.3)	0.10 (10.5)	0.11 (9.3)
robust1 s.e. (t-ratio)	0.23 (4.4)	0.26 (3.6)	0.22 (4.9)	0.26 (4.1)
robust2 s.e. (t-ratio)	0.32 (3.1)	0.36 (2.6)	0.31 (3.5)	0.35 (3.0)
Threshold Variable	− 2.60	− 2.56	− 2.35	− 2.30
standard s.e. (t-ratio)	0.09 (− 30.1)	0.09 (− 27.6)	0.09 (− 26.0)	0.10 (− 23.7)
robust1 s.e. (t-ratio)	0.26 (− 10.0)	0.26 (− 9.8)	0.26 (− 9.1)	0.26 (− 8.8)
robust2 s.e. (t-ratio)	0.43 (− 6.1)	0.42 (− 6.0)	0.69 (− 3.4)	0.69 (− 3.3)
threshold value	0.20	0.20	0.20	0.20
${\mathcal{R}}_0$ numbers (Constant Terms)
common [robust2 s.e.]	5.33 [0.23]	5.33 [0.23]
specific [robust2 s.e.]:
Belgium			5.42 [0.65]	5.46 [0.66]
France			5.32 [0.67]	5.33 [0.69]
Germany			5.17 [0.68]	5.11 [0.70]
Italy			5.51 [0.67]	5.47 [0.69]
Netherlands			5.37 [0.66]	5.41 [0.68]
Poland			5.17 [0.66]	5.15 [0.68]
Portugal			5.44 [0.67]	5.45 [0.68]
Spain			5.48 [0.66]	5.49 [0.67]
UK			5.49 [0.66]	5.49 [0.67]
R-squared	0.39	0.35	0.40	0.36

Number of observations is 5716 with $N=9$ countries, $T_{min}=624$ and $T_{max}=646$ days. The estimation sample is unbalanced at the beginning. Starting dates of individual country samples are: 7-March-2020 (Belgium), 3-March-2020 (France), 2-March-2020 (Germany), 24-February-2020 (Italy), 7-March-2020 (Netherlands), 17-March-2020 (Poland), 15-March-2020 (Portugal), 4-March-2020 (Spain), and 3-March-2020 (UK). The last period is 30-November-2021 for all countries. “Robust1” standard errors are robust to serial correlation only (Newey-West type correction), whereas “robust2” standard errors are robust to serial correlation as well as any cross-sectional correlation. See Online Appendix for a description of the estimation of standard errors. Figures in parentheses are t-ratios. The figures in square brackets of the common intercept or the country-specific fixed effects are the standard errors robust to serial correlation as well as cross-sectional correlation (robust2). Oxford stringency and economic support indices are divided by 100 so that they take values between zero and one. Lag order is set to $p=10$ days in all regressions

Table 3 provides summary statistics for all covariates used in the regressions. It reports the sample means and standard deviations (in brackets) for the pre-vaccination sub-sample ending January 31, 2021, and for the remainder of the sample (February 1, 2021 to November 30, 2021).22 Multiplying the average values of the regressors in Table 3 with the estimated coefficients in Table 2 (using the specification with common intercept and MF declining from 5 to 2), we find the threshold effect to be quantitatively important and when it is switched on reduces ${\beta }_t/\gamma$ by about a half.23 The second largest reduction comes from the stringency policy index (with a − 1.2 average contribution to the reduction of ${\beta }_t/\gamma$). In contrast, the contribution from the economic support index is smaller, only by −0.2 on average. According to our estimates, vaccination contributed − 0.5 on average in the second sample (February–November, 2021), with its contribution increasing in magnitude throughout the sample ending in − 1.3, as share of vaccinated population increased over time (see Table S2 in the online supplement).

Table 3.

Summary statistics: regressors sample means and standard deviations (in brackets) for pre- and post-vaccination samples

	Stringency index	Economic support	Vaccinated share	Delta share	Threshold indicator
Pre-vaccination sample ending January 31 2021
Belgium	0.59 (0.15)	0.77 (0.22)	0.00 (0.00)	0.00 (0.00)	0.97 (0.18)
France	0.63 (0.18)	0.67 (0.26)	0.00 (0.00)	0.00 (0.00)	0.95 (0.22)
Germany	0.61 (0.15)	0.41 (0.17)	0.00 (0.00)	0.00 (0.00)	0.94 (0.23)
Italy	0.73 (0.12)	0.62 (0.23)	0.00 (0.00)	0.00 (0.00)	0.96 (0.20)
Netherlands	0.59 (0.17)	0.76 (0.22)	0.00 (0.00)	0.00 (0.00)	0.96 (0.19)
Poland	0.58 (0.21)	0.50 (0.21)	0.00 (0.00)	0.00 (0.00)	0.95 (0.22)
Portugal	0.65 (0.12)	0.73 (0.11)	0.00 (0.00)	0.00 (0.00)	0.97 (0.17)
Spain	0.65 (0.16)	0.80 (0.23)	0.00 (0.00)	0.00 (0.00)	0.96 (0.21)
UK	0.67 (0.18)	0.92 (0.27)	0.00 (0.00)	0.00 (0.00)	0.94 (0.23)
All 9 countries	0.63 (0.17)	0.69 (0.26)	0.00 (0.00)	0.00 (0.00)	0.95 (0.21)
1 February 2021–30 November 2021 sample
Belgium	0.53 (0.09)	0.75 (0.00)	0.36 (0.30)	0.45 (0.46)	1.00 (0.00)
France	0.62 (0.09)	0.43 (0.11)	0.32 (0.26)	0.44 (0.46)	1.00 (0.00)
Germany	0.66 (0.13)	0.38 (0.00)	0.33 (0.26)	0.45 (0.47)	1.00 (0.00)
Italy	0.69 (0.09)	0.75 (0.00)	0.34 (0.27)	0.44 (0.45)	1.00 (0.00)
Netherlands	0.58 (0.17)	0.65 (0.12)	0.32 (0.27)	0.45 (0.47)	1.00 (0.00)
Poland	0.54 (0.15)	0.84 (0.12)	0.28 (0.21)	0.42 (0.46)	1.00 (0.00)
Portugal	0.63 (0.13)	0.75 (0.00)	0.40 (0.34)	0.53 (0.46)	1.00 (0.00)
Spain	0.56 (0.12)	0.88 (0.00)	0.38 (0.31)	0.43 (0.45)	1.00 (0.00)
UK	0.58 (0.16)	0.88 (0.28)	0.38 (0.26)	0.57 (0.46)	1.00 (0.00)
all 9 countries	0.60 (0.14)	0.70 (0.21)	0.35 (0.28)	0.47 (0.46)	1.00 (0.00)

This table report sample means (main entries) and sample deviations (in brackets) of the individual regressors in pooled regressions presented in Table 2. The top panel reports summary statistics for the pre-vaccination sample (ending January 31 2021), and the bottom panel reports summary statistics for the remainder of the full sample—February 1, 2021, to November 30, 2021. Table S4 in the online supplement reports additional summary statistics (minimum and maximum values)

We conclude from this evidence that all the factors considered in this paper as drivers of the epidemic did in fact contributed to abating it, and no single driver on its own could have been effective in bringing the transmission of the virus under control. Thus also explaining the different country experiences we documented in the previous section. Mandatory and voluntary social distancing and policy support together were generally quite effective in abating the spread of the virus at the early stages of the epidemic to the end 2020, but vaccination was the most important factor toward the end of 2021.

Alternative Specifications of the Threshold Effects

Given the importance of the threshold variable for the evolution of the transmission rate of the virus, it seemed of interest to consider other forms of the threshold variable to further investigate its effects.24 Accordingly, we here consider one specification with two threshold indicators, and another with smooth threshold parametric specification.

Table 4 reports estimation results for panel regressions featuring two thresholds indicators. Namely, we replace the single threshold variable in (15) with the linear combination of the two threshold indicators, ${\kappa }_{1}I(f_{j,t-p}>{\tau }_{1,f})+{\kappa }_{2}I(f_{j,t-p}>{\tau }_{2,f})$. To conserve space, we focus on the full sample results only. The findings in Table 4 continue to show strong support for threshold effects. In the baseline specifications, with the MF declining from 5 to 2, one of the two threshold values (${\tau }_{2,f}=0.2$) is identical to the single threshold specification, and the other one is even smaller (${\tau }_{1,f}=0.05$). Both threshold indicators are statistically significant. When we use the larger values of MF (8 to 2.5), only one of the two threshold variables is statistically significant with the estimated threshold, 0.20, being the same as before.25 Overall, estimated coefficients and estimated ${\mathcal{R}}_0$ numbers are similar to those reported in Table 2. These results suggest that threshold effects are occurring at relatively low levels, but nonlinear effects are possibly more nuanced than a single 0/1 threshold representation.

Table 4.

Panel regressions of effective transmission rates using two 0/1 threshold indicators (Full sample ending November 30, 2021)

Multiplication factor	Pooled estimates		Fixed effects estimates
	5 to 2	8 to 2.5	5 to 2	8 to 2.5
Stringency index	− 1.91	− 2.26	− 2.03	− 2.33
standard s.e. (t-ratio)	0.09 (− 22.3)	0.10 (− 23.7)	0.09 (− 22.3)	0.10 (− 22.8)
robust1 s.e. (t-ratio)	0.17 (− 11.3)	0.18 (− 12.6)	0.17 (− 11.9)	0.19 (− 12.6)
robust2 s.e. (t-ratio)	0.18 (− 10.4)	0.20 (− 11.5)	0.33 (− 6.1)	0.43 (− 5.5)
Economic Support	− 0.25	− 0.26	− 0.53	− 0.55
standard s.e. (t-ratio)	0.05 (− 5.2)	0.05 (− 4.9)	0.06 (− 8.2)	0.07 (− 7.9)
robust1 s.e. (t-ratio)	0.10 (− 2.6)	0.10 (− 2.5)	0.14 (− 3.9)	0.14 (− 3.8)
robust2 s.e. (t-ratio)	0.12 (− 2.2)	0.12 (− 2.2)	0.17 (− 3.1)	0.20 (− 2.7)
Vaccinated Share	− 1.51	− 1.51	− 1.72	− 1.67
standard s.e. (t-ratio)	0.16 (− 9.6)	0.17 (− 8.8)	0.16 (− 10.8)	0.17 (− 9.7)
robust1 s.e. (t-ratio)	0.35 (− 4.3)	0.38 (− 4.0)	0.35 (− 5.0)	0.38 (− 4.4)
robust2 s.e. (t-ratio)	0.53 (− 2.9)	0.59 (− 2.6)	0.50 (− 3.4)	0.57 (− 3.0)
Delta Variant Share	1.00	1.00	1.10	1.07
standard s.e. (t-ratio)	0.10 (9.8)	0.11 (9.0)	0.10 (10.5)	0.11 (9.6)
robust1 s.e. (t-ratio)	0.23 (4.4)	0.25 (4.0)	0.22 (4.9)	0.25 (4.3)
robust2 s.e. (t-ratio)	0.32 (3.2)	0.36 (2.8)	0.31 (3.6)	0.35 (3.1)
Threshold Variable 1	− 1.23	− 2.61	− 1.19	− 2.35
standard s.e. (t-ratio)	0.15 (− 8.2)	0.09 (− 28.3)	0.15 (− 7.9)	0.10 (− 24.3)
robust1 s.e. (t-ratio)	0.23 (− 5.4)	0.25 (− 10.5)	0.17 (− 6.8)	0.18 (− 12.8)
robust2 s.e. (t-ratio)	0.32 (− 3.9)	0.36 (− 7.3)	0.34 (− 3.5)	0.44 (− 5.4)
threshold value	0.05	0.20	0.05	0.20
Threshold Variable 2	− 1.76	0.29	− 1.55	0.26
standard s.e. (t-ratio)	0.13 (− 13.1)	0.03 (10.0)	0.14 (− 11.4)	0.03 (8.6)
robust1 s.e. (t-ratio)	0.14 (− 12.9)	0.14 (2.1)	0.17 (− 9.1)	0.18 (1.4)
robust2 s.e. (t-ratio)	0.16 (− 10.7)	0.17 (1.8)	0.35 (− 4.5)	0.44 (0.6)
threshold value	0.20	2.40	0.20	2.40
${\mathcal{R}}_0$ numbers (Constant Terms)
common [robust2 s.e.]	5.68 [0.16]	5.39 [0.17]
specific [robust2 s.e.]:
Belgium			5.75 [0.31]	5.47 [0.40]
France			5.65 [0.30]	5.37 [0.39]
Germany			5.50 [0.28]	5.19 [0.36]
Italy			5.83 [0.34]	5.56 [0.44]
Netherlands			5.70 [0.31]	5.44 [0.40]
Poland			5.51 [0.29]	5.25 [0.38]
Portugal			5.77 [0.33]	5.48 [0.43]
Spain			5.81 [0.34]	5.52 [0.44]
UK			5.82 [0.35]	5.54 [0.44]
R-squared	0.39	0.36	0.40	0.37

See notes to Table 2

For the smooth threshold specification, we adopt the popular parametric representation from the literature on smooth transition regression models (e.g., Teräsvirta 1998) and adapt it to our empirical application to ensure zero values when $f_{j,t-p}=0$, regardless of the shape parameters. Specifically, we consider

$$\begin{array}{c}\hfill h\left(f_{j,t-p},,,{\tau }_f,,,{\delta }_f\right)=\left[\frac{1}{1+e^{-{\delta }_f\left(f_{j,t-p},-,{\tau }_f\right)}},-,h_0,\left({\tau }_f,,,{\delta }_f\right)\right]/\left[1,-,h_0,h_0,\left({\tau }_f,,,{\delta }_f\right)\right]\text{,}\end{array}$$ 16

where ${\delta }_f,{\tau }_f>0$, and

$$\begin{array}{c}\hfill h_0\left({\tau }_f,,,{\delta }_f\right)=\frac{1}{1+e^{{\delta }_f{\tau }_f}}\text{.}\end{array}$$

This specification replaces the fixed threshold function $I\left(f_{j,t-p},>,{\tau }_f\right)$ in (15) with the more flexible smooth transition function (16). We refer to the parameter ${\tau }_f$ in (16) as the smooth threshold and refer to ${\delta }_f$ as the shape parameter.26 For sufficiently large values of the shape parameter ${\delta }_f$, $h\left(f_{j,t-p},,,{\tau }_f,,,{\delta }_f\right)$ resembles $I\left(f_{j,t-p},>,{\tau }_f\right)$, whereas for small values of ${\delta }_f$ the transition process becomes smoother and more gradual.

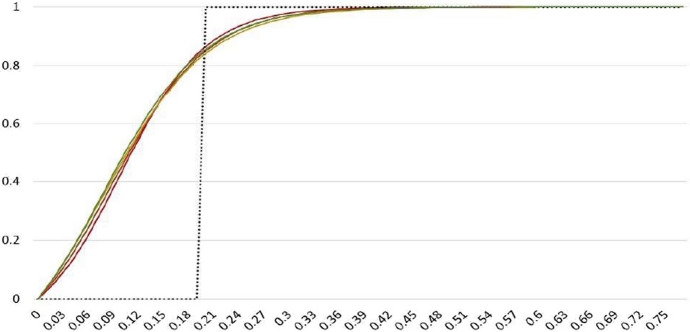
Table 5 summarizes results for the smooth threshold specification. The results complement earlier estimates in Tables 2 and 4 and confirm that threshold effects kick in at very low levels new infections. The estimates of ${\tau }_f$ lie in the range 0.08 to 0.10, and the estimated threshold shape parameter ${\delta }_f$ is quite large, in the range 16 to 20. Smooth threshold functions for these parameter values are plotted in Fig. 4, alongside the fixed threshold function from Table 2. Allowing for a smooth threshold transition function suggests that the threshold effects are slightly more gradual compared with the fixed 0/1 transition, but they start to kick in at even lower values.

Table 5.

Panel regressions of effective transmission rates using smooth threshold specification (Full sample ending November 30, 2021)

Multiplication factor	Pooled estimates		Fixed effects estimates
	5 to 2	8 to 2.5	5 to 2	8 to 2.5
Stringency index	− 1.89	− 1.90	− 2.00	− 1.97
standard s.e. (t-ratio)	0.09 (− 21.9)	0.09 (− 20.6)	0.09 (− 21.8)	0.10 (− 19.9)
robust1 s.e. (t-ratio)	0.18 (− 10.7)	0.19 (− 10.0)	0.18 (− 11.4)	0.19 (− 10.3)
robust2 s.e. (t-ratio)	0.27 (− 6.9)	0.29 (− 6.6)	0.27 (− 7.3)	0.30 (− 6.7)
Economic Support	− 0.26	− 0.20	− 0.54	− 0.54
standard s.e. (t-ratio)	0.05 (− 5.3)	0.05 (− 3.9)	0.06 (− 8.3)	0.07 (− 7.8)
robust1 s.e. (t-ratio)	0.10 (− 2.5)	0.11 (− 1.9)	0.15 (− 3.6)	0.15 (− 3.6)
robust2 s.e. (t-ratio)	0.16 (− 1.6)	0.16 (− 1.2)	0.21 (− 2.6)	0.20 (− 2.8)
Vaccinated Share	− 1.54	− 1.24	− 1.75	− 1.48
standard s.e. (t-ratio)	0.16 (− 9.8)	0.17 (− 7.3)	0.16 (− 11.0)	0.17 (− 8.6)
robust1 s.e. (t-ratio)	0.36 (− 4.3)	0.40 (− 3.1)	0.35 (− 5.0)	0.39 (− 3.8)
robust2 s.e. (t-ratio)	0.52 (− 2.9)	0.58 (− 2.2)	0.51 (− 3.4)	0.57 (− 2.6)
Delta Variant Share	1.02	0.95	1.12	1.06
standard s.e. (t-ratio)	0.10 (9.9)	0.11 (8.6)	0.10 (10.8)	0.11 (9.5)
robust1 s.e. (t-ratio)	0.23 (4.4)	0.26 (3.6)	0.23 (4.9)	0.26 (4.1)
robust2 s.e. (t-ratio)	0.31 (3.3)	0.35 (2.7)	0.30 (3.8)	0.34 (3.2)
Smooth Threshold	− 3.09	-3.01	− 2.83	− 2.77
standard s.e. (t-ratio)	0.10 (− 31.1)	0.11 (− 28.5)	0.10 (− 27.1)	0.11 (− 24.7)
robust1 s.e. (t-ratio)	0.27 (− 11.5)	0.27 (− 11.1)	0.27 (− 10.3)	0.28 (− 10.0)
robust2 s.e. (t-ratio)	0.35 (− 8.9)	0.35 (− 8.5)	0.65 (− 4.4)	0.66 (− 4.2)
threshold value ${\tau }_f$	0.09	0.10	0.08	0.08
shape parameter ${\delta }_f$	17.7	20.0	16.2	17.0
${\mathcal{R}}_0$ numbers (Constant Terms)
common [robust2 s.e.]	5.76 [0.14]	5.73 [0.14]
specific [robust2 s.e.]:
Belgium			5.83 [0.55]	5.87 [0.57]
France			5.73 [0.56]	5.73 [0.58]
Germany			5.58 [0.57]	5.52 [0.59]
Italy			5.91 [0.55]	5.87 [0.57]
Netherlands			5.78 [0.56]	5.82 [0.58]
Poland			5.58 [0.56]	5.56 [0.58]
Portugal			5.85 [0.55]	5.86 [0.58]
Spain			5.89 [0.55]	5.90 [0.57]
UK			5.90 [0.54]	5.90 [0.56]
R-squared	0.39	0.35	0.40	0.37

Smooth threshold specification is given by the smooth transition function (16) with threshold parameter ${\tau }_f>0$ and the shape parameter ${\delta }_f>0$. See notes to Table 2

Fig. 4.

Estimated smooth (solid lines) and the 0/1 threshold indicator (black dotted line). Notes: The figure plots 0/1 threshold indicator $I\left(f_{j,t-p},>,{\tau }_f\right)$ for estimated threshold value of ${\tau }_f=0.2$ in Table 2 and the smooth threshold function, $h\left(f_{j,t-p},,,{\tau }_f,,,{\delta }_f\right),$ defined by (16) using the estimated values of ${\tau }_f$ and ${\delta }_f$ in Table 5

Conclusions

This paper first estimates effective transmission rates and reproduction numbers for a number of countries based on a moment condition that can be derived from an agent-based stochastic network epidemic model. It then models their evolution for selected European countries with similar experiences at the outset of the pandemic but different outcomes subsequently as a function of social distancing, incentives to comply, the emergence of mutations, and vaccine uptake.

From a methodological perspective, the estimation approach that we propose permits distinguishing, at any jurisdictional level, between changes in the effective reproduction number due to herd immunity and changes due to variations in the average contact or the susceptibility to infection, which are the structural determinants of the epidemic diffusion. At the empirical level, using only daily COVID-19 case statistics, the paper provides estimates of transmission rates, allowing for the under-reporting of infected cases in officially reported COVID case statistics.

Evidence based on panel data modeling indicates that the diversity of outcomes that we document likely resulted from the nonlinear interaction of mandated and voluntary social distancing and the economic incentives that governments provided to support isolation through the end of 2020. The importance of these factors declined over time, with vaccine uptake driving the observed heterogeneity in country experiences during 2021. Our estimates suggest that no one factor alone was sufficient to bring the effective R number below one and to keep it there without substantial contributions from the other factors. Our panel regressions also allow us to identify the basic reproduction number, $R_0$, providing estimates that are very similar across the nine European countries, and all well in excess of the values of 2.4 to 3.9 assumed in the extant literature. Our estimates also confirm the higher transmission rate of the Delta variant.27 The main conclusions of the paper are robust to misreporting, alternative specifications of the threshold effect, controlling for actual population mobility patterns, error heteroskedasticity, and error serial correlation.

Supplementary Information

Below is the link to the electronic supplementary material.

Biographies

Alexander Chudik

is an economic policy advisor and senior economist at the Federal Reserve Bank of Dallas. His main research interests lie in the field of econometrics, and cover a variety of topics, including analysis of panel data models, aggregation, cross-section dependence, and macroeconometric modeling with a global perspective.

Hashem Pesaran

is the John Elliott Distinguished Chair in Economics at University of Southern California, an Emeritus Professor of Economics at Cambridge University, and a Fellow of Trinity College, Cambridge. His research covers national and global macro-econometric modelling, analysis of panel data models with cross-sectional dependence, and the Iranian economy.

Alessandro Rebucci

is Associate Professor at the Johns Hopkins Carey Business School, holding a joint appointment in the Economics Department of the Johns Hopkins Krieger School of Art and Science. He is a NBER Faculty Research Fellow (IFM Program), a CEPR Research Fellow (IMF Programme), a Research Fellow of the Center for Urban & Real Estate Management, and Globalization of Real Estate (University of Zurich), and the Centre for Applied Financial Economics (University of Southern California). Prof. Rebucci is Associate editor of the Journal of Money, Credit and Banking, Journal of Banking and Finance, and the Journal of International Money and Finance.

Appendix

In this appendix, we motivate the time-varying specification of the effective reproduction number and the transmission rate spelled out in the main text and provide the moment condition that we use for estimation based on the network-model of Pesaran and Yang’s (2021, PY). We also set up a simple decision-theoretic model of social distancing to motivate the choice of economic support variable and the threshold indicator used in the panel-data model used to explain the evolution of the transmission rates in Europe.

A Time-Varying Specification of the Single-Group PY Model

PY consider both single- and multi-group models built from the bottom up from an individual stochastic network model of interaction and COVID-19 contagion. After spelling out the critical assumptions on the infection diffusion process, here, we focus on the moment conditions for the estimation of the single-group model that tracks very closely the multi-group model in PY’s simulations.

Consider n individuals indexed by $i=1,2,\dots ,n$. Some are initially infected while the rest are susceptible to be infected at a later date, indexed by t. An individual i infected at date $t=t_i^{\ast }$ is represented by

$$\begin{array}{c}\hfill x_{\mathit{it}}=0,\text{for all}t<t_i^{\ast };\text{ and }{x}_{\mathit{it}}=1,\text{for all}t\ge t_i^{\ast }.\end{array}$$ A.1

The event of recovery or death of the individual i will be represented by the variable $y_{\mathit{it}}$, which is equal to zero unless the individual is “removed,” i.e., recovered or dead. The indicator variable

$$\begin{array}{c}\hfill z_{\mathit{it}}=\left(1,-,y_{\mathit{it}}\right)x_{\mathit{it}}\end{array}$$ A.2

then denotes “an active” infection, namely if the individual i is infected and not yet recovered. Specifically, $z_{\mathit{it}}$ takes the value of 1 if individual i is infected and not yet recovered at time t. It takes the value of 0 if individual i has not yet been infected, or has been infected but recovered/died. It follows that $x_{\mathit{it}}=z_{\mathit{it}}+y_{\mathit{it}}$.

Individual i becoming infected is modeled using the following Markov switching process as a function of the latent variable $x_{i,t+1}^{\ast }$,

$$\begin{array}{c}\hfill x_{i,t+1}=x_{\mathit{it}}+\left(1,-,x_{\mathit{it}}\right)I\left(x_{i,t+1}^{\ast },>,0\right),\end{array}$$ A.3

where $I\left(\mathcal{A}\right)$ is the indicator function that takes the value of unity if $\mathcal{A}$ holds and zero otherwise, and $x_{i,t+1}^{\ast }$ is given by:

$$\begin{array}{c}\hfill x_{i,t+1}^{\ast }={\tau }_{\mathit{it}}\sum _{j=1}^n{d}_{\mathit{ij}}\left(t\right)z_{\mathit{jt}}-{\mu }_{\mathit{it}}{\xi }_{i,t+1}.\end{array}$$

Since $I\left(x_{i,t+1}^{\ast },>,0\right)$ is unaffected by re-scaling of $x_{i,t+1}^{\ast }$, and by assumption ${\mu }_{\mathit{it}}>0$, then the above expression can also be written equivalently as

$$\begin{array}{c}\hfill \frac{x_{i,t+1}^{\ast }}{{}^{{\mu }_{\mathit{it}}}}=\left(\frac{{\tau }_{\mathit{it}}{k}_t}{{\mu }_{\mathit{it}}}\right)\sum _{j=1}^n\left(\frac{d_{\mathit{ij}}\left(t\right)}{k_t}\right)z_{\mathit{jt}}-{\xi }_{i,t+1}.\end{array}$$ A.4

The component ${\sum }_{j=1}^n\left(\frac{d_{\mathit{ij}}\left(t\right)}{k_t}\right)z_{\mathit{jt}}$ captures the contact pattern of individual i with all actively infected individuals, $z_{\mathit{jt}}$ for $j\ne i$. $\mathbf{D}(t)=\left[d_{\mathit{ij}},\left(t\right)\right]$ is a contact network matrix, such that $d_{\mathit{ij}}\left(t\right)=1$ if individual i is in contact with individual j at time t. It is assumed that the elements of the $n\times n$ network matrix $\mathbf{D}\left(t\right)$ are independent draws with $E\left[d_{\mathit{ij}},\left(t\right),/,k_t\right]=p_t/k_t=1/n$, where $k_t$ is the mean daily contact number during day t. The term ${\tau }_{\mathit{it}}$ is an individual-specific measure of exposure intensity, scaled by ${\mu }_{\mathit{it}}$ which in turn measures the individual’s immunity, either inherent or induced by vaccination.

The ${\xi }_{i,t+1}$ term in (A.4) is an unobserved individual-specific strictly positive random variable, which captures the unobservable characteristics that leads to different probabilities of infection, even for individuals with the same contact patterns and exposures. Following PY, we assume ${\xi }_{i,t+1}$ is exponentially and independently distributed over i and t with the cumulative distribution function given by

$$\begin{array}{c}\hfill Pr\left({\xi }_{i,t+1},<,a\right)=1-exp\left(-,a\right),\text{ for}a>0,\end{array}$$ A.5

where $E\left({\xi }_{i,t+1}\right)=1$.

Since individual i becomes infected if $x_{i,t+1}^{\ast }>0$, what matters most for the spread of the virus is the ratio $k_t{\tau }_{\mathit{it}}/{\mu }_{\mathit{it}}$ in Eq. (A.4) which captures both social distancing (voluntary or mandatory) and vaccination. Note also that, at a theoretical level, it is not possible to distinguish between reducing interactions via $k_t$, or reducing the intensity of these exposures via ${\tau }_{\mathit{it}}$ , or via vaccination that increases ${\mu }_{\mathit{it}}$. So these three factors are not separately identified.

The recovery or death from COVID-19—the exit from the infection state that we label removal—depends on the number of days since infection. Specifically, the removal process for individual i is given by

$$\begin{array}{c}\hfill y_{i,t+1}=y_{\mathit{it}}+z_{\mathit{it}}{\zeta }_{i,t+1}\left(t_i^{\ast }\right),\end{array}$$ A.6

where ${\zeta }_{i,t+1}\left(t_i^{\ast }\right)=1$ if individual i recovers at time $t+1$, having been infected exactly at time $t_i^{\ast }$ and not before, and ${\zeta }_{i,t+1}\left(t_i^{\ast }\right)=0,$ otherwise. Furthermore, it is assumed that the time to removal, denoted by $T_{\mathit{it}}^{\ast }=t-t_i^{\ast },$ follows the geometric distribution (for $t-t_i^{\ast }=1,2,\dots$)

$$\begin{array}{c}\hfill Pr\left[{\zeta }_{i,t+1},\left(t_i^{\ast }\right),=,1\right]=Pr\left(T_{\mathit{it}}^{\ast },=,t,-,t_i^{\ast }\right)=\gamma {\left(1,-,\gamma \right)}^{t-t_i^{\ast }-1},\end{array}$$ A.7

where $\gamma$ can be interpreted as the probability of recovering or dying at time $t+1$ having remained infected for $t-t_i^{\ast }-1$ days. This implies the following removal micro-moment condition

$$\begin{array}{c}\hfill E\left(y_{i,t+1},\left|y_{\mathit{it}},,,z_{\mathit{it}}\right)\right)=y_{\mathit{it}}+\gamma z_{\mathit{it}}\text{.}\end{array}$$ A.8

Noting that a susceptible individual can now be denoted by $s_{\mathit{it}}=1-z_{\mathit{it}}-y_{\mathit{it}}$, and using the definitions above we have that the cumulative number of infections is $C_t={\sum }_{i=1}^n{x}_{\mathit{it}}$, the total number of removed (recovered or deceased) is $R_t={\sum }_{i=1}^n{y}_{\mathit{it}}$, and the total number of active cases is $I_t={\sum }_{i=1}^n{z}_{\mathit{it}}=C_t-R_t$, while the number of “susceptible” individuals is $S_t={\sum }_{i=1}^n{s}_{\mathit{it}}=n-I_t-R_t$.

Assuming that ${\tau }_{\mathit{it}}=\tau$, $k_t=k$ and ${\mu }_t=\mu$ are time invariant, PY derive the following approximation for the aggregate moment condition for the population share of the total cumulative confirmed cases, $c_t=C_t/n$ (see Eq. (48) of PY)

$$\begin{array}{c}\hfill E\left(\left(\frac{1-c_{t+1}}{1-c_t}\right|,,i_t\right)=e^{-\beta i_t}+O\left(n^{-1}\right),\end{array}$$ A.9

where

$$\begin{array}{c}\hfill \beta =\frac{\left(1,-,e^{-\tau }\right)k}{\mu }\approx \frac{\tau k}{\mu },\end{array}$$ A.10

and $i_t=I_t/n$ is the per capita number of active cases. In our empirical analysis, we allow for time variations in k, $\tau$ and $\mu$ and accordingly obtain the following mean transmission rate

$$\begin{array}{c}\hfill {\beta }_t\approx \frac{k_t{\tau }_t}{{\mu }_t},\end{array}$$ A.11

where $k_t$ is the average number of contact during day t, ${\tau }_t$ is the average exposure intensity of the susceptible population to the virus, and ${\mu }_t\ge 1$ expected to be an increasing function of the proportion of susceptible population vaccinated, thus capturing the effects of vaccination. It is also worth noting that, in the above set up, the basic reproduction number, ${\mathcal{R}}_0$, is given by

$$\begin{array}{c}\hfill {\mathcal{R}}_0\approx {\beta }_0/\gamma =k_0{\tau }_0/\gamma ,\end{array}$$ A.12

with ${\mu }_0=1$ at the start of the epidemic.

A Simple Decision-Theoretic Model of Voluntary Social Distancing

To motivate the choice of the variables to be used in the panel data model of the transmission rate in Europe, in this appendix, we introduce a simple decision-theoretic model of social distancing.

Consider an individual i from a fixed population of size n in the epidemic day t, and suppose the individual in question is faced with the voluntary decision of whether to isolate or not. Under self-isolation, an individual that does not telework incurs the loss of wages net of any COVID-19 economic support amounting to $(1-{\theta }_{\mathit{it}})w_{\mathit{it}}$, plus the inconvenience cost, $a_{\mathit{it}}$, of being isolated, where $w_{\mathit{it}}$ is the wage and ${\theta }_{\mathit{it}}$ is the percentage of income lost which is compensated by the government support. For those individuals who can work from home ${\theta }_{\mathit{it}}$ is likely to be 1 or very close to it. But for many workers who are furloughed or become unemployed, ${\theta }_{\mathit{it}}$ is likely to be close to zero, unless they are compensated by transfers from the government.

On the other hand, if the individual decides not to self-isolate, then he/she receives the uncertain pay-off of $(1-x_{\mathit{it}})w_{\mathit{it}}-x_{\mathit{it}}{\varphi }_{\mathit{it}}$, where $x_{\mathit{it}}$ is an indicator which takes the value of unity if the individual contracts the disease and zero otherwise. The parameter ${\varphi }_{\mathit{it}}$ represents the cost of contracting the disease and is expected to be quite high. We are ruling out the possibility of death as an outcome and also assume that if the individual does not isolate and get sick does not earn the wage.

In this setting, the individual decides to self-isolate if the sure loss of self-isolating is less than the expected loss of not self-isolating, namely if

$$\begin{array}{c}\hfill \left(1,-,{\theta }_{\mathit{it}}\right)w_{\mathit{it}}+a_{\mathit{it}}<E\left[x_{\mathit{it}},{\varphi }_i,-,(1-x_{\mathit{it}}),w_{\mathit{it}},\left|{\mathcal{I}}_{t-1}\right)\right],\end{array}$$ A.13

where ${\mathcal{I}}_{t-1}$ is the publicly available information that includes $c_{t-1},$ the total number of infections. Assume now for simplicity that the probability of anyone contracting the disease is uniform across the population and this is correctly perceived to be given by ${\pi }_{t-1}$. Hence, $E\left(x_{\mathit{it}},\left|{\mathcal{I}}_{t-1}\right)\right)={\pi }_{t-1}$, and the condition for self-isolating in any day t can be written as

$$\begin{array}{c}\hfill (2-{\theta }_{\mathit{it}})w_{\mathit{it}}+a_{\mathit{it}}<{\pi }_{t-1}(w_{\mathit{it}}+{\varphi }_{\mathit{it}}),\end{array}$$

or as

$$\begin{array}{c}\hfill \frac{2-{\theta }_{\mathit{it}}+\left(a_{\mathit{it}},/,w_{\mathit{it}}\right)}{1+\left({\varphi }_{\mathit{it}},/,w_{\mathit{it}}\right)}={\lambda }_{\mathit{it}}<{\pi }_{t-1}.\end{array}$$ A.14

Since ${\pi }_{t-1}\le 1$, then for individual i to self-isolate we must have ${\lambda }_{\mathit{it}}<1$ (note that ${\lambda }_{\mathit{it}}\ge 0$, with ${\lambda }_{\mathit{it}}=0$ when ${\varphi }_{\mathit{it}}\to \infty$) or if

$$\begin{array}{c}\hfill {\varphi }_{\mathit{it}}/w_{\mathit{it}}>a_{\mathit{it}}/w_{\mathit{it}}+(1-{\theta }_{\mathit{it}}).\end{array}$$ A.15

This condition clearly illustrates that an individual is more likely to self-isolate if the relative cost of contracting the disease, ${\varphi }_{\mathit{it}}/w_{\mathit{it}},$ is higher than the inconvenience cost of self-isolating plus the proportion of wages being lost due to self-isolation. Also, an individual is more likely to self-isolate voluntarily if the wage loss, measured by ${\theta }_{\mathit{it}},$ is low thus showing that compensating some workers for the loss of their wages encourages a larger fraction of the population to comply with mandatory social distancing. The above formulation could easily accommodate the differential incentive to self-isolate across different age groups and sectors of economic activity. Given that the epidemic affects the young and the old differently, with the old being more at risk as compared to the young, then ${\varphi }_{\mathit{old}}>{\varphi }_{\mathit{young}}$, and the old are more likely to self-isolate. Similarly, low-wage earners are more likely to self-isolate as compared to high-wage earners with the same preferences (${\varphi }_{\mathit{it}}$ and $a_{\mathit{it}}$), and facing the same transfer rates, ${\theta }_{\mathit{it}}$. But the reverse outcome could occur if low-wage earner faces a higher rate of transfer as compared to the high-wage earners.

According to this simple model, the fraction of population that are willing to socially isolate voluntarily is given by

$$\begin{array}{c}\hfill p_{n,t}=n^{-1}\sum _{i=1}^{n}I\left[(1-{\theta }_{\mathit{it}}),w_{\mathit{it}},<,\left({\varphi }_{\mathit{it}},-,a_{\mathit{it}}\right)\right],\end{array}$$

where I(A) is an indicator function that takes the value of 1 if A holds and zero otherwise. It is clear that the extent of voluntary social distancing, $p_{n,t}$, is positively related to the size of the economic support, ${\theta }_{\mathit{it}}$, and the perceived net cost of contracting the virus, $\left({\varphi }_{\mathit{it}},-,a_{\mathit{it}}\right)$, which could rise sharply when epidemic surges and/or if better messaging by health authorities about the true costs of contracting the disease is provided. The inclusion of the economic support variable and the threshold indicator in our empirical analysis are intended to capture such effects, with the indicator taking the value of unity when people become more fearful of catching the virus.