Macrofinancial Causes of Optimism in Growth Forecasts

Abstract

We analyze the causes of the apparent bias toward optimism in growth forecasts underpinning the design of IMF-supported programs, which has been documented in the literature. We find that financial variables observable to forecasters are strong predictors of growth forecast errors. The greater the expansion of the credit-to-GDP gap in the years preceding a forecast, the greater its over-optimism about growth over the next two years. This result is strongest among forecasts that were most optimistic, where errors are also increasing in the economy’s degree of liability dollarization. We find that the inefficient use of financial information applies to growth forecasts more broadly, including the IMF’s forecasts in the World Economic Outlook and those produced by professional forecasters compiled by Consensus Economics. We conclude that improved macrofinancial analysis represents a promising avenue for reducing over-optimism in growth forecasts.

Introduction

An important function of the International Monetary Fund (IMF) is to assist member countries in implementing macroeconomic programs designed to smooth their external adjustment, which usually involves the disbursement of financing tranches as policy conditionality is met. While assessing the success of these fund-supported programs is a multi-dimensional exercise, an important backbone of a successful and credible program is a realistic set of projections for macroeconomic variables such as output and inflation. In this paper, we are—to the best of our knowledge—the first to document that financial variables observable at the time of program design are strong predictors of growth forecast errors in IMF-supported programs.

The previous literature has evaluated the IMF’s program forecasts for accuracy, bias and efficiency, with some finding evidence of over-optimism (e.g., Kim et al. 2021). Over-optimism has been found to be most significant in samples of large programs (Musso and Phillips 2002), at longer horizons (Ho and Mauro 2016) and when planned policy adjustments were large (Ismail et al. 2020). Over-optimism in growth forecasts is problematic not only because it can undermine the calibration of macroeconomic policies, but also because it may itself cause future recessions by incentivizing the accumulation of public and private debt (Beaudry and Willems 2022).

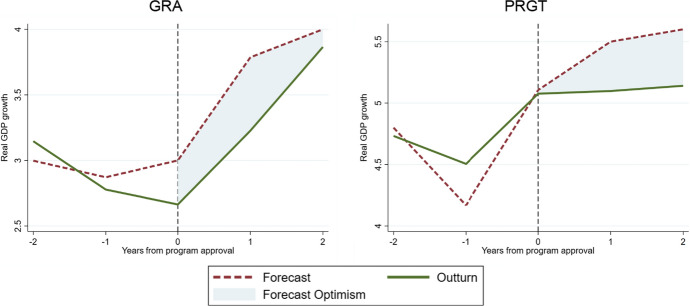
Figure 1 shows forecasts and outturns for real GDP growth surrounding the approval of IMF-supported programs. Over-optimism is a feature of the median forecast made in the context of both programs implemented in advanced and emerging economies and those programs made available on concessional terms to the IMF’s lower-income member countries.1 Across 306 programs approved from 2000 to 2019, the mean annual growth rate over the next two years ended up being 0.76 percentage points lower than initially forecast at the time of the program request. That is, the level of output two years hence ended up being 1.5 percentage points lower than forecast.

Fig. 1.

Evolution of real output growth surrounding the approval of IMF-supported programs. Sources: WEO, MONA and authors’ calculations. Figure shows median across 129 IMF-supported programs supported by GRA resources and 177 programs supported by PRGT resources that were approved between 2000 and 2019. Forecasts are those made at program request and accessed from the IMF’s MONA database, while outturns are from the October 2021 vintage of the World Economic Outlook

Over-optimism of growth forecasts may reflect several factors, which are likely to be sample specific. Growth is affected by shocks that could not have been foreseen by the forecaster, such as a fall in the world price of an exported commodity, the emergence of a civil conflict or a global financial crisis (IMF 2019). To the extent that these unanticipated shocks do not have a zero mean in a particular sample, this can give rise to a biased forecast. Growth forecasts may also err because they are inefficient, in the sense that the forecaster did not make full use of the information that was available at the time of the forecast.2 This can arise because a planned policy change ends up not having the expected impact on future growth, because a planned policy change does not get implemented or alternatively because the forecaster did not correctly model the relationship between the past and future evolution of observable variables.

We present forecast efficiency tests that check whether ex post growth forecast errors are correlated with characteristics of the financial system that were observable when a program was designed. Methodologically, our approach is similar to Blanchard and Leigh (2013), who document that the size of planned fiscal consolidation was a good predictor of growth over-optimism in IMF-supported programs in the euro zone following the global financial crisis. They conclude that this forecast inefficiency is suggestive that IMF forecasters had underestimated the size of the fiscal multiplier in this sample. A similar approach has more recently been adopted by Ismail et al. (2020), who additionally document a nonlinearity in the relationship between forecast optimism and the size of the planned fiscal adjustment. Our main contribution is to apply this approach to study the role of financial variables, specifically the evolution of credit to the private sector, which will allow us to infer whether macrofinancial analysis is being properly incorporated into the IMF’s program forecasts.

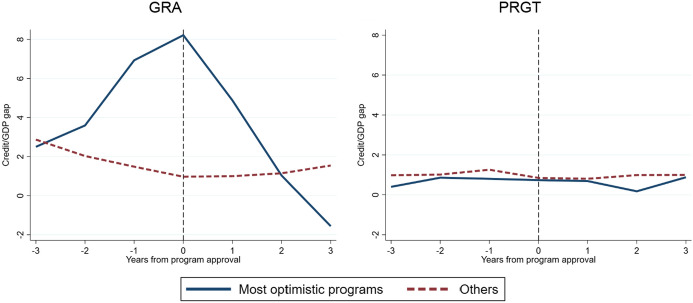
Why might one suspect that inefficient use of financial variables could be driving forecast optimism? Figure 2 plots the evolution of the credit-to-GDP gap surrounding the approval of IMF-supported programs.3 We have separated the sample based on the ex post error of the program’s growth forecast, splitting the sample at the top quartile of the empirical distribution. For those GRA programs that ended up being most optimistic, we notice a large swing in the credit cycle surrounding program approval. For the median program in this subsample, the credit-to-GDP gap increases by 6 percentage points in the three years prior to program approval and reverts sharply in the following years. This pattern is not observed in programs that featured little or no forecast optimism; nor is it observed in the sample of PRGT programs, whose low-income beneficiaries tend to have less developed financial systems.

Fig. 2.

Evolution of the credit-to-GDP gap surrounding the approval of IMF-supported programs. Sources: WEO, MONA, BIS, IFS, BOP and authors’ calculations. Figure shows medians across programs for which the credit-to-GDP gap could be estimated using available data. “Most optimistic programs” in each panel are those in the top quartile of growth forecast errors ${\widehat{g}}_i$ defined in Eq. 1

Our motivation for testing the efficient use of financial variables originates in the large literature on their predictive power for forecasting output growth, prominently explored by Stock and Watson (2003) for the case of the G7 economies. Adrian et al. (2019) show that financial indicators are good predictors of the conditional mean and variance of future output growth in the USA, arguing that this feature is driven by amplification mechanisms between the financial sector and real economy. Schularick and Taylor (2012) show that financial credit expansions forecast declines in real activity in a sample of 14 countries over the past 130 years. Chen and Rancière (2019) present simple models incorporating financial variables including credit growth that provide good out-of-sample accuracy when forecasting output in a sample of 62 countries. Closely related to our work, they show that the models outperform the IMF’s World Economic Outlook (WEO) in an out-of-sample horserace of forecast accuracy for 85 percent of the countries they study. Kirti (2018) finds that strong credit growth is a good predictor of future growth and unemployment three years hence. He also documents that this relationship is compounded by the strength of lending standards: When strong credit growth is accompanied by a deterioration of lending standards, this is followed by even weaker growth and higher unemployment.

But if the literature has documented that financial conditions are good predictors of future output growth, is this fact being fully incorporated into macroeconomic forecasts? Kirti (2018) tests this hypothesis on a sample of WEO forecasts for 38 countries and finds that the documented relationship between financial and real variables is not anticipated by forecasters, with past credit developments correlating strongly with ex post forecast errors.

We believe our paper is the first to examine whether growth forecasts made in the context of IMF-supported programs efficiently use the information contained in observable financial variables. These programs offer an interesting context that may differ from forecasts produced in the IMF’s World Economic Outlook surveillance forecasts and those produced by professional forecasters in the private sector. A first way programs differ is that they are usually designed in a context where a negative shock has already materialized, creating a gap in the balance of payments and prompting the country’s authorities to seek financial assistance from the international community. There is an extensive literature documenting the failure of professional economists—including those at the IMF—to anticipate recessions (Loungani 2001; An et al. 2018). This stylized fact generates an optimism bias that is particularly pronounced in samples with many large negative shocks. Programs thus offer an interesting context because the accuracy of their forecasts relies less on ability to anticipate a negative shock, but rather from anticipating the depth of downturns and the strength of recoveries following a realized shock.

A second way IMF-supported program growth forecasts differ is that they involve a unique class of agency issues and incentives. Programs must be jointly agreed between the fund and the member country’s government, and this process may involve political incentives to bias a forecast toward optimism or pessimism, as discussed by Musso and Phillips (2002). Rules established in IMF policy prevent the institution from lending if public debt is assessed to be on a unsustainable path, and require stricter policy conditionality when loans are made to countries that have vulnerabilities from existing debt. Since debt sustainability assessments are heavily influenced by growth forecasts, an incentive toward optimism may exist for the manager wishing to facilitate a loan to a country with vulnerabilities. Finally, forecasters may perceive a professional advantage from the prestige associated with managing a large program loan. This may create an incentive to overstate the growth forecast that underpins the borrower’s ability to repay a larger loan to the fund.4

Our paper also relates to the literature on sources of bias and inefficiency in macroeconomic forecasts made by the IMF and by other forecasters (Timmermann 2007; Eicher et al. 2019). Blanchard and Leigh (2013) provide a prominent example of inefficient program forecasts: the underestimation of the impact of a planned fiscal consolidation on growth during the Euro area crisis of 2010–2011. Our paper confirms that misestimation of fiscal multipliers may have been a factor in explaining optimistic program forecasts, though the result is not statistically significant in our sample.

Our main result is that financial variables observable during program design are reliable and strong predictors of growth forecast errors. A program preceded by a one-standard-deviation increase in the credit-to-GDP gap—approximately 8.1 percentage points in our sample—is associated with an annualized forecast error that is approximately 0.60 percentage points more optimistic, such that the level of output is over-estimated by about 1.2 percentage points at a two-year horizon. This result is about twice as strong among those programs whose growth forecasts turned out to be optimistic. While our analysis is focused on the credit-to-GDP gap, we also find evidence of inefficiency in the use of other financial variables, including the degree of liability dollarization and the recent growth of residential property prices.

While we do not attempt to provide a comprehensive decomposition of the drivers of forecast errors, we explore plausible explanations for the inefficient use of information in financial variables. A plausible mechanism underlying this result is that a program’s policy adjustments are endogenous to the financial cycle, such that programs following a credit boom are calibrated to tighten financial conditions. This could give rise to inefficient forecast optimism if the impact of these tighter policies on growth was underestimated. Relatedly, more restrictive policies may be less likely to be implemented due to political resistance, making programs approved after a credit boom more likely to go “off track” with agreed policies not being implemented as planned. We present some evidence that these explanations are unlikely to explain our result. Rather, we deduce that forecasters do not correctly model the relationship between the past and future evolution of observable variables—possibly underestimating the tendency of credit to revert to its trend—and the interactions of the credit cycle and real economy.

We show that our result also applies outside the context of IMF-supported programs, including in a large panel of WEO forecasts made in the IMF’s surveillance role and in forecasts made in the private sector by professional forecasters surveyed by Consensus Economics. However, the size of the effect appears to be smaller in these samples than what is estimated in our event study of IMF-supported programs. We take this external validity test as an indication that improved macrofinancial analysis could alleviate the optimism of growth forecasts across the profession.

The paper is organized as follows. In Sect. 2, we document stylized facts about growth forecast errors in IMF-supported programs and present our main empirical approach based on an event study. In Sect. 3, we test the validity of our result in other contexts using a broad panel of IMF forecasts that spans both program and non-program situations, as well as forecasts made by professional forecasters. Section 4 concludes.

Event Study of IMF-Supported Programs

Our empirical approach studies forecasts made upon approval of IMF-supported programs initiated between 2000 and 2019, as reported in the IMF’s Monitoring of Fund Arrangements (MONA) database.5 During this period there were 306 IMF-supported programs approved, of which 129 were supported by GRA resources and 177 by concessional PRGT resources reserved for low-income member countries.6

Following Blanchard and Leigh (2013), we summarize growth performance using the annualized growth rate of real output over the two years following the approval of program i in year t, which we denote $g_i$. That is, we consider the change in the level of real output $y_i$ from years t-1 to t+1:

$$g_i=\left(\sqrt{\left[y_{i,t+1}/y_{i,t-1}\right]}-1\right)\times 100.$$

The choice of a two-year horizon is meant to capture short- to medium-term outcomes, which can be thought to be most directly affected by the approval of the IMF-supported program.7 We then define the forecast error ${\widehat{g}}_i$ as the difference between the forecast made at the time of the program approval and the outturn:

$${\widehat{g}}_i=E_b{g}_i-g_i,$$ 1

where $E_b$ is the expectations operator conditional on the information set available at date b, when the program was approved by the IMF’s Executive Board, and $g_i$ is the outturn based on the October 2021 vintage of the World Economic Outlook database. A positive value of ${\widehat{g}}_i$ denotes an optimistic growth forecast (that is, growth turned out to be lower than anticipated), while a negative value denotes a pessimistic growth forecast (that is, growth was higher than anticipated).

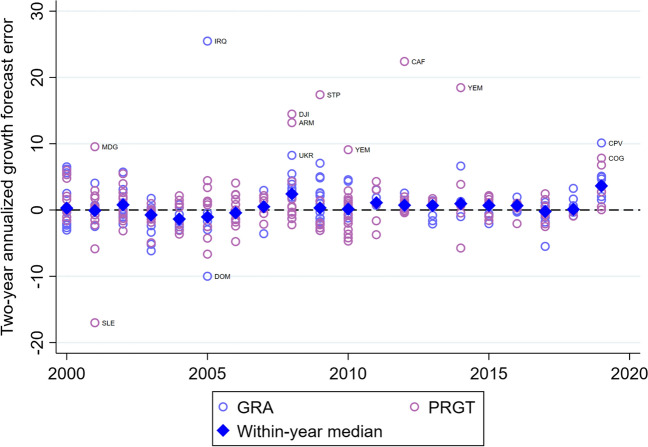
Figure 3 plots ${\widehat{g}}_i$ for all IMF-supported programs since 2000, with GRA programs marked by blue circles and PRGT programs marked in purple. The average of ${\widehat{g}}_i$ in the full sample of programs over this period is 0.8, with a median of 0.4 and standard deviation of 3.9; this is the optimism bias that has been identified in the literature (Kim et al. 2021). It is also worth noting that many programs contain growth forecasts that turned out to be remarkably accurate: One quarter have a value of ${\widehat{g}}_i$ that is within 0.68 percentage points of zero. The within-year median value of ${\widehat{g}}_i$ is shown in blue diamonds, with values that are generally close to zero except for years associated with major global crises (notably, 2008 and 2019).8 Indeed, GRA programs approved outside these two years have a median value of ${\widehat{g}}_i$ of 0.07 over 2000–2019. That is, in the absence of an unanticipated global crisis, about half of IMF-supported programs contained growth forecasts that turned out to be optimistic, while the other half were too pessimistic.

Fig. 3.

Forecast errors following approval of IMF-supported programs. Sources: WEO, MONA and authors’ calculations. For each program, we plot the annualized forecast error over the two years following program approval (${\widehat{g}}_i$). Forecast errors based on forecasts from the IMF’s Monitoring of Fund Arrangements database and outturns from the October 2021 vintage of the World Economic Outlook

Programs in low-income economies supported by concessional PRGT resources exhibit larger variance of forecast errors, with a number displaying extremely large annualized forecast errors of upwards of 10–20 percentage points. This could stem from characteristics of the borrowing countries, such as their vulnerability to large shocks such as civil conflicts and natural disasters, as well as their less diversified production structures and lower data quality (Eicher et al. 2019). There are 13 programs in this sample for which ${\widehat{g}}_i$ is more than two standard deviations from zero, and these have been labeled with the country code. According to data from the Uppsala Conflict Data Program (UCDP), eight of these program requests took place within three years of an episode of organized violent conflict.9

Our baseline specification is an event study that regresses program i’s growth forecast error on a set of explanatory variables:

$${\widehat{g}}_i=\alpha +\mathit{\delta }{\mathit{X}}_i+\beta C_i+\gamma {\dot{y}}_{i,t-1}+{\gamma }_{2019}+{\epsilon }_i,$$ 2

where ${\widehat{g}}_i$ is defined in Eq. 1 and time t is the year of program approval. The vector ${\mathit{X}}_i$ contains macrofinancial variables that belong to the information set observable to the forecaster at the time of approval for program i at date b. This is the basis for our forecast efficiency test. The null hypothesis of an efficient forecast is that the coefficients $\mathit{\delta }$ on regressors in ${\mathit{X}}_i$ are equal to zero and that forecasts are unbiased with intercept $\alpha$ equal to zero. If the null is rejected, this would suggest that information contained in these variables has not been properly incorporated into program forecasts and that this is a source of forecast error.

In our baseline specification, ${\mathit{X}}_i$ includes a single variable: the change in the credit-to-GDP gap over the two years preceding program approval (that is, from t−3 to t−1). The credit-to-GDP gap is computed as the deviation of the ratio of credit to the private sector to GDP from its trend. To ensure that the variable belongs to the information set, we construct it using two features. First, the GDP series used in the denominator of the credit-to-GDP ratio is taken from the WEO vintage immediately preceding program approval at date b. This avoids the introduction of data revisions to the output series, which would not have been in the information set available to the forecaster. Second, the trend of the ratio is computed using a one-sided five-year moving average, which does not incorporate information on subsequent data.10

The decision to focus on aggregate credit-to-GDP rather than other market-based financial indicators may lead to some information loss, but is motivated by two considerations. First, this variable has been widely used in the literature as a summary indicator of the domestic financial cycle (Borio 2014) and has been shown to be a good indicator of risks in the financial sector (Kaminsky and Reinhart 1999; Borio and Lowe 2002; Sufi and Taylor 2021). Indeed, the Basel III framework for banking supervision includes specific guidance for national regulators to use the credit-to-GDP gap to measure the financial cycle and calibrate the stance of macroprudential policy tools (BCBS 2010). Second, its widespread availability over long periods allows us to study a large sample of countries—twice as large as previous papers such as Kirti (2018) and Chen and Rancière (2019)—including low-income economies with less developed financial systems.11 Our full estimation sample consists of 218 programs (89 GRA and 129 PRGT) for which credit aggregate series are available for at least seven years prior to program approval, allowing us to compute our measure of the real-time credit-to-GDP gap.

The baseline specification includes dummy variables to capture events that may be correlated with financial and output developments, but which are not directly caused by them and which we do not consider as being feasibly predicted or modeled by the forecaster. The dummy variable ${\gamma }_{2019}$ denotes that the program was approved during the year preceding the COVID-19 pandemic, which led to very large growth forecast errors shown in Figure 3. The dummy variable $C_i$ indicates that an episode of violent conflict occurred within three years of the program’s approval.12 We also include the lagged growth rate of real output, to control for the economic cycle that prevailed prior to program approval. This is potentially important because it has been documented that growth forecasts may be revised inefficiently slowly during downturns (An et al. 2018).

Equation 1 is estimated by ordinary least squares, with estimates reported in Table 1. Standard errors are estimated using a sandwich estimator that allows for cross-correlation of the error terms within country groups. Our rationale for using this approach is that IMF forecasts are derived from country-specific forecasting models that are slow to evolve. This introduces a source of country-level variation in the data across time and forecast vintages.

Table 1.

Results from event study regressions

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Credit-to-GDP gap (change from t−3 to t−1)	0.07***	0.14**	0.10**	0.07***	0.08	0.05**	0.10**	0.08***
	(0.02)	(0.06)	(0.05)	(0.02)	(0.10)	(0.02)	(0.05)	(0.02)
Dummy: Civil conflict	1.67**	1.79**	2.04***	0.79	2.34**	1.53**	2.41**	1.82**
	(0.65)	(0.68)	(0.66)	(0.64)	(0.93)	(0.68)	(1.03)	(0.71)
Output growth (t−1)	0.12**	0.13	0.10*	0.13**	0.17**	0.08*	0.10	0.12**
	(0.05)	(0.08)	(0.06)	(0.06)	(0.08)	(0.04)	(0.07)	(0.05)
Dummy: 2008						1.12
						(1.18)
Interact: Dummy 2008* Credit-to-GDP gap						0.37**
						(0.16)
Dummy: 2011						1.46*
						(0.78)
Interact: Dummy 2011* Credit-to-GDP gap						−0.08
						(0.07)
Dummy: 2019	3.87***	2.29**	3.19***	3.88***	4.07***	4.06***	3.15***
	(0.91)	(0.96)	(0.63)	(1.18)	(1.41)	(0.92)	(1.10)
Constant	−0.45	1.17***	−0.47	0.15	−1.22**	−0.49*	0.06	−0.50*
	(0.27)	(0.35)	(0.29)	(0.30)	(0.50)	(0.27)	(0.30)	(0.29)
Sample	Full	${\widehat{g}}_i>0$	Credit gap > 0	GRA	PRGT	Full	Post-GFC	Excl. COVID
Observations	218	128	160	89	129	218	105	206
Time period	2000–2019	2000–2019	2000–2019	2000–2019	2000–2019	2000–2019	2010–2019	2000–2018
R2	0.13	0.15	0.17	0.22	0.13	0.17	0.20	0.09
Mean of dep. variable (${\widehat{g}}_i$)	0.70	2.57	0.68	0.82	0.63	0.70	1.32	0.49

White heteroskedasticity-robust standard errors clustered by country are shown in parentheses. The use of *** denotes a coefficient significantly different from zero at the 0.01 confidence level; **0.05; *0.10

The baseline specification reported in column 1 indicates that the change in the credit-to-GDP gap over the two years prior to the program is correlated with more optimistic growth forecasts in the full sample of 218 programs.13 For every percentage point that the credit-to-GDP gap increases in the two years prior to program approval, forecasts for annualized growth over the next two years display increased optimism of 0.075 percentage points. This elasticity is highly economically significant. A program preceded by a one-standard-deviation increase in the credit-to-GDP gap—approximately 8.1 percentage points in our sample—is associated with an annualized forecast error that is approximately 0.6 percentage points more optimistic, such that the level of output is over-estimated by about 1.2 percentage points at a two-year horizon.

Programs undertaken surrounding an episode of violent conflict and those approved in 2019 (prior to the global COVID-19 pandemic) display highly significant over-optimism on average.14 The conditional mean—estimated by the constant—is found to be insignificantly different from zero, indicating that there is no residual bias after controlling for these variables.

In column 2, we estimate the same specification on a sample that includes only those programs that ended up with optimistic growth forecasts, with ${\widehat{g}}_i>0$. In this sample, the size of the coefficient on the credit-to-GDP gap is nearly twice as large as in the baseline. That is, the strength of the information inefficiency of growth forecasts with respect to financial variables is more pronounced among programs that end up being optimistic. Among these programs, a one-standard-deviation increase in the credit-to-GDP gap is associated with an over-estimation of the level of output by about 2.3 percentage points at a two-year horizon. Among the 90 programs that had pessimistic growth forecasts (${\widehat{g}}_i\le 0$; not reported in Table 2), the credit-to-GDP gap is no longer statistically significant and the coefficient becomes slightly negative, indicating that the inefficiency we document applies only to those programs whose growth forecasts end up being optimistic.

Table 2.

Results controlling for aspects of program design

	(1)	(2)	(3)	(4)	(5)
Credit-to-GDP gap (change from t−3 to t−1)	0.15**	0.16**	0.08**	0.07***	0.14***
	(0.07)	(0.08)	(0.04)	(0.03)	(0.05)
Dummy: Civil conflict	2.05**	2.02**	1.80*	1.67**	1.82***
	(0.80)	(0.81)	(0.98)	(0.66)	(0.67)
Output growth (t−1)	0.21***	0.21***	0.13	0.11**	0.08
	(0.08)	(0.08)	(0.09)	(0.06)	(0.05)
Dummy: 2019	3.38***	3.49***	2.52***	3.86***	3.98***
	(1.11)	(0.96)	(0.69)	(0.91)	(0.84)
Expected real growth of base money (t−1 to t+1)	−0.02
	(0.04)
Expected change in money multiplier (t−1 to t+1)		0.18
		(0.88)
Expected fiscal adjustment (t−1 to t+1)			0.17
			(0.14)
Loan amount (Access/GDP)				−0.03
				(0.16)
Debt outstanding to IMF (t; Debt/GDP)					−0.29***
					(0.09)
Interact: Debt outstanding * Credit-to-GDP gap					−0.01***
					(0.00)
Constant	−0.63	−0.70*	−0.78*	−0.33	0.23
	(0.43)	(0.42)	(0.43)	(0.60)	(0.36)
Observations	91	92	136	218	216
R2	0.27	0.27	0.10	0.13	0.19
Time period	2002–2019	2002–2019	2000–2019	2000–2019	2000–2019
Sample	Full	Full	Full	Full	Full

White heteroskedasticity-robust standard errors clustered by country are shown in parentheses. The use of *** denotes a coefficient significantly different from zero at the 0.01 confidence level; **0.05; *0.10

In the third column, we restrict the sample to programs that have a positive credit-to-GDP gap in the year prior to their approval, which allows us to test the symmetry of our result over the credit cycle. We find that the coefficient here is also somewhat larger than in the full sample. Among the 58 programs that were preceded by a negative credit-to-GDP gap (results not reported in Table 2), the coefficient of the credit-to-GDP gap is positive but is no longer statistically significant, indicating that the inefficiency we document is strongest among those programs that are preceded by a positive credit-to-GDP gap.

The next two columns estimate the same equation, but separate the full sample according to whether programs are supported by GRA or PRGT resources.15 The results show that while the coefficient on the credit-to-GDP gap is of a similar magnitude across the two groups—0.07 for GRA programs versus 0.08 for PRGT-supported programs—its statistical significance is only confirmed in the first group. This may reflect the greater relative importance of the financial system in advanced and emerging economies—which rely on GRA resources—in comparison with the low-income economies that can opt for more concessional PRGT facilities, or simply the greater volatility in the data for the latter sample. Other factors appear to be important in the latter group. Notably, PRGT-supported programs that coincide with violent conflict are associated with significantly greater optimism, with the annualized growth forecast error 2.3 percentage points larger in these cases. The conflict variable is not significantly related to growth forecast errors in the sample of GRA-supported programs.

While our baseline finding may reflect the well-documented link between booming financial conditions prior to major global crises and the impact of these crises on growth, we wish to ensure that the result is not exclusively driven by these global events. In column 6, we introduce additional dummy variables indicating programs approved prior to two major global financial shocks: 2008 for the global financial crisis and 2011 for the euro area crisis. We also include interaction terms for each of these dummies with our credit-to-GDP gap variable. While conditional forecast errors following the 2011 crisis are 1.5 percentage points more optimistic than the rest of the sample, this optimism does not appear to be associated with excessively inefficient use of financial information. In the case of the 2008 crisis, the interaction term is highly significant, signaling that the size of the credit boom prior to that event is strongly correlated with the size of growth forecast errors. Importantly, the null hypothesis of an efficient forecast in which $\delta$ = 0 can still be rejected for the rest of the sample, with a point estimate of 0.05. We conclude that our inefficiency result holds outside of global crisis episodes, and is significantly stronger in the context of the global financial crisis.

In column 7, we estimate the model on the subset of programs that were approved after the Global Financial Crisis, between 2010 and 2019. Following the GFC, understanding and awareness of macrofinancial linkages increased substantially among academics and policymakers. For instance, it became well established that credit booms and busts interact with the real economy to determine the depth and persistence of recessions (Claessens et al. 2009, 2012; Jordà et al. 2013). However, we find that forecast errors made in the post-GFC period remain highly correlated with the past evolution of the credit-to-GDP gap, with the size of the coefficient increasing to 0.10. This suggests that growth forecasters have not become more efficient at incorporating the information in financial variables. Notably, our parsimonious specification explains a higher share of the variance in ${\widehat{g}}_i$ over the more recent period, with the R² increasing from 0.13 in the full sample to 0.20 in the shorter sample.

Finally, in column 8 we re-estimate the baseline specification on a sample that excludes programs whose outturns were influenced by the onset of the COVID-19 pandemic. This unexpected global event had a substantial impact on growth in 2020, leading to large forecast errors for the 12 programs in our sample that were approved in 2019. Excluding these programs from our sample does not have a meaningful impact on our inefficiency result.

Appendix Table 5 reports a set of robustness tests for the baseline results in which we construct the credit-to-GDP gap variable using alternative filtering techniques, including the Hodrick–Prescott filter proposed by Borio and Lowe (2002) and the linear projection method proposed by Hamilton (2018). Our baseline results are robust to these alternative specifications. We also consider alternative timings of the lagged credit-to-GDP gap variable and consider the variable in levels rather than changes. The results are broadly robust to these specifications, though the use of a much longer lag length for the credit-to-GDP gap (5 or 6 years) reduces their significance.

Table 5.

Robustness: results from event study regressions using alternative definitions of the credit-to-GDP gap

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Credit-to-GDP gap (baseline) (change from t−3 to t−1)	0.07***
	(0.02)
Credit-to-GDP gap (HP filter) (change from t−3 to t−1)		0.07***
		(0.03)
Credit-to-GDP gap (Hamilton) (change from t−3 to t−1)			0.07***
			(0.02)
Credit-to-GDP gap (change from t−2 to t−1)				0.05*
				(0.03)
Credit-to-GDP gap (change from t−4 to t−1)					0.05*
					(0.03)
Credit-to-GDP gap (change from t−5 to t−1)						0.02
						(0.02)
Credit-to-GDP gap (change from t−6 to t−1)							0.04
							(0.03)
Credit-to-GDP gap (t−1)								0.07**
								(0.03)
Credit-to-GDP gap (t−2)								0.02
								(0.05)
Credit-to-GDP gap (t−3)								−0.08
								(0.05)
Dummy: Civil conflict	1.67**	1.68**	1.69**	1.64**	1.56	1.51**	1.64**	1.71**
	(0.65)	(0.66)	(0.66)	(0.65)	(0.68)	(0.69)	(0.72)	(0.66)
Output growth (t−1)	0.12**	0.12**	0.12**	0.11**	0.11**	0.11**	0.13**	0.12**
	(0.05)	(0.05)	(0.05)	(0.05)	(0.05)	(0.05)	(0.06)	(0.05)
Dummy: 2019	3.87***	3.89***	3.91***	3.74***	3.87***	3.80***	3.77***	3.90***
	(0.91)	(0.91)	(0.90)	(0.90)	(0.91)	(0.90)	(0.91)	(0.92)
Constant	−0.45	−0.43	−0.44	−0.39	−0.44	−0.37	−0.42	−0.53*
	(0.27)	(0.27)	(0.27)	(0.27)	(0.28)	(0.30)	(0.30)	(0.30)
Sample	Full	Full	Full	Full	Full	Full	Full	Full
Observations	218	218	218	218	214	211	204	218
Time period	2000–2019	2000–2019	2000–2019	2000–2019	2000–2019	2000–2019	2010–2019	2000–2019
R2	0.13	0.13	0.14	0.12	0.12	0.11	0.12	0.13
Mean of dep. variable (${\widehat{g}}_i$)	0.70	0.70	0.70	0.70	0.67	0.69	0.76	0.70

White heteroskedasticity-robust standard errors clustered by country are shown in parentheses. The use of *** denotes a coefficient significantly different from zero at the 0.01 confidence level; **0.05; *0.10

Potential channels of macrofinancial inefficiency: the role of program design

What mechanism explains the inefficient use of financial information in growth forecasts? A plausible hypothesis is that pre-program credit expansions are met with particularly restrictive program policy conditionality. These policy adjustments may in turn lead to forecast optimism if they are more politically challenging to implement, or if their impact on growth is underestimated. To test this hypothesis, we augment the baseline equation to include measures of expected monetary, financial and fiscal policy adjustment, reporting the results in Table 2.

In column 1, we proxy for programmed monetary adjustment using the expected rate of growth of the monetary base over the next two years, deflated by the expected growth of the consumer price index. Most IMF-supported programs include monetary conditionality that sets an upper bound on the growth rate of the monetary base, with this becoming the operational target by which the stance of monetary policy is implemented. We find that this variable is not significantly correlated with growth forecast errors and that the economic and statistical significance of the pre-program credit-to-GDP gap is unaffected.16 This allows us to conclude that the inefficiency we have identified is not generated by the endogenous calibration of program conditionality in response to pre-program credit conditions.

Monetary policy may provide an incomplete measure of the programmed policy adjustment’s impact on financial conditions. For instance, a build-up in credit may be met by a tightening of macroprudential policies such as reserve requirements, which can moderate credit intermediation for a given stance of monetary policy. In column 2, we proxy for the programmed adjustment of financial conditions using the expected change in the money multiplier—that is, the ratio of broad money to the monetary base—from period t−1 to t+1. Again, we find that this variable is not significantly correlated with growth forecast errors. In a final exercise reported in column 3, we introduce a measure of programmed fiscal adjustment, as in Blanchard and Leigh (2013) and Ismail et al. (2020). We construct the expected change in the overall fiscal balance as a share of GDP from t−1 to t+1, capturing the expected fiscal effort over the forecast horizon.17 We confirm that planned fiscal adjustments appear positively correlated with forecast optimism—suggesting that fiscal multipliers may be somewhat underestimated—but the result is not statistically significant in this sample.18 Even after controlling for programmed adjustment of monetary, financial and fiscal policies, forecast optimism remains significantly correlated with the pre-program evolution of the credit-to-GDP gap.

These exercises have focused on planned policy adjustments, but an alternative mechanism for our baseline result could be that a pre-program credit boom makes it harder to implement agreed policies, making it more likely that the program goes “off track.” Since forecasts at program approval must assume that policies will be implemented as planned, this could lead to a source of optimism in growth forecasts. To test this hypothesis, we compute the forecast errors for the two proxies of monetary and financial policy adjustment described above, and regress these on our measure of pre-program credit developments. We find that neither variable is significantly correlated. Likewise, policy adjustment forecast errors are not significantly correlated with the degree of planned policy adjustment. Taken together, we conclude that the inefficiency we have identified is unlikely to be explained by the degree of program implementation.

In introduction, we discussed some plausible incentive and agency issues that could lead to biased forecasting in the context of IMF-supported lending programs. We now test for two of these potential mechanisms. In column 4, we include the size of the loan reported in MONA, measured as the total access to IMF resources over the duration of the program as a share of the country’s GDP in year t. Inconsistent with the previous result documented in Musso and Phillips (2002), we find that larger loans are not associated with more optimistic growth forecasts. In column 5, we include the debt outstanding to the IMF in the month prior to program approval at date b as a share of the country’s GDP in year t, using information made publicly available by the fund through its Financial Data Query Tool. We also include an interaction term between our measure of debt outstanding and the credit-to-GDP gap variable. This exercise reveals that forecast optimism is decreasing in the country’s prior debt to the fund incurred during previous loans. Likewise, the inefficiency in growth forecasts with respect to lagged credit-to-GDP gap developments is also decreasing in the country’s prior debt to the fund. This suggests that there may be some degree of learning by doing in IMF program forecasts, in which forecasters become less biased toward optimism and make more efficient use of financial information when working with a country that has made repeated use of IMF financing.

An alternative explanation for the inefficient use of financial variables in growth forecasts is the inherent difficulty in distinguishing in real time between an ongoing credit expansion that is structural—reflecting a process of financial development—from a cyclical boom that will soon revert.19 Our interpretation of the relationship we identify in this section is that forecasters are biased toward the structural interpretation of credit expansions. They thus fail to forecast either the mean reversion of private credit or the impact of this cyclical credit reversion on growth.20

Panel Analysis of Growth Forecasts

Our second empirical approach tests the robustness, generality and external validity of the findings in Sect. 2. We build a much larger set of IMF growth forecasts that allows us to include a set of more granular control variables and to explore some of the possible channels through which financial conditions are associated with forecast errors. We also wish to understand whether the forecast inefficiency found in the previous section is specific to the context of an IMF-supported program approval, or whether it prevails in other forecasting contexts as well.

We start by building a dataset of semiannual IMF forecasts from successive vintages of the World Economic Outlook (WEO) for 130 countries. The WEO is the flagship report providing the IMF’s view on the global economy and is published twice each year at regular intervals in the Spring and Fall. The publication includes forecasts for standard macroeconomic variables—including growth, inflation and the current account balance—over the next five years for all IMF member countries, which are produced by the institution’s staff of economists as part of the institution’s multilateral surveillance function. We combine the WEO forecasts with forecasts made in the context of IMF-supported programs reported in the MONA database over the sample period. This includes the forecasts made in the context of program approvals studied in Sect. 2 and also includes another 398 forecasts made upon completion of program reviews.21 These program forecasts are produced as an input to decisions made by the IMF’s Executive Board and occur at irregular intervals over the year.

The unit of observation in our panel is defined by a country c, forecast vintage v and year t. For each 3799 vintage-country pairs, our specification admits a single observation of the dependent variable ${\widehat{g}}_{\mathit{vc}}$, which as defined in equation 1 measures the forecast error for the annualized growth rate in years t and t+1. The empirical distributions of ${\widehat{g}}_{\mathit{vc}}$ in our panel are plotted by the histograms in Figure 4, where we distinguish forecasts made in the context of an IMF-supported program from those made in other contexts. The sample mean and median of ${\widehat{g}}_{\mathit{vc}}$ is 0.00 and −0.11 in the program sample, and 0.32 and 0.03 in the non-program sample.22

Fig. 4.

Distributions of IMF growth forecast errors; 2003–2019. Sources: WEO, MONA and authors’ calculations. Distribution of the annualized forecast errors over a two-year horizon (${\widehat{g}}_{\mathit{vc}}$). Forecasts from the IMF’s Monitoring of Fund Arrangements and World Economic Outlook databases, and outturns from the October 2021 vintage of the World Economic Outlook. Values of ${\widehat{g}}_{\mathit{vc}}$ above 10 percentage points or below −10 percentage points have been omitted from the histograms for readability

We regress ${\widehat{g}}_{\mathit{vc}}$ on a vector of observable financial variables ${\mathit{X}}_{\mathit{vc}}$ that were part of the forecaster’s information set and a vector of additional control variables ${\mathit{Y}}_{\mathit{vc}}$:

$${\widehat{g}}_{\mathit{vc}}=\alpha +{\mathit{\delta }\mathit{X}}_{\mathit{vc}}+{\mathit{\rho }\mathit{Y}}_{\mathit{vc}}+{\epsilon }_{\mathit{vc}}.$$ 3

In the baseline specification, the vector ${\mathit{X}}_{\mathit{vc}}$ contains the recent evolution of the credit-to-GDP gap—defined the same way as in Sect. 2—as well as the lagged share of loans by banks to non-financial corporates that are denominated in foreign currency, as reported in the IMF’s Monetary and Financial Statistics database. The latter is a state variable that captures a financial vulnerability that may amplify the impact of real and financial shocks on output. Both variables are part of the information set available at date b, when the forecast is made.

The coverage of the WEO and MONA variables in this more recent period includes a richer set of vintage-specific forecasts that we can include in the vector of additional controls ${\mathit{Y}}_{\mathit{vc}}$. A first variable is the ex post forecast error for the growth rate of country c’s trading partners. These forecasts are taken from the IMF’s internal Global Economic Environment (GEE) database, which forecasters are instructed to use as an input in their preparation of WEO forecasts for country c.23 This country-specific variable captures global shocks affecting the country’s external demand conditions.24 A second variable is the change in the fiscal balance as a share of GDP from t−1 to t+1 that is expected in vintage v, which was also employed in estimations reported in Table 2 above. We again include in ${\mathit{Y}}_{\mathit{vc}}$ a dummy variable indicating that civil conflict took place in the forecast period, as well as the growth of real output prior to program approval. Finally, we include ex post revisions made to the level of real GDP in period t−1, which controls for forecast errors reflecting base effects from statistical revisions to national accounts.

The results from this exercise are presented in Table 3. Column 1 reports the baseline specification estimated on the panel of 1425 country-vintage forecasts made in the context of an active IMF-supported program. We confirm the relationship identified in our event study of IMF-supported programs presented in the previous section: The recent evolution of the credit-to-GDP gap is significantly correlated with forecast errors, with a coefficient of 0.06. Just as the point estimate is highly consistent with the result from the event study, so too is the economic significance: A forecast preceded by a one-standard-deviation increase in the credit-to-GDP gap—about 6.6 percentage points in this larger sample—is associated with an annualized forecast error that is 0.40 percentage points more optimistic. However, the share of loans denominated in foreign currency is not found to be significant, with a coefficient that is very close to zero.

Table 3.

Results from panel forecast efficiency tests

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Credit-to-GDP gap (change from t−3 to t−1)	0.06***	0.02**	0.03***	0.02**	0.03***	0.03***	0.03***	0.02***
	(0.02)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)
Share of loans denom. FX (t−1)	−0.00	−0.00	−0.00	0.00	0.01**	−0.01**	−0.00	−0.00
	(0.00)	(0.00)	(0.00)	(0.01)	(0.01)	(0.00)	(0.00)	(0.00)
Real house price growth (t−3 to t−1)				0.05**
				(0.02)
Dummy: Civil conflict	0.05	−0.30	−0.14	−0.10	−0.09	−0.36	−0.17	−0.12
	(0.32)	(0.33)	(0.25)	(0.33)	(0.43)	(0.31)	(0.25)	(0.25)
Exp. fiscal adjustment (t−1 to t+2)	0.01	−0.02	−0.01	0.04	0.03	−0.04	0.02	−0.01
	(0.05)	(0.04)	(0.03)	(0.06)	(0.04)	(0.05)	(0.02)	(0.03)
FE trade partners’ growth (t+1)	0.50***	0.50***	0.50***	0.49***	0.23***	0.52***	0.50***	0.49***
	(0.06)	(0.05)	(0.04)	(0.06)	(0.04)	(0.05)	(0.04)	(0.04)
Ex post revision to real GDP (t−1)	−0.05	0.21**	0.08	0.01	0.08	0.06	0.04	0.08
	(0.09)	(0.11)	(0.07)	(0.18)	(0.09)	(0.07)	(0.07)	(0.07)
Real GDP growth (t−1)	0.09**	0.08**	0.08**	0.01	0.07	0.01	0.09***	0.08**
	(0.04)	(0.04)	(0.03)	(0.04)	(0.06)	(0.03)	(0.03)	(0.03)
REER Gap (change from t−3 to t−1)							0.05***
							(0.01)
Interact: REER * Hi FX loans							−0.05**
							(0.02)
Dummy: Banking crisis (t−1 or t−2)								0.06
								(0.51)
Dummy: Banking crisis (t or t+1)								1.21***
								(0.41)
Constant	−0.24	0.02	−0.05	−0.13	2.39***	0.19	−0.09	−0.09
	(0.31)	(0.16)	(0.14)	(0.17)	(0.28)	(0.15)	(0.14)	(0.15)
Sample	Program	No program	All	All	${\widehat{g}}_{c,t}^v$>pct75	Consensus Forecasts	All	All
Observations	1425	2374	3799	1429	948	2056	3727	3799
R2	0.23	0.26	0.24	0.35	0.15	0.34	0.26	0.25
Time period	2003–2019	2003–2019	2003–2019	2003–2019	2003–2019	2003–2019	2003–2019	2003–2019
Mean of dep. variable (${\widehat{g}}_{\mathit{vc}}$)	0.00	0.32	0.20	0.23	3.51	0.07	0.22	0.20

The dependent variable is ${\widehat{g}}_{\mathit{vc}}$, the forecast error for annualized growth of real output from t−1 to t+1. White heteroskedasticity-robust standard errors clustered by country are shown in parentheses. The use of *** denotes a coefficient significantly different from zero at the 0.01 confidence level; **0.05; *0.10. Full sample includes all forecast vintages from WEO and MONA databases covering 130 countries. Consensus Forecasts includes semiannual forecasts for 67 countries

From our vector of controls, we find that the forecast errors of trading partners’ growth are tightly correlated with forecast errors. This intuitive result reflects the fact that common global shocks—including to commodity prices and financial conditions—are an important source of forecast errors in individual countries. When the GEE forecast for country c’s partners turns out to be 1 percentage point too optimistic, this leads to an annualized growth forecast that is 0.5 percentage points more optimistic in the two following years.

The expected fiscal consolidation is not significantly correlated with forecast errors for growth, which is consistent with the results presented by Blanchard and Leigh (2013). As Blanchard and Leigh (2013) discuss, the macroeconomic and financial conditions surrounding the euro area crisis were particularly suited to generating larger-than-normal fiscal multipliers, and this does not seem to have been correctly anticipated by IMF growth forecasts at the time. However, they show that this result did not hold in other samples of WEO forecasts, including those that covered a longer period and a sample of emerging market economies. Our finding that expected fiscal consolidation is not significantly associated with more optimistic forecasts is suggestive that the IMF may be moving toward more realistic assumptions about fiscal multipliers.25

In column 2, we estimate the panel on the 2374 country-vintage forecasts that were made in the absence of an active fund-supported program, in the institution’s surveillance role. The lagged change in the credit-to-GDP gap remains statistically significant, but the size of the coefficient is somewhat smaller at 0.02. In column 3, we estimate Eq. 3 on the full sample to 3799 country-vintage forecasts—about 63 percent of which are generated outside the context of a IMF-supported program—covering 130 countries. The inefficiency result documented so far in the context of fund-supported programs also holds in the fund’s surveillance forecasts and the average effect is significant across all fund forecasts. However, its economic significance appears to be smaller, with a forecast preceded by a one-standard-deviation increase in the credit-to-GDP gap—about 8.8 percent in this sample—associated with an annualized forecast error that is 0.18 percentage points more optimistic, which is about half the effect found in the sample of program forecasts.

We then test whether the inefficiency result we have presented with respect to the lagged credit-to-GDP gap also applies to another commonly used financial variable: residential property prices deflated by the national consumer price index. These data are compiled by the Bank for International Settlements (BIS) using comparable methodology, but the available sample remains relatively scarce in its coverage of emerging and developing economies.26 The inclusion of the biannual growth rate of real house prices (taken over the periods t−3 to t−1 to align with the timing of our credit-to-GDP gap variable) as an additional regressor in Column 4 cuts the sample size in half from 3799 to 1429 observations. Interestingly, both lagged real house price growth and the lagged credit-to-GDP gap are significantly correlated with forecast errors, with recent growth in both variables associated with greater optimism.

In column 5, we return to our baseline specification but restrict the sample to forecasts that ended up being most optimistic, with a value of ${\widehat{g}}_{\mathit{vc}}$ that is in the top quartile of the empirical distribution of forecast errors (that is, ${\widehat{g}}_{\mathit{vc}}>1.3$). Among this sample of optimistic forecasts, the coefficient on the credit-to-GDP gap remains 0.03 and is statistically significant at the 0.01 level. In addition, the share of loans denominated in foreign current becomes positively correlated with forecast optimism. In this sample, a one-standard-deviation increase in the FX share (approximately 27 percentage points in this sample) is associated with an annualized growth forecast error that is 0.3 percentage points more optimistic.

As discussed in Introduction, IMF forecasts may be subject to unique agency issues and incentives, particularly when these are made in the context of lending programs. To test the external validity of our inefficiency result, we investigate whether it holds in a sample of forecasts made by professional forecasters in the private sector. To do so, we estimate Eq. 3 on a sample of 2056 semiannual forecasts reported in Consensus Forecasts publications for 67 countries. We merge these forecast vintages with information on control variables from the closest preceding GEE and WEO vintages to complete vector ${\mathit{Y}}_{\mathit{vc}}$.27 The result in column 6 is consistent with the baseline, despite the differences in country coverage across samples. We conclude that the inefficient use of financial information in growth forecasts is not confined to those made for IMF-supported programs, but applies to a variety of contexts and forecasters. The size of the coefficient in column 6 is very close to our estimate based on the full sample of IMF forecasts reported in column 3, which is smaller than the subsample based only on IMF-supported program forecasts. This is suggestive that any IMF-specific incentives leading to stronger forecast inefficiency with respect to macrofinancial information are predominant only in the context of its lending operations.

We then explore a possible channel through which financial vulnerabilities could result in larger forecast errors. If forecasts are preceded by a period of real exchange rate misalignment, financial vulnerabilities may cause exchange rate movements in subsequent years to have stronger impacts on growth, introducing a source of forecast errors if the forecaster has not properly modeled this mechanism. To test this, we introduce additional variables in the vector ${\mathit{X}}_{\mathit{vc}}$, including the change in the real effective exchange rate gap from t−3 to t−1, with the gap estimated as a percentage deviation from a one-sided five-year moving average to ensure that it was available at the time of the forecast. We also include an interaction between this variable and a dummy indicating that the lagged share of loans denominated in foreign currency is above the sample median.

Column 7 shows that the recent evolution of the REER gap is positively correlated with forecast optimism, but only when liability dollarization is low. When liability dollarization is high, this relationship is completely negated. A possible interpretation of this result is that the prevalence of this particular financial vulnerability may draw the attention of the forecaster to an exchange rate misalignment, whereas a disruptive external imbalance receives less attention when liability dollarization is low. In any case, the significance of lagged credit developments remains unchanged.

In a final exercise, we study the role of banking crises in explaining growth forecast errors.28 To do so, we introduce two dummy variables. The first indicates that a banking crisis documented by Laeven and Valencia (2020) took place in the two years prior to the forecast. The second indicates that a banking crisis took place in the two years following the forecast. In column 8, we show that the former is not significant, such that post-crisis forecasts are not conclusively more biased than others. The occurrence of crises during the forecast horizon is of course highly correlated with optimistic forecast errors, since such events are difficult to anticipate. However, it is noteworthy that even after controlling for the occurrence of banking crises, the past evolution of the credit-to-GDP gap remains significantly correlated with forecast errors. That is, the information contained in this financial variable is informative for growth forecast errors outside of situations in which a banking crisis is triggered.

Robustness: fixed effects estimation

The dimensionality of the panel dataset used in this section allows us to undertake additional robustness tests that were not possible in the event study of fund-supported programs presented in Sect. 2. In Table 4, we report our baseline specification with the introduction of alternative vectors of fixed effects. In the first column, we reproduce the baseline result from Table 3, column 3, showing the estimate of equation 3 in the full sample of IMF forecasts. In columns 2–3, we introduce country and year fixed effects, respectively. In column 4, we introduce country and year fixed effects. And in column 5, we introduce country and forecast vintage fixed effects. In all these specifications, the point estimate and standard error of the lagged credit-to-GDP gap variable are unaffected.

Table 4.

Robustness—panel forecast efficiency tests with fixed effects

	(1)	(2)	(3)	(4)	(5)	(6)
Credit-to-GDP gap (change from t−3 to t−1)	0.03***	0.03***	0.03***	0.03***	0.03***	0.03**
	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)
Share of loans denominated in FX (t−1)	−0.00	0.00	−0.00	0.00	−0.00	−0.01*
	(0.00)	(0.01)	(0.00)	(0.01)	(0.01)	(0.01)
Dummy: Civil conflict	−0.14	0.29	−0.11	0.28	0.25	0.49
	(0.25)	(0.30)	(0.25)	(0.28)	(0.32)	(0.54)
Expected fiscal adjustment (t−1 to t+2)	−0.01	−0.02	0.02	0.02	0.00	0.02
	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.04)
Forecast error: Trade partners’ growth (t+1)	0.50***	0.54***	0.09	0.17**	0.19**	0.44***
	(0.04)	(0.04)	(0.08)	(0.08)	(0.09)	(0.07)
Ex post revision to real GDP (t−1)	0.08	−0.04	0.07	−0.06	0.06	−0.08
	(0.07)	(0.07)	(0.07)	(0.07)	(0.09)	(0.08)
Real GDP growth (t−1)	0.08**	0.15***	0.05*	0.16***	0.16***	0.12***
	(0.03)	(0.03)	(0.03)	(0.03)	(0.04)	(0.03)
Constant	−0.05	−0.09	−1.68***	−1.50***	−0.96**	0.05
	(0.14)	(0.11)	(0.39)	(0.35)	(0.44)	(0.33)
Fixed effects	None	Country	Year	Country and Year	Country and Vintage	Forecaster
Observations	3799	3799	3799	3799	3799	2717
R-squared	0.24	0.38	0.30	0.42	0.55	0.44
Time period	2003–2019	2003–2019	2003–2019	2003–2019	2003–2019	2003–2015

The dependent variable is ${\widehat{g}}_{\mathit{vc}}$, the forecast error for annualized growth of real output from t−1 to t+1. White heteroskedasticity-robust standard errors clustered by country are shown in parentheses. The use of *** denotes a coefficient significantly different from zero at the 0.01 confidence level; **0.05; *0.10. Sample includes all forecast vintages from WEO and MONA databases covering 130 countries

Finally, we test the robustness of our result to the inclusion of individual forecaster fixed effects. As Beaudry and Willems (2022) show, some IMF mission chiefs tend be more optimistic than others over the course of their careers. There are many reasons that forecasting ability and bias may differ across individual forecasters, including predisposition toward certain models or forecasting approaches, and natural variation in cognitive ability (D’Acunto et al. 2022). To the extent that mission chief assignments are correlated with the credit cycle—say, if some individuals gravitate toward work on countries experiencing a financial crisis—then cross-forecaster variation could plausibly explain our inefficiency result. In Table 4, column 6, we expand our specification to include the vector of anonymized mission chief fixed effects built by Beaudry and Willems (2022) over the period 2003–2015.29 Here again, the point estimate and standard error of the lagged credit-to-GDP gap variable are unaffected.

We note that the fit of the specification with mission chief fixed effects (R² = 0.44) is substantially higher than the baseline specification with no fixed effects (R² = 0.24), and is comparable to the specification that includes country and time fixed effects (R² = 0.42). The best fit is offered by the specification including country and vintage fixed effects (R² = 0.55). This suggests an important role for these dimensions in explaining forecast errors, while the significance of the credit-to-GDP gap is maintained across all of these different sources of variation.

Conclusions and Policy Implications

The previous literature has identified an optimism bias in certain samples of growth forecasts made by the IMF in the design of programs supported by the institution. Alternative explanations have been put forward for this inefficiency, including mistakes made in modeling the impact of fiscal policy adjustment on future growth. Our paper is the first to study the role of financial variables in explaining optimism in growth forecasts made in IMF-supported programs.

We find that commonly available financial variables are correlated with subsequent forecast errors made in the design of IMF-supported programs. Specifically, an expansion of the credit-to-GDP gap in the years preceding a program request is associated with a significantly more optimistic growth forecast for the next two years. This result is strongest among forecasts that were most optimistic, where errors are also increasing in the economy’s degree of liability dollarization.

Our results are indicative that the IMF’s program growth forecasts do not efficiently incorporate information found in observable financial variables. This may reflect deficiencies in the macrofinancial modeling that underpins program design. We test whether this inefficiency result reflects the endogenous calibration of monetary and financial policies in response to credit conditions, and find that it does not.

While we show that the inefficient use of financial variables is strongest among growth forecasts made in the context of fund-supported programs, we document similar inefficiencies in growth forecasts produced in the IMF’s surveillance activities, as well as in forecasts made by professional forecasters in the private sector. We posit that a likely mechanism behind this result is the inherent difficulty in distinguishing in real time between an ongoing credit expansion that is structural—reflecting a process of financial development—from a cyclical boom. Additional research is needed into distinguishing these credit dynamics in real time and developing models of their short-term macroeconomic implications that could better inform growth forecasts.

Biographies

Yan Carrière-Swallow

is a Senior Economist in the Asia and Pacific Department at the International Monetary Fund. Prior to joining the IMF in 2012, he worked at the Central Bank of Chile.

José Marzluf

is a Research Assistant in the Strategy, Policy and Review Department at the International Monetary Fund. Before joining the IMF in 2020, he was a consultant at the World Bank.

Appendix

See Table 5.