Abstract
Novel Coronavirus (COVID-19) has affected stock markets around the globe, adding serious challenges to asset allocations and hedging strategies. This investigation analyses the dynamic correlations and portfolio implications among the S&P 500 index and various commodities (gold, WTI crude oil, Brent oil, beverages, and wheat) before and during the COVID-19 era. Using multivariate asymmetric GARCH models, the results show weak correlations during the standard period. However, the correlations intensify and become more complicated during the COVID-19 era, especially between gold and S&P 500. Similarly, bidirectional return and volatility spillovers across stock-commodity markets are more pronounced during the COVID-19 outbreak. Analysis involving the optimal portfolio weights and time-varying hedge ratios indicates that a $1long position in the S&P 500 can be hedged for 15 cents in crude oil during the standard period and for 33 cents in gold during the COVID-19 era. A portfolio of S&P 500 – beverages displays the highest VaR, while a portfolio of S&P 500 – gold displays the lowest VaR, especially during the COVID-19 era. This finding suggests that gold offers better portfolio diversification benefits and downside risk reductions, which are useful in determining strategies for portfolio investors during the COVID-19 outbreak.
Keywords: Mean and volatility spillovers, Crude oil, Gold, Commodity markets, S&P 500 index, Value at risk, VAR-DCC-MEGARCH model
1. Introduction
Today, the world faces a new pandemic identified as Novel Coronavirus (COVID-19), which has restructured global financial markets (Daube, 2020). Particularly, the S&P 500 and Nasdaq 100 index saw 14.9% and 12.4% declines in their market value from March 6, 2020, to March 18, 2020, respectively (Shehzad et al., 2020a).1 Shehzad et al. (2020b) reveal that the COVID-19 crisis has been more harmful than the global financial crisis (GFC) of 2007–2009. However, commodity futures have different return and volatility patterns from stock markets and diversify financial risk (Kang et al., 2017). Accordingly, financial institutions and investors invest large amounts in commodity futures, leading to the emergence of these markets as a valued asset class. Hence, a suitable portfolio can be found for US investors through commodity futures during the COVID-19 era. For this purpose, the study selects S&P 500, wheat futures, beverages futures, West Intermediate Texas (WTI) oil futures, Brent oil futures, and gold futures. Batten et al. (2017) reveal the importance of oil markets for diversifying financial risk. Moreover, Mensi et al. (2013) show that commodities, i.e., wheat, beverages, crude oil, and gold, improve investors' returns during a regular period. Sadorsky (2012) argues that oil markets offer discounted hedges for emerging markets. Moreover, Baur and McDermott (2010) state that gold not only possesses hedging properties but also acts as a safe haven for US and European stock markets; though these findings are not confirmed for BRICS, Australian, or Canadian equities. Reboredo (2013) reveals that gold acts as a safe haven and hedge against US dollar price movements. El Hedi Arouri et al. (2015) show that gold is a vital instrument against Chinese stock to reduce financial risk. Therefore, revealing the hedge properties, time-varying correlations, spillover impacts, and downside risks of these markets becomes essential during the normal period and COVID-19 era. The most corroborated approach to measuring the downside risk of financial markets is the value at risk (VaR) method established by Jorion (1996). However, Cheng et al. (2004) argue about its inefficiency owing to its convexity; nonetheless, no authenticated instrument can quantify the downside risk of financial markets except VaR (Sampid and Hasim, 2018). The correct estimation of VaR is substantially dependent on the nature of the volatility model. An accurate volatility model not only deals with the fat-tailed properties of the distribution but also with outsized financial instruments (Malz, 2011). To specify the VaR of financial markets, a multivariate approach to the generalized autoregressive conditional heteroskedasticity (GARCH) model can be taken. Numerous multivariate GARCH approaches have been established to compute the covariance between financial markets, such as CCC-GARCH, DCC-GARCH, GO-GARCH, and BEKK-GARCH models. This study implements the dynamic conditional correlation (DCC) multivariate exponential generalized autoregressive conditional heteroskedasticity (MEGARCH) approach established by Engle (2002) and Nelson (1991). The investigation employs the vector autoregressive (VAR) approach to capture the effect of returns transmission among the commodity futures and stock markets. It applies the student-t distribution to model the fat-tailed properties of the returns distribution. The DCC model is capable of dynamically handling the time-varying correlation between financial assets and many matrices (Ahmad et al., 2013). In addition, the MEGARCH approach correctly calculates the leverage impact (Sikhosana and Aye, 2018).
Various studies ascertain the returns transmission and volatility spillover effects between financial markets, gold, oil, and other commodities for the standard period, e.g., Chan et al. (2011), and Aruga and Managi (2011). However, past research does not consider the optimal portfolio, hedging, or portfolio VaR of these markets during the COVID-19 era. Furthermore, no study compares the behavior of these markets before and during the first wave of the COVID-19period.2 The contribution of this analysis is evaluating and comparing investment strategies during the normal and COVID-19 eras. The research studies the bidirectional and unidirectional returns and volatility transmission effects between the stock market and commodity futures to conclude which markets are the net receivers and transmitters of financial risk. The examination scrutinizes portfolio VaR through normal and student-t density at 95% and 99% confidence levels. The research assesses the power of DCC-MEGARCH to estimate the exact VaR for a portfolio of S&P 500 and commodity futures. The author believes that analyzing these markets before and during the COVID-19 period brings essential facts in the field of finance. The essential research queries of this project are, firstly: Is the return transmission effect between stock markets and commodity futures the same for both periods? Secondly, do the shocks which occur in the variance of returns spillover across markets in both periods? Thirdly, does the correlation among these markets change during the period of the COVID-19 crisis? Fourthly, what are the average weights of S&P 500 and commodities, and do the optimal weights have different values for the two eras? Fifthly, should hedging the stock market with commodity futures be preferred, or vice versa? Sixthly, do the hedging ratios change over these periods? Seventhly, has COVID-19 caused an upsurge in the downside risk of these markets? Eighthly, can the DCC-MEGARCH approach evaluate the exact VaR of these markets? The answers to these questions would enable policy-makers, investors, and academicians to heighten their awareness of the risk configuration of these markets and make more timely decisions involving the stock markets and commodities. According to the authors' best information, no research deals with these markets during the standard era and COVID-19 period in a single article. The findings of this inquiry are significant for speculators, financial management firms, and policy-makers.
The remainder of this study is organized as follows: Section 2, 3 deal with the literature review and data and methodology, respectively; Section 4 presents comprehensive results; Section 5 concludes.
2. Literature review
The COVID-19 has significantly damaged the economy of the globe. Keeping in view the scope COVID-19 crisis, the dynamic association among stock markets and commodities have gained significant attention from researchers due to their significance to portfolio diversification. For instance, Okorie and Lin (2021) analyzed the contagion effect during the COVID-19 pandemic. The study found significant evidence of the contagion effect in the stock markets due to COVID-19. Particularly, an investigation documented that these effects were noted in both returns and volatility of stock markets. Nguyen et al. (2021) evaluated the contagion effect and variance spillover effect from the US and Chinese stocks to other financial markets of the world. The outcomes of the study revealed that there was a significant contagion effect from the Chinese and the US stock markets to global stock markets; nevertheless, the study found weak evidence of variance spillover effect among them.
Kang and Lee (2019) examine the dynamic volatility spillovers and network connectivity between stock index and commodity futures markets using the multivariate DECO-FIGARCH model and the spillover index method. The estimation findings show a positive equivalence between the Index and commodity futures. In addition, it is seen that the highest spillover was during the 2008–2009 global financial crisis and the 2010–2012 European debt crisis. An et al. (2020) reveal the magnitude and direction of spreads in nineteen bulk of metal futures prices using a network theory approach that includes a bivariate spillover model. According to the findings, energy bulk mineral commodities such as natural gas acts as the highest net spillover transmitter, while an industrial metal commodity such as US Steel acts as the net highest spillover receiver. Mensi et al. (2021) examine the short-, medium- and long-term volatility spillovers between developed and developing countries for equity markets and strategic commodity futures markets. The results provide evidence of time-varying volatility spillovers that intensify under major events. (ii) Moreover, overall volatility spillovers are higher in the short run than in the medium and long run. (iii) A mixed portfolio provides a higher level of hedging effectiveness for both emerging and developed markets.
Vo and Hung (2021) examined the volatility spillovers effect among the gold, crude oil, and S&P 500 index. The investigation used the wavelet approach and found that the returns transmission pattern is more thickened during the COVID-19 era than the pre-COVID-19 era. Wen et al. (2021) evaluated the spillovers impact between the Chinese commodities and Chinese stock markets. The investigation used the TVP-VAR approach and found that Chinese stock markets are the net recipient of the variance spillovers effect. The study nominated that volatility association among these markets becomes more critical after a major crisis. Also, the study stated that the hedging properties of Chinese commodity markets have been weakened during the COVID-19 pandemic era. Erdem (2020) analyzed the adverse effects of COVID-19 on the stock markets of independent and less independent nations. The findings expressed that financial markets of partially independent nations have been affected more because of the same size of COVID-19 cases. Adekoya and Oliyide (2021) employed the time-varying parameter vector autoregression approach (TVP-VAR) to ascertain the spillovers effect among commodity and stock markets. The examination confirmed that gold is the significant receiver of the shocks transmitted from the financial markets. The study employed a quantile-based linear and non-linear causality test. The verdicts of this test announce that COVID-19 is greatly responsible for volatility transmission among the stock markets and commodity markets.
Farid et al. (2021) inspected stock markets (S&P 500) and commodity markets of the US, i.e., natural gas, gold, oil, and silver by utilizing the MCS-GARCH and Diebold and Yilmaz (2012) volatility index model. The investigation explores the behavior of risk transmission among these markets before and during the COVID-19 pandemic era. The results showed that volatility connectedness among these markets was at peaked during the COVID-19 era. Notably, the stock market and gold is the significant contributor of variance shocks to the volatility connectedness system. Narayan et al. (2020) articulated the association between depreciation of the Yen (Japanese currency) and the stock markets of Japan. The investigation unrevealed that depreciation of the Japanese Yen against the US dollar imperatively increases the stock returns during the COVID-19 period (January 2020–August 2020). Salisu et al. (2020) employed the panel vector autoregressive model to discover the oil-stock affiliation during the COVID-19 era. The investigation discovered that both stock markets and oil returns have faced long-term shocks happened due to their own and cross volatility effects. Similarly, Shehzad et al. (2021b) estimated the impact of COVID-19 and the global financial crisis on the Dow Jones index and WTI crude oil returns. The study employed the E-GARCH model and found that the variance of both markets is high during the COVID-19 era in comparison with the global financial crisis of 2007–2009. Moreover, the study exposed that the trade war between China and the US showed an insignificant impact on the returns of both markets.
Kinateder et al. (2021) used to DCC-GARCH model to evaluate the safe-haven properties of gold and government sovereign bonds. The investigation elaborated that sovereign bonds of the UK, US, and Germany have significant safe haven properties for properties. Ashraf (2020) analyzed the response of the stock markets to the COVID-19 cases and deaths that happened due to COVID-19. The investigation confirmed that stock market returns goes down when the COVID-19 cases increased. Moreover, the study documented that COVID-19 cases have a greater negative impact than COVID-19 deaths on the stock market's returns. Similarly, Shehzad et al., (2020a) analyzed the impact of the health crisis generated due to COVID-19 on the stock markets of the US and European nations. The investigation announced that COVID-19 deaths have significantly affected the Nasdaq composite index returns. However, increases in COVID-19 cases were proved to be more dangerous for S&P 500 returns. Hence, the above-summarized literature exposed that COVID-19 has imperatively affected the stock markets and commodity markets. Consequently, it becomes important to explore the time-varying correlation and volatility spillovers among the stock markets and commodities; additionally, to find suitable hedging opportunities and safe haven for investors during the COVID-19 period.
3. Data and methodology
3.1. Data
This examination is based on the sample period January 04, 2010, to May 10, 2020, divided into two sections, segment A and segment B. In the analysis, segment A represents the stable period (January 04, 2010, to November 30, 2019), while segment B represents the COVID-19 era (December 1, 2019, to May 10, 2020).3 The data used in the analysis is collected from the database of the US Energy Information Administration, Investing. Com, and Yahoo Finance.
3.2. Methodology
This investigation computes daily returns as follows:
| (1) |
where is the day-wise returns of the study variables at time t, and , and are the daily prices of the study variables at time t and t-1, respectively. There are numerous multivariate GARCH (MGARCH) models, e.g., the diagonal and full vector-half (VECH) models(Bollerslev et al., 1988) and the BEKK-GARCH model (Engle and Kroner, 1995), which deal with returns and volatility transmission impacts. Sadorsky (2012) contends that these models have various restrictions such as complications estimating the parameters, and poor performance of the likelihood function (for more detail, see Bauwens et al. (2006)). In order to find evidence of the risk transmission effect, this study applies the dynamic conditional correlation (DCC) multivariate exponential generalized autoregressive conditional heteroskedasticity (MEGARCH) model introduced by Engle (2002). It amalgamates the DCC-MEGARCH model with the vector autoregressive (VAR) model to capture evidence of returns transmission from one market to another. The DCC-MEGARCH model has several advantages over other GARCH models. Firstly, the standard MGARCH model ignores the parametric change in the returns and computes instability through the magnitude of stock returns. However, the MEGARCH approach follows a parametric method to ascertain conditional variance. Secondly, the standard MGARCH model cannot evaluate the exact volatility persistence in the market (Nelson, 1991). Although MEGARCH does not impose non-negativity conditions on the parameters, it significantly evaluates stock returns' asymmetric behavior (Sikhosana and Aye, 2018). On the other hand, the correlation between two securities has a domineering role in managing these markets' financial risk and needs a wide range of correlation series (BenSaïda et al., 2018). Similarly, portfolio optimization requires the covariance and standard deviation information of financial assets. The DCC-MEGARCH approach calculates the time-varying correlation between financial assets. It first analyses the univariate GARCH model then computes the time-varying conditional correlation among returns (Engle, 2002). In the DCC-GARCH model, the number of parameters evaluated does not hinge on the number of variables. Hence, a large number of correlations can be computed at a time (Engle, 2002).
3.2.1. Reckoning the VAR approach
This investigation evaluates the mean equation and quantifies the one lagged VAR model for both segments as follows(El Hedi Arouri et al., 2011):
| (2) |
where and indicate the returns and constant coefficient of financial asset i at time t in the mean equation, respectively. Similarly, when i 0, it estimates the returns transmission impact from asset j to asset i. Conversely, if i = j, it characterizes the lagged returns' transmission effect on its subsequent returns. Additionally, and are the error term and number of variables, respectively.
3.2.2. Computation of the DCC-MEGARCH model
This examination evaluates the variance equation through the MEGARCH (1, 1) model-based onthe Akaike information criterion as follows:
| (3) |
where and arethe variance term and constant of series i at time t, respectively. If i j, represents a parameter that captures the volatility spillover effect from series j to i. Moreover, in the case where i = j, it calculates the influence of shocks in the return series i at time t, on its own next-day variance, i.e. the ARCH effect. Also, isthe impact of variations occurring in the variance of series i at time t on its own next-day variance, i.e. the GARCH effect. Although, representsthe news effect on returns of financial asset j, it is also the leverage or asymmetric effect. The standardized student-t density for a random vector Ycan be written as follows:
| (4) |
where and arethe gamma function and degree of freedom, respectively, andn isthe number of instruments analyzed. This project assesses the conditional correlation following the procedure of Engle (2002):
| (5) |
where indicates the covariance matrix and conditional variance, and and arethe diagonal matrix of time dissimilar standard deviation and conditional correlation matrix, respectively. and are specified as:
| (6) |
;nd
| (7) |
where is a symmetric positive definite matrix:
| (8) |
can also be delineated as:
| (9) |
where , and symbolize the unconditional correlation matrix of standardized residuals of the return series included in the study and an matrix of standardized residuals, respectively. Furthermore, and are the DCC coefficients, which are expected to be positive, and their sum should not exceed the limit of 1. Consequently, the time dissimilar DCCs between series i and j can be ascertained as:
| (10) |
Thus, the VAR-DCC-MEGARCH model along with the student-t distribution and asymmetric spillovers allows the investigation to calculate more accurate multivariate time series data parameters.
3.2.3. Optimal hedging calculations
The research evaluates the optimal hedging solutions for the long position of asset i with a short position of asset j as follows (Kroner and Sultan, 1993):
| (11) |
where and point towards the covariance among asset i and j at time t and the conditional variance of asset j at time t.
3.2.4. Portfolio optimization
This examination derives the best possible portfolio weights of commodity markets and financial markets for both segments. Kroner and Ng (1998)show that the conditional volatility and covariance findings of multivariate GARCH models can ascertain the time divergent optimal weights as follows:
| (12) |
| (13) |
where is the weight of asset i at time t in the time-varying portfolio of two assets, i.e., asset i and j. In Eq. (11) , and arethe conditional volatility of asset j,the covariance between asset i and j, and the conditional variance of asset i at time t, respectively. Hence, the weight of asset j can be premeditated as 1-
3.2.5. Forecasting time-varying value at risk (VaR)
Numerous research studies, e.g., Jorion (2007), use VaR to ascertain financial loss. This study forecasts the one-day ahead time-varying VaR through an in-sample estimation approach, as it provides more exact VaR (Mensi et al., 2016). The analysis uses the student-t and normal distribution to stipulate the portfolio VaR between asset i and j. Consequently, the variance-covariance VaR for a two asset portfolio can be quantified as follows:
| (14) |
where , and are the optimal portfolio weights of asset i and j, respectively, , and represent the sigma value of asset i and j at time t, respectively, and is the conditional correlation between asset i and j at time t. The analysis computes the student-t and normal distribution quantile after assuming the series mean equals0 and the variance is equal to 1 at the 95% and 99% confidence levels. Hence, to derive the portfolio VaR of two assets, Eq. (13) can be redesigned as:
| (15) |
where is the distribution function is usedto estimate the VaR.
3.2.6. Back-testing value at risk model
This study applies the “hit process” to verify the robustness of the estimated VaR, where the projected values of downside risk are compared with the real loss figures, and the number of VaR exceptions are derived. VaR exceptions designate the number of real loss values that exceed the projected VaR. The hit process can be defined statistically as follows:
| (16) |
If n denotes the sample size, then the number of exceptions can be quantified as . Consequently, the VaR model is accurate if the hit rate is near the destined coverage level (), and it is i.i.d, e.g.:
| (17) |
The study also employs Kupiec (1995) and Christoffersen's (1998) approaches to ascertaining VaR model constancy. The likelihood ratio of Kupiec (1995) can be defined as:
| (18) |
The null hypothesis of Kupiec (1995) states that the hit rate is equal to or near a specified coverage level, i.e., . The likelihood ratio of Christoffersen's (1998) approach can be specified as:
| (19) |
where isthe likelihood of two incessant factors from variable i (0) to j (1), assuming the first-order Markov chain transition probability matrix among two plausible parameters. Likewise, and specify the transitions from parameter i to j and maximum likelihood calculations, respectively. Christoffersen's (1998) null hypothesis identifies that exceptions are equal to a predestined coverage level and behave independently. This approach follows a chi-square distribution .
4. Results and discussion
4.1. ADF, descriptive parameters, and ARCH-LM test results
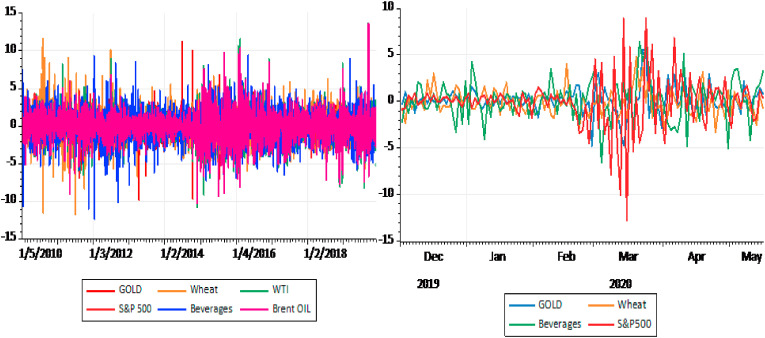
Table 1 gives the summary parameters of the variables used in this analysis. The statistics reveal that the average returns of the S&P 500 are negative during the COVID-19 era. Segment A indicates that the skewness value of gold, S&P 500, and beverages is negative with a high kurtosis parameter, implying that the chances of loss are higher in these markets. Nevertheless, during the COVID-19 period, gold shows positive skewness. The study applies the autoregressive conditional heteroskedasticity Lagrange multiplier (ARCH-LM) test (Engle, 1982) and the Breusch and Pagan (2006) test to evaluate the ARCHeffect and serial correlation in the study variables, respectively. These methodologies show that a significant ARCHeffect and serial correlation exist in these markets for both segments. Fig. 1 shows evidence of volatility clustering for both periods. Accordingly, the VAR-DCC-MEGARCH model is suitable for this examination. Moreover, the outcomes of the Jarque-Bera test show that the data are not normally distributed in the period. The student-t distribution is a perfect solution to deal with data holding these properties. The investigation applies the augmented Dickey-Fuller (ADF) test (Dickey et al., 1979) to analyze the unit root status of the data and find that all the data are stationary at level, i.e., I(1).
Table 1.
Descriptive statistics of daily returns.
| Segment A | GOLD | WHEAT | WTI | S&P 500 | Beverages | Brent OIL |
|---|---|---|---|---|---|---|
| Mean | 0.011353 | −0.001132 | −0.015662 | 0.040918 | −0.010644 | −0.010011 |
| Std. Dev. | 1.074085 | 1.918065 | 2.072594 | 0.935073 | 2.056939 | 1.937899 |
| Skewness | −0.132487 | 0.281606 | 0.064814 | −0.494692 | −0.069759 | 0.020691 |
| Kurtosis | 19.67619 | 6.310315 | 6.409943 | 7.555823 | 5.499097 | 6.892037 |
| Jarque-Bera | 28882.84 | 1170.762 | 1209.089 | 2256.755 | 650.5109 | 1573.04 |
| Probability | 0 | 0 | 0 | 0 | 0 | 0 |
| ADF-Statistics | −54.83861 | −50.35374 | −53.33578 | −52.33022 | −46.64852 | −53.87815 |
| P-values | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 |
| Q(20) | 28.725 | 6.1442 | 20.339 | 28.346 | 20.205 | 29.298 |
| P-values | 0.00138 | 0.04632 | 0.0262 | 0.001589 | 0.02737 | 0.001115 |
| Arch(10) (χ2) | 144.37 | 168.84 | 240.42 | 462.22 | 119.98 | 203.75 |
| P-values | 0 | 0 | 0 | 0 | 0 | 0 |
| Segment B | GOLD | WHEAT | WTI | S&P 500 |
|---|---|---|---|---|
| Mean | 0.146963 | −0.070991 | 0.196152 | −0.080366 |
| Std. Dev. | 1.512386 | 1.42474 | 2.219108 | 2.923971 |
| Skewness | 0.283249 | 0.688886 | −0.126623 | −0.556146 |
| Kurtosis | 6.529875 | 4.142998 | 3.66854 | 3.668543 |
| Jarque-Bera | 61.24201 | 15.35586 | 2.448942 | 105.9409 |
| Probability | 0 | 0.000463 | 0.293913 | 0 |
| ADF-Statistics | −9.206867 | −9.803819 | −11.19283 | −9.177288 |
| P-values | 0 | 0 | 0 | 0 |
| Q(20) | 49.205 | 14.005 | 31.156 | 42.421 |
| P-values | 0.0002 | 0.8302 | 0.05317 | 0.002436 |
| Arch(10) (χ2) | 11.719 | 15.287 | 4.7085 | |
| P-values | 0 | 0 | 0.03001 |
Notes: Segment A (January 04, 2010, to November 30, 2019); segment B (December 1, 2019, to May 10, 2020).
Fig. 1.
Returns distribution plots before and during the COVID-19 era.
4.2. Findings of the VAR model
Table 2 shows the consequences of the mean equation (Eq. (2)) for segment A. The mean equation for gold shows that WTI returns (ψ1, 3) have a negative association with gold returns; while, Brent oil returns (ψ1, 6) upsurge WTI returns. The upshot is that a 1unit increase in S&P 500 returns (ψ2, 4) expands wheat unit returns by 0.08, while the transmission of the return from other markets to wheat remains insignificant during the standard period. The returns transmission effects from wheat (ψ3, 2) and Brent oil (ψ3, 6) to WTI are significant, and the one period lagged return of WTI oil (ψ3, 3) affects its own returns. Previous changes in WTI (ψ4, 3) and Brent oil returns (ψ4, 6) have positive and negative impacts on S&P 500 returns, respectively. Also, the one-period lagged returns of S&P 500 (ψ4, 4) harmfully affect its own returns. The previous returns of S&P 500 (ψ5, 4) and gold (ψ5, 1) positively influence current beverages returns. On the other hand, the mean equation of Brent oil exposes inconsequential results, which are in line with Khalfaoui et al. (2019) andMensi et al. (2013).
Table 2.
Results of the VAR model (segment A: January 04, 2010, to November 30, 2019).
| Coefficient | Std. Error | P-values | Coefficient | Std. Error | P-values | ||
|---|---|---|---|---|---|---|---|
| Mean equation of GOLD (1) | Mean equation of S&P 500 (4) | ||||||
| ψ1,1 | −0.0663733 | 0.01527082 | 0.00 | Coefficient | Std. Error | P-Values | |
| ψ1,2 | 0.01390 | 0.00853102 | 0.10 | ψ4,1 | −0.005943 | 0.01375043 | 0.67 |
| ψ1,3 | −0.03240 | 0.01817647 | 0.07 | ψ4,2 | 0.01239701 | 0.00768165 | 0.11 |
| ψ1,4 | −0.01164 | 0.01872308 | 0.53 | ψ4,3 | 0.05689102 | 0.01636679 | 0.00 |
| ψ1,5 | 0.01089 | 0.00789565 | 0.17 | ψ4,4 | −0.0781875 | 0.01685897 | 0.00 |
| ψ1,6 | 0.03595 | 0.01929815 | 0.06 | ψ4,5 | −0.0038499 | 0.00710955 | 0.59 |
|
ψ1,0 |
0.00012 |
0.01615287 |
0.99 |
ψ4,6 |
−0.0543505 |
0.0173768 |
0.00 |
| Mean equation of Wheat (2) | ψ4,0 | 0.09434912 | 0.01454467 | 0.00 | |||
| Coefficient | Std. Error | P-Values | Mean equation of Beverages (5) | ||||
| ψ2,1 | 0.0089 | 0.03233804 | 0.78 | Coefficient | Std. Error | P-values | |
| ψ2,2 | −0.0144746 | 0.01806558 | 0.42 | ψ5,1 | 0.0799311 | 0.0364337 | 0.03 |
| ψ2,3 | −0.0571547 | 0.03849114 | 0.14 | ψ5,2 | −0.0405845 | 0.02035362 | 0.05 |
| ψ2,4 | 0.08921727 | 0.03964865 | 0.02 | ψ5,3 | 0.00560199 | 0.0433661 | 0.90 |
| ψ2,5 | 0.01618946 | 0.01672011 | 0.33 | ψ5,4 | 0.07789655 | 0.04467021 | 0.08 |
| ψ2,6 | −0.0029766 | 0.04086645 | 0.94 | ψ5,5 | 0.06411897 | 0.01883774 | 0.00 |
|
Ψ2,0 |
−0.0369324 |
0.0342059 |
0.28 |
ψ5,6 |
−0.0296621 |
0.04604225 |
0.52 |
| Mean equation of WTI (3) | Ψ5,0 | 0.00550858 | 0.03853813 | 0.89 | |||
| Coefficient | Std. Error | P-Values | Mean equation of Brent OIL (6) | ||||
| ψ3,1 | 0.00375597 | 0.0317581 | 0.91 | Coefficient | Std. Error | P-values | |
| ψ3,2 | 0.00468819 | 0.0177416 | 0.079 | ψ6,1 | −0.0108263 | 0.02945432 | 0.71 |
| ψ3,3 | 0.01760762 | 0.0378008 | 0.064 | ψ6,2 | 0.00370866 | 0.0164546 | 0.82 |
| ψ3,4 | 0.02076169 | 0.0389376 | 0.59 | ψ6,3 | 0.00593504 | 0.03505872 | 0.87 |
| ψ3,5 | −0.0110908 | 0.01642026 | 0.50 | ψ6,4 | 0.04890852 | 0.03611301 | 0.18 |
| ψ3,6 | −0.0628865 | 0.04013357 | 0.012 | ψ6,5 | −0.0011576 | 0.01522911 | 0.94 |
| Ψ3,0 | 0.04399024 | 0.03359246 | 0.19 | ψ6,6 | −0.0569309 | 0.03722222 | 0.13 |
| ψ6,0 | 0.06723677 | 0.03115561 | 0.03 | ||||
Notes: This table presents the estimated results from Eq. (2), where ψ is the returns transmission impact from asset i to j.
Table 3 shows the outcomes of the mean equation (Eq. (2)) for segment B. The beverages returns (ψ1, 3/ψ3, 1) have an undesirable and bidirectional impact on gold returns during the COVID-19 era, and the one-period lagged return of gold (ψ1, 1) remarkably affects its own current returns. The previous day returns of S&P 500 (ψ1, 4) show an adverse impact on the current day-wise returns of gold. Consistently, the one period lagged values of S&P 500 (ψ2, 3) control the current values of wheat. Previous day gold returns (ψ3, 1) and S&P 500 (ψ3, 3) returns negatively impact current beverages market returns. Moreover, the one-period lagged return of S&P (ψ4, 4) affects its own current returns.
Table 3.
Results of the VAR model (segment B: December 1, 2019, to May 10, 2020).
| Coefficient | Std. Error | P-values | Coefficient | Std. Error | P-values | ||
|---|---|---|---|---|---|---|---|
| Mean equation of GOLD (1) | Mean equation of Beverages (3) | ||||||
| ψ1,1 | 0.13431825 | 0.05340982 | 0.011907949 | ψ3,1 | −0.2698256 | 0.11832684 | 0.02258746 |
| ψ1,2 | −0.0212304 | 0.05429481 | 0.695782297 | ψ3,2 | 0.11336057 | 0.12028748 | 0.34598088 |
| ψ1,3 | −0.0691169 | 0.03579603 | 0.053501242 | ψ3,3 | 0.02090481 | 0.07930434 | 0.79208636 |
| ψ1,4 | −0.1237191 | 0.02718473 | 0.000000000 | ψ3,4 | −0.2053252 | 0.06022643 | 0.00065149 |
|
ψ1,0 |
0.07062292 |
0.07745578 |
0.361882557 |
ψ3,0 |
0.20601155 |
0.17159947 |
0.22993076 |
| Mean equation of Wheat (2) | Mean equation of S&P 500 (4) | ||||||
| Coefficient | P-Values | Coefficient | P-Values | ||||
| ψ2,1 | 0.04556561 | 0.08417355 | 0.588280667 | ψ4,1 | 0.0895458 | 0.08902059 | 0.31446372 |
| ψ2,2 | −0.0314454 | 0.08556828 | 0.713254501 | ψ4,2 | 0.02782379 | 0.09049563 | 0.75849321 |
| ψ2,3 | −0.0630312 | 0.05641432 | 0.263870201 | ψ4,3 | 0.00916501 | 0.05966287 | 0.87791461 |
| ψ2,4 | 0.01603922 | 0.04284296 | 0.070812727 | ψ4,4 | −0.4238919 | 0.04531002 | 0 |
| ψ2,0 | −0.1370524 | 0.12206983 | 0.261548955 | ψ4,0 | 0.10978993 | 0.12909908 | 0.39508519 |
See notes to Table 2.
4.3. Results of DCC-MEGARCH approach
Table 4 shows the results of the variance equation (Eq. (3)) for segment A. The outcome is that gold (Φ1, 4) and S&P 500 (Φ4, 1) have a bidirectional volatility spillover relationship. Moreover, the volatility that befalls wheat returns (Φ1, 2) indicates a negative association with gold instability. The current shocks befalling the S&P 500 significantly impact the instability level of wheat (Φ2, 4) and WTI (Φ3, 4). The study reports that the volatility of beverages (Φ4, 5) strongly spills over to S&P 500 index volatility. Moreover, the volatility of Brent oil (Φ5, 6) has a generous impact on the volatility of beverages. The volatility of the gold market (Φ6, 1) and the S&P 500 index (Φ1, 4) have unidirectional impacts on the variability of Brent oil. Kang et al. (2017) state that commodity futures have bidirectional spillover effects.
Table 4.
Estimated results for the DCC-MEGARCH model (segment A: January 04, 2010, to November 30, 2019).
| Coefficient | Std. Error | P-values | Coefficient | Std. Error | P-values | ||
|---|---|---|---|---|---|---|---|
| Φ1,0 | 0.0015065 | 0.0012938 | 0.2442590 | Φ1,6 | −0.0112416 | 0.0139845 | 0.4214775 |
| Φ2,0 | 0.0194733 | 0.0024916 | 0.0000000 | Φ,2,1 | −0.0070186 | 0.0123245 | 0.5690254 |
| Φ3,0 | 0.0103419 | 0.0014027 | 0.0000000 | Φ2,2 | 0.1019333 | 0.0053522 | 0.0000000 |
| Φ4,0 | −0.0096983 | 0.0050295 | 0.0538219 | Φ2,3 | 0.0113915 | 0.0142704 | 0.4247201 |
| Φ5,0 | 0.0204070 | 0.0022456 | 0.0000000 | Φ2,4 | −0.0333759 | 0.0159810 | 0.0367551 |
| Φ6,0 | 0.0115055 | 0.0015092 | 0.0000000 | Φ2,5 | −0.0008163 | 0.0055055 | 0.8821265 |
| φ1 | 0.0057930 | 0.0243177 | 0.8117081 | Φ2,6 | −0.0003882 | 0.0147838 | 0.9790525 |
| φ2 | −0.0462437 | 0.0233033 | 0.0472081 | Φ3,1 | 0.0070512 | 0.0091288 | 0.4398672 |
| φ3 | 0.0192164 | 0.0187004 | 0.3041415 | Φ3,2 | 0.0020928 | 0.0047339 | 0.6584312 |
| φ4 | −0.0722325 | 0.0292464 | 0.0135193 | Φ3,3 | 0.0607834 | 0.0029658 | 0.0000000 |
| φ5 | 0.0254593 | 0.0374822 | 0.4969890 | Φ3,4 | −0.0479555 | 0.0133896 | 0.0003416 |
| φ6 | 0.0179553 | 0.0175186 | 0.3053977 | Φ3,5 | 0.0042544 | 0.0043789 | 0.3312645 |
| χ1 | 0.9952340 | 0.0000316 | 0.0000000 | Φ3,6 | −0.0111796 | 0.0116775 | 0.3383869 |
| χ2 | 0.9826640 | 0.0003580 | 0.0000000 | Φ4,1 | 0.0305729 | 0.0175344 | 0.0812298 |
| χ3 | 0.9924373 | 0.0000326 | 0.0000000 | Φ4,2 | −0.0064030 | 0.0089581 | 0.4747530 |
| χ4 | 0.9640474 | 0.0071564 | 0.0000000 | Φ4,3 | 0.0162979 | 0.0190760 | 0.3928997 |
| χ5 | 0.9848981 | 0.0000237 | 0.0000000 | Φ4,4 | 0.1784329 | 0.0250443 | 0.0000000 |
| χ6 | 0.9913882 | 0.0000588 | 0.0000000 | Φ4,5 | 0.0137242 | 0.0074363 | 0.0649544 |
| ϱ1 | 3.7221498 | 0.2881143 | 0.0000000 | Φ4,6 | −0.0193653 | 0.0203580 | 0.3414861 |
| ϱ2 | 8.4981509 | 1.2771676 | 0.0000000 | Φ5,1 | 0.0172892 | 0.0127173 | 0.1739878 |
| ϱ3 | 8.1669190 | 1.4198396 | 0.0000000 | Φ5,2 | −0.0020361 | 0.0064172 | 0.7510222 |
| ϱ4 | 7.7295823 | 1.0988079 | 0.0000000 | Φ5,3 | −0.0216032 | 0.0161081 | 0.1798755 |
| ϱ5 | 5.1608997 | 0.5157703 | 0.0000000 | Φ5,4 | 0.0047443 | 0.0178454 | 0.7903517 |
| ϱ6 | 6.4600079 | 0.8772858 | 0.0000000 | Φ5,5 | 0.0859164 | 0.0050379 | 0.0000000 |
| υ | 0.0128527 | 0.0028665 | 0.0000073 | Φ5,6 | 0.0125204 | 0.0166815 | 0.0452921 |
| σ | 0.9785853 | 0.0065626 | 0.0000000 | Φ6,1 | 0.0046026 | 0.0102906 | 0.0654685 |
| ϱ | 8.5683314 | 0.4837990 | 0.0000000 | Φ6,2 | 0.0025944 | 0.0053889 | 0.6302072 |
| Φ1,1 | 0.0571145 | 0.0083733 | 0.0000000 | Φ6,3 | −0.0193410 | 0.0123405 | 0.1170510 |
| Φ1,2 | −0.0105955 | 0.0057069 | 0.0633657 | Φ6,4 | −0.0640642 | 0.0159675 | 0.0000602 |
| Φ1,3 | 0.0102259 | 0.0135706 | 0.4511284 | Φ6,5 | 0.0039857 | 0.0049917 | 0.4245945 |
| Φ1,4 | −0.0535963 | 0.0162815 | 0.0009953 | Φ6,6 | 0.0745716 | 0.0164883 | 0.0000061 |
| Φ1,5 | −0.0030498 | 0.0045790 | 0.5053939 |
Notes: The estimated results are based on Eq. (3), where Φ, φ, χ, and ϱ, are the volatility spillover effect from asset i to j (when i = j, representing the ARCH effect), news effect, GARCH effect, and degree of freedom, respectively, while υ and σ are the DCC coefficients.
The results for segment A show that shocks measured through standardized residuals of gold (Φ1, 1), wheat (Φ2, 2), WTI (Φ3, 3), S&P 500 (Φ4, 4), beverages (Φ5, 5), and Brent oil (Φ6, 6) at time t, affect their own returns at time t+1. Hence, it is clear that these markets have extensive ARCH effects. Fluctuations that follow today in the variance of gold (χ1), wheat (χ2), WTI (χ3), S&P 500 (χ4), beverages (χ5), and Brent oil (χ6) have a salient influence on the volatility of these markets in the subsequent period. This information shows the resilient GARCH effects in these markets. The investigation finds that negative news in the economy has superior control over the wheat and S&P 500 returns equal to positive news of an analogous magnitude, implying that these markets have a strong leverage effect. The sum of the DCC parameters (υ, σ) of this study is less than 1, implying that our DCC-MEGARCH model is mean-reverting. The significant statistics of the degree of freedom parameter (ϱ), from 3.72 to 8.5showthat the study effectively captures the fat-tailed returns distributions of these markets. These results are in line with Sadorsky (2014) andMensi et al. (2015).
Table 5 shows the results of the variance equation (Eq. (3)) for segment B. Wheat volatility (Φ1, 2) has a bidirectional spillover association with gold (Φ2, 1). The volatility of WTI (Φ1, 3) has a significant effect on gold volatility and vice versa (Φ3, 1). Shocks occurring in the variance of S&P 500 (Φ1, 4) upsurge the uncertainty of gold returns and vice versa (Φ4, 1). The investigation indicates that the volatility of WTI (Φ2, 3) and S&P 500 (Φ2, 4) substantially spillover to the volatility of wheat and vice versa (Φ3, 2) (Φ4, 2). The variance of S&P 500 (Φ3, 4) positively impacts the variance of WTI, while the volatility of WTI negatively impacts the volatility of S&P 500 (Φ4, 3).
Table 5.
Estimated results for the DCC-MEGARCH model (segment B: December 1, 2019, to May 10, 2020).
| Coefficient | Std. Error | P-values | Coefficient | Std. Error | P-values | ||
|---|---|---|---|---|---|---|---|
| Φ1,0 | 0.712897 | 0.000122 | 0.000000 | ϱ | 4.616349 | 0.791302 | 0.000000 |
| Φ2,0 | 0.897263 | 0.250481 | 0.000341 | Φ1,1 | 0.234377 | 0.000002 | 0.000000 |
| Φ3,0 | 2.512174 | 0.001176 | 0.000000 | Φ1,2 | 0.299408 | 0.000057 | 0.000000 |
| Φ4,0 | −0.075124 | 0.000253 | 0.000000 | Φ1,3 | −0.084512 | 0.000008 | 0.000000 |
| φ1 | −0.353745 | 0.000011 | 0.000000 | Φ1,4 | 0.031671 | 0.000013 | 0.000000 |
| φ2 | 0.146579 | 0.089037 | 0.099709 | Φ2,1 | 0.250916 | 0.082754 | 0.002429 |
| φ3 | −0.028292 | 0.002129 | 0.000000 | Φ2,2 | 0.022837 | 0.231710 | 0.092149 |
| φ4 | −0.620520 | 0.002840 | 0.000000 | Φ2,3 | 0.016762 | 0.048438 | 0.729309 |
| χ1 | 0.804073 | 0.000219 | 0.000000 | Φ2,4 | −0.039471 | 0.018540 | 0.033255 |
| χ2 | 0.784019 | 0.053021 | 0.000000 | Φ3,1 | −0.086009 | 0.000010 | 0.000000 |
| χ3 | 0.892759 | 0.000493 | 0.000000 | Φ3,2 | −0.091750 | 0.000041 | 0.000000 |
| χ4 | 0.999183 | 0.001936 | 0.000000 | Φ3,3 | 0.016521 | 0.000049 | 0.000000 |
| ϱ1 | 3.227725 | 0.000036 | 0.000000 | Φ3,4 | 0.003957 | 0.000313 | 0.000000 |
| ϱ2 | 9.999958 | 45.915869 | 0.029414 | Φ4,1 | 0.260073 | 0.000806 | 0.000000 |
| ϱ3 | 9.883477 | 0.306339 | 0.000000 | Φ4,2 | −0.110368 | 0.000744 | 0.000000 |
| ϱ4 | 2.100005 | 0.003171 | 0.000000 | Φ4,3 | −0.079702 | 0.000313 | 0.000000 |
| υ | 0.022011 | 0.006969 | 0.001585 | Φ4,4 | 0.179754 | 0.000549 | 0.000000 |
| σ | 0.987824 | 0.711051 | 0.000000 |
See notes to Table 4.
Kang et al. (2017) show that there is a bidirectional volatility transmission effect between commodity markets and that it is multifaceted during financial turmoil. The study variables have strong ARCH and GARCH effects. The study shows that negative news due to COVID-19 has a greater impact on the returns of gold (φ1), wheat (φ2), and S&P 500 (φ3). The DCC coefficients (υ, σ) are significant, and their sum is less than 1, which means the DCC-MEGARCH model is mean-reverting. The degree of freedom parameter (ϱ) contains moderate values from 2.1 to 9.8, which confirms that this investigation successfully captures the markets' fat-tailed properties.
4.4. Time-varying correlation
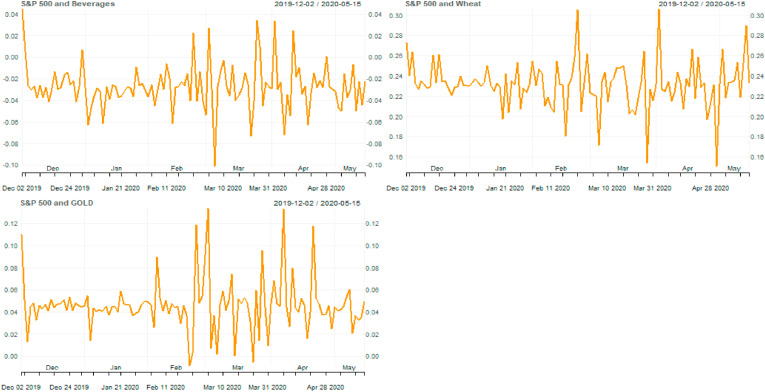
Fig. 2 shows the time-varying correlation among the study variables for segment A. The correlation between the S&P 500 and gold is highly positive at the end of 2010, while it is highly negative during 2016. Although the time-varying correlation between S&P 500 and Brent oil remains positive throughout the sample period, the time-varying correlation between the S&P 500 and WTI becomes highly negative at the beginning of 2011. Moreover, the association of S&P 500 with wheat and beverages is highly negative at the beginning of 2013. Fig. 3 shows the time-varying correlation among these markets during the COVID-19 era. These plots show that the relationship of S&P 500 to wheat and gold remains positive during the COVID-19 era. Conversely, the time-varying correlation between S&P 500 and beverages becomes negative during the COVID-19 outbreak in the US.
Fig. 2.
Time-varying correlation between S&P 500 and commodity markets during the standard period.
Fig. 3.
Correlation between the S&P 500 index and commodity markets during the COVID-19 era.
4.5. Summary parameters of time-varying portfolio weights
Table 6 shows the summary parameters of time-varying optimal weights for the S&P 500 with commodity markets in segment A. The statistics show that the mean weight of the S&P 500 is higher in these optimal portfolios. Notably, it has the highest mean value of 0.99 in the S&P 500 and Brent oil portfolio, which means investors can invest 99% of their investments in S&P 500 and 1% in Brent oil during the standard period. The optimal weights of gold, wheat, WTI, and beverages are38%, 5%, 1%, and 22%, respectively.
Table 6.
Summary parameters of time-varying weights for each portfolio (segment A: January 04, 2010, to November 30, 2019).
| S&P500/GOLD | S&P 500/Wheat | S&P500/WTI | S&P500/Beverages | S&P500/Brent OIL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S&P500 | GOLD | S&P500 | Wheat | S&P500 | WTI | S&P500 | Beverages | S&P500 | Brent OIL | |
| Mean | 0.61862 | 0.3813 | 0.94615 | 0.0538 | 0.98094 | 0.0190 | 0.78 | 0.22 | 0.99 | 0.01 |
| Maximum | 1 | 0.9588 | 1 | 0.9136 | 1 | 0.4235 | 1 | 0.3257 | 1 | 0.22 |
| Minimum | 0.04118 | 0 | 0.086352 | 0 | 0.57649 | 0 | 0.68 | 0 | 0.78 | 0 |
Note: This table shows summary statistics of time-varying weights calculated using Eq. (13).
Table 7 gives a summary of the optimal portfolio weights of gold, wheat, beverages, and S&P 500 during the COVID-19 era. These parameters show that the average weight of commodity markets is higher than the S&P 500 during the COVID-19 era, implying that investors should invest more in commodity futures than stock markets during the crisis. Notably, the highest mean weight value of 0.89 is for wheat in the S&P 500 portfolio, which means investors can invest 89% of their investment in wheat and 11% in the S&P 500 during the economic crisis. The mean optimal weights of gold and beverages are0.85 and 0.71, respectively.
Table 7.
Summary parameters of time-varying weights for each portfolio (segment B: December 1, 2019, to May 10, 2020).
| S&P500/GOLD | S&P 500/Wheat | S&P500/Beverages | ||||
|---|---|---|---|---|---|---|
| S&P500 | GOLD | S&P500 | Wheat | S&P500 | Beverages | |
| Mean | 0.1444703 | 0.8555297 | 0.1005143 | 0.8994857 | 0.2818532 | 0.7181468 |
| Maximum | 1 | 1 | 1 | 1.024796 | 1 | 0.9966803 |
| Minimum | 0 | 0 | 0 | 0 | 0.0033197 | 0 |
See notes to Table 6.
4.6. Summary statistics for time-varying hedging
Table 8 lists the summary statistics of the time-varying hedging ratios before the COVID-19 era (segment A). The average value of the hedging ratio of S&P 500 with WTI crude oil is 0.14, and S&P 500 with Brent oil is 0.15, implying that, on average, a $1 long position can be hedged for 14 cents in the WTI and 15 cents in Brent oil. The investigation suggests that risk-averse investors can invest in a portfolio of S&P 500 – beverages and Gold – S&P 500. However, medium-term investments can be made in S&P 500 – Brent oil and WTI – S&P 500 portfolios. Fig. 4 shows the time-varying hedging ratios for these markets before the COVID-19 era. These plots indicate that the optimal hedge ratios of these portfolios frequently relapse to their mean values. Śmiech and Papież (2017) argue that gold is a feeble hedge for stocks. Similar results are reported by Shehzad et al. (2021a).
Table 8.
Summary coefficients of time-varying hedging (segment A: January 04, 2010, to November 30, 2019).
| S&P500/GOLD | S&P500/Wheat | S&P500/WTI | S&P500/Beverages | S&P500/Brent OIL | |
|---|---|---|---|---|---|
| Minimum | −0.368325146 | −0.08306358 | −0.075627216 | −0.058666744 | 0.020320739 |
| Mean | 0.036644007 | 0.041304621 | 0.148755736 | 0.035427735 | 0.15337303 |
| Maximum |
0.474642493 |
0.4361979 |
0.683449336 |
0.423462685 |
0.689438076 |
|
GOLD/S&P500 |
Wheat/S&P 500 |
WTI/S&P500 |
Beverages/S&P500 |
Brent OIL/S&P500 |
|
| Minimum | −0.463681187 | −0.311608665 | −0.195982736 | −0.393391656 | 0.068605115 |
| Mean | 0.059503454 | 0.252088656 | 0.815892421 | 0.208946136 | 0.736528397 |
| Maximum | 0.664964014 | 1.727540552 | 2.245786607 | 1.185605397 | 2.189608561 |
Note: This table presents summary information of hedging ratios based on Eq. (11).
Fig. 4.
Hedging ratios during the standard period.
Table 9 gives a summary of the time-varying hedging ratios of the study variables during the COVID-19 era. The hedging ratio between S&P 500 and gold is 0.33, implying that, on average, a $1 long position in S&P 500 can be hedged for 33 cents in gold futures during financial calamities such as the COVID-19 era. Additionally, the hedging ratios between gold and S&P 500 and wheat and S&P 500 are0.01 and 0.081, respectively, meaning that, on average, a $1 long position in gold could be hedged for 1 cent in S&P 500, and a $1 long position in wheat can be hedged for 8 cents in S&P 500 during the COVID-19 era. The hedging ratio of S&P 500 with wheat has the highest average value of 1.23, implying that long-term investments can be made in this portfolio. Fig. 5 shows that the hedging ratio of S&P 500 with gold and wheat is highest at the time of the COVID-19 outbreak.
Table 9.
Summary coefficients of time-varying hedging (segment B: December 1, 2019, to May 10, 2020).
| S&P500/GOLD | S&P500/Wheat | S&P500/Beverages | |
|---|---|---|---|
| Minimum | −0.044073076 | 0.173193352 | −1.264344925 |
| Mean | 0.338279368 | 1.398702434 | −0.107042369 |
| Maximum |
4.716066214 |
15.5890666 |
0.182535245 |
| GOLD/S&P500 | Wheat/S&P 500 | Beverages/S&P500 | |
| Minimum | −0.001490486 | 0.003655792 | −0.130678521 |
| Mean | 0.01603454 | 0.081718291 | −0.014354809 |
| Maximum | 0.080940009 | 0.30889762 | 0.036688718 |
See notes to Table 8.
Fig. 5.
Hedging ratios during the COVID-19 era.
4.7. Summary statistics of value-at-risk (VaR)
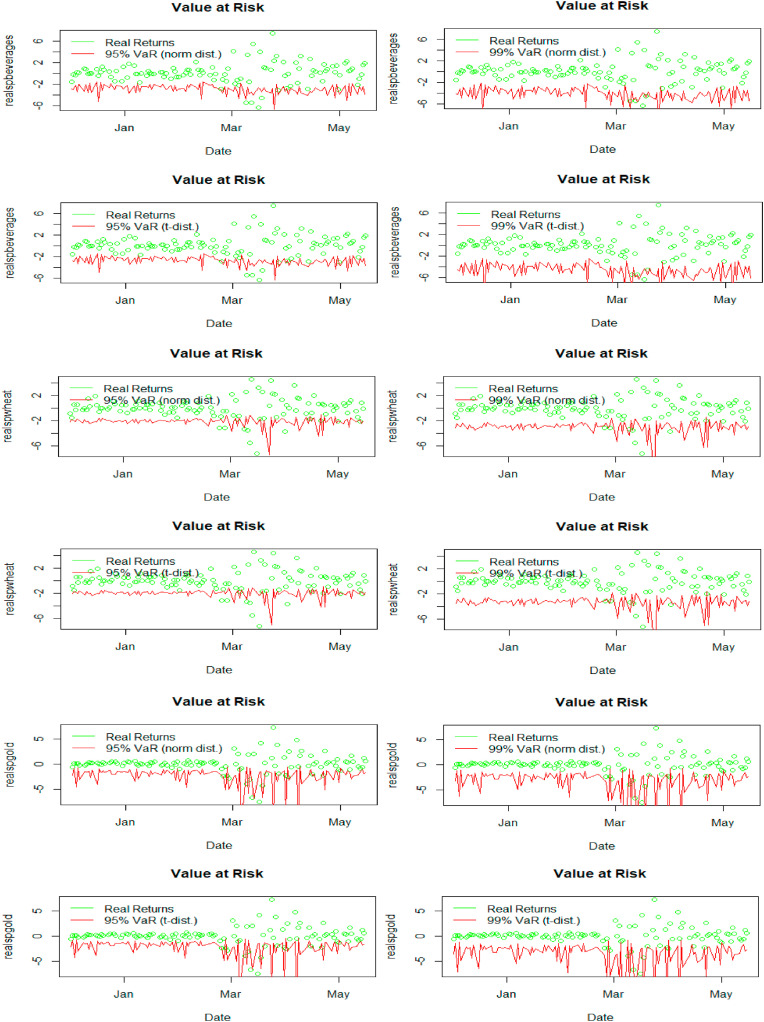
Fig. 6, Fig. 7 show the portfolio downside risk pattern for the normal and COVID-19 periods, respectively. Table 10 shows the summary statistics of the VaR for both periods. The findings show that a portfolio of S&P 500 and beverages has the highest mean VaR at the99% and 95% confidence levels during the standard period. However, as per the student-t distribution, the average portfolio VaR of gold, wheat, WTI, and Brent oil is-0.78, −0.96, −0.92, and −0.91, respectively. During the COVID-19 era (segment B), the highest mean value of portfolio VaR of S&P 500 and beverages is −2.39, followed by wheat and gold.
Fig. 6.
Time-varying VaR during the normal period.
Fig. 7.
Time-varying VaR during the COVID-19 era.
Table 10.
Summary statistics for VaR.
| Student-t distribution |
Normal distribution |
|||||
|---|---|---|---|---|---|---|
| Segment A: January 04, 2010, to November 30, 2019 | ||||||
| S&P500/GOLD | Max | Min | Mean | Max | Min | Mean |
| 95% | −2.9239309 | −0.9971852 | −0.4725904 | −3.0812948 | −1.0508531 | −0.4980249 |
| 99% | −4.8826732 | −1.6652 | −0.789179 | −4.3579341 | −1.4862415 | −0.7043662 |
| S&P500/Wheat | ||||||
| 95% | −38.74684 | −2.6989203 | −0.5752493 | −40.832169 | −2.8441743 | −0.6062089 |
| 99% | −64.703362 | −4.5069279 | −0.9606091 | −57.749715 | −4.02257 | −0.8573728 |
| S&P500/WTI | ||||||
| 95% | −542.05047 | −5.5292806 | −0.5554945 | −571.22325 | −5.8268627 | −0.5853908 |
| 99% | −905.17027 | −9.2333476 | −0.9276204 | −807.89195 | −8.2410431 | −0.8279294 |
| S&P500/Beverages | ||||||
| 95% | −7.2633792 | −2.7259162 | −1.5913491 | −7.6542893 | −2.8726232 | −1.6769945 |
| 99% | −12.12912 | −4.5520085 | −2.6573945 | −10.825607 | −4.0628058 | −2.3718053 |
| S&P500/Brent OIL | ||||||
| 95% | −279.10057 | −4.4206787 | −0.5504531 | −294.12158 | −4.6585966 | −0.5800782 |
| 99% |
−466.07015 |
−7.382093 |
−0.9192019 |
−415.98176 |
−6.5887421 |
−0.8204156 |
| Segment B: December 1, 2019, to May 10, 2020 | ||||||
| S&P500/GOLD | ||||||
| 95% | −12.292924 | −2.2675941 | −0.4434445 | −12.954521 | −2.3896344 | −0.4673104 |
| 99% | −20.527959 | −3.7866562 | −0.7405082 | −18.321827 | −3.3797056 | −0.660926 |
| S&P500/Wheat | ||||||
| 95% | −7.091334 | −2.0429247 | −0.98664 | −7.4729848 | −2.1528735 | −1.0397403 |
| 99% | −11.841821 | −3.4114807 | −1.6475906 | −10.569185 | −3.0448501 | −1.4705246 |
| S&P500/Beverages | ||||||
| 95% | −6.310023 | −2.8000732 | −1.4323912 | −6.6496241 | −2.9507712 | −1.5094815 |
| 99% | −10.53711 | −4.6758433 | −2.3919506 | −9.4046903 | −4.1733321 | −2.1348885 |
Note: These results are calculated based on Eq. (15).
4.8. Back-testing value at risk and VAR-DCC-MEGARCH model
The Kupiec (1995) and Christoffersen (1998) test results for both segments are given in Table 11 . These statistics show that the DCC-MEGARCH model, along with student-t and normal distribution, measures the exact VaR for the S&P 500 – gold portfolio at a 95% confidence level, and an accurate VaR for the S&P 500 – wheat portfolio at a 95% confidence level. However, they do not ascertain correct and independent VaRs for other portfolios during the standard period. The results for segment B show that the DCC-MEGARCH model accurately predicts the downside risk of the S&P 500 – gold portfolio, S&P 500 – wheat portfolio, and S&P 500 – beverages portfolio at a 99% confidence level. The VaR limitations of these portfolios given in Fig. 6 show that the DCC-MEGARCH model underestimates the downside risk of the S&P 500 – WTI portfolio, S&P 500 – beverages portfolio, and S&P – Brent oil portfolio for the standard era. On the other hand, the VaR limitation given in Fig. 7 verifies that the projected downside risk does not exceed the actual loss during the COVID-19 era. Hence, this investigation argues that the DCC-MEGARCH model is perfect for evaluating the portfolio VaR during crisis circumstances.
Table 11.
Back-testing for the VaR.
| Student-t distribution |
Normal distribution |
|||||||
|---|---|---|---|---|---|---|---|---|
| Segment A: January 04, 2010, to November 30, 2019 | ||||||||
| Confidence level | Expected Exceed | Actual Exceed | LRuc | LRcc | Expected Exceed | Actual Exceed | LRuc | LRcc |
| GOLD | ||||||||
| 95% | 124 | 132 | 0.4541905 | 0.6191286 | 124 | 114 | 0.9758747 | 0.9859311 |
| 99% | 124 | 31 | 104.603** | 105.304** | 124 | 45 | 70.1861** | 71.4780** |
| Wheat | ||||||||
| 95% | 124 | 113 | 1.171848 | 1.175275 | 124 | 99 | 5.9380** | 5.9392** |
| 99% | 124 | 21 | 136.88** | 137.24** | 124 | 31 | 104.60** | 105.38** |
| WTI | ||||||||
| 95% | 124 | 64 | 37.461** | 47.989** | 124 | 52 | 56.522** | 64.591** |
| 99% | 124 | 8 | 194.92** | 194.97** | 124 | 16 | 156.42** | 156.63** |
| Beverages | ||||||||
| 95% | 124 | 32 | 101.77** | 108.96** | 124 | 25 | 123.02** | 133.04** |
| 99% | 124 | 6 | 206.64** | 206.67** | 124 | 6 | 206.64** | 206.67** |
| Brent OIL | ||||||||
| 95% | 124 | 79 | 20.078** | 23.898** | 124 | 73 | 26.257** | 29.263** |
| 99% |
124 |
9 |
189.45** |
189.51** |
124 |
20 |
140.57** |
142.63** |
| Segment B: December 1, 2019, to May 10, 2020 | ||||||||
| GOLD | ||||||||
| 95% | 5 | 11 | 4.0277** | 4.032149 | 5 | 10 | 2.735223 | 5.9914** |
| 99% | 5 | 7 | 0.268301 | 0.9218936 | 5 | 9 | 3.841459 | 1.787974 |
| Wheat | ||||||||
| 95% | 5 | 12 | 5.5215** | 5.52153** | 5 | 11 | 4.0277** | 4.032149 |
| 99% | 5 | 6 | 3.841459 | 0.6782979 | 5 | 7 | 0.268301 | 0.9218936 |
| Beverages | ||||||||
| 95% | 5 | 6 | 0.0112879 | 0.6782979 | 5 | 5 | 3.841459 | 0.5663942 |
| 99% | 5 | 2 | 3.40306 | 3.474492 | 5 | 2 | 3.40306 | 3.474492 |
In order to determine the serial correlation in the standardized and squared standardized residuals of the model, this investigation applies the Breusch and Pagan (2006) test at lag 20. The measurements presented in Table 12 show no serial correlation in the residuals or squared residuals of the DCC-MEGARCH model for either segment. Consequently, the parameters resulting from VAR-DCC-MEGARCH are accurate, and the model is impeccably fitted.
Table 12.
Back-testing of the VARX-DCC-MEGARCH model.
| Segment A: January 04, 2010, to November 30, 2019 |
Segment B: December 1, 2019, to May 10, 2020 |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Q (20) | P-values | Q2 (20) | P-values | Q (20) | P-values | Q2 (20) | P-value | ||
| GOLD | 13.94 | 0.8334 | 50.985 | 0.0001 | GOLD | 0.094225 | 0.7589 | 6.9315 | 0.7319 |
| Wheat | 9.042 | 0.9824 | 8.2043 | 0.9904 | Wheat | 0.47683 | 0.4899 | 7.2129 | 0.7052 |
| WTI | 13.96 | 0.8324 | 7.8183 | 0.6466 | Beverage | 6.9315 | 0.7319 | 13.016 | 0.2228 |
| S&P500 | 1.462 | 0.2265 | 16.734 | 7.4878 | S&P500 | 15.432 | 0.1171 | 13.786 | 0.183 |
| Beverage | 0.912 | 0.3395 | 14.437 | 0.8077 | |||||
| Brent OIL | 7.414 | 0.6858 | 17.243 | 0.6372 | |||||
Note: This table presents the results for serial correlation and heteroskedasticity in standardized residuals (Q) and its square (Q2) at lag 20.
4.9. Robustness check
This paper also explores the relations between the S&P 500 index and various commodities (gold, WTI crude, Brent oil, beverages, and wheat) for robustness check with the Granger causality test based on the vector error correction (VECM) model. In this way, possible causal relationships between the assets in the portfolio can be revealed.VECM provides information on both short- and long-run relationships between variables. The VECM is based on a VAR model powered by the first-difference single-lag error correction term. Wald statistics provide information about the short-run causality relationship. The long-term causality relationship is based on the statistical significance of the error correction coefficient. Table 13 reports Granger causality results based on VECM. According to the results,(i) there is a long-run unidirectional causality from other assets to GOLD and WTI. According to the short-term results, (ii), there is a bidirectional/feedback relationship between S&P500 and WTI, Brent OIL and WTI, and GOLD and WTI.
Table 13.
Granger causality test results.
| Panel Granger causality test based on VECMab |
|||||||
|---|---|---|---|---|---|---|---|
| Short-run |
Long-run |
||||||
| ΔS&P500 | ΔGOLD | ΔWheat | ΔWTI | ΔBeverages | ΔBrent OIL | ECT | |
| ΔS&P500 | – | 0.771 (0.379) | 0.787 (0.380) | 20.460* (0.000) | 0.099 (0.752) | 2.775*** (0.092) | 3.41E-05 [0.38] |
| ΔGOLD | 0.465 (0.493) | – | 1.770 (0.183) | 10.060* (0.000) | 1.868 (0.172) | 3.251*** (0.072) | −0.0013** [-2.15] |
| ΔWheat | 1.131 (0.251) | 0.869 (0.351) | – | 0.375 (0.540) | 0.255 (0.611) | 2.729*** (0.097) | 3.41E-05 [0.75] |
| ΔWTI | 4.150** (0.041) | 3.417*** (0.065) | 0.387 (0.533) | – | 1.534 (0.215) | 28.688* (0.000) | −4.18E-05* [-5.69] |
| ΔBeverages | 0.116 (0.733) | 0.366 (0.544) | 0.705 (0.400) | 0.066 (0.796) | – | 0.365 (0.545) | 1.31E-05 [1.14] |
| ΔBrent OIL | 1.579 (0.210) | 0.260 (0.609) | 0.132 (0.715) | 10.903* (0.000) | 0.228 (0.632) | – | 5.60E-06 [1.03] |
a The values in parentheses are P values.
b The values in brackets are t-statistics. *,** and *** indicate 1%, 5% and 10% significance.
5. Conclusion and policy recommendations
COVID-19 has strongly affected the stock markets of the world. Accordingly, defining stock market behavior, commodity futures, and investment opportunities have become imperative. This investigation applies the VAR-DCC-MEGARCH model to ascertain the spillover effects, time-varying correlations, VaR, optimal portfolios, and hedging of S&P 500 with the commodities, i.e., gold, beverages, wheat, and oil futures before and during the COVID-19 era. The analysis shows that there is no bidirectional return spillover effect among these markets during the standard period. However, the S&P 500 index transmission effect on wheat, beverages, and Brent oil is significant during the standard period. The one period lagged return of gold does not affect the current returns of other markets except beverages. However, returns of S&P 500 expressly control the returns of gold, wheat, and beverages during the COVID-19 era. The returns of gold and beverages show bidirectional returns transmission. During the regular period, the volatility of gold and S&P 500 have a bidirectional association with each other. Furthermore, the variability of gold prices significantly spills over to the instability of Brent oil; however, wheat volatility does not push the uncertainty of these markets, except gold. Variations in the variance of the S&P 500 have far-reaching effects on the variance of wheat, WTI, and Brent oil, whereas the variance of beverages has a unidirectional spillover impact on the variance of the S&P 500. During the COVID-19 era, volatility occurred in the stock markets leading to instability of commodity markets and vice versa. Consequently, this investigation concluded that during circumstances of financial turmoil, market behaviors become more complex, and they dramatically affect the constancy of each other. The hedging ratios of S&P500– gold and S&P 500– wheat remain high during the COVID-19 era. The study suggests that commodities should be preferred for portfolios during crisis eras and that the VAR-DCC-MEGARCH model along with the student-t distribution and normal distribution can estimate the exact VaR at a 99% confidence level during times of crisis. These findings are important for investors and financial managers who consistently aim to build optimal portfolios and refine their hedging strategies during stressful periods. Future research could consider the direct impact of economic and financial uncertainties on stock-commodity correlations and their implications for optimal hedging. Other future studies can consider sector data of the stock market also.
Credit author statement
Khurram Shehzad: Conceptualization, Methodology, Software, Data Curation, Writing- Original draft preparation, Visualization, Investigation, Software, Validation. Xiaoxing Liu: Supervision. Emrah Kocak: Writing revised draft, Validation. Umer Zaman: Data Curation, Writing- Original draft preparation.
Funding
“The study is supported by National Natural Science Foundation of China (No.72173018).
Declaration of competing interest
“The authors reported no potential conflict of interest”.
Footnotes
The ten-year US Treasury bond market price dramatically dropped to its lowest level in history (Gupta et al., 2021).
Salisu and Akanni (2020 construct a global fear index for the COVID-19 pandemic.
Due to the excess number of variables and the limited number of observations, the investigation excludes the energy markets in segment B.
References
- Adekoya O.B., Oliyide J.A. How COVID-19 drives connectedness among commodity and financial markets: evidence from TVP-VAR and causality-in-quantiles techniques. Resour. Pol. 2021;70 doi: 10.1016/j.resourpol.2020.101898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmad W., Sehgal S., Bhanumurthy N.R. Eurozone crisis and BRIICKS stock markets: contagion or market interdependence? Econ. Modell. 2013;33:209–225. doi: 10.1016/j.econmod.2013.04.009. [DOI] [Google Scholar]
- An S., Gao X., An H., Liu S., Sun Q., Jia N. Dynamic volatility spillovers among bulk mineral commodities: a network method. Resour. Pol. 2020;66 doi: 10.1016/j.resourpol.2020.101613. [DOI] [Google Scholar]
- Aruga K., Managi S. Tests on price linkage between the U.S. and Japanese gold and silver futures markets. Econ. Bull. 2011 [Google Scholar]
- Ashraf B.N. Stock markets' reaction to COVID-19: cases or fatalities? Res. Int. Bus. Finance. 2020;54 doi: 10.1016/j.ribaf.2020.101249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batten J.A., Kinateder H., Szilagyi P.G., Wagner N.F. Can stock market investors hedge energy risk? Evidence from Asia. Energy Econ. 2017;66:559–570. doi: 10.1016/j.eneco.2016.11.026. [DOI] [Google Scholar]
- Baur D.G., McDermott T.K. Is gold a safe haven? International evidence. J. Bank. Finance. 2010 doi: 10.1016/j.jbankfin.2009.12.008. [DOI] [Google Scholar]
- Bauwens L., Laurent S., Rombouts J.V.K. Multivariate GARCH models: a survey. J. Appl. Econom. 2006;21:79–109. doi: 10.1002/jae.842. [DOI] [Google Scholar]
- BenSaïda A., Litimi H., Abdallah O. Volatility spillover shifts in global financial markets. Econ. Modell. 2018;73:343–353. doi: 10.1016/j.econmod.2018.04.011. [DOI] [Google Scholar]
- Bollerslev T., Engle R.F., Wooldridge J.M. A capital asset pricing model with time-varying covariances. J. Polit. Econ. 1988 doi: 10.1086/261527. [DOI] [Google Scholar]
- Breusch T.S., Pagan A.R. Econometrica; 2006. A Simple Test for Heteroscedasticity and Random Coefficient Variation. [DOI] [Google Scholar]
- Chan K.F., Treepongkaruna S., Brooks R., Gray S. Asset market linkages: evidence from financial, commodity and real estate assets. J. Bank. Finance. 2011 doi: 10.1016/j.jbankfin.2010.10.022. [DOI] [Google Scholar]
- Cheng S., Liu Y., Wang S. Progress in risk Measurement1. Adv. Model. Optim. 2004 [Google Scholar]
- Christoffersen P.F. Int. Econ. Rev.; Philadelphia: 1998. Evaluating Interval Forecasts. [DOI] [Google Scholar]
- Daube C.H. 2020. The Corona Virus Stock Exchange Crash. [Google Scholar]
- Dickey D.A., Fuller W.A. Distribution of the estimators for autoregressive time series with a unit root. JJournal Am. Stat. Assoc. 1979;74:427–431. [Google Scholar]
- Diebold F.X., Yilmaz K. Better to give than to receive: predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012;28(1):57–66. [Google Scholar]
- El Hedi Arouri M., Jouini J., Nguyen D.K. Volatility spillovers between oil prices and stock sector returns: implications for portfolio management. J. Int. Money Finance. 2011 doi: 10.1016/j.jimonfin.2011.07.008. [DOI] [Google Scholar]
- El Hedi Arouri M., Lahiani A., Nguyen D.K. World gold prices and stock returns in China: insights for hedging and diversification strategies. Econ. Modell. 2015;44:273–282. doi: 10.1016/j.econmod.2014.10.030. [DOI] [Google Scholar]
- Engle R. Dynamic conditional correlation: a simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002;20:339–350. doi: 10.1198/073500102288618487. [DOI] [Google Scholar]
- Engle R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica. 1982;50:987. doi: 10.2307/1912773. [DOI] [Google Scholar]
- Engle R.F., Kroner K.F. 1995. Multivariate Simultaneous Generalized Arch. Econom. Theory. [DOI] [Google Scholar]
- Erdem O. Freedom and stock market performance during Covid-19 outbreak. Finance Res. Lett. 2020;36 doi: 10.1016/j.frl.2020.101671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farid S., Kayani G.M., Naeem M.A., Shahzad S.J.H. Intraday volatility transmission among precious metals, energy and stocks during the COVID-19 pandemic. Resour. Pol. 2021;72 doi: 10.1016/j.resourpol.2021.102101. [DOI] [Google Scholar]
- Gupta R., Shahzad S.J.H., Sheng X., Subramaniam S. The role of oil and risk shocks in the high‐frequency movements of the term structure of interest rates: evidence from the US Treasury market. Int. J. Finance Econ. 2021 [Google Scholar]
- Jorion P. third ed. McGraw-Hill; 2007. Philippe Jorion: Value at Risk – the New Benchmark for Managing Financial Risk. [Google Scholar]
- Jorion P. Risk2: measuring the risk in value at risk. Financ. Anal. J. 1996 doi: 10.2469/faj.v52.n6.2039. [DOI] [Google Scholar]
- Kang S.H., Lee J.W. The network connectedness of volatility spillovers across global futures markets. Phys. A Stat. Mech. its Appl. 2019;526 doi: 10.1016/j.physa.2019.03.121. [DOI] [Google Scholar]
- Kang S.H., McIver R., Yoon S.M. Dynamic spillover effects among crude oil, precious metal, and agricultural commodity futures markets. Energy Econ. 2017;62:19–32. doi: 10.1016/j.eneco.2016.12.011. [DOI] [Google Scholar]
- Khalfaoui R., Sarwar S., Tiwari A.K. Analysing volatility spillover between the oil market and the stock market in oil-importing and oil-exporting countries: implications on portfolio management. Resour. Pol. 2019;62:22–32. doi: 10.1016/j.resourpol.2019.03.004. [DOI] [Google Scholar]
- Kinateder H., Campbell R., Choudhury T. Safe haven in GFC versus COVID-19: 100 turbulent days in the financial markets. Finance Res. Lett. 2021;101951 doi: 10.1016/j.frl.2021.101951. [DOI] [Google Scholar]
- Kroner K.F., Ng V.K. Modeling asymmetric comovements of asset returns. Rev. Financ. Stud. 1998 doi: 10.1093/rfs/11.4.817. [DOI] [Google Scholar]
- Kroner K.F., Sultan J. Time-varying distributions and dynamic hedging with foreign currency futures. J. Financ. Quant. Anal. 1993 doi: 10.2307/2331164. [DOI] [Google Scholar]
- Kupiec P.H. Techniques for verifying the accuracy of risk measurement models. J. Deriv. 1995 doi: 10.3905/jod.1995.407942. [DOI] [Google Scholar]
- Malz A.M. John Wiley & Sons; 2011. Financial Risk Management: Models, History, and Institutions. [Google Scholar]
- Mensi W., Beljid M., Boubaker A., Managi S. Correlations and volatility spillovers across commodity and stock markets: linking energies, food, and gold. Econ. Modell. 2013;32:15–22. doi: 10.1016/j.econmod.2013.01.023. [DOI] [Google Scholar]
- Mensi W., Hammoudeh S., Kang S.H. Precious metals, cereal, oil and stock market linkages and portfolio risk management: evidence from Saudi Arabia. Econ. Modell. 2015;51:340–358. doi: 10.1016/j.econmod.2015.08.005. [DOI] [Google Scholar]
- Mensi W., Hammoudeh S., Nguyen D.K., Kang S.H. Global financial crisis and spillover effects among the U.S. and BRICS stock markets. Int. Rev. Econ. Finance. 2016;42:257–276. doi: 10.1016/j.iref.2015.11.005. [DOI] [Google Scholar]
- Mensi W., Shafiullah M., Vo X.V., Kang S.H. Volatility spillovers between strategic commodity futures and stock markets and portfolio implications: evidence from developed and emerging economies. Resour. Pol. 2021;71 doi: 10.1016/j.resourpol.2021.102002. [DOI] [Google Scholar]
- Narayan P.K., Devpura N., Wang H. Japanese currency and stock market—what happened during the COVID-19 pandemic? Econ. Anal. Pol. 2020;68:191–198. doi: 10.1016/j.eap.2020.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson D.B. Conditional heteroskedasticity in asset returns: a new approach. Econometrica. 1991 doi: 10.2307/2938260. [DOI] [Google Scholar]
- Nguyen D.T., Phan D.H.B., Ming T.C., Nguyen V.K.L. An assessment of how COVID-19 changed the global equity market. Econ. Anal. Pol. 2021;69:480–491. doi: 10.1016/j.eap.2021.01.003. [DOI] [Google Scholar]
- Okorie D.I., Lin B. Stock markets and the COVID-19 fractal contagion effects. Finance Res. Lett. 2021;38 doi: 10.1016/j.frl.2020.101640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reboredo J.C. Is gold a safe haven or a hedge for the US dollar? Implications for risk management. J. Bank. Finance. 2013;37:2665–2676. doi: 10.1016/j.jbankfin.2013.03.020. [DOI] [Google Scholar]
- Sadorsky P. Modeling volatility and correlations between emerging market stock prices and the prices of copper, oil and wheat. Energy Econ. 2014;43:72–81. doi: 10.1016/j.eneco.2014.02.014. [DOI] [Google Scholar]
- Sadorsky P. Correlations and volatility spillovers between oil prices and the stock prices of clean energy and technology companies. Energy Econ. 2012 doi: 10.1016/j.eneco.2011.03.006. [DOI] [Google Scholar]
- Salisu A.A., Ebuh G.U., Usman N. Revisiting oil-stock nexus during COVID-19 pandemic: some preliminary results. Int. Rev. Econ. Finance. 2020;69:280–294. doi: 10.1016/j.iref.2020.06.023. [DOI] [Google Scholar]
- Sampid M.G., Hasim H.M. Estimating value-at-risk using a multivariate copula-based volatility model: evidence from European banks. Int. Econ. 2018;156:175–192. [Google Scholar]
- Shehzad K., Bilgili F., Zaman U., Kocak E., Kuskaya S. Is gold favourable than bitcoin during the COVID-19 outbreak? Comparative analysis through wavelet approach. Resour. Pol. 2021;73 doi: 10.1016/j.resourpol.2021.102163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shehzad K., Xiaoxing L., Arif M., Rehman K.U. Investigating the psychology of financial markets during COVID-19 era. A Case Study of the US and European Markets. 2020;11:1–13. doi: 10.3389/fpsyg.2020.01924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shehzad K., Xiaoxing L., Kazouz H. COVID-19's disasters are perilous than Global Financial Crisis: a rumor or fact? Finance Res. Lett. 2020;101669 doi: 10.1016/j.frl.2020.101669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shehzad K., Zaman U., Liu X., Jarosław G. 2021. Examining the Asymmetric Impact of COVID-19 Pandemic and Global Financial Crisis on Dow Jones and Oil Price Shock. [Google Scholar]
- Sikhosana A., Aye G.C. Asymmetric volatility transmission between the real exchange rate and stock returns in South Africa. Econ. Anal. Pol. 2018;60:1–8. doi: 10.1016/j.eap.2018.08.002. [DOI] [Google Scholar]
- Śmiech S., Papież M. In search of hedges and safe havens: revisiting the relations between gold and oil in the rolling regression framework. Finance Res. Lett. 2017;20:238–244. doi: 10.1016/j.frl.2016.10.006. [DOI] [Google Scholar]
- Vo X.V., Hung N.T. Directional spillover effects and time-frequency nexus between oil, gold and stock markets: evidence from pre and during COVID-19 outbreak. Int. Rev. Financ. Anal. 2021;76 doi: 10.1016/j.irfa.2021.101730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen F., Cao J., Liu Z., Wang X. International Review of Financial Analysis Dynamic volatility spillovers and investment strategies between the Chinese stock market and commodity markets. Int. Rev. Financ. Anal. 2021;76 doi: 10.1016/j.irfa.2021.101772. [DOI] [Google Scholar]