A Numerical Scheme for Anisotropic Reactive Nonlinear Viscoelasticity

Abstract

Reactive viscoelasticity is a theoretical framework based on the theory of reactive constrained mixtures that encompasses nonlinear viscoelastic responses. It models a viscoelastic solid as a mixture of strong and weak bonds that maintain the cohesiveness of the molecular constituents of the solid matter. Strong bonds impart the elastic response while weak bonds break and reform into a stress-free state in response to loading. The process of bonds breaking and reforming is modeled as a reaction where loaded bonds are the reactants and bonds reformed into a stress-free state are the products of a reaction. The reaction is triggered by the evolving state of loading. The state of stress in strong bonds is a function of the total strain in the material, whereas the state of stress in weak bonds is based on the state of strain relative to the time that these bonds were reformed. This study introduces two important practical contributions to the reactive nonlinear viscoelasticity framework: (1) normally, the evaluation of the stress tensor involves taking a summation over a continually increasing number of weak bond generations, which is poorly suited for a computational scheme. Therefore, this study presents an effective numerical scheme for evaluating the strain energy density, the Cauchy stress, and spatial elasticity tensors of reactive viscoelastic materials. (2) We provide the conditions for satisfying frame indifference for anisotropic nonlinear viscoelasticity, including for tension-bearing fiber models. Code verifications and model validations against experimental data provide evidence in support of this updated formulation.

1 Introduction

Reactive viscoelasticity is a theoretical framework that can model nonlinear viscoelasticity [1,2], derived using concepts introduced in the theory of reactive constrained mixtures [3,4], and sharing some qualitative analogies with the earlier work of Wineman and Rajagopal [5,6]. It models a viscoelastic solid as a mixture of strong and weak bonds that maintain the cohesiveness of the molecular constituents of solid matter. Strong bonds impart the elastic response while weak bonds break and reform into a stress-free state in response to loading. This formulation is consistent with the molecular interpretation of viscoelasticity first proposed by Tobolsky [7,8]. The process of bonds breaking and reforming is modeled as a reaction where loaded bonds are the reactants and bonds reformed into a stress-free state are the products of a reaction. The reaction is triggered by the evolving state of deformation and reaction kinetics are governed by a reduced relaxation function whose temporal evolution may depend on the state of strain at the time of changing deformation. The state of stress in strong bonds is a function of the total strain in the material, whereas the state of stress in weak bonds is based on the state of strain relative to the time that weak bonds were reformed. The residual dissipation constraint imposed by the axiom of entropy inequality is satisfied automatically by the adoption of relaxation functions that decrease monotonically with time.

Nonlinear viscoelasticity is characterized by the dependence of the viscoelastic relaxation time on the state of strain. This response stands in contrast to quasi-linear viscoelasticity [9–11] where the elastic response may be nonlinear but the relaxation time remains invariant to the state of strain. Experimentally, nonlinear viscoelastic responses have been reported in biological soft tissues such as articular cartilage [12], ligament [13], tendon [14], intervertebral disk [15], and aortic wall [16], among others. In addition to reactive viscoelasticity, theoretical approaches to modeling nonlinear viscoelasticity have been proposed by various investigators, most notably in the work of Vanderby and coworkers [17–20], Reese and Govindjee [21], Liu et al. [22], and Amabili et al. [16].

Soft tissue damage is an important topic of investigation in biomechanics, which is often complicated by the nonlinear nature of a tissue's viscoelastic response. Damage mechanics in soft tissues may be formulated using theoretical frameworks that relate damage to intrinsic material behavior, most notably the material's strain energy density or scalar invariants related to it [23,24]. Therefore, among the various theoretical frameworks available for modeling nonlinear viscoelasticity it may be more beneficial to employ those that provide explicit expressions for the strain energy density [1,21,22]. Even among those, some are limited to modeling isotropic materials [21], thereby limiting their applicability to the wider range of material behaviors found in soft tissue mechanics. Thus, in practice, constrained reactive mixture theory is currently one of the few frameworks that have the versatility to model the nonlinear viscoelasticity of anisotropic biological soft tissues, with potential extension to damage mechanics.

Whereas efficient numerical methods have been presented before for quasi-linear viscoelasticity with an exponential relaxation function [25,26], no standard scheme exists for efficient numerical computation of nonlinear viscoelastic responses, or quasi-linear viscoelasticity with nonexponential relaxation functions. In our reactive nonlinear viscoelasticity framework, the evaluation of the strain energy density, stress, and elasticity tensors involves taking a summation over a number of weak bond generations that tracks with the number of time steps in an analysis, producing increasingly inefficient calculations as time increases. To address this limitation, this study presents an improved numerical scheme for limiting the number of generations needed to evaluate the strain energy density, and the Cauchy stress and spatial elasticity tensors of reactive viscoelastic materials.

A review of the governing equations of reactive nonlinear viscoelasticity is first provided, updated to enforce frame indifference [27], followed by descriptions of a basic and an improved numerical scheme for calculating the response of such materials. Then we provide code verification problems that ascertain the accurate calculation of the responses in representative problems, followed by a validation of models against representative experimental data obtained from prior experimental studies [12,18,28]. These validations serve to illustrate the application of nonlinear viscoelasticity to experimental measurements in biomechanics.

2 Governing Equations

2.1 Review of Reactive Viscoelasticity.

As presented in our earlier study [1], the strain energy density ${\Psi }_r$ of a reactive viscoelastic solid is given by

$${\Psi }_r(\mathbf{F}(t))={\Psi }_r^e(\mathbf{F}(t))+\sum _u{w}^u{\Psi }_0^a({\mathbf{F}}^u(t))$$ (2.1)

Here, $\mathbf{F}(t)$ is the observable deformation gradient at the current time t, and t^u represents the time t when all currently reformed (nonbreaking) weak bonds break and start reforming into a stress-free state; we refer to it as bond generation u, with $-\infty <t^u\le t$. The deformation gradient ${\mathbf{F}}^u(t)$ of generation u is a suitably chosen deformation gradient relative to the time that $u-$ generation bonds are reformed, based on a constitutive modeling assumption. The function ${\Psi }_0^a$ in Eq. (2.1) represents the strain energy density of solid matter associated with weak bonds, whereas ${\Psi }_r^e$ is that of strong (elastic) bonds. The mass fraction w^u of each weak bond generation u increases from generation u to the subsequent generation v as those bonds are reforming in a stress-free state; this increase takes place during the time interval $t^u\le t<t^v$. In particular, at time t^u, ${\mathbf{F}}^u(t^u)$ must be a proper orthogonal tensor in order to satisfy the stress-free reformation of weak bonds, ${\Psi }_0^a({\mathbf{F}}^u(t^u))=0$. In our earlier study [1] we had proposed that ${\mathbf{F}}^u(t)=\mathbf{F}(t)·{\mathbf{F}}^{-1}(t^u)$, which satisfies ${\mathbf{F}}^u(t^u)=\mathbf{I}$ where I is the identity tensor. As presented in Sec. 2.1.1, we revise our formulation of ${\mathbf{F}}^u(t)$ to properly enforce frame indifference based on concepts introduced in our more recent studies [29,30].

Loading that takes place at generation v leads to a subsequent decay of w^u with time $t\ge t^v$ due to the evolving bond-breaking-and-reforming reaction, as governed by a user-defined reduced relaxation function $g(\mathbf{F}(t^v),t-t^v)$ for $t\ge t^v$. By definition, the reduced relaxation function must satisfy $\underset{t\to 0}{\lim }g(\mathbf{F},t)=1$, whereas $\underset{t\to \infty }{\lim }g(\mathbf{F},t)=0$. To accommodate nonlinear viscoelasticity this relaxation function may depend on some suitable measure of the state of strain at the time of bond breaking, as embodied in the dependence of g on $\mathbf{F}(t^v)$. The general recursive relation for the bond mass fractions w^u is

$$\begin{array}{c}{w}^u(t)=\{\begin{array}{cc}0& t<t^u\\ f^u(t)& t^u\le t<t^v\\ f^u(t^v)g(\mathbf{F}(t^v),t-t^v)& t\ge t^v\end{array}\\ f^u(t)=1-\sum _{\gamma <u}{w}^{\gamma }(t)\end{array}$$ (2.2)

In this expression, $f^u(t)$ represents the mass fraction of all past generations of weak bonds which have reformed in a stress-free state in the time interval $t^u\le t<t^v$, and which start breaking at t^v. This recursive relation starts with the earliest generation $u\to -\infty$, which is at rest (no deformation). In particular, the right stretch tensor U satisfies $\mathbf{U}(-\infty )=\mathbf{I}$; U is also the right stretch tensor of the oldest generation, ${\mathbf{U}}^{-\infty }(t)=\mathbf{U}(t)$, while $f^{-\infty }(t)=1$ since no weak bonds have broken before the initiation of loading. If the material is instantaneously loaded at $t^v=0^{+}$, it follows that $w^{-\infty }(t)=g(\mathbf{F}(0^{+}),t-0^{+})$ for t > 0. Thus, the bond mass fraction $w^{-\infty }(t)$ is equal to the relaxation function g for the given amount of prescribed strain inferred from $\mathbf{F}(0^{+})$, providing a means to formulate a constitutive model for $g(\mathbf{F}(t^v),t-t^v)$ from experimental measurements of the relaxation response to an instantaneous deformation at time t^v. Regardless of the choice of a constitutive model for g, the weak bond mass fractions in Eq. (2.2) satisfy

$$\sum _u{w}^u(t)=1$$ (2.3)

over all generations u, as required by the axiom of mass conservation for the mixture. A numerical illustration of the weak bond mass fractions $w^u(t)$ and the function $f^u(t^v)$ in a finite deformation stress-relaxation analysis is provided later in this presentation (Fig. 5(a)).

Fig. 5.

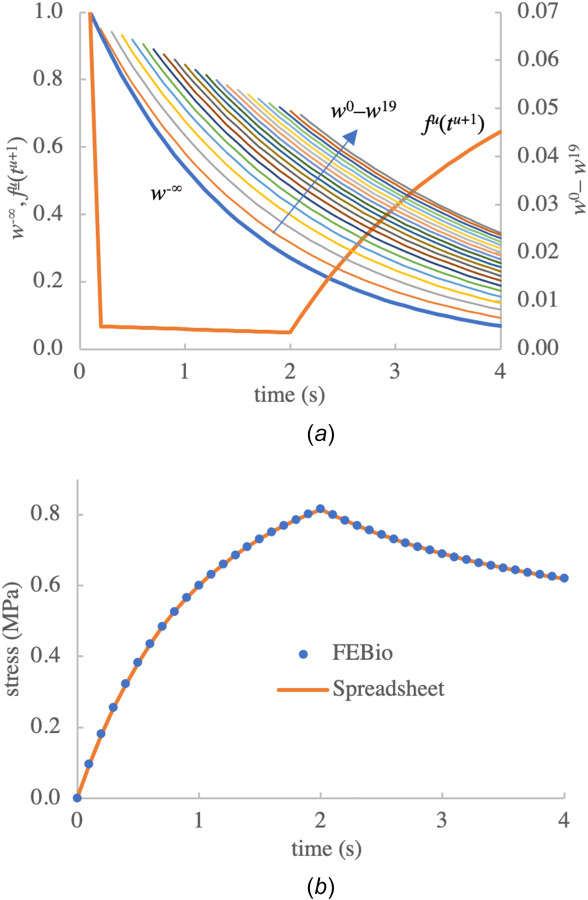
(a) Spreadsheet calculation of bond mass fractions $w^u(t_{n+1})$ for $u=-\infty ,1,2,\dots ,19$ for the stress-relaxation problem outlined in Sec. 3.1.2. Uniform time increments $t_{n+1}$ were used in this analysis ( $0\le n<40$), in the range $0\le t\le 4$. The deformation of this material was increased linearly until time t = 2. $f^u(t^{u+1})$ represents the mass fraction of previously broken weak bonds which have reformed in a stress-free state and start breaking at $t^{u+1}$. Since weak bond mass fractions w^u for $u=0-19$ span a smaller range than $w^{-\infty }$ and $f^u(t^{u+1})$, they are plotted on separate scales. (b) Verification of febio implementation of the stress response in reactive nonlinear viscoelasticity against calculations performed in the spreadsheet.

Example 1. In the special case of quasi-linear reactive viscoelasticity with an exponential reduced relaxation function, the function g has the form $g(t)=e^{-t/\tau }$, where τ is the time constant for the relaxation; this relaxation function is thus independent of the strain. Substituting this expression in Eq. (2.2) simplifies the recursive relation to

$$w^u\left(t\right)=\{\begin{array}{cc}0& t\le t^u\\ 1-e^{-\frac{t-t^u}{\tau }}& t^u\le t<t^v\\ e^{-\frac{t-t^v}{\tau }}-e^{-\frac{t-t^u}{\tau }}& t^u<t^v\le t\end{array}$$ (2.4)

as reported in our earlier study [1].

2.1.1 Frame Indifference and Material Symmetry.

In our recent study [30] on constrained reactive mixtures, we presented general arguments for enforcing frame indifference in these types of mixtures. In this section, we present the specific constraints needed to satisfy frame indifference for reactive viscoelasticity and we show that these constraints remain valid for any material symmetry. We also examine the special case of fibrous materials that can only sustain tensile stresses, as their strain origin may evolve with each generation u.

The reference configuration ${\mathbf{X}}^u$ of generation u in a constrained mixture of solids whose motion is $\mathit{\chi }$ is associated with the deformation gradient ${\mathbf{F}}^u=\partial \mathit{\chi }/\partial {\mathbf{X}}^u$. Since this relative deformation gradient is evaluated based on a constitutive model, neither ${\mathbf{F}}^u$ nor ${\mathbf{X}}^u$ are observable variables [30]. Let u = s denote the master constituent, with deformation gradient ${\mathbf{F}}^s=\partial \mathit{\chi }/\partial {\mathbf{X}}^s$, where ${\mathbf{F}}^s\equiv \mathbf{F}$ in the notation of Sec. 2.1. These deformation gradients are related by

$${\mathbf{F}}^s=\frac{\partial \mathit{\chi }}{\partial {\mathbf{X}}^s}=\frac{\partial \mathit{\chi }}{\partial {\mathbf{X}}^u}·\frac{\partial {\mathbf{X}}^u}{\partial {\mathbf{X}}^s}={\mathbf{F}}^u·{\mathbf{F}}^{us}$$ (2.5)

where ${\mathbf{F}}^{us}=\partial {\mathbf{X}}^u/\partial {\mathbf{X}}^s$ is a time-invariant mapping between ${\mathbf{X}}^u$ and ${\mathbf{X}}^s$. This time invariance follows from the assumption that mixture constituents are constrained to share the same velocity.

To examine frame indifference we first recognize that the transformation of the deformation gradient ${\mathbf{F}}^s$ by an orthogonal transformation Q is

$${\mathbf{F}}^{s*}=\mathbf{Q}·{\mathbf{F}}^s$$ (2.6)

from which it follows that the right Cauchy–Green tensor ${\mathbf{C}}^s={({\mathbf{F}}^s)}^{\mathrm{T}}·{\mathbf{F}}^s$ satisfies:

$${\mathbf{C}}^{s*}={({\mathbf{F}}^{s*})}^{\mathrm{T}}·{\mathbf{F}}^{s*}={({\mathbf{F}}^s)}^{\mathrm{T}}·{\mathbf{Q}}^T·\mathbf{Q}·{\mathbf{F}}^s={\mathbf{C}}^s$$ (2.7)

Thus, the material measure of strain ${\mathbf{C}}^s$ (and its associated right stretch tensor ${\mathbf{U}}^s$, where ${\mathbf{C}}^s={({\mathbf{U}}^s)}^2$) is invariant to Q. Similarly, the transformation of ${\mathbf{F}}^u$ by Q is ${\mathbf{F}}^{u*}=\mathbf{Q}·{\mathbf{F}}^u$ so that the associated right Cauchy–Green tensors satisfy ${\mathbf{C}}^{u*}={\mathbf{C}}^u$, implying that ${\mathbf{C}}^u$ (and its associated right-stretch tensor ${\mathbf{U}}^u$) is invariant to Q. Accordingly, the expression of Eq. (2.5) satisfies frame indifference if ${\mathbf{F}}^{us*}={\mathbf{F}}^{us}$ is invariant, implying that it maps a material vector into another material vector [27]. Therefore, a constitutive model for ${\mathbf{F}}^{us}$ must not violate this invariance.

In general, using the polar decomposition theorem we let

$${\mathbf{F}}^s={\mathbf{R}}^s·{\mathbf{U}}^s\hspace{0.17em},{\mathbf{F}}^u={\mathbf{R}}^u·{\mathbf{U}}^u$$ (2.8)

so that Eq. (2.5) implies

$${\mathbf{F}}^{us}={({\mathbf{U}}^u)}^{-1}·\mathbf{R}·{\mathbf{U}}^s\hspace{0.17em},\mathbf{R}={({\mathbf{R}}^u)}^{\mathrm{T}}·{\mathbf{R}}^s$$ (2.9)

The rotations ${\mathbf{R}}^s$ and ${\mathbf{R}}^u$ transform according to ${\mathbf{R}}^{s*}=\mathbf{Q}·{\mathbf{R}}^s$ and ${\mathbf{R}}^{u*}=\mathbf{Q}·{\mathbf{R}}^u$ [27]. Based on Eq. (2.9) it follows that the proper orthogonal tensor R, which represents a relative rotation, is necessarily invariant to transformations Q, thus ${\mathbf{R}}^{*}=\mathbf{R}$, implying that ${\mathbf{F}}^{us}$ in Eq. (2.9) is also invariant to Q. This conclusion derives from our constitutive assumption that ${\mathbf{F}}^u$ actually represents a deformation gradient that can be decomposed according to the polar decomposition theorem, as presented in Eq. (2.8).

In reactive viscoelasticity, we adopt the constitutive assumption that ${\mathbf{U}}^u=\mathbf{I}$, thus ${\mathbf{F}}^u={\mathbf{R}}^u$, at time t^u when generation u must come into existence in a stress-free state. According to Eq. (2.9), at time t^u we have

$${\mathbf{F}}^{us}=\mathbf{R}(t^u)·{\mathbf{U}}^s(t^u)$$ (2.10)

Then, at subsequent times we have ${\mathbf{F}}^u(t)={\mathbf{F}}^s(t)·{({\mathbf{F}}^{us})}^{-1}$. In order to satisfy the invariance ${\mathbf{R}}^{*}=\mathbf{R}$ while also requiring R to be a proper orthogonal transformation, we may select

$$\mathbf{R}(t^u)=\mathbf{I}\hspace{0.17em},{\mathbf{F}}^{us}={\mathbf{U}}^s(t^u)$$ (2.11)

Since this choice is invariant to any transformation Q it remains valid for all material symmetries, ranging from triclinic to isotropic. Therefore, reverting to our earlier notation where ${\mathbf{F}}^s\equiv \mathbf{F}$, our revised constitutive model for the relative deformation gradient in reactive viscoelasticity is

$${\mathbf{F}}^u(t)=\mathbf{F}(t)·{\mathbf{U}}^{-1}(t^u)$$ (2.12)

where U is the right stretch tensor of F.

2.1.2 Tension-Bearing Fiber Models.

There remains one special case that must be addressed with a separate choice for $\mathbf{R}(t^u)$. In biomechanics, we often find it convenient to model fibrous or fibrillar materials using one-dimensional fibers that can only sustain tension. Typically, such fibers are represented with a strain energy density function

$${\Psi }_0(\mathbf{C})=H(I_n-1){\Psi }_n(I_n)\hspace{0.17em},I_n={\mathbf{n}}_r·\mathbf{C}·{\mathbf{n}}_r$$ (2.13)

where ${\mathbf{n}}_r$ is the unit vector along the fiber in its reference configuration, and I_n is the square of the stretch ratio along the fiber. The Heaviside unit step function $H(I_n-1)$ in Eq. (2.13) ensures that the fiber contributes strain energy only when it is under tension (I_n > 1); thus, the constitutive model ${\Psi }_n(I_n)$ for the tensile response of the fiber must reduce to zero when I_n = 1.

In the reactive viscoelasticity framework presented in this study, each generation u comes into existence at time t^u, thus the constitutive model for the fiber must account for the fact that the fiber orientation is no longer along ${\mathbf{n}}_r$ at time t^u. Indeed, the total weak bond free energy in a reactive viscoelastic material now reduces to

$$\begin{array}{c}\sum _u{w}^u{\Psi }_0^a({\mathbf{F}}^u(t))=\sum _u{w}^{u}H(I_n^u-1){\Psi }_n(I_n^u)\\ I_n^u={\mathbf{n}}_r^u·{\mathbf{C}}^u·{\mathbf{n}}_r^u\end{array}$$ (2.14)

where ${\mathbf{n}}_r^u$ is the fiber orientation at time t^u and $I_n^u$ is the square of the stretch ratio of the fiber relative to its reference configuration at time t^u. Recall that the elemental line along ${\mathbf{n}}_r$ gets transformed in the material frame at any time t by U to ${\lambda }_n\mathbf{n}=\mathbf{U}·{\mathbf{n}}_r$ where

$${\lambda }_n=\sqrt{{\mathbf{n}}_r·\mathbf{C}·{\mathbf{n}}_r}\hspace{0.17em},\mathbf{n}=\frac{1}{{\lambda }_n}\mathbf{U}·{\mathbf{n}}_r$$ (2.15)

At time t^u when generation u forms in a stress-free state, it follows that the fiber material is now based on the orientation ${\mathbf{n}}_r^u\equiv \mathbf{n}(t^u)$, evaluated using $\mathbf{U}(t^u)$ as shown in Eq. (2.15). In general, ${\mathbf{n}}_r^u$ and ${\mathbf{n}}_r$ need not be collinear, therefore we can find the rotation $\mathbf{R}(t^u)$ that transforms ${\mathbf{n}}_r^u$ to ${\mathbf{n}}_r$

$$\mathbf{R}(t^u)=(1-\text{cos}\hspace{0.17em}\gamma )\mathbf{m}\otimes \mathbf{m}+\text{cos}\hspace{0.17em}\gamma \mathbf{I}-\mathbb{E}·(\text{sin}\hspace{0.17em}\gamma \hspace{0.17em}\mathbf{m})$$ (2.16)

with $\text{cos}\hspace{0.17em}\gamma ={\mathbf{n}}_r^u·{\mathbf{n}}_r$ and $\text{sin}\hspace{0.17em}\gamma \hspace{0.17em}\mathbf{m}={\mathbf{n}}_r^u\times {\mathbf{n}}_r$. In this expression, m is the unit vector along the rotation axis, γ is the rotation angle about the axis, and $\mathbb{E}$ represents the (pseudo-)third-order permutation tensor whose components are equal to the permutation symbol ${\epsilon }_{\mathit{ijk}}$. Thus, $-\mathbb{E}·\mathit{\omega }$ is the antisymmetric second-order tensor $\Omega$ whose dual vector is $\mathit{\omega }$, from which it follows that $\Omega ·\mathbf{a}=\mathit{\omega }\times \mathbf{a}$ for any vector a. Here again, since $\mathbf{R}(t^u)$ represents a relative rotation between the material vectors ${\mathbf{n}}_r^u$ and ${\mathbf{n}}_r$, it is invariant to any transformation Q.

In practice it is not necessary to evaluate $\mathbf{R}(t^u)$ in Eq. (2.9) for each generation u of each fiber in a material model; instead one can reset the fiber direction from ${\mathbf{n}}_r$ to ${\mathbf{n}}_r^u=\mathbf{n}(t^u)$, where n is evaluated as per Eq. (2.15), requiring only the storage of $\mathbf{U}(t^u)$ for each generation u. This scheme may also be used with continuous fiber distributions [31].

2.1.3 Stress and Elasticity Tensors.

Given ${\Psi }_r$ in Eq. (2.1), the stress may be evaluated from the strain energy density using standard relations of hyperelasticity. In particular, the Cauchy stress $\mathit{\sigma }$ and spatial elasticity tensor $\mathcal{C}$ are evaluated from

$\begin{array}{c}\mathit{\sigma }=2J^{-1}\mathbf{F}·\frac{\partial {\Psi }_r}{\partial \mathbf{C}}·{\mathbf{F}}^T=\frac{2}{J}\frac{\partial {\Psi }_r}{\partial \mathbf{C}}:\left({\mathbf{F}}^T\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}{\mathbf{F}}^T\right)\\ \mathcal{C}=\frac{4}{J}\left(\mathbf{F}\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}\mathbf{F}\right):\frac{{\partial }^2{\Psi }_r}{\partial \mathbf{C}\partial \mathbf{C}}:\left({\mathbf{F}}^T\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}{\mathbf{F}}^T\right)\end{array}$ (2.17)

where $\mathbf{C}={\mathbf{F}}^T·\mathbf{F}$ is the right Cauchy–Green tensor, $J=\det \mathbf{F}$, and $\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}$ is the dyadic product of tensors that yields Cartesian components ${(\mathbf{A}\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}\mathbf{B})}_{\mathit{ijkl}}=A_{ik}{B}_{jl}$ for arbitrary second-order tensors A and B. In the expression for ${\Psi }_r$ in Eq. (2.1), ${\Psi }_r^e$ depends on F (and thus on C), facilitating the evaluation of the corresponding strong bond contributions to the stress, ${\mathit{\sigma }}^e$, and elasticity tensor, ${\mathcal{C}}^e$, using Eq. (2.17). However, the strain energy density of weak bonds ${\Psi }_0^a$ is evaluated for each generation u using the relative deformation gradient in Eq. (2.12). Using the chain rule of differentiation

$$\begin{array}{c}\frac{\partial {\Psi }_0^a}{\partial \mathbf{C}}=\frac{\partial {\Psi }_0^a}{\partial {\mathbf{C}}^u}:\left({\mathbf{U}}^{-1}\left(t^u\right)\odot {\mathbf{U}}^{-1}\left(t^u\right)\right)\\ \frac{{\partial }^2{\Psi }_0^a}{\partial \mathbf{C}\partial \mathbf{C}}=\left({\mathbf{U}}^{-1}\left(t^u\right)\odot {\mathbf{U}}^{-1}\left(t^u\right)\right):\frac{{\partial }^2{\Psi }_0^a}{\partial {\mathbf{C}}^u\partial {\mathbf{C}}^u}\\ :\left({\mathbf{U}}^{-1}\left(t^u\right)\odot {\mathbf{U}}^{-1}\left(t^u\right)\right)\end{array}$$ (2.18)

where we used ${\mathbf{C}}^u={({\mathbf{F}}^u)}^{\mathrm{T}}·{\mathbf{F}}^u={\mathbf{U}}^{-1}(t^u)·\mathbf{C}·{\mathbf{U}}^{-1}(t^u)$ and the dyadic product of tensors $\odot$ that yields Cartesian components ${(\mathbf{A}\odot \mathbf{B})}_{\mathit{ijkl}}=\frac{1}{2}(A_{ik}{B}_{jl}+A_{il}{B}_{jk})$. Substituting these relations into Eq. (2.17) and making use of the identities $(\mathbf{A}\odot \mathbf{A}):(\mathbf{B}\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}\mathbf{B})=(\mathbf{A}·\mathbf{B})\odot (\mathbf{A}·\mathbf{B})$ and $(\mathbf{B}\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}\mathbf{B}):(\mathbf{A}\odot \mathbf{A})=(\mathbf{B}·\mathbf{A})\odot (\mathbf{B}·\mathbf{A})$ shows that the contributions of ${\Psi }_0^a({\mathbf{F}}^u)$ to $\mathit{\sigma }$ and $\mathcal{C}$ take the form

$$\begin{array}{c}\frac{2}{J}\mathbf{F}·\frac{\partial {\Psi }_0^a}{\partial \mathbf{C}}·{\mathbf{F}}^T=J^{-1}\left(t^u\right)\frac{2}{J^u}{\mathbf{F}}^u·\frac{\partial {\Psi }_0^a}{\partial {\mathbf{C}}^u}·{\left({\mathbf{F}}^u\right)}^T\\ \equiv J^{-1}\left(t^u\right){\mathit{\sigma }}_0^a\left({\mathbf{F}}^u\right)\hspace{0.17em}\\ \frac{4}{J}\left(\mathbf{F}\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}\mathbf{F}\right):\frac{{\partial }^2{\Psi }_0^a}{\partial \mathbf{C}\partial \mathbf{C}}:\left({\mathbf{F}}^T\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}{\mathbf{F}}^T\right)=J^{-1}\left(t^u\right)\frac{4}{J^u}\left({\mathbf{F}}^u\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}{\mathbf{F}}^u\right)\\ :\frac{{\partial }^2{\Psi }_0^a}{\partial {\mathbf{C}}^u\partial {\mathbf{C}}^u}:\left({\left({\mathbf{F}}^u\right)}^{\mathrm{T}}\hspace{0.17em}\mathrm{\oslash }\hspace{0.17em}{\left({\mathbf{F}}^u\right)}^{\mathrm{T}}\right)\\ \equiv J^{-1}\left(t^u\right){\mathcal{C}}_0^a\left({\mathbf{F}}^u\right)\end{array}$$ (2.19)

In other words, the stress and elasticity tensors for the weak bond generations may be evaluated from standard hyperelasticity relations for ${\Psi }_0^a({\mathbf{F}}^u)$, but their respective contributions to $\mathit{\sigma }$ and $\mathcal{C}$ need to be scaled by $J^{-1}(t^u)$. Therefore,

$\begin{array}{c}\mathit{\sigma }\left(\mathbf{F}\right)={\mathit{\sigma }}^e\left(\mathbf{F}\right)+\sum _u{w}^u{J}^{-1}\left(t^u\right){\mathit{\sigma }}_0^a\left({\mathbf{F}}^u\right)\hspace{0.17em}\\ \mathcal{C}\mathbf{\left(}\mathbf{F}\mathbf{\right)}={\mathcal{C}}^e\left(\mathbf{F}\right)+\sum _u{w}^u{J}^{-1}\left(t^u\right){\mathcal{C}}_0^a\left({\mathbf{F}}^u\right)\end{array}$ (2.20)

2.1.4 Thermodynamics.

The thermodynamics of constrained reactive mixtures was presented in our earlier studies [4,30]. Under isothermal conditions, the residual dissipation statement emerging from the Clausius–Duhem inequality takes the form

$$\sum _u{\widehat{\rho }}_r^u{\mu }^u\le 0\hspace{0.17em}$$ (2.21)

where ${\mu }^u=\partial {\Psi }_r/\partial {\rho }_r^u$ is the chemical potential of the $u-$ generation, ${\rho }_r^u$ is the referential apparent density of solid matter associated with weak bonds of that generation, and ${\widehat{\rho }}_r^u$ is the referential mass density supply for the bond-breaking reaction of that generation. As shown previously [1], ${\rho }_r^u$ is related to the bond mass fraction w^u via ${\rho }_r^u/{\rho }_0^a=w^u$, where ${\rho }_0^a$ is the referential mass density of solid matter associated with all weak bonds of a material (which remains constant in the absence of damage). Based on the axiom of mass balance, the referential mass density supply satisfies ${\widehat{\rho }}_r^u={\dot{\rho }}_r^u$, where the dot operator represents the material time derivative [4]. Substituting these relations, along with Eq. (2.1), into the residual dissipation inequality in Eq. (2.21) produces the equivalent form

$$\sum _u{\dot{w}}^u\frac{\partial {\Psi }_r}{\partial w^u}=\sum _u{\dot{w}}^u{\Psi }_0^a\left({\mathbf{F}}^u\left(t\right)\right)\le 0\hspace{0.17em}$$ (2.22)

Since the strain energy density ${\Psi }_0^a$ is always strictly positive or zero (the latter being the case during the bond reformation in the time interval $t^u\le t<t^v$), this inequality is satisfied if and only if ${\dot{w}}^u\le 0$ whenever ${\Psi }_0^a>0$, for all u. According to Eq. (2.2), this requirement is satisfied as long as the relaxation function g monotonically decreases for all times.

In fact, this thermodynamic requirement is the reason why the relaxation function $g(\mathbf{F}(t^v),t-t^v)$ evaluated for $t\ge t^v$ in Eq. (2.2) can only depend on the state of strain $\mathbf{F}(t^v)$ at the time that $u-$ generation bonds start breaking. Had g depended on an evolving $\mathbf{F}(t)$, the monotonic decrease in w^u could not be enforced unconditionally; such a dependence could also produce nonsensical negative bond mass fractions [1].

2.2 Computational Scheme

2.2.1 Basic Scheme.

The earliest generation corresponds to $u\to -\infty$. Sequential discrete generations may therefore be denoted by $u=-\infty ,0,1,2,\dots$ whose breaking-and-reforming times may be denoted by t^u starting from t⁰, which is the time that generation $u\to -\infty$ breaks and reforms. Then, the bond generation v that follows u is equivalent to u + 1 and the bond mass fractions evolve recursively as

$$\begin{array}{c}{w}^{-\infty }(t)=\{\begin{array}{cc}1& -\infty \le t<t^0\\ g(\mathbf{F}(t^0),t-t^0)& t^0\le t\end{array}\\ f^{-\infty }(t)=1\\ {\mathbf{F}}^{-\infty }(t)=\mathbf{F}(t)\\ w^0(t)=\{\begin{array}{cc}0& t<t^0\\ f^0(t)& t^0\le t<t^1\\ f^0(t^1)& \\ ·g(\mathbf{F}(t^1),t-t^1)& t^1\le t\end{array}\\ f^0(t)=1-w^{-\infty }(t)\\ {\mathbf{F}}^0(t)=\mathbf{F}(t)·{\mathbf{U}}^{-1}(t^0)\\ ⋮⋮\\ w^u(t)=\{\begin{array}{cc}0& t<t^u\\ f^u(t)& t^u\le t<t^v\\ f^u(t^v)& \\ ·g(\mathbf{F}(t^v),t-t^v)& t^v\le t\end{array}\\ f^u(t)=1-\sum _{\gamma =-\infty }^{u-1}{w}^{\gamma }(t)\\ {\mathbf{F}}^u(t)=\mathbf{F}(t)·{\mathbf{U}}^{-1}(t^u)\end{array}$$ (2.23)

These bond mass fractions can be used to evaluate the strain energy density ${\Psi }_r^a$ of weak bonds as shown in Eq. (2.1), ${\Psi }_r^a(\mathbf{F}(t))=\sum _u{w}^u{\Psi }_0^a({\mathbf{F}}^u(t))$.

Let the initial time-step in a finite element analysis be $t_0=0$, the current time-step be $t_{n+1}$ and previous time-step be t_n ( $n\ge 0$). Bond generation u = –∞ pre-exists at the start of an analysis, whereas generations $u=0,1,2,\dots$ are produced at times t^u that represent a subset of the discrete times $t_{n+1}$.

Let u = m represent the latest generation produced in an analysis, with $m=0,1,2,\dots$. Since the state of strain need not change at every time-step, whereas a change in strain triggers a new generation u, it follows that $\mathbf{F}(t_{n+1})=\mathbf{F}(t^m)$ for the latest generation, even when $t_{n+1}\ge t^m$. Generation m is created at a time t^m in a stress-free state. Until the next generation m + 1 is produced at $t^{m+1}$, the bond mass fraction $w^m(t)=f^m(t)$ is not needed in the evaluation of ${\Psi }_r^a$ since ${\mathbf{F}}^m(t_{n+1})=\mathbf{F}(t_{n+1})·{\mathbf{U}}^{-1}(t^m)=\mathbf{R}(t^m)$ and ${\Psi }_0^a({\mathbf{F}}^m(t_{n+1}))=0$ in this stress-free state. Therefore, the response of weak bonds b in Eq. (2.1) may be evaluated from

$$\begin{array}{c}{\Psi }_r^a(t_{n+1})=\sum _{u=-\infty }^{m-1}{w}^u(t_{n+1}){\Psi }_0^a({\mathbf{F}}^u(t_{n+1}))\\ t_{n+1}\ge t^m\end{array}$$ (2.24)

The mass fractions $w^u(t_{n+1})$ appearing in this summation are obtained from the recursive formula in Eq. (2.2), adapted to discretized times

$$\begin{array}{c}{w}^u(t_{n+1})=f^u(t^{u+1})g(\mathbf{F}(t^{u+1}),t_{n+1}-t^{u+1})\\ f^u(t)=1-\sum _{\gamma =-\infty }^{u-1}{w}^{\gamma }(t)\\ t_{n+1}\ge t^m\end{array}$$ (2.25)

As noted above, the mass fraction $w^m(t_{n+1})=f^m(t_{n+1})$ of the latest generation is not needed for the evaluation of ${\Psi }_r^b(t_{n+1})$, however, it is given by

$$w^m(t_{n+1})=1-\sum _{\gamma =-\infty }^{m-1}{w}^{\gamma }(t_{n+1})\hspace{0.17em}$$ (2.26)

Therefore, with the inclusion of $w^m(t_{n+1})$, the mass balance constraint of Eq. (2.3) is automatically satisfied by the recursive relation of Eq. (2.2).

Based on Eq. (2.1) this basic computational scheme requires us to store $t^{u+1},\hspace{0.17em}{f}^u(t^{u+1})$ and $\mathbf{U}(t^{u+1})$ for all generations $u=-\infty ,0,1,2,\dots$ to allow the computation of $w^u(t_{n+1})$ and ${\mathbf{F}}^u(t_{n+1})$, from which the strain energy density, stress and elasticity tensor of the breakable bonds may be evaluated. Evidently, though this scheme may use fewer bond generations m than there are time steps n, there is no upper bound on m. Therefore, this basic computational approach becomes increasingly more inefficient and memory-consuming as the number of generations increases. In Secs. 2.2.2–2.2.4, we consider three schemes that may reduce m. The pseudo-code implementing this framework is given in Algorithm 1, with Eq. (2.25) specifically implemented in Function ReformingBondMassFraction.

2.2.2 Strain Threshold for Triggering New Generation.

A new generation u can be detected by evaluating the incremental deformation gradient from the most recent weak bond generation at t^m to the current time $t_{n+1}$ as $\Delta \mathbf{F}=\mathbf{F}(t_{n+1})·{\mathbf{F}}^{-1}(t^m)$. When $\Delta \mathbf{F}$ is not a pure rotation ( $\Delta {\mathbf{F}}^T·\Delta \mathbf{F}\ne \mathbf{I}$), a new generation may be triggered at $t^u=t_{n+1}$. To restrict viscoelastic responses to specific kinematic conditions, we may also choose more specialized conditions for triggering a new generation, such as incremental deformations that are purely dilatational, or purely distortional [1]. The following triggering cases are considered:

$$\{\begin{array}{cc}\Vert \Delta \mathbf{E}\Vert >e_{\min }& \text{any}\hspace{0.17em}\text{strain}\\ \Vert \text{dev}\Delta \mathit{\eta }\Vert >e_{\min }& \text{distortional}\hspace{0.17em}\text{strain}\\ |\ln (\det \Delta \mathbf{F})|>e_{\min }& \text{dilatational}\hspace{0.17em}\text{strain}\end{array}\hspace{0.17em}$$ (2.27)

where $\Delta \mathbf{E}=\frac{1}{2}(\Delta {\mathbf{F}}^T·\Delta \mathbf{F}-\mathbf{I})$ is the incremental Lagrange strain, and $\Delta \mathit{\eta }=\ln \Delta \mathbf{V}$ is the incremental natural strain, where $\Delta \mathbf{V}$ is the left stretch tensor of $\Delta \mathbf{F}$. The deviatoric part of the natural strain is nonzero only when the strain is distortional [32]. Here, the norm of any tensor A is evaluated as $\Vert \mathbf{A}\Vert =\sqrt{\mathbf{A}:\mathbf{A}}$. In the above expression $e_{\min }$ represents the strain threshold above which a new generation is triggered. When not specified by the user, its default is set to ten times machine epsilon (in double precision). When $e_{\min }$ becomes greater than the typical increment in strain between t_n and $t_{n+1}$, the number of generations produced may become significantly smaller than the number of steps in an analysis. However, this limiting scheme does not place a specific cap on the number of generations. This scheme is represented in the pseudo-code of Algorithm 1, in Function NewGeneration.

2.2.3 Merging and Culling Oldest Generation.

We may also seek to limit the number of generations by merging the oldest two generations and then culling the oldest. We take advantage of the concept of fading memory, whereby the reduced relaxation function g decays monotonically over time. According to Eq. (2.25), this relation implies that the bond mass fraction of the $u-$ generation, which is in the range $0\le w^u(t)\le 1$, also decays with time after bonds of that generation start breaking ( $t\ge t^{u+1}$).

The strategy is to push generations on a stack each time a new one is created. When a new generation is added we check if the oldest extant generation u satisfies $w^u<w_{\min }$, where $w_{\min }$ is a user-selected parameter in the range $[0,1]$. If this condition is satisfied, we merge the oldest generation u with the second oldest, u + 1, then pop the oldest generation out of the stack, thereby keeping the stack size constant. In practice, merging and culling should only be done when there are at least three generations in the stack.

Merging the two oldest generations 0 and 1 is done efficiently using weighted averages, where the weights are the bond mass fractions corresponding to those two oldest generations. As mentioned above, for each generation u we store the set ${\mathcal{S}}^u=\{t^{u+1},f^u(t^{u+1}),\mathbf{U}(t^{u+1})\}$ onto stacks (or more precisely, C++ double-ended queues called deque). Upon the addition of a new generation at $t_{n+1}$ we can set the second oldest generation (u = 1) to

$${\mathcal{S}}^1\leftarrow \frac{w^0\left(t_{n+1}\right){\mathcal{S}}^0+w^1\left(t_{n+1}\right){\mathcal{S}}^1}{w^0\left(t_{n+1}\right)+w^1\left(t_{n+1}\right)}$$ (2.28)

then pop generation u out of the stack. This scheme is represented in the pseudo-code of Algorithm 1, in Function CullGenerations.

This strategy does not assign a specific cap on the number of generations. Instead, generations are created as needed until the oldest satisfies the given condition on its bond mass fraction. This simple weighted average is justified by the fact that $w^u(t_{n+1})$ and $w^{u+1}(t_{n+1})$ tend toward the same value as $t_{n+1}-t^{u+1}$ and $t_{n+1}-t^{u+2}$ increase significantly beyond the characteristic relaxation time of the function g. Other strategies for merging the two oldest generations could also be considered in principle, such as a strategy of matching the value and first-time derivative of the merged bond mass fraction with that of the two oldest generations. In practice, however, such alternative strategies would be computationally expensive, requiring iterative solutions of nonlinear equations for matching those values. These computational costs would severely compromise the computational efficiency that we seek to achieve with this merging and culling scheme.

There are two potentially negative consequences of the strategy proposed here. First, the number of generations m needed in an analysis is not fixed in advance, implying that it could still increase to unreasonably large values with increasing times steps. Second, regardless of its actual value, the maximum number of generations m achieved during an analysis cannot be allowed to decrease with culling as $t_{n+1}$ keeps increasing, because the smoothness of the response would then be compromised. In the Results section below we illustrate the temporal evolution of m and the conditions under which m remains small or increases to unreasonably large values.

2.2.4 Bond Mass Fraction Threshold for Triggering New Generation.

As noted in the recursive relation of Eq. (2.2), the bond mass fraction $w^u(t)$ of the $u-$ generation is proportional to the fraction $f^u(t^v)$ of reformed weak bonds that are available to break at time t^v. We may forgo the triggering of a new generation whenever this fraction is sufficiently small, such as $f^u(t^v)<w_{\min }$, where $w_{\min }$ may be conveniently set to the same user-selected parameter as in Sec. 2.2.3.

2.3 Multiple Weak Bond Families.

So far we have assumed that the viscoelastic material is a mixture of strong bonds and one family of weak bonds. All reformed bonds in the weak bond family break simultaneously in response to a change in strain between consecutive time points. Let us contemplate the implication of this modeling assumption in a stress-relaxation analysis where, starting from rest, step changes in strain occur at two distinct consecutive time points t_a and t_b. At time t_a all the weak bonds break and start reforming and the viscoelastic response is entirely governed by the time constant for the reformation of these weak bonds, as governed by the reduced relaxation function g. If the characteristic relaxation time of g is large compared to the relative time increment between t_a and t_b, the fraction of weak bonds that have reformed during the time interval $t\in [t_a,t_b]$ and are available to break again at time t_b will be small. In that case, the viscoelastic stress-relaxation response after the second step change in strain, as assessed from the peak-to-equilibrium stress ratio, may be weak, possibly contradicting experimental observations.

To produce a better agreement between our reactive viscoelasticity framework and experimental data, we may find it necessary to include multiple weak bond families, each of which engages with loading, and breaks to start reforming, at a different threshold of strain. This strain threshold may be a positive scalar strain measure Ξ consistent with the measure used to determine the triggering of new weak bond generations as given in Eq. (2.27). Thus, we may pick one of the following choices for Ξ:

$$\Xi (\mathbf{F})=\{\begin{array}{cc}\Vert \mathbf{E}\Vert & \text{any}\hspace{0.17em}\text{strain}\\ \Vert \text{dev}\mathit{\eta }\Vert \equiv K_2& \text{distortional}\hspace{0.17em}\text{strain}\\ |\ln (\det \mathbf{F})|& \text{dilatational}\hspace{0.17em}\text{strain}\end{array}\hspace{0.17em}$$ (2.29)

where F is the total deformation gradient, E is the Green–Lagrange strain tensor and $\mathit{\eta }$ is the left Hencky tensor. The underlying physical basis for this modeling approach is that biological tissues often exhibit a toe region where the tissue's extracellular matrix (ECM) is crimped. Whereas the elastic response of this toe region may be captured with a suitably nonlinear constitutive model for ${\Psi }_r^e$, it is reasonable to assume that weak bonds in the crimped ECM don't contribute to the viscoelasticity until the ECM becomes uncrimped. A nonlinear function ${\Psi }_0^a$ for weak bonds would not capture this weak bond recruitment mechanism according to the constitutive model of Eq. (2.1).

There is little benefit to introducing a discrete set of weak bond families, as this modeling assumption would needlessly increase the number of material parameters needed to describe the response of such materials in proportion to the number of families in the discrete set. Instead, we assume for simplicity that weak bond families exist over a continuous spectrum of the strain threshold Ξ and that the total fraction of weak bonds in the mixture that break at strain thresholds below Ξ is given by some function $F(\Xi )$. Furthermore, we assume that all a weak bond families share the same relaxation function $g(\mathbf{F}(t^v),t-t^v)$, and that the influence of the strain measure Ξ may be embodied in the dependence of g on $\Xi (\mathbf{F}(t^v))$. Thus, this approach only introduces additional material parameters as needed to describe $F(\Xi )$. For example, we may use a function such as

$$F(\Xi )=1+\mu {\left(\frac{\Xi }{{\Xi }_0}\right)}^{\alpha }\hspace{0.17em}$$ (2.30)

where $\mu \ge 0$, α, and ${\Xi }_0$ are material constants. Here, $F(0)=1$ represents the fraction of weak bonds available to break at Ξ = 0. With increasing Ξ, this fraction increases as long as $\alpha >0$, implying that more weak bonds get recruited with increasing strain. In the special case μ = 0, we recover the behavior of a single weak bond family. We may adopt other choices of constitutive models, such as $F(\Xi )=\text{exp}\hspace{0.17em}[\mu {(\Xi /{\Xi }_0)}^{\alpha }]$, or $F(\Xi )$ could be provided as a user-specified function that satisfies $F(0)=1$. This strain-dependent weak bond recruitment mechanism also represents a characteristic feature of nonlinear viscoelasticity, even when g does not depend on strain.

Without delving into details, it can be shown that the incorporation of a continuous spectrum of weak bond families into the constitutive model of Eq. (2.2) can be achieved by simply incorporating $F(\Xi )$ into the reforming bond mass fraction $f^u(t)$ as

$$\begin{array}{c}{f}^u(t^v)=F({\Xi }_m(t^v))-\sum _{\gamma <u}{w}^{\gamma }(t)\\ {\Xi }_m(t)=\underset{s\le t}{\max }\Xi (\mathbf{F}(s))\end{array}$$ (2.31)

This expression, which should be used for the calculation of w^u as per Eq. (2.2), shows that each generation u has recruited weak bond mass fraction $F({\Xi }_m(t^v))$ into the mixture, where ${\Xi }_m(t^v)$ is the highest strain level achieved over the loading history of this material up until generation u started breaking at time t^v. In particular, for the earliest generation u = –∞, we have ${\Xi }_m(t^{-\infty })=0$, for which $F(0)=1$, thus guaranteeing a viscoelastic response starting from zero strain. In effect, the function $F(\Xi )$ serves as a strain-dependent scale factor on the weak bond strain energy density ${\Psi }_0^a$. This modification to the calculation of Eq. (2.25) is performed in Function Update of the pseudo-code of Algorithm 1, with the result of Eq. (2.31) being represented in Function ReformingBondMassFraction.

Algorithm 1 Pseudo-code summarizing the numerical algorithms described in this study. These functions are called by Function Update described in Algorithm 2. The number of generations m is the current size of the stack $t^{u+1}$.

Function ReformingBondMassFraction

//Implement Eq. (2.25)

Let $m=$number of generations

If (m = 0) Let $f^{m-1}(t_{n+1})=1$

Else Let $f^{m-1}(t_{n+1})=F({\Xi }_m(t_{n+1}))$

For u = 0 to m – 1    $f^{m-1}(t_{n+1})$ $-=$

$f^{u-1}(t^u)g(\mathbf{F}(t^u),t_{n+1}-t^u)$     Return $f^{m-1}(t_{n+1})$

Function NewGeneration

//Implement Sec. 2.2.4

Let $f^{m-1}(t_{n+1})=$

ReformingBondMassFraction

If $f^{m-1}(t_{n+1})<w_{\min }$ Return false

//Implement Sec. 2.2.2

Evaluate $\Delta \mathbf{F}=\mathbf{F}(t_{n+1})·{\mathbf{F}}^{-1}(t^m)$

Evaluate e from Eq. (2.27)

If $e>e_{\min }$ Return True

Return False

Function CullGenerations

//Implement Sec. 2.2.3

Let $m=$number of generations

If m < 3 Return

Let $w^0(t_{n+1})=g(\mathbf{U}(t^0),t_{n+1}-t^0)$

If $w^0(t_{n+1})<w_{\min }$ Let $w^1(t_{n+1})=f^0(t^1)g(\mathbf{U}(t^1),t_{n+1}-t^1)$

Update t1, $f^0(t^1)$, $\mathbf{U}(t^1)$

and $F({\Xi }_m(t^1))$ per Eq. (2.28)

Pop t0, $\mathbf{U}(t^0)$, $f^{-\infty }(t^0)$

and $F({\Xi }_m(t^0))$ out of

$t^{u+1}$, $f^u(t^{u+1})$, $\mathbf{U}(t^{u+1})$

and $F({\Xi }_m(t^{u+1}))$ stacks

Return

Algorithm 2 The Function Update is called at each iteration of the nonlinear solver until convergence is achieved at the current time $t_{n+1}$. The Function ${\Psi }_r$ is called when evaluating the mixture free energy density at each iteration of the nonlinear solver. This function serves as a template for similar calculations of the stress $\mathit{\sigma }$ and elasticity $\mathcal{C}$ as described in Eq. (2.20) of Sec. 2.1.3. When u = 0 in this function, u – 1 is equivalent to the superscripted $-\infty$ in the text, see Eq. (2.23). These functions depend on those presented in Algorithm 1.

Function update

Let $m=$number of generations

If (m = 0) Or ( $t_{n+1}>t^{m-1}$)   If NewGeneration is True

Push $t_{n+1}\equiv t^m$ onto $t^{u+1}$ stack

Push $\mathbf{U}(t_{n+1})$ onto ${\mathbf{U}}^{u+1}$ stack

//Implement Sec. 2.3

Update ${\Xi }_m(\mathbf{U}(t_{n+1}))$ using Eq. (2.31)

Push $F({\Xi }_m(\mathbf{U}(t_{n+1})))$

onto $F^{u+1}$ stack

Push $f^{m-1}(t^m)=$

ReformingBondMassFraction

onto $f^{u+1}$ stack

Call CullGenerations

Else if $t_{n+1}=t^m$

Update previously pushed

$\mathbf{U}(t^m)$, $F({\Xi }_m(\mathbf{U}(t^m)))$ and $f^{m-1}(t^m)$

Function ${\Psi }_r$

Let $m=$number of generations

If m = 0 Return ${\Psi }_r={\Psi }_r^e(\mathbf{F}(t_{n+1}))+{\Psi }_0^a(\mathbf{F}(t_{n+1}))$

Let ${\Psi }_r={\Psi }_r^e(\mathbf{F}(t_{n+1}))$

For u = 0 to m – 1

Evaluate $w^{u-1}(t_{n+1})=f^{u-1}(t^u)g(\mathbf{F}(t^u),t_{n+1}-t^u)$

Evaluate ${\mathbf{F}}^{u-1}(t_{n+1})=\mathbf{F}(t_{n+1})·{\mathbf{U}}^{-1}(t^{u-1})$

Evaluate ${\Psi }_r$+= $w^{u-1}(t){\Psi }_0^a({\mathbf{F}}^{u-1}(t_{n+1}))$

Return ${\Psi }_r$

3 Results

The computational scheme for reactive nonlinear viscoelasticity described in Sec. 2 was implemented in the open source finite element software febio [33]. The material type for this framework is reactive viscoelastic; this material type is a container that allows users to select any desired constitutive model for strong bonds, ${\Psi }_r^e$, for weak bonds, ${\Psi }_0^a$, and for the relaxation function g. A select list of available choices for the relaxation function is given in Table 1. A material was also implemented for an uncoupled strain energy density formulation, under the material type uncoupled reactive viscoelastic, where ${\Psi }_r$ is split into deviatoric and dilatational contributions, ${\Psi }_r(\mathbf{F})={\tilde{\Psi }}_r(\tilde{\mathbf{F}})+U(J)$, where $\tilde{\mathbf{F}}=J^{-1/3}\mathbf{F}$ and $U(J)$ is the dilatational strain energy density that typically depends on a single bulk modulus κ. This split carries over to ${\Psi }_r^e$ and ${\Psi }_0^a$. This uncoupled formulation is better suited numerically for the modeling of nearly incompressible material responses.

Table 1.

Subset of currently available relaxation functions $g(\mathbf{F}(t^v),t-t^v)$ for nonlinear reactive viscoelasticity in febio

Name	$g(\mathbf{F}(t^v),t-t^v)$	Material constants (units)
Exponential	$e^{-(t-t^v)/\tau }$	$\tau \hspace{0.17em}\left(\text{time}\right)$
Exp-distortion	$\begin{array}{c}\text{exponential}\\ \tau (K_2(t^v))={\tau }_0+{\tau }_1{K}_2^{\alpha }(t^v)\end{array}$	$\begin{array}{c}{\tau }_0(\text{time})\\ {\tau }_1(\text{time})\\ \alpha (\text{time})\end{array}$
Power	${(1+\frac{t-t^v}{\tau })}^{-\beta }$	$\begin{array}{c}\tau (\text{time})\\ \beta (\text{time})\end{array}$
Power-dist-user	$\begin{array}{c}\text{power}\\ \tau (K_2(t^v))=\text{user}-\text{specified}\\ \beta (K_2(t^v))=\text{user}-\text{specified}\end{array}$	$\begin{array}{c}\tau (\text{time})\\ \beta (\text{time})\end{array}$
Malkin	$\frac{(\beta -1)t^{1-\beta }}{{\tau }_1^{1-\beta }-{\tau }_2^{1-\beta }}\left[\Gamma \left(\beta -1,\frac{t}{{\tau }_2}\right)-\Gamma \left(\beta -1,\frac{t}{{\tau }_1}\right)\right]$	$\begin{array}{c}{\tau }_1(\text{time})\\ {\tau }_2(\text{time})\\ \beta (\text{time})\end{array}$
Malkin-distortion	$\begin{array}{c}\text{Malkin}\\ {\tau }_1={\tau }_{10}+{\tau }_{11}\hspace{0.17em}\text{exp}\left(-\frac{K_2(t^v)}{s_1}\right)\\ {\tau }_2={\tau }_{20}+{\tau }_{21}\hspace{0.17em}\text{exp}\left(-\frac{K_2(t^v)}{s_2}\right)\end{array}$	$\begin{array}{c}{\tau }_{10}(\text{time}){\tau }_{20}(\text{time})\\ {\tau }_{11}(\text{time}){\tau }_{21}(\text{time})\\ s_1(\text{time})s_2(\text{time})\end{array}$

In these relations, $K_2(t^v)$ is the second invariant of the natural (Hencky) strain tensor, which represents a kinematic measure of distortion [32]. Specifically, $K_2=\Vert \text{dev}\mathit{\eta }\Vert$ where $\mathit{\eta }=\ln \mathbf{V}$ is the spatial natural strain tensor (also known as the left Hencky strain tensor) and V is the left stretch tensor. Here, K₂ is evaluated at the time t^v when $u-$ generation bonds start breaking. In febio user-specified functions, such as those needed for $\tau (K_2)$ and $\beta (K_2)$, may be given either as a mathematical formula or a curve (piecewise linear or cubic) passing through data points. The function $\Gamma (s,x)$ represents the upper incomplete gamma function.

3.1 Verifications.

In all the verification problems that employed uniaxial loading in the presentation below, unless specified otherwise the finite element model consisted of a unit cube ( $1\hspace{0.17em}\hspace{0.17em}\text{mm}\times 1\hspace{0.17em}\hspace{0.17em}\text{mm}\times 1\hspace{0.17em}\hspace{0.17em}\text{mm}\hspace{0.17em}$) meshed with a single eight-node hexahedral element, whose faces are parallel to the coordinate planes. Symmetry conditions were prescribed on three of the orthogonal faces (zero displacements normal to the coordinate planes) while the positive z-face was subjected to a prescribed displacement or load.

3.1.1 Linear Viscoelasticity.

As shown previously [1], in the limit of infinitesimal strains the reactive viscoelasticity framework reduces to classical linear viscoelasticity. Therefore the code may be verified against standard solutions, such as those for creep and stress-relaxation, using the “exponential” relaxation function in Table 1. As reviewed in [2], the linear viscoelastic stress-relaxation response of an isotropic elastic solid to a step increase ${\epsilon }_0$ in strain under uniaxial loading produces the normal stress response

$$\sigma \left(t\right)=E^e{\epsilon }_{0}H\left(t-t_1\right)\left(1+\frac{E^a}{E^e}{e}^{-\left(t-t_1\right)/\tau }\right)$$ (3.1)

where E^e and E^a are Young's moduli for strong and weak bonds, respectively, and $H(t)$ is the Heaviside unit step function. This analytical solution accounts for the fact that the step strain in the finite element analysis is applied at the first time-step t₁. We used this solution to verify the finite element code using the material properties $\tau =1\hspace{0.17em}\mathrm{s}$, and $E^e=E^a=1\hspace{0.17em}\text{MPa}$ and prescribed strain ${\epsilon }_0={10}^{-4}$. We examined the response for $0\le t\le 8\hspace{0.17em}\mathrm{s}$, using n uniform time increments ( $n=16,32,64,128$).

The material model used in febio for strong and weak bonds was the compressible neo-Hookean solid described in [34]. Since febio is inherently a finite deformation code, even a small strain ${\epsilon }_0$ can produce a slight deviation from that of the linear model. As explained below, this small error is taken into account when reporting these verification results. The neo-Hookean models require the specification of Young's modulus and Poisson's ratio. We set the latter to 0.3, for both strong and weak bonds. The febio code optionally allows the user to prescribe the strain threshold $e_{\min }$ described in Sec. 2.2.2. For the stress-relaxation verification problems, this strain threshold was set to $e_{\min }={10}^{-4}\times {\epsilon }_0$. Based on the nature of this problem, only one generation breaks as a result of the step increase in strain, namely, generation u = –∞ which breaks at the first time-step $t^0=t_1$. Therefore, there was no need to set, nor explore a nonzero value for $w_{\min }$ in this verification problem.

Upon running these models the numerical solutions for this stress-relaxation problem agreed exactly with the analytical solution (save for the slight nonlinearity induced by the finite strain formulation, producing a relative error magnitude less than $\sim 0.002\hspace{0.17em}\%$) for all four values of n. This result was expected since the analytical solution of Eq. (3.1) produces exactly the same relaxation function as $w^{-\infty }$ in Eq. (2.23). We also confirmed that only a single breaking generation was produced in the febio analysis.

Next, we verified the code against the linear viscoelastic creep response of the same material to a step increase in stress, σ₀, under uniaxial loading, which produces the creep strain

$$\begin{array}{c}\epsilon \left(t\right)=\frac{{\sigma }_0}{E^e}H\left(t-t_1\right)\left(1-\xi e^{-\zeta \left(t-t_1\right)/\tau }\right)\\ \zeta =\frac{E^a}{E^e+E^a}\end{array}$$ (3.2)

Since the strain evolves continuously with time in this solution, this verification problem could be used to test the proposed methods for limiting the number of generations. This problem was analyzed using ${\sigma }_0={10}^{-4}$, over the time range $0\le t\le 16\hspace{0.17em}\mathrm{s}$, using $n=32,64,128,256$ uniform time increments. For further comparison, we used febio's quasi-linear viscoelastic (QLV) material, whose numerical implementation was described by Puso and Weiss [25]. This comparison was justified by the fact that the QLV theory is also expected to reproduce classical linear viscoelasticity within the limit of infinitesimal strains.

Results showed that the reactive viscoelasticity (RVE) model slightly underestimated the analytical solution, with the relative error in $\epsilon (t)$ showing a peak magnitude of –3.0%, –1.5%, –0.73%, and –0.36% for the four increasing values of n. In contrast, the QLV model slightly overestimated the analytical solution, showing peak relative errors of 11.9% with n = 32 and 1.6% with n = 256. Plots of $\epsilon (t)$ and relative errors are presented in Figs. 1(a) and 1(b) for n = 32 and n = 256, respectively. The temporal evolution of the relative error differed between RVE and QLV, with the latter showing a monotonic decrease starting from the first time-step, whereas RVE showed a relative error peaking in magnitude at an intermediate time in the range $0\le t\le 16\hspace{0.17em}\mathrm{s}$.

Fig. 1.

Influence of the number of time steps n on the creep response of a linear viscoelastic material, comparing the analytical response of Eq. (3.2) to the reactive viscoelastic (RVE) framework, as well as standard QLV [25] as implemented in febio: (a) n = 32 and (b) n = 256

Next, we examined the influence of setting a nonzero value for $w_{\min }$ to reduce the number of generations in the RVE model with n = 256 time steps, as presented in Fig. 2(a). As expected, the default value of $w_{\min }=0$ produced a linearly increasing number of breaking generations m with increasing time steps, reaching a maximum value of $m=n=256$. With $w_{\min }=0.01$ the number of generations increased linearly with the number of time steps and then held constant at m = 74 starting at time t = 4.625. The peak magnitude of the relative error against the analytical solution remained at –0.36%, as shown in Fig. 2(b). Similarly, with $w_{\min }=0.05$, the number of generations held constant at m = 48 starting at $t=3\hspace{0.17em}\mathrm{s}$, with the relative error against the analytical solution now peaking at 1.4%. The creep responses $\epsilon (t)$ for these four cases are not displayed here since they were nearly indistiguishable. For completeness, we also examined $w_{\min }=0.1$ as a representative case with poorer outcomes due to excessive culling. Though the peak number of generations produced in this case was only 37 (out of a maximum of 256), the creep response showed a kink at the time when the number of generations plateaued (Fig. 2(c)). Moreover, the error relative to the analytical solution increased to 2.9%, implying that values $w_{\min }$ at 0.1 or above should not be used.

Fig. 2.

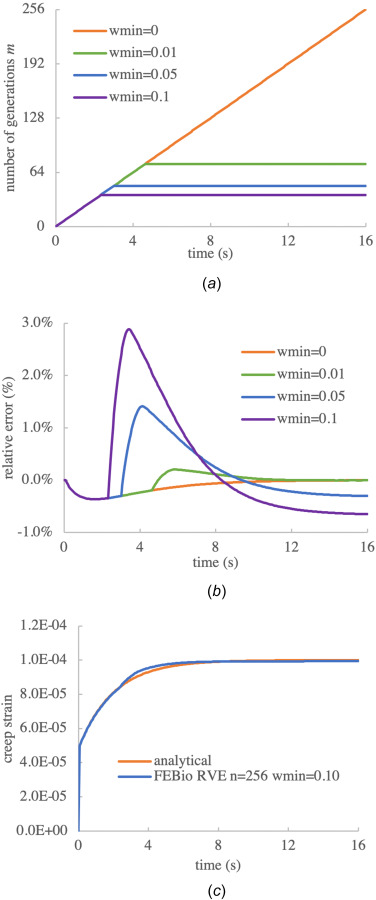
Influence of $w_{\min }$ on the creep response of a linearly viscoelastic material, using n = 256 time steps: (a) number of generations m, (b) relative error between numerical response and analytical solution of Eq. (3.2), and (c) creep strain when $w_{\min }=0.1$, showing deviation from the analytical solution

Finally, we examined the influence of changing the minimum threshold strain for triggering new generations, using $e_{\min }={10}^{-8}-{10}^{-5}$ with n = 256 uniform time increments. These values of $e_{\min }$ are at least ten times smaller than the equilibrium creep strain ${\sigma }_0/E^e={10}^{-4}$ achieved in this analysis. The temporal evolution of maximum generations m for these four cases is shown in Fig. 3(a), with peak values of 7, 43, 118, and 190 for the four respective values of $e_{\min }={10}^{-5},{10}^{-6},{10}^{-7},{10}^{-8}$. The temporal evolution of the error relative to the analytical solution is presented in Fig. 3(b), showing peak magnitudes of –4.2%, –0.57%, –0.36%, and –0.36% at $e_{\min }={10}^{-5},{10}^{-6},{10}^{-7},{10}^{-8}$, respectively. These results suggest that $e_{\min }={10}^{-6}$ (100 times smaller than the equilibrium creeps strain) represents a good compromise between reducing the relative error and reducing the maximum number of generations. For completeness, we show the creep response for the poorest outcome corresponding to $e_{\min }={10}^{-5}$ in Fig. 3(c), which displays unacceptable jaggedness resulting from the relative coarseness of strain increments in consecutive generations.

Fig. 3.

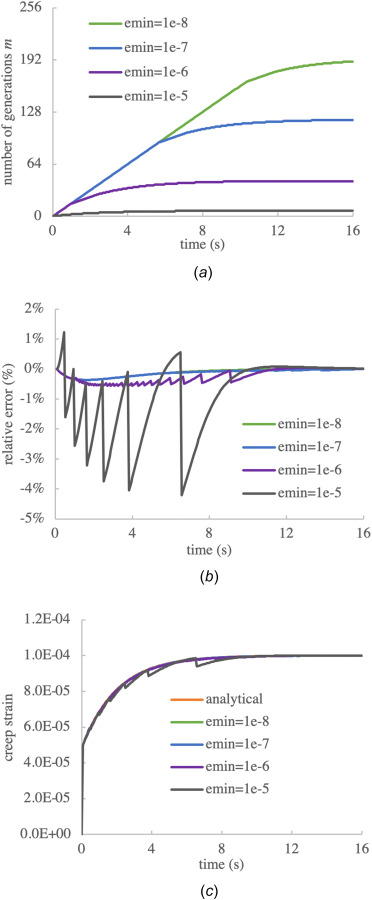
Influence of $e_{\min }$ on the creep response of a linearly viscoelastic material, using n = 256 time steps: (a) number of generations m, (b) relative error between numerical response and analytical solution of Eq. (3.2), and (c) the creep strain response when $e_{\min }={10}^{-5}$ (one-tenth of the equilibrium strain ${10}^{-4}$) shows unacceptable deviations from the analytical solution, while lower values of $e_{\min }$ (one-hundredth or lower) produce more acceptable agreements

3.1.2 Nonlinear Viscoelasticity.

As noted in Sec. 2.1, when an RVE material is loaded uniaxially with a prescribed step stretch ${\lambda }_{0}H(t-t_1)$, only one bond generation breaks at time t₁, corresponding to u = –∞, with its bond mass fraction given by $w^{-\infty }(t)=g(\mathbf{F}(t_1),t-t_1)$ for $t\ge t_1$. The resulting stress response may be evaluated from Eq. (2.20) as

$$\begin{array}{c}\mathit{\sigma }(\mathbf{F}(t))={\mathit{\sigma }}^e(\mathbf{F}(t))+g(\mathbf{F}(t_1),t-t_1){\mathit{\sigma }}_0^a(\mathbf{F}(t))\\ t\ge t_1\end{array}$$ (3.3)

Now consider that we employ the same constitutive model for the stress in strong and weak bonds, based on the isotropic hyperelastic constitutive model proposed by Criscione et al. [32], where the principal normal stresses are given by

$${\sigma }_i=\frac{\left(3\kappa +4\mu \right)\ln {\lambda }_i+\left(3\kappa -2\mu \right)\left(\ln {\lambda }_j+\ln {\lambda }_k\right)}{3J}$$ (3.4)

Here, i, j, k form a permutation over x, y, z, κ is the bulk modulus and μ is the shear modulus in the limit of infinitesimal strains. They can be related to Young's modulus and Poisson's ratio using standard formulas. Under uni-axial loading along the z-direction the principal directions may be given by $i,j,k\to x,y,z$. Then, by setting ${\sigma }_x={\sigma }_y=0$ under an axial stretch ${\lambda }_z={\lambda }_0$, we find that the natural strain tensor $\mathit{\eta }$ is given by

$$[\mathit{\eta }]=\left[\begin{array}{ccc}-\nu & 0& 0\\ 0& -\nu & 0\\ 0& 0& 1\end{array}\right]\ln {\lambda }_0$$ (3.5)

where ν is Poisson's ratio. It follows that $J={\lambda }_0^{1-2\nu }$ under this uniaxial loading configuration. The corresponding nonzero stress along z is

$${\sigma }_z=E\frac{\ln {\lambda }_0}{{\lambda }_0^{1-2\nu }}$$ (3.6)

where E is Young's modulus.

For the verification problem employed in this section, we choose the “exp-distortion” relaxation function g from Table (1), which requires us to evaluate $K_2=\Vert \text{dev}\mathit{\eta }\Vert$ from Eq. (3.5)

$$K_2=\sqrt{\frac{2}{3}}\left(1+\nu \right)\left|\ln {\lambda }_0\right|$$ (3.7)

Combining these relations, and assuming that Poisson's ratio is the same for strong and weak bonds, produces the closed-form analytical solution for the nonlinear viscoelastic stress response to a step stretch in uniaxial loading

$$\begin{array}{c}\frac{\sigma \left(t\right)}{E^e}\frac{{\lambda }_0^{1-2\nu }}{\ln {\lambda }_0}=1+\frac{E^a}{E^e}{e}^{-\left(t-t_1\right)/\tau \left(K_2\right)}\\ t\ge t_1\end{array}$$ (3.8)

where

$$\tau (K_2)={\tau }_0+{\tau }_1{K}_2^{\alpha }$$

In the expression of Eq. (3.8) we have normalized the stress by its equilibrium value.

For illustrative purposes we used $E^e=E^a=1\hspace{0.17em}\text{MPa},\hspace{0.17em}\nu =0.3$, ${\tau }_0=1\hspace{0.17em}\mathrm{s},\hspace{0.17em}{\tau }_1=2\hspace{0.17em}\mathrm{s}$ and $\alpha =\frac{1}{2}$. We performed febio analyses with ${\lambda }_0=1.02$, 1.2 and 2 and compared the results to the above analytical solution for the time range $0\le t\le 8\hspace{0.17em}\mathrm{s}$, using n = 256 uniform time steps. We set the generation trigger to distortional strain in Eq. (2.27), with $e_{\min }={10}^{-2}\times \ln {\lambda }_0$, to ensure that only one breaking generation was produced. Accordingly, there was no motivation to adjust $w_{\min }$ in these analyses. A comparison of the febio and analytical responses for these three values of λ₀ is presented in Fig. 4, showing perfect agreement between the numerical and analytical solutions. (Relative errors between febio and analytical solutions were within numerical roundoff values for the convergence parameters adopted for the iterative solution of the nonlinear equations, with the highest relative error at $\sim 0.0004\%$.)

Fig. 4.

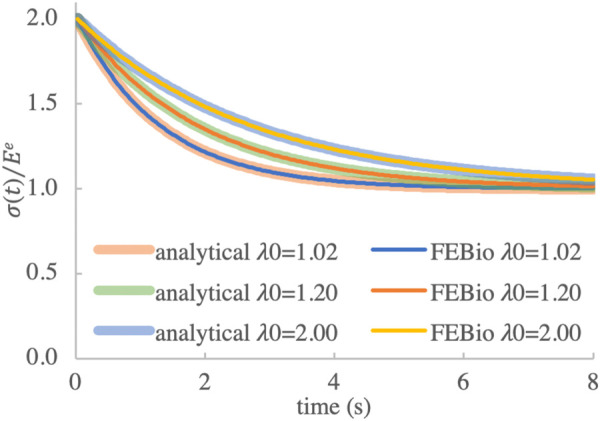
Normalized stress for analytical and febio responses, using the nonlinear viscoelastic model of Eq. (3.8), for three different values of the prescribed stretch ratio λ₀

To verify the febio code for multiple breaking bond generations in nonlinear viscoelasticity we analyzed the uniaxial stress-relaxation response to a linearly increasing stretch ratio ${\lambda }_0(t)$, in the range $1\le {\lambda }_0(t)\le 2$, subsequently kept constant, using n = 40 uniform time increments in the range $0\le t\le 4\hspace{0.17em}\mathrm{s}$. We used the same nonlinear material models employed above. The verification of the febio code was performed against a calculation of the response using a spreadsheet, following the basic computational scheme described in Sec. 2.2.1. This analysis produced m = 20 breaking generations $u=-\infty ,1,2,\dots ,m-1$. The spreadsheet thus contained 40 × 20 rows and columns to store the axial stretch ratios ${\lambda }^u(t_{n+1})$ and relative volumes $J^u(t_{n+1})$ evaluated from ${\mathbf{F}}^u(t_{n+1})=\mathbf{F}(t_{n+1})·{\mathbf{U}}^{-1}(t^u)$ at the time steps $t_1-t_{40}$. A single column was used to store $K_2(t^{u+1})$ evaluated from Eq. (2.20). Additional 40 × 20 blocks were created to evaluate the bond mass fractions $w^u(t_{n+1})$ (Fig. 5(a)) using the recursive relation of Eq. (2.2) and the exp-distortion relaxation function in Table 1, as well as the axial normal stresses ${\sigma }_0^a({\lambda }^u(t_{n+1}))$ evaluated from Eq. (3.6). A single additional column was needed to evaluate ${\sigma }^e(\lambda (t_{n+1}))$ from Eq. (3.6), although this value equaled ${\sigma }_0^a({\lambda }^{-\infty }(t_{n+1}))$ in this particular problem because of our choice of identical material models for the strong and weak bonds. Finally, another 40 × 20 blocks was used to store the product $w^u(t_{n+1})J^{-1}(t^u){\sigma }_0^a({\lambda }^u(t_{n+1}))$ appearing in Eq. (2.20). The final result for the stress, $\sigma (t_{n+1})={\sigma }^e(\lambda (t_{n+1}))+{\sum }_{u=-\infty }^{m-1}{w}^u(t_{n+1})J^{-1}(t^u){\sigma }_0^a({\lambda }^u(t_{n+1}))$ according to Eq. (2.20), was evaluated by summing rows across columns.

Results for $\sigma (t_{n+1})$ of the spreadsheet and febio analyses are presented in Fig. 5(b), showing perfect agreement between the two methods, with the error in febio relative to the spreadsheet analysis falling within numerical roundoffs, $\sim 0.00014\%$.

3.1.3 Frame Indifference Verification.

One of the characteristics of reactive viscoelasticity theory is its formulation in the spatial frame, as shown in Sec. 2.1.3. This form conveniently arises due to the use of mass bond fractions w^u as observable scalar state variables which are independent of the deformation gradient $\mathbf{F}(t)$. To verify the frame indifference of this formulation and its febio implementation we analyzed uni-axial cyclical loading of an anisotropic material consisting of a ground matrix (compressible neo-Hookean with $E=1\hspace{0.17em}\text{MPa}$ and $\nu =0.3$ for strong and weak bonds) and two fiber bundles that could sustain tension only, each with strain energy density

$${\Psi }_n=\frac{\xi }{2}{\left(I_n-1\right)}^2$$ (3.9)

where I_n is defined in Eq. (2.13), and $\xi =5\hspace{0.17em}\text{MPa}$ for strong and weak bonds. The reduced relaxation function for reactive viscoelasticity was set to an exponential function with $\tau =1\hspace{0.17em}\mathrm{s}$. The unit cube was meshed uniformly with $3\times 3\times 3$ eight-node hexahedral elements. The negative z-face was anchored to a rigid body while the positive z-face was subjected to a cyclical tensile normal traction $t_n=\frac{t_0}{2}(1-\text{cos}\hspace{0.17em}2\pi t)$ with $t_0=5\hspace{0.17em}\text{MPa}$. The rigid body had a prescribed rotation about the origin, $\mathbf{R}(t)=(1-\text{cos}\hspace{0.17em}\theta )\mathbf{m}\otimes \mathbf{m}+\text{cos}\hspace{0.17em}\theta \mathbf{I}-\mathbb{E}·(\text{sin}\hspace{0.17em}\theta \hspace{0.17em}\mathbf{m})$, and the time-varying axial rotation $\mathit{\theta }=\theta \mathbf{m}$ was set to $\mathit{\theta }(t)=\pi (1-\text{cos}\hspace{0.17em}2\pi t){\mathbf{e}}_x-\pi (1-\text{cos}\hspace{0.17em}2\pi t){\mathbf{e}}_y+\pi (1-\text{cos}\hspace{0.17em}\pi t){\mathbf{e}}_z$ in the global Cartesian basis $\{{\mathbf{e}}_x,{\mathbf{e}}_y,{\mathbf{e}}_z\}$. In the reference configuration the fiber bundles were oriented along the global directions ${\mathbf{n}}_r=(\pm {\mathbf{e}}_x+2{\mathbf{e}}_z)/\sqrt{5}$, thus conferring orthotropic material symmetry. The finite element analysis used n = 400 uniform time increments over the range $0\le t\le 10\hspace{0.17em}\mathrm{s}$. Results of this analysis were compared to the equivalent loading of a non-rotating cube, $\mathbf{R}(t)=\mathbf{I}$. For the purpose of verifying frame indifference we set $w_{\min }=0$ and $e_{\min }=0$.

We examined principal normal natural strains of the central element of the mesh. Results showed identical temporal evolutions of the three principal strains, with the rotating model matching the nonrotating model within numerical roundoff errors (maximum relative error magnitude of $\sim 0.0004\%$, Fig. 6(a)). A plot of the maximum principal stress versus maximum principal natural strain shows similarly good agreement, also exhibiting the characteristic “preconditioning” behavior of viscoelastic soft tissues (Fig. 6(b)). Since this analysis ran for a total of 1200 time steps with continually varying strain, the number of generations for this analysis reached m = 1200. By setting $w_{\min }=0.05$ the number of generations was reduced to m = 293 (Fig. 6(c)). In comparison to the case with $w_{\min }=0$, the difference in the calculated maximum principal stress ranged from $-0.011\hspace{0.17em}\text{MPa}$ to $0.002\hspace{0.17em}\text{MPa}$ over the $10\hspace{0.17em}\mathrm{s}$ of this analysis (or –0.25% to 0.04% of the peak stress achieved in these cycles).

Fig. 6.

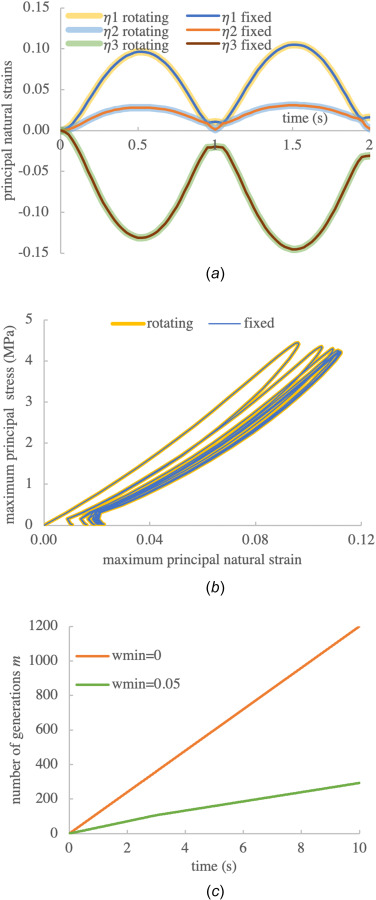
Verification of frame indifference for an orthotropic fibrous material subjected to cyclical stress, comparing outcomes between a cubic material domain with fixed versus rotating substrates. (a) Comparison of principal natural strains over two cycles of loading. (b) Comparison of maximum principal stress versus maximum principal strain for ten cycles of loading, showing a distinct preconditioning response. (c) The number of generations for two different values of $w_{\min }$. All results are shown for the central element of a cubic mesh with $3\times 3\times 3$ elements. The cycle period was $1\hspace{0.17em}\mathrm{s}$ and the time increment was set to $0.025\hspace{0.17em}\mathrm{s}$ (40 time increments per cycle).

3.2 Validations

3.2.1 Nonlinear Viscoelasticity of the Rat Medial Collateral Ligament.

Provenzano et al. [18] reported experimental data in support of nonlinear viscoelastic stress-relaxation and creep responses of Sprague–Dawley rat medial collateral ligaments (MCL). For stress relaxation they prescribed a tensile strain ${\epsilon }_0$ to the ligament in $\sim 0.32\hspace{0.17em}\mathrm{s}$ then reported the stress response from $\sim 3\hspace{0.17em}\mathrm{s}$ to $100\hspace{0.17em}\mathrm{s}$. In their Fig. 3 they showed stress-relaxation responses on a single sample, performed using four distinct applied strains ${\epsilon }_0$. They fitted their data successfully to an equation of the form $\sigma (t)={\sigma }_0{t}^{-n}$, where σ₀ and n both depended on the applied strain ${\epsilon }_0$, as summarized in Table 2. In our treatment here, we consider those fitted curves to represent their experimental data, and we seek to provide a validation of the reactive nonlinear viscoelastic framework using their data sets.

Table 2.

Provenzano et al. [18] reported their experimental MCL stress-relaxation data as fitted faithfully to the function $\sigma (t)={\sigma }_0{t}^{-n}$

${\epsilon }_0$	$\sigma ={\sigma }_0{t}^{-n}\hspace{0.17em}(\text{MPa})$	${\sigma }^a({\epsilon }_0)\hspace{0.17em}(\text{MPa})$	K 2	τ	β
0.82 %	$1.474t^{-0.141}$	2.395	$1.00\times {10}^{-2}$	0.032	0.141
1.74 %	$5.700t^{-0.053}$	6.841	$2.11\times {10}^{-2}$	0.032	0.053
2.38 %	$10.103t^{-0.025}$	11.011	$2.88\times {10}^{-2}$	0.032	0.025
3.74 %	$15.015t^{-0.012}$	15.648	$4.50\times {10}^{-2}$	0.032	0.012

Their data was represented by our RVE framework using the power-dist-user model in Table 1, to produce ${\sigma }^a({\epsilon }_0)$ and $\beta (K_2)$, assuming that $\tau (K_2)=0.032\hspace{0.17em}\mathrm{s}$ for all ${\epsilon }_0$. The function $\beta (K_2)$ employed in febio was piecewise linear over the range of K₂ values shown here, and held constant outside of that range.

To maintain unit consistency we may assume that their formula is more accurately represented by $\sigma (t)={\sigma }_0{(t/t_0)}^{-n}$ where $t_0=1\hspace{0.17em}\mathrm{s}$. To fit their experimental data to a model consistent with the RVE approach of this study we chose the reduced relaxation function g to be the “power-dist-user” relaxation model presented in Table 1, since it represented the closest approximation to their fitted equation. For the purpose of modeling their experimental data we assumed that the strain ${\epsilon }_0$ was applied instantaneously at time $t^v=0.32\hspace{0.17em}\mathrm{s}$. In that case, the stress response evaluated from Eq. (2.20) predicts

$$\sigma \left(t\right)={\sigma }^e\left({\epsilon }_0\right)+{\left(1+\frac{t-t^v}{\tau \left(K_2\right)}\right)}^{-\beta \left(K_2\right)}{\sigma }^a\left({\epsilon }_0\right)$$ (3.10)

For an incompressible response to uniaxial loading, it can be shown that K₂ at t^v is given by $K_2({\epsilon }_0)=\sqrt{3/2}|\ln (1+{\epsilon }_0)|$.

We considered the following simplified RVE model to represent their data: In a strict sense, Provenzano et al.'s fitted function $\sigma (t)$ expects that the stress reduces to zero as $t\to \infty$, which is more consistent with the response of a viscoelastic fluid, not a solid. Since their experimental stress response did not extend in time sufficiently to produce a reliable estimate of ${\sigma }^e({\epsilon }_0)$, we adopted a negligibly small value for ${\sigma }^e({\epsilon }_0)$ in Eq. (3.10) and assumed that $\tau \ll t^v$. Then it would follow that β is approximately equal to their parameter n, while ${\sigma }^a{\tau }^{\beta }$ is approximately equal to their ${\sigma }_0{t}_0^n$.

In febio we modeled this MCL tissue using a Mooney-Rivlin incompressible solid for ${\sigma }^e({\epsilon }_0)$, with a negligibly low shear modulus of $0.2\hspace{0.17em}\text{MPa}$. We assumed that $\tau (K_2)={10}^{-1}\times t^v\sim 0.032\hspace{0.17em}\mathrm{s}$ for all K₂. Consequently, the RVE response to uniaxial tensile stress relaxation under a prescribed step strain ${\epsilon }_0$ at t^v could be approximated from Eq. (3.10) using ${\sigma }^a({\epsilon }_0)$ and $\beta (K_2)$ as presented in Table 2. Plotting the calculated values for ${\sigma }^a({\epsilon }_0)$ in Table 2, we found a nearly linear response with strain ${\epsilon }_0$. We fitted this response to the fiber model in Eq. (3.9), yielding a fiber modulus $\xi =97.83\hspace{0.17em}\text{MPa}$ that produced a response that passed approximately through the four strain data points, as shown in Fig. 7(a) (Young's modulus for this material model would be $2\xi$ in the limit of zero strain). This value of ξ for the fiber tensile modulus was consistent with our assumption that a shear modulus of $0.2\hspace{0.17em}\text{MPa}$ for the ground matrix would be negligible.

Fig. 7.

Fitting of RVE model to stress-relaxation of rat MCL reported by Provenzano et al. [18]. (a) Symbols represent the discrete values of the RVE weak bond stress ${\sigma }^a({\epsilon }_0)$ calculated from σ₀ and n at various ${\epsilon }_0$, as reported in Sec. 3.2.1 and column 3 of Table 2; the solid curve is a fit of those tabulated values using the constitutive fiber model of Eq. (3.9), with $\xi =97.83\hspace{0.17em}\text{MPa}$. (b) febio prediction of the RVE model stress-relaxation response $\sigma (t)$ (thick curves), using this fitted model for ${\sigma }^a({\epsilon }_0)$ and the relaxation parameters τ and β as summarized in Table 2. Nonlinear regression analyses of the form $\sigma (t)={\sigma }_0{t}^n$ are presented for each febio prediction (dotted curves and superposed equations), allowing a comparison of σ₀ and n with column 2 of Table 2.

Using these material models and parameters in febio, we simulated Provenzano's MCL stress-relaxation experiments at the four prescribed strains ${\epsilon }_0$ (Fig. 7(b)), producing excellent agreement for the values of n as expected (since $\beta (K_2)$ was set to match the values of n), and good agreement with the values of σ₀ in Table 2. The slightly imperfect agreement found for σ₀ was due to the minor deviation of our fitted ${\sigma }^a({\epsilon }_0)$ compared to the exact values evaluated from Provenzano et al.'s experimental data, as seen in Fig. 7(a). This successful fit represented a necessary condition toward validation of the reactive viscoelasticity framework as applied to this problem.

Provenzano et al. [18] also reported the creep response of other MCL samples to prescribed stresses σ₀ in the range 3.3–9.9 MPa. Unlike their Fig. 3 results in stress-relaxation, they did not report multiple creep tests on the same MCL sample at various values of σ₀. Their aggregate results in creep were similarly fitted to functions $\epsilon (t)={\epsilon }_0{t}^{-n}$ and they reported that n decreased with increasing σ₀, from $\sim 0.06$ to $\sim 0.007$ in the range $3.3\le {\sigma }_0\le 9.9\hspace{0.17em}\text{MPa}$. When we simulated the creep response of the above RVE material, we found that fitting $\epsilon (t)={\epsilon }_0{t}^{-n}$ to these simulated responses produced decreasing values of n, ranging from n = 0.045 at ${\sigma }_0=3.3\hspace{0.17em}\text{MPa}$ down to n = 0.018 at ${\sigma }_0=9.9\hspace{0.17em}\text{MPa}$. Extending the range of σ₀ as low as $1.65\hspace{0.17em}\text{MPa}$ and as high as $19.9\hspace{0.17em}\text{MPa}$ extended the range of n from 0.074 down to 0.011, confirming the trend found by Provenzano et al. [18]. This successful prediction of the trend observed by these authors served as a sufficient condition for validating the nonlinear reactive viscoelasticity framework as applied to this problem. From preliminary investigations, we found that closer agreement with the specific values of n found in their study could be achieved by attributing a non-negligible contribution to the elastic (strong bond) response of the MCL, ${\sigma }^e({\epsilon }_0)$ in Eq. (3.10). In practice, this effort would require a more extensive experimental dataset, such as longer relaxation times and creep measurements performed on the same set of samples.

3.2.2 Quasi-Linear Viscoelasticity of Immature Bovine Cartilage in Tension.

Park and Ateshian [12] previously reported extensive experimental data for the tensile response of immature bovine articular cartilage. Based on earlier theoretical and experimental observations [35,36], these authors deemed that the tensile response of articular cartilage was dominated by intrinsic viscoelasticity of the collagen-proteoglycan matrix, in contrast to interstitial fluid flow-dependent viscoelasticity which dominates in compression. Here, we examined one particular dataset where stress-relaxation responses were obtained under five different strain increments on the same tissue sample, ranging from 2% to 10% tensile strains (Fig. 8(a)). The objective of this investigation was to determine if the response of immature bovine cartilage in tension was indeed nonlinearly viscoelastic, as indicated by those authors based on their fits of those data [12], and if so, to examine the extent of the strain-dependence of the reduced relaxation function $g(\mathbf{F}(t^v),t-t^v)$.

Fig. 8.

Stress-relaxation analysis of immature bovine cartilage in tension, from the study of Park and Ateshian [12]. (a) Symbols represent experimental data from a single tissue sample subjected to a series of prescribed strains (each sample was allowed to recover while unloaded for 2000s prior to the next test). Orange solid curve represents febio curvefit of the experimental data at 10% strain (four-parameter fit, see text); green solid curves represent febio predictions of experimental data at remaining strains, using curvefitted properties from 10% strain. (b) febio prediction of the strain energy density (SED) response of strong and weak bonds using the model fitted to 10% stress-relaxation data. The sum of strong and weak bond SED is equal to the total SED.

For this analysis cartilage was modeled simply as a constrained mixture of a compressible neo-Hookean ground matrix [34] and a single fiber bundle oriented along the loading direction. The ground matrix was ascribed only elastic properties, implying that it contributed only to ${\Psi }_r^e$ in Eq. (2.1). Its Young's modulus was set to $0.663\hspace{0.17em}\text{MPa}$ based on the mean cartilage equilibrium compressive modulus reported in [12], and its Poisson's ratio was set to zero based on prior observations of negligibly small immature bovine cartilage equilibrium Poisson's ratio in compression [37]. The single fiber model, which contributed to the strong and weak bond responses in Eq. (2.1), obeyed the response of Eq. (3.9), leaving only ξ as an unknown material coefficient for the elastic response (ξ^e) and the weak bond response (ξ^a). The reduced relaxation function was assumed to be of type 'power' or 'power-dist-user' in Table 1, with unknown parameters τ and β.

Initially, the goal was to fit each of the five stress-relaxation responses to extract the four parameters ξ^e, ξ^a, τ, and β, with the expectation that τ and β could vary with the distortional strain measure K₂. Fitting the response at 10% strain using the “power” reduced relaxation model produced ${\xi }^e=1.484\hspace{0.17em}\text{MPa},{\xi }^a=6.400\hspace{0.17em}\text{MPa},\hspace{0.17em}\tau =0.1328\hspace{0.17em}\mathrm{s}$, and $\beta =0.2590$. A linear regression analysis of the fitted stress versus the experimental stress responses (evaluated at the same time points) produced a coefficient of determination $R^2=0.9996$. These fitted material properties were subsequently used to predict the responses at the remaining strain levels (2%, 4%, 6%, and 8%) and remarkable agreement was found between those predictions and the experimental data, as shown in Fig. 8(a). We concluded that the viscoelastic response of immature bovine articular cartilage is in fact quasi-linear in the range of strains examined here, since the same parameters τ and β could be used for all those strains. Furthermore, the ability to predict the stress-relaxation responses at four distinct strain values by only fitting the fifth response on the same tissue sample served to conclusively validate the reactive viscoelastic framework as applied to this problem.

Finally, for the 10% stress-relaxation fitted model, a plot of the strain energy densities ${\Psi }_r$ (total), ${\Psi }_r^e$ (strong bonds) and ${\Psi }_r^a=\sum _u{w}^u{\Psi }_0^a$ (weak bonds) in Fig. 8(b), showed that weak bonds contributed most significantly to ${\Psi }_r$ in the early time response ( $\sim 76\%$), though this contribution eventually decayed toward zero as t increased. In contrast, ${\Psi }_r^e$ rose to a relatively smaller fraction of ${\Psi }_r$ ( $\sim 24\%$) during the initial increase in strain, then remained constant.

3.2.3 Nonlinear Viscoelasticity of Bovine Nucleus Pulposus.

The response of the bovine nucleus pulposus to unconfined compression stress relaxation was reported in a recent study by Jacobsen [28]. A tissue sample was subjected to five consecutive ramp-and-hold displacement profiles that each resulted in 5% compression of the initial sample thickness, for a total compression of 25%. The engineering stress response was fitted to a reactive viscoelastic model using an uncoupled (nearly incompressible) neo-Hookean material for the strong and weak bond responses, with ${\tilde{\Psi }}_r=\frac{\mu }{2}({\tilde{I}}_1-3)$, where μ is the shear modulus and ${\tilde{I}}_1=\text{tr}\tilde{\mathbf{C}}$, $\tilde{\mathbf{C}}={\tilde{\mathbf{F}}}^T·\tilde{\mathbf{F}}$, and $\tilde{\mathbf{F}}=J^{-1/3}\mathbf{F}$. The reduced relaxation function was set to the continuous relaxation spectrum first proposed by Fung [38], which may be reproduced by the Malkin relaxation function [39] given in Table 1 when β = 1. To accommodate strain-dependent relaxation, the parameters τ₁ and τ₂ of this function were allowed to generally depend on $K_2(t^v)$ as given in 'Malkin-distortion' in that table, though we deduced by trial and error that ${\tau }_1={\tau }_{10}$ was independent of K₂. The weak bond recruitment function $F(\Xi )$ of Eq. (2.30) was also used, with $\Xi \equiv K_2$ and α = 2.

The experimental data were fitted to this model to extract the material parameters μ^e and μ^a (shear moduli of the strong and weak bonds), τ₁₀, τ₂₀, τ₂₁, and s₂ for the reduced relaxation function, and μ and ${\Xi }_0$ for the recruitment function. This eight-parameter fit produced ${\mu }^e=1.63\hspace{0.17em}\text{kPa}$, ${\mu }^a=6.90\hspace{0.17em}\text{kPa},{\tau }_{10}=0.0684\hspace{0.17em}\mathrm{s},\hspace{0.17em}{\tau }_{20}=203\hspace{0.17em}\mathrm{s}$, ${\tau }_{21}=2549\hspace{0.17em}\mathrm{s},\hspace{0.17em}{s}_2=0.0109,\hspace{0.17em}\mu =28.0$ and ${\Xi }_0=1.012$. The nonlinear regression coefficient between the fit and data was $R^2=0.990$ and the fit is shown in Fig. 9(a). To better understand the strain-dependence of ${\tau }_2(K_2)$ and $F(K_2)$ for this fit, these functions are shown in Fig. 9(b), calculated using τ₂₀, τ₂₁, and s₂ for ${\tau }_2(K_2)$, and μ, ${\Xi }_0$ and α for $F(K_2)$.

Fig. 9.

Curve-fitting of nucleus pulposus unconfined compression stress-relaxation response to data from Ref. [28]. (a) Experimental data and reactive viscoelasticity curvefit of the compressive engineering stress, for five consecutive increases of 5% in the compressive engineering strain. (b) Dependence of weak bond recruitment F and relaxation time τ₂ on distortional strain K₂. Symbols represent the values of K₂ corresponding to each engineering strain increment in the stress-relaxation response.

4 Discussion

The primary objective of this study was to develop computational schemes for our existing reactive nonlinear viscoelasticity framework [1] that offer improved efficiency compared to the basic method where the number of generations may increase indefinitely (Sec. 2.2). This implementation was made available in the open source finite element software febio [33]. Based on recent theoretical developments [29,30], we also updated the theoretical formulation to satisfy frame indifference for any material symmetry (Sec. 2.1.1). Finally, we validated this framework against some experimental data (Sec. 3), which had not been done previously.

The overarching motivation for improving numerical algorithms for this reactive nonlinear viscoelasticity framework was the dearth of available theories and open-source computational tools for anisotropic nonlinear viscoelasticity, despite the pervasiveness of anisotropic nonlinear viscoelastic responses in biological tissues as reviewed in the Introduction. Indeed, nonlinear viscoelasticity has remained a challenging problem to address in biomechanics and other fields of mechanics. Furthermore, future investigations of damage mechanics in viscoelastic materials may require viscoelasticity theories that provide an explicit evaluation of the strain energy density, as illustrated in Fig. 8(b).

Three numerical improvements were introduced in this study: (1) Setting a strain threshold $e_{\min }$ for triggering a new generation in the bond-breaking-and-reforming reaction, (2) merging and culling older generations whose bond mass fraction has fallen below a specified threshold $w_{\min }$, and (3) setting a minimum threshold $w_{\min }$ on the reformed bond mass fraction for triggering a new generation. First, we verified that the febio implementation of the basic scheme described in Sec. 2.2.1 produced a good agreement with closed-form analytical solutions from linear viscoelasticity, including stress-relaxation and creep as summarized in Sec. 3.1.1. Results presented in Fig. 1 confirmed that the implementation worked correctly, producing errors that decreased with smaller time steps.

Next, we investigated the influence of $w_{\text{min}}$ on the linear viscoelastic creep response. Creep was chosen since the number of generations m for this mode of loading normally increases indefinitely with time, thus serving as a good test of the effectiveness of the proposed numerical schemes. Based on the results presented in Fig. 2 we concluded that values of $w_{\min }\le 0.05$ produced significant improvements in computational efficiency, placing a cap on m for this mode of loading while maintaining acceptably low errors. An examination of the influence of $e_{\min }$ on the numerical response similarly showed significant improvements, as long as $e_{\min }$ was set no greater than one-hundredth of the equilibrium strain in a particular loading sequence, as shown in Fig. 3.

Since these verification problems were performed using linear viscoelasticity, additional verifications were performed for quasi-linear viscoelasticity (Fig. 4) as well as nonlinear viscoelasticity (Fig. 5) in the range of finite deformations. These results similarly confirmed that the finite element implementation was consistent with the formulated equations presented in Sec. 2.2.

To verify our formulation of a frame-indifferent framework, we introduced a novel benchmark problem whereby a block of anisotropic material was rotated while being cyclically loaded in tension. We compared its response to the same loading regimen in the absence of rotation. As shown in Sec. 3.1.3, the prescribed rotations were in the finite range. Excellent agreement was found between the rotating and fixed models, as presented in Fig. 6. In fact, it was this benchmark problem that made us realize that our original formulation for ${\mathbf{F}}^u(t)$, presented in Sec. 2.1 and in Ref. [1], needed to be corrected as shown in Sec. 2.1.1 and Eq. (2.12) to enforce frame indifference. Since the orthotropic material model of this benchmark problem employed tension-bearing fiber materials, we used the technique described in Sec. 2.1.2 to properly reset the strain origin for each bond-breaking-and-reforming generation. Had we failed to implement this correction for the fiber strain origin, we would have found that tensile cyclical loading of this fibrous material could produce compressive stresses in the material's cyclical response as the number of loading cycles increased.

We found that stress-relaxation problems place a natural cap on the number of generations m, which was achieved once the prescribed deformation became fixed. For these problems, it was helpful to set a suitably small value of $e_{\min }$ to prevent spurious triggering of generations due to numerical roundoffs in the strain calculation. Creep problems theoretically require a continually increasing number of generations as time increases, but setting suitably small values for either $w_{\min }$ or $e_{\min }$ could successfully place a cap on the number of generations, as illustrated in Figs. 2(a) and 3(a), respectively. However, cyclical loading did not provide a natural bound on the number of generations m since it caused continually changing strains. Nevertheless, by setting a minimum threshold $w_{\min }$ on the mass fraction of reformed bonds for triggering a new generation, it was possible to considerably reduce the value of m in an analysis, as illustrated in Fig. 6(c).

Finally, we examined three sets of experimental data as a means of validating the reactive nonlinear viscoelasticity framework. As presented in Sec. 3.2.1, we were able to fit MCL tensile stress-relaxation data from Provenzano et al. [18] using strain-dependent relaxation parameters (Table 2 and Fig. 7) and reproduce their observed trend under tensile creep, whereby the exponent of a power-law fit to the creep response decreased in magnitude with increasing applied stress. This outcome is not unique to the reactive viscoelasticity framework, as Provenzano et al. previously demonstrated similar success using their own choices of models for nonlinear viscoelasticity [19].

The second dataset employed for validating our framework was based on our prior experimental tensile stress-relaxation data on immature bovine articular cartilage [12], as presented in Sec. 3.2.2 and Fig. 8. Here, we had anticipated that the viscoelastic response would be nonlinearly varying with the prescribed tensile strain. Interestingly, it turned out that a single fit of the data at 10% strain could then be used to successfully predict the stress-relaxation responses at lower strains.

The third dataset, presented in Sec. 3.2.3, was a representative tissue sample from a recent experimental study of the stress-relaxation response of bovine nucleus pulposus from Jacobsen and Chahine [28]. This sample's response illustrated the need to include weak bond recruitment as a function of distortional strain, as described in Sec. 2.3, in order to achieve a good curvefit of the experimental data (Fig. 9). It was also found that the relaxation time τ₂ of its reduced relaxation function needed to depend on the distortional strain K₂, further underscoring the nonlinear viscoelastic response of this tissue.

In all these cases our aim was to provide a modicum of validation of the reactive nonlinear viscoelasticity framework and its implementation in febio. Thus, the analysis of experimental data did not cover the full complement of samples tested in the respective studies from which we extracted those data. In practice, we expect that more elaborate models would be needed for comprehensive modeling of the rat MCL or immature bovine articular cartilage.

As acknowledged in the above presentation, there are some limitations to the numerical implementation presented in this study. First, setting useful values for the parameters $w_{\min }$ and $e_{\min }$ may require some trial and error to achieve a satisfactory compromise between accuracy and efficiency. Second, the methods presented here do not guarantee that there will be a cap on the number m of generations needed to model a particular response. Even when a cap is achieved, as shown in Figs. 2 and 3, there is no guarantee that the number will remain low. Nevertheless, despite these limitations, having a computational scheme that can handle any desired reduced relaxation function represents a major advantage for investigators who seek to identify the best model for their experimental data.

In summary, we have formulated and implemented a reasonably efficient numerical scheme for modeling nonlinear anisotropic viscoelasticity using the framework of constrained reactive mixtures. The implementation of this scheme in the open source finite element software febio1 helps to disseminate this tool to the wider community of researchers who need to model nonlinear viscoelastic responses, especially in relation to biological tissues.

Funding Data

• National Institute of General Medical Sciences (R01 GM083925; Funder ID: 10.13039/100000057).