Abstract
DNA replication and the related processes of genome expression require binding, assembly, and function of protein complexes at and near single-stranded (ss)–double-stranded (ds) DNA junctions. These central protein–DNA interactions are likely influenced by thermally induced conformational fluctuations of the DNA scaffold across an unknown distribution of functionally relevant states to provide regulatory proteins access to properly conformed DNA binding sites. Thus, characterizing the nature of conformational fluctuations and the associated structural disorder at ss–dsDNA junctions is critical for understanding the molecular mechanisms of these central biological processes. Here, we describe spectroscopic studies of model ss–dsDNA fork constructs that contain dimers of “internally labeled” cyanine (iCy3) chromophore probes that have been rigidly inserted within the sugar–phosphate backbones of the DNA strands. Our combined analyses of absorbance, circular dichroism, and two-dimensional fluorescence spectroscopy permit us to characterize the local conformational parameters and conformational distributions. We find that the DNA sugar–phosphate backbones undergo abrupt successive changes in their local conformations—initially from a right-handed and ordered DNA state to a disordered splayed-open structure and then to a disordered left-handed conformation—as the dimer probes are moved across the ss–dsDNA junction. Our results suggest that the sugar–phosphate backbones at and near ss–dsDNA junctions adopt specific position-dependent local conformations and exhibit varying extents of conformational disorder that deviate widely from the Watson–Crick structure. We suggest that some of these conformations can function as secondary-structure motifs for interaction with protein complexes that bind to and assemble at these sites.
I. INTRODUCTION
The Watson–Crick (W–C) B-form double-helix1 is the most stable of the myriad structures that DNA can (and must) adopt in order to function both as a template for gene expression and as a vehicle for transmitting heredity. Under physiological conditions, double-stranded (ds) DNA exists primarily as a narrow, Boltzmann-weighted distribution of base-sequence-dependent conformations, for which the W–C structure represents an approximate free energy minimum. The molecular interactions that stabilize dsDNA include cooperative stacking of adjacent nucleotide (nt) bases, internal strain that stacking induces in the sugar–phosphate backbones, W–C hydrogen bonding between opposite complementary strands, intra- and inter-chain repulsion between adjacent backbone phosphates, counterion condensation, and orientation of polar water molecules within the nearest solvation layers at exposed DNA surfaces. All these interactions are subject to thermally induced fluctuations (i.e., DNA “breathing”), which may lead to local segments adopting transiently unstable conformations over time scales spanning tens of microseconds to several seconds.2 For example, on sub-second time scales and depending on temperature relative to the overall melting temperature of the DNA duplex, the interior of local AT-rich regions of dsDNA may become exposed to the surrounding aqueous environment by spontaneously disrupting the W–C structure and forming open “bubble-like” conformations. On the time scale of multiple seconds, segments of dsDNA may undergo higher order sequence-dependent distortions of the local conformation, such as the formation of a local “bubble,” “bend,” or “kink.”
The spontaneous formation of an unstable local dsDNA conformation is very likely a key initial step in the assembly mechanisms of complexes of gene regulatory proteins that recognize and bind to specific nt base sequences. In contrast, protein–DNA assembly mechanisms that occur largely independently of specific nucleotide base sequences must utilize the ability of the protein or protein complex to recognize certain secondary-structure motifs that can be adopted by the sugar–phosphate backbones of the DNA.3 For example, the assembly of DNA replication complexes involves the preferential binding of proteins to single-stranded (ss)–dsDNA forks and junctions.2 In principle, various types of DNA breathing near ss–dsDNA junctions may facilitate the interconversion between various unstable conformations, of which one or more may be expected to resemble that of the DNA framework within a stable protein–DNA complex. Such an unstable conformational species may serve as a “transition state” for the interaction of DNA binding sites with replication proteins.
In this work, we present spectroscopic studies of the distributions of structural parameters that characterize the local conformations of the sugar–phosphate backbones at and near ss–dsDNA fork junctions. These experiments use DNA constructs in which carbocyanine dye Cy3 has been covalently attached as a dimer pair within the sugar–phosphate backbones at specific positions relative to the ss–dsDNA junction (see Fig. 1). The Cy3 chromophore is often used as a fluorescent marker for DNA sequencing and other biotechnological applications due to its relatively high absorption cross section and favorable fluorescence quantum yield.4 The Cy3 chromophore consists of a conjugated trimethine bridge that cojoins two indole-like substituents [see Fig. 1(a)]. The lowest energy π → π* electronic transition between the ground state g and the excited state e occurs when the molecule is in its all-trans ground state configuration.
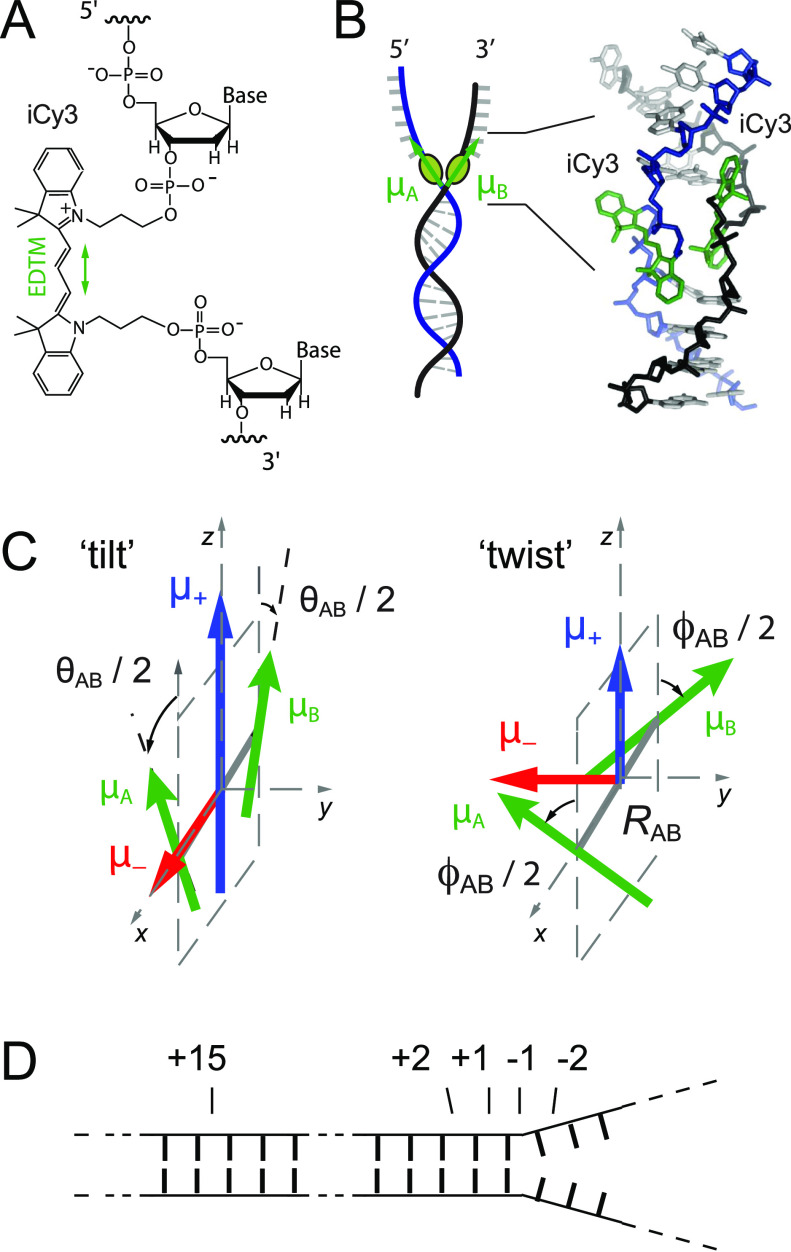
FIG. 1.
Labeling chemistry and nomenclature of the internal (iCy3)2 dimer probes positioned within the sugar–phosphate backbones of model ss–dsDNA fork constructs. (a) The Lewis structure of the iCy3 chromophore is shown with its 3′ and 5′ linkages to the sugar–phosphate backbone of a local segment of ssDNA. The double-headed green arrow indicates the orientation of the electric dipole transition moment (EDTM). (b) An (iCy3)2 dimer-labeled DNA fork construct contains the dimer probe near the ss–dsDNA fork junction. The conformation of the (iCy3)2 dimer probe reflects the local secondary structure of the sugar–phosphate backbones at the probe insertion site position. The sugar–phosphate backbones of the conjugate DNA strands are shown in black and blue, the bases are shown in gray, and the iCy3 chromophores are shown in green. (c) The structural parameters that define the local conformation of the (iCy3)2 dimer probe are the inter-chromophore separation vector RAB, the tilt angle θAB, and the twist angle ϕAB. The electrostatic coupling between the iCy3 chromophores gives rise to the anti-symmetric (−) and symmetric (+) excitons, which are indicated by the red and blue arrows, respectively, and whose magnitudes and transition energies depend on the structural parameters. (d) The insertion site position of the iCy3 dimer probe is indicated relative to the pseudo-fork junction using positive integers in the direction toward the double-stranded region and negative integers in the direction toward the single-stranded region.
The linear absorbance spectrum of the free Cy3 chromophore in solution, as well as when it is attached covalently to a nucleic acid, exhibits a pronounced vibronic progression, which can be simulated using a Holstein–Frenkel Hamiltonian with electronic transition energy ɛeg = ∼18 250 cm−1, vibrational mode energy ℏω0 = ∼1100 cm−1, and Huang–Rhys electronic–vibrational coupling parameter λ2 = ∼0.55.5 The electric dipole transition moment (EDTM) has magnitude μeg = ∼12.8 D and orientation that lies parallel to the Cy3 trimethine bridge [see Fig. 1(a)]. Cy3 can be chemically attached “internally” to the DNA with “iCy3” acting as a molecular bridge between bases as an extension of the sugar–phosphate backbone.6 When two complementary single strands of DNA with opposed iCy3 labeling positions are annealed, an (iCy3)2 dimer probe is formed within the DNA duplex. If the sequence of nt bases at or near one side of the (iCy3)2 dimer is non-complementary, the labeling location occurs at a ss–dsDNA fork junction, as schematically shown in Fig. 1(b). iCy3 monomer-labeled ss–dsDNA constructs are similarly prepared with a thymine (T) base at the position opposite to the probe within the complementary strand.
Because of the relatively small separation between iCy3 chromophores within the (iCy3)2 dimer-labeled ss–dsDNA fork constructs, the monomer EDTMs [labeled sites A and B in Fig. 1(c)] can couple through a resonant electrostatic interaction J. This coupling gives rise to symmetric (+) and anti-symmetric (−) excitons with orthogonally polarized dipole moments and with relative magnitudes that depend on the local conformation of the (iCy3)2 dimer probe. The symmetric and anti-symmetric excitons consist of a manifold of delocalized electronic-vibrationally coupled states, which are superpositions of electronic–vibrational product states of the A and B monomer sites.7,8 The absorbance and circular dichroism (CD) spectra of (iCy3)2 dimer-labeled ss–dsDNA constructs are well-described using the Holstein–Frenkel model and can be used to determine local conformational parameters.5,7 The structural parameters that characterize the dimer conformation are the “tilt” angle θAB, the “twist” angle ϕAB, and the separation RAB. In our previous spectroscopic studies of (iCy3)2 dimer-labeled ss–dsDNA constructs, we calculated the resonant electrostatic coupling by treating the EDTMs as point dipoles.7 We later repeated these calculations using an “extended-dipole” model9,10 that more accurately accounted for the extension of the transition charge density across the length of the molecule and that yielded nearly identical results to those provided by the point-dipole approximation.5 We note that more accurate models of electrostatic coupling for Cy3, which are based on ab initio calculations of atomic transition charges, have recently become available and provide future opportunities to test the validity of point-dipole and extended dipole models.11
Here, we focus on the distributions of structural parameters obtained from theoretical analyses of absorbance, CD, and two-dimensional fluorescence spectroscopy (2DFS) of (iCy3)2 dimer-labeled ss–dsDNA fork constructs. While absorbance and CD can be used to determine the mean structural parameters of the (iCy3)2 dimer probes, 2DFS provides additional information about the distributions of these parameters. The underlying optical principles of 2DFS resemble those of 2D nuclear magnetic resonance (NMR)12,13 and 2DIR, with the latter providing structural and dynamic information about local vibrational modes in proteins,14,15 nucleic acids,16,17 and biomolecular hydration shells.18 2DIR has been used to distinguish sequence-dependent inter-base H-bonds in duplex DNA16,17 and the rearrangements of water molecules at or near the exposed surfaces of DNA strands.18 While these relatively fast processes likely contribute to nucleic acid stability and dynamics, they do not directly probe the DNA breathing fluctuations involved in protein recognition events.19,20 In contrast, the signals detected by 2DFS on (iCy3)2 dimer probe-labeled ss–dsDNA constructs do directly monitor DNA backbone conformations and conformational disorder, which likely play a central role in protein recognition and binding events.
In the following experiments, we studied several different ss–dsDNA fork constructs in which we varied the (iCy3)2 dimer labeling position, as shown in Fig. 1(d), and for some of these constructs, we varied the temperature. In contrast to the (iCy3)2 dimer ss–dsDNA constructs, the linear spectra of the iCy3 monomer ss–dsDNA constructs are relatively insensitive to probe labeling position and temperature, as previously reported.5,7 These findings suggest that for the (iCy3)2 dimer ss–dsDNA constructs, the sensitivity of the homogeneous line shapes to labeling position and temperature is largely due to variations of the coupling interaction J, which is sometimes referred to as “off-diagonal disorder” in the reference frame of the monomer sites.15,21
In our prior studies, we established that a combination of absorbance and CD spectra contain sufficient information to determine mean values of the structural parameters , , and , in addition to an estimate of the inhomogeneous line broadening parameter σI.5,7 Inhomogeneous line broadening is a direct measure of structural heterogeneity due to individual molecules of the sample exhibiting uniquely different homogeneous line shapes, which depends on the local conformation of the (iCy3)2 dimer probe. Our prior estimates of σI were obtained from a deconvolution of absorbance and CD spectra and were based on the value of the homogeneous linewidth ΓH = ∼186 cm−1. We determined the latter value from room temperature 2DFS experiments on iCy3 monomer and (iCy3)2 dimer-labeled DNA constructs in which the probe labeling position was deep within the double-stranded region and for which the laser bandwidth was ΔλL = ∼16 nm.7 In the current work, we perform a more accurate analysis of 2DFS data in which the laser bandwidth was ΔλL = ∼33 nm. This increase in the laser bandwidth permits us to simultaneously determine the homogeneous and inhomogeneous line shape parameters as a function of probe labeling position and temperature. In addition, we here extend our line shape analysis to model the distributions of the structural parameters RAB, θAB, and ϕAB because variation in these parameters “builds in” the structural heterogeneity measured by our 2DFS experiments. In the analyses that follow, we have assumed that the distributions of structural parameters can be successfully modeled as Gaussians, which can be characterized using the standard deviations σR, σθ, and σϕ.
It is useful to briefly review here the general dependence of the homogeneous line shapes of the absorbance, CD, and 2DFS observables on the (iCy3)2 dimer conformation and associated electrostatic couplings.5,7 As previously mentioned, the optical transitions of an isolated iCy3 monomer probe are well-described using a simple Hamiltonian model based on a two-electronic level system coupled to a single vibrational (harmonic) mode. The iCy3 monomer has its lowest-lying optical transition centered at ∼18 250 cm−1 (the “0–0” line with no vibrational excitation) and sequentially higher lying optical transitions (e.g., “0–1” and “0–2” with one and two vibrational excitations, respectively) spaced apart by the vibrational mode energy ∼1100 cm−1. The absorbance spectrum of the iCy3 monomer, therefore, exhibits a vibronic progression with relative peak intensities determined by the associated Franck–Condon factors. The corresponding 2D fluorescence spectrum is a contour diagram that reflects the transition probability-weighted correlations between successive optical transitions of the vibronic sub-bands. The 2D fluorescence spectrum, thus, exhibits peaks and cross-peaks associated with the optical transitions with relative intensities determined by both the Franck–Condon factors and the spectral overlaps between the optical transitions and the spectrum of the exciting laser. Because CD depends on the presence of chiral asymmetry of the transition dipole moments, the (achiral) iCy3 monomer exhibits an approximately featureless CD spectrum.
For the (iCy3)2 dimer-labeled ss–dsDNA constructs studied in this work, the strength of the electrostatic interactions lies within the so-called “intermediate-coupling regime”22 so that the absorbance spectrum of the dimer has a similar shape to that of the monomer. However, the electrostatic interaction leads to each of the vibronic features (i.e., 0–0 and 0–1) being split and additionally broadened into the symmetric (+) and anti-symmetric (−) exciton subbands. The relative peak intensities of the absorbance spectrum depend on (in addition to the above-mentioned factors that affect the iCy3 monomer) the local conformation of the dimer, which determines the magnitudes of the symmetric and anti-symmetric transition dipole moments μ± [see Fig. 1(c)]. The 2D fluorescence spectrum of the (iCy3)2 dimer probe, thus, exhibits a higher density of peaks and cross-peaks, which are associated with the relatively high density of symmetric and anti-symmetric excitons, when compared to the spectrum of the iCy3 monomer. In contrast to the CD of the iCy3 monomer, which is featureless, the CD of the (iCy3)2 dimer generally exhibits features characteristic of the chiral asymmetry of the exciton-coupled transition dipole moments.
Among the significant findings of this work is that the (iCy3)2 dimer is a reliable probe of the local conformation of the sugar–phosphate backbones at and near ss–dsDNA fork junctions, which sensitively depends on the labeling site position and temperature. We studied the temperature-dependence of the local conformation of (iCy3)2 dimer-labeled ss–dsDNA constructs, both at positions deep within the duplex region (+15) and near the ss–dsDNA fork junction (−1). We find that local conformations and conformational disorder of the sugar–phosphate backbones at the +15 position are minimized at room temperature (23 °C) and change rapidly as the temperature is either raised or lowered away from room temperature under physiological salt conditions (100 mM NaCl and 6 mM MgCl2), permitting for the development of local conformations that deviate significantly from the W–C duplex DNA structure, such as bubbles, bends, and kinks. In contrast, local conformations and conformational disorder of the ss–dsDNA junction at the −1 position do not vary significantly with increasing temperature, suggesting that the distribution of thermally accessible states is relatively narrow. Moreover, the mean local conformation and conformational disorder vary systematically with the (iCy3)2 dimer-labeling position [from +2 to −2, refer to Fig. 1(d) for probe labeling nomenclature]. This transition is characterized by an increase in conformational disorder and a loss of cylindrical symmetry characterized by the mean tilt angle , followed by a change in the local symmetry of the DNA backbones from right-handed to left-handed, as reflected by the mean twist angle . Perhaps contrary to expectations, regions of the ss–dsDNA junction extending into the single strands appear to be relatively well-ordered.
II. EXPERIMENTAL METHODS
A. Sample preparation
The sequences and nomenclature of the iCy3 monomer and (iCy3)2 dimer-labeled ss–dsDNA constructs used in our studies are shown in Table I. Oligonucleotide samples were purchased from Integrated DNA Technologies (IDT, Coralville, IA) and used as received. Solutions were prepared containing ∼1 µM oligonucleotide in the 10 mM TRIS buffer with 100 mM NaCl and 6 mM MgCl2. Complementary strands were combined in equimolar concentrations. The samples were heated to 95 °C for 4 min and left to cool slowly on a heat block overnight prior to data collection. The annealed iCy3 monomer and (iCy3)2 dimer-labeled ss–dsDNA fork constructs contained both ds and ss DNA regions, with the probe labeling positions indicated by the nomenclature described in Fig. 1(d). The iCy3 monomer-labeled constructs contained a thymine base (T) in the complementary strand at the position directly opposite to the probe chromophore.
TABLE I.
Base sequences and nomenclature for the iCy3 monomer and (iCy3)2 dimer ss–dsDNA fork constructs used in these studies. The horizontal lines indicate regions of complementary base pairing.
| DNA construct | Nucleotide base sequence |
|---|---|
| +15 (iCy3)2 | 3′-GTC AGT ATT ATA CGC TCy3C GCT AAT ATA TAC GTT TTT TTT TTT TTT TTT TTT TTT TTT TTT T-5′ |
| dimer | 5′-CAG TCA TAA TAT GCG ACy3G CGA TTA TAT ATG CTT TTA CCA CTT TCA CTC ACG TGC TTA C-3′ |
| +15 iCy3 | 3′-GTC AGT ATT ATA CGC TCy3C GCT AAT ATA TAC GTT TTT TTT TTT TTT TTT TTT TTT TTT TTT T-5′ |
| monomer | 5′-CAG TCA TAA TAT GCG A T G CGA TTA TAT ATG CTT TTA CCA CTT TCA CTC ACG TGC TTA C-3′ |
| −1 (iCy3)2 | 3′-GAG GGA GCA CAG CAG AGG TCA GTA TTA TAC GCT Cy3CG CTG GTA TAC CAC GTT (T)28–5′ |
| dimer | 5′-CTC CCT CGT GTC GTC TCC AGT CAT AAT ATG CGA Cy3AT GCT TTT ACC ACT TTC ACT CAG GTG CTT A-3′ |
| −1 iCy3 | 3′-GAG GGA GCA CAG CAG AGG TCA GTA TTA TAC GCT Cy3CG CTG GTA TAC CAC GTT (T)28–5′ |
| monomer | 5′-CTC CCT CGT GTC GTC TCC AGT CAT AAT ATG CGA T AT GCT TTT ACC ACT TTC ACT CAG GTG CTT A-3′ |
| −2 (Cy3)2 | 3′-GAG GGA GCA CAG CAG AGG TCA GTA TTA TAC GCT Cy3CG CTG GTA TAC CAC GTT (T)28–5′ |
| dimer | 5′-CTC CCT CGT GTC GTC TCC AGT CAT AAT ATG CGC Cy3AT ACT TTC GCC ACT TTC ACT CAC GTG CTT A-3′ |
| +1 (Cy3)2 | 3′-GAG GGA GCA CAG CAG AGG TCA GTA TTA TAC GCT Cy3CG CTG GTA TAC CAC GTT (T)28–5′ |
| dimer | 5′-CTC CCT CGT GTC GTC TCC AGT CAT AAT ATG CGA Cy3GT ACT TTC GCC ACT TTC ACT CAC GTG CTT A-3′ |
| +2 (Cy3)2 | 3′-GAG GGA GCA CAG CAG AGG TCA GTA TTA TAC GCT Cy3CG CTG GTA TAC CAC GTT (T)28–5′ |
| dimer | 5′-CTC CCT CGT GTC GTC TCC AGT CAT AAT ATG CGA Cy3GC ACT TTC GCC ACT TTC ACT CAC GTG CTT A-3′ |
B. Absorbance and circular dichroism (CD) measurements
We performed linear absorbance measurements using a Cary 3E UV–vis spectrophotometer and CD measurements with a JASCO model J-720 CD spectrophotometer. Series of temperature-dependent measurements were performed over the range of 1–75 °C. For all absorbance and CD measurements, the samples were housed in a 1 cm quartz cuvette. CD measurements over the temperature range 1–25 °C were performed using a JASCo J-1500 CD spectrophotometer equipped with a Koolance EXOS liquid cooling system, which can operate reliably at near-freezing temperatures.
C. Two-dimensional fluorescence spectroscopy (2DFS)
Phase-modulation 2DFS experiments were performed on the iCy3 labeled ss–dsDNA fork constructs listed in Table I using methods and procedures described previously.5,7,23–26 The train of four collinear laser pulses used to excite the sample was centered on wavelength λL = ∼532 nm (∼18 800 cm−1), with bandwidth ΔλL = ∼33 nm (∼1100 cm−1). The pulses were generated using a custom-built non-collinear optical parametric amplifier (NOPA) that was pumped using a 140 kHz Ti:Sa regenerative amplifier (Coherent, RegA). The NOPA output was divided into two paths using a 50/50 beam splitter, and each beam was directed to a separate Mach–Zehnder interferometer (MZI). Acousto-optic Bragg cells, placed within the beam paths of each MZI, were used to apply a relative temporal phase sweep to the pulses exiting the MZI. Thus, the relative phase of pulses 1 and 2 and that of pulses 3 and 4 were swept continuously at the frequencies Ω21 = 5 kHz and Ω43 = 8 kHz, respectively. The relative paths of the pulses were varied using computer-controlled translation stages to step the time delay t21 between the first pair of pulses and the delay t43 between the second pair of pulses. For all our measurements, the time delay t32 between the second and third pulse was set to zero. For each combination of time delays, the four pulses were used to excite resonant electronic transitions of the iCy3 probes, and the ensuing fluorescence was detected and demodulated simultaneously at the sum frequency Ω43 + Ω21 = 13 kHz and the difference frequency Ω43 − Ω21 = 3 kHz, which correspond, respectively, to the fourth-order non-rephasing (NRP) and rephasing (RP) signals.24,26,27
The optical pulses were compressed using a quadruple-pass fused-silica prism pair to compensate for dispersive media in the optical paths preceding the sample. Pulse widths were characterized by placing a beta-barium borate (BBO) frequency doubling crystal at the sample position where a phase-modulated train of pulse pairs was incident. The frequency-doubled signal output was detected using a lock-in amplifier, which was referenced to the waveform signal used to modulate the relative phase of the pulses.23,26 The pulse compressor was adjusted so that the full-width-at-half-maximum (FWHM) of the pulse–pulse autocorrelation, for each of the pulse pairs, was ΔτL = ∼28 fs. We measured the laser bandwidth ΔλL = ∼33 nm (∼1100 cm−1) centered at λL = ∼532 nm using an Ocean Optics spectrometer. The measured time–bandwidth product was = ∼0.98, which is larger than the optimal value (0.44) for Fourier-transform limited Gaussian pulses and indicates the presence of some third-order dispersion that was not compensated by the prism compressor.
The laser pulse spectrum with the above spectral properties was reproducibly maintained and continuously monitored during each 2DFS measurement described in this work. Samples were housed in a 1 mm quartz cuvette that was mounted to a small aluminum heating block, which was itself placed in thermal contact with a copper block equipped with internally circulating cooling water. The temperature of the sample was maintained to within ∼±0.1 °C using two thermoelectric chips, which were mounted directly to the aluminum block. Fluorescence was detected at a 45° angle of incidence relative to the front face of the sample cuvette using a 5 mm collection lens and a 615 nm long-pass filter (Chroma, HQ615LP), which served to minimize scattered excitation light. A light stream of nitrogen was continuously flowed across the front face of the cuvette to prevent condensation of vapor for measurements performed at reduced temperatures.
III. THEORETICAL MODELING
A. Simulation of absorbance and CD spectra
We simulated the absorbance and CD spectra of the iCy3 monomer and (iCy3)2 dimer ss–dsDNA fork constructs (see Table I) by applying the Holstein–Frenkel (H–F) model,8,28 as described in our previous studies.5,7 The H–F model treats each iCy3 monomer as a two-electronic-level molecule with ground state and excited state , which are coupled to a single harmonic vibrational mode of frequency ω0. The electronic–vibrational coupling is characterized by the Huang–Rhys parameter, , where d is the displacement of the minimum of the electronically excited vibrational potential energy surface relative to that of the ground state surface. The Huang–Rhys parameter physically corresponds to the number of vibrational quanta absorbed by the system upon electronic excitation. Each monomer (M, labeled A and B) is chemically identical with electronic transition energy, ɛeg, and electric dipole transition moment (EDTM), . The Hamiltonian operator representing the monomer is given by
| (1) |
where and are, respectively, the operators for creating and annihilating a vibrational excitation in the electronic potential energy surfaces. These operators obey the commutation relation , where is the Kronecker delta function and the monomer labels .
The monomer absorbance spectrum is a weighted sum of homogeneous line shapes associated with the individual vibronic transitions from the initially unexcited ground state, ,
| (2) |
In Eq. (2), the index is the vibrational quantum number of the electronically excited (unexcited) potential energy surface, the homogeneous line shape is given by the Lorentzian , with the FWHM linewidth equal to ΓH, and the individual peak intensities depend on the Franck–Condon factors, .
To account for the influence of varying local environments on the transition energy (i.e., spectral inhomogeneity), we describe the total absorbance spectrum as a Voigt convolution integral29
| (3) |
In Eq. (3), the Gaussian distribution, , represents the probability that a given monomer has its transition energy relative to an average value and σI is the standard deviation of the inhomogeneously broadened spectrum.
The Hamiltonian of the AB dimer is written as
| (4) |
where the final term couples the singly excited electronic transitions of the monomers through an electrostatic interaction J. In our nomenclature used here, represents the product state in which monomer A is electronically excited and monomer B is unexcited. The electronic coupling parameter J depends on the dimer conformation and can be modeled in terms of the Coulomb interaction between the individual monomer transition charge densities ,
| (5) |
where RAB = rB − rA. In the current work, we approximate the electrostatic coupling parameter using the “extended” transition dipole–dipole model, which accounts for the finite size of the iCy3 chromophore by including a one-dimensional displacement vector l that lies parallel to the monomer EDTM,9,10
| (6) |
Equation (6) assumes that the transition charge density for each monomer is composed of two point charges of equal magnitude (q) and opposite sign separated by the distance l such that .5,10 The distances between point charges are given by and , where and are unit vectors that lie parallel to the monomer EDTMs. For the calculations that follow, we used the values = 12.8 D, l = 7 Å, and q = 0.38e (where e is the electronic charge unit), as in our previous studies.5 In the extended dipole model, the value of J depends on the inter-chromophore separation RAB, the twist angle ϕAB, and the tilt angle θAB [see Fig. 1(c)], which collectively specify the (iCy3)2 dimer conformation.
For a given value of the coupling parameter J, we determined the eigen-energies and the eigen-states of the dimer Hamiltonian given in Eq. (4). The singly excited states are symmetric (+) and anti-symmetric (−) superpositions of electronic–vibrational products of site-basis states , where the coefficients depend on the vibrational coordinates of the monomers, is the vibrational product state, and β = (0, 1, …) is a state index that advances in order of increasing energy.8
The dimer absorbance spectrum is the sum of symmetric (+) and anti-symmetric (−) exciton features,
| (7) |
where , is the collective EDTM, and is a Lorentzian function that represents the homogeneous line shape of the transition with eigen-energy and FWHM linewidth ΓH. Similarly, the dimer CD spectrum is the sum of symmetric and anti-symmetric rotational strengths,
| (8) |
where . In the above expressions, we have defined the ground vibrational–electronic state of the AB dimer .
The (iCy3)2 dimer conformation may vary from molecule to molecule due to local DNA “breathing” fluctuations so that the homogeneous dimer absorbance and CD line shapes are convolved with an inhomogeneous distribution function , which is centered at the average transition energy and has standard deviation σI. The final expressions for the absorbance and CD spectra are given, respectively, by the Voigt profiles,
| (9) |
| (10) |
B. Simulation of two-dimensional fluorescence spectra (2DFS)
We applied the H–F model to simulate our 2D fluorescence spectra according to methods developed previously.24,27 The 2DFS signals are written in terms of the rephasing (RP) and non-rephasing (NRP) fourth-order response functions,
| (11) |
and
| (12) |
In Eqs. (11) and (12), the first two terms on the right-hand sides of the proportionalities represent, respectively, the ground state bleach (GSB) and stimulated emission (SE) contributions. The final two terms represent excited state absorption (ESA) contributions for the singly and doubly excited state manifolds, respectively. The parameter Γ2D represents the fluorescence quantum yield of the doubly excited state-manifold relative to that of the singly excited state manifold. The possible values of Γ2D may range from 0 to 2, which have the effect of modifying the sign and magnitude of the ESA contributions relative to those of the GSB and SE. In our analyses of the 2D spectral line shapes of the iCy3 monomer and (iCy3)2 dimer ss–dsDNA constructs discussed below, we treated Γ2D as one of three parameters (the others being the homogeneous and inhomogeneous linewidth parameters, ΓH and σI, respectively) that were optimized to our experimental data. For all our calculations, we found that the optimized value for Γ2D was ∼0.3 (see Fig. S1 of the supplementary material).
In writing the response functions, we designate as the dimer state with both monomers electronically unexcited and with vibrational quantum number v = vA + vB such that, for example, state is the electronic ground state with zero vibrational occupancy. The states and represent any two of the symmetric and anti-symmetric excitons within the singly excited state manifold, and the state represents any one state within the doubly excited state manifold. When the effects of inhomogeneous broadening are included, the individual terms of the RP response functions can be written as follows:30–32
| (13) |
| (14) |
| (15) |
and for NRP,
| (16) |
| (17) |
| (18) |
In Eqs. (13)–(18), the factor denotes the orientationally averaged four-point product, , which accounts for the projections of the (iCy3)2 dimer transition dipole moments onto the (parallel) plane polarizations of the four laser pulses and includes an average over the isotropic distribution of dimer orientations in solution.33 The factor is the product of the intensities of the laser at the transition frequencies ωab and ωcd.
An important feature of the RP and NRP response functions is their distinct dependences on the homogeneous and inhomogeneous linewidth parameters, ΓH and σI, respectively31,34 (see Fig. 2). The RP response functions [Eqs. (13)–(15)] contain the line shape factor , which decays exponentially at the homogeneous dephasing rate along the diagonal axis (t21 + t43) and as a Gaussian envelope with inhomogeneous decay constant along the anti-diagonal axis (t21 − t43) [see Fig. 2(a), top panel]. In contrast, the NRP response functions [Eqs. (16)–(18)] contain the line shape factor , which decays along the diagonal axis with rate constants that depend on both the homogeneous and inhomogeneous parameters [see Fig. 2(a), bottom panel]. Examples of the RP and NRP response functions are shown in Fig. 2(b). The RP and NRP 2D fluorescence spectra, which are functions of the optical frequencies and , are obtained by performing two-dimensional Fourier transforms of the response functions with respect to the delay variables t21 and t43 given in Eqs. (11) and (12), respectively [see Fig. 2(c)].
FIG. 2.
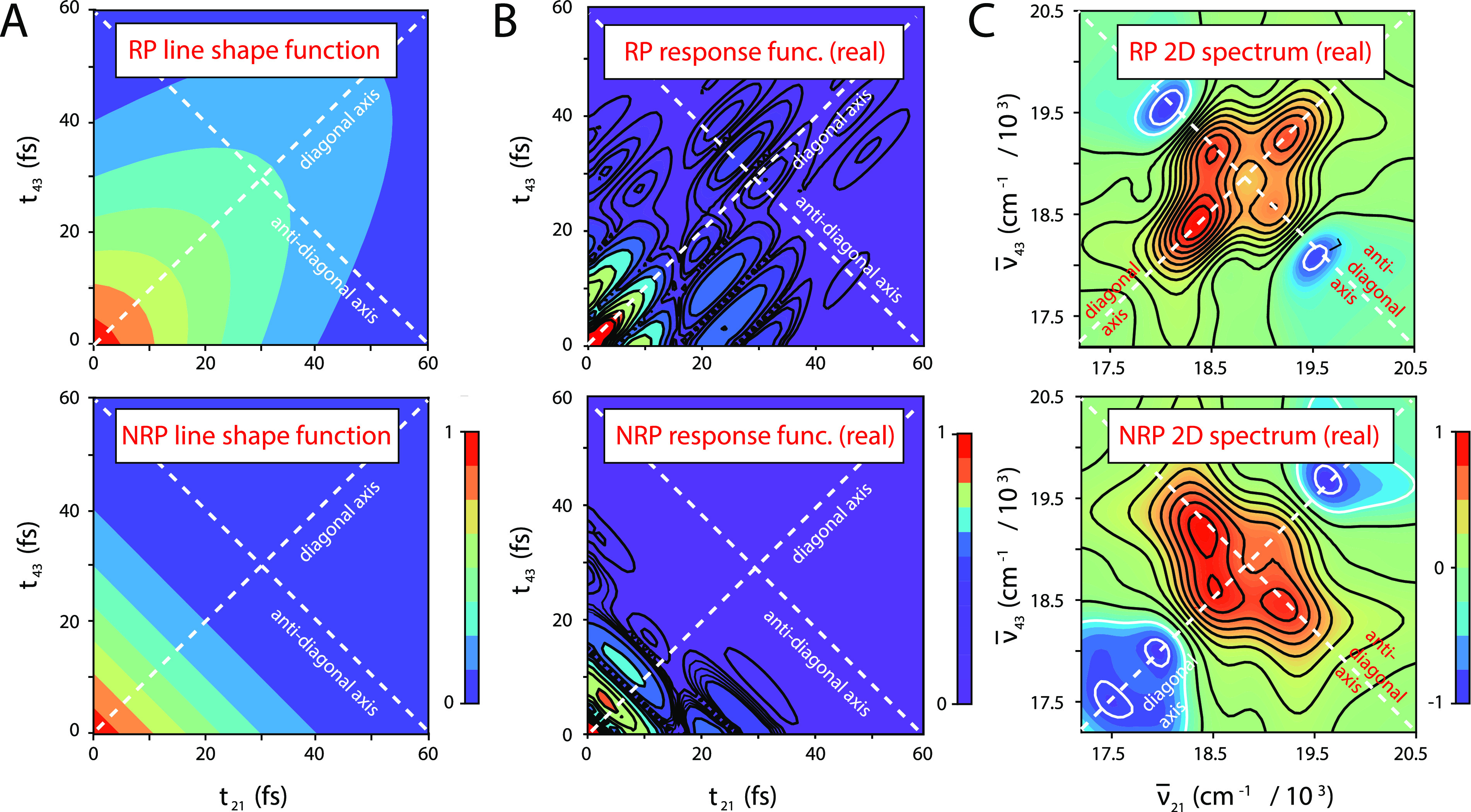
Example calculations of the 2DFS rephasing (RP) and non-rephasing (NRP) response functions and 2D spectra for the −1 iCy3 monomer ss–dsDNA construct at 25 °C. The iCy3 monomer Hamiltonian parameters used in these calculations are given in Table S2 of the supplementary material and include the values ΓH = 105 cm−1 and σI = 198 cm−1. All functions are displayed as two-dimensional contour plots with diagonal and anti-diagonal axes indicated as the white dashed lines. (a) The RP line shape function (top panel), , contains two independent factors, one representing an exponential (homogeneous) decay along the diagonal axis (t21 + t43) and the other representing a Gaussian (inhomogeneous) decay along the anti-diagonal axis (t21 − t43). The NRP line shape function (bottom panel), , depends on both the homogeneous and inhomogeneous linewidth parameters, which contribute to the decays along both diagonal and anti-diagonal axes. (b) The absolute value of the real parts of the RP response function [Eq. (11), top panel] and the NRP response function [Eq. (12), bottom panel] contain the line shape functions shown in (a) and the transition frequency phase factors given in Eqs. (13)–(18). (c) The RP 2D spectrum (top panel) and the NRP spectrum are calculated by performing a two-dimensional Fourier transform of the response functions shown in (b) with respect to the time variables t21 and t43.
In the limiting case for which spectral inhomogeneity greatly exceeds the homogeneous linewidth (σI ≫ ΓH), individual features of the RP 2D spectrum exhibit a Lorentzian line shape in the direction of the anti-diagonal axis () and an inhomogeneously broadened line shape in the direction of the diagonal axis ().31 In this limit, the homogeneous and inhomogeneous linewidth parameters can be determined directly from the RP 2D spectrum by fitting the anti-diagonal and diagonal cross sections of the 2D spectral line shape to model Lorentzian and Gaussian functions, respectively. However, in the more general case of moderate inhomogeneity (σI ≃ ΓH), the homogeneous and inhomogeneous broadening mechanisms each contributes to the RP 2D line shape in both the diagonal and anti-diagonal directions. In our analyses of the 2D spectral line shapes of the iCy3 monomer and (iCy3)2 dimer ss–dsDNA constructs presented below, we determined the homogeneous and inhomogeneous line shape parameters by simultaneously fitting experimental RP and NRP 2DFS spectra to the numerical Fourier transforms of the model response functions given in Eqs. (11) and (12). This approach provided an accurate description of the 2D spectra without imposing any assumed restrictions on the degree of inhomogeneity present.
C. Numerical optimization procedures
In previous work,5,7 we characterized the iCy3 monomer absorbance spectrum using four independent parameters: the mean electronic transition energy 18 250 cm−1, the Huang–Rhys vibronic coupling parameter λ2 ≅ 0.57, the vibrational frequency ω0 ≅ 1100 cm−1, and the spectral inhomogeneity parameter σI ≅ 300 cm−1. We determined these values by performing a numerical optimization procedure in which we directly compared the simulated spectra [Eq. (3)] to experimental data. In our previous studies, we assumed constant values for the homogeneous FWHM linewidth ΓH = 186 cm−1 and the monomer EDTM = 12.8 D, which we determined in separate experiments.7 We used these monomer parameters as inputs to our analyses of the absorbance and CD spectra of the (iCy3)2 dimer ss–dsDNA constructs [Eqs. (9) and (10), respectively]. In our calculations of the dimer spectra, we included six vibrational levels in the monomer electronic–vibrational manifold of states to ensure numerical convergence.7 The dimer absorbance and CD spectra were, thus, used to obtain optimized values of the mean structural parameters , , and , which determined the mean electrostatic coupling [Eq. (6)].
We next used the set of optimized structural coordinates as inputs to our model analyses of the RP and NRP 2DFS data, which are described in Eqs. (11) and (12), respectively. The transition frequencies, ωab and ωcd, appearing in the RP and NRP response functions [Eqs. (13)–(18)], in addition to the laser spectral overlap factors and the transition-dipole orientation factors , are all constants determined by the values of the mean structural coordinates. For our simulations of the 2DFS data, it was necessary to carry out the sums of Eqs. (13)–(18) over the space of transition pathways between the dimer ground electronic–vibrational state manifold (labeled , with dimension 6 × 6 = 36), the singly excited electronic–vibrational state manifold (labeled and , with dimension 36 + 36 = 72), and the doubly excited electronic–vibrational state manifold (, with dimension 36). Nevertheless, the actual number of terms needed to simulate the response functions accurately is a small fraction of the total number of possible pathways due to the resonance conditions imposed by the laser pulse spectrum [reflected by the factors ]. In practice, for each response function, the summation over transition pathways was calculated and stored as a two-dimensional interferogram that was multiplied by the line shape function in the case of the RP response functions [Eqs. (13)–(15)] and the line shape function in the case of the NRP response functions [Eqs. (16)–(18)]. We, thus, performed optimization analyses of our 2DFS data to obtain accurate values for the homogeneous and inhomogeneous linewidth parameters, ΓH and σI, respectively.
For our optimization calculations, we implemented an automated multi-variable regression analysis to efficiently explore the parameter space of the spectroscopic models. We have applied similar procedures in past studies,5,7,24,27,35–37 in which a random search algorithm was used to select an initial set of input parameters that were refined iteratively using commercial software (KNITRO).38 For each set of input trial parameters, we calculated a linear least squares error function χ2, which was minimized to obtain the optimized solution. Thus, for our optimizations of the absorbance and CD spectra of the (iCy3)2 dimer ss–dsDNA constructs, we minimized the function
| (19) |
and for our optimizations of 2DFS data, we minimized the function
| (20) |
We performed error-bar analyses of the optimized parameters, which we determined by a 1% deviation of the χ2 function from its optimized value.
D. Modeling conformational heterogeneity of (iCy3)2 dimer-labeled ss–dsDNA constructs
As discussed in Secs. III A–III C, the information provided by the linear absorbance and CD spectra of the (iCy3)2 dimer permits us to determine the mean values of the conformational coordinates , , and . By expanding the analysis to include 2DFS data, we determined additional information about the inhomogeneously broadened distribution of homogeneous line shapes, which is due primarily to the variation of local (iCy3)2 dimer conformations within the ensemble of ss–dsDNA molecules. To develop our interpretation of the inhomogeneous line shape in terms of structural disorder, we assumed that the conformational coordinates, RAB, θAB, and ϕAB, can be treated as independent variables and that their distributions can be described as a product of Gaussians,
| (21) |
We emphasize that by assuming that the structural coordinates are independent variables—i.e., possible covariance terms are negligible—Eq. (21) may only be used to determine estimates of the standard deviations.
To model our inhomogeneously broadened 2DFS data, we calculated a library of “homogeneous” RP and NRP 2D fluorescence spectra spanning a range of equally spaced values for the conformational coordinates and for which the homogeneous and inhomogeneous linewidth parameters were set equal—i.e., ΓH = σI = 100 cm−1. In Fig. 3(a), we show examples of simulated homogeneous RP and NRP 2D fluorescence spectra of the +2 (iCy3)2 dimer ss–dsDNA construct corresponding to three different values of the mean twist angle = 80.6°, 82.6°, and 84.6° and for mean tilt angle = 5.1° and mean separation = 2.8 Å. From the library of homogeneous 2D spectral line shapes, we simulated inhomogeneously broadened RP and NRP 2D spectra by numerically sampling the library according to the Gaussian distribution given in Eq. (21). We, thus, followed a procedure similar to that described in Sec. III C to iteratively calculate the linear least squares error function between simulated and experimental spectra, which we minimized to obtain optimized values for the standard deviations of the conformational parameters, σR, σθ, and σϕ. Optimized values were obtained according to the definitions discussed below, which depended on the functional dependence of the error function on the standard deviation parameter.
FIG. 3.
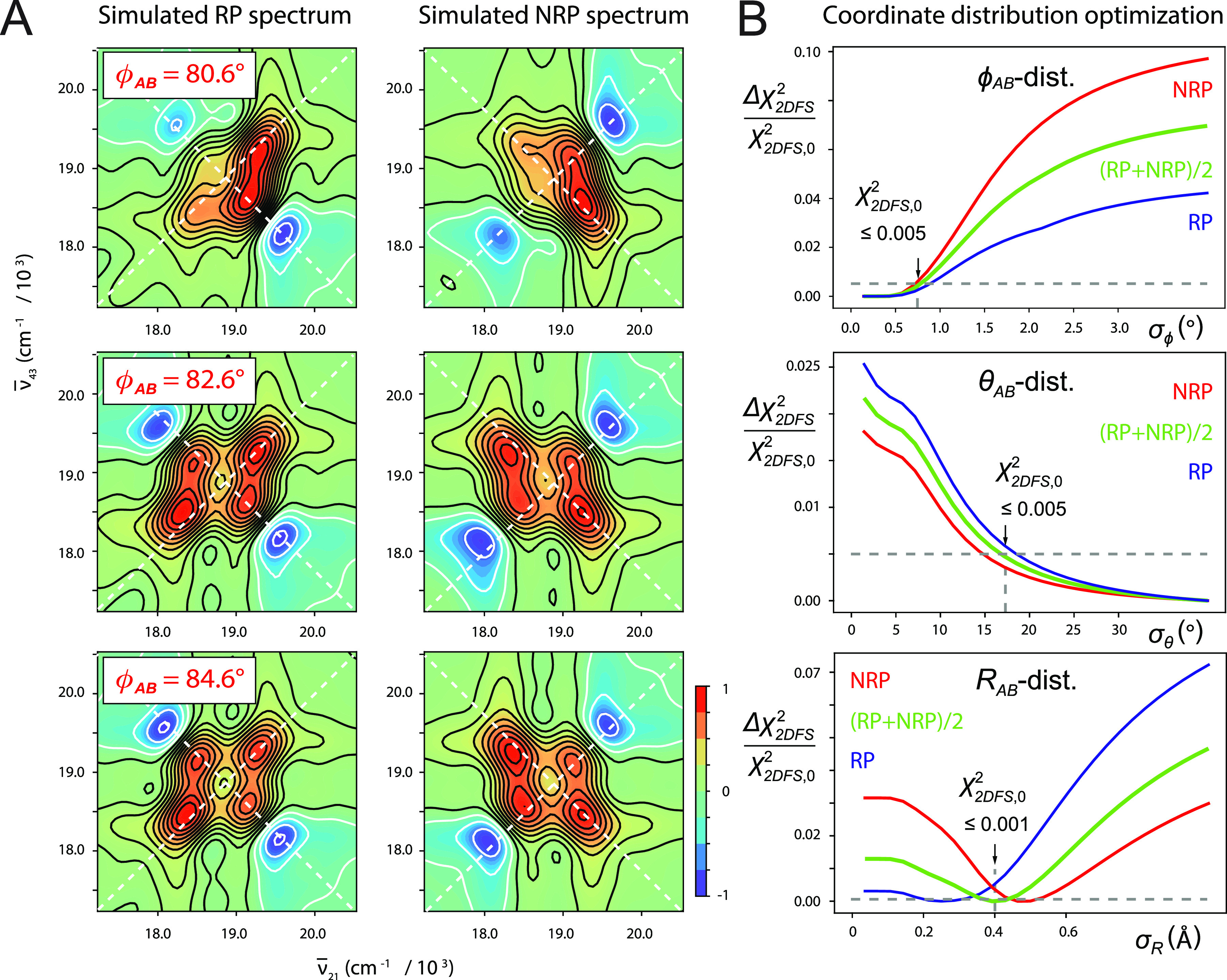
(a) Simulated RP and NRP “homogeneous” 2D fluorescence spectra (real part) of the +2 (iCy3)2 dimer ss–dsDNA construct for various values of the mean twist angle: = 80.6° (top row), 82.6° (middle), and 84.6° (bottom); mean tilt angle = 5.1°; mean separation = 2.8 Å; and homogeneous and inhomogeneous linewidth parameters ΓH = σI = 100 cm−1. (b) Cross sections of the relative deviation of the linear least squares error function, , are shown as functions of the standard deviations σϕ (top), σθ (middle), and σR (bottom). Inhomogeneously broadened spectra of the +2 (iCy3)2 dimer ss–dsDNA construct were simulated by numerically sampling the library of “homogeneous” 2D fluorescence spectra according to the Gaussian distribution of structural coordinates given in Eq. (21). Error function cross sections are shown plotted relative to their “optimized” values, (indicated by vertical arrows), which are defined as the 0.5% threshold for cases in which the function approached its minimum asymptotically (as do the σϕ and σθ cross sections) and the 0.1% threshold for cases in which the function exhibited a distinct minimum (as shown for the σR cross section).
In Fig. 3(b), we show example cross sections of the relative deviation of the linear least squares error function and their RP and NRP contributions, and , respectively, with . These functions are plotted relative to their “optimized” values, , which we defined as the 0.5% threshold (i.e., ) in cases for which the minimum is approached asymptotically. In cases for which the function exhibited a distinct minimum, we defined the optimized value such that . For the error function plotted along the σϕ axis [Fig. 3(b), top], we see that approaches an asymptotic minimum for small values of the standard deviation and increases abruptly for σϕ ≥ 0.7°. This indicates that the distribution of the local twist angle parameter for the +2 (iCy3)2 ss–dsDNA construct is relatively narrow and that the optimized value for σϕ is an upper bound. In contrast, the cross section plotted along the σθ axis [Fig. 3(b), middle] decreases monotonically with increasing standard deviation, indicating that the optimized value σθ = 17° is a lower bound. The average cross section plotted along the RAB-distribution axis [Fig. 3(b), bottom] exhibits a distinct minimum with optimized value σR = 0.4 Å. In all the panels shown in Fig. 3(b), threshold values are indicated by the horizontal dashed lines.
E. Determination of the relative fluorescence quantum yield parameter Γ2D
The value used for the parameter Γ2D, which characterizes the relative fluorescence quantum yield of the doubly vs singly excited state populations [described in Eqs. (11) and (12)], is important for fitting 2DFS data to theoretical models.24,27,39,40 To determine the value of Γ2D, we performed an optimization analysis of our temperature-dependent 2DFS data for the (iCy3)2 dimer-labeled +15 (duplex) ss–dsDNA construct based on the H–F Hamiltonian model. In these calculations, we minimized the function described in Eq. (20) while varying the parameter Γ2D. The procedure was carried out for datasets taken at five different temperatures (5, 15, 23, 35, and 45 °C). The remaining input parameters for the H–F model were obtained from the optimized fits to the linear absorbance and CD spectroscopic measurements taken at the same temperatures, as discussed further below. We show the results of these calculations in Fig. S1 of the supplementary material. For each temperature, we observe a progression of the parameter Γ2D that favors lower values except for 25 °C, for which the analysis is relatively insensitive to the value of Γ2D. We, therefore, adopted the value Γ2D = 0.3 for all the (iCy3)2 dimer calculations presented in the remainder of this work.
IV. RESULTS AND DISCUSSION
A. Local conformations and spectral inhomogeneity of the iCy3 monomer and (iCy3)2 dimer ss–dsDNA constructs labeled at the +15 “duplex” and −1 “fork” positions
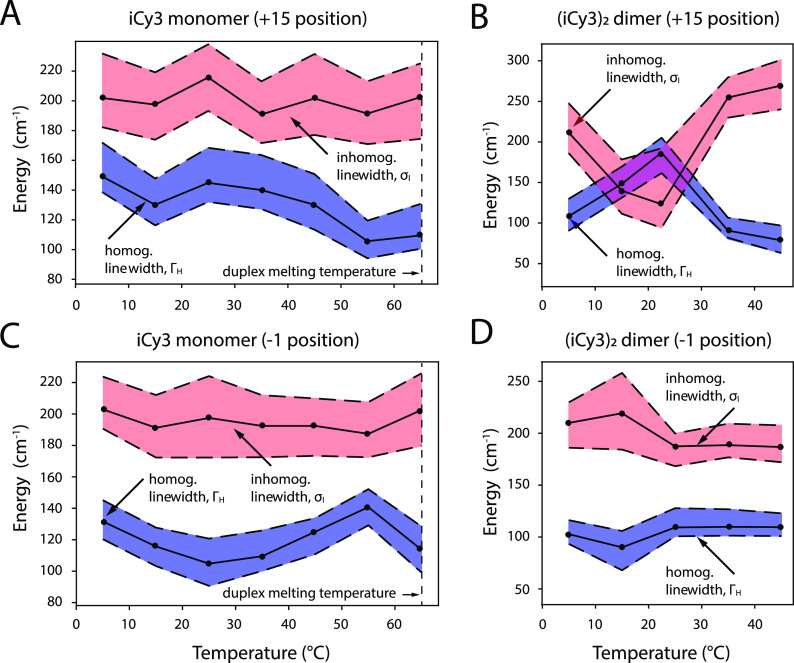
In previous studies, we examined the temperature-dependent absorbance and CD spectra of iCy3 monomer and (iCy3)2 dimer-labeled ss–dsDNA constructs, in which the chromophore probes were positioned either at the +15 position (deep within the duplex region) or at the −1 position relative to the ss–dsDNA fork junction [see Fig. 1(c) and Table I].5,7 We found that the structural parameters and coupling strengths that characterized the absorbance and CD spectra of the (iCy3)2 dimer ss–dsDNA constructs varied with probe labeling position and temperature. In Fig. 4, we compare our results for the room temperature (25 °C) CD, absorbance, and 2DFS measurements of the iCy3 monomer and (iCy3)2 dimer-labeled +15 “duplex” and −1 “fork” ss–dsDNA constructs.
FIG. 4.
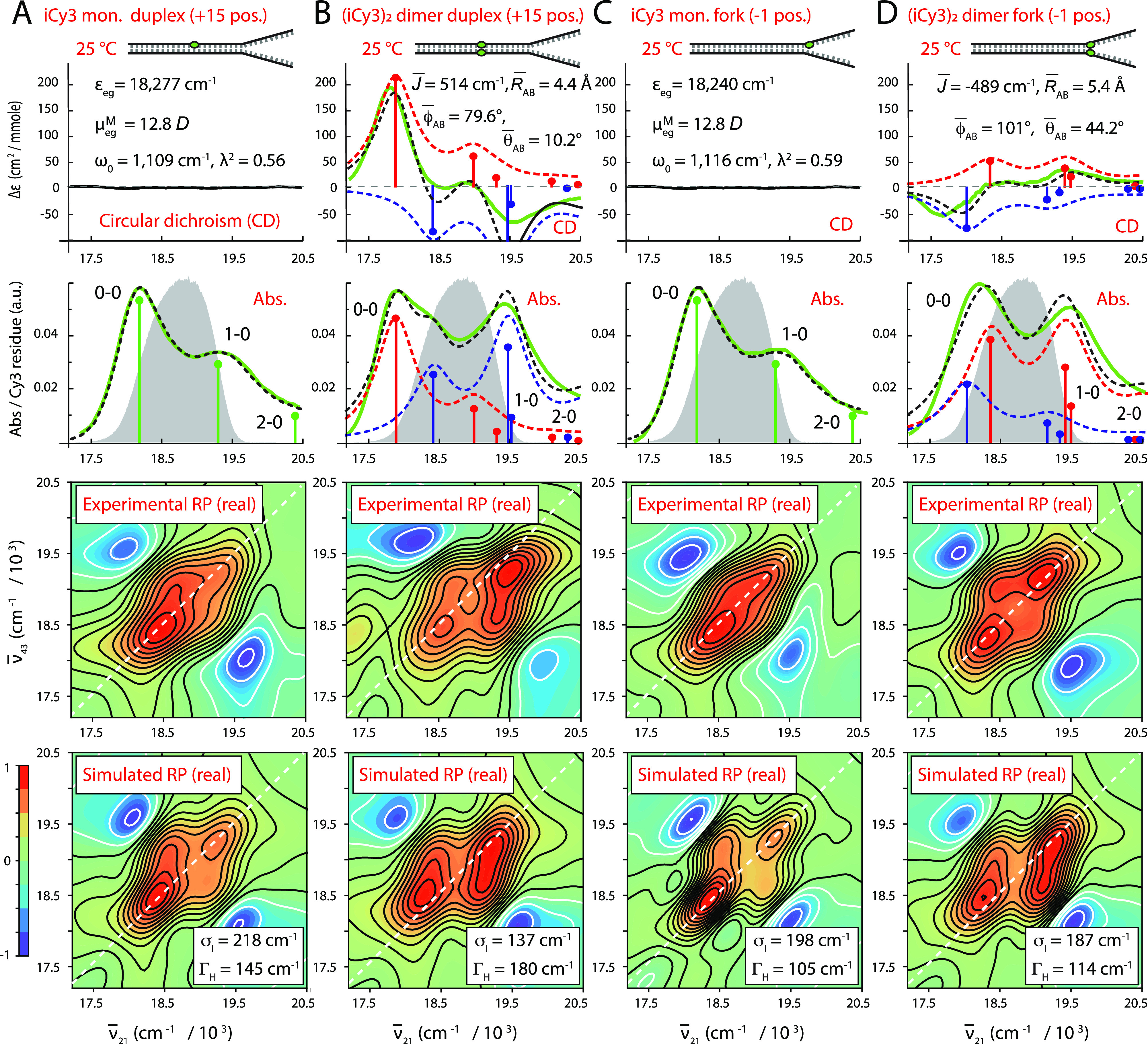
Experimental and simulated spectroscopic measurements of iCy3 monomer and (iCy3)2 dimer-labeled +15 “duplex” and −1 “fork” ss–dsDNA constructs performed at room temperature (25 °C). (a) iCy3 monomer +15 ss–dsDNA construct, (b) (iCy3)2 dimer +15 ss–dsDNA construct, (c) iCy3 monomer −1 ss–dsDNA construct, and (d) (iCy3)2 dimer −1 ss–dsDNA construct. The experimental CD (top row) and absorbance spectra (second row) are shown (in green) overlaid with vibronic spectral features (black dashed curves) obtained from the optimized fits to the H–F model. For the monomer constructs [(a) and (c)], the vibronic features are shown in green, and for the dimer constructs [(b) and (d)], the symmetric (+) and anti-symmetric (−) excitons are shown in blue and red, respectively. Values of optimized parameters are shown in the insets of the corresponding panels. The laser spectrum, with center frequency = 18 796 cm−1 (λL = 532 nm) and FWHM bandwidth = 1100 cm−1 (ΔλL = ∼33 nm), is shown (in gray) overlaid with the absorbance spectra and spans a region containing both the 0–0 and 1–0 vibronic subbands, as shown. Experimental RP spectra (third row) are compared to the optimized simulated RP spectra (fourth row). Simulated spectra are based on the structural parameters obtained from our optimization analyses of the CD and absorbance spectra, the fluorescence quantum yield parameter Γ2D = 0.3, and the homogeneous and inhomogeneous linewidth parameters (ΓH and σI, respectively), which are listed for the (iCy3)2 dimer-labeled constructs in Tables II and III and for the iCy3 monomer-labeled constructs in Tables S1 and S2 of the supplementary material.
We first consider the CD, absorbance, and 2D fluorescence spectra of the iCy3 monomer-labeled +15 “duplex” and −1 “fork” ss–dsDNA constructs [see Figs. 4(a) and 4(c), respectively], which are well-described using the monomer Hamiltonian [Eqs. (1)–(3)], as expected. Values obtained from model fits to the absorbance and CD spectra for the mean electronic transition energy ɛeg, electric dipole transition moment = 12.8 D, vibrational frequency ω0, and Huang–Rhys parameter λ2 are shown in the insets. The laser spectrum used for the 2DFS experiments is shown (in gray) overlaid with the absorbance spectra (second row) and spans the spectral region containing the 0–0 and 0–1 vibronic transitions of the monomer (shown as green line segments). The signatures of these transitions are present in the experimental 2DFS data (RP spectra, third row). We simulated the 2DFS data (fourth row) using the monomer Hamiltonian and the optimized parameters obtained from the CD and absorbance spectra, as described in Sec. III B. We note the good agreement between simulated and experimental 2D spectra shown in Figs. 4(a) and 4(c), although in both cases the simulation predicts slightly higher cross-peak intensities and weaker inhomogeneous broadening than we observed experimentally. For the iCy3 monomer-labeled ss–dsDNA constructs, we obtained the optimized values: ΓH = 145 cm−1 and σI = 218 cm−1 for the +15 ss–dsDNA construct and ΓH = 105 cm−1 and σI = 198 cm−1 for the −1 ss–dsDNA construct. Optimized values for the iCy3 monomer Hamiltonian parameters for the +15 and −1 ss–dsDNA constructs, and their associated error bars, are listed in Tables S1 and S2 of the supplementary material, respectively.
For the (iCy3)2 dimer-labeled +15 “duplex” and −1 “fork” ss–dsDNA constructs, the CD, absorbance, and 2DFS data are well described using the H–F dimer Hamiltonian [Eqs. (4)–(10)] [see Figs. 4(b) and 4(d), respectively]. Mean values of the structural parameters and electronic coupling are shown in the insets. The simulated symmetric (+) and anti-symmetric (−) vibronic manifolds are shown overlaid with the experimental spectra as the blue and red dashed curves, respectively. The symmetries of the CD spectra, and the corresponding signs of the electrostatic couplings , determine the handedness of the (iCy3)2 dimer conformation. The optimization of the H–F model to the +15 “duplex” ss–dsDNA construct provides values for the mean separation, twist, and tilt angles = 4.4 Å, = 79.6°, and = 10.2°, respectively, which indicates that the sugar–phosphate backbones adopt a right-handed, cylindrically symmetric local conformation at the +15 position consistent with the Watson–Crick B-form crystallographic structure of duplex DNA. In contrast, the optimized values obtained for the −1 “fork” ss–dsDNA construct are = 5.4 Å, = 101°, and = 44.2°, which indicates that the sugar–phosphate backbones at the −1 position adopt, on average, a left-handed, splayed open conformation. The experimental 2DFS data (third row) exhibit diagonal and off-diagonal peaks, which are due to optically resonant transitions involving the symmetric and anti-symmetric vibronic manifolds. The 2DFS data were simulated (fourth row) using the same optimized structural parameters obtained from the CD and absorbance spectra according to the procedure discussed in Sec. III B. From our analyses of the 2DFS line shapes, we obtained optimized values of the homogeneous and inhomogeneous linewidth parameters for the (iCy3)2 dimer-labeled ss–dsDNA constructs: ΓH = 180 cm−1 and σI = 137 cm−1 for the +15 ss–dsDNA construct and ΓH = 114 cm−1 and σI = 187 cm−1 for the −1 ss–dsDNA construct.
We note that the simulated and experimental 2DFS data shown in Figs. 4(b) and 4(d) are in good agreement. However, like the results we obtained for the iCy3 monomer-labeled constructs described above, the simulations for the (iCy3)2 dimer-labeled constructs predict slightly higher cross-peak intensities than we observed experimentally. The most likely explanation for the discrepancy is the presence of third-order dispersion in the laser spectrum, which is not accounted for in our modeling procedure. An additional simplification of our model is the assumption that the system is solely comprised of the exciton-coupled (iCy3)2 dimer. While the dimer model is necessary to account for the CD spectrum of the −1 (iCy3)2 ss–dsDNA construct, it is possible that a minor fraction of the dimer probes exists in an uncoupled (monomer-like) configuration. A slightly more complicated model, which describes the system as a heterogeneous mixture of (iCy3)2 dimer and iCy3 monomer sub-populations, would more realistically represent the experimental absorbance and 2DFS data. Nevertheless, we have found that including an iCy3 monomer “background” contribution to the absorbance and 2DFS simulations is not by itself sufficient to explain the discrepancies we observe between simulated and experimental spectra. The third-order dispersion of the laser spectrum, which was maintained constant for all our measurements, is the most likely source of the additional line broadening that we observed in our 2DFS measurements.
The spectral inhomogeneity that we determined from our room temperature 2DFS line shape analyses was generally larger for the iCy3 monomer-labeled constructs than for the (iCy3)2 dimer-labeled constructs. This finding is especially evident for the +15 ss–dsDNA constructs and suggests that the local environment of the sugar–phosphate backbones of the iCy3 monomer probes is more disordered than that of the (iCy3)2 dimer probes. We note that the (iCy3)2 dimer ss–dsDNA constructs have the two monomer probes positioned directly opposite to one another in a symmetric manner, while the monomer-labeled ss–dsDNA constructs have a single thymine (T) base positioned on the conjugate strand directly opposite to the iCy3 probe. Monomer substitution may, thus, introduce a “defect site,” which may be more disruptive to the local conformation and dynamics of the sugar–phosphate backbones than dimer substitution at the same probe labeling positions at room temperature. This finding is consistent with recent studies of the sensitivity of cyanine monomer substituted DNA constructs to the local environment,41 which can influence fluorescence intensity, local mobility, and photostability.6
B. Temperature-dependent local conformations and spectral linewidth parameters of iCy3 monomer and (iCy3)2 dimer ss–dsDNA constructs labeled at the +15 “duplex” and −1 “fork” positions
We carried out temperature-dependent absorbance, CD, and 2DFS measurements of both the iCy3 monomer and the (iCy3)2 dimer-labeled +15 and −1 ss–dsDNA constructs. In previous work, we reported the results of our temperature-dependent studies of the absorbance and CD spectra of these constructs to determine optimized structural and spectroscopic parameters using the monomer and H–F Hamiltonian models.5,7 Although these studies determined the mean values of the monomer and dimer Hamiltonian parameters, including the mean structural parameters , , and , they could not provide accurate assessments for the homogeneous and inhomogeneous linewidths as we report in the current study. Comparisons between our temperature-dependent experimental 2DFS data and optimized simulations for the monomer and dimer-labeled +15 “duplex” ss–dsDNA constructs are shown in Figs. S2–S5 and S6–S9 of the supplementary material, respectively. Similar comparisons for the monomer and dimer labeled −1 “fork” ss–dsDNA constructs are shown in Figs. S10–S13 and S14–S17 of the supplementary material, respectively. In Tables II and III, we list for these same constructs the mean structural parameters obtained from the absorbance and CD spectra and the associated linewidth parameters obtained from our analyses of the 2DFS data over the full range of temperatures studied. The optimized monomer Hamiltonian parameters for the +15 and −1 ss–dsDNA constructs are listed in Tables S1 and S2 of the supplementary material.
TABLE II.
Mean structural parameters and 2DFS linewidths determined for the (Cy3)2 dimer-labeled +15 “duplex” ss–dsDNA construct. The parameters determined from model analyses of linear absorbance and CD spectra are the mean resonant coupling , the mean twist angle , the mean tilt angle , and the mean interchromophore separation . The parameters determined from the 2DFS data are the inhomogeneous and homogeneous linewidths σI and ΓH. Error bars were calculated based on a 1% deviation of the χ2 function from its minimum (optimized) value.
| Optimized parameters for (iCy3)2 dimer +15 “duplex” ss–dsDNA constructs | ||||||
|---|---|---|---|---|---|---|
| From absorbance and CD optimization | From 2DFS optimization | |||||
| T (°C) | (cm−1) | (deg) | (deg) | (Å) | σI (cm−1) | ΓH (cm−1) |
| 1 | 493 | 78.3 + 0.3/−0.1 | 44.2 + 1.4/−0.4 | 3.49 + 0.9/−0.6 | 121.5 + 35.4/−32.4 | 105.1 + 22.2/−17.4 |
| 5 | 488 | 79.3 + 0.2/−0.1 | 39.3 + 0.7/−0.4 | 2.7 + 1.1/−0.4 | 212.7 + 36.8/−31.0 | 109.5 + 21.2/−17.9 |
| 15 | 532 | 80.7 + 0.2/−0.1 | 18.1 + 2.9/−2.1 | 3.7 ± 0.1 | 141.8 + 34.3/−33.4 | 149.4 + 19.7/−18.7 |
| 23 | 514 | 79.6 ± 0.2 | 10.2 + 6.4/−27 | 4.4 ± 0.1 | 136.7 + 45.8/−40.1 | 180.4 + 25.0/−20.3 |
| 35 | 496 | 76.0 ± 0.3 | 3.0 + 13/−19 | 5.5 ± 0.1 | 253.2 + 27.6/−25.3 | 91.8 + 14.0/−14.4 |
| 45 | 483 | 71.9 ± 0.4 | 7.7 + 8.5/−24 | 6.4 ± 0.1 | 268.4 + 31.8/−26.4 | 78.5 + 17.0/−12.0 |
| 55 | 467 | 70.4 ± 0.5 | 7.0 + 8.4/−22 | 6.8 ± 0.1 | 253.2 + 36.2/−33.9 | 60.8 + 18.7/−13.6 |
| 65 | 354 | 73.7 ± 0.6 | 5.4 + 11/−22 | 7.1 ± 0.1 | 217.8 + 31.4/−25.2 | 56.3 + 16.7/−14.1 |
TABLE III.
Mean structural parameters and 2DFS linewidths determined for the (Cy3)2 dimer-labeled −1 “fork” ss–dsDNA construct. The parameters determined from model analyses of spectroscopic data are the same as defined in Table II.
| Optimized parameters for (iCy3)2 dimer −1 “fork” ss–dsDNA constructs | ||||||
|---|---|---|---|---|---|---|
| From absorbance and CD optimization | From 2DFS optimization | |||||
| T (°C) | (cm−1) | (deg) | (deg) | (Å) | σI (cm−1) | ΓH (cm−1) |
| 1 | −340 | 96.1 ± 0.3 | 39.9 + 2.2/−2.4 | 5.0 ± 0.1 | 187.3 + 14.5/−15.3 | 118.35 + 12.2/−9.6 |
| 5 | −339 | 97.5 + 0.2/−0.7 | 35.5 + 1.8/−7.6 | 5.3 + 0.2/−0.1 | 207.6 + 22.3/−19.6 | 105.1 + 15.1/−11.7 |
| 15 | −537 | 101 ± 0.7 | 47.3 + 4.2/−4.5 | 5.3 ± 0.1 | 217.7 + 39.1/−37.8 | 87.3 + 17.1/−18.3 |
| 23 | −489 | 101 ± 0.8 | 44.2 + 5.4/−6.5 | 5.4 ± 0.1 | 187.3 + 20.5/−22.0 | 113.9 + 13.6/−11.6 |
| 35 | −390 | 101 ± 0.7 | 44.4 + 6.1/−7.4 | 6.1 ± 0.1 | 192.4 + 19.8/−18.1 | 113.9 + 13.8/−10.6 |
| 45 | −352 | 96 ± 0.5 | 58.2 + 3.2/−3.5 | 5.6 ± 0.1 | 187.3 + 17.7/−15.0 | 113.9 + 11.8/−9.5 |
In Fig. 5, we illustrate the temperature-dependence of the absorbance (a), CD (b), experimental 2DFS data (c), and simulated 2DFS data (d) for the (iCy3)2 dimer-labeled +15 ss–dsDNA construct. The data presented in Fig. 5 and the corresponding parameters listed in Table II show that for this construct, the mean coupling strength is maximized at 15 °C ( = 532 cm−1) and decreases systematically with increasing and decreasing temperature. At the lowest temperatures (1–25 °C), the absorbance and CD spectra exhibit, respectively, the intensity borrowing and bi-signate line shapes that are characteristic of the vibronically coupled iCy3 dimer system.7,8 The H–F analysis of the absorbance and CD data indicates that the sugar–phosphate backbones of the duplex adopt a progressively increasing mean tilt angle with decreasing temperature, while the mean twist angle does not change significantly (Table II). Moreover, the 2DFS data at low temperatures show well-separated and relatively narrow peaks and cross-peaks, which indicate the presence of the delocalized symmetric (+) and anti-symmetric (−) excitons.
FIG. 5.
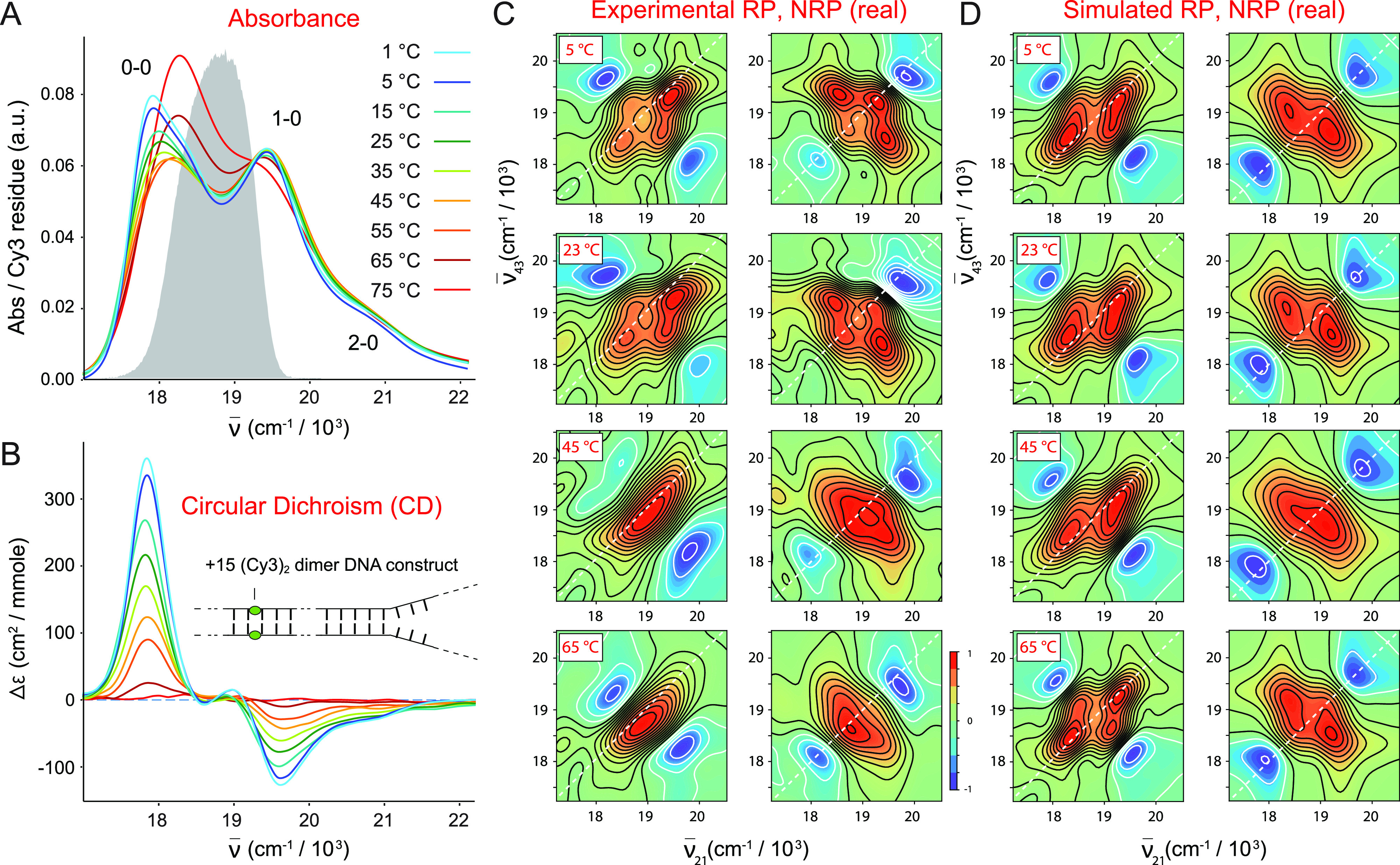
Temperature-dependent spectroscopic measurements of the (iCy3)2 dimer +15 ss–dsDNA construct. (a) Absorbance. (b) CD. (c) Experimental 2DFS. (d) Simulated 2DFS. The gray curve in (a) is the same laser spectrum, as shown in Fig. 4. In (c) and (d), both RP (left columns) and NRP (right columns) 2D spectra are shown. An additional comparison between the experimental 2DFS data and the optimized simulated spectra for the (iCy3)2 dimer +15 ss–dsDNA construct is presented in Figs. S6–S9 of the supplementary material.
The simulated 2DFS data shown in Fig. 5(d), which assumes the optimized structural parameters obtained from the H–F analysis of the absorbance and CD, are in very good agreement with the experimental data at low temperatures (5–23 °C) and provide an accurate determination of the homogeneous and inhomogeneous line shape parameters. We note the agreement is less good for the 1 °C data (see Figs. S6 and S7 of the supplementary material), which may be the result of experimental error introduced due to the proximity of the freezing point. As the temperature is increased (35–65 °C), the absorbance and CD spectral line shapes change systematically to reflect the decrease in the mean coupling strength. At the highest temperature for which the single strands of the duplex have fully separated (75 °C), the absorbance and CD spectra resemble those of the iCy3 monomer substituted ss–dsDNA constructs. The spectral features of the 2DFS data, which are well-defined at low temperatures, become progressively less pronounced as the temperature is increased. We note an abrupt change in the experimental 2DFS line shapes at temperatures above 23 °C in which the intensities of the off-diagonal features decrease and the exciton-split diagonal features appear to merge into a single diffuse feature. While our simulations predict the observed broadening of the 2DFS line shapes with increasing temperature, they do not fully capture the merging of the diagonal peaks into a single diffuse feature. The discrepancies are likely due to minor shortcomings of our model, which does not account for laser pulse dispersion or contributions to the signal from the iCy3 monomer. Nevertheless, the simulated spectra do reflect the observed broadening of the 2D line shapes for most temperatures that we studied and, thus, provide valid estimates of the homogeneous and inhomogeneous linewidth parameters at these temperatures.
As mentioned previously, we simulated our 2DFS data for the iCy3 monomer and (iCy3)2 dimer +15 “duplex” and −1 “fork” labeled ss–dsDNA constructs using the same temperature-dependent Hamiltonian parameters that we determined from analyses of absorbance and CD data (see Tables II and III).5,7 Our simulations of the 2DFS (iCy3)2 dimer spectra exhibited peaks and cross-peaks with positions and relative intensities that matched closely our experimental results for the temperature range 5–45 °C and for the iCy3 monomer spectra over the range 5–65 °C. We, thus, performed optimization calculations on our 2DFS data to determine the best fit homogeneous and inhomogeneous linewidth parameters, ΓH and σI, respectively, as a function of temperature. These results are presented in Tables II and III, and the linewidth parameters are plotted in Fig. 6. Our simulations of the 2DFS data for the (iCy3)2 dimer +15 ss–dsDNA “duplex” construct do not entirely capture the observed merging of the exciton-split diagonal features at temperatures above 45 °C. At these elevated temperatures ranging through the melting point of the double-stranded region of the ss–dsDNA constructs (Tm ∼ 65 °C), our simulations appear to underestimate the experimentally observed inhomogeneous linewidths, as discussed above. Moreover, for the (iCy3)2 dimer −1 ss–dsDNA “fork” construct, the highest temperature that we investigated is 45 °C, which is ∼20° lower than the duplex melting point. This is due to the relatively low CD signals of this ss–dsDNA construct at elevated temperatures, which prevented us from obtaining accurate values of the structural parameters above 45 °C. As we discuss further below, the structural parameters of the (iCy3)2 dimer −1 construct appear to have converged to plateau values at temperatures below 45 °C.
FIG. 6.
Optimized homogeneous and inhomogeneous linewidth parameters as a function of temperature obtained from 2DFS line shape analyses. (a) iCy3 monomer +15 ss–dsDNA construct, (b) (iCy3)2 dimer +15 ss–dsDNA construct, (c) iCy3 monomer −1 ss–dsDNA construct, and (d) (iCy3)2 dimer −1 ss–dsDNA construct. Shaded regions bounded by the dashed lines indicate error bars, which were calculated based on a 1% deviation of the function [Eq. (20)] from its minimum value. The vertical dashed line at 65 °C indicates the melting temperature Tm of the duplex regions of the DNA constructs. Direct comparisons between experimental and optimized simulated 2DFS data are presented in Figs. S2–S17 of the supplementary material.
In our previous studies, we estimated the inhomogeneous linewidths solely based on analyses of linear spectroscopic data, for which we assumed that the homogeneous linewidth was constant (ΓH = 186 cm−1) for all temperatures and probe labeling positions.7 The results of those studies suggested that for both the iCy3 monomer and (iCy3)2 dimer-labeled +15 (duplex) ss–dsDNA constructs, the inhomogeneous linewidth parameter increased monotonically with temperature over the range 15–65 °C. However, for the iCy3 monomer and (iCy3)2 dimer-labeled −1 (fork) ss–dsDNA constructs, the inhomogeneous linewidth parameter remained relatively constant over this same temperature range.
In Fig. 6, we present the results of our 2DFS line shape analysis, which provides a far more detailed picture of the temperature- and position-dependent behavior of the homogeneous and inhomogeneous linewidth parameters (shown as blue- and teal-shaded regions, respectively). The optimized values of the linewidth parameters are presented as points, and the shaded regions bounded by dashed lines indicate error bars, which are based on a 1% deviation of the function [see Eq. (20)] from its optimized value. As mentioned previously, our results at 1 °C appear to behave as “outliers” from the remaining temperature-dependent data shown over the range ∼5–65 °C, which we next discuss.
We first consider the linewidth parameters corresponding to the iCy3 monomer-labeled +15 “duplex” [Fig. 6(a)] and the −1 “fork” [Fig. 6(c)] ss–dsDNA constructs. Our results indicate that the two iCy3 monomer-labeled constructs exhibit qualitatively similar temperature dependencies of the inhomogeneous linewidths. At the lowest temperatures (∼5–15 °C), the inhomogeneous linewidth (σI ∼ 200 cm−1) is significantly larger in magnitude than the homogeneous linewidth (ΓH ∼ 100–140 cm−1), which suggests that there is significant conformational disorder of the sugar–phosphate backbones labeled by the iCy3 monomer probe in both the duplex region and at the fork −1 position. Furthermore, the inhomogeneous linewidths undergo very little variation over the temperature range 5–65 °C, indicating a relatively constant level of conformational disorder of the sugar–phosphate backbones as the temperature is increased toward the melting point.
The homogeneous linewidths of both iCy3 monomer-labeled ss–dsDNA constructs exhibit more complicated temperature-dependent behavior. In the case of the iCy3 monomer-labeled +15 “duplex” ss–dsDNA construct, the value of the homogeneous linewidth decreases rapidly from ΓH ∼ 190 to ∼130 cm−1 over the temperature range 5–15 °C, followed by a slight increase from ΓH ∼ 130 to ∼145 cm−1 over the range 15–25 °C, and a gradual decrease from ΓH ∼ 145 to ∼105 cm−1 over the range 25–55 °C. The highest temperature of 65 °C corresponds to the melting point of the duplex region, for which 50% of the single strands are expected to be completely separated. At the melting point, we observe a significant reduction of the homogeneous linewidth (ΓH ∼ 114 cm−1) in comparison to the value we obtained for the same constructs at room temperature (ΓH ∼ 145 cm−1). In contrast, for the iCy3 monomer-labeled −1 “fork” ss–dsDNA construct, the homogeneous linewidth decreases gradually from ΓH ∼ 132 to ∼105 cm−1 over the range 5–25 °C, followed by an increase from ΓH ∼ 105 to ∼140 cm−1 over the range 25–55 °C. It is interesting to note that while the homogeneous linewidth of the iCy3 monomer +15 ss–dsDNA construct is maximized at room temperature (ΓH ∼ 145 cm−1), the value of the homogeneous linewidth of the −1 “fork” ss–dsDNA construct is minimized at room temperature (ΓH ∼ 105 cm−1).
The homogeneous linewidth is related to the total dephasing time (T2) according to (100 fs for ΓH ≈ 100 cm−1). The total dephasing time can be written in terms of the population relaxation time (T1) and the pure dephasing time () according to .34 The value of T1 can be estimated from the room temperature fluorescence lifetime τF ∼ 162 ps.4 Although the fluorescence lifetime of iCy3 labeled DNA constructs can vary with temperature due to, for example, thermally activated photoisomerization,4,42–44 such processes are many orders of magnitude slower than the tens-of-femtosecond time scales of pure dephasing. The homogeneous linewidth is, thus, dominated by pure dephasing, which depends on interactions between the electronic transitions and the phonon bath. This suggests that we may interpret the temperature-dependent variation of the homogeneous linewidth in terms of changes to the iCy3 probe’s direct interactions with its local environment, which is primarily comprised of the sugar–phosphate backbones.
We next turn to the homogeneous and inhomogeneous linewidth parameters of the (iCy3)2 dimer-labeled +15 “duplex” [Fig. 6(b)] and −1 “fork” [Fig. 6(d)] ss–dsDNA constructs. These data show that the 2D spectral line shapes of the (iCy3)2 dimer-labeled duplex and fork ss–dsDNA constructs exhibit strikingly different and more complex temperature-dependent behavior than the iCy3 monomer-labeled ss–dsDNA constructs discussed above. The results shown in Fig. 6(b) were obtained from our analysis of 2DFS data of the (iCy3)2 dimer-labeled +15 duplex ss–dsDNA construct shown in Figs. 5(c) and 5(d) and Figs. S6–S9 of the supplementary material. In this case, both the homogeneous and inhomogeneous line shape parameters undergo sensitive temperature-dependent variations. For the temperature range 5–23 °C, the inhomogeneous linewidth decreases rapidly from the value σI ∼ 213 cm−1 to σI ∼ 137 cm−1. The room temperature value of the inhomogeneous linewidth appears to be a local minimum since increasing the temperature from 23–35 °C leads to a rapid increase to the value, σI ∼ 253 cm−1, suggesting a dramatic increase of local conformational disorder just above room temperature. This relatively high value of the inhomogeneous linewidth parameter persists (σI ∼250 cm−1) over the temperature range 35–45 °C. In contrast, the homogeneous linewidth parameter increases over the range 5–23 °C to its maximum value ΓH ∼180 cm−1, followed by an abrupt decrease to ΓH ∼ 92 cm−1 over the range 23–35 °C. This relatively low value of the homogeneous linewidth persists (ΓH ∼70 cm−1) over the temperature range 35–45 °C.
We note that the homogenous and inhomogeneous linewidth parameters appear to depend on temperature in a reciprocal manner, with extremum values attained at room temperature. Evidently, at room temperature, the local conformation of the (iCy3)2 dimer probes at the +15 position, which is deep within the duplex region of the ss–dsDNA construct, is minimally disordered such that the probes interact uniformly with their local environments to maximize the electronic dephasing rate. The room temperature condition appears to be unique. As the temperature is raised or lowered from 23 °C, the local conformational disorder increases abruptly, while the mean coupling strength between the electronic transitions of the probe chromophores and the phonon bath decreases. These results suggest that the W–C local conformation of the (iCy3)2 dimer-labeled sugar–phosphate backbones at sites deep within the duplex region is the optimally stable structure at 23 °C and that the distribution of conformations broadens substantially at temperatures just above or below room temperature. These findings indicate that the activation barriers for thermally induced breathing at these positions are readily surmounted just above room temperature. At the same time, decreasing the temperature below 23 °C destabilizes the W–C local conformation in the duplex region, like “cold denaturation” in proteins.45–47
We next discuss the temperature-dependent optimized linewidth parameters for the (iCy3)2 dimer-labeled −1 “fork” ss–dsDNA construct, shown in Fig. 6(d). Like the (iCy3)2 dimer-labeled +15 duplex construct, the homogeneous and inhomogeneous linewidths appear to vary with temperature in a reciprocal manner. However, in this case, the principal variation occurs over the temperature range 5–23 °C for which the inhomogeneous linewidth increases from σI ∼ 208 cm−1 to σI ∼ 218 cm−1 and then decreases to σI ∼ 187 cm−1. Over this temperature range, the homogeneous linewidth initially decreases from ΓH ∼ 105 cm−1 to ΓH ∼ 87 cm−1, followed by an increase to ΓH ∼ 114 cm−1. Upon further increasing the temperature above 23 °C, the inhomogeneous and homogeneous linewidth parameters do not undergo significant additional changes, suggesting that—unlike the duplex labeled ss–dsDNA constructs—the distribution of local conformations of the (iCy3)2 labeled fork construct is not broadened by thermally activated processes near room temperature.
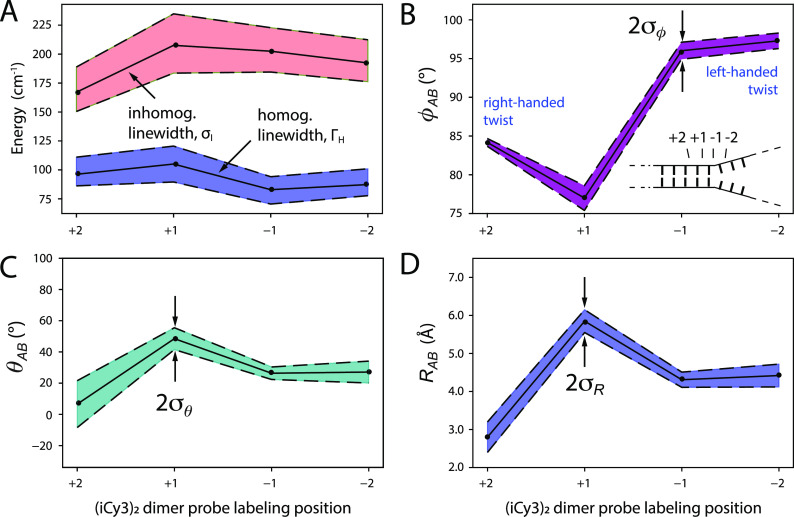
C. Local conformations and spectral linewidth parameters of (iCy3)2 dimer ss–dsDNA constructs labeled at the +2, +1, −1, and −2-positions
We next performed room temperature absorbance, CD, and 2DFS experiments on (iCy3)2 dimer-labeled ss–dsDNA constructs in which the dimer probe position was systematically varied across the ss–dsDNA fork junction. The results of these studies are summarized in Fig. 7, in which columns A–D correspond to the probe label positions: +2, +1, −1, and −2, respectively. The corresponding optimized values for the mean structural parameters and homogeneous and inhomogeneous linewidths are listed in Table IV. Comparisons between the experimental and optimized simulated 2DFS data are presented in Figs. S18–S21 of the supplementary material, respectively. In the top two rows of Fig. 7, the experimental CD and absorbance spectra (green curves) are shown overlaid with simulated spectra resulting from our H–F model analyses. The color schemes are the same as those used in Fig. 4. Experimental and simulated 2DFS data using the laser spectrum with FWHM = 1100 cm−1 (ΔλL = ∼33 nm, overlaid with absorbance spectra in gray) are shown in the third and fourth rows, respectively.
FIG. 7.
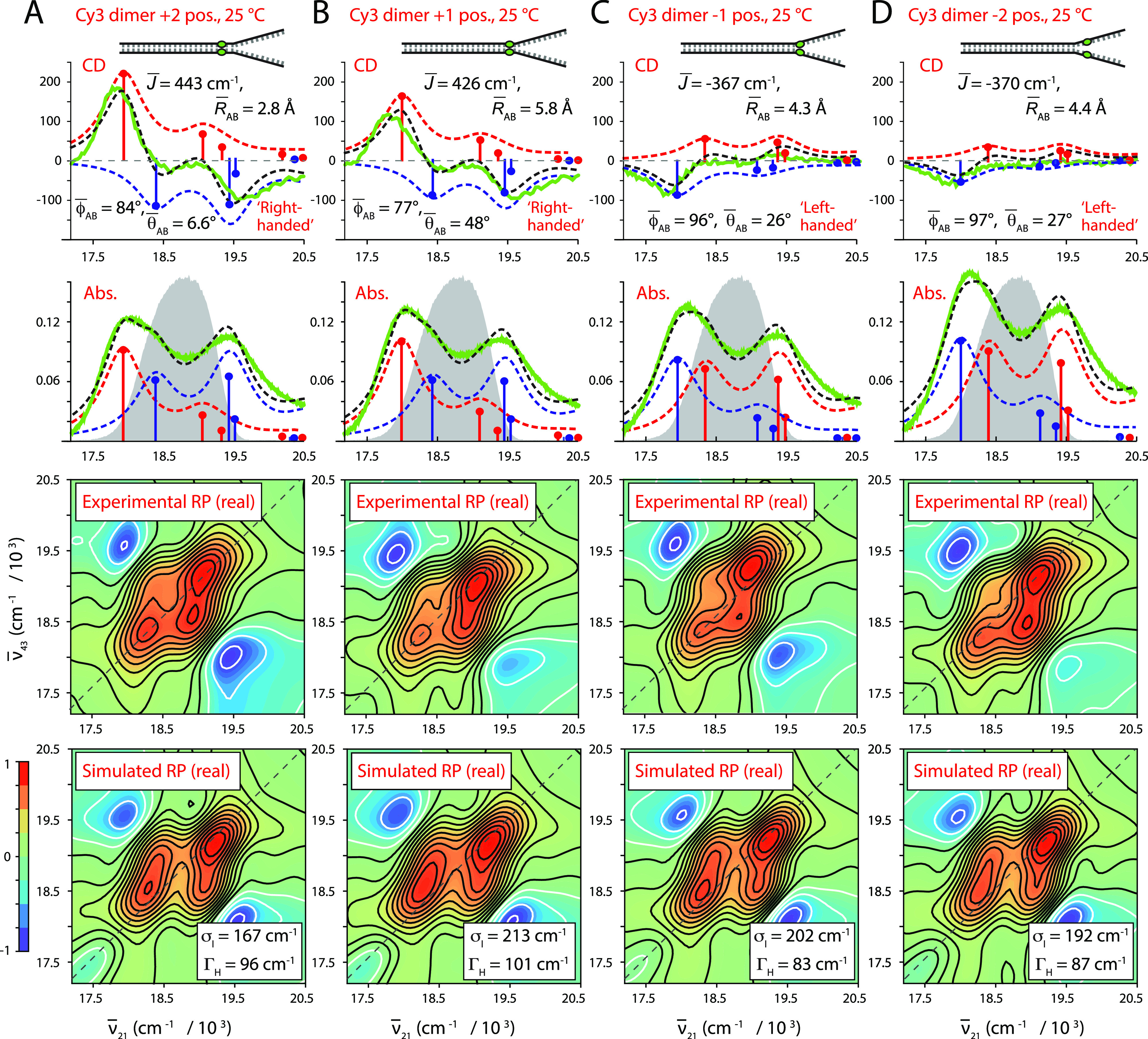
Experimental and simulated spectroscopic measurements performed at room temperature (25 °C) for (iCy3)2 dimer ss–dsDNA constructs as a function of probe labeling position. (a) +2, (b) +1, (c) −1, and (d) −2. The experimental CD (top row) and absorbance spectra (second row) are shown (in green) overlaid with vibronic spectral features (black dashed curves) obtained from optimized fits to the H–F model. The symmetric (+) and anti-symmetric (−) excitons are shown in blue and red, respectively. Values of the optimized parameters are shown in the insets of the corresponding panels. The laser spectrum (in gray) is shown overlaid with the absorbance spectrum and is the same as in Fig. 4. Experimental RP spectra (third row) are compared to the optimized simulated RP spectra (fourth row). Simulated spectra are based on the structural parameters obtained from our optimization analyses of the CD and absorbance spectra, the fluorescence quantum yield parameter Γ2D = 0.3, and the homogeneous and inhomogeneous linewidth parameters (ΓH and σI, respectively) listed in Table IV. Comparisons between experimental and optimized simulated 2DFS data are presented in Figs. S18–S21 of the supplementary material.
TABLE IV.
Mean conformational parameters and 2D spectral linewidths determined from H–F model analyses of absorbance, CD, and 2DFS of (iCy3)2 dimer-labeled ss–dsDNA fork constructs.
| Construct | (deg) | (deg) | σI | ΓH | ||
|---|---|---|---|---|---|---|
| +2 | 443 | 84.2 ± 0.1 | 6.6 ± 32 | 2.8 ± 0.1 | 167.1 + 21.8/−16.6 | 96.2 + 14.8/−10 |
| +1 | 426 | 77.0 ± 0.3 | 48.5 ± 3.3 | 5.8 ± 0.1 | 212.6 + 28.2/−22.8 | 100.6 + 18.2/−12.9 |
| −1 | −367 | 96.0 ± 0.2 | 26.4 ± 2.5 | 4.3 ± 0.1 | 202.5 + 20.3/−18.0 | 82.9 + 11.2/−12.4 |
| −2 | −420 | 97.3 ± 1.8 | 27.1 ± 54 | 4.4 ± 0.7 | 192.4 + 20.0/−16.2 | 87.3 + 13.6/−9.6 |
From our H–F model analyses of the absorbance and CD data, we see that the mean electrostatic coupling undergoes a sign inversion as the (iCy3)2 dimer probe position is changed from the +1 to −1 position across the ss–dsDNA junction. This is accompanied by non-continuous changes of the local conformational coordinates: the mean interchromophore separation [2.8 (+2), 5.8 (+1), 4.3 (−1), and 4.4 Å (−2)], the mean twist angle [84° (+2), 77° (+1), 96° (−1), and 97° (−2)], and the mean tilt angle [6.6° (+2), 48° (+1), 26° (−1), and 27 (−2)]. The sign inversion of the electrostatic coupling between the +1 and −1 positions indicates that the conformation of the (iCy3)2 dimer probe, and presumably that of the sugar–phosphate backbones labeled at these sites, changes from right-handed to left-handed. This change of handedness is correlated to a change of the mean twist angle from values that are less than 90° (right-handed) to values that are greater than 90° (left-handed). In addition, the mean tilt angle undergoes an abrupt increase from 7° to 48° between the +2 and +1 positions, followed by a decrease to ∼27° at the −1 and −2 positions. This indicates that the local conformation of the sugar–phosphate backbones within the ss–dsDNA fork constructs undergoes an abrupt loss of cylindrical symmetry at the interface between the +2 and +1 positions. However, some of the cylindrical symmetry is recovered at the −1 and −2 positions.
The simulated and experimental 2DFS measurements shown in Fig. 7 are in very good agreement, although for the −1 and −2 positions the simulated cross-peak intensities are slightly greater than those observed experimentally. Our analyses of the 2DFS spectral line shapes show how local conformational disorder of the (iCy3)2 dimer probes, in addition to interactions between the electronic transitions and the phonon bath, depend on the probe labeling position. In Fig. 8(a), we plot the position-dependent values of the inhomogeneous and homogeneous linewidth parameters. For the +2 ss–dsDNA fork construct, the inhomogeneous linewidth σI ∼ 167 cm−1 and the homogeneous linewidth ΓH ∼ 96 cm−1. The value for the inhomogeneous linewidth is significantly larger than the one we obtained for the +15 ss–dsDNA construct (σI ∼ 137 cm−1), while the value for the homogeneous linewidth is smaller [compared to the 23 °C point of Fig. 6(b)], indicating a higher degree of conformational disorder at the +2 position relative to +15. When the probe labeling position is changed to +1, the inhomogeneous linewidth parameter increases: σI ∼ 213 cm−1, while the homogeneous linewidth undergoes only a slight increase: ΓH ∼ 101 cm−1. This finding suggests that although the sugar–phosphate backbones at the +1 position maintain the right-handed local conformations seen at the +2 and +15 positions (characteristic of the B-form double-helix), the distribution of local conformations is further broadened at the +1 position in comparison to the +2 position. When the probe labeling position is changed to −1, we see that both the inhomogeneous and homogeneous linewidth parameters decrease to the values σI ∼ 202 cm−1 and ΓH ∼ 83 cm−1. These values do not change significantly when the probe labeling sites are shifted to the −2 position: σI ∼ 192 cm−1 and ΓH ∼ 87 cm−1. These findings suggest that the distribution of local conformations decreases slightly at the −1 and −2 positions relative to the +1 position. Thus, the abrupt change in average local conformation that we observe across the +2 to +1 ss–dsDNA junction (from right-handed cylindrically symmetric to right-handed cylindrically asymmetric) is accompanied by the appearance of local conformational disorder at the +1 position. An additional change in the average local conformation occurs across the +1 to −1 positions (from right-handed to left-handed) for which the local conformational disorder persists for positions extending into the single-stranded region of the ss–dsDNA constructs.
FIG. 8.
Optimized spectral linewidth and mean structural parameters of (iCy3)2 dimer-labeled ss–dsDNA constructs for varying label position obtained from 2DFS line shape analyses. (a) Homogeneous and inhomogeneous linewidth parameters. (b) Mean twist angle . (c) Mean tilt angle . (d) Mean inter-chromophore separation . In (a), the shaded regions bounded by the dashed lines indicate error bars, which were calculated based on a 1% deviation of the function [Eq. (20)] from its minimized value. In (b)–(d), the shaded regions bounded by the dashed lines indicate the standard deviations of the structural parameter distributions obtained from analyses of the 2DFS spectral line shapes, which are listed in Table V. These values were obtained by minimizing the least squares error functions shown in Fig. S23 of the supplementary material.
D. Distribution of local conformational parameters of (iCy3)2 dimer ss–dsDNA constructs labeled at the +2, +1, −1, and −2-positions
We used the 2DFS data shown in Figs. 7 and S18–S22 of the supplementary material to model the distributions of conformational parameters according to the method outlined in Sec. III D. The results of these studies are summarized in Table V and are shown together with the optimized values for the inhomogeneous and homogeneous linewidth parameters in Fig. 8. In Figs. 8(b)–8(d), the optimized values for the mean conformational parameters, which we determined from our analyses of absorbance and CD spectra, are presented as points. Shaded regions represent the optimized Gaussian widths of the corresponding distributions, which we determined by minimizing the least squares error functions shown in Fig. S23 of the supplementary material. In Fig. 8(a), the inhomogeneous and homogeneous linewidth parameters and 1% deviation error bars are presented, which we determined according to the 2D line shape analysis presented in Secs. IV A and IV B.
TABLE V.
Standard deviations of conformational parameters determined from H–F model analyses of absorbance, CD, and 2DFS data of (iCy3)2 dimer-labeled ss–dsDNA fork constructs. The optimized values were obtained by minimizing the least squares error function described in Sec. III D, which are shown in Fig. S23 of the supplementary material.
| Construct | σϕ (deg) | σθ (deg) | σR (Å) |
|---|---|---|---|
| +2 | 0.8 | 17 | 0.4 |
| +1 | 1.8 | 7.0 | 0.28 |
| −1 | 1.1 | 4.0 | 0.22 |
| −2 | 1.0 | 5.5 | 0.32 |
In Fig. 8(b), we plot the position-dependence of the mean twist angle and standard deviation σϕ. For the +2 ss–dsDNA construct, the mean twist angle has the value = 84.2°, which is very close to that obtained for the +15 position (79.6°). The value we determined for the standard deviation at this position is relatively small, σϕ = ∼0.7°. As the position is changed to +1, the twist angle decreases to = 77.0° with standard deviation σϕ = ∼1.7°. When the position is changed to −1, the mean twist angle undergoes a significant increase to = 96.0° (from right-handed to left-handed) with standard deviation σϕ = ∼1.1°. The values for both the mean twist angle and standard deviation do not change significantly when the probe labeling position is changed from −1 to −2. From these results, we conclude that while the mean twist angle undergoes significant changes as the probe labeling position is varied across the ss–dsDNA fork junction, the distribution of twist angles remains relatively narrow (σϕ < ∼2°) for these positions.
We next consider the position-dependent behavior of the mean tilt-angle and its standard deviation σθ, as shown in Fig. 8(c). For the +2 labeled ss–dsDNA construct, the mean tilt angle is = 6.6° and the standard deviation is σθ = ∼17°, indicating that there is a significant degree of conformational disorder in the tilt angle parameter at this position, although the sugar–phosphate backbones occupy, on average, a cylindrically symmetric local conformation. When the label position is changed to +1, the mean tilt angle increases dramatically to = 48.5° and the standard deviation decreases slightly to σθ = ∼7°. This indicates that the cylindrical symmetry of the sugar–phosphate backbones, which is normally found in the duplex region, is no longer present at the +1 position and that the conformational disorder of the tilt angle has decreased slightly. When the label position is changed to −1, the mean tilt angle decreases significantly to = 26.4° and the standard deviation decreases to σθ = ∼3.5°. When the label position is changed from −1 to −2, the mean tilt angle does not change significantly ( = 27.1°), although the standard deviation increases to σθ = ∼6°.
In Fig. 8(d), we show the position-dependent behavior of the mean interchromophore separation . For the +2 labeled construct, the mean separation is = 2.8 Å and the standard deviation is σR = ∼0.4 Å. We acknowledge that this value for the mean separation is unrealistically small as it lies below the van der Walls contact distance of ∼3.5 Å. This inconsistency is likely due to a breakdown of our H–F model analysis that underestimates the coupling strength for small interchromophore separations.11 When the probe label position is changed to +1, the mean separation decreases slightly to = 5.8 Å and the standard deviation decreases slightly to σR = ∼0.3 Å. However, when the position is changed from +1 to −1, the mean separation decreases significantly to = 4.3 Å and the standard deviation decreases to σR = ∼0.2 Å. When the position is changed further from −1 to −2, the mean separation does not change significantly ( = 4.4 Å) and the standard deviation is relatively unchanged: σR = ∼0.2 Å.
It is interesting to compare our results for the distributions of local conformational parameters, as summarized in Figs. 8(b)–8(d), to the optimized values we obtained for the homogeneous and inhomogeneous linewidths shown in Fig. 8(a). The position-dependencies of the linewidth parameters are discussed in Sec. IV C and show that there is relatively little variation in the inhomogeneous linewidth σI as the probe label position is changed from the +2 to −2 positions across the ss–dsDNA junction. Although the mean structural coordinates vary sensitively across the ss–dsDNA junction, the standard deviations of the structural coordinates that we obtained from our 2DFS line shape analysis indicate that the distributions of conformational coordinates at these positions remain relatively narrow at room temperature.
V. CONCLUSIONS
The conservation of base sequence integrity within genomic DNA is critical to maintaining well-regulated gene expression and replication. However, the structure of DNA within the cell must be dynamic, allowing for thermally induced fluctuations (i.e., DNA “breathing”) to facilitate productive interactions, including binding-site recognition and the assembly of functional protein–DNA complexes. For example, at ss–dsDNA fork junctions, transient local conformation fluctuations of the sugar–phosphate backbones are likely transition states for the formation of a stable helicase–primase (primosome) sub-assembly during DNA replication, with the existence of multiple DNA conformers working to facilitate competition between different protein regulatory factors and replisome proteins.
In this work, we have probed the average local conformations and the degree of conformational disorder at and near model ss–dsDNA replication fork junctions through site-specific internal labeling with two cyanine dyes (iCy3) rigidly inserted within the sugar–phosphate backbones at opposite positions within complementary single strands. We performed linear (absorbance and CD) and nonlinear (2DFS) spectroscopic studies of iCy3 monomer and (iCy3)2 dimer-labeled ss–dsDNA constructs as a function of temperature and probe label position (see Table I). Our analyses of the absorbance spectra of the iCy3 monomer-labeled ss–dsDNA constructs indicate that the monomer Hamiltonian parameters (i.e., the mean electronic transition energy , the Huang–Rhys vibronic coupling parameter λ2, and the vibrational frequency ω0) are largely insensitive to temperature and probe label position (see Tables S1 and S2 of the supplementary material). In contrast, the absorbance and CD spectra of (Cy3)2 dimer-labeled ss–dsDNA constructs respond sensitively to changing temperature and probe label position, from which we observed systematic changes of the optimized dimer Hamiltonian parameters (i.e., the mean resonant coupling , the mean twist angle , the mean tilt angle , and the mean interchromophore separation ; see Tables II–IV). Our 2DFS experiments have provided information about the local conformational disorder of the Cy3 probes at the probe label positions, from which we found that the Cy3 monomer-labeled ss–dsDNA constructs are significantly more disordered than the corresponding (Cy3)2 dimer-labeled constructs at room temperature (see Fig. 6). The relatively high disorder that we observed in the iCy3 monomer-labeled ss–dsDNA constructs is likely due to a mismatch of the W–C base pairing in the vicinity of the probe labeling site. In the iCy3 monomer-labeled ss–dsDNA constructs, a single thymine (T) base was positioned directly opposite to the iCy3 probe on the conjugate strand to act as a spacer. Nevertheless, normal W–C pairing is likely perturbed by the incorrect spacing between complementary bases introduced by the presence of the single iCy3 monomer probe. In contrast, we found that the (iCy3)2 dimer-labeled ss–dsDNA constructs are minimally disordered at room temperature and physiological buffer salt conditions, and their conformation-dependent spectroscopic properties appear to reflect the site-specific local conformations of the sugar–phosphate backbones at positions relatively close to the ss–dsDNA fork junction.
From our temperature-dependent studies of the (iCy3)2 dimer-labeled ss–dsDNA +15 “duplex” construct, we found that local conformations of the sugar–phosphate backbones deep within the double-strand region occupy a minimally disordered, right-handed B-form conformation at room temperature (23 °C). The B-form conformation is destabilized when the temperature is either raised or lowered from room temperature [see Fig. 6(b) and Table II]. These observations are consistent with the notion that the room temperature stability of the B-form conformation results from a nearly equal balance between opposing thermodynamic forces (entropy–enthalpy compensation) and that small departures from room temperature (in either the positive or negative direction) alter the free energy landscape and serve to populate non-B-form conformations. Such a picture is sometimes invoked in “DNA breathing and trapping models,” in which non-canonical local conformations of the DNA framework are transiently populated under physiological conditions and function as activated states required for the protein–DNA complex assembly.2,37,48
Our temperature-dependent studies of the (iCy3)2 dimer-labeled ss–dsDNA −1 “fork” construct showed that the average local conformation of the sugar–phosphate backbones at this probe position is left-handed and relatively disordered (in comparison to the +15 position) at room temperature. Increasing the temperature above 23 °C did not significantly change the average local conformation or conformational disorder at the −1 position, suggesting that the free energy landscape in this region of the construct is relatively insensitive to increasing temperature. However, like our observation for the +15 duplex ss–dsDNA construct, decreasing temperature below 23 °C did lead to a significant increase of the conformational disorder at the −1 position. These observations suggest, as has been studied in protein systems, that the concept of “cold denaturation” (defined as positions in the phase diagram for the folding–unfolding transition of the protein where changes in temperature in either direction decrease the stability of the folded form) might be productively applied to investigations of the stability of ss–dsDNA transitions as well.46,47,49–51 Future studies of nucleic acid stability, using the 2DFS approach described in the current work to investigate conformational disorder at nucleic acid positions of possible physiological interest, may help to shed new light on the underlying molecular mechanisms of some of the central processes of genome expression.
The results of our position-dependent studies of the (iCy3)2 dimer-labeled ss–dsDNA constructs at room temperature provide detailed information about the local conformations of the sugar–phosphate backbones at positions across the ss–dsDNA fork junction and are summarized in Fig. 9. The mean local conformations of the sugar–phosphate backbones are right-handed (with mean twist angle, < 90°) for positive integer positions and left-handed ( > 90°) for negative integer positions. Local conformations deep within the duplex region are cylindrically symmetric (with mean tilt angle 5°–10°) and minimally disordered (with inhomogeneous linewidth, σI = 137 cm−1). The disorder increases significantly for positive positions approaching the ss–dsDNA fork junction (σI = 167 cm−1 at the +2 position). At the +1 position, we observe an abrupt loss of cylindrical symmetry ( 48°), which coincides with an additional gain in conformational disorder (σI = 213 cm−1). The left-handed conformations at the −1 and −2 positions exhibit somewhat smaller mean tilt angles ( 27° and 26°, respectively) and decreasing conformational disorder (σI = 202 and 192 cm−1, respectively), suggesting that the peak perturbation to secondary structure within the ss–dsDNA fork junction occurs at the +1 position. Our 2DFS experiments provide additional information about the standard deviations of the distributions of conformational coordinates (see Fig. 8 and Table V). Perhaps surprisingly, our analyses indicate that the distributions of conformational parameters at positions traversing the ss–dsDNA fork junction are narrow, suggesting that regions of the junction extending into the single strands are relatively well-ordered. We emphasize that while the above conclusions are based on the interpretation of ensemble spectroscopic measurements, future single-molecule experiments performed on (iCy3)2 dimer ss–dsDNA constructs can, in principle, directly probe the individual conformational states that underlie the distributions reported here.
FIG. 9.
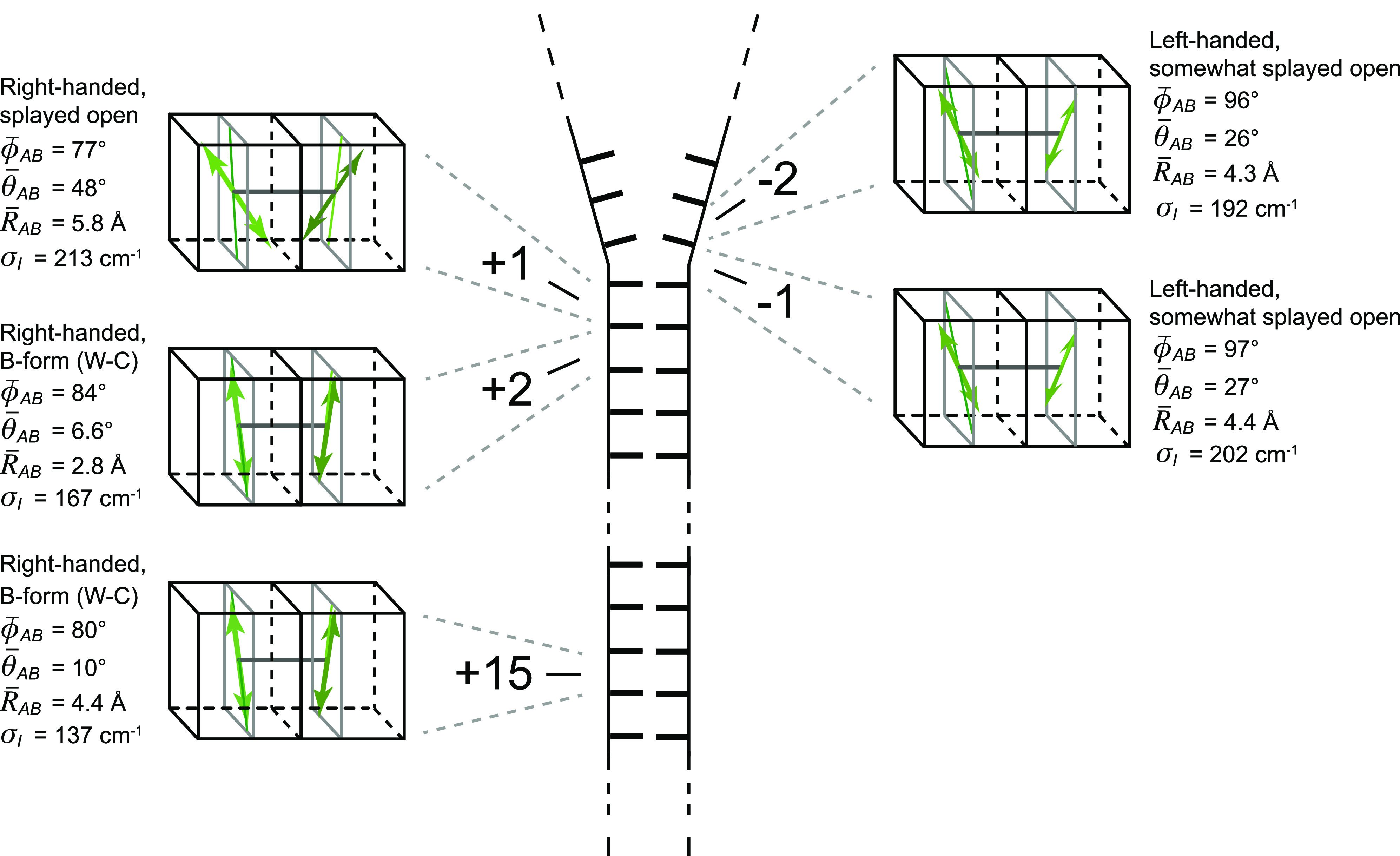
Schematic illustration of the average local conformations of the (iCy3)2 dimer-labeled ss–dsDNA junction at positions +15, +2, +1, −1, and −2 at room temperature.
Our findings provide a detailed picture of the variation of local conformation and conformational disorder of the sugar–phosphate backbones at and near the ss–dsDNA fork junction. The relatively narrow distributions of local conformations at such key positions imply that the number of possible states that mediates protein binding may be rather limited and suggests a possible structural framework for understanding the roles of transient DNA junction conformations in driving the processes of DNA–protein complex assembly and function.
SUPPLEMENTARY MATERIAL
See the supplementary material for the following: additional temperature-dependent optimized parameters and simulations of the Holstein–Frenkel model fit to absorbance, CD, and 2DFS data of iCy3 monomer and (iCy3)2 dimer ss–dsDNA constructs; results are shown for an optimization analysis of the relative quantum yield parameter Γ2D; values are shown for the temperature-dependent Hamiltonian parameters of the iCy3 monomer-labeled +15 “duplex” and −1 “fork” ss–dsDNA constructs; comparisons are shown between optimized fits to 2DFS data of the +15 and −1 ss–dsDNA constructs [both the iCy3 monomer and the (iCy3)2 dimer] for the temperature range 1–65 °C and to 2DFS data of the (iCy3)2 dimer-labeled −2, −1, +1, and +2 ss–dsDNA constructs at 23 °C; and results are shown for the optimization analyses and fits to 2DFS data to determine standard deviations of the conformational coordinates as a function of the (iCy3)2 dimer-labeling position relative to the ss–dsDNA junction.
ACKNOWLEDGMENTS
The authors are grateful to their laboratory colleagues in the Marcus and von Hippel groups for many helpful discussions. This work was supported by grants from the National Institutes of Health General Medical Sciences (Grant No. GM-15792 to A.H.M. and P.H.v.H.) and the National Science Foundation Chemistry of Life Processes Program (Grant No. CHE-1608915 to A.H.M.). P.H.v.H. is an American Cancer Society Research Professor of Chemistry.
Note: This paper is part of the JCP Special Topic on Time-Resolved Vibrational Spectroscopy.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.Watson J. D. and Crick F. H. C., “Molecular structure of nucleic acids,” Nature 171, 737–738 (1953). 10.1038/171737a0 [DOI] [PubMed] [Google Scholar]
- 2.von Hippel P. H., Johnson N. P., and Marcus A. H., “50 years of DNA “breathing”: Reflections on old and new approaches,” Biopolymers 99, 923–954 (2013). 10.1002/bip.22347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gnatt A. L., Cramer P., Fu J., Bushnell D. A., and Kornberg R. D., “Structural basis of transcription: An RNA polymerase II elongation complex at 3.3 Å resolution,” Science 292, 1876–1882 (2001). 10.1126/science.1059495 [DOI] [PubMed] [Google Scholar]
- 4.Levitus M. and Ranjit S., “Cyanine dyes in biophysical research: The photophysics of polymethine fluorescent dyes in biomolecular environments,” Q. Rev. Biophys. 44, 123–151 (2011). 10.1017/s0033583510000247 [DOI] [PubMed] [Google Scholar]
- 5.Heussman D., Kittell J., Kringle L., Tamimi A., von Hippel P. H., and Marcus A. H., “Measuring local conformations and conformational disorder of (Cy3)2 dimers labeled DNA fork junctions using absorbance, circular dichroism and two-dimensional fluorescence spectroscopy,” Faraday Discuss. 216, 211–235 (2019). 10.1039/c8fd00245b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lee W., von Hippel P. H., and Marcus A. H., “Internally labeled Cy3/Cy5 DNA constructs show greatly enhanced photostability in single-molecule FRET experiments,” Nucleic Acids Res. 42, 5967–5977 (2014). 10.1093/nar/gku199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kringle L., Sawaya N. P. D., Widom J., Adams C., Raymer M. G., Aspuru-Guzik A., and Marcus A. H., “Temperature-dependent conformations of exciton-coupled Cy3 dimers in double-stranded DNA,” J. Chem. Phys. 148, 085101 (2018). 10.1063/1.5020084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kistler K. A., Pochas C. M., Yamagata H., Matsika S., and Spano F. C., “Absorption, circular dichroism, and photoluminescence in perylene diimide bichromophores: Polarization-dependent H- and J-aggregate behavior,” J. Phys. Chem. B 116, 77–86 (2011). 10.1021/jp208794t [DOI] [PubMed] [Google Scholar]
- 9.Czikklely V., Forsterling H. D., and Kuhn H., “Extended dipole model for aggregates of dye molecules,” Chem. Phys. Lett. 6, 207–210 (1970). 10.1016/0009-2614(70)80220-2 [DOI] [Google Scholar]
- 10.Didraga C., Pugžlys A., Hania P. R., von Berlepsch H., Duppen K., and Knoester J., “Structure, spectroscopy, and microscopic model of tubular carbocyanine dye aggregates,” J. Phys. Chem. B 108, 14976–14985 (2004). 10.1021/jp048288s [DOI] [Google Scholar]
- 11.Sorour M. I., Kistler K. A., Marcus A. H., and Matsika S., “Accurate modeling of excitonic coupling in cyanine dye Cy3,” J. Phys. Chem. A 125, 7852–7866 (2021). 10.1021/acs.jpca.1c05556 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ernst R. R., Bodenhausen G., and Wokaun A., Principles of Nuclear Magnetic Resonance in One and Two Dimensions (Oxford University Press, Oxford, 1990). [Google Scholar]
- 13.Brown S. P. and Wimperis S., “Inhomogeneously broadening of two-dimensional NMR lineshapes,” Chem. Phys. Lett. 237, 509–515 (1995). 10.1016/0009-2614(95)00330-7 [DOI] [Google Scholar]
- 14.Reppert M. and Tokmakoff A., “Computational amide I 2D IR spectroscopy as a probe of protein structure and dynamics,” Annu. Rev. Phys. Chem. 67, 359–386 (2016). 10.1146/annurev-physchem-040215-112055 [DOI] [PubMed] [Google Scholar]
- 15.Ghosh A., Ostrander J. S., and Zanni M. T., “Watching proteins wiggle: Mapping structures with two-dimensional infrared spectroscopy,” Chem. Rev. 117, 10726–10759 (2017). 10.1021/acs.chemrev.6b00582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sanstead P. J., Stevenson P., and Tokmakoff A., “Sequence-dependent mechanism of DNA oligonucleotide dehybridization resolved through infrared spectroscopy,” J. Am. Chem. Soc. 138, 11792–11801 (2016). 10.1021/jacs.6b05854 [DOI] [PubMed] [Google Scholar]
- 17.Sanstead P. J. and Tokmakoff A., “Direct observation of activated kinetics and downhill dynamics in DNA dehybridization,” J. Phys. Chem. B 122, 3088–3100 (2018). 10.1021/acs.jpcb.8b01445 [DOI] [PubMed] [Google Scholar]
- 18.Laage D., Elsaesser T., and Hynes J. T., “Water dynamics in the hydration shells of biomolecules,” Chem. Rev. 117, 10694–10725 (2017). 10.1021/acs.chemrev.6b00765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.McConnell B. and von Hippel P. H., “Hydrogen exchange as a probe of the dynamic structure of DNA. I. General acid-base catalysis,” J. Mol. Biol. 50, 297–316 (1970). 10.1016/0022-2836(70)90194-4 [DOI] [PubMed] [Google Scholar]
- 20.McConnell B. and von Hippel P. H., “Hydrogen exchange as a probe of the dynamic structure of DNA. II. Effects of base composition and destabilizing salts,” J. Mol. Biol. 50, 317–332 (1970). 10.1016/0022-2836(70)90195-6 [DOI] [PubMed] [Google Scholar]
- 21.Ganim Z. and Tokmakoff A., “Spectral signatures of heterogeneous protein ensembles revealed by MD simulations of 2DIR spectra,” Biophys. J. 91, 2636–2646 (2006). 10.1529/biophysj.106.088070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Förster T., Delocalized Excitation and Excitation Transfer, Division of Biology and Medicine: Bulletin, United States/Atomic Energy Commission (Florida State University, Tallahassee, FL, 1965), Vol. 18. [Google Scholar]
- 23.Tamimi A., Landes T., Lavoie J., Raymer M. G., and Marcus A. H., “Fluorescence-detected Fourier transform electronic spectroscopy by phase-tagged photon counting,” Opt. Express 28, 25194–25214 (2020). 10.1364/oe.400245 [DOI] [PubMed] [Google Scholar]
- 24.Perdomo-Ortiz A., Widom J. R., Lott G. A., Aspuru-Guzik A., and Marcus A. H., “Conformation and electronic population transfer in membrane supported self-assembled porphyrin dimers by two-dimensional fluorescence spectroscopy,” J. Phys. Chem. B 116, 10757–10770 (2012). 10.1021/jp305916x [DOI] [PubMed] [Google Scholar]
- 25.Tekavec P. F., Dyke T. R., and Marcus A. H., “Wave packet interferometry and quantum state reconstruction by acousto-optic phase modulation,” J. Chem. Phys. 125, 194303 (2006). 10.1063/1.2386159 [DOI] [PubMed] [Google Scholar]
- 26.Tekavec P. F., Lott G. A., and Marcus A. H., “Fluorescence-detected two-dimensional electronic coherence spectroscopy by acousto-optic phase modulation,” J. Chem. Phys. 127, 214307 (2007). 10.1063/1.2800560 [DOI] [PubMed] [Google Scholar]
- 27.Lott G. A., Perdomo-Ortiz A., Utterback J. K., Widom J. R., Aspuru-Guzik A., and Marcus A. H., “Conformation of self-assembled porphyrin dimers in liposome vesicles by phase-modulation 2D fluorescence spectroscopy,” Proc. Natl. Acad. Sci. U. S. A. 108, 16521–16526 (2011). 10.1073/pnas.1017308108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Spano F. C., “The spectral signatures of Frenkel polarons in H- and J-aggregates,” Acc. Chem. Res. 43, 429–439 (2010). 10.1021/ar900233v [DOI] [PubMed] [Google Scholar]
- 29.Valcunas L., Abramavicius D., and Mančal T., Molecular Excitation Dynamics and Relaxation: Quantum Theory and Spectroscopy (Wiley VCH, 2013). [Google Scholar]
- 30.Mukamel S., “Femtosecond optical spectroscopy: A direct look at elementary chemical events,” Annu. Rev. Phys. Chem. 41, 647–681 (1990). 10.1146/annurev.pc.41.100190.003243 [DOI] [Google Scholar]
- 31.Siemens M. E., Moody G., Li H., Bristow A. D., and Cundiff S. T., “Resonance lineshapes in two-dimensional Fourier transform spectroscopy,” Opt. Express 18, 17699–17708 (2010). 10.1364/oe.18.017699 [DOI] [PubMed] [Google Scholar]
- 32.Grégoire P., Kandada A. R. S., Vella E., Tao C., Leonelli R., and Silva C., “Incoherent population mixing of contributions to phase-modulated two-dimensional coherent excitation spectra,” J. Chem. Phys. 147, 114201 (2017). 10.1063/1.4994987 [DOI] [PubMed] [Google Scholar]
- 33.Cho M., Two-Dimensional Optical Spectroscopy, 1st ed. (CRC Press, Boca Raton, 2009). [Google Scholar]
- 34.Mukamel S., Principles of Nonlinear Optical Spectroscopy, edited by Lapp M. (Oxford University Press, Oxford, 1995). [Google Scholar]
- 35.Widom J. R., Lee W., Perdomo-Ortiz A., Rappoport D., Molinski T. F., Aspuru-Guzik A., and Marcus A. H., “Temperature-dependent conformations of a membrane supported “zinc porphyrin tweezer” by 2D fluorescence spectroscopy,” J. Phys. Chem. A 117, 6171–6184 (2013). 10.1021/jp400394z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Phelps C., Israels B., Jose D., Marsh M. C., von Hippel P. H., and Marcus A. H., “Using microsecond single-molecule FRET to determine the assembly pathways of T4 ssDNA binding protein onto model DNA replication forks,” Proc. Natl. Acad. Sci. U. S. A. 114, E3612–E3621 (2017). 10.1073/pnas.1619819114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Israels B., Albrecht C. S., Dang A., Barney M., von Hippel P. H., and Marcus A. H., “Sub-millisecond conformational transitions of single-stranded DNA lattices by photon correlation single-molecule FRET,” J. Phys. Chem. B 125, 9426–9440 (2021). 10.1021/acs.jpcb.1c04119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Byrd R. H., Nocedal J., and Waltz R. A., KNITRO: An Integrated Package for Nonlinear Optimization, Large-Scale Nonlinear Optimization (Springer-Verlag, Berlin, 2006), pp. 35–59. [Google Scholar]
- 39.Kunsel T., Tiwari V., Matutes Y. A., Gardiner A. T., Cogdell R. J., Ogilvie J. P., and Jansen T. L. C., “Simulating fluorescence-detected two-dimensional electronic spectroscopy of multichromophoric systems,” J. Phys. Chem. B 123, 394–406 (2019). 10.1021/acs.jpcb.8b10176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tiwari V., Matutes Y. A., Konar A., Yu Z., Ptaszek M., Bocian D. F., Holten D., Kirmaier C., and Ogilvie J. P., “Strongly coupled bacteriochlorin dyad studied using phase-modulated fluorescence-detected two-dimensional electronic spectroscopy,” Opt. Express 26, 22327–22341 (2018). 10.1364/oe.26.022327 [DOI] [PubMed] [Google Scholar]
- 41.Pace N. A., Hennelly S. P., and Goodwin P. M., “Immobilization of cyanines in DNA produces systematic increases in fluorescence intensity,” J. Phys. Chem. Lett. 12, 8963–8971 (2021). 10.1021/acs.jpclett.1c02022 [DOI] [PubMed] [Google Scholar]
- 42.Spiriti J., Binder J. K., Levitus M., and van der Vaart A., “Cy3-DNA stacking interactions strongly depend on identity of the terminal basepair,” Biophys. J. 100, 1049–1057 (2011). 10.1016/j.bpj.2011.01.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Aramendia P. F., Negri R. M., and Roman E. S., “Temperature dependence of fluorescence photoisomerization in symmetric carbocyanines. Influence of medium viscosity and molecular structure,” J. Phys. Chem. 98, 3165–3173 (1994). 10.1021/j100063a020 [DOI] [Google Scholar]
- 44.Waldeck D. H. and Fleming G. R., “Influence of viscosity and temperature on rotational reorientation. Anisotropic absorption of 3,3′-diethyloxadicarbocyanine iodide,” J. Phys. Chem. 85, 2614–2617 (1981). 10.1021/j150618a009 [DOI] [Google Scholar]
- 45.von Hippel P. H. and Waugh D. F., “Casein: Monomers and polymers,” J. Am. Chem. Soc. 77, 4311–4319 (1955). 10.1021/ja01621a041 [DOI] [Google Scholar]
- 46.Privalov P. L., Griko Y. V., Venyaminov S. Y., and Kutyshenko V. P., “Cold denaturation of myoglobin,” J. Mol. Biol. 190, 487–498 (1986). 10.1016/0022-2836(86)90017-3 [DOI] [PubMed] [Google Scholar]
- 47.Mikulecky P. J. and Feig A. L., “Cold denaturation of the hammerhead ribozyme,” J. Am. Chem. Soc. 124, 890–891 (2002). 10.1021/ja016878n [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Phelps C., Lee W., Jose D., von Hippel P. H., and Marcus A. H., “Single-molecule FRET and linear dichroism studies of DNA “breathing” and helicase binding at replication fork junctions,” Proc. Natl. Acad. Sci. U. S. A. 110, 17320–17325 (2013). 10.1073/pnas.1314862110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Vaitiekunas P., Crane-Robinson C., and Privalov P. L., “The energetic basis of the DNA double helix: A combined microcalorimetric approach,” Nucleic Acids Res. 43, 8577–8589 (2015). 10.1093/nar/gkv812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mikulecky P. J. and Feig A. L., “Heat capacity changes associated with nucleic acid folding,” Biopolymers 82, 38–58 (2006). 10.1002/bip.20457 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mak C. H., “Unraveling base stacking driving forces in DNA,” J. Phys. Chem. B 120, 6010–6020 (2016). 10.1021/acs.jpcb.6b01934 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for the following: additional temperature-dependent optimized parameters and simulations of the Holstein–Frenkel model fit to absorbance, CD, and 2DFS data of iCy3 monomer and (iCy3)2 dimer ss–dsDNA constructs; results are shown for an optimization analysis of the relative quantum yield parameter Γ2D; values are shown for the temperature-dependent Hamiltonian parameters of the iCy3 monomer-labeled +15 “duplex” and −1 “fork” ss–dsDNA constructs; comparisons are shown between optimized fits to 2DFS data of the +15 and −1 ss–dsDNA constructs [both the iCy3 monomer and the (iCy3)2 dimer] for the temperature range 1–65 °C and to 2DFS data of the (iCy3)2 dimer-labeled −2, −1, +1, and +2 ss–dsDNA constructs at 23 °C; and results are shown for the optimization analyses and fits to 2DFS data to determine standard deviations of the conformational coordinates as a function of the (iCy3)2 dimer-labeling position relative to the ss–dsDNA junction.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.