Abstract
Feature Selection (FS) is considered as an important preprocessing step in data mining and is used to remove redundant or unrelated features from high-dimensional data. Most optimization algorithms for FS problems are not balanced in search. A hybrid algorithm called nonlinear binary grasshopper whale optimization algorithm (NL-BGWOA) is proposed to solve the problem in this paper. In the proposed method, a new position updating strategy combining the position changes of whales and grasshoppers population is expressed, which optimizes the diversity of searching in the target domain. Ten distinct high-dimensional UCI datasets, the multi-modal Parkinson's speech datasets, and the COVID-19 symptom dataset are used to validate the proposed method. It has been demonstrated that the proposed NL-BGWOA performs well across most of high-dimensional datasets, which shows a high accuracy rate of up to 0.9895. Furthermore, the experimental results on the medical datasets also demonstrate the advantages of the proposed method in actual FS problem, including accuracy, size of feature subsets, and fitness with best values of 0.913, 5.7, and 0.0873, respectively. The results reveal that the proposed NL-BGWOA has comprehensive superiority in solving the FS problem of high-dimensional data.
Keywords: Feature selection, Hybrid bionic optimization algorithm, Biomimetic position updating strategy, Nature-inspired algorithm, High-dimensional UCI datasets, Multi-modal medical datasets
Introduction
Nowadays, with the rapid accumulation of massive data in different fields, data are being produced at a never seen before scale in dimensions [1]. High-dimensional data usually contain an increasing amount of information, but many unrelated or weakly correlated features also exist, which affect the data processing [2]. Therefore, it is urgent to develop effective data mining technology to reduce the dimension of high-dimensional data in various fields, such as medicine, bioinformatics, text mining, and internet of drones [3, 4]. FS is an effective data dimensional reduction method, which has been widely used and plays an important role in machine learning and pattern recognition fields [5]. By reducing the dimension of the dataset, it improves the calculation speed of the model. As a preprocessing step, FS is essentially a combinatorial optimization problem [6]. The purpose of FS aims to remove irrelevant and redundant attributes of specific datasets [7]. Different FS methods can be selected for data processing due to different learning algorithms. When dealing with high-dimensional data, the search strategy in the FS method is particularly important [8]. Recently, meta-heuristics with various search strategies have been largely employed to solve FS problems [9]. With the global search ability, the Swarm Intelligence (SI)-based heuristic search methods can better alleviate the time complexity and computing costs in FS [10]. The SI optimization algorithms are inspired by natural animal communities’ behavior and simulate the foraging and predation law continuously [11].
At present, many popular SI algorithms have been employed to solve the FS problems, such as: Genetic Algorithm (GA) [12], Particle Swarm Optimization (PSO) [13], and Grey Wolf Optimization algorithm (GWO) [14]. Recently, some algorithms including Whale Optimization Algorithm (WOA) [15], Butterfly Optimization Algorithm (BOA) [16], and Grasshopper Optimization Algorithm (GOA) are proposed [17]. These optimization algorithms based on population generate a set of candidate solutions in each run. This can lead the better consequences in FS.
Similarly, Abualigah et al. propose a novel nature-inspired meta-heuristic optimizer, called Reptile Search Algorithm (RSA), which is motivated by the hunting behavior of crocodiles [18]. The Dwarf Mongoose Optimization algorithm (DMO) algorithm is proposed to mimic the foraging behavior of the dwarf mongoose and displays the bionic behavior for searching [19]. Using a bionic disease transmission strategy, a meta-heuristic algorithm named Ebola Optimization Search Algorithm (EOSA) is proposed, which is based on the propagation mechanism of the Ebola virus disease [20]. Moreover, the distributed behavior of the major arithmetic operators can also establish a meta-heuristic approach to optimization problems, which is called Arithmetic Optimization Algorithm (AOA) [21]. Besides, a population-based optimization method is proposed, called Aquila Optimizer (AO), which is inspired by the natural behavior of aquila during prey capture [22]. Table 1 describes the bionic behavior differences of some nature-inspired meta-heuristic algorithms.
Table 1.
Differences in bionic behavior between some nature-inspired meta-heuristic algorithms
| Algorithm | Inspiration | References |
|---|---|---|
| Aquila Optimizer (AO) | Aquila Bird | [22] |
| Arithmetic Optimization Algorithm (AOA) | Arithmetic Operators | [21] |
| Butterfly Optimization Algorithm (BOA) | Food Search and Mating Behavior of Butterflies | [16] |
| Dwarf Mongoose Optimization algorithm (DMO) | Behavior of The Dwarf Mongoose | [19] |
| Ebola Optimization Search Algorithm (EOSA) | Ebola Virus | [20] |
| Genetic Algorithm (GA) | Evolutionary Biology | [12] |
| Grasshopper Optimization Algorithm (GOA) | Foraging and Swarming Behavior of Grasshoppers | [17] |
| Grey Wolf Optimization (GWO) | Hunting Process of Grey Wolves | [14] |
| Particle Swarm Optimization (PSO) | Simplified Social Model | [13] |
| Reptile Search Algorithm (RSA) | Behavior of Crocodiles | [18] |
| Whale Optimization Algorithm (WOA) | Social Behavior of Humpback Whales | [15] |
However, considering that many optimization problems are set in a binary space, the above SI optimization algorithms cannot meet this condition. Here, calculating the optimal position is the key to completing FS problems when employing SI optimization algorithms. Besides, appropriately balancing exploration and exploitation will lead to the improvement of the search algorithm’s performance. Therefore, how to explore the space of the search and exploit the optimal solutions are two contradictory principles to be considered [23].
To deal well with this issue, the majority of SI optimization algorithms have been further optimized. It is a common method to improve the location update in a binary way and redefine the space of position updating. A binary PSO (BPSO) in which a particle moves in a state space restricted to zero and one on each dimension is proposed [24]. To solve the diverse FS problems, Hussien et al. design two novel binary variants of the WOA called BWOA-S and BWOA-V [25]. By combining a mutation operator into the GOA, a novel version called binary GOA (BGOA) is proposed [26]. The BGOA can enhance the exploratory behavior of the original GOA. Although binary variant algorithms can solve the binary optimization problem in feature subset selection of high-dimensional datasets, it still makes errors because of careless search facing complex FS problems. New solutions are still urgently needed to solve the search problem in FS.
The combination of the advantages of SI optimization algorithms can also balance the relationship between exploration and exploitation. Hybrid algorithms have attracted more and more attention in the field of optimization algorithms [27]. Table 2 summarizes the relevant studies on hybrid optimization algorithms in recent years. Marfarja et al. propose a hybrid WOA and simulated annealing (SA) algorithm in a wrapper feature selection method to enhance the exploitation of the WOA [28]. Al-Tashi et al. improve a binary version of the hybrid PSO and GWO as an FS method, which employs suitable operators to solve binary problems [29]. To surmount the inconveniences in dimensional space and non-informational peculiarities, Purushothaman et al. introduce a hybrid between the GWO and the GOA for text feature selection and clustering [30]. Besides the simple combination in the hybrid algorithms, some studies have improved the bionic variation by improving the coefficients in the function.
Table 2.
Some hybrid optimization algorithms
Hence, a system for FS based on a hybrid Monkey Algorithm (MA) with Krill Herd Algorithm (KHA) is proposed [31]. The fitness function of the proposed algorithm incorporates both classification accuracy and feature reduction size. Jia H et al. propose three hybrid algorithms to solve FS problems based on Seagull Optimization Algorithm (SOA) and Thermal Exchange Optimization (TEO) [32]. A hybrid feature subset selection algorithm called the Maximum Pearson’s Maximum Distance Improved Whale Optimization Algorithm (MPMDIWOA) is proposed by designing two parameters to adjust the weights of the relevance and redundancy [33]. Hybrid bionic optimization algorithms perform well in feature subset selection, but there is no concrete practice in practical application. Recently, some practical feature selection problems have begun to focus on using hybrid algorithms.
Considering the strengths of GWO and Crow Search Algorithm (CSA), a hybrid GWO with CSA, namely GWOCSA is proposed, which aims to generate promising candidate solutions and achieve global optima efficiently [34]. A new hybrid binary version of bat (BA) and enhanced PSO is proposed to solve FS problems, called Hybrid Binary Bat Enhanced Particle Swarm Optimization Algorithm (HBBEPSO) [35]. It combines the bat algorithm with its capacity for echolocation into the version of the particle swarm optimization. Moreover, Cy et al. introduce a hybrid model called BCROSAT for FS in high-dimensional biomedical datasets, in which the tournament selection mechanism and SA algorithm are combined with Binary Coral Reef Optimization (BCRO) [36]. Shunmugapriya and Kanmani propose a novel swarm-based hybrid algorithm named AC-ABC Hybrid, which combines the characteristics of Ant Colony Optimization (ACO) and Artificial Bee Colony (ABC) algorithms to optimize FS [37]. Although these hybrid bionic optimization algorithms solve the feature subset selection in some problems, they still fall into local optimum in high-dimensional datasets.
In brief, the SI optimization algorithm has an excellent performance in FS, it is easy to fall into the local optimal condition in the process of feature selection and fail to select the most representative feature subset. Therefore, how to solve the defect and select the least feature subset is a crucial problem [38]. To improve this problem existing in most optimization algorithms, this paper proposes a nonlinear binary grasshopper whale optimization algorithm, namely NL-BGWOA, which combines the whale individual updating method in WOA with GOA and optimizes the position updating strategy. The proposed NL-BGWOA incorporates the adaptive weight and nonlinear adjustment coefficients. To verify the reliability of the proposed NL-BGWOA, it is compared with several other state-of-the-art algorithms in FS experiments, such as GOA, WOA, BGOA, and BWOA. Moreover, the proposed algorithm is also tested on high-dimensional UCI datasets, multi-modal Parkinson's speech datasets, and COVID-19 symptom dataset, whose experimental results are evaluated.
The rest of the paper is organized as follows. Section 2 gives an outline of the standard GOA, WOA, and the corresponding binary version of them. Section 3 presents the proposed NL-BGWOA algorithm and its procedures. Section 4 describes the experimental design, results, and analysis of the basic FS problem and the actual problem in medical datasets. Finally, Sect. 5 draws some conclusions for this paper and presents the further work.
Background
Grasshopper Optimization Algorithm
The Original Algorithm
In nature, grasshoppers often gather in large-scale ways to prey. The characteristics of grasshoppers are related to their movement. The swarm in the nymph phase is characterized by slow movement with small steps by the grasshoppers. In contrast, the swarm in the adult phase is characterized by abrupt and long-distance movement, which corresponds to the exploration and exploitation phase of the nature-inspired algorithms.
The grasshopper optimization algorithm gives a mathematical model that simulates the movement of grasshopper populations:
| 1 |
where is the distance between the ith and the jth grasshopper: ; s is the strength of social forces: , where f indicates the intensity of attraction and l is the attractive length scale; and are the upper and lower bound, respectively; is the value of the best solution, and is a decreasing coefficient to shrink the comfort zone, repulsion zone, and attraction zone.
The parameter is the core parameter of the GOA algorithm, and the parameter update strategy has an important influence on the convergence performance of the algorithm. The linearly decreasing parameter can realize the process of the algorithm from exploration to development and the ability to reduce the comfort zone between grasshoppers.
| 2 |
where is the maximum value, is the minimum value, the value of is 1 or 2, indicates the current iteration, and is the maximum number of iterations.
The outer is used to reduce the search coverage toward the target grasshopper as the iteration count increases, while the inner is used to reduce the effect of the attraction and repulsion forces between grasshoppers proportionally to the number of iterations.
Binary Grasshopper Optimization Algorithm
The grasshopper optimization algorithm has strong local development capabilities, so it has good performance in solving continuous optimization problems. However, according to the nature of the FS problem, the search space can be represented by binary values [0,1]. Since binary operators are expected to be much simpler than continuous counterparts, the GOA algorithm needs to be discretized. Therefore, Majdi Mafarja et al. propose a method by modifying the population update strategy of the GOA algorithm to obtain the Binary Grasshopper Optimization Algorithm (BGOA).
Here, sigmoidal and hyperbolic tan functions are two transfer functions, which play key roles in BGOA. This paper takes the sigmoidal function as an example:
| 3 |
The position of the current grasshopper will be updated based on the probability value :
| 4 |
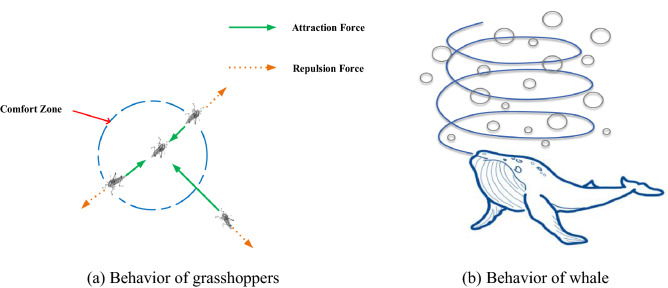
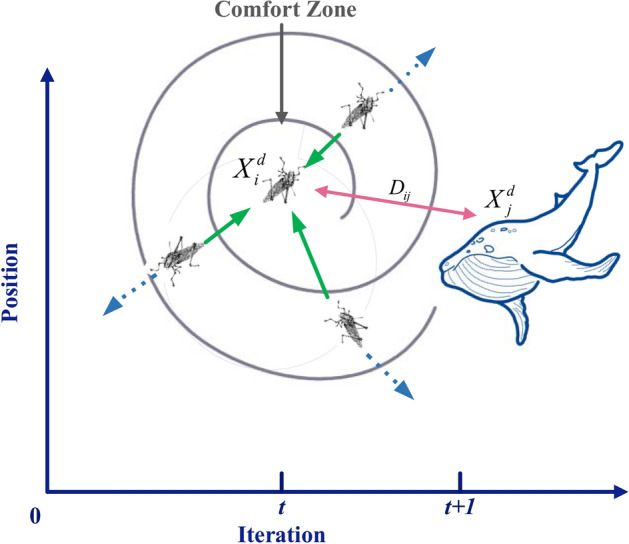
where represents the dth dimension of the grasshopper in the next iteration and is a random number in the range . A conceptual model of the interactions between grasshoppers and the comfort zone is illustrated in Fig. 1a.
Fig. 1.
Behavior of individual grasshoppers and whale
Whale Optimization Algorithm
The Original Algorithm
The WOA is a SI optimization algorithm that imitates humpback whale predation, which includes the encircling prey phase, the exploitation phase, and the exploration phase. During the encircling prey phase, individual whales can identify the location of prey and enclose them. The corresponding computation is as follows:
| 5 |
where is the number of iteration. is the optimal whale position and is the current whale position. is the corresponding step size.
In the exploitation phase, the WOA designs two ways to simulate the bubble-net attacking method of whales. The first way is similar to the encircling prey phase when is established. The second way is called the spiral updating position, where the whale moves to the current optimal individual in a spiral movement. The corresponding process for position updating is defined as follows:
| 6 |
where is the distance between the individual whale and the current optimal whale. is the logarithmic spiral shape constant, in general, is set to 1. is a random number in interval .
In conclusion, the whale position can be updated by the above two cases:
| 7 |
where is a random number in , which represents a probability value. When is less than 0.5, the whales use the first case to shrink and surround. Otherwise, the whales use the second case to spirally update their position.
During the exploration phase, if there is no optimal prey in the shrinking range, the whale will jump out of the range and search randomly. When is true, the mathematical model is as follows:
| 8 |
where is the position of a random whale in the current population.
Binary Whale Optimization Algorithm
The WOA has a simple structure and uses a few coefficients, so it is often used for various situations. However, the original WOA may exist local optimization. Therefore, the binary WOA for the feature selection redefined the space of position updating.
In binary WOA, the positions of the individual whale in solution space are restricted to the binary space :
| 9 |
where is the number in the interval . is the updated binary position at iteration. is a combination of the position updating and the sigmodal function, which is defined as follows:
| 10 |
The general movement of the individual whale as it hunts and preys through the bubble-net attacking method is illustrated in Fig. 1b.
The Proposed Method
According to the fundamental purpose of the FS problem, the proposed NL-BGWOA finds the least optimal feature subset from the original datasets, improves the accuracy of the optimization algorithm, and simplifies the data processing. Besides, the proposed method improves the nonlinear decline coefficient and the adaptive weight that changes in the iteration process. The specific improvement contents are as follows.
The Related Work
(1) The nonlinear coefficient
The swarm intelligence optimization algorithm is mainly divided into two stages: the exploration stage and the exploration stage. These two important stages determine the performance of the algorithm, so how to effectively balance them is a key consideration.
However, there is a major problem in most swarm intelligence optimization algorithms: the core coefficient decreases linearly at a constant rate, which will slow down the convergence speed and easily make the algorithm fall into a local optimum. To tackle the above problem, this paper proposes a nonlinear change strategy, which adjusts the linear change of the coefficient by combining the change trend of the cosine function.
The proposed nonlinear coefficient is described by the following equation:
| 11 |
where and is the maximum and minimum, the value of is 1 or 2, respectively, indicates the current iteration, and is the maximum number of iterations.
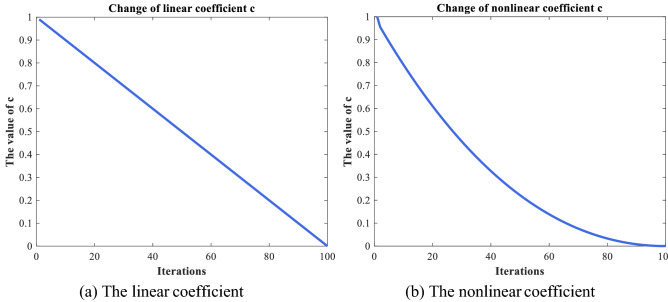
The proposed nonlinear coefficient speeds up the search speed in the exploitation stage, which enables the individual to obtain the target quickly. During the exploration phase, the speed of the coefficient slows down, so the population can carefully search the surrounding space. Therefore, the proposed method can effectively avoid falling into the local optimum and better balance the global and local search. The comparison between the nonlinear and linear coefficients is shown in Fig. 2.
Fig. 2.
The comparison between the nonlinear and linear coefficients
2. The adaptive weight
The movement of individuals in the swarm intelligence optimization algorithm during position updating is also very important. During iterating, it should be considered that the position updating method in different iteration cycles and the degree of dependence between individuals. In this paper, the adaptive weight is integrated into the updating position, which is defined as follows:
| 12 |
where is the number of current iteration and is the number of the maximum iterations.
The position update after the adoption of adaptive weights will dynamically adjust the size of the weights according to the increase in the number of iterations, so that the current optimal position guides individuals differently. As the number of iterations increases, the individual with a larger weight will speed up the movement, which speeds up the convergence speed.
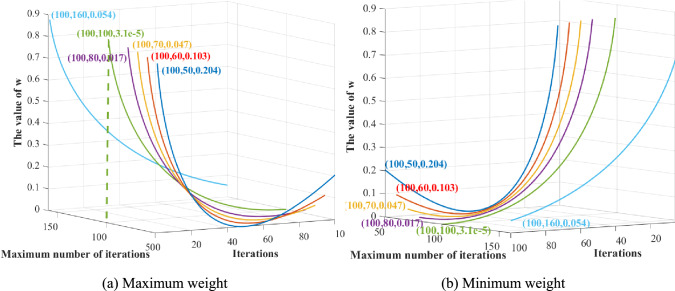
As shown in Fig. 3, different has a great influence on the adaptive weight . The weight is large at the beginning and gradually become smaller, which is affected by the number of the maximum iteration . By comparison, it can be seen that when is 100, the condition can be met simultaneously. The optimal is highlighted in green.
Fig. 3.
Comparison of adaptive weight with different
The Proposed NL-BGWOA
The purpose of the feature selection is to select relevant features and eliminate redundant ones. The BWOA remains the better performance in low-dimensional datasets, but it cannot select the effective features to handle the high-dimensional datasets. The BGOA has certain advantages in processing high-dimensional data, which can make up for the deficiencies of BWOA. Therefore, this paper proposes a novel algorithm named NL-BGWOA that combines the advantages of BGOA and BWOA.
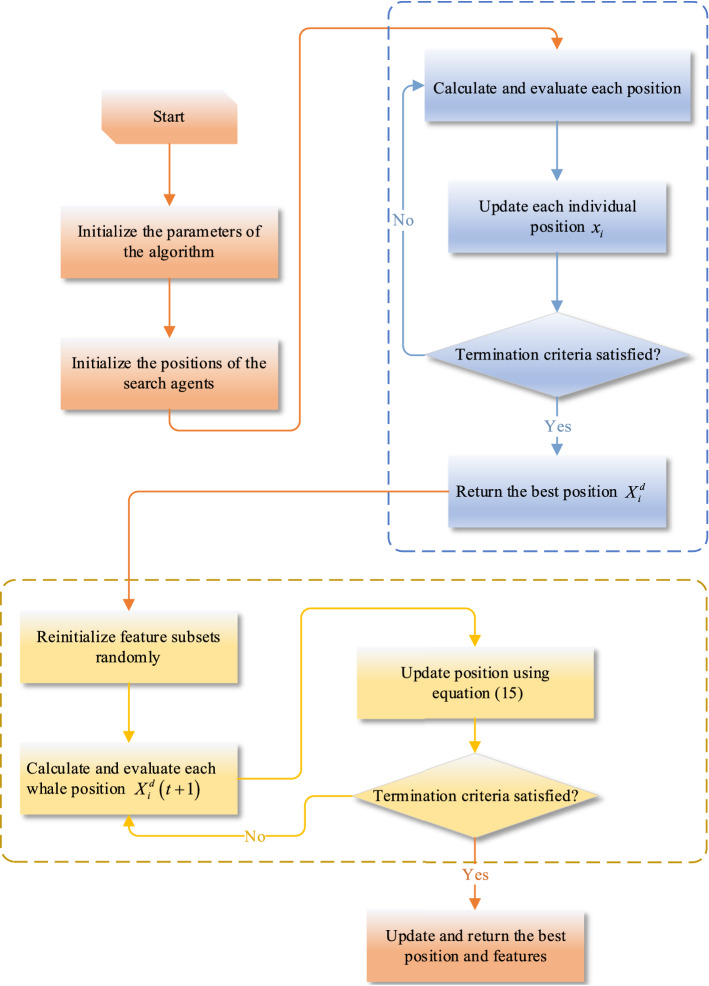
The proposed method can select the representative salient features of the adopted datasets and can find more optimal solutions in the search space. Concretely, features are selected from generated features that are potential solutions in the search space. The salient features are further selected by the NL-BGWOA to produce more representative and significant feature subsets. In the proposed NL-BGWOA, multiple influences are analyzed for optimal locations, with the aim of conducting more detailed searches in high-dimensional datasets. The proposed method can improve the efficiency of the search. Besides, the optimization between the current optimal position and the next one during each search can improve the accuracy of FS. Figure 4 shows the process of the proposed NL-BGWOA.
Fig. 4.
The proposed NL-BGWOA
(1) Mathematical model of the proposed method
In the proposed method, the selection of the significant feature subsets focuses on the updating position. Here, the new position update strategy is transformed by changing the calculation of the distance between individuals in the force function. In the position update strategy, the position of the individual in a potential search space depends on a variety of factors:
| 13 |
Here, is the gravity, is the wind force, and is the interaction force between two individuals in populations:
| 14 |
where is the number of individuals. is the distance between the individual to the individual: . is the corresponding unit vector, which is set by .
Consequently, the individual position is determined by the position, distance, force, and the last optimal position between the populations. The position update model in the NL-BGWOA algorithm is defined as:
| 15 |
In the proposed method, is the optimal position after selection, and are the two nonlinear coefficients used to balance the search, and are the upper and lower bound, respectively. or is initial position vector of the NL-BGWOA. or is the current position of the next optimal position in NL-BGWOA. is the adaptive weight in iteration, is the value of the best solution. In this paper, and are expressed by Eqs. 7 and 8, respectively.
(2) The corresponding flowchart and pseudo-procedure
The proposed method can expand its searching capability and locate the near global optimum solution. The architecture and the corresponding steps of the proposed NL-BGWOA are explained in Fig. 5. The specific steps of the proposed method are as follows:
Fig. 5.
The overall structure of the proposed NL-BGWOA
Step 1: Initialize parameters , , , , and .
Step 2: Initialize the positions of the search agents and the number of iterations.
Step 3: Sort by the fitness of each individual and calculate the adaptive weight .
Step 4: According to the probability number , update the position using the shrinking encircling mechanism or the spiral equation.
Step 5: If the iteration gets to the maximum, then output the result. Otherwise, go to Step 3.
Step 6: Randomly reinitialize the feature subset.
Step 7: Calculate the fitness of initial features and keep the recent best fitness value and position in NL-BGWOA.
Step 8: Enter the iterative process of NL-BGWOA, update the optimal solution, and return the best features.
Step 9: Update the current optimal position and fitness value, then return the optimal features.
Step 10: If the iteration gets to the maximum, then output the result. Otherwise, go to Step 6.
The corresponding pseudo-code is illustrated as follows:
The proposed NL-BGWOA fully integrates the strengths of BWOA and BGOA and tackles the FS of high-dimensional data. Besides, the proposed method expresses the datasets in the iteration and computes the fewer features. Therefore, it can guarantee the goodness of the feature subsets and increase the performance of the optimization algorithm.
Experimental Results and Evaluation
Data Description and Parameters’ Setting
To verify the performance of the proposed algorithm and extensively investigate the application, other state-of-the-art algorithms are selected for comparison experiments with the proposed algorithm. By analyzing some results in the feature selection experiment, such as the accuracy rate and the number of feature selections, the advantages between the proposed algorithm and other algorithms can be compared. The corresponding parameter settings are shown in Table 3. Each algorithm is conducted in 20 independent experiments with the following parameter settings.
Table 3.
Parameter settings of the algorithms used for comparison in the current study
| Algorithm | Parameter | Values |
|---|---|---|
| PSO(BPSO) | Number of particles | 10 |
| Maximum number of iterations | 100 | |
| Inertia weight in PSO(BPSO) | 1 | |
| Acceleration constants in PSO(BPSO) | [2,2] | |
| WOA(BWOA) | Number of whales | 10 |
| Maximum number of iterations | 100 | |
| Classification quality coefficient in WOA(BGOA) | 0.99 | |
| GOA(BGOA) | Number of grasshoppers | 10 |
| Maximum number of iterations | 100 | |
| Linear decrease coefficient and | (1, 1.0E−04) | |
| Classification quality coefficient in GOA(BGOA) | 0.99 | |
| NL-BGWOA | Number of individuals | 10 |
| Maximum number of iterations | 100 | |
| Classification quality coefficient in NL-BGWOA | 0.99 | |
| Linear decrease coefficient and | (1, 1.0E−04) |
Here, several basic feature selection experiments have been performed over ten distinct high-dimensional UCI datasets [39]. The details of ten datasets are depicted in Table 4.
Table 4.
Benchmark datasets
| No. of datasets | Name | No. of features | No. of samples |
|---|---|---|---|
| D1 | Arrhythmia | 279 | 452 |
| D2 | BreastEW | 32 | 596 |
| D3 | Clean1 | 165 | 476 |
| D4 | Clean2 | 165 | 6598 |
| D5 | Dermatology | 34 | 366 |
| D6 | Hill-Valley | 100 | 606 |
| D7 | LonosphereEW | 34 | 351 |
| D8 | SonarEW | 60 | 208 |
| D9 | Spambase | 57 | 4601 |
| D10 | WaveformEW | 40 | 5000 |
Meanwhile, the multi-modal Parkinson's speech datasets from the UCI repository and COVID-19 symptom dataset are used to verify the specific practical problem of the proposed algorithm, which are described as follows:
Here, the datasets P1 [40] and P2 [41] in Table 5 contain a group of linear and time–frequency-based features, measures of variation in fundamental frequency, amplitude, and so on. Especially for P1, besides the above fundamental features, the disease speech data set includes speech intensity, resonance frequencies, bandwidth-based features, and other specific features. The comprehensive multi-modal Parkinson's datasets can be referred to in Appendix A.
Table 5.
Multi-modal Parkinson's disease speech datasets
| No. of datasets | No. of features | No. of samples |
|---|---|---|
| P1 | 754 | 756 |
| P2 | 26 | 1040 |
Table 6 describes the information of the COVID-19 patient symptom dataset from Kaggle [42]. COVID-19 patient’s dataset is collected from a nearby hospital, where there are a total of 2575 positive and negative symptoms. The symptoms include age, fever, body pain, runny nose, difficult breath, and the infection probability of COVID-19 patients, of which the value is either 1 or 0. In difficult breathing, there are three types of values, which are no difficulty breathing problem, severe problem, and moderate problem.
Table 6.
COVID-19 symptom dataset
| No. of samples | Label | Symptoms |
|---|---|---|
| 2575 | Boolean (COVID-19 positive or negative) | Age, fever, body pain, runny nose, difficult breathing, and the infection probability of COVID-19 patients |
Evaluation Criteria
(a) Accuracy
Accuracy is the criterion for comparing the classification accuracy when performing feature selection experiments, which is obtained from the 5-KNN classifier on the test data. Average accuracy is calculated in the total runs:
| 16 |
where is the number of runs, is classification accuracy in the experiment.
(b) The size of selected features subsets
The size of selected feature subsets is another indicator to evaluate algorithms. It is an average value of the selected feature subsets when algorithms run times:
| 17 |
where is the number of selected features in the experiment.
(c) Fitness value
The fitness value of the optimal solution is not only used to update the position of individuals, but also to evaluate the performance of the algorithms. It is the average of the fitness values acquired after running all the iterations of the optimization algorithms:
| 18 |
where is the fitness value in the experiment.
Performance Evaluation
Feature Selection for Benchmark Datasets
In this paper, the 5-KNN classifier is used to measure the performance. All datasets are divided into two parts: 80% of the instances are devoted to training and 20% of the instances are used to test.
Table 7 presents the average classification accuracy for feature selection after running 20 times. Note that the best results are highlighted in bold. From Table 7, it can be clearly seen that the proposed algorithm has advantages over other algorithms on the majority of high-dimensional datasets, especially D3 and D7.
Table 7.
Mean classification accuracy
| Datasets | Algorithms | ||||||
|---|---|---|---|---|---|---|---|
| PSO | WOA | GOA | BPSO | BWOA | BGOA | NL-BGWOA | |
| D1 | 0.5841 | 0.5911 | 0.5833 | 0.5810 | 0.5977 | 0.5926 | 0.5994 |
| D2 | 0.9588 | 0.9566 | 0.9737 | 0.9558 | 0.9823 | 0.9824 | 0.9823 |
| D3 | 0.8549 | 0.9100 | 0.8931 | 0.9021 | 0.9205 | 0.9180 | 0.9258 |
| D4 | 0.9465 | 0.9713 | 0.9645 | 0.9692 | 0.9723 | 0.9604 | 0.9725 |
| D5 | 0.9863 | 0.9863 | 0.9534 | 0.9863 | 0.9786 | 0.9863 | 0.9895 |
| D6 | 0.5816 | 0.5560 | 0.5818 | 0.5597 | 0.6237 | 0.6045 | 0.6320 |
| D7 | 0.9307 | 0.9420 | 0.8893 | 0.9200 | 0.9371 | 0.9164 | 0.9443 |
| D8 | 0.8667 | 0.8988 | 0.8667 | 0.8654 | 0.8805 | 0.9002 | 0.8857 |
| D9 | 0.9105 | 0.8850 | 0.8934 | 0.8787 | 0.9160 | 0.9167 | 0.9239 |
| D10 | 0.7120 | 0.8056 | 0.7582 | 0.7610 | 0.8120 | 0.8104 | 0.8125 |
To describe the experimental results more intuitively, several representative datasets are selected in Fig. 6. Here, the red lines and the corresponding numbers represent the proposed NL-BGWOA. It can see the advantages of the proposed NL-BGWOA in classification accuracy compared with other algorithms.
Fig. 6.
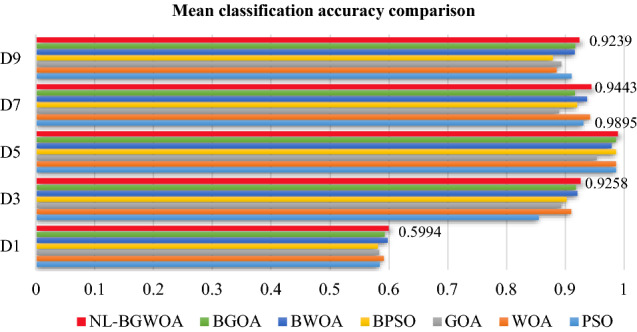
Mean classification accuracy for several representative datasets
Table 8 shows the average size of selected feature subsets on ten different high-dimensional datasets, where the best values are in bold. Meanwhile, several representative datasets are selected to represent the size of selected feature subsets, as shown in Fig. 7. As can be observed in Table 8 and Fig. 7, the proposed NL-BGWOA performs superior in the mean size of feature subsets on almost all the datasets.
Table 8.
Mean size of selected feature subsets
| Datasets | Algorithms | ||||||
|---|---|---|---|---|---|---|---|
| PSO | WOA | GOA | BPSO | BWOA | BGOA | NL-BGWOA | |
| D1 | 137.6 | 143.0 | 128.1 | 140.0 | 134.3 | 173.9 | 108.3 |
| D2 | 14.7 | 13.5 | 12.8 | 14.8 | 10.2 | 10.9 | 5.6 |
| D3 | 104.9 | 86.8 | 78.7 | 82.1 | 64.9 | 86.6 | 35.8 |
| D4 | 109.4 | 78 | 79.7 | 84.6 | 68.3 | 71.5 | 43.0 |
| D5 | 19.7 | 22.1 | 17.3 | 18.3 | 20.5 | 15.8 | 11.9 |
| D6 | 51.3 | 48.5 | 47.9 | 46.0 | 39.6 | 55.0 | 22.3 |
| D7 | 14.7 | 13.6 | 15.4 | 15.0 | 5.1 | 13.1 | 3.2 |
| D8 | 37.6 | 28.6 | 29.1 | 27.6 | 14.5 | 27.4 | 7.4 |
| D9 | 29.9 | 31.2 | 27 | 29.9 | 24.9 | 29.5 | 16.4 |
| D10 | 35.8 | 32.5 | 17.7 | 22.7 | 11.0 | 21.7 | 9.1 |
Fig. 7.
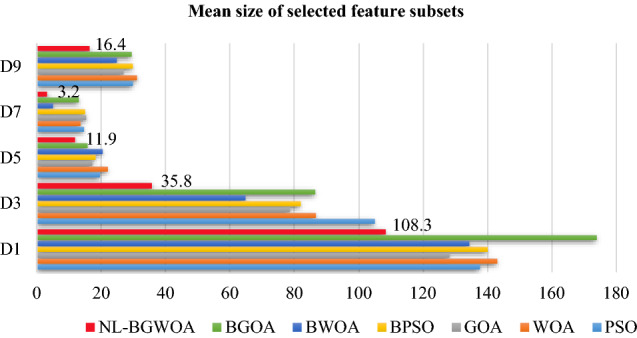
Mean size of selected feature subsets for several representative datasets
Especially on D3 and D9, the size of selected feature subsets obtained by the NL-BGWOA is far less than the results from other algorithms. This indicates that the proposed method can effectively reduce the number of features, select the most relevant optimal feature subsets, and implement the purpose of FS problems. The numbers in Fig. 7 specify the size of feature subsets selected by the proposed NL-BGWOA.
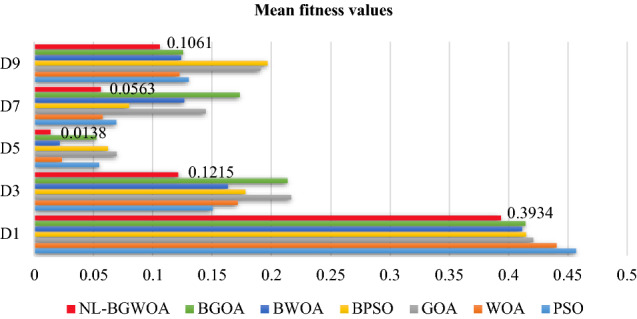
Table 9 and Fig. 8 summarize the experimental results of the fitness for the proposed method. The best fitness values are in bold. Note that some representative datasets are also selected, as shown in Fig. 8.
Table 9.
Mean fitness values
| Datasets | Algorithms | ||||||
|---|---|---|---|---|---|---|---|
| PSO | WOA | GOA | BPSO | BWOA | BGOA | NL-BGWOA | |
| D1 | 0.4569 | 0.4404 | 0.4207 | 0.4147 | 0.4113 | 0.4141 | 0.3934 |
| D2 | 0.0412 | 0.0434 | 0.0659 | 0.0442 | 0.0205 | 0.0154 | 0.0205 |
| D3 | 0.1508 | 0.1719 | 0.2170 | 0.1783 | 0.1636 | 0.2139 | 0.1215 |
| D4 | 0.0596 | 0.0382 | 0.0800 | 0.0368 | 0.0371 | 0.0747 | 0.0336 |
| D5 | 0.0549 | 0.0234 | 0.0697 | 0.0623 | 0.0215 | 0.0526 | 0.0138 |
| D6 | 0.4468 | 0.4450 | 0.4243 | 0.4405 | 0.4256 | 0.4109 | 0.3614 |
| D7 | 0.0693 | 0.0579 | 0.1449 | 0.0800 | 0.1268 | 0.1736 | 0.0563 |
| D8 | 0.1382 | 0.1112 | 0.1684 | 0.1378 | 0.1207 | 0.2305 | 0.1143 |
| D9 | 0.1305 | 0.1227 | 0.1911 | 0.1970 | 0.1241 | 0.1258 | 0.1061 |
| D10 | 0.2871 | 0.1944 | 0.3063 | 0.2243 | 0.1965 | 0.2249 | 0.1876 |
Fig. 8.
Mean fitness values comparison for several representative datasets
It can be observed from Table 9 and Fig. 8 that the majority of the best results highlighted in bold are obtained by the proposed NL-BGWOA. For instance, the NL-BGWOA provides average fitness values of 0.0336 and 0.0563 on D4 and D7, respectively. The numbers highlighted in Fig. 8 represent the values of fitness for the proposed algorithm.
As can be seen in Table 9 and Fig. 8, the NL-BGWOA’s superior performance in mean fitness values demonstrates the ability to search and select the optimal objectives, which has a high potential to solve the promising problems. Overall, the average fitness values of NL-BGWOA prove the competency to efficiently find the optima in the search space.
Feature Selection Experiment for Medical Datasets
Table 10 and Fig. 9 show the results of three evaluation criteria obtained from the proposed method in comparison to other algorithms on the multi-modal Parkinson datasets, where the bold represents the best method. According to the results reported in Table 10 and Fig. 9, there is a significant contrast between the proposed NL-BGWOA and other algorithms, especially the number of selected features (Num-FS). The values of Num-FS are highlighted in Fig. 9, which are presented in the form of numbers around the corresponding algorithm.
Table 10.
Evaluation of the current study on the multi-modal Parkinson datasets
| Algorithms | D1 | D2 | ||||
|---|---|---|---|---|---|---|
| Accuracy | Num-FS | Fitness | Accuracy | Num-FS | Fitness | |
| PSO | 0.765 | 378.6 | 0.2354 | 0.694 | 13.6 | 0.3060 |
| WOA | 0.782 | 183.4 | 0.2179 | 0.665 | 11.5 | 0.3351 |
| GOA | 0.866 | 365.5 | 0.2393 | 0.665 | 11.1 | 0.3437 |
| BPSO | 0.766 | 371.1 | 0.2341 | 0.688 | 13.1 | 0.3118 |
| BWOA | 0.905 | 180.7 | 0.0955 | 0.695 | 10.5 | 0.3053 |
| BGOA | 0.911 | 485.7 | 0.0900 | 0.692 | 9.2 | 0.3151 |
| NL-BGWOA | 0.913 | 111.7 | 0.0873 | 0.698 | 5.7 | 0.3034 |
Fig. 9.
The comparison of different algorithms on the multi-modal Parkinson datasets
Similarly, the proposed NL-BGWOA is tested on the COVID-19 symptom dataset, with experimental results shown in Table 11 and Fig. 10. The results show that the proposed method can improve the accuracy, the number of feature subsets, and fitness. The best values are shown in bold in Table 11. Especially the value of fitness and the number of feature subsets are improved significantly, which the optimal values are 1.0 and 0.4191, respectively. The numbers around the algorithms in Fig. 10 show a comparison using the number of selected features as an example.
Table 11.
Evaluation of the COVID-19 symptom dataset
| Algorithms | Accuracy | Num-FS | Fitness |
|---|---|---|---|
| PSO | 0.5184 | 2.0 | 0.4805 |
| WOA | 0.5073 | 3.0 | 0.4629 |
| GOA | 0.5188 | 2.0 | 0.4431 |
| BPSO | 0.5167 | 3.0 | 0.4386 |
| BWOA | 0.5204 | 3.0 | 0.4837 |
| BGOA | 0.5201 | 2.0 | 0.4353 |
| NL-BGWOA | 0.5217 | 1.0 | 0.4191 |
Fig. 10.
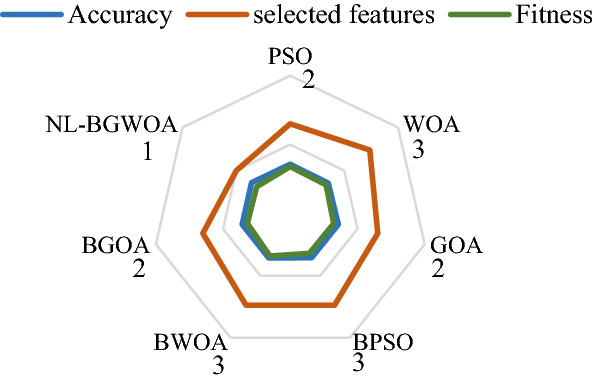
The comparison of different algorithms on the COVID-19 symptom datasets
The above experimental results indicate that the proposed NL-BGWOA has superior performance to the other algorithms in terms of three evaluation criteria during processing the medical datasets. The results mean that the proposed NL-BGWOA can tackle the foremost purpose of feature selection problems. Besides, it selects the features that can represent patients accurately. This application is also used the selected related features to determine whether the patient has a disease.
Statistical Test
Moreover, for further analysis of the proposed method, the statistical test is used to show the comparison statistically. It is a non-parametric test that provides a statistical value indicating whether the proposed method is significantly different from other methods.
Table 12 summarizes the results of the Friedman test based on classification accuracy, with the optimal values in bold. From the above discussion and results, it can be observed that the best rank is given to NL-BGWOA corresponding to their mean rank, which is followed by BWOA, BGOA, BPSO, WOA, GOA, and PSO. It is concluded that the proposed NL-BGWOA has better performance on search quality.
Table 12.
Results of Friedman test
| Algorithms | Mean | Ranking |
|---|---|---|
| PSO | 2.0000 | 7 |
| WOA | 2.8077 | 5 |
| GOA | 2.0385 | 6 |
| BPSO | 3.2091 | 4 |
| BWOA | 4.3462 | 2 |
| BGOA | 4.0769 | 3 |
| NL-BGWOA | 5.7308 | 1 |
Conclusion
For the FS problem, BWOA and BGOA may select a large number of features and fall into optima. Therefore, they will add a certain degree of difficulty to subsequent data processing. In this paper, a novel FS method called NL-BGWOA is proposed, which integrates the strengths of BWOA and BGOA in the FS problem and tackles the FS of high-dimensional data. The proposed method expresses the datasets in the iteration by computing the fewer features, which can increase the performance of optimization algorithm and guarantee the goodness of the feature subsets. To verify the effectiveness of the proposed method, this paper conducts experiments on 10 benchmark datasets, multi-modal Parkinson datasets, and COVID-19 symptom datasets. The results demonstrated the superiority of the proposed method compared to most state-of-the-art algorithms in terms of the selected feature subsets. However, the classification accuracy and fitness still need to be improved facing datasets with fewer features, especially in various actual applications. As further work, the proposed method can be applied to more practices to solve the problems in the real life such as disease diagnosis, prediction, and engineering optimization problems.
Appendix A
Description of multi-modal Parkinson's disease speech datasets.
| No. of datasets | Features | Description |
|---|---|---|
| P1 | Baseline features |
Jitter variants Shimmer variants Fundamental frequency parameters Harmonicity parameters Recurrence period density entropy (RPDE) Detrended fluctuation analysis (DFA) Pitch period entropy (PPE) |
| Time frequency features |
Intensity parameters Formant frequencies Bandwidth |
|
| Mel frequency cepstral coefficients | MFCCs | |
| Wavelet transform based features |
Wavelet transform (WT) features related with F0 |
|
| Vocal fold features |
Glottis quotient (GQ) Glottal to noise excitation (GNE) Vocal fold excitation ratio (VFER) Empirical mode decomposition (EMD) |
|
| P2 | Frequency features |
Jitter (local) Jitter (local, absolute) Jitter (rap) Jitter (ppq5) Jitter (ddp) |
| Amplitude features |
Shimmer (local) Shimmer (local, dB) Shimmer (apq3) Shimmer (apq5) Shimmer (apq11) Shimmer (dda) |
|
| Harmonicity features |
Autocorrelation Noise-to-harmonic Harmonic-to-noise |
|
| Pitch features |
Median pitch Mean pitch Standard deviation Minimum pitch Maximum pitch |
|
| Pulse features |
Number of pulses Number of periods Mean period Standard deviation of period |
|
| Voicing features |
Fraction of locally unvoiced frames Number of voice breaks Degree of voice breaks |
Author contributions
LF contributed to conceive and design the experiments. Author XL contributed to perform the experiments and acquire the data.
Funding
This work was supported by Natural Science Foundation of Liaoning Province under Grant 2021-MS-272 and Educational Committee project of Liaoning Province under Grant LJKQZ2021088.
Data availability statement
The collected datasets are available at http://archive.ics.uci.edu/ml/datasets.php.
Declarations
Conflict of Interest
Lingling Fang declares that she has no conflict of interest. Author Xiyue Liang declares that she has no conflict of interest.
Ethical Approval
This article does not contain any studies with human participants performed by any the authors.
Informed Consent
Informed consent was not required as no human or animals were involved.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Abualigah L, Diabat A. Chaotic binary group search optimizer for feature selection. Expert Systems with Applications. 2022;192:116368. doi: 10.1016/j.eswa.2021.116368. [DOI] [Google Scholar]
- 2.Song XF, Zhang Y, Guo YN, Sun XY, Wang YL. Variable-size cooperative coevolutionary particle swarm optimization for feature selection on high-dimensional data. IEEE Transactions on Evolutionary Computation. 2020;24(5):882–895. doi: 10.1109/TEVC.2020.2968743. [DOI] [Google Scholar]
- 3.Abu Khurma R, Aljarah I, Sharieh A, Abd Elaziz M, Damaševičius R, Krilavičius T. A review of the modification strategies of the nature inspired algorithms for feature selection problem. Mathematics. 2022;10(3):464. doi: 10.3390/math10030464. [DOI] [Google Scholar]
- 4.Abualigah L, Diabat A, Sumari P, Gandomi AH. Applications, deployments, and integration of internet of drones (iod): a review. IEEE Sensors Journal. 2021;21(22):25532–25546. doi: 10.1109/JSEN.2021.3114266. [DOI] [Google Scholar]
- 5.Tawhid MA, Ibrahim AM. Feature selection based on rough set approach, wrapper approach, and binary whale optimization algorithm. International Journal of Machine Learning and Cybernetics. 2020;11(3):573–602. doi: 10.1007/s13042-019-00996-5. [DOI] [Google Scholar]
- 6.Agrawal P, Ganesh T, Mohamed AW. A novel binary gaining–sharing knowledge-based optimization algorithm for feature selection. Neural Computing and Applications. 2021;33(11):5989–6008. doi: 10.1007/s00521-020-05375-8. [DOI] [Google Scholar]
- 7.Rostami M, Berahmand K, Forouzandeh S. A novel community detection based genetic algorithm for feature selection. Journal of Big Data. 2021;8(1):1–27. doi: 10.1186/s40537-020-00398-3. [DOI] [Google Scholar]
- 8.Deng XL, Li YQ, Weng J, Zhang JL. Feature selection for text classification: A review. Multimedia Tools and Applications. 2019;78(3):3797–3816. doi: 10.1007/s11042-018-6083-5. [DOI] [Google Scholar]
- 9.Sharma M, Kaur P. A comprehensive analysis of nature-inspired meta-heuristic techniques for feature selection problem. Archives of Computational Methods in Engineering. 2021;28(3):1103–1127. doi: 10.1007/s11831-020-09412-6. [DOI] [Google Scholar]
- 10.Ma WP, Zhou XB, Zhu H, Li LW, Jiao LC. A two-stage hybrid ant colony optimization for high-dimensional feature selection. Pattern Recognition. 2021;116(1):107933. doi: 10.1016/j.patcog.2021.107933. [DOI] [Google Scholar]
- 11.Abualigah L. Group search optimizer: A nature-inspired meta-heuristic optimization algorithm with its results, variants, and applications. Neural Computing and Applications. 2021;33(7):2949–2972. doi: 10.1007/s00521-020-05107-y. [DOI] [Google Scholar]
- 12.Yang J, Honavar V. Feature subset selection using a genetic algorithm. In: Liu H, Motoda H, editors. Feature extraction, construction and selection. Springer; 1998. pp. 117–136. [Google Scholar]
- 13.Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. In Proceedings of ICNN'95-international conference on neural networks (Vol. 4, pp. 1942–1948)
- 14.Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Advances in Engineering Software. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
- 15.Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- 16.Arora S, Singh S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Computing. 2019;23(3):715–734. doi: 10.1007/s00500-018-3102-4. [DOI] [Google Scholar]
- 17.Saremi S, Mirjalili S, Lewis A. Grasshopper optimisation algorithm: Theory and application. Advances in Engineering Software. 2017;105:30–47. doi: 10.1016/j.advengsoft.2017.01.004. [DOI] [Google Scholar]
- 18.Abualigah L, Abd Elaziz M, Sumari P, Geem ZW, Gandomi AH. Reptile search algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Systems with Applications. 2022;191:116158. doi: 10.1016/j.eswa.2021.116158. [DOI] [Google Scholar]
- 19.Agushaka JO, Ezugwu AE, Abualigah L. Dwarf mongoose optimization algorithm. Computer Methods in Applied Mechanics and Engineering. 2022;391:114570. doi: 10.1016/j.cma.2022.114570. [DOI] [Google Scholar]
- 20.Oyelade ON, Ezugwu AES, Mohamed TI, Abualigah L. Ebola optimization search algorithm: A new nature-inspired metaheuristic optimization algorithm. IEEE Access. 2022;10:16150–16177. doi: 10.1109/ACCESS.2022.3147821. [DOI] [Google Scholar]
- 21.Abualigah L, Diabat A, Mirjalili S, Abd Elaziz M, Gandomi AH. The arithmetic optimization algorithm. Computer Methods in Applied Mechanics and Engineering. 2021;376:113609. doi: 10.1016/j.cma.2020.113609. [DOI] [Google Scholar]
- 22.Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-Qaness MA, Gandomi AH. Aquila optimizer: A novel meta-heuristic optimization algorithm. Computers & Industrial Engineering. 2021;157:107250. doi: 10.1016/j.cie.2021.107250. [DOI] [Google Scholar]
- 23.Abu Khurmaa R, Aljarah I, Sharieh A. An intelligent feature selection approach based on moth flame optimization for medical diagnosis. Neural Computing and Applications. 2021;33(12):7165–7204. doi: 10.1007/s00521-020-05483-5. [DOI] [Google Scholar]
- 24.Mirjalili S, Lewis A. S-shaped versus V-shaped transfer functions for binary particle swarm optimization. Swarm and Evolutionary Computation. 2013;9:1–14. doi: 10.1016/j.swevo.2012.09.002. [DOI] [Google Scholar]
- 25.Hussien AG, Oliva D, Houssein EH, Juan AA, Yu X. Binary whale optimization algorithm for dimensionality reduction. Mathematics. 2020;8(10):1821. doi: 10.3390/math8101821. [DOI] [Google Scholar]
- 26.Mafarja M, Aljarah I, Faris H, Hammouri AI, Ala’M AZ, Mirjalili S. Binary grasshopper optimisation algorithm approaches for feature selection problems. Expert Systems with Applications. 2019;117:267–286. doi: 10.1016/j.eswa.2018.09.015. [DOI] [Google Scholar]
- 27.Wang, J., Li, Y., & Hu, G. (2021). Hybrid seagull optimization algorithm and its engineering application integrating Yin–Yang Pair idea. Engineering with Computers, 1–37
- 28.Mafarja MM, Mirjalili S. Hybrid whale optimization algorithm with simulated annealing for feature selection. Neurocomputing. 2017;260:302–312. doi: 10.1016/j.neucom.2017.04.053. [DOI] [Google Scholar]
- 29.Al-Tashi Q, Kadir SJA, Rais HM, Mirjalili S, Alhussian H. Binary optimization using hybrid grey wolf optimization for feature selection. IEEE Access. 2019;7:39496–39508. doi: 10.1109/ACCESS.2019.2906757. [DOI] [Google Scholar]
- 30.Purushothaman R, Rajagopalan SP, Dhandapani G. Hybridizing Gray Wolf Optimization (GWO) with Grasshopper Optimization Algorithm (GOA) for text feature selection and clustering. Applied Soft Computing. 2020;96:106651. doi: 10.1016/j.asoc.2020.106651. [DOI] [Google Scholar]
- 31.Hafez, A. I., Hassanien, A. E., Zawbaa, H. M., & Emary, E. (2015). Hybrid monkey algorithm with krill herd algorithm optimization for feature selection. In 2015 11th international computer engineering conference (ICENCO) (pp. 273–277)
- 32.Jia HM, Xing ZK, Song WL. A new hybrid seagull optimization algorithm for feature selection. IEEE Access. 2019;7:49614–49631. doi: 10.1109/ACCESS.2019.2909945. [DOI] [Google Scholar]
- 33.Zheng YF, Li Y, Wang G, Chen YP, Xu Q, Fan JH, Cui XT. A novel hybrid algorithm for feature selection based on whale optimization algorithm. IEEE Access. 2018;7:14908–14923. doi: 10.1109/ACCESS.2018.2879848. [DOI] [Google Scholar]
- 34.Arora S, Singh H, Sharma M, Sharma S, Anand P. A new hybrid algorithm based on grey wolf optimization and crow search algorithm for unconstrained function optimization and feature selection. IEEE Access. 2019;7:26343–26361. doi: 10.1109/ACCESS.2019.2897325. [DOI] [Google Scholar]
- 35.Tawhid MA, Dsouza KB. Hybrid binary bat enhanced particle swarm optimization algorithm for solving feature selection problems. Applied Computing and Informatics. 2018;16(1):117–136. doi: 10.1016/j.aci.2018.04.001. [DOI] [Google Scholar]
- 36.Yan CK, Ma JJ, Luo HM, Patel A. Hybrid binary coral reefs optimization algorithm with simulated annealing for feature selection in high-dimensional biomedical datasets. Chemometrics and Intelligent Laboratory Systems. 2019;184:102–111. doi: 10.1016/j.chemolab.2018.11.010. [DOI] [Google Scholar]
- 37.Shunmugapriya P, Kanmani S. A hybrid algorithm using ant and bee colony optimization for feature selection and classification (AC-ABC hybrid) Swarm and Evolutionary Computation. 2017;36:27–36. doi: 10.1016/j.swevo.2017.04.002. [DOI] [Google Scholar]
- 38.Wang ZG, Xiao X, Rajasekaran S. Novel and efficient randomized algorithms for feature selection. Big Data Mining and Analytics. 2020;3(3):208–224. doi: 10.26599/BDMA.2020.9020005. [DOI] [Google Scholar]
- 39.Dua, D., & Graff, C. (2017). Parkinsons Data Set. UCI machine learning repository. http://archive.ics.uci.edu/ml
- 40.Sakar CO, Serbes G, Gunduz A, Tunc HC, Nizam H, Sakar BE, Tutuncu M, Aydin T, Isenkul E, Apaydin H. A comparative analysis of speech signal processing algorithms for Parkinson’s disease classification and the use of the tunable Q-factor wavelet transform. Applied Soft Computing. 2019;74:255–263. doi: 10.1016/j.asoc.2018.10.022. [DOI] [Google Scholar]
- 41.Sakar BE, Isenkul ME, Sakar CO, Sertbas A, Gurgen F, Delil S, Apaydin H, Kursun O. Collection and analysis of a Parkinson speech dataset with multiple types of sound recordings. IEEE Journal of Biomedical and Health Informatics. 2013;17(4):828–834. doi: 10.1109/JBHI.2013.2245674. [DOI] [PubMed] [Google Scholar]
- 42.Alam, T. (2021). Covid-19 patients symptom dataset. Kaggle. https://www.kaggle.com/datasets/takbiralam/covid19-symptoms-dataset
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The collected datasets are available at http://archive.ics.uci.edu/ml/datasets.php.