Abstract
The importance of the graphical convolution network in multi-label classification has grown in recent years due to its label embedding representation capabilities. The graphical convolution network is able to capture the label dependencies using the correlation between labels. However, the graphical convolution network suffers from an over-smoothing problem when the layers are increased in the network. Over-smoothing makes the nodes indistinguishable in the deep graphical convolution network. This paper proposes a normalization technique to tackle the over-smoothing problem in the graphical convolution network for multi-label classification. The proposed approach is an efficient multi-label object classifier based on a graphical convolution neural network that tackles the over-smoothing problem. The proposed approach normalizes the output of the graph such that the total pairwise squared distance between nodes remains the same after performing the convolution operation. The proposed approach outperforms the existing state-of-the-art approaches based on the results obtained from the experiments performed on MS-COCO and VOC2007 datasets. The experimentation results show that pairnorm mitigates the effect of over-smoothing in the case of using a deep graphical convolution network.
Keywords: Deep Learning, Multi-label classification, Graphical convolution neural network, Over-smoothing
Introduction
The multi-label classification problem is a well-known problem in the research field which provides the set of labels associated with the unseen input instance. Multi-label classification is useful in different domains such as image (Pham et al. 2017), genome , bioinformatics (Zhang and Kabuka 2020), and text classification (Zhang and Zhou 2006). Among these domains, image recognition with multiple labels aims to find multiple objects in the given image. Multi-label classification is different and more challenging than multi-class classification, where only one object is predicted in the given image (Liu et al. 2017; Ristin et al. 2015). Multi-label classification for the image domain is useful in the field of human attributes (Li et al. 2016), medical diagnosis (Guan and Huang 2020), and retail checkout recognition (George and Floerkemeier 2014). Multi-label problem is considered the generalized form of the multi-class problem because there is more than one label associated with each instance in multi-label classification. Labels may have a strong cooccurrence dependency characteristic; e.g., Sea and sand are different in meaning but usually appear together in an image of a beach.
The performance of single-label classification in the image domain has been greatly improved using the deep convolution neural networks (CNNs) (He et al. 2016; Simonyan and Zisserman 2014). However, these approaches provide good results, but the correlation among labels is an important factor that is missing in these approaches. The first approach based on the neural networks for the multi-label classification is known as backpropagation based multi-label classification (BP-MLL) (Zhang and Zhou 2006). This approach modifies the backpropagation to incorporate the multi-label data. This approach is iterative in nature because of the backpropagation operation. In multi-label literature, some non-iterative approaches are introduced for fast training procedures, such as Multi-label Kernelized extreme learning machine(ML-KELM) (Luo et al. 2017) and Kernelized random vector functional link network(ML-KRVFL) (Chauhan and Tiwari 2022). These non-iterative approaches use the closed-form solutions such as pseudoinverse and ridge-regression for the computation of the network parameters. The pseudoinverse uses the inverse of a matrix to compute the parameters of the network. Due to this, non-iterative solutions are difficult to use for large-size multi-label datasets. The deep learning approaches are useful for working on a large amount of data, such as raw images in the image domain. For the computer vision based tasks, a deep-learning based convolutional neural network (CNN) can be trained with the softmax function at the output layer (Krizhevsky et al. 2012). These approaches consider the multi-label classification problem as a single-label classification for each label, which uses the ranking loss or cross-entropy loss for the training (Gong et al. 2013). For multi-label classification, when the number of classes increases, the distinction between classes becomes unclear. These approaches are limited in their scalability as the number of classes or labels grows continuously. In multi-label classification, The labels are dependent on each other in various manners, such as correlation, prior knowledge related to neighbor nodes, and geometric information of graphs. Among these dependencies, correlation is the key dependency for multi-label classification. The approaches discussed above fail to consider the correlations among labels.
A graphical convolution neural network (GCN) based classifier is proposed to resolve the scalability and correlation issues (Kipf and Welling 2017; Chen et al. 2019). The hybrid approaches combining the GCN with CNN have been explored in recent times for classification tasks. In these approaches, the Image level representation is combined with the GCN to represent the Relation Aware Representation (RAR). These hybrid approaches are applied in healthcare domains to diagnose the COVID 19 (Wang et al. 2021) and breast cancer (Zhang et al. 2021) which provides better diagnosis capability in comparison to those approaches which use the CNN model alone for diagnosis of disease. In another application related to anomaly detection, GCN is used with the Internet of things (IoT) to monitor efficiently the entire network infrastructure (Protogerou et al. 2021). The graphical convolution neural network-based classifiers suffer from the over-smoothing problem (Zhu et al. 2017; Li et al. 2018). The over-smoothing problem occurs due to the increment in the number of layers in GCN. The convolution operators are analogous to laplacian smoothing. When the convolution operation is applied many times to the functions, then the functions converge to similar values. The same scenario happens when the layers are increased in the GCN then the features of nodes converge to similar values due to the convolution operations. This behavior is known as over-smoothing. Over-smoothing makes it difficult to make the GCN deep and decreases the performance of the deep classifier if it is not tackled in the initial phase of network design.
We propose a semantic embedding-based hybrid approach named a multi-label graphical convolution neural network with pairnorm () to classify multi-label images. The main contributions of this paper are mentioned below.
We propose an end-to-end multi-label classifier that represents the labels as a semantic embedding in GCN.
The proposed approach incorporates the normalization technique pairnorm in GCN for multi-label classification to mitigate the effect of over-smoothing.
The proposed approach is able to perform multi-label classification in the case of a large number of labels present in an image. The semantic embeddings provide the scalability to the multi-label classification.
The proposed approach prevents the nodes from becoming similar after applying the convolution operator in GCN. The over-smoothing is alleviated by applying a simple normalization after the convolution operation. This approach is inspired by pairnorm, which keeps the total pairwise squared distance among the nodes similar before and after convolution operation (Zhao and Akoglu 2020). The proposed approach incorporates the pairnorm to resolve the over-smoothing issue in the multi-label image domain. Over-smoothing happens when the numbers of layers increase in the graphical neural network. This is the first time when pairnorm is incorporated for multi-label computer vision tasks using graphical convolution neural networks. The proposed approach designs an inter-dependent classifier having the graphical neural network with the convolution neural network. Image representation-based classifiers based on CNN have a limitation in making the distinction between labels when the number of labels grows to a large number. In CNN-based approaches, the difference among the labels becomes very insignificant (Yeh and Li 2019) when the number of labels increases. The semantic embedding-based representation of labels in proposed is able to tackle this limitation. The proposed approach creates the interdependent object classifier using GCN, and the generated classifiers learn to maintain the label cooccurrence. Thus the proposed can benefit the multi-label classification in case of a large number of labels.
Experiments performed on two large-size image datasets (MS-COCO and VOC 2007) show that the proposed approach alleviates the over-smoothing problem and performs better than other multi-label classification approaches. The proposed approach addresses the correlation of labels and over-smoothing problems for multi-label classification. We use the benefits of graph data structure to explore and capture the label correlation and dependency. The proposed approach is scalable for a large number of labels as these labels are represented as nodes in the GCN with their corresponding features ( I.e., semantic embedding). This paper further discusses the related work in the multi-label classification in Sect. 2. The proposed approach is discussed in Sect. 3 followed by the experiments and results in Sect. 4. Concluding remarks are presented in Sect. 5.
Related work
In this section, we summarize the prior work related to multi-label classification in the computer vision domain, graphical convolution network, and formal problem definition of multi-label classification.
Multi-label image recognition
In recent times, rapid progress has been achieved in the development of large image datasets. These datasets are manually labeled, such as PASCAL VOC (Everingham et al. 2010) and MSCOCO (Lin et al. 2014). These datasets are available to explore the research using a deep convolution network (Sharif Razavian et al. 2014). A simple approach for multi-label classification is to consider it as independent binary classifiers for each label. In these approaches, the label set grows exponentially and lacks the ability to capture the correlation between labels (Yeh and Li 2019).
Deep learning based approaches have great potential for computer-vision recognition and verification-related tasks. These approaches use the learned features from the input instances. CNN is extended for multi-label classification using various approaches fed the images directly into the CNN using the support vector machine pipeline (Sharif Razavian et al. 2014; Gong et al. 2013) and computes various losses using the CNN as a feature extractor. The top-k ranking provides the improvement in the performance of the multi-label classifiers (Li et al. 2017). All these mentioned approaches ignore the semantic relationship among labels. The semantic relationship between labels is considered using the visual semantic embeddings in recent times (Frome et al. 2013; Yeh and Li 2019).
The semantic label space can be designed by the information obtained from the unannotated text. This information preserves the semantic relationship among labels while visual-semantic embeddings are learned in multi-label classification (Frome et al. 2013).
Recurrent neural network (RNN) is utilized to consider the label dependencies (Wei et al. 2015) using the correlation among labels by creating the link of label embeddings in the joint embedding space. A single CNN-based paradigm for multi-label classification is proposed to learn from the transformation of an image rather than a representation of the image (Yeh and Li 2019). For the semantic embedding representation of labels, we use the graph-based GCN architecture. A brief survey of GCN is presented in the next section.
Graph convolutional network
The CNN-based approaches are used to analyze the visual image data. This data represents the euclidean data, and CNN can not process the non-euclidean data (e.g., social network data), which is present in the real world in huge amounts (Kipf and Welling 2017). The GCN is proposed to deal with this non-euclidean data. The GCN has two types of construction, spectral construction and spatial construction. The CNN can be explained in terms of spectral construction with the help of a mathematical foundation. The CNN can be used to design localized fast convolutions on graphs (Defferrard et al. 2016). The process of convolution operators on graphs is improved by the convolution operator and stacking the layer. Kipf and Welling (2017) proposed the GCN, and later it was confirmed by Li et al. (2018) that GCN is actually a variant of Laplacian smoothing. The GCN has the potential to capture the contextual information between the graph generation of labels and images. As shown in Fig. 1, the probability of the presence of a cricketer in an image is high if a bat, ball, stumps, and helmet occur together. The left image of bat and ball in Fig. 1 helps to provide the semantic that if a ball is present, then the bat is present in an image. These types of semantics help to create the graph of labels as the nodes and the dependencies as the edges. The formal description of multi-label classification in the image domain is discussed in the next section.
Fig. 1.
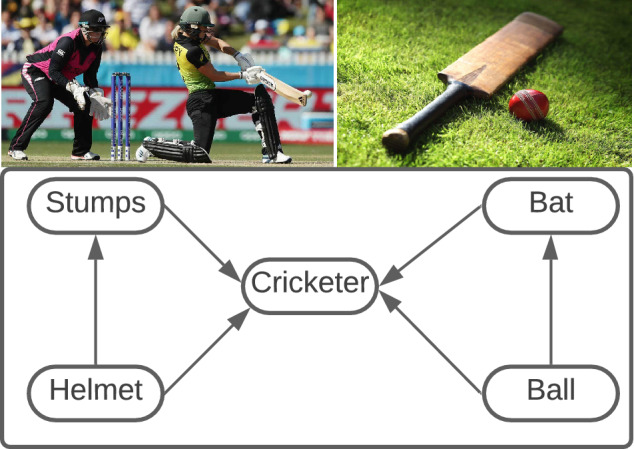
Example of label dependencies in multi-label classification. In this direct graph, we demonstrate a directed graph over the object labels to denote label dependencies in multi-label image recognition. In this figure, “Label A Label B” means when Label A appears, Label B is likely to appear, but its reverse may not be true
Problem description
We describe the formal discussion of multi-label classification in this section. Lets denotes the training set of data where denotes the training instance and denotes the corresponding labels. There can be more than one entry of 1 in Y is possible for the input instance. For a given image, we aim at partitioning labels into two disjoint sets according to the image-label relevance. In simple words, the proposed pairnorm-based multi-label classifier separates the relevant and irrelevant labels of an input image using the GCN. The GCN suffers from over-smoothing problems because the nodes in the graphs are unable to differentiate themselves from the neighbor nodes when the number of layers increases in the network. The pairnorm-based proposed approach is able to reduce the effect of over-smoothing for the multi-label classification.
Proposed work
In this section, we describe the proposed multi-label classifier using a pairnorm-based graphical convolution network (). The proposed is able to alleviate the effect of the over-smoothing problem. The over-smoothing problem arises when more than two layers are used in the structure of GCN. When the number of layers is increased in the GCN, then the nodes are unable to discriminate among themselves and represent the same features. The graphical convolutional network works on the information flow among nodes with the correlation information. It is important to consider the correlation among labels effectively for multi-label classification. Hence, we use a GCN-based structure to capture the correlation dependency among the labels.
In the GCN, each label is denoted as a node and represents the semantic embeddings. We propose a GCN-based model which directly maps these embeddings to the image features for the multi-label classification, and these mapping parameters are shared across all the labels. The main idea of GCN is to provide feature description and correlation matrix A as an input to the function f(., .) and learn it for the graph G. The correlation matrix A is used to represent the correlation among nodes. In the GCN, usually, this correlation matrix is predefined based on the adjacency properties of nodes in a graph. The nodes in the GCN graphs represent the labels for multi-label classification. So as per the need for multi-label classification, the correlation matrix A is derived based on the cooccurrence of labels in the dataset. The matrix A represents the semantic embedding among the labels. This matrix is named as a cooccurrence matrix because it represents the correlation relationship between labels. If the labels i and j cooccurs together then the probability P(j|i) is not necessarily equals to the probability . This can be understand from the Fig. 2 that and are different. These correlation behaviors are captured by the matrix A. Let label i occurs times in training set and co-occurrence of two labels i and j is represented by . Using this information, the correlation among label i and j can be denoted by . This computation provides the following matrix, which contains the conditional probabilities
| 1 |
In the above mathematical expression, the cooccurance measure may be very rare if two labels are not correlated. The cooccurance of labels may be different between test set and training set. So using the value as cooccurance becomes difficult to generalize. To alleviate these problems, the binary correlation matrix A can be defined as follows
| 2 |
where represents the binary representation of the correlation and denotes the threshold to filter the noisy edges. Every layer in GCN can be written by a non-linear function as
| 3 |
The function f(., .) after applying the convolution operation is denoted by
| 4 |
where denotes the learnable transformation matrix, is the normalized version of matrix A, and h(.) represents the nonlinear operation. In the experiments, h(.) can be any nonlinear function. We have used the LeakyReLU activation function for nonlinear transformations in our experiments. As the over-smoothing problem occurs in GCN when the number of layers is increased to create the deep GCN structure. The features of nodes become indistinguishable due to the over-smoothing problem. In other words, for the visual data, over-smoothing refers that the features become similar after applying the convolution operation in the graph.
Fig. 2.

Cooccurance between labels. The denotes probability , which means the probability of occurring stumps when a label cricketer occurs in an image. The denotes probability , which means the probability of label cricketer occurring when label stumps occurs in the image. The probability P(Cricketer|Stumps) does not need to be equal to the probability P(Stumps|Cricketer)
We propose the multi-label classification approach to reduce the effect of over-smoothing using pairnorm with GCN. Pairnorm can be considered as the normalization of the output of the graph convolution output. The graph convolution can be formulated as a graph regularized least square and considered an optimization problem. The convolution procedure measures the variation of new features for the graph structure. Due to the convolution, the nodes with similar properties come in the same cluster, known as smoothing. The convolution procedure cannot distinguish the nodes from different clusters and performs the smoothing procedures on the nodes from different clusters. This smoothing process on distant nodes is termed as over-smoothing.
In the proposed approach, represents the output of the graph convolution process, which is the input to the pairnorm. The output of the pairnorm process is denoted by . This flow is shown in Fig. 3. In simple words, pairnorm is a normalization procedure that is applied after the convolution operation. This normalization process is a two-step process as follows.
Fig. 3.

Flow diagram of pair norm
Step 1: In the first step, we subtract the row-wise mean from each as follows
| 5 |
where denotes the centered representation of nodes and n is the total number of nodes in the graph which denotes the labels.
Step 2: Using the step two, scaling operation on centered representation is performed as follows.
| 6 |
where denotes the output of pairnorm and s is the scaling parameter. We have imposed more restrictions on node representation in the GCN and used the following form of scaling
| 7 |
After applying the convolution operation, the total squared pairwise distance (TPSD) in and becomes different in GCN. The steps mentioned in Eq. (5) and (7) make the TPSD same in and . The aim of pairnorm is to keep the TPSD among nodes constant before and after the convolution operation. The operations center in step 1 and scaling in step 2 are performed after every convolution operation in the graph. In this way, the effect of over-smoothing is reduced in the GCN. In the GCN-based multi-label inter-dependent classifier, a matrix is learned from the label representation using a GCN based mapping function. The GCN is used as stacking the layer l where the output of current layer is processed by pairnorm, then it is provided to the next layer as an input. The input for the first layer is the embedding of labels matrix, and is the output of the last layer having dimensions . The output represents the generated interdependent object classifiers C. The predicted score of the classifier is obtained by applying the learned classifier to the image feature representation. It can be denoted as
| 8 |
The binary cross entropy (BCE) loss function is used to train the proposed model. The true labels are denoted by and has the vaues 0 or 1 as per the association of labels. The BCE loss is defined below
| 9 |
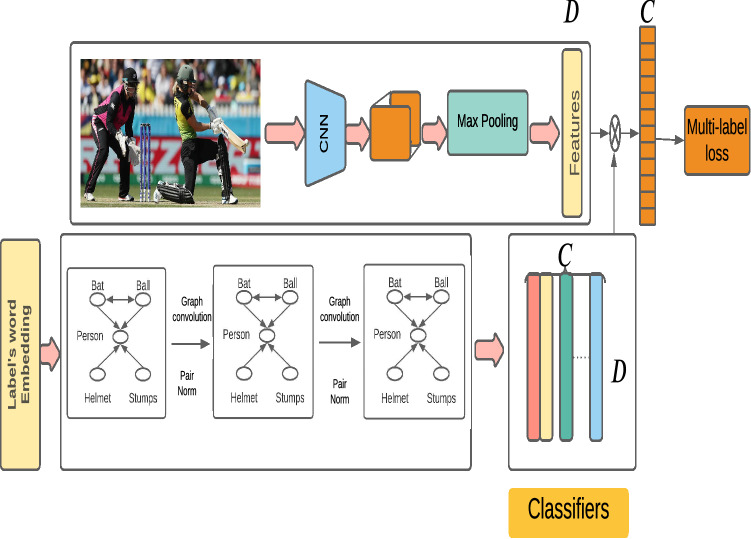
As shown in Fig. 4, the proposed approach has two parts. The first one is the image representation, and the second part is the GCN which uses the semantic embedding representation of labels as an input. In the image representation part, any CNN-based model can be used to transform the images into a feature vector. We use the ResNet-101 (Simonyan and Zisserman 2014) to transform the images into the feature vectors. These generated feature vectors have the same dimension as the dimension D of the generated classifiers produced by GCN. In the second part, the embedding is learned using GCN, and C classifiers are generated. The dot product is computed between the feature vectors and each classifier C for training and prediction. In the proposed approach, the network is trained using BCE loss as shown in Eq. (9).
Fig. 4.
Proposed classifier with pairnorm. The overall flow of the proposed approach for multi-label classification image recognition is illustrated in this figure. The label embeddings are provided in GCN as an input, and it generates the inter-dependence object classifiers in the form of trained feature vectors of labels. The image features are generated using the backbone network such as CNN. It generates the features as a fully connected layer. The dot product is performed between each generated classifier and the feature vector generated by the backbone network. The Stacked GCNs are learned over the label graph to map these label representations into a set of inter-dependent object classifiers which are applied to the image representation extracted from the input image via a backbone network for multi-label image recognition
Experiments and results
The experimental details of the proposed approach are discussed in this section. All the experiments of the are conducted on Intel Xeon Gold XUbuntu 18.04 server with TITAN Xp 16 GB GPU and 192 GB RAM. The PyTorch framework is used to implement the proposed approach. The images are fed into the network in the size of 32 batches, and the network is trained for 100 epochs. In each epoch, there are multiple iterations () using the stochastic gradient descent optimizer. After the experiments, the average of the evaluation measures is reported as a result using the evaluation metrics mean average precision(mAP), per class average precision (CP), per class average recall(CR), per class average F1 score(CF1), overall precision(OP), overall recall(OR), and overall F1 score(OF1). LeakyReLU function is used for faster convergence in the image representation for nonlinear representation of data. The slope of LeakyReLU is negative for faster convergence. The pretrained ResNet101 architecture trained on the imagenet is used for feature extraction. The parameters of the network are shown in Table 1. The VOC 2007 (Everingham et al. 2010), and MS-COCO (Lin et al. 2014) datasets are used to perform the experimentation and comparison with state-of-the-art approaches.
Table 1.
Parameter values of the classifier
| Parameters | Parameter values |
|---|---|
| Hidden layer dimensions | 1024, 2048 |
| 0.4 | |
| LeakyReLU slope | 0.2 |
| Momentum | 0.9 |
| Weight decay | 0.0001 |
| Initial learning rate | 0.01 |
The per class precision () for i th class is computed by using the following expression
| 10 |
where true positive is an outcome when the model correctly predicts the positive class and false positive is an outcome when the model incorrectly predicts the positive class. The overall precision is computed by weighting the per class precision with the number of instances of corresponding class. The overall precision is denoted by the following mathematical expression
| 11 |
where denotes the per class precision for i th class, denotes the total no. of sample belong to i th class, and C denotes total no. of labels. The per class recall () for i th class is computed by using the following expression
| 12 |
where false negative is an outcome when the model incorrectly predicts the negative class. The overall recall is computed by weighting the per class recall with the number of instances of corresponding class. The overall recall is denoted by the following mathematical expression
| 13 |
where denotes the per class recall for i th class, denotes the total no. of sample belong to i th class, and C denotes total no. of labels. The average per class precision is denoted by the following mathematical expression
| 14 |
where C denotes the total number of classes or labels. The average per class recall is denoted by the following mathematical expression
| 15 |
where C denotes the total number of classes or labels. The per class F1 score is computed by the following mathematical expression
| 16 |
The overall F1 score is computed by the following mathematical expression
| 17 |
The mean average precision is denoted by the following mathematical expression
| 18 |
where mAP is the mean average precision and OP denotes the overall precision. The per-class precision and per-class recall are computed for each label. The overall class precision, overall class recall, and overall F1 scores are computed for all labels. The GCN-related experimentation is performed using two layers, three layers, and four layers to test the effect of over-smoothing. In the GCN, the labels are represented by the pretrained Glove embedding (Pennington et al. 2014), which are trained on the Wikipedia dataset. We can represent the labels in numerical features using embedding, so mathematical operations such as average, addition, and deletion can be used for the labels. For those labels which have multiple similar words in embedding, we have taken an average of all the word features for similar words. We have taken the benefits of the mathematical properties of word embeddings for these labels. We first discuss the performance of the proposed approach on the MS-COCO dataset in Sect. 4.1 and VOC 2007 in Sect. 4.2. The ablation study for over-smoothing is discussed in Sect. 4.3.
Results on MS-COCO dataset
Microsoft-Common Objects in Context (MS-COCO) dataset is a widely used dataset for image classification tasks. This dataset contains the visual scenes. This dataset has been used for multi-label classification in recent times. There are 82,081 images present in the training set and 40,504 in the validation set. There are 80 classes in the MS-COCO dataset and an average of 2.9 objects per label. There are no specific labels available for multi-label learning for the test set, so multi-label approaches use the validation set for testing purposes.
The experimental results for all the classes are reported in Table 3. The mAP is significantly improved by the proposed classifier using pairnorm. The proposed pairnorm based outperforms all other classifiers for mAP CP, CR, CF1, OP, OR, and OF1 for all classes. The results for the top 3 classes are described in Table 2. We compare the results with RNN-Attention (Wang et al. 2017), CNN-RNN (Wang et al. 2016), ML-ZSL (Lee et al. 2018), Order free RNN (Chen et al. 2018a), SRN (Zhu et al. 2017), Multi-evidence (Ge et al. 2018), and ML-CGCN (Chen et al. 2019).
Table 3.
The comparison results for top 3 labels on MS-COCO dataset
| Methods | CP | CR | CF1 | OP | OR | OF1 |
|---|---|---|---|---|---|---|
| CNN-RNN | 66.0 | 55.6 | 60.4 | 69.2 | 66.4 | 67.8 |
| RNN-Attention | 79.1 | 58.7 | 67.4 | 84.0 | 63.0 | 72.0 |
| Order-Free RNN | 71.6 | 54.8 | 62.1 | 74.2 | 62.2 | 67.7 |
| ML-ZSL | 74.1 | 64.5 | 69.0 | – | – | – |
| SRN | 85.2 | 58.8 | 67.4 | 87.4 | 62.5 | 72.9 |
| ResNET-101 | 84.1 | 59.4 | 69.7 | 89.1 | 62.8 | 73.6 |
| Multi-Evidence | 84.5 | 62.2 | 70.6 | 89.1 | 64.3 | 74.7 |
| ML-CGCN | 89.2 | 64.1 | 74.6 | 90.5 | 66.5 | 76.7 |
| 91.55 | 66.83 | 77.26 | 94.21 | 70.04 | 80.35 |
Table 2.
The comparison results for all labels on MS-COCO dataset
| Methods | mAP | CP | CR | CF1 | OP | OR | OF1 |
|---|---|---|---|---|---|---|---|
| CNN-RNN | 61.2 | – | – | – | – | – | – |
| SRN | 77.1 | 81.6 | 65.4 | 71.2 | 82.7 | 69.9 | 75.8 |
| ResNET-101 | 77.3 | 80.2 | 66.7 | 72.8 | 83.9 | 70.8 | 76.8 |
| Multi-evidence | – | 80.4 | 70.2 | 74.9 | 85.2 | 72.5 | 78.4 |
| ML-CGCN | 83.0 | 85.1 | 72.0 | 78.0 | 85.8 | 75.4 | 80.3 |
| 85.114 | 87.86 | 75.54 | 81.23 | 89.66 | 79.78 | 84.43 |
The compared approaches contain the hybrid approaches as well, such as CNN-RNN, and RNN Attention, which are hybrid approaches of various deep learning approaches such as CNN-RNN is a hybrid combination of CNN and RNN. RNN Attention is a hybrid combination of RNN and attention mechanisms. The results show that the proposed performs better than other approaches for the top 3 classes also. It is observed that labels that are closer to each other become closer and distant labels remain distant from each other after applying the normalization using pairnorm. This is the reason that the performance of is significantly better than other state-of-the-art approaches.
Results on VOC 2007 dataset
The VOC 2007 dataset is the collection of consumer photographs taken from the photo-sharing website Flickr. This dataset is well used for multi-label classification tasks. There are 9963 images from the 20 classes in the VOC dataset. We use the trainval set to train the model and the test set to test the proposed approach. The results of CP, CR, CF1, OP, OR, and OF1 for all classes are shown in Fig. 5. The CP, CR, CF1, OP, OR, and OF1 are 91.63 %, 78.05 %, 84.29%, 98.03%, 96.14%, and 97.07 % respectively for all the classes of VOC 2007 dataset.
Fig. 5.
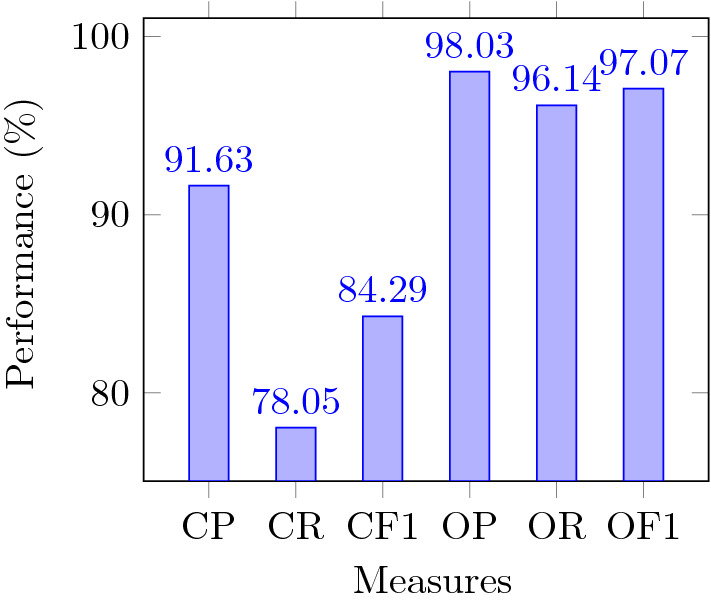
Results provided by the approach for all classes of VOC 2007 dataset
The results of CP, CR, CF1, OP, OR, and OF1 for top 3 classes are shown in Fig. 6. The CP, CR, CF1, OP, OR, and OF1 are 94.62 %, 76.58 %, 84.65%, 96.07%, 94.97%, and 95.51% respectively for top 3 classes of VOC 2007 dataset.
Fig. 6.
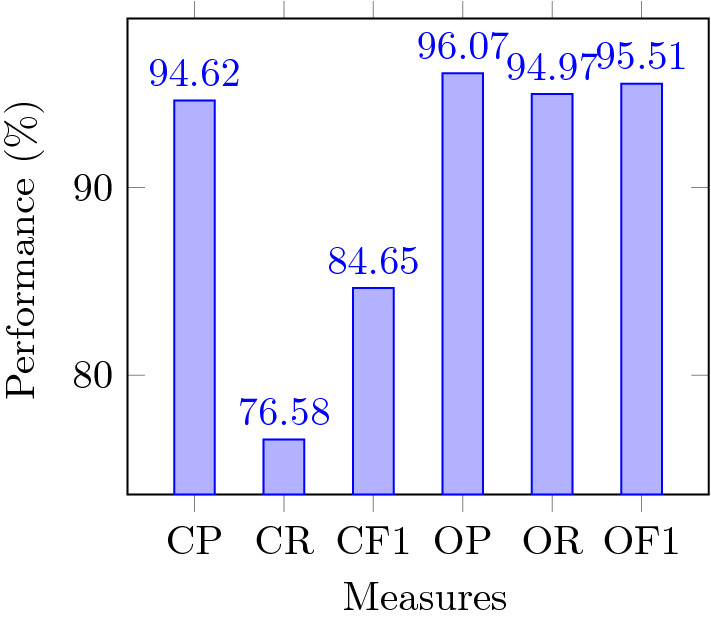
Results provided by the approach for top 3 classes of VOC 2007 dataset
For a fair comparison, we report the mean average precision (mAP) of the proposed approach with CNN-RNN (Wang et al. 2016), RLSD (Zhang et al. 2018), VeryDeep (Simonyan and Zisserman 2014), ResNet101 (Simonyan and Zisserman 2014), FeV+LV (Yang et al. 2016), HCP (Wei et al. 2015), RNN-Attention (Wang et al. 2017), Atten-Reinforce (Chen et al. 2018b), and ML-CGCN (Chen et al. 2019). The experimental results are shown in Table 4 which shows that for the VOC 2007 dataset outperforms all other approaches.
Table 4.
Comparison of mAP with state-of-the-art approaches on VOC 2007 dataset
| Methods | mAP |
|---|---|
| CNN-RNN | 84.0 |
| RLSD | 88.5 |
| VeryDeep | 89.7 |
| ResNet101 | 89.9 |
| FeV+LV | 90.6 |
| HCP | 90.9 |
| RNN-attention | 91.9 |
| Atten-reinforce | 92.0 |
| ML-CGCN | 94.0 |
| 94.47 |
Ablation studies
The over smoothing problem is considered in the computer vision domain when the difference among classes becomes indistinguishable. The hidden layers in the network capture the nonlinear transformation, and in the case of graphs, it provides the same value for all the nodes. Here nodes represent the labels. In this way, the labels become indistinguishable. The solution to the problem related to over-smoothing is still being explored in recent times (Li et al. 2018). We propose a multi-label classifier based on a graphical convolution neural network with an efficient method to minimize the effect of the over-smoothing problem.
The result of increasing the layers in is described in Table 5 for the MS-COCO dataset and in Table 6 for VOC 2007 dataset. For the MS-COCO dataset, the effect of over-smoothing is minimized by having two layers. The pairnorm is applied to the two-layer GCN, and the value of mAP, CF1, and OF1 for all labels are 81.23%, 84.43%, 77.26%, respectively, and for the top 3 labels is, CF1 and OF1 are reported as 80.34% and 75.67% respectively. For VOC 2007, the dataset mAP for two layers is reported as 94.47%, and for 3 and 4 layer networks, the reported mAP is 94.12% and 93.98%, respectively. These metrics are decreased when the number of layers is increased in the GCN network for the training of the classifier. It is observed that in the GCN-based approaches, the deeper networks are not always better. Even in most of the scenarios, it suffers from the over-smoothing problem. So it’s better to choose the appropriate approaches to minimize the effect of over-smoothing from the fewer layers itself so that the effect of over-smoothing can be alleviated for more layers. The pairnorm-based interdependent classifier is able to alleviate over-smoothing for the two-layer network, and its performance becomes superior to other approaches when the layers are increased. The proposed approach has the following strengths
The proposed approach is scalable in the case of a large number of classes or labels. The semantic embeddings are used to represent the labels in GCN. The GCN generates the interdependent object classifiers, which are used to classify the multi-label images.
The proposed algorithm mitigates the effect of the over-smoothing problem in the image domain. Due to the over-smoothing, the labels are difficult to distinguish. The pairnorm is able to tackle the over-smoothing in deep GCN.
The proposed approach is a deep learning approach, and it requires hardware computational resources such as a graphical processor unit (GPU) for experimentation. This high computational resource (Macedonia 2003) requirement is also considered the weakness of other deep learning based approaches that are applied to large datasets. We consider only one inter-label relationship correlation between labels. In the future, the other inter-label relationship, such as prior information about labels using bayesian and geometrical information, can be explored. The proposed approach is a deep learning approach, and the parameter tuning of deep learning techniques has become a time-consuming and cumbersome task. The deep learning algorithms contain a lot of parameters, and it is difficult to use grid search to try various combinations of parameters. In recent times, to tackle this issue, various evolutionary algorithms have been used for parameter optimization of deep learning techniques. One possible direction for parameter tuning is to use evolutionary techniques such as Aquila optimizer (Abualigah et al. 2021), Dwarf mongoose optimization algorithm (Agushaka et al. 2022), Ebola optimization search algorithm (Oyelade et al. 2022), and Reptile Search Algorithm (RSA) (Abualigah et al. 2022). Further, the proposed approach has the potential to be explored in the future for zero-shot learning when input instances are unavailable for rare labels. In this case, the transfer of knowledge using semantic embedding can be used for multi-label classification in case of unavailable training instances.
Table 5.
The effect of over-smoothing on MS-COCO dataset
| All | top 3 | ||||
|---|---|---|---|---|---|
| mAP | CF1 | OF1 | CF1 | OF1 | |
| 2 layer | 81.23 | 84.43 | 77.26 | 80.34 | 75.67 |
| 3 layer | 80.00 | 84.12 | 76.98 | 80.12 | 75.67 |
| 4 layer | 79.82 | 83.88 | 76.42 | 79.88 | 75.67 |
Table 6.
The effect of over-smoothing on VOC 2007 datset
| # Layers | mAP |
|---|---|
| 2 layer | 94.47 |
| 3 layer | 94.12 |
| 4 layer | 93.98 |
Conclusion
In this paper, we have tackled the over-smoothing problem in multi-label classification by incorporating pairnorm in GCN. The pairnorm is a normalization technique that is applied after the convolution operation in GCN. The proposed approach generates the interdependent object classifiers using the label embedding, which provides the strength that the label itself is enriched by the features. We have incorporated the correlation matrix to consider the interrelationship among labels. The effectiveness of a pairnorm-based multi-label classifier is verified by the experimental results performed on MS-COCO and VOC 2007 datasets. The GCN with pairnorm outperforms other state-of-the-art approaches for multi-label classification. The proposed approach is able to limit the effect of over-smoothing in multi-label classification. The aim of using this approach is to maintain the inter-dependence relationship between labels to alleviate the effect of over-smoothing. The proposed approach is a deep learning-based approach. Hence the parameter tuning of the proposed algorithm is a cumbersome task. One possible future direction for parameter tuning is to use evolutionary techniques with the proposed approach. In , we consider only one interdependent relationship, which is cooccurrence among labels. In the future, other possible interdependent relationships among labels, such as prior information using bayesian and geometrical transformation, can be used for better consideration of interrelationship among labels. The proposed approach can be extended with other embeddings to represent the graph nodes using Google News and FastText. The proposed approach has the potential to be extended for zero-shot learning in the future.
Declarations
Conflict of interest
The authors declare that they have no conflict of interest, and there is no data generated in this research work. The datasets MS-COCO and VOC 2007 used in this work are benchmark image datasets and are cited in this manuscript.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Abualigah L, Yousri D, Abd Elaziz M et al (2021) Aquila optimizer: a novel meta-heuristic optimization algorithm. Comput Ind Eng 157(107):250 [Google Scholar]
- Abualigah L, Abd Elaziz M, Sumari P et al (2022) Reptile search algorithm (RSA): a nature-inspired meta-heuristic optimizer. Expert Syst Appl 191(116):158 [Google Scholar]
- Agushaka JO, Ezugwu AE, Abualigah L (2022) Dwarf mongoose optimization algorithm. Comput Methods Appl Mech Eng 391(114):570 [Google Scholar]
- Chauhan V, Tiwari A (2022) Randomized neural networks for multilabel classification. Appl Soft Comput 115(108):184 [Google Scholar]
- Chen SF, Chen YC, Yeh CK, et al (2018a) Order-free RNN with visual attention for multi-label classification. In: Proceedings of the AAAI conference on artificial intelligence
- Chen T, Wang Z, Li G, et al (2018b) Recurrent attentional reinforcement learning for multi-label image recognition. In: Proceedings of the AAAI conference on artificial intelligence, pp 6730–6737
- Chen ZM, Wei XS, Wang P, et al (2019) Multi-label image recognition with graph convolutional networks. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp 5177–5186
- Defferrard M, Bresson X, Vandergheynst P (2016) Convolutional neural networks on graphs with fast localized spectral filtering. In: NIPS, pp 3844–3852
- Everingham M, Van Gool L, Williams CK et al (2010) The pascal visual object classes (VOC) challenge. Int J Comput Vis 88(2):303–338 [Google Scholar]
- Frome A, Corrado GS, Shlens J et al (2013) Devise: a deep visual-semantic embedding model. Adv Neural Inf Process Syst 26:2121–2129 [Google Scholar]
- Ge W, Yang S, Yu Y (2018) Multi-evidence filtering and fusion for multi-label classification, object detection and semantic segmentation based on weakly supervised learning. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 1277–1286
- George M, Floerkemeier C (2014) Recognizing products: a per-exemplar multi-label image classification approach. In: European conference on computer vision. Springer, pp 440–455
- Gong Y, Jia Y, Leung T et al (2013) Deep convolutional ranking for multilabel image annotation, pp 1–9. arXiv:1312.4894
- Guan Q, Huang Y (2020) Multi-label chest X-ray image classification via category-wise residual attention learning. Pattern Recognit Lett 130:259–266 [Google Scholar]
- He K, Zhang X, Ren S et al (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 770–778
- Kipf TN, Welling M (2017) Semi-supervised classification with graph convolutional networks. In: International conference on learning representations, ICLR, pp 1–14
- Krizhevsky A, Sutskever I, Hinton GE (2012) Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Syst 25:1097–1105 [Google Scholar]
- Lee CW, Fang W, Yeh CK et al (2018) Multi-label zero-shot learning with structured knowledge graphs. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 1576–1585
- Li Q, Han Z, Wu XM (2018) Deeper insights into graph convolutional networks for semi-supervised learning. In: Proceedings of the AAAI conference on artificial intelligence
- Li Y, Huang C, Loy CC, et al (2016) Human attribute recognition by deep hierarchical contexts. In: European conference on computer vision. Springer, pp 684–700
- Li Y, Song Y, Luo J (2017) Improving pairwise ranking for multi-label image classification. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 3617–3625
- Lin TY, Maire M, Belongie S et al (2014) Microsoft coco: Common objects in context. In: European conference on computer vision. Springer, pp 740–755
- Liu L, Wang P, Shen C et al (2017) Compositional model based fisher vector coding for image classification. IEEE Trans Pattern Anal Mach Intell 39(12):2335–2348 [DOI] [PubMed] [Google Scholar]
- Luo F, Guo W, Yu Y et al (2017) A multi-label classification algorithm based on kernel extreme learning machine. Neurocomputing 260:313–320 [Google Scholar]
- Macedonia M (2003) The GPU enters computing’s mainstream. Computer 36(10):106–108 [Google Scholar]
- Oyelade ON, Ezugwu AES, Mohamed TI et al (2022) Ebola optimization search algorithm: a new nature-inspired metaheuristic optimization algorithm. IEEE Access 10:16,150-16,177 [Google Scholar]
- Pennington J, Socher R, Manning CD (2014) Glove: global vectors for word representation. In: Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP), pp 1532–1543
- Pham AT, Raich R, Fern XZ (2017) Dynamic programming for instance annotation in multi-instance multi-label learning. IEEE Trans Pattern Anal Mach Intell 39(12):2381–2394 [DOI] [PubMed] [Google Scholar]
- Protogerou A, Papadopoulos S, Drosou A et al (2021) A graph neural network method for distributed anomaly detection in iot. Evol Syst 12(1):19–36 [Google Scholar]
- Ristin M, Guillaumin M, Gall J et al (2015) Incremental learning of random forests for large-scale image classification. IEEE Trans Pattern Anal Mach Intell 38(3):490–503 [DOI] [PubMed] [Google Scholar]
- Sharif Razavian A, Azizpour H, Sullivan J et al (2014) CNN features off-the-shelf: an astounding baseline for recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pp 806–813
- Simonyan K, Zisserman A (2014) Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556
- Wang J, Yang Y, Mao J, et al (2016) CNN-RNN: a unified framework for multi-label image classification. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 2285–2294
- Wang SH, Govindaraj VV, Górriz JM et al (2021) Covid-19 classification by FGCnet with deep feature fusion from graph convolutional network and convolutional neural network. Inf Fus 67:208–229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Chen T, Li G et al (2017) Multi-label image recognition by recurrently discovering attentional regions. In: Proceedings of the IEEE international conference on computer vision, pp 464–472
- Wei Y, Xia W, Lin M et al (2015) HCP: a flexible CNN framework for multi-label image classification. IEEE Trans Pattern Anal Mach Intell 38(9):1901–1907 [DOI] [PubMed] [Google Scholar]
- Yang H, Tianyi Zhou J, Zhang Y et al (2016) Exploit bounding box annotations for multi-label object recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 280–288
- Yeh MC, Li YN (2019) Multilabel deep visual-semantic embedding. IEEE Trans Pattern Anal Mach Intell 42(6):1530–1536 [DOI] [PubMed] [Google Scholar]
- Zhang D, Kabuka MR (2020) Protein family classification from scratch: a CNN based deep learning approach. IEEE/ACM Trans Comput Biol Bioinform 18(5):1996–2007 [DOI] [PubMed] [Google Scholar]
- Zhang J, Wu Q, Shen C et al (2018) Multilabel image classification with regional latent semantic dependencies. IEEE Trans Multim 20(10):2801–2813 [Google Scholar]
- Zhang ML, Zhou ZH (2006) Multilabel neural networks with applications to functional genomics and text categorization. IEEE Trans Knowl Data Eng 18(10):1338–1351 [Google Scholar]
- Zhang YD, Satapathy SC, Guttery DS et al (2021) Improved breast cancer classification through combining graph convolutional network and convolutional neural network. Inf Process Manag 58(2):102–439 [Google Scholar]
- Zhao L, Akoglu L (2020) Pairnorm: tackling oversmoothing in GNNS. In: International conference on learning representations, pp 1–17
- Zhu F, Li H, Ouyang W et al (2017) Learning spatial regularization with image-level supervisions for multi-label image classification. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 5513–5522