LassoNet: Neural Networks with Feature Sparsity

Abstract

Much work has been done recently to make neural networks more interpretable, and one approach is to arrange for the network to use only a subset of the available features. In linear models, Lasso (or ℓ₁-regularized) regression assigns zero weights to the most irrelevant or redundant features, and is widely used in data science. However the Lasso only applies to linear models. Here we introduce LassoNet, a neural network framework with global feature selection. Our approach achieves feature sparsity by allowing a feature to participate in a hidden unit only if its linear representative is active. Unlike other approaches to feature selection for neural nets, our method uses a modified objective function with constraints, and so integrates feature selection with the parameter learning directly. As a result, it delivers an entire regularization path of solutions with a range of feature sparsity. In experiments with real and simulated data, LassoNet significantly outperforms state-of-the-art methods for feature selection and regression. The LassoNet method uses projected proximal gradient descent, and generalizes directly to deep networks. It can be implemented by adding just a few lines of code to a standard neural network.

1. Introduction

1.1. Background

In many problems of interest, much of the information in the features is irrelevant for predicting the responses and only a small subset is informative. Feature selection methods provide insight into the relationship between features and an outcome while simultaneously reducing the computational expense of downstream learning by removing features that are redundant or noisy.

With high-dimensional data sets becoming ever more prevalent, feature selection has seen widespread usage across a variety of real-world tasks, including speech (Cai et al., 2018), object recognition (Li et al., 2017), and disease detection from protein data (Wulfkuhle et al., 2003). The benefits of feature selection include reducing experimental costs, enhancing interpretability, computational speed up, memory reduction and even improving model generalization on unseen data (Min et al., 2014). For example, feature selection is especially valuable in biomedical studies where the data with the full set of features is expensive or difficult to collect, as it can alleviate the need to measure irrelevant or redundant features, and allows to identify a small set of features while maintaining prediction performance – this can significantly save on future data collection costs. While feature selection methods have been extensively studied in the setting of linear regression (e.g. LASSO), identifying relevant features for highly nonlinear models remains an open challenge.

As a motivating example, consider a data set that consists of the expression levels of various proteins across tissue samples. Such measurements are increasingly carried out to assist with disease diagnosis, as biologists measure a large number of proteins with the aim of discriminating between disease classes. Yet, it remains expensive to conduct all of the measurements that are needed to fully characterize proteomic diseases. It is natural to ask: Are there redundant or unnecessary features? What are the most effective and representative features to characterize the disease? Furthermore, when a small number of proteins are selected, their biological relationship with the target diseases is more easily identified. These ”marker” proteins thus provide additional scientific understanding of the problem.

Figure 1 shows an example of feature selection path produced by our method on the MICE Protein Dataset (Higuera et al., 2015), which contains protein expression levels of normal and trisomic mice exposed to different experimental conditions. We see that only about 35 proteins are needed to obtain maximal classification accuracy. This kind of steeply concave curve explains why feature selection is a key pre-processing step in many machine learning tasks.

Figure 1. Feature selection path produced by our method on the MICE Protein Dataset.

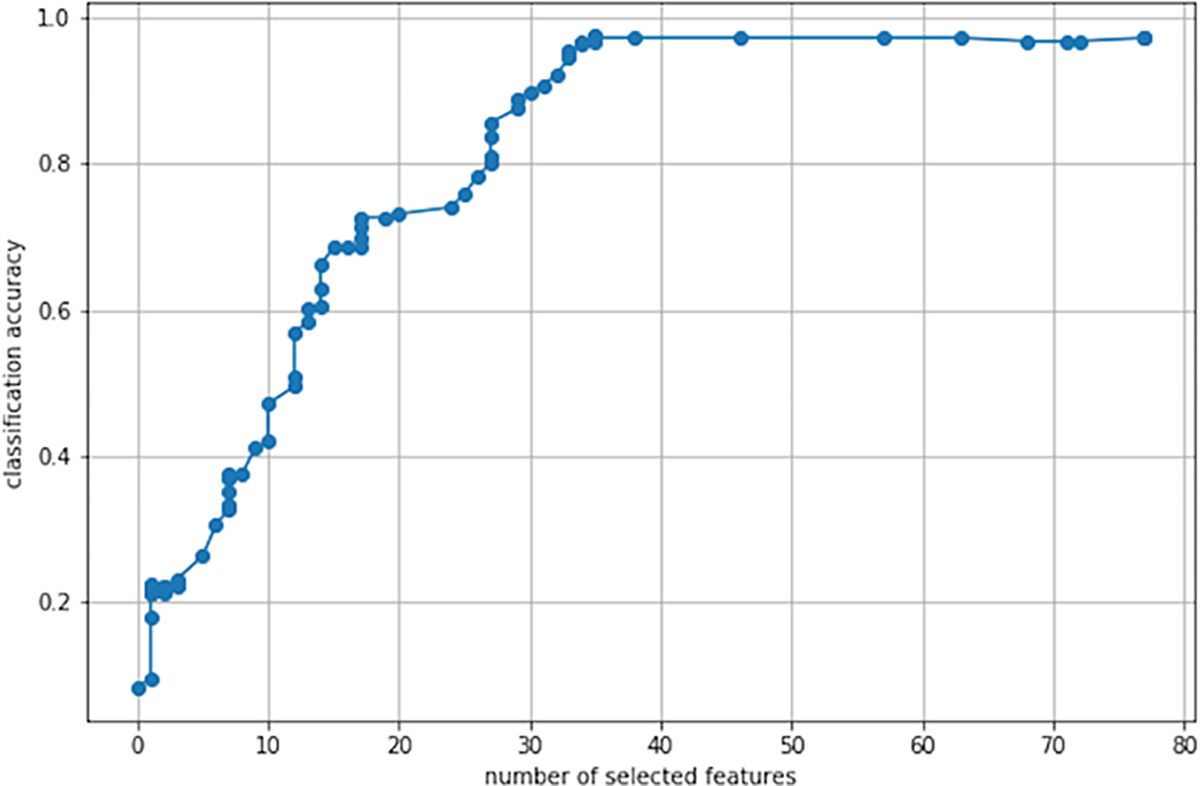
Considering the cost of proteomic measurements, a trade-off between the number of features kept and statistical performance is often desirable. In this example, the method captures 70% of the signal with about 20% of the features. This allows to narrow down the list of important features, making the conclusions of the prediction task more actionable.

Section 1 discusses related works on feature selection. Section 2 formulates the problem. Section 3 introduces our main proposal, and Section 4 the optimization strategy. In Section 5, we conduct experiments on several real-world datasets. Finally, Sections 6 and 7 extend LassoNet to the unsupervised learning and matrix completion problems, respectively.

1.2. Related Works

Feature selection methods can generally be divided into three groups: filter, wrapper and embedded methods.

• Filter methods operate independently of the choice of the predictor by selecting individual features that maximize the desired criteria. For example, the popular Fisher score (Gu et al., 2012) selects features such that in the data space spanned by the selected features, the distances between data points in different classes are as large as possible, while the distances between data points in the same class are as small as possible. Filter methods select features independently of the learning method to be used, and this is a major limitation. For example, since filter methods evaluate individual features, they generally do not detect features that participate mainly in interactions with other features.

• Wrapper methods use learning algorithms to evaluate subsets of features based on their predictive power. For example, the recently proposed HSIC-LASSO (Yamada et al., 2014) uses kernel learning to discover non-linear feature interactions.

• Similarly to wrapper methods, embedded methods use specific predictors to select features, and are generally able to detect interactions and redundancies among features. However, embedded methods tend to do so more efficiently as they combine feature selection and learning into a single problem. A well-known example is the lasso (Tibshirani, 1996), which can be used to select features for regression by varying the strength of l₁ regularization. The limitation of lasso, however, is that it only applies to linear models. Recently, Feng and Simon (2017) proposed an input-sparse neural network, where the input weights are penalized using the group LASSO penalty. As will become evident in Section 3, our proposed method extends and generalizes this approach in a natural way.

1.3. Proposed Method

We propose a new approach that extends lasso regression and its feature sparsity to feed-forward neural networks. We call our procedure LassoNet. The method is designed so that only a subset of the features are used by the network. Our procedure uses an input-to-output residual connection and allows a feature to have non-zero weight in a hidden unit only if its linear connection is active.

The linear and nonlinear components are optimized jointly, allowing to capture arbitrary nonlinearity. As we show through experiments in Section 5, this leads to lower classification errors on real-world datasets compared to the aforementioned methods. A visual example of results from our method is shown in Fig. 2, where LassoNet selects the most informative pixels on a subset of the MNIST dataset, and classifies the original images with high accuracy.

Figure 2. Demonstrating LassoNet on the MNIST dataset.

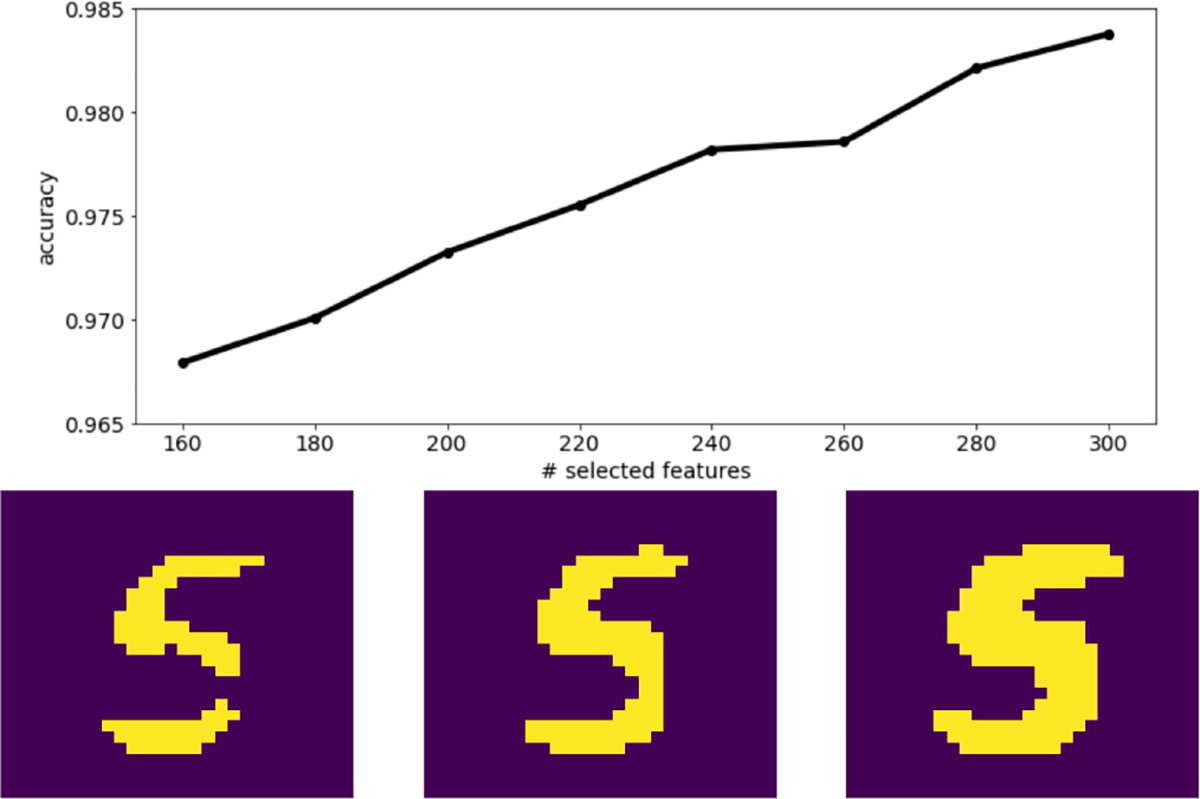
Here, we show the results of using LassoNet to simultaneously select informative pixels and classify digits 5 and 6 from the MNIST dataset. Top: The classification accuracy by number of selected features. Bottom: 3 samples from the model with 84, 110 and 158 active features out of the 784 features respectively.

We test LassoNet on a variety of datasets, and find that it generally outperforms state-of-the-art methods for feature selection and regression.

2. Problem Formulation

We now describe the problem of global feature selection. Although global feature selection is relevant for both supervised and unsupervised settings, we describe here the supervised case, which is the focus of this paper, and defer discussion of the unsupervised case to Section 6.

We assume a data-generating model p(x, y) over a d-dimensional space, where $\mathbf{x}\in {ℝ}^d$ is the covariate and y is the response, such as class labels. The goal is to find the best function f*(x) for predicting y. We emphasize that the problem of learning f* is non-parametric, so that for example no linear or quadratic restriction is assumed. We seek to minimize the empirical reconstruction error:

$$\underset{f\in \mathcal{F},S}{\min }\widehat{\mathbb{E}}\left[L\left(y,f\left({\mathbf{x}}_S\right)\right)\right]$$ (1)

where S ⊆ {1, 2 . . . d} is a subset of features, x_S denotes the vector x with elements x_i set to zero for i ∉ S, and L is a loss function specified by the user. For example, in a univariate regression problem, the function class might be the set of all linear functions, and the loss function might be the squared error loss L(y, f(x)) = (y − f(x))². The principal difficulty in solving (1) is due to the combinatorial nature of the minimization—the choice of possible subsets S grows exponentially in d, making the problem NP-hard even for simple choices of f, such as linear regression (Amaldi et al., 1998), and exhaustive search is intractable if the number of features is large. In addition, the function class $\mathcal{F}$ needs to exhibit strong expressive power—that is, we seek to develop a method that can approximate the solution for any given class of functions, from linear regression to deep fully-connected neural networks.

3. Our proposal: LassoNet

3.1. Background and notation

Here we choose $\mathcal{F}$ to be the class of residual feedforward neural networks:

$$\mathcal{F}=\left\{f:f(\mathbf{x})={\theta }^T\mathbf{x}+f_W(\mathbf{x})\right\},$$

where the width and depth of the network are arbitrary. Residual networks are known to be easier to train (He et al., 2016a). Furthermore, they act as universal approximators to any function class (Raghu et al., 2017; Lin and Jegelka, 2018).

For the reader’s convenience, we collect key notation and background here. Throughout the paper n denotes the total number of training points, d denotes the data dimension, f_W denotes a fully connected feed-forward network with parameters W, K denotes the size of the first hidden layer, $W^{(1)}\in {ℝ}^{d\times K}$ denotes the first hidden layer, and $\theta \in {ℝ}^d$ denotes the residual layer. $L(\theta ,W)=\frac{1}{n}{\sum }_{i=1}^n\ell \left({\mathbf{x}}_{\mathbf{i}},y_i;\theta ,W\right)$ is the loss on the training data set, where ℓ denotes the loss on individual training samples. ${\mathcal{S}}_{\lambda }(x)=\mathrm{sign}(x)\cdot \max \{|x|-\lambda ,0\}$ is the soft thresholding operator.

The general architecture of LassoNet is illustrated in Fig. 3. The method consists of two main ingredients:

1. A penalty is introduced to the original empirical risk minimization that encourages feature sparsity. The formulation transforms the combinatorial search to a continuous search by varying the level of the penalty.

2. A proximal gradient algorithm is applied in a mathematically elegant way, so that it admits a simple and efficient implementation. The method can be implemented by adding just a few lines of code to a standard neural network. The mathematical derivation of this algorithm is detailed in Section 5.

Figure 3. The architecture of LassoNet.

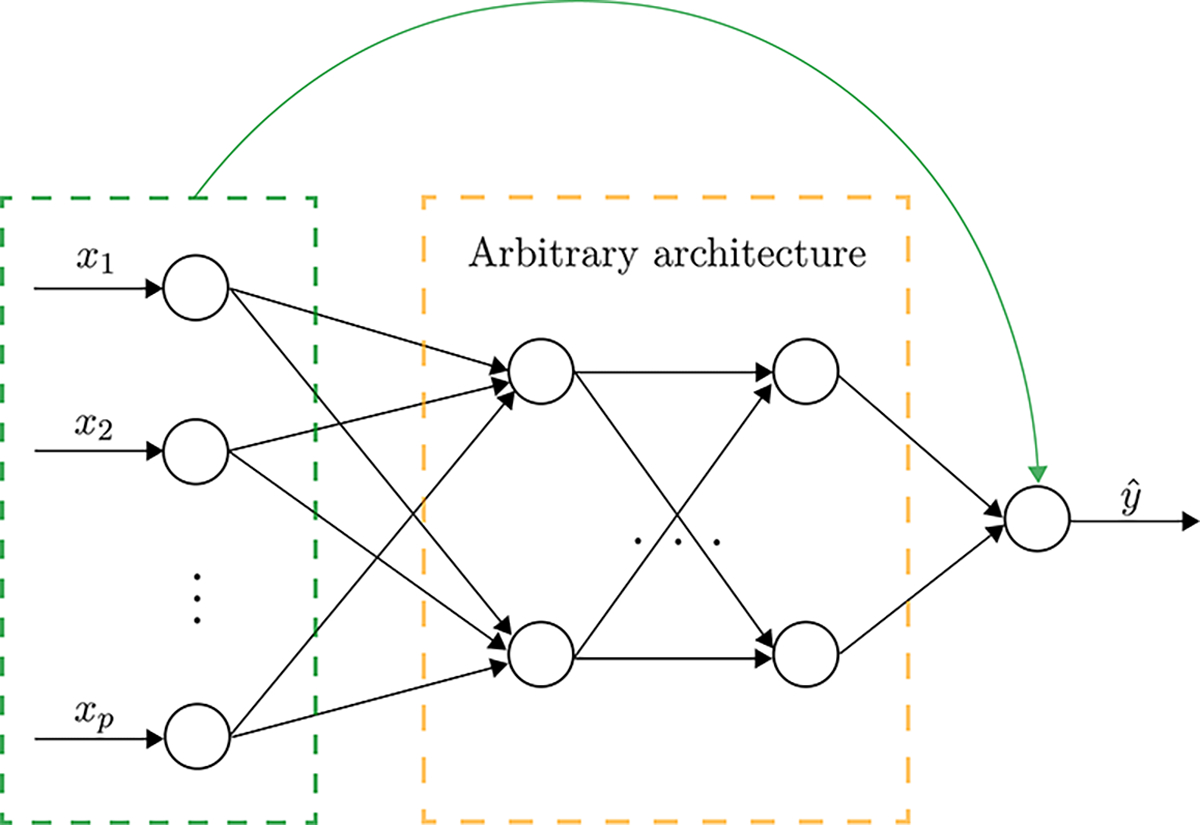
The architecture of LassoNet consists of a single residual connection, shown in green and an arbitrary feedforward neural network, shown in black. The residual layer and the first hidden layer are jointly passed through a hierarchical soft-thresholding optimizer.

3.2. Formulation

The LassoNet objective function is defined as

$$\begin{array}{l}\underset{\theta ,W}{\mathrm{minimize}}L(\theta ,W)+\lambda \Vert \theta {\Vert }_1\\ \text{subject}\text{to}{\Vert W_j^{(1)}\Vert }_{\infty }\le M\left|{\theta }_j\right|,j=1,\dots ,d.\end{array}$$ (2)

where the loss function L(θ, W) was defined in Section 3.1, and W⁽¹⁾ denotes the first hidden layer. We emphasize that our goal is not just to sparsify the network, but to do so in a structured way that selects the relevant input features. Since the network is feedforward, we do not need to penalize the remaining hidden layers in any particular way.

The constraint

$$\left|W_{jk}^{(1)}\right|\le M\cdot \left|{\theta }_j\right|,k=1,\dots ,K$$

budgets the total amount of non-linearity involving feature j according to the relative effect importance of X_j as a main effect. An immediate consequence is that W_j = 0 as soon as θ_j = 0. In other words, feature j is completely inactive from the model without the need for an explicit penalty on W, hence efficient feature selection. In this framework, feature sparsity becomes possible with a controllable trade-off between the linear and nonlinear components. In the extreme where M = 0, the formulation recovers exactly the LASSO; in the other extreme (by letting M → +∞), one recovers a standard feed-forward neural network with ℓ₁-penalty on the first layer.

This formulation has several benefits. First, it promotes the linear component of the signal above the nonlinear one and uses it to guide feature sparsity. Such a strategy is not new, and bears close resemblance to the hierarchy principle which has been extensively studied in statistics (Choi et al., 2010; Radchenko and James, 2010; Lim and Hastie, 2014; She et al., 2016; Yan and Bien, 2017). In addition, the formulation leverages the expressive power of residual neural networks (He et al., 2016a). These are easier to train and can uniformly approximate any measurable function, unlike fully-connected networks which are not universal approximators (Lin and Jegelka, 2018). Finally, by tying every feature to a single coefficient (the linear component), our formulation provides a natural framework for feature selection.

One added benefit of the formulation is that the linear and non-linear components are fitted simultaneously, allowing to capture arbitrary nonlinearity in the data. If the best fitting model would have ∥W_j∥ large but |θ_j| only moderate, this can be accommodated with a reasonable choice of M. Furthermore, Fig. 4 suggests that the demand for hierarchy is analogous to the demand for sparsity—a form of “regularization.”

Figure 4.

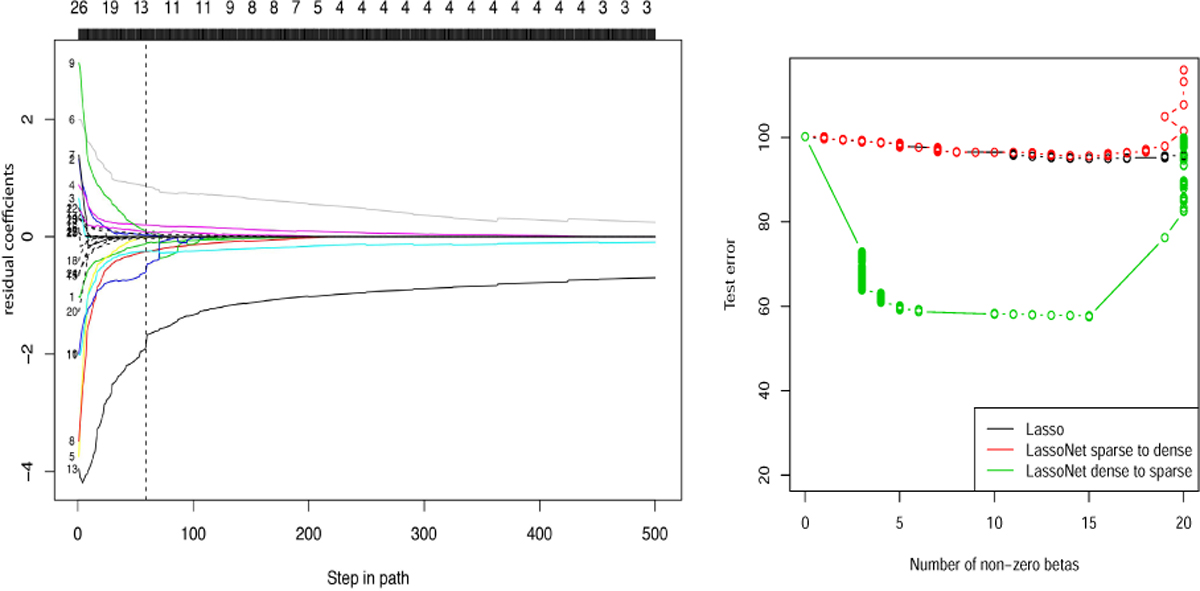
Left: The path of residual coefficients for the Boston housing dataset. We augmented the Boston Housing dataset from p = 13 features to 13 additional Gaussian noise features (corresponding to the broken lines). The number of features selected by LassoNet is indicated along the top. LassoNet achieves the minimum test error (at the vertical broken line) at 13 predictors. Upon inspection of the resulting model, 12 of the 13 selected features correspond to the true predictors, confirming the model’s ability to perform controlled feature selection. Right: Comparing two kinds of initialization. The test errors for Lasso and LassoNet using the sparse-to-dense (in red) and dense-to-sparse (in green) strategies are shown. The dense-to-sparse strategy achieves superior performance, confirming the importance of a dense initialization in order to efficiently explore the optimization landscape.

Training LassoNet involves two steps. First, all the model parameters are updated by stochastic gradient descent. Then, a hierarchical proximal operator is applied to the input layer pair (θ, W⁽¹⁾⁾. This sequential nature makes the procedure extremely simple to implement in popular machine learning frameworks, and requires only modifying a few lines of code from a standard residual network. The procedure is summarized in Alg. 1.

An added benefit of the method is its computational attractiveness. The LassoNet regularization path can be trained at a cost that is essentially that of training a single model. This is achieved thanks to the use of warm starts in a specific direction, as outlined in Section 4.1.

3.3. Hyper-parameter tuning

LassoNet has two hyper-parameters:

• the ℓ₁-penalty coefficient, λ, controls the complexity of the fitted model; higher values of λ encourage sparser models;

• the hierarchy coefficient, M, controls the relative strength of the linear and nonlinear components.

It may be difficult to set the hierarchy coefficient, M, without expert knowledge on the domain or task. We can circumvent this situation easily, by treating the hierarchy coefficient as a hyper-parameter. We may use a naive search, which exhaustively evaluates the accuracy for the predefined hyper-parameter candidates with a validation dataset. This procedure can be performed in parallel.

Algorithm 1.

Training LassoNet

1:	Input: training dataset $X\in {ℝ}^{n\times d}$, training labels Y, feed-forward neural network fW(·), number of epochs B, hierarchy multiplier M, path multiplier ϵ, learning rate α
2:	Initialize and train the feed-forward network on the loss L(X, Y; θ, W)
3:	Initialize the penalty, λ = ϵ, and the number of active features, k = d
4:	while k > 0 do
5:	Update λ ← (1 + ϵ)λ
6:	for b ∈ {1... B} do
7:	Compute gradient of the loss w.r.t to (θ, W) using back-propagation
8:	Update θ ← θ − α∇θL and W ← W − α∇W L
9:	Update (θ, W(1)) ← Hier-Prox(θ, W(1), λ, M)
10:	end for
11:	Update k to be the number of non-zero coordinates of θ
12:	end while
13:	where Hier-Prox is defined in Alg. 2

4. Optimization

4.1. Warm starts: a path from dense to sparse

The technique of warm starts is very effective in optimizing models over an entire regularization path. For example, this technique is employed in Lasso ℓ₁-regularized linear regression (Friedman et al., 2010). In this approach, optimization is carried out for each fixed value of λ on a logarithmic scale from sparse to dense, and using the solution from the previous λ as a warm start for the next. This is effective, since the sparse models are easier to optimize and the sparse solution is also of main interest.

Not surprisingly, for optimizing LassoNet, we find that a dense-to-sparse warm start approach is far more effective than a sparse-to-dense approach, in the sense that the former approach returns models that generalize better than those returned from the latter. This phenomenon is illustrated in Fig. 4, where the standard sparse-to-dense approach gets caught in local minima with poor generalization ability. On ther other hand, the dense-to-sparse approach leverages the favorable generalization properties of the dense solution and preserves them after drifting into sparse local minima.

4.2. Hierarchical proximal optimization

The objective is optimized using proximal gradient descent, as outlined in Alg. 1. The key novelty is a numerically efficient algorithm for the proximal inner loop. We call the proposed algorithm HIER-PROX and detail it in Alg. 2. Underlying its development is the derivation of equivalent optimality conditions that completely characterize the global solution of the non-convex minimization problem defining the proximal operator. As it turns out, the inner loop is decomposable across features. As we show in Appendix B, HIER-PROX finds the global minimum of an optimization problem of the form

$$\begin{array}{l}\underset{b\in ℝ,W\in {ℝ}^K}{\mathrm{minimize}}L(b,W)\equiv \frac{1}{2}{(v-b)}^2+\frac{1}{2}\Vert u-W{\Vert }_2^2+\lambda |b|,\\ \text{subject}\text{to}\Vert W{\Vert }_{\infty }\le M\left|b\right|\end{array}$$

Remarkably, the complexity of Hier-Prox is controlled by O(dK·log(dK)), where dK is the total number of the parameters being updated. This overhead is negligible compared to the computation of the gradients with respect to the same parameters. Furthermore, implementing the optimizer is straightforward in most standard deep learning frameworks. We provide more information about our implementation in Appendix C.

Algorithm 2.

Hierarchical Proximal Operator

1:	procedure Hier-Prox(θ, W(1); λ, M)
2:	for j ∈ {1,..., d} do
3:	Sort the entries of $W_j^{(1)}$ into $|W_{(j,1)}^{(1)}|\ge \dots \ge |W_{(j,K)}^{(1)}|$
4:	for m ∈ {0, ..., K} do
5:	Compute $w_m\equiv \frac{M}{1+m{M}^2}\cdot {\mathcal{S}}_{\lambda }\left(\left|{\theta }_j\right|+M·{\sum }_{i=1}^m|W_{(j,i)}^{(1)}|\right)$
6:	Find the first m such that $|W_{(j,m+1)}^{(1)}|\le w_m\le |W_{(j,m)}^{(1)}|$
7:	end for
8:	${\tilde{\theta }}_j\leftarrow \frac{1}{M}\cdot \mathrm{sign}\left({\theta }_j\right)\cdot w_m$
9:	${\tilde{W}}_j^{(1)}\leftarrow \mathrm{sign}\left(W_j^{(1)}\right)\cdot \min \left(w_m,W_j^{(1)}\right)$
10:	end for
11:	return $\left(\tilde{\theta },{\tilde{W}}^{(1)}\right)$
12:	end procedure
13:	Notation: d denotes the number of features; K denotes the size of the first hidden layer.
14:	Conventions: Ln. 6, $W_{(j,K+1)}^{(1)}=0$, $W_{(j,0)}^{(1)}=+\infty$; Ln. 9, minimum is applied coordinate-wise.

4.3. Computational Complexity

In most existing hierarchical models, computation remains a major challenge. Indeed, the complex nature of the regularizers used to enforce hierarchy prevents most current optimization algorithms from scaling with d. In contrast, training LassoNet is performed at an attractive computational cost. Namely:

• The bulk of the computational cost occurs when training the dense network;

• Subsequently, training over the λ path is computationally cheap. By leveraging warm starts and the efficient HIER-PROX solver, the method effectively prunes the dense model. In practice, predictions across consecutive solutions in the path are usually close, which explains the speed-ups we observe in our experiments.

The use of warm starts dramatically reduces the number of rounds of gradient descent needed during each iteration, as the solution with penalty λ is often very similar to the solution with penalty λ(1 + ϵ). This added benefit distinguishes LassoNet from many competing feature selection methods, which require advance knowledge of the optimal number of features to select, and do not exhibit any computational savings over the path of features. Finally, the computational complexity of the method improves with hardware acceleration and parallelization techniques commonplace in deep learning.

5. Experiments

In this section, we show experimental results on real-world datasets. These are drawn from several domains including protein data, image data and voice data, and have been used for benchmarking feature selection methods in prior literature (Abid et al., 2019) ¹:

• Mice Protein Dataset consists of protein expression levels measured in the cortex of normal and trisomic mice who had been exposed to different experimental conditions. Each feature is the expression level of one protein.

• MNIST and MNIST-Fashion consist of 28-by-28 grayscale images of hand-written digits and clothing items, respectively. We choose these datasets because they are widely known in the machine learning community. Although these are image datasets, the objects in each image are centered, which means we can meaningfully treat each 784 pixels in the image as a separate feature.

• ISOLET consists of preprocessed speech data of people speaking the names of the letters in the English alphabet, and is widely used as a benchmark in the feature selection literature. Each feature is one of the 617 quantities produced as a result of preprocessing, including spectral coefficients and sonorant features.

• COIL-20 consists of centered grayscale images of 20 objects. Images of the objects were taken at pose intervals of 5 degrees amounting to 72 images for each object. During preprocessing, the images were resized to produce 20-by-20 images, with each feature being one of the 400 pixels.

• Smartphone Dataset for Human Activity Recognition consists of sensor data collected from a smartphone mounted on subjects while they performed several activities such as walking upstairs, standing and laying. Each feature represents one of the 561 raw or processed quantities from the sensors on the phone.

We compare LassoNet with several supervised feature selection methods mentioned in Related Works, including HSIC-LASSO and the Fisher Score. We also include principal feature analysis (PFA), a popular method for selecting discrete features based on PCA, proposed by Lu et al. (2007). Where available, we made use of the scikit-feature implementation (Li et al., 2018) of each method. Fig. 5 shows the results on the ISOLET data set, which is widely used as a benchmark in prior feature selection literature.

Figure 5. Results on the ISOLET dataset.

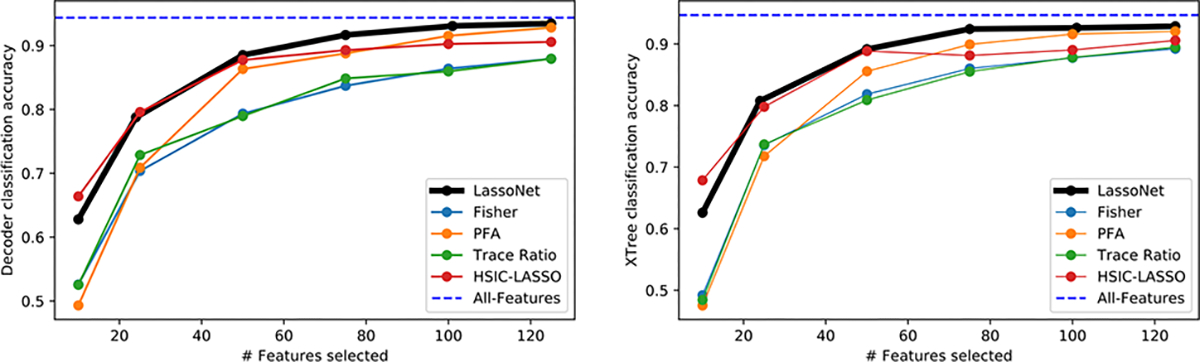
Here, we compare LassoNet to other feature selection methods using a 1-hidden layer neural network (left) and an Extremely Randomized Trees (a variant of random forests) classifier (right). We find that across all values of k tested, and for both learners, LassoNet has highest classification accuracy.

In our experiments, we also include, as an upper-bound on performance, reconstruction methods that are not restricted to choosing individual features. In experiments with decoders, we use a standard feed-forward auto-encoder with all the input features, and in tree-based learners, we use equivalent full trees.

We benchmarked each feature selection method with varying number of features. Although LassoNet is an integrated procedure — simultaneously performing feature selection and learning, most other feature selections are not, and therefore we explore the use of the selected feature set as input into two separate downstream learners. For every task, we run each algorithm being evaluated to extract the k features selected. We measure classification accuracy by passing the resulting matrix X_S to a one-hidden-layer feed-forward network and to an extremely randomized trees classifier (Geurts et al., 2006), a variant of random forests that has been used with feature selection methods in prior literature (Drotár et al., 2015). For all of the experiments, we use Adam optimizer with a learning rate of 10⁻³.

For LassoNet, we did not use the network that was learned during training, but re-trained the feedforward network from scratch to remove the bias introduced by ℓ₁ regularization (Zhang et al., 2008). We divide each data set randomly into train, validation and test with a 70–10-20 split. The number of neurons in the hidden layer of the feed-forward network was varied within [k/3, 2k/3, k, 4k/3], and the network with the highest validation accuracy was selected and measured on the test set.

The resulting classification errors are shown in Fig. 5 for the decoder network on the ISOLET dataset, and in Appendix 3 for other datasets and downstream learners. Overall, we find that our method is the strongest performer in the large majority of cases. While occasionally more than one method achieves the best accuracy, we find that our method either ties or overtakes the remaining methods in all instances, suggesting that the hierarchical objective may be widely applicable for different learning tasks.

6. Application to Unsupervised Feature Selection

In certain applications, specific prediction tasks may not be known ahead of time, and thus it is important to develop methods that can identify a subset of features while allowing imputation of the remaining features with minimal distortion. Thus, an unsupervised approach becomes relevant in order to identify the most important features in the dataset for arbitrary downstream tasks.

LassoNet adapts to the unsupervised setting conveniently by replacing the neural network classifier with a decoder network. The main difference is the use of the GROUP-LASSO rather than LASSO penalty in order to enforce the same set of selected features across all reconstructed inputs. We provide more details on this setting in Appendix B.

7. Application to Matrix Completion

In several problems of contemporary interest, arising, for instance, in biomedical settings where measurements are costly or otherwise limited, the observed data are in the form of a large sparse matrix, Z_ij, (i, j) ∈ Ω, where Ω ⊂ {1, ..., m} × {1, ..., n}. Popularly dubbed the matrix completion problem (Candès and Recht, 2008), the task is to predict the unobserved entries.

Most existing approaches, including the popular Soft-Impute algorithm (Mazumder et al., 2010) require low-rank assumptions about the underlying data. In this section, we show how to use LassoNet to perform matrix completion without any low-rank assumption. Instead, the method exploits feature sparsity, i.e., only a small number of input features are used for reconstruction. Additionally, our method differs from existing solutions in another major way. While both methods are iterative, Soft-Impute performs singular value thresholding to find a linear low-dimensional structure. In contrast, our method allows to use arbitrary nonlinear manifolds through the network’s hidden layers.

To investigate the method’s performance, we run both LassoNet and Soft-Impute on the MICE Protein Dataset. This dataset was previously used in Section 5 for the supervised prediction task, and here the goal is to impute the entries that are missing from the training data. The results are displayed in Fig. 7, where LassoNet achieves about a 50% reduction in the number of proteins measured for an equivalent test MSE.

Figure 7. Imputation errors of LassoNet and and Soft-Impute.

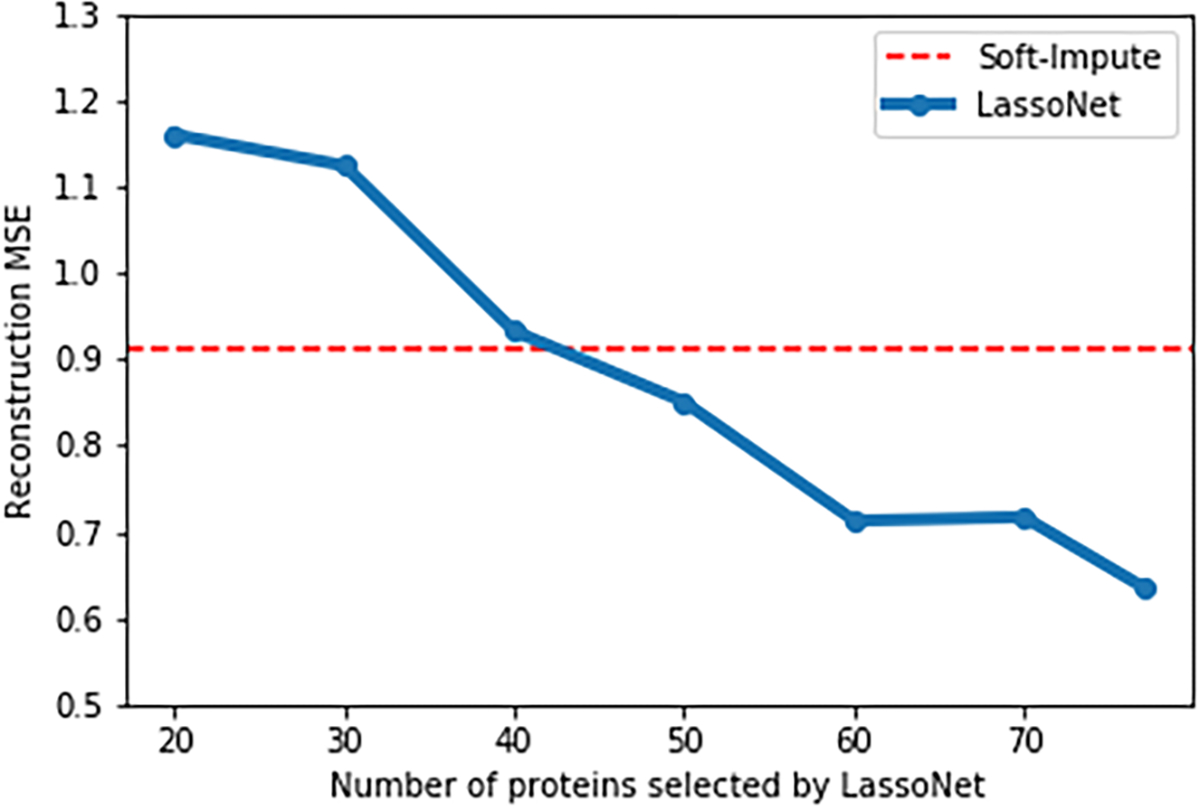
We report the performance of LassoNet with different numbers of selected features using the MSE on the test set. We find that we can achieve a similar MSE to Soft-Impute using only about 40 proteins, a 50% reduction in the number of proteins measured.

Our results show that the low-rank assumption underlying most existing matrix imputation methods is not always appropriate. More worryingly, when the linear assumption is violated, the statistical performance of standard imputation methods may be severely impaired. Therefore, modeling nonlinear low-dimensional structures may improve the imputation power. If the underlying data effectively admits nonlinear structure, LassoNet will outperform linear reconstruction.

8. Discussion

In this paper, we have proposed a new feature selection method for neural networks. Unlike most other feature selection methods, our method provides a path of regularized models at essentially the same cost as training a single model. At its core, LassoNet involves a nonconvex optimization problem with hierarchy constraints to satisfy feature sparsity. The nonconvex optimization problem is decomposed into two subproblems that are solved iteratively, one using stochastic gradient descent and the other analytically. The stochasticity of the initial dense model allows it to efficiently explore and converge over an entire regularization path with varying number of input features. This makes LassoNet different from many feature selection methods, which assume prior knowledge of the number of features to select.

Advantages of LassoNet include its generality and ease of use. First, the generality of the method allows it to extend to several other learning tasks, such as unsupervised reconstruction and matrix completion. Second, implementing the architecture in popular machine learning frameworks requires only modifying a few lines of code from a standard feed-forward neural network. Furthermore, the runtime of LassoNet over an entire path of feature sizes is similar to that of training a single model and improves with hardware acceleration and parallelization techniques commonplace in deep learning. Finally, the only additional hyper-parameter of LassoNet is the hierarchy coefficient. We find that the default value, M = 10, used in this paper works well for a variety of datasets.

In several fields including computer vision (He et al., 2016b) and speech recognition (Chan et al., 2016), the trend has moved from inserting expert knowledge toward general-purpose methods that learn these biases from data. Currently, the state-of-the-art is based on learning convolutional filters. In this setting, it would be desirable to achieve ”filter sparsity”, that is, select the most relevant convolutional filters to improve interpretability. This constitutes an important direction for future work.

LassoNet, like the other feature selection methods we compared with in this paper, does not provide p-values or statistical significance quantification. Features discovered through LassoNet should be validated through hypothesis testing or additional analysis using relevant domain knowledge. In this regard, a growing body of research about hypothesis testing for Lasso (Lockhart et al., 2014; Javanmard and Montanari, 2014) could serve as a fruitful starting point.

Figure 6. Demonstrating the unsupervised LassoNet on the MNIST dataset.

Left: 3 test images from each class of digits are shown. Right: the reconstructed versions of the images using LassoNet with an intermediate penalty level (corresponding to about 50 active features) show that generally the digit is identified correctly and some stylistic features, such as the orientation in the digit ”5” and the thickness in the digit ”7”, are preserved.

A. Classification accuracies for downstream lerners

A.1. Classification accuracies using decoder networks

Here we show the classification accuracies of the various feature selection methods on six publicly available datasets, using feedforward neural networks as the learner.

Table 1: Classification accuracies of feature selection methods using decoder networks as the learner.

Here Fisher refers to the Fisher score, PFA refers to principal feature analysis and All-Feature refers to the learner that uses all input features. For each method, we select k = 50 features and use a 1-hidden layer neural network for classification. All reported values are on a hold-out test set. (Higher is better.)

Dataset	(n, d)	# Classes	All-Feature	Fisher	HSIC-Lasso	PFA	LassoNet
Mice Protein	(1080, 77)	8	0.990	0.944	0.958	0.939	0.958
MNIST	(10000, 784)	10	0.928	0.813	0.870	0.873	0.873
MNIST-Fashion	(10000, 784)	10	0.833	0.671	0.785	0.793	0.800
ISOLET	(7797, 617)	26	0.953	0.793	0.877	0.863	0.885
COIL-20	(1440, 400)	20	0.996	0.986	0.972	0.975	0.991
Activity	(5744, 561)	6	0.853	0.769	0.829	0.779	0.849

A.2. Classification accuracies using tree-based classifiers

We also report the equivalent table to Table 1, but using the extremely randomized tree classifier as downstream learner. The results are competitive, as Lassonet continues to have high (but not always highest) classification accuracy.

Table 2: Classification accuracies of feature selection methods using the tree-based learner.

Here, we show the classification accuracies of the various feature selection methods on six publicly available datasets. Here Fisher refers to the Fisher score, PFA refers to principal feature analysis, and All-Feature refers to the learner that uses all input features. For each method, we select k = 50 features. The classifier used here was an Extremely Randomized Tree classifier (a variant of random forests) with the number of trees being 50. All reported values are on a hold-out test set. (Higher is better.)

Dataset	(n, d)	# Classes	All-Feature	Fisher	HSIC-Lasso	PFA	LassoNet
Mice Protein	(1080, 77)	8	0.997	0.996	0.996	0.997	0.997
MNIST	(10000, 784)	10	0.941	0.818	0.869	0.879	0.892
MNIST-Fashion	(10000, 784)	10	0.831	0.66	0.775	0.784	0.794
ISOLET	(7797, 617)	26	0.951	0.818	0.888	0.855	0.891
COIL-20	(1440, 400)	20	0.996	0.996	0.993	0.993	0.993
Activity	(5744, 561)	6	0.859	0.794	0.845	0.808	0.860

B. Proofs

Proof of Correctness of the Hier-Prox and Group-Hier-Prox Operators

At its core, LassoNet performs a step of vanilla gradient descent and subsequently solves a constrained minimization problem. Since the problem is decomposable across features, each iteration of the algorithm decouples into d single-feature optimization problems. Here we show the following:

1. Hier-Prox returns the global optimum of the following optimization problem:

   $$\begin{array}{l}\underset{b\in ℝ,W\in {ℝ}^K}{\mathrm{minimize}}L(b,W)\equiv \frac{1}{2}{(v-b)}^2+\frac{1}{2}\Vert u-W{\Vert }_2^2+\lambda |b|,\\ \text{subject}\text{to}\Vert W{\Vert }_{\infty }\le M\left|b\right|\end{array}$$ (3)

   where $v\in ℝ$ is a scalar and $u\in {ℝ}^K$ is a vector.
2. Group-Hier-Prox returns the global optimum of the following problem:

   $$\begin{array}{l}\underset{(b,W)}{\mathrm{minimize}}\frac{1}{2}\left(\Vert v-b{\Vert }_2^2+\Vert U-W{\Vert }_2^2\right)+\lambda \Vert b{\Vert }_2,\\ \text{subject}\text{to}\Vert W{\Vert }_{\infty }\le M\Vert b{\Vert }_2\end{array}$$ (4)

   where $v\in {ℝ}^K$, $U\in {ℝ}^K$ are vectors of the same size.

It turns out that the aforementioned two results are special cases of the following proposition. They can be easily recovered by setting $\overline{\lambda }=0$.

Proposition 1

Fix $v\in {ℝ}^K$ and $U\in {ℝ}^K$. (Note: the two integers k, K can be different) Let us consider the problem

$$\begin{array}{l}\underset{(b,W)}{\mathrm{minimize}}\frac{1}{2}\left(\Vert v-b{\Vert }_2^2+\Vert U-W{\Vert }_2^2\right)+\lambda \Vert b{\Vert }_2+\overline{\lambda }\Vert W{\Vert }_1\\ \text{subject}\text{to}\Vert W{\Vert }_{\infty }\le M\cdot \Vert b{\Vert }_2.\end{array}$$

We derive the sufficient and necessary condition for characterizing the global optimum (b*, W*) of the above optimization problem:

1. Let us order the coordinates ${\left\{\left|U_i\right|\right\}}_{i\in [K]}$ in decreasing order

   $$\left|U_{(1)}\right|\ge \left|U_{(2)}\right|\ge \dots \ge \left|U_{(K)}\right|.$$
   Define a₀ = λ, and for each s ∈ {1, 2, . . ., K}, the value $a_s\in ℝ$ by

   $$a_s=\lambda -M\sum _{i=1}^s\left(\left|U_{(i)}\right|-\overline{\lambda }\right).$$
   Define the vector $b_s\in {ℝ}^k$ for each s ∈ [K] = {0, 1, . . ., K} by

   $$b_s=\frac{1}{1+s{M}^2}{\left(1-\frac{a_s}{\Vert v{\Vert }_2}\right)}_{+}\cdot v.$$
   Then $b^{*}=b_{s^{*}}$ where s* ∈ [K] is the unique s ∈ [K] such that

   $$M{\Vert b_s\Vert }_2\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(|U_{(s+1)}|\right),{\mathcal{S}}_{\overline{\lambda }}\left(|U_{(s)}|\right)\right).$$

   By convention ${\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(K+1)}\right|\right)=0$ and ${\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(0)}\right|\right)=\infty$.

2. The W* must satisfy

   $$W^{*}=\mathrm{sign}(U)\min \left\{M{\Vert b^{*}\Vert }_2,{\mathcal{S}}_{\overline{\lambda }}(|U|)\right\}.$$

Proof

We start by proving the claim below: for some $w\in {ℝ}_{+}$

$$\text{Claim}:W^{*}=\mathrm{sign}(U)\min \left\{M\Vert b{\Vert }_2,{\mathcal{S}}_{\overline{\lambda }}(|U|)\right\}.$$ (5)

Denote w = M ∥b*∥₂. By definition, W* is the minimum of the below optimization problem:

$$\begin{array}{l}\underset{W}{\mathrm{minimize}}\frac{1}{2}\Vert U-W{\Vert }_F^2+\overline{\lambda }\Vert W{\Vert }_1\\ \text{subject}\text{to}\Vert W{\Vert }_{\infty }\le M{\Vert b^{*}\Vert }_2=w.\end{array}$$ (6)

The optimization problem is convex in W. Further, since the nonlinear constraint ∥W∥_∞ ≤ w can be equivalently expressed into the following linear constraints

$$-w\le W_j\le w\text{for}\text{all}j\in \{1,2,\dots ,K\}$$

Slater’s condition and hence strong duality hold for the optimization problem (6). As a result, we know for some dual variable $s\in {ℝ}_{+}^K$, W* minimizes the following Lagrangian:

$$W^{*}=\underset{W\in {ℝ}^K}{\mathrm{argmin}}\frac{1}{2}\Vert U-W{\Vert }_2^2+\sum _{j=1}^K{s}_j\left|W_j\right|+\overline{\lambda }\sum _{j=1}^K\left|W_j\right|.$$

Now, let’s take the subgradient and get that W* needs to satisfy for all j ∈ {1, 2, . . ., K}:

$$\begin{array}{l}{W}_j^{*}-U_j+\left(\overline{\lambda }+s_j\right)v_j^{*}=0\text{for}\text{some}{v}_j^{*}\in \partial (|W_j^{*}|).\\ s_j(|W_j^{*}|-w)=0.\\ s_j\ge 0,\text{and}|W_j^{*}|\le w.\end{array}$$ (7)

Now we divide our discussion into two cases:

1. s_j = 0. The KKT condition (Eq. (7)) shows $U_j=W_j^{*}+\overline{\lambda }{v}_j^{*}$ for some $v_j^{*}\in \partial (|W_j^{*}|)$. This implies that $W_j^{*}={\mathcal{S}}_{\overline{\lambda }}\left(U_j\right)$, which is possible if and only if $\left|{\mathcal{S}}_{\overline{\lambda }}\left(U_j\right)\right|\le w$.

2. s_j > 0. The KKT condition (Eq. (7)) gives $|W_j^{*}|=w$. Since $U_j=W_j^{*}+\left(\overline{\lambda }+s_j\right)v_j^{*}$ for $v_j^{*}\in \partial (|W_j^{*}|)$, it implies $\mathrm{sign}(v_j^{*})=\mathrm{sign}(W_j^{*})=\mathrm{sign}\left(U_j\right)$. Hence $W_j^{*}=\mathrm{sign}\left(U_j\right)w$. Note if w ≠ 0, then we must have $v_j^{*}=\mathrm{sign}(W_j^{*})=\mathrm{sign}(U_j)$. Thus, having some s_j > 0 with $U_j=W_j^{*}+\left(\overline{\lambda }+s_j\right)v_j^{*}$ is equivalent to that $\left|{\mathcal{S}}_{\overline{\lambda }}\left(U_{i,j}\right)\right|>w$.

Summarizing the above discussion, we see that W* must satisfy

$$W_j^{*}=\mathrm{sign}\left(U_j\right)\min \left\{w,{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_j\right|\right)\right\}.$$

This proves the claim at Eq (5). Introduce the mapping $W:{ℝ}^k\to {ℝ}^K$

$$W_j(b)=\mathrm{sign}\left(U_j\right)\cdot \min \left\{M\Vert b{\Vert }_2,{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_j\right|\right)\right\}.$$

The claim at Eq (5) shows that it suffices to find b that minimizes

$$F(b)=\frac{1}{2}\left(\Vert v-b{\Vert }_2^2+\Vert U-W(b){\Vert }_F^2\right)+\lambda \Vert b{\Vert }_2+\overline{\lambda }\Vert W(b){\Vert }_1.$$

Denote w = M ∥b∥₂. Order the coordinates ${\left\{\left|U_i\right|\right\}}_{i\in [K]}$ in decreasing order

$$\left|U_{(1)}\right|\ge \left|U_{(2)}\right|\ge \dots \ge \left|U_{(K)}\right|.$$

Define by convention that U₍₀₎ = ∞ and U_(K)+1 = 0. Now, we compute the value F(b) when $w=M\Vert b{\Vert }_2\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s+1)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s)}\right|\right)\right)$. Indeed, we have

$$F(b)=\frac{1}{2}\left(1+s{M}^2\right){\Vert b-\frac{1}{1+s{M}^2}v\Vert }_2^2+\left(\lambda -M\sum _{i=1}^s\left(\left|U_{(i)}\right|-\overline{\lambda }\right)\right)\Vert b{\Vert }_2+r_s.$$

where r_s denotes the remainder term, which is independent of b but can be dependent of U, v, M, s, λ,$\overline{\lambda }$. Now, let’s define for s ∈ [K]

$$F_s(b)=\frac{1}{2}\left(1+s{M}^2\right){\Vert b-\frac{1}{1+s{M}^2}v\Vert }_2^2+\left(\lambda -M\sum _{i=1}^s\left(\left|U_{(i)}\right|-\overline{\lambda }\right)\right)\Vert b{\Vert }_2.$$

and denote $b_s\in {ℝ}^k$ to be the global minimum of F_s on ${ℝ}^k$, i.e.,

$$b_s=\frac{1}{1+s{M}^2}{\left(1-\frac{a_s}{\Vert v{\Vert }_2}\right)}_{+}v\text{where}{a}_s=\lambda -M\sum _{i=1}^s\left(\left|U_{(i)}\right|-\overline{\lambda }\right).$$

Now we show the two claims below, which implies the desired proposition.

1. There exists one unique s* ∈ [K] such that

   $$M{\Vert b_{s^{*}}\Vert }_2\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{\left(s^{*}+1\right)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{\left(s^{*}\right)}\right|\right)\right).$$ (8)

2. The global minimum $b^{*}=b_{s^{*}}$.

Proof of Point (a) Denote s_max ∈ [K] to be the one that satisfies

$${\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{\left(s_{\max }+1\right)}\right|\right)=0<{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{\left(s_{\max }\right)}\right|\right).$$

It suffices to prove the existence and uniqueness of s* ∈ [s_max] satisfying Eq (8). Introduce the function $h:\left[s_{\max }\right]\to ℝ$ by

$$h(s)=M\left(\Vert v{\Vert }_2-\lambda \right)+\overline{\lambda }-\left|U_{(s)}\right|+M^2\sum _{i=1}^s\left(\left|U_{(i)}\right|-\left|U_{(s)}\right|\right).$$

It is clear that h is increasing w.r.t. s ∈ [s_max]. Moreover, by algebraic manipulation, one can show that s ∈ [s_max] satisfies

$$M{\Vert b_s\Vert }_2\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s+1)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s)}\right|\right)\right).$$

if and only if (set by convention h(0) = −∞, h(s_max + 1) = ∞)

$$h(s)\le 0<h(s+1).$$

This proves the existence and uniqueness of s* that satisfies Eq (8).

Proof of Point (b) Introduce the function

$$f(w)=\underset{b:M\Vert b{\Vert }_2=w}{\min }F(b).$$

We will show that

1. f(w) is strictly increasing when $w\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s+1)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s)}\right|\right)\right)$ and s < s*.

2. f(w) is strictly decreasing when $w\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s+1)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s)}\right|\right)\right)$ and s > s*.

The above two facts imply that the global minimum w* of f(w) must belong to the interval $w^{*}\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{\left(s^{*}+1\right)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{\left(s^{*}\right)}\right|\right)\right]$. Thus $b=b_{s^{*}}$ is the global minimum of F(b) since $b=b_{s^{*}}$ achieves the minimum over all b that satisfy $w=M\Vert b{\Vert }_2\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{\left(s^{*}+1\right)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{\left(s^{*}\right)}\right|\right)\right)$.

Now we prove point (i) and point (ii). For $w\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s+1)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s)}\right|\right)\right)$, we know that F(b) = F_s(b)+r_s. From all b satisfying M ∥b∥₂ = w, it is clear that $b=\frac{wv}{M\Vert v{\Vert }_2}$ minimizes F_s(b). Therefore, for $w\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s+1)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s)}\right|\right)\right)$,

$$f(w)=F\left(\frac{wv}{M\Vert v{\Vert }_2}\right)=\frac{1+s{M}^2}{2M^2}{\left(w-w_s\right)}^2+r_s^{\prime }\text{for}{w}_s=\frac{M\left(\Vert v{\Vert }_2-a_s\right)}{1+s{M}^2},$$

where r_s denotes the remainder term, which is independent of b but can be dependent of U, v, M, s, λ,$\overline{\lambda }$. Now, by definition of s*, we know that

1. h(s) ≤ 0 for s ≤ s*.

2. h(s) > 0 for s > s*.

Simple algebraic manipulation shows that this implies that

1. $w_s\le {\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s+1)}\right|\right)$ for s < s*.

2. $w_s>{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s)}\right|\right)$ for s > s*.

Note that f(w) is quadratic centered at w = w_s for $w\in \left[{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s+1)}\right|\right),{\mathcal{S}}_{\overline{\lambda }}\left(\left|U_{(s)}\right|\right)\right)$. This proves the desired deferred point (i) and point (ii).

C. Experimental Details

All experiments were run on a single computer with NVIDIA Tesla K80 and Intel Xeon E5–2640. The average runtime for each result was 4.5 minutes.

C.1. LassoNet Architecture

The implementation was conducted in the PyTorch framework. For LassoNet, we use a one-hidden-layer feedforward neural network with ReLU activation function. We also included a two-hidden-layer network in Section 7 for the matrix completion problem. The number of neurons in the hidden layer was varied within [d/3, 2d/3, d, 4d/3], where d is the total number of features, and the network with the highest validation accuracy was selected and measured on the test set. The learning rate was set to 0.001 and the number of epochs was set to 200. Although the hierarchy parameter could in principle be selected on a validation set as well, we have found that the default value M = 10 works well for a variety of datasets.

C.2. Benchmark Datasets

The MNIST and MNIST-Fashion datasets were retrieved using the Keras library. The remaining datasets were retrieved from the UCI Repository (Dua and Graff, 2017).