Dinitrogen Binding and Activation: Bonding Analyses of Stable V(III/I)–N₂–V(III/I) Complexes by the EDA–NOCV Method from the Perspective of Vanadium Nitrogenase

Abstract

The FeVco cofactor of nitrogenase (VFe₇S₈(CO₃)C) is an alternative in the molybdenum (Mo)-deficient free soil living azotobacter vinelandii. The rate of N₂ reduction to NH₃ by FeVco is a few times higher than that by FeMoco (MoFe₇S₉C) at low temperature. It provides a N source in the form of ammonium ions to the soil. This biochemical NH₃ synthesis is an alternative to the industrial energy-demanding production of NH₃ by the Haber–Bosch process. The role of vanadium has not been clearly understood yet, which has led chemists to come up with several stable V–N₂ complexes which have been isolated and characterized in the laboratory over the past three decades. Herein, we report the EDA–NOCV analyses of dinitrogen-bonded stable complexes V(III/I)–N₂ (1–4) to provide deeper insights into the fundamental bonding aspects of V–N₂ bond, showing the interacting orbitals and corresponding pairwise orbital interaction energies (ΔE_orb(n)). The computed intrinsic interaction energy (ΔE_int) of V–N₂–V bonds is significantly higher than those of the previously reported Fe–N₂–Fe bonds. Covalent interaction energy (ΔE_orb) is more than double the electrostatic interaction energy (ΔE_elstat) of V–N₂–V bonds. ΔE_int values of V–N₂–V bonds are in the range of −172 to −204 kcal/mol. The V → N₂ ← V π-backdonation is four times stronger than V ← N₂ → V σ-donation. V–N₂ bonds are much more covalent in nature than Fe–N₂ bonds.

Introduction

Nitrogen is one of the most important and essential elements for microorganisms, plants, and animals.^1,2 Dinitrogen (N₂) is the major component of the earth atmosphere (78%). All of these can breathe air but cannot directly utilize dinitrogen (N₂) from the inhaled gas and hence have to expel it as is without converting it to other forms of N compounds in their cell except for a few organisms like rhizobium, azotobacter, etc.¹ These bacteria have developed a variety of species genomes, which can form different protein-containing enzymes such as nitrogenase, which can nurture protein-encapsulated inorganic metal complexes such as P clusters, 4Fe–4S, and FeMoco/FeVco cofactors in oxygen free environments.² The evolution of FeMoco, FeVco, and FeFeco in sea water via genetic analyses has been recently summarized.³ FeVco and FeFeco have been less extensively studied compared to FeMoco. However, it has been concluded that FeVco needs more electrons to produce similar equivalents of NH₃ since it also produces more H₂ gas. Very recently, the structural aspects of FeVco have been confirmed with a 1.35 Å structure of vanadium nitrogenase from azotobacter vinelandii.⁴ Combined with sunlight and Mg–ATM, nitrogenase can direct the electron carriers P clusters, 4Fe–4S, and ferredoxin to transport required numbers of electrons to the FeMoco/FeVco cofactors (Scheme 1) within the nitrogenase with some conformational changes in the protein folding, bringing them closer to facilitate the electron transfer to the inorganic core of FeMoco/FeVco cofactors.^1,2 The most common nitrogenase cofactor is FeMoco,⁵ which is actually an anionic heterobimetallic coordination cluster MoFe₇S₉C^1– containing a μ₆-C atom in the center of it.^6,7 This light element (C) bridges between six mixed-valence Fe ions, which are antiferromagnetically coupled via μ-S^2– and μ₆-C^4– bridges. FeMoco possesses two heterocubanes Fe₄S₄ and MoFe₃S₃, which are connected via three μ-S^2– and μ₆-C^4– bridges.^6,7 Until now, the exact mode of N₂ binding, activation, and mode of the reduction of N₂ to NH₃ have not been confirmed.¹ Kinetic studies showed that N₂ binding is most likely at one of the Fe ions of the (μ₆-C^4–)Fe₆ unit. Further studies showed that a similar vanadium analogue of FeMoco (MoFe₇S₉C) can do a similar job in the Mo-deficient soil, which is known as FeVco.^3,4 The structural analyses of vanadium nitrogenase obtained from azotobacter vinelandii showed that one of the belt sulfide ions is replaced by a carbonate anion having different proteins to adopt this carbonate anion to fit in the cavity.⁴ Over the last four decades, several Mo, V, and Fe ion-containing complexes have been synthesized, isolated, and characterized, containing stable Mo/V/Fe–N₂ bonds.⁸⁻²⁹ Some of these complexes have been stepwise reduced with electrons and subsequent addition of protons, and the corresponding intermediate species have been even isolated and characterized too. The M → N₂ π-backdonations and elongation of N–N bond have been discussed from density functional theory (DFT) calculations, WBI values, and NBO analyses.^{21−23,30−34} However, the nature and strength of σ/π M ← N₂/M → N₂ donation/backdonations and exact orbitals involved in bonding have been rarely studied until very recently for M=Fe.^35,37 There are over 20 reports⁹⁻²⁹ purely on V–N₂-containing systems, and there are several mixed vanadium and other metals containing end-on N₂ bridges. A distinct feature has been observed for V–N₂−V complexes. V(III) or V(I) complexes with end-on N₂ bridges possess a diamagnetic ground state, while Fe–N₂–Fe complexes are paramagnetic/diamagnetic in nature. It is hence suspected that the nature of bonding interaction between V and N₂ is quite different and possibly very strong where a strong antiferromagnetic coupling¹¹⁻²² is mediated via an end-on N₂ bridge or has something to do with the electron pairing due to the chemical bonding.²² The DFT calculations of the V(II)–N₂–V(II) complex²² showed that due to V → N₂ ← V π-backdonation (π*) interactions, the V(d_xy) + N₂(π*) and V(d_yz) + N₂(π*) orbitals became lower in energy, accommodating two pairs of electrons from two V(III) (d²) ions, leading to a S = 0 spin ground state.²² The geometry optimization and theoretical calculations involving vanadium ions is quite challenging too.²¹⁻²³ However, a V(II)–N₂–V(II) complex has been shown to have a diamagnetic singlet spin ground state (S = 0) with a suggested canonical structure V(III)–N₂^2––V(III), which has been concluded from DFT calculations and computation of Mulliken spin densities.²³ V(III)–N₂^2––V(III) has been suggested to have antiferromagnetic coupling between two V(III) centers having the lower energy d_z² and d_x²–y² orbitals with electrons on each V(III) ion.²³

Scheme 1. Nitrogenase Cofactors P Cluster (a, b), [4Fe–4S] (c), and FeVco (d) Cofactors of the Nitrogenase Enzyme.

The most crucial step for activation of dinitrogen with binding of a transition metal complex is the weakening of the strong N ≡ N bond by π-backdonation (M → N₂) from metal into antibonding molecular orbitals of N₂. CH₃C[(CH₂)N(i-Pr)Li]₃ or TIAME and VCl₃(THF)₃ react to form the dinitrogen complex (TIAME)V–N₂–V(TIAME) (1) containing an end-on bridging N₂ molecule.¹¹ In the presence of nitrogen, the reaction of VCl₃(THF)₃ with three moles of Me₃CCH₂Li in diethylether produces the bridging nitrogen complex [(Me₃CCH₂)₃V]₂(μ-N₂) (2).¹² When VCl₃(THF)₃ is suspended in THF and treated with lithium di-isopropyl-amide (LDA), it forms the bridge dinitrogen complex [((i-Pr)₂N)₃V]₂(μ-N₂) (3).¹³ When [5,1-(C₅H₄CH₂CH₂NMe₂)VCl₂(PMe₃)] is reduced under a nitrogen atmosphere in the presence of diphenylacetylene, a bridging dinitrogen complex {[5-(C₅H₄CH₂CH₂NMe₂)]V(PhC≡CPh)(PMe₃)₂}₂(μ-N₂) (4) is formed.¹⁴ All four complexes possess a singlet (diamagnetic) spin ground state. These complexes have not been previously studied by theoretical calculations. For these complexes, the V–N bond length is between 1.704 and 1.767 Å, and the N–N bond length is in the range of 1.204–1.280 Å. The N₂ unit in these compounds has a longer N–N bond length than a free N₂ molecule (1.102 Å), which is due to the effect of V→N₂ π-backdonation corresponding to N−N bond activation.¹¹⁻¹⁴ When complex (2) is protonated with HCl, instead of hydrazine or ammonia, neopentane is produced. Due to a sterically packed ligand, neopentyl is protonated instead of nitrogen, generating neopentane.¹² It prompted us to look into the bonding characteristics of these complexes. Herein, we report on the DFT, QTAIM calculations, and EDA–NOCV analyses of these four diamagnetic complexes (1–4) possessing an end-on μ-bridging N₂ molecule to shed light on the V–N₂ bonding with the computations of intrinsic interaction energy (ΔE_int) and pairwise orbital interaction energy of the V–N₂–V bonds. The formal oxidation states of V ions are +3 (1–3) and +1 (4), respectively.

Results and Discussion

In addition to the literature review,⁸⁻²⁹ we used computational methods such as optimization, NBO, QTAIM, and EDA–NOCV to investigate the geometrical parameters and bonding nature of the complexes (see Scheme 2). Our calculations were done at the BP86-D3(BJ)/Def2-TZVPP level of theory. We also checked that the geometrical parameters computed at the BP86 and TPSS levels of theory are very similar (see SI).

Scheme 2. Previously Reported Modeled Complexes Containing N₂ as a Bridged Ligand between Two Vanadium Metal Centers.

For the complexes presented in Scheme 2, we carried out geometry optimization and vibrational frequency computations in singlet and triplet electronic states. Complexes 1–4 are more stable in their singlet states¹¹⁻¹⁴ than their triplet states by 16.0–35.9 kcal/mol.

Each V atom of complexes 1–3 adopts¹¹⁻¹³ a pseudotetrahedral coordination geometry with a N₄ or C₃N donor set. Two V(III/I) centers are connected/bridged by a 1,2-μ-N₂ (end-on) molecule. The coordination geometry of the V center in 4 appears¹⁴ to be similar although it is bonded to a η⁵-cp ring and a C≡C triple bond of diphenylacetylene. The C_Ph–C–C–C_Ph torsion angle (4.4°) in 4 is significantly lower than that of a free diphenylacetylene ligand, suggesting a significant charge flow from the V(I) center to the acetylene triple bond via V → C≡C (side-on) π-backdonation. Two phenyl groups are cis to each other. Two N atoms of the amino group attached to the cp ring are not bonded to the V(I) centers of 4. Six neopentyl ^tBu groups are oriented toward the bridging N≡N unit, shielding this core. The V–N₂ bond lengths of complexes 1–4 in their optimized geometries, as shown in Figure 1, lie in the range of 1.705–1.765 Å, which are very similar to those of the experimentally observed V–N₂ bond length (1.704–1.767 Å)¹⁻⁴ obtained from X-ray single-crystal diffraction (Figure 1). The V–N₂ bond lengths in 1–4 are significantly different than that of the rarely isolated stable V≡N complex (1.565(4) Å).²³ The V−N_N2 bond lengths are in the order 1 < 2 < 3 < 4. The significant backdonation from metal to nitrogen causes the shorter bond lengths in complexes 1–3 when these values are compared with that (1.103) of the free N₂ molecule.¹¹⁻¹⁴

Figure 1.

Optimized geometries of complexes 1–4 at the BP86-D3(BJ)/Def2-TZVPP level of theory at their singlet states. Bond lengths are in Å and bond angles are in degree (°). Nitrogen atoms are represented with blue spheres, vanadium metal atoms with violet spheres, and carbon atoms with gray-colored spheres. Hydrogen atoms are omitted for clarity.

In complex 1,¹¹ there is a strong backdonation from metal to nitrogen, which could be due to the donation of a lone pair of electrons from the nitrogen atom of the TIAME ligand to vanadium. It causes an increase in electron density in vanadium, enabling more electron backdonation from vanadium to the dinitrogen unit of the complex, consequently shortening the bond. Although the same thing can happen in complex 3,¹³ namely, the transfer of a lone pair of electrons from a diisopropylamide’s nitrogen atom to the vanadium metal. However, the donation may not be as strong as in complex 3 due to waging nature of a ⁱPr substituent in three noncyclic N(ⁱPr₂) ligands (3), whereas in complex 1, the ligand is directionally chelating, resulting in stronger donations of electron densities of lone pair of electrons of adjacent N atoms in complex 1 as opposed to complex 3. Due to the nonchelating nature of the ligand in complex 3, backdonation from vanadium metal to the nitrogen ligand is likely to be less than that in complex 2,¹² resulting in a longer V–N₂ bond length in complex 3. Note that the formal oxidation states of 1–3 and 4 are +3 and +1, respectively. The formal charges on the V metals may also be the reason for different V–N bond lengths. It is apparent that due to the poor backdonation from vanadium metal to the dinitrogen ligand, the V–N₂ bond length in complex 4 is longer than those of the other three complexes 1, 2, and 3. The PMe₃ and acetylene ligands, which are known as π-acceptor ligands, also compete for V → PMe₃/acetylene π-backdonations. As a result, the effective share of electron densities reduces, possibly resulting in a lesser extent of π-backdonation to the dinitrogen ligand from vanadium. As a result, the V–N₂ bond length is slightly longer in complex 4 than those of the other complexes. The N–N bond length follows the order 4 < 3 < 2 < 1.¹¹⁻¹⁴ However, their values are very close to each other, 1.215–1.246 Å, which are slightly different than experimentally reported N–N bond lengths (1.204–1.280 Å).¹¹⁻¹⁴ These differences can be attributed to the solvation and/or intermolecular forces in solid states.^35b The V–N–N bond angle measured for these complexes is nearly equal to 180°, implying that four atoms, two vanadium atoms, and two nitrogen atoms of the N₂ unit are linearly bonded.

The V–N bond dissociation energy, as shown in Table 1, of these complexes is found to be in the order 1 (D_e = +110.48 kcal/mol) > 2 (D_e = +102.78 kcal/mol) > 3 (D_e = +88.64 kcal/mol) > 4 (D_e = +79.38 kcal/mol), which is expected after observing that the V–N bond length and the dissociation of the N₂ unit is endergonic (Table 2(1)) and follow the same order as that of the V–N bond dissociation energy, i.e., 1 (ΔG = +82.70 kcal/mol) > 2 (ΔG = +67.12 kcal/mol) > 3 (ΔG = +50.92 kcal/mol) > 4 (ΔG = +48.29 kcal/mol). The endergonicity of dissociation of the N₂ unit is the highest in 1, followed by 2 and 3, and the lowest in 4, which indicates that complex 1 is thermodynamically more stable than complexes 2, 3, and 4. The energy gap between FMO (frontier molecular orbitals), i.e., the energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) (Δ_H–L), can also be used to evaluate a system’s electronic stability. For these species, the HOMO–LUMO energy gap follows the order 1 (Δ_H–L = 2.077 eV) > 2 (Δ_H–L = 1.991 eV) > 3 (Δ_H–L = 1.836 eV) > 4 (Δ_H–L = 1.470 eV) suggesting that complex 1 is more electronically stable and less reactive than 2, 3, and 4 based on the HOMO–LUMO energy gap (Scheme 3). This stability order could be owing to the bulky character of the ligands connected to the vanadium metal center. Chelation in a complex is an entropy-friendly process. As we move on from complex 2 to complex 4, the bulkiness of the ligand increases, causing complex 4 to lose stability. As a result, we can deduce that the HOMO–LUMO energy gap of a complex reduces as the bulky nature of the ligand increases.^22,23

Table 1. Dissociation Energy (V−N₂−V Bonds) and Gibbs Free Energy of Dissociation of N₂ in the Complexes at the BP86-D3(BJ)/Def2-TZVPP Level of Theory^a.

complex	dissociation energy, De (kcal/mol)	Gibbs energy, ΔG (kcal/mol)
1	110.48	82.70
2	102.78	67.12
3	88.64	50.92
4	79.38	48.29

^aEnergy is given in kcal/mol.

Table 2. NBO Analysis of Complexes 1–4 at the BP86-D3(BJ)/Def2-TZVPP Level of Theory^a.

complex	bond	ON	polarization and hybridization (%)		WBI	q(N2)
1	V–N σ	1.95	V: 22.50% s(31.6%), p(13.2%) d(55.2%)	N: 77.50% s(63.6%), p(36.4%)	1.70	–0.312
	V–N π	1.74	V: 28.66% p(29.1%), d(70.9%)	N: 71.34% p(99.96%)
	V–N π	1.75	V: 29.13% p(27.4%), d(72.6%)	N: 70.87% p(99.96%)
	N–N σ	1.97	N: 50.22% s(36.3%), p(63.7%)	N: 49.78% s(35.2%), p(64.8%)	1.500
2	V–N σ	1.96	V: 20.5% s(25.3%), p(12.8%), d(61.9%)	N: 79.5% s(63.8%), p(36.2%)	1.67	–0.415
	V–N π	1.80	V: 31.7% p(3.8%), d(96.2%)	N: 68.3% p(100.0%)
	V–N π	1.80	V: 31.7% p(3.8%), d(96.2%)	N: 68.3% p(100.0%)
	N–N σ	1.98	N: 50.0% s(36.1%), p(63.9%)	N: 50.0% s(36.1%), p(63.9%)	1.52
3	V–N σ	1.92	V:15.7% s(25.0%), p(31.4%), d(43.6%)	N: 84.3% s(64.7%), p(35.3%)	1.48	–0.638
	V–N π	1.78	V: 31.5% p(17.0%), d(83.0%)	N: 68.5% p(100.0%)
	V–N π	1.69	V: 22.2% p(36.0%), d(64.0%)	N: 77.8% p(100.0%)
	N–N σ	1.98	N: 50.0% s(34.9%), p(65.1%)	N: 50.0% s(34.9%), p(65.1%)	1.52
4	V–N				1.53	–0.001
	N–N				1.73

^aThere was no solvent media included. Wiberg bond indices (WBI), polarization, hybridization of distinct bonds, occupation number (ON), and partial charges (q).

Scheme 3. Effect on the HOMO–LUMO Energy Gap on Changing the Ligand Coordinated to the Vanadium Metal Center from Complexes 1–4.

To determine the nature of chemical bonding and orbital interaction of these complexes, we used energy and charge density methods such as NBO, QTAIM, and EDA–NOCV to perform quantum chemical computations. Figure 2 shows the orbital images of these complexes from the NBO calculations performed at the BP86-D3(BJ)/Def2-TZVPP level of theory. The Wiberg bond indices (WBI) of the N–N bond for these complexes are in the range of 1.50–1.73 Å, which are significantly smaller than that of the free N₂ molecule (3.03), suggesting the transfer of a significant amount of charge densities from V(III/I) → N₂ π-backdonation. The WBI values of the N–N bonds in these complexes are in the sequence 1 > 2 = 3 > 4, suggesting that complex 1 possesses higher π-backdonation than complexes 2, 3, and 4. The WBI values for corresponding V–N₂ bonds are in the range of 1.48–1.70 (Table 2). These V–N_N2 bonds are significantly polarized toward N₂ due to differences in their electronegativity values. The NBO analyses revealed an accumulation of electron/charge densities (−0.638 to −0.001) on the N₂ units of 1–4, again suggesting that vanadium to dinitrogen (V → N₂) π-backdonations are stronger than V ← N₂ σ-donations. In complex 4, there is a negligible charge accumulation on the N₂ unit. The computed NPA charges are 0.504 (1), 0.711 (2), and 0.885 (3) on each vanadium, and −0.687 and −0.681 on two V atoms of 4.

Figure 2.

NBOs of complexes 1–4 at the BP86-D3(BJ)/Def2-TZVPP level of theory.

The BCP at the (3, −1) topological point (bond critical point; small green sphere) in the Laplacian of the electron density contour plot of these complexes (1–4), shown in Figure 3, is directed away from the center of the bond, indicating that the bond is slightly polarized (Figure 4), which is compatible with the NBO analysis. The V–N_N2 bond is polarized toward the N atom of the N₂ unit, according to NBO analysis, due to higher π-backdonation from vanadium to nitrogen (V → N₂) than σ-donation from nitrogen to vanadium (V → N₂). The electron density is concentrated on the nitrogen atom in these complexes, as demonstrated by the contour plot shown in Figure 3, which is in good agreement with the charge concentration revealed by the NBO analysis. There is a bond parameter, called bond ellipticity (ε = λ₁/λ₂–1), where λ₁ and λ₂ are the eigenvalues of the Hessian matrix, which measure the deviation of the distribution of electron densities from the cylindrical shape as a measure of the bond order. If the bond ellipticity value at BCP (3, −1) ε_BCP is close to zero, then the bond will be either a single or a triple bond due to the cylindrical contours of electron density (ρ(r)) along the bond path, but if the ε_BCP is greater than zero, then the bond will be a double bond. The bond ellipticity value (ε_BCP) for the V–N_N2 bond of these complexes is given in Table 2(3), which lies in the range of 0.000–0.177.

Figure 3.

For V–N–N–V, a contour plot of the Laplacian distribution [∇²ρ(r)] in complexes 1–4 is given. The charge concentration (∇²ρ(r) < 0) is depicted by blue solid lines, while charge depletion (∇²ρ(r) > 0) is depicted by red dotted lines. The small green sphere represents the bond critical point (BCP) along the bond path, and the thick solid blue lines linking the atomic basins depict the zero-flux surface crossing the molecular plane. Nitrogen atoms are symbolized by blue atoms, while vanadium atoms are symbolized by pink atoms.

Figure 4.

MEP surface plots of complexes 1–4 in Cartesian coordinates calculated with DFT at the BP86-D3(BJ)/Def2-TZVPP level of theory. Electronegative regions are shown in various colors. The minimum electrostatic potential (i.e., more electron charge density) is depicted in red, while the maximum electrostatic potential (i.e., less electron charge density) is depicted in dark blue. Yellow and light blue show the intermediate.

Table 2 does not include the occupancy of the V–N_N2 bond and the N–N bond of complex 4 because NBO computations were unable to determine these values as they were lower than the threshold occupancy. Molecular electrostatic potential (MEP) surface plots of these complexes’ positively and negatively charged electrostatic potential are shown in Figure 4.

The triple bond between vanadium and nitrogen in the N₂ unit is confirmed by NBO analysis. Table 3 further shows that the bond ellipticity value (BCP) for these complexes’ N–N bond is very near to zero, indicating the possibility of either a single or a triple bond. The single bond between two nitrogen atoms in N₂ is confirmed by the NBO analysis. The parameter η, which can be computed using the ratio |λ₁|/λ₃, where λ₁ and λ₃ are the eigenvalues of the Hessian matrix, represents the bond type and softness. If the number is less than 1.0, it implies closed-shell interactions, as the electron density shrinks away from the BCP for these interactions. If the value is more than 1, then the bond is said to be covalent. The η value for the V–N bond is in the range of 0.174–0.196, which is less than 1.0, signifying that these bonds are formed via closed-shell interactions. The fact that the value for the N–N bond is greater than 1.0 and falls between 1.172 and 2.496 suggests the covalent nature of the N–N bond. The covalent character of the N–N bond is further shown by the relatively high electron density ρ(r) and total energy density H(r) near the bond critical point (BCP). The positive Laplacian of BCP electron density, ∇²ρ(r), and the relatively lower electron density ρ(r) at BCP (Table 3) of V–N show that charge is ejected from that region, covalency is weak, and electrostatic interactions are present. The negative Laplacian of BCP electron density, ∇²(r), for the N–N bond of these complexes implies shared interaction between two N atoms of the N₂ unit (Table 3). The higher the electron density is at the bond critical point, the stronger the bond. Table 2(3) shows that the V–N_N2 bond strength of the complexes is in the order 1 ≈ 2 > 3 > 4, which is consistent with the V–N bond dissociation energy given in Table 1, and the electron density at BCP for the N–N bond of these complexes is in the order 1 < 2 < 3 < 4, indicating that the N–N bond strength follows the same order as the V–N_N2 bond dissociation energy. The ratio |2G(r)/V(r)| also provides details of the nature of interactions. If the value is less than 1, the interaction is covalent. If the −G(r)/V(r) ratio is greater than 1.0, the interaction is totally noncovalent. Table 3 shows that for these complexes, the ratio |2G(r)/V(r)| for the N–N bond is smaller than 1.0, indicating that the interaction between two N atoms is covalent.

Table 3. Electron Density (ρ(r)), Laplacian (∇²ρ(r)), Total Energy Density (H(r)), Potential Energy Density (V(r)), Kinetic Energy Density (G(r)), Ellipticity (ε_BCP), and Eta (η) Values from AIM Analysis of Complexes 1–4 (Singlet State)^a.

complex	bond	ρ(r)	∇2ρ(r)	H(r)	V(r)	G(r)	εBCP	η	|2G(r)/V(r)|	–G(r)/V(r)
1	V–N	0.181	0.902	–0.074	–0.374	0.300	0.000	0.174	1.604	0.802
	N–N	0.463	–1.267	–0.616	–0.914	0.298	0.000	1.172	0.652	0.326
2	V–N	0.182	0.886	–0.075	–0.372	0.297	0.000	0.183	1.597	0.798
	N–N	0.471	–1.306	–0.633	–0.940	0.307	0.000	2.496	0.653	0.326
3	V–N	0.171	0.864	–0.064	–0.345	0.281	0.129	0.185	1.629	0.814
	N–N	0.474	–1.306	–0.640	–0.953	0.313	0.004	1.186	0.657	0.328
4	V–N	0.157	0.788	–0.052	–0.301	0.249	0.177	0.196	1.654	0.827
	N–N	0.503	–1.452	–0.710	–1.057	0.347	0.010	1.249	0.656	0.328

^aValues are in a.u.

It has been established that NBO and QTAIM often may not be able to accurately provide the nature of chemical bonds and orbital involved in the formation of the chemical bonds of interest. We investigated the V–N₂ bond of complexes 1–4 by EDA–NOCV (energy decomposition analyses coupled with natural orbital for chemical valence)^{50,51,56−60} analyses to estimate the intrinsic interaction energy (ΔE_int) and pairwise orbital interaction energies to shed light on the nature of the metal–dinitrogen bond. EDA–NOCV calculations (one complex (4); see SI) showed that the nature of the bonds between V and N₂ are dative σ/π-bonds rather than electron-sharing σ/π-bonds. The ((L)V)₂ and N₂ fragments prefer to form bonds in their singlet states rather than in quintet states, which has been confirmed from the lower absolute value of orbital interaction energy (ΔE_orb).

L = TIAME (1), (Me₃CCH₂)₃ (2), ((ⁱPr)₂N)₃ (3), {η⁵-(C₅H₄CH₂CH₂NMe₂)}(PhC≡ CPh)(PMe₃) (4).

The interaction energy (ΔE_int) of the complexes 1–4 lies between −172.1 and −204.0 kcal/mol in the order 1 > 2 > 3 > 4, suggesting that the ΔE_int values of V(III)–N₂–V(III) bonds in 1–3 are significantly higher than those of V(I)–N₂–V(I) bonds in 4. Note that 4 possesses an olefin bonded to each V(I) center. The V–N₂ bond dissociation energies (D_e) of 1–4 are in the range of 79–110 kcal/mol having an order of 1 > 2 > 3 > 4 (Table 1). The D_e of the V–N₂−V bond in 1 is higher by 30 kcal/mol that that of 4, which could be partially due to the competitive V–olefin interactions in 4. The interaction energy is larger than the dissociation energy of the V–N₂−V bond (Table 1). The interactions energy (ΔE_int) (−116.9 kcal/mol)^35a of Fe(I)–N₂–Fe(I) bonds³⁶ previously reported singlet diiron–N₂ complex is significantly lower than those of V(III/I)–N₂–V(III/I) bonds in 1–4 (−172.1 and −204.0 kcal/mol). The V → N₂ ← V π-backdonation is four times stronger than V ← N₂ → V σ-donation. V–N₂ bonds are much more covalent in nature than Fe–N₂–Fe bonds.^35a,36

This difference arises due to the preparative energy, which requires fragment preparation energy and additional energy for electronic excitation to the reference spin energy states of all of the fragments. The attractive dispersion energies of two V–N₂ bonds of 1–4 are approximately 2–3% of the total interaction energy. The average Pauli repulsion energy (ΔE_Pauli) of 1–4 is nearly 65% of the overall attractive interaction energies, following the order 1 > 2 > 3 > 4. The contribution due to the electrostatic interaction energies (ΔE_elstat) and orbital interaction energies (ΔE_orb) between 2(L)V(III/I) and N₂ fragments to the overall ΔE_int in 1–4 is in the range of ∼27–33 and ∼63–71%, respectively, suggesting that the latter is 2.5 times higher than the former. The V–N₂ bonds of 1–4 are dominated by covalent interactions, which decrease in the order 1 < 2 < 3 < 4 (Table 4).

Table 4. EDA–NOCV Results at the BP86-D3(BJ)/TZ2P Level of V–N₂ Bonds of (LV)₂(μ-N₂) Complexes 1–4 Using Neutral (LV)₂ in the Electronic Singlet State and Neutral N₂ Fragments in the Electronic Singlet State as Interacting Fragments^a.

energy	interaction	1	2	3	4
ΔEint		–204.0	–204.9	–196.6	–172.1
ΔEPauli		393.29	357.7	339.6	332.2
ΔEdispb		–13.4 (2.2%)	–14.09 (2.5%)	–15.0 (2.8%)	–15.1 (3.0%)
ΔEelstatb		–160.6 (26.9%)	–164.9 (29.3%)	–167.4 (31.2%)	–167.6 (33.2%)
ΔEorbb		–423.3 (70.9%)	–383.6 (68.2%)	–353.8 (66.0%)	–321.4 (63.8%)
ΔEorb(1)c	(LV)2 ← N2(3σg+) σ e– donation	–40.7 (9.6%)	–42.3 (11.0%)	–35.6 (10.1%)	–33.7 (10.5%)
ΔEorb(2)c	(LV)2 ← N2(2σu+) σ e– donation	–26.0 (6.2%)	–26.2 (6.8%)	–23.1 (6.5%)	–22.1 (6.9%)
ΔEorb(3)c	(LV)2 → N2(1πg) π e– backdonation	–173.8 (41.1%)	–154.8 (40.4%)	–150.4 (42.5%)	–154.8 (48.2%)
ΔEorb(4)c	(LV)2 → N2(1πg′) π e– backdonation	–173.8 (41.1%)	–144.7 (37.7%)	–125.3 (35.4%)	–91.3 (28.4%)
ΔEorb(rest)c		–9.0 (2.1%)	–4.1 (3.9%)	19.4 (5.5%)	–19.5 (5.7%)

^aEnergy is given in kcal/mol.

^bValues in the parentheses indicate the contribution to the total attractive interaction ΔE_elstat + ΔE_orb+ ΔE_disp.

^cValues in parentheses show the contribution to the total orbital interaction ΔE_orb..

The breaking of the total orbital interaction energy (ΔE_orb) into pairwise interaction energy identifies the exact orbitals on the fragments and gives pairwise stabilization energy of each set of interactions as (ΔE_orb(n)) (n = 1–4). The symbols 3σ_g⁺, 2σ_u⁺, 1π_g, and 1π_u represent molecular orbitals σ_2p–2p, σ_2s–2s^*, π_2p–2p, and π_2p–2p of N₂, respectively. NOCV analyses of 1–4 revealed that there are two sets of interactions between two (L)V(III/I) and one N₂ fragment: V ← N₂ σ-donation (ΔE_orb(1–2)) and V → N₂ π-backdonation (ΔE_orb(3–4)). The V ← N₂ σ-donation ΔE_orb(1) [(LV)₂ ← N₂(3σ_g⁺)] and ΔE_orb(2) [(LV)₂ ← N₂(2σ_u⁺)] of 1–4 contribute 9–11% and 6–7%, respectively, to the total orbital interaction energy (ΔE_orb). The V → N₂ π-backdonation ΔE_orb(3) [(LV)₂ → N₂(1π_g)] and ΔE_orb(4) [(LV)₂ → N₂(1π_g′)] of 1–4 contribute 40–48% and 28–41%, respectively, to the total orbital interaction energy (ΔE_orb). The V → N₂ π-backdonation (∼75–82%) is nearly four times stronger than V ← N₂ σ-donation (∼16–17%). However, ΔE_orb(3)/ΔE_orb(4) of 1–4 show a synergistic effect [V → N₂ and V ← N₂]. Figures 5–8 show how the deformation densities and related molecular orbitals reveal the direction of the charge flow for complexes 1–4.¹¹⁻¹⁴ The first two orbital terms ΔE_orb(1) and ΔE_orb(2) represent σ-electron donation from HOMO (3σ_g⁺) and HOMO – 2 (2σ_u⁺) of N₂ into vacant d-orbitals (LUMO, LUMO + 1, LUMO + 2 and LUMO + 3) of the vanadium metal center. The last two terms ΔE_orb(3) and ΔE_orb(4) represent the V → N₂ π-backdonations from occupied d-orbitals (HOMO, HOMO – 1) of vanadium metal into the unoccupied degenerate π*-orbital LUMO (1π_g and 1π_g′) of dinitrogen following the order 1 > 2 > 3 > 4. However, the deformation densities (Figures 5–8) suggest the involvement of simultaneous V ← N₂ π-donation (Scheme 4) [from filled bonding π-orbitals of N₂ (1π_u; π_2p–2p) to vacant antibonding orbitals of vanadium], resulting in the increased π-contributions to the total orbital interactions. This observation from EDA–NOCV analysis explains the two π-occupancies from the NBO analysis. The shapes of the orbitals of the ((L)V)₂ fragment in 1 and 3 significantly differ due to the participation of lone pairs of electrons on N atoms in π-bonding (d_vanadium – p_ligand) with the d-orbitals of V(III) centers when they are compared with those of 2. The splitting of the two V–alkyne bonds show that intrinsic interaction energy (ΔE_int) of V–alkyne is significantly higher, suggesting that V → alkyne/V ← alkyne interactions (Figure 9) are stronger than those of the V–N₂ bond of 4 (Table 5). The ΔE_orb(1–4) shows V ← alkyne σ-donation of 4, while the ΔE_orb(5-6) represents V → alkyne π-backdonations, which are four times higher than V ← alkyne σ-donation. These competitive V−alkyne interactions may have reduced the V → N₂ π-backdonations in 4; otherwise, V center of 4 being at the formal oxidation state of +1 will be able to exert N₂ V → alkyne π-backdonations, leading to the lower V−N₂ intrinsic interaction energy (ΔE_int) when it is compared with those of 1−3.

Figure 5.

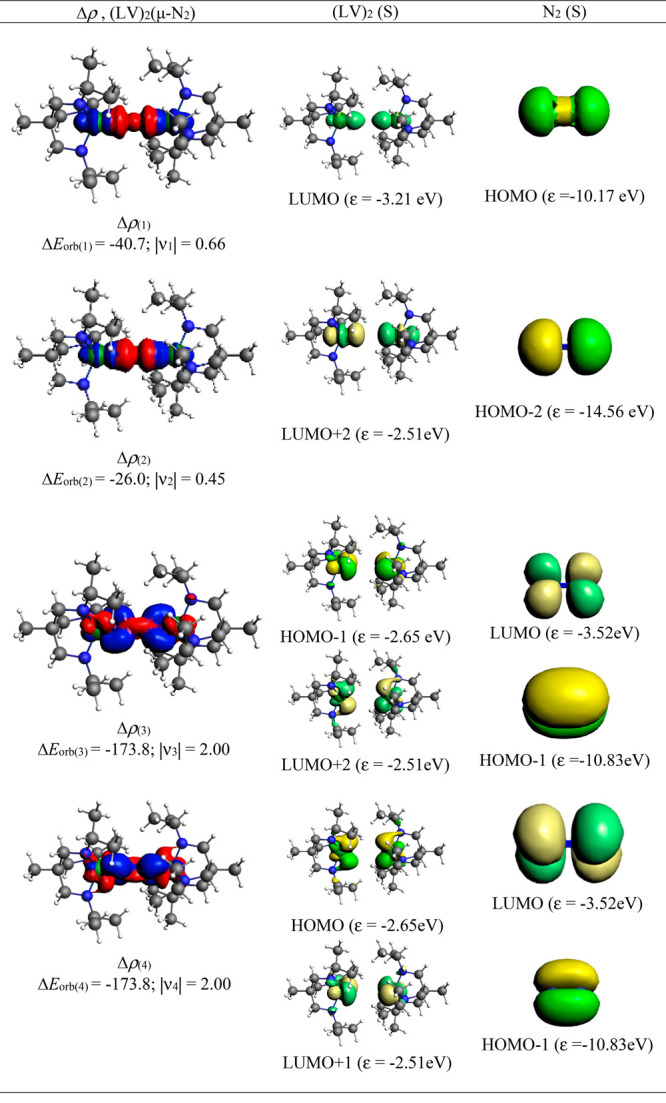
Shape of the deformation densities Δρ_(1)–(4) that correspond to ΔE_orb(1)–(4), and the associated MOs of (LV)₂(μ-N₂) (1), and the fragment orbitals of (LV)₂ and N₂ in the singlet state at the BP86-D3(BJ)/TZ2P level. Isosurface values of 0.003 au for Δρ_(1–4). The size of the charge migration in e is determined by the eigenvalues |ν_n|. The direction of the charge flow of the deformation densities is red → blue.

Figure 8.

Shape of the deformation densities Δρ_(1)–(4) that correspond to ΔE_orb(1)–(4), and the associated MOs of (LV)₂(μ-N₂) (4), and the fragment orbitals of (LV)₂ in the singlet state and N₂ in the singlet state at the BP86-D3(BJ)/TZ2P level. Isosurface values of 0.003 au for Δρ_(1–4). The size of the charge migration in e is determined by the eigenvalues |ν_n|. The direction of the charge flow of the deformation densities is red → blue.

Scheme 4. Orbital Interactions for the Formation of V–N₂–V σ/π-Bonds in Complexes 1–4.

Figure 9.

Shape of the deformation densities Δρ_(1)–(6) that correspond to ΔE_orb(1)–(6), and the associated MOs of L₂V₂(C₂Ph₂)₂ (1-S), and the fragment orbitals of [L₂V₂] in the singlet state and (C₂Ph₂) in the singlet state at the BP86-D3(BJ)/TZ2P level. Isosurface values of 0.001 au for Δρ_(1–6) The eigenvalues ν_n give the size of the charge migration in e. The direction of the charge flow of the deformation densities is red → blue. ΔE_orb energies are given in kcal/mol.

Table 5. EDA–NOCV Results at the BP86-D3(BJ)/TZ2P Level of L₂V₂–(C₂Ph₂)₂ Bonds of (L₂(C₂Ph₂)₂)V Complex 4 Using Neutral (L₂(C₂Ph₂)₂)V in the Singlet State and Neutral C₂Ph₂ in the Singlet State as Fragments^a.

energy	interaction	[L2V2] (S) + (C2Ph2)2 (S) (4)
ΔEint		–239.5
ΔEPauli		401.9
ΔEdispb		–62.3 (9.7%)
ΔEelstatb		–263.1 (41.0%)
ΔEorbb		–316.0 (49.3%)
ΔEorb(1)c	[L2V2] ← (C2Ph2) σ e– donation	–21.8 (7.0%)
ΔEorb(2)c	[L2V2] ← (C2Ph2) σ e– donation	–20.3 (6.4%)
ΔEorb(3)c	[L2V2] ← (C2Ph2) π e– donation	–10.8 (3.4%)
ΔEorb(4)c	[L2V2] ← (C2Ph2) π e– donation	–8.2 (2.6%)
ΔEorb(5)c	[L2V2] → (C2Ph2) π e– backdonation	–118.4 (37.5%)
ΔEorb(6)c	[L2V2] → (C2Ph2) π e– backdonation	–115.1 (36.4%)
ΔEorb(rest)c		–21.4 (6.7%)

^aEnergy is given in kcal/mol.

^bValues in the parentheses show the contribution to the total attractive interaction ΔE_elstat + ΔE_orb + ΔE_disp.

^cValues in parentheses show the contribution to the total orbital interaction ΔE_orb.

Figure 6.

Shape of the deformation densities Δρ_(1)–(4) that correspond to ΔE_orb(1)–(4), and the associated MOs of (LV)₂(μ-N₂) (2), and the fragment orbitals of (LV)₂ and N₂ in the singlet state at the BP86-D3(BJ)/TZ2P level. Isosurface values of 0.003 au for Δρ_(1–4). The size of the charge migration in e is determined by the eigenvalues |ν_n|. The direction of the charge flow of the deformation densities is red → blue.

Figure 7.

Shape of the deformation densities Δρ_(1)–(4) that correspond to ΔE_orb(1)–(4), and the associated MOs of (LV)₂(μ-N₂) (3), and the fragment orbitals of (LV)₂ and N₂ in the singlet state at the BP86-D3(BJ)/TZ2P level. Isosurface values of 0.003 au for Δρ_(1–4). The size of the charge migration in e is determined by the eigenvalues |ν_n|. The direction of the charge flow of the deformation densities is red → blue.

In conclusion, the current study elucidates the bonding and stability of experimentally reported stable vanadium–dinitrogen complexes 1–4 by employing DFT, NBO, QTAIM, and EDA–NOCV techniques. The quantum computations suggest that complexes 1–4 are more stable in the singlet state. The WBI and bond ellipticity values (from QTAIM) correlate well, suggesting a triple bond character between each vanadium and dinitrogen and a single/weak triple bond between two nitrogen atoms of the N₂ unit. There is an accumulation of charge on the N₂ unit, which also signifies that there is a flow of charge from vanadium to nitrogen. The NBO analysis also suggests that the V−N₂−V bonds of complex 1 are stronger than those of 2, 3, and 4. The electronic stability order for the complexes is expected to be in the order 1 > 2 > 3 > 4. The η value suggests that the V–N₂ bond is formed via closed-shell interactions and the N–N bond has a covalent character as expected. The NBO and QTAIM analyses both suggest that the V–N₂ bond is polarized towards N₂ unit due to the charge flow. The EDA–NOCV analysis predicts that the covalent character between vanadium and dinitrogen decreases from complex 1 to complex 4. It also predicts that there is stronger π-backdonation (V → N₂) than the σ-donation (V ← N₂) in all of the complexes and it follows the order 1 > 2 > 3 > 4; in addition, there is simultaneously π-donation from degenerate occupied HOMO – 1 (1π_u and 1π_u′) of dinitrogen to vacant d-orbitals of vanadium, resulting in an increase in the π-contributions to the total orbital interactions. The EDA–NOCV analyses of all four complexes (1–4) revealed that intrinsic interaction energy (ΔE_int) of V–N₂–V bonds (−172 to −204 kcal/mol) is significantly higher than that of the previously reported Fe–N₂–Fe bonds (−116.9 kcal/mol). The V → N₂ ← V π-backdonation is four times stronger than V ← N₂ → V σ-donation. V–N₂ bonds are more covalent in nature than Fe–N₂ bonds. These results are significant from the point of view of vanadium nitrogenase (FeVco) since very little has been studied about FeVco. The N₂ binding site in FeVco has not been confirmed yet. It is worth mentioning that previously reported^37b cyclic Ti₃(CO)₃ was theoretically predicted to have σ+π aromaticity, having the cyclic Ti₃ unit stabilized via entirely π-backdonation from Ti₃ → (CO)₃, which is remarkable.

Computational Method

Geometry optimizations and vibrational frequencies calculations of four previously reported stable dinitrogen-bonded vanadium complexes 1, 2, 3, and 4 in different spin states (singlet (S) and triplet (T)) have been carried out in the gas phase at the BP86-D3(BJ)/Def2-TZVPP³⁸⁻⁴³ level using the Gaussian 16 program package.⁴⁴ The NBO 6.0 program⁴⁵ has been used to perform NBO analysis^46,47 to evaluate natural bond orbitals, partial charges(q) on the atoms, Wiberg bond indices (WBI),⁴⁸ and occupation numbers (ON). The absence of imaginary frequencies ensures the minima on the potential energy surfaces. The nature of V(III/I)–N₂–V(III/I) bonds of all of the species has been analyzed by energy decomposition analysis (EDA)⁴⁹ coupled with natural orbital for chemical valence (NOCV)^50,51 using the ADF 2018.105 program package.⁵⁵ EDA–NOCV calculations have been performed at the BP86-D3(BJ)/TZ2P⁵²⁻⁵⁴ level of theory utilizing the geometries optimized at the BP86-D3(BJ)/Def2-TZVPP level. Generalized gradient approximations (GGAs)³⁸⁻⁴¹ include both the electron density and its gradient at each point. The distribution of electron densities due to differences between the electronegativity values of an atom pair like V–N, C–V, or C–N is hence also more accurately taken care of in the GGA BP86 functional.⁵⁶⁻⁶⁰ The EDA–NOCV method involves the decomposition of the intrinsic interaction energy (ΔE_int) between two fragments into four energy components, as follows

1

where the electrostatic ΔE_elstat term originates from the quasi-classical electrostatic interaction between the unperturbed charge distributions of the prepared fragments; the Pauli repulsion ΔE_Pauli is the energy change associated with the transformation from the superposition of the unperturbed electron densities of the isolated fragments to the wavefunction, which properly obeys the Pauli principle through explicit antisymmetrization and renormalization of the production of the wavefunction. Dispersion interaction, ΔE_disp, is also obtained since we included empirical dispersion with D3(BJ). The orbital term ΔE_orb comes from the mixing of orbitals, charge transfer, and polarization between the isolated fragments. This can be further divided into contributions from each irreducible representation of the point group of an interacting system, as follows

2

The combined EDA–NOCV method is able to partition the total orbital interactions into pairwise contributions of the orbital interactions, which are important in providing a complete picture of the bonding. The charge deformation Δρ_k(r), which comes from the mixing of the orbital pairs ψ_k(r) and ψ_–k(r) of the interacting fragments, gives the magnitude and the shape of the charge flow due to the orbital interactions (eq 3), and the associated orbital energy ΔE_orb presents the amount of orbital energy coming from such interactions (eq 4).

3

4

Readers are further referred to the recent review articles to know more about the EDA–NOCV method and its application.⁵⁶⁻⁶⁰ However, the EDA–NOCV analysis of paramagnetic species is quite challenging.^35,37 N₂ has been considered in singlet and ligand vanadium in different spin states for our EDA–NOCV fragmentations and analyses (see Table S1 in the SI). The charge flow has been shown by deformation densities, red → blue.⁵⁶

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c04472.

• EDA–NOCV results at the BP86-D3(BJ)/TZ2P level of V–N₂ bonds, optimized coordinates for complexes 1–4 at the BP86 level of theory, QTAIM, and optimized coordinates (PDF)

The authors declare no competing financial interest.