Significance
Several strategies for low-cost solar energy conversion/storage systems are based upon redox-active molecules on semiconductor electrodes. Understanding charge transfer between such molecules and semiconductors is crucial for next-generation energy technologies. However, the immense difficulty in untangling the device physics, electrostatics, and chemical kinetics involved in the current-potential responses of these systems has been a long-standing challenge. In this work, we discovered a method for analyzing such data quantitatively and comprehensively. In doing so, we discovered an aspect of these systems that has been overlooked for more than a half century. Specifically, the act of passing one electron between the semiconductor and an adsorbed molecule can affect the ability to move the next electron to/from another adsorbed molecule.
Keywords: electrochemistry, redox adsorbates, semiconductor
Abstract
A detailed framework for modeling and interpreting the data in totality from a cyclic voltammetric measurement of adsorbed redox monolayers on semiconductor electrodes has been developed. A three-layer model consisting of the semiconductor space-charge layer, a surface layer, and an electrolyte layer is presented that articulates the interplay between electrostatic, thermodynamic, and kinetic factors in the electrochemistry of a redox adsorbate on a semiconductor. Expressions are derived that describe the charging and faradaic current densities individually, and an algorithm is demonstrated that allows for the calculation of the total current density in a cyclic voltammetry measurement as a function of changes in the physical properties of the system (e.g., surface recombination, dielectric property of the surface layer, and electrolyte concentration). The most profound point from this analysis is that the faradaic and charging current densities can be coupled. That is, the common assumption that these contributions to the total current are always independent is not accurate. Their interrelation can influence the interpretation of the charge-transfer kinetics under certain experimental conditions. More generally, this work not only fills a long-standing knowledge gap in electrochemistry but also aids practitioners advancing energy conversion/storage strategies based on redox adsorbates on semiconductor electrodes.
The transfer of charge between an adsorbed redox species and a semiconductor electrode (Fig. 1A) is of great fundamental and applied interest in electrochemistry. This process is the key step underpinning two of the most researched directions in semiconductor photoelectrochemistry: dye-sensitized solar cells (1–5) and fuel-forming photoelectrochemical systems that utilize molecular electrocatalysts (6–11). Charge transfer between semiconductors and redox adsorbates is also the essence of several types of nonvolatile electrochemical memory technologies (12–18). Curiously, such charge-transfer reactions are rarely studied by cyclic voltammetry, by far the most popularly employed electroanalytical method by researchers of all disciplines (19).
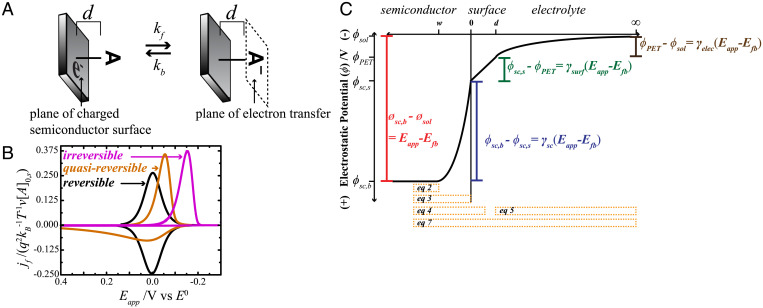
Fig. 1.
A) Simplified depiction of a reducible molecule, A, persistently adsorbed onto a semiconductor surface through a molecular tether of length d. Electron transfer occurs at the plane of electron transfer (PET). (B) Normalized faradaic current vs. applied potential, Eapp, profiles for reversible, quasireversible, and irreversible regimes. (C) A depiction of the electrostatics of the semiconductor–molecule–electrolyte system at an Eapp value that is positive of the flat-band potential, Efb. The total applied potential is partitioned into three regions. The electrostatic potential (ϕ) difference between the semiconductor bulk and surface occurs in the semiconductor space-charge region. The difference in ϕ between the semiconductor surface and the PET occurs in the surface layer. The difference in ϕ between the PET and an infinite distance into the bulk electrolyte occurs in the diffuse layer. The electrostatic potential difference in each region is proportional to the total applied potential by a respective γ-term. The orange boxes denote the Gauss regions that can be defined to generate the respective equations listed in the text.
The general weakness of cyclic voltammetry in the electrochemistry of redox adsorbates on semiconductors is that several different complex phenomena individually and collectively affect and define the current-potential (j-Eapp) data. Semiconductor device physics underpin the delivery of charge carriers to the electrode interface. Electrostatics govern the behavior of both charge carriers and ions at the interface. The reaction rate itself is a function of the forward and back charge-transfer rate constants. Despite interest dating back several decades (20, 21), a single unifying description of how these phenomena influence/dictate the observable data has never been presented.
Some limited strategies to predict and to understand the voltammetric behavior of adsorbed redox monolayers on semiconductor electrodes have been reported sporadically (22–25). These reports relied on a combination of (up to) four oversimplifications in their analyses. One assumption is that the applied potential drops exclusively in the semiconductor (24) (i.e., neglecting the dielectric properties of the rest of the system). Another common assumption is that the faradaic current of a semiconductor electrode is equivalent to the faradaic current of a metal electrode in series with a rectifying diode (22, 24). This supposition obscures how the innate properties of the semiconductor/electrolyte interface affect the reaction. A third assumption is to neglect the possible influence of surface states for simplicity or ascribe all the features to the behavior of surface states (23). A final assumption is to treat the charging current as totally separate from the faradaic current (i.e., the charging of the electrode and the redox reaction of the adsorbate are totally separable). Although this last assumption is inaccurate for the voltammetric responses of redox adsorbates on metal electrodes (26–30), it curiously has never been challenged in semiconductor electrochemistry.
We recently identified an analytical solution for the faradaic current density, jf, in cyclic voltammetric measurements of redox adsorbates on semiconductors that described how the interplay between the rate of the faradaic reaction and the rate of the experiment dictated the magnitude and potential dependence of jf (31). The approach did not require the first two assumptions, instead recognizing that jf was explicitly a function of how the applied potential partitions across the semiconductor space-charge region, the surface tether, and the electrolyte layer. The key insight from that work was that the potential dependence of jf explicitly described the interplay between the charge-transfer kinetics and the timescale of the experiment (Fig. 1B) (31). Experiments where the rates of forward and back charge transfer are much faster than the experiment timescale appear “reversible.” These voltammograms exhibit waves that overlap with the Gaussian shape familiar in the electrochemistry of redox adsorbates on metal electrodes (32). Experiments where the rate of charge transfer and the experiment are comparable exhibit a “quasireversible” character. In this case, neither wave appears Gaussian and each has distinct positions and shapes. Experiments where the charge-transfer rates are much slower than the experiment timescale exhibit “irreversible” behavior (Fig. 1B). That is, the experiment is sufficiently fast that the forward reaction can proceed, but the reverse reaction cannot. However, our previous work did not describe the charging current density, jc, or how to calculate the total current density, j, in a voltammetric measurement.
Eq. 1 describes the starting point for the work here, where j is equal to the sum of jf and jc:
| [1] |
In Eq. 1, both the faradaic and charging components of the total current density are understood as capacitances with units of Farads centimeter−2 multiplied by the experimental voltammetric scan rate (v). Fig. 1A illustrates the reality that the charge densities stored at the surface of the semiconductor, σsc, and at the plane of electron transfer, σPET, are separated only by a distance d. If these charge densities are not entirely screened from each other, the possibility exists that the charge at one location influences the behavior of charge at the other location.
The first derivative term in Eq. 1 involving σPET describes how the charge density at the plane of electron transfer changes with the applied potential as a result of the redox reaction. This “reaction” derivative is a function that is explicitly defined by the voltammetric shapes in Fig. 1B. The derivative of σPET with applied potential defines a charge-transfer (faradaic) reaction capacitance, Cf (i.e., ). The magnitude of Cf reflects the number of redox adsorbates reacting at each potential (31).
The other derivative term in Eq. 1 involves σsc and defines how the charge density at the semiconductor electrode surface changes with the applied potential. This capacitance is explicitly the total measurable electrode capacitance, CT (i.e., ). The magnitude of CT describes the number of electrons needed to change the Fermi level of charge carriers at the electrode surface. A complete understanding of experimental voltammetric data from redox adsorbates on semiconductor electrodes, therefore, explicitly requires understanding how Cf and CT contribute to the total current.
Herein, we present a solution for the electrochemical behavior of redox adsorbates on semiconductor electrodes based on Gauss’s law applied to the space-charge region of the semiconductor, the parallel plate capacitance of the surface layer, and the electrolyte (Fig. 1C). This approach does not rely on discretized, finite-element modeling (33–36). Instead, the functional forms that connect physical parameters are defined. For this purpose, the following information is presented. First, an expression for the charging current density is derived from the application of Gauss’s law. An algorithm that utilizes Eq. 1 and generates the total current measured in a cyclic voltammetry experiment is then detailed. Second, for the more pragmatic readers, the net insights from the algorithm are described through examples of voltammetric j-Eapp responses as a function of band-edge energetics, surface and electrolyte dielectrics, and the presence of surface states. Third, conditions where the charging and faradaic currents are and are not independent are described. The effect of “coupling” between the charging of a semiconductor surface and the faradaic reaction of an adsorbate on the observable j-Eapp data is detailed. For completeness, aspects that are specific to semiconductor electrodes are distinguished and highlighted from those specific to metal (37, 38) electrodes.
Theory
Gauss’s Law Analysis.
Fig. 1C visually describes the electrostatic potential drops across the system depicted in Fig. 1A. In Fig. 1C, the fractional potential drops across the semiconductor space-charge region, the surface, and the electrolyte are denoted as γsc, γsurf, and γelec, respectively. In this picture, the difference between the electrostatic potential at the left and right extremes (i.e., the semiconductor bulk and the electrolyte bulk, respectively) represents the total applied potential. For simplicity, the electrostatic potential of the solution (ϕsol) is assumed equivalent to the point of zero charge of the counterelectrode so that we only need to focus on the semiconductor working electrode to understand the total current-potential behavior. For further ease, the value of ϕsol is set to the point of zero charge of the semiconductor electrode (i.e., the flat-band potential [Efb]). Hence, the applied potential changes only the electrostatic potential of the bulk semiconductor (ϕsc,b) and not ϕsol. These statements are equivalent to , Efb = 0, and , respectively.
The values of γsc, γsurf, and γelec are affected by the charge densities (Coulombs centimeter−2) at each location shown in Fig. 1C (i.e., at the front edge of the space-charge layer [σsc,b], at the surface of the semiconductor electrode [σsc,s], at the plane of electron transfer [σPET], and across the electrolyte [σelec]). Through Gauss’s law (30, 32), the electrostatic potentials throughout the semiconductor/adsorbate/solution interface are defined by the charge densities and the electric fields (i.e., the electrostatic potential drop dropped over the region thickness). In this case, Gauss’s law is applied to the various boxed regions indicated at the bottom of Fig. 1C to determine the values of σsc,b, σsc,s, and σelec. Each charge density is simply the product of the net electric field multiplied by the dielectric constants of that region:
| [2] |
| [3] |
| [4] |
| [5] |
| [6] |
| [7] |
The definitions of all individual terms in these expressions are given in Table 1. Eqs. 5 and 6 for σelec are the Gouy–Chapman description of the potential drop in the diffuse layer of an electrolyte (30).
Table 1.
Summary of symbol definitions and units
| Symbol | Units | Description | Symbol | Units | Description |
|---|---|---|---|---|---|
| β | Angstroms−1 | Tunneling constant | Csc | Farads centimeter-2 |
Differential capacitance of the space-charge layer in the semiconductor |
| b | — | Css | Farads centimeter-2 | Differential capacitance of surface states | |
| d | Centimeters | Length of the tether | Csurf | Farads centimeter-2 | Differential capacitance of the surface layer |
| ε 0 | Farads centimeter−1 | Permittivity of free space | Celec | Farads centimeter-2 | Differential capacitance of the electrolyte |
| εsc,b | — | Relative dielectric constant of the bulk semiconductor | Cf | Farads centimeter-2 | Differential capacitance of the faradaic reaction |
| εsc,scl | — | Relative dielectric constant at the edge of the semiconductor space-charge layer | Eapp | Volts | Applied potential relative to the flat-band potential |
| εsurf | — | Relative dielectric constant of the surface layer | Ecb | Volts | Conduction-band potential for the corresponding value of Eapp |
| εelec | — | Relative dielectric constant of the electrolyte | Ecb,fb | Volts | Conduction-band potential when Eapp = Efb |
| ϕsc,b | Volts | Electrostatic potential in the bulk of the semiconductor | Efb | Volts | Flat-band potential ≡ 0 |
| ϕsc,s | Volts | Electrostatic potential at the surface of the semiconductor | E 0 fb | Volts | Standard potential of redox adsorbate when Eapp = Efb |
| ϕPET | Volts | Electrostatic potential at the plane of electron transfer | Fs | — | Potential-dependent probability function for the integrated charge across the space-charge layer in the semiconductor |
| ϕsol | Volts | Electrostatic potential at the edge of the diffuse layer in solution | fs | — | Potential-dependent probability function for the integrated charge held in surface states |
| Γlower(x,y) | — | Lower incomplete Γ function with arguments x and y | j | Amps centimeter−2 | Total measured current density |
| Γupper(x,y) | — | Upper incomplete Γ function with arguments x and y | jf | Amps centimeter−2 | Faradaic current density |
| κ | Centimeters−1 | Reciprocal thickness of the double layer | jc | Amps centimeter−2 | Charging current density |
| σsc,s | Coulombs centimeter−2 | Charge density at the surface of the semiconductor | kf | Seconds−1 | Forward charge-transfer rate constant |
| σsc,b | Coulombs centimeter−2 | Charge density in the semiconductor bulk | kb | Seconds−1 | Back charge-transfer rate constant |
| σPET | Coulombs centimeter−2 | Charge density at the plane of electron transfer | ket | Centimeters4 second−1 | Electron transfer rate constant from the conduction band |
| σelec | Coulombs centimeter−2 | Charge density in the electrolyte | k 0 | Seconds−1 | Heterogeneous rate constant when Eapp = E0 |
| σscl | Coulombs centimeter−2 | Charge density stored in the semiconductor space-charge layer | kss | Centimeters3 second−1 | Rate constant for filling/emptying surface states |
| σss | Coulombs centimeter−2 | Charge density stored in surface states | m | — | Normalized experimental timescale, |
| χA | — | Fraction of oxidized adsorbed redox species | Nd | Centimeters−3 | No. of dopants per unit volume |
| χA- | — | Fraction of reduced adsorbed redox species | nelec | Molecules centimeters−3 | Concentration of supporting electrolyte |
| γsc | — | Fraction of the time-dependent applied potential dropped across the space-charge layer of the semiconductor | ns, 0 | Centimeters−3 | Majority carrier concentration when Eapp = E0 |
| γsurf | — | Fraction of the time-dependent applied potential dropped across the surface layer | Nss | Centimeters−2 | Density of surface states per unit area |
| γelec | — | Fraction of the time-dependent applied potential dropped across the electrolyte layer | u | — | Normalized applied potential that directly moves the Fermi level |
| [A]s,0 | Molecules centimeter−2 | Total surface concentration of redox species | v | Volts second−1 | Scan rate (+ and − on cathodic and anodic sweeps, respectively) |
| q | Coulombs | Unsigned charge of an electron | Centimeters | Potential-dependent width of semiconductor space-charge layer | |
| kB | Joules Kelvin−1 | Boltzmann's constant | zA | — | Oxidation state of oxidized form of redox species |
| T | Kelvin | Temperature | zA- | — | Oxidation state of reduced form of redox species |
| CT | Farads centimeters-2 |
Total measured capacitance of the semiconductor electrode | z | — | Type of electrolyte (=1 for a 1:1 electrolyte) |
| Z | — |
The assumptions underlying this analysis are that 1) electrolyte ions can access A and A− at the plane of electron transfer but cannot permeate through the surface layer between the electrode surface and the plane of A/A− molecules, that 2) all molecules are treated as point charges without dipoles, and that 3) charge is delocalized across the planes of the surface and electron transfer and not at any other plane closer to/farther from the surface. These assumptions are not necessary to apply Gauss’s law to this system. In addition, these assumptions are not specific to semiconductors. Nevertheless, these assumptions simplify the analysis so that the main points are clear.
A key difference between metal and semiconductor electrodes is the definition of the surface charge density. For a metal electrode, by definition, there is no internal electric field. Instead, Eq. 4 is the only expression that describes the electrode charge density at the surface, and Eq. 3 is omitted (30). However, for a semiconductor electrode, there is an internal electric field that requires inclusion of Eq. 3. The width of the region that experiences the electric field, , is not a constant like d. Instead, is a function of the electrostatic potential difference between the bulk and the surface of the semiconductor, as is the effective dielectric constant at the edge of the semiconductor space-charge layer, . Accordingly, σsc,s has a more nuanced potential dependence than a metal electrode and requires further definition beyond Eq. 3.
Rather than define a complex function for , it is simpler to recognize that σsc,s is the sum of several contributions to the total surface charge density that are each functions of the potential dropped within the semiconductor. For all semiconductors, the charge over the entire space-charge layer (σscl) necessarily contributes to σsc,s. For nearly every known semiconductor interface, there is also the possibility of charge being stored in surface states within the bandgap (σss). Accordingly, Eq. 8 is arguably the better description of σsc,s:
| [8] |
Although σscl and σss are distinct terms, they are also each functions of potential-dependent electron occupancy functions and , respectively, that relate to the electrostatic potential drop in the semiconductor space-charge layer. For uniformly doped semiconductors, the occupancy probability function has different forms depending on the operating condition (i.e., depletion vs. accumulation vs. inversion) (39, 40). Nevertheless, the general relation between σscl and Fs is given in Eq. 9:
| [9] |
Separately, the occupancy probability function depends explicitly on the types and distributions of surface states present at the semiconductor interface. The general relation between σss and fs is shown in Eq. 10:
| [10] |
where Nss describes the total number of surface states.
The value of does not come from Gauss’s law but instead, from the faradaic reaction (Fig. 1A). The potential dependence of the faradaic reaction has been described recently (31), and Eq. 11 is the important result here:
| [11] |
where the total number of redox active molecules on the surface is and the charge states of the oxidized and reduced forms of the redox species are and , respectively. The fraction of the total adsorbed molecules in the oxidized form is . This last term is potential dependent. For metal electrodes, an expression for based on the Butler–Volmer formalism was recently detailed (41) but is not applicable for semiconductor electrodes. Instead, the exact expressions for for a lightly doped semiconductor electrode in depletion or mild accumulation during the forward and reverse sweeps were recently identified in terms of incomplete Γ-functions (31):
| [12a] |
| [12b] |
There are two key features of Eq. 12 that make it highly useful. First, Eq. 12 holds for any scan rate. Second, Eq. 12 relates the faradaic reaction to γsc, γsurf, and γelec through the terms m, Z, and b. Table 1 summarizes the definitions and algebraic relationships of these terms that were derived previously (31). The germane point here is that the combination of Eqs. 11 and 12 yields σPET at any value of Eapp.
With Eqs. 2–12, expressions for Cf and CT are possible through differentiation of each charge density with respect to Eapp:
| [13] |
| [14] |
| [15] |
| [16] |
| [17] |
| [18] |
| [19] |
The right-hand side of each expression in Eqs. 14–18 is the product of a differential capacitance term and a derivative that describes a change in an electrostatic potential drop relative to a change in the total applied potential. Most of these individual differential capacitance terms are familiar to experimentalists. The expressions for the space-charge capacitance (Csc) used here correspond to either depletion or mild accumulation conditions. The functional form of the surface-state capacitance (Css) employed in this work corresponds to monoenergetic surface states located in the middle of the band gap. The Gouy–Chapman model of the diffuse layer was used for electrolyte capacitance (Celec). For compactness, the expressions for these terms are detailed in SI Appendix. Still, the presented framework shown here is general and can accommodate other descriptions of Csc, Css, and Celec if needed. In contrast, the description of the faradaic capacitance, Cf, is central to this work and is described in more detail here.
As defined in Eq. 18, Cf arises from the change in the fraction adsorbates in the oxidized state with changing potential (i.e., ). For redox adsorbates, this derivative is necessarily a function of both the forward and back rate constants (kf and kb, respectively), the scan rate, and itself (38, 42):
| [20] |
To be useful, kf and kb in Eq. 20 must be known. Expressions for kf and kb in terms of γsc, γsurf, and γelec were recently identified (31):
| [21] |
| [22] |
Accordingly, Eq. 23 defines Cf in the following way:
| [23] |
The negative sign arises because the value of decreases as more A is reduced to A−. The combination of Eqs. 12 and 21–23 allows determination of Cf at any potential when γsc, γsurf, and γelec are known.
A potentially confounding aspect of Eqs. 14–18 is the presence of , , and until it is recognized that these derivatives define γsc, γsurf, and γelec:
| [24] |
| [25] |
| [26] |
To be clear, γsc, γsurf, and/or γelec may or may not depend on the applied potential. Neither condition is required for obtaining a real final expression for CT. However, the following restatement of the conservation of charge is a necessary constraint on the values of γsc, γsurf, and γelec:
| [27] |
Although tedious, Eqs. 13–19 and 24–27 can be distilled down into a set of four unique expressions for γsc, γsurf, γelec, and CT in terms of Csc, Css, Csurf, Celec, and Cf. Algebraic compacting of these expressions originating from Gauss’s law results in the following expressions:
| [28] |
| [29] |
| [30] |
| [31] |
Notably, Csc, Css, Celec, and Cf themselves are functions of one or more γ-terms (SI Appendix). Nevertheless, despite the admittedly extensive set of chemical and physical details that underlie these four equations (e.g., the dielectric constants of all materials, solution concentration, surface-state density, etc.), they represent a solvable system of expressions that define both CT and the connection between CT and Cf. That is, only one set of nonzero, real values of γsc, γsurf, γelec, and CT is possible at each applied potential for a given physical semiconductor electrode/adsorbate/electrolyte system. The simplest method to find γsc, γsurf, γelec, and CT is through iterative calculation of Eqs. 28–31 with Eq. 27 as the constraint, which can be performed with any spreadsheet software.
Eqs. 1, 23, and 31 together yield the total current density, j, at every applied potential without assumption or ambiguity. In the following section, these three expressions are used to generate voltametric data for a hypothetical n-type semiconductor electrode operating in the dark and featuring a population of redox adsorbates. However, a few insights from Eq. 31 are highlighted up front.
The first insight is that nothing in Eq. 31 pertains to a specific kinetic condition. That is, Eq. 31 remains valid for charge-transfer reactions that are irreversible as well as those at equilibrium. Hence, the analysis presented here is applicable to all experimental timescales.
The second insight is that a semiconductor electrode can exhibit a markedly different CT than an analogous metal electrode experiencing the exact same surface and diffuse layers because of the influence of “Csc + Css.” The expression for a metal electrode [i.e., ] (27, 30, 43–45) can be recovered from Eq. 31 only when Csc + Css is much larger than the other capacitances. In practice, even for semiconductors in accumulation, Csc will rarely be that large, and Css will only be appreciable if the surface states are present at a significant density and located near midbandgap. Conversely, when Csc + Css is much smaller than the other capacitances, Eq. 31 simplifies to . In this case, the capacitance of the surface layer has no bearing on the electrode behavior.
The third insight is that CT will be equal to one over the sum of the reciprocal capacitances when = 0 (i.e., ). This statement is equivalent to the total capacitance of a network of independent capacitances in series. That is, this “uncoupled” expression will only apply if the faradaic reaction capacitance is negligible. As presented, there are three obvious physical conditions and one implicit physical condition where Eq. 31 would collapse into this uncoupled regime. First, since Cf relates to the change in concentrations of A and A−, Cf is zero when the charge-transfer reaction either has not begun or is completed. Second, decreasing the surface concentration of redox adsorbates would necessarily diminish Cf. Third, increasing the concentration of the electrolyte to augment Celec would make the impact of Cf negligible in Eq. 31. A fourth subtle condition is also possible. Eq. 31 explicitly applies only to a redox adsorbate that is held rigidly within the plane of electron transfer throughout the entire experiment. Any deviation from this condition could possibly minimize Cf. This scenario is not considered here further but may be a property of real systems, where the redox adsorbate has some finite mobility (46–48).
Results
Influence of the Faradaic Reaction on CT.
The consequence of whether the condition = 0 is fulfilled or not on the value of CT is examined in Fig. 2. Fig. 2 presents the calculated values of γsc, γsurf, γelec, and CT at each potential for a lightly doped (Nd = 1017 cm−3) n-type semiconductor electrode with a medium-sized bandgap (Eg = 1.17) operating under strong depletion. In these calculations, the semiconductor electrode features both a single type of surface state at a moderate surface density (i.e., Nss = 1010 cm−2) and a layer of adsorbed redox molecules (i.e., [A]s,0 = 10−9 mol cm−2) and is immersed in a moderately polar electrolyte. To be clear, the nuanced potential dependencies of the γ- and CT terms are a result of the physical parameters of the semiconductor/adsorbate/electrolyte system. SI Appendix, Table S1 summarizes the full list of physical parameters used in the calculations of these plots. For clarity, the x-axis scale is defined with reference to the potential of the conduction-band edge when the applied potential is equal to the flat-band potential, Ecb,fb. The use of Ecb,fb as the reference point is more innate to the semiconductor than using the flat-band potential as the reference since Efb depends directly on the semiconductor dopant density, while Ecb,fb does not. Additionally, Ecb,fb is specified because any applied potential that does not drop across the semiconductor will shift the conduction-band edge from the perspective of an ion in solution.
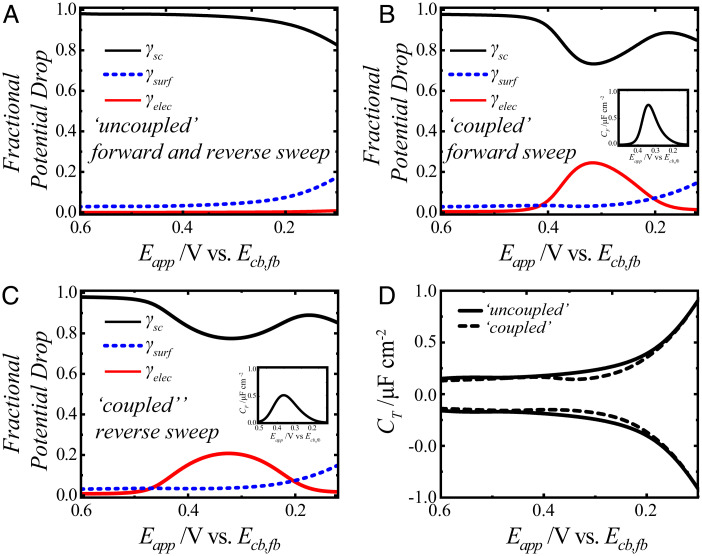
Fig. 2.
(A–C) Plots of the fractional potential drop profiles calculated using Eqs. 28–31 for the (A) uncoupled case with Cf = 0 and for the (B and C) coupled case with Cf ≠ 0. The fractional potential drops are represented as γsc (black solid lines), γsurf (blue dashed lines), and γelec (red solid lines). For the coupled case, the fractional potential drops have to be calculated separately for (B) the forward and (C) the reverse sweeps since the chosen Cf values (Insets) are different in the forward and reverse sweeps. The full list of physical parameters is contained in SI Appendix, Table S1. (D) Calculated total capacitance, CT, vs. applied potential using the specific γsc, γelec, and γsurf values from (solid black lines) A and from (dashed black lines) B and C.
Fig. 2A presents the calculated potential-dependent γsc, γsurf, and γelec values for the uncoupled case [i.e., Eqs. 28–31, where = 0] for both the forward and reverse sweeps of a voltammogram. Fig. 2 B and C presents the potential-dependent γsc, γsurf, and γelec values for the “coupled” case [i.e., Eqs. 28–31, where ≠ 0] during the forward and reverse sweeps, respectively, of a cyclic voltammetric measurement. For the purposes of comparison, the functional forms of arbitrary quasireversible forward and reverse faradaic reactions are used for Cf in Fig. 2 B and C, respectively.
As apparent in Fig. 2 A–C, the fractional potential drops are identical except in the potentials where the faradaic reaction occurs. In this potential range, γsc specifically decreased and γelec increased to maintain the condition described in Eq. 27. The values of γsurf were largely unchanged across the two plots. These changes indicate that when the faradaic reaction is appreciable, the net effect is to shift the applied potential from dropping within the semiconductor space-charge layer to dropping selectively across the diffuse layer.
Fig. 2D presents the difference in CT for the coupled and uncoupled cases. As presented, these plots assume no uncompensated solution resistance. In practice, any uncompensated resistance will result in a finite rise time (32), imparting a rounded appearance at the start of each sweep and possible distortion of the data. Several points are notable in Fig. 2D. First, CT is not constant with potential but instead, slowly increases at progressively more negative potentials because the capacitance of the space-charge layer is the dominating factor in CT. Second, the coupled and uncoupled cases are indistinguishable except in the potential ranges where the faradaic reaction occurs. This point is a natural corollary of the same observation for Fig. 2 A–C. Third, in the potential range where faradaic current flows, the values of CT between the coupled and uncoupled cases are slightly different on the forward and reverse sweeps at the same applied potential. Consequently, the coupling of faradaic and charging current does not appreciably change CT and by extension, the magnitude and profile of the charging current density. Instead, the primary effect of coupling is to alter the operative γsc, γsurf, and γelec values. This point is quite distinct from the case of a metal electrode (27, 29, 30, 44, 49), where it is the change in the charging current that primarily affects the total current.
Because the faradaic reaction depends intimately on γsc, γsurf, and γelec (through Eqs. 21–23), the shape of the total voltammogram will change even if the charging current does not change. To appreciate this point more clearly, the total voltammetric current densities for adsorbed redox molecules in the absence and presence of coupling are described in the following sections.
Voltammetric Responses of a Redox Adsorbate on a Semiconductor without Coupling between the Faradaic and Charging Current Densities.
In this section, the potential dependence of the total (observed) current density in cyclic voltammetry experiments was generated through the outputs of Eqs. 1, 23, and 31. By setting in Eq. 31 to zero, these calculations produced the profiles of cyclic voltammograms where the charging and faradaic currents were uncoupled.
Fig. 3 presents a set of calculated γ-terms and total voltammetric responses (j-Eapp) that share the same base physical properties. Fig. 3A presents the calculated values of γsc, γsurf, and γelec at each potential from the midbandgap out to the conduction-band edge. Fig. 3B presents the voltammograms that would be expected when v = 0.1 V s−1 if the redox adsorbate had a standard potential +0.3 V relative to the conduction-band edge (i.e., E0fb = +0.3 V vs. Ecb,fb). Fig. 3C displays the corresponding voltammograms if the redox adsorbate instead had E0fb = +0.5 V vs. Ecb,fb. These differences between Ecb,fb and E0fb dictated the values of kf and kb at E0fb (i.e., k0). As discussed previously (31), when “k0kBT/qγsc” is much larger than the scan rate, the voltammetry appears reversible. When k0kBT/qγsc is much smaller than the scan rate, the voltammetry is irreversible, where no oxidation wave is observed because the experiment outpaces the reverse reaction. In this case, the values of +0.3 and +0.6 V for E0fb vs. Ecb,fb translate to quasireversible and irreversible voltammograms.
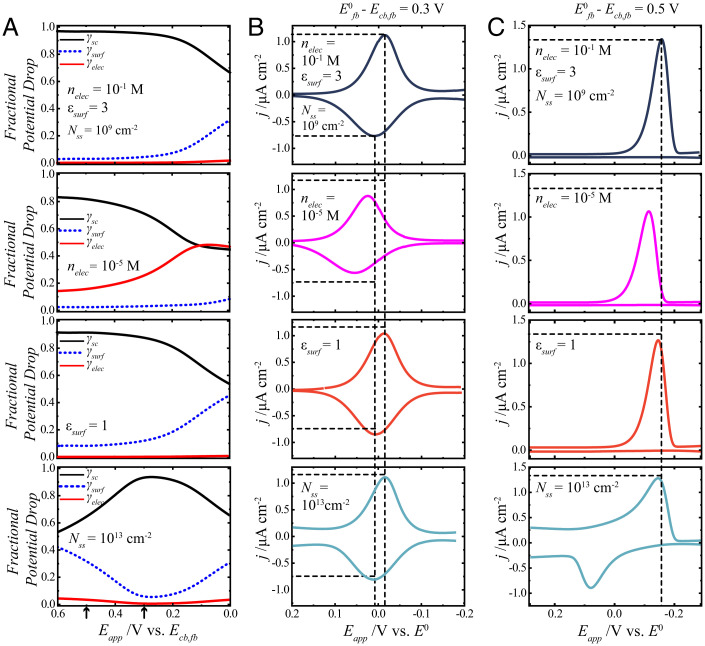
Fig. 3.
Summary of the effect of changing selected physical parameters (nelec, εsurf, and Nss) that define a redox adsorbate on a lightly doped n-type semiconductor electrode without coupling. The full list of calculation values is contained in SI Appendix, Table S1. (A) The fractional potential drops are represented as γsc (black solid lines), γsurf (blue dashed lines), and γelec (red solid lines) as a function of potential. The potential scale is referenced to the conduction band–edge value at the flat band, Ecb,fb. The arrows on the x axis denote the zero point of the voltammograms in C and B, respectively. (B) Calculated j-Eapp responses for a redox adsorbate with a standard potential that is +0.3 V relative to Ecb,fb. These plots use the specific γsc, γelec, and γsurf values from A and B in Eqs. 1, 23, and 31 and assume a scan rate of 0.1 V s−1. (C) Calculated j-Eapp responses for a redox adsorbate with a standard potential that is +0.5 V relative to Ecb,fb. The top row represents a reference condition with the relevant parameter values listed on the plots. The subsequent rows indicate the effect of changing one parameter to the value indicated on each plot.
In Fig. 3, the top row represents a reference condition where three parameters (nelec = 10−1 M, εsurf = 3, and Nss = 1013 cm−2) that dictate the properties of the diffuse, surface, and space-charge layers, respectively, are listed. In each of the lower three rows, a single parameter of interest is changed to show the effect of changing just that parameter on the distribution of the applied potential and the corresponding voltammetric response. The purpose of the vertical and horizontal dashed lines is to facilitate comparison of each voltammogram with the reference condition. The vertical dashed lines in Fig. 3 denote the positions of the peak cathodic and anodic currents for the reference condition. The horizontal dashed lines in Fig. 3 denote the cathodic and anodic peak current densities for the reference condition.
The second row from the top in Fig. 3 summarizes the influence of a change in the diffuse layer by decreasing the concentration of electrolyte to 10−5 M. An electrolyte concentration of 10−5 M specifically changed the magnitudes of γsc and γelec, with less potential dropping within the semiconductor space-charge layer and appreciably more potential dropping in the diffuse layer. For both voltammograms, the consequence of the different profiles of γsc and γelec was not to change the character (i.e., overall shape) of the voltammogram. Instead, the decrease in the electrolyte concentration effected a positive shift in the voltammetric wave positions. In addition, all of the peak currents in both voltammograms were lower than in the reference condition (SI Appendix, Table S2).
The third row from the top in Fig. 3 illustrates the effect of a change in the surface-layer properties by lowering the dielectric constant of the surface layer to its absolute minimum value. This change effected a uniform drop in γsc and increase in γsurf, with γelec essentially the same as in the reference condition. For the voltammogram where E0fb = +0.3 V vs. Ecb,fb, the cathodic and anodic peak positions were nearly unchanged (SI Appendix, Table S2). However, the cathodic peak current density decreased notably, while the anodic peak current density increased. For the voltammogram where E0 = +0.5 V vs. Ecb,fb, cathodic peak position was slightly shifted more positive, and the cathodic peak current density was lowered.
The bottom row in Fig. 3 details the effect from a change in the space-charge region of the semiconductor by increasing the surface-state density to Nss = 1013 cm2 when the surface states are located near the middle of the bandgap. (Additional calculations with other Nss values indicated that no discernable effects could be observed when Nss < 1011 cm2 s−1.) For a trapping/detrapping rate constant of 10−8 cm3 s−1, this value of Nss would correspond to an apparent surface recombination velocity of 105 cm s−1 as compared with 101 cm s−1 for the reference condition. The γsc, γsurf, and γelec profiles were unlike any other condition. At the most positive potentials, γsurf and γsc were comparable. The profiles of both γsurf and γsc possessed either a global maximum or minimum in this potential range. For the voltammogram with E0fb = +0.3 V, the background charging current density was noticeably larger. The peak positions were slightly shifted positive relative to the reference condition. For the voltammogram with E0fb = +0.5 V, the changes were more pronounced. The background charging current was much larger at positive potentials, and the entire voltammogram character changed. A pronounced anodic current was apparent, with an overall voltammetric shape with appreciable peak splitting akin to a metal electrode with a slow charge-transfer rate constant (41).
Voltammetric Responses of a Redox Adsorbate on a Semiconductor with Coupling between the Faradaic and Charging Current Densities.
Additional calculations were performed using the same presented framework and combination of Eqs. 1, 23, and 31 but with deliberately not set to zero. Accordingly, these calculations produced the profiles of voltammograms where the charging and faradaic processes were coupled.
In the coupled case, Cf ideally should be calculated simultaneously with the faradaic current density. Operationally, such calculations are difficult because the capacitive current density is determined iteratively, while the faradaic current density evaluation involves numerical integration. An alternative approach was adopted. Simply, the values of CT, γsc, γsurf, and γelec were first calculated at each applied potential value assuming the uncoupled case. These γsc, γsurf, and γelec values were then used to calculate the initial faradaic current density. This initial faradaic current density was then used to approximate Cf at every potential. CT, γsc, γsurf, and γelec at each potential were then determined again. These new CT, γsc, γsurf, and γelec values were used to recalculate the potential dependence of the faradaic current density. This process was repeated as many times as necessary until the output faradaic current densities were indistinguishable from the input values.
Fig. 4 corntrasts the uncoupled and coupled voltammetric responses for the same lightly doped n-type semiconductor electrode described in Fig. 3. The key difference among the plots in Fig. 4 is that the surface concentration of the redox adsorbates ([A]s,0) is varied, which effects different values of Cf. Fig. 4 A and B shows the profiles of γsc, γsurf, and γelec for the forward and reverse sweeps. Fig. 4C shows the corresponding voltammograms for the case where E0 = +0.3 V vs. Ecb,fb. The current density axes of these voltammograms are normalized by surface concentration so that they can be compared quantitatively. In this case, the top row represents the reference condition where the faradaic and charging current densities are uncoupled. Again, the vertical and horizontal dashed lines assist in comparison of each voltammogram with the reference condition.
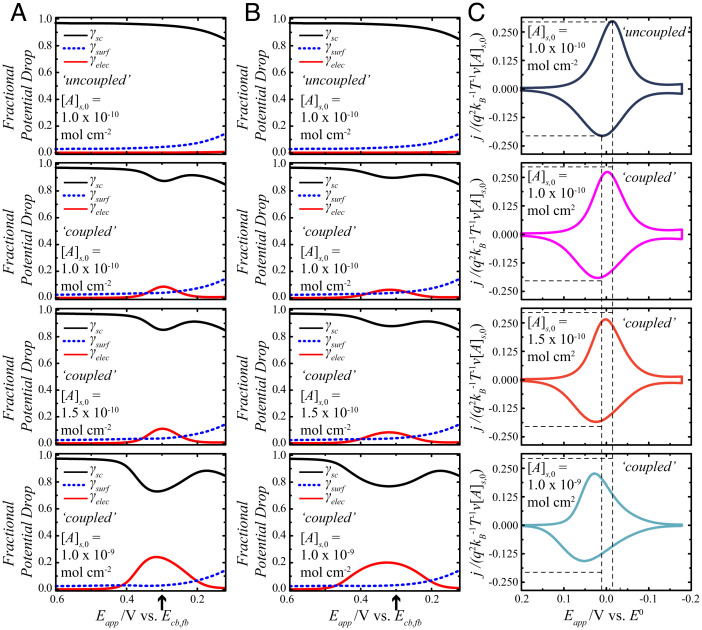
Fig. 4.
Effect of electrostatic coupling between the charges at the planes of the semiconductor electrode and of electron transfer for a redox adsorbate on a lightly doped n-type semiconductor electrode. The full list of calculation values is contained in SI Appendix, Table S1. (A) The fractional potential drops on the forward sweep are represented as γsc (black solid lines), γsurf (blue dashed lines), and γelec (red solid lines) as a function of potential. The potential scale is referenced to the conduction band–edge value at the flat band, Ecb,fb. The arrow on the x axis denotes Eapp = E0. (B) The corresponding fractional potential drops on the reverse sweep are shown as a function of potential. The arrow on the x axis denotes Eapp = E0. (C) Calculated j-Eapp responses for a redox adsorbate with a standard potential that is +0.3 V relative to Ecb,fb. The y axes on these plots are normalized so as to compare directly the current densities at different concentrations of the redox adsorbate, [A]s,0. These plots use the specific γsc, γelec, and γsurf values from A and B in Eqs. 1, 23, and 31 and assume a scan rate of 0.1 V s−1. The top row represents the results for a reference condition where the charges are uncoupled. The subsequent rows indicate the effect of increasing [A]s,0 with electrostatic coupling.
Fig. 4 A and B shows distortions in the potential-dependent profiles of γsc, γsurf, and γelec as [A]s,0 (and correspondingly, Cf) increased. Specifically, a local minimum appeared in the profile of γsc, and a local maximum appeared in the profile of γsurf, although these changes were different for the forward and reverse sweeps. Three obvious changes in the voltammetry (Fig. 4C) were noted from the changes in the profiles of γsc and γsurf. First, the cathodic and anodic peaks shifted progressively toward more positive potentials (SI Appendix, Table S3). Second, both the cathodic and anodic current densities decreased as [A]s,0 increased. Third, the cathodic and anodic waves broadened, exhibiting obvious asymmetry. The cathodic wave attained an almost “diffusive” shape at the highest [A]s,0 value. Further analysis of this asymmetry indicates a connection to the position of E0 relative to the flat-band potential (SI Appendix). Additionally, the peak splitting values (ΔEp) of the voltammograms demonstrating coupled behavior were all equal to or smaller than the ΔEp value for the uncoupled case.
Discussion
There are three primary findings from this work that significantly advance the electrochemistry of redox adsorbates on semiconductors. First, the physical properties of the semiconductor electrode, the surface, and the electrolyte influence the voltammetry in complex but entirely predictable ways. Second, the assumption that electrostatics and faradaic reaction kinetics are always separable at a semiconductor electrode is false. Third, practitioners now have the ability to predict whether the possibility of coupled charging and faradaic current densities is determinant in their systems of interest. These points are discussed individually below.
Influence of Physical Properties on the Form of the Voltammetric Response.
For a semiconductor electrode in depletion or mild accumulation, the dielectric properties of the surface and electrolyte do not grossly change the general character of the voltammetric response. That is, even when their properties translate to small surface- and diffuse-layer capacitances, the j-Eapp data still largely report on the operative heterogeneous charge-transfer kinetics of a lightly doped semiconductor. Even in the absence of exhaustive knowledge on the surface and electrolyte properties, the voltammetric data are useful for estimating interfacial rate constants.
Factors that affect the semiconductor space-charge region do change the general form of the voltammetric response. Clearly, the presence of a high density of surface states renders the voltammetric response similar to the behavior of a metal electrode, even if the governing charge-transfer reaction itself is nothing like that on a metal electrode and there is no charge transfer through the surface states. Simply, for surface states at a sufficiently high density, their capacitance results in a smaller potential drop across the semiconductor space-charge region (i.e., a lower value of γsc). However, this occurrence only significantly alters the voltammetry when the unfilled surface-state position within the bandgap is close to the standard potential of the redox adsorbate. When those quantities are significantly different, the impact of filling surface states on the faradaic current is minimal. The role of surface states can, therefore, be diagnosed by examining the voltammetry of several types of redox adsorbates that differ in their standard potentials. In this way, this work makes clear that invoking exotic mechanisms, like tunneling through the depletion region, may not be warranted when assessing voltammograms that exhibit unexpected “metallic” behavior.
Nevertheless, the exact form of the voltammogram for a redox adsorbate on a semiconductor electrode operating in depletion or mild accumulation is sensitive to the specific features of the semiconductor, the surface, and the electrolyte. Cathodic and anodic voltammetric peak positions and/or peak current densities clearly shift when the properties of the diffuse layer change. Low electrolyte concentrations induce a positive shift in the voltammetry, even past the standard potential. This point should not be construed as an “underpotential” or catalyzed redox event (50). Rather, it reflects the fact that the potential drop across the diffuse layer is sufficient to make the standard potential of the redox adsorbate shift relative to the reference electrode. That is, the standard potential of the redox adsorbate is now a function of the applied potential. The change in peak current values separately reflects what the fractional potential drop is in each layer. When γsc decreases, the cathodic current peak drops. The anodic peak changes because the rate of the back reaction is a function of γsurf and γelec. When γsurf increases, the anodic peak increases. When γelec increases, the anodic peak decreases. Since these features of the voltammetry are influenced by the specific makeup of the system, the simplified analyses methods of plotting peak positions vs. scan rate (i.e., the method of Laviron) (37, 51, 52) are too simplistic. Despite its prevalence in the literature (53–57), this work makes clear that the method of Laviron (37, 51, 52) is not universally appropriate for redox adsorbates on semiconductor electrodes.
The Difference between the Behavior of Redox Adsorbates on Semiconductor and Metal Electrodes.
The analyses presented here argue that coupled behavior is an intrinsic aspect of redox adsorbates on semiconductor electrodes. Although this premise is well established in the voltammetry of metal electrodes (26–30), it has not previously been discussed at any length for semiconductor electrodes. Simply, the concept of coupled charging and faradaic current densities is a profundity in the electrochemistry of semiconductors.
Although the concept of coupled behavior follows naturally from a Gauss’s law analysis of both metal and semiconductor electrodes, there is no potential drop within a metal electrode. For metal electrodes, coupling the charging and faradaic current densities shifts the potential drop from the surface layer to the diffuse layer (30). On a metal electrode, the potential drop across the surface layer is the driving force for the faradaic reaction in both the forward and back reactions. Consequently, more extensive coupling makes it harder to perform both the forward and back reduction/oxidation reactions as the potential moves closer to the point of zero charge (30, 49).
On a semiconductor electrode, coupling of the charging and faradaic currents and its consequences are different. Semiconductor electrodes are more prone to coupled behavior because “(Csc + Css)−1” amplifies the “Cf/Celec” term in Eq. 31. For a semiconductor electrode, the potential drop across the surface layer remains largely unchanged when the faradaic and charging currents are coupled. Instead, coupling shifts the potential drop from the semiconductor space-charge region to the diffuse layer (i.e., γsc decreases, while γelec increases). Because charge transfer at a semiconductor electrode occurs at the band edges rather than at the Fermi level (58), the smaller potential drop across the space-charge region affects the forward reaction. However, a larger potential drop across the electrolyte layer decelerates the back charge-transfer reaction and shifts the voltammetry toward positive potentials. Additionally, since the changes in the forward and back reaction rates are asymmetric, the impacts on the forward and reverse voltammetric waves are not always visually equivalent, as shown in the figures.
Interdependence of Charging and Faradaic Current Densities at a Semiconductor Electrode.
Although the quantitative peak splitting values of Fig. 4 and SI Appendix, Table S3 specifically pertain to the listed conditions, the qualitative changes in voltammetry are generally informative. For example, a shift toward more positive potentials (for reduction reactions) with higher surface loadings of redox adsorbates is consistent with coupling. Additionally, the direction of asymmetry also contains information about the value of the flat-band potential relative to where the faradaic current passes, with the asymmetry directed toward the flat-band potential (SI Appendix). A final point should be made about the sensitivity of cyclic voltammetric data toward redox adsorbate concentration. A persistent observation in the literature is that the voltammetric response is sensitive to the surface concentration (22, 59). Although several factors may contribute to this observation, the analysis here shows that increased coupling of the faradaic and charging currents that occurs at higher surface loadings may also obfuscate the interpretation of charge-transfer kinetics unless taken into account.
The presented treatment should not be construed as sufficiently comprehensive to describe all possible systems. For example, the analysis presupposes no potential drop within the bulk semiconductor. For semiconductors with poor charge-carrier mobilities, this point may not be true. Similarly, complex phenomena, like the flipping of adsorbate orientation during redox reactions (47), ion pairing (45, 49), possible repulsive/attractive interactions between adsorbates at high surface concentrations (60–63), and alternate descriptions of the electrolyte capacitance (44, 63), may be operative for a particular system. Nevertheless, these phenomena are not necessary to appreciate the point of this work (i.e., identifying the connectivity of the charging and faradaic currents). The presented framework represents the simplest baseline from which data can be contextualized for insight on and consideration of what additional detail (if any) is necessary to understand the system at hand.
For illustration, the presented treatment can be applied to existing data in the literature of semiconductor redox adsorbates. A popular system of interest is ferrocene tethered to Si (12). Several reports show asymmetric anodic and cathodic wave shapes across a range of scan rates (12, 14, 15, 57, 64–67). To date, no rationalization of this feature has been provided. However, the presented treatment suggests that the asymmetry denotes coupling between the charges of the ferriceniums and Si surface. Moreover, the slant of the asymmetry suggests that the Si valence band–edge potential is close to (but more positive than) the standard potential of the ferrocene/ferricenium couple. A detailed analysis of some of the reported voltammetry for vinylferrocene bonded to p-type Si, including effects of uncompensated resistance distortion, is the subject of a forthcoming report.
Conclusions
This work applies Gauss’s law analysis to semiconductor electrodes featuring redox adsorbates. Expressions are introduced that describe the total voltammetric responses of semiconductor electrodes operating in depletion. Specifically, Eqs. 1, 23, and 31 describe how the faradaic and charging current densities are a function of the potential drops across the semiconductor space-charge, surface, and electrolyte layers. The discussion presented here makes clear electrochemical features that are unique to semiconductors and absent in metal electrodes. Several global conclusions can be drawn from these expressions.
First, a major understanding afforded here is a proof for how and why the charging and faradaic currents at a semiconductor electrode are natively linked. Specifically, Eq. 31 shows that the act of passing one electron between the semiconductor and an adsorbed molecule at a fixed position necessarily affects the ability to shuttle the next electron to/from another adsorbed molecule. This coupling between the charging and faradaic processes may or may not be advantageous for a particular application, but its possibility is inherent to this type of electrochemistry. This analysis defines general conditions when this should and should not be a dominant phenomenon.
Second, the presented approach does not require finite-difference approximations of differential equations, nor does it rely on forcing the data to conform to the diode equations (68) commonly used in the solid-state device literature. There are two advantages to these features. Solving the network of equations could be performed with a common spreadsheet program, facilitating its use by experimentalists who want to model their data but may not be versed in continuum-level models. Additionally, the presented framework shows the connectivity between the relevant chemistry and physics, providing more intuition on their impact on cyclic voltammetry data without abstraction.
Third, despite the seemingly large number of inputs in the calculation of a voltammogram, all inputs can be experimentally measured and physically identified. That is, this approach does not require “nonideality” factors to justify why the data do not conform to the sum of a metal electrode in series with a diode. Rather, this framework illustrates how physicochemical properties of redox adsorbate and semiconductor contribute to the observed behavior. As a result, it is possible to assess voltammetric data globally rather than just at specific inflection points. If the features of a given system are sufficiently defined/controlled, then the presented analysis could afford a direct way to obtain various types of information from the voltammogram (e.g., the potential difference between the majority carrier-band edge and the standard potential of the redox adsorbate). Voltammetry cannot only be more complementary to other standard methods (e.g., impedance spectroscopy) but may be more suitable for quantitative analysis under certain conditions (e.g., when the electrode capacitance and/or charge-transfer resistance are too small) (69).
Fourth, the present analysis provides a reference point for the interpretation of voltammetry of redox adsorbates on semiconductors. Some of the simplifying assumptions used at the outset of this work (vide supra) may not be suitable for a given system. Still, the presented framework provides both context to justify adding further levels of detail and the process necessary for data interpretation. The algorithm presented here allows for consideration of the entire voltammetric form, which can provide further insight on the semiconductor interface if the relevant physical properties are known. Excessive scrutiny of a single voltammogram in isolation is not recommended since there are clearly several possible system configurations that could produce similar/indistinguishable voltammetric shapes. Analysis of multiple voltammograms in their entirety over a range of different conditions (e.g., scan rates, solvents, ionic strengths, etc.) will yield more confidence in the interpretation. The framework here provides experimentalists guidance for formulating readily testable hypotheses to evaluate a semiconductor/redox adsorbate system.
Materials and Methods
The calculations presented in this work were executed with a custom script written in MATLAB version R2021a (with the Symbolic Math Toolbox and the Parallel Computing Toolbox) and computer workstations with the following specifications: Intel i7-8750H central processing unit running at 2.20 GHz with 8 GB of random access memory running Windows 10. A description of the calculations is presented in SI Appendix.
The numerous physical terms used throughout the analysis presented below are contained and defined in Table 1 for brevity and ease of reading. Additionally, the discussion centers on n-type electrodes, but all points apply to the case where charge transfer of majority carriers occurs through the relevant band edge. Accordingly, this analysis applies equally to the oxidation of redox adsorbates on p-type electrodes in the dark.
Supplementary Material
Acknowledgments
S.M. acknowledges support from Department of Energy Grant DE-SC0006628.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2202395119/-/DCSupplemental.
Data, Materials, and Software Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Grätzel M., Dye-sensitized solar cells. J. Photochem. Photobiol. Photochem. Rev. 4, 145–153 (2003). [Google Scholar]
- 2.Zeng K., et al. , Molecular engineering strategies for fabricating efficient porphyrin-based dye-sensitized solar cells. Energy Environ. Sci. 13, 1617–1657 (2020). [Google Scholar]
- 3.Huaulmé Q., et al. , Photochromic dye-sensitized solar cells with light-driven adjustable optical transmission and power conversion efficiency. Nat. Energy 5, 468–477 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tomar N., Agrawal A., Dhaka V. S., Surolia P. K., Ruthenium complexes based dye sensitized solar cells: Fundamentals and research trends. Sol. Energy 207, 59–76 (2020). [Google Scholar]
- 5.Ren Y., et al. , A stable blue photosensitizer for color palette of dye-sensitized solar cells reaching 12.6% efficiency. J. Am. Chem. Soc. 140, 2405–2408 (2018). [DOI] [PubMed] [Google Scholar]
- 6.Duan L., Tong L., Xu Y., Sun L., Visible light-driven water oxidation—from molecular catalysts to photoelectrochemical cells. Energy Environ. Sci. 4, 3296–3313 (2011). [Google Scholar]
- 7.Alibabaei L., et al. , Solar water splitting in a molecular photoelectrochemical cell. Proc. Natl. Acad. Sci. U.S.A. 110, 20008–20013 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang Y., et al. , Highly efficient photoelectrochemical water splitting with an immobilized molecular Co4 O4 cubane catalyst. Angew. Chem. Int. Ed. Engl. 56, 6911–6915 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Petit J.-P., Chartier P., Beley M., Deville J.-P., Molecular catalysts in photoelectrochemical cells: Study of an efficient system for the selective photoelectroreduction of CO2: p-GaP or p-GaAs/Ni(cyclam)2+, aqueous medium. J. Electroanal. Chem. Interfacial Electrochem. 269, 267–281 (1989). [Google Scholar]
- 10.Niu F., et al. , Hybrid photoelectrochemical water splitting systems: From interface design to system assembly. Adv. Energy Mater. 10, 1900399 (2020). [Google Scholar]
- 11.Klepser B. M., Bartlett B. M., Anchoring a molecular iron catalyst to solar-responsive WO3 improves the rate and selectivity of photoelectrochemical water oxidation. J. Am. Chem. Soc. 136, 1694–1697 (2014). [DOI] [PubMed] [Google Scholar]
- 12.Fabre B., Ferrocene-terminated monolayers covalently bound to hydrogen-terminated silicon surfaces. Toward the development of charge storage and communication devices. Acc. Chem. Res. 43, 1509–1518 (2010). [DOI] [PubMed] [Google Scholar]
- 13.Huang K., et al. , Ferrocene and porphyrin monolayers on Si(100) surfaces: Preparation and effect of linker length on electron transfer. ChemPhysChem 10, 963–971 (2009). [DOI] [PubMed] [Google Scholar]
- 14.Li Q., et al. , Capacitance and conductance characterization of ferrocene-containing self-assembled monolayers on silicon surfaces for memory applications. Appl. Phys. Lett. 81, 1494–1496 (2002). [Google Scholar]
- 15.Li Q., et al. , Electrical characterization of redox-active molecular monolayers on SiO2 for memory applications. Appl. Phys. Lett. 83, 198–200 (2003). [Google Scholar]
- 16.Roth K. M., et al. , Comparison of electron-transfer and charge-retention characteristics of porphyrin-containing self-assembled monolayers designed for molecular information storage. J. Phys. Chem. B 106, 8639–8648 (2002). [Google Scholar]
- 17.Roth K. M., Lindsey J. S., Bocian D. F., Kuhr W. G., Characterization of charge storage in redox-active self-assembled monolayers. Langmuir 18, 4030–4040 (2002). [Google Scholar]
- 18.Vilan A., Cahen D., Chemical modification of semiconductor surfaces for molecular electronics. Chem. Rev. 117, 4624–4666 (2017). [DOI] [PubMed] [Google Scholar]
- 19.Marken F., Neudeck A., Bond A. M., “Cyclic voltammetry” in Electroanalytical Methods: Guide to Experiments and Applications, Scholz F., et al., Eds. (Springer, Berlin, Germany, 2010), pp. 57–106. [Google Scholar]
- 20.Gerischer H., Michel-Beyerle M. E., Rebentrost F., Tributsch H., Sensitization of charge injection into semiconductors with large band gap. Electrochim. Acta 13, 1509–1515 (1968). [Google Scholar]
- 21.Gerischer H., Electrochemical techniques for thie study of photosensitization. Photochem. Photobiol. 16, 243–260 (1972). [Google Scholar]
- 22.Vogel Y. B., Molina A., Gonzalez J., Ciampi S., Quantitative analysis of cyclic voltammetry of redox monolayers adsorbed on semiconductors: Isolating electrode kinetics, lateral interactions, and diode currents. Anal. Chem. 91, 5929–5937 (2019). [DOI] [PubMed] [Google Scholar]
- 23.Bertoluzzi L., Badia-Bou L., Fabregat-Santiago F., Gimenez S., Bisquert J., Interpretation of cyclic voltammetry measurements of thin semiconductor films for solar fuel applications. J. Phys. Chem. Lett. 4, 1334–1339 (2013). [DOI] [PubMed] [Google Scholar]
- 24.Santangelo P. G., Miskelly G. M., Lewis N. S., Cyclic voltammetry at semiconductor photoelectrodes. 1. Ideal surface-attached redox couples with ideal semiconductor behavior. J. Phys. Chem. 92, 6359–6367 (1988). [Google Scholar]
- 25.Vogel Y. B., et al. , Reproducible flaws unveil electrostatic aspects of semiconductor electrochemistry. Nat. Commun. 8, 2066 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Creager S. E., Rowe G. K., Solvent and double-layer effects on redox reactions in self-assembled monolayers of ferrocenyl—alkanethiolates on gold. J. Electroanal. Chem. (Lausanne) 420, 291–299 (1997). [Google Scholar]
- 27.Fawcett W. R., Discreteness-of-charge effects at an electrode covered with a self-assembled monolayer containing a simple redox couple. J. Electroanal. Chem. (Lausanne) 378, 117–124 (1994). [Google Scholar]
- 28.Forster R. J., Faulkner L. R., Electrochemistry of spontaneously adsorbed monolayers. Equilibrium properties and fundamental electron transfer characteristics. J. Am. Chem. Soc. 116, 5444–5452 (1994). [Google Scholar]
- 29.Honeychurch M. J., Effect of the interfacial potential distribution on the measurement of the rate constant for electron transfer between electrodes and redox adsorbates. Langmuir 14, 6291–6296 (1998). [Google Scholar]
- 30.Smith C. P., Dwhite H. S., Theory of the interfacial potential distribution and reversible voltammetric response of electrodes coated with electroactive molecular films. Anal. Chem. 64, 2398–2405 (1992). [DOI] [PubMed] [Google Scholar]
- 31.Waelder J., Vasquez R., Liu Y., Maldonado S., A description of the faradaic current in cyclic voltammetry of adsorbed redox species on semiconductor electrodes. J. Am. Chem. Soc. 144, 6410–6419 (2022). [DOI] [PubMed] [Google Scholar]
- 32.Bard A. J., Faulkner L. R., Electrochemical Methods: Fundamentals and Applications (Wiley, New York, NY, ed. 2, 2001). [Google Scholar]
- 33.Iqbal A., Bevan K. H., Simultaneously solving the photovoltage and photocurrent at semiconductor–liquid interfaces. J. Phys. Chem. C 122, 30–43 (2018). [Google Scholar]
- 34.Anz S. J., Krüger O., Lewis N. S., Gajewski H., Conditions under which heterogeneous charge-transfer rate constants can be extracted from transient photoluminescence decay data of semiconductor/liquid contacts as determined by two-dimensional transport modeling. J. Phys. Chem. B 102, 5625–5640 (1998). [Google Scholar]
- 35.Anz S. J., Lewis N. S., Simulations of the steady-state current density vs potential characteristics of semiconducting electrodes. J. Phys. Chem. B 103, 3908–3915 (1999). [Google Scholar]
- 36.Mills T. J., Lin F., Boettcher S. W., Theory and simulations of electrocatalyst-coated semiconductor electrodes for solar water splitting. Phys. Rev. Lett. 112, 148304 (2014). [DOI] [PubMed] [Google Scholar]
- 37.Laviron E., General expression of the linear potential sweep voltammogram in the case of diffusionless electrochemical systems. J. Electroanal. Chem. 101, 19–28 (1979). [Google Scholar]
- 38.Myland J. C., Oldham K. B., Quasireversible cyclic voltammetry of a surface confined redox system: A mathematical treatment. Electrochem. Commun. 7, 282–287 (2005). [Google Scholar]
- 39.Goldstein M., Semiconductor Surfaces (John Wiley & Sons, Inc., New York, NY, 1965). [Google Scholar]
- 40.Lancaster M., AlQurashi A., Selvakumar C. R., Maldonado S., Quantitative analysis of semiconductor electrode voltammetry: A theoretical and operational framework for semiconductor ultramicroelectrodes. J. Phys. Chem. C 124, 5021–5035 (2020). [Google Scholar]
- 41.Waelder J., Maldonado S., Beyond the laviron method: A new mathematical treatment for analyzing the faradaic current in reversible, quasi-reversible, and irreversible cyclic voltammetry of adsorbed redox species. Anal. Chem. 93, 12672–12681 (2021). [DOI] [PubMed] [Google Scholar]
- 42.Honeychurch M. J., Rechnitz G. A., Voltammetry of adsorbed molecules. Part 2. Irreversible redox systems. Electroanalysis 10, 453–457 (1998). [Google Scholar]
- 43.Honeychurch M. J., Rechnitz G. A., Voltammetry of adsorbed molecules. Part 1. Reversible redox systems. Electroanalysis 10, 285–293 (1998). [Google Scholar]
- 44.Andreu R., Calvente J. J., Fawcett W. R., Molero M., Discreteness of charge and ion association effects on electroactive self-assembled monolayers. Langmuir 13, 5189–5196 (1997). [Google Scholar]
- 45.Ohtani M., Kuwabata S., Yoneyama H., Voltammetric response accompanied by inclusion of ion pairs and triple ion formation of electrodes coated with an electroactive monolayer film. Anal. Chem. 69, 1045–1053 (1997). [Google Scholar]
- 46.Ruther R. E., Cui Q., Hamers R. J., Conformational disorder enhances electron transfer through alkyl monolayers: Ferrocene on conductive diamond. J. Am. Chem. Soc. 135, 5751–5761 (2013). [DOI] [PubMed] [Google Scholar]
- 47.Sampaio R. N., Li G., Meyer G. J., Flipping molecules over on TiO2 surfaces with light and electric fields. J. Am. Chem. Soc. 141, 13898–13904 (2019). [DOI] [PubMed] [Google Scholar]
- 48.Garín C., León A., Pacheco M., Riveros G., Electronic transfer mechanism in self-assembled monolayers of silicon. J. Solid State Electrochem. 23, 3099–3106 (2019). [Google Scholar]
- 49.Andreu R., Calvente J. J., Fawcett W. R., Molero M., Role of ion pairing in double-layer effects at self-assembled monolayers containing a simple redox couple. J. Phys. Chem. B 101, 2884–2894 (1997). [Google Scholar]
- 50.Barman K., et al. , Voltage-driven molecular catalysis of electrochemical reactions. J. Am. Chem. Soc. 143, 17344–17347 (2021). [DOI] [PubMed] [Google Scholar]
- 51.Laviron E., A.C. polarography and faradaic impedance of strongly adsorbed electroactive species. Part II. Theoretical study of a quasi-reversible reaction in the case of a Frumkin isotherm. J. Electroanal. Chem. 105, 25–34 (1979). [Google Scholar]
- 52.Laviron E., A.C. polarography and faradaic impedance of strongly adsorbed electroactive species. Part I. Theoretical and experimental study of a quasi-reversible reaction in the case of a Langmuir isotherm. J. Electroanal. Chem. 97, 135–149 (1979). [Google Scholar]
- 53.Fabre B., Functionalization of oxide-free silicon surfaces with redox-active assemblies. Chem. Rev. 116, 4808 (2016). [DOI] [PubMed] [Google Scholar]
- 54.Lattimer J. R. C., Brunschwig B. S., Lewis N. S., Gray H. B., Redox properties of mixed methyl/vinylferrocenyl monolayers on Si(111) surfaces. J. Phys. Chem. C 117, 27012–27022 (2013). [Google Scholar]
- 55.Bellec N., Faucheux A., Hauquier F., Lorcy D., Fabre B., Redox-active organic monolayers deposited on silicon surfaces for the fabrication of molecular scale devices. Int. J. Nanotechnol. 5, 741–756 (2008). [Google Scholar]
- 56.Ahmad S. A. A., Ciampi S., Parker S. G., Gonçales V. R., Gooding J. J., Forming ferrocenyl self-assembled monolayers on Si(100) electrodes with different alkyl chain lengths for electron transfer studies. ChemElectroChem 6, 211–220 (2019). [Google Scholar]
- 57.Decker F., et al. , Electrochemical reversibility of vinylferrocene monolayers covalently attached on H-terminated p-Si(100). J. Phys. Chem. B 110, 7374–7379 (2006). [DOI] [PubMed] [Google Scholar]
- 58.Lancaster M., MacInnes M., Vasquez R., Maldonado S., Springer Handbook of Inorganic Photochemistry, Bahnemann D., Patrocinio A. O., Eds. (Springer, Berlin, Germany, 2022). [Google Scholar]
- 59.Ciampi S., et al. , The impact of surface coverage on the kinetics of electron transfer through redox monolayers on a silicon electrode surface. Electrochim. Acta 186, 216–222 (2015). [Google Scholar]
- 60.Fawcett W. R., Fedurco M., Kovacova Z., Double layer effects at molecular films containing acid/base groups. Langmuir 10, 2403–2408 (1994). [Google Scholar]
- 61.Macdonald J. R., Barlow C. A., Theory of work‐function change on adsorption of polarizable ions. J. Chem. Phys. 44, 202–206 (1966). [Google Scholar]
- 62.MacDonald J. R., Barlow C. A., Penetration parameter for an adsorbed layer of polarizable ions. J. Appl. Phys. 37, 3471–3482 (1966). [Google Scholar]
- 63.Calvente J. J., Andreu R., Molero M., López-Pérez G., Domínguez M., Influence of spatial redox distribution on the electrochemical behavior of electroactive self-assembled monolayers. J. Phys. Chem. B 105, 9557–9568 (2001). [Google Scholar]
- 64.Fontanesi C., et al. , Redox-active ferrocene grafted on H-terminated Si(111): Electrochemical characterization of the charge transport mechanism and dynamics. Sci. Rep. 9, 8735 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Dalchiele E. A., et al. , XPS and electrochemical studies of ferrocene derivatives anchored on n- and p-Si(100) by Si–O or Si–C bonds. J. Electroanal. Chem. (Lausanne) 579, 133–142 (2005). [Google Scholar]
- 66.Sano H., et al. , Formation of uniform ferrocenyl-terminated monolayer covalently bonded to Si using reaction of hydrogen-terminated Si(111) surface with vinylferrocene/n-decane solution by visible-light excitation. J. Colloid Interface Sci. 361, 259–269 (2011). [DOI] [PubMed] [Google Scholar]
- 67.Marrani A. G., et al. , Functionalization of Si(100) with ferrocene derivatives via “click” chemistry. Electrochim. Acta 53, 3903–3909 (2008). [Google Scholar]
- 68.Herrera M. U., Ichii T., Murase K., Sugimura H., Use of diode analogy in explaining the voltammetric characteristics of immobilized ferrocenyl moieties on a silicon surface. ChemElectroChem 2, 68–72 (2015). [Google Scholar]
- 69.Farjardo A. M., Lewis N. S., Rate constants for charge transfer across semiconductor-liquid interfaces. Science 274, 969–972 (1996). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.