Mechanism of temperature-induced asymmetric swelling and shrinking kinetics in self-healing hydrogels

Significance

Self-healing hydrogels are increasingly finding use in diverse applications, such as artificial biological tissues, soft machines, and biosensors. Understanding the physical principle that governs the swelling and shrinking kinetics of self-healing hydrogels is indispensable for their applications but quite limited. Here, we show that the shrinking and swelling kinetics of self-healing hydrogels could be intrinsically asymmetric. The swelling kinetics is governed by the permanently crosslinked network structure, whereas the shrinking kinetics is governed by structure frustration, formed due to large differences in the heat and solvent diffusions. This study provides a useful step toward elucidating the essential physics governing the swelling and shrinking of self-healing hydrogels upon temperature change.

Abstract

Understanding the physical principle that governs the stimuli-induced swelling and shrinking kinetics of hydrogels is indispensable for their applications. Here, we show that the shrinking and swelling kinetics of self-healing hydrogels could be intrinsically asymmetric. The structure frustration, formed by the large difference in the heat and solvent diffusions, remarkably slows down the shrinking kinetics. The plateau modulus of viscoelastic gels is found to be a key parameter governing the formation of structure frustration and, in turn, the asymmetric swelling and shrinking kinetics. This work provides fundamental understandings on the temperature-triggered transient structure formation in self-healing hydrogels. Our findings will find broad use in diverse applications of self-healing hydrogels, where cooperative diffusion of water and gel network is involved. Our findings should also give insight into the molecular diffusion in biological systems that possess macromolecular crowding environments similar to self-healing hydrogels.

Swelling and shrinking caused by solvent uptake and release in response to environmental changes are among the most fundamental properties of polymer gels (1, 2). Understanding the physical principle governing the swelling and shrinking kinetics of gels is indispensable for their applications as stimuli-responsive materials (3–5). It further provides an important insight into molecular diffusion in biological systems that have macromolecular crowding environments similar to gels (6, 7). The equilibrium swelling volume of gels is governed by thermodynamics, whereas the kinetics of the volume change is governed by the cooperative diffusion process (8–11). In many cases, environmental stimuli induce structural changes in gels governed by thermodynamics, which result in rich and complex kinetics of volume change through thermodynamic–kinetic coupling (12–14). One typical example is found in thermally sensitive poly(N-isopropylacrylamide) (PNiPAAm) hydrogels having low critical solution temperature (LCST) (15, 16). The shrinking kinetics of the PNiPAAm hydrogels above the LCST is much slower than the swelling kinetics below the LCST owing to the volume phase transition (14).

In recent decades, self-healing hydrogels having dynamic bonds, such as ionic bonds, hydrogen bonds, or hydrophobic bonds, have been developed (17–22). The dynamic bonds are reversible, endowing these gels with many unique properties, such as self-healing ability, viscoelasticity, and high toughness. In the presence of abundant reversible dynamic bonds, self-healing hydrogels have a macromolecular crowding environment with a much lower equilibrium water content (typically ∼50 wt.%) than conventional chemical gels (typically >90 wt.%) (23–25). These gels typically have a monotonous and weak temperature dependence of swellability in water and do not exhibit a volume phase transition at specific temperatures (26, 27).

Recently, we discovered that some self-healing hydrogels containing dynamic bonds, for example, polyampholyte (PA) hydrogels synthesized from different cationic and anionic monomer combinations and hydrogen bonding hydrogel synthesized from 2-ureidoethyl methacrylate and methacrylic acid (27), show strongly asymmetric swelling–shrinking kinetics with temperature change: when heated they swell fast but shrink very slowly when cooled abruptly (26, 27). In accompaniment with the slow shrinking, these gels show cooling-induced turbidity change. The transparent sample immediately transitions to a cloudy state after abrupt cooling and then slowly regains its transparency when reaching the swelling equilibrium. This phenomenon is observed over a wide range of temperatures whenever a cooling temperature jump larger than several degrees is provided. Based on this unique phenomenon, several promising applications have been proposed, including dynamic memory-forgetting devices, thermal imaging, security paper, and prolonged drug delivery (26, 27). Exploring the mechanism underlying this unique phenomenon will significantly merit the application of this class of hydrogels.

Here, we focus on the mechanism behind the asymmetric swelling–shrinking kinetics of self-healing hydrogels. We assume that the structure frustration formed during sudden cooling, exhibited as a transient turbidity change, was responsible for the slow shrinking kinetics. Because the self-healing gels studied are able to absorb more water at high temperatures, abrupt cooling results in, thermodynamically, an excess amount of water molecules in the gels. Owing to the sample size–dependent slow diffusion process, these water molecules are temporarily entrapped in the gels. Consequently, abrupt cooling results in the local aggregation of excess water molecules to form a frustrated structure (26, 27). To verify this hypothesis, in this work, we tune the structure frustration and investigate its role in the swelling and shrinking behavior of self-healing hydrogels. We assume that increasing the elasticity of the polymer network should suppress structure frustration and, thereby, the asymmetric swelling–shrinking kinetics. This is because the structure frustration in self-healing gels is essentially a nonequilibrium liquid–liquid microphase separation, governed by the competition between the mixing free energy gain of the polymer and solvent and the elastic energy penalty by introducing microphase separation (28–30).

In this study, we tune the elasticity of gels by changing the permanent cross-linking density. First, we study its effect on the structure frustration and then compare the cooperative diffusion constants of swelling and shrinking of the gels at the same temperature and its correlation with the structure frustration, after which we study the heating history (temperature and time) effects on the cooperative diffusion constant of shrinking. Finally, we compare the activation energies of the cooperative diffusion constants of swelling and shrinking.

Structure Frustration Modulated by Gel Elasticity

We use hydrogels composed of PA as a model system. PA gels were synthesized by radical polymerization of anionic monomer, sodium p-styrenesulfonate (NaSS), and cationic monomer, methyl chloride quarternized N,N-dimethylamino ethyl acrylate (DMAEA-Q), in a concentrated aqueous solution at the charge-balanced point (31–35). The gels, which have an abundance of ionic bonds, are permanently cross-linked by a chemical cross-linker or entrapped entanglement. A previous study has shown that the permanent cross-linking density, which determines the plateau modulus of viscoelastic gels, can be tuned by the chemical cross-linker concentration, C_MBAA, and total monomer concentration, C_m, at sample synthesis (34). Increasing C_m of PA gel brings more topological entanglements, which act as equivalent chemical cross-linking. In this study, the samples are coded as PA-C_m-C_MBAA. We prepared two sets of samples to change the elasticity: one is PA-2.5-C_MBAA, where C_m is fixed at 2.5 M and C_MBAA is varied from 0 to 5 mol% relative to C_m, and the other is PA-C_m-0.1, where C_m is varied from 1.6 to 2.8 M and C_MBAA is fixed at 0.1 mol%. Note here the PA gel network can be formed without MBAA, due to the long lifetime of entanglements. The relaxation dynamics of entanglements is significantly delayed by high density and high strength of ionic bonds, and thus, these entanglements act as permanent crosslinking in the observation time window. Water-equilibrated gels were used in the present study. The equilibrated water content of these gels at 25 °C was ∼45 wt.%, showing weak dependence on C_MBAA and C_m (SI Appendix, Figs. S1 and S2, (34)). Disk-shaped samples with a diameter of 50 mm and a thickness in the range from 1.1 to 1.3 mm at room temperature were used.

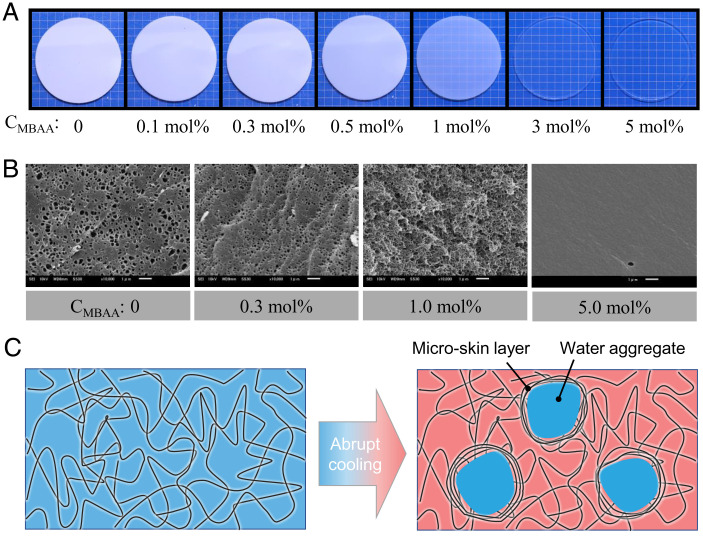
The PA-2.5-C_MBAA gels in the equilibrium swelling state are transparent, except for the sample with C_MBAA = 0, because of the relatively large phase-separation structure (34). These gels were first heated at 80 °C in a water bath for 2 h to reach equilibrium and then moved to a 25 °C water bath for shrinking. Fig. 1A and SI Appendix, Fig. S3 show the optical images of PA-2.5-C_MBAA gels after being moved to a 25 °C water bath for 1 min. For a C_MBAA smaller than 0.5 mol%, the gels exhibited a turbid appearance, indicating structural frustration upon cooling. When the C_MBAA is 1.0 mol%, the gel becomes semitransparent, indicating the suppression of structure frustration by the increase in chemical cross-linking density. When the C_MBAA equals or exceeds 3.0 mol%, the gels maintain the transparency upon cooling, implying that the structure frustration is fully suppressed.

Fig. 1.

Structure frustration kinetically induced by abrupt cooling of self-healing gels and the effect of gel elasticity. (A) Optical images showing the gels 1 min after abrupt cooling from 80 to 25 °C. The gels used here were PA-2.5-C_MBAA series. Except for PA-2.5-0.0, the gels were transparent at their equilibrium state in the temperature range studied. Background lattice: 5 mm. (B) Corresponding scanning electron microscopy (SEM) images of gels with several selected C_MBAA. Scale bars: 1 μm. (C) Schematic illustration to show structure frustration upon abrupt cooling in self-healing gels. The hydration of the polymer network decreases at low temperatures, and the extra water molecules are expelled to form aggregates (frustrated structure). The structure frustration can be suppressed and even prohibited by increasing the elastic constraint of the polymer network.

Fig. 1B and SI Appendix, Fig. S4 show the scanning electron microscopy (SEM) images of the cut cross-sections of PA-2.5-C_MBAA gels with four representative C_MBAA, 0, 0.3, 1.0, and 5.0 mol%, respectively, upon cooling from 80 to 25 °C for 1 min. For gels with a C_MBAA smaller than 1.0 mol%, the SEM images show a porous structure, further confirming the presence of structure frustration. For the gel with a C_MBAA of 5.0 mol%, the SEM image shows a smooth appearance, suggesting the absence of structure frustration. The structure change observed by SEM is well consistent with the transparency change in optical measurement. The pore size, d, can be estimated from the SEM images, which decreases from ∼500–100 nm by increasing the C_MBAA from 0.0 to 1.0 mol%. It should be noted that the SEM results showed the trend of the structure size change rather than the accurate structure size.

To directly correlate the elasticity of the gels with the structure frustration, we further determine the shear modulus of the PA gels. As PA gels are highly viscoelastic, we measured the frequency dependence of the storage modulus (shear modulus) $G\prime$ and loss modulus $G″$ (Fig. 2A and SI Appendix, Figs. S5–S7). The plateau modulus at low frequency, $G{\prime }_{\text{pla}}$, is considered as the shear modulus from the permanently cross-linked polymer network, owing to chemical cross-linking and trapped entanglements (34).

Fig. 2.

Competition between the interfacial energy and elastic constraint determines the pore size. (A) An example of linear dynamic behavior of a PA-2.5-0.1 gel at 25 °C to obtain the plateau modulus, $G{\prime }_{\text{pla}}$. The master curves of the storage modulus $G\prime$, loss modulus $G″$, and loss factor tan δ were constructed from the frequency sweep data at different temperatures from 8 to 88 °C, following the principle of time−temperature superposition (36). (B) The product $G{\prime }_{\text{pla}}$ × d versus $G{\prime }_{\text{pla}}$. The pore size, d, was obtained from the SEM images in Fig. 1B.

Dimensional considerations suggest that the pore size of water aggregates, $d$, should take the form $d\sim \frac{\gamma }{G{\prime }_{\text{pla}}}$. The interfacial energy $\gamma$ favors to maximize the pore size. On the contrary, the elastic constraint favors to minimize the pore size. We plotted the product $G{\prime }_{\text{pla}}$ × d as a function of $G{\prime }_{\text{pla}}$ (Fig. 2B). $G{\prime }_{\text{pla}}$ × d is near constant, confirming that the pore size was determined by the competition between the interfacial energy and elastic constraint of the gel. $G{\prime }_{\text{pla}}$ × d was ∼6 mJ/m², which is in a reasonable range for interfacial energy.

Let us recall the driving force for shrinking and structure frustration. By moving a PA gel from a hot water bath to a cold one, the amount of water in the gel is greater than the water content corresponding to the equilibrium degree at the cold bath. The temperature of the gel decreases rapidly, owing to fast heat conduction, whereas the excess water cannot be expelled from the gel instantly, owing to the sample size–dependent slow diffusion of water molecules. The thermal diffusion coefficient is approximately three orders higher than that of water diffusion (26, 27). Consequently, these excess water molecules are locally expelled from the polymer network to form aggregates. The formation of water aggregates leads to local deformation of the network chains and therefore could induce the formation of a microskin layer at the boundary of the water aggregates (Fig. 1C). The microskin layer builds a barrier to water diffusion out of the gel, resulting in a slow shrinking kinetics. When the elastic modulus of the polymer network is sufficiently high, the structure frustration is suppressed because of the high energy cost in the deformation of the polymer network. This well explains our experimental observation that structure frustration disappears at a large shear modulus, which, in turn, should reduce the asymmetry between swelling and shrinking. Here, we emphasize that such structure frustration has a kinetic origin, and it forms upon cooling at any temperature. This differs from the equilibrium phase separation that occurs only at a critical temperature in typical thermally responsive hydrogels (37, 38).

Swelling and Shrinking Kinetics at the Same Temperature

Next, we study the swelling and shrinking kinetics of PA gels with different structure frustrations. The size change of the PA gels during swelling and shrinking is exceedingly small, within 10% of the original diameter (SI Appendix, Fig. S8). In our previous study, swelling was performed at high temperatures, whereas shrinking was performed at low temperatures. To avoid the effect brought by the temperature difference, in this study, we studied the swelling and shrinking kinetics at the same temperature. For this purpose, we prepared three water baths with temperatures of 7, 25, and 80 °C, respectively. A piece of PA gel was placed in the 7 °C water bath and another in the 80 °C water bath (Fig. 3A). The two samples were respectively kept in the water baths for 24 and 2 h to reach swelling equilibrium first. Then they were moved to a 25 °C water bath, and this time is taken to be zero. For the gel being moved from 7 to 25 °C, it swells and keeps the transparency during swelling, while for the gel being moved from 80 to 25 °C, the gel turns to turbid instantly. The turbid gel shrinks with time and changes to transparent gradually.

Fig. 3.

Swelling and shrinking of PA gels at the same temperature. (A) Schematic illustration showing the experimental procedure to achieve swelling and shrinking at the same temperature. Two PA gels were first equilibrated at 7 °C water bath for 24 h and 80 °C water bath for 2 h to reach swelling equilibrium, respectively, both of which show a transparent appearance. Then they were moved to a 25 °C water bath. For the gel moved from 7 to 25 °C, it keeps transparency and swells, while for the gel moved from 80 to 25 °C, it changes to turbid instantly and shrinks with time. (B and C) Relative change of diameter of PA gels during swelling (B) and shrinking (C), as a function of time after being moved to the 25 °C water bath. The gray lines are the fitting results with Eq. 1. (D) The calculated swelling and shrinking cooperative diffusion coefficients at 25 °C. The PA-2.5-0.1 gel was used.

The kinetics of swelling and shrinking at 25 °C were monitored by measuring the gel diameter, with a digital camera equipped in a photo stage (SI Appendix, Fig. S9). The change in diameter of the disk-shaped gel was extracted from the optical images using ImageJ software. Fig. 3 B and C shows the time evolutions of gel diameters during swelling and shrinking with the PA-2.5-0.1 gel as a typical example, and the others are shown in SI Appendix, Figs. S10 and S11. As shown in Fig. 3 B and C and SI Appendix, Figs. S10 and S11, the time profiles can be well described by the swelling–shrinking kinetics equation for disk-shaped gels (Eq. 1 in ref. (14) or Eq. 44 in ref. (11)) derived from the Tanaka–Filmore theory (10):

$$\left|\frac{d_{\text{t}}-d_{\infty }}{d_0-d_{\infty }}\right|\cong \frac{8}{{\pi }^2}exp\left(-\frac{t}{\tau }\right),$$ [1]

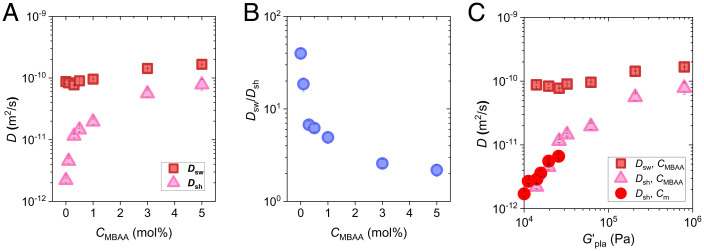
where $d_0$, $d_{\text{t}}$, and $d_{\infty }$ denote the gel diameters at time 0, time $t$, and equilibrium state, respectively. $\tau$ denotes the characteristic time of swelling or shrinking. Although Tanaka–Fillmore theory was formulated for simple chemically crosslinked hydrogels, the result indicates that it is also applicable for self-healing gels with dynamic bonds. Our previous study confirmed that $\tau$ is proportional to the square of the sample thickness, following cooperative diffusion (27). We estimated the cooperative diffusion coefficients, $D$, from the relation $\tau =\frac{h_{\infty }^2}{{\pi }^{2}D}$, where $h_{\infty }$ is the gel thickness at equilibrium state. The cooperative diffusion coefficient of swelling, $D_{\text{sw}}$, increases slightly from 8.8 × 10⁻¹¹ to 1.7 × 10⁻¹⁰ m²/s by increasing C_MBAA from 0 to 5.0 mol% (Fig. 4A). In contrast, the cooperative diffusion coefficient of shrinking, $D_{\text{sh}}$, increases dramatically from 2.2 × 10⁻¹² to 7.8 × 10⁻¹¹ m²/s with increasing C_MBAA. Here, we define the ratio $D_{\text{sw}}/D_{\text{sh}}$ as a parameter of the asymmetry between shrinking and swelling. $D_{\text{sw}}/D_{\text{sh}}$ initially declines rapidly and then slows down with the increase in C_MBAA (Fig. 4B). $D_{\text{sw}}/D_{\text{sh}}$ decreases from 39.8 to 4.9 by increasing the C_MBAA from 0 to 1 mol%, whereas it decreases from 4.9 to 2.2 by increasing the C_MBAA from 1.0 to 5.0 mol%. $D_{\text{sw}}/D_{\text{sh}}$ approaches 1 at high chemical cross-linker concentrations, suggesting that the asymmetry between swelling and shrinking kinetics is suppressed by the suppression of structure frustration in gels with high elasticity.

Fig. 4.

Asymmetry between swelling and shrinking kinetics after temperature jumping. (A and B) Cooperative diffusion coefficients for swelling and shrinking (A) and their ratios (B) at 25 °C for gels with different C_MBAA. (C) Cooperative diffusion coefficients for swelling and shrinking versus plateau modulus $G{\text{'}}_{\text{pla}}$ for gels with different C_MBAA and C_m at 25 °C.

Because the size of structure frustration is inversely related to the elasticity of the gels, we plot the $G{\prime }_{\text{pla}}$ dependence of shrinking and swelling cooperative diffusion coefficients at 25 °C, as shown in Fig. 4C. For the swelling process, $D_{\text{sw}}$ has a weak increase with $G{\prime }_{\text{pla}}$. For the shrinking process, $D_{\text{sh}}$ dramatically decreases with $G{\prime }_{\text{pla}}$, and all the results of the PA-C_m-0.1 (SI Appendix, Figs. S12–S14) and PA-2.5-C_MBAA sets collapse on the same curve in Fig. 4C, which further confirms that the elasticity of the gels governs the structure frustration and thereby the shrinking kinetics.

Based on the Tanaka–Fillmore theory (10, 11), the cooperative diffusion coefficient of a gel is related to its bulk osmotic modulus, $K_{\text{os}}$, and shear modulus, $\mu$ (equals to $G{\prime }_{\text{pla}}$ of PA gel here), and the friction, $f$, between the network and solvent, by Eq. 2:

$$D=\frac{K_{\text{os}}+4\mu /3}{f}.$$ [2]

For the swelling process in which no frustration structure is formed, it is reasonable to assume that $K_{\text{os}}$ and $f$ do not change significantly for the gels with different $G{\prime }_{\text{pla}}$, as the PA gels with different C_MBAA and C_m have similar polymer volume fractions at the same temperature in the equilibrium state in water (SI Appendix, Fig. S2B) (34). Meanwhile, the bulk modulus, $K_{\text{os}}$, is typically one order of magnitude larger than the shear modulus $G{\prime }_{\text{pla}}$ in gels (39), which results in a weak dependence of $D_{\text{sw}}$ on $G{\prime }_{\text{pla}}$. The experimental observation of the weak dependence of $D_{\text{sw}}$ on $G{\prime }_{\text{pla}}$ suggests that the swelling kinetics of self-healing hydrogels is basically governed by the permanent cross-linked structure, and the dynamic bonds play a weak role. For the shrinking process in which a frustrated structure is formed, Eq. 2 cannot be applied directly, owing to the heterogeneous structure in the gel.

Is the Cooperative Diffusion Coefficient of Shrinking an Intrinsic Parameter?

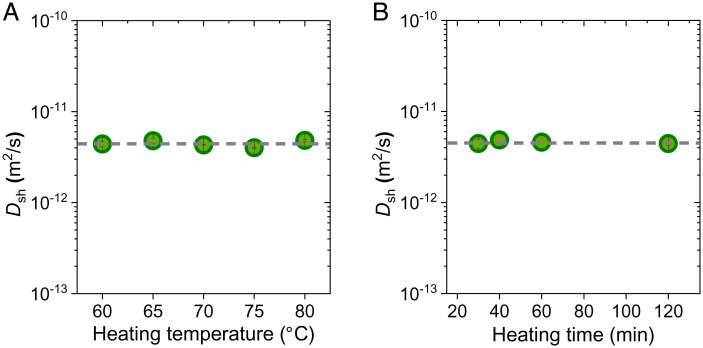
To elucidate whether the cooperative diffusion coefficient, in the presence of structure frustration, is an intrinsic parameter or a heating history–dependent parameter, we varied the heating temperature of the hot bath. Five hot baths with temperatures ranging from 60 to 80 °C were used. PA-2.5-0.1 gels were heated in hot baths for 2 h to reach swelling equilibrium and then moved to the same cold bath with a temperature of 25 °C for shrinking (SI Appendix, Fig. S15). All the gels show transparent to turbid changes after being moved to the 25 °C cold bath, suggesting the formation of structure frustration upon cooling. As shown in Fig. 5A, although the heating temperatures are different, the cooperative diffusion coefficients extracted from the shrinking process at 25 °C are almost the same. This result indicates that, although delayed shrinking is induced by structure frustration that is heating history–dependent, the cooperative diffusion constant of shrinking, $D_{\text{sh}}$, is independent of the heating history.

Fig. 5.

Effect of heating temperature and heating time on the shrinking cooperative diffusion coefficients. (A) PA gels were heated in water baths with different temperatures for 2 h to reach equilibrium and then moved to a 25 °C water bath for shrinking. (B) PA gels were heated in 60 °C water baths for different heating time and then moved to a 25 °C water bath for shrinking. The PA-2.5-0.1 gel was used.

To understand such a seemingly contradictory phenomenon, we performed SEM measurement of gels with different heating temperatures. SI Appendix, Fig. S16 shows the SEM images of the cut cross-section of gels upon cooling from different hot baths to the same 25 °C cold bath for 1 min. With increasing heating temperature, the pore sizes from the SEM images remain unchanged, whereas the number density increases. The constant pore size is consistent with our dimensional analysis, where the pore size depends on the competition between the interfacial energy and elastic constraints, but not the heating temperature. The same pore size gives the same microskin layer around the water aggregate. Because the diffusion is dominated by this microskin layer, the gels under different heating temperatures have the same shrinking cooperative diffusion coefficient.

We further explore the role of swelling extent on the shrinking kinetics by performing experiments with varying heating times of the gel in the hot bath. The gels equilibrated at 25 °C were heated in a 60 °C hot bath for a specific time, after which they were moved back to the 25 °C water bath for shrinking. The heating time was varied from 20 to 120 min, covering the range from swelling nonequilibrium to swelling equilibrium (SI Appendix, Fig. S17). As swelling is a water diffusion–controlled process, water absorption occurs from the surface layers of the gel and develops gradually into the inner region, finally reaching swelling equilibrium at a prolonged time. We found that, within the experimental accuracy, the cooperative diffusion coefficients for shrinking at 25 °C are almost the same for different swelling times (Fig. 5B and SI Appendix, Fig. S18).

These results give a conclusion that, once the shrinking temperature is fixed, neither the heating temperature nor the swelling extent influences the shrinking cooperative diffusion coefficient, $D_{\text{sh}}$. Therefore, $D_{\text{sh}}$ can be considered as an intrinsic parameter for self-healing hydrogels with an abundance of physical bonds.

Activation Energies of Swelling and Shrinking

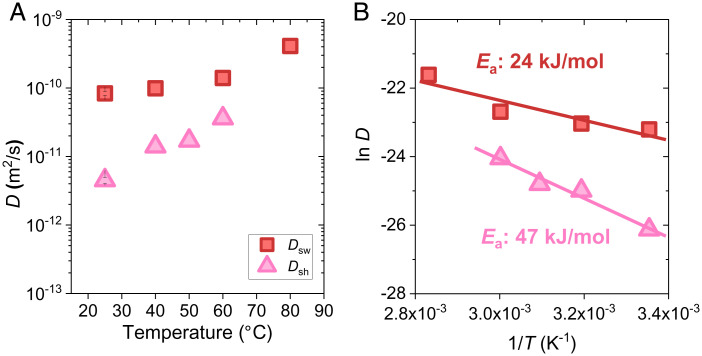
Because the shrinking cooperative diffusion coefficient is an intrinsic material parameter, we can discuss its temperature dependence. We performed swelling and shrinking experiments at different temperatures, using PA-2.5-0.1 gels as an example. In the swelling experiments, four destination temperatures were used, ranging from 25 to 80 °C (SI Appendix, Fig. S19). For swelling at 25 °C, the gel was equilibrated at 7 °C first and then it was moved to the 25 °C water bath for swelling. For swelling at the other three temperatures, the gels were equilibrated at 25 °C, first considering the experimental convenience, and then they were moved to the destination temperature for swelling. The cooperative diffusion coefficient for swelling, $D_{\text{sw}}$, increases slightly from 8.35 × 10⁻¹¹ to 4.1 × 10⁻¹⁰ m²/s in the studied temperature range (Fig. 6A). The increase in $D_{\text{sw}}$ with increasing temperature can be explained by the decreased water viscosity and increased network relaxation kinetics with increasing temperature, which accelerates the swelling kinetics.

Fig. 6.

Activation energies of swelling and shrinking. (A) Cooperative diffusion coefficients for swelling and shrinking at different temperatures. (B) Plots of swelling and shrinking cooperative diffusion coefficients versus temperature. The slopes produce the energies for swelling and shrinking. The PA-2.5-0.1 gel was used.

In the shrinking experiment, the gels were equilibrated at 80 °C, after which they were moved to water baths with destination temperatures ranging from 25 to 60 °C for shrinking (SI Appendix, Fig. S20). All gels exhibit transparent to turbid changes upon cooling, owing to the formation of structure frustration. The cooperative diffusion coefficient for shrinking, $D_{\text{sh}}$, increases from 4.5 × 10⁻¹² to 3.6 × 10⁻¹¹ m²/s in the studied temperature range (Fig. 6A). $D_{\text{sh}}$ increases significantly faster with temperature than that of $D_{\text{sw}}$, because of the different mechanisms controlling the swelling and shrinking kinetics. At the same temperature, $D_{\text{sh}}$ is significantly smaller than $D_{\text{sw}}$, suggesting the presence of asymmetric swelling–shrinking kinetics in the studied temperature range.

The temperature dependence of both the swelling and shrinking cooperative diffusion coefficients obeys the Arrhenius relation (40),

$$D=\mathit{Aexp}\left(-\mathrm{\Delta }E/k_{B}T\right),$$ [3]

where $A$ is a constant, $\mathrm{\Delta }E$ denotes activation energy, $k_B$ is the Boltzmann constant, and $T$ denotes the temperature in Kelvin. $D_{\text{sw}}$ and $D_{\text{sh}}$ are plotted versus $1/T$ in Fig. 6B, where the slopes produce the activation energies (24 and 47 kJ mol⁻¹ for swelling and shrinking, respectively). The activation energy for swelling is higher than that of pure water (18 kJ mol⁻¹) (9), suggesting that the swelling is a synergistic movement of the gel network and solvent, rather than the diffusion of solvent only. The swelling activation energy of PA gels containing abundant ionic bonds is similar however slightly higher than that of common chemical poly(methyl methacrylate) gels (22 kJ mol⁻¹) (41), demonstrating that physical bonds have a minor effect on swelling. On the contrary, the shrinking activation energy of PA gels is approximately twice that of swelling, clearly indicating the structure frustration, which induces a high barrier to water diffusion.

Conclusions

Our work provides a useful first step towards elucidating the essential physics governing the swelling and shrinking of self-healing hydrogels upon temperature change. It was found that the shrinking and swelling kinetics show strong asymmetry, even at the same temperature, which is related to the structure frustration upon abrupt cooling. The swelling kinetics is near independent of the plateau modulus of viscoelastic self-healing gels. The shrinking kinetics is mainly governed by the structure frustration beyond the polymer network scale. The huge rate difference in water diffusion and heat diffusion upon cooling leads to the formation of water aggregates, which is considered to enhance the network chain density around them and suppresses the rate of water release from the gel. Consequently, the gel exhibits a slow shrinking kinetics.

It is also interesting to point out that the shrinking kinetics, characterized by the shrinking cooperative diffusion coefficient, depends only on the shrinking temperature, independent of the heating temperature and heating duration. This suggests that not only the swelling diffusion coefficient but also the shrinking diffusion coefficient are intrinsic material parameters for self-healing gels. The elasticity of the gel network is found to be a key parameter governing the formation of structure frustration and, therefore, the asymmetric swelling and shrinking kinetics. This is because the structure frustration is a result of competition between the local desolvation, which drives the structure frustration, and the elastic deformation of the polymer network, which suppresses the structure frustration. This finding is general and should be applicable to gels with an inverse thermal property, that is, swelling at low temperatures and shrinking at high temperatures.

Self-healing hydrogels are increasingly finding use in diverse applications, such as artificial biological tissues, contact lenses, and biosensors, where the diffusion of small molecules or polymer networks or their cooperative diffusion is inevitably involved. We believe that this work provides fundamental understandings on the temperature-triggered transient structure formation of self-healing hydrogels and expect that our findings will find broad use in diverse applications of these hydrogels where cooperative diffusion of water and gel network is involved. Diffusion is also a ubiquitous process in nature and has important biological consequences. For example, diffusion provides all the reactants required for chemical and physical reactions in biotissues and transports the products and metabolic waste (6, 7). The findings in self-healing hydrogels should provide insight into molecular diffusion in biological systems that are essentially physical hydrogels consisting of water and macromolecular components, such as fibrous collagen and proteoglycans that are cross-linked by reversible bonds.

Methods

Gel Preparation.

PA hydrogels were prepared in the following way. A mixed aqueous solution containing NaSS, DMAEA-Q, MBAA, and α-keto was injected into a reaction cell consisting of two glass plates separated by a silicone rubber spacer and irradiated with ultraviolet light (wavelength 365 nm, light intensity ∼4 mW cm⁻²) for 11 h under an argon atmosphere. The concentration of MBAA used in this work is from 0.1 to 5 mol%, relative to the total monomer concentration. During polymerization, the samples show homogeneous appearance and no whitening happens (SI Appendix, Fig. S21). After radical polymerization, the as-prepared gels were immersed in a large amount of water to remove counterions and residual chemicals, during which strong ion interaction forms and the gels shrink (31). The total monomer concentration of NaSS and DMAEA-Q, C_m, changed from 1.6 to 2.8 M, and the ratio between NaSS and DMAEA-Q remained at 0.514:0.486. The concentration of MBAA, C_MBAA, changed from 0 to 5 mol%, and the concentration of α-keto remained at 0.1 mol%, relative to C_m. The thickness of the spacer used was 1.5 mm. The water-equilibrated gels had balanced charges and were strong and tough. The thickness of water-equilibrated gels at 25 °C was in the ranging of 1.1∼1.3 mm, depending on the sample composition.

All details associated with SEM, water content measurement, and rheology measurement are available in SI Appendix.

Data, Materials, and Software Availability

All data are included in the manuscript and/or SI Appendix.