Environmental context dependency in species interactions

Significance

Interactions between species in nature can vary in strength and direction and may be driven by environmental variation. We use kelp forests as an example to show how varying species-interaction strengths, estimated directly from time-series data on species abundances, can be related to low-frequency variation in environmental drivers. Our approach has relevance to the study of species interactions in other ecological systems where environmental and monitoring data exist, but experimental studies of species interactions are infeasible.

Abstract

Ecological interactions are not uniform across time and can vary with environmental conditions. Yet, interactions among species are often measured with short-term controlled experiments whose outcomes can depend greatly on the particular environmental conditions under which they are performed. As an alternative, we use empirical dynamic modeling to estimate species interactions across a wide range of environmental conditions directly from existing long-term monitoring data. In our case study from a southern California kelp forest, we test whether interactions between multiple kelp and sea urchin species can be reliably reconstructed from time-series data and whether those interactions vary predictably in strength and direction across observed fluctuations in temperature, disturbance, and low-frequency oceanographic regimes. We show that environmental context greatly alters the strength and direction of species interactions. In particular, the state of the North Pacific Gyre Oscillation seems to drive the competitive balance between kelp species, asserting bottom-up control on kelp ecosystem dynamics. We show the importance of specifically studying variation in interaction strength, rather than mean interaction outcomes, when trying to understand the dynamics of complex ecosystems. The significant context dependency in species interactions found in this study argues for a greater utilization of long-term data and empirical dynamic modeling in studies of the dynamics of other ecosystems.

Interactions between species drive patterns of diversity, stability, resilience, and productivity in nature (1–4). In any ecosystem, the collection of species interactions determines community dynamics. Yet, since environmental conditions can influence these species interactions and environmental conditions can vary greatly over space or time (5–9), shifting interspecies dynamics can drive complex ecosystem changes. For example, the Stress Gradient Hypothesis (10–12) posits that interactions among species within a trophic level can shift from competitive to facilitative across large gradients of stress (e.g., thermal, nutrient, or water stress), with important implications for community dynamics. Similar hypotheses have been posited about shifts in other key species-interaction types, like parasitism and mutualism (13, 14), and consumer–prey interactions (15).

Although ecologists have long recognized that many important species interactions may vary greatly over time and space, this context dependency remains very difficult to effectively measure and describe. Field experiments that measure interactions can generally be performed at only a few places over a relatively short window of time. They are therefore inevitably subject to only a subset of potential environmental contexts that may not encompass the full range of conditions experienced by that ecosystem over longer time scales or broader geographies (16). The resulting constraints increase the chance that the profound influence of environmental context on the outcome of species interactions ranging from keystone predation (8) to competition (6, 17, 18) to protective symbioses (19–21) will remain underappreciated. Since expanding the temporal and spatial scales of such experiments to rectify these challenges is a daunting task, we need additional tools.

Moreover, even when context dependency of species interactions has been examined explicitly, studies commonly focus on estimating mean interaction strengths, rather than more comprehensive examinations of interaction variance and dynamics (9). This averaging approach may be appropriate for answering certain questions, but if species interactions are highly variable in both magnitude and direction—and therefore “weak” when averaged—key species interactions that are important drivers of community change may be dismissed as insignificant observational noise (4).

Meeting these significant challenges requires placing interspecific interactions into their appropriate full environmental contexts. Controlled experiments can sort out the relative and interactive effects of a few orthogonal environmental drivers at a time; for example, examination of the effects of ocean warming and acidification on algal competition (22). But as species-interaction webs and lists of important environmental variables grow in size, fully factorial experimental designs quickly become unwieldy, if not impossible, to implement. One potential solution may lie in coupling long-term ecological observations that span a large range of environmental contexts with analytical methods that can directly estimate context-dependent species interactions from those time-series observations of changing abundances. Since long-term records of species abundances exist for a wide range of ecosystems, such an approach could help to characterize environmental contingencies in species interactions far more rapidly and could explicitly examine interaction variability in both strength and direction in a broader array of contexts.

Here, we explore this alternative approach through a case study, by examining the effects of environmental context on species interactions using nonlinear time-series analyses applied to long-term monitoring data from a southern California kelp forest (23). Kelp forests are diverse and temporally dynamic ecosystems, in which many important species interactions are well-documented through decades of experimental and comparative studies (24–26). The study of kelp forests has been foundational to ecological theory, especially regarding the relative influence of top-down and bottom-up structuring forces in ecosystems (27–31). Recently, however, findings from long-term kelp-forest research programs have begun to challenge many long-held beliefs about the drivers of kelp-forest ecosystem dynamics (32). In particular, a longer-term perspective has led to growing hints about the critical importance of environmental context—such as the level of physical disturbance or the current state of El Niño conditions—for understanding kelp-forest processes (33–37).

To explore the insights that can be gleaned from time-series data to determine patterns of variation in species interactions and their relationships to environmental drivers, we use empirical dynamic modeling [EDM (38)]. EDM uses information from single or multiple time series to empirically model relationships between variables through the reconstruction of dynamic attractors . The general modeling framework for all EDM methods is readily adaptable to many different sorts of time-series variables, including environmental variables manifesting at different scales (39–41). Because the methods are specifically designed for nonlinear dynamic systems, EDM—in theory—should be able to illuminate context-dependent patterns across diverse types of species interactions. Recently developed EDM methods exist for uncovering dynamic species interactions from time-series data (38), but these methods have, to date, been applied only to simulated and planktonic communities. Their utility to the study of other ecological systems remains untested. We use EDM to explore how a kelp-forest species-interaction network varies over time and to establish environmental context dependency in interaction strength and direction.

Results

To characterize environmental context dependency in kelp-forest interactions between species, we take three general steps (Materials and Methods; a full step-by-step description and reproducible code used to produce all analyses and figures are available on GitHub [https://github.com/owenrliu/env_context_dependency]). First, we use dynamic inferred causality tests called convergent cross-mapping (CCM) (42) to construct a kelp-forest species-interaction network directly from time-series data. In so doing, we test for all unidirectional inferred causal signals between five common kelp-forest species, as well as between five exogenous environmental variables and those species. Second, for each identified inferred causal link between species, we reconstruct species interactions over time, using another EDM tool called multivariate S-maps (sequential locally weighted global linear maps) (38, 43). Finally, we show how variability in key species interactions and overall kelp-forest dynamics can be related back to the environmental context under which they took place.

Our analyses focus on the dynamics of five common southern California kelp-forest species, whose interactions are thought to be important in structuring kelp-forest ecosystems (24, 26, 44) (Fig. 1). Specifically, we analyze time-series monitoring data from San Nicolas Island, an uninhabited island that is part of the northern Channel Islands in southern California. Data collected there (45) have contributed to significant insights on the influence of environmental and biological drivers of kelp-forest dynamics (32, 46, 47).

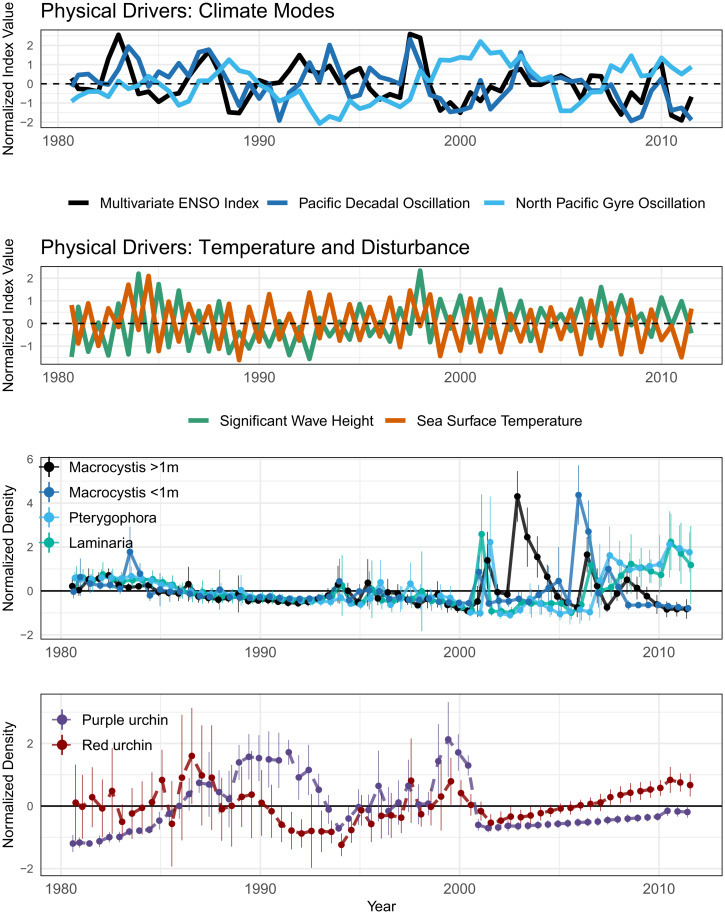
Fig. 1.

Raw data for species and physical drivers included in the study. Points represent mean values across 10 spatial replicates, while vertical lines represent ± 1 SD. All variables normalized to zero mean and unit variance, with linear time trends removed. Dashed lines distinguish herbivore (sea urchin) time series from time series of algae species.

The giant kelp Macrocystis pyrifera is the eponymous foundation species of kelp forests (48), the primary canopy- and habitat-forming kelp along most of the central and southern coast of California (25). The monitoring data include both adult Macrocystis and recruits [sporophytes identified as M. pyrifera, but less than 1 m tall (45)]. We include both size classes of Macrocystis to separate the effects of herbivory and competition on adult Macrocystis versus Macrocystis recruitment. We explore Macrocystis dynamics and its interactions with two presumptive competitors and two abundant herbivores. The understory kelp species Laminaria farlowii and Pterygophora californica compete with Macrocystis for space, light, and nutrients (49–51). The two herbivores—the purple sea urchin Strongylocentrotus purpuratus and the red sea urchin Mesocentrotus franciscanus—are thought in many places to control Macrocystis density and can sometimes wipe out entire giant kelp forests, leading to the alternative ecosystem state known as an urchin barren (46, 52). Finally, although secondary consumers (among them, California sea otters, California spiny lobsters, and California sheephead) exist in this system, recent work in the same system showed no relationship between predator dynamics and kelp-forest ecosystem state change (47). In light of that finding and a lack of sufficient temporal resolution in data on predator abundances, they are excluded from our analyses.

In southern California, Macrocystis population dynamics can be driven by nutrient availability and physical disturbance (31, 36). The availability of nitrate is inversely related to seawater temperature (53) and, over longer time scales, is associated with oscillations in patterns of upwelling and oceanic currents. Accordingly, we include five environmental variables in our analyses to test their relationship to kelp-forest species dynamics and interactions: sea-surface temperature (SST), physical disturbance (measured by maximum seasonal wave height [SWH]), and three indices of low-frequency climate modes: the Multivariate El Niño Index (MEI) (54), the Pacific Decadal Oscillation (PDO) (55), and the North Pacific Gyre Oscillation (NPGO) (56).

Drivers of Kelp-Forest Species Interactions.

The time series of species densities at San Nicolas Island (Fig. 1) shows evidence of a number of dynamic ecosystem states, in contrast to other kelp-forest literature that describes kelp forests as having only two alternative stable states—a denuded urchin barren or a healthy kelp forest (52).

More specifically, in Fig. 1, it is clear that, although sea urchins were abundant early in the time series, they declined in abundance by the mid-1990s, likely due to predation by reintroduced sea otters (47). However, for a number of subsequent years, there was little evidence of the establishment of a mature kelp forest, which might be expected under the simple assumption of two alternative kelp-forest states. Instead, kelp-forest succession was not observed until 2001, when, first, the smaller, understory kelp species P. californica and L. farlowii increased in abundance, followed the next year by an extreme increase in the density of mature giant kelp M. pyrifera. However, this high density of Macrocystis was short-lived, and although there was a large recruitment of small Macrocystis sporophytes observed in late 2005, the subsequent years saw a decline in Macrocystis and the establishment instead of a Pterygophora- and Laminaria-dominated forest.

The data suggest that kelp-forest ecosystem structure at San Nicolas Island is more dynamic than a two-state system. The multiple ecosystem states observed raise important questions. Why did Macrocystis not flourish after the decline in abundance of two of its primary herbivores, the red urchin M. franciscanus and the purple urchin S. purpuratus? Subsequently, when a mature kelp forest did establish, why was it so short-lived? More generally, what drives these observed shifts in ecosystem structure?

Typically, the three kelp species considered here are thought to exhibit a competitive dominance hierarchy, where M. pyrifera is the dominant competitor for light and nutrients when these resources are abundant, but Macrocystis is also more susceptible to physical stress than Pterygophora and Laminaria (49, 51). Additionally, laboratory studies suggest that Macrocystis is preferred to Pterygophora and Laminaria as a food source for the urchin species, given its greater relative palatability (57, 58). Therefore, the strength of competition between Macrocystis, Pterygophora, and Laminaria is likely dependent upon ambient environmental conditions, as well as the top-down burden of herbivory.

Overall, we seek to uncover whether the dynamic history of kelp-forest ecosystem states at San Nicolas Island can be appropriately described through nonstatic species interactions, which themselves are underpinned by varying environmental context.

Empirical Interaction Network.

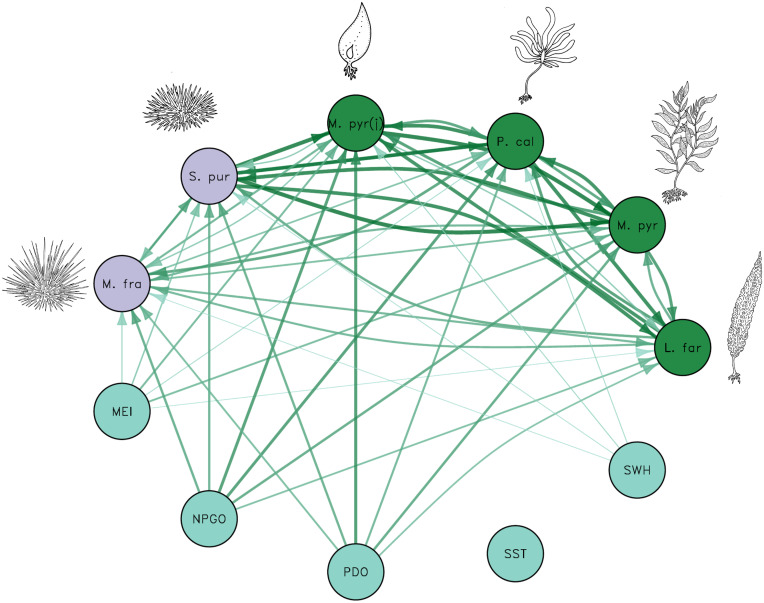
To establish significant species interactions from the monitoring time series, we use CCM (42). Applying CCM to the set of six biological and five physical variables, we find a dense interaction network (Fig. 2). Out of 60 possible unidirectional links among species and between species and the environmental variables, 52 are significant. Adult Macrocystis dynamics are driven by three of the five environmental variables, with the PDO and the NPGO showing the strongest inferred causal signals. This finding aligns with recent work by others using different methods (36, 59) that found that the NPGO and mean nitrate concentrations were primary controls of giant kelp biomass dynamics across the California coast. More generally, although the included physical variables, except for SST, show significant links to many of the biological variables, the NPGO shows the strongest links to almost all of the biological variables. Our analysis suggests that more attention should be focused on the effects of the state of the NPGO in southern California.

Fig. 2.

Reconstructed interaction web using results of CCM. Each arrow represents a significant inferred causal signal and link width and opacity scale with the strength of causal forcing (see full results in SI Appendix). Species abbreviations: L. far, L. farlowii; M. fra, M. franciscanus; M. pyr, M. pyrifera; P. cal, P. californica; S. pur, S. purpuratus. Physical drivers: NPGO, MEI, PDO, SST, and SWH.

In turn, adult Macrocystis shows strong inferred causal links to every other biological variable, suggesting that Macrocystis dynamics affect the dynamics of the other study species. This is despite the fact that the study site at San Nicolas Island does not have a stable giant kelp forest (raw time series, Fig. 1); rather, the site has transitioned from an urchin barren (46) to a Pterygophora- and Laminaria-dominated state to a Macrocystis forest at various times throughout the 30-y time series. The implication is that, despite not maintaining dominance in the typical ecological sense of the word (large abundance and biomass), Macrocystis remains a key foundation species in this ecosystem. Its dynamics are fundamentally important in driving the dynamics of all the other kelp-forest species in this time-series dataset (25). This result is relevant to other ecosystems that experience great variability in structure over time. With a sufficient past record of changes in abundance, the CCM approach can help to propose the most important inferred causal species in ecosystem-interaction networks. For example, analyses of this sort could help identify key species for ecosystem-restoration projects.

CCM analysis confirms that the kelp-forest system studied represents a complex array of significant interactions between algal species and their herbivores. However, CCM alone does not elucidate the direction and magnitude of individual species interactions. To obtain estimates of the interaction strengths themselves, we use multivariate S-maps (38, 43) (Materials and Methods). S-maps reconstruct dynamic “attractors” by casting the abundances of inferred causally related species or environmental variables into n-dimensional state space, where n is the number of inferred causal variables, including the focal species itself. For a set of inferred causally related species, a point in multivariate space can be plotted by using each species’ abundance as an axis. The attractor is then created by tracing this multispecies trajectory forward in time (see example attractor in SI Appendix). For each point along the attractor, S-maps compute a Jacobian matrix, the elements of which are the estimated partial derivatives between species’ normalized densities. These interaction-matrix elements are our measure of species interactions. Because Jacobians are computed sequentially for every point along reconstructed attractors, we obtain estimates of interaction strength that can vary nonlinearly with ecosystem state.

There are a few important characteristics of S-maps that deserve mention. First, the S-map estimation procedure, like all EDM methods, is specifically designed for nonlinear systems and is therefore an appropriate tool for investigating ecosystems, like kelp forests, that exhibit nonlinear dynamics, such as alternative stable states or hysteresis (38). Secondly, because S-maps utilize reconstructed multispecies attractors, each estimated interaction is fundamentally based on observations of similar past ecosystem states—where each state is represented as a multivariate vector of species densities—rather than a phenomenological extrapolation of the most recent dynamics in time. This property distinguishes S-maps from multivariate autoregressive approaches to time-series analysis (60, 61). Finally, like all modeling approaches, interaction strengths derived from S-maps can be sensitive to the specific embedding (i.e., set of predictors) utilized and limited by available data. Our models utilize predictor variables that are 1) known from previous empirical research to be important kelp-forest interactors; 2) show good out-of-sample predictability in both univariate and multivariate embeddings (Materials and Methods and SI Appendix, Table S1); and 3) are confirmed by CCM to drive interspecies dynamics.

S-map models performed well in out-of-sample prediction (SI Appendix, Table S1), providing evidence that the dynamics of the multispecies system are nonlinear, predictable, and able to be captured with the subset of species available in this study. All models performed better than simple linear models with no state-dependence (SI Appendix, Table S1). Interestingly, the model for red sea urchin M. franciscanus did not perform markedly better than a simple linear model. This may be because red urchins at San Nicolas Island are harvested by both a small population of sea otters and by a commercial fishery, whose dynamics are not captured in our models. Future work on red urchin dynamics should consider fishing and predation impacts, in addition to the ecological processes captured here.

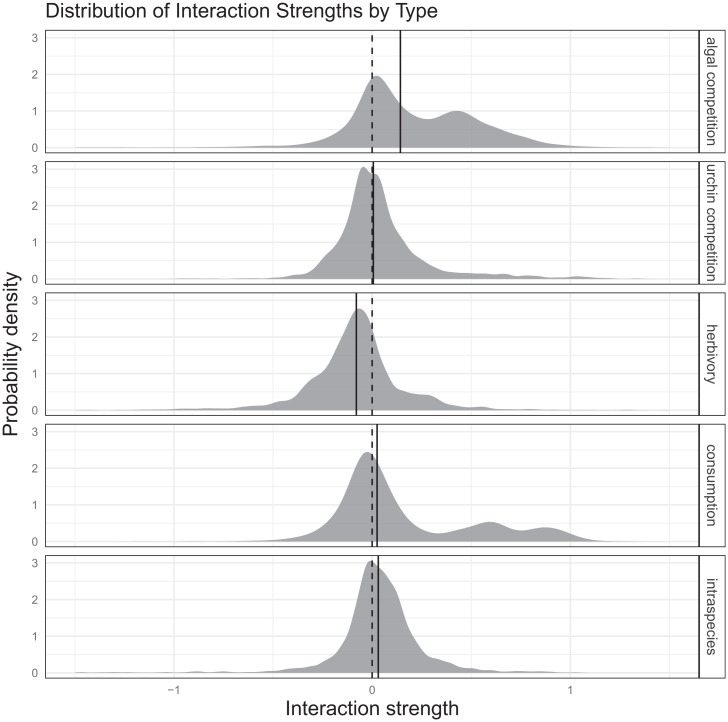
In the case of the San Nicolas kelp forest, we find a striking prevalence of neutral and positive species interactions (Fig. 3). After grouping species interactions by type, only herbivory (the effect of urchins on algal species) is predominantly estimated as a negative interaction. Conversely, the effects of the algal species on the urchin species, and the urchin species on each other, are centered around zero. Likewise, contrary to our expectations, interactions between the algal species (presumptive competition) are not always antagonistic. Together, these results suggest that facilitation—direct or indirect—can arise in kelp forests in multiple contexts (62). For example, since there is evidence here of strong herbivory, then there may be indirect facilitation between algal species because of a shared herbivore: A greater algal density, in general, could ameliorate the negative effect of herbivory on any one species. Indeed, ref. 46 suggested a potential mechanism for this observation. As drift kelp (discarded algal detritus) becomes more available, urchins can shift their mode of feeding from active and roving to stationary and passive and cease their destructive grazing. This type of indirect, associative facilitation between algal species may sometimes outweigh the strength of direct algal competition. Additionally, Macrocystis forests can mediate wave and current strength and, as a result, can also help retain reproductive propagules of other species (25). Indirect facilitation in kelp forests has received comparatively little attention (63, 64) relative to the strong focus on exploitative competition between these species for light and nutrients (49, 51), but similar facilitative effects have been documented in other ecosystems (65). Our analysis does not contradict the importance of competition in kelp-forest ecosystems. Rather, it suggests that facilitation, especially indirect facilitation, may be an additional important structuring force in some environmental contexts (63). Furthermore, the estimated interactions remain broadly consistent under two alternative model specifications for each multispecies model, one with an additional variable-selection process (SI Appendix, Figs. S9–S12) and one using first-differenced abundance data (SI Appendix, Figs. S13 and S14). Together, these alternative specifications provide robust evidence for state-dependent interspecies interactions in the San Nicolas Island kelp-forest community.

Fig. 3.

Smoothed kernel-density histograms of all estimated interactions by type. From top to bottom: Algal competition, urchin competition, herbivory, consumption (i.e., effects of algae on urchins), and intraspecies. Solid lines denote medians across all estimated interactions of that type.

Effect of Environment on Interactions.

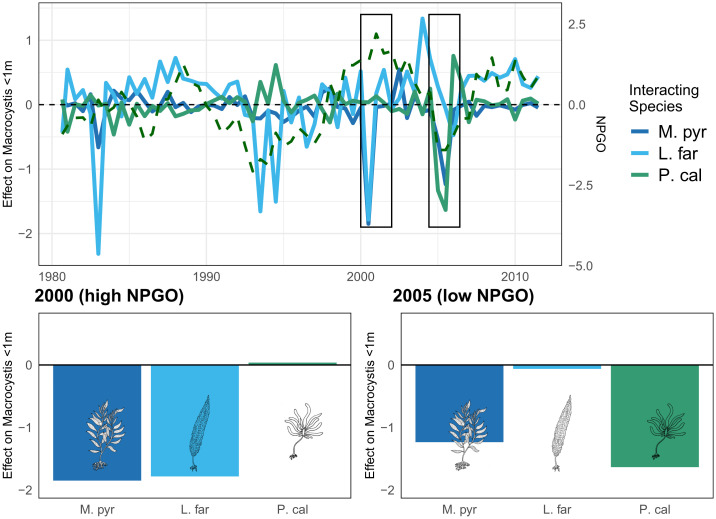
The estimated kelp-forest interactions vary in time. As an example, consider the effects of Laminaria and Pterygophora on Macrocystis recruitment (in our analysis, represented by the density of Macrocystis sporophytes <1 m tall; Fig. 4). Previous research suggests that intact kelp canopies of Pterygophora and Macrocystis itself can inhibit Macrocystis recruitment through competition for space and light (51). During certain periods in the time series, interactions between the three kelp species are fleetingly strong. Moreover, the algal species interactions seem to covary with extreme values of the NPGO, which is a dynamic driver of all of these species, according to our CCM analysis. For example, during the highest positive observed NPGO value just after the year 2000, adult Macrocystis and Laminaria both have strong negative effects on Macrocystis recruitment, while Pterygophora has a neutral or small positive effect. Then, in 2005 to 2006, during a low phase of the NPGO, all three species suppress Macrocystis recruitment (Fig. 4). Negative values of the NPGO are associated with decreases in wind-driven upwelling and nutrient availability in the southern California Current (36, 56), so we can postulate that these conditions intensify the interspecies suppression of Macrocystis recruitment—a hypothesis that warrants field tests.

Fig. 4.

Interaction of Macrocystis, Pterygophora, and Laminaria with Macrocystis recruits over time (solid lines). Normalized NPGO index is shown with dashed line. Boxes zoom in on the interactions in a year with elevated NPGO (2000) and a year with low NPGO (2005). Abbreviations are as in Fig. 2.

The observed pattern supports the idea that the NPGO, which we have already established as an important driver of individual species dynamics, also drives the strengths of their interactions over time. This may be true of the other environmental drivers as well. However, one difficulty with assigning direct relationships between individual environmental variables and particular species interactions (in any ecosystem) is that all interactions are context-dependent, and those contexts involve more than one environmental variable and species at a time. For example, in the San Nicolas case study, we could hypothesize that adult Macrocystis may be a better competitor with Laminaria and Pterygophora under elevated nutrient levels, indicated by high values of the NPGO index in the study area (36). Using our models, we can identify the Macrocystis interactions that occurred under high values of the NPGO, but these observations may be somewhat confounded with other elements of the environmental or ecological context at that particular time (e.g., whether the high NPGO values co-occur with high versus low SST values). Therefore, we use a state-space neighborhood-averaging procedure, adapted from ref. 66, to temper the influence of individual observations and determine how environmental context may affect species interactions (Materials and Methods).

We use these neighborhood-averaged interactions to investigate the relationship between physical and biological interactions in the San Nicolas kelp forest. For the sake of consistency, we continue with our focus on interactions between Macrocystis, Pterygophora, and Laminaria (Fig. 4), a subset of the overall CCM interaction network. Fig. 5 shows how each inferred causal interaction between algae species varies as a function of the effect of the NPGO. Similar figures investigating the effects of the PDO and purple urchins are provided in SI Appendix.

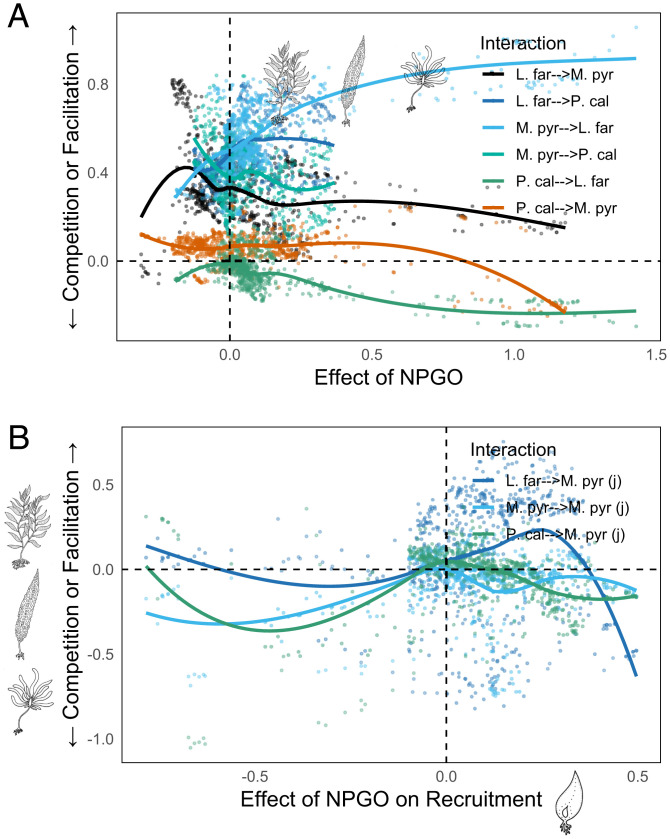
Fig. 5.

(A) Variation in the strength of competition between adult Macrocystis, Laminara, and Pterygophora, relative to the effect of the NPGO on those species. Shown are all significant inferred causal interactions between algae species. (B) Variation in the effect of adult Macrocystis, Laminara, and Pterygophora on Macrocystis recruitment, relative to the effect of the NPGO. Points indicate individual interaction strengths averaged among the 30 nearest state-space neighbors, as described in Materials and Methods. Solid lines are loess smooths.

In Fig. 5A, there are clear relationships between the effect of the NPGO and the strength and direction of interactions between algal species. As the NPGO’s beneficial effect on Laminaria, Pterygophora, and Macrocystis increases, apparent competition between the species becomes more likely, particularly in the effects of Pterygophora on Laminaria. Conversely, under the presumably stressful conditions associated with negative effects of the NPGO on these species, positive species interactions—apparent facilitation—are more common. These findings for the mature algae species align with ecological theory suggesting that facilitation may be more common under environmentally stressful conditions, supporting the Stress Gradient Hypothesis (5, 11, 62). However, we stress that these contextual results are complex—the fundamentally nonlinear relationships between species illuminated in this study warrant careful consideration when resolving causal linkages, because each unique context may result in distinct, state-dependent dynamics.

There is evidence in our models that, in some contexts, the strengths of environmental forcing and species interactions are positively, rather than negatively, associated. Consider the relationship between NPGO context and algal effects on Macrocystis recruitment (Fig. 5B). When NPGO conditions are poor for Macrocystis sporophytes, we also observe intensified negative impacts of Pterygophora and Laminaria on Macrocystis recruitment and an increasingly negative intraspecific effect of adult Macrocystis. Overall, Fig. 5 suggests that the balance between growth, competition, and recruitment among the major algal species vary significantly with environmental context.

The relationships of algal species-interaction strength with herbivory are less clear-cut. SI Appendix, Fig. S8 shows how algal species interactions vary with the effects of the purple urchin S. purpuratus on each algal species. Under an assumption of top-down control in this kelp forest, we might expect that a greater negative effect of herbivory would decrease competition and increase facilitation between the algae species as a result of associative protection from herbivory (67). Instead, while most estimated algal interactions suggest facilitation on average, we do not observe many strong associations between the strength of herbivory and the strength of those interactions (SI Appendix, Fig. S8). One exception is the estimated effect of Macrocystis on Laminaria, which becomes more positive when the negative herbivory effect of S. purpuratus is strong.

Clearly, for many species interactions, there are strong associations between environmental stress and the strength of species interactions, but some of these relationships are the opposite of what we expect from theory. At the same time, it appears that variations in bottom-up forcing indicated by the NPGO and PDO may be just as important in driving species-interaction strength in this kelp forest than the top-down influence of herbivory. Such findings show the value of analytical approaches that can clearly document how species interactions change in magnitude and direction over time. Further investigations of the relative dynamic effects of top-down versus bottom-up forcing in other cases, especially in ecosystems [such as the rocky intertidal (68)], where important species interactions have been previously described, would be a worthwhile future endeavor.

Discussion

Ecosystem dynamics are composed of nonlinear species relationships, played out within shifting environmental contexts. A significant challenge in the study of ecosystem dynamics has been the difficulty in appropriately extrapolating experimental results to real ecosystems, where multiple species–species and species–environment interactions are operating simultaneously. We have used this study to illustrate how EDM, in combination with rich time-series ecosystem data, can help to tackle this challenge. Long-term time-series data are not uncommon for many ecosystems and locations. As illustrated here, such monitoring data therefore provide platforms for identifying inferred causal interaction networks and investigating the influence of large-scale environmental drivers on interaction strengths using existing datasets, rather than requiring long-term experiments in the future. In this particular ecosystem, our analyses of time-series data confirmed many results from previous experimental work regarding the foundation species M. pyrifera. Perhaps more importantly, they also revealed patterns of substantial variability in multiple species-interaction strengths related to variation in underlying environmental conditions that were previously unobserved.

The accumulated evidence suggests that in the San Nicolas kelp forest, environmental context drives positive-feedback loops in species interactions that maintain ecosystem states. Consider the effects of the NPGO on the interactions between Macrocystis, Pterygophora, and Laminaria (Figs. 4 and 5). Lower values of the NPGO index in the study area are associated with lower nutrient availability and reduced upwelling (36). In this nutrient-stressed context, apparent facilitation between the algae species is common, and the ability of Macrocystis to compete with the understory species declines. Furthermore, there can be strong negative intraspecies and interspecies effects on Macrocystis recruitment during low NPGO phases. This creates a self-reinforcing loop that suppresses Macrocystis abundance and promotes Pterygophora and Laminaria. Even under low herbivory pressure on Macrocystis, this positive feedback remains. The implication is that under nutrient-stressed conditions, Laminaria and Pterygophora should be favored over Macrocystis in competition, a result consistent with previous findings in other kelp forests (49). Importantly, because of the positive feedback, this ecosystem state—an understory forest instead of a Macrocystis forest—should be stable as long as the environmental context does not substantially change (46).

Alternatively, under elevated NPGO values, the nature of competition shifts among the kelp species. Pterygophora’s effect on Laminaria and adult Macrocystis becomes more competitive, but Pterygophora’s ability to suppress Macrocystis recruitment is reduced. These conditions create an opportunity for successful Macrocystis recruitment and the potential establishment of a kelp forest replete with both canopy-forming and understory kelp species. Considered in a dynamic framework, then, the ultimate outcome of elevated nutrient availability for kelp-forest relative species abundances will depend on priority effects. Negative interactions between some algal species means that whichever species is able to establish first in such a situation should be able to continue to dominate.

We have shown how environmental context underpins the strength of species interactions that, in turn, drive ecosystem dynamics. The effects of large-scale environmental signals like the NPGO and PDO are clearly related to the strength of species interactions in the San Nicolas kelp forest. Moreover, the relationship of algal species interactions to increased herbivory pressure (SI Appendix, Fig. S8) suggests that herbivory may reinforce or stabilize existing ecosystem states, rather than driving ecosystem change. This finding echoes other early (46) and recent (47) work done at San Nicolas Island, showing that nutrient regimes and available drift algae drive sea urchin feeding behavior, rather than herbivory driving kelp dynamics directly. Overall, we found that environmental context determines the balance of facilitation and competition and conclude that changes in environmental forcing can alter the likelihood of ecosystem state change. Therefore, we argue [in agreement with others (34–37, 69)] that bottom-up control is particularly important in driving kelp-forest ecosystem dynamics in southern California.

One important implication of our study is that if a research goal is to understand the dynamics of entire ecosystems, studying solely the mean outcome of single-species interactions may be highly misleading. We showed how varying species interactions in the San Nicolas kelp forest are key to a deep understanding of ecosystem dynamics. In kelp forests and other ecosystems, indirect associations between multiple species and shifting environmental contexts may give rise to rare, critical moments when fleetingly strong interactions determine ecosystem shifts. Rather than being viewed as purely stochastic events, our results suggest that we may be able to understand and perhaps predict the likelihood of these events through monitoring of large-scale environmental fluctuations and current ecosystem states. This idea needs further investigation in multiple systems, but if widely applicable, it means that context dependency—and its role in mediating varying species-interaction strengths—deserves more attention than the identification of mean species-interaction strengths (9).

Furthermore, it is the confluence of multiple species interactions that determines overall ecosystem dynamics, and no one interaction can necessarily be considered in isolation. It is clear from our results that when environmental context changes, the entire balance of species interactions changes as well, potentially precipitating ecosystem shifts or triggering the types of positive-feedback loops described above. This is likely the case in every ecosystem. A lesson from those findings, then, is that when investigating ecosystem shifts, it may be misleading to focus too intently on single interactions that are determined to be important a priori, without a careful analysis of how and why other interaction links may be changing concurrently.

We began in this study with a complex set of dynamics observed directly in long-term monitoring data. From those data, we established causation, built interaction networks, and investigated the influence of large-scale environmental drivers on species-interaction strengths. As a result, we were able to better understand why ecosystem shifts occurred, in relation to the environmental context at the time of those shifts. There is rich dynamic information contained in seemingly simple records of species densities over time, information that can and should be uncovered in ecosystems with existing long-term monitoring data to advance our understanding of key species, interactions, and environmental drivers.

Our study and others using EDM state-space reconstruction do not take the place of experimentation. Appropriate application of EDM requires relatively lengthy time series, which may not be available in many ecosystems. The San Nicolas Island dataset includes more than 30 y of data, a time-series length that could be considered a luxury in many systems. Moreover, there are detailed biological and ecological mechanisms and fine spatial- and temporal-scale dynamics that we cannot capture solely from such data analytics. That being said, the reverse is also true—even the most rigorous field experiments of ecosystem dynamics can be compromised by context dependencies, like we observed in this system. Multivariate EDM can help to both contextualize and guide insights from short-term experiments. Our analyses are a proof of concept: We started with time-series data from a monitoring dataset in a well-studied, but complex, ecosystem and showed how previous experimental results play out over a longer time period in a variable environment. The consistency of our findings with other kelp-forest studies and ecological theories, such as the Stress Gradient Hypothesis, argues for the potential of this approach to provide credible insights into other ecosystems, where time-series data exist, but where important interactions may not be nearly as well-established. Where important interactions are known, EDM can help to explore whether environmental context matters in interaction variance. Where ecosystem interactions are not as well-known, EDM may be a helpful first step in identification of ecosystem links, whose mechanisms can then be further established through other experimental and observational methods.

Materials and Methods

Data Standardization.

San Nicolas Island is a small, remote island situated about 100 km offshore from southern California. The data in the analysis are from a sampling station on the western end of San Nicolas Island. The benthic monitoring data herein have been collected more or less every 6 mo for more than 35 y by the US Geological Survey (USGS) and its Western Ecological Research Center (45). The monitoring site consists of 10 permanent transects (see ref. 45 for full monitoring protocols). Data from the 10 transects were manually stitched together to produce single long time series, leveraging spatial replication to create denser manifolds, a technique called dewdrop regression (70, 71). Each species’ time series therefore consisted of 630 total observations (63 monitoring periods across 10 replicates).

Physical data included historical SST from the National Oceanic and Atmospheric Administration’s Optimally Interpolated Sea Surface Temperature (https://www.ncei.noaa.gov/products/optimum-interpolation-sst), the MEI (54), the PDO (55), and the NPGO (56). The actual measures included in analyses for these four indices were the average values for the 4 mo preceding each period in the benthic monitoring data. This metric was chosen to approximate the general environmental conditions under which species interactions were occurring. The measure for maximum SWH combined modeled wave-height data from the USGS Geophysical Fluid Dynamics Laboratory (https://cmgwindwave.usgsportals.net/) with updated modeled data from the California Coastal Data Information Program [CDIP MOPv1.1 (72)], both based on data from an array of buoys distributed across the Southern California Bight. Significant wave height is here defined as the average height, in meters, of the one-third highest waves in the same 4 mo preceding each benthic monitoring period. This is meant to capture any large storm events and provide a general measure of physical disturbance. Unlike the biological data, where there are unique spatial replicates, the physical data have only 1 value for each of the 63 monitoring periods. Hence, the time series for the physical drivers are identical for each of the 10 spatial replicates. Missing data in the time series (about 15% of data points) were linearly interpolated between available observations. It is worth noting that, although there are other approaches to the handling of datasets with missing data in EDM, simple linear interpolation is expected to perform adequately for our situation, in which there are few missing points and those missing observations are irregular, never occurring more than twice in a row (73).

For attractor reconstruction, all time series were standardized to zero mean and unit variance, common practice in EDM (40). Additionally, the time series were detrended, removing any linear time trend from the biological variables’ time series.

CCM.

We used CCM to infer causal relationships between variables (42). CCM is described in detail elsewhere (40, 42), but is introduced here.

All EDM analyses, including the CCM and multispecies S-map algorithms used in this study, are based on extensions of Takens’ theorem of nonlinear dynamic systems (43, 74). Takens showed that a dynamic system could be accurately represented by using “shadow attractors,” or manifolds, built from time series of observed variables in that system. In basic terms, an attractor or manifold is built from a set of E-length state-space vectors, where E is the number of progressive lags of a single variable (for CCM) or the number of separate variables (for multispecies S-maps) used in the reconstruction. E is called the “embedding dimension.” Each E-length vector—for example, ${\mathbf{x}}_{\mathbf{t}}=<x_t,x_{t-1},x_{t-2}>$ —is a point on the attractor, and the set of E-length vectors used for the reconstruction is called the “library.” Takens showed that these reconstructions are topologically invariant to the “true” (unobserved) dynamic system, with a one-to-one mapping between points on the attractor and points on the true manifold. This powerful theory is what allows EDM to draw inference about nonlinear dynamic systems through attractor reconstruction.

Before variables were included in CCM-inferred causality tests, we ensured that each variable could be properly embedded using univariate simplex projection (40) (SI Appendix). Univariate simplex projection uses attractors built from multiple lags of single time series (e.g., for variable x, an attractor with an E of 3 would consist of vectors ${\mathbf{x}}_{\mathbf{t}}=<x_t,x_{t-1},x_{t-2}>$). To predict ${\mathbf{x}}_{\mathbf{t}+\mathbf{1}}$, the simplex algorithm finds the E + 1 nearest neighbors of ${\mathbf{x}}_{\mathbf{t}}$ in the library of vectors, and the prediction ${\widehat{\mathbf{x}}}_{\mathbf{t}+\mathbf{1}}$ is the average of those nearest neighbors’ values at ${\widehat{\mathbf{x}}}_{\mathbf{t}+\mathbf{1}}t+1$, weighted by their Euclidean distance from ${\mathbf{x}}_{\mathbf{t}}$ at t. This is the essence of simplex projection: A forecast for a given point in state space is surmised from the forward trajectories of observed nearby points. Keep in mind that because of the way attractors are reconstructed, the nearest neighbors are not necessarily nearby in time, but, rather, close in ecosystem “state” to the predicted point. Applying this method, all variables in the analysis showed significant univariate predictability based on out-of-sample prediction skill (SI Appendix, Fig. S1). The best embedding dimension (that is, the number of lags included for each variable that gave optimal predictability) was extracted for each variable. These best E’s are an estimate of the dimensionality of the dynamic system experienced by each species.

Extensions of Takens’ theory state that if two variables (in our case, species or physical variables) are part of the same dynamic system, their univariate attractors should be topologically invariant from the true attractor and, therefore, should be topologically invariant from one another (39, 42). This means that there will be a one-to-one mapping (“cross-mapping”) between points on the reconstructed attractor of one variable and the corresponding points on the other variable’s attractor. Taking advantage of this property, significant cross-mapping is evidence of causation. In practical terms, if (for example) giant kelp is causally forced by sea urchins, that forcing should leave a signature on the giant kelp time series. CCM tests for causation by using the same simplex algorithm as described above, except that now we use an attractor/manifold built from the time series of one variable (X) to predict contemporaneous values of another variable (Y). If the attractor can accurately predict the dynamics of the second variable, we infer that the second variable has a causal influence on the first. In simple terms, the inferred causal effect of X on Y is determined by how well Y cross-maps X (42). In this way, the inference from cross-mapping is the converse direction of causation. In our example, if sea urchins drive giant kelp, the dynamic information from the urchin time series should be reflected in the kelp dynamics, and, therefore, we should be able to recover (cross-map) dynamic information about sea urchins using the kelp time series (which, indeed, we can; SI Appendix, Fig. S3). Moreover, as we use more data in the cross-mapping, the predictive skill should increase. This is because with more data, the attractor “fills in,” or becomes denser, and, consequently, predictions made from nearest neighbors become more accurate. This property is called “convergence” (hence, “CCM”) and is an essential criterion for causation and what distinguishes correlation from causation (42). We assessed convergence by testing whether cross-mapped prediction accuracy (Pearson’s ρ between observations and predicted values of the cross-mapped variable) improves with library length (the number of embedded vectors used to construct the attractor). If two variables are spuriously correlated and not causally linked, CCM will not display convergence.

Following Sugihara et al. (42), each separate CCM test used an attractor built from one variable to predict another. Causation was tested by plotting predictive skill ρ against library size. For simplex and CCM analyses, we used leave-one-out cross-validation to assess model skill, where models were built excluding one observation at a time and used to predict that observation. Then, the process was repeated for all observations. We used three restrictive criteria for CCM to establish inferred causality, to ensure to the extent practicable that CCM did not simply represent spurious correlation between time-series variables (75). The criteria were, first, that cross-map skill using all available data were significantly greater than zero; second, that predictability was convergent, defined by whether the predictive skill at maximum library size was significantly greater than predictive skill at minimum library size (71); and, third, that that CCM significance was robust to the use of a seasonal null model and, hence, did not simply represent effects of shared seasonality in species dynamics (see the online repository at GitHub [https://github.com/owenrliu/env_context_dependency] for details). Any species interactions that failed any of these tests were deemed noncausal. All species–species and species–environment interactions were tested by using CCM (Fig. 2 and SI Appendix, Fig. S4), and significant interactions among species that met inferred causality criteria were retained for use in building multispecies attractors.

Multivariate S-Maps.

Multivariate attractors follow the same logic as the attractors described above, except that, instead of using single variables to reconstruct the attractors, we use contemporaneous values of multiple variables (38). That is, instead of library vectors or points in state-space taking the form of, for example, $<x_t,x_{t-1},x_{t-2}>$, they now are formed in true multivariate space, e.g., $<\mathit{Kel}{p}_t,\mathit{Urchi}{n}_t,\mathit{Nutrient}{s}_t>$. Additionally, instead of making predictions using only nearest neighbors, S-maps [sequential locally weighted global linear maps (43)] use all library vectors and exponentially weight them by their distance to the prediction vector before using linear regression to make a forecast; vectors closest to the prediction vector have the greatest weight. Because library vectors are weighted individually in this manner, a separate linear map is created for each predicted vector. This is why the procedure is called “sequentially weighted global linear maps.” Conceptually, as the dynamic system moves along the surface of the attractor, S-maps sequentially compute new linear maps to the next point. The varying species interactions (the measure of interest) are the coefficients of these local linear maps.

Mathematically, when making a prediction for a target point ${\mathbf{x}}^{*}$, each library vector (point on the attractor) ${\mathbf{x}}_{\mathbf{k}}$ is given a weight

$$w_k=\mathit{exp}\frac{-\theta \left|\right|{\mathbf{x}}_{\mathbf{k}}-{\mathbf{x}}^{*}\left|\right|}{\overline{d}},$$

where $\left|\right|{\mathbf{x}}_{\mathbf{k}}-{\mathbf{x}}^{*}\left|\right|$ is the Euclidean distance between the library and target vector, and $\overline{d}$ is the average distance to all library vectors. By controlling the strength of local weighting, the single parameter θ controls the nonlinearity of the model (38, 43).

As described in Results, the multivariate model for each species consisted of all the species that showed significant causation through CCM analysis. An example of a multispecies attractor is shown in SI Appendix, Fig. S5. Additionally, the preferred model for each species was then constructed by finding the value of θ (the amount of nonlinearity) that optimized out-of-sample prediction using leave-one-out cross-validation. Each S-map model resulted in 500 to 520 estimated interactions for each significant link in Fig. 2 across the entire dataset, which were then compared to the environmental conditions under which they took place. For individual model θ and performance metrics, see SI Appendix, Fig. S2 and SI Appendix, Table S1.

State-Space Interaction Averaging.

To compare Jacobian elements to each other (i.e., to compare the effect of environmental drivers to the effect of biological drivers on target species’ dynamics), we adapt a method from ref. 66. For each multispecies S-map model, we extract all estimated species and environment–species interactions (coefficients from local Jacobians). Then, for each estimated interaction, we find its 30 nearest neighbors in the multivariate model space—its 30 most similar environmental and biological contexts—and then calculate the average value of the interaction among those 30 neighbors. By doing this for all estimated interactions, we can observe the general environmental contexts that give rise to stronger or weaker species interactions, while smoothing across individual observations.

Supplementary Models.

In the above analyses, we are interested in the influence of causal environmental variables on species interactions in kelp forests. We use causation tests (CCM) and multivariate embeddings to explore how important interactions vary along environmental gradients. However, as a robustness check, we want to ensure that the results are not overly determined by the particular choice of variables to include in each model. In the main analysis, we choose to include in multivariate models all the physical and biological variables that showed inferred causal signals, as determined by CCM. Another feasible choice for model selection in EDM is to try to find a combination of predictor variables that best predict the target biological variable. We performed a variable-exclusion model-selection process that started with all candidate-inferred causal variables for each species and removed variables sequentially until predictability began to decay. In the course of model selection, if model dimensionality (total number of included variables) falls below the optimal embedding dimension for that species (derived from univariate simplex; SI Appendix, Fig. S1), we add lags of the focal variable to retain the optimal embedding dimension.

Variable reduction through model selection does not strongly affect the direction and variability of the remaining estimated species-interaction coefficients (SI Appendix, Figs. S10–S12), providing further confidence that the Jacobian estimates of specific species interactions are robust to alternative embeddings. For the main-text results, we retain the full models that include interactions of each species with all physical and biological variables that showed inferred causal signals in CCM analyses because in this study, we are interested primarily in variation in species interactions driven by environmental fluctuations, and not exclusively in maximizing the predictability of any one species’ dynamics.

As an additional robustness check, we rerun the multivariate S-map models using a version of the data that is first-differenced (SI Appendix, Figs. S13 and S14). Often, EDM uses first-differencing to detrend long time series and focus on dynamics. The same variables were chosen for each species’ model, as in the multivariate models from the main analysis.

All analyses in the study were performed in R (76), especially utilizing the rEDM package [version 1.11.0 (77)]. All code and reproducible analyses are included in SI Appendix.

Data, Materials, and Software Availability

Time-series data and code data have been deposited in GitHub (https://github.com/owenrliu/env_context_dependency) (78).