Abstract
Recent studies have advocated for the use of connected speech in clinical voice and speech assessment. This suggestion is based on the presence of clinically relevant information within the onset, offset, and variation in connected speech. Existing works on connected speech utilize methods originally designed for analysis of sustained vowels and, hence, cannot properly quantify the transient behavior of connected speech. This study presents a non-parametric approach to analysis based on a two-dimensional, temporal-spectral representation of speech. Variations along horizontal and vertical axes corresponding to the temporal and spectral dynamics of speech were quantified using two statistical models. The first, a spectral model, was defined as the probability of changes between the energy of two consecutive frequency sub-bands at a fixed time segment. The second, a temporal model, was defined as the probability of changes in the energy of a sub-band between consecutive time segments. As the first step of demonstrating the efficacy and utility of the proposed method, a diagnostic framework was adopted in this study. Data obtained revealed that the proposed method has (at minimum) significant discriminatory power over the existing alternative approaches.
I. INTRODUCTION
Voice and speech are the primary methods for communicating ideas, thoughts, and emotions and degradation in their perceived quality by the listener can significantly reduce a person's communicative effectiveness and quality of life.1–3 In instances where a voice abnormality exists, comprehensive evaluation is an integral part of the clinical assessment4 with auditory-perceptual assessments and acoustic measures serving as the primary methods of voice evaluations.5,6 However, auditory-perceptual assessment is a subjective index that is prone to high degrees of inter-rater and intra-rater variability.7 Conversely, acoustic measures are objective approaches which are robust to factors such as human bias and variability that can provide a fast, automatic, and low-cost tool for voice assessment.
Acoustic measures can be categorized into four main groups. First, perturbation measures quantify the cycle-to-cycle variations in the amplitude and frequency of vibration of the vocal folds with shimmer and jitter being the most well-known examples, respectively.8 Second, noise parameters quantify the irregular component of the voice. Some examples from this category are signal-to-noise ratio,9 harmonic-to-noise ratio,10 and energy of the noise in different sub-bands.11 Third, cepstral and spectral measures capture spectral characteristics of the acoustic signal with cepstral peak prominence (CPP),12 long-term average spectrum (LTAS),13 and temporal-spectral dynamics of speech14 being the most common methods. Fourth, non-linear measures such as the largest Lyapunov exponent15 and parameters of the shape of phase-space have also been used.16
Considering the type of token, acoustic measures can be applied to either sustained vowels or connected speech (i.e., spoken phrases or sentences). Sustained phonation is minimally affected by intonation, speech rate, and dialect,17 as the phonatory mechanism is less variable during its production which may lead to more reliable measures.18 Also, its production requires less instruction from the clinician,19 and thus, sustained vowels have traditionally been the stimulus of choice for acoustic analysis. Conversely, connected speech is associated with variations in frequency, intensity, intonation, prosody, phonation onsets and offsets, and other temporal and spectral variations. Ecological validity has been among the primary reasons for advocating the usage of connected speech for acoustic analyses of the voice.20,21 For example, using sustained vowels rather than connected speech may lead to more severe auditory-perceptual ratings,19,22,23 a finding that may lead to bias during voice assessment. Additionally, non-stationary characteristics of speech (e.g., onsets) are a significant source of information for voice assessment24 and connected speech is the more likely context for manifestation of certain voice disorders that result in dysphonia.25
At present, several different approaches are available for the evaluation of connected speech.9,21,26–33 One possibility is to use perturbation measures,26,30,32,34 however, perturbation requires accurate estimation of the fundamental frequency (F0) which is increasingly unstable for dysphonic vowels35 and the dynamic nature of connected speech would make such an application even more challenging. Additionally, intonation and prosody are inherent characteristics of running speech, and hence perturbation measures in connected speech would be higher. However, distinguishing between normal and dysphonia-induced perturbations is not a trivial task and may perform inferiorly in comparison to spectral and noise measures.26
Despite several disadvantages, other widely used measures for evaluation of connected speech are LTAS13,26,29,31–33 and CPP and its smoothed version (CPPs).20,21,27,28,31 The underlying assumption behind CPP and CPPs is the existence of a voicing component, whereas connected speech includes both voiced and unvoiced phonemes. One remedy is to detect the voiced segments and then concatenate them for the analysis.13,26,32–34 However, because the unvoiced segments are removed, artificial sharp transitions are introduced into the stimuli being analyzed. More importantly, this evaluation does not give a full representation of the speech sample. Second, LTAS, CPP, and CPPs only provide the general (i.e., the long-term and average) characteristics of the speech sample, while spectral and temporal dynamics of speech (e.g., onsets, offsets, pitch, and intensity variations) are the main distinguishing factors between connected speech and sustained vowels. Unfortunately, to date, none of these methods have been designed to capture and model these non-stationary phenomena.
Continuing our seminal work14 this study proposes a novel non-parametric approach for quantification of the dynamics and variation of connected speech in temporal and spectral domains with possible clinical applications. However, given the “methodological” computational nature of the current study we have adopted a diagnostic framework as the first step of validating the proposed method and demonstrating that it has (at minimum) significant discriminatory advantages over existing alternative acoustic measures.
II. MATERIALS AND METHODS
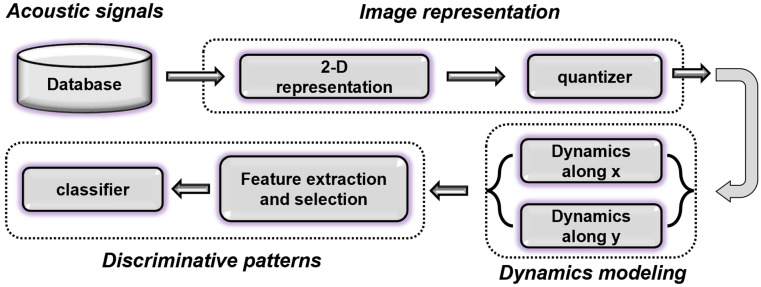
The acoustic speech signal is often displayed as a time-dependent amplitude signal. This one-dimensional (1D) representation has a perfect time resolution. However, it is possible to exchange the temporal resolution and to derive a two-dimensional (2D) temporal-spectral representation of the signal. The potency of this approach for cryptanalysis of scrambled speech was demonstrated recently36 and intelligibility of 92.9% was reported for the recovered samples.37 This value was 50.9% higher than methods based on 1D representation of the speech.37 Considering the inherent difficulty of the cryptanalysis problem, this result suggests the potential of the 2D representation of an acoustic signal. The 2D representation of speech makes the visual tracking of the temporal-spectral variations possible. Owing to this characteristic, spectrograms (which are 2D representations) have been an important tool in voice science and phonetics.38,39 The current study is based on a similar rationale and proposes a novel approach for objective measurement of the dynamics of connected speech from its 2D representation. There are many benefits to this approach, for example, the trade-off between temporal and spectral resolutions could be adjusted to achieve the best result. Also, the conversion from 1D to 2D representation is very flexible and could be implemented based on filter banks in a suitable domain,40 short-time Fourier transform,37 and wavelet.41 Finally, many image processing techniques become applicable to acoustic signals. Figure 1 shows a block diagram of the proposed method. First, the acoustic signal is transformed into its 2D image representation, and then its variation and dynamics along the x (time) and y (frequency) axes are modeled. Supervised learning is employed for finding discriminative patterns between dynamics of different classes.
FIG. 1.
(Color online) Block diagram of the proposed method.
A. Database
Based on our rationale, the performance of the proposed method was evaluated using three different speech datasets. Details of each data set are presented in Table I.
TABLE I.
Summary of the included datasets. M: Male, F: Female. The numbers reported before and after the ± are mean and standard deviation. Amyotrophic lateral sclerosis (ALS), Parkinson’s disease (PD), adductor laryngeal dystonia (AdLD), unilateral vocal fold paralysis (UVFP), and vocal hyperfunction (VHF).
| Dataset | Classes | Participants' information | Recording information | Severity score | ||||
|---|---|---|---|---|---|---|---|---|
| Number | Gender | Age | Number | Length(s) | Token | |||
| ALS-DB | Control | 12 | 6 M, 6 F | 66.1 ± 9.5 | 1197 | 1.6 ± 0.3 | Say [target words] again | 98.5 ± 0.7 |
| ALS | 8 | 4 M, 4 F | 64.6 ± 10.2 | 1197 | 1.8 ± 0.5 | 72.7 ± 12.1 | ||
| PD-DB | Control | 33 | 15 M, 18 F | 61.3 ± 14.7 | 33 | 48.9 ± 5.9 | Grandfather Passage | 98.5 ± 0.8 |
| PD | 57 | 29 M, 28 F | 68.7 ± 9.0 | 57 | 55.4 ± 16.5 | 89.9 ± 10.6 | ||
| VD-DB | Control | 32 | 16 M, 16 F | 39.3 ± 8.8 | 32 | 32.0 ± 5.8 | First paragraph of the Rainbow Passage | 13.3 ± 1 |
| UVFP | 24 | 10 M, 14 F | 58.2 ± 9.4 | 24 | 42.8 ± 9.7 | 10.4 ± 1.2 | ||
| AdLD | 20 | 4 M, 16 F | 58.3 ± 9.7 | 20 | 43.3 ± 6.7 | 11.2 ± 0.9 | ||
| VHF | 49 | 23 M, 26 F | 44.2 ± 10.9 | 49 | 37.0 ± 6.9 | 11.9 ± 1.6 | ||
The first dataset was a two-class set, and it included speech recordings from participants with amyotrophic lateral sclerosis (ALS) with bulbar symptoms and age-matched controls. The ALS group consisted of eight individuals recorded over three sessions (baseline, 3 months, and 6 months later). The control group consisted of 12 vocally healthy individuals recorded over two sessions (baseline and 6 months later). Due to dropout, some participants had recordings only from some of the sessions. All participants completed the Word-In-Phrase portion of the Speech Intelligibility Test for Windows®47 and the acoustic signals were recorded using a head mounted microphone (AKG C410) positioned 6 cm from the mouth at a 45° azimuth and a digital recorder (Zoom H4N, 24-bit/96 kHz). For this task 57 target words were selected randomly and inserted into the carrier phrase, “say [target words] again” and each subject was asked to read them using their typical pitch and loudness. Severity of speech impairment was measured from these stimuli as percent speech intelligibility;47 interested readers may refer to Refs. 48 and 49 for further information about this dataset.
The second dataset was a two-class set that included speech recordings from participants with Parkinson's disease (PD) and controls. The PD and control groups consisted of 57 and 33 participants, respectively. All participants were asked to read the Grandfather Passage50 at a comfortable pitch and loudness level. The Grandfather Passage contains 129 words and is a standard passage for the evaluation of motor speech disorders. The acoustic signals were recorded using a headset microphone (Shure SM150) positioned 15 cm from the mouth and a Tascam DA-P1 DAT recorder (16 bit/48 kHz). Severity of speech impairment was measured using the Speech Intelligibility Test for Windows®47 and interested readers may refer to Ref. 51 for further information about this dataset.
The third dataset was a four-class set, and it included speech recordings from participants with voice disorders [adductor laryngeal dystonia (AdLD), unilateral vocal fold paralysis (UVFP), and vocal hyperfunction (VHF)] and controls. All participants were asked to read the first paragraph of the Rainbow Passage52 at their comfortable pitch and loudness. The Rainbow Passage is a standard passage used for the evaluation of voice disorders and its first paragraph contains 98 words. The acoustic signals were recorded using a cardioid condenser microphone (SHURE PG81) positioned 15 cm from the mouth and a laptop running Kay-Pentax Sona Speech II (16 bit/ 44.1 kHz). No perceptual evaluation was available for this dataset; therefore, CPP12 was used as a corollate for the overall severity.
B. 2D image-representation
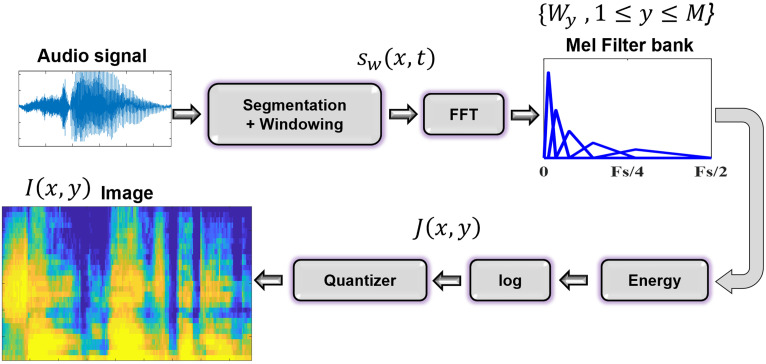
This study adopted a filter bank approach for creating the 2D representation of speech, as filters with different frequency resolutions (e.g., Mel,42 R-Mel,40 uniform11) can be used. Also, the output of each filter is expressed using a single number (i.e., energy) which would reduce the number of spectral measures (the number of vertical pixels in the image). This is especially useful for short recordings. Figure 2 represents the steps.
FIG. 2.
(Color online) Block diagram of image representation steps.
The audio signal was segmented and then multiplied with a Hamming window. Fast Fourier transform (FFT) of each segment was then multiplied with a set of filters constructed based on the Mel scale which provides high spectral resolution at low frequencies and low spectral resolution at high frequencies.40 Equation (1) shows the conversion of a frequency f from Hz into Mel,
| (1) |
The number of filters in the bank determines the spectral resolution (i.e., the number of vertical pixels) in the final image. Detailed information regarding the construction of the filter bank may be found in an earlier work.43 The energy of each filter was computed by summing its output in the frequency domain. A column of the image was created by vertical concatenation of energy of all filters. Repeating these steps for all segments results in the 2D representation of the signal, where x and y axes correspond to temporal and spectral domains, respectively. Let {Wy: y = 1,…,M} be a bank of M filters, and denotes the FFT. Also, assume that the acoustic signal has been divided into N segments, with sw(x,t) denoting segment x after applying the Hamming window. Equation (2) shows the relationship between these variables, where J(x,y) is the output of Fig. 2 after log operation. Equation (3) shows the relationship between N, the length of the signal (L), the segment length (ρ), and the amount of overlap (λ),
| (2) |
| (3) |
J(x,y) is a 2D representation with real values. To use image processing techniques, they should be mapped into a limited set of numbers. This was done by applying a quantizer ( ) on J(x,y),
| (4) |
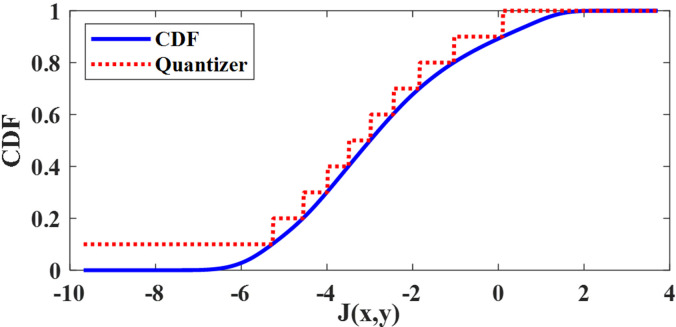
A scalar non-uniform quantizer with l levels was constructed by dividing the range of [0, 1] from the cumulative distribution function (CDF) of into l equal-length intervals. The values corresponding to those intervals were selected as steps of the quantizer. Implications of different values of l are discussed later in the simulations and results section. Figure 3 shows an example.
FIG. 3.
(Color online) A non-uniform scalar quantizer with l = 10 levels.
C. Dynamics modeling
The image I(x,y) has N × M pixels, and given the dependence of N on the recording length comparison between different recordings would require some temporal normalization first. Additionally, evaluating individual pixels provides limited information and most of the information is present at a larger scale. Therefore, the value of each pixel with respect to its neighbors were quantified using their joint distributions. The 1-neighborhood defined along x and y axes would capture temporal and spectral variations of the signal. The mathematical definition of temporal ( ) and spectral ( ) models are shown in Eqs. (5) and (6), where denotes the Dirac delta function and ,
| (5) |
| (6) |
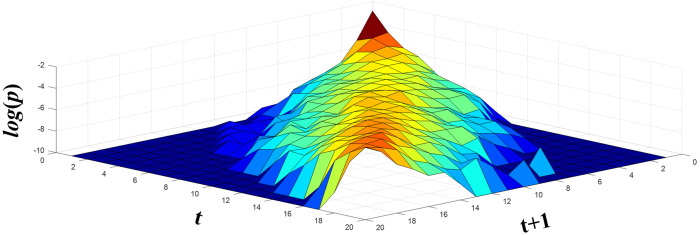
It is worthwhile to elaborate on the interpretation of the models. means that if the energy of a sub-band at time t is equal to i, the energy of the same sub-band at time t + 1 would change to j with a probability of k. means that if the energy of a sub-band at time t is equal to i, the energy of the next sub-band at the same time t would change to j with a probability of k. Figure 4 depicts the spectral model of a test sample on a logarithmic scale. The small values have been replaced with −10 for better illustration.
FIG. 4.
(Color online) Spectral model of a test sample with l = 20 levels.
D. Feature extraction procedure
The proposed approach yielded two statistical models and their components (l2 values per model) can be used for finding discriminative patterns, but they can only capture simple phenomena. However, the holistic properties of the model can capture more complex characteristics. Further, the two models will produce 2l2 values. Training a classifier with many features increases its computational complexity, requires more training samples, and introduces the possibility of redundant or irrelevant features. Therefore, features were extracted from the shape of the models instead. A model with just diagonal values represents a static phenomenon. Therefore, dispersion from the diagonal would be a good holistic feature. The first rows of the model represent low energy values and variation in that region is more likely to happen and therefore less informative. Hence, dispersions at higher energies were weighted more. Equation (7) shows the formula for diagonal dispersion. Values of and were used in this paper,
| (7) |
A model with many zeros and just a few large values indicate a predictable signal, whereas model with many small values indicates a less predictable signal. Entropy can quantify these and Eq. (8) shows its computation,44
| (8) |
Diagonal dispersion and entropy provide macro-level information of the models. To capture local information, values of the mean ( ), standard deviation ( ), and inertia ( ) for every row r of the models were also computed,
| (9) |
| (10) |
| (11) |
In summary, 3l + 2 features (a diagonal dispersion, an entropy, l means, l standard deviations, and l inertias) were extracted from each model.
E. Finding discriminative patterns
To find discriminative patterns between target classes, a support vector machine (C-SVM) with radial basis function (RBF) kernel was used. The kernel scale was set to auto in matlab. Feature normalization could improve the performance of classifiers.16 Equation (12) was used for this purpose, where μ and σ denote the mean and standard deviation of a feature f estimated from the training samples,
| (12) |
Finally, feature selection was used to remove the irrelevant and redundant features. This step significantly reduces the number of features in the final model and is a necessary step for achieving the interpretability of the framework and understanding the underlying differences between classes. The present study used a genetic algorithm (GA) due to its superior performance.16,45 This decision was made primarily due to the fact that unlike sequential feature selection, GA-feature selection directly works in the target sub-space and can benefit from the existence of any high-dimensional interaction between the selected features. Parameters of our GA were as follows: accuracy of classifier as the fitness function, 200 individuals, two-point crossover,46 tournament selection, and mutation with a rate of 1%. The GA algorithm was stopped if the fitness function did not improve after five consecutive generations.
F. Cross-validation approach
Generalization of the outcomes on PD-DB and VD-DB were evaluated using a stratified ten-fold cross-validation, where all samples from each class were evenly and randomly divided into ten disjoint sets. Each set constituted the testing set of that fold, and all the remaining samples were included into its corresponding training set. Referring to Table I, participants from the ALS-DB had multiple speech tokens; therefore, using a ten-fold cross-validation would lead to data overlap between training and testing sets. Therefore, a leave-one-subject-out method was used for ALS-DB. That is, for control participants, recordings from both sessions (2 × 57 samples) were excluded from their relevant training set and only included in their relevant testing set. For participants with ALS, however, each recording session was treated separately and only 57 samples were excluded from the training set and included in the testing set. The rationale for this choice was that ALS is a progressive disease and the 3-month gap between different recording sessions was leading to significant degradation in the speech recorded during later sessions. Investigating the intelligibility and speech rate of participants with ALS over different sessions provided confirmation.49
III. SIMULATIONS AND RESULTS
Four different experiments were conducted to demonstrate the application and performance of the proposed method.
A. Experiment 1: Dynamics models of synthetic signals
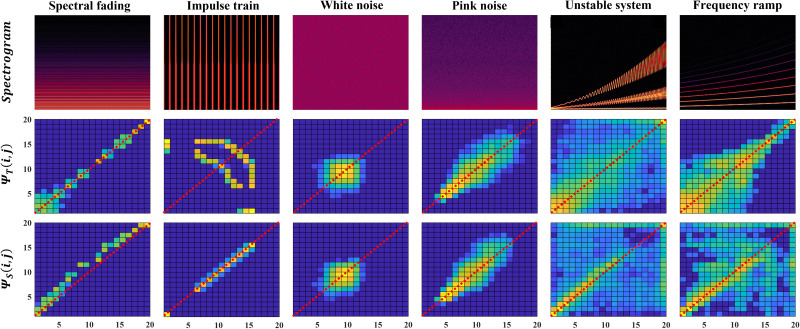
To provide better insights into the proposed method, temporal and spectral models of different synthetic signals are shown in Fig. 5. The first signal was a series of finely spaced harmonics with decreasing amplitudes at higher frequencies. Its temporal model has values primarily on the diagonal indicating little temporal variation. On the other hand, its spectral model has a concave shape (i.e., values are above the main diagonal), meaning that with high probability the next sub-band has lower energy. Both observations agree with the expectations for this signal. The second signal was an impulse train (i.e., fast temporal variation but a constant spectrum). The temporal model shows large values (yellowish color) for off diagonal entries, indicating that with high probability a high-energy time segment is followed by a low-energy time segment. In contrast, the spectral model only has values on the main diagonal, revealing similar energy between consecutive sub-bands. Both observations agree with the expectation for an impulse train. The next two signals were white and pink noises, respectively. White noise exhibits similar temporal and spectral models which concur with visual inspection of the spectrogram. The models also have Gaussian-like shapes. Samples of white noise are independent and identically distributed, and elements of our models are constructed using a sum [Eqs. (5), (6)]; therefore, the Gaussian-like peak was expected. Pink noise has a much wider range of variations and, hence, its models exhibit more dispersed patterns. Finally, the spectrograms of the last two signals are more complex which is depicted in their temporal and spectral models. Finding discriminative patterns for the last two examples are more challenging; therefore, machine learning was used for the remaining experiments where the discriminative power of the proposed method was investigated.
FIG. 5.
(Color online) Spectrogram, temporal, and spectral model of some synthesized signals. Diagonal of each model is represented with a red dotted line.
B. Experiment 2: Parameter tuning
This experiment demonstrates effects of parameters of the proposed method and serves as a sensitivity analysis. We started with 30 ms segments, 15 ms overlap, and 20 filters, and sequentially optimized a set of parameters at a time. This experiment was conducted using the ALS-DB with a forward feature selection16 due to its lower computational complexity and good performance.45 The number of quantizer levels (l) determines the number of intensity levels in the image, and hence the resolution of changes that can be captured. A larger value of l leads to an image with more temporal-spectral details, which is desirable. However, it also increases the number of entries in the models. The value of l was changed from 10 to 80 levels in increments of 5. Table II presents the results for selected values of l.
TABLE II.
Effect of quantizer level on the accuracy of the classifier.
| Number of selected features | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| l | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 10 | 68.2 | 77.5 | 81.2 | 83.6 | 83.9 | 84.4 | 85 | 84.7 | |
| 20 | 66.2 | 73.5 | 75.9 | 80.2 | 82.6 | 83.5 | 84.5 | 85.1 | |
| 30 | 66.8 | 74.2 | 75.4 | 76.8 | 78.4 | 80.8 | 81.9 | 83.2 | |
| 40 | 69.2 | 75.9 | 80.6 | 81.6 | 84.2 | 84.7 | 85.6 | 86.3 | |
| 50 | 69.8 | 78.7 | 82.7 | 83.3 | 84.3 | 85.4 | 86.3 | 87 | |
| 60 | 77.9 | 82.1 | 83.7 | 85.4 | 85.8 | 86.4 | 87.7 | 88 | |
| 65 | 83.2 | 84.6 | 85.6 | 86.9 | 87.5 | 89.1 | 90.1 | 90.7 | |
| 70 | 84.6 | 85.9 | 87.2 | 87.3 | 88.5 | 90 | 90.1 | 90.7 | |
| 75 | 85.7 | 87.1 | 87.8 | 88.2 | 88.8 | 89.6 | 90.4 | 90.2 | |
| 80 | 86.5 | 88.6 | 89.4 | 90.1 | 90.9 | 91.2 | 91.2 | 91.1 | |
| 10 | 57.8 | 63.2 | 69.3 | 72.7 | 75.6 | 77.2 | 78.7 | 79.4 | |
| 20 | 59.7 | 47 | 56.1 | 63.8 | 65.1 | 65 | 67.2 | 71.5 | |
| 30 | 63.3 | 55.3 | 67.4 | 73.1 | 77.5 | 79.7 | 80.8 | 81.4 | |
| 40 | 66.2 | 62.5 | 73.9 | 78.8 | 81.5 | 82.8 | 83.6 | 83.9 | |
| 50 | 66.1 | 73.2 | 77.3 | 79.6 | 82.4 | 84.2 | 84.6 | 85.6 | |
| 60 | 75.7 | 83.8 | 85.9 | 87 | 87 | 88.4 | 89 | 89.2 | |
| 65 | 81.4 | 84.5 | 86.6 | 86.7 | 87.7 | 88.6 | 88.9 | 89.4 | |
| 70 | 84 | 87 | 88.1 | 88.3 | 88.5 | 89 | 89.1 | 89.2 | |
| 75 | 84.1 | 87.3 | 87.3 | 87.5 | 88 | 88.8 | 89.6 | 89.6 | |
| 80 | 85 | 87.8 | 88.1 | 89.3 | 89.2 | 89.7 | 90.3 | 90.5 | |
Based on Table II, the performance of both models improves as l increases, with the largest improvement occurring around l = 60. However, the number of features increases with l and longer recordings are also required for reliable estimation of the joint distributions [Eqs. (5), (6)]. Hence, the value of l = 65 was selected.
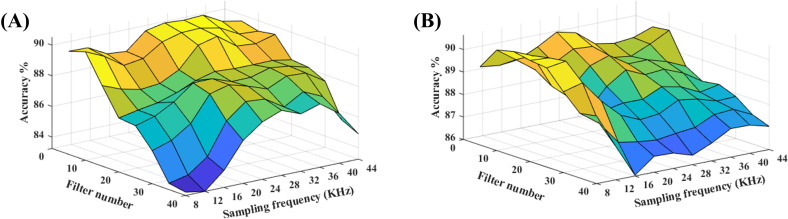
The spectral resolution depends on the sampling frequency (Fs) of the signal and the number of filters (M), where Fs determines the bandwidth of the signal and M determines how finely that bandwidth is divided into different frequency bands. That is, we could increase the spectral resolution of the produced image by increasing the value of M. Alternatively, we can derive a high-resolution representation from the low-frequency regions of the signal (i.e., discarding its high-frequency components) by keeping the M constant and instead downsampling the signal from the original Fs into a lower one. The value of target Fs (i.e., the downsampled version) was changed from 8 to 44.1 kHz in 8 kHz-increments, and the value of M was changed from 5 to 40 in increments of 5. Figure 6 presents the results smoothed by an averaging filter with the size of 2 × 2.
FIG. 6.
(Color online) Effect of spectral resolution when eight features are selected: (A) Spectral model, (B) Temporal model.
Based on Fig. 6 performance of the spectral model generally improves with an increase in Fs, but the temporal model is relatively robust to variations in Fs. Additionally, both models perform better with a low number of filters. The two models are independent of each other and could be computed with different parameters, but for simplicity, the same set of parameters (Fs=28 000 Hz and M = 10) was used for both models.
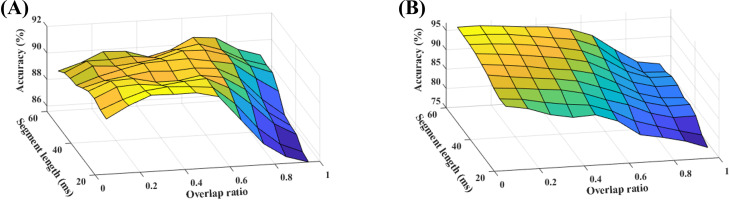
Segment length and the value of overlap determine the temporal resolution and smoothness of the produced image. The value of segment length was varied from 20 to 60 ms in 5 ms-increments, and the value of overlap was varied from 5% to 95% of the segment length in 5%-increments. Figure 7 presents the results smoothed by an averaging filter with the size of 2 × 2.
FIG. 7.
(Color online) Effect of temporal resolution when eight features are selected: (A) Spectral model, (B) Temporal model.
Based on Fig. 7, the spectral model has its best performance at moderate values of segment length and overlap, whereas a larger segment length with a small overlap is optimum for the temporal model. The two models are independent of each other and could be computed with different parameters, but for simplicity, the same set of parameters (45 ms and 35% overlap) was used for both models.
C. Experiment 3: Comparison with alternative approaches
This experiment was conducted to compare the performance of the proposed method with some existing alternatives. Recently, LTAS was used for analysis of connected speech of PD.33 We followed the same methodology and extracted ten features from speech. CPP and CPPs12 are also popular acoustic measures for evaluation of connected speech. We used their mean, standard deviation, skewness, and kurtosis as classification features. The distribution of F0 could be discriminative too, therefore, the same four statistical moments were also computed from the F0 of speech samples. Computations of CPP, CPPs, and F0 have an implicit assumption about the presence of a voicing component in the speech. Therefore, these measures may be extracted only from the voiced segments of the speech. This routine has been recommended in some studies,20,32 while others did not make such distinction.4,12,21,27 To account for this discrepancy and to measure the effect of including unvoiced segments on the performance of features, both cases were investigated. Conversely, computation of the LTAS does not have such assumption and it can be computed from the whole signal. Yet, some studies have computed LTAS only from voiced segments;13,26,33 therefore, the performance of both cases was investigated. Voiced segments were detected using a combination of zero-crossing rate, energy, and autocorrelation.26 Wavelet analysis is another method that had promising results on sustained vowels,41 but it can also be applied to connected speech. Features were computed as entropy and energy of all sub-bands.41 Modulation spectra is another technique that is suitable for the analysis of connected speech and has already been used for evaluation of PD.53 Features were computed as the mean and standard deviation of modulation spectra centroids and their energy.
Table III compares the performance of the proposed method with some existing alternatives on three speech datasets. It is noteworthy that, the main goal of classification for ALS-DB was to discriminate between ALS and controls and the proposed method used six features. The main goal of classification for PD-DB was to discriminate between PD and controls and the proposed method used four features. Finally, the main goal of classification for VD-DB was to discriminate among controls and the three groups of voice disorders (Table I) and the proposed method used seven features. A series of two-sample t-tests were used to compare performance of the proposed method (Spectral+Temporal) with Wavelet, which was the best existing alternative on all three datasets. The proposed method significantly outperformed the Wavelet method on ALS-DB (p = 0.006, t = 2.8), PD-DB (p = 0.0001, t = 5.4), and VD-DB (p = 0.006, t = 3.1). These promising results confirm the advantage of the proposed method.
TABLE III.
Performance of different methods in terms of sensitivity (Sen.), specificity (Spe.), accuracy (Acc.), and balanced accuracy (BAcc.). The best results are shown in boldface.
| ALS-DB | PD-DB | VD-DB | ||||||
|---|---|---|---|---|---|---|---|---|
| Feature set | Sen. (%) | Spe. (%) | Acc. (%) | Sen. (%) | Spe. (%) | Acc. (%) | Acc. (%) | BAcc (%) |
| LTAS | 72.0 ± 23.7 | 73.1 ± 19.3 | 72.4 ± 21.9 | 93.0 ± 12.0 | 24.2 ± 23.7 | 67.8 ± 7.8 | 39.8 ± 10.0 | 31.1 ± 11.8 |
| LTASa | 63.2 ± 23.6 | 50.3 ± 20.3 | 58.5 ± 23.0 | 93.3 ± 11.7 | 9.2 ± 14.9 | 62.3 ± 9.1 | 40.8 ± 11.9 | 30.8 ± 13.1 |
| F0 | 51.1 ± 27.4 | 34.6 ± 14.2 | 45.1 ± 24.6 | 82.0 ± 18.2 | 9.2 ± 14.9 | 55.4 ± 14.1 | 37.0 ± 10.7 | 31.8 ± 13.0 |
| F0a | 46.4 ± 23.9 | 36.9 ± 23.2 | 43.0 ± 23.8 | 91.3 ± 12.1 | 27.5 ± 22.2 | 67.7 ± 13.3 | 29.7 ± 9.7 | 22.0 ± 13.0 |
| CPP | 60.4 ± 18.6 | 50.3 ± 12.6 | 56.7 ± 17.2 | 91.3 ± 9.2 | 18.3 ± 16.1 | 64.7 ± 8.7 | 46.6 ± 8.2 | 42.0 ± 5.6 |
| CPPa | 44.0 ± 14.1 | 41.5 ± 12.2 | 43.1 ± 13.3 | 94.3 ± 13.2 | 45.0 ± 28.7 | 76.7 ± 12.0 | 53.0 ± 18.8 | 48.0 ± 13.6 |
| CPPs | 61.5 ± 21.8 | 47.8 ± 22.6 | 56.5 ± 22.7 | 87.7 ± 12.8 | 3.3 ± 10.5 | 56.5 ± 8.9 | 43.6 ± 15.3 | 40.8 ± 21.4 |
| CPPsa | 51.0 ± 22.5 | 47.8 ± 16.6 | 49.8 ± 20.3 | 90.3 ± 19.3 | 33.3 ± 17.1 | 70.1 ± 12.7 | 48.8 ± 9.1 | 44.5 ± 10.6 |
| Modulation spectra | 80.5 ± 23.4 | 62.4 ± 30.9 | 73.9 ± 27.4 | 87.7 ± 15.0 | 44.2 ± 31.9 | 71.2 ± 15.7 | 47.8 ± 15.2 | 44.4 ± 13.9 |
| Wavelet | 85.0 ± 23.3 | 80.3 ± 21.3 | 83.3 ± 22.4 | 82.7 ± 8.0 | 75.0 ± 25.5 | 79.2 ± 9.9 | 57.0 ± 13.7 | 51.3 ± 12.6 |
| Spectral | 94.0 ± 10.2 | 86.0 ± 18.7 | 91.1 ± 14.1 | 96.3 ± 7.8 | 82.5 ± 15.4 | 91.1 ± 7.1 | 69.4 ± 14.3 | 64.9 ± 15.3 |
| Temporal | 96.2 ± 5.7 | 90.3 ± 13.4 | 94.1 ± 9.5 | 96.3 ± 7.8 | 100.0 ± 0.0 | 97.8 ± 4.7 | 72.8 ± 6.7 | 66.9 ± 8.4 |
| Spectral+Temporal | 96.8 ± 4.7 | 92.1 ± 13.0 | 95.1 ± 8.8 | 98.3 ± 5.3 | 97.5 ± 7.9 | 97.9 ± 4.7 | 73.0 ± 8.9 | 65.8 ± 10.8 |
Features were extracted from only voiced segments of the speech.
D. Experiment 4: Effect of different classifiers
Experiment 4 was conducted to investigate robustness of the proposed method to different classifiers. Features of the proposed method were fed into different classifiers including the naive Bayes, neural network, tree, and random forest (Table IV). The overall observation supports the robustness of the outcome for different classifiers. Naive Bayes showed the largest degradation in performance while random forest followed the performance of SVM closely.
TABLE IV.
Performance of Spectral+Temporal model with different classifiers in terms of accuracy.
| Classifier | ALS-DB | PD-DB | VD-DB |
|---|---|---|---|
| SVM | 95.1 ± 8.8 | 97.9 ± 4.7 | 73.0 ± 8.9 |
| Naive Bayes | 93.2 ± 10.0 | 76.2 ± 17.0 | 59.2 ± 10.3 |
| Neural network | 94.1 ± 9.6 | 90.1 ± 9.5 | 55.4 ± 16.2 |
| Tree | 91.5 ± 11.5 | 84.4 ± 9.4 | 57.5 ± 13.1 |
| Random forest | 94.5 ± 9.3 | 92.1 ± 7.6 | 62.3 ± 10.3 |
IV. DISCUSSION
This study was motivated by the observation that existing approaches to clinical evaluation of connected speech utilize methods that were originally designed for analysis of sustained vowels, a method that is inadequate for quantification of transient behaviors within the speech signal. Based on the data obtained, some important observations can be made. First, reviewing Table III the temporal models had better discriminative power than their spectral counterparts. This observation suggests that the temporal variation is the more likely place to find more powerful measures for reliable diagnosis and maybe even for a more accurate prognosis of voice and speech disorders. Interestingly, this was true for the voice disorder database which represents an impairment of the larynx and the vibratory characteristics of the vocal folds and not necessarily an issue with the vocal tract. This conclusion is consistent with studies suggesting that connected speech is the more valid context for the evaluation of voice disorders.9,19–25 Second, when features from the temporal model were augmented with features from the spectral model, the discriminative power did not improve significantly. This observation suggests that (at least in the proposed method), the spectral information is redundant and only the temporal information is required. This contrasts with contemporary clinical voice and speech research that has focused on the quantification of the spectral characteristics of the signal. Third, the more conventional clinical acoustic measures of LTAS, CPP, and F0 had the lowest discriminative power. The average accuracy improvement of the proposed method over these conventional measures was 35.1%. This finding highlights their limited statistical powers for research and clinical evaluation and supports the need for the development and utilization of more robust acoustic measures. Fourth, Table III does not show a meaningful trend for computation of LTAS, CPP, and F0. Specifically, computation of CPP and F0 from only the voiced portions of samples increased their discriminative powers only for some of the databases, whereas, for the remaining ones it either did not change or decreased their discriminative powers. The same observation is true for LTAS features. Based on these data, we are not able to establish a recommendation regarding the computation of these commonly used features in clinical voice science research. One reason for this behavior could be that the commonly used technique of concatenation of the voiced phonemes introduces abrupt and sharp transitioning at the boundaries of phonemes, a process which would dilute computation of the subsequent measures.
The proposed method is a non-parametric approach without any implicit or explicit assumptions about the type of stimuli being analyzed and, therefore, it offers a general framework for the analysis of both connected speech and sustained vowels. The proposed framework has several potential applications and the present experiments offer preliminary findings on its feasibility and discriminatory powers. However, most aspects of the method are still unexplored. For example, the definition of the neighborhood is a key factor of the proposed method, and it determines the phenomenon that is being captured. This study used one-neighborhood in the x and y directions which in turn led to short-time temporal and spectral models of the speech. However, it is possible to capture other phenomena of speech by defining other appropriate neighborhoods. For example, long-term spectral and temporal behaviors may be captured using a higher-order neighborhood combined with a vector quantizer, or the spectro-temporal interactions and patterns (e.g., upward pitch-glides) may be captured by defining proper diagonal neighborhoods. Another possible part of the method that could be revised to provide more granularity is its temporal model. Referring to Eq. (5), the temporal model was defined as the overall variation of all rows of the image along the x axis, meaning temporal variations in all sub-bands were treated equally and were mixed together; this is probably why the temporal model of pink noise in Fig. 5 had an elliptic shape rather than a circular one. However, if different sub-bands have dissimilar temporal variations a separate temporal model could be computed for each sub-band. The efficacy of this approach remains a valuable question for future research. Finally, the performance of the system may improve by using a different quantization approach (e.g., vector quantization, or having smaller step sizes for certain energy intervals) or more sophisticated image processing techniques for capturing more complex phenomena in future studies.
Deep networks such as convolutional neural networks (CNNs) have been a recent mainstream in the machine learning community with very promising results, yet the present work did not consider such approaches. Those new architectures do not require the application of hand-crafted features (similar to those presented here) and also could achieve better classification outcomes; however, their applications for clinical purposes and basic science research may be limited. That is, clinical and basic science studies are often hypothesis driven, whereas these new machine learning architectures seem to be incompatible with hypothesis-driven research. Specifically, these networks learn the “feature extraction” process based on the data and during the learning phase itself. In contrast, in hypothesis-driven research, a premise needs to be formed about the outcome before conducting any analyses on the data. Lacking the interpretability of the outcome is another disadvantage of these new architectures. For example, the final features of a CNN are the results of different kernels from different layers propagated through many layers and mixed in a very complex fashion with each other. Therefore, it is not clear (if possible at all) to identify what the final features are capturing. While each individual CNN kernel may be visualized and “some of them” could be “approximated” with well-understood operations (e.g., low-pass, high-pass), such realizations are only a very tiny fraction of the possible space and most of the kernels will not be well-behaved and well-understood. Therefore, even if the behavior of some of the kernels can be understood, their complex combinations and interactions with the remaining kernels would hinder understanding and interpretation of the final features.
Despite the importance of our current findings, several limitations are noted. First, the relatively small sample size of the database and the lack of an independent test set raises the possibility of overfitting and the risk of overtraining. However, investigating the performance of the method on multiple datasets and with different classifiers, and comparing the performance of the method on the training set and testing set suggest that the degree of over-fitting should be small. Looking at the performance of the method on the training sets showed a small variance (about 2%) for the ALS-DB and PD-DB. However, the difference between the training and testing accuracies on the VD-DB was much higher (about 9%). This high variance could be attributed to the small sample and the complexity of the problem (a four-class classification). The imbalanced PD dataset and the age range differences between controls and participants with UVFP and AdLD are some other points that should be mentioned. Referring to Table III, we see comparable sensitivity and specificity for the proposed method on PD-DB which translates into its robustness to PD-DB being imbalanced. Regarding age differences in VD-DB, speech of patients with UVFP and AdLD have distinct perceptual attributes and it is more likely for the machine learning to train on these more prominent attributes rather than nuanced differences associated with age. However, there is some possibility for age-related differences to contribute to the performance of those two classes. As a final note, the proposed method has clear interpretation in the signal processing sense and relative to the rich existing literature on the spectral analysis of voice and speech; consequently, such data could be used to make informed hypothesis about the behavior of the spectral model, but the possibility of its physiological interpretation remains as a question for future studies.
V. CONCLUSION
Evaluation of voice and speech is an integral part of the clinical voice assessment. Recent studies have advocated for the use of connected speech for this purpose. Unfortunately, existing works on the evaluation of connected speech have only changed the type of stimuli from sustained vowel to connected speech, without changing the employed evaluation methodology. Considering that voicing onsets, offsets, and temporal variations of speech are the main advantages of using connected speech over vowels, methods for quantification of the dynamics of connected speech are needed. To address this gap, a novel method based on image-representation of speech was proposed and empirically evaluated. Dynamics and variations of the produced image along x and y axes were captured using the joint distribution of properly defined neighborhoods. These models captured variations in the energy of speech between two consecutive time segments and two consecutive frequency sub-bands. As the first step of demonstrating the efficacy and utility of the proposed method, a diagnostic framework was adopted. At minimum, the proposed method has significant discriminatory power. To this end, features were extracted from each model and were fed into an SVM seeking discriminative patterns for three different clinical databases. The performance of the proposed method was compared with a wide range of existing approaches covering the commonly used methods for clinical evaluation of voice and speech, and some alternatives based on 2D representations of the signal. The proposed method outperformed alternative approaches with a high margin on all investigated databases. The average accuracy improvement of the proposed method over the more conventional clinical acoustic measures of LTAS, CPP, and F0 was 35.1%.
ACKNOWLEDGMENTS
This work was supported in part by T32 DC013017 from the National Institute of Deafness and Other Communication Disorders, the National Center for Advancing Translational Sciences, University of Kansas Medical Center, Frontiers: The Heartland Institute for Clinical and Translational Research, Grant No. UL1TR000001 (formerly Grant No. UL1RR033179). This work was partially supported by a grant from the American Speech-Language-Hearing Foundation.
References
- 1. Murry T. and Rosen C. A., “ Outcome measurements and quality of life in voice disorders,” Otolaryngol. Clin. North America 33(4), 905–916 (2000). 10.1016/S0030-6665(05)70251-6 [DOI] [PubMed] [Google Scholar]
- 2. Scott S., Robinson K., Wilson J. A., and Mackenzie K., “ Patient-reported problems associated with dysphonia,” Clin. Otolaryngol. 22(1), 37–40 (1997). 10.1046/j.1365-2273.1997.00855.x [DOI] [PubMed] [Google Scholar]
- 3. Hogikyan N. D. and Sethuraman G., “ Validation of an instrument to measure voice-related quality of life (V-RQOL),” J. Voice 13(4), 557–569 (1999). 10.1016/S0892-1997(99)80010-1 [DOI] [PubMed] [Google Scholar]
- 4. Patel R. R., Eadie T., Paul D., Hillman R. E., Barkmeier-Kraemer J., Awan S. N., Courey M., Deliyski D., and Švec J. G., “ Recommended protocols for instrumental assessment of voice: American Speech-Language-Hearing Association expert panel to develop a protocol for instrumental assessment of vocal function,” Am. J. Speech. Lang. Pathol. 27(3), 887–905 (2018). 10.1044/2018_AJSLP-17-0009 [DOI] [PubMed] [Google Scholar]
- 5. Behrman A., “ Common practices of voice therapists in the evaluation of patients,” J. Voice 19(3), 454–469 (2005). 10.1016/j.jvoice.2004.08.004 [DOI] [PubMed] [Google Scholar]
- 6. Oates J., “ Auditory-perceptual evaluation of disordered voice quality,” Folia Phoniatr. Logop. 61(1), 49–56 (2009). 10.1159/000200768 [DOI] [PubMed] [Google Scholar]
- 7. Kent R. D., “ Hearing and believing: Some limits to the auditory-perceptual assessment of speech and voice disorders,” Am. J. Speech. Lang. Pathol. 5(3), 7–23 (1996). 10.1044/1058-0360.0503.07 [DOI] [Google Scholar]
- 8. Ludlow C. L., Bassich C., Connor N., Coulter D., and Lee Y., “ The validity of using phonatory jitter and shimmer to detect laryngeal pathology,” in Laryngeal Function in Phonation and Respiration, edited by Baer T. and Sasaki C. and Harris K. (Little, Brown & Co., Boston, 1987). [Google Scholar]
- 9. Qi Y., Hillman R. E., and Milstein C., “ The estimation of signal-to-noise ratio in continuous speech for disordered voices,” J. Acoust. Soc. Am. 105(4), 2532–2535 (1999). 10.1121/1.426860 [DOI] [PubMed] [Google Scholar]
- 10. Qi Y. and Hillman R. E., “ Temporal and spectral estimations of harmonics-to-noise ratio in human voice signals,” J. Acoust. Soc. Am. 102(1), 537–543 (1997). 10.1121/1.419726 [DOI] [PubMed] [Google Scholar]
- 11. Ghasemzadeh H. and Arjmandi M. K., “ Toward optimum quantification of pathology-induced noises: An investigation of information missed by human auditory system,” IEEE/ACM Trans. Audio. Speech. Lang. Process. 28, 519–528 (2020). 10.1109/TASLP.2019.2959222 [DOI] [Google Scholar]
- 12. Hillenbrand J. and Houde R. A., “ Acoustic correlates of breathy vocal quality: Dysphonic voices and continuous speech,” J. Speech. Lang. Hear. Res. 39(2), 311–321 (1996). 10.1044/jshr.3902.311 [DOI] [PubMed] [Google Scholar]
- 13. Löfqvist A. and Mandersson B., “ Long-time average spectrum of speech and voice analysis,” Folia Phoniatr. Logop. 39(5), 221–229 (1987). 10.1159/000265863 [DOI] [PubMed] [Google Scholar]
- 14. Ghasemzadeh H. and Searl J., “ Modeling dynamics of connected speech in time and frequency domains with application to ALS,” in 11th International Conference on Voice Physiology and Biomechanics (ICVPB) (2018). [Google Scholar]
- 15. Vaziri G., Almasganj F., and Behroozmand R., “ Pathological assessment of patients' speech signals using nonlinear dynamical analysis,” Comput. Biol. Med. 40(1), 54–63 (2010). 10.1016/j.compbiomed.2009.10.011 [DOI] [PubMed] [Google Scholar]
- 16. Ghasemzadeh H., Tajik Khass M., Arjmandi M. K., and Pooyan M., “ Detection of vocal disorders based on phase space parameters and Lyapunov spectrum,” Biomed. Sign. Process. Control 22, 135–145 (2015). 10.1016/j.bspc.2015.07.002 [DOI] [Google Scholar]
- 17. Fritzell B., Hammarberg B., Gauffin J., Karlsson I., and Sundberg J., “ Breathiness and insufficient vocal fold closure,” J. Phon. 14(3-4), 549–553 (1986). 10.1016/S0095-4470(19)30705-3 [DOI] [Google Scholar]
- 18. Murry T. and Doherty E. T., “ Selected acoustic characteristics of pathologic and normal speakers,” J. Speech. Lang. Hear. Res. 23(2), 361–369 (1980). 10.1044/jshr.2302.361 [DOI] [PubMed] [Google Scholar]
- 19. Zraick R. I., Wendel K., and Smith-Olinde L., “ The effect of speaking task on perceptual judgment of the severity of dysphonic voice,” J. Voice 19(4), 574–581 (2005). 10.1016/j.jvoice.2004.08.009 [DOI] [PubMed] [Google Scholar]
- 20. Maryn Y., De Bodt M., and Roy N., “ The acoustic voice quality index: Toward improved treatment outcomes assessment in voice disorders,” J. Commun. Disord. 43(3), 161–174 (2010). 10.1016/j.jcomdis.2009.12.004 [DOI] [PubMed] [Google Scholar]
- 21. Awan S. N., Roy N., and Dromey C., “ Estimating dysphonia severity in continuous speech: Application of a multi-parameter spectral/cepstral model estimating dysphonia severity in continuous speech,” Clin. Ling. Phon. 23(11), 825–841 (2009). 10.3109/02699200903242988 [DOI] [PubMed] [Google Scholar]
- 22. Maryn Y. and Roy N., “ Sustained vowels and continuous speech in the auditory-perceptual evaluation of dysphonia severity,” J. Soc. Bras. Fonoaudiol. 24(2), 107–112 (2012). 10.1590/S2179-64912012000200003 [DOI] [PubMed] [Google Scholar]
- 23. Lederle A., Barkmeier-Kraemer J., and Finnegan E., “ Perception of vocal tremor during sustained phonation compared with sentence context,” J. Voice 26(5), 668.E1–668.E9 (2012). 10.1016/j.jvoice.2011.11.001 [DOI] [PubMed] [Google Scholar]
- 24. Krom G. D., “ Consistency and reliability of voice quality ratings for different types of speech fragments,” J. Speech. Lang. Hear. Res. 37(5), 985–1000 (1994). 10.1044/jshr.3705.985 [DOI] [PubMed] [Google Scholar]
- 25. Roy N., Gouse M., Mauszycki S. C., Merrill R. M., and Smith M. E., “ Task specificity in adductor spasmodic dysphonia versus muscle tension dysphonia,” Laryngoscope 115(2), 311–316 (2005). 10.1097/01.mlg.0000154739.48314.ee [DOI] [PubMed] [Google Scholar]
- 26. Parsa V. and Jamieson D. G., “ Acoustic discrimination of pathological voice, sustained vowels versus continuous speech,” J. Speech. Lang. Hear. Res. 44(2), 327–339 (2001). 10.1044/1092-4388(2001/027) [DOI] [PubMed] [Google Scholar]
- 27. Heman-Ackah Y. D., Michael D. D., and G. S. Goding, Jr. , “ The relationship between cepstral peak prominence and selected parameters of dysphonia,” J. Voice 16(1), 20–27 (2002). 10.1016/S0892-1997(02)00067-X [DOI] [PubMed] [Google Scholar]
- 28. Murton O., Hillman R. E., and Mehta D., “ Cepstral peak prominence values for clinical voice evaluation,” Am. J. Speech. Lang. Pathol. 29(3), 1596–1607 (2020). 10.1044/2020_AJSLP-20-00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Eadie T. L. and Doyle P. C., “ Classification of dysphonic voice: Acoustic and auditory-perceptual measures,” J. Voice 19(1), 1–14 (2005). 10.1016/j.jvoice.2004.02.002 [DOI] [PubMed] [Google Scholar]
- 30. Ma E. P. M. and Yiu E. M. L., “ Multiparametric evaluation of dysphonic severity,” J. Voice 20(3), 380–390 (2006). 10.1016/j.jvoice.2005.04.007 [DOI] [PubMed] [Google Scholar]
- 31. Eadie T. L. and Baylor C. R., “ The effect of perceptual training on inexperienced listeners' judgments of dysphonic voice,” J. Voice 20(4), 527–544 (2006). 10.1016/j.jvoice.2005.08.007 [DOI] [PubMed] [Google Scholar]
- 32. Maryn Y., Corthals P., Van Cauwenberge P., Roy N., and Bodt M. D., “ Toward improved ecological validity in the acoustic measurement of overall voice quality: Combining continuous speech and sustained vowels,” J. Voice 24(5), 540–555 (2010). 10.1016/j.jvoice.2008.12.014 [DOI] [PubMed] [Google Scholar]
- 33. Smith L. K. and Goberman A. M., “ Long-time average spectrum in individuals with Parkinson disease,” NeuroRehabilitation 35(1), 77–88 (2014). 10.3233/NRE-141102 [DOI] [PubMed] [Google Scholar]
- 34. Askenfelt A. G. and Hammarberg B., “ Speech waveform perturbation analysis: A perceptual-acoustical comparison of seven measures,” J. Speech. Lang. Hear. Res. 29(1), 50–64 (1986). 10.1044/jshr.2901.50 [DOI] [PubMed] [Google Scholar]
- 35. Titze I. R., “ Summary statement: Workshop on acoustic voice analysis, National Center for Voice and Speech,” https://ncvs.org/archive/freebooks/summary-statement.pdf (1995) (Last viewed 7/17/2022).
- 36. Ghasemzadeh H., Mehrara H., and Tajik Khass M., “ Cipher-text only attack on hopping window time domain scramblers,” in Proceedings of the 4th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, IEEE; (2014), pp. 194–199, available at https://ieeexplore.ieee.org/abstract/document/6993428. 10.1109/ICCKE.2014.6993428 [DOI] [Google Scholar]
- 37. Ghasemzadeh H., Tajik Khass M., and Mehrara H., “ Cipher text only attack on speech time scrambling systems using correction of audio spectrogram,” ISC Int. J. Inf. Security 9(2), 33–47 (2017). [Google Scholar]
- 38. Baken R. J. and Orlikoff R. F., Clinical Measurement of Speech and Voice ( Cengage Learning, Boston, 2000). [Google Scholar]
- 39. Jakielski K. J. and Gildersleeve-Neumann C. E., Phonetic Science for Clinical Practice, 1st ed. ( Plural Publishing, San Diego, 2018). [Google Scholar]
- 40. Ghasemzadeh H., Tajik Khass M., and Arjmandi M. K., “ Audio steganalysis based on reversed psychoacoustic model of human hearing,” Digital Signal Process. 51, 133–141 (2016). 10.1016/j.dsp.2015.12.015 [DOI] [Google Scholar]
- 41. Arjmandi M. K. and Pooyan M., “ An optimum algorithm in pathological voice quality assessment using wavelet-packet-based features, linear discriminant analysis and support vector machine,” Biomed. Signal Process. Control 7(1), 3–19 (2012). 10.1016/j.bspc.2011.03.010 [DOI] [Google Scholar]
- 42. Stevens S. S., Volkmann J., and Newman E. B., “ A scale for the measurement of the psychological magnitude pitch,” J. Acoust. Soc. Am. 8(3), 185–190 (1937). 10.1121/1.1915893 [DOI] [Google Scholar]
- 43. Ghasemzadeh H. and Arjmandi M. K., “ Universal audio steganalysis based on calibration and reversed frequency resolution of human auditory system,” IET Sign. Proc. 11(8), 916–922 (2017). 10.1049/iet-spr.2016.0690 [DOI] [Google Scholar]
- 44. Cover T. M., Elements of Information Theory ( Wiley & Sons, New York, 2012). [Google Scholar]
- 45. Ghasemzadeh H., “ Calibrated steganalysis of mp3stego in multi-encoder scenario,” Inf. Sci. 480, 438–453 (2019). 10.1016/j.ins.2018.12.035 [DOI] [Google Scholar]
- 46. Ghasemzadeh H., “ A metaheuristic approach for solving jigsaw puzzles,” in Iranian Conference on Intelligent Systems (ICIS2014), Bam, Iran, IEEE; (2014), available at https://ieeexplore.ieee.org/abstract/document/6802604. 10.1109/IranianCIS.2014.6802604 [DOI] [Google Scholar]
- 47. Yorkston K. M., Beukelman D. R., Hakel M., and Dorsey M., Speech Intelligibility Test for Windows ( Communication Disorders Software, Lincoln, NE, 1996). [Google Scholar]
- 48. Searl J., Knollhoff S., and Barohn R. J., “ Lingual–alveolar contact pressure during speech in amyotrophic lateral sclerosis: Preliminary findings,” J. Speech. Lang. Hear. Res. 60(4), 810–825 (2017). 10.1044/2016_JSLHR-S-16-0107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Searl J. and Knollhoff S., “ Changes in lingual-alveolar contact pressure during speech over six months in amyotrophic lateral sclerosis,” J. Commun. Disord. 70, 49–60 (2017). 10.1016/j.jcomdis.2017.10.004 [DOI] [PubMed] [Google Scholar]
- 50. Darley F. L., Aronson A. E., and Brown J. R., Motor Speech Disorders, 3rd ed. ( W.B. Saunders Company, Philadelphia, PA, 1975). [Google Scholar]
- 51. Searl J. and Dietsch A. M., “ Tolerance of the VocaLogTM vocal monitor by healthy persons and individuals with Parkinson disease,” J. Voice 29(4), 518.E13–518.E20 (2015). 10.1016/j.jvoice.2014.09.011 [DOI] [PubMed] [Google Scholar]
- 52. Fairbanks G., Voice and Articulation Drillbook, 2nd ed. ( Harper & Row, New York, 1960). [Google Scholar]
- 53. Villa-Cañas T., Orozco-Arroyave J. R., Vargas-Bonilla J. F., and Arias-Londoño J. D., “ Modulation spectra for automatic detection of Parkinson's disease,” in 2014 XIX Symposium on Image, Signal Processing and Artificial Vision (2014), pp. 1–5. [Google Scholar]