RUV-III-NB: normalization of single cell RNA-seq data

Abstract

Normalization of single cell RNA-seq data remains a challenging task. The performance of different methods can vary greatly between datasets when unwanted factors and biology are associated. Most normalization methods also only remove the effects of unwanted variation for the cell embedding but not from gene-level data typically used for differential expression (DE) analysis to identify marker genes. We propose RUV-III-NB, a method that can be used to remove unwanted variation from both the cell embedding and gene-level counts. Using pseudo-replicates, RUV-III-NB explicitly takes into account potential association with biology when removing unwanted variation. The method can be used for both UMI or read counts and returns adjusted counts that can be used for downstream analyses such as clustering, DE and pseudotime analyses. Using published datasets with different technological platforms, kinds of biology and levels of association between biology and unwanted variation, we show that RUV-III-NB manages to remove library size and batch effects, strengthen biological signals, improve DE analyses, and lead to results exhibiting greater concordance with independent datasets of the same kind. The performance of RUV-III-NB is consistent and is not sensitive to the number of factors assumed to contribute to the unwanted variation.

INTRODUCTION

Single-cell RNA-seq (scRNA-seq) technologies have gained popularity over the last few years as more and more studies interrogate transcriptomes at the single cell level. Just as with other omics data, scRNA-seq data inevitably contains unwanted variation which can compromise downstream analyses if left unaddressed. As in the case with bulk RNA-seq data, library size is the major source of unwanted variation in scRNA-seq data and consequently, removing library size effects is the first priority in preprocessing scRNA-seq data. The successful removal of library size effects is crucial for the validity of downstream analyses such as clustering, cell-type annotation, differential expression and trajectory analyses. Several studies (1–4) have found that the bulk RNA-seq procedures for removing library size effects do not work well for scRNA-seq data. This is because the relationship between gene expression and library size in scRNA-seq data is typically complex and gene-specific, a feature of the data that has necessitated the development of methods using gene-specific scaling factors (3–5), as opposed to methods that use global scaling factors e.g. (1,6). In addition to library size effects, scRNA-seq data can exhibit batch effects (7) due to variation between cell counts within a study (e.g. due to plate-to-plate variation) and variation between cell counts across studies (e.g. due to platform and sample preparation variation). In this paper, we concentrate on dealing with the first, although we show that our method has the potential to perform data integration by adjusting for library size and batch effects across studies.

Like Vallejos et al. (2), in this paper we will use the term ‘normalization’ to refer to a procedure that attempts to remove all kinds of unwanted variation and not only that due to library size. One of the key challenges when performing normalization is to remove the right kind and amount of variation. Removing the wrong or too much variation risks removing biology, especially if biological variation is associated with unwanted variation. Most methods that adjust scRNA-seq data for batch effects (8–11) proceed in two steps: library size effects are removed first, and then batch effects are removed from data that has been adjusted for library size. This approach is reasonable if there is little or no association between library size, batch and biology, but when there are such associations, its effectiveness may be reduced. For example, when different cell-types have quite different library size distributions, the first step may adjust the data too aggressively and remove library size differences arising as differences between cell-types. ZINB-WaVE (12) can be used to perform simultaneous adjustment for library size and batch effects. However, it requires that the batches are known a priori, and its adjustment is carried out without considering the possibility that library size, biology and batch may be associated. Furthermore, most normalization methods remove the effects of unwanted variation for the cell embedding used for clustering-based analysis but may severely distort gene-level data used for differential expression (DE) analysis used to identify marker genes (13).

In this paper, we propose RUV-III-NB that simultaneously adjusts scRNA-seq gene counts for library size and within study batch differences. As with RUV-III (14) which inspired this work, we do not assume that batch details are known, but seek to use replicates and negative control genes to capture and adjust for the unwanted variation. Negative controls are genes whose variation is (largely) unwanted and not of biological interest, while we necessarily modify our notion of replicates, for the gene expression levels in single cells cannot be measured in replicate. To ensure that the right kind and amount of variation is removed from gene counts we estimate the effect of unwanted variation on these counts using suitably defined using either pseudo-replicates of cells or pseudo-cells that have the same biology. The use of pseudo-replicates and negative control genes to adjust for unwanted variation is not unique to RUV-III-NB. These features were introduced in RUV-III (14) and subsequently were also used in scMerge (10). The principal novel aspect of the RUV-III-NB is the use of a negative binomial (NB) generalized linear model (GLM) directly on count data bringing the RUV-III framework in line with widely-used methods such as edgeR (15), DESeq2 (16) and sctransform (4). The GLM framework also allows RUV-III-NB to return the adjusted data in the form of percentile-adjusted counts (PAC), making the adjusted data suitable for downstream analyses that uses gene-level count such as differential expression (DE) analyses.

Using five publicly available datasets, we compare RUV-III-NB to several popular methods for normalizing scRNA-seq data and demonstrate its ability to retain biological signals and remove unwanted variation both in terms of cell embedding and gene-level count data, when biology and unwanted variation are associated.

MATERIALS AND METHODS

We describe the RUV-III-NB model and algorithm here, with more details can be found in the Supplementary Methods. RUV-III-NB takes raw sequencing counts as input and models the counts y_gc for genes g and cells c, as independent Negative Binomial (NB), y_gc ∼ NB(μ_gc, ψ_g) or Zero-Inflated Negative Binomial (ZINB) random variables, g = 1, …, G, c = 1, …, N. Here, we will only discuss the NB model for UMI data and leave the ZINB model for read count data to the Supplementary Methods section. Without loss of generality, we further assume there are m groups among the N cells with the same underlying biology within and different underlying biology across groups. We will refer to these groups as pseudo-replicate sets, that is, sets of cells whose members will be regarded as replicates for the purposes of normalization. Let 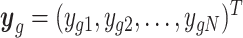be the vector of counts for gene g and 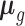be its vector of mean (i.e. expected value) parameters under the NB model. We use a generalized linear model with log link function to relate these mean parameters to the unobserved unwanted factor levels captured by the matrix 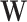while the biology of interest will be embodied in the matrix 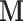, these being related by

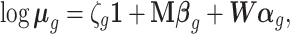(1)

where 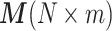is the pseudo-replicate design matrix with 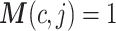if the cth cell is part of the jth pseudo-replicate set and 0 otherwise, 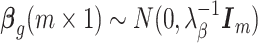is the vector of biological parameters, with values for each of the m replicate sets, 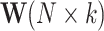is the unobserved matrix of k-dimensional unwanted factor levels and 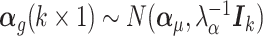is the vector of regression coefficient associated with the unwanted factors, and finally ζ_g is the location parameter for gene g after adjusting for unwanted factors, g = 1, …, G. In our applications we found that setting λ_α = 0.01 and λ_β = 16 yield good results.

For a given number k of unwanted factors we use a double-loop iteratively re-weighted least squares (IRLS) algorithm, where in the inner loop, given current estimates of the dispersion parameters, we estimate the parameters of the loglinear model above, including the unobserved unwanted factor levels (see Supplementary Methods for details). Once convergence is achieved there, we update the dispersion parameters in the outer loop. Two important constructs enable the algorithm to estimate the unobserved unwanted factor levels and their gene-specific effects on the sequencing count. These are the pseudo-replicate design matrix and the set of negative control genes.

The pseudo-replicate design matrix plays an important role for estimating the effect of the unwanted factors on the data (14,17). This effect is represented by 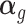and in RUV-III-NB it is estimated after projecting the current IRLS working vector onto the orthogonal complement of the subspace spanned by the columns of 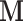. Given an estimate of 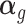, we use the set of negative control genes to estimate the unobserved unwanted factor levels 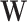. As stated above, negative controls are genes whose variation is (largely) unwanted and not of biological interest, (18), i.e, 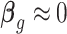for all negative control genes g. The model for these genes thus reduces to

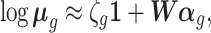We recommend the use of single-cell housekeeping genes (19) as the negative controls but users can (and may need to) devise their own negative control set. The important property of such genes is that they are affected by the same sources of unwanted variation as the other genes, and that their variation is not related to the biology of interest in the study.

Strategies for defining pseudo-replicate sets

To estimate the effects of the unwanted variation on the gene counts, the RUV-III-NB algorithm requires users to specify one or more sets of cells with relatively homogeneous biology, and these are called pseudo-replicate sets. In cases where the biological factor of interest for each cell is known, e.g when different treatments are compared across the same cell type, or when two or more cell lines are being compared, then cells with the same level of the biological factor of interest can be declared to be a pseudo-replicate set . There will be situations where the biology of interest is not known a priori at the single cell level. For example, it is often the case that cell type information is unavailable in advance, especially for droplet-based technologies. For such situations we outline some strategies that can be used to define pseudo-replicate sets.

Single batch

When the data comes from a single batch, users can cluster the cells into distinct biologically homogeneous sets of cells. The clustering could be done using the log  (normalized count + 1) where the scaling factor for normalization is calculated using computeSumFactors function in scran package (1). For clustering we recommend the use of a graph-based method such as the Louvain algorithm (20). Cells allocated to the same cluster can then be considered to form a pseudo-replicate set. We illustrate this strategy in Supplementary Figure S1.

Multiple batches

When the data comes multiple batches, we need to match clusters containing cells with similar biology located in different batches. We recommend that users use the scReplicate function in the Bioconductor package scMerge (10) for this purpose. This function takes log (normalized count + 1) as input and performs clustering for each batch separately followed by identification of clusters in different batches that are mutual nearest clusters (MNCs) (10). This approach implicitly assumes that technical variability does not dominate biological variability, so we can expect cells with the same biological conditions in different batches to still be close to one another relative to different cell types from different batches.

Once these mutual nearest clusters (MNC) are identified, cells from the same MNC can be considered to form a pseudo-replicate set. We illustrate this strategy in Supplementary Figure S2.

Strengthening pseudo-replicate sets using pseudo-cells

Even when pseudo-replicate sets can be defined by clustering, the clustering may at times be imprecise, with considerable biological heterogeneity across cells in the same cluster. Thus declaring all such cells to be a pseudo-replicate set may risk removing some of the biological signal of interest. To address this issue, we introduce the idea of basing pseudo-replicate sets on pseudo-cells. These are synthetic single cells with homogeneous biology (see explanation below), quite distinct from the metacells (21) which are groups of scRNA-seq cell profiles that are statistically equivalent to samples derived from the same RNA pool, designed for a quite different purpose.

It can be shown that the counts assigned to these pseudo-cells will still have the quadratic mean-variance relationship typical of negative binomial random variables. The difference between these pseudo-cells and the real cells lies in the overdispersion parameter. For the same gene, the overdispersion parameter for pseudo-cells will be smaller, reflecting the reduced variability resulting from the pool-and-divide strategy (see Supplementary Methods).

We would like to emphasize that using pseudo-cells to remove unwanted variation is an optional feature of RUV-III-NB. RUV-III-NB can be used when only real cells are used to define the pseudo-replicates matrix. However, the performance of RUV-III-NB can potentially be improved when pseudo-cells are used to define the matrix. To accommodate pseudo-cells into RUV-III-NB fitting algorithm, the count matrix needs to be expanded with columns associated with the pseudo-cells appended to the right of the count matrix for the real cells. The pseudo-replicate matrix also needs to be expanded with rows associated with the pseudo-cells added below the rows for the (real) cells. Finally, for each gene, the pseudo-cells are assumed to have different dispersion parameters from the (real) cells. More details about this can be found in the Supplementary Methods.

Pseudo-cells: single batch

Within a single batch and biology, we suppose that the major source of unwanted variation is library size, and that other intra-batch variation (e.g., well-to-well variation within a plate) is minimal. The idea is to form pseudo-replicates of pseudo-cells that have been constructed to have as much variation as possible in their library size while keeping their biology as homogeneous as possible, more homogeneous than we might see in actual single cells in a pseudo-replicate set. Suppose we have identified m pseudo-replicate sets using either known single cell biology or the strategy that we have just described above. For each of the pseudo-replicate sets, we form pseudo-cells that represent the pseudo-replicate set using the following pool-and-divide strategy:

1. Assign each cell to one of the J = 10 pools based on its library size, where pool j contains n_j cells, j = 1…, J.

2. Pooling: Let 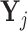be the matrix of counts for cells belonging to pool j = 1, 2, …J , where rows corresponds to genes and columns corresponds to cells. We aggregate the counts for these cells by forming row totals of 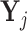and denote the vector containing these row totals by 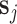with components s_gj = ∑_{c ∈ poolj}y_gc.

3. Dividing: For each gene g, we generate a count z_gj using the pool-aggregated counts as follows: z_gj∣s_gj ∼ Binomial(s_gj, p = 1/n_j), where s_gj is the aggregated count for gene g in pool j consisting of n_j cells. This step is formally equivalent to randomly dividing the aggregated counts for the pool into counts for n_j pseudo-cells and choosing one of the pseudo-cells at random. The hope is that the pseudo-cell so defined will exhibit average and so stabler biology in its gene counts, while concentrating the unwanted variation in the pool, here library size.

4. We thus obtain counts 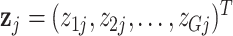for the pseudo-cell that represents pool j.

5. We repeat steps 1-4 for all J pools and declare the J pseudo-cells so defined to be a pseudo-replicate set.

6. Finally, we carry out steps 1–5 above for the other pseudo-replicate sets, at the end of which we will have m pseudo-replicate sets each containing J pseudo-cells.

Pseudo-cells: multiple batches

When there are multiple batches, the procedure for forming pseudo-cells just described needs to follow the stratification of our cells into sets of MNC. Then we construct pseudo-cells for each of the clusters that makes up an MNC. For example, suppose we have b = 2 batches A, and B and we identified three clusters for each batch with the following MNC: (A₁, B₂), (A₂, B₁) and (A₃, B₃) where A₁ refers to the first cluster in batch A, etc. The procedure for forming the pseudo-cells would then be as follows:

1. Start with the first MNC (A₁, B₂)

2. Assign each cell in A₁ into one of the J groups based on its library size, where group j contains n_j cells.

3. Pooling: Let 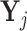be the matrix of counts for cells belonging to pool j where rows correspond to genes and columns corresponds to cells. Aggregate the gene counts in these cells by forming the row totals of 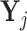and denote this new vector by s_gj.

4. Dividing: For each gene g, we generate a count z_jg using the pool-aggregated counts as follows: z_jg ∼ Binomial(s_jg, p = 1/n_j) where s_jg is the pool-aggregated count for gene g. As above, this step is equivalent to randomly dividing the aggregated counts for the pool into those for n_j pseudo-cells and choosing one of the pseudo-cells randomly.

5. We thus obtain 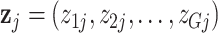as the count data for pseudo-cell that represent pool j.

6. Repeat steps 2–5 for cells in B₂.

7. Declare all the pseudo-cells formed in step 2–6 above to be a pseudo-replicate set.

8. Go to step 1 and repeat steps 2–6 for the second MNC (A₂, B₁) and third MNC (A₃, B₃)

When this procedure is completed, we will have as many pseudo-replicate sets as we have MNC sets and each pseudo-replicate set is made up of b × J pseudo-cells. We illustrate this strategy for b = 2 batches and J = 2 groups in Supplementary Figure S3.

Adjusted counts

Once we obtain the estimates of unwanted factors 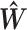and their effects 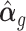, we remove their effects from the raw data. RUV-III-NB provides two forms of adjusted data. These adjusted data can be used as input to downstream analyses such as clustering, trajectory and differential expression analyses.

• Pearson residuals:

  

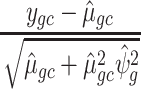
  where .

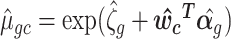  When k = 1 and 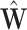is approximately equal to log library size (up to a scaling factor), these Pearson residuals will roughly agree with those of (4), although different shrinkages of parameter estimates may lead to small differences. When k > 1 and some columns of 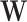reflect batch effects, our Pearson residuals will also adjust for unwanted variation other than library size, such as batch effects.

• Log of percentile-invariant adjusted counts (log PAC):

  
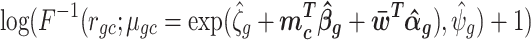  where r_gc ∼ U(a_gc, b_gc) and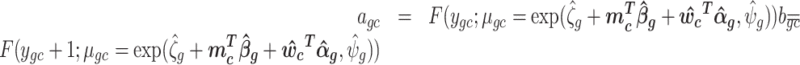

  

  where F(.) is the negative binomial c.d.f and F⁻¹(.) its inverse, 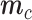is the c^th row of the matrix 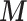, 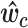the c^th row of the matrix 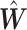and 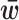is vector of entries equal to the average level 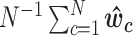of unwanted variation. Here U(a, b) denoted a random variable uniformly distributed over the interval (a, b).

  The intuition behind this adjustment is as follows. We first obtain the percentiles of the observed counts under the fitted NB model, where the mean value parameter includes terms for unwanted variation. Since negative binomials are discrete distributions, percentiles can only be determined up to an interval. To come up with an estimate of a percentile for practical use, we simply select a uniformly distributed random value from this interval in a manner suggested in (22). We then find the corresponding counts for that estimated percentile under a different NB model, namely one where the mean parameter is free from unwanted variation, i.e. where 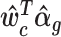is replaced by 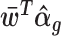. We then add 1 and log. Our definition of percentile-invariant adjusted counts explicitly derives the counts as percentiles of a full NB distribution and in this regard it is similar to that in (23) who proposed this approach to obtain batch-corrected bulk RNA-seq data. Their adjustment was only applied to non-zero counts, and left the zero counts intact. That was not expected to pose significant problems for bulk RNA-seq data where zero counts are relatively scarce, but because zero counts are very prominent in scRNA-seq data, we broaden their approach and also adjust zero counts. On the other hand, sctransform’s corrected counts (4) is calculated by taking away from the observed counts the difference between the predicted counts at the observed and at the average log library size, followed by rounding to avoid non-integer values.

  We recommend that the log PAC transformation is used as corrected data for UMI counts, while the Pearson residuals can be used as alternative for non-UMI counts.

Datasets for benchmarking

To benchmark our methods against others, we use the following five datasets that encompass different technological platforms, illustrate different strategies for identifying pseudo-replicates and pose different challenges for normalization due to association between different unwanted factors and biology (Table 1).

Table 1.

Characteristics of datasets used for benchmarking

Study	Platform	UMI	Unwanted Fac.	Biological Fac.	Pseudo-replicate strategy	LS × batch	LS × Bio	Batch × Bio
NSCLC	10x	Yes	LS	Cell-type	pseudo-cells	No	Yes	No
Cell line	10x	Yes	LS, batch	Cell lines	MNCs from scMerge::scReplicate	No	No	Yes
CLL	Celseq2	Yes	LS, plate	Treatment	Granta+pseudo-cells	Yes	Yes	Yes
Gaublomme	SmartSeq2	No	LS, batch	Pathogenicity	Biol. Factor	Yes	No	Yes
Pancreas	inDrop,CelSeq2	Yes	LS, batch	Cell-type	MNCs from scMerge::scReplicate	Yes	No	No

LS = library size, LS × batch = presence of LS and batch association, LS × Bio = presence of LS and biological factor association, Batch × Bio = presence of batch and biological factor association.

Prior to normalization all datasets were subjected to quality control checks using Bioconductors’s scater package (24) to remove low quality cells. Low abundance genes were also removed and additional parameters for each method were set to their default.

• Non-small cell lung cancer cells (NSCLC): The dataset was generated using 10x and is freely available from the 10x Genomics website (www.10xgenomics.com). The sequencing was done in one batch, so there should be no batch effects, but the cells are a mixture of cells with larger size such as epithelial cells and smaller cells such as T cells. The challenge here is to normalize when library size is associated with the biology, namely, cell-type. The raw data were downloaded from https://www.10xgenomics.com/resources/datasets/nsclc-tumor-5-gene-expression-1-standard-2-2-0. After QC, there were 10,019 genes and 6,622 cells.

• Cell line: The 10x technology was used to sequence cells in three batches. One batch contained only the Jurkat cell line, another contained only the 293T cell line, while the third batch contained 50–50 mixture of both cell lines. The data were downloaded from the following websites:

  • - Batch with Jurkat cells only were downloaded from https://www.10xgenomics.com/resources/datasets/jurkat-cells-1-standard-1-1-0

  • - Batch with 293T cells only were downloaded from https://www.10xgenomics.com/resources/datasets/293-t-cells-1-standard-1-1-0

  • - Batch containing mixture of Jurkat and 293T cells were downloaded from https://www.10xgenomics.com/resources/datasets/50-percent-50-percent-jurkat-293-t-cell-mixture-1-standard-1-1-0

  After QC, there were 7,943 genes and 9,027 cells.

• Chronic lymphocytic leukemia (CLL): This in-house dataset was generated using the CelSeq2 technology as part of a study investigating the transcriptomic signature of Venetoclax resistance. The cells were pre-sorted so that the vast majority are B-cells and were treated with dimethyl sulfoxide (DMSO) as well as single treatment (TRT) and combination treatments (TRT+) for one week, before being sequenced on six different plates. In addition to this, a small number of cells from the Granta cell line were included on each plate. After QC, there were 11,470 genes and 1,644 cells. The dataset is included as CLLdata object in the ruvIIInb R package.

• Gaublomme: Th17 cells derived under a non-pathogenic condition (TGF-β1+IL-6, unsorted: 130 cells from two batches and TGF-β1+IL-6; sorted for IL-17A/GFP+: 151 cells from three batches) and a pathogenic condition (Il-1β1+IL-6+IL-23, sorted for IL-17A/GFP+: 139 cells from two batches) were sequenced using the SMARTseq technology (25). The raw FASTQ is available from GEO website (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE74833). We obtain the raw count data from the author. After QC, there were 7,590 genes and 337 cells.

• Pancreas: Human pancreas islet cells from two different studies that used inDrop (26) and CELSeq2 technology (27). The datasets were downloaded from https://hemberg-lab.github.io/scRNA.seq.datasets/human/pancreas/. After QC, there were 11,542 genes and 10.687 cells.

Benchmarking methods

For the NSCLC study where there should be no batch effect and the only task is removing library size effects, we compared RUV-III-NB with the following methods: scran (1), sctransform (4), ZINBwave (12) and Dino (5). For the other studies where batch effects are present, we compare RUV-III-NB to the following batch correction methods: mnnCorrect and fastMNN (8), Seurat3 (11) coupled with sctransform normalization, ZINBwave (12) and scMerge (10). These methods have been selected because all of them return the gene-level normalized data required to calculate the benchmarking metrics (see below). This is in contrast with other methods such as Harmony (9), where the normalized data is only available as an embedding. Some of the methods produce multiple versions of normalized data and in Supplementary Table S1, we provide details on which normalized data we used for calculating the various metrics in our benchmarking exercise.

We use the following criteria for assessing the performance of the different normalization methods:

• Genewise correlations between the normalized data and log library size: We expect a good normalization to remove any association between gene expression levels and log library size, especially when cells with the same biology are considered.

• R² between log library size and the leading cumulative PCs: For each cell-type, the coefficient of determination (R²) when regressing log library size on the first k PCs simultaneously (PC₁,PC₂,...PC_k), k = 1, 2, …10 should be as low as possible. This is because we believe that a good normalization should reduce the association between the normalized data and log library size, so within a group of cells with similar biology, the leading PCs cumulatively should contain little information about library size. In this case, the leading PC of the data on all the cells would be associated with library size only to the extent that library size is associated with biology (e.g. cell type), indicating that the normalization has brought biology to the forefront and relegated the unwanted variation (here library size) not associated with biology to the higher order (lower variance) PC.

• Silhouette statistics for clustering by batch (Technical Silhouette): When batch effects are reduced, we should expect a lower degree of clustering by batch, within a set of cells with homogeneous biology. To assess this, we calculated median silhouette statistics for clustering by batch for each set of cells with the same biological factor. The silhouette statistics were calculated based on the first k PCs (k =1,2,...10).

• Silhouette statistics for clustering by biology (Biological Silhouette): When batch effects are removed, we expect biological signals to be strengthened and lead to better clustering by biology. To assess this, we calculated median silhouette statistics for clustering by biological factor for each set of cells with the same biological factor. The silhouette statistics were calculated based on the first k PCs (k = 1, 2, ..., 10). For the cell line, Gaublomme and CLL studies, the information on biological factors is available and this is used to calculate silhouette scores. For the NSCLC and Pancreatic studies, cell type is the biological factor of interest. Because they are not available, we use the Bioconductor package SingleR (28) to estimate the cell types and use the estimated cell types for calculating the silhouette score.

  For all methods, to calculate the first 10 PC we used Euclidean distance based on genes whose normalized expression variance lies in the top 50%. For Seurat3-Integrated, we use all anchor features for calculating PC. The number of anchor features is typically 2000, much less than the half of the total number of genes. PC were derived using the R package irlba.

• Differential expression vs unwanted factors (DE-UF): When comparing cells of the same cell-type across batches (DE-batch) or smaller vs larger library size (DE-LS), a good normalization should decrease the proportion of differentially expressed genes (DEG). To calculate the proportion of DEG, we first performed DE analysis using the nonparametric Kruskal-Wallis test. The choice of Kruskal–Wallis test is because we would like to avoid the DE test favoring a certain normalization method based on the similarity in their parametric assumptions. The P-values from each DE analysis are obtained and then these are used to estimate π₀, the proportion of DEG using Storey and Tibshirani’s method (29) as implemented in the qvalue Bioconductor package.

• Differential expression vs biology (DE-Bio): When comparing cells across different biologies, a good normalization should increase the concordance between the results found with the current and those of an independent study, as measured by the number of DEG. The Kruskal–Wallis test was used to perform DE analysis against biological factors.

• RLE metrics: Correlation between relative log expression (RLE) statistics with unwanted factors Because of the exquisite sensitivity of RLE plots to unwanted variation (30), it can often pick unwanted variation not evident from methods such as PCA (14). With good normalization we expect that within a set of cells with homogeneous biology, the median and interquartile ranges (IQR) of RLE to have little association with unwanted factors. We used three metrics to measure this association:

  • - Squared correlation (r²) between log library size and RLE medians. A lower value of this metric indicates better normalization.

  • - Squared correlation (r²) between log library size and RLE IQR. A lower value of this metric indicates better normalization.

  • - The squared of total canonical correlation (31) between log library size and batch variables on one side and RLE median and IQRs on the other. This last metric is used as an overall measure of association between RLE summary statistics and unwanted factors (log library size and batch) when there are multiple batches. A lower value of this metric indicates better normalization.

  Since RLE calculation requires subtracting log of gene-specific median expression (30), the RLE plots were calculated using only genes with non-zero median expression.

Overall score

For each metric above except DE-bio which will be presented separately, we calculated an overall score as follows:

• For biological silhouette, we use the average of median silhouette scores across different number of cumulative PCs to represent the overall score.

• For technical silhouette and R² between log library size and the leading cumulative PCs: within each cell-type, we calculate the average of the metric across different cumulative PCs. The cell-type specific averages are further averaged across different cell-types to create a score and finally we take 1 – score so that higher score for these metrics represent higher performance.

• For correlation between normalized data and log library size, we first take the average within each cell-type. The cell-type specific averages are further averaged across different cell-types to create a score and finally we take 1 – score so that higher score for these metrics represent higher performance.

• For DE vs unwanted factors, we estimate the proportion of null genes within each cell-type. The cell-type specific estimates are then averaged across t cell-types to create a score and finally we take 1 – score so that higher score for these metrics represent higher performance.

• For RLE metrics, we first calculate the average of the three RLE-related metrics above for each cell-type. These cell-type specific metrics are then averaged across cell-types to create a score and finally we take 1 – score so that higher score for these metrics represent higher performance.

‘Gold-standard’ DE genes

We compare the concordance of differentially-expressed genes (DEG) obtained from the different methods to the following ‘gold standard’ DEG:

• Cell line: ‘Gold standard’ DEG in this case were derived by comparing Jurkat and 293T cells from batch 3, which has cells from both cell lines. The assumption is that cells assayed in the same batch will exhibit similar batch effects that will, to some extent, cancel when we compare cells of different types. The DE analysis was performed using the Kruskal-Wallis test on the log (scran-normalized data + 1).

• Gaublomme: ‘Gold standard’ DEG here were derived from an external dataset. We downloaded the raw Affymetrix CEL files from the GEO website (ID: GSE39820). The microarray data were normalized using the GCRMA package version 2.58.0 and DE analysis comparing non-pathogenic (TGF-β1+IL-6) vs pathogenic (Il-1β1+IL-6+IL-23) microarray samples was performed using the limma package (32).

• Pancreas: ‘Gold standard’ DEG here were also derived from an external dataset. Normalized Agilent microarray expression data were downloaded from https://www.omicsdi.org/dataset/arrayexpress-repository/E-MTAB-465 and DE analysis comparing Alpha vs Beta cells was performed using limma.

RESULTS

RUV-III-NB preserves biology when library size and biology are associated

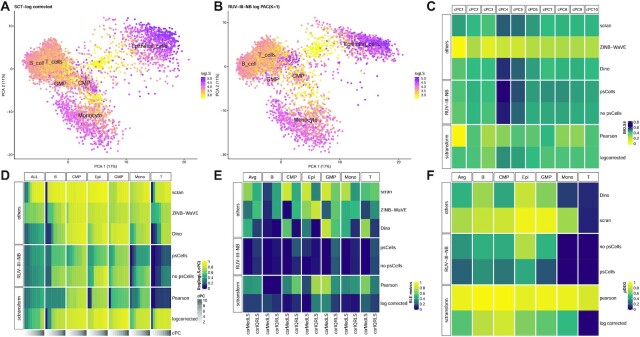
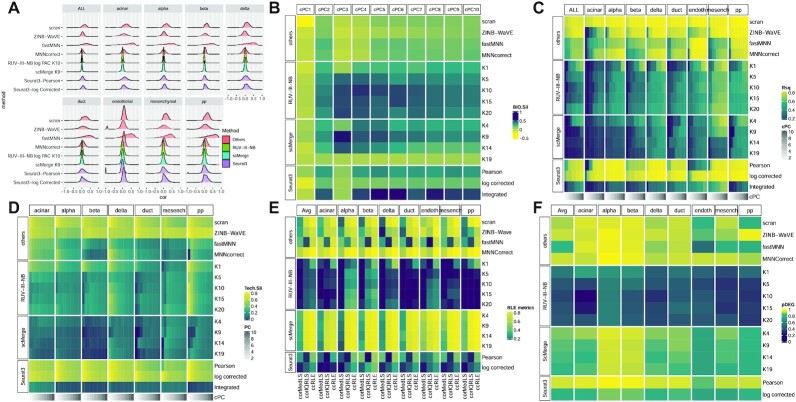
In the NSCLC study, library size is associated with biology because the large epithelial cells have larger library sizes than those of the immune cells, and among the immune cells, monocytes are the largest, and they also have the largest average library size (Figure 1A). RUV-III-NB identified log library size as a source of unwanted variation (Supplementary Figure S4A) and managed to separate the larger monocytes from the rest of the immune cells (Figure 1B) better than sctransform-log corrected data (Figure 1A) and other methods (Supplementary Figure S5). Most methods achieve the highest median biological silhouette score when four PCs are used (Figure 1C) with RUV-III-NB log PAC and Dino being the only normalization methods that improve the optimal biological signals over that of the simple scran normalization. For RUV-III-NB, using pseudo-cells to form pseudo-replicates lead to improved biological signals (Figure 1C) as well as other metrics (Figures 1D–F). Apart from enhancing biological signals, a good normalization method should reduce effects of the unwanted factors in the normalized data. To investigate this, within cells of the same type, we examine the remaining effects of the library size in the normalized data using several metrics. Figure 1D shows that the leading principal components of sctransform-Pearson, RUV-III-NB log PAC and Dino-normalized data have the least association with log library size, with RUV-III-NB normalized data consistently having the lowest correlation with log library size across all genes (Supplementary Figure S6A). RUV-III-NB log PAC also produces median and IQR of relative log expression (RLE) that have the least association with library size (Figure 1E) and the smallest proportion of differentially-expressed genes (DEG) when cells with below and above median log library size are compared (Figure 1F). Looking across all metrics, RUV-III-NB clearly has the best overall performance. Not only does it enhance the biological signals, it is also the most successful in removing library size effects from the data and in the differential expression analysis between cells of differing library sizes (Figure 2).

Figure 1.

NSCLC study. (A) PC of sctransform-log corrected count. Colour refers to log library size. (B) PC of RUV-III-NB log percentile adjusted count (PAC). These show that monocytes are better separated from the rest of the cells. (C) Median biological silhouette score for different numbers of cumulative PCs. Most methods achieve the highest median score when four PCs are used, with RUV-III-NB and Dino the only methods that improve the biological silhouette relative to scran normalization. (D) Heatmap of R-squared between logLS and cumulative PC of normalized data. RUV-III-NB (with pseudo-cells) and sctransform-Pearson have the lowest correlation, with RUV-III-NB still retaining some of the size-related heterogeneity within a cell type. (E) Squared correlation between median (corMedLS) and IQR (corIQRLS) of relative log expression (RLE) and log library size. (F) Proportion of DEG between cells with below and above median log library size.

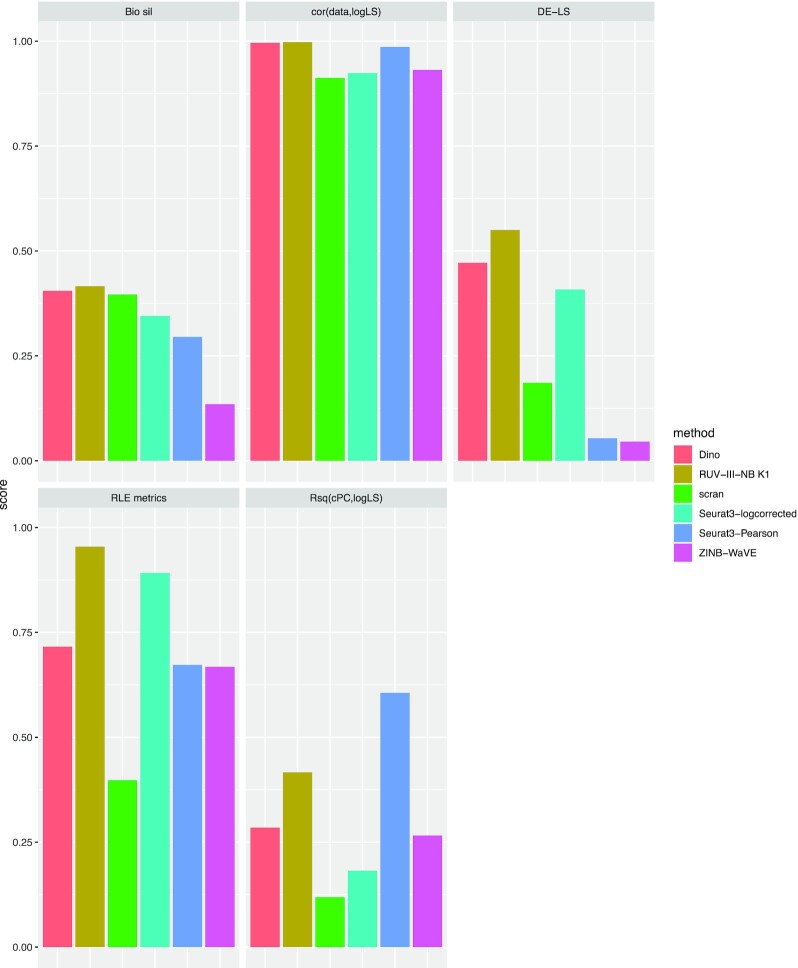
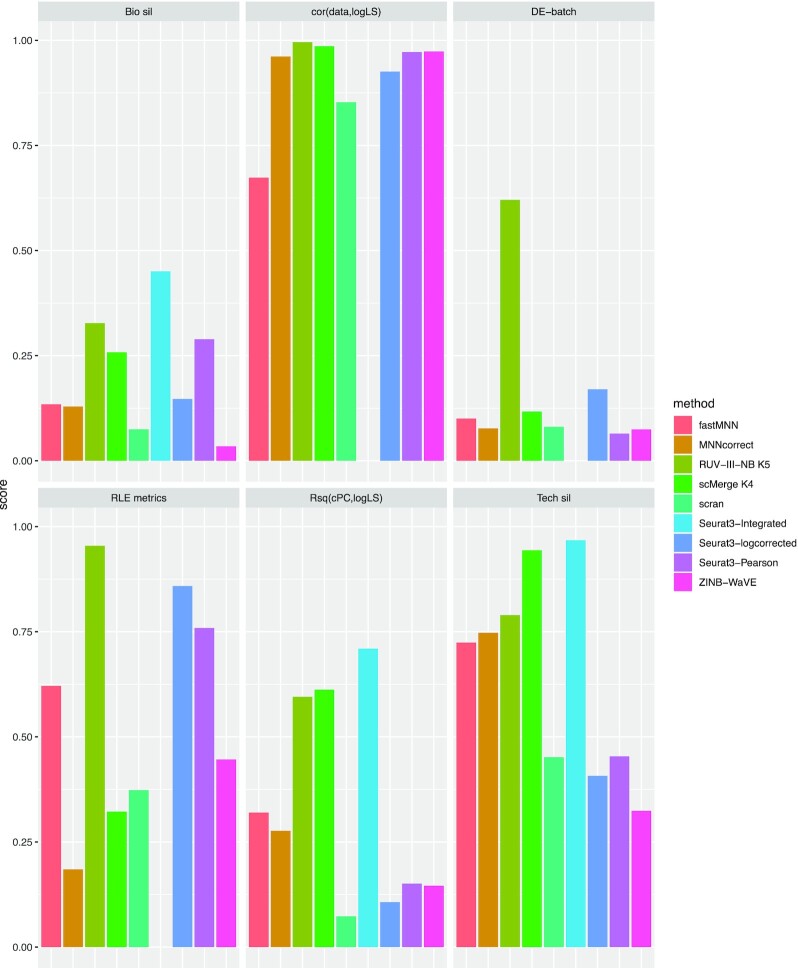
Figure 2.

Overall performance of normalization methods in the NSCLC study. Each panel represents a metric with methods represented by differently-colored bars. The length of the bar corresponds to level of performance with respect to the metric in 0–1 scale.

RUV-III-NB preserves biology when batch and biology are associated

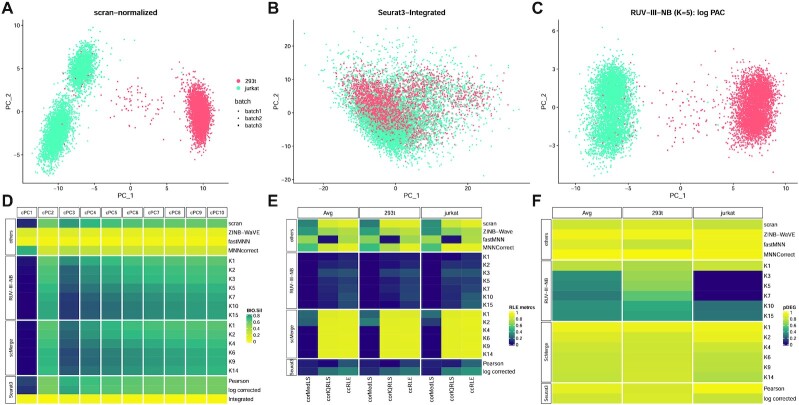
In the cell line study, there are two cell types but the cell types were sequenced in different pairs of the three batches. This creates an association between biology and batch. RUV-III-NB identified log library size (Supp Figure S4B) and batch (Supp Figure S4C) as major sources of unwanted variation. After scran normalization, the leading PC still clearly exhibit batch effects (Figure 3A). RUV-III-NB removes the batch effects from the leading PC (Figure 3C) as does scMerge (Supplementary Figure S7). MNNCorrect, Seurat3-Pearson and Seurat3-log corrected do not remove the batch effects (Supplementary Figure S7), while fastMNN (Supplementary Figure S7) and Seurat3-Integrated (Figure 3B) remove batch effects but also remove biology. The tendency of Seurat3-Integrated, MNNCorrect and ZINB-WaVE in removing biology is also observed in the CLL study (Supplementary Figure S8) and Gaublomme study (Supplementary Figure S13) in which the biological factors and batch are associated.

Figure 3.

Cell line study. (A) The first two PCs of scran-normalized data. Colour refers to cell type. Batch effects are visible for the Jurkat cells. (B) PCs of Seurat3-Integrated data removes cell type separation. (C) PCs of RUV-III-NB log percentile adjusted counts (PAC). Clustering by cell type is clearly visible with batch effects removed. (D) Median biological silhouette score for different numbers of cumulative PCs. RUV-III-NB and scMerge improve the biological signal relative to scran and increasing the number of unwanted factors beyond a certain point only slightly degrades performance. (E) Squared correlation between median (corMedLS) and IQR (corIQRLS) of relative log expression (RLE) with log library size and squared of total canonical correlation (ccRLE) between median and IQR of RLE and log library size and batch variables. (F) Proportion of DEG when comparing cells of the same type across batches.

In the cell line study, only RUV-III-NB and scMerge improve the biological signals when compared with simple scran normalization (Figure 3D), with RUV-III-NB being slightly better at reducing correlation between the normalized data and log library size (Supplementary Figure S6B), and much better at removing the effect of the unwanted factors from the RLE (Figure 3E) and from the differential expression analysis (Figure 3F). Considering all the different metrics together, we see a clear advantage of RUV-III-NB and scMerge over the other methods, and an advantage of RUV-III-NB over scMerge for the RLE and differential expression metrics (Figure 4).

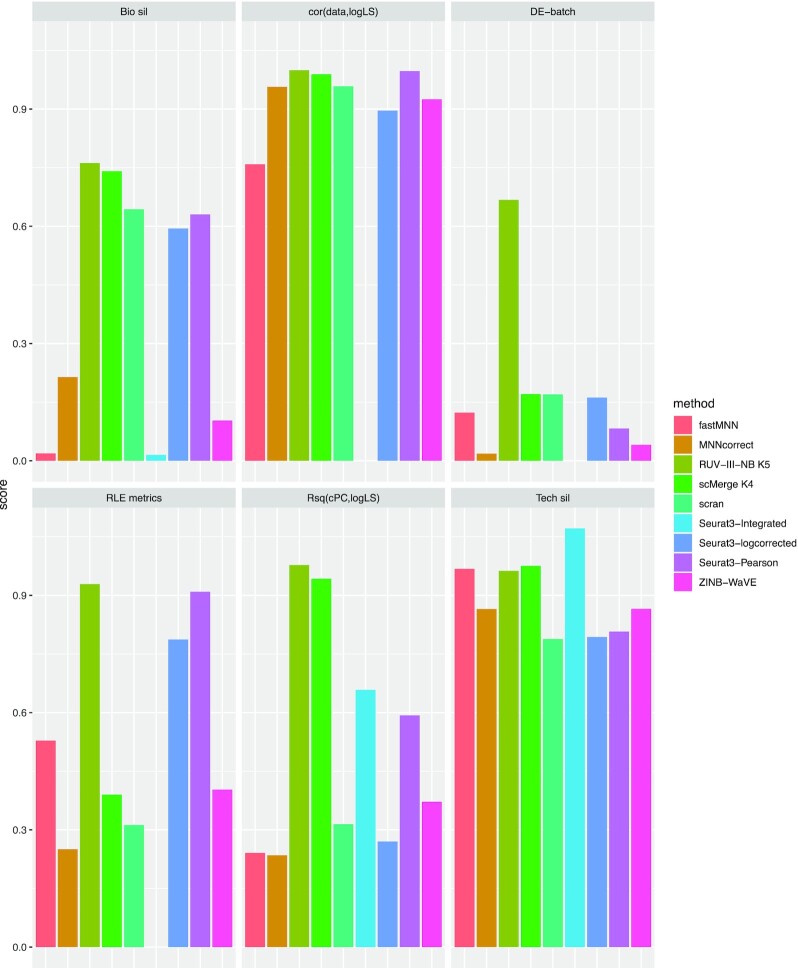
Figure 4.

Overall performance of normalization methods in the cell line study. Each panel represents a metric with methods represented by differently-colored bars. Metrics that require gene-level corrected data are not available for Seurat3-Integrated. The length of the bar corresponds to level of performance with respect to the metric in 0–1 scale.

The ability of RUV-III-NB to preserve biological signals and its excellent performance in terms of the RLE and differential expression metrics is also observed in the CLL study (Supplementary Figures S9–S11, S17B), another study with UMI count where biology and batch are associated. However, in the Gaublomme study that does not have UMI counts, scMerge is slightly better than RUV-III-NB for almost all metrics, including the RLE and differential expression analyses (Supplementary Figures S12, S14 and S17C).

RUV-III-NB preserves biology when biology is not associated with unwanted factors

The statistical model behind RUV-III-NB is designed so that removal of unwanted variation takes into account their potential association with biology. It is therefore of interest to examine how RUV-III-NB fares when the unwanted factors and biology are not associated. In the pancreas study, the eight cell types are present in both of the batches that correspond to different technological platform, and within each platform there is little difference in the average library size distribution between cell types (Supplementary Figure S15). Thus, there is only small amount of association between unwanted factors, in this case log library size and batch (Supplementary Figures S4H and I), with biology.

The leading PC of the scran-normalized data shows that cells of the same type are split by their batch of origin (Supplementary Figure S16A). RUV-III-NB, scMerge and Seurat3-Integrated integrate the two batches well so that cells of the same type are clustered together (Supplementary Figures S16B, H and I). RUV-III-NB, together with scMerge consistently manage to reduce the correlation between normalized data and log library size for homogeneous cell types (Figure 5A). Seurat3-Integrated, RUV-III-NB and scMerge are the most successful in improving biological signals (Figure 5B). But in terms of R² between cumulative PCs and log library size (Figure 5C) and technical silhouette (Figure 5D), scMerge and Seurat3-Integrated are slightly better than RUV-III-NB. This suggests that the more cautious approach of RUV-III-NB slightly reduces its ability to remove unwanted factors from the embedding, although RUV-III-NB is still the best method for removing the effect of unwanted factors from the gene-level count data, resulting in better RLE and differential expression analysis (Figures 5E and F). When all metrics are considered together, RUV-III-NB still has the best overall performance (Figure 6).

Figure 5.

Pancreas study. (A) Densities of Spearman correlations between log library size and normalized data for ALL and each cell type. RUV-III-NB has the most concentrated density around zero, followed by scMerge. (B) Median biological silhouette score for different numbers of cumulative PCs. Seurat3-Integrated performs the best, followed by scMerge and RUV-III-NB (C) Heatmap of R² between logLS and cumulative PCs of normalized data. scMerge has the lowest correlation, followed by Seurat3-Integrated and RUV-III-NB. (D) Technical silhouette scores for each cell-type. scMerge has the lowest silhouette, followed by Seurat3-Integrated and RUV-III-NB. (E) Squared correlation between median and IQR of relative log expression (RLE) with log library size and squared of total canonical correlation (ccRLE) between median and IQR of RLE and log library size and batch. (F) Proportion of DEG when comparing cells of the same type across batches.

Figure 6.

Overall performance of normalization methods in the pancreatic study. Each panel represents a metric with methods represented by differently-colored bars. Metrics that require gene-level corrected data are not available for Seurat3-Integrated. The length of the bar corresponds to level of performance with respect to the metric in 0–1 scale.

RUV-III-NB accommodates size heterogeneity within a cell type

With UMI counts the library size corresponds closely to the number of molecules inside a cell and cell size. Hence, library size in experiments with UMI contain information about size-related heterogeneity as well as being affected by technical variation such as differences in molecule capture rates. Previous work (33) used cellular detection rates (CDR), i.e. the proportion of expressed genes to both model and adjust for potential size-related heterogeneity. They found that CDR is highly correlated with an RUV-estimated unwanted factor and while the variation due to size-related heterogeneity is less than variation due to technical factors, its magnitude is still considerable.

Here, we investigate the ability of the different normalization methods to isolate these biologically meaningful library size effects from the unwanted (technical) library size effects. To do this, for the NSCLC study we performed DE analysis comparing monocytes with smaller (< median) vs larger (≥ median) library size. The results show that RUV-III-NB has the lowest proportion of DEG (Figure 1F), which suggests that RUV-III-NB removed the unwanted library size effects most effectively. We then performed KEGG pathway analysis among the DEG to investigate whether the DEG obtained are biologically meaningful. We found that only DEG from RUV-III-NB log PAC and sctransform-log corrected were significantly enriched with terms from the phagosome pathway (Supplementary Figure S18). This is consistent with an earlier report (34) that larger monocytes have increased phagocytic activity. We carried out a similar analysis for the pancreas study where we compared beta cells with above and below median library sizes from the inDrop experiment (26). Sasaki et al., (35) reported that patients with type II diabetes have reduced beta cells size. We found that that only the DEG from RUV-III-NB log PAC were significantly enriched with terms from the insulin resistance pathway (Supplementary Figure S19). We conclude that only RUV-III-NB normalization can reliably reveal size-related heterogeneity among cells of the same type.

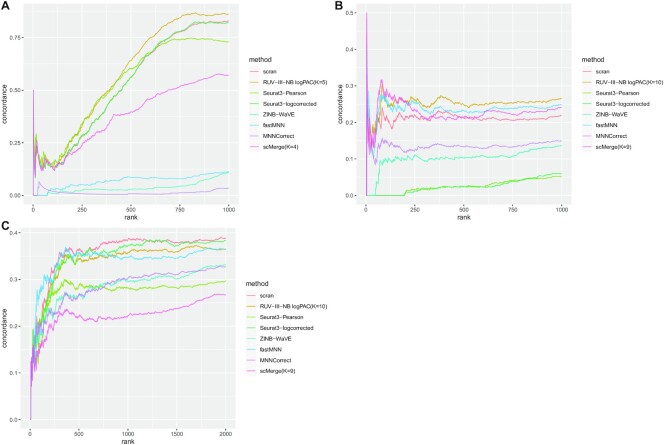
RUV-III-NB improves concordance with ‘gold standard’ DEG

For the Cell line, Gaublomme and Pancreas studies, we also compared the concordance of DEG based on data normalized by the different methods with the ‘gold standard’ DEG. For the Cell line study, the DEG are from the 293T vs Jurkat cell comparison, for the Gaublomme study we compare pathogenic vs sorted non-pathogenic Th-17 cells, while for the Pancreas study we compare alpha and beta cells. We found that for the Cell line and Gaublomme studies where batch is associated with biology, RUV-III-NB has the best concordance (Figures 7A, B), while for the Pancreas study (Figure 7C) where batch and biology are not associated, none of the batch-effect removal methods improve on scran normalization, with RUV-III-NB ranking second after Seurat3 with log-corrected counts.

Figure 7.

Concordance of DEG. (A) Jurkat vs 293T cells in the cell line study. RUV-III-NB has the best concordance, followed by Seurat3-Pearson. (B) Pathogenic vs Sorted Non-Pathogenic cells in the Gaublomme study. RUV-III-NB has the best concordance followed by fastMNN and scMerge. (C) Alpha versus Beta cells in the Pancreas study. fastMNN and scran have the best concordance followed by Seurat3-log corrected and RUV-III-NB.

RUV-III-NB performance is robust

The RUV-III-NB algorithm require users to specify the negative control gene set and the number of unwanted factors. Using the cell line dataset, we investigate the sensitivity of the key performance metrics against these parameters. We use five different strategies to identify the negative control gene set and varying K from 1 to 20. Supplementary Figure S20A demonstrate that for four negative control gene sets, including set 2 that uses the default single-cell housekeeping genes, the R² between log library size and leading principal component of normalized data is relatively robust when K is increased and thus potentially overestimated. Set 4, in which the negative control gene set was identified as non-DEG from the batch with two cell lines (batch 3), is the only one where the R² is affected by overestimation of K. In terms of average batch (Supp Figure S20B) and biological silhouette width (Supp Figure S20C), its performance is quite similar across different negative control gene sets, for K ≥ 2. RUV-III-NB performance also appears to be robust when λ_α ≥ 0.01 and λ_β ≥ 16 as regularization parameters (Supplementary Figure S21). Based on these results, λ_α = 0.01 and λ_β = 16 are used as default parameters in ruvIIInb package.

Computing time

The original implementation of RUV-III-NB requires a High-Performance Computing (HPC) environment. For the examples used in this paper, the running time on an HPC environment with 15 cores and 120 Gb total RAM (8Gb RAM per core), ranges from approximately 120 min for the CLL dataset with around 1650 cells to around 280 minutes for the Pancreas dataset with more than 10,000 cells (Supplementary Figure S22A). The running time is approximately a square root, rather than a linear function of the number of cells. Studies involving scRNA-seq are growing in size and it is now not uncommon to have studies with several hundred thousands of cells. To meet this challenge, we also provide a fast implementation of RUV-III-NB, which we call fastRUV-III-NB. For K ≤ 10, the fast implementation is faster than MNNCorrect and scMerge and about half as fast as Seurat3 (Supplementary Figure S22B). Importantly, judging from several key metrics (Supplementary Figure S23), fastRUV-III-NB achieves the same level performance as the original RUV-III-NB. The speed-up is achieved primarily by estimating gene-level parameters using a subset of cells (default = 20%). To reduce memory requirements fastRUV-III-NB processes the data as a DelayedArray object.

DISCUSSION

Single-cell RNA-seq offers us an unparalleled opportunity to advance our understanding of the transcriptome at the single cell level. However, scRNA-seq data contains significant amounts of unwanted variation that, when left unaddressed, may compromise downstream analyses. Most methods for removing unwanted variation from scRNA-seq data implicitly assume that the unwanted factors are at worst weakly associated with the biological signals of interest. In this paper, we have proposed RUV-III-NB, a statistical method for normalizing scRNA-seq data which does not make this assumption. The method adjusts for unwanted variation using pseudo-replicate sets, which should ensure that it does not remove too much biology when biology and unwanted variation are associated. Using publicly available data from five studies we show this to be the case.

We have benchmarked RUV-III-NB against methods that return gene-level normalized data as well as lower dimensional embedding. Both metrics are equally important in scRNA-seq experiments. While embedding is important and useful for clustering-based analysis to identify cells with similar biology, gene-level normalized data is used to identify markers genes to characterize the clusters. We have shown the distinct advantage of RUV-III-NB for UMI data in terms of embedding and normalized data when the unwanted variation is associated with biology. When biology is not associated with unwanted variation, RUV-III-NB has similar level of performance to Seurat3 and scMerge in terms of embedding and better in terms of normalized data.

A novel feature of RUV-III-NB is that it returns an adjusted count after adjusting every count for the unwanted variation. We call this the percentile-invariant adjusted count (PAC). These adjusted counts can be used as input to downstream analyses such as differential expression (DE), cell-type annotation and pseudotime analyses. In this paper, we have shown that when used for DE analysis, it delivers good control of false discoveries and improved power to detect ‘gold standard’ DE genes. In the vignette that accompanies the R package, we also demonstrated how the adjusted counts can be used to perform cell-type annotation.

RUV-III-NB can be used for both data with and without UMI, but its improvement relative to other methods is especially evident for UMI data. When using RUV-III-NB users need to specify the number of unwanted factors in the data (K) and the set of negative control genes. We have shown that RUV-III-NB performance is relatively robust to overestimation of K and the choice of negative control gene sets. As a general guidance, when there are B batches in the dataset, we recommend setting K slightly larger than B + 1 and then seeing if it can be reduced. The reason is because one unwanted factor is needed to model the log library size effect, up to B − 1 unwanted factors may be needed to model between-batch differences and the last unwanted factors are reserved to model unwanted factors that we do not foresee a priori.

While RUV-III-NB is developed primarily to remove within-study batch effects, it can also be used to integrate datasets from different studies where platform difference is a major source of unwanted variation. Using the Pancreas study, we have shown that the performance of RUV-III-NB for data integration purposes is quite competitive.

DATA AVAILABILITY

The method is implemented as a publicly available R package available from https://github.com/limfuxing/ruvIIInb. All datasets used in this paper are published datasets available for downloads from sources outlined in the Methods section above.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: Australian Health and Medical Research Council.

Conflict of interest statement. None declared.