Summary
We developed a computational approach to find the best intervention to achieve transcription factor (TF) mediated transdifferentiation. We construct probabilistic Boolean networks (PBNs) from single-cell RNA sequencing data of two different cell states to model hematopoietic transcription factors cross-talk. This was achieved by a “sampled network” approach, which enabled us to construct large networks. The interventions to induce transdifferentiation consisted of permanently activating or deactivating each of the TFs and determining the probability mass transfer of steady-state probabilities from the departure to the destination cell type or state. Our findings support the common assumption that TFs that are differentially expressed between the two cell types are the best intervention points to achieve transdifferentiation. TFs whose interventions are found to transdifferentiate progenitor B cells into monocytes include EBF1 down-regulation, CEBPB up-regulation, TCF3 down-regulation, and STAT3 up-regulation.
Subject areas: Biological sciences, cell engineering
Graphical abstract
Highlights
-
•
Differentially expressed transcription factors are the best for transdifferentiation
-
•
Probabilistic Boolean networks (PBNs) are used to model transdifferentiation using the scRNAseq data at one time point
-
•
A new approach works for a large number of network nodes
Biological sciences; cell engineering.
Introduction
Transdifferentiation, the direct transition of one mature cell type into another, has been widely observed in metazoa, either spontaneously or experimentally induced (Addis et al., 2013; Vierbuchen et al., 2010; Zhou et al., 2008). The attribute “direct” is defined as a cell type switching without passage through a common progenitor state of the two respective cell types, let alone an embryonic or induced pluripotent state (iPS) (Nicholas and Kriegstein, 2010). Such a detour would require two steps, induced dedifferentiation (commonly referred to as “reprogramming”) followed by the guided differentiation into a “destination” cell type. The redirection via a pluripotent state is inefficient and associated with the risk of teratoma formation (Cieślar-Pobuda et al., 2017).
Inducing transdifferentiation from one cell type to another has a variety of applications in tissue engineering, regenerative medicine, or cancer reversion to a normal (postmitotic) state (Cho et al., 2017; Grath and Dai, 2019). Like reprogramming, transdifferentiation can be achieved by ectopic overexpression of transcription factors (TF) because they regulate the expression of genes, collectively establishing the complex gene regulatory network (GRN) of the genome. The GRN governs gene activation programs, thereby establishing the gene expression profile that in turn determines the cell phenotype (Grath and Dai, 2019). Although cell-lineage determining TFs in development have long been described, evaluating which TF can serve as a switch to induce a given transdifferentiation is still largely empirical. As trial-and-error experiments to determine which TFs induce destination transdifferentiation are time-consuming, there is a need for the theoretical prediction of the specific (set of) TF(s) that can serve as intervention points for inducing transdifferentiation from a given cell type to another based on their distinct gene expression patterns.
The simplest method is to overexpress a TF that is known to be strongly associated with a cell type, i.e. a TF that acts as a canonical cell type-specific marker (Neph et al., 2012). Overexpression in the departure cell type A of such a lineage-defining TF that is specific for the destination cell type B has in many cases successfully converted cells from type A to type B (Heinäniemi et al., 2013). Such interpretation of correlation (cell type-specific expression) as causation, and its use for actuation, has proven surprisingly successful (Grath and Dai, 2019). Herein the intervention is typically the permanent switching on (ectopic overexpression) or off (genetic knockout) of an appropriate putative fate-determining TF (Ledford, 2015). This qualitative approach has limitations: it ignores the particular nature of the high-dimensional departure cell state, notably the information offered by the genome-wide gene expression profiles, as well as possible causal regulatory relationships, and is thus often inefficient. More recent computational prioritization of the TFs to be actuated in transdifferentiation protocols consider the gene expression profile (transcriptome) of cell lineages (Consortium et al., 2018; Rackham et al., 2016) or explicitly utilize curated gene regulatory circuit models to predict the required TF perturbation (Cahan et al., 2014; Zhou et al., 2013).
Single-cell transcriptome measurements now offer a new opportunity for refining transcriptome-based prioritization of the TFs to be used for intervention. The dispersion of cellular transcriptomes among isogenic cells of the same nominal cell type exposed by single-cell RNA sequencing (scRNAseq) is more than just “noise.” The structure of the dispersion in the high-dimensional expression space also reflects intrinsic constraints imposed by the GRN that controls the stability of cell states and changes in cell transcriptomes (Huang, 1999; Huang and Ingber, 2000; Kauffman, 1969). Moreover, the heterogeneity of cell states within one population of cells of the same type has emerged as one of the major reasons for the inefficiency of cell reprogramming (Chen, 2020; Francesconi et al., 2019). Thus, for a model of cell transdifferentiation to be successful, heterogeneity within the cell type needs to be taken into account.
We present a method based on the framework of probabilistic Boolean networks (PBNs) (Shmulevich et al., 2002a) to prioritize the TFs for genetic interventions that trigger transdifferentiation based on observed single-cell transcriptomes in populations of cells. Boolean networks (BN) had been used since their introduction by Kauffman in 1969 to deterministically model large (artificial) GRNs and to study fundamental properties of their dynamics, notably the settling of the network dynamics into a stable attractor state, a stable GRN-wide gene activation configuration that represents a biologically observable stable steady-state, or notably, a cell type (Braccini et al., 2017; Enciso et al., 2017; Huang et al., 2005; Joo et al., 2018; Krumsiek et al., 2011).
PBNs were originally proposed to capture the ability to explicitly represent biological regulation using rules, a way to absorb uncertainty into the model, the ability to use the model to study dynamics in a stochastic framework (enabling one to determine long-term behavior and steady states), and as a means of determining how a perturbation to a gene in the network affects system behavior. The latter is particularly important for driving the system toward a destination endpoint, such as in therapeutic intervention (Shmulevich et al., 2002a, 2002b).
With the advent of single-cell transcriptomics, we now have the opportunity to observe the heterogeneity of cell populations. Although PBNs naturally capture the uncertainty that may be either contextual (e.g., environmental inputs) or related to measurement noise in the case of model inference from data, the described approach lies in constructing many PBNs by directly making use of stochastic cell-to-cell variability of transcriptomes of individual cells. We focus only on genes capable of transcriptional regulation, as mediated by TFs. Thus, we focus on regulators that form the “core” of the PBNs constructed within our framework. By contrast, the “peripheral” genes that do not control other genes, such as structural proteins, do not directly contribute to driving the dynamics of the PBN.
We develop a stochastic dynamical model that generates the observed steady-state distribution of cell states, applied to the transdifferentiation scenario. Thus, we model two steady-state distributions representing the two dispersed cell populations within two GRN attractors: that of the departure cell type and that of the destination cell type. With the PBN formalism, we built an ensemble of BNs from randomly chosen pairs of cells of each of the two observed distributions in the single-cell transcriptomics data, representing the departure and destination state, respectively. The PBN constructed solely based on such static single-cell resolution gene expression data was then used for modeling transdifferentiation. We used a new PBN construction mechanism that we call the sampled network approach, which reduces computational costs compared to methods involving the full network, affording a significant increase in the number of nodes that can be considered. Using synthetic data, we demonstrated that the sampled and the full (not sampled) network identified the same cell types and also yielded consistent results in the intervention analysis.
This article is organized as follows. In the results section, we first present the process of building BNs from data and the merging of a set of BNs into a PBN using the two different approaches, the full and sampled network. We then show findings from the analyses of synthetic data as a validation of the method, followed by results of the analysis of published scRNAseq data for the case of progenitor B cells and monocytes and the transdifferentiation between these two cell types. In the discussion section, we offer additional thoughts on our algorithm and compare the results with that of the literature. The Star Methods section describes the details of the implementation. The supplementary data contain further analysis and an introduction to the basic formalism of BNs and PBNs.
Results
Overview of the procedure
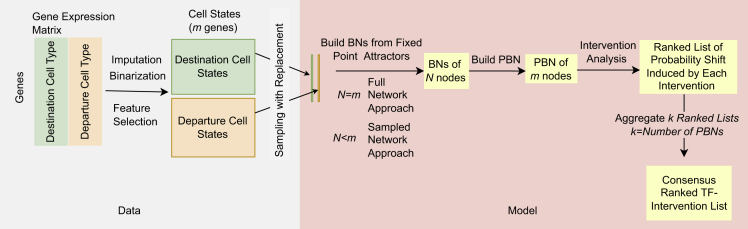
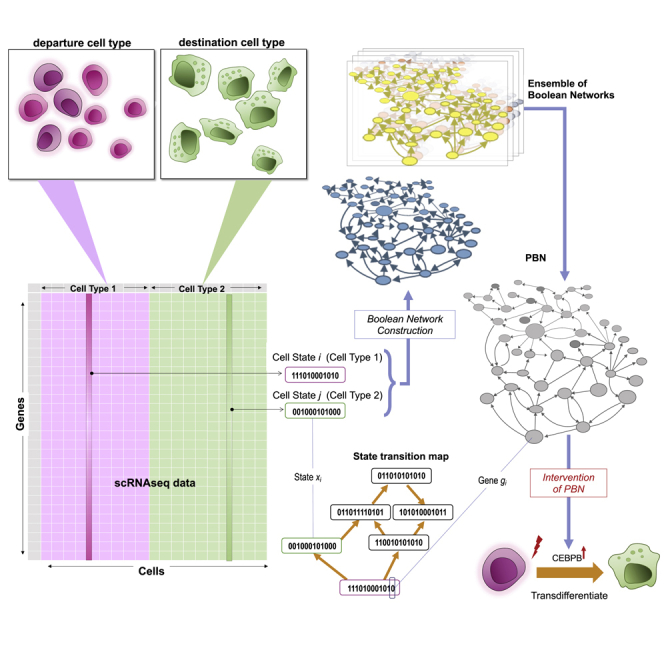
To exploit static scRNAseq data for modeling transdifferentiation, we used probabilistic Boolean networks (PBNs) with the goal of identifying the set of TFs whose activity needs to be permanently set to ON or OFF (“permanent intervention”) to achieve transdifferentiation from the departure to the destination cell type. As a limited number of TFs play a prominent role in controlling a cell type-specific transcriptional state by autoregulation, cross-regulating each other, and regulating cell type-specific gene expression, we restricted the analysis of gene regulatory networks only to TFs. “Permanent intervention” models gene deletion or ectopic overexpression which are still the most common and reliable genetic manipulations (Afzal et al., 2020; Ledford, 2015). The overall approach is shown in Figure 1.
Figure 1.
The methodology overview
The left panel shows the data preprocessing part. The binarized gene expression of relevant transcription factors (TFs) is fed into the model. The right panel shows the sequential steps of the modeling. First, n BNs are built based on one randomly picked cell state pair and one PBN is built based on the n BNs. This process of picking random cell state pairs is repeated k times resulting in k PBNs. Intervention analysis is performed on each PBN separately and the results are aggregated into one consensus list that represents the TF interventions that are most likely to induce the transdifferentiation of the departure cell type into the destination cell type. N is the number of nodes in a BN, m is the number of genes after feature selection.
In order to build the PBNs, every Boolean function from every Boolean network constructed by the BN construction algorithm was used. We used two different approaches, namely, the full and the sampled network approaches. In the full network approach, every TF in the system is a node in every BN. In the sampled network approach, a different randomly sampled subset of TFs constitutes the nodes of each BN. We showed, with synthetic data, that the intervention results using the sampled network approach are consistent with the results using the entire network that contains all the nodes (i.e., full network approach).
To the best of our knowledge, this is the first study that subsamples the cell states at the node level in order to reduce the state space, thus addressing the scalability problem of all network models, including PBNs, that have an exponentially growing state space relative to the number of nodes.
In order to use PBNs starting from the single-cell gene expression data that contains the transcript counts for each gene in every cell, we first impute and binarize the data by setting the expression of a gene in a cell to 1 if there is an expression, otherwise to 0, obtaining two gene-by-cell binary data matrices, for the destination and the departure cell population, respectively (Figure 1, left). To evaluate the approach we also generated synthetic data in the same binary form by randomly generated pairs of Boolean vectors that represent cell states from cells in the departure and destination cell types. In both cases, the cell-type gene expression matrices, observed or synthetic, are interpreted as steady states to build the PBN (Figure 1, right).
Analysis of synthetic data
This analysis validates the “sampled network” approach. We first randomly generated multiple pairs of Boolean vectors, which represent the steady-state cells in the population of departure and destination cell types, respectively. These steady-states are the starting point to construct PBNs that will be used to model the transition of the states by representing each gene with a node. A node’s value can be updated by a Boolean function that is sampled with a selection probability among a set of Boolean functions taken from the Boolean networks, constructed as follows. First, Boolean networks (BN) are constructed from the gene expression data of each departure-destination pair of states using the BN construction algorithm developed by Pal et al. (2005), which uses states extracted from steady-state gene expression data to build BNs that possess these states as their attractors (the states that a BN eventually reaches). We then construct a PBN by using the Boolean functions (for each node) from the constructed BNs. In the PBN, a node’s value is updated by a Boolean function that is sampled with a selection probability among a set of Boolean functions that have been found by the BN construction algorithm. In the full network approach, every TF in the system is a node in every BN. To reduce the computational cost, we also used the sampled network approach in which a different randomly sampled subset of the TFs constitutes the nodes of each BN.
Evaluation of probabilistic Boolean networks constructed by using the full and sampled network approach
We first had to determine whether the PBNs constructed using the full and the sampled network approaches consistently predict the highest steady-state probabilities for the cell states from which they have been built. We also determined whether the two approaches are consistent in terms of the probability shifts achieved by the intervention and of the steady-state probability distributions induced by the different interventions. Intervention means setting a node’s (gene) value to 0 or 1 forever, representing a “constitutive” genetic manipulation. We also verified the consistency of the sampled network approach by building multiple PBNs on the same cell state pairs in the synthetic data and showing that the probability shifts are highly concordant.
We first determined which intervention caused the highest probability of mass shift from the departure to the destination cell states. There are eight possible intervention types for a given TF: the TF can have value 0 or 1 in the departure cell state and 0 or 1 in the destination cell state and the intervention can be either setting the TF’s value to 0 (TF = 0) or to 1 (TF = 1). We evaluated the consistency between the full and sampled network approaches in terms of both steady-state distribution and probability mass shift from departure to destination cell states caused by the interventions. To do so, 100 PBNs on 100 different cell state pairs were built using the full network and the sampled network approaches. Each cell state is represented by a vector of random binary values of length 10 and a cell state pair represents two states randomly assigned to departure and destination cell types. We applied permanent intervention to each TF by fixing it to a value of 0 or 1.
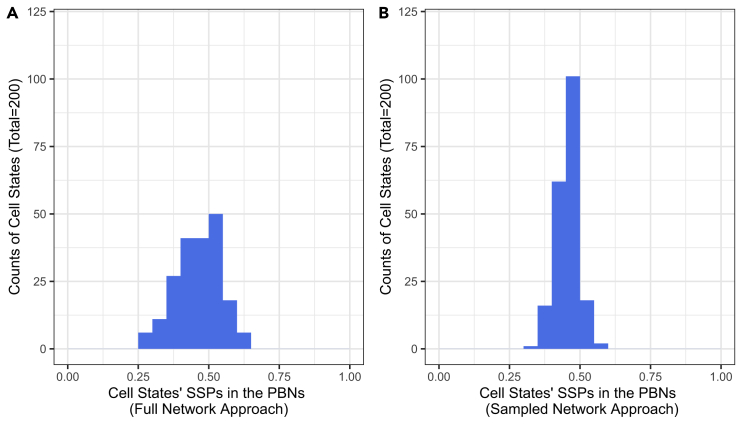
We then investigated the concordance of the sampled network approach by building 100 PBNs on the same cell pair. We also showed one example of the steady-state distribution induced by each intervention type. For all cell state pairs, the cell states were correctly characterized as the states with the highest steady-state probability by both full and sampled network approaches. As two cell states were used to build each BN, the states of the PBN corresponding to these cell states were expected to have steady-state probability of around 0.5. The mean and SD of the steady-state probabilities of cell states from full and sampled networks were 0.4664, 0.0773 and 0.4568, 0.0412, respectively. The histogram of probabilities, at the steady state, of the cell states across all PBNs is shown in Figure 2.
Figure 2.
The histogram of steady-state probabilities (SSPs) of cell states in the constructed PBNs
(A and B) (A) Shows counts of cell states with the probability on the x axis using the full network approach; (B) shows counts of cell states with the probability on the x axis using the sampled network approach; The total number of cell states is 200 in each case (100 cell state pairs). Two cell states are used to build each BN. The states of the PBN corresponding to these cell states are expected to have steady-state probability of around 0.5 before any intervention. The steady-state probabilities being around 0.5 validate the BN and PBN construction mechanisms.
Probability shift induced by interventions in the probabilistic Boolean network from synthetic data
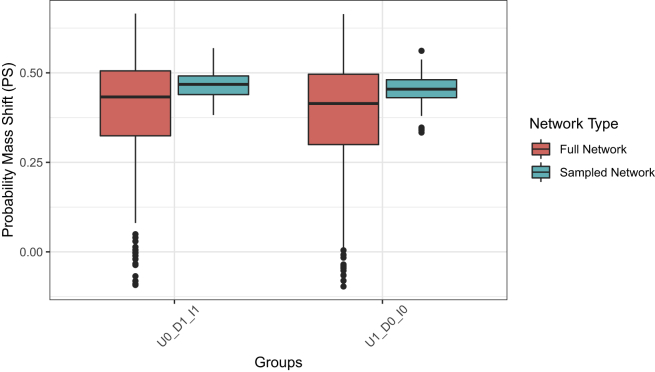
We next quantified the shift of the probability of the steady-state of the departure to that of the destination cell type following an intervention. We calculated the probability of mass shift induced by interventions (TF = 0 or TF = 1) on which the TF has different values in the departure and destination cell states and the intervention is performed consistently with the destination cell states. Figure 3 shows the probability of mass shift for the two relevant cases mentioned above.
Figure 3.
The probability shift (PS) from departure to destination cell states
The boxplots show the probability of mass shift from departure to destination cell states caused by interventions in which the TF has different values in the departure and destination cell states and the intervention is performed consistently with the target, where the TF’s binary status in the destination cell state is referred to as the target. U0_D1_I1: TF has value 0 in the departure cell states, and 1 in the destination cell states, and TF = 1 (its value is set to 1 permanently) U1_D0_I0: TF has value 1 in the departure cell states, and 0 in the destination cell states, and TF = 0 (its value is set to 0 permanently).
The results show that both the full network and sampled network approaches find that the probability mass shift from departure to destination cell states computed from different PBNs is centered at 0.5 and, interestingly, that the sampled network approach is more consistent as evidenced by the narrower distribution. We believe that the reason for this phenomenon is that the sampled network has a smaller search space than the full network.
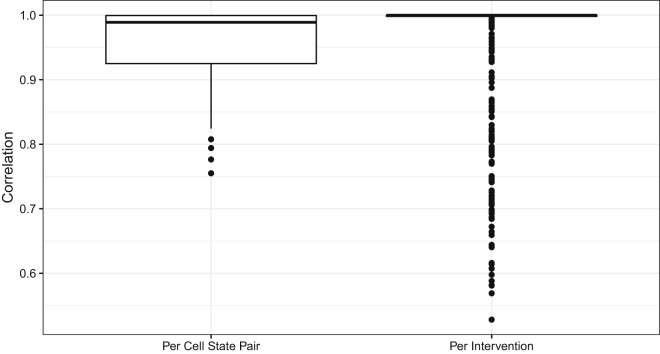
Figure 4 shows the distribution of Pearson correlation coefficients between steady-state probabilities of the states in the full and sampled networks after the same intervention. The interventions considered for each TF are the ones that have different values in the departure and destination cell states and the intervention is performed consistently with the target value (for each intervention). It also shows the distribution of Pearson correlation coefficients between steady-state probabilities of the states in the full and sampled network after the same interventions per cell pair. One correlation is produced over all desired interventions for one cell state pair. As can be seen, the correlations are consistently high.
Figure 4.
The boxplot of the correlations for 100 cell state pairs. Correlations between πf and πs for all cell pairs where πf and πs are the steady-state probability distributions after intervention on PBNs built by the full and sampled network approaches
One correlation is produced for each of the desired interventions (518 correlations in total) (Per Intervention). The correlations between the steady-state probability vectors after desired interventions corresponding to the full and the sampled networks for each cell state pair are plotted (100 correlations in total) (Per Cell State Pair).
Probability shifts and steady-state distributions after different types of interventions on one example pair of departure and destination cell states
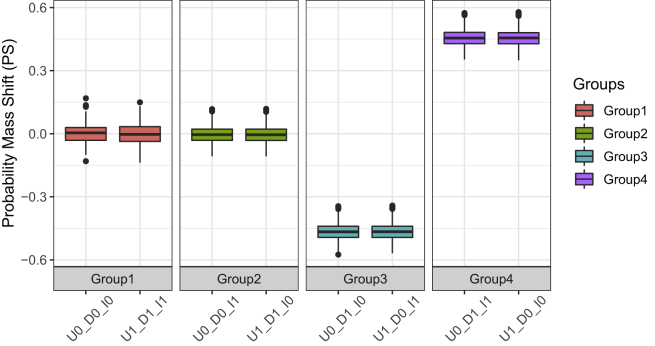
This analysis was performed on the PBNs built using the sampled network approach in order to understand how the probability mass shifts after different intervention types and to compute the steady-state distributions of the PBN induced by them. We built 100 PBNs using the sampled network approach on one cell state pair (Departure: 1010101110, Destination: 1001010011). Different types of intervention were performed on each PBN. Figure 5 shows the probability of mass shift and the steady-state distributions of the PBNs induced by different interventions. There are four groups of behaviors caused by the eight types of intervention. Only one group (Group 4) results in the desired probability shift. The small inter-quartiles in the boxplots show the consistency of our results.
Figure 5.
The probability of mass shift induced by different intervention types
100 PBNs were built on the same cell state pair (Departure: 1010101110, Destination: 1001010011) using the sampled network approach. The boxplots show the probability of mass shift induced by different intervention types: The intervention types are denoted by UX_DY_IZ where U and D stand for departure and destination cell states, X and Y are the values of the TF in the departure and destination cell states and I stands for Intervention and Z is the value that the TF is set to after intervention, where X, Y, and Z are binary values. Example representation: U1_D1_I0: TF’s value in departure cell state = 1, TF’s value in destination cell state = 1 and Intervention is setting the TF to 0. Group 1 (U0_D0_I0 and U1_D1_I1) has almost no effect on the steady-state distribution while in Group 2 (U0_D0_I1 and U1_D1_I0) the steady-state probability mass of cell states is distributed over other states and the initial cell states are lost. In Group 3 (U0_D1_I0 and U1_D0_I1), the steady-state probability mass is moved toward the departure cell state while in Group 4 (U1_D0_I0 and U0_D1_I1), most of the steady-state probability distribution is moved toward the destination cell state.
Analysis of biological data
We applied our approach to the scRNAseq data (GSE116256) which was generated by the study (Van Galen et al., 2019). We only used gene expression data from healthy donors. We sought to find the interventions that would induce the shift with highest probability from a progenitor B cell state (departure) to a monocytic state (destination) utilizing single-cell transcriptome data available for these two cell types. Transdifferentiation from progenitor B cells to monocytes has previously been observed (Cirovic et al., 2017; Stoilova et al., 2013). Using the scRNAseq dataset to determine the TF intervention most likely to induce the transdifferentiation of progenitor B cells into monocytes, we randomly picked one progenitor B cell state and one monocyte cell state from the single-cell transcriptomes and constructed one PBN for each such cell state pair. We repeated this multiple times so as to capture the heterogeneity in the scRNAseq data within each cell type. We used 30 hematopoiesis-related TFs that were retrieved from a comprehensive literature review (Hannah et al., 2011) and built our model using the sampled network approach, as the full network approach becomes computationally prohibitive (with 230 states). We found that the two states predicted to have the highest steady-state probability indeedhad specific gene expression profiles of the progenitor B cell and monocyte state pair from which the PBNs were constructed.
Intervention to achieve progenitor B cell to monocyte transition
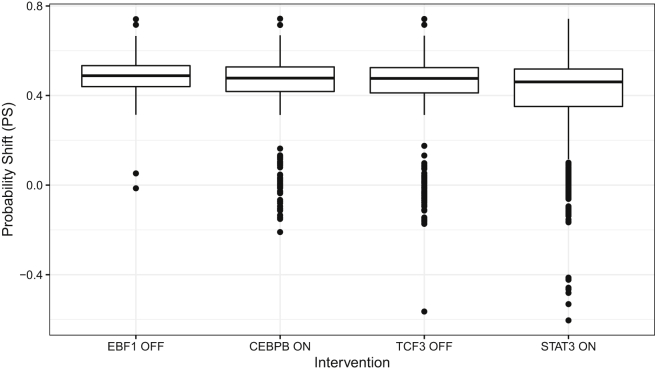
We next analyzed the intervention on each of the 500 sampled cell state pairs. The PBNs built on each cell pair were subjected to 60 possible TF-interventions (TF = 0 and TF = 1 for each of the 30 TFs), obtaining a ranked list of TF interventions from each PBN based on the probability shift they induced. Finally, we aggregated the lists using the RobustRankAggregation method (Kolde et al., 2012) to obtain one consensus list. In the consensus list, we found that EBF1 down-regulation, CEBPB up-regulation, TCF3 down-regulation, and STAT3 upregulation are the interventions (in decreasing order) that are most likely to achieve transdifferentiation from progenitor B cells into monocytes. The probability shifts of the interventions that cause transdifferentiation with the highest probability over the sampled data points are shown in Figure 6.
Figure 6.
The distributions of the probability mass shift (PS) from progenitor B cell to monocyte induced by each of the indicated interventions on PBNs that are constructed using the scRNAseq data
A positive value of PS indicates a shift toward the destination state.
Discussion
In this study, we have developed a PBN-based approach to identify the gene in a gene regulatory network whose manipulation (permanent activation or inactivation) is most likely to induce the transdifferentiation of one cell type into another. We limited our networks to the subgraphs representing TFs because these regulatory genes control the activity of other genes and thus, collectively dictate the dynamics of the global gene activity profiles, in which stable gene expression states embody the stable cell types. We show that the new sampled network approach, which offers the facility to efficiently examine large networks, produces consistent results with the full network approach (Figure 5).
Our analysis was designed to focus on “permanent interventions” and thus will naturally not find regulators whose transient activation (pulsed expression) would have sufficed to cause transdifferentiation. For instance, some factors can be upregulated to initiate the transdifferentiation and then can or must be down-regulated again when the destination state is reached. In the biological context of (patho)physiological transitions, such regulatory factors that are induced transiently in response to regulatory signals from the tissue and thus define a transition state have been amply described. For instance, immediate-early genes (IEG), typically signal transduction and transcriptional regulators, are rapidly induced on receiving a differentiation signal and then subside within minutes to hours, thus defining an unstable transition state (Moris et al., 2016). In contrast to such natural transitions, transdifferentiation by the experimental manipulation of lineage-specific TFs, as modeled by our interventions, may represent a brute, external imposition of a desired state.
Nevertheless, the fact that a (permanent) alteration of a cell type-specific TF can induce transdifferentiation into a stable state may reflect a deeper biological organization through which the GRN governs development. One could envisage that the evolutionary innovation that adds a new cell type (along with its novel distinct gene expression state) to the existing cell type repertoire of a metazoan must also guarantee that the new cell type can be reached during development in an effective manner from an existing cell type as the departure state. A simple implementation of this requirement would be a dual role for the distinct molecular feature both in specifying the new trait as well as in implementing its development.
The approach we took captures two types of uncertainty. The first is the uncertainty of our knowledge of TF-TF interactions. A TF’s expression state can be determined by different upstream TFs and rules with different probabilities. This type of uncertainty is handled by each PBN of an ensemble of BNs. Second, there is uncertainty in scRNAseq data owing to experimental variability as well as the physical stochasticity of gene expression. To address both uncertainties we randomly sampled the cell type states, which capture the frequency of the different cell states in the scRNAseq data, where a state is defined by the binary expression status of 30 hematopoiesis-related TFs. We then constructed one PBN from each pair of cells (one drawn from the distribution of the departure and one from that of the destination cells) and performed intervention analysis for each pair of cells independently. We then aggregated the results from the set of different PBNs thus generated and built a consensus-ranked list of the interventions most likely to induce the transdifferentiation of progenitor B cells into monocytes. This approach can easily be applied to any cell state pair from two cell types for which an intervention that triggers a transition is sought.
A most intriguing finding is that the TFs that are differentially expressed between departure and destination cell types are also the ones that are more likely to induce the transdifferentiation of one cell type into another when targeted by our intervention. This finding that TFs differentially expressed in destination state X are also the levers for achieving that state X by overexpression essentially means that in cell fate regulation, “correlation is causation” as implicitly assumed in reprogramming efforts (Crespo and Del Sol, 2013; Okawa et al., 2016; Rackham et al., 2016) that aim to find the best TF intervention for cell reprogramming. Indeed, lineage-specific TFs are also the master fate-determining regulators (Guerrero-Ramirez et al., 2018). This complementary approach for identifying stringent cell type-specific markers has identified TFs that are also enriched for those that have been utilized for reprogramming into the respective cell types (Consortium et al., 2020). This consistent finding lends further support to the mapping between TFs that act as cell type-specific “markers” and the (same) TFs that act as lineage determining factors sufficient to drive transdifferentiation into said cell type. Our computational approach harnesses the information immanent in the observed cell states that in turn reflects the regulatory constraints imparted by the GRN and makes predictions that are consistent with this empirical assumption. Such fundamental robustness in development and its evolution, which randomly rewires the gene regulatory network and evaluates the functional consequence on developmental paths (evolutionary developmental biology) (Torres-Sosa et al., 2012), may also be reflected in the PBN that we used.
The identity of the factor needed to induce a state (“lineage-determining factor”) with that of being a distinct feature of said state (“lineage marker”) has a long history in experimental biology, starting with the seminal work of Weintraub who used the muscle-cell specific TF MyoD to induce the transdifferentiation of fibroblasts into myoblasts (Stadtfeld et al., 2008). However, this collapse of correlation with causation is far from universal. First, successful transdifferentiation requires the departure state to be permissive, which is more likely the case when it is developmentally related to the destination state (Weintraub et al., 1989). Specifically, MyoD does not produce myoblasts when overexpressed, e.g., in epithelial cells. Here, we study the transition from B cells to monocytes, both of which are immune cells that share functional features, such as antigen-presentation. Thus, the initial state, that is the departure state, also plays a role in determining the feasibility of given transdifferentiation.
The biological principle that transdifferentiation can be achieved simply by upregulating the cell type-specific transcription factor of the destination cell type (Fu et al., 2017; Grath and Dai, 2019) is in line with the complementary notion that repression of regulators that establish the resident cell type can also cause transdifferentiation away from it (Aydin and Mazzoni, 2019). Our analysis also supports this empirical property.
For the specific transdifferentiation of progenitor B cells into monocytes, our findings indicate that EBF1 down-regulation, CEBPB up-regulation, TCF3 down-regulation, and STAT3 up-regulation promote this transdifferentiation. Indeed, EBF1 (Ceredig et al., 2009; Laurenti et al., 2013) and TCF3 (Somasundaram et al., 2015) whose inactivation triggers exit from the B cell state, has been shown to be critical for differentiation into B cells and for maintenance of B cell lineage identity. Conversely, the upregulation of CEBPB is known to transdifferentiate progenitor B cells into monocytes (Cirovic et al., 2017). STAT3 is also known to have a role in monocyte differentiation (Bigley et al., 2011; Miranda et al., 2005; Paul et al., 2016).
EBF1 is a regulator known to be required for B cell formation from its precursors, while also disallowing their differentiation into other cell lineages (Boller et al., 2018) and is also essential for the maintenance of the B cell state. Furthermore, knockout of EBF1 causes myeloid development, whereas the restoration of EBF1 expression inhibits myeloid differentiation (Pongubala et al., 2008). EBF1 regulates B-lymphoid versus myeloid and other fates by enforcing B cell-related gene expression while reducing the expression of myeloid-related genes like PU.1 and EBP (Dorantes-Acosta and Pelayo, 2012). Thus, it represents a hypothesized target the suppression of which is predicted to lead to monocyte differentiation.
CEBPB is known to induce transdifferentiation in murine cells (Cirovic et al., 2017; Stoilova et al., 2013) but to the best of our knowledge, it has not been tested in human cells. CEBPA, however, is known to transdifferentiate pre-B cells into macrophages in humans with 100% efficiency in the absence of stroma (Bussmann et al., 2009). In the dataset that we used, CEBPA has low expression and it is known that the lack of CEBPA can be compensated by the activation of CEBPB (Cirovic et al., 2017). As CEBPA and CEBPB have overlapping roles, it may explain why we found CEBPB as a candidate target and not CEBPA. Thus, CEBPB represents another candidate for experimental validation.
CEBPA expression levels were very low in the entire dataset including progenitor B cells and monocytes although CEBPA is known to be highly expressed in monocytes (Krumsiek et al., 2011). Moreover, CEBPA is not specific to B cells but rather appears to be a generic regulator in the development of lineages with wide-ranging pioneer factor activity involved in fate determination of cell types ranging from lung, adipose, to T- and myeloid cells (Ohlsson et al., 2016).
TCF3 is a B cell fate determinant and one of the regulators of EBF1 (Laslo et al., 2008). Thus, downregulation of TCF3 could be desired intervention for the same reason as downregulating EBF1. Both TCF3 and EBF1 are transcription factors that play a role in transdifferentiation from B cells to macrophages (Eguizabal et al., 2013).
Several approaches that have utilized bulk transcriptome data for finding the TFs most likely to induce cell type conversions or reprogramming have been proposed. Mogrify (Rackham et al., 2016), CellNet (Cahan et al., 2014), and the study by D'Alessio et al. (D’Alessio et al., 2015) do not consider TF-TF interactions in their models. By contrast, several Boolean network approaches explicitly model cell (trans)-differentiation (Collombet et al., 2017; Enciso et al., 2020; Krumsiek et al., 2011) based on a rule set extracted from the literature to define the presumed ground truth Boolean functions for every gene. Our method departs from these two approaches: while the PBN approach is inherently also data-driven and models transdifferentiation within a dynamical system framework, it does not seek to infer any GRN architecture. Put another way, it is not our aim to determine from the data how each gene is regulated by other genes in order to formulate the dynamical system equations that explicitly model the attractor transition dynamics. Moreover, unlike all previous work with PBNs that utilize the “bulk transcriptome” of an entire population of cells as aggregate, we now specifically exploit the dispersion of transcriptomic states of cells of the same type as observed in single-cell transcriptome data. To the best of our knowledge, the only computational method for prioritizing candidate transcription factors using the scRNAseq data is TransSynW (Ribeiro et al., 2021), which considers source and target cell types, but unlike our method, does not include TF interactions.
Limitations of the study
A limitation of the study is that our approach does not explicitly utilize the gene expression counts from the RNAseq data, but is based on a binary representation of gene expression values. This binary discretization may be an oversimplification of gene expression but this trade-off is necessary for the efficient simulation of large ensembles of networks. Moreover, a long history of modeling gene complex regulatory networks as Boolean networks with binary-valued gene expression suggests that the network architecture and the Boolean function as such capture much of the emerging biological behavior of the regulatory network. Although our system is limited to the subnetwork comprising the TFs, it can be extended to lineage-specific gene signatures and encompass other classes of regulators, like miRNAs.
STAR★Methods
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Single-cell RNA-seq reveals AML hierarchies relevant to disease progression and immunity | (Van Galen et al., 2019) | https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE116256 |
| Software and algorithms | ||
| R Programming Language | https://cran.r-project.org | |
| Julia Programming Language | https://julialang.org | |
| Generating Boolean networks with a prescribed attractor structure | (Pal et al., 2005) | https://doi.org/10.5281/zenodo.6954489 |
| Sampled Network Approach | This paper | https://doi.org/10.5281/zenodo.6954489 |
Resource availability
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Ilya Shmulevich (ilya.shmulevich@isbscience.org).
Materials availability
-
•
This study did not generate new unique reagents.
Method details
BN construction
BNs were originally proposed by Kauffman in 1969 for representing gene regulatory networks, where a gene is quantized as 1 (0) if it is ON (OFF) (Kauffman, 1969). A Boolean network is a directed graph (G, E) where each node xi is a binary variable that is updated at each time point and each edge Eij represents regulation of xj by xi (Schwab et al., 2020). The value that xi takes at time t+1 is determined by its regulators’ values at time t with a Boolean function that is assigned to xi. This update can be synchronous or asynchronous with other genes depending on whether all nodes’ values are updated simultaneously or sequentially. In this study we used synchronous updates. The values of all nodes at time point t together represent the state of the network at time point t. A Boolean network has 2n states, where n is the number of nodes and a transition from a state (time point t) has to lead to only one state (time point t+1) as determined by the values of the input nodes for each node at time point t.
In the long term, depending on the initial conditions, Boolean networks reach some state(s) and stay there forever unless a perturbation/intervention is introduced to the network. These stable states are called attractors and can be fixed points or cycles. If it is a fixed point attractor, then the state at time point t+1 will always be the same as the state at time t while if it is a cyclic attractor, the cycle will have a finite number of states and every state in the cycle will eventually be revisited. Fixed point attractors represent stable cell types (or cell states) in homeostasis (Zhou et al., 2013), which we assume in this study. Another reason to use only fixed point attractors is that cycle attractors are mostly artifacts of synchronous updating (Greil and Drossel, 2005; Greil et al., 2007).
Before constructing the PBN, we first built a set of BNs using static single cell gene expression data and the algorithm developed by Pal et al. (2005). This algorithm uses a set of (observed) states extracted from steady state gene expression data and builds BNs that possess these states as their attractors. This is an ill-posed inverse problem because many or no BNs may have these attractors. The algorithm randomly samples attractors from the observed states and picks a random subset of genes Wi that, when used as inputs, collectively determine the value of gene xi via the Boolean function fi assigned to gene xi and then checks the compatibility of the set Wi with the given attractors. If the set is not compatible with the attractors, it picks a new set Wi. The algorithm generates the truth table that corresponds to the attractors and randomly assigns the remaining entries. It checks for cycling attractors and if found, it refills the truth table. In addition to the attractors, the maximum connectivity in the network and the minimum and maximum number of level sets of the states in the BNs are also constrained. Level sets of states represent the number of transitions required to reach one of the attractors and are computed from the state transition diagram; e.g., level set Ij consists of the states that can reach one of the attractors in j transitions (Pal et al., 2005). In our study, we constructed PBNs using only those Boolean functions that exist in any of the BNs that have been constructed from the given two attractors, each of which is specified by the two single cells’ transcriptional states.
PBN construction
PBNs are generalizations of BNs where a node’s value can be updated by a Boolean function that is sampled with a selection probability among a set of Boolean functions (“predictors”) (Shmulevich et al., 2002a). The set of Boolean functions for a node xi is represented as
where fj(i) is one of the predictors that determine the value of node xi and is the number of predictors of node xi.
We constructed one PBN using the set of BNs constructed from the gene expression data of each pair of attractor states representing the cell state pair from the two cell types that defines the destination transition. We then performed the interventions that achieve the transition. Intervention analysis then serves to predict the TFs that can be used for inducing transdifferentiation.
We used the so-called independent PBN approach (Shmulevich et al., 2002a), which assumes independence of the predictors. This assumption is needed for the sampled network approach.
The state into which a PBN will transition is determined by the joint probability of the node predictors. The dynamics of the PBN correspond to a Markov chain (Shmulevich et al., 2002a). To be able to escape from an irreducible sub-chain, the system needs to have a small random perturbation probability p > 0. The random perturbation of a node is the flipping of its value from 0 to 1 or vice versa independently of other nodes. The Markov chain induced by the PBN becomes ergodic (every state becomes reachable) with the introduction of such small random perturbations to the system. The ergodicity implies the existence of a unique steady state distribution, which represents long term behavior. We estimate the steady state distribution by running the network for a sufficiently long time (until convergence, after a burn-in period) and calculating the time spent in each state.
Permanent intervention
A permanent intervention is the setting of a gene’s value and fixing it permanently in this value. For a PBN, this means that the Boolean function that determines the gene’s value has selection probability 1 and is set to the identity function, and the initial value is set to a desired value of 0 or 1. This intervention reduces the state space by half since the states in which the intervened gene has the value that is not equal to the fixed value cannot be observed. The permanent intervention has no effect on the other genes’ predictive Boolean functions or selection probabilities of these functions (Shmulevich et al., 2002b).
Synthetic data analysis methods
Construction of synthetic PBNs
We generated 100 cell state pairs where each cell state is represented by 10 binary TFs, i.e., a binary vector of length 10. In the full network approach, we built 50,000 BNs using these 10 TFs together for each cell state pair (100 cell state pairs, 5000 BNs for each, 500,000 BNs, 5,000,000 Boolean functions). In the sampled network approach, for each cell state pair, we sampled 5 TFs out of 10, built 100 BNs and repeated this 100 times (100 cell state pairs, 100 subsets, 100 BNs = 1,000,000 BNs, 5,000,000 Boolean functions). We used the same number of Boolean functions for each of the approaches. The number of inputs for each TF (number of inputs to the Boolean function) was picked randomly among 1, 2, 3; the number of levels of the BNs ranged between 2 and 10 and the perturbation probability was 0.002 for both full and sampled network approaches. We had many synthetic networks, we set a high perturbation probability to accelerate convergence, without changing the overall results.
The Markov chain was simulated for 100,000 iterations with a burn-in period of 50,000 iterations. We divided the visited states into two groups: between 50,000 and 75,000th iterations and between 75,001 and 100,000th iterations. Then we had two distributions of length 1024 (2ˆ10), each element of which is the number of visits to a state. We performed the Kolmogorov-Smirnov test on the two distributions for each of 100 cell state pairs (both full network and sampled network approaches) to determine whether the distributions are statistically indistinguishable (p > 0.05) to assess convergence. The steady state probability (SSP) of states was calculated by simulation. We calculated the number of visits to each state to find the states where the PBN has spent its time the most and checked whether they correspond to the attractors of the constituent BNs of the PBN.
Permanent intervention
Permanent intervention was performed by setting a TF to a value and not updating its value during the iterations (a frozen node in the network). The Boolean function for that TF can be represented as a fixed constant Boolean function: f=0 or f=1 with selection probability 1. In the intervention analysis, we calculated the number of visits to each state just like we did for finding attractors except that each state consisted of 9 TFs since we excluded the TF with which we intervened. There are 512 steady state probabilities in each intervention analysis.
The amount of probability that is shifted from the departure to the destination state is defined as,
where PS is the probability mass moved from the departure state to the destination state.πFB, πFA, πTB, πTA represent the probability mass on the departure state before and after intervention and the probability mass on the destination state before and after intervention, respectively.
There are 8 types of intervention per TF: the TF can be 0 or 1 in the departure cell state and 0 or 1 in the destination cell state and the intervention is denoted as TF = 0 or TF = 1. We are interested in the following relevant interventions for the cases where the TF has different values in departure and destination cell states. The intervention is performed consistently with the destination cell state (i.e., if the target bit is 1, then the intervention is also 1). The relevant cases are the TFs whose value is 0 in the departure cell state, and 1 in the destination cell state, and TF = 1 and the TFs whose value is 1 in the departure cell state, and 0 in the destination cell state, and TF = 0.
We monitor convergence in the same way we do for PBN construction.
Biological data analysis methods
Data preparation for PBN construction
The scRNAseq data (GSE116256) in this analysis was generated by the study (Van Galen et al., 2019), the aim of which was to understand the AML micro-environment, distinguish healthy and malignant cell types and illustrate subclonal evolution using transcriptomics and mutational data from AML patients and healthy donors. The dataset includes 38,410 cells from 40 bone marrow aspirates from 16 AML patients (30,712 cells) and 5 healthy samples (7,698 cells) as well as genotyping for 3,799 cells. The cell types from healthy donors that we used are progenitor B cell and monocyte. In our analysis we used combined data from progenitor B cells and monocytes from four healthy donors since one healthy donor was used for enriching progenitors (CD34+CD38– and CD34+).
We performed drop-out imputation with the R-Bioconductor package scRecover (Miao et al., 2019) using scImpute imputation option (Li and Li, 2018). Different imputation options like MAGIC (Van Dijk et al., 2018) and SAVER (Huang et al., 2018) did not change the overall results. Not employing data imputation caused data inconsistency, meaning that after feature selection and binarization, cell states from some progenitor B and monocyte cell types had the same binary sequence. 12 unique data points had the same binary sequence with two labels (progenitor B and monocyte).
We used the 30 hematopoiesis related transcription factors from the comprehensive literature review of genome-wide hematopoietic transcription factors from the work by (Hannah et al., 2011). These TFs are listed in Table S1.
We also attempted k-means and TF-IDF (Moussa and Măndoiu, 2018) binarization approaches. Both resulted in inconsistent data. We decided to set the expression of a gene in a cell to 1 if there is an expression, otherwise to 0, similar to the approaches used in (Fisher et al., 2015; Woodhouse et al., 2018).
The 30 TF gene expression matrix of progenitor B cells and monocytes had 18806 zero and 1864 non-zero counts. 3678 entries in the matrix have been imputed resulting in 15128 zero and 5542 non-zero counts.
The histogram of counts before and after imputation can be seen in Figure S1.
This resulted in two binary gene expression matrices, the 30 TFs of 124 progenitor B cells and 30 TFs of 565 monocytes. Many of the data points are repeated in the dataset owing to a limited set of TFs and binarization. Figure S2 shows the t-SNE plot of the binarized gene expression matrix with these 30 TFs. This data is used to build BNs using the algorithm of (Pal et al., 2005). We sampled 500 cell state pairs in order to build 500 PBNs thus capturing the heterogeneity in the scRNAseq dataset. Each PBN is built using an aggregate of Boolean rules from 50,000 BNs each of which has one cell pair as their attractors. To construct each PBN, we sampled one progenitor B cell state and one monocyte state with replacement, proportionally to their counts in the cell type specific gene expression matrix.
For PBN construction, we used the sampled network approach and for each PBN, we subsampled 10 TFs out of 30 and built 100 BNs for each of the cell states that are composed of the sampled 10 TFs. We repeated this process 500 times and produced 50,000 BNs to construct each of the PBNs.
For computing the steady state distribution before and after permanent intervention, we use a perturbation probability of 0.0001. The Markov chain was simulated for 300,000 iterations with a burn-in period of 100,000 iterations because the state space is larger than it was in the analysis on synthetic data. After permanent intervention analysis, each state consisted of 29 TFs owing to one TF being fixed.
Aggregation of ranked lists in biological data analysis
In order to find the best intervention for inducing transdifferentiation of a progenitor B cell into a monocyte for each PBN, we calculated the probability shift after each intervention (TF = 0 or TF = 1) on each TF using Equation 2, where the departure cell type is progenitor B and the destination cell type is monocyte. We sorted the TF and intervention type (downregulation (TF = 0) and upregulation (TF = 1)) pairs in descending order based on the probability shift from departure to destination cell type they induced. We used the RobustRankAggregation method (Kolde et al., 2012) to produce a consensus list from all the lists, one from each PBN.
Acknowledgments
This work was supported by the National Cancer Institute’s Office of Cancer Genomics Cancer Target Discovery and Development (CTD2) initiative. Ilya Shmulevich and Bahar Tercan have been supported by Personalized Cancer Models to Discover and Develop New Therapeutic Targets as part of the Cancer Target Discovery And Development Consortium (NCI U01 CA217883) and Molecular Determinants of Cancer Therapeutic Response (NCI P01 CA077852) projects. Bahar Tercan has also been supported by the Institute for Systems Biology Innovator Awards Program. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors would like to thank Ranadip Pal for providing the code for the BN construction algorithm, David Gibbs and Theo Knijnenburg for their insightful discussions, and Matti Nykter for his suggestions for performing the sampled network consistency analysis.
Author contributions
Conceptualization and methodology, BT, IS, BA; data analysis and implementation, BT; writing original draft, BT; writing, review & editing, BT, IS, SH, BA, ERD; supervision, IS.
Declaration of interests
The authors declare no competing interests.
Published: September 16, 2022
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.isci.2022.104951.
Supplemental information
Data and code availability
-
•
Data availability: The data is available at GEO repository with GEOID GSE116256 https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE116256.
-
•
Code availability: The code is freely available on https://github.com/IlyaLab/CellReprogramming. Archived code as at time of publication: https://doi.org/10.5281/zenodo.6954489.
-
•
Any additional information required to reanalyze the data reported in this paper is available from the Lead Contact upon request.
References
- Addis R.C., Ifkovits J.L., Pinto F., Kellam L.D., Esteso P., Rentschler S., Christoforou N., Epstein J.A., Gearhart J.D. Optimization of direct fibroblast reprogramming to cardiomyocytes using calcium activity as a functional measure of success. J. Mol. Cell. Cardiol. 2013;60:97–106. doi: 10.1016/j.yjmcc.2013.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afzal S., Sirohi P., Singh N.K. A review of CRISPR associated genome engineering: application, advances and future prospects of genome targeting tool for crop improvement. Biotechnol. Lett. 2020;42:1611–1632. doi: 10.1007/s10529-020-02950-w. [DOI] [PubMed] [Google Scholar]
- Aydin B., Mazzoni E.O. Cell reprogramming: the many roads to success. Annu. Rev. Cell Dev. Biol. 2019;35:433–452. doi: 10.1146/annurev-cellbio-100818-125127. [DOI] [PubMed] [Google Scholar]
- Bigley V., Haniffa M., Doulatov S., Wang X.-N., Dickinson R., McGovern N., Jardine L., Pagan S., Dimmick I., Chua I., et al. The human syndrome of dendritic cell, monocyte, B and NK lymphoid deficiency. J. Exp. Med. 2011;208:227–234. doi: 10.1084/jem.20101459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boller S., Li R., Grosschedl R. Defining B Cell Chromatin: Lessons from EBF1. Trends Genetics. 2018;34:257–269. doi: 10.1016/j.tig.2017.12.014. [DOI] [PubMed] [Google Scholar]
- Braccini M., Roli A., Villani M., Serra R. Advances in Artificial Life, Evolutionary Computation, and Systems Chemistry. Springer International Publishing; 2017. Automatic design of Boolean networks for cell differentiation; pp. 91–102. [Google Scholar]
- Bussmann L.H., Schubert A., Vu Manh T.P., De Andres L., Desbordes S.C., Parra M., Zimmermann T., Rapino F., Rodriguez-Ubreva J., Ballestar E., Graf T. A robust and highly efficient immune cell reprogramming system. Cell Stem Cell. 2009;5:554–566. doi: 10.1016/j.stem.2009.10.004. [DOI] [PubMed] [Google Scholar]
- Cahan P., Li H., Morris S.A., Lummertz da Rocha E., Daley G.Q., Collins J.J. CellNet: network biology applied to stem cell engineering. Cell. 2014;158:903–915. doi: 10.1016/j.cell.2014.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceredig R., Rolink A.G., Brown G. Models of haematopoiesis: seeing the wood for the trees. Nat. Rev. Immunol. 2009;9:293–300. doi: 10.1038/nri2525. [DOI] [PubMed] [Google Scholar]
- Chen J. Perspectives on somatic reprogramming: spotlighting epigenetic regulation and cellular heterogeneity. Curr. Opin. Genet. Dev. 2020;64:21–25. doi: 10.1016/j.gde.2020.05.016. [DOI] [PubMed] [Google Scholar]
- Cho K.-H., Lee S., Kim D., Shin D., Joo J.I., Park S.-M. Cancer reversion, a renewed challenge in systems biology. Curr. Opin. Struct. Biol. 2017;2:49–58. [Google Scholar]
- Cieślar-Pobuda A., Knoflach V., Ringh M.V., Stark J., Likus W., Siemianowicz K., Ghavami S., Hudecki A., Green J.L., Łos M.J. Transdifferentiation and reprogramming: overview of the processes, their similarities and differences. Biochim. Biophys. Acta Mol. Cell Res. 2017;1864:1359–1369. doi: 10.1016/j.bbamcr.2017.04.017. [DOI] [PubMed] [Google Scholar]
- Cirovic B., Schönheit J., Kowenz-Leutz E., Ivanovska J., Klement C., Pronina N., Bégay V., Leutz A. C/EBP-Induced transdifferentiation reveals granulocyte-macrophage precursor-like plasticity of B cells. Stem Cell Rep. 2017;8:346–359. doi: 10.1016/j.stemcr.2016.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collombet S., van Oevelen C., Sardina Ortega J.L., Abou-Jaoudé W., Di Stefano B., Thomas-Chollier M., Graf T., Thieffry D. Logical modeling of lymphoid and myeloid cell specification and transdifferentiation. Proc. Natl. Acad. Sci. USA. 2017;114:5792–5799. doi: 10.1073/pnas.1610622114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Consortium T.T.M., The Tabula Muris Consortium. Coordination O., Coordination L., Organ Collection and Processing. Library Preparation and Sequencing. Analysis C.D., Annotation C.T., Writing Group. Supplemental Text Writing Group Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature. 2018;562:367–372. doi: 10.1038/s41586-018-0590-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Consortium T.T.M., The Tabula Muris Consortium. Pisco A.O., McGeever A., Schaum N., Karkanias J., Neff N.F., Darmanis S., Wyss-Coray T., Quake S.R. A single cell transcriptomic atlas characterizes aging tissues in the mouse. Nature. 2020;583:590–595. doi: 10.1038/s41586-020-2496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crespo I., Del Sol A. A general strategy for cellular reprogramming: the importance of transcription factor cross-repression. Stem Cell. 2013;31:2127–2135. doi: 10.1002/stem.1473. [DOI] [PubMed] [Google Scholar]
- D’Alessio A.C., Fan Z.P., Wert K.J., Baranov P., Cohen M.A., Saini J.S., Cohick E., Charniga C., Dadon D., Hannett N.M., et al. A systematic approach to identify candidate transcription factors that control cell identity. Stem Cell Rep. 2015;5:763–775. doi: 10.1016/j.stemcr.2015.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorantes-Acosta E., Pelayo R. Lineage switching in acute leukemias: a consequence of stem cell plasticity? Bone Marrow Res. 2012:406796. doi: 10.1155/2012/406796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eguizabal C., Montserrat N., Veiga A., Izpisua Belmonte J.C. Dedifferentiation, transdifferentiation, and reprogramming: future directions in regenerative medicine. Sem. Reprod. Med. 2013;31:82–94. doi: 10.1055/s-0032-1331802. [DOI] [PubMed] [Google Scholar]
- Enciso J., Álvarez-Buylla E., Pelayo R. A multi-modular Boolean network for the study of acute lymphoblastic leukemia. Exp. Hematol. 2017;53:S109. [Google Scholar]
- Enciso J., Mendoza L., Álvarez-Buylla E.R., Pelayo R. Dynamical modeling predicts an inflammation-inducible CXCR7+ B cell precursor with potential implications in lymphoid blockage pathologies. PeerJ. 2020;8:e9902. doi: 10.7717/peerj.9902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher J., Köksal A.S., Piterman N., Woodhouse S. Computer Aided Verification. Springer International Publishing; 2015. Synthesising executable gene regulatory networks from single-cell gene expression data; pp. 544–560. [Google Scholar]
- Francesconi M., Di Stefano B., Berenguer C., de Andrés-Aguayo L., Plana-Carmona M., Mendez-Lago M., Guillaumet-Adkins A., Rodriguez-Esteban G., Gut M., Gut I.G., et al. Single cell RNA-seq identifies the origins of heterogeneity in efficient cell transdifferentiation and reprogramming. Elife. 2019;8:e41627. doi: 10.7554/eLife.41627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu X., He F., Li Y., Shahveranov A., Hutchins A.P. Genomic and molecular control of cell type and cell type conversions. Cell Regen. 2017;6:1–7. doi: 10.1016/j.cr.2017.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grath A., Dai G. Direct cell reprogramming for tissue engineering and regenerative medicine. J. Biol. Eng. 2019;13:1–15. doi: 10.1186/s13036-019-0144-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greil F., Drossel B. Dynamics of critical Kauffman networks under asynchronous stochastic update. Phys. Rev. Lett. 2005;95:048701. doi: 10.1103/PhysRevLett.95.048701. [DOI] [PubMed] [Google Scholar]
- Greil F., Drossel B., Sattler J. Critical Kauffman networks under deterministic asynchronous update. New J. Phys. 2007;9:373. [Google Scholar]
- Guerrero-Ramirez G.-I., Valdez-Cordoba C.-M., Islas-Cisneros J.-F., Trevino V. Computational approaches for predicting key transcription factors in targeted cell reprogramming (Review) Mol. Med. Rep. 2018;18:1225–1237. doi: 10.3892/mmr.2018.9092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannah R., Joshi A., Wilson N.K., Kinston S., Göttgens B. A compendium of genome-wide hematopoietic transcription factor maps supports the identification of gene regulatory control mechanisms. Exp. Hematol. 2011;39:531–541. doi: 10.1016/j.exphem.2011.02.009. [DOI] [PubMed] [Google Scholar]
- Heinäniemi M., Nykter M., Kramer R., Wienecke-Baldacchino A., Sinkkonen L., Zhou J.X., Kreisberg R., Kauffman S.A., Huang S., Shmulevich I. Gene-pair expression signatures reveal lineage control. Nat. Methods. 2013;10:577–583. doi: 10.1038/nmeth.2445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S. Gene expression profiling, genetic networks, and cellular states: an integrating concept for tumorigenesis and drug discovery. J. Mol. Med. 1999;77:469–480. doi: 10.1007/s001099900023. [DOI] [PubMed] [Google Scholar]
- Huang S., Ingber D.E. Shape-dependent control of cell growth, differentiation, and apoptosis: switching between attractors in cell regulatory networks. Exp. Cell Res. 2000;261:91–103. doi: 10.1006/excr.2000.5044. [DOI] [PubMed] [Google Scholar]
- Huang M., Wang J., Torre E., Dueck H., Shaffer S., Bonasio R., Murray J.I., Raj A., Li M., Zhang N.R. SAVER: gene expression recovery for single-cell RNA sequencing. Nat. Methods. 2018;15:539–542. doi: 10.1038/s41592-018-0033-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S., Eichler G., Bar-Yam Y., Ingber D.E. Cell fates as high-dimensional attractor states of a complex gene regulatory network. Phys. Rev. Lett. 2005;94:128701. doi: 10.1103/PhysRevLett.94.128701. [DOI] [PubMed] [Google Scholar]
- Joo J.I., Zhou J.X., Huang S., Cho K.-H. Determining relative dynamic stability of cell states using Boolean network model. Sci. Rep. 2018;8:12077–12114. doi: 10.1038/s41598-018-30544-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kauffman S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 1969;22:437–467. doi: 10.1016/0022-5193(69)90015-0. [DOI] [PubMed] [Google Scholar]
- Kolde R., Laur S., Adler P., Vilo J. Robust rank aggregation for gene list integration and meta-analysis. Bioinformatics. 2012;28:573–580. doi: 10.1093/bioinformatics/btr709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krumsiek J., Marr C., Schroeder T., Theis F.J. Hierarchical differentiation of myeloid progenitors is encoded in the transcription factor network. PLoS One. 2011;6:e22649. doi: 10.1371/journal.pone.0022649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laslo P., Pongubala J.M.R., Lancki D.W., Singh H. Gene regulatory networks directing myeloid and lymphoid cell fates within the immune system. Sem. Immunol. 2008;20:228–235. doi: 10.1016/j.smim.2008.08.003. [DOI] [PubMed] [Google Scholar]
- Laurenti E., Doulatov S., Zandi S., Plumb I., Chen J., April C., Fan J.-B., Dick J.E. The transcriptional architecture of early human hematopoiesis identifies multilevel control of lymphoid commitment. Nat. Immunol. 2013;14:756–763. doi: 10.1038/ni.2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledford H. CRISPR, the disruptor. Nature. 2015;522:20–24. doi: 10.1038/522020a. [DOI] [PubMed] [Google Scholar]
- Li W.V., Li J.J. An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat. Commun. 2018;9:997–999. doi: 10.1038/s41467-018-03405-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao Z., Li J., Zhang X. scRecover: discriminating true and false zeros in single-cell RNA-seq data for imputation. bioRxiv. 2019 doi: 10.1101/665323. Preprint at. [DOI] [Google Scholar]
- Miranda M.B., Xu H., Torchia J.A., Johnson D.E. Cytokine-induced myeloid differentiation is dependent on activation of the MEK/ERK pathway. Leuk. Res. 2005;29:1293–1306. doi: 10.1016/j.leukres.2005.03.016. [DOI] [PubMed] [Google Scholar]
- Moris N., Pina C., Arias A.M. Transition states and cell fate decisions in epigenetic landscapes. Nat. Rev. Genet. 2016;17:693–703. doi: 10.1038/nrg.2016.98. [DOI] [PubMed] [Google Scholar]
- Moussa M., Măndoiu I.I. Single cell RNA-seq data clustering using TF-IDF based methods. BMC Genom. 2018;19:569–645. doi: 10.1186/s12864-018-4922-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neph S., Stergachis A.B., Reynolds A., Sandstrom R., Borenstein E., Stamatoyannopoulos J.A. Circuitry and dynamics of human transcription factor regulatory networks. Cell. 2012;150:1274–1286. doi: 10.1016/j.cell.2012.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholas C.R., Kriegstein A.R. Cell reprogramming gets direct. Nature. 2010;463:1031–1032. doi: 10.1038/4631031a. [DOI] [PubMed] [Google Scholar]
- Ohlsson E., Schuster M.B., Hasemann M., Porse B.T. The multifaceted functions of C/EBPα in normal and malignant haematopoiesis. Leukemia. 2016;30:767–775. doi: 10.1038/leu.2015.324. [DOI] [PubMed] [Google Scholar]
- Okawa S., Nicklas S., Zickenrott S., Schwamborn J.C., Del Sol A. A generalized gene-regulatory network model of stem cell differentiation for predicting lineage specifiers. Stem Cell Rep. 2016;7:307–315. doi: 10.1016/j.stemcr.2016.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pal R., Ivanov I., Datta A., Bittner M.L., Dougherty E.R. Generating Boolean networks with a prescribed attractor structure. Bioinformatics. 2005;21:4021–4025. doi: 10.1093/bioinformatics/bti664. [DOI] [PubMed] [Google Scholar]
- Paul F., Arkin Y., Giladi A., Jaitin D.A., Kenigsberg E., Keren-Shaul H., Winter D., Lara-Astiaso D., Gury M., Weiner A., et al. Transcriptional heterogeneity and lineage commitment in myeloid progenitors. Cell. 2016;164:1663–1677. doi: 10.1016/j.cell.2015.11.013. [DOI] [PubMed] [Google Scholar]
- Pongubala J.M.R., Northrup D.L., Lancki D.W., Medina K.L., Treiber T., Bertolino E., Thomas M., Grosschedl R., Allman D., Singh H. Transcription factor EBF restricts alternative lineage options and promotes B cell fate commitment independently of Pax5. Nat. Immunol. 2008;9:203–215. doi: 10.1038/ni1555. [DOI] [PubMed] [Google Scholar]
- Rackham O.J.L., Firas J., Fang H., Oates M.E., Holmes M.L., Knaupp A.S., FANTOM Consortium. Suzuki H., Nefzger C.M., Daub C.O., et al. A predictive computational framework for direct reprogramming between human cell types. Nat. Genet. 2016;48:331–335. doi: 10.1038/ng.3487. [DOI] [PubMed] [Google Scholar]
- Ribeiro M.M., Okawa S., Del Sol A. TransSynW: a single-cell RNA-sequencing based web application to guide cell conversion experiments. Stem Cells Transl. Med. 2021;10:230–238. doi: 10.1002/sctm.20-0227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwab J.D., Kühlwein S.D., Ikonomi N., Kühl M., Kestler H.A. Concepts in Boolean network modeling: what do they all mean? Comput. Struct. Biotechnol. J. 2020;18:571–582. doi: 10.1016/j.csbj.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmulevich I., Dougherty E.R., Kim S., Zhang W. Probabilistic Boolean Networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics. 2002;18:261–274. doi: 10.1093/bioinformatics/18.2.261. [DOI] [PubMed] [Google Scholar]
- Shmulevich I., Dougherty E.R., Zhang W. Gene perturbation and intervention in probabilistic Boolean networks. Bioinformatics. 2002;18:1319–1331. doi: 10.1093/bioinformatics/18.10.1319. [DOI] [PubMed] [Google Scholar]
- Somasundaram R., Prasad M.A.J., Ungerbäck J., Sigvardsson M. Transcription factor networks in B-cell differentiation link development to acute lymphoid leukemia. Blood. 2015;126:144–152. doi: 10.1182/blood-2014-12-575688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadtfeld M., Maherali N., Breault D.T., Hochedlinger K. Defining molecular cornerstones during fibroblast to iPS cell reprogramming in mouse. Cell Stem Cell. 2008;2:230–240. doi: 10.1016/j.stem.2008.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoilova B., Kowenz-Leutz E., Scheller M., Leutz A. Lymphoid to myeloid cell trans-differentiation is determined by C/EBPβ structure and post-translational modifications. PLoS One. 2013;8:e65169. doi: 10.1371/journal.pone.0065169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torres-Sosa C., Huang S., Aldana M. Criticality is an emergent property of genetic networks that exhibit evolvability. PLoS Comput. Biol. 2012;8:e1002669. doi: 10.1371/journal.pcbi.1002669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk D., Sharma R., Nainys J., Yim K., Kathail P., Carr A.J., Burdziak C., Moon K.R., Chaffer C.L., Pattabiraman D., et al. Recovering gene interactions from single-cell data using data diffusion. Cell. 2018;174:716–729.e27. doi: 10.1016/j.cell.2018.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Galen P., Hovestadt V., Wadsworth Ii M.H., Hughes T.K., Griffin G.K., Battaglia S., Verga J.A., Stephansky J., Pastika T.J., Lombardi Story J., et al. Single-cell RNA-seq reveals AML hierarchies relevant to disease progression and immunity. Cell. 2019;176:1265–1281.e24. doi: 10.1016/j.cell.2019.01.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vierbuchen T., Ostermeier A., Pang Z.P., Kokubu Y., Südhof T.C., Wernig M. Direct conversion of fibroblasts to functional neurons by defined factors. Nature. 2010;463:1035–1041. doi: 10.1038/nature08797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weintraub H., Tapscott S.J., Davis R.L., Thayer M.J., Adam M.A., Lassar A.B., Miller A.D. Activation of muscle-specific genes in pigment, nerve, fat, liver, and fibroblast cell lines by forced expression of MyoD. Proc. Natl. Acad. Sci. USA. 1989;86:5434–5438. doi: 10.1073/pnas.86.14.5434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodhouse S., Piterman N., Wintersteiger C.M., Göttgens B., Fisher J. SCNS: a graphical tool for reconstructing executable regulatory networks from single-cell genomic data. BMC Syst. Biol. 2018;12:59–67. doi: 10.1186/s12918-018-0581-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J.X., Qiu X., d’Herouel A.F., Huang S. In: Computational Systems Biology: Chapter 12. Second edition. Eils R., Kriete A., editors. Elsevier Inc. Chapters; 2013. Discrete gene network models for understanding multicellularity and cell reprogramming: from network structure to attractor landscape; pp. 241–276. [Google Scholar]
- Zhou Q., Brown J., Kanarek A., Rajagopal J., Melton D.A. In vivo reprogramming of adult pancreatic exocrine cells to β-cells. Nature. 2008;455:627–632. doi: 10.1038/nature07314. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
-
•
Data availability: The data is available at GEO repository with GEOID GSE116256 https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE116256.
-
•
Code availability: The code is freely available on https://github.com/IlyaLab/CellReprogramming. Archived code as at time of publication: https://doi.org/10.5281/zenodo.6954489.
-
•
Any additional information required to reanalyze the data reported in this paper is available from the Lead Contact upon request.