Abstract
The COVID-19 pandemic exacerbated the erratic demand, supply, and prices of energy. It is unlikely that these effects would subside post-pandemic, especially with the pre-existing climate change crisis that also needs to be addressed. Emissions policies aimed at mitigating climate change place economic pressures on already disrupted energy systems, which could worsen energy insecurity. Configuring disrupted energy systems to build robustness to supply chain-related uncertainties and economic pressures of emissions policies are desired to simultaneously address these problems. To this end, this study introduces a robust mixed-integer linear program that simultaneously incorporates the abovementioned needs for configuring energy production systems. The proposed model is tested through a demonstrative case study that deals with a biomass-based polygeneration plant design problem. The scenario analysis and sensitivity test on the model concerning the case under consideration yields the following results: (1) setting ambitious target profits reduces the probability of the resulting plant configuration to achieving the set targets in the presence of supply chain-related uncertainties, while conservative targets promote the opposite; (2) the inoperability of the plant’s process units reduces the robustness of optimal process configurations, and drastic configurations may be required to achieve targets despite the inoperability of process units; (3) a hybrid cap-and-trade and emissions tax policy yields approximately similar implications to the robustness of the resulting optimal plant configurations compared to a pure cap-and-trade policy, but the rate of decrease in robustness with respect to the initial emissions cap is lesser in the hybrid policy than in the pure cap-and-trade policy.
Keywords: Energy, Climate change, Process integration, Polygeneration, Risk, Optimization
1. Introduction
The energy sector is at the receiving end of the impacts of the COVID-19 pandemic (Klemeš et al., 2020, Mastropietro et al., 2020). The challenges introduced by the pandemic on energy systems include high voltage levels and inaccurate load forecasting, which are direct results of irregular consumption patterns, high ramp rates, and fluctuations in frequency (Navon et al., 2021). Furthermore, the volatility in energy supply and demand during the pandemic has resulted in fluctuations in energy prices (International Energy Agency (IEA), 2020, Navon et al., 2021). The severe disruption dealt by the COVID-19 pandemic to energy supply chains has exacerbated energy demand and supply uncertainties, which has profound economic implications, especially in the energy sector. Even as lockdowns ease, travel bans persist, and some industries remain closed, while others are operating at less than full capacity due to various forms of social distancing or a lack of demand (Szczygielski et al., 2021). Selerio and Maglasang (2021) showed that these disruptions ripple and result in disruptions and uncertainties in industries like the energy sector, which are also evidenced by other studies (i.e., Salisu and Adediran, 2020, Szczygielski et al., 2021, Liu et al., 2022). This issue makes the development of engineering strategies that increase the robustness of energy systems critical.
On top of the uncertainties associated with the pandemic, the energy sector is also susceptible to uncertainties consequent from climate change (Laghari, 2013). For instance, as the average global atmospheric temperature increases, an increase in the energy demand for essential utilities (i.e., electricity, water, heating, and cooling) is almost inevitable in the long run (Schaeffer et al., 2012, Koljonen and Lehtilä, 2012). Long-term climatic changes make these uncertainties in energy demand (i.e., uncertainty in the extent of increase in energy demand) and uncertainties consequent to limited energy supply lasting (Carvajal et al., 2019). The looming climate change crisis would eventually require countries to expedite cleaner energy production technology investments. Based on the previous discussions, cleaner energy production should be implemented in view of post-COVID-19 conditions. While several methodological studies have addressed strategies for post-COVID-19 recovery efforts in various sectors of the economy (e.g., Ocampo et al., 2021a, Ocampo et al., 2021b, Selerio, Caladcad, Catamco, Capinpin, & Ocampo, 2022), investigations in the energy production research domains remain to be scarcely explored, especially in view of process optimization, climate change, and post-COVID-19 uncertainties.
The energy sector is one of the largest emitters of greenhouse gases (GHG). For instance, in 2020, 76.2 % of direct GHG emissions originated from energy production (IEA, 2020). Furthermore, about 70 % of total global GHG emissions are in the form of CO2 originating from the combustion of fossil fuels (Olivier et al., 2017). The massive GHG emissions of the energy sector warrant the acceleration of investments in cleaner energy production technologies in response to the climate change crisis. Among the popular technologies promoted to address this problem are polygeneration technologies (Jana et al., 2017).
Polygeneration technologies can deliver multiple utilities from a single feedstock to obtain an efficient multi-utility system. It has been recognized as a promising pathway for resolving problems associated with GHG emissions (Jana et al., 2017). Polygeneration is a thermochemical process that simultaneously produces at least two different products in non-trivial quantities. However, polygeneration is not a petroleum refining process, a co-generation process, or a tri-generation process; at least one product is a chemical or fuel, and at least one is electricity (Adams & Ghouse, 2015). The purpose of polygeneration is to increase energy yield (Ubando et al., 2020), promote potential carbon drawdown (Jana et al., 2017), and decrease energy production costs (Wang et al., 2017).
On the other hand, despite the increasing public concern over climate change and the availability of technologies that could potentially address it, the actions undertaken by the energy industry to address this crisis are considered largely inadequate (Buso & Stenger, 2018). This scenario is commonly known as the adaptation gap (UNEP, 2016). Furthermore, market failures caused by environmental externalities have likely worsened the adaptation gap. These challenges increase the need for government interventions (e.g., subsidies, economic policy, energy consumption policy) to address these GHG emissions concerns in the energy sector. Governments opt for either emissions tax or cap-and-trade policies to address these challenges.
The emissions tax policy assigns a cost-per-ton of GHG emissions across all emitters (Wood, 2018). On the other hand, the cap-and-trade policy assigns carbon emissions allowances (or caps) to firms at a given planning horizon (Zhou & Wang, 2016). At the same time, firms can also purchase carbon allowances from a carbon trading market if it needs to increase production. Consequently, the firm can trade-off (or sell) its surplus allowances to those who need them (Chai et al., 2018). The adoption of these emissions policies in many countries has motivated industry practitioners and academics to investigate methods to optimally configure operations (Ubando et al., 2020, Zhou and Wen, 2020).
Carbon-constrained planning models are usually employed to address process integration/synthesis problems (Foo & Tan, 2016). Process integration techniques are a family of methodologies for synthesizing several operations to increase the efficiency of resource consumption and/or reduce harmful emissions (Klemeš, 2013). Foo and Tan (2016) performed a comprehensive review of process integration techniques for carbon-constrained operations planning. So far, the consideration of emissions policies in process integration has been performed only in the macro planning context (see Manesh et al., 2013). Furthermore, the consideration of economic pressures consequent to emissions policies in configuring plant-wide energy production systems, i.e., polygeneration plants, is not yet explored in the domain literature. Implementing emissions policies to motivate the adoption of clean energy production technologies, i.e., polygeneration, makes the configuration of operations challenging, especially in view of the economic pressures introduced by these policies to recovering energy firms and the uncertainties associated with the post-COVID-19 conditions.
During the brunt of the COVID-19 pandemic, many renewable energy production plants worldwide have laid off their workers to keep operations (Graff & Carley, 2020). These lay-offs have reduced their operational capacities, making them inoperable and highly vulnerable. In addition, long-term inoperability can also arise from the lack of supplies for the replacement and repair of damaged process units, especially when the suppliers were bankrupt during the pandemic. The process units of energy production plants involve expensive heavy-duty equipment whose parts are usually sourced from specialized suppliers. This is relevant because a disruption in the operations of these suppliers could cut off specialized equipment maintenance services essential to keeping energy production operations running. The reality of situations wherein disruptions ripple from one production entity to another has been recently documented in the context of the COVID-19 pandemic (Selerio & Maglasang, 2021). This issue exacerbates the need to configure operations in response to the long-term operational challenges introduced by post-COVID-19 conditions.
The above discussions imply the need to simultaneously consider the influence of emissions policies, process inoperability, and supply chain-related uncertainties to obtain a robust configuration of polygeneration plants in response to both climate change risks and post-COVID-19 conditions. In this work, supply chain-related uncertainties are defined by uncertainties in both the demand for energy products and the supply of raw materials to produce them. These uncertainties could be represented by uncertainties in demand quantity and price of goods, just like in the work of Sy et al. (2016). Developing a modeling framework that addresses the problems expounded above is essential to managers, policymakers, and engineers as it maps the effects of emissions policies on energy systems design. Furthermore, the need to implement policies that promotes flexibility for polygeneration plants has been proposed as a way for the energy sector to become resilient against extreme disruptive events (e.g., COVID-19 pandemic) (Heffron et al., 2021). In the context of emissions policies, a consensus is not yet achieved regarding which among emissions tax and cap-and-trade is better at drawing down GHG emissions in response to climate change.
Promoting a hybrid policy that integrates the two previously mentioned emissions policies is increasingly studied in the literature (Wood, 2018, Cao et al., 2019). Canada implemented a hybrid policy wherein firms have the flexibility to choose which among the existing emissions policies to subscribe to – either emissions tax or cap and trade (Wood, 2018). It has allowed firms to choose the more economically viable policy for their scale of operations and has addressed the volatility of the price of emissions allowance (Wood, 2018). Hybrid emissions policies have also been implemented in China (Cao et al., 2019) and the USA (Brooks & Keohane, 2020). Whether hybrid emissions policies are better than pure emissions policies in promoting energy systems’ robustness is not yet investigated in the literature. Investigating this question in the context of polygeneration plants and the other gaps highlighted previously can provide useful insights into developing a robust and resilient energy system.
This work contributes to the carbon-constrained process integration literature by introducing a novel mathematical programming-based process integration model for the automated configuration of polygeneration plants while incorporating the implications of emissions policies, supply chain uncertainties, and inoperability in view of post-disaster conditions (e.g., post-COVID-19). This work is also the first to investigate the effects of hybrid emissions policies on the optimal configuration of polygeneration plants. The proposed model is tested through a demonstrative case study that deals with a biomass-based polygeneration plant design problem. In this work, the measures adopted to promote robustness against supply chain-related uncertainties in polygeneration plants are investigated by conducting a scenario analysis where target profit is varied, and the robustness of the resulting plant design associated with the target profit is recorded. The influence of the inoperability of process units on the robustness of plant configurations is also investigated through the scenario analysis by comparing the robustness of configurations for a disrupted and undisrupted plant scenario. Lastly, the effects of hybrid and “pure” emissions policies are investigated by obtaining a manifold of polygeneration plant designs associated with the implementation of each policy type and recording how key parameters, i.e., robustness, are affected by each policy type.
The rest of the paper is outlined as follows: Section 2 presents the detailed formulation of the proposed process integration model. Section 3 presents the material and methods used to test the viability of the proposed model for obtaining polygeneration plant designs. Section 4 presents the results of the tests. Section 5 presents the discussions of the results. Lastly, Section 6 presents the conclusion and suggestions for future works.
2. The model
2.1. Problem statement
Let be the set of all production materials (e.g., raw materials, final outputs, and by-products) in the system and be the set of environmental by-products, i.e., emissions, such that . Also, let be the set of all process units in the system. The specific problem tackled in this study can be formally stated as follows:
-
▪
A multi-functional energy production system utilizes inputs, i.e., biomass feedstocks, to produce multiple outputs, e.g., power and heat.
-
▪
The technological performance of the process units of the system is defined by a fixed set of proportions of input and output streams.
-
▪
The demand and price of material streams are subject to uncertainty.
-
▪
Production disturbances are in the form of process failures (e.g., damaged equipment), which lead to abnormal operations and reduced operational capacity.
-
▪
Cap-and-trade or emissions tax policies are in effect and applied to the environmental emissions (elements in ) of the system.
The objective is to determine the energy production system that maximizes profit (i.e., revenue less costs) while considering uncertainties in supply chain-related parameters and economic pressures of emissions policies throughout the duration of abnormal operations.
2.2. Notations
From here on out, Greek letters denote decision variables, while the conventional Alphabetical letters denote model parameters. Uncertain variables are characterized by the accent tilde (~). The transpose of matrices is characterized by the superscript . The diagonalization of a matrix is denoted by the operator . Furthermore, the indices used in this study are as follows: and , representing production materials and process units, respectively. The notations are briefly presented in the following subsections.
2.2.1. Coefficients
is the technology matrix that describes the input–output streams of materials to process units.
are vectors denoting the lower limit of the part-load operating level of a process unit and spare operating capacity from the application of safety factors, respectively.
is the variable capital cost vector.
is the fixed capital cost vector.
is the fractional inoperability vector.
is the vector denoting the price (per ton) of emissions allowance.
is the vector denoting the emissions tax rate.
is the vectors denoting the initial emissions cap.
, are the nominal value and maximum perturbation value of the uncertain material price vector, respectively.
, are the nominal value and maximum perturbation value of the uncertain production limit vector, respectively.
are the total annual plant operating hours and the annualizing factor of total capital expenditure, respectively.
is the predefined target profit.
2.2.2. Decision variables
is the part-load operating level vector.
is the binary unit selection vector.
is the scalar binary emissions policy selection variable.
is the vectors denoting the emissions allowance.
is the vector denoting the total emissions.
is the robustness index.
2.2.3. State variables
is the vector denoting the total emissions.
is the profit.
is the uncertain material price vector.
is the uncertain production limit vector.
2.3. Model assumptions
The following assumptions are followed in this modeling work:
-
▪
is scale-invariant. Thus, reductions (or increases) in the operational capacity of process units do not affect the proportions of the input–output streams in . The values of are predetermined during the design stage.
-
▪
The entire feasible operating range of process units is bounded by a lower limit (i.e., the minimum part-load capacity) and an upper limit (i.e., the rated capacity with safety factor).
-
▪
The price and demand of material streams are uncertain.
-
▪
The firm does not produce outputs above the demand limit. Similarly, the firm does not generate environmental emissions above the emissions cap.
-
▪
The capital cost of each process unit is annualized and described by a piecewise linear function of capacity.
-
▪
Two emissions policies are considered, namely emissions tax and cap-and-trade.
-
▪
The price of an emissions allowance in the cap-and-trade program is constant.
-
▪
Emission allowances are sold in competitive markets. There is a readily available demand for emissions allowances whenever the firm decides to sell its on-hand allowances.
2.4. Model development
This study considers the economic implications of inoperability, capital costs arising from process configurations, and emissions policies. The profit obtained from the configuration of the energy production plant is calculated as follows:
| (1) |
The total capital cost arising from decisions on vectors and is denoted by the term . The term represents the variable capital cost of scaling the production, while represents the fixed capital cost of operating the process units. The cost arising from the emissions policies is represented by the term . Specifically, the cost arising from emissions tax is presented by while the costs arising from cap-and-trade are represented by . The model is linear when is fixed because in the term , the multiplication of the variable to another decision variable is avoided. Fixing the value of indicate that only one of the two emissions policies can take effect. However, when a hybrid emissions policy is in effect where an energy firm is given the flexibility to choose which policy to subscribe to, like the Canadian policy discussed in Wood (2018), ψ becomes a decision variable that makes the model quadratic (nonlinear). The quadratic term in Equation (1) can be easily linearized by letting and adding the following constraints: , , , where , , and is a known large number (i.e., ). It should be noted that because . The details of the decision variable are presented in the subsequent discussions. Although the linearization of the nonlinear term in the objective function is apparent and straightforward, as previously demonstrated, it is not reflected in the succeeding models to keep the models’ form concise and as simple as possible.
On the other hand, revenue is represented by the term , where represents the total input-output streams (production) of the plant. In this study, production is limited by the annual demand and emissions limits as follows:
| (3) |
The production limit vector contains the annualized limits on the demand of outputs (final products) and emissions (environmental by-products). From the term , the total emissions can be isolated as follows:
| (4) |
In the cap-and-trade policy, energy firms are restricted by regulators in their generation of emissions. However, they have the option to purchase emissions allowances to increase their emissions cap from the initial cap that they previously acquired. They may also sell the allowance that they have on hand for profit. Following these policy conditions, the emissions limit is represented as follows:
| (5) |
From Equation (5), the emissions limit can be extracted from vector as follows:
| (6) |
The emissions limit is meaningful when the cap-and-trade policy is in effect. When the emissions tax policy is in effect, is a variable with a sufficiently large value, which prevents it from interfering with production decisions under the emissions tax policy.
On the other hand, by performing some substitutions on Equations , the scalar form of Equation that is solely on the emissions production limit can be obtained as follows:
| (7) |
Under this cap-and-trade policy, the development of negative emissions technologies is incentivized by providing firms with free allowances equivalent to their negative emissions. Such allowances can then be sold for profit. To regulate the amount of emissions allowances circulating in the carbon market, the government may interfere by reducing the amount of emissions allowances present in the system in the next planning horizon. In this way, this proposed policy can function in a stable fashion – at least in principle.
In this study, the production of an energy plant is subjected to process failures or inoperability in the form of damaged process units. These damages may be caused by climate change-induced extreme weather conditions. Such types of inoperability may be sustained throughout the entire planning horizon, i.e., one year, especially with the mobility restrictions or supply chain disruptions that may still linger after a disaster; or especially when the supplier of rare/specialized replacement parts for repair has been bankrupted because of the disaster. Inoperability is modeled as the reduction of the part-load operating level of process units, which is represented as follows:
| (8) |
The part-load operating level scales the operations of the energy production plant. It is defined in an interval with a minimum part-load operating level (lower limit) denoted by . Below the lower limit, the part-load operation is assumed to be unstable. On the other hand, the maximum part-load operating level (upper limit) is denoted by . The spare operating capacity comes from the safety factors incorporated in the design of process units, which are predetermined at the design stage. The fractional inoperability level originates from disturbances that affect the process units. It indicates whether a process unit is fully operable, i.e., , partially operable, i.e., , or fully inoperable, i.e., . On the other hand, the binary unit selection vector indicates whether a process unit operates, i.e., , or not, i.e., . It switches off a process unit whenever it cannot operate within the limits of its part-load operating level.
The deterministic model follows:
Model.
subject to:
The uncertainty of the supply chain-related parameters, i.e., price and demand of the material streams, are modeled here using the target-oriented robust optimization (TORO) framework (Ng & Sy, 2014). The uncertain material price vector and production limit vector are represented as follows:
| (9) |
| (10) |
The vectors and represent the most optimistic values of the material prices and production limits, respectively. On the other hand, the vectors and represent the perturbations of the nominal values such that:
| (11) |
The robustness index determines the perturbation of the uncertain values. It can be observed that the largest perturbations are obtained when . The largest perturbations take the values and . Thus, under the most favorable case, the values of and would be at the maximum. It is also apparent that larger perturbations correspond to a higher value of . Some practical insights can be obtained from these observations. First, an uncertainty-averse attitude would prefer a higher value of . Second, a risk-seeking attitude would prefer a lower value of . Lastly, this model provides a way to address uncertainties in process configuration by representing uncertainty as an interval.
The TORO framework hinges on robust optimization theory and satisficing theory, which promotes target-oriented decision making (Ng & Sy, 2014). It is desired to configure energy production plants that are under risk so that they can remain feasible for as wide a range of uncertainties as possible. To this end, target-oriented decision making is reflected by transforming the original objective function in Model into a constraint that corresponds to a target profit . The modification of the model is presented as follows:
Model.
| (12) |
subject to:
| (13) |
| (14) |
| (15) |
Equation represents the objective function mentioned earlier which describes robustness. Equations represents the transformation of the objective function of Model into a constraint that corresponds to a target profit . Unlike conventional optimization procedures wherein the objectives are either maximized or minimized, a target-oriented approach is adopted here. In particular, the value which is maximized in Model (1), is converted into a fixed value, and, thus, represented as , which corresponds to the target profit. Setting targets instead of aiming for the theoretically best possible outcome (i.e., maximum ) is a standard procedure employed in practice. This is commonly known as the “satisficing behavior” in economics (Ng & Sy, 2014). It means that decision-makers, in practice, tend to settle for good enough solutions (determined by the target) instead of seeking to achieve the theoretically best solution. On the other hand, Equations and are modifications of Equations and , respectively, for incorporating the conditions on the uncertain parameters. The condition for their transformation is based on the definitions in Equations (9)-(11).
The terms and require the evaluation of infinitely many constraints to solve Model . It is because of the uncertain constraints containing and that would lead to the creation of individual constraints for each of their infinite possible realizations in . There is, therefore, a need to convert Model into an equivalent model that is amenable to solving using traditional mathematical programming techniques. To this end, the property of duality is employed.
To demonstrate the application of duality, Equation is modified such that the perturbation of is maximized through the term . The resulting expression is as follows:
| (16) |
The term could then be represented as an isolated optimization (maximization) problem by following the conditions set in Equation . The maximization problem is as follows:
Model.
| (17) |
subject to:
| (18) |
Equation (17) represents the maximization term in Equation (16) which is treated as an objective function of a separate optimization problem. Equation (18) is the constraint derived from Equation (11). The duality property of linear programming is applied to this model to obtain its dual counterpart as follows:
Model.
| (19) |
subject to:
| (20) |
The specific procedures of applying the duality property are omitted here for brevity. Instead, the readers are referred to the work of Bertsimas and Sim (2003) for a more detailed discussion on the property of weak and strong duality, which proves the equivalence of Model and Model . The translation of the demand constraints in Equation and Equation follows the same procedure. After the application of the duality property on the uncertain constraints and the substitution of the dual models into Model , the resulting robust optimization model is obtained as follows:
Model.
subject to:
| (21) |
| (22) |
| (23) |
| (24) |
where and are dual variables.
Equations are obtained by substituting the dual models that correspond to the maximization of the perturbations of the uncertain variables and . Specifically, Equation (21) is the result of substituting the objective function in Equation (19) for the term in Equation (16). On the other hand, Equation (22) and Equation (23) are the results of repeating the procedures applied to Equation (13), which was demonstrated through Equations (16)-(20), to Equation (14), and Equation (15), respectively. Lastly, Equation (24) represents the dual variables associated with Equations (21), (22), (23), which are obtained from the transformations performed on Equations (13), (14), (15).
whenever . Thus, if a policy is feasible for an uncertainty set defined by , then it will be feasible for all perturbations that would fall within this range. It can also be observed that given a fixed value of and , Model is linear concerning the decision variables , , and . Model could thus be conveniently solved for the maximum value of by performing a line search on . We could utilize well-known search algorithms like the bisection or golden search method to solve this model.
The bisection search method takes an interval in which the root of a function is believed to lie, such that and have opposite signs. The method then proceeds to find the midpoint of and then checks whether the root lies in , or . In contrast, the golden search method selects two points on the interval, , and compares and to determine whether the root lies in , or . Ng and Sy (2014) introduced an efficient bisection search algorithm that is readily adaptable for solving TORO models. In this study, the bisection search algorithm promoted by Ng and Sy (2014) is applied to solve Model (5). The bisection search algorithm is implemented in this study using the following pseudo-code:
Model.
Set tolerance level into a sufficiently small number;
Initialize and ;
WHILE DO:
;
Solve Model 5 using ;
IF a feasible solution exists THEN.
ELSE
END
END
3. Material and methods
The applicability of the proposed model is tested in this study. A biomass-based polygeneration plant is considered a case in point.
3.1. System description
The case study considers a polygeneration system for producing syngas, power, heat, bio-oil, and biochar using biomass as the primary feedstock. The biomass considered in this study is forest residue. The scenario presented here is hypothetical. However, the assumptions used are based on realistic and plausible parameters; thus, this case should be seen as an illustrative example that demonstrates the advantages of the proposed model for this type of problem. The plant consists of the following process units:
-
•
Co-generation (Cogen) module – an integrated unit comprised of a gas turbine (GT) generator to produce electricity from synthetic gas (syngas), coupled with a heat recovery steam generator (HRSG) to generate heat from the residual heat in the GT exhaust.
-
•
Boiler – an auxiliary gas-fired boiler considered to potentially produce the additional heat demand on top of the heat generated from the Cogen module.
-
•
Gasification unit – a gasifier with a reactor temperature greater than 500 °C to produce bio-oil and syngas, with biochar co-production from biomass.
-
•
Pyrolysis unit – a pyrolizer for producing the same products as the gasifier at varying production yields using biomass as input.
-
•
Torrefaction – forest residue was torrefied at 250 °C in this process unit for 60 min with a calorific value of 19.56 MJ/kg (Ubando et al., 2019). The torrefaction upgrades the biomass to biochar with bio-oil co-production from the condensable gases.
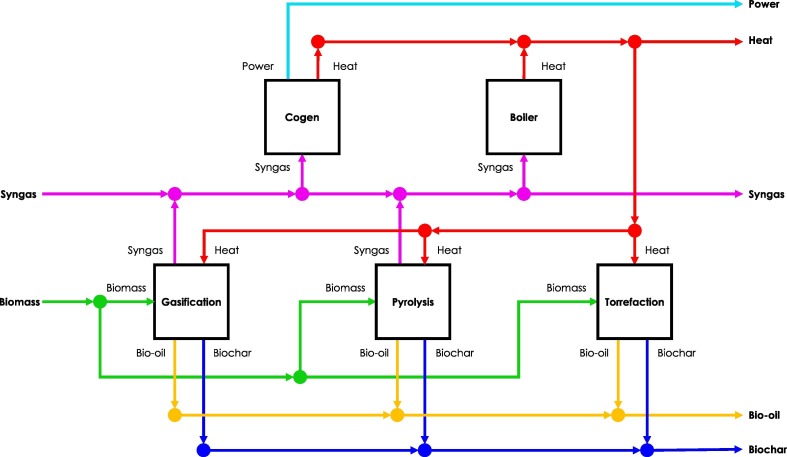
The calorific value of syngas produced from the thermochemical processing of forest residues is 5.90 (Kostúr & Kačur, 2015). The operational setting of the process units considered here is sourced from Ubando et al. (2020). The input and output streams of the process units, their capital costs (fixed and variable), and part-load operating levels are presented in Table 1 . The prices of materials streams, along with their maximum perturbation values, are shown in Table 2 . The flowsheet of the polygeneration plant described here is presented in Fig. 1 .
Table 1.
Process Parameters.
| a | Unit | Cogen | Boiler | Gasification | Pyrolysis | Torrefaction |
|---|---|---|---|---|---|---|
| Biomass | 0.00 | 0.00 | −24.87 | −179.62 | −9.10 | |
| Syngas | −1,199.46 | −4.97 | 24.09 | 24.09 | 0.00 | |
| Power | 362.69 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Heat | 282.90 | 6.51 | −2.76 | −7.50 | −0.10 | |
| Bio-oil | 0.00 | 0.00 | 1.58 | 23.69 | 0.55 | |
| Biochar | 0.00 | 0.00 | 2.76 | 21.71 | 5.00 | |
| CO2 | 65.28 | 0.52 | −7.41 | −58.19 | −13.40 | |
| b | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| b | 0.15 | 0.20 | 0.10 | 0.12 | 0.00 | |
| b | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| a | 1,204.13 | 9.05 | 108.60 | 84.72 | 12.34 | |
| a | 481.65 | 2.35 | 43.44 | 33.89 | 4.93 |
The input-output proportions and their corresponding capital costs are obtained from Ubando et al. (2020).
Assumed values for the baseline case.
Table 2.
Price and Demand Limits of Material Steams with their Assumed Perturbation Values.
| Material | Unit | () | b() | b () | b () |
|---|---|---|---|---|---|
| Biomass | c20.00 | 10.00 | 35.00 | 17.50 | |
| Syngas | d29.83 | 14.92 | 0.11 | 55.00 | |
| Power | a92.10 | 46.05 | 3.96 | 1.98 | |
| Heat | a51.58 | 25.79 | 4.40 | 2.20 | |
| Bio-oil | a40.00 | 20.00 | 26.40 | 13.20 | |
| Biochar | a329.00 | 164.50 | 0.55 | 0.28 | |
| CO2 | a0.00 | 0.00 | 0 |
Obtained from Ubando et al. (2020).
Assumed values for the baseline case.
Obtained from the U.S. Department of Energy (2011).
Obtained from Pei et al. (2016).
Fig. 1.
Flowsheet of the Polygeneration Plant.
The values of the parameters pertaining to emissions policy for the baseline scenario of this study are as follows: 8.24 (Zeng et al., 2017), 8 (Jenkins, 2014), 0 (assumed). For the benchmark case, is assumed. The following further case-specific assumptions are followed in this study:
-
•
All economic parameters used here are expressed in 2021 U.S. Dollars (USD).
-
•
The emissions considered in this case study are only CO2 emissions.
-
•
It is assumed that the maximum perturbation values are and .
-
•
The polygeneration plant is assumed to operate for 8000 with a target profit of .
-
•
It is assumed that the process units have no salvage value at the end of their service lives (40 years), and their respective book values follow straight-line depreciation, with an annualizing factor of 0.06 .
-
•
The fixed capital cost of process units is estimated using the average fixed-to-variable (FtV) cost ratio of the main and auxiliary process units in Sy et al. (2016). This assumes that the polygeneration plant investigated here follows the cost structure (Aboody et al., 2018) of the polygeneration plant in Sy et al. (2016), which has an FtV cost ratio of 0.4 for main process units (e.g., Cogen) and 0.26 for auxiliary process units (e.g., boiler).
-
•
In the torrefaction process, the generated non-condensable gases were assumed negligible in the analysis because they are relatively minimal compared with the biochar and bio-oil produced (Stelte, 2012) by the unit.
3.2. Analyses
3.2.1. Scenario analysis
Four scenarios are considered in this analysis to illustrate the influence of target setting (i.e., setting different target profits) on the robustness of the resulting plant design associated with it. The first scenario (CS1) corresponds to the optimal design of the baseline case (). The second scenario (CS2) corresponds to an ambitious target setting () in . The third scenario (CS3) corresponds to a conservative target setting () in . The fourth scenario (CS4) corresponds to a conservative target setting (similar to CS3) but under severe process failure of the boiler leading to its inoperability equivalent to 0.60. This scenario presupposes that the nominal plant design is the one obtained in CS3, but the design is struck by an unexpected failure of the boiler unit. The plant manager is pressured to take a course of action to abate the effects of the disruption and achieve targets amidst it. Repairing the boiler requires the purchase of customized replacement parts for the cyclone separator. However, the operations of the parts supplier are currently in an indefinite postponement due to the economic challenges induced by the pandemic. The plant manager could invest in other fully operational and available process units to buffer lost production due to boiler inoperability. Due to the circumstances mentioned earlier, it is assumed that the inoperability of the boiler covers at least the entire planning horizon, i.e., at least one year. CS2 and CS3 aim to demonstrate the design implications of target setting, while CS4 intends to espouse process failure (inoperability) in a polygeneration plant. Model is solved for all the scenarios. The results of the four scenarios are compared based on their resulting material flow configurations, robustness, and economic (i.e., revenue, capital cost, emissions cost, and profit) and environmental (i.e., CO2 emissions) performance.
3.2.2. Monte Carlo simulation
In this analysis, the Monte-Carlo simulation is performed on the resulting polygeneration plant designs of the four scenarios (CS1-CS4) to assess the efficacy of the proposed model in addressing supply chain uncertainties in the price and demand of material streams. This analysis is performed assuming a uniform distribution of values of the uncertain variables. Uniform distribution is assumed to safely approximate how uncertainties in the real world could occur. The adoption of skewed distributions could result in large errors, especially when the estimation of the distribution’s skewness is incorrect. Also, several works that deployed Monte Carlo simulation as a post-analysis to TORO models have also assumed uniform distribution (Ng and Sy, 2014, Sy et al., 2016). Model is then solved for random realizations of the uncertain variables, then a tally is made whenever the design from the scenario that is being evaluated is feasible concerning the constraints of Model (5). Suppose there are number of instances where the design is feasible out of the simulations, the estimation of the simulated robustness of the design that is being evaluated is, therefore, equivalent to .
3.2.3. Sensitivity analysis
Two sets of sensitivity analyses are performed in this study. The first analysis (SA1) simultaneously solves Model while setting and for a range of values of the price of emissions allowance in and emissions cap in . This analysis intends to assess the robustness of the optimal system design and its resulting total emissions under various policy conditions concerning cap-and-trade. The second analysis (SA2) simultaneously solves Model for a range of values of the emissions tax rate in , price of emissions allowance in , and emissions cap while setting as a decision variable. This analysis intends to assess the robustness of the optimal system design under various policy conditions concerning a hybrid cap-and-trade and emissions tax policy compared to the pure cap-and-trade policy.
3.3. Device and software
The mathematical program of Model and the search algorithm in Model (6) is coded using LINGO programming language and ran in the Global Solver of LINGO 19.0 software (Educational License) using a Dell (G5 5500) Laptop whose specifications are presented in Table 3 . The LINGO code used is presented in Appendix A. Furthermore, the Monte Carlo simulation is performed in Microsoft Excel using the Data Table feature to propagate the simulation instances. The file containing Monte Carlo simulation results is provided in the supplementary file.
Table 3.
Device Specifications.
| Feature | Specifications |
|---|---|
| Processor | Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz 2.59 GHz |
| Installed Random Access Memory (RAM) | 16.0 GB (15.8 GB usable) |
| System Type | 64-bit operating system, x64-based processor |
| Operating System (OS) | Windows 11 Home Single Language |
| OS Version and Build | 22000.258 |
4. Results
4.1. Influence of target setting and process inoperability on process configuration
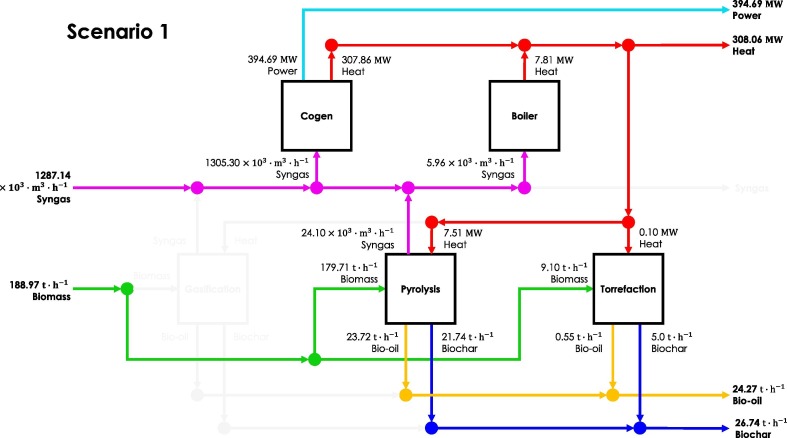
The optimal configuration of the baseline scenario (CS1) is presented in Fig. 2 . The gasification unit is inactivated in this design. Syngas (1287.14 ) is outsourced along with biomass (188.97 ) as primary feedstock. While the polygeneration plant produces all four outputs, it is a primary power-producing plant with a capacity of 394.69 . In this regard, the co-generation unit is operated the most for power production. The secondary product of the plant is heat (308.06 ). Some of the heat is utilized as intermediate inputs for the pyrolysis and torrefaction units for the thermochemical processing of biomass. The two thermochemical process units produce bio-oil (24.27 ). They also sequester CO2 to produce biochar (26.74 ) resulting in CO2 neutrality. The baseline design is considered the benchmark in the analysis of the succeeding scenarios (CS2-CS4).
Fig. 2.
Optimal Configuration for CS1,.
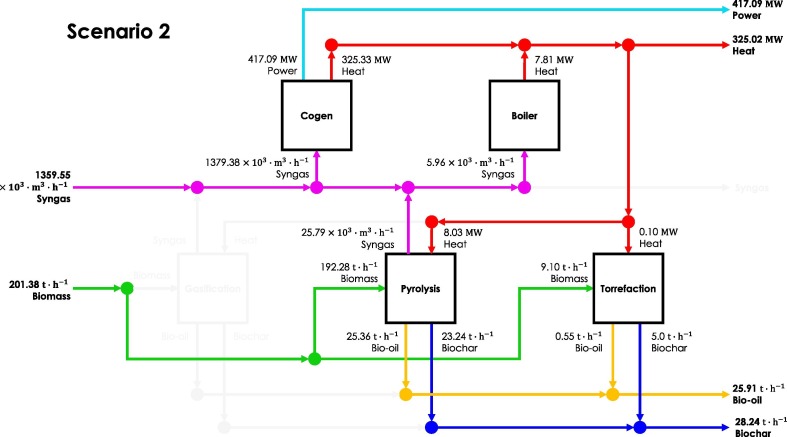
Fig. 3 presents the optimal configuration of the second scenario (CS2). This configuration shows a 5.67 % and 6.92 % increase in the operating capacity of the co-generation and pyrolysis units, respectively. It is apparent that the increase in operating capacities of these process units is in response to the ambitious target profit that characterizes this scenario, . Consequently, biomass (201.38 ) and syngas (1359.55 ) consumption increased by 6.58 % and 5.63 %, respectively. On the other hand, power (417.09 ), heat (325.02 ), biochar (28.24 ), and bio-oil (25.91 ) production increased by 5.67 %, 5.50 %, 5.62 %, and 6.76 %, respectively. The increase in production capacity also resulted in the emissions of CO2 amounting to 15.16 .
Fig. 3.
Optimal Configuration for CS2,.
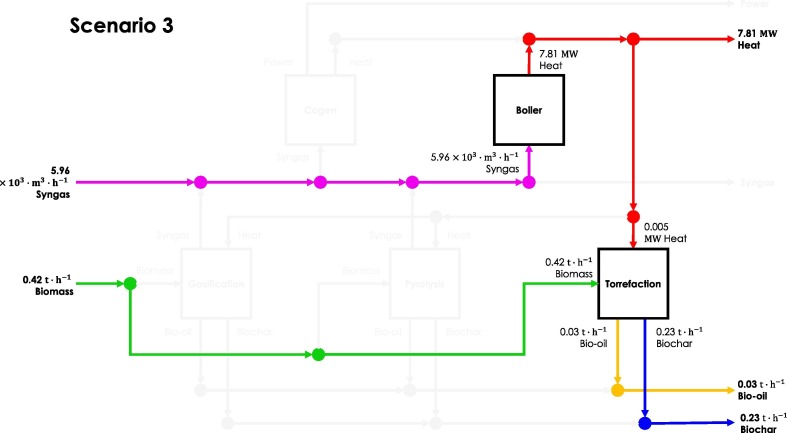
Fig. 4 presents the optimal configuration of the third scenario (CS3). In this configuration, the co-generation, gasification, and pyrolysis units are inactivated. The boiler unit operates at the same level as the baseline scenario, while the operating capacity of the torrefaction unit is reduced by 95 %. The syngas (5.96 ) and biomass (0.42 ) consumption is reduced by 99.54 % and 99.78 %, respectively. Power production is completely ceased due to the inactivation of the co-generation unit while the heat (7.81 ), bio-oil (0.03 ), and biochar (0.23 ) production are reduced by 97.47 %, 99.89 %, and 99.13 %, respectively. It is apparent that the operational capacity of the process units is reduced in response to the low target profit that characterizes the scenario, . The configuration is CO2 neutral, and the primary product of the polygeneration plant is heat, along with bio-oil and biochar.
Fig. 4.
Optimal Configuration for CS3,.
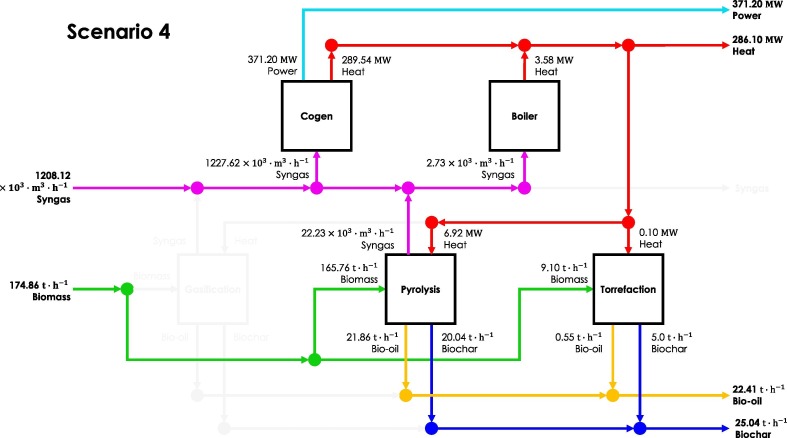
The optimal configuration of the last scenario (CS4) is presented in Fig. 5 . Note that this scenario has the same target profit as CS3, i.e., , but is under the condition of process inoperability of the boiler unit equivalent to 0.60. Unlike CS3, in this configuration, only the gasification unit is inactivated. However, compared to the baseline case, the operational capacity of the co-generation, boiler, and pyrolysis units are reduced by 5.95 %, 54.17 %, and 7.85 %, respectively. The operating capacity of the torrefaction unit is the same as the baseline scenario. The CO2 emissions of this configuration amount to 47.37 . The economic and environmental performance of the four configurations discussed in this section is summarized in Table 4 .
Fig. 5.
Optimal Configuration for CS4, , 0.60.
Table 4.
Economic and Environmental Performance of the Obtained Configurations.
| Variable | Unit | CS1 | CS2 | CS3 | CS4 |
|---|---|---|---|---|---|
| Revenue | 126.45 | 151.29 | 1.32 | 111.24 | |
| Capital Cost | 116.45 | 121.29 | 1.12 | 111.04 | |
| Emissions Cost | 0.00 | 124.90 | 7.19 | 390.37 | |
| Profit | 10.00 | 30.00 | 0.20 | 0.20 | |
| Robustness | 0.41 | 0.19 | 0.88 | 0.50 | |
| Emissions | 0.00 | 15.16 | 0.00 | 47.37 |
4.2. Viability of the robustness metric in the practical setting
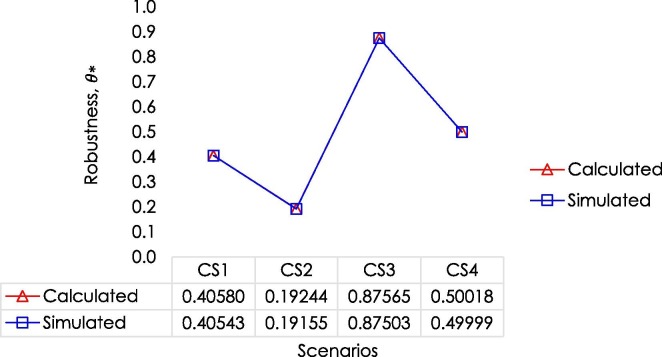
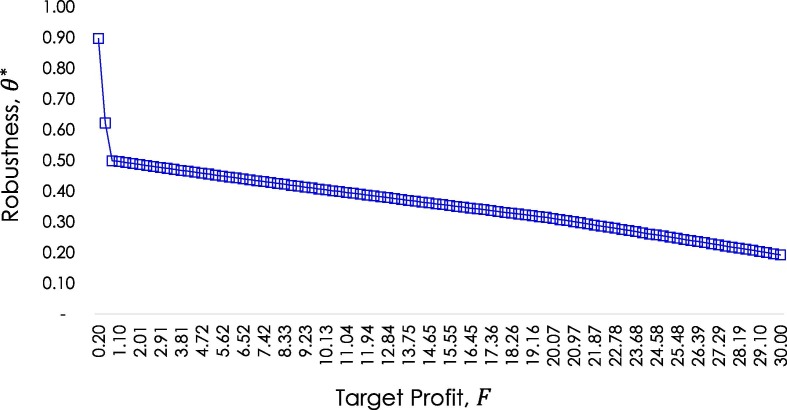
The comparison of the calculated values of the robustness index for each of the four previously presented configurations against the obtained robustness from the Monte Carlo simulations performed on each of them is presented in Fig. 6 . Clearly, the calculated robustness is validated by the simulations. On the other hand, the robustness of the optimal configuration for the baseline case under various target profits is presented in Fig. 7 . The plot clearly shows that robustness decreases as the target profit increases.
Fig. 6.
Comparison of the Calculated and Simulated Values of Robustness of each Configuration.
Fig. 7.
Robustness of Configurations as Target Profit Increases.
4.3. Influence of emissions policies on the robustness of process configuration
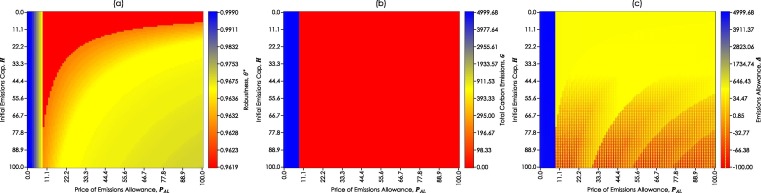
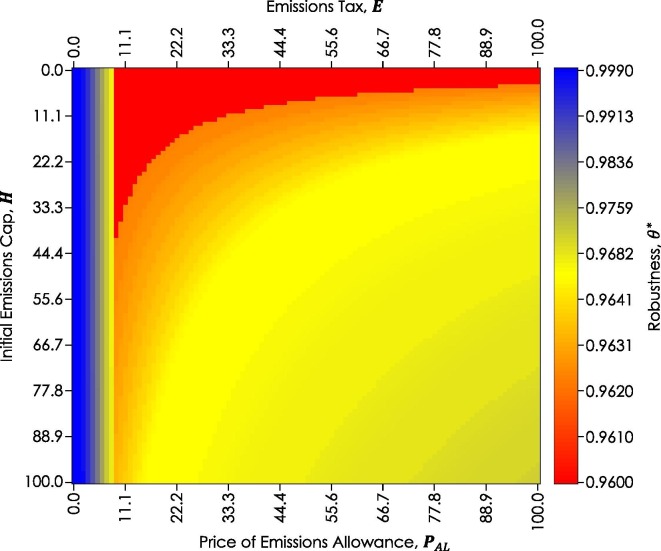
The results of SA1 are summarized in Fig. 8 . The finding in Fig. 8(b) suggests that the optimal configuration that employs strategies to drawdown CO2 emissions is motivated by the price of emissions allowance . It is also observed in Fig. 8(a) that robustness of the optimal configurations decreases as the price of emissions allowance increases. Robustness also decreases as the initial carbon emissions cap decreases. The economic pressures introduced by these parameters on the polygeneration firm are the apparent cause of this influence on the robustness of optimal configurations. It is also important to note that the model may choose to configure the capacities of activated process units or activate process units that have CO2 sequestration capabilities, i.e., pyrolysis, gasification, or torrefaction, in response to the disincentives of CO2 emissions introduced by the cap-and-trade policy. The activation of the CO2 sequestrating process unit may lead to neutral or negative CO2 emissions. Hence, the red shade patterns observable in Fig. 8(c) are attributable to the activation of these process units. On the other hand, Fig. 9 shows that a hybrid emissions policy that provides the polygeneration firm with the flexibility to subscribe either to a cap-and-trade or emissions tax has a relatively similar impact on the robustness of the resulting optimal process configuration compared to pure cap-and-trade.
Fig. 8.
Robustness of Configurations under a Multitude of Values of Emissions Allowance and Emissions Cap of the Cap-and-Trade.
Fig. 9.
Robustness of Configurations under a Multitude of Values of Emissions Allowance , Emissions Tax Rate , and Emissions Cap of the Hybrid Cap-and-Trade and Emissions Tax Policy.
5. Discussion
5.1. Risk aversion and the role of target setting in process configuration
The robustness of the optimal process configurations decreases as the target profit increases. Although setting conservative target profits increases the robustness of the resulting configuration, it limits the amount of profit that the polygeneration plant can obtain. The robustness of the resulting configuration also suffers from extremely ambitious targets. Thus, a risk-averse attitude would lean towards conservative targets, while a risk-seeking attitude would lean towards ambitious targets. A decision-maker would benefit economically, i.e., in terms of achieving desired profits, and psychologically, i.e., confidence towards the probability of achieving target profits, from a decision within their risk appetite – the level of risk that the decision-maker is willing to absorb. In the context of post-pandemic energy supply chains, which are permeated by manifold uncertainties, a moderately ambitious target profit setting, i.e., with (CS1) would be desirable. The value of can be considered the probability of achieving the target profit given the implementation of the resulting process configuration. The observed trade-off between target profit setting and robustness is an obvious idea in practice. The utility of the proposed model of this study is that it obtains optimal process configurations that adhere to this obvious and practical idea. It should be noted that the process design implications of robustness and target profit setting are not readily available in practice.
5.2. The cost efficiency of process configuration under boiler inoperability
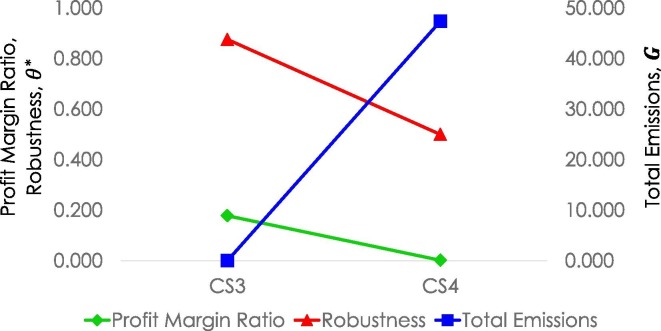
The analysis performed in CS4 demonstrated the influence of process inoperability on the optimal configuration of processes in the polygeneration plant. Fig. 10 compares CS3 (zero inoperability) and CS4 (the boiler is inoperable). Both scenarios are capable of achieving the target profit ; however, the inoperability of the boiler unit incurred major drawbacks to the optimal process configuration in CS4. In CS3, the optimal process configuration is a primarily heat-producing polygeneration plant. The inoperability of the boiler unit introduced a challenge to heat production. Instead of relying solely on the boiler for heat production, in CS4, the co-generation unit is activated to produce heat and power. To sequester the CO2 emissions consequent to the activation of the co-generation unit, the pyrolysis unit is also activated. The activation increased the production of auxiliary products such as bio-oil and biochar. However, the activation of capital-intensive units in response to the inoperability of the boiler unit drastically reduced the cost-efficiency of the resulting optimal configuration, which is evidenced by the dip in the value of the profit margin ratio of the plant (see Fig. 10). It has also reduced the robustness of the resulting configuration and made it less “clean” in terms of CO2 emissions. Nevertheless, the target profit can be achieved through this design at a relatively high probability of achievement despite the challenges introduced by the inoperability of the boiler unit. Table 5 presents the performance of the polygeneration plant in scenario CS3 if not configured regardless of the inoperability of the boiler unit ( 0.60). In comparison to CS4, the polygeneration plant would have lost 180,663.08 USD in profit if its design was not configured to achieve targets amidst the inoperability of the boiler unit. The incorporation of inoperability analysis in process configuration is among the advantages of the proposed model. It introduces a viable approach to designing the polygeneration plant that adapts to the risks associated with process failures without compromising target profit.
Fig. 10.
Comparison of Optimal Process Configurations in CS3 and CS4.
Table 5.
The Performance of the Polygeneration Plant if CS3 is not Configured Regardless of the 0.60 Inoperability.
| Variable | Unit | CS3 ( 0.60) |
|---|---|---|
| Revenue | 0.82 | |
| Capital Cost | 0.78 | |
| Emissions Cost | −2.57 | |
| Profit | 0.019 | |
| Robustness | n/a | |
| Emissions | −0.31 |
Table 5 presents the performance of the polygeneration plant in scenario CS3 if not configured regardless of the inoperability of the boiler unit ( 0.60). In comparison to CS4, the polygeneration plant would have lost 180,663.08 USD in profit if its design was not configured to achieve targets amidst the inoperability of the boiler unit. The incorporation of inoperability analysis in process configuration is among the advantages of the proposed model. It introduces a viable approach to automatically generate designs for the polygeneration plant that can adapt to the operational challenges introduced by severe process failures without compromising target profit.
5.3. Influence of economic pressures of emissions policies on process configuration
The findings obtained from SA1 demonstrated the straightforward effect of emissions policies on polygeneration plants. The robustness of polygeneration plants suffers from strict emissions policies, i.e., policies with a high carbon price. While this observation is apparent in practice, its implication on process configuration is not easily determined. For instance, the findings suggest that investments in technologies that draw down CO2 emissions are motivated by sufficiently high carbon prices. Although this finding is evident in practice, the selection of specific technologies and the decision on its operational capacity in such a way that meets economic targets are not readily apparent. The advantage of the proposed model lies in the integration of this analysis in response to emissions policies. On the other hand, the tests employed in SA2 showed that different emissions policies, i.e., pure or hybrid policies, have an approximately similar impact on the robustness of the resulting optimal process configurations. This is largely due to the “carbon price” set for both cap-and-trade and emissions tax policies being almost equivalent. However, it is noticeable that the rate of decrease in robustness with respect to the initial emissions cap is lesser (see Fig. 9) in the hybrid policy than in the pure cap-and-trade policy (see Fig. 8(a)). This is a consequence of the flexibility of the polygeneration firm under the hybrid policy, which allows it to subscribe to emissions tax, which incurs a lesser cost per ton of CO2 when the initial emissions cap decreases to sufficiently low levels. The effect of a hybrid policy on the robustness of the resulting configuration may be more pronounced under conditions where there is a disparity between the price of emissions allowance and the carbon tax rate.
5.4. Viability of the proposed model
The previous discussions highlighted the practicality of the performance of the designs produced by the proposed model, which means that it follows what is expected of a polygeneration plant when it becomes operational in the real world. The sophisticated aspect of the model is its ability to execute an optimal process configuration in response to the factors considered in the modeling work while producing a practical performance. The computed performance of the model was assessed using Monte Carlo simulation. The findings from the analysis suggest that the robustness metric used in the study is a viable metric to assess the performance of the obtained polygeneration plant designs against uncertainties in supply chain-related factors (i.e., price and demand).
6. Conclusion and future works
Simultaneous consideration of the influence of supply chain-related uncertainties, inoperability, and the economic pressures of emissions policies on the configuration of polygeneration plants receives minimal attention in the current literature. The risks brought by the COVID-19 pandemic exacerbated the need to address this gap. This study approached this problem in view of target-oriented robust optimization, which hinges on the satisficing behavior of decision-makers. An illustrative case study is undertaken involving process integration for a clean biomass-based polygeneration plant. The case study elucidated the following findings:
-
•
Setting ambitious targets reduces the probability of the resulting configuration to achieving the set targets in the presence of supply chain-related uncertainties, while conservative targets promote the opposite.
-
•
Inoperability of process units reduces the robustness of optimal process configurations. The case study has shown that drastic process configurations may be required to achieve targets despite the inoperability of process units. While targets may be achieved through these configurations, the cost-efficiency of the plant may suffer from the configuration of capital-intensive process units.
-
•
For the specific case undertaken in this study, a hybrid cap-and-trade and emissions tax policy yields approximately similar implications to the robustness of resulting optimal process configurations compared to a pure cap-and-trade policy.
-
•
However, it was observed that the rate of decrease in robustness with respect to the initial emissions cap is lesser in the hybrid policy than in the pure cap-and-trade policy.
The viability of the robustness metric used in the study is validated using Monte Carlo simulation. The computed robustness has been validated by the performed simulation. It suggests that the designs obtained using the proposed model effectively address supply chain-related uncertainties. However, the results of this work are limited. First, the results of this study are based on a hypothetical case and may vary in actuality. Thus, these results should be interpreted as estimates of how the polygeneration system could perform in actuality. Second, the parameters are based on secondary data and, thus, must be adjusted if applied to specific and real-case applications. Future works may use the proposed model for configuring actual systems that resemble a production network to address these limitations. The model may also be extended to account for the elasticity of the price of emissions allowance and its influence on obtaining optimal process configurations. Lastly, it might be worthwhile to determine ways to extend the proposed model for use in energy planning at the macro scale.
CRediT authorship contribution statement
Egberto Selerio: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. Joerabell Lourdes Aro: Conceptualization, Writing – original draft, Writing – review & editing. Samantha Shane Evangelista: Conceptualization, Writing – original draft, Writing – review & editing. Fatima Maturan: Conceptualization, Writing – original draft, Writing – review & editing. Lanndon Ocampo: Conceptualization, Project administration, Supervision, Writing – original draft, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.cie.2022.108637.
Appendix A. . LINGO code for model (5) and model (6)
Appendix B. Supplementary material
The following are the Supplementary data to this article:
References
- Aboody D., Levi S., Weiss D. Managerial incentives, options, and cost-structure choices. Review of Accounting Studies. 2018;23(2):422–451. [Google Scholar]
- Adams T.A., II, Ghouse J.H. Polygeneration of fuels and chemicals. Current Opinion in Chemical Engineering. 2015;10:87–93. [Google Scholar]
- Bertsimas D., Sim M. Robust discrete optimization and network flows. Mathematical Programming. 2003;98(1):49–71. [Google Scholar]
- Brooks S.A., Keohane N.O. The political economy of hybrid approaches to a US carbon tax: A perspective from the policy world. Review of Environmental Economics and Policy. 2020;14(1):67–75. [Google Scholar]
- Buso M., Stenger A. Public-private partnerships as a policy response to climate change. Energy Policy. 2018;119:487–494. [Google Scholar]
- Cao J., Ho M.S., Jorgenson D.W., Nielsen C.P. China’s emissions trading system and an ETS-carbon tax hybrid. Energy Economics. 2019;81:741–753. [Google Scholar]
- Carvajal P.E., Li F.G., Soria R., Cronin J., Anandarajah G., Mulugetta Y. Large hydropower, decarbonisation and climate change uncertainty: Modelling power sector pathways for Ecuador. Energy Strategy Reviews. 2019;23:86–99. [Google Scholar]
- Chai Q., Xiao Z., Lai K., Zhou G. Can carbon cap and trade mechanism be beneficial for remanufacturing? International Journal of Production Economics. 2018;203:311–321. [Google Scholar]
- Foo D.C., Tan R.R. A review on process integration techniques for carbon emissions and environmental footprint problems. Process Safety and Environmental Protection. 2016;103:291–307. [Google Scholar]
- Graff M., Carley S. COVID-19 assistance needs to target energy insecurity. Nature Energy. 2020;5(5):352–354. [Google Scholar]
- Heffron R.J., Körner M.F., Schöpf M., Wagner J., Weibelzahl M. The role of flexibility in the light of the COVID-19 pandemic and beyond: Contributing to a sustainable and resilient energy future in Europe. Renewable and Sustainable Energy Reviews. 2021;140:110743. doi: 10.1016/j.rser.2021.110743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Energy Agency (IEA) (2020). Global energy review 2020. IEA, Paris. Accessed at: https://www.iea.org/reports/global-energy-review-2020.
- Jana K., Ray A., Majoumerd M.M., Assadi M., De S. Polygeneration as a future sustainable energy solution–A comprehensive review. Applied Energy. 2017;202:88–111. [Google Scholar]
- Jenkins J.D. Political economy constraints on carbon pricing policies: What are the implications for economic efficiency, environmental efficacy, and climate policy design? Energy Policy. 2014;69:467–477. [Google Scholar]
- Klemeš J.J., editor. Handbook of process integration (PI): minimization of energy and water use, waste and emissions. Woodhead Publishing; Cambridge, UK: 2013. [Google Scholar]
- Klemeš J.J., Van Fan Y., Tan R.R., Jiang P. Minimising the present and future plastic waste, energy and environmental footprints related to COVID-19. Renewable and Sustainable Energy Reviews. 2020;127:109883. doi: 10.1016/j.rser.2020.109883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koljonen T., Lehtilä A. The impact of residential, commercial, and transport energy demand uncertainties in Asia on climate change mitigation. Energy Economics. 2012;34:S410–S420. [Google Scholar]
- Kostúr K., Kačur J. May). Indirect measurement of syngas calorific value. IEEE; 2015. pp. 229–234. [Google Scholar]
- Laghari J. Climate change: Melting glaciers bring energy uncertainty. Nature. 2013;502(7473):617–618. doi: 10.1038/502617a. [DOI] [PubMed] [Google Scholar]
- Liu T., Nakajima T., Hamori S. The impact of economic uncertainty caused by COVID-19 on renewable energy stocks. Empirical Economics. 2022;62(4):1495–1515. doi: 10.1007/s00181-021-02087-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manesh M.H.K., Abadi S.K., Amidpour M., Ghalami H., Hamedi M.H. New emissions targeting strategy for site utility of process industries. Korean Journal of Chemical Engineering. 2013;30(4):796–812. [Google Scholar]
- Mastropietro P., Rodilla P., Batlle C. Emergency measures to protect energy consumers during the Covid-19 pandemic: A global review and critical analysis. Energy Research & Social Science. 2020;68:101678. doi: 10.1016/j.erss.2020.101678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Navon A., Machlev R., Carmon D., Onile A.E., Belikov J., Levron Y. Effects of the COVID-19 pandemic on energy systems and electric power grids—A review of the challenges ahead. Energies. 2021;14(4):1056. [Google Scholar]
- Ng T.S., Sy C. An affine adjustable robust model for generation and transmission network planning. International Journal of Electrical Power & Energy Systems. 2014;60:141–152. [Google Scholar]
- Ocampo L., Aro J.L., Evangelista S.S., Maturan F., Selerio E., Atibing N.M., Yamagishi K. On k-means clustering with IVIF datasets for post-COVID-19 recovery efforts. Mathematics. 2021;9(20):2639. [Google Scholar]
- Olivier, J. G., Schure, K. M., & Peters, J. A. H. W. (2017). Trends in global CO2 and total greenhouse gas emissions. PBL Netherlands Environmental Assessment Agency. Accessed at: https://www.pbl.nl/en/trends-in-global-co2-emissions.
- Ocampo L., Tanaid R.A., Tiu A.M., Selerio E., Jr., Yamagishi K. Classifying the degree of exposure of customers to COVID-19 in the restaurant industry: A novel intuitionistic fuzzy set extension of the TOPSIS-Sort. Applied Soft Computing. 2021;113:107906. doi: 10.1016/j.asoc.2021.107906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pei P., Korom S.F., Ling K., Nasah J. Cost comparison of syngas production from natural gas conversion and underground coal gasification. Mitigation and Adaptation Strategies for Global Change. 2016;21(4):629–643. [Google Scholar]
- Salisu A., Adediran I. Uncertainty due to infectious diseases and energy market volatility. Energy Research Letters. 2020;1(2):14185. [Google Scholar]
- Schaeffer R., Szklo A.S., de Lucena A.F.P., Borba B.S.M.C., Nogueira L.P.P., Fleming F.P.…Boulahya M.S. Energy sector vulnerability to climate change: A review. Energy. 2012;38(1):1–12. [Google Scholar]
- Selerio E., Jr., Caladcad J.A., Catamco M.R., Capinpin E.M., Ocampo L. Emergency preparedness during the COVID-19 pandemic: Modelling the roles of social media with fuzzy DEMATEL and analytic network process. Socio-Economic Planning Sciences. 2022;82(Part A) doi: 10.1016/j.seps.2021.101217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selerio E., Maglasang R. Minimizing production loss consequent to disasters using a subsidy optimization model: A pandemic case. Structural Change and Economic Dynamics. 2021;58:112–124. [Google Scholar]
- Stelte W. Energy & Climate Centre for Renewable Energy and Transport Section for Biomass. Danish Technological Institute. 2012. Torrefaction of Unutilized Biomass Resources and Characterization of Torrefaction Gasses: Resultat Kontrakt Report. [Google Scholar]
- Sy C.L., Aviso K.B., Ubando A.T., Tan R.R. Target-oriented robust optimization of polygeneration systems under uncertainty. Energy. 2016;116:1334–1347. [Google Scholar]
- Szczygielski J.J., Brzeszczyński J., Charteris A., Bwanya P.R. The COVID-19 storm and the energy sector: The impact and role of uncertainty. Energy Economics. 2021;109:105258. doi: 10.1016/j.eneco.2021.105258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- U.S. Department of Energy (August 2011). U.S. Billion-Ton Update: Forest Biomass and Woodwastes. U.S. Department of Energy. Accessed at: https://www1.eere.energy.gov/bioenergy/pdfs/btu_forest_biomass.pdf.
- Ubando A.T., Chen W.H., Ong H.C. Iron oxide reduction by graphite and torrefied biomass analyzed by TG-FTIR for mitigating CO2 emissions. Energy. 2019;180:968–977. [Google Scholar]
- Ubando A.T., Chen W.H., Tan R.R., Naqvi S.R. Optimal integration of a biomass-based polygeneration system in an iron production plant for negative carbon emissions. International Journal of Energy Research. 2020;44(12):9350–9366. [Google Scholar]
- United Nations Environmental Programme (UNEP) (2016). The adaptation (finance) gap report. Technical report, United Nations Environment Programme (UNEP), Nairobi. Accessed at: https://www.unep.org/resources/adaptation-gap-report-2020.
- Wang Y., Chen W., Liu B. Manufacturing/remanufacturing decisions for a capital-constrained manufacturer considering carbon emission cap and trade. Journal of Cleaner Production. 2017;140:1118–1128. [Google Scholar]
- Wood J. The pros and cons of carbon taxes and cap-and-trade systems. The School of Public Policy Publications. 2018;11(30):1–19. [Google Scholar]
- Zeng S., Nan X., Liu C., Chen J. The response of the Beijing carbon emissions allowance price (BJC) to macroeconomic and energy price indices. Energy Policy. 2017;106:111–121. [Google Scholar]
- Zhou P., Wang M. Carbon dioxide emissions allocation: A review. Ecological Economics. 2016;125:47–59. [Google Scholar]
- Zhou P., Wen W. Carbon-constrained firm decisions: From business strategies to operations modeling. European Journal of Operational Research. 2020;281(1):1–15. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.