Effects of clot contraction on clot degradation: A mathematical and experimental approach

Abstract

Thrombosis, resulting in occlusive blood clots, blocks blood flow to downstream organs and causes life-threatening conditions such as heart attacks and strokes. The administration of tissue plasminogen activator (t-PA), which drives the enzymatic degradation (fibrinolysis) of these blood clots, is a treatment for thrombotic conditions, but the use of these therapeutics is often limited due to the time-dependent nature of treatment and their limited success. We have shown that clot contraction, which is altered in prothrombotic conditions, influences the efficacy of fibrinolysis. Clot contraction results in the volume shrinkage of blood clots, with the redistribution and densification of fibrin and platelets on the exterior of the clot and red blood cells in the interior. Understanding how these key structural changes influence fibrinolysis can lead to improved diagnostics and patient care. We used a combination of mathematical modeling and experimental methodologies to characterize the process of exogenous delivery of t-PA (external fibrinolysis). A three-dimensional (3D) stochastic, multiscale model of external fibrinolysis was used to determine how the structural changes that occur during the process of clot contraction influence the mechanism(s) of fibrinolysis. Experiments were performed based on modeling predictions using pooled human plasma and the external delivery of t-PA to initiate lysis. Analysis of fibrinolysis simulations and experiments indicate that fibrin densification makes the most significant contribution to the rate of fibrinolysis compared with the distribution of components and degree of compaction (p < 0.0001). This result suggests the possibility of a certain fibrin density threshold above which t-PA effective diffusion is limited. From a clinical perspective, this information can be used to improve on current therapeutics by optimizing timing and delivery of lysis agents.

Significance

Diseases and illnesses such as cancer, diabetes, and coronavirus disease 2019 (COVID-19) infection can lead to a prothrombotic environment, resulting in excessive blood clotting and risk of heart attacks and strokes. Current therapies (fibrinolytic agents) have limited time frames for effective administration, and bleeding complications can occur. Clot contraction, a result of platelet-fibrin interaction, is known to be altered in prothrombotic conditions and has been shown to impair external fibrinolysis. A combination of modeling simulations and experimental validation allowed us to manipulate a physiologically relevant, yet simplified, blood clot structure to identify underlying mechanisms of resistance to degradation. Our findings suggest an opportunity to develop t-PA variants with an optimal affinity for fibrin for more effective clot resolution treatment.

Introduction

Thromboembolic diseases, such as acute stroke and myocardial infarction, are directly associated with excess clotting (hypercoagulability) and insufficient clot degradation (hypofibrinolysis) (1, 2, 3, 4, 5, 6, 7, 8). Blood coagulation, or clotting, is the process by which blood transforms into an insoluble gel consisting of platelets and red blood cells (RBCs) interspersed within a fibrin network. Monomeric fibrin molecules polymerize, in a half-staggered formation, as fibrinopeptides are cleaved by the coagulation factor thrombin, to form the fibrin network (9). Fibrinolysis, the enzymatic degradation of the fibrin network, occurs as a result of the conversion of plasminogen into plasmin by tissue plasminogen activator (t-PA) (10,11). Plasmin then degrades fibrin, which has the dual effect of removing fibrin from the clot and exposing additional binding sites for t-PA, which creates a positive-feedback loop of clot degradation (10,12,13). External fibrinolysis, a model for the intravenous delivery of thrombolytic drugs such as t-PA, is used to activate the fibrinolysis process clinically as a treatment for thrombotic conditions (14,15). Despite the fact that fibrinolytic drugs are US Food and Drug Administration (FDA) approved, they are only utilized in ∼5% of ischemic stroke patients due to the short time window of effectiveness (∼73% of patients do not make it to the hospital within the time window), the significantly increased risk for bleeding (intracranial hemorrhage occurs in 6.4% of t-PA-treated patients compared with 0.6% of placebo-treated patients) (16), and a recanalization rate ceiling of only ∼80% (17). Thus, it is critical to determine features of blood clots that influence the efficacy and specificity of thrombolytic drugs.

Mathematical and experimental methodologies have been used to explore the mechanisms of fibrinolysis to varying degrees. Mathematical modeling and computer simulations provide a platform to easily modify variables, run a plethora of parameter combinations, and identify the optimal and meaningful parameters for experiments. Previous microscale models of a single fibrin fiber were used to study the length of time individual t-PA molecules can stay bound during lysis, and the time it takes a single fiber exposed to t-PA to degrade (18,19). Model results confirmed that individual thick fibers take longer to degrade than thin fibers (19). Data from the microscale model were incorporated into a macroscale model developed to study the entire fibrin network, including the front-like degradation of a clot undergoing external lysis (18,19). Model results led to the conclusion that coarse clots composed of thick fibers lyse faster than fine clots composed of thin fibers when a small number of t-PA molecules are used to initiate lysis, but the reverse is true when many t-PA molecules are used. This multiscale modeling framework contributes to knowledge about degradation rates and t-PA distribution across fibers in different regions of the clot. Importantly, the model was used to compare the effect of t-PA mutants with standard treatments (18). While existing models help provide insights into the mechanisms underlying the external lysis of clots made of only fibrin, whole blood clots are structurally more complex than fibrin alone.

Fibrin, platelets, and RBCs form the structural basis of whole blood clots, which undergo dynamic changes that alter the clot structure over the course of time. Platelets generate contractile forces that are transmitted through the fibrin mesh, due to platelet-fibrin interactions (20, 21, 22). This clot contraction process results in 1) volume shrinkage of the clot (compaction), 2) the spatial redistribution of fibrin and platelets to the clot exterior and RBCs to the clot core, and 3) a reduction in pore sizes between fibers, termed fiber densification. The extent of clot contraction is reduced in thrombotic conditions, such as ischemic stroke, deep vein thrombosis, systemic lupus erythematosus, and asthma, compared with healthy subjects (20,23, 24, 25, 26, 27, 28, 29, 30). The rate of external fibrinolysis is reduced in contracted clots compared with those where contraction is impaired (20). We speculate that the extent of altered contraction of blood clots in thrombotic conditions may play a role in the efficacy of thrombolytic treatments (20,31); however, the underlying mechanism driving impaired fibrinolysis of contracted blood clots remains unknown. Thus, there is a need to determine how the changes in clot structure that occur during the contraction process influence the rate of fibrinolysis.

It is known that the fibrin network structure and the number of t-PA molecules influence the rate of fibrinolysis (11,18,32,33), but most fibrinolysis studies have been focused on fibrin in the absence of blood cells. For example, clots composed of thick fibers have been shown experimentally to degrade faster than clots composed of thin fibers, despite the fact that individual thick fibers degrade more slowly than individual thin fibers (11,18,34,35). This suggests that densification of the fibrin fibers may play a role in altering the rate of fibrinolysis in contracted blood clots. Furthermore, the compaction of RBCs into the clot core during contraction may reduce t-PA effective diffusion throughout the clot (31), leading to reduced fibrinolytic activity. Last, the redistribution of fibrin to the exterior of the blood clot may influence t-PA’s ability to access the entire clot. Determining how the structural changes of fibrin densification, clot compaction, and fibrin redistribution that occur during clot contraction affect the rate of external fibrinolysis is fundamental in pinpointing the role that clot contraction plays in thrombolytic efficacy.

Here, we combine mathematical modeling and experimental approaches to determine how the dynamic structural changes that occur during the contraction process influence fibrinolysis. We develop a macroscale model to incorporate RBCs and examine how clot composition influences lysis rates. This modified model, together with turbidimetric assays and confocal microscopy, helps us to study mechanisms of external fibrinolysis. We manipulate key parameters such as pore size, distribution and densification of fibrin fibers, and the presence of RBCs to delineate the key mechanisms underlying impaired fibrinolysis of contracted blood clots.

Methods

Development of a multiscale mathematical model of contracted blood clots

In order to recapitulate the structural changes that occur during the contraction process, we significantly upgrade our previously described mathematical model to 1) incorporate RBCs and 2) reflect the clot contraction driven volume shrinkage and changes in fibrin fiber distribution and densification. Briefly, this multiscale model of an occlusive blood clot under static flow conditions combines a two-dimensional microscale model that represents a single fiber cross section and a three-dimensional (3D) macroscale model that represents a blood clot (18,19). Fibrin, t-PA, plasminogen, and plasmin are tracked as they change in space and time following the addition of a t-PA bolus at the edge of the clot to initiate fibrinolysis. Motivated by the development of a fibrinolysis model with increasing physiological relevance, we modified the macroscale model (18,19) by first homogeneously distributing RBCs into the clot volume as portions of the volume that were not degradable and through which t-PA could not diffuse. Additional model details are found in Section SAi (Fig. S1 and Table S1). Reproducible equations for the microscale and macroscale model can be found in (18,19).

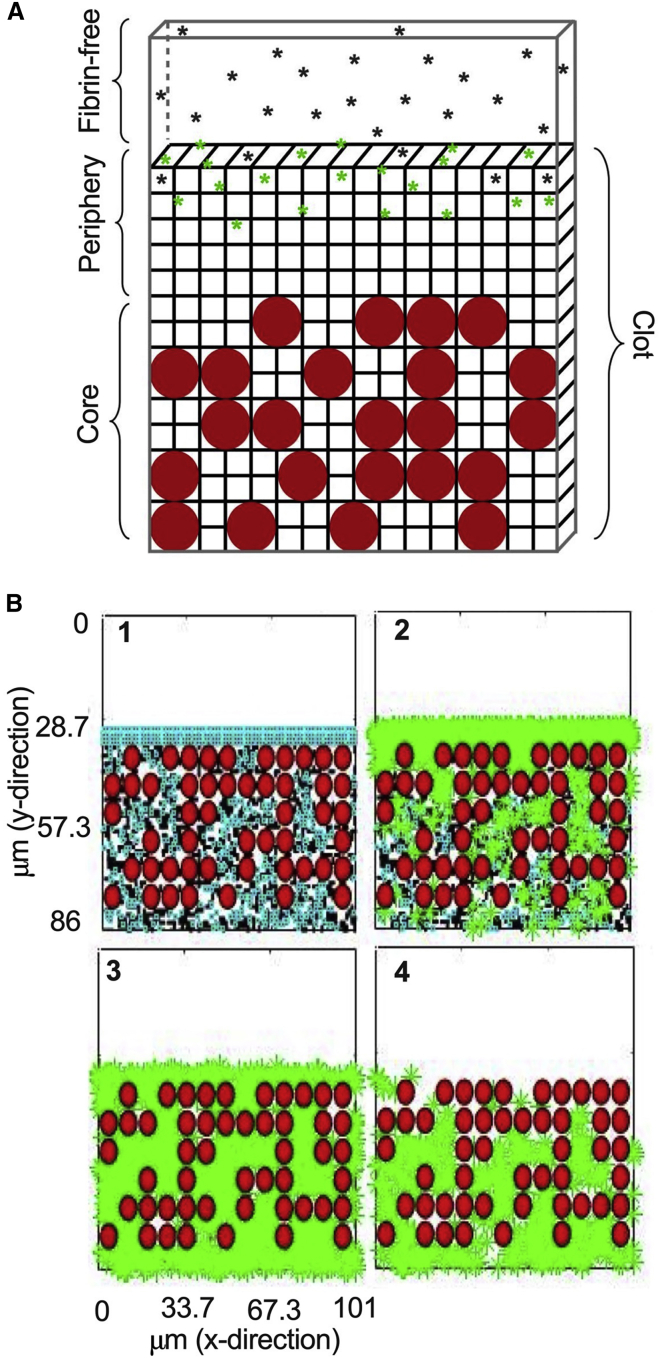
During the clot contraction process, the blood clot volume shrinks, resulting in the compaction of the constitutive components of the clot, and the fibrin network is redistributed and densified on the periphery of the clot (Fig. 2; Table 1) (31,36). To mimic these structural changes, we have divided the model clot into two regions: the periphery and the core (Fig. 1 A). For an uncontracted clot (with volume 5620 μm³ and pore size 1.014 μm; Table S1), the RBCs and fibrin are homogeneously distributed in the core region. For contracted clots, the overall clot volume was reduced to 882.8 μm³ to reflect the volume shrinkage of the clot, the pore size was reduced to 0.22 μm to reflect the densification of fibrin, and 90% of the fibrin was placed in the periphery region, to reflect the spatial redistribution that occurs during the contraction process (Fig. 3 A).

Figure 2.

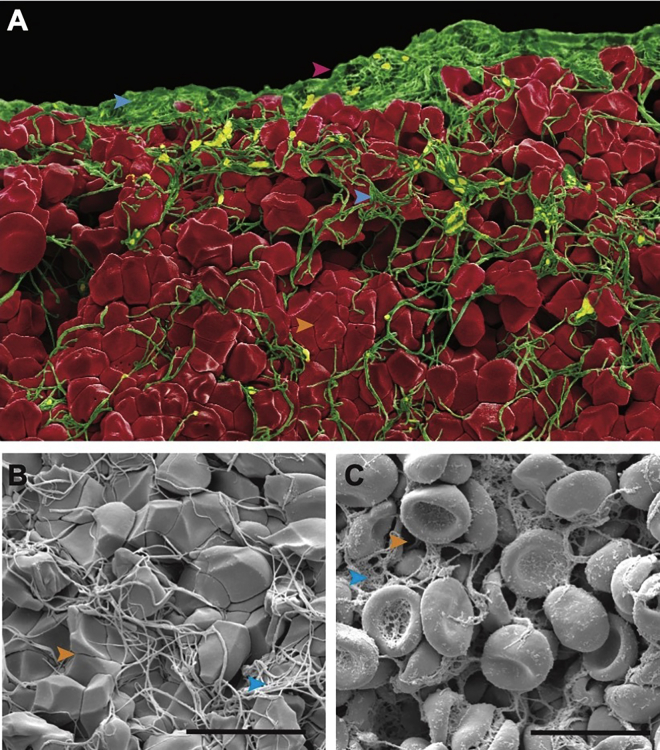
Clot contraction results in structural changes. (A) Colorized scanning electron microscopy image of a contracted blood clot. (B) Magnified view of a contracted clot and (C) uncontracted clot. Pink arrowhead, periphery edge; blue arrowhead, fibrin; orange arrowhead, pores. Scale bar: 10 μm. To see this figure in color, go online.

Table 1.

Clot contraction results in three structural changes, which can be modeled by varying three key parameters

	Redistribution: percentage of fibrin in the exterior/periphery	Volume shrinkage: compaction of RBCs	Densification: pore size
Contracted	↑	↑	↓
Uncontracted	↓	↓	↑

Figure 1.

Schematic of 3D mathematical model of external fibrinolysis. (A) The model is composed of the fibrin-free region containing unbound t-PA (black asterisks), the fibrin network periphery with unbound and bound t-PA (green stars), and the core containing fibrin and RBCs (red circles). (B) Time series of t-PA diffusion (green stars) into the fibrin network (blue and black) and RBC region (180, 240, 300, 360 s). To see this figure in color, go online.

Figure 3.

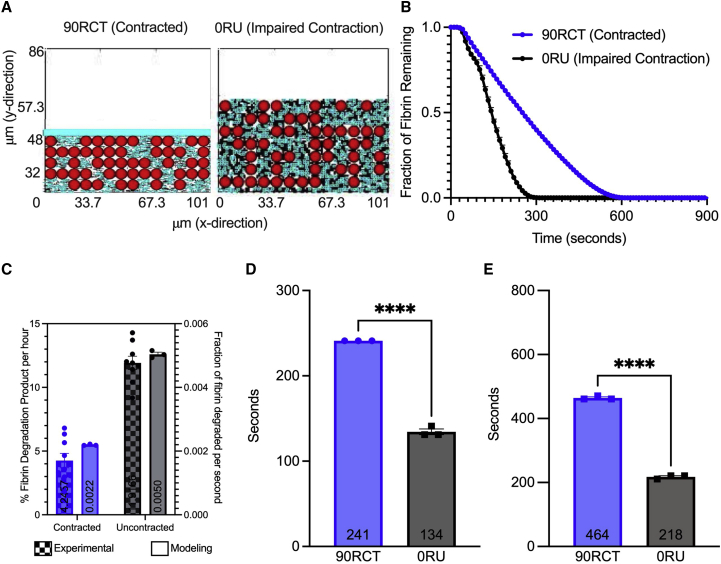
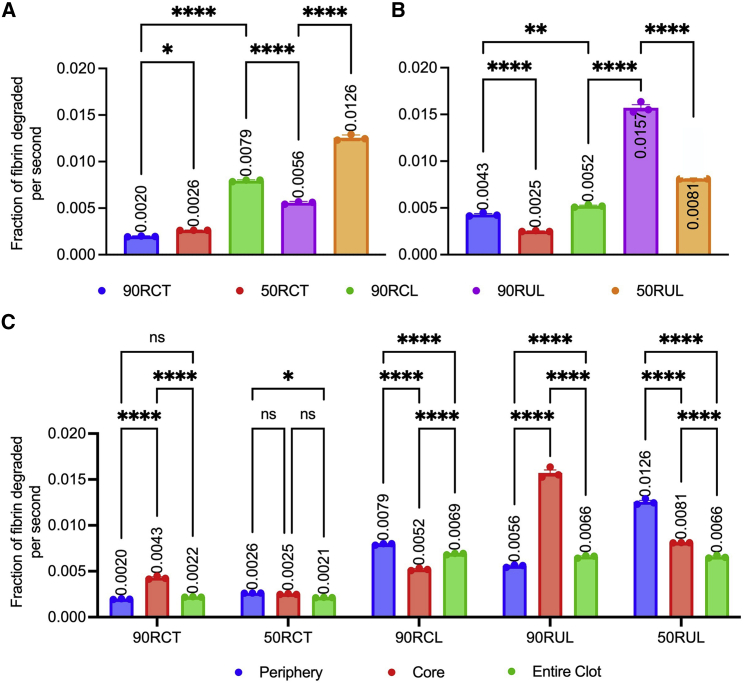
Fibrinolysis in contracted versus uncontracted clot simulations. Model contracted (A, left) and uncontracted (A, right) clots are built to mimic the experimental clots. Three independent simulations were conducted for both contracted and uncontracted clots with t-PA added at the clot’s edge, and degradation of the clot was measured by the fraction of fibrin remaining in the clot over the course of time (B). The experimental rate of clot degradation (contracted versus impaired contraction with blebbistatin, a myosin inhibitor (22)), and modeling rate of clot degradation (90RCT versus 0RU) are compared (C); experimental degradation is measured as percentage of fibrin degradation products (% FDP) per hour; modeling degradation was measured in fraction of fibrin degraded per second (ff/s), and was determined by calculating the slope of the linear portion of (B). Time to 50% degradation (D) and 90% degradation (E) were analyzed. Data are represented as mean $\pm$ SEM. Data were analyzed using a one-way ANOVA followed by a Tukey’s multiple comparison test. ^∗∗∗∗p < 0.0001. To see this figure in color, go online.

The goal of the present study was to examine the role of three different clot parameters: fibrin fiber densification, fiber redistribution, and clot compactness. Six different scenarios were evaluated in the first set of analyses: 90RCT, 50RCT, 90RCL, 50RUL, 90RUL, and 0RU (Table 2). The naming scheme was as follows: the number at the front followed by an R (for redistribution) represented the percentage of total fibrin that was distributed in the clot periphery; the second letter was either U (for an uncontracted clot, which had a larger volume) or C (for a contracted clot, which was more compact due to volume shrinkage); the third letter was either L (for loosely packed peripheral fibrin; pore size 1.014 μm) or T (for tightly packed peripheral fibrin; pore size 0.22 μm). A model scenario without the third letter (e.g., 0RU) did not have a peripheral fibrin region, but rather was a homogeneous mixture of fibrin and RBCs. Results of the various model scenarios were compared in order to understand the relative contributions of densification, redistribution, and compactness. For example, by comparing 90RCT and 90RCL—which were both contracted clots with 90% of the fibrin in the periphery—we can investigate the effect of densification. Comparing these scenarios, in which the clots were strictly composed of fibrin, with our original scenarios elucidates the effect of RBCs on lysis.

Table 2.

Clot scenario descriptions with varying parameters

Scenario	% fibrin in clot periphery redistributed (R)	Contracted (C) (i.e., volume shrinkage)	Uncontracted (U)	Tightly packed periphery (T)	Loosely packed periphery (L)
90RCT	90	X		X
50RCT	50	X		X
90RCL	90	X			X
90RUL	90		X		X
50RUL	50		X		X
0RU	0		X	NA	NA

Fibrin redistribution on the clot periphery: 90% of total fibrin is in the periphery (90R)/50% of total fibrin is in periphery (50R)/clot is a homogeneous mixture of RBCs and fibrin, with 0% of fibrin in the periphery (0R). Volume shrinkage: contracted (C)/uncontracted (U). Fibrin structure: tight, pore size between fibers is 0.22 μm (T)/loose, pore size between fibers is 1.014 μm (L). All contracted clots have tightly packed core regions, and all uncontracted clots have loosely packed core regions. 0RU represents a clot where contraction is impaired; 90RCT corresponds to a fully contracted clot. NA, not available.

Initiation of fibrinolysis and post-processing

Model simulations were run in Fortran and postprocessed in MATLAB (Section SAii). Fibrinolysis was initiated through the addition of a bolus delivery of 9350 t-PA molecules (uncontracted clot, 92.2 molecules/μm² or 5 nM; contracted clot, 425.5 molecules/μm² or 86.2 nM). Plasminogen and plasmin are included implicitly in this macroscale model via their effect on the microscale model data (details in Section SA). Three simulations were run for each scenario, with measurements taken every 10 s with very little variability between each simulation.

We track the time to 50% and 90% lysis (in seconds), degradation rate (measured in fraction of fibers degraded per second, which we will denote ff/s), and t-PA distributions. The degradation rate was determined by calculating the slope of the linear portion of the degradation curves (Fig. S4); the 50% and 90% lysis times were determined using the fraction of remaining fibrin data.

We created time series plots such as the one in Fig. 1 B to showcase fibrin fibers lysing across a front (Figs. S2 and S3). For each of the six scenarios simulated, we produced time series plots and corresponding degradation plots that showcase the lysis data for the periphery, core, and entirety of the clot (Figs S5 and S6).

Sample preparation

Citrated human blood was obtained from the blood banks at the University of Pennsylvania and the State University of New York - Stony Brook. Platelet-free plasma was isolated by plasmapheresis and diluted 1:4 citrate phosphate dextrose:plasma and frozen within 8 h. Plasma was thawed, pooled for 25 donors, filtered, aliquoted, and refrozen at −80°C. Prior to experiments, pooled plasma was warmed to 37°C. Samples were prepared by mixing the necessary ratios of plasma to buffer (50 mM Tris, 140 mM NaCl, 1 mg/mL bovine serum albumin [BSA]) to achieve the different fibrinogen concentrations (0.22, 1.38, 1.68, 1.94 mg/mL final concentration). A stock activation mix was created with 25 mM CaCl₂ (final concentration), 0.1U/mL thrombin (final concentration), and buffer. Then 80 μL of the plasma mix was added to each well of a standard 96-well plate, and 20 μL of the activation mix was added to each sample, creating a total of 100-μL clot with height of 3 mm in a standard 96-well plate, and rapidly mixed to initiate clotting, as previously described (37, 38, 39).

Clot formation and fibrinolysis

Clot formation was tracked kinetically using a SpectraMax Microplate Reader at 405 nm with 15-s intervals. Clots were allowed to form for at least 30 min in a humid chamber within the plate reader at 37°C to track clotting and ensure full clot formation (i.e., plateau); 100 $\mu$L of a t-PA (75 nM final concentration) or control solution was gently overlaid on top of each sample to initiate lysis. Lysis was tracked by recording the changes in optical density (OD) at 405 nm for at least 7 h with 15-s intervals. Experiments were performed in triplicate with technical triplicates for each individual experiment (37,39,40). Replicates were removed if the clot did not fully form, if delivery of external t-PA resulted in a suspected collapsed clot, or outliers found using the robust regression and outlier removal (ROUT) method (Fig. S8).

Clot lysis analysis

Clot lysis curves were normalized to the maximum OD, such that this point was set equal to 1 and a fully degraded clot approached an OD of 0. Degradation rate was defined as the slope of the linear region of the normalized curves, with units of fraction of fibrin remaining per second (ff/s). The time to 50% lysis was defined as the time, in seconds, at which the fraction of fibrin remaining was 0.5. Fig. S9 shows an exemplary curve and respective analysis. All analysis was completed using GraphPad Prism 9.0.

Confocal microscopy

Plasma was prepared as described previously. Samples contained the necessary ratios of plasma to buffer (50 mM Tris, 140 mM NaCl, 1 mg/mL BSA) to achieve the different fibrinogen concentrations (0.22, 1.38, 1.68, 1.94 mg/mL final concentration), 25 mM CaCl₂, 0.5U/mL thrombin, and labeled fibrinogen (1:100 volume). The z stack (9-$\mu$m range with 1-μm interval) images were taken with a Zeiss LSM 780 confocal microscope with a 40× water immersion objective and numerical aperture of 1.20. Maximum intensity projections of the z stack sections were converted to binary and the percentage areas of fibers were calculated using Fiji.

Statistical analysis

All statistical analysis was completed using GraphPad Prism 9.0. All data are represented as mean ± standard error of the mean unless otherwise noted. For all statistical tests, an alpha value of 0.05 was used. Normality was assumed for mathematical modeling. A one-way analysis of variance (ANOVA) was conducted to determine differences between simulation scenarios. A two-way ANOVA was performed to determine differences within/between regions of the simulated clots. After confirming normality through a Shapiro-Wilk test for all experimental data, a two-tailed t-test or a one-way ANOVA was conducted to determine differences between fibrin density groups. Experimental differences for quantified parameters were compared using a one-way ANOVA. A two-way ANOVA was used to directly compare model scenarios and experimental results.

Results

3D mathematical model

Utilizing the 3D model developed here, we initiated a t-PA bolus (green stars) at the peripheral edge of the simulated clot to mimic external fibrinolysis (Fig. 1 B). This initialization occurred in the fibrin-free region where t-PA diffused and then bound to a fibrin fiber (fibrin is indicated by black and blue in Fig. 1 B) in the outermost clot region. This outermost clot region is the edge of the RBC-and-fibrin region in the baseline uncontracted clot scenario (0RU), and the fibrin-only periphery in all other scenarios (Figs. S2 and S3). The t-PA molecules either kinetically unbound or were forced to unbind due to the presence of plasmin after initializing degradation on the corresponding fibrin fiber. Based on data collected from the previous microscale model about how frequently t-PA was forced to unbind (18), we assumed that 8.48% of t-PA unbinding events in the model are due to plasmin. We assumed that the t-PA in these cases was bound to a small piece of fibrin, which could freely diffuse into or away from the clot. Eventually, the t-PA would kinetically unbind from this small piece of fibrin and be free to bind elsewhere.

Effect of clot contraction on external fibrinolysis

We previously showed experimentally that the rate of external fibrinolysis is reduced by twofold in contracted blood clots compared with those with impaired clot contraction (p < 0.001) (20). However, the mechanism underlying this reduction remains unknown. Clot contraction results in the volume shrinkage of the blood clot and the spatial redistribution and densification of fibrin on the exterior of the clot (Fig. 2). We modified the mathematical model described above to be able to compare contracted and uncontracted clots, varying amounts of fibrin in the subregions (periphery and core) of the whole clot, and tightness of the fibrin network. The baseline contracted clot simulation reflects a reduction in clot volume and 90% of fibrin redistributed and densified on the periphery of the clot (90RCT), whereas the baseline clot with impaired contraction had a homogenous distribution of fibrin and RBCs (0RU) (Fig. 3 A and B). Simulations revealed that the rate of fibrinolysis was reduced in the contracted clot scenario by more than twofold (0.0022 versus 0.0050 fraction of fibrin degraded per second; p < 0.0001; Fig. 3 C), which corresponds to our previously reported experimental results (20). The 50% and 90% degradation times were delayed by more than 1.5- and twofold, respectively (241 versus 134 s, p < 0.0001, Fig. 3 D; and 464 versus 217 s, p < 0.0001, Fig. 3 E). Collectively, these findings help to validate the modified model of external fibrinolysis in contracted blood clots.

Mechanism of delayed fibrinolysis in simulations of contracted blood clots

To delineate the structural mechanisms that drive the reduction in fibrinolysis of contracted clots, we developed a series of scenarios that systematically and independently varied volume shrinkage, fibrin redistribution to the periphery, and fibrin densification (Table 2; Fig. 4 A; Table S1).

Figure 4.

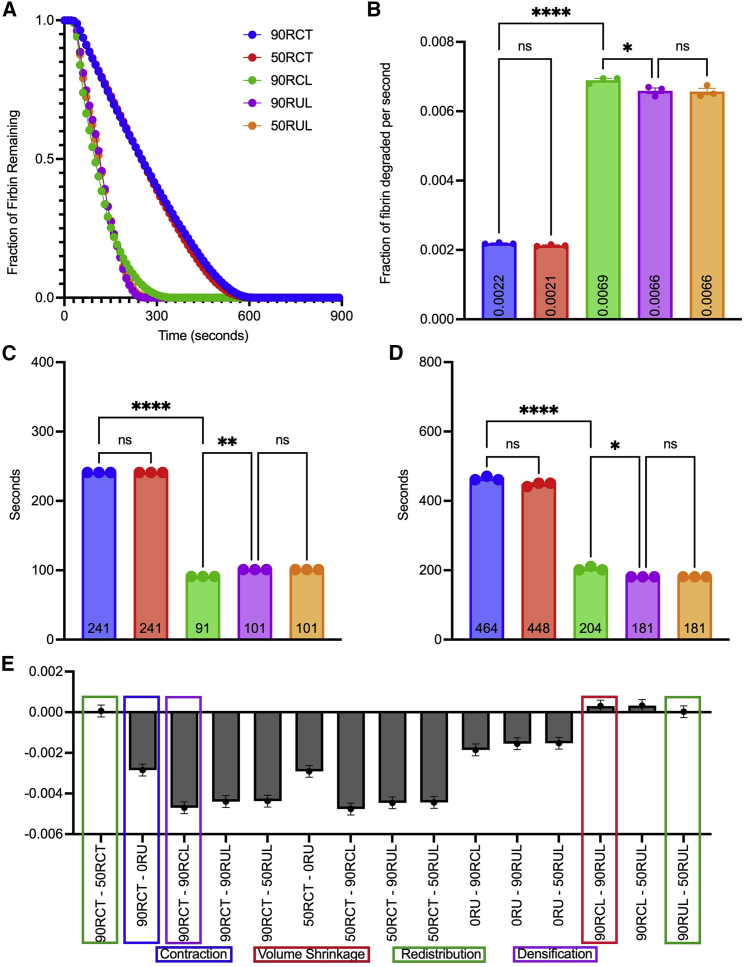
Influence of clot structure on external fibrinolysis. Additional simulations were developed to understand the role of contraction, redistribution, and densification on the lysis of blood clots. Fraction of fibrin remaining in the clot is plotted as a function of time for simulations described in Table 2 (A). Clot degradation rate (fraction of fibrin degraded per second) was determined as described previously (B). Time to 50% degradation (C), and time to 90% degradation (D) were analyzed. Ns, p > 0.05; ^∗p < 0.05; ^∗∗p < 0.01; ^∗∗∗p < 0.001; ^∗∗∗∗p < 0.0001. Data represented as mean ± SEM. (E) The column mean differences for the degradation rates of the entire clot. Scenarios with only one dissimilar component are highlighted in green, red, and purple for comparison. The comparison highlighted in blue represents the baseline contracted and uncontracted clots. To see this figure in color, go online.

Volume shrinkage

In order to assess the effect of volume shrinkage, we compared scenarios 90RCL and 90RUL, where fibrin redistribution and densification are held constant, and the clot volume is reduced due to contraction. There was a slight, but statistically significant, difference in the degradation rate (0.0069 versus 0.0066 ff/s, p < 0.05; Fig. 4 B), 50% degradation time (91 versus 101 s, p < 0.01; Fig. 4 C), and 90% degradation time (204 versus 181 s, p < 0.05; Fig. 4 D). This suggests that, while volume shrinkage does influence the rate of fibrinolysis, the effect is limited, as reflected by a small mean difference between scenarios in all three calculations (0.0003 ff/s, 10 s, 20 s, respectively; Fig. 4 E). Moreover, the degradation rate is surprisingly slightly faster when volume shrinkage occurs (90RCL versus 90RUL). Previous experiments have shown that contracted clots, despite their shrinkage in volume, degrade slower than uncontracted clots. Since the model showed that isolation of volume shrinkage by itself increases the rate of lysis, we can conclude that volume shrinkage does not contribute to limiting fibrinolysis.

Intriguingly, when there is no fibrin in the periphery of the contracted and uncontracted clot (0RC versus 0RU; see Fig. S7 for 0RC), there are statistically significant differences in degradation rate (0.0015 versus 0.005 ff/s, p < 0.0001), 50% degradation time (358 versus 134 s, p < 0.0001), and 90% degradation time (671 versus 218 s, p < 0.0001) (Fig. S7). However, it is impossible to remove the influence of fibrin densification from this comparison since the fibrin is more densely packed in the core of the contracted clot compared with the uncontracted one. It is likely that fibrin densification is playing a larger role than clot volume in slowing lysis of the 0RC clot.

Fibrin redistribution

We next examined the direct effect of fibrin redistribution by comparing scenarios in which clot volume/contraction and fibrin density are kept constant, while the distribution of the fibrin network to the periphery of the clot is varied between 0% and 90%. When comparing 90RUL versus 50RUL and 90RCT versus 50RCT, there are insignificant differences in degradation rate (0.0022 versus 0.0021 and 0.0066 versus 0.0066 ff/s, p > 0.05; Fig. 4 B), time to 50% lysis (241 versus 241 and 101 versus 101 s, non-significant [ns]; Fig. 4 C), and time to 90% lysis (464 versus 448 and 181 versus 181 s, ns; Fig. 4 D), suggesting that fibrin distribution does not play an evident role in altering fibrinolysis of contracted clots.

Surprisingly, when there is 0% of the fibrin in the periphery (0RU and 0RC), the entire clot has a slower degradation rate (p < 0.0001) than the respective clots with 90% and 50% of fibrin in the periphery. This suggests that, while the degree of redistribution does not seem to matter when the clot has some fibrin in the periphery region, an entirely homogeneous clot does have different lysis characteristics than a clot with a fibrin periphery.

Fibrin densification

Last, we studied the effect of densification of fibrin by comparing scenarios with similar fibrin distribution but different pore sizes, distinguished by tight versus loose fibrin networks. We observed a statistically significant difference between contracted clot scenarios 90RCT and 90RCL in degradation rates (0.0022 versus 0.0069 ff/s, p < 0.0001; Fig. 4 B), 50% degradation times (241 versus 91 s, p < 0.0001; Fig. 4 C), and 90% degradation times (464 versus 204 s, p < 0.0001; Fig. 4 D). This implies a slower (>threefold) and delayed (>twofold) lysis in contracted clots with dense fibrin on the periphery. The mean differences calculated between scenarios comparing densification of the periphery is qualitatively the largest (Fig. 4 E), suggesting that fibrin densification plays the dominant role in enzymatic degradation.

Influence of clot spatial distribution on the rate of fibrinolysis

To further probe the mechanism underlying impaired external fibrinolysis in contracted clots, we analyzed the fibrinolytic process in two distinct subregions: the fibrin-rich periphery and the RBC-rich core (Fig. 1 A). We performed the same scenario comparisons as for the entire clot (in the previous section) to understand the role of clot contraction, redistribution, and densification in the clot subregions.

Volume shrinkage

First, we focused on contracted versus uncontracted clots in which fibrin density and redistribution were held constant (90RCL and 90RUL). We observed a faster degradation rate in the periphery of the contracted clot compared with the uncontracted clot (0.0079 versus 0.0056 ff/s, p < 0.0001; Fig. 5 A) and a more than threefold slower degradation rate in the core of the contracted clot (0.0052 versus 0.0157 ff/s, p < 0.0001; Fig. 5 B). These competing rates in the different regions of the clot account for the insignificant difference in the entire clot degradation rates noted earlier.

Figure 5.

Analysis of fibrinolysis in the periphery and core of the clot. Degradation rates (ff/s) of the different subregions of the clots—periphery (A) and core (B)—are compared for the scenarios in Table 2. Degradation rates of the periphery, core, and entire clot are compared with each other for each scenario in Table 2 (C). Data represented as mean ± SEM. ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001, ^∗∗∗∗p < 0.0001. To see this figure in color, go online.

Fibrin redistribution

Next, we analyzed the effect of fibrin redistribution by looking at scenarios where clot volume and fibrin density were kept constant and the percentage of fibrin in the periphery was varied (90RCT versus 50RCT and 90RUL versus 50RUL). Comparing the contracted clots with 90% or 50% fibrin in the periphery (90RCT versus 50RCT) showed a slower degradation rate in the periphery with more fibrin (0.0020 versus 0.0026 ff/s, p < 0.05; Fig. 5 A) and a faster degradation rate in the core of the clot with more fibers in the periphery (0.0043 versus 0.0025 ff/s, p < 0.0001; Fig. 5 B). We found similar results in the uncontracted clots. Comparing the uncontracted clots with 90% or 50% fibrin in the periphery (90RUL versus 50RUL), we observed more than a twofold slower degradation rate in the periphery of the clot with more peripheral fibrin (90RUL) (0.0056 versus 0.012 ff/s, p < 0.0001; Fig. 5 A) and a more than 1.5-fold faster degradation rate in the core of the clot with more peripheral fibrin (90RUL) (0.016 versus 0.0081 ff/s, p < 0.0001; Fig. 5 B). While fibrin redistribution plays a limited role in altering the lysis of the overall clot, it does seem to influence the lysis rate of the periphery versus the core subregions.

Fibrin densification

To study the effect of fibrin densification, we compared contracted clot simulations with 90% of the fibrin in the periphery, one clot with a densely packed periphery and the other with a loosely packed periphery (90RCT versus 90RCL, respectively). The periphery of a contracted clot with a densely packed periphery (90RCT) degraded fourfold slower than its loosely packed counterpart (90RCL) (0.002 versus 0.0079 ff/s, p < 0.0001; Fig. 5 A). Furthermore, the otherwise identical densely packed core—due to volume shrinkage—in both scenarios was affected by the densification of the periphery. Degradation in the core of the clot with the tighter periphery was significantly slower (0.0043 versus 0.0052 ff/s, p < 0.01; Fig. 5 B).

Interconnecting roles of contraction and densification

Next, we assessed differences within simulations to determine which portions of the clot (periphery versus core) limit the rate of fibrinolysis. In contracted clots with a loosely packed periphery (90RCL), degradation rate in the periphery was faster than in the core, resulting in an intermediate rate of lysis for the entire clot (0.0079 versus 0.0052 versus 0.0069 ff/s, p < 0.0001; Fig. 5 C). This highlights the important role of fibrin densification: the periphery of the clot (which is loosely packed) degraded much faster than the core of the clot (which is tightly packed). Recall that, in the contracted clot with the tight periphery (90RCT), which has both a tightly packed core and periphery, the degradation rate of the periphery was slower than the degradation rate of the core. This indicates that tight packing of fibrin has the biggest effect when located on the periphery. The opposite was true for the contracted clot with loose periphery (90RCL), suggesting that contraction status of a clot affects which subregion degrades fastest. Finally, recall that, in the uncontracted clot with loose periphery (90RUL), the core degraded faster than the periphery. This analysis highlights the interconnecting roles of contraction and densification. All three scenarios (90RCT, 90RUL, and 90RCL) have the same distribution—90% of the fibrin is found in the periphery—but different combinations of contraction and densification.

A faster degradation rate in the periphery than the core, resulting in a midpoint rate of lysis, was not seen for any other clot scenarios. In the remaining scenarios (50RCT and 50RUL), the entire clot lysed slower than both the periphery and the core. At first, this seems counterintuitive that the lysis rate of the entire clot could be slower than its constituents; however, observations of the 50% and 90% degradation times show that the entire clot lysis is delayed by slow effective diffusion through the periphery and into the core (Figs. S2–S4). In other words, lysis cannot be initiated in the core until at least one t-PA molecule has traveled through the peripheral region, causing the overall process to take longer and thus resulting in a slower degradation of the entire clot. Importantly, in the contracted scenario (50RCT), there was an insignificant difference between the degradation rate in the periphery and in the core due to densification (0.0026 versus 0.0025 ff/s, ns). The tight network in the periphery and the volume shrinkage due to contraction in the core result in an overall dense clot. The overall dense clot exhibits a slower rate of degradation. Unsurprisingly, the same was not true for the scenario where partial redistribution occurred in the absence of densification and contraction (50RUL); the onset of degradation in the uncontracted core was dependent on the complete degradation of the loose periphery. There was a statistically significant difference in the time to 90% degradation time in the periphery and core for both 50RCT and 50RUL (50RCT, 117 versus 291 s, p < 0.0001; 50RUL, 121 versus 211, p < 0.0001). The lysis of the entire clot was delayed and slowed down by the lagging degradation of the core.

The distinction between what was seen in scenarios 90RCT and 90RUL and scenarios 50RCT and 50RUL is representative of the role of redistribution. When there was an unequal distribution of fibrin in the subregions (90RCT and 90RUL), the degradation in the core, with few fibers, has less of an influence on the entire clot’s degradation rate. However, when there was an equal distribution of fibrin (50RCT and 50RUL), the entire clot degradation reflects both regions.

Notably, in the baseline contracted clot (90RCT), the degradation of the entire clot was reduced due to a significantly slower degradation rate in the periphery (Fig. 5 C). 90RCT had the overall slowest degradation rate in the periphery, confirming that a densely packed periphery with a high number of fibers hinders lysis. The rates of the subregions were statistically insignificantly different (90RCT core versus periphery: 0.0020 versus 0.0022 ff/s, ns). Keeping the percentage of fibrin in the periphery fixed at 90% but now considering an uncontracted clot with loosely packed fibrin (90RUL), the degradation rate of the core was more than twofold faster than the rates of the periphery and the entire clot.

Experimental verification of the role of fibrin density in the rate of fibrinolysis

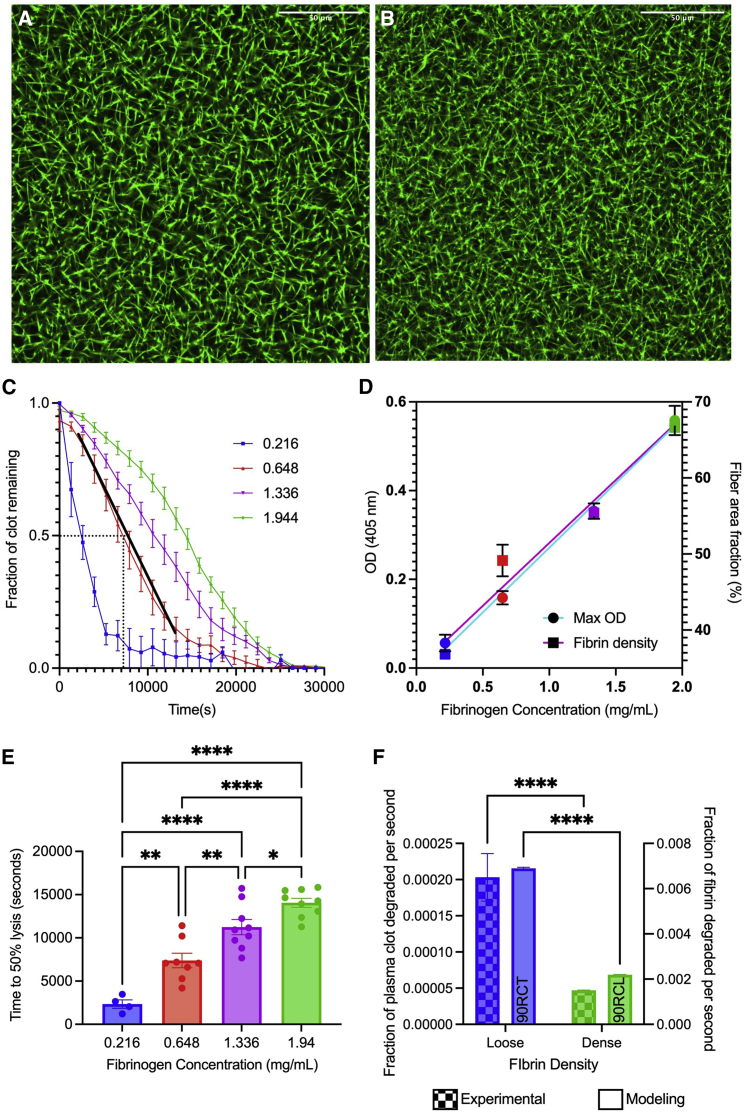
To validate the modeling results, with an emphasis on our discovery of fibrin densification in the periphery playing the key role in limiting external fibrinolysis, we turned to experiments. Since the model predicted the importance of fibrin densification in the periphery on limiting external fibrinolysis of contracted clots, we utilized platelet-poor plasma samples with varying fibrinogen concentrations to mimic the redistributed and densified periphery in the model. As we were probing the role of the dense fibrin periphery, these experiments only represent the clot periphery’s fibrin network, thus they do not include the RBCs that are found in the core region. The network density of fibrin was altered by changing the fibrinogen concentration up to ninefold. To assess the relationship between fibrinogen concentration and fibrin network density, we used confocal microscopy to determine the area density and turbidity measurements to quantify the maximum OD (Fig. 6 A–C, Fig. S10). We observed a positive linear correlation between initial fibrinogen concentration and both percentage area fraction (R² = 0.955, Fig. 6 C) and maximum OD (R² = 0.900), confirming that fibrin density increases with increasing fibrinogen concentration. The highest concentration of fibrinogen (1.94 mg/mL) leads to a 1.8-fold denser fibrin network than the lowest concentration (0.22 mg/mL) (Fig. 6 C, p < 0.0001).

Figure 6.

Model verification using experiments to study the role of densification. Confocal microscopy images showing loose (A) and tight (B) fibrin networks. Maximum OD and fiber area fraction were used to verify densification with varying fibrinogen concentrations. (C) Normalized lysis curves of the different fibrinogen concentrations after the delivery of t-PA and initiation of lysis, with black dotted lines showing time at 50% lysis (in seconds), and a representative linear fit for degradation rate analysis (in terms of fraction of clot remaining per second) (D). Time at 50% lysis (E) and degradation rate (F) are used to assess clot lysis. A side-by-side comparison of experiments (0.22 versus 1.94 mg/mL) and modeling (90RCL versus 90RCT) of loose and dense clot degradation rates (F). Data represented as mean ± SEM. ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001, ^∗∗∗∗p < 0.0001. For all figures, blue, red, purple, and green represent 0.22, 0.65, 1.34, and 1.94 mg/mL, respectively. To see this figure in color, go online.

Clot lysis curves (Fig. 6 D) started with a normalized fully formed clot at t = 0 s, corresponding to t = 7200 s after initiation of clotting. The maximum OD was used to normalize the clot lysis curves as the fraction of clot degraded over time. Therefore, an OD of 1 represents a fully formed clot and an OD of 0 represents a fully lysed clot. These lysis curves were used to calculate time to 50% lysis and clot degradation rate. The 50% lysis time became longer as the fibrin density increased, showing a delay in lysis (Fig. 6 E). For example, the lowest fibrin density reached 50% lysis sixfold faster than the highest density (2300 versus 14,000 s, respectively, p < 0.001; Figs. 6 E and S11). Degradation rate was measured as the slope of the linear region, from the maximum OD to the start of the plateau (R² < 0.9 for all slopes; Fig. 6 B). A side-by-side comparison of the degradation rates for experimental and model loose and tight fibrin networks reveals a consistently faster degradation rate in the loose fibrin networks (0.00020 versus 0.000047 ff/s for the experimental loosest and most dense clots, respectively, p < 0.0001; Figs. 6 F and S11).

Discussion

We developed a 3D mathematical model of external fibrinolysis that accounts for the structural changes of contracting blood clots. During the contraction process, platelets pull on the fibrin network, resulting in its densification (41). Collectively, any individual changes in clot structure have the potential to influence the rate of fibrinolysis. Our implementation of a multiscale model enabled us to systematically and independently vary volumetric shrinkage, fibrin distribution, and fibrin densification in a way that cannot be done experimentally. Results of our modeling work demonstrated that densification of fibrin in the peripheral region is the primary mechanism behind impaired external fibrinolysis of contracted clots (90RCT/90RCL; Fig. 4 A–E). Through our model, we identified that volumetric shrinkage and distribution of the fibrin network alone have limited impact on fibrinolysis (90RCL/90RUL for volumetric shrinkage and 90RCT/50RCT & 90RUL/50RUL for distribution; Fig. 4 A–E). It has previously been observed that the thickness and length of the fibers influence degradation rate: tight networks composed of thin fibers typically degrade slowly while looser networks of thicker fibers support t-PA permeability and degrade more quickly (18,20,34,35). Our model solidified this conclusion with the observation that digestion of higher densities of fibrin fibers (90RCT) was significantly delayed and these clots degraded significantly slower than those with lower densities (90RCL).

We confirmed experimentally that, as fibrin density increases, the time it takes to reach 50% lysis increases and the overall degradation rate of the fibrin network slows (Fig. 6 C–E). Higher fibrinogen concentrations resulted in a denser fibrin network (Fig. 6 C), which could be equated to 90RCT (the baseline contracted and dense clot).

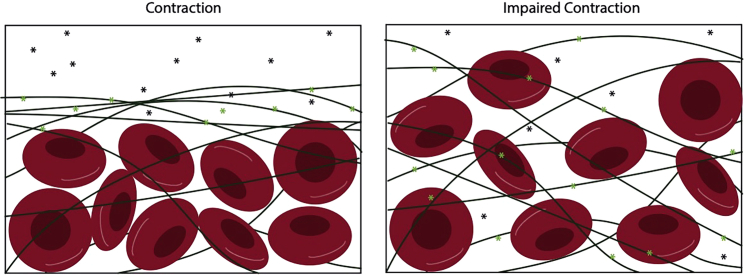
We propose that the dense peripheral fibrin network acts as an attractive substrate for t-PA binding, and therefore as a temporary barrier for t-PA diffusion farther into the clot. Consider two clots that contain the same number of RBCs and fibrin in the core and the same total amount of fibrin in the entire clot, but one clot has a dense peripheral fibrin network while the other has a loose peripheral fibrin network (Fig. 7). When t-PA is introduced to the fibrin-free region abutting the peripheral region of the clot, it quickly diffuses until its movement is hindered by fibrin. t-PA binds strongly to fibrin; when a t-PA molecule is bound, it is “stuck” in that location until it unbinds, after which it can continue diffusing. Because a dense peripheral network has more fibrin per unit clot volume than a loose peripheral network, t-PA is more likely to encounter fibrin as it diffuses, and hence is more likely to bind. In this case, the effective diffusion of t-PA through the clot is slowed, because the random movement due to diffusion is interrupted by periods of stillness, when t-PA is bound to fibrin. Furthermore, even though a t-PA molecule that has bound to a dense fibrin network will have the same kinetic unbinding rate as a t-PA molecule bound to a loose fibrin network (in other words, the t-PA molecule will unbind, on average, in the same amount of time in each scenario), the molecule that unbinds from the dense network is more likely to quickly encounter more fibrin to which it can bind, again slowing its progression farther into the clot. Hence, we propose that slower effective diffusion of t-PA is the mechanism by which fibrin densification reduces degradation rate and increases the times to 50% and 90% lysis. Support for this mechanism is provided by previous work that showed that fine fibrin clots composed of thin, tightly packed fibers degrade slower than coarse fibrin clots composed of thick, loosely packed fibers (same total amount of fibrin in each clot), despite the fact that individual thin fibers degrade faster than individual thick fibers (18). If the t-PA was evenly distributed between both clots, the fine clot would degrade faster since its constituent pieces degrade faster; instead, in the present study in which all fibers are the same thickness, the t-PA is “trapped” in the dense periphery, unable to move farther into the clot. It should be noted that although individual thin fibers are digested faster (18), here we have more fibers in the entire network that need to be digested (Table S1). Furthermore, experimental results reveal a reduced permeability in contracted clots (31), and we propose that external fibrinolysis is limited due to the reduced permeability and limited interaction of fibrin and t-PA in contracted clots (20). Physiologically, blood clots and thrombi are exposed to blood flow, which will result in the perfusion of fibrinolytic enzymes into the clot volume in addition to diffusion. In the future, we can modify the model to include blood flow so that we may investigate the contributions of both diffusion and perfusion.

Figure 7.

Proposed mechanism for limited diffusion of t-PA molecules in tight fibrin networks. More bound t-PA molecules (green stars) get stuck in the tight clot periphery because of high affinity for fibrin (left, contracted clot) and are unable to diffuse through the core.

For a Figure360 author presentation of Figure 7, see https://doi.org/10.1016/j.bpj.2022.07.023.

Clots with impaired contraction have large enough pores that unbound t-PA molecules (black stars) are less likely to encounter a fiber while diffusing, and hence are less likely to have their diffusion interrupted by a binding event; this results in the t-PA displaying faster effective diffusion than in dense clots. In the above scenarios, the core of the clot is left constant with uniform, circular RBCs and identical fibrin network. To see this figure in color, go online.

Thrombosis, which results in the blockage of blood flow to downstream organs, is a leading cause of death worldwide (42,43). A therapeutic approach to enzymatically dissolve the thrombus and restore blood flow is the administration of a thrombolytic agent (t-PA). However, this treatment is limited due to the short time window for treatment (16). Intravenous delivery of t-PA must be given within ∼4.5 h to be effective; it is challenging to know the exact onset of strokes, and stroke victims do not always make it to the hospital within this period, limiting the ability to administer treatment (16). Clot contraction may play a role in the limited time window for therapeutic t-PA administration, due to the structural changes of the thrombus that occur during the contraction process (20). Determining the mechanism through which clot contraction influences the rate and efficacy of fibrinolysis has the potential to influence patient care and inform the development of novel therapeutics. Contraction, volume shrinkage of the clot, results in a compressed clot structure, redistribution of fibrin to the periphery of the clot, and decreased pore size, all of which may limit the effective diffusion of t-PA (Fig. 2 A–C) (10,20,22,23,31). Our model can be used to explore the efficacy of thrombolytic treatments with an array of clot structures and environmental conditions, also considering the differences between in vitro and in vivo clots.

Clot contraction occurs not only in vitro, but also in vivo, and thus it is highly likely to influence the efficacy of responsiveness to thrombolytic agents (20,44). Patients with thrombotic conditions have elevated fibrinogen concentrations, denser fibrin networks, and subsequent resistance to lysis (35,45, 46, 47). More specifically, in vitro contracted clots, and ex vivo murine and patient thrombi, have been shown to have distinct regions of fibrin and RBCs, specifically leading to the packing of RBCs into the core (8,31,48, 49, 50). While here we focus on two distinct layers as described in contracted blood clots (20), in the future, a model clot could be utilized to independently vary the location and density of fibrin within distinct layers to assess how increasing complexity of thrombi further modulates the rate of fibrinolysis.

The novel model of fibrinolysis presented here is an important advance from existing 3D models (18,51, 52, 53) for several reasons. First, with the addition of RBCs to our biochemically detailed macroscale model, our new model contains more features of a pathophysiological blood clot than previous models that contain only fibrin and lytic proteins (18,52,53), or only RBCs (51). A notable difference in our model is the presence of RBCs in the core interacting with the fibrin network, a fibrin-only region in the periphery, and a fibrin-free region where t-PA molecules are introduced and can freely diffuse. Our model includes RBCs, distributed in the core region in a grid-like fashion (Fig. 1 A). As platelets compress the fibrin network, RBCs deform and contribute to a reduction in t-PA permeability (31). Previous studies using NMR have shown that contracted clots are impermeable (31). Contrary to this, our present study suggests that RBCs (in the quantity and distribution we used) do not significantly impair t-PA diffusion; this could be attributed to the gap of at least one pore size between all our RBCs. However, if we allowed RBCs to abut one another in a deformed or polyhedral configuration (36), and if we restricted the free volume in the thrombi to be just 2% of the total volume (1), it is likely we would see an impairment in t-PA diffusion. Also, experimental studies have suggested that the presence of RBCs suppresses t-PA activation of plasminogen (54, 55, 56), which could be included in a future model. The model that includes RBCs recapitulates the experimental results observed previously where clot contraction results in a reduction in the rate of fibrinolysis and delayed lysis times (Fig. 3 E–G), validating our model of fibrinolysis in blood clots.

Second, our model considers the structural complexity of distinct regions of a clot—core and periphery—and allows for the predetermined fibrin density in each region to be set independently. Hence, we can investigate a wider range of clots, encompassing pathological clot structures. The current model reasonably approximates venous thrombosis where the thrombus is primarily composed of polyhedrocytes (deformed RBCs as a result of contraction) and fibrin, with minimal free space compared with arterial thrombi, which have more platelets and fibrin along with polyhedrocytes (1). Going forward, the model can be modified to incorporate these structural differences between venous and arterial thrombi. Moreover, venous thrombi form during stagnation (57), suggesting that the effective diffusion (rather than perfusion) of t-PA may be relevant to the success of lysis in these thrombi. In the future, we can include the effects of blood flow and the resulting perfusion of t-PA molecules, making the model more relevant for other thrombi.

Additionally, varying specific structural parameter values such as pore size, fiber diameter, clot volume, and total amount of fibrin is more straightforward with a model than what can be done experimentally. Many simulations can be run with different parameter values, and those with the most interesting results can be identified as candidates for laboratory experimentation, some of which have been discussed here. Taken together, these model innovations provide an important new framework for studying the effect of macroscale structure on external lysis, and combining this approach with experimental techniques allows for a deeper understanding of the mechanisms of fibrinolysis. Our results highlight the benefit and importance of combining modeling and experimental approaches. The simulations can be used to suggest underlying mechanisms in interesting experimental data previously without a clear mechanistic cause. Future studies could investigate volumetric shrinkage, fibrin redistribution, and fibrin densification in conjunction to understand their confounding and independent influences.

The work presented here focused on external fibrinolysis, but internal fibrinolysis (where t-PA is present throughout the clot, rather than added after formation, a model for physiological fibrinolysis), is also important. Previous experiments (20) showed that internal and external fibrinolysis differ in response to contraction and t-PA delivery. In particular, contracted clots undergoing internal fibrinolysis had accelerated degradation compared with uncontracted clots. While this difference has been described experimentally, the mechanism underlying this difference remains unknown. The model developed here can be expanded to consider internal lysis to understand the differing roles of contraction, fibrin redistribution, and fibrin densification in both processes.

The discovery that densification plays a critical role in external fibrinolysis can lead to the development of novel therapeutics to target the hindered diffusion of t-PA molecules into the clot, caused by binding to fibrin. For example, we propose that the development of a t-PA variant with a lower, optimal affinity for fibrin will prevent the molecules from getting stuck in the periphery and better diffuse into the core, while still allowing t-PA to bind often enough to initiate lysis. A variant with a binding affinity that is too low would easily diffuse through the clot, but also would not bind to fibrin, and hence would not start the necessary lytic cascade. On the other hand, a variant with a binding affinity that is too high would bind so strongly to fibrin that its effective diffusion through the clot would be severely hindered, greatly slowing down clot lysis. Nonetheless, it is important to consider clinical scenarios. First, when t-PA delivery is intravenous and thus dependent on blood flow to reach the thrombi, there is a need for a high affinity for fibrin to make sure the molecules can stick or “latch” onto the fibrin. With systemic delivery of thrombolytics, there is the risk of excess bleeding if the t-PA molecules have a low affinity. However, with local administration, such as through a direct catheter, the efficacy is dependent on the thrombolytic’s ability to diffuse through the complex structure of the clot. Based on the results of our model and the newfound mechanistic understanding of clot contraction, we propose the existence of an optimal t-PA variant binding affinity that allows for more efficient diffusion through the clot while also initiating lysis. This would allow for lower concentrations of fibrinolytic agents and could provide a critical advancement in effectively treating people with prothrombotic conditions.

Author contributions

B.B. and V.T. developed model simulations. B.B. and A.A. performed modeling. V.T. and R.R. designed experiments. R.R. performed experiments. R.R., V.T., B.B., and J.W. analyzed data. All authors contributed to the preparation of the manuscript.

Editor: Jing Chen.