Nucleation causes an actin network to fragment into multiple high-density domains

Abstract

Actin networks rely on nucleation mechanisms to generate new filaments because spontaneous nucleation is kinetically disfavored. Branching nucleation of actin filaments by actin-related protein (Arp2/3), in particular, is critical for actin self-organization. In this study, we use the simulation platform for active matter MEDYAN to generate 2000 s long stochastic trajectories of actin networks, under varying Arp2/3 concentrations, in reaction volumes of biologically meaningful size (>20 μm³). We find that the dynamics of Arp2/3 increase the abundance of short filaments and increases network treadmilling rate. By analyzing the density fields of F-actin, we find that at low Arp2/3 concentrations, F-actin is organized into a single connected and contractile domain, while at elevated Arp2/3 levels (10 nM and above), such high-density actin domains fragment into smaller domains spanning a wide range of volumes. These fragmented domains are extremely dynamic, continuously merging and splitting, owing to the high treadmilling rate of the underlying actin network. Treating the domain dynamics as a drift-diffusion process, we find that the fragmented state is stochastically favored, and the network state slowly drifts toward the fragmented state with considerable diffusion (variability) in the number of domains. We suggest that tuning the Arp2/3 concentration enables cells to transition from a globally coherent cytoskeleton, whose response involves the entire cytoplasmic network, to a fragmented cytoskeleton, where domains can respond independently to locally varying signals.

Significance

Dendritic actin networks are essential to generate protrusive forces in cells. However, the micron-level spatial organization that results from nanometer-level Arp2/3 dynamics is still poorly understood. To address this, we use a computational model, MEDYAN, to study the spatial organization of actin at various Arp2/3 concentrations and discover that elevated Arp2/3 levels favor formation of short filaments (<1 μm). Consequently, while at low Arp2/3 concentrations, actin filaments come together processively to form a globally contractile network, at high Arp2/3 concentrations, multiple, spatially separated actin networks form, leading to network fragmentation. We propose that such disconnected network states could enable cells to sustain spatially heterogeneous chemical fluxes and force transmission, facilitating spatially tuned responses to a wide range of signaling cues.

Introduction

Biological systems rely on specific patterns of self-organization to produce cell shapes and distributions of cellular constituents that perform physiological functions effectively. The structural properties of cells are controlled by the cytoskeleton, which is a network of filamentous proteins such as actin, microtubules, and intermediate filaments. Actin, the most abundant cytoskeletal protein, enables critical biological processes through assembly and disassembly of filaments, motor proteins (myosin) that walk along filaments to exert forces, and passive crosslinkers that tune the connectivity of the network (1,2). These molecules self-assemble under the guidance of precisely controlled signaling pathways to form micron-scale structures that give structural stability and dynamic adaptability to cells. As the collective behavior of the multi-component actin network in vivo is exceptionally complex, in vitro studies using minimal sets of reconstituted components have been essential to reveal the detailed biophysical mechanisms that underly actin organization. A great challenge, however, is to understand how these simple components come together to produce the diversity of large-scale structures observed in cells.

The cytoskeleton is extremely versatile in that its components can form a wide array of structures that are optimized for specific needs. For example, in eukaryotic cells that lack a cell wall, actin forms a pseudo-planar network of filaments right under the plasma membrane to form the actin cortex. Together with myosins and other actin-binding proteins, the cortex offers mechanical stability to the cell. The actin organization and dynamics in this architecture have been studied extensively (3, 4, 5). Another, very different, actin-dependent structure is found in the axonal growth cones of neurons. The growth cone is the highly branched, filamentous structure at the tip of a growing axon that produces protrusive forces to promote extension of the axon and steer its growth through the extracellular medium to reach specific neuronal targets. Extensive experimental studies have identified many cytoskeletal components involved in growth cone motility. However, it has been challenging to link the nano-scale chemical processes these molecules control with the micron-scale network organization they produce in the growing axon.

Genetic and cell biological experiments suggest that the branched actin nucleating factor, actin-related protein 2/3 (Arp2/3), and myosin are particularly important for growth cone function. As spontaneous nucleation of actin filaments is kinetically disfavored, cells rely on nucleating factors such as Arp2/3, formin, spire, and liemodulin to generate new filaments (6). Thus, cells dynamically assemble actin networks by tightly controlled spatial localization and activation of such nucleation factors. Among the various nucleating factors, branched actin nucleation has been implicated in maintaining a coherent growth cone and is highly regulated as a downstream effector in key signaling pathways (7,8). Branched nucleation proceeds by nucleating new offspring filaments on the side of preexisting parent filaments at an angle of approximately 70° (9,10), primarily by the Arp2/3 complex, which accelerates nucleation by mimicking the presence of two actin monomers (11). Branching and debranching activities have profound effects on cell shape and dynamics (12,13) and indeed are commonly found to be central targets of the external signals that regulate cytoskeletal events (8,14, 15, 16). This mechano-sensitive process is necessary to generate forces against the plasma membrane to drive motility (17). Moreover, as the elongation capacity of an actin network is limited by the number of filaments, mechanisms such as actin nucleation and severing lead, respectively, to a surge in extensible filaments and, in the abundance of the polymerizable actin pool, resulting in a dynamic actin network with augmented turnover. Hence, it is essential to understand the effects of Arp2/3 in determining actin network architecture, which, in turn, gives rise to its salient mechanical properties.

In conjunction with actin architecture, forming stable and dynamic cytoskeletal structures also requires a delicate balance between motor-driven forces and viscoelastic dissipation (18, 19, 20, 21). Thus, large-scale remodeling of networks through contractile forces and actin turnover is crucial for effective force production that leads to locomotion and growth. Studies of actin networks, and their interaction with crosslinkers and myosins, have uncovered fundamental organizational principles of linear and planar actin structures (2,4,22, 23, 24, 25). However, just as the crosstalk between contractility and actin turnover has proven to be essential for dissecting cortical tension (26), to understand the mechanics of the growth cone cytoskeleton, it is essential to study a minimal growth cone mimic with actin, crosslinkers, myosins, and constitutively active Arp2/3 to dissect the crosstalk between actin turnover and myosin contractility.

While computational studies on actin networks have helped identify kinetic (27) and mechanical (28) differences between linear and dendritic actin networks, computational limitations have prevented understanding network organization in the large-scale dendritic networks that form in vivo. Therefore, inspired by the actin organization observed from in vivo imaging of a growth cone in the developing Drosophila wing (called TSM1 (29,30)), we set out to computationally prepare actin filaments, crosslinked by α-actinin and myosin, and subject them to varying concentrations of the branching nucleator Arp2/3 in a cylindrical volume whose dimensions approximate that of an in vivo TSM1 growth cone. We reasoned that investigation of the properties of such a network at larger, multi-micron-length scales might reveal emergent properties that are not readily apparent from order parameters estimated at sub-micron length scales (such as nematic order parameter, contact number, coordination number, and radial distribution function). Hence, we chose to employ spatial density field analysis (pixel intensity analog) to understand spatial and temporal patterns in the micron-level network organization of disordered actin networks.

Here, we demonstrate that Arp2/3-driven nucleation drastically alters network organization in a concentration-dependent manner between a connected, globally contractile state versus a more fragmented association of distinguishable domains that are only relatively weakly linked to one another. We show that the global actin network is characterized by actin-rich local domains of heterogeneous volume that dynamically exchange filamentous actin with one another and with the actin-depleted surrounding. We further find that conditions with reduced Arp2/3 tend toward a smaller number of larger domains, while higher levels of Arp2/3 fragment the network into larger numbers of smaller domains. We further establish that the mechanism by which nucleation activity controls the size and number of high-density domains is mediated through modulating the distribution of actin filament lengths, which acts cooperatively with myosin contractility to regulate the organization of the overall actomyosin network at the multi-micron scale. Thus, at low Arp2/3 concentrations, where long actin filaments are abundant, myosin-driven forces favor globally contractile networks. In contrast, the predominance of short filaments at high Arp2/3 concentrations limits long-range, myosin-dependent interactions, favoring condensation of actin into a multiplicity of small, locally contractile domains. Treating the time evolution of the number of actin domains as a stochastic process with state-dependent drift and diffusion, we show that the fragmented state evolves stochastically due to the delicate balance between domain-split and domain-merge events. Finally, we discuss the biological significance of toggling actin network organization between globally connected versus relatively fragmented states.

Materials and methods

All simulations performed in this work were carried out using MEDYAN (31), a mechano-chemical force field, to simulate active networks. MEDYAN encodes an explicit filament model that is coupled with a diffusive phase of reactive molecules. The transport dynamics of the diffusive phase and its chemical interactions with the filament phase are evolved using an efficient version of the Gillespie algorithm called the next reaction method (32). MEDYAN’s stochastic reaction-diffusion framework also accounts for the force-sensitive changes to the reaction rates. This comprehensive modeling strategy has been instrumental in understanding thermodynamic principles of self-organization of actin networks (18) and mechanistic details that aid formation and contractility in specific actin structures, including bundles (33,34), rings (35), and isotropic networks (31,36).

Inspired by axonal growth cones (29,30) and microvilli (37) observed in vivo, we chose to simulate actin networks in a cylindrical reaction volume of 2-μm diameter and 7.5-μm height to avoid artificial edge-dependent biases found in cuboidal systems and to allow for emergent effects of larger absolute physical scale (31). Simulations contained 20-μM diffusing G-actin and were initialized with 400 randomly located and randomly oriented F-actin seed filaments, each 40-monomers long (108 nm). These seed filaments represent ∼5.3% of the total actin initially present in the volume and allow the simulations to bypass an otherwise lengthy lag period for initial actin nucleation. We note, however, that the actin monomers contained in these seeds are turned over by treadmilling within the first 300 s of the simulations. In MEDYAN, filaments are represented as rigid cylinders that are joined at hinge points. The latter helps us define bending deformations, tuned to reproduce F-actin’s persistence length (38). While longitudinal stretching and compression are also modeled, they are small in amplitude because of very high stiffness of actin polymers (31,39). Each cylindrical element is 40 (actin) monomers long, exposing four binding sites for binding linkers, motors, or brancher molecules.

Stochastic chemical evolution in MEDYAN is achieved through the next reaction method (32). Diffusion and reaction events are modeled at single-molecule resolution. Structural description of filaments along with necessary mechanical forcefields describe stress build-up during chemical evolution (31). The network is mechanically equilibrated every 25 ms of chemical evolution using a gradient descent algorithm, accounting for mechano-chemical effects and feedbacks. In MEDYAN, unbinding of α-actinin and myosin minifilaments are mechano-sensitive, modeled as slip and catch bonds, respectively. Unbinding rates are calculated at the end of every minimization cycle based on corresponding instantaneous forces. Chemical evolution and mechanical equilibration steps are iterated to generate 2000-s-long trajectories. Please refer to the supporting methods for a detailed description of key features of MEDYAN, along with the chemical reactions considered in this study.

In order to create conditions for the formation of a contractile network, we introduced non-muscle myosin IIA minifilaments (mole ratio of myosin heads to actin = 0.1) and α-actinin (mole ratio of α-actinin to actin = 0.01). Linear networks described above were evolved for 1 s before activating Arp2/3 molecules. In cells, Arp2/3 activation is restricted to membranes, which are rich in Arp2/3 activators such as WASP, WAVE, and N-WASP. In axons and growth cones, experimental images have revealed a dense concentration of internal membranes, including membrane-bound organelles such as endoplasmic reticulum and cytoplasmic transport vesicles, among others, which presumably can serve this function (29,40). We, therefore assume that constitutively active Arp2/3 is readily available throughout the growth cone cytoplasm since explicit consideration of Arp2/3 association with such complex membrane surfaces would be computationally expensive and would require extensive assumptions about the internal organization of the growth cone cytoplasm. Thus, we model bulk nucleation of actin filaments mediated by Arp2/3 binding.

In our model, Arp2/3 binding produces an offspring along the side of the mother filament at a 70° angle, forming a nascent dendrite (9,41). The offspring filament’s minus end is protected from (de)polymerization events in the Arp2/3-bound state. Conversely, Arp2/3 unbinding results in a free offspring filament, a diffusing Arp2/3 molecule, and a free binding site on the parent filament. We model Arp2/3 unbinding as a force-sensitive slip bond with a characteristic unbinding force of 6pN([42]). All simulation parameters and the number of replicates generated in this study are elaborated on in Table S1.

Note that the simulations analyzed in detail here are a sub-set of the simulations used to model actin architecture in a developing axon in vivo in a parallel publication from our group (43). The results of the two papers, while consistent, are entirely independent; no analysis is repeated in both manuscripts.

Results

Increased Arp2/3 activity reduces the dispersity of filament lengths and increases network treadmilling rate

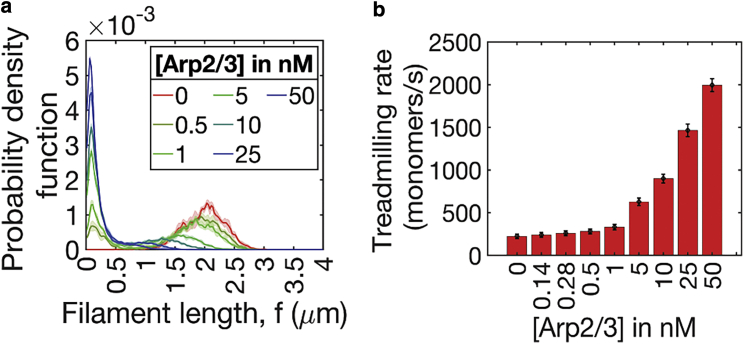
To understand the impact Arp2/3 branching has at the filament level, we simulated actin networks at Arp2/3 concentrations 0, 1, 5, 10, 25, and 50 nM (six replicates per concentration). To ensure that our simulations have reached steady state, we looked at structural and chemical properties of the network (filament length distribution [Fig. 1 a], network treadmilling rate [Fig. 1 b, explained below], and radius of gyration [Fig. S2]). The low variability of these parameters both between trajectories and in the last 500 s of our trajectories confirmed that the actin network has attained a steady state. As expected, in linear networks ([Arp2/3] = 0 nM), the seed filaments extended into long filaments by consuming the diffusing pool of G-actin. With the addition of Arp2/3, filament distribution bifurcates into a population of short filaments nucleated by Arp2/3 and a population of extended seed filaments (Figs. 1 and S1; supporting material). A further increase in Arp2/3 concentration results in networks dominated by dendritic nucleation and characterized by extremely short filaments (<0.5 μm). Thus, increasing Arp2/3 activity increases the filament nucleation rate, resulting in a steady state characterized by short filaments.

Figure 1.

Dendritic activity in networks causes a reduction in filament length and increases monomer replacement by treadmilling. (a and b) The plot of (a) filament length and (b) network treadmilling rate of networks at various Arp2/3 concentrations. (a) Solid lines and shaded areas represent the mean and standard deviation, respectively, of filament lengths from six replicates. (b) Mean treadmilling rate of the network is plotted as a bar graph, with error bars representing standard deviation. Networks' approach to steady state was quantified based on time invariance of mean treadmilling rate. As the treadmilling rate stabilized around 1500 s, data from the last 500 s of trajectories (six replicates, sampling frequency = 5 s) was employed in (a) and (b). To see this figure in color, go online.

We wondered whether actin treadmilling could account for the effect of Arp2/3 on filament length. We therefore investigated how the treadmilling rate of the network depends on the Arp2/3 concentration. Treadmilling is a steady-state behavior where filaments have stable average lengths as the retraction rate of minus ends matches the extension rate of plus ends. Hence, we define treadmilling rate as the average of the number of monomers that have depolymerized from the minus end and the number of monomers that have polymerized onto the plus end in 1 s (27). We find that the treadmilling rate (Fig. 1 b) at steady state increases with Arp2/3 concentration due to the increase in the number of filament ends from Arp2/3-based nucleation. (27) Additionally, Arp2/3 unbinding exposes the minus end to fluctuations from filament polymerization and depolymerization reactions. We therefore speculate that the combination of finite-bound lifetimes for the Arp2/3-parent-offspring filament complex (τ = 50 s) (42) and mechano-sensitive offspring unbinding that are incorporated in our model (based on experimental observations (44)) contribute further to the enhanced treadmilling rate. Varying Arp2/3-unbinding rates at [Arp2/3] = 25 nM, we find that slower unbinding leads to increased abundance of longer filaments, reduced number of filaments, and diminished treadmilling rates (supporting material; Fig. S3). Taken together, the results shown in Fig. 1 suggest that under the influence of Arp2/3, branching activity produces a population of short filaments and that the networks experience enhanced treadmilling rate.

Arp2/3 alters the hierarchical organization of actin networks

Having seen how Arp2/3 affects the properties of actin filaments, we then investigated the influence of Arp2/3 on the network-level organization of actin. To achieve this, we mapped the high-resolution actin filament coordinates onto a coarse-grained density field. Dividing the reaction volume into voxels of size (x, y, z = 100, 100, 100 nm), we counted the number of F-actin monomers enclosed in each voxel to define local actin density through mean filtering. The mean-filtering technique is helpful to prevent large voxel-to-voxel variation in local densities that might arise from mapping fine filament structure to coarse density field (45,46).

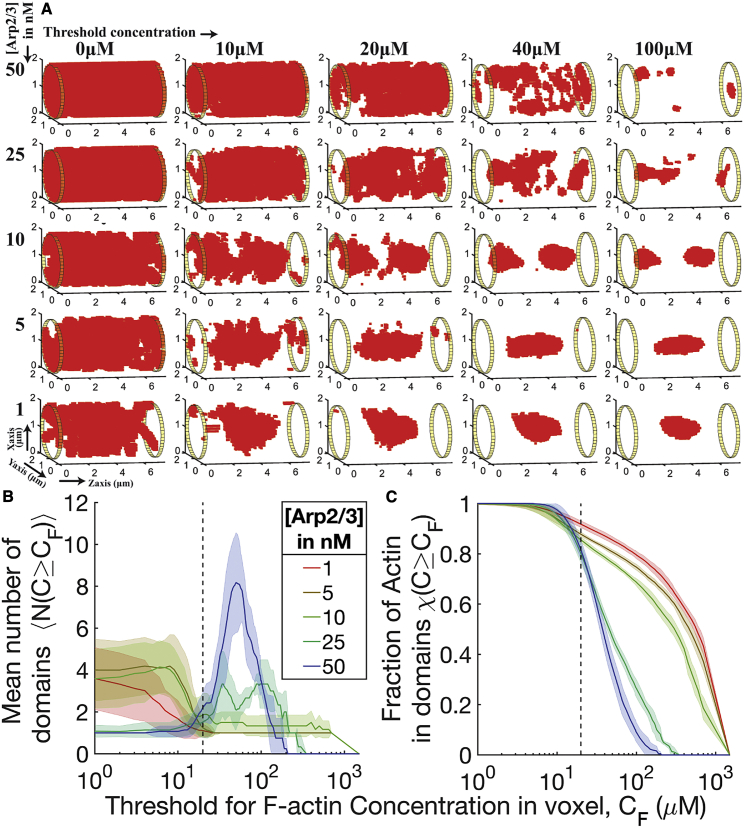
To understand how actin is organized in the reaction volume, we visualize the density field at various voxel concentration thresholds (Fig. 2 a). This visualization is similar to observing fluorescently labeled experimental actin networks at varying intensity thresholds. When all voxels with F-actin are considered (threshold of 0 μM), we see minor differences from changing the Arp2/3 concentration; there is actin present throughout the reaction volume. Density fields at higher thresholds, however, reveal drastic differences in actin organization. When the threshold is set to the bulk actin concentration of our simulations (20 μM) (Fig. 2 a), we see that actin is not distributed uniformly throughout the volume but rather is concentrated in spatially distinguishable clusters of voxels, here termed domains, whose size and number vary over the Arp2/3 concentrations studied.

Figure 2.

Visualization of actin density field reveals Arp2/3-driven changes to actin organization. (a) We visualize representative final snapshots from our simulations at various Arp2/3 concentrations as a density field. Cylindrical reaction volume is discretized into voxels of size (100, 100, 100) nm to define local F-actin density. The ends of cylindrical volume are shown as 50-nm-thick yellow cylinders. Please refer to the materials and methods for more information on the actin density field computation. Red squares represent the center of mass of voxels that contain actin above the threshold concentrations (listed above). (b) Plot of the number of domains identified when viewing the actin density field at various threshold concentrations from last 100 s of snapshots (sampling frequency = 5 s) of six replicates. Solid line represents mean, and shaded area represents standard deviation. The X axis is shown on a logarithmic scale, and the bulk actin concentration is shown as a dotted line. Note that the apparent fine structure of fluctuations observed in 25- and 50-nM profiles between 40- and 200-μM thresholds correspond to small (1–2 unit) fluctuations in the number of domains identified. (c) The fraction of total actin monomers included in identified domains was found by integrating over the density field and is plotted versus threshold actin concentrations. The dotted line represents bulk actin concentration (20 μM). Solid lines represent mean, and shaded area represents standard deviation. The fraction of total actin included in the domains reduces with increasing [Arp2/3]. To see this figure in color, go online.

Examining actin organization at the 40-μM threshold, we see stark differences depending on branching activity. At low Arp2/3 concentrations, F-actin contracts globally into a single domain. Increasing Arp2/3 concentration to 10 nM results in a network that is composed of two high-density actin domains. At higher Arp2/3 concentrations ([Arp2/3] = 25 nM and [Arp2/3] = 50 nM), the number of domains increases, suggesting that the actin distribution is spatially heterogeneous. Increasing thresholds to 5× bulk actin concentration (100 μM) does not reveal significant changes in trends observed compared with the 40-μM threshold.

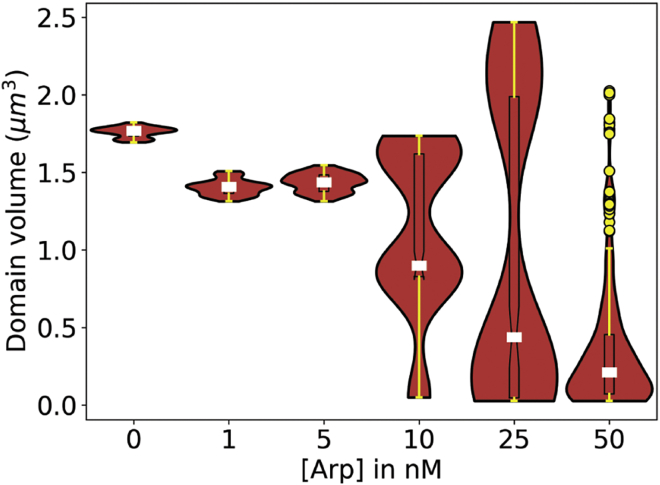
To characterize further the trends in network organization observed above, we quantified the number of distinguishable domains as we varied the threshold actin concentration. Using a breadth-first search algorithm, we identified domains formed of voxels where actin concentration is greater than a threshold and with a minimum volume (27 voxels, corresponding to ∼0.03 μm³) and termed them high-density actin domains. The choice of minimum volume threshold does not affect the qualitative trends observed (Fig. S4.) Figs. 2 b and c elucidate the nature of actin organization over a wide range of threshold concentrations. We see that the trends in the number of domains from changing Arp2/3 levels do not change when the actin density field is visualized at 2–10× bulk actin concentration (40–200 μM). We also find that under all Arp2/3 concentrations studied, most of the actin (>80%) is found in regions where the local voxel density is 20 μM and above (Fig. 2 c). Thus, actin’s overall hierarchical organization is dictated by a combination of filament length and, as we will show below, myosin activity. To quantify further the trends in network organization observed above, we investigated the actin density fields at a threshold concentration of 40 μM, twice the bulk actin concentration in the network. This threshold was selected to provide maximum sensitivity for identifying the number of domains at various [Arp2/3] while ensuring that the domains contain the majority of total actin in the network. Please refer to the supporting results (Fig. S9) for a discussion on the role of threshold concentration. The distribution of domain volume from the last 100 s (sampling frequency = 5 s) of trajectories under a threshold concentration of 40 μM revealed remarkable differences in domain organization (Fig. 3). As Arp2/3 concentration is increased, two trends are observed. First, median domain size decreases. Second, heterogeneity of domain size initially increases, peaking at intermediate concentrations of Arp2/3, before beginning to reduce again at the highest concentrations. We postulate that heterogeneity arises from the stochastic fluctuation of a balanced set of competing factors that drive domain expansion and contraction, respectively, but which resolve in favor of domain condensation versus fragmentation at the two extremes of Arp2/3 level. The results discussed above suggest that Arp2/3 alters the organization of the F-actin network, effectively causing fragmentation into domains with heterogeneous size distributions. This conjecture will be examined in more detail below and in the discussion.

Figure 3.

Distribution of high-density actin domain volume reveals differences in actin organization resulting from Arp2/3 activity. Volume distributions of high-density actin domains identified at 40-μM threshold at various Arp2/3 concentrations from the last 100 s of the trajectories (six replicates, sampling frequency = 5 s) are represented as violin plots. The boxplot shows the 25^th–75^th percentile represented as a box with the median shown as white lines. Whiskers are shown as solid yellow lines, with outlier data points represented as yellow circles. Data shown are collected from last 100 s of all six replicates per [Arp2/3]. To see this figure in color, go online.

Increased Arp2/3 activity results in multiple, fragmented high-density domains in actin network

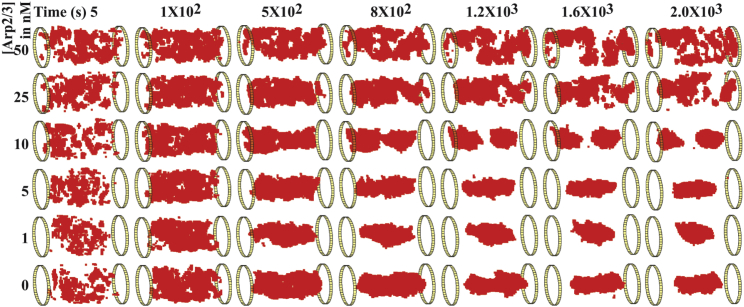
To understand the mechanism by which networks at higher Arp2/3 concentrations fragment into multiple domains, we investigated the time profile of the actin density field at a concentration threshold of 40 μM. Fig. 4 shows representative time-dependent snapshots at various Arp2/3 concentrations. We see that, initially, networks at all Arp2/3 concentrations are composed of spatially fragmented domains. As the simulation proceeds, we find that spatial segregation of the network into actin-rich and actin-depleted regions occurs in an Arp2/3-concentration-dependent manner. In networks with <10 nM Arp2/3 concentrations, the domains merge with time, resulting in a single, connected domain. At Arp2/3 concentrations of 10 nM and above, actin networks initially contract and merge through agglomeration of preexisting domains. However, at later stages in the simulation, these high-density actin domains separate from one another, resulting in a network where high-actin-concentration regions are again spatially fragmented. Together, these results demonstrate that the mechanism of actin organization changes depending on Arp2/3 concentration.

Figure 4.

Time profiles of actin density field reveal altered network organization leading to actin fragmentation at elevated Arp2/3 concentrations. At various time points in our simulations with different Arp2/3 concentrations, representative snapshots are converted into actin density fields to reveal actin organization. The actin density field is visualized at a 40-μM threshold concentration in each case. The voxels that have a local actin concentration higher than the threshold concentration are shown in red. Timestamp in seconds is shown to the top, while Arp2/3 concentrations are mentioned on the left. Data shown here are from the final snapshot of a single replicate corresponding to each [Arp2/3]. To see this figure in color, go online.

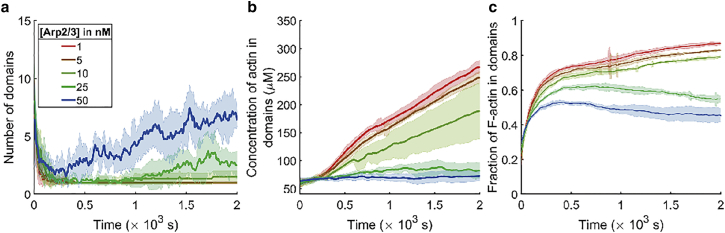
To gain more insights into the Arp2/3-driven fragmentation of high-density domains, we calculated the number of distinguishable domains found in the density field at snapshots taken every 5 s (Fig. 5 a) using a breadth-first search algorithm over the voxels that satisfy the concentration threshold. Looking at the fraction of total F-actin that is contained in high-density domains (Fig. 5 c), we first see a sharp increase until 500 s. This is consistent with the idea that myosin activity throughout the volume first stochastically condenses the actin into local clumps whose actin concentration is above that of the bulk background (as seen in Fig. 4, columns 1–3), and these, in turn, coalesce into larger units. After this initial collection of actin into domains of enhanced density, the rate of F-actin accumulation slows down or even reverses slightly, dependent on the Arp2/3 level. At low Arp2/3 concentrations (≤5 nM), the initial aggregation of actin is accompanied by a steady decrease in the number of domains until the entire network is composed of a single, connected domain that remains connected for the rest of the simulation. In this condition, the absolute actin concentration within the domains continues to show a steady increase with time (Fig. 5 b). In contrast, at higher Arp2/3 concentrations, networks evolve with a biphasic domain count profile where, during the initial phase (until 200 s), we again see a reduction in the number of high-density actin domains, but it is followed by a maturation phase where the number of domains increases. In this condition, however, increasing Arp2/3 concentration progressively limits the final actin concentration in domains (Fig. 5 b).

Figure 5.

Analysis of high-density actin domains reveals Arp2/3 dependent differences in network organization. (a) Number of actin domains found from actin density field analyses is plotted as a time profile at various Arp2/3 concentrations. (b) Time profiles of actin concentration in the domains are plotted at various Arp2/3 concentrations. (a and b) Solid lines and shaded areas represent mean and standard deviation, respectively. (c) Time profiles of the fraction of total actin in the domains at various Arp2/3 concentrations. The solid line and shaded area represent mean and standard deviation, respectively. (a–c) Data shown are calculated from six replicates per Arp2/3 concentration, and data sampling frequency = 5 s. To see this figure in color, go online.

Cooperation between myosin and Arp2/3 dynamics modulates actin organization

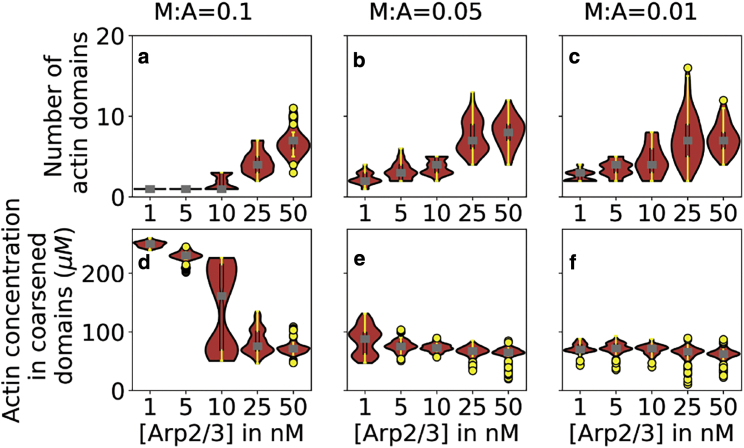
The pattern of Arp-dependent changes to actin concentration in high-density actin domains led us to wonder if there was crosstalk between nucleation-driven treadmilling and myosin-driven contractility. To understand the role of myosin in the mechanism of Arp2/3-driven fragmentation, we studied actin networks by reducing myosin concentrations to 50% and 10% of the myosin concentration employed in simulations discussed so far and generated five replicates per [Arp2/3] myosin mole ratio pair. The number of domains from the last 100 s of the 2000-s trajectories is plotted in Fig. 6 a–c, and the time profiles are shown in Fig. S5. At all myosin concentrations studied, increasing Arp2/3 results in a fragmented network characterized by an elevated number of high-density actin domains. We also looked at actin concentration in the high-density actin domains to understand myosin’s impact in organizing filamentous actin (Fig. 6 d–f). Consistent with Fig. 5 b, increasing Arp2/3 reduces F-actin concentration in domains. Additionally, we find that at any given Arp2/3 concentration, reducing myosin decreases actin concentration in domains consistent with the reduced contractility of the networks. The actin concentration in these domains (Fig. 6 d–f) reduces with increasing Arp2/3, particularly at high concentrations of myosin, but has a diminished effect as myosin level decreases, suggesting that Arp2/3 reduces actin density primarily by hindering myosin-driven contractility. We also find that the heterogeneity of these measurements within a condition tends to be maximal in parameter ranges where opposing, stochastic processes are roughly balanced, much as we found for the domain volume measurement in Fig. 3 (above).

Figure 6.

Cooperation between myosin and actin leads to network fragmentation. (a–c) Violin plots showing the number of domains in the actin density field obtained at a threshold concentration of 40 μM at different Arp2/3 concentrations (X axis). Myosin mole ratios are mentioned above each panel. (d–f) Violin plots showing actin concentration in high-density actin domains. Note that the domains are determined based on the mean concentration threshold, while the concentration plotted here is calculated based on actin concentration determined from filament data. Hence, the actin concentration in domains can be below the mean concentration threshold. (a–f) Plots also show median values (gray) and 25% and 75% quantiles as boxplots (black). Whiskers represent data ranges (yellow lines), and outlier data are plotted as yellow circles (mole ratio of myosin heads to actin = 0.1, Nsimulations = 6, mole ratio of myosin heads to actin = 0.05 and 0.01, Nsimulations = 5, data points = last 100 s, sampling frequency = 5 s). To see this figure in color, go online.

We then asked if reducing myosin levels increases fragmentation of the actin network. Decreasing myosin to 50% and 10% causes significantly increased fragmentation of actin networks up to [Arp2/3] = 10 nM (Fig. 6 a–c; Wilcoxon test; all p values are listed in Table S2). At higher Arp2/3 concentrations, we find that reducing myosin to 50% does significantly increase fragmentation, but a further reduction to 10% does not affect the network fragmentation from that observed at 50% reduction (p range = 0.86–1.00). It is interesting to note, however, that under all conditions studied, reducing myosin did increase fragmentation in the initial phase (<500 s) of the trajectories (Fig. S5). This is suggestive of timescale differences in the dominant mechanism that drives actin organization in dendritic networks, perhaps accounting for the biphasic temporal evolution of domain number under conditions of high Arp2/3 (Fig. 5 a).

The activity of Arp2/3 alters dynamics of high-density actin domains toward fragmented states

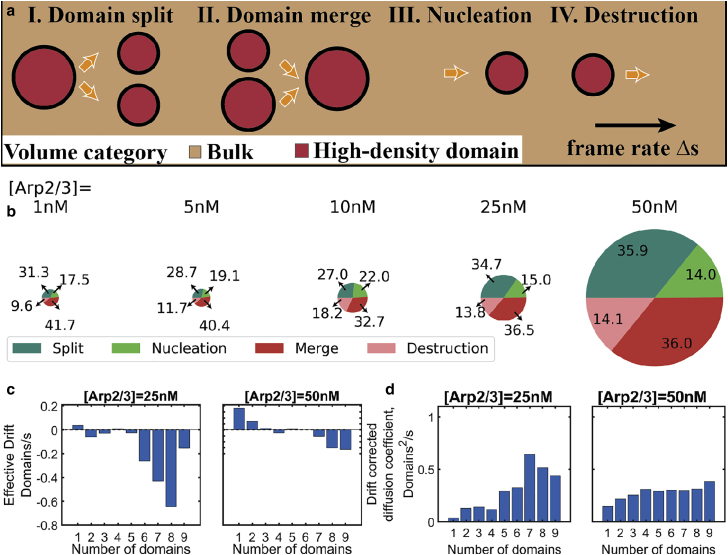
The results above show how overall network properties evolve over time, with Arp2/3 causing global spreading and myosin producing local condensation. But how does this combination give rise to the final fragmented states that we observe? To understand the mechanism by which high-density actin domains evolve, we studied the trajectories of the density field. We classified each domain’s birth as either coming from a domain-splitting or domain-nucleation event and the loss of a domain as resulting from either domain-domain merge or domain-destruction event (Fig. 7 a). While domain nucleation happens when actin in a region within the reaction volume condenses above the chosen threshold, destruction happens as actin in a high-density domain relaxes from events such as myosin/crosslinker unbinding, thereby lowering actin concentration to below our chosen threshold. Fig. 7 b shows that increasing Arp2/3 concentration increases the frequency of occurrence for all four elementary events that alter domain number. It is interesting to note that the mechanisms that lead to an increase in domain number are roughly as prevalent as mechanisms that cause a decrease in domain number. Also, we see that among the two processes that lead to increase in domain number, namely domain splitting and domain nucleation, the former is more probable. Similarly, the reduction in number of domains between two consecutive snapshots is more often due to domain-domain merges than domain-destruction events. The probability of split and merge events as a function of minimum distance between domains (Fig. S7) shows that at [Arp2/3] = 25 and 50 nM, the domain-split and -merge events primarily happen between domains that are ≤200 nm from one another and that the probability quickly falls at larger distances. This suggests that domains reassort only when their boundaries are spatially close and that long-range interaction of domains via background, unincorporated actin is minimal.

Figure 7.

Analysis of domain dynamics reveals the underlying mechanism of F-actin organization into high-density actin domains. (a) The cartoon rendering describes elementary transition mechanisms showing F-actin domains in red, with brown regions representing low-density actin background. (aI–aIV) Four different transition mechanisms in a reference snapshot that affect the number of clusters in the following snapshot. (b) Pie charts showing the percentage of transitions observed throughout the trajectory at different Arp2/3 concentrations. The size of the pie chart is proportional to the total number of transitory events. (Fig. S6 shows data from entire trajectory in addition to specific time ranges as bar graph along with the standard deviation) (c and d) Estimation of (c) drift and (d) drift-corrected diffusion coefficients (bottom row) at various cluster sizes from trajectories of high Arp2/3 concentrations, 25 (left column) and 50 nM (right column) show how the instantaneous change (drift) and spread in number of domains (diffusion coefficient) depends on the number of domains present in the snapshot. (b–d) Entire trajectories of all replicates corresponding to each of the Arp2/3 concentrations are employed to compute these results. To see this figure in color, go online.

To understand the differences in domain dynamics between networks from low and high Arp2/3 concentrations, we plotted distributions of domain-number-altering events accumulated over 500-s intervals (Fig. S6). We see that at low Arp2/3 concentrations, the high-density actin domains are highly dynamic in the first 500 s of trajectories. Although all four domain-birth and -death mechanisms occur, domain-domain-merge events happen at a higher frequency. As a result, within the first 500 s of trajectories, networks with [Arp2/3] < 10 nM experience a steady decrease in the number of domains, resulting in a single, connected domain. The space-spanning domain is significantly less dynamic, suggesting that domain merges are irreversible in networks with low Arp2/3 concentration. This observation is consistent with experiments where actin condensates merge irreversibly with time, causing a steady increase in actin mass within condensates (4,47).

On the other hand, networks with high Arp2/3 concentrations are more dynamic than their low Arp2/3 counterparts. As the domain-birth and -death events roughly balance each other throughout the trajectories, we postulate that elevated Arp2/3 levels stochastically favor a fragmented network state with multiple, high-density actin domains. To investigate this, we employed a stochastic modeling framework assuming that the change in the number of domains in a given time interval depends on a combination of effective drift and random fluctuations (48). Further, we consider that the effective drift and diffusion terms depend on the number of domains at a given time point, N(t). Drift measures the mean number of domains in the system at time t+1, when N(t) = n. Positive (negative) drift indicates that the number of domains increases (decreases) at time t+1 when compared with N(t). Additionally, the drift-corrected diffusion coefficient measures the squared fluctuation of the of the deviation of N(t+1)-n from the drift A(n,t). Thus, a drift-corrected diffusion coefficient of zero suggests that the number of high-density domains are constant, while a large diffusion coefficient indicates high variability in N(t+1). Please refer to the supporting material for a discussion on the stochastic model and parameter estimation. Analyzing timeseries of the number of domains from trajectories, we see that the drift is lowest for states with an intermediate level of fragmentation, with minimum drift when the snapshot has three, four, and five fragmented domains for networks at 25 nM [Arp2/3] and three to six domains for 50 nM [Arp2/3] (Fig. 7 c). Also, for networks with more than six domains, the drift parameter is negative, indicating that the system favors domain-death events, while at values lower than the minima, drift is positive, suggesting that the system favors the birth events. Thus, the fragmented state is the result of a balance of domain dynamics. We also see that the drift-corrected diffusion coefficient term is significant at all domain number values studied (Fig. 7 d), highlighting the role that random noise plays in the process and leading to enhanced variability.

Relative roles of geometric branching versus kinetic nucleation in the effect of Arp2/3

The fragmentation of networks in our simulations can be explained as a combination of two distinct phenomena: myosin-driven contractility and Arp2/3-driven nucleation. We find that increasing dendritic activity in a network results in short filaments (<1 μm) (Fig. 1 a). In a parallel analysis (presented elsewhere; (43)), we find that short filaments such as these organize into a non-percolated network through which myosin-driven contractile forces cannot propagate effectively. Such non-percolated networks contract locally due to myosin-driven contractility, resulting in a fragmented network with multiple high-density actin domains, as observed above.

Arp2/3-driven nucleation of an offspring filament can be viewed as the combination effect of a minus-end-bound nucleator (similar to leiomodin (6)) and an angle-sensitive filament-filament crosslinker. To understand the relative importance of these two mechanisms, we simulated actin networks with varying concentrations of synthetic minus-end nucleators with the same kinetics as Arp2/3 but lacking the capacity to bind a mother filament and generate a branched structure. These nucleators nucleate filaments and stay attached to the minus end until unbinding. The resulting networks have distributions of filament lengths, treadmilling rate, and total number of filaments consistent with those reported above for a branching nucleator (Fig. S8 a–c). Analyzing the density fields at 40-μM threshold, we also find that high nucleator concentrations reproduced the network fragmentation seen with a branching nucleator (Fig. S4 d), suggesting that the nucleation activity alone, independent of a branching geometry, is sufficient to generate network fragmentation. Nevertheless, we see interesting quantitative differences in the organization of high-density actin domains between the two nucleators studied in a [nucleator]-dependant manner. While the number of domains initially (<200 s) decreases with time for all nucleator concentrations, and it remains low at [nucleator] ≤10 nM (both Arp2/3 and synthetic minus-end nucleator) (Fig. S8 d), we see that differences in Arp2/3 concentration consistently exhibit more extreme effects on large-scale actin distribution than do differences in the concentration of the non-branching nucleator. Thus, we observe higher actin concentrations inside domains at low [Arp2/3], but lower concentrations at high [Arp2/3], than with the equivalent levels of the synthetic nucleator (Fig. S8 e). Similarly, we see a higher fraction of F-actin contained in the domains at low Arp2/3 than low nucleator (≤10 nM), but a lower fraction at high (25 nM) Arp2/3 (Fig. S8 f) (though at the highest level of nucleator, 50 nM, the variance becomes too large for comparison). Additionally, at higher nucleator concentrations (25 and 50 nM), Arp2/3 trajectories fragment into a higher number of domains than the synthetic minus-end nucleators. These results suggest that the branching nature of Arp2/3 enhances the sensitivity of large-scale actin organization to changes in the protein’s level and activity. It may be that as Arp2/3 nucleation reinforces actin closer to regions with preexisting filaments, we see enhanced local actin concentration, leading to higher F-actin concentration in domains at low [Arp2/3] and a higher number of domains at higher [Arp2/3].

Discussion

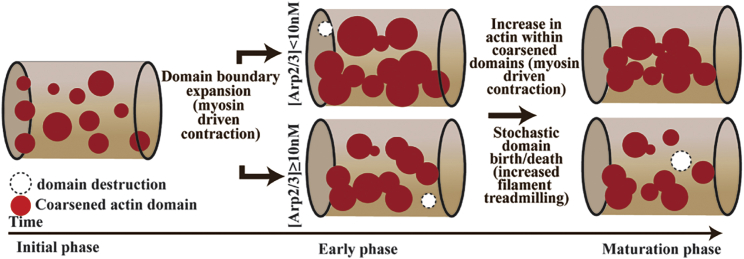
We studied the influence of Arp2/3 in tuning the micron-scale spatial organization of actin using MEDYAN, a mechano-chemical forcefield that simulates the stochastic time evolution of cytoskeletal networks. Analyzing filament-level data and density fields resulting from 2000-s-long simulations of actin networks at various Arp2/3 concentrations, we found that network organization depends on the interaction between Arp2/3-dependent actin fragmentation and myosin-dependent contractility (Fig. 8). At a given myosin concentration, the nucleation activity and finite-bound lifetime of Arp2/3 lead to an overall reduction in filament length and diversity when we increase Arp2/3. Thus, at low or intermediate Arp 2/3 concentrations (e.g., 1–10 nM), actin networks are composed of mixed populations of long (≥1 μm) and short filaments (<1 μm). In contrast, at high Arp2/3 (e.g., 50 nM), the network consists almost exclusively of short, sub-micron filaments. These changes at the filament level, when coupled with the effects of myosin activity, at elevated Arp2/3, lead to a network organization where actin is organized into separated spatial domains due to the reduced connectivity of a network composed of short filaments. In contrast, the long actin filaments presented at lower Arp2/3 concentrations allow the actin to form a single, connected, globally contractile network. In essence, actin networks become kinetically trapped in a spatially fragmented state in networks with high Arp2/3 activity due to the difference in the spatial range over which contractility can operate.

Figure 8.

Cartoon of the proposed mechanism to explain Arp2/3-dependent network organization at micron-length scale. Cylindrical reaction volumes are shown with red blobs representing high-density actin domains. The dominant mechanism for transitions along a trajectory is mentioned, along with the filament level interaction mentioned within parenthesis. Domain destruction events are mentioned as empty circles with dotted lines. To see this figure in color, go online.

The similar but interacting effects of Arp2/3-dependent fragmentation and myosin-dependent contractility are perhaps demonstrated most clearly by their temporally segregated effects on the time evolution of the network. On short timescales (≤500 s), our analyses show that actin organization is determined primarily by myosin-driven contractility (Fig. 5). During this phase, myosin activity brings filaments closer to one another, leading to delocalized contractility of the entire actin network at all Arp2/3 concentrations studied in this work. The impact of Arp2/3 then becomes apparent at longer timescales, where the progressive reduction of average filament length causes the network to fragment into separately contractile domains. Therefore, networks with low Arp2/3 activity, having a sizable population of long filaments, continue contracting globally, generating a single domain with an actin concentration about an order of magnitude above bulk (>100 μM). At high Arp2/3 concentrations, in contrast, networks stochastically lose global connectivity and instead exhibit enhanced localized contractility that favors a fragmented state composed of multiple, separated domains.

In this work, we find that both reductions in myosin and increase in Arp2/3 favor fragmented network organization, but the nature of their effects depends on the absolute level of both. Specifically, myosin plays a substantial role in determining fragmentation of actin networks at low Arp2/3 conditions, while at elevated Arp2/3, myosin has less of an impact. Thus, reducing myosin by 50% relative to our starting baseline significantly increases network fragmentation at all Arp2/3 concentrations analyzed. In contrast, further decrease of myosin to 10% of its baseline at the starting level only increases fragmentation of low [Arp2/3] networks (≤10 nM) and has no further effect on high [Arp2/3] networks. In essence, the data suggest that the effectiveness of myosin becomes saturated as the Arp2/3 level is increased and the mean actin filament length decreases. Stated otherwise, while contractile forces of myosin are crucial to organize actin filaments into high-density domains, the efficacy of that condensation is limited by the shortening of actin filaments caused by Arp2/3. We also note that increasing Arp2/3 at any given myosin concentration gives a broader variance of actin organization patterns (range: 1–15 domains; median values), while altering myosin at any Arp2/3 has a milder impact on the number of high-density actin domains. Transitions to fragmented network states similar to those we describe have been observed experimentally (4,23). They have also been explained computationally for linear actin networks as either a sol-gel transition or coarsening-driven domain growth processes (1,4,19,23,24).

How dynamic are the high-density actin domains we observe in our simulations? To address this question, we have to discriminate between two different levels of actin organization. At the microscopic level, at all Arp2/3 concentrations, we see that individual actin monomers and filament segments are constantly exchanged between contractile domains. At the mesoscopic level (0.5–5 μm), we observe more complex and more interesting dynamics that depend on the activity of Arp2/3 and that are likely to have significant implications for downstream biological processes. At low concentrations of Arp2/3, the entire network quickly collapses into a single, connected, contractile domain whose properties remain relatively static over time despite the continual exchange of molecular components. At somewhat higher concentrations of Arp2/3, however, a fragmented network state emerges from the underlying actin network, and it remains highly dynamic at the multi-micron level of resolution. These domains have a wide range of volumes, they merge and split continually, and they continue to exchange actin with both the neighboring domains and background actin (actin below threshold concentration). The actin network in this condition can be thought of as being in a metastable state, where, at any given Arp2/3 concentration, the network drifts stochastically toward a preferred level of fragmentation.

At the elevated levels of Arp2/3 investigated here, the network shows diffusion across a broad range of domain sizes and numbers, even at steady state. We believe that the properties of these high-density domains, such as their contractility and inter-domain dynamics, are representative of the actin network as a whole as they contain the large majority of total actin in the volume (>80% at 20 μM threshold and >50% at 40 μM threshold, relative to the 20-μM bulk concentration of actin in the simulation) and inform us of the principles of actin organization at a multi-micron spatial scale that is relevant to the processes occurring in cells. In this analysis, we chose to compute the density fields at a 100-nm-length scale due to its concordance with physical properties of actin used in our computational method. We note, however, that it is also not so different from the resolution of typical fluorescent imaging experiments. As a result, it offers us the possibility of validating the biological relevance of our computational observations by comparing our results with experimental observations (29,30). Indeed, in a study we have recently presented elsewhere (43), we have shown that the simulations investigated here, together with additional, related simulations, generate mesoscopic patterns of actin distribution that effectively mimic the actin distributions observed experimentally by quantitative live imaging of single axonal growth cones in vivo in the developing Drosophila wing (30,43).

One possible implication from our analysis is that the limited lifetime of the parent-Arp2/3-offspring filament complex may significantly affect the hierarchical organization of actin from sub-micron- to micron-length scales. Diffusing Arp2/3 complexes modeled in our simulations are treated as active and readily bind to the sides of parent filaments to generate offspring filaments. Upon unbinding, Arp2/3 molecules are released and can bind to a new filament and continue to nucleate offspring filaments.(49) Thus, the finite-bound lifetime of Arp2/3 (42) presumably contributes to an enhanced nucleation rate, particularly at higher Arp2/3 concentrations, and promotes overall reduction in filament lengths. However, Arp2/3 molecules modeled with infinite-bound lifetimes have been shown to accumulate significant stresses in the network that are released instantaneously, causing large deformations in a mechanism similar to avalanches (28,50). As the branches in our study unbind at with a 50-s residence time (42), we do not observe such large deformations in the force-sensitive unbranching model used in the current work. It remains to be seen if our networks exhibit non-Gaussian stress-relaxation patterns in a phenomenon similar to cytoquakes found in other studies (18,51, 52, 53, 54), and if not, does that contribute to the domain dynamics that we observe.

Perhaps surprisingly, by performing simulations in which we model the nucleating activity of Arp2/3 but remove its branching function, we find that the nucleation activity of Arp2/3 alone is sufficient to reproduce the spatial fragmentation patterns observed under Arp2/3 conditions, even in the absence of a dendritic branching geometry. Thus, we believe that our findings here could be relevant to other actin nucleators as well. These findings are critical to understanding the relationship between network architecture and functional consequence in filamentous biological active matter by separating the contributions of network dynamics from those of network geometry (2,55,56).

The ability of actin modifiers to alter actin architecture from the sub-micron to the multi-micron level has critical implications for biological systems. For example, we hypothesize that under such fragmented conditions, actin networks can work cooperatively with transport myosins such as Myosin V (57) and Myosin X (58) to create spatially diverse and disconnected fluxes of critical biological molecules within a single cytoplasm. Moreover, we hypothesize that the emergent property of a fragmented cellular cytoskeleton under high Arp2/3 activity may facilitate local responses to signaling cues within small, kinetically confined domains (59,60). In contrast, the connected networks generated at low Arp2/3 concentrations may favor a unitary response involving the entire cytoplasmic network over multi-micron-length scales (61, 62, 63). Additionally, network remodeling between the globally connected versus fragmented states can be crucial to modulate both the intensity and spatial range of signaling processes and morphological transitions. We suggest that cells may employ changing levels of Arp2/3 activity to tune the network between connected and fragmented states of actin to reorganize the structural and, as a result, functional roles of the cytoskeleton.

Conclusion

Our work demonstrates how large-scale actin network organization can be drastically altered by the presence of the branching nucleator, Arp2/3. Changing the concentration of Arp2/3 alters overall network connectivity by altering the proportion of sub-micron-long filaments. We show that irrespective of Arp2/3 concentration, networks initially (t < 100 s) evolve with localized contraction, leading to multiple domains of condensed actin. As the network evolves, we initially observe contractile domain-merge events, resulting in fewer actin domains. As network evolution progresses, we see that networks with low Arp2/3 activity are trapped in the connected, globally contractile state. In contrast, high Arp2/3 activity promotes domain-level processes that cause the networks to evolve stochastically toward fragmented network states. This study suggests that signaling pathways that affect Arp2/3 levels tune the overall network architecture, switching between a globally coherent state versus a fragmented state with enhanced local responsiveness.

Author contributions

A.C., E.G., and G.A.P. designed research; A.C. performed research; A.C. and G.A.P. contributed analytical tools; A.C. analyzed data; A.C., E.G., and G.A.P wrote the manuscript.

Editor: Timo Betz.

Data availability

The details of MEDYAN model implementation can be accessed online (https://github.com/medyan-dev/medyan-public), and a link to the source code can be found under the releases tab of the repository.

The analysis scripts used for this study and the input files can be found at https://github.com/achansek/readMEDYANtraj and https://github.com/achansek/MEDYANArp23_2021.