Skip to main content
PMC home page
International Journal of Methods in Psychiatric Research logoLink to International Journal of Methods in Psychiatric Research
. 2022 May 18;31(3):e1916. doi: 10.1002/mpr.1916

An empirical evaluation of alternative approaches to adjusting for attrition when analyzing longitudinal survey data on young adults' substance use trajectories

Yajuan Si 1,✉, Brady T West 1, Philip Veliz 2, Megan E Patrick 1, John E Schulenberg 1, Deborah D Kloska 1, Yvonne M Terry‐McElrath 1, Sean E McCabe 3
PMCID: PMC9464329  PMID: 35582963

Abstract

Objectives

Longitudinal survey data allow for the estimation of developmental trajectories of substance use from adolescence to young adulthood, but these estimates may be subject to attrition bias. Moreover, there is a lack of consensus regarding the most effective statistical methodology to adjust for sample selection and attrition bias when estimating these trajectories. Our objective is to develop specific recommendations regarding adjustment approaches for attrition in longitudinal surveys in practice.

Methods

Analyzing data from the national U.S. Monitoring the Future panel study following four cohorts of individuals from modal ages 18 to 29/30, we systematically compare alternative approaches to analyzing longitudinal data with a wide range of substance use outcomes, and examine the sensitivity of inferences regarding substance use prevalence and trajectories as a function of college attendance to the approach used.

Results

Our results show that analyzing all available observations in each wave, while simultaneously accounting for the correlations among repeated observations, sample selection, and attrition, is the most effective approach. The adjustment effects are pronounced in wave‐specific descriptive estimates but generally modest in covariate‐adjusted trajectory modeling.

Conclusions

The adjustments can refine the precision, and, to some extent, the implications of our findings regarding young adult substance use trajectories.

Keywords: attrition, longitudinal trajectory modeling, selection bias, substance use, weighting

1. INTRODUCTION

Substance use becomes more common in adolescence and typically peaks in young adulthood (Jager et al., 2013; McCabe et al., 2016, 2019; Schulenberg & Maggs, 2002; Schulenberg et al., 2005). Longitudinal surveys collect rich data about individual characteristics and enable the estimation of substance use prevalence and trajectory modeling, a key approach to understanding the developmental course and etiology of substance use. Examples include the Monitoring the Future (MTF) panel study (Schulenberg et al., 2021), the Population Assessment of Tobacco and Health Study (Hyland et al., 2017), and the National Longitudinal Study of Adolescent to Adult Health (Harris et al., 2019). However, the quality of prevalence and trajectory estimates can be attenuated by panel attrition. With declining response rates in surveys (Brick & Williams, 2013; de Leeuw et al., 2018), study respondents could be systematically different from attriters in terms of substance use outcomes, causing potential bias in estimates of developmental trajectories (Feldman & Rabe‐Hesketh, 2012). Moreover, sample selection procedures for longitudinal studies are often complex in nature, including design features such as stratification, cluster sampling, and survey weights for probability samples and auxiliary variables that affect selection and response propensities for nonprobability samples. A failure to account for these selection features in estimation could affect the inferential validity and generalizability of descriptive summary measures and estimates of trajectory models.

Weighting approaches have been proposed in the survey statistics literature to simultaneously adjust for these complex sample design features and panel attrition (Heeringa et al., 2017). However, there is no clear consensus in the literature on whether or how to apply weighting adjustments for attrition in longitudinal trajectory modeling. The role of weighting adjustments in regression models has been a long‐debated topic (Bollen et al., 2016). Longitudinal trajectory estimation introduces methodological challenges and may require wave‐specific weighting adjustments. Alternative to weighting, multiple imputation (MI; Rubin, 1987) allows for the inclusion of variables that can be incomplete into the imputation model but is subject to computational burdens. The common practice is to use weighting adjustment for attrition and MI for item nonresponse when individuals only answer partial questions (Si et al., 2022a, 2022b).

Of the prior studies that have examined long‐term trajectories of alcohol, marijuana, and prescription drug misuse during the transition from adolescence to young adulthood, analyses have generally been restricted to respondents providing complete information in all waves and ignored attrition (e.g., McCabe et al., 2018). More recent studies focusing on long‐term substance use trajectories have addressed attrition, typically using inverse propensity score weighting (McCabe et al., 2019; Patrick et al., 2018, 2016; Terry‐McElrath et al., 2017). Using the MTF panel data, Keyes et al. (2020) estimated bias by imputing nonrespondents' outcomes. Nevertheless, appropriate statistical approaches to adjusting for attrition when estimating longitudinal trajectories with a model adjusting for various risk factors have received relatively little focus, especially for subgroups of particular interest to substance use researchers.

Various sociodemographic characteristics are known to be associated with substance use (e.g., Roghani et al., 2021), and there are differences in substance use behaviors among young adults as a function of college attendance (e.g., Schulenberg et al., 2021). In general, binge drinking and non‐medical misuse of prescription stimulants have higher prevalence among college students than non‐college young adults, although levels have converged some in recent years. In contrast, non‐college young adults tend to have higher prevalence of cigarette use, daily cannabis use, non‐medical misuse of prescription sedatives/tranquilizers, and other illicit drugs, including heroin and methamphetamine, than those attending college.

Research has also focused on how key sociodemographic differences like educational attainment alter the developmental course of substance use with longitudinal data (e.g., Linden‐Carmichael et al., 2019), and some of these studies include various remedies to account for differential attrition. However, attrition still remains a strong concern with such panel studies, given that some groups with different substance use patterns (e.g., non‐college attenders) are more likely to drop out of these long‐term studies and may ultimately bias the results when assessing these key sociodemographic differences. This paper contributes to the literature by developing guidelines on the use of different attrition adjustment methods when analyzing longitudinal survey data.

The multi‐cohort MTF panel study of teens and adults offers a unique data source that can be used to evaluate attrition effects on longitudinal trajectory modeling, when accounting for diverse socio‐demographics and examining specific substance use outcomes of interest. Inverse propensity score weighting procedures can address attrition and have been used in many recent MTF substance use trajectory publications (Patrick et al., 2016, 2021; Terry‐McElrath & Patrick, 2016a, 2016b; Terry‐McElrath et al., 2019).

Using seven waves of longitudinal data from the MTF panel study as an example, we seek to (1) perform a systematic comparison of alternative approaches to analyzing longitudinal survey data with a wide range of substance use outcomes, and (2) examine the sensitivity of inferences about differences in estimated substance use prevalence and trajectories to the approaches used, focusing on trajectory differences as a function of college attendance. Our methodological examination focuses on three aspects:

  1. Whether to use the complete cases (CCs) that respond to all waves (including those who do not answer all questions) or the available cases (ACs) that respond in any wave.

  2. Comparing approaches to accounting for the correlation of repeated measures on the same individual.

  3. Whether to apply weighting adjustments for attrition.

We investigate eight different methods based on these aspects, shown in Table 1. Appropriate decisions depend on the underlying missing data mechanism and the trajectory model specification (Little & Rubin, 2019). We evaluate the effects of the different adjustments on estimated prevalence and trajectories, and corresponding substantive inferences.

TABLE 1.

Comparison and names of eight approaches investigated

Method CC AC Selection features Correlation Attrition‐adjusted weight
CC √ √
AC √ √
CC‐gee √ √ √
AC‐gee √ √ √
CC‐ID cluster √ √ √
AC‐ID cluster √ √ √
CC‐attr‐w √ √ √ √
AC‐attr‐w √ √ √ √
Open in a new tab

Abbreviations: AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; AC‐gee, GEE with available cases; AC‐ID cluster, available case analysis accounting for the cluster structure by individuals; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases; CC‐gee, GEE with complete cases; CC‐ID cluster, complete case analysis accounting for the cluster structure by individuals.

2. METHODS

2.1. Data

The MTF study began in 1975 and has been an ongoing epidemiological and etiological research project to study changes in the beliefs, attitudes, and behaviors of U.S. young people regarding substance use and other health risks (Miech et al., 2021; Schulenberg et al., 2021). Each year, about 15,000 12th grade students in approximately 133 public and private high schools nationwide participate in the MTF study. The data from students are collected with a multi‐stage random sampling procedure, designed to secure new nationwide samples of 12th grade students each year. Beginning with the class cohort of 1976, a subsample from each 12th grade class (modal age 18) was followed up after high school on a continuing basis, with oversampling of students who report drug use.

The subsample selected for the panel study is a sample of U.S. individuals with modal age 18 who provided their sex and contact information. There were important features that affected the sample selection (e.g., drug use reporting, sex, and geographical strata of schools). One random half of each cohort began follow‐up assessments 1 year after high school (modal age [hereafter referred to simply as “age”] 19) and the other random half 2 years after high school (age 20), with all being followed every 2 years through age 29/30; in this study, the two random halves were combined (e.g., follow‐up 1 includes ages 19/20). The longitudinal follow‐ups permitted examination of developmental changes within cohorts. We analyzed the MTF panel data to examine trajectories of substance use from late adolescence through young adulthood. We focused on four cohorts whose baseline data were collected from 2002 to 2005 (age 29/30 data collected in 2013–2017) to allow for six possible follow‐up waves for any participant (i.e., first follow‐up at 19/20 sixth follow‐up at 29/30). We chose these specific cohorts because they were the first to include the latest updates to the wording of existing questions about specific substance use (i.e., non‐medical misuse of prescription medications).

2.2. Measures

Our goal was to estimate the trajectories of substance use, adjusting for key risk factors for different subgroups defined by college attendance status. By virtue of the sampling design, at baseline respondents were all in high school. We began the trajectory modeling at the first follow‐up of age 19/20. The outcomes were longitudinal measures of the following substance use behaviors: binge drinking (five or more drinks in a row during the past 2 weeks), cigarette smoking (in the past 30 days), marijuana use (in the past 12 months), non‐medical prescription opioid misuse (in the past 12 months), a composite indicator of any non‐medical prescription drug (NMPD) misuse (of four specific drug classes that included amphetamines, sedatives, tranquilizers, or opioids, in the past 12 months), and a composite indicator of any use of other selected illicit drugs, including lysergide, other hallucinogens, cocaine, or heroin (in the past 12 months). The time‐varying covariates included follow‐up wave indicators, full‐time 4‐year college attendance, and marital status. The time‐invariant covariates were baseline characteristics including cohort (2002–2005), age in months, sex, race/ethnicity, high school grades, parental education, baseline measures of corresponding substance outcomes, and reported intent to attend a 4‐year college. The covariates were selected based on the substance use literature where the conditional interpretations adjusting other variables will be substantively meaningful. The candidate covariates in the attrition adjustment included all selection features and baseline characteristics related to the substance use outcomes. The full lists are available in eTables 1 and 2. Most of these measures are subject to item nonresponse, and our strategies for handling missing values are discussed in the eAppendix. We found that our findings are robust under different imputation methods, including MI, mainly due to the low rates of item nonresponse.

2.3. Substance use trajectory modeling

The developmental course of substance use can be affected or moderated by sociodemographic characteristics. Across six follow‐up wave indicators defined by t ij (= 1, 2, 3, 4, 5, 6), we considered marginal (or population‐averaged) logistic regression models for each of these binary outcome variables Y, where Y ij  = 1 if individual i indicated use of substances at measurement j, and otherwise, Y ij  = 0:

logitPrYij=1=β0+β→1tij+β→2xi+β3collij+β4marryij+β→5tij∗collij. (1)

Here the marginal model includes the primary coefficients of interest that identify possible differences in trajectories based on college status: the coefficients β→5 for the interaction t ij  × coll ij between college attendance (coll ij ) and wave (t ij ). Treating the first follow‐up wave (age 19/20) as the reference level, we introduced five dummy variables for the wave indicators, and the quantities of interest were the odds ratios, expβ→1,expβ→5, which were exponentials of the coefficients as five‐dimensional vectors. The model adjusted for a vector of time‐invariant individual‐level measures x i described above and a time‐varying indicator of being married (marry ij ).

We compared different estimation approaches and evaluated their effects on the trajectory modeling of substance use outcomes. We first fit simple logistic regression models ignoring the correlation of the repeated measures within a sampled student. For both CCs and ACs, we considered unweighted analyses, unweighted analyses accounting for the correlation of the repeated observations on each individual, and weighted analyses accounting for attrition adjustments and individual clustering. Due to computational challenges in achieving estimation convergence using existing software, we do not explicitly consider multilevel modeling as an alternative subject‐specific trajectory modeling approach (e.g., Heeringa et al., 2017) in this study.

2.4. Attrition adjustment

We use the baseline sample as the benchmark and adjust for attrition. For both CC and AC weight construction, we treated the response indicators as binary outcomes and considered two approaches to predicting the probability of response: classification trees based on recursive partitioning (Breiman et al., 1984) and classical logistic regression models. The tree‐based approach selects variables and their higher‐order interactions through splitting rules that sequentially maximize predictive performance for the overall decision tree. The predictive performance of the classification tree depends on balancing the tree size and the true error rate based on a new test dataset, the goal of which is to avoid overfitting the training data used to construct the tree. We applied a conditional tree method that automatically stops splitting based on hypothesis tests and eliminates the pruning step (Hothorn et al., 2006).

The logistic regression model includes only main effects of the same set of covariates, enabling an assessment of whether any additional higher‐order interactions in the tree‐based approach improves our overall ability to predict response propensity. We performed forward selection techniques to select the best predictors in the logistic regression model. The candidate covariates in the attrition adjustment included all selection features and baseline characteristics related to the substance use outcomes, including the cohort indicator, the MTF sample stratification code, the oversampling indicator for 12th grade drug users for the panel, school type, age, sex, race/ethnicity, marital status, family structure, parental education, future plans after high school graduation (military or technical schools, etc.), frequencies of missing class due to different reasons, working status, weekly pay amounts from jobs and other sources, binge drinking in the past 2 weeks, use of various substances in the past 30 days/12 months/lifetime, and a host of variables concerning beliefs, high school activities and performance, and other problematic behaviors at baseline. The attrition adjustment will be effective if the selected covariates are strongly related to the aforementioned substance use outcomes.

For probability samples, the base weights adjust for the sample composition at baseline to match the target student population, and the attrition‐adjusted weights are constructed by multiplying the base weights by the inverses of predicted probabilities of participating at a given wave (or for all follow‐up waves). Here, we treated the MTF panel study as a quasi‐probability sample by assigning base weights as 1 and using the inverse response propensity scores at each wave as the attrition‐adjusted weights. In CC analyses, we created an indicator of whether the individual had participated in all six follow‐up waves, and used the inverse of the predicted response propensities p cc to construct the attrition‐adjusted CC weight: wcc=1/pcc. In AC analyses, we created wave‐specific response indicators of whether the individual has responded in one particular wave and constructed multiple attrition‐adjusted AC weights based on the inverses of predicted AC response propensities p ac as the attrition‐adjusted AC weights: wac=1/pac, to fully utilize all available observations.

These adjustment approaches make different assumptions about the underlying response mechanism. The unweighted analysis assumes that the attrition results in data that are missing completely at random, and the attrition‐adjusted weighting analysis assumes that the attrition results in data that are missing at random conditional on the baseline characteristics. The CC and AC analyses thus differ in terms of whether the response mechanisms and the variables that predict response propensities change across the follow‐up waves.

2.5. Accounting for clustering

To account for the correlation within each individual, we applied two methods: (1) a design‐based approach, treating individuals as clusters in all of the weighted analyses incorporating the attrition adjustments and applying Taylor Series Linearization for variance estimation (Binder, 1983); and (2) generalized estimating equations (GEE) accounting for the clustering structure due to multiple responses per person with an exchangeable working correlation matrix specification. For the purpose of our comparison, we chose the exchangeable working correlation here to approximate the design‐based analysis. We note that inferences related to the fixed coefficients in models fitted using GEE are generally robust against the possible misspecification of this working correlation structure, and model diagnostics and goodness of fit measures should be used to inform model selection in practice (Liang & Zeger, 1986).

We implemented tree‐based methods using the contributed R package party (Hothorn et al., 2021) and fitted GEE models with the R package geepack (Halekoh et al., 2006). We accounted for the clustering via the individual numeric identifiers (MTF ID) and the (possibly adjusted) weights in the logistic regression models for the longitudinal substance use outcomes via the R package survey (Lumley, 2020), which utilizes weighted estimating equations assuming an exchangeable correlation structure within clusters and Taylor Series Linearization for variance estimation. We performed model diagnostics and evaluated prediction performance of the tree models based on the area under the Receiver Operating Characteristic curve (AUC), an aggregate measure of performance across all possible classification thresholds. We implemented MI via chained equations to handle item nonresponse with the R package mice (Van Buuren & Oudshoorn, 1999) with details given in the eAppendix. All analyses were performed in R 4.0.3 (R Core Team, 2020).

3. RESULTS

The MTF study collected baseline data from 9802 sampled individuals in the 2002–2005 12th grade cohorts who were aged 29/30 in 2013–2017. The CC analyses included 2257 individuals who responded in all six waves: 642 from the 2002 cohort, 549 from the 2003 cohort, 547 from the 2004 cohort, and 519 from the 2005 cohort. Considering all 9802 sampled individuals who responded at baseline, the attrition rates across the six follow‐up waves were 43.6%, 48.4%, 52.1%, 55.9%, 59.0%, and 61.8%, respectively, resulting in a total of 27,372 available observations for the AC analyses from 6787 individuals who participated in at least one of the follow‐up waves.

The eAppendix includes a detailed description of the constructed weights and the variables used in the tree methods. The AUC values and the descriptive summaries of the six AC weights and the one CC weight are shown in Table 2. The AUC values ranged between 0.65 and 0.68, indicating moderate prediction power of the tree models, the fit of which is determined by a tradeoff between prediction accuracy and tree sizes. The attrition‐adjusted CC weights had the largest variability, and the distributions of the AC weights were similar, except for Wave 6 (age 29/30), where there was increased variability in the weights.

TABLE 2.

AUC values of the classification tree models for the attrition adjustment and descriptive summaries of different weights

Sample size AUC Weight
Min 25th Pctl Median 75th Pctl Max
Baseline‐18 9802
CC 2257 0.65 1.2 2.6 3.1 5.2 7.8
AC‐19/20 5529 0.66 1.3 1.3 1.8 2.0 2.8
AC‐21/22 5058 0.67 1.3 1.5 2.0 2.3 3.7
AC‐23/24 4700 0.66 1.2 1.5 2.1 2.4 3.5
AC‐25/26 4324 0.67 1.3 1.6 2.2 2.8 3.8
AC‐27/28 4019 0.67 1.4 1.7 2.4 3.0 4.6
AC‐29/30 3742 0.68 1.5 1.8 2.6 3.2 6.3
Open in a new tab

Abbreviations: AC, available case analysis; AUC, Area Under the Curve; CC, complete case analysis; Pctl, percentile.

3.1. Wave‐specific descriptive statistics

We first considered prevalence estimates for each specific wave. The three groups of individuals (9802 sampled individuals, 2257 CC individuals, 6787 AC individuals) had different sociodemographic characteristics, given in Table 3. Compared to all sampled baseline individuals (baseline), the majority of the CC respondents were female (66% in CC, 52% at baseline, and 57% in AC), white (81% in CC, 71% at baseline, and 75% in AC), and less likely to report any drug use (20% in CC, 28% at baseline, and 26% in AC). The AC individuals did not generally present different characteristics from all sampled individuals at baseline. However, the differences became apparent when we examined the respondents in each follow‐up wave. We compared unweighted CCs and ACs, as well as the CCs and ACs with attrition‐adjusted weights, in the descriptive summaries for college attendance status and substance use outcomes from the first (age 19/20) to the sixth (age 29/30) follow‐up.

TABLE 3.

Descriptive summaries of selected baseline sociodemographics

Baseline CC AC AC waves
19/20 21/22 23/24 25/26 27/28 29/30
Sample size 9802 2257 6787 5529 5058 4700 4324 4019 3742
Age in months (SD) 217 (6) 216 (5) 217 (6) 217 (5) 217 (5) 216 (5) 216 (5) 216 (5) 216 (5)
Drug use reporting
Yes 28% 20% 26% 25% 25% 25% 25% 24% 24%
No 72% 80% 74% 75% 75% 75% 75% 76% 76%
Sex
Male 48% 34% 43% 41% 41% 40% 40% 39% 39%
Female 52% 66% 57% 59% 59% 60% 60% 61% 61%
Race/ethnicity
Black 10% 5% 8% 8% 7% 7% 6% 6% 6%
White 71% 81% 75% 75% 77% 77% 78% 79% 79%
Asian 4% 4% 4% 4% 4% 4% 4% 4% 4%
Hispanic 11% 7% 9% 9% 9% 8% 8% 8% 8%
Other 4% 3% 4% 4% 4% 4% 4% 3% 3%
Open in a new tab

Abbreviations: AC, available case analysis; AC waves, six follow‐up waves marked by the modal ages; Baseline, sampled baseline individuals; CC, complete case analysis; SD, standard deviation.

Figure 1 depicts the estimated proportions of individuals attending college across time based on these four methods. The estimated proportions of individuals with full‐time college attendance increased from age 19/20 to age 29/30. However, different approaches resulted in different values of the proportion estimates. The CC analysis yielded the highest estimated proportions of individuals attending college, around 60%–72%, while the AC analysis yielded estimates around 50%–67%. The attrition‐adjusted, weighted analyses reduced both estimates, showing that the attritors were less likely to attend college across young adulthood.

FIGURE 1.

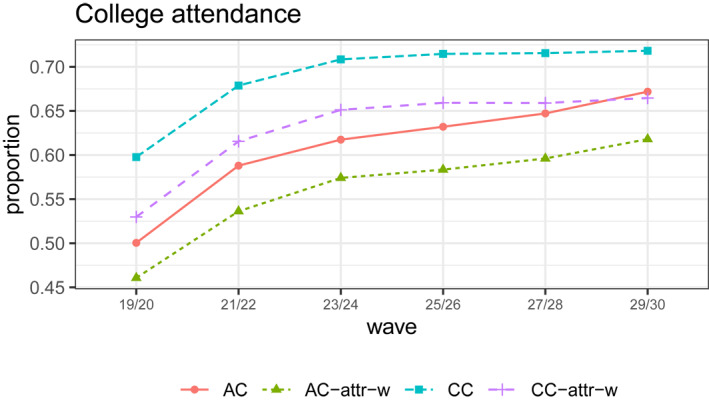
FIGURE 1

Open in a new tab

Estimated proportion of participants with full‐time 4‐year college attendance across six follow‐up waves marked by the modal ages. AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases

The prevalence estimates of substance use across time based on these four methods are presented in Figure 2. Across all analyses the prevalence of binge drinking increased and peaked at age 21/22, and then decreased in a monotone fashion, and the attrition weighting adjustments did not affect the trends. The AC and CC analyses presented similar decreasing trends in the proportions of 30‐day cigarette smokers. The prevalence of annual marijuana use decreased from age 19/20 to age 25/26, remained similar until age 27/28, and decreased again through age 29/30. Weighting increased the prevalence most strongly in CC analyses. The attrition‐adjusted CC weighting reduced the differences between CC and AC estimates of annual non‐medical prescription opioid misuse prevalence, and the reduction effect was apparent between age 23/24 and 29/30.

FIGURE 2.

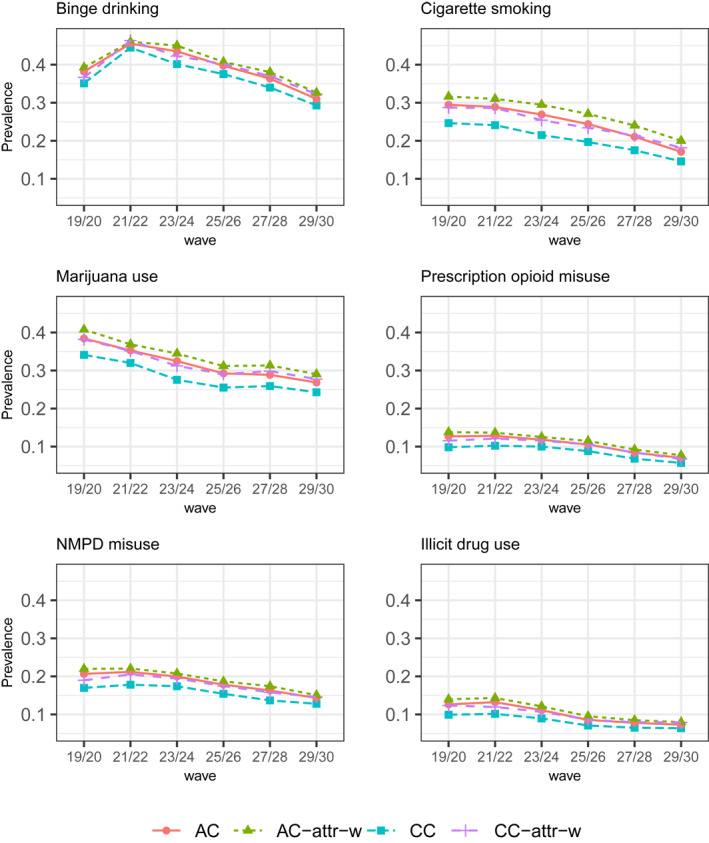
FIGURE 2

Open in a new tab

Prevalence estimates of substance use at baseline and six follow‐up waves marked by the modal ages. The substance use measures include: binge drinking (five or more drinks in a row during the past 2 weeks), cigarette smoking (in the past 30 days), marijuana use (in the past 12 months), non‐medical prescription opioid misuse (in the past 12 months), a composite indicator of any NMPD misuse (of four specific drug classes that included amphetamines, sedatives, tranquilizers, or opioids, in the past 12 months), and a composite indicator of any use of other selected illicit drugs, including LSD, other hallucinogens, cocaine, or heroin (in the past 12 months). AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases; LSD, lysergide; NMPD, non‐medical prescription drug

We found similar results for the prevalence of composite annual NMPD misuse. As for composite annual illegal drug use, the prevalence substantially decreased between age 21/22 and age 25/26 and then remained similar, where the AC estimates were higher than those of the CCs and weighting tended to inflate the estimated rates.

Overall, across the six different substance use outcomes, the AC estimates were higher than the CC estimates with varying trajectories over time; attrition‐adjusted weighting increased both estimates, and the effect was larger for CC than for AC. This indicates that the attriters who missed follow‐up waves tended to be substance users, and the CC analysis underestimated prevalence as a result.

3.2. Trajectory modeling

For each of the eight trajectory models, we collected the coefficients of the wave indicators and the interactions between wave and the college attendance indicators estimated based on the mean structure given in Equation (1). We present the odds ratios of the five categorical panel wave indicators for college attenders and non‐attenders and their 95% confidence intervals in Figures 3, 4, 5, 6, 7, 8. The y‐axis was set at the same range for all eight plots inside each figure to facilitate comparison, and the plots with different scales are presented in the eAppendix. The trajectories varied across different methods and outcomes. Generally, AC estimates had lower variances than CC analyses due to larger sample sizes in the follow‐up waves. The inclusion of weights increased variances in CC analyses, but the variance inflation was negligible in AC analyses.

FIGURE 3.

FIGURE 3

Open in a new tab

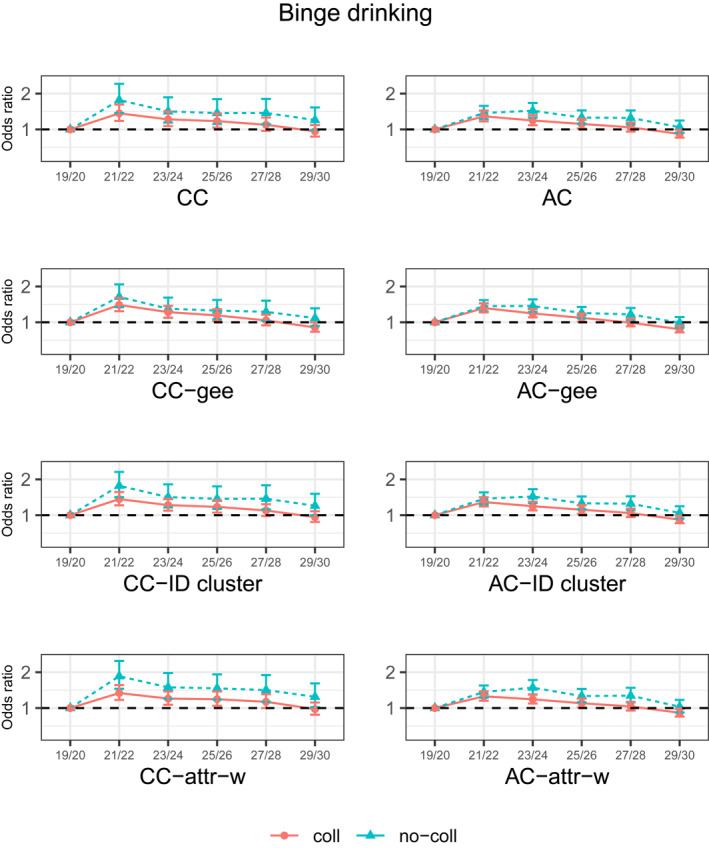
Odds ratio estimates of panel effects on binge drinking (five or more drinks in a row during the past 2 weeks) prevalence for college attenders and non‐attenders. AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; AC‐gee, GEE with available cases; AC‐ID cluster, available case analysis accounting for the cluster structure by individuals; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases; CC‐gee, GEE with complete cases; CC‐ID cluster, complete case analysis accounting for the cluster structure by individuals

FIGURE 4.

FIGURE 4

Open in a new tab

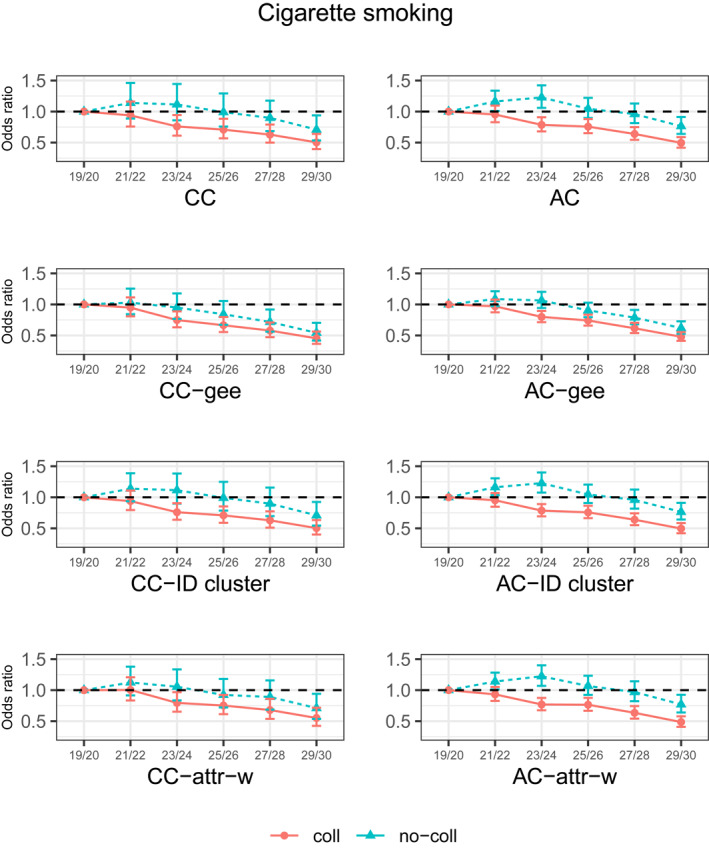
Odds ratio estimates of panel effects on cigarette smoking (in the past 30 days) prevalence for college attenders and non‐attenders. AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; AC‐gee, GEE with available cases; AC‐ID cluster, available case analysis accounting for the cluster structure by individuals; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases; CC‐gee, GEE with complete cases; CC‐ID cluster, complete case analysis accounting for the cluster structure by individuals

FIGURE 5.

FIGURE 5

Open in a new tab

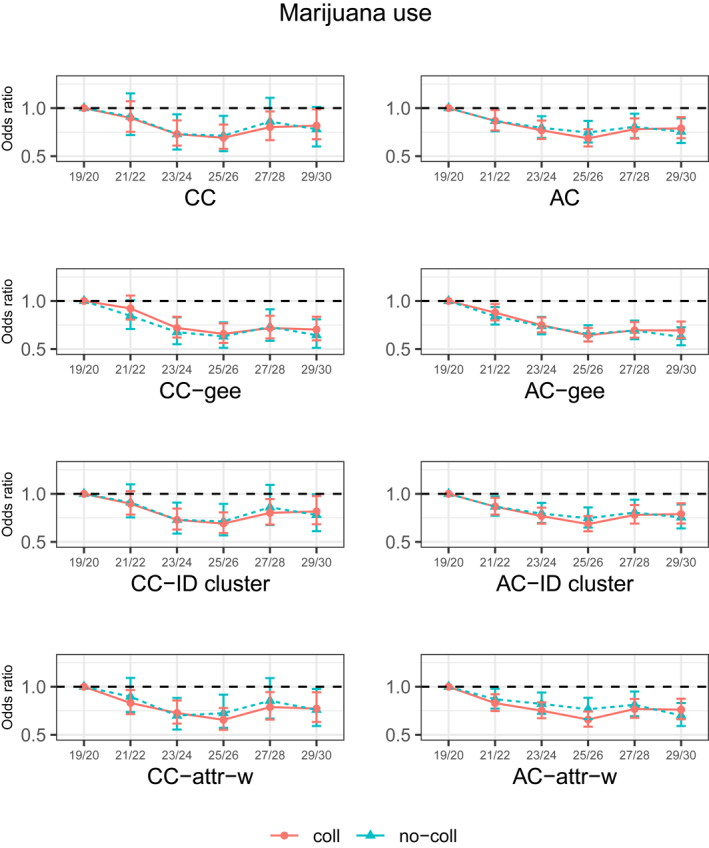
Odds ratio estimates of panel effects on the use of marijuana (in the past 12 months) for college attenders and non‐attenders. AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; AC‐gee, GEE with available cases; AC‐ID cluster, available case analysis accounting for the cluster structure by individuals; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases; CC‐gee, GEE with complete cases; CC‐ID cluster, complete case analysis accounting for the cluster structure by individuals

FIGURE 6.

FIGURE 6

Open in a new tab

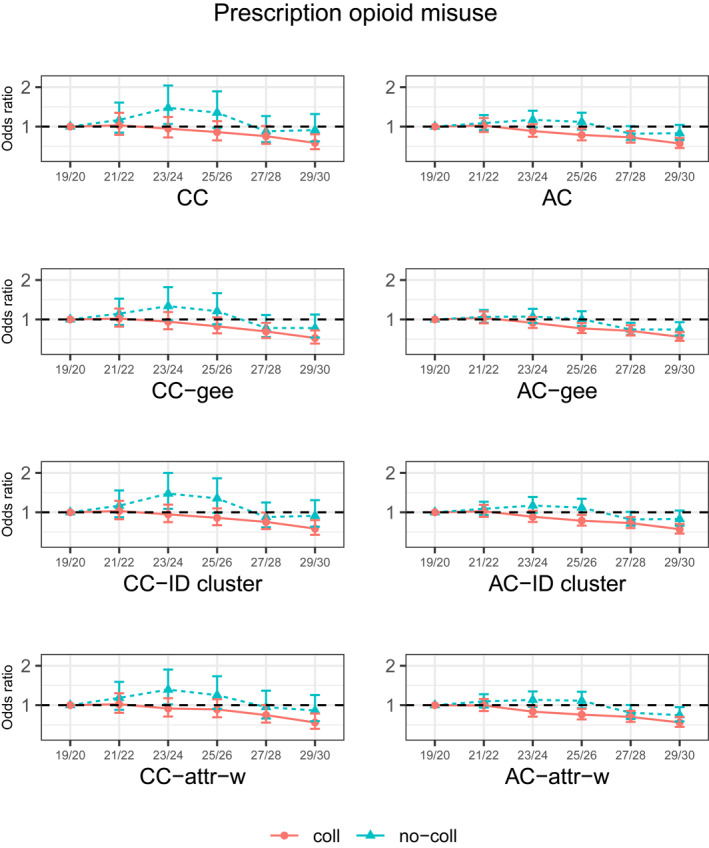
Odds ratio estimates of panel effects on the non‐medical misuse of prescription opioids (in the past 12 months) for college attenders and non‐attenders. AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; AC‐gee, GEE with available cases; AC‐ID cluster, available case analysis accounting for the cluster structure by individuals; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases; CC‐gee, GEE with complete cases; CC‐ID cluster, complete case analysis accounting for the cluster structure by individuals

FIGURE 7.

FIGURE 7

Open in a new tab

Odds ratio estimates of panel effects on the non‐medical misuse of prescription drugs (NMPD) for four specific drug classes that included amphetamines, sedatives, tranquilizers, or opioids, (in the past 12 months) for college attenders and non‐attenders. AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; AC‐gee, GEE with available cases; AC‐ID cluster, available case analysis accounting for the cluster structure by individuals; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases; CC‐gee, GEE with complete cases; CC‐ID cluster, complete case analysis accounting for the cluster structure by individuals

FIGURE 8.

FIGURE 8

Open in a new tab

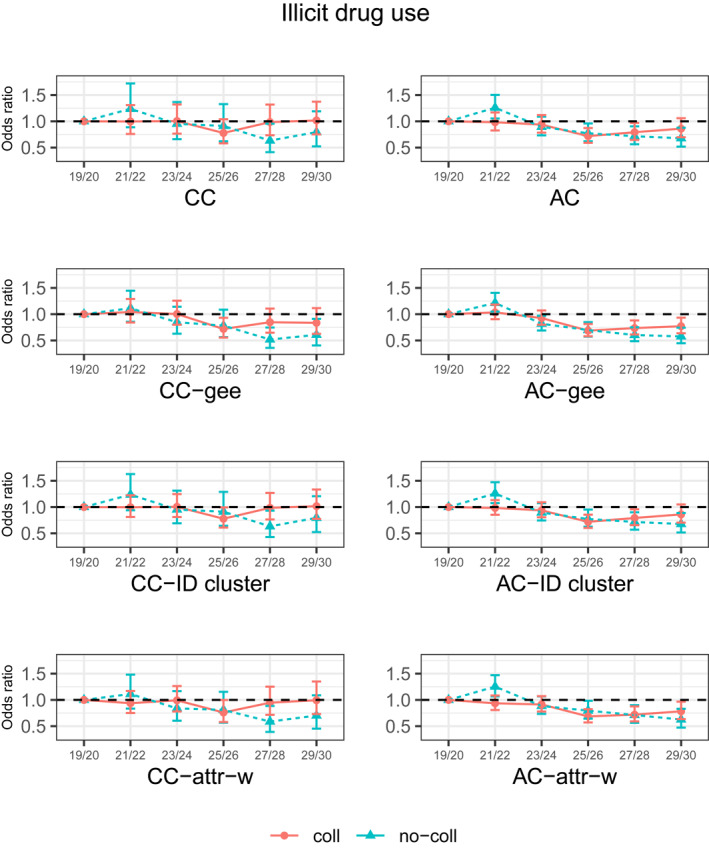
Odds ratio estimates of panel effects on the use of illicit drugs (a composite indicator of any use of other selected illicit drugs, including LSD, other hallucinogens, cocaine, or heroin, in the past 12 months) for college attenders and non‐attenders. AC, available case analysis; AC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with available cases; AC‐gee, GEE with available cases; AC‐ID cluster, available case analysis accounting for the cluster structure by individuals; CC, complete case analysis; CC‐attr‐w, attrition‐adjusted weighted analysis accounting for the cluster structure by individuals with complete cases; CC‐gee, GEE with complete cases; CC‐ID cluster, complete case analysis accounting for the cluster structure by individuals; LSD, lysergide

Figure 3 shows that the prevalence of binge drinking followed a non‐linear trend, first increasing through age 23/24 in the AC analyses, and then decreasing after that through age 29/30. The attrition‐adjusted AC analysis showed that college attendance reduced the prevalence of binge drinking at age 23/24 and age 27/28. All CC analyses showed that the peak was at age 21/22 and did not display any substantial differences between college attenders and non‐attenders. The AC analyses yielded more efficient trajectory estimates of binge drinking with smaller variances than the CC analyses, and weighting slightly changed the estimates.

Figure 4 shows that the estimated cigarette smoking rate for those attending college generally decreased over time under both CC and AC analyses. However, in the AC analyses, the trend was a non‐linear, inverted U shape for college non‐attenders, where the rates of cigarette smoking substantially increased from age 21/22 through 23/24. College attenders had a significantly lower probability of smoking than those who did not attend. Weighting did not affect these analyses. Like binge drinking, the AC estimates of cigarette smoking trajectories had lower variability than the CC estimates.

The AC and CC analyses in Figure 5 for marijuana use yielded different findings. The CC methods failed to detect the decreasing trends at age 21/22 for college non‐attenders. However, the AC analyses showed that the age effects on the prevalence of marijuana use decreased from age 19/20 through age 29/30. Weighting with attrition adjustments slightly increased the uncertainty of the odds ratio estimates for this outcome.

In the AC analyses, non‐medical prescription opioid misuse started decreasing for college attenders at age 23/24 through age 29/30, and the decrease started for non‐college attenders at age 27/28, as shown in Figure 6. The CC analyses of prescription opioid misuse indicated that the rate increased between age 21/22 and age 25/26 for those without college education. The attrition‐adjusted weighting had negligible effects on the trend and estimation uncertainty.

The trends of NMPD misuse shown in Figure 7 are similar to those of prescription opioid misuse, except that in the AC analyses the decreases started at age 25/26 for college attenders and at age 29/30 for non‐college attenders. The CC analyses had larger variances and failed to show the age variation. The effect of the weighting adjustments was small in this case.

The AC estimates of the composite illicit drug use trends were also more efficient than those under the CC approach. Figure 8 indicates that the AC analysis of the composite illicit drug use showed that the prevalence increased between age 19/20 and 21/22 and then decreased between age 23/24 and 29/30 for non‐college attenders, and the decrease occurred between age 23/24 and 27/28 for college attenders. The CC analyses did not show any age differences until age 27/28 for college non‐attenders. We did not observe substantial effects of weighting adjustments for the illicit drug use outcomes.

Overall, the AC analyses with the clustering features and attrition‐adjusted weights resulted in the most efficient estimates. The attrition‐adjusted weighted AC analyses utilized more data and, more importantly, corrected attrition bias in the estimates, even though the effect is generally minor on the trend estimates. The CC analyses yielded different estimates with large variances, with less statistical power to detect age effects or moderation effects of college attendance.

The AC analyses showed decreasing age effects on the use of cigarettes, marijuana, prescription opioids, NMPDs, and illicit drugs, and moderation effects of college attendance on rates of binge drinking, the use of cigarettes, marijuana use, prescription opioid misuse, NMPD misuse, and illicit drug use. The CC‐GEE analysis provided evidence supporting that the decreasing trends were significant, potentially because of the correlation adjustment, where individuals had participated in all follow‐up waves and provided complete trajectories. However, the variance estimates under CC‐GEE failed to account for the attrition‐adjusted weights that inflate the variances. The weights played a negligible role in AC analyses of the trajectory modeling, which would generally be expected if the models are well‐specified (Korn & Graubard, 1999), but weights were essential in the descriptive summary estimates.

4. DISCUSSION

Using national U.S. data from the MTF study, we evaluated the effects of attrition adjustment on longitudinal trajectory estimates of substance use from adolescence through young adulthood, and compared different approaches to this type of analysis. The eight methods considered varied in terms of using CCs or ACs, using GEE or not, and using attrition‐adjusted weights or not. Their performances depended on the relationship between attrition and the substance use outcomes, the trajectory model specification and covariates included in the model, the variability of the weights, and the sample size. Overall, the weighted AC analysis adjusting for clustering and attrition appeared to be the most effective approach. These findings have important methodological, clinical, and policy implications.

4.1. Methodological implications

We recommend using all available cases and including variables strongly related to the outcome in longitudinal trajectory modeling. The attrition weight construction accounts for all sample selection features and baseline characteristics related to the substance use outcomes. The role of weights is prominent in the descriptive prevalence estimates, but modest in the trajectory modeling. When we added the features that affect sample selection (e.g., strata) as covariates in the trajectory modeling, using the weights in estimation did not change the estimates, and the interpretation of coefficients became conditional on these features (results are not presented here and available upon request). When one has concerns about the outcome model specification, accounting for weights in the model can offer protection against model misspecification (Korn & Graubard, 1999; Kott, 2007; Pfeffermann, 2011; Winship & Radbill, 1994), in the sense that estimates will be unbiased with respect to the sample design. It is important to simultaneously adjust for correlations of repeated observations and attrition bias with weights, especially if weights are informative about the outcomes. Hence, the AC analysis with the attrition‐adjusted weights appears to be the most effective approach. Yet, validation of empirical findings requires additional evidence.

The empirical comparison suggests a few directions for future methodological research. First, ideally a full factorial design based on Table 1 with 16 different approaches should be examined.

We include IDs as a clustering variable in the design‐adjusted weighted analyses, essentially mimicking GEE with an exchangeable correlation structure. The point estimates will be similar to those of weighted GEEs (Robins et al., 1995). However, the programs enabling weighted GEEs may give misleading variance estimates (Natarajan et al., 2008). Multilevel models could serve as subject‐specific (as opposed to marginal) alternatives if there is interest in the explicit estimation of between‐individual variances in trajectories. However, the appropriate implementation of multilevel modeling in this context requires weights for multiple levels of the data hierarchy: baseline weights and time‐varying weights (Heeringa et al., 2017; Pfeffermann, 1993; Rabe‐Hesketh & Skrondal, 2006). The estimation of multilevel models in our application cannot achieve convergence, and the computation of generalized linear mixed effects models with weights needs further developments, such as using Bayesian paradigms. Second, all methods considered here assumed missingness at random. Other studies have evaluated adjustment techniques assuming missingness not at random (e.g., Feldman & Rabe‐Hesketh, 2012; Terry‐McElrath et al., 2017; Deng et al., 2013; etc.), which allows for sensitivity analyses. However, different assumptions have been introduced for model estimation. Rigorous evaluation of different methods through simulation studies is still needed, and this work is ongoing. Third, MI approaches can be generalized to simultaneously handle attrition and item nonresponse (Si et al., 2015, 2016, 2020, 2021). Extensions of current MI approaches are required to accommodate the complex challenges in trajectory modeling and implementation in practice, such as accounting for complex survey design features, non‐monotone attrition, and a large number of mixed types of variables.

4.2. Substantive implications

Our investigation can be extended to other substance use outcomes (e.g., substance use disorder) and other longitudinal studies to enhance estimates for clinical and policy purposes. Our results show different trajectories and implications for different drug classes. Consistent with other research (Arterberry et al., 2020), we observe decreasing trends with age in the use of cigarettes, marijuana use, prescription opioid misuse, NMPD misuse, and illicit drug use, and that college attenders have lower prevalences of cigarette smoking and use of some substances during particular age periods. The differences based on college attendance have real‐world implications for making clinical and policy decisions, such as determining population‐level estimates and community resources that should be allocated for substance‐related screening and interventions. The moderating effects vary across substance use outcomes and time. The non‐linear trend of binge drinking prevalence showed the importance of trajectory modeling across multiple time points, with a peak value at age 21/22 (Patrick et al., 2019). It will also be valuable to examine other national longitudinal probability‐based studies (e.g., Harris et al., 2019; Hyland et al., 2017), with different survey designs, instruments, measures, response patterns, and response rates.

CONFLICT OF INTEREST

The authors declared that they have no conflicts of interest to this work.

HUMAN STUDIES AND SUBJECTS

The study is exempted from the Independent Review Board as the secondary data analysis does not involve human subjects.

Supporting information

Supporting Information S1

Click here for additional data file. (353.8KB, docx)

ACKNOWLEDGEMENT

The work was supported by research grants R01DA001411, R01DA016575, and R01DA031160 from the National Institute on Drug Abuse, National Institutes of Health.

Si, Y. , West, B. T. , Veliz, P. , Patrick, M. E. , Schulenberg, J. E. , Kloska, D. D. , Terry‐McElrath, Y. M. , & McCabe, S. E. (2022). An empirical evaluation of alternative approaches to adjusting for attrition when analyzing longitudinal survey data on young adults' substance use trajectories. International Journal of Methods in Psychiatric Research, 31(3), e1916. 10.1002/mpr.1916

DATA AVAILABILITY STATEMENT

The restricted‐use panel data of the Monitoring the Future study are analyzed via the NAHDAP Virtual Data Enclave Management System maintained by the Inter‐university Consortium for Political and Social Research at the University of Michigan. The codes are publicly accessible at https://github.com/yajuansi‐sophie/MTFattrition.

REFERENCES

  1. Arterberry, B. J. , Boyd, C. J. , West, B. T. , Schepis, T. S. , & McCabe, S. E. (2020). DSM‐5 substance use disorders among college‐age young adults in the United States: Prevalence, remission and treatment. Journal of American College Health, 68(6), 650–657. 10.1080/07448481.2019.1590368 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Binder, D. A. (1983). On the variances of asymptotically normal estimators from complex surveys. International Statistical Review, 51(3), 279–292. 10.2307/1402588 [DOI] [Google Scholar]
  3. Bollen, K. A. , Biemer, P. P. , Karr, A. F. , Tueller, S. , & Berzofsky, M. E. (2016). Are survey weights needed? A review of diagnostic tests in regression analysis. Annual Review of Statistics and Its Application, 3(1), 375–392. 10.1146/annurev-statistics-011516-012958 [DOI] [Google Scholar]
  4. Breiman, L. , Friedman, J. H. , Olshen, R. A. , & Stone, C. J. (1984). Classification and regression trees. Wadsworth and Chapman & Hall. [Google Scholar]
  5. Brick, J. M. , & Williams, D. (2013). Explaining rising nonresponse rates in cross‐sectional surveys. The Annals of the American Academy of Political and Social Science, 645(1), 36–59. 10.1177/0002716212456834 [DOI] [Google Scholar]
  6. deLeeuw, E. , Hox, J. , & Luiten, A. (2018). International nonresponse trends across countries and years: An analysis of 36 years of labour force survey data. Survey Insights: Methods from the Field. Retrieved from https://surveyinsights.org/?p=10452 [Google Scholar]
  7. Deng, Y. , Hillygus, D. S. , Reiter, J. P. , Si, Y. , & Zheng, S. (2013). Handling attrition in longitudinal studies: The case for refreshment samples. Statistical Science, 22(2), 238–256. 10.1214/13-sts414 [DOI] [Google Scholar]
  8. Feldman, B. J. , & Rabe‐Hesketh, S. (2012). Modeling achievement trajectories when attrition is informative. Journal of Educational and Behavioral Statistics, 37(6), 703–736. 10.3102/1076998612458701 [DOI] [Google Scholar]
  9. Halekoh, U. , Højsgaard, S. , & Yan, J. (2006). The R package geepack for generalized estimating equations. Journal of Statistical Software, 15(2), 1–11. 10.18637/jss.v015.i02 [DOI] [Google Scholar]
  10. Harris, K. M. , Halpern, C. T. , Whitsel, E. , Hussey, J. M. , Killeya‐Jones, L. A. , Tabor, J. , & Dean, S. C. (2019). Cohort profile: The national longitudinal study of adolescent to adult health (add health). International Journal of Epidemiology, 48(5), 1415–1415k. 10.1093/ije/dyz115 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Heeringa, S. G. , West, B. T. , & Berglund, P. A. (2017). Applied survey data analysis (2nd ed.). CRC Press. [Google Scholar]
  12. Hothorn, T. , Hornik, K. , Strobl, C. , & Zeileis, A. (2021). Party: A laboratory for recursive partytioning. Version 1.3‐6. http://cran.r‐project.org/web/packages/party/ [Google Scholar]
  13. Hothorn, T. , Hornik, K. , & Zeileis, A. (2006). Unbiased recursive partitioning: A conditional inference framework. Journal of Computational & Graphical Statistics, 15(3), 651–674. 10.1198/106186006x133933 [DOI] [Google Scholar]
  14. Hyland, A. , Ambrose, B. K. , Conway, K. P. , Borek, N. , Lambert, E. , Carusi, C. , Taylor, K. , Crosse, S. , Fong, G. T. , Cummings, K. M. , Abrams, D. , Pierce, J. P. , Sargent, J. , Messer, K. , Bansal‐Travers, M. , Niaura, R. , Vallone, D. , Hammond, D. , Hilmi, N. , , & Compton, W. M. (2017). Design and methods of the Population Assessment of Tobacco and Health (PATH) study. Tobacco Control, 26(4), 371–378. 10.1136/tobaccocontrol-2016-052934 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Jager, J. , Schulenberg, J. E. , O'Malley, P. M. , & Bachman, J. G. (2013). Historical variation in drug use trajectories across the transition to adulthood: The trend toward lower intercepts and steeper, ascending slopes. Development and Psychopathology, 25(2), 527–543. 10.1017/s0954579412001228 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Keyes, K. M. , Jager, J. , Platt, J. , Rutherford, C. , Patrick, M. E. , Kloska, D. D. , & Schulenberg, J. (2020). When does attrition lead to biased estimates of alcohol consumption? Bias analysis for loss to follow‐up in 30 longitudinal cohorts. International Journal of Methods in Psychiatric Research, 29(4), 1–9. 10.1002/mpr.1842 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Korn, E. , & Graubard, B. (1999). Analysis of health surveys. John Wiley & Sons. [Google Scholar]
  18. Kott, P. S. (2007). Clarifying some issues in the regression analysis of survey data. Survey Research Methods, 1, 11–18. [Google Scholar]
  19. Liang, K. Y. , & Zeger, S. L. (1986). Longitudinal data analysis using generalized linear models. Biometrika, 7(1), 13–22. 10.1093/biomet/73.1.13 [DOI] [Google Scholar]
  20. Linden‐Carmichael, A. N. , Kloska, D. D. , Evans‐Polce, R. , Lanza, S. T. , & Patrick, M. E. (2019). College degree attainment by age of first marijuana use and parental education. Substance Abuse, 40(1), 66–70. 10.1080/08897077.2018.1521354 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Little, R. J. A. , & Rubin, D. B. (2019). Statistical analysis with missing data (3rd ed.). John Wiley & Sons. [Google Scholar]
  22. Lumley, T. (2020). Survey: Analysis of complex survey samples. R package version 4.0. [Google Scholar]
  23. McCabe, S. E. , Kloska, D. D. , Veliz, P. , Jager, J. , & Schulenberg, J. A. (2016). Developmental course of non‐medical use of prescription drugs from adolescence to adulthood in the United States: National longitudinal data. Addiction, 111(12), 2166–2176. 10.1111/add.13504 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. McCabe, S. E. , Veliz, P. T. , Dickinson, K. , Schepis, T. S. , & Schulenberg, J. E. (2019). Trajectories of prescription drug misuse during the transition from late adolescence into adulthood: A national longitudinal multi‐cohort study. The Lancet Psychiatry, 6(10), 840–850. 10.1016/s2215-0366(19)30299-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. McCabe, S. E. , Veliz, P. , & Schulenberg, J. E. (2018). How collegiate fraternity and sorority involvement relates to substance use during young adulthood and substance use disorders in early midlife: A national longitudinal study. Journal of Adolescent Health, 62(3S), S35–S43. 10.1016/j.jadohealth.2017.09.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Miech, R. A. , Johnston, L. D. , O'Malley, P. M. , Bachman, J. G. , Schulenberg, J. E. , & Patrick, M. E. (2021). Monitoring the future national survey results on drug use, 1975–2020: Volume I, Secondary school students. Institute for Social Research. [Google Scholar]
  27. Natarajan, S. , Lipsitz, S. , Fitzmaurice, G. , Moore, C. , & Gonin, R. (2008). Variance estimation in complex survey sampling for generalized linear models. Journal of the Royal Statistical Society. Series C (Applied Statistics), 57(1), 75–87. 10.1111/j.1467-9876.2007.00601.x [DOI] [Google Scholar]
  28. Patrick, M. E. , Kloska, D. D. , Mehus, C. , Terry‐McElrath, Y. M. , O'Malley, P. M. , & Schulenberg, J. E. (2021). Key subgroup differences in age‐related change from 18 to 55 in alcohol and marijuana use: U.S. National data. Journal of Studies on Alcohol and Drugs, 82(1), 93–102. 10.15288/jsad.2021.82.93 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Patrick, M. E. , Terry‐McElrath, Y. M. , Kloska, D. D. , & Schulenberg, J. E. (2016). High‐Intensity drinking among young adults in the United States: Prevalence, frequency, and developmental change. Alcoholism: Clinical and Experimental Research, 40(9), 1905–1912. 10.1111/acer.13164 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Patrick, M. E. , Terry‐McElrath, Y. M. , Lanza, S. T. , Jager, J. , Schulenberg, J. E. , & O'Malley, P. M. (2019). Shifting age of peak binge drinking prevalence: Historical changes in normative trajectories among young adults aged 18 to 30. Alcoholism: Clinical and Experimental Research, 43(2), 287–298. 10.1111/acer.13933 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Patrick, M. E. , Veliz, P. , Linden‐Carmichael, A. , & Terry‐McElrath, Y. M. (2018). Alcohol mixed with energy drink use during young adulthood. Addictive Behaviors, 84, 224–230. 10.1016/j.addbeh.2018.03.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Pfeffermann, D. (1993). The role of sampling weights when modeling survey data. International Statistical Review, 61(2), 317–337. 10.2307/1403631 [DOI] [Google Scholar]
  33. Pfeffermann, D. (2011). Modelling of complex survey data: Why model? Why is it a problem? How can we approach it? Survey Methodology, 37(2), 115–136. [Google Scholar]
  34. Rabe‐Hesketh, S. , & Skrondal, A. (2006). Multilevel modelling of complex survey data. Journal of the Royal Statistical Society: Series A, 169(4), 805–827. 10.1111/j.1467-985x.2006.00426.x [DOI] [Google Scholar]
  35. R Core Team . (2020). R: A language and environment for statistical computing. https://www.R‐project.org/ [Google Scholar]
  36. Robins, J. M. , Rotnitzky, A. , & Zhao, L. P. (1995). Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association, 90(429), 106–121. 10.1080/01621459.1995.10476493 [DOI] [Google Scholar]
  37. Roghani, A. , Nyarko, S. H. , & Potter, L. (2021). Smoking cigarettes, marijuana, and the transition to marriage among cohabiters in the USA. Global Social Welfare, 8(3), 279–286. 10.1007/s40609-021-00211-w [DOI] [Google Scholar]
  38. Rubin, D. B. (1987). Multiple imputation for nonresponse in surveys. John Wiley & Sons. [Google Scholar]
  39. Schulenberg, J. E. , & Maggs, J. L. (2002). A developmental perspective on alcohol use and heavy drinking during adolescence and the transition to young adulthood. Journal of Studies on Alcohol, 14(s14), 54–70. 10.15288/jsas.2002.s14.54 [DOI] [PubMed] [Google Scholar]
  40. Schulenberg, J. E. , Merline, A. C. , Johnston, L. D. , O'Malley, P. M. , Bachman, J. G. , & Laetz, V. B. (2005). Trajectories of marijuana use during the transition to adulthood: The big picture based on national panel data. Journal of Drug Issues, 35(2), 255–279. 10.1177/002204260503500203 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Schulenberg, J. E. , Patrick, M. E. , Johnston, L. D. , O'Malley, P. M. , Bachman, J. G. , & Miech, R. A. (2021). Monitoring the future national survey results on drug use, 1975–2020: Volume II, college students and adults ages 19–60. Institute for Social Research. [Google Scholar]
  42. Si, Y. , Heeringa, S. , Johnson, D. , Little, R. J. A. , Liu, W. , Pfeffer, F. , & Raghunathan, T. (2021). Multiple imputation with massive data: An application to the panel study of income dynamics. Journal of Survey Statistics and Methodology. 10.1093/jssam/smab038 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Si, Y. , Little, R. , Mo, Y. , & Sedransk, N. (2022a). A case study of nonresponse bias analysis in educational assessment surveys. Under review. https://arxiv.org/abs/2104.04432 [Google Scholar]
  44. Si, Y. , Little, R. , Mo, Y. , & Sedransk, N. (2022b). Nonresponse bias analysis in longitudinal educational assessment studies. Under review. http://arxiv.org/abs/2204.07105 [Google Scholar]
  45. Si, Y. , Palta, M. , & Smith, M. (2020). Bayesian profiling multiple imputation for missing hemoglobin values in electronic health records. Annals of Applied Statistics, 14(4), 1903–1924. 10.1214/20-aoas1378 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Si, Y. , Reiter, J. P. , & Hillygus, D. S. (2015). Semi‐Parametric selection models for potentially non‐ignorable attrition in panel study with refreshment samples. Political Analysis, 23(1), 92–112. 10.1093/pan/mpu009 [DOI] [Google Scholar]
  47. Si, Y. , Reiter, J. P. , & Hillygus, D. S. (2016). Bayesian latent pattern mixture models for handling attrition in panel studies with refreshment samples. Annals of Applied Statistics, 10(1), 118–143. 10.1214/15-aoas876 [DOI] [Google Scholar]
  48. Terry‐McElrath, Y. M. , O'Malley, P. M. , Johnston, L. D. , Bray, B. C. , Patrick, M. E. , & Schulenberg, J. E. (2017). Longitudinal patterns of marijuana use across ages 18–50 in a US national sample: A descriptive examination of predictors and health correlates of repeated measures latent class membership. Drug and Alcohol Dependence, 171, 70–83. 10.1016/j.drugalcdep.2016.11.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Terry‐McElrath, Y. M. , & Patrick, M. E. (2016a). Intoxication and binge and high‐intensity drinking among U.S. young adults in their mid‐twenties. Substance Abuse, 37(4), 597–605. 10.1080/08897077.2016.1178681 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Terry‐McElrath, Y. M. , & Patrick, M. E. (2016b). Trends and timing of cigarette smoking uptake among U.S. young adults: Survival analysis using annual national cohorts from 1976 to 2005. Addiction, 110(7), 1171–1181. 10.1111/add.12926 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Terry‐McElrath, Y. M. , Patrick, M. E. , Johnston, J. D. , & Schulenberg, J. E. (2019). Young adult longitudinal patterns of marijuana use among U.S. National samples of 12th grade frequent marijuana users: A repeated‐measures latent class analysis. Addiction, 114(6), 1035–1048. 10.1111/add.14548 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Van Buuren, S. , & Oudshoorn, C. (1999), Flexible multivariate imputation by MICE, Technical report, Leiden: TNO Preventie en Gezondheid, TNO/VGZ/PG 99.054. [Google Scholar]
  53. Winship, C. , & Radbill, L. (1994). Sampling weights and regression analysis. Sociological Methods & Research, 23(2), 230–257. 10.1177/0049124194023002004 [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information S1

Click here for additional data file. (353.8KB, docx)

Data Availability Statement

The restricted‐use panel data of the Monitoring the Future study are analyzed via the NAHDAP Virtual Data Enclave Management System maintained by the Inter‐university Consortium for Political and Social Research at the University of Michigan. The codes are publicly accessible at https://github.com/yajuansi‐sophie/MTFattrition.

Articles from International Journal of Methods in Psychiatric Research are provided here courtesy of Wiley

RESOURCES