Haplotype-resolved assembly of diploid genomes without parental data

Abstract

Routine haplotype-resolved genome assembly from single samples remains an unresolved problem. Here we describe an algorithm that combines PacBio HiFi reads and Hi-C chromatin interaction data to produce a haplotype-resolved assembly without the sequencing of parents. Applied to human and other vertebrate samples, our algorithm consistently outperforms existing single-sample assembly pipelines and generates assemblies of similar quality to the best pedigree-based assemblies.

The advances in long-read sequencing technologies have laid the foundations for high-quality de novo genome assembly^1,2. For diploid or polyploid genomes, most long-read assemblers collapse different homologous haplotypes into a consensus assembly, completely losing the phasing information. A few assemblers use heterozygous differences between haplotypes to retain local phasing^3-6. However, owing to the limited read length, these assemblers can only generate short phased blocks for samples of low heterozygosity. To obtain long contigs, they stitch part of these short blocks to produce a primary assembly with homologous haplotypes randomly switching in each contig, and dump the remaining blocks into an alternate assembly. The alternate assembly is fragmented and often contains excessive sequence duplications. It is ignored in most downstream analysis. To this end, a primary/alternate assembly still represents a single haplotype, not a diploid genome. For a diploid genome, we prefer to derive a haplotype-resolved assembly which consists of two sets of contigs with each set representing a complete homologous haplotype. Each contig in a haplotype-resolved assembly supposedly comes from one haplotype, also known as a haplotig. Trio binning⁷ is the first algorithm to produce a haplotype-resolved assembly but the requirement of parental sequencing often limits its application in practice. This limitation motivates the recent development of single-sample haplotype-resolved assembly using additional Hi-C or Strand-Seq data^8-10. These methods all start with a collapsed assembly and ignore the rich information in phased assembly graphs. They are not as good as graph trio binning employed by hifiasm⁵ for all metrics measured. In addition, the published single-sample methods all involve multiple steps in a long pipeline, which complicates their installation and deployment.

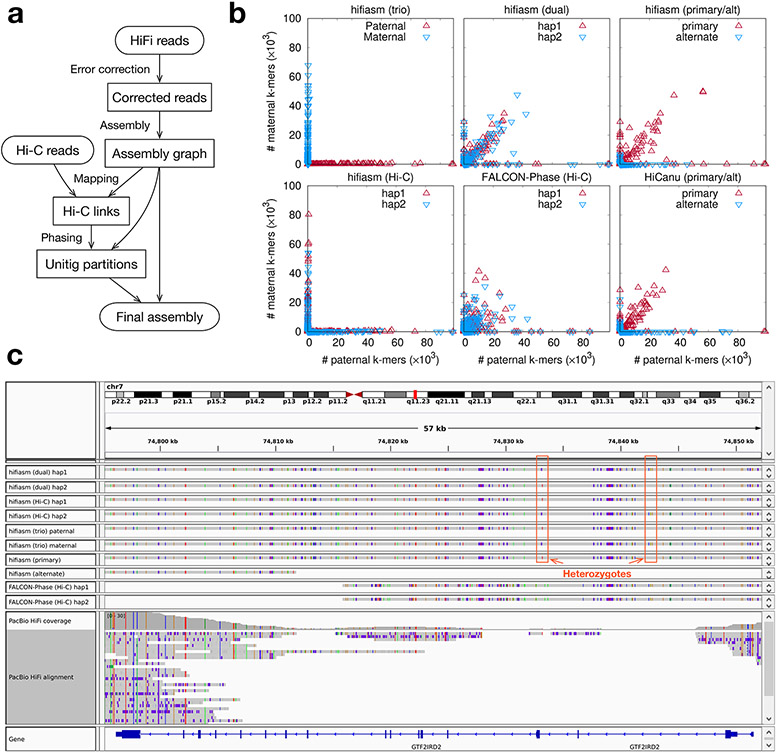
To overcome the limitations of earlier methods, we extended our hifiasm assembler to single-sample haplotype-resolved assembly using HiFi and Hi-C data both at around 30-fold coverage of the haploid genome size. Our new Hi-C based algorithm, called hifiasm (Hi-C) here, is built on top of phased hifiasm assembly graphs⁵ but differs from the published hifiasm (trio) algorithm in sequence partition. In a hifiasm graph, each node is a unitig assembled from HiFi reads with correct phasing and each edge represents an overlap between two unitigs. While hifiasm (trio) labels reads in unitigs with parental k-mers, hifiasm (Hi-C) partitions relatively short unitigs in the graph with Hi-C short reads (Fig. 1a). Specifically, we index 31-mers in unitigs and map Hi-C short reads to them without detailed base alignment. If a pair of reads from a Hi-C fragment matches two distant heterozygotes on two unitigs, we add a haplotype-specific “link” between the unitigs, which provides long-range phasing information. We then bipartition the unitigs such that unitigs in each partition have little redundancy and share many Hi-C links. We reduce such a unitig bipartition problem to a graph max-cut problem¹¹ and find a near optimal solution with a stochastic algorithm¹²; we also consider the topology of the assembly graph to reduce the chance of local optima (Online Methods). In the end, we reuse the same graph binning strategy in hifiasm (trio) to produce the final hifiasm (Hi-C) assembly. Unlike existing methods, our algorithm directly operates on a HiFi assembly graph and tightly integrates Hi-C read mapping, phasing and assembly into one single executable program with no dependency to external tools. It is easier to use and runs faster (Supplementary Table 2).

Figure 1. Haplotype-resolved assembly using Hi-C data.

(a) Assembly workflow. Hifiasm corrects reads and produces a phased assembly graph. It then maps Hi-C short reads to the graph, links unitigs in the assembly graph that share mapped Hi-C fragments, and finds a bipartition of unitigs such that unitigs linked by many Hi-C fragments tend to be grouped together. Hifiasm finally emits a haplotype-resolved assembly jointly considering the unitig partition and the assembly graph. (b) Phasing accuracy of HG002 assemblies. Each point corresponds to a contig. Its coordinate gives the number of paternal- and maternal-specific 31-mers on the contig, with these 31-mers derived from parental short reads. Hifiasm (trio): haplotype-resolved hifiasm assembly with trio binning. Hifiasm (dual): paired hifiasm assembly without Hi-C. Hifiasm (primary/alt): primary and alternate hifiasm assembly without Hi-C. Hifiasm (Hi-C): haplotype-resolved hifiasm assembly with Hi-C. FALCON-Phase (Hi-C): FALCON-Phase assembly with Hi-C based on IPA contigs, acquired from its publication¹⁰. HiCanu (primary/alt): primary and alternate HiCanu assembly without Hi-C. All assemblies use the same HiFi and Hi-C datasets. (c) Screenshot of contig and read alignment to GRCh38 around gene GTF2IRD2.

We also adapted our max-cut based phasing algorithm to HiFi-only data without Hi-C, trio or additional data. In this mode, hifiasm assumes the sequence divergence between repeat copies on the same haplotype is higher than the heterozygosity of the diploid sample. It effectively produces a pair of non-redundant primary assemblies representing a complete diploid genome with imperfect phasing. We call such a pair of assemblies as a dual assembly, or hifiasm (dual). A hifiasm (dual) assembly is often not haplotype-resolved because most long contigs are not haplotigs for a diploid sample of low heterozygosity. Different from the traditional primary/alternate format, a dual assembly represents a complete diploid genome and it is more contiguous, more accurate and more powerful in downstream analysis as is shown below. The idea of the dual assembly format was first introduced in a later version of Peregrine¹³, though our algorithm to derive the assembly is distinct.

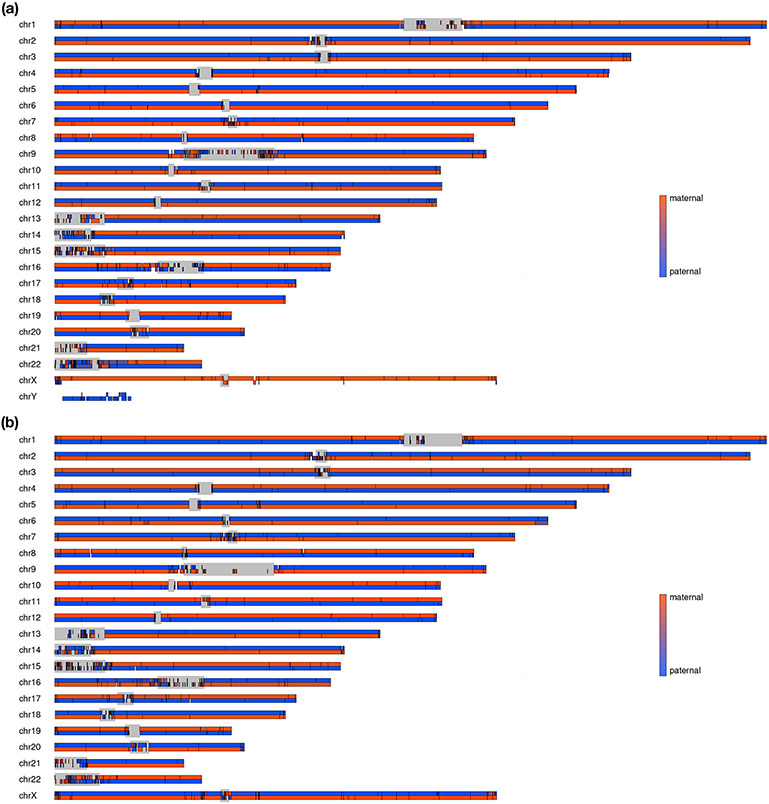
We first evaluated the phasing accuracy on the human HG002 dataset (Fig. 1b), taking trio phasing as the ground truth. We found that hifiasm (Hi-C) or hifiasm (trio) contigs are largely haplotigs with no contigs joining long stretches of paternal and maternal haplotypes. Hifiasm (Hi-C) is able to achieve chromosome-level phasing: for all chromosomes, contigs from the same haplotype are mostly partitioned to the same phase except at some centromeres (Extended Data Fig. 1). It also resolves asymmetric sex chromsomes in the male HG002 sample. Hifiasm (Hi-C) may put paternal and maternal contigs from different chromosomes in one partition. This is an innate ambiguity in Hi-C phasing as paternal and maternal chromosomes are indistinguishable in the cells of an offspring. In the hifiasm and HiCanu primary/alternate assembly settings (Fig. 1b), primary contigs are long but are not haplotigs; alternate contigs are haplotigs but are fragmented. In comparison, both hap1 and hap2 assemblies in hifiasm (dual) behave like a primary assembly as is expected.

The advantage of hifiasm (Hi-C) and hifiasm (dual) is more apparent around segment duplications. We examined the contig and read alignments around GTF2IRD2 (Fig. 1c), a key gene to the Williams-Beuren syndrome¹⁶. This gene has a close paralog GTF2IRD2B downstream. Most HiFi reads from GTF2IRD2 are mismapped to its paralog, leaving a coverage gap (Fig. 1c). Alternate contigs have a similar issue. Although FALCON-Phase Hi-C-based assemblies are not as fragmented as alternate contigs, it is still unable to resolve GTF2IRD2. Only hifiasm (Hi-C) and hifiasm (dual) can go through this region on both haplotypes and reveal the variations on this gene. Many challenging medically-relevant genes in segmental duplications like GTF2IRD2 can only be resolved by hifiasm¹⁷.

In comparison to other single-sample haplotype-resolved assembly pipelines including FALCON-Phase¹⁰, DipAsm⁸ and PGAS⁹, hifiasm Hi-C-based assemblies are more contiguous and have fewer phasing errors for human samples HG002 and HG00733 (Table 1). Hifiasm assemblies also miss fewer multi-copy genes, consistent with our earlier finding⁵.

Table 1.

Statistics of different assemblies

Dataset	Assembler	Size (Gb)	N50 (Mb)	Hamming error (%)	Multicopy genes missed (%)	Gene completeness
						Complete (%)	Duplicated (%)
HG002 (HiFi + trio/Hi-C)	hifiasm (Hi-C)	3.075/2.909	50.0/55.1	1.42/0.82	19.82/19.98	99.28/99.08	0.32/0.32
	Falcon-Phase (Hi-C)	3.027/3.027	32.1/32.1	18.66/19.15	40.13/39.25	99.29/99.26	3.14/3.13
	hifiasm (trio)	2.936/3.033	57.9/57.8	0.75/0.74	21.18/16.72	99.17/99.24	0.29/0.33
HG002 (HiFi only)	hifiasm (dual)	3.033/3.015	57.8/44.7	28.25/21.59	18.47/20.30	99.11/99.04	0.35/0.31
	hifiasm (primary/alt)	3.112/2.910	89.9/0.4	22.30/1.99	13.14/32.25	99.44/88.10	0.34/2.67
	HiCanu (primary/alt)	2.960/3.143	48.4/0.3	27.76/0.68	34.95/20.62	98.88/85.63	0.19/5.15
HG00733 (HiFi + trio/Hi-C/Strand-seq)	hifiasm (Hi-C)	3.024/3.062	44.5/40.6	1.79/1.48	14.97/18.31	99.44/99.51	0.31/0.35
	DipAsm (Hi-C)	2.934/2.933	26.3/28.2	2.81/2.57	66.08/67.44	99.03/99.04	0.39/0.40
	PGAS (Strand-seq)	2.905/2.900	30.1/25.9	3.25/2.60	66.48/68.31	99.15/99.18	0.16/0.15
	hifiasm (trio)	3.047/3.026	52.3/45.6	0.78/0.99	14.57/18.87	99.50/99.28	0.42/0.32
HG00733 (HiFi only)	hifiasm (dual)	3.027/3.049	48.3/36.4	38.08/36.40	19.82/17.52	99.36/99.18	0.34/0.42
	hifiasm (primary/alt)	3.077/3.018	68.3/0.3	39.63/2.23	12.18/28.98	99.58/84.95	0.51/2.89
	HiCanu (primary/alt)	2.918/3.312	44.5/0.2	38.79/1.00	42.75/14.81	98.89/82.78	0.14/6.29
European badger (HiFi + trio/Hi-C)	hifiasm (Hi-C)	2.731/2.536	84.5/73.6	1.51/2.09		96.77/94.33	1.68/1.63
	hifiasm (trio)	2.633/2.560	91.5/57.2	0.65/3.28		94.44/95.11	1.70/1.68
European badger (HiFi only)	hifiasm (dual)	2.628/2.643	80.6/70.9	16.56/16.13		95.32/96.14	1.65/1.65
	hifiasm (primary/alt)	2.724/1.711	85.0/0.2	12.88/1.83		96.82/51.59	1.67/1.35
	HiCanu (primary/alt)	2.690/1.371	67.1/0.1	11.36/1.12		96.75/38.30	1.96/2.57
Sterlet (HiFi + trio/Hi-C)	hifiasm (Hi-C)	1.869/1.879	10.4/9.3	3.48/2.52		93.05/93.16	57.83/58.35
	hifiasm (trio)	1.865/1.853	11.3/11.4	0.75/0.44		93.30/93.27	59.15/57.91
Sterlet (HiFi only)	hifiasm (dual)	1.873/1.869	10.6/9.2	11.32/11.34		93.41/92.80	56.92/58.79
	hifiasm (primary/alt)	1.927/1.885	27.7/1.5	24.94/0.87		93.43/92.64	59.01/55.66
	HiCanu (primary/alt)	1.724/2.114	7.3/2.2	12.31/1.99		91.48/90.25	42.47/59.97
South Island takahe (HiFi + trio/Hi-C)	hifiasm (Hi-C)	1.315/1.154	12.5/13.2	0.70/0.64		97.01/90.27	0.54/0.46
	hifiasm (trio)	1.237/1.236	12.9/12.6	1.87/0.19		91.22/92.29	0.64/0.61
South Island takahe (HiFi only)	hifiasm (dual)	1.237/1.257	13.8/10.7	6.03/5.06		92.56/94.45	0.49/0.52
	hifiasm (primary/alt)	1.320/0.644	16.3/0.3	5.12/1.01		97.11/45.33	0.59/0.73
Black Rhinoceros (HiFi + trio/Hi-C)	hifiasm (Hi-C)	2.992/3.056	31.6/28.9	1.16/1.44		96.49/96.82	0.82/0.78
	hifiasm (trio)	3.014/3.050	30.1/31.3	0.93/0.33		96.13/96.81	0.89/0.90
Black Rhinoceros (HiFi only)	hifiasm (dual)	2.929/3.047	26.8/27.3	35.05/34.13		94.49/95.99	0.80/0.87
	hifiasm (primary/alt)	3.055/2.846	38.9/0.7	36.44/3.42		96.79/84.76	0.80/1.01
	HiCanu (primary/alt)	3.058/2.560	22.2/0.3	31.55/0.61		96.79/70.11	1.53/1.38

All assemblies of the same sample use the same HiFi and Hi-C reads, except PGAS which relies on strand-seq data for phasing. Each assembly consists of two sets of contigs. The two sets may represent paternal/maternal with trio binning, haplotype 1/haplotype 2 with haplotype-resolved assembly or hifiasm dual assembly, or represent primary/alternate contigs. The two numbers in each cell give the metrics for the two sets of contigs, respectively. FALCON-Phase HG002 assembly, DipAsm and PGAS HG00733 assemblies were acquired from their associated publications. For South Island takahe, HiCanu could not produce assembly in 3 weeks so it is excluded. The N50 of an assembly is defined as the sequence length of the shortest contig at 50% of the total assembly size. The completeness scores of all human assemblies were calculated by the asmgene method¹⁴ with GRCh38 as the reference genome. The completeness of non-human assemblies were evaluated by BUSCO¹⁵. All samples have parental short reads, which were used to calculate the phasing switch error rates (Supplementary Table 1) and phasing hamming error rates with yak⁵. The hamming error rate equals Σ_i min{p_i, m_i}/Σ_i(p_i + m_i) where p_i and m_i are the number of paternal- and maternal-specific 31-mers on contig i, respectively. ‘Multicopy genes missed’ is the percentage of multi-copy genes in GRCh38 (multiple mapping positions at ≥99% sequence identity) that are not multi-copy in the assembly. This metric is only reported for human samples as other species lack high-quality reference genomes and good gene annotations.

We further applied hifiasm to several non-human datasets with parental data, including two mammals (European badger¹⁸, Meles meles and Black rhinoceros, Diceros bicornis ), a fish (Sterlet², Acipenser ruthenus), and bird (South Island takahe, Porphyrio hochstetteri). The takahe is endangered, and the black rhinoceros is critically endangered, making it all the more imperative to obtain a more complete phased diploid assembly.

On these diverse datasets, hifiasm Hi-C assemblies are broadly comparable to hifiasm trio assemblies in terms of completeness, contiguity, phasing accuracy and base accuracy (QV), except for sterlet whose Hi-C assembly has a noticeably higher hamming error rate (Table 1 and Supplementary Table 1). We speculate this may be caused by residual tetraploidy whereby the ends of several chromosomes behave like a tetraploid organism¹⁹. Such a genome organization would violate the diploid assumption of hifiasm (Hi-C) and mislead the phasing to mix opposite parental sequences in one contig. Hifiasm dual assemblies have similar contiguity and phasing switch error rates to the Hi-C assemblies on both haplotypes (Supplementary Table 1), but their hamming error rates are higher as we are unable to correctly phase through regions of low heterozygosity with long reads alone. Hi-C and dual assemblies aim to reconstruct both homologous haplotypes. They will introduce a contig break if there is a random coverage drop on one of the two homologous haplotypes. A primary assembly on the other hand only aims to reconstruct one haplotype. If there is a coverage drop on one haplotype, it will switch to the other haplotype at higher coverage. This makes primary assemblies less sensitive to uneven coverage and more contiguous. Nonetheless, the focus of primary assembly on one haplotype greatly lowers the quality of the other haplotype. The corresponding alternate contigs are often only <300kb in length and incomplete (Table 1). A primary/alternate assembly does not represent a whole diploid genome.

The original hifiasm⁵ was the first assembler that could construct an assembly graph faithfully encoding the phasing of accurate long reads. With the addition of Hi-C phasing on top of our earlier work, hifiasm is so far the only assembler that can fully exploit the rich information in phased assembly graphs and robustly produce unmatched high-quality haplotype-resolved assemblies for single individuals of various species in several hours (Supplementary Table 2). Eliminating the barrier of the parental data requirement, hifiasm has paved the way for population-scale haplotype-resolved assembly which may shed light on the evolution and functionality of segmental duplications and complex gene families omitted in most analyses.

Methods

Overview of hifiasm assembly graphs.

As is described in our earlier work⁵, a hifiasm assembly graph is a simplified string graph consisting of unitigs with overlaps between them. Given a string graph, nodes are HiFi reads and edges are the overlaps between the corresponding reads. Unitigs correspond to non-branching paths in the string graph and they have no phasing errors if generated correctly. For a diploid sample, there are two types of unitigs: unitigs from heterozygous regions and unitigs from homozygous regions. The two types can be distinguished based on their read coverage. If we can determine the phase of each heterozygous unitig, we may use the existing hifiasm graph-binning algorithm to derive a haplotype-resolved assembly by spelling contigs only composed of unitigs in the same phase. The haplotype-resolved assembly is thus reduced to the unitig phasing problem (Supplementary Fig. 1).

Producing a dual assembly with HiFi reads only.

Recall that a dual assembly is a pair of non-redundant primary assemblies with each assembly representing a complete homologous haplotype. At the overlapping step, hifiasm records two types of HiFi read overlaps: cis read overlaps and trans read overlaps. An overlap between HiFi read A and B is cis if A and B are inferred to come from the same homologous haplotype; otherwise it is trans. We refer to our earlier work⁵ for more information about this procedure. Hifiasm only uses cis overlaps to build the assembly. Let U_st be the number of trans read overlaps between two heterozygous unitigs s and t. It is a proxy to the similarity between the two unitigs. For each heterozygous unitig t, let variable δ_t ∈ {1, −1} be its phase. Hifiasm tries to maximize the following objective function to determine the phases of heterozygous unitigs:

$$F(\overrightarrow{\delta })=-\sum _{s,t}{\delta }_s{\delta }_t{U}_{st}$$ (1)

where $\overrightarrow{\delta }$ is the vector of all heterozygous unitig phases. With this optimization, hifiasm tries to maximize the sequence similarity across the two phases, or equivalently, to minimize the similarity within each phase. The objective function above takes a form similar to the Hamiltonian of Ising models and can be transformed to a graph maximum cut problem. It can be approximately solved by a stochastic algorithm which will be explained later. After determining the phases, hifiasm spells contigs composed of unitigs in the same phase. This gives a dual assembly.

Our optimization-based method has stronger power to deal with complex repetitive regions. There are several existing tools for other applications which also need to identify the overlaps between homologous regions like purge_dups²⁰. These tools use fixed similarity thresholds to filter out wrong overlaps. However, it is very hard to select appropriate thresholds for repetitive regions as they are highly similar to each other. Our optimization-based method tries to globally consider all unitigs and overlaps so that it is able to more robustly filter out wrong overlaps within the same haplotype. Supplementary Fig. 1(a) and Supplementary Fig. 1(b) show an example. With our optimization, hifiasm assigns both unitig a0 and a1 to the same phase, so that the trans overlap between them can be removed. The straightforward solution without optimization may regard the overlap between a0 and a1 as a real one if a wrong similarity threshold is selected.

Mapping Hi-C reads to assembly graphs.

Given a diploid sample, the total length of unitigs in the assembly graph approximately doubles the haploid genome size. The majority of 31-mers in the graph have two copies and are not unique. Unique 31-mers tend to harbor haplotype-specific heterozygous alleles. Because for the purpose of phasing we only care about Hi-C read pairs that bridge two or more heterozygous alleles, we only index unique 31-mers in the assembly graph. We map a Hi-C short read pair if it harbors two or more non-overlapping 31-mers and discard the remaining reads that are not informative to phasing. The Hi-C reads mapped to homozygous unitigs are also discarded as homozygous unitigs are not informative to phasing.

Existing phasing and scaffolding tools use general-purpose read mappers to align Hi-C reads. These standalone mappers maximize the alignment sensitivity and accuracy but they are slow, often taking a day to map Hi-C reads to a mammal genome. Hi-C is intrinsically noisy data, much noisier than read mapping errors. We may not need high mapping accuracy for the phasing purpose. Furthermore, with the graph structure and the max-cut formulation, we can filter out many Hi-C mapping errors. Our k-mer based alignment only takes a few hours and has been shown to perform well.

Suppose a Hi-C short read is mapped to a heterozygous unitig t with the algorithm above. Such a mapping is a cis mapping in that the Hi-C read is in the same phase as unitig t. If HiFi reads around the Hi-C read mapping positions have trans overlaps with HiFi reads on unitig t′, we can infer the Hi-C read has a trans mapping to t′, suggesting the Hi-C read is on the opposite phase of t′. Essentially, we need cis mappings to cluster unitigs coming from the same haplotypes together, and trans mappings to separate unitigs from different haplotypes. If there are massive Hi-C cis mappings bridging two heterozygous unitigs s and t, it is likely that s and t originate from the same haplotype. By contrast, large numbers of Hi-C trans mappings bridging s and t indicate they should be assigned to different haplotypes.

Modeling Hi-C phasing.

For a Hi-C read pair r, let x_rt = 1 if it has a cis mapping to unitig t or let x_rt = −1 if the Hi-C read has a trans mapping to t; otherwise x_rt = 0. Similar to the formulation of dual assembly, let δ_t ∈ {1, −1} denote the phase of a heterozygous unitig t. {x_rt} are observations while {δ_t} are variables whose values will be determined.

A Hi-C read pair may occasionally bridge two loci on different homologous haplotypes. Such a Hi-C pair is called a trans Hi-C pair. Suppose a Hi-C read pair r bridges unitig s and t and the probability of its being trans is ε_r. By the definition of x, x_rs and x_rt can be either 1 or −1. We have

$$P(x_{rs},x_{rt}\mid {\delta }_s,{\delta }_t)=\{\begin{array}{cc}(1-{\epsilon }_r)∕2\hfill & \text{if}{x}_{rt}{x}_{rs}{\delta }_t{\delta }_s=1\hfill \\ {\epsilon }_r∕2\hfill & \text{if}{x}_{rt}{x}_{rs}{\delta }_t{\delta }_s=-1\hfill \end{array}\phantom{\}}$$

or equivalently

$$P(x_{rs},x_{rt}\mid {\delta }_s,{\delta }_t)=\frac{1}{2}\sqrt{{\epsilon }_r(1-{\epsilon }_r)}\cdot {\left(\frac{1-{\epsilon }_r}{{\epsilon }_r}\right)}^{\frac{1}{2}{x}_{rt}{x}_{rs}{\delta }_t{\delta }_s}$$

The composite log likelihood of $\overrightarrow{\delta }$ over all unitigs is

$$\log L(\overrightarrow{\delta })=\sum _r\sum _{s,t}\log P(x_{rs},x_{rt}\mid {\delta }_s,{\delta }_t)=C+\frac{1}{2}\sum _{s,t}{\delta }_s{\delta }_t\sum _r{x}_{rs}{x}_{rt}\log \frac{1-{\epsilon }_r}{{\epsilon }_r}$$

where C is not a function of δ. Define $w_r=\log \frac{1-{\epsilon }_r}{{\epsilon }_r}$, which is effectively the weight of Hi-C read pair r. And introduce the cis and trans weights between unitigs:

$$\begin{gathered} W_{st}=\sum _{r\in \{r\mid x_{rs}{x}_{rt}=1\}}{w}_r \\ {\overline{W}}_{st}=\sum _{r\in \{r\mid x_{rs}{x}_{rt}=-1\}}{w}_r \end{gathered}$$

The equation above can be written as

$$\log L(\overrightarrow{\delta })=C+\frac{1}{2}\sum _{s,t}{\delta }_s{\delta }_t(W_{st}-{\overline{W}}_{st})$$ (2)

Maximizing the log-likelihood can be achieved by solving a max-cut problem again. The derivation above extends reference-based phasing of the linker¹² algorithm to unitig phasing.

As the probability of a Hi-C pair being trans depends on the insert size¹¹, we calculate ε_r = ε(d_r) where d_r is the distance between the two mapping positions of Hi-C fragment r on the unitig graph. We use an empirical multiple rounds method to iteratively fit function ε(d), assuming all unitigs are haplotigs. In each round of log-likelihood optimization, a trans Hi-C read pair r would be mapped to two heterozygous unitigs with different phases, where their phases are determined by the last round of log-likelihood optimization. We can then group Hi-C mappings around distance d and calculate the fraction of trans mappings in the group as $\widehat{\epsilon }(d)$. Note that in the initial round of optimization, all Hi-C read pairs are simply set to be cis due to the lack of phase for each unitig.

Finding near optimal solutions to the max-cut problem.

Statistical physicists often optimize an equation like Eq. (1) and (2) with stochastic algorithms. Hifiasm follows a similar route:

1. For each unitig t, randomly set δ_t to 1 or −1.

2. Arbitrarily choose a unitig t. Flip its phase (i.e. changing δ_t from 1 to −1 or vice versa) if doing so improves the objective function.

3. Repeat step 2 until the objective function cannot be improved. This reaches a local maximum. If the new local maximum is better than the best maximum so far, set it as the best maximum.

4. Perturb the best maximum either by randomly flipping a fraction of unitigs or by flipping all neighbors of a random unitig. Go to step 2 to look for a new local maximum.

5. Repeat steps 2 through 4 for 10,000 times by default and report the best local maximum in this process.

In practical implementation at step 3, hifiasm may flip a pair of unitig sets at the same time if the two sets of unitigs are inferred to come from opposite phases and to be homologous to each other. Such pairs can be identified based on a “bubble” structure¹⁴ in the assembly graph and all-versus-all pairwise alignment between unitigs. This heuristic speeds up convergence. To reduce the effect of erroneous homologous unitig identification, hifiasm does not apply the heuristic in the last round of optimization.

Assembly of test samples.

For all samples, we ran “hifiasm hifi.fa.gz” to produce primary/alternate assemblies and dual assemblies, and ran “hifiasm --h1 hic_1.fq.gz --h2 hic_2.fq.gz hifi.fa.gz” to produce Hi-C based assemblies. For trio binning assemblies, we used “yak count -b37 -o parent.yak parent.fq.gz” to count k-mers for both parents and ran “hifiasm -1 father.yak -2 mother.yak hifi.fa” for assembly. We ran HiCanu with “canu genomeSize=$GS useGrid=false -pacbio-hifi hifi.fa.gz”, where “$GS” is the genome size which is set to 3.1g for human, 2.65g for European badger, 1.85g for Sterlet and 3.05g for Black rhinoceros. We applied purge_dups²⁰ to the initial HiCanu assemblies of HG002, HG00733 and sterlet as this improves their assemblies. Purge_dups and additional evaluation command lines can be found in the supplementary materials.

Extended Data

Extended Data Fig. 1. Chromosome-level phasing results for hifiasm (Hi-C) human assemblies.

All contigs were aligned to the T2T CHM13 reference and the Y chromosome of GRCh38, and then the corresponding regions of contigs on the reference were determined based on the alignment results. For each chromosome, the top track and the bottom track indicate haplotype 1 contigs and haplotype 2 contigs, respectively. The phase density of contigs was calculated by the parental short reads. Gray bars indicate centromeric regions. (a) Chromosome-level phasing results for HG002 with 30X HiFi and 30X Hi-C. (b) Chromosome-level phasing results for HG00733 with 30X HiFi and 30X Hi-C.

Data availability

Human reference genome: GRCh38; HG002 HiFi reads: SRR10382244, SRR10382245, SRR10382248 and SRR10382249; HG002 Hi-C reads: “HG002.HiC_1*.fastq.gz” from https://github.com/human-pangenomics/HG002_Data_Freeze_v1.0; HG002 Parental short reads: from the same HG002 data freeze; HG00733 HiFi reads: ERX3831682; HG00733 Hi-C reads: SRR11347815; HG00733 Parental short reads: ERR3241754 for HG00731 (father) and ERR3241755 for HG00732 (mother); European badger: PRJEB46293; Sterlet: PRJEB19273; South Island takahe: https://vgp.github.io/genomeark/Porphyrio_hochstetteri/; Black Rhinoceros: https://vgp.github.io/genomeark/Diceros_bicornis/; All evaluated assemblies are available at https://zenodo.org/record/5948487 and https://zenodo.org/record/5953248.