Methods for modelling excess mortality across England during the COVID-19 pandemic

Abstract

Excess mortality is an important measure of the scale of the coronavirus-2019 pandemic. It includes both deaths caused directly by the pandemic, and deaths caused by the unintended consequences of containment such as delays to accessing care or postponements of healthcare provision in the population. In 2020 and 2021, in England, multiple groups have produced measures of excess mortality during the pandemic. This paper describes the data and methods used in five different approaches to estimating excess mortality and compares their estimates.

The fundamental principles of estimating excess mortality are described, as well as the key commonalities and differences between five approaches. Two of these are based on the date of registration: a quasi-Poisson model with offset and a 5-year average; and three are based on date of occurrence: a Poisson model without offset, the European monitoring of excess mortality model and a synthetic controls model. Comparisons between estimates of excess mortality are made for the period March 2020 through March 2021 and for the two waves of the pandemic that occur within that time-period.

Model estimates are strikingly similar during the first wave of the pandemic though larger differences are observed during the second wave. Models that adjusted for reduced circulation of winter infection produced higher estimates of excess compared with those that did not. Models that do not adjust for reduced circulation of winter infection captured the effect of reduced winter illness as a result of mobility restrictions during the period. None of the estimates captured mortality displacement and therefore may underestimate excess at the current time, though the extent to which this has occurred is not yet identified. Models use different approaches to address variation in data availability and stakeholder requirements of the measure. Variation between estimates reflects differences in the date of interest, population denominators and parameters in the model relating to seasonality and trend.

Introduction

The global spread and subsequent impact of coronavirus-2019 (COVID-19) has been profound. By early April 2021, there had been over 130 million confirmed cases of infection and nearly three million deaths among confirmed cases globally.^1,2 The impact of COVID-19 on mortality in the UK has been one of the highest in Europe. Data from May 2021 indicates that the UK has seen the largest number of deaths among confirmed cases of COVID-19 compared to any other European country and the 7th-highest case fatality rate globally.^2–4

A sole focus on COVID-19 confirmed deaths might underestimate the impact that this pandemic has had on mortality, as deaths in confirmed cases are highly dependent on testing patterns. In the early stages of the pandemic in England, testing was targeted at hospitalised cases; so, COVID-19 deaths among cases that were not confirmed by testing⁵ will have been missed. In addition, focusing solely on confirmed cases fails to include the indirect mortality resulting from the unintended consequences of containment, such as delays to accessing care or postponements of healthcare provision in the population.⁶ It also fails to account for potential positive indirect effects of social mobility restrictions such as reduced circulation of other viruses.⁷

Mortality from all causes, in particular the excess mortality over what would be expected from historical trends, is a more realistic measure of the pandemic burden. Monitoring of excess mortality from all causes throughout the COVID-19 pandemic can provide an objective and comparable measure of the impact of the pandemic, overcoming the issues of variation in testing and coding of cause of death.⁸ It is important retrospectively, to quantify the burden experienced in different population strata and to identify inequalities,^9,10 as well as prospectively, to inform policy.^5,11

Excess mortality is estimated by comparing the number of observed deaths to the number of deaths that would have been expected based on previously observed trends. Typically, the expected number of deaths is estimated through a model that uses historical data by assuming that historical trends would still pertain to the current time if the COVID-19 pandemic had not occurred. The discrepancy resulting from the difference or the ratio between the expected (counterfactual) and observed number of deaths is then taken as an estimate of the excess mortality.

During the COVID-19 pandemic, multiple academic, government and public health groups have estimated excess deaths in England.¹⁰⁻¹² Due to variation in the methodologies employed to construct the counterfactual, the type of data used, and the format of reporting of results, different estimates of excess have been published.¹⁰⁻¹⁵

In this paper, we review five different approaches adopted in England to estimating excess mortality. We describe their rationale and the assumptions they rely on as well as the data they use, to clarify the potential difference in results and interpretation between approaches. We present times series and relative cumulative estimates of excess for the first two waves of the pandemic in England and among English regions; we compare relative cumulative excess estimates at the end of each wave and discuss differences between estimates. Finally, we compare estimates of excess to observed COVID-confirmed deaths.

Data and methods

Estimation of excess mortality requires data on all-cause mortality in the current period, paralleled by comparable data for earlier years. Data on all-cause mortality come from the General Registry Office (GRO). As a death is registered, the record is available from the GRO by age in years, date of death, date of registration, gender and region of residence. After registration, the death is reported to the Office for National Statistics (ONS) where information on cause and place of death from the death certificate is added. This process adds a delay, making the report of the death less timely, but provides additional details. The number of deaths registered each week by sex, age group and region (of place of death) are regularly made publicly available via the ONS.¹² The ONS also publishes annual mortality data files for England and Wales containing counts of deaths by age, gender and region dating back to 2006.¹⁵

Date of interest

Excess mortality may be estimated either by date of death (DOD) or date of registration (DOR). The time series by date of death accurately reflects how the mortality burden evolves over time. However, since each death event is only recorded at the point of registration, this time series is typically incomplete, due to the delay between the occurrence of a death and the time it is registered at the general registry office.¹⁶ This delay is typically around 3 weeks, but can be much longer when coronial investigation is required.¹⁷ Furthermore, delays between death and registration may be even more subject to variation during pandemic periods.¹⁸ Therefore, when analysis by DOD is undertaken to monitor the burden of an emerging epidemic in a timely manner, observed deaths need to be corrected to account for the deaths not yet reported. This adds uncertainty to estimation of the excess deaths. Alternatively, analyses by DOD without a correction would require discarding 3 weeks of incomplete data, affecting the timeliness of the estimation. Estimating excess by DOR avoids any additional uncertainty introduced by delay correction and can produce robust estimates of excess once deaths have been registered, particularly among subgroups. These estimates are more difficult to interpret because these counts represent a mixture of deaths that happened on different days and do not therefore provide direct information on the evolution of the burden.

Delay adjustment

To adjust for the delay between DOR and DOD, a procedure is implemented by re-weighting the observed counts, with weights derived from the reporting delay distribution estimated using data from the past time periods using the observed delay distribution (i.e. the proportion of deaths registered at a lag of k weeks (k = 0,1,2,3,4,…, 52) by age and region) appropriately accounting for the right truncated nature of the data.¹⁹ Such weights are then applied to the observed death counts to estimate the total number of deaths, including those already occurred but not yet reported, for the corresponding age, region and interval from death to the day of the last registrations. Complications arise when this distribution is affected by sudden and unexpected shocks to the reporting system and the subsequent changes to registration procedures.¹⁰ In this case, more sophisticated statistical models may estimate the delay distribution and the resulting weights.¹⁹

Methods to construct the counterfactual

The key difference between alternative approaches to the estimation of excess mortality is in how the expected or baseline is estimated. Approaches based on statistical models express μ_t,s, the mean number of deaths y_t,s at time t (typically taken as a day or a week of the current period) for the subpopulation s (indexed by e.g. age-group, sex, geographic region, ethnicity and/or deprivation), as a function of number at risk N_t,s, historical mortality rate X_t,s (where t refers to the corresponding day or week of earlier periods, e.g. the previous year), a component f_t,s which takes different forms to describe time trends (e.g. trigonometric function or splines), and relevant covariates Z_j,s for j = 1,…,p, i.e. g(μ_t,s) = function(N_t,s, X_t,s, f_t,s, Z_t,s). Expected counts of deaths $\hat{\mu }$_t,s are derived separately for each population subgroup s, and excess deaths are then obtained as ED_t,s = y_t,s − $\hat{\mu }$_t,s. Alternatively, relative excess deaths are defined as RED_t,s = y_t,s /$\hat{\mu }$_t,s. Note that t could represent either the time of death occurrence (DOD model) or the time at which a death is registered (DOR model); so, each model specifies the covariate appropriate to the outcome being considered.

Time of registration models

1. Weekly quasi-Poisson generalised linear model with offset based on DOR (Quasi-Poisson model)

This method estimates the daily counts of expected deaths based on DOR for population subgroups defined by age, sex, geographic area of residence (Regions (former Government Office Regions) and Upper Tier Local Authority), ethnic group, deprivation quintile and place of death.⁹ Variation in registration patterns (e.g. weeks when there are days when deaths are not routinely registered) needs to be incorporated into the structure of DOR models. The model includes historical mortality rate (X_t,s) and a component f_t,s composed of a number of independent time-related variables: a continuous covariate for calendar time, t, accounting for systematic changes in the rate of death with time; 12 binary dummy variables, one per calendar month, taking value 0 for any week except for the two associated with the months whose midpoints are closest to that date, which take values between 0 and 1, the higher value relating to the month that's closest and always summing to 1, describing seasonality;²⁰ dummy variables indicating weeks containing public holidays, weeks ahead of and following a week with a public holiday. The final form of the model is

$$ln({\mu }_{t,s})=ln(N_{t,s})+{\beta }_s{X}_{t,s}+{\eta }_s{f}_{t,s}$$ [1]

Parameters β_s and η_s are estimated under the assumption that the observed count of deaths y_t,s are a draw from a quasi-Poisson distribution;²¹ here, variance increases linearly with the predicted mean (i.e. equivalent to a Poisson distribution) but the model also incorporates an estimated scale parameter (φ), which can be >1 allowing for overdispersion.

The expected total deaths $\hat{\mu }$_t in a chosen week are obtained by summing the samples across subgroups. To quantify uncertainty, a prediction interval for the expected number of deaths in a week is generated using a Monte Carlo approach. Multiple samples are drawn from a negative binomial distribution, which is itself a form of the quasi-Poisson model. These draws are obtained by making a minor modification to the usual rnbinom(.) function in R, which generates pseudorandom draws from a negative binomial distribution: specifically, the arguments are set to be equivalent to making draws from a quasi-Poisson distribution with the required expected count and scale parameter. Working week by week these sampled values are summed over all subpopulations (e.g. by age and sex) and the empirical 0.00135 and 0.99865 probability quantiles based across all the multiple samples are used as upper and lower prediction intervals. These quantiles correspond to ±3 standard deviations for a normal standardised deviate, which is the metric of variability/uncertainty generally used by Public Health England to produce weekly reports of excess deaths nationally and among population subgroups.⁹

2. Weekly 5-year Average based on DOR (5-year average)

Daily or weekly number of expected deaths based on DOR can be simply estimated using the average of the observed counts of death in the corresponding day or week in each of the five baseline years. Denoting by t[year] the t^th day (or week) for a generic year, the estimated count is

$${\hat{Y}}_{t[year]}={\displaystyle \frac{{\sum }_{j=year-5}^{year-1}{y}_{t[j]}}{5}}$$ [2]

Here, “corresponding” implies, for example, that the relevant days of the week are aligned between the target year (in our case 2020) and each of the baseline years (2015–2019). This method is used by the Office for National Statistics (ONS) to report excess deaths in England and Wales.¹² In line with what is presented by the ONS, no uncertainty estimates are calculated.¹²

Time of deaths models

1. Weekly Application of the European monitoring of excess mortality algorithm based on date of death (EuroMOMO model)

In the European monitoring of excess mortality (EuroMOMO) algorithm, introduced to allow for timely comparisons across European countries for public health action,¹³ the baseline of weekly expected counts is defined through a Serfling model²² and weekly deaths from the past 5 years (X_t,s):

$$ln({\mu }_{t,s})=ln(N_{t,s})+{\beta }_s{X}_{t,s}+{\eta }_{1,s}t+{\eta }_{2,s}sin(2\pi t/k)+{\eta }_{3,s}cos(2\pi t/k)$$ [3]

Sine and cosine terms represent seasonality, with periodicity generally selected to have a full period in 1 year. This model is generally fitted to counts of deaths observed in spring and autumn over the past 5 years, allowing estimation of baseline mortality during a period not affected by winter-specific factors. The estimated trigonometric function is then used to derive, through extrapolation, the baseline mortality in that period. The 2 and 3 standard deviation prediction intervals are computed, and daily excess is considered to be significant whenever observed counts exceed the 3 standard deviation upper bound of the interval. Three standard deviation prediction intervals are presented in time series charts. For cumulative estimates, the same method described for the quasi-Poisson model was used for calculating prediction intervals.

Here, a correction for delay from death to registration based on historic delays¹³ is applied to Y_t,s, and the model is fitted using an over-dispersed Poisson distribution as in equation 1. The estimated number of excess deaths and the corresponding standard deviations (z-scores) above the expected baseline²³ are included in the routine weekly monitoring of all-cause excess mortality in England.

2. Daily quasi-Poisson generalised linear model with offset based on date of death (Poisson model)

This method estimates daily counts of expected deaths by DOD assuming they are independently distributed, with the mean µ_t,s modelled through a quasi-Poisson generalized linear model, similar to the one in equation 1.

A log-linear time trend adjusts for changes in deaths over time due to demographic factors, whereas death counts around the same day of the year (±7 days) from the past 5 years allow accounting for seasonality. These components of the model are equivalent to the corresponding elements of the model underpinning approach 1.

The 2 and 3 standard deviation prediction intervals are computed, and daily excess is considered to be significant whenever observed counts exceed the 3 standard deviation upper bound of the interval. The model and threshold calculation is the same as the Farrington method used for outbreak detection but with daily rather than weekly data and without any reweighting based on outlier data. Three standard deviation prediction intervals are presented in time series charts. For cumulative estimates the same method described for the quasi-Poisson model was used for calculating prediction intervals. This model is published as part of Public Health England's (PHE) surveillance cell weekly reports.¹⁰

3. Daily synthetic controls model based on DOD (synthetic controls model)

Daily baseline mortality here is estimated by fitting a model to the observed mortality before the outbreak, identifying the most suitable predictors. Such variables must fulfil the condition of being potentially good predictors of mortality in the absence of COVID-19, and not being affected by COVID-19 itself. The counterfactual, that is, baseline mortality in the absence of COVID-19, can then be forecast. Beyond daily death rates in the past 4 epidemic years (X_t,s), factors closely associated with mortality such as weather conditions (temperature and rainfall) and incidence of viral infections (influenza and Respiratory Syncytial Virus (RSV)) are included in the matrix Z_t,s along with their lagged values up to 7 days, as some covariates might lead to delayed effects. If all of the assumptions of the above are met, the estimated excess deaths can then be interpreted as a result of the pandemic, not confounded by variation in weather or circulating pathogens in the current season.

These predictors are included as control time series in a Bayesian structural time series model (BSTS), an alternative to the more traditional regression models:

$$\begin{array}{rl}& Y_{t,s}={\mu }_{t,s}+{\beta }_s{X}_{t,s}+{\zeta }_s{Z}_{t,s}+e_{t,s}\\ & {\mu }_{t,s}={\mu }_{t-1,s}+{\gamma }_{t,s}\end{array}$$ [4]

Daily deaths are expressed as a linear combination of a time-varying mean μ_t,s, which describes the outcome dependency over time through an evolution equation. Here, the evolution equation is expressed as a random walk, and the noise components are assumed to be Gaussian both in the evolution and the observation equation. A Bayesian variable selection allows including many time series as covariates without selecting them a priori, as their predictive contribution can be estimated through a spike-and-slab prior²⁴ and combined into a weighted average, whose weights are derived to maximise model fit to observed data.

Uncertainty is quantified through credible intervals for the mean, whereas excess mortality is quantified as the difference between observed counts y_t,s and the estimated counterfactual (${\hat{}}_{t,s}$), for t > t₁, and the corresponding credible intervals are obtained from the posterior predictive distribution.

Results

To describe excess in the different population subgroups over time we consider two critical time periods within the first 12 months of the pandemic: March 2020 to June 2020 and September 2020 to March 2021, representing the first and second wave, respectively. To make comparisons between estimates for DOD and DOR models at similar time points, we describe weekly and cumulative estimates of excess from DOD models at time point t and corresponding estimates of DOR models at t + 5 days (Supplementary Table 1). Full details of cumulative estimates for each model are available in Supplementary Tables 2 (Wave 1) and 3 (Wave 2).

Cumulative estimates of excess mortality

During the period of the pandemic March 2020 through to March 2021, all five models estimated cumulative excess mortality in excess of 100,000 deaths. The synthetic controls model estimated the highest excess (116,103.3), while the quasi-Poisson model estimated the lowest excess (101,301.6).

Cumulative estimates of excess for the first and second wave of the pandemic

During the first wave of the pandemic all models provided similar cumulative estimates for each population subgroup (Figure 5), quantifying that mortality in England was 50% higher than expected for that time of the year. The variation across genders is small, with a slightly more pronounced excess in men compared to women, whereas relative excess differs markedly across age groups: non-significant in the youngest, below 25% in the 15-44, around 40% in the 44–64 and 65–74, and above 50% in the elderly. Regional variation was also generally consistently estimated: all models estimate over 70% excess deaths in London, while the South-West saw a 25–30% excess. The synthetic control model estimates lower excess for some regions compared to other models: this could be due to the estimates accounting for meteorological conditions, as 2020 saw a mild spring in some parts of the country.

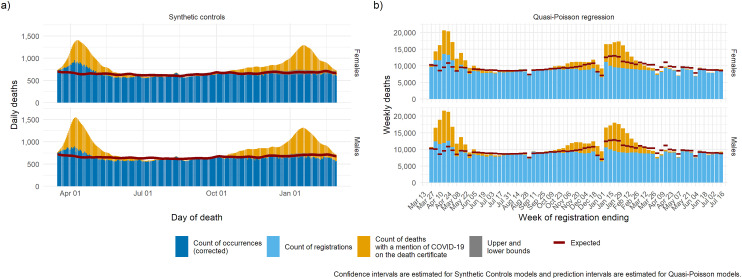
Figure 5.

Expected deaths and delay-corrected deaths (DOD models) or registered deaths (DOR models) by gender for the period March 2020 through to March 2021: (a) synthetic controls, (b) quasi-Poisson regression.

DOD: date of death; DOR: date of registration.

Agreement between models in wave 2 is weaker, with nation-wide excess estimated to range between 20% and 35%. Generally, the synthetic controls model produces a higher excess because it has factored in the lower flu circulation of winter 2020/2021. Interestingly, all models indicate no clear pattern of more sustained relative excess as age increases: the largest excess (over 30% for all models) is observed in the 45–64 years old, while for other age groups the excess mostly ranges between 20% and 30% (except for the youngest). Region-wise, London above 30% and North East below 20% represent the two extremes; however, weekly reporting has shown that different English regions experienced very different epidemics during the second wave.^9,13

While the differences in estimates of excess are larger for the second wave due to different approaches to modelling, all model estimates become less reliable as the baseline is projected further over time. This is driven by two factors. The first is that trends in mortality over previous years become less stable as they are projected over longer periods. The second is that any increase in mortality is inevitably followed by some reduction in mortality from other causes in the subsequent time period. This is because deaths of some individuals will occur among those who, in the absence of the event causing the increase in mortality, would have died of an alternative cause, and likely on an alternative date. This concept is often described as mortality displacement or harvesting.²⁵ Extensive periods of mortality displacement make population denominator estimates and therefore baseline rates of mortality less reliable. This is particularly disruptive to estimates of excess by cause of death as these estimates are affected by displacement of mortality by time and cause.

Time series estimates of excess in England March 2020 through March 2021

Time series estimates of excess for all persons

We present plots of observed deaths from all causes and predicted trends as estimated by the five models for the period March 2020 through to March 2021, using data as observed on 22 March 2021. For each model we present daily or weekly time series (depending on the unit of analysis used within the model).

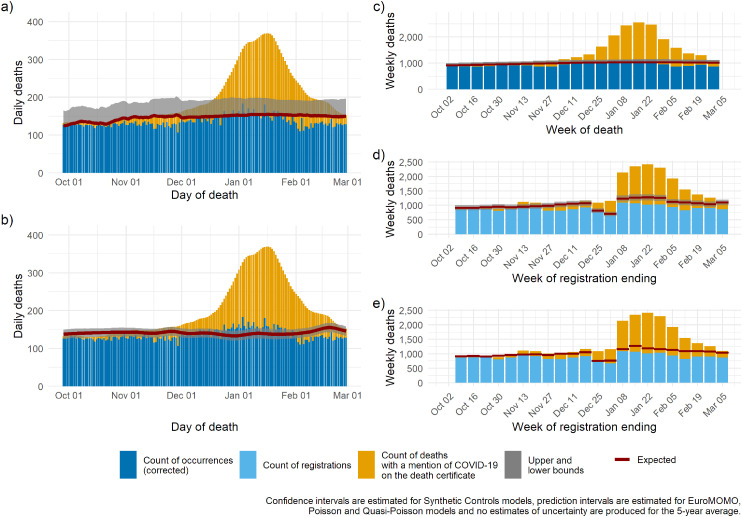
The smooth baseline of DOD models (daily and weekly) reflects the consistent nature of deaths day to day, while the baseline of DOR models reflects the changing pattern of death registrations over holiday periods and during weeks with public holidays. Comparing the two DOD models on the left, synthetic controls capture a lower baseline in winter (second wave) as it accounts for lower viral circulation. Comparing the two DOR models, the baseline of the quasi-Poisson model increases slightly over time as it adjusts for an ageing population within the population denominators, while the 5-year average based on counts does not. The baseline of the quasi-Poisson model fluctuates around public holiday dates specific to the current period while the 5-year average model fluctuates around the public holiday dates of the previous 5 years. This difference is highlighted by the movement in the quasi-Poisson model baseline around April 2020: because Easter weekend has occurred in a different week each year for the previous five years this movement smoothed out over five weeks in the 5-year average model.

Time series estimates of excess showing COVID-19 mentions on the death certificate

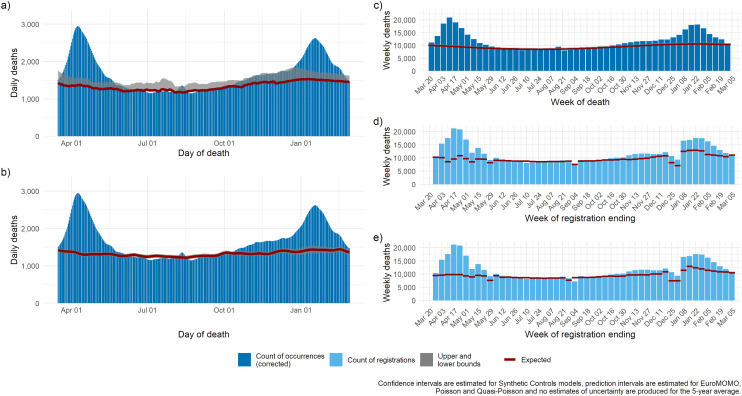
We select one daily model by DOD and one weekly model by DOR, and we compare their estimates to the number of deaths with mention of COVID-19 on the death certificate (Figure 2). Both models highlight an excess mortality over and above those with a mention of COVID-19 during the first wave, whereas the situation reverts during the second wave: the number of deaths that would have happened in absence of COVID-19 estimated by the synthetic controls model mimics the observed non-COVID-19 deaths, while the quasi-Poisson estimates a higher baseline, as it models a counterfactual based on a ‘normal’ winter, with influenza circulation and both models ignore mortality displacement consequent upon premature deaths occurring earlier in the pandemic.

Figure 2.

Expected deaths and delay-corrected deaths (DOD models) or registered deaths (DOR models) for five models for the period March 2020 through to March 2021: (a) Poisson regression; (b) synthetic controls, (c) EuroMOMO, (d) quasi-Poisson regression, (e) 5-year average.

DOD: date of death; DOR: date of registration; EuroMOMO: European monitoring of excess mortality.

Figure 1.

Relative cumulative excess mortality for England and selected subgroups for the first and second waves of the pandemic using five different models: synthetic controls, Poisson regression, quasi-Poisson regression, 5-year average and European monitoring of excess mortality.

Time series estimates of excess by age and sex

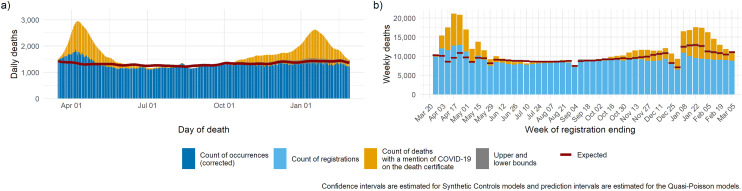
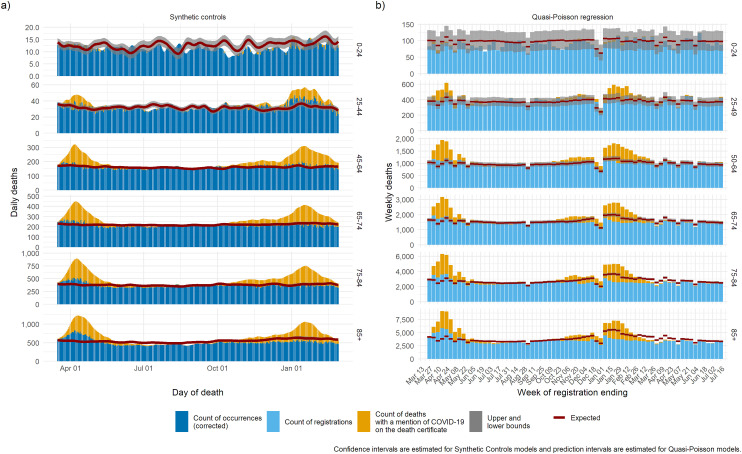
We then present the trend in mortality split by age group (Figure 3) and by gender (Figure 4) for the synthetic controls model and the quasi-Poisson model. Both models estimate the baseline to a precise level of detail in all age groups except the age group 0–24 years, where mortality is low, and the uncertainty is high. Mortality below baseline was observed during the summer in the 85+  age group, suggesting a possible mortality displacement caused by the first wave.

Figure 3.

Expected deaths and delay-corrected deaths (DOD models) or registered deaths (DOR models) and Covid-19 mentions for the period March 2020 through to March 2021: (a) synthetic controls, (b) quasi-Poisson regression.

DOD: date of death; DOR: date of registration; Covid-19, coronavirus-2019.

Figure 4.

Expected deaths and delay-corrected deaths (DOD models) or registered deaths (DOR models) by age group for the period March 2020 through to March 2021: (a) synthetic controls, (b) quasi-Poisson regression.

DOD: date of death; DOR: date of registration.

Excess mortality where COVID-19 was not mentioned on the death certificate was more pronounced among the elderly (75–84 and 85+) and among women during the first wave. This may be due to limited access to testing or limited access to treatment during periods when services were overwhelmed. During the second wave both models highlight deaths in excess of what were expected where COVID-19 was mentioned on the death certificate among the group aged 25–44, as well as potential mortality displacement among the group aged 85+.

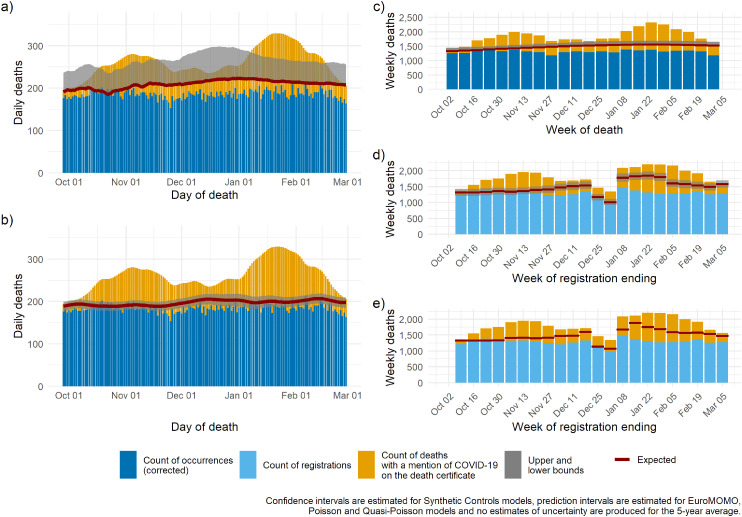
To illustrate regional heterogeneity in the epidemic during the second wave, we present region-specific time series estimates of the baseline from the five models: plots for London and the North West are presented in Figures 6 and 7, figures for other English regions are available in Supplementary Figures 1–7. The two regions recorded very different trends in deaths: London (Figure 6), similar to other southern regions, had one substantial increase in mortality over and above the expected between December and March. Conversely, the North West (Figure 7), similar to Yorkshire and Humber and the North East (Supplementary Figures 2 and 4), experienced early and sustained excess over the period of the second wave characterised by two flat sub-waves, the first rising in October and the second in December. The overlaid estimated baselines facilitate identification of periods characterised by excess: despite important differences in the size of the uncertainty around the estimated baseline, all five models detect excess mortality at similar times; however, only the synthetic controls, and to some extent EuroMOMO produce estimates similar to number of deaths with COVID-19 mentioned on the death certificate.

Figure 6.

London: expected deaths and delay-corrected deaths (DOD models) or registered deaths (DOR models) for five models for the period October 2020 through to March 2021: (a) Poisson regression; (b) synthetic controls, (c) EuroMOMO, (d) quasi-Poisson regression, (e) 5-year average.

DOD: date of death; DOR: date of registration; EuroMOMO: European monitoring of excess mortality.

Figure 7.

The North West: expected deaths and delay-corrected deaths (DOD models) or registered deaths (DOR models) for five models for the period October 2020 through to March 2021: (a) Poisson regression; (b) synthetic controls, (c) EuroMOMO, (d) quasi-Poisson, (e) 5-year average.

DOD: date of death; DOR: date of registration; EuroMOMO: European monitoring of excess mortality.

Time series estimates of excess by region

Discussion

We present descriptions of data and methods as well as results from five key models for estimating excess mortality in England from March 2020 through to March 2021. Among the five models presented, estimates were strikingly similar during the first wave of the pandemic. As the pandemic progressed into the second wave, models that adjusted for reduced circulation of winter infection produced higher estimates of excess mortality.

The choice of whether to use methodologies to adjust for circulating winter infections is dependent on the overarching aims of the model. For models aiming to capture the overall direct and indirect impact of the pandemic including the impact of restriction on movement, adjusting for reduced pathogen circulation through the winter months would be counter to the model aims. For those models that aim to provide near-real time surveillance of the pandemic, the adjustment for lower circulation of other pathogens aims to allow for more sensitivity in detecting excess mortality attributable to COVID-19. However, this is done retrospectively and relies on completeness of ascertainment and reporting.

Near-real time surveillance of mortality for epidemic surveillance is most easily interpreted using DOD as the date of interest. However, DOD models are estimated from DOR data using a delay correction to estimate the number of deaths that have occurred. This delay correction can be unreliable during times of rapid increase or decrease in deaths. An example of this occurred early in the pandemic, when deaths increased rapidly in London, the EuroMOMO delay correction initially substantially overestimated excess mortality. This happened because the delay correction algorithm employed methods to account for increased delays to registration during periods of increased mortality but in reality, changes to registration processes in England during the pandemic reduced the delay in death registrations¹⁶; this resulted in the delay correction producing inaccurate projections.

The methodologies adopted by each of the models presented in this paper provide estimates of excess that meet different stakeholder needs. DOD daily models (Poisson and synthetic controls) provide epidemiological surveillance of the pandemic in near real time. This is particularly important for key decision makers in government and groups interested in modelling the impact of interventions on mortality. While all models would produce a fair retrospective international comparison, limited data availability and inconsistency of data between countries restricts which models can be implemented. The EuroMOMO model adopts a flexible methodology allowing for a reduction in the input data required thereby enabling comparisons between countries.²³ The quasi-Poisson model provides robust estimates among small subgroups and, because it uses DOR, can present excess among cause of death, place of death and down to small geographical units Upper Tier Local Authorities (UTLAs). As a result, this model proves to be a useful pragmatic tool for policy makers to monitor and respond to rapid changes in the number of registered deaths at such times, and to interpret these results in the light of their implications for monitoring excess deaths from non-COVID-19 causes. Finally, the 5-year average is quick to produce, particularly from a standing start at the beginning of the pandemic; however, because it does not properly account for fluctuations in death registrations around bank holidays, during holiday periods, estimates should be interpreted with caution at these times.

While excess mortality models are a key tool for monitoring and assessing the impact of the pandemic, there are some limitations shared by all models. For example, the data used in all of these approaches (DOR or DOD) fail to deal rigorously with deaths that require coronial investigation (e.g. suicides or accidents) when those data are to be analysed within 12 months of the date of occurrence. Models are unable to differentiate excess mortality that are indirectly caused by the pandemic (e.g. delays to treatment) from COVID-19 deaths that have not been classified as COVID-19. Another important limitation of excess mortality is that the estimates are not strictly appropriate for direct comparisons between groups. Excess mortality is estimated for each group given the age structure within each group. For direct comparisons between groups that control for the age (and other factors) between groups, a further step to standardise estimates is required.² Finally, as the pandemic continues, estimates of expected deaths based on estimates of mortality from years prior to the pandemic cannot fully account for the impact the pandemic will have on future trends in mortality when those trends are inevitably perturbed by the premature deaths caused by the pandemic.

This is the first paper to describe and differentiate the methods to help clarify the different measures of excess mortality that have been published during the COVID-19 pandemic in England. It provides detail of the data and methodologies applied to five key measures used in England and differentiates the results with reference to the methods used. We present each model as they are published to enable comparisons of real outputs. However, it does have some limitations. We could not compare an exhaustive list of methods of estimating excess; instead, we have focused on five key methods. In the absence of a gold standard methodology for comparison, we were unable to formally assess the accuracy of the models. Finally, the different data used in DOD and DOR models limit direct comparisons of excess between methods using DOD and those using DOR; however, this does provide a pragmatic and realistic approach to comparisons between models.

The various approaches to estimating excess mortality we have investigated, all produce similar estimates that provide a robust estimate of the true extent of the impact of the pandemic on mortality. Differences between the approaches used by each model reflect differences in data availability and stakeholder requirements of the measure. Differences between the results of each method reflect the use of DOD, DOR, population denominators and parameters in the model relating to seasonality and trend. These approaches are all complementary and any of them may be used when their particular characteristics best reflect the required aim of analysis and the particular data available to underpin that analysis.

Table 1.

Cumulative excess mortality for England using five different models for all persons in England: synthetic controls, Poisson regression, quasi-Poisson regression, 5-year average and EuroMOMO. DOD models 16/03/2020–28/02/2021, DOR models 21/03/2020–05/03/2021.

Model	Cumulative estimates of Excess Mortality	Credible intervals
Synthetic controls	116,130.3	(105,597.9–126,673.2)
Poisson regression	111,619.1	(109,566.5, 113,640.3)
Quasi-Poisson regression	101,301.6	(99,168.3, 103,293.9)
5-year average	107,780.0	(Not calculated)
EuroMOMO	113,693.5	(111,740.8, 115,805.6)

EuroMOMO: European monitoring of excess mortality; DOD: date of death; DOR: date of registration.