Abstract
Quiescent cancer cells are rare nondiving cells with the unique ability to evade chemotherapies and resume cell division after treatment. Despite the associated risk of cancer recurrence, how cells can reversibly switch between rapid proliferation and quiescence remains a long‐standing open question. By developing a unique methodology for the cell sorting‐free separation of metabolic profiles in cell subpopulations in vitro, we unraveled metabolic characteristics of quiescent cells that are largely invariant to basal differences in cell types and quiescence‐inducing stimuli. Consistent with our metabolome‐based analysis, we show that impairing mitochondrial fatty acid β‐oxidation (FAO) can induce apoptosis in quiescence‐induced cells and hamper their return to proliferation. Our findings suggest that in addition to mediating energy and redox balance, FAO can play a role in preventing the buildup of toxic intermediates during transitioning to quiescence. Uncovering metabolic strategies to enter, maintain, and exit quiescence can reveal fundamental principles in cell plasticity and new potential therapeutic targets beyond cancer.
Keywords: cellular quiescence, fatty acid oxidation, metabolic adaptation, trimetazidine, quiescence-proliferation transition
Subject Categories: Cancer, Cell Cycle, Metabolism
Analyses of the metabolic adaptation of human cell lines transitioning into quiescence reveal a metabolic signature common to different cell types and quiescence‐inducing stimuli, indicating fatty acid oxidation as a key vulnerability in quiescent‐induced cancer cells.
Introduction
Cellular quiescence (G0) is a fundamental operating principle in cells to enable long‐term survival in a reversible nondividing state following cell cycle arrest in G1 phase (Hua & Thompson, 2001; Coller et al, 2006; Liu et al, 2007; Valcourt et al, 2012; Cheung & Rando, 2013). Essential functions in the human body, such as the immune response (Hua & Thompson, 2001; Chapman et al, 2020), hematopoiesis (Pietras et al, 2011), tissue repair, and regeneration (Li & Clevers, 2010; Cheung & Rando, 2013; Cho et al, 2019) rely on the ability of cells to enter a quiescent, nondividing state, and subsequently switch back to proliferation. Paradoxically, nonproliferating cells can be found also among tumor cells (Jackson, 1989; Aguirre‐Ghiso, 2007; Giancotti, 2013; Zeuner, 2015). While rare, quiescent cancer cells exhibit increased radio‐ and chemoresistance (Dembinski & Krauss, 2009; Chen et al, 2012; Brown et al, 2017), and when reactivated from their dormant state can be responsible for cancer recurrence and metastasis (Mellor et al, 2005; Chen et al, 2012; Sosa et al, 2014; Ramirez et al, 2016; Brown et al, 2017), posing a major challenge in cancer therapy.
Environmental signals indicating unfavorable conditions, including nutrient limitation (Zhang et al, 2015), stress (Yang et al, 2020), cell–cell contact, or the absence of growth factors (Coller et al, 2006; Mitra et al, 2018), can trigger the entry into quiescence. A key feature of quiescent cells is the ability to maintain cellular homeostasis in a nondividing state for long periods (i.e., years). Despite their apparent dormancy, quiescent cells remain viable and have the ability to rapidly switch back to fast proliferation. It is hence not surprising that metabolism in quiescence is more active than previously thought. However, while rewiring of metabolism has become a hallmark of rapidly proliferating cancer cells (Vander Heiden et al, 2009; Hanahan & Weinberg, 2011; DeBerardinis & Chandel, 2016; Keibler et al, 2016; Pavlova & Thompson, 2016; Vander Heiden & DeBerardinis, 2017; Fendt et al, 2020), a similar description of the metabolic characteristics in quiescent cancer cells is lagging behind.
Mounting evidence suggests an involvement of metabolism in mediating cellular quiescence across multiple cell types. Quiescent fibroblasts, endothelial cells, adult stem cells, and B‐lymphocytes reportedly exhibit active energy generation and homeostasis‐related metabolic processes (Lemons et al, 2010; Coloff et al, 2016; Lee et al, 2017; Kalucka et al, 2018) like fatty acid degradation (Ito et al, 2012; Knobloch et al, 2017; Kalucka et al, 2018), TCA cycle, and oxidative phosphorylation. However, most studies relied on genomic or proteomic measurements, and systematic and direct characterization of the metabolic features of quiescence is missing. Moreover, to what extent does metabolism play a role in the adaptation of nondividing cancer cells to microenvironmental challenges (Hu et al, 2011; Carmona‐Fontaine et al, 2017; Lyssiotis & Kimmelman, 2017; Kumar et al, 2019) or treatment‐induced stress and drug tolerance (Dembinski & Krauss, 2009; Chen et al, 2012; Ramirez et al, 2016; Brown et al, 2017; Yang et al, 2020) have remained key open questions.
Here, we monitored metabolic changes in six largely different cell types, including cancer cells, transitioning from rapid proliferation into a quiescent state induced by three different environmental stimuli. To overcome technical limitations in preserving and profiling the metabolic state of quiescent cells, we developed an original methodology that allows differentiating metabolic signatures of cell subpopulations without the need for physical separation (i.e., cell sorting). This approach allowed us to generate an unprecedented compendium of metabolic profiles of quiescent cells in six different cell lines and three quiescence‐inducing conditions. Remarkably, we found direct evidence for a common metabolic adaptation to quiescence that is shared among different cell types and is largely independent of the quiescence stimulus. Consistent with previous findings (Ito et al, 2012; Knobloch et al, 2017; Kalucka et al, 2018), our metabolome‐based analysis revealed a key difference in fatty acid degradation in quiescence. We show that fatty acid β‐oxidation (FAO) becomes a vulnerability in quiescence‐induced cells and suggest that beyond its roles in mediating energy and redox balance, FAO can also prevent the accumulation of toxic intermediates in cells transitioning to quiescence.
Results
Quiescent cells rapidly exit growth arrest and resume proliferation
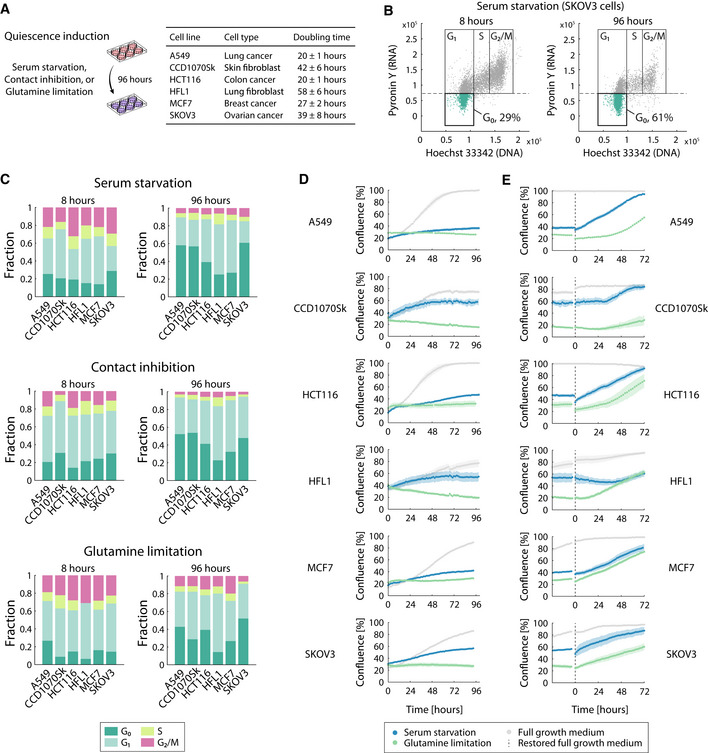
A reversible cell cycle exit in G1 phase and the ability to resume proliferation are defining characteristics of quiescent (G0) cells (Jackson, 1989; Coller et al, 2006; Coller, 2011; Zeuner, 2015; Cho et al, 2019). However, whether these abilities depend on the cell type or specific quiescence‐inducing stimuli remains unclear. Here, we monitored the transition between rapid proliferation and quiescence in a diverse set of adherently growing human cell lines and under quiescence‐inducing conditions (Fig 1A). We chose six human cell lines exhibiting different proliferation rates, i.e., doubling times between 20 and 58 h (Fig 1A). Specifically, we included four cancer cell lines of different tissue origins (i.e., A549 lung, HCT116 colon, MCF7 breast, and SKOV3 ovarian cancer cells, Fig 1A) with largely different genetic backgrounds (i.e., mutations (Ikediobi et al, 2006)) and basal metabolic states (Ortmayr et al, 2019) (Appendix Fig S1), and two nontransformed fibroblast cell lines (i.e., CCD1070Sk (Liu et al, 2007) and HFL1 (Coller et al, 2006)) previously used to model cellular quiescence in vitro (Coller et al, 2006; Liu et al, 2007). As environmental stimuli inducing a transition from proliferation into a quiescent state, we selected two that are well‐established: serum starvation (Coller et al, 2006; Liu et al, 2007; Mitra et al, 2018) and contact inhibition (Coller et al, 2006; Leontieva et al, 2014; Mitra et al, 2018), and a less conventional stimulus that is more directly linked to cellular metabolism, i.e., glutamine limitation. All three conditions also mimic in vivo shifts in the cancer environment (Carmona‐Fontaine et al, 2017; Lyssiotis & Kimmelman, 2017), i.e., the lack of growth signals in a foreign niche, space limitations in an intact tissue or solid tumor, or nutrient gradients in tissue regions secluded from blood vessels, respectively. To induce quiescence, we exposed the cell lines separately to each of the three quiescence stimuli for 96 h. Cells were seeded and maintained at confluence (contact inhibition), or subconfluent cells were incubated with media lacking fetal bovine serum (serum starvation) or glutamine (glutamine limitation), respectively. We quantified the end‐point fraction of quiescent (G0) cells in each condition using a previously established flow cytometry‐based assay (Kim & Sederstrom, 2001) (Fig 1B, Dataset EV1).
Figure 1. A collection of in vitro models for cellular quiescence in diverse human cell types.
-
ASchematic illustration of the experimental setup for the induction of quiescence in six different adherently growing cell types using three quiescence stimuli (i.e., serum starvation, contact inhibition, or glutamine limitation) for 96 h. Cell‐type and basal growth characteristics of the six cell lines are reported in the table.
-
BFlow cytometry‐based stratification of cells in different cell cycle phases and in G0 (quiescence, 2n DNA, and low RNA content), shown for SKOV3 cells in serum starvation conditions at 8 and 96 h, respectively. Cells were detached, fixed with ethanol, and stained with Hoechst 33342 and Pyronin Y prior to flow cytometry analysis.
-
CDistribution of cell cycle phases in six cell lines exposed to quiescence‐inducing conditions (see Panel A) for 8 and 96 h, respectively. Each stacked bar plot reports the fraction of cells in G0, G1, S, and G2/M phases, estimated using the assay depicted in panel B.
-
DCell confluence of adherent cell cultures in quiescence‐inducing conditions (i.e., serum starvation and glutamine limitation) was monitored using time‐lapse microscopy in a plate reader (TECAN Spark 10M) in 1.5‐h intervals. Contact‐inhibited cells no longer grow in monolayers and could not be accurately imaged with this approach. Data points and shaded areas indicate mean ± standard deviation (SD) over three biological replicates. Approximately 9,500, 4,500, 19,500, 6,700, 19,500, and 9,500 cells/well were seeded for glutamine limitation and serum starvation of A549, CCD1070Sk, HCT116, HFL1, MCF7, and SKOV3 cells, respectively.
-
EDynamic changes in cell confluence (as described in panel D) after restoring normal growth conditions (at 0 h, i.e., fresh growth media containing both fetal bovine serum and glutamine) after 96 h of quiescence induction. Data points and shaded areas indicate (mean ± SD) over three biological replicates.
At 96 h after exposure to quiescence stimuli, cell populations consisted for the vast majority (~90%) of cells in either G1 or G0 phase (2n DNA content) (Fig 1B and C, and Appendix Fig S1, Dataset EV1). The fraction of G0 phase cells in the population increased in all tested conditions, on average 2.25‐fold, reaching between 30 and 60% G0 cells (Fig 1C). Next, we asked whether the dynamics of the transition between rapid proliferation and quiescence is affected by the diversity in cell types and physiology (i.e., basal growth rates), as well as quiescence‐inducing conditions. After inducing quiescence by either serum starvation or glutamine limitation, we observed a rapid reduction in growth rates (Fig 1D and Appendix Fig S1, Dataset EV2), and a near‐complete growth arrest after approximately 72 h. To probe the ability to spontaneously resume proliferation, after 96 h of quiescence induction we restored normal growth conditions (i.e., full growth media containing both glutamine and serum). Remarkably, we observed an almost instantaneous exit from growth arrest and a return to a rapid proliferation in all cancer cell models (Fig 1E, Dataset EV2), with the two fibroblast cell lines exhibiting a slight delay and resuming growth within 24 h. Hence, our in vitro model allows reliably probing key functional characteristics of quiescent cells, and the collected growth phenotypic data uncovered largely similar growth dynamics upon entry and exit from quiescence. This similarity hinted at adaptive processes that are largely independent of cell types and quiescence‐inducing stimuli and potentially, not only mediate the switch from proliferation to quiescence but can also prepare for regrowth (Fig 1E and Appendix Fig S1).
Cells in G0 phase display a common metabolic signature
The ability of cells to rapidly switch between proliferation and quiescence requires highly coordinated metabolic adaptation to maintain homeostasis and avoid exhaustion of essential intermediates and/or the buildup of toxic intermediates, and at the same time prepare to rapidly resume growth by providing the necessary energy and biosynthetic precursors for cell division (Vander Heiden et al, 2009; Boroughs & DeBerardinis, 2015; Keibler et al, 2016; Pavlova & Thompson, 2016). However, despite mounting evidence for quiescence‐specific transcriptional programs (Coller et al, 2006; Liu et al, 2007), direct and systematic evidence of universal metabolic characteristics mediating adaptation of cells in G0 phase is missing.
Measuring metabolic differences between quiescent and proliferating cell subpopulations remains a major challenge. Like in an in vivo context, quiescence‐induced cell cultures in vitro harbor mixed populations with co‐occurring cells in G0 and other cell cycle phases (Fig 1, Dataset EV1). While cell sorting of heterogeneous populations allows for selection of cells in different cell cycle phases (e.g., only G0 cells), this technique implies lengthy and invasive steps, which, as previously shown (Llufrio et al, 2018; Binek et al, 2019), can profoundly alter the metabolic state of cells. We found that the necessary initial step of enzymatic cell detachment commonly used to generate single‐cell suspensions for cell sorting, induced metabolic changes that can mask the differences between cell lines from different tissues of origin (Appendix Fig S2, Dataset EV3). In addition, we noted increased technical variability in ion intensity measurements of detached‐cell extracts (Appendix Fig S2), presumably arising from the multiple sample processing steps (e.g., centrifugation and washing). Thereby, while suitable for genome or proteome profiling (Coller et al, 2006; Ly et al, 2017; Hoogendijk et al, 2019; Herr et al, 2020) where the consequences of perturbations manifest within minutes to hours (Sabatier et al, 2018), classical cell sorting approaches hamper a systematic and unbiased metabolic characterization of quiescent cell subpopulations. To overcome this limitation and enable direct metabolome profiling in quiescent cells, we sought to develop a novel approach for the sorting‐free separation of metabolic signatures in distinct cell subpopulations.
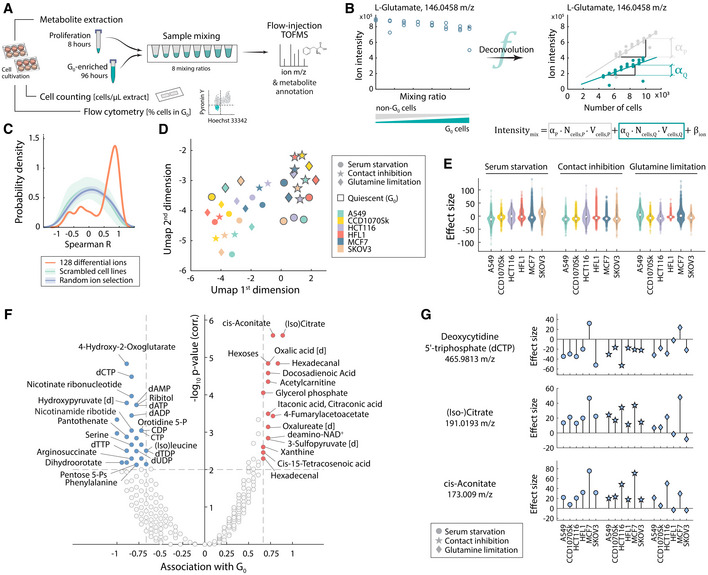
In a metabolite extract from a homogeneous cell population, the total abundance of any given metabolite is linearly dependent on the number of cells extracted and can be measured and compared between cell types using mass spectrometry techniques (Ortmayr et al, 2019). Similarly, we can assume that in a mixed cell population, the total measured metabolite abundance is a linear combination of the characteristic metabolite abundances in each individual cell subpopulation, provided that the presence or relative abundance of each distinct population in the culture does not affect the metabolism or general cell biology of the other in a way that might change the amount of any given metabolite per cell. Here, building on this general principle, we conceived an experimental‐computational framework based on a series of cell extract samples containing different relative amounts of two subpopulations of interest, and a linear regression model to separate in silico the characteristic metabolic profiles of the individual subpopulations. In brief, the method consists of three steps (Fig 2A and B). First, metabolites are extracted separately from two cell cultures enriched for either of the two subpopulations. In the second step, the two cell extract samples are mixed at several defined ratios and analyzed by high‐throughput nontargeted metabolomics (FIA‐TOFMS (Fuhrer et al, 2011)). In the third and final step, we solve a multilinear regression model to obtain coefficients representative of the relative metabolite abundance in the individual cell subpopulations (Fig 2B).
Figure 2. Metabolic profiling of quiescent (G0) cell subpopulations using sorting‐free in silico deconvolution.
-
A, BSchematic representation of the multistep approach for the in silico separation of subpopulation metabolic signatures without physical separation. The mixing of cell extracts obtained from cultures at 8 h (mostly G1, S, and G2/M phase cells) and 96 h (quiescence‐enriched, mainly cells in G0 and G1, see Fig 1C) allows for controlling the number of G0 and non‐G0 cells in each sample prior to FIA‐TOFMS analysis (Fuhrer et al, 2011). Panel B depicts the linear regression model used to determine separate estimates αQ and αP describing the relative intracellular abundance of individual metabolites in quiescent and proliferating cells, respectively.
-
CComparison (Spearman correlation) of reconstructed metabolome profiles of five cell lines after mixing and deconvolution (Appendix Fig S4) to known metabolic differences between the five cell lines (Ortmayr et al, 2019). The plot shows the probability density (kernel smoothing function) of Spearman correlation coefficients for 128 ions with characteristic variance across cell lines (orange curve). Distributions expected at random, i.e., correlations obtained after scrambling cell line labels, or randomly selecting putatively annotated metabolites are shown in green and blue, respectively. Shaded errors represent the standard deviation across 100,000 permutations.
-
DDimensionality reduction (Uniform Manifold Approximation and Projection, UMAP (preprint: McInnes et al, 2018)) of deconvoluted metabolic profiles of quiescent (G0) vs. non‐G0 cells (panel A and B), using Z‐scored relative abundances of 1940 putatively annotated metabolites in 6 cell lines × 3 stimuli × 2 cell states and Spearman similarity metric.
-
EDistribution of metabolic differences (effect size) between G0 and non‐G0 cells in six cell lines exposed to three different quiescence‐inducing stimuli, depicted as a violin plot. The violin shape is given by the Kernel density, overlaid data points represent individual metabolites (in total 1940 putatively annotated metabolites), and white circles indicate the median.
-
FVolcano plot of common metabolic changes in G0 cells. X‐axis values indicate the association with G0, i.e., the fraction of G0 models in which a metabolite is found at higher (positive association) or lower (negative value) abundance in G0 cells across the 18 cell models. The statistical significance (y‐axis) of the quiescence association was estimated for each metabolite using a hypergeometric test and an iterative testing scheme (see Materials and Methods section and Appendix Fig S4). Highlighted metabolites change consistently in two‐thirds or more conditions (G0 association >= 0.667, P‐value < 0.01, Benjamini–Hochberg correction). Only ions annotated to metabolites listed in the KEGG database are shown in the plot. The suffix [d] indicates α‐keto acids detected as phenyl hydrazine derivatives (Zimmermann et al, 2014).
-
GEffect size profiles for selected putatively annotated metabolites showing significantly quiescence‐associated patterns across six cell lines and three quiescence stimuli (see panel F).
The approach relies on two key assumptions, i.e., that the key metabolic characteristics of each subpopulation are not affected by the relative proportion of subpopulations, and that metabolite concentrations lie within the range where measured ion intensities linearly increase with the number of cells (i.e., extracted biomass). It is worth noting that when either of the two assumptions is not fulfilled, we expect the relationship between metabolite concentration and ion intensity to significantly deviate from linearity. We verified that the linearity of MS measurements (R 2 > 0.9) was preserved across multiple cell line extracts (i.e., different sample matrices, Appendix Fig S3, Dataset EV3) by spiking metabolites into extracts of three cell lines exhibiting different basal levels of high‐abundant metabolites like glutamate, glutathione, and 2‐oxoglutarate (Appendix Fig S3 and Materials and Methods, Dataset EV3). For all metabolites, the linear range extended two orders of magnitude beyond metabolite concentrations in a typical cell extract (Appendix Fig S3). Deviations from linearity were observed for only 18% of metabolites on average (Appendix Fig S3), supporting the validity of our assumptions. Ions not following a linear dependency between cell number and ion intensity are filtered out during data processing.
To benchmark the methodology for the separation (deconvolution) of subpopulation metabolic profiles, we mimicked co‐occurring signals by mixing metabolite extracts from different cell lines and applied the deconvolution approach to reconstruct the individual cell line metabolic profiles (Appendix Fig S4). To that end, we generated cell extracts from five cell lines grown individually, prepared mixes in all possible pairwise combinations of cell lines, and applied the workflow described above to reconstruct the individual cell line profiles (Dataset EV3). After deconvolution, we compared (Spearman correlation) the relative metabolite abundances derived from mixed metabolite extracts against previously measured characteristic metabolic differences between the five cell lines (Ortmayr et al, 2019) (Appendix Fig S4, Dataset EV3). For 128 metabolites exhibiting large variation in abundance across cell lines in pure extracts (greater than 3 standard deviations variance across the 5 cell lines), we observed high correlations (median Spearman correlation 0.7) that were significantly higher than for ions exhibiting no characteristic difference across these five cell lines (622 metabolites, P‐value 8.9e‐13). Hence, we validated the ability of our approach to resolve distinct metabolic characteristics of different cell types from the profiling of mixed extracts.
We applied the sorting‐free deconvolution method to profile the relative difference in the abundance of 1940 putatively annotated metabolites between quiescent (G0) and proliferating (G1, S, and G2/M phases) cell subpopulations, in the six cell types and three quiescence stimuli (Fig 1, Dataset EV4). To that end, we generated cell extracts at 8 and 96 h after applying quiescence‐inducing conditions, enriched for non‐G0 and G0 cells, respectively (Fig 1C). Deconvolution using the mixing scheme revealed a distinct signature of G0‐cell populations (Appendix Fig S4) that was not discernible by simply comparing the metabolic profiles at 8 and 96 h after quiescence induction (i.e., without deconvolution, Appendix Fig S4, Dataset EV4). This further reinforces that conventional approaches used for the metabolome profiling of quiescent cells, where the bulk population is measured, may overlook characteristic differences in quiescent cell subpopulations.
Interestingly, we found that the differences in metabolite abundances were mostly due to the cell state (i.e., G0 vs. non‐G0) rather than cell type or quiescence stimulus (Fig 2D), while only 31 ions showed significant variation across stimuli (ANOVA P‐value <0.05, Benjamini–Hochberg correction, Appendix Fig S5, Dataset EV4). A common metabolic signature of cells in G0 that is largely invariant to cell type or quiescence‐inducing stimuli suggests a universal metabolic program underlying the proliferation‐quiescence transition, consistent with our observation of largely similar growth dynamics (Fig 1, Dataset EV1).
To systematically identify common features of the metabolic adaptation to quiescence, for each metabolite we estimated how frequently cells exhibit higher or lower levels in G0 (effect size, Fig 2E) across the 18 conditions (Fig 2F, Appendix Fig S4, Dataset EV4, Materials and Methods section). We identified 164 putatively annotated metabolites exhibiting an association with G0, i.e., that showed consistently increased or decreased abundances in G0 cells, irrespective of cell type or quiescence stimulus (Fig 2F, abs. G0 association > = 2/3, Benjamini–Hochberg corrected P‐value <0.01, hypergeometric statistical test).
While consistently reduced pool sizes of several nucleotides and intermediates of nucleotide biosynthesis (precursors dihydroorotate and pentose 5‐phosphates) are likely the result of the arrest of DNA replication, quiescence‐associated metabolites reflected adaptive changes in metabolism that likely go beyond an indirect effect of growth arrest (Fig 2F). For example, we found metabolites that exhibited consistently higher levels in G0 cells, such as cis‐aconitate and (iso‐)citrate (in 15 and 16 out of 18 quiescence models, respectively, Fig 2G). On average, citrate and aconitate accumulations were slightly lower in glutamine limitation as compared to serum starvation and contact inhibition (Fig 2G), potentially reflecting the indirect effect of an interrupted supply of a major anaplerotic TCA cycle substrate like glutamine (DeBerardinis et al, 2007; DeBerardinis & Cheng, 2010; Daye & Wellen, 2012). Maintaining large metabolite pools can report on active strategies supporting cell survival in the quiescent state, and possibly prepare quiescent cells for resuming growth (e.g., xanthine (Link et al, 2015)). Together with citrate and aconitate, we noted a significantly quiescence‐associated accumulation (corrected P‐value <0.01) of several metabolites located in lipid metabolism (acetylcarnitine, glycerol 3‐phosphate, and hexadecanal, Fig 2F). These changes suggest for differential regulation of lipid metabolism in quiescent cells. Interestingly, fatty acid β‐oxidation has been associated with quiescence in cell models other than cancer, i.e., in endothelial (Kalucka et al, 2018) and stem cells (Ito et al, 2012; Knobloch et al, 2017; Shyh‐Chang & Ng, 2017). However, its fundamental functional role, and whether fatty acid degradation also plays a role in cancer cell quiescence remains to be elucidated. Here, we observed increased levels of acetylcarnitine that could indicate an engagement of the carnitine system (Melone et al, 2018) responsible for fatty acid transport across the mitochondrial membrane, consistent with a possible role of fatty acid β‐oxidation and its product acetyl‐CoA in the accumulation of aforementioned TCA intermediates (e.g., citrate).
Altogether, our data uncover common metabolome characteristics of quiescent cells across several quiescence‐inducing conditions and multiple cell types, including cancer cells. While previous studies have focused on cellular quiescence in a physiological (i.e., noncancer) setting, here we show global metabolic rearrangements that hint at the involvement of fatty acid degradation also in cancer cells reversibly transitioning between proliferation and quiescence.
With quiescence entry, FAO becomes a metabolic vulnerability
Fatty acid β‐oxidation (FAO) is a major pathway in the degradation of fatty acids (as fatty acyl‐CoAs) into acetyl‐CoA units (Fig 3A) (Houten et al, 2016). Acetyl‐CoA can further be converted to citrate, forming a key intermediate not only in energy generation (TCA cycle) but also in the regeneration of redox equivalents (NADPH, isocitrate dehydrogenase reaction) in mitochondria or the cytosol. Thus, FAO can ensure cellular energy and redox homeostasis, and also provides citrate for lipogenesis, protein, or histone acetylation (Melone et al, 2018). While FAO has been associated with different functions in cellular quiescence in noncancer cells (Knobloch et al, 2017; Shyh‐Chang & Ng, 2017; Kalucka et al, 2018), its function in the adaptation of cancer cells to quiescence remains to be clarified.
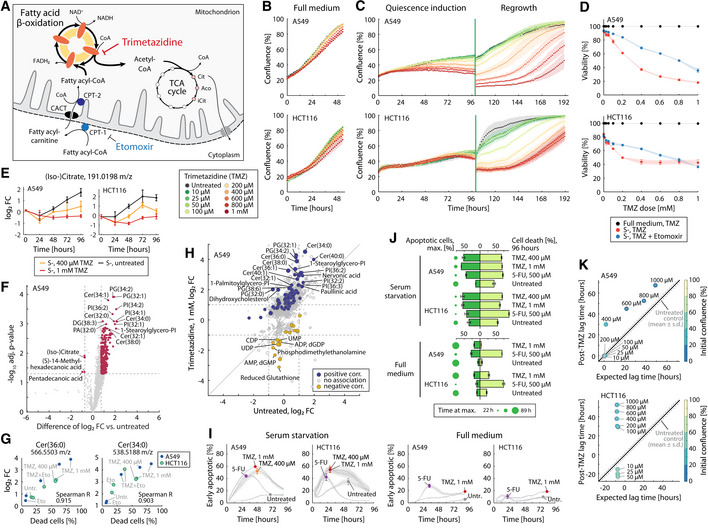
Figure 3. FAO inhibitor trimetazidine (TMZ) impairs viability and regrowth of quiescent cancer cells.
-
ASchematic representation of mitochondrial fatty acid β‐oxidation. In the cytosol, long‐chain fatty acids are conjugated to carnitine by carnitine palmitoyltransferase 1 (CPT1, irreversibly inhibited by the CoA conjugate of etomoxir) for transport across the mitochondrial membrane by acylcarnitine translocase (CACT). In the mitochondrial matrix, the fatty acyl chain is released from carnitine and conjugated to coenzyme A by CPT2. Fatty acyl‐CoAs are shortened stepwise by β‐oxidation enzymes acyl‐CoA dehydrogenase, enoyl‐CoA hydratase, and 3‐ketoacyl‐CoA thiolase, generating FADH2, NADH, and one molecule of acetyl‐CoA per reaction cycle. Trimetazidine competitively inhibits the last step of FAO, the cleavage of acetyl‐CoA by 3‐keto acyl‐CoA thiolase.
-
BGrowth phenotypic changes induced by TMZ treatment in A549 and HCT116 cells grown in full growth medium (RPMI‐1640 with 5% dialyzed FBS). Cell confluence as a proxy of cell numbers was monitored using automated time‐lapse microscopy in a plate reader (TECAN Spark 10M). Data points and shaded areas indicate mean ± SD over three biological replicates.
-
CGrowth phenotypic changes induced by TMZ treatment in quiescence‐inducing conditions (serum starvation) in A549 and HCT116 cancer cells. Growth was monitored via cell confluence as described in panel B. At 96 h, cells were stimulated to exit quiescence by replacing serum‐free media with a fresh growth medium without TMZ (regrowth). Data points and shaded areas indicate mean ± SD over three biological replicates.
-
DViability of quiescence‐induced cells treated with TMZ, or with TMZ plus 10 μM etomoxir was assessed using a fluorescence imaging assay involving two fluorescent dyes: Hoechst 33342 (all nuclei) and propidium iodide (dead cells). Data points and error bars indicate mean ± SD over three biological replicates.
-
EDynamic changes in the intracellular levels of citrate in A549 and HCT116 cells induced to enter quiescence by serum starvation with or without TMZ. Fold changes were estimated relative to steady‐state levels in full medium (Dubuis et al, 2018). Data points and error bars indicate mean ± SD over three biological replicates.
-
FVolcano plot showing TMZ‐induced metabolic changes (1 mM, 48 h) in A549 cells in serum starvation (see also Appendix Fig S8). Shown are differences in log2 fold change between TMZ treatment and serum starvation alone (x‐axis), and their statistical significance (y‐axis, adjusted P‐value, t‐test, and Benjamini–Hochberg correction).
-
GCorrelation of ceramide levels (log2 fold change, y‐axis) with the loss of viability under TMZ treatment (fraction of dead cells at 96 h, x‐axis, see panel D).
-
HComparison of relative changes (log2 fold‐change) in the abundance of 1791 putatively annotated metabolites upon TMZ treatment (1 mM, y‐axis) against untreated quiescence‐induced A549 cells (x‐axis). Fold‐changes are calculated relative to the expected ion intensity in full medium at a steady state (Dubuis et al, 2018). Significant positive and negative correlations (Spearman, P < 0.01) with cell death at 96 h are highlighted in blue and yellow, respectively.
-
IFractions of early apoptotic cells in A549 or HCT116 cancer cell cultures in quiescence‐inducing conditions (serum starvation, left panels) or full growth medium (5% dFBS, right panels), treated with TMZ (0.4 or 1 mM), 5‐fluorouracil (5‐FU, 0.5 mM, positive control), or medium (untreated). Early apoptotic cells were detected using ApoTracker Green under co‐staining with Hoechst 33342 (nuclei) and propidium iodide (dead cells). Cell staining was continuously monitored in 3‐h intervals for 96 h using automated fluorescence microscopy in a TECAN Spark Cyto. The full time course is shown in Appendix Fig S8. Data points and shaded areas indicate mean ± SD over three biological replicates. Approximately 3,400 and 7,500 cells/well were seeded of A549 and HCT116 cells, respectively.
-
JSummarized differences in the dynamics of apoptosis induction by TMZ treatment between quiescence‐inducing conditions (upper panel) and full growth medium (lower panel). In each treatment, the maximum fraction of apoptotic cells and the time at which the maximum was reached (dark green bars) is reported alongside the fraction of dead cells at 96 h (light green bars, full time course in Appendix Fig S8). Apoptosis induction was assessed as described in panel I. Bar length and error bars indicate mean ± SD over three biological replicates.
-
KComparison of lag times (i.e., time to resume cell duplication) after serum starvation with or without TMZ treatment in A549 and HCT116 cancer cells. Lag times were estimated from cell confluence data shown in panel C, by first estimating the maximum growth rate (see Materials and Methods section for a detailed description), and subsequently finding the intersection between the tangent to the point with the highest growth rate and the initial confluence (i.e., after media change at 96 h). To correct for the intrinsic dependency of lag time on the initial confluence (Appendix Fig S9), expected lag times (x‐axis) were determined by linear interpolation of lag times measured in untreated cells at different initial confluences (Appendix Fig S9).
The common metabolic characteristics of G0 cells (Fig 2F) hint at a differential regulation of fatty acid degradation, reflected in the accumulation of citrate and cis‐aconitate, which exhibit the most significant association with G0 (Fig 2F and G, Benjamini–Hochberg corrected P‐value 4.87e‐9 and 6.65e‐9, respectively). To test whether this quiescence‐associated accumulation of FAO‐related metabolites in G0 cells reports an increased activity of fatty acid β‐oxidation in quiescence, we used trimetazidine, a competitive inhibitor of 3‐ketoacyl‐CoA thiolase (Lopaschuk et al, 2003) catalyzing the third and last enzymatic step of FAO (Fig 3A). Cells in full growth media were insensitive to trimetazidine across a wide range of concentrations (Fig 3B, Dataset EV5), indicating that FAO is dispensable during rapid cell proliferation. By contrast, in A549 and HCT116 cancer cells under serum starvation conditions, trimetazidine treatment caused drastic dynamic changes in cell confluence (Fig 3C, Dataset EV5) and induced cell death in a dose‐dependent manner (Fig 3D, Dataset EV5). Similarly, trimetazidine impaired viability also when applied 96 h after quiescence induction, and also in cultures enriched for G0 cells by glutamine limitation (Appendix Fig S6, Dataset EV5). Using dynamic metabolome profiling (Dubuis et al, 2018), we found that trimetazidine treatment abolished the time‐dependent accumulation of citrate during G0 induction by serum deprivation (Fig 3E, Dataset EV6). Targeted LC–MS/MS measurements confirmed this observation (Appendix Fig S7, Dataset EV6), providing supportive evidence that the G0‐associated citrate accumulation reflects an increased activity of fatty acid β‐oxidation in G0 cells. Moreover, in line with our observation that fatty acid β‐oxidation is dispensable during proliferation (Fig 3B), trimetazidine did not alter citrate levels in cells in full medium containing 5% dFBS and 2 mM glutamine (Appendix Fig S7). Collectively, these results indicate that fatty acid degradation plays a central role in cells transitioning from rapid proliferation to G0 phase.
Previous studies exploring the function of FAO in quiescence models outside of cancer identified a link to energy production in adult stem cells (Ito et al, 2012; Knobloch et al, 2017) or redox homeostasis in endothelial cells (Kalucka et al, 2018). Downstream metabolism of FAO‐derived citrate can fuel oxidative phosphorylation and ATP synthesis, as well as the NADP+‐dependent isocitrate dehydrogenase reaction to regenerate NADPH. To test whether FAO is required to supply citrate for these functions, we supplemented serum‐starved and trimetazidine‐treated cells with citrate or reduced glutathione (GSH), a key endogenous antioxidant. Remarkably, the strong toxicity induced by trimetazidine was rescued neither by citrate nor by GSH (Appendix Fig S7, Dataset EV5), indicating that in our quiescence models, the role of FAO likely goes beyond the previously suggested functions to maintain redox homeostasis or use of FAO‐derived acetyl‐CoA/citrate as an energy source.
We hypothesized that if the inhibition of FAO affects mitochondrial metabolic intermediates, the toxicity of trimetazidine for quiescence‐induced cells is linked to accumulating FAO substrates in mitochondria, which can impair mitochondrial function and trigger apoptosis (Ostrander et al, 2001; Penzo et al, 2002; Artwohl et al, 2009). To test this possibility, we investigated whether a reduced transport of FAO substrates into mitochondria can alleviate trimetazidine‐induced toxicity. To this end, we used etomoxir, an irreversible inhibitor of carnitine palmitoyltransferase CPT1A, the limiting component of the carnitine system for the import of longer‐chain fatty acids into mitochondria (Melone et al, 2018) (Fig 3A). Co‐treatment with etomoxir reduced the toxic effect of trimetazidine in quiescence‐induced cells (Fig 3D and Appendix Fig S7, Dataset EV5), indicating that trimetazidine‐induced toxicity is at least partially caused by increased levels of potentially toxic intermediates in mitochondria. Nevertheless, etomoxir is not able to completely abolish trimetazidine toxicity (Fig 3D). The residual toxicity is consistent with a remaining citrate accumulation (Appendix Fig S7, Dataset EV6) and is likely due to incomplete inhibition of fatty acid‐driven respiration by etomoxir (Divakaruni et al, 2018), or a compensatory role of peroxisomal FAO (Violante et al, 2013, 2019).
To shed light on the mechanism underlying trimetazidine‐induced toxicity, we measured metabolic changes in quiescence‐induced cells treated with trimetazidine at 24, 48, 72, and 96 h (Fig 3F and Appendix Fig S8, Dataset EV6). Already at 24 and 48 h, we detected significantly higher levels (adjusted P‐value <0.05, Benjamini–Hochberg correction) of several metabolites related to lipid metabolism and phospholipids in trimetazidine‐treated as compared to untreated quiescence‐induced cells (Fig 3F and Appendix Fig S8, Dataset EV6). Among these early metabolic responses to trimetazidine, we found accumulations of several bioactive lipid species with signaling functions, such as lysophospholipids (stearoyl and arachidonoyl phosphoinositol, Fig 3F and Appendix Fig S8) and ceramides containing long‐chain fatty acids (e.g., sum compositions 32:0, 32:1, 34:0, 34:1, 38:0). Elevated levels of certain ceramides have been associated with the progression of apoptotic cell death (Rudd & Devaraj, 2018) by promoting the permeabilization of the mitochondrial membrane (Chang et al, 2015; Ogretmen, 2018; Dadsena et al, 2019). Hence, we hypothesized that impaired FAO can lead to the generation of cytotoxic intermediates such as ceramides, thus potentially exposing quiescence‐induced cells to apoptotic cell death.
To test this hypothesis, we systematically searched for metabolic changes associated with trimetazidine‐induced toxicity. To that end, we estimated the correlation (Spearman) between the reduction in viability at 96 h (Fig 3D) and characteristic relative changes in metabolite abundances in G0‐induced A549 and HCT116 cells treated with trimetazidine (400 μM or 1 mM), alone or in combination with 10 μM etomoxir (Dataset EV6). We found that the metabolic signature associated with cell death consists of several ceramide species (Fig 3G and H), reinforcing a potential link between FAO inhibition by trimetazidine and the accumulation of toxic metabolites such as apoptosis‐inducing ceramides. To verify apoptosis as the cell death mechanism triggered by trimetazidine, we monitored the induction of apoptosis by detecting externalized phosphatidylserine (PS) residues with ApoTracker Green (BioLegend, (Barth et al, 2020)) in a fluorescence imaging assay (Fig 3I and Appendix Fig S8, Dataset EV6). Consistent with the accumulation of ceramides (Fig 3G), we observed a rapid significant (P‐value = 6.8e‐08) increase in the fraction of early apoptotic cells (i.e., displaying PS) in trimetazidine‐treated quiescence‐induced cells as compared to untreated serum‐starved cells (Fig 3I and J), reaching up to 60% of all cells within the first 48 h in both A549 and HCT116 cells (Fig 3I and Appendix Fig S8). Subsequently, we observed a large increase in the number of cells with compromised plasma membranes (additional staining by live cell‐impermeable propidium iodide, Fig 3J and Appendix Fig S8, Dataset EV6), indicating late stages of apoptosis and cell death in agreement with the previous viability analysis (Fig 3D). Interestingly, co‐treatment with etomoxir did not abolish the increase in early apoptotic cells but reduced cell death at 96 h (Fig 3D and Appendix Fig S8). The lower rate of apoptotic cell death reinforces the hypothesis that trimetazidine‐induced toxicity is at least in part caused by the action of toxic intermediates in mitochondria. Hence, a co‐treatment with etomoxir, by reducing the import of fatty acids into mitochondria, can slow down the buildup of toxic metabolites. Altogether, these results suggest that maintaining homeostasis by controlling fatty acid degradation is critical to preserve mitochondrial integrity and avoid induction of the apoptotic cascade in cells reversibly transitioning into quiescence.
Several metabolites showing a reduced abundance after trimetazidine treatment are intermediates of nucleotide, energy, and redox metabolism (e.g., ADP, AMP, NADPH, reduced glutathione, 2‐oxoglutarate, Fig 3H and Appendix Fig S8), potentially indicating that FAO is involved in maintaining homeostasis of cofactors and metabolite pools that are not only relevant to survival in quiescence but also to rapidly resume proliferation. Furthermore, citrate, whose abundance was decreased by FAO inhibition (Fig 3E), is a key intermediate not only in energy metabolism but also in lipid biogenesis (Bauer et al, 2005). Hence, we hypothesized that, in addition to maintaining homeostasis during quiescence induction, fatty acid degradation also plays a role in preparing cells for reversing quiescence. We tested whether the ability to exit quiescence and switch back to rapid proliferation is affected by prior trimetazidine treatment, by restoring normal growth conditions (i.e., complete growth medium containing 5% dialyzed FBS) after 96 h of trimetazidine treatment in serum starvation. Strikingly, while untreated serum‐starved cells readily escaped the growth arrest, prior treatment with more than 200 μM trimetazidine increased the time necessary to restart cell proliferation (i.e., lag time, Fig 3C and K, Dataset EV5). Although we observed a basal dependency of lag time on the starting cell density (Appendix Fig S9, Dataset EV5), lag times observed after trimetazidine treatment exceeded the expected delay in regrowth simply due to reduced cell confluence caused by trimetazidine toxicity in quiescence‐induced cells (Fig 3K). Similarly, because most dead cells are removed during media change at 96 h (green vertical line in Fig 3C, Appendix Fig S9), we concluded that the increased lag time was not a mere consequence of higher numbers of dead cells in the population after trimetazidine treatment. Supplementation of citrate, whose abundance is decreased by trimetazidine treatment, did not restore rapid regrowth (Appendix Fig S9), indicating that the growth lag is not simply linked to a decreased citrate availability for lipid biosynthesis and/or generation of energy and redox cofactors. Not only the levels of citrate were decreased by trimetazidine but also levels of other intermediates of oxidative energy metabolism (e.g., 2‐oxoglutarate), nucleotides (e.g., AMP, ADP), and redox cofactors (e.g., NADPH, NAD/H), potentially indicating a key role of mitochondrial metabolism and respiration in mediating the rapid switch of nongrowing cells back to proliferation and cell cycle progression (Ahn et al, 2017).
Our experimental evidence suggests that while fatty acid degradation is dispensable during rapid proliferation, its proper function and maintenance of mitochondrial integrity becomes crucial for homeostasis during quiescence‐induced growth arrest, and also for preparing cells for rapid growth resumption. Thus, our findings demonstrate that the transition into cellular quiescence can impose metabolic dependencies that are fundamentally different from proliferating cells, and potentially offer unique opportunities to selectively target quiescent cancer cells.
Discussion
While cancer cells are typically associated with rapidly proliferating cell states, nondividing, quiescent cancer cells pose a serious risk for cancer recurrence and represent a key challenge to conventional anticancer therapies. Moreover, because in vivo identification and selective isolation of quiescent cancer cells is complicated, the metabolic characteristics of quiescent cancer cells are largely unexplored. Here, to bypass major technical bottlenecks, we developed an innovative approach to systematically chart fundamental metabolic characteristics that differentiate proliferating from quiescent cells in vitro. This new methodology enables delineating metabolic differences between coexisting cell subpopulations without the need for laborious, time‐consuming, and invasive cell sorting procedures. Compared with other in silico frameworks able to remove contaminations of cancer tissue samples with nontumor cells or vice versa in metabolome profiling data (Wang et al, 2016), our framework is able to directly establish relative metabolite abundances in distinct cell subpopulations, and can in principle be applied to deconvolute more than 2 coexisting subpopulations.
It is noteworthy that our approach does not require samples of pure cell populations. Instead, a relative enrichment of individual subpopulations is sufficient to generate gradients of each subpopulation with the aid of the mixing scheme. Hence, we envisage that our approach could complement single‐cell technologies, like single‐cell transcriptomics (Aldridge & Teichmann, 2020), that allow defining different cell types in complex tissue samples, expanding the deconvolution of metabolic signatures in bulk measurements beyond in vitro systems. Here, this method enabled us to systematically characterize differential metabolic profiles in six cell types and three quiescence‐inducing conditions, generating an unprecedented resource to directly investigate the role of metabolism in mediating the transition from rapid proliferation into quiescence.
While more cell lines and conditions need to be tested to further support the generalization of our findings, we discovered characteristic metabolic adaptive changes that are common to diverse quiescence‐inducing environmental conditions and largely different cell types, suggesting a central role of metabolism in the reversible transitioning between proliferation and quiescence (G0). Our analysis uncovered quiescence‐associated changes in central metabolic pathways (e.g., from nucleotide and amino acid to energy, redox, and cofactor metabolism) and storage metabolism (e.g., xanthine, hexose sugars) (Fig 2F), suggesting widespread adaptive changes to mediate (Andrade et al, 2021) cellular homeostasis in quiescence, and potentially aid rapid regrowth (Link et al, 2015). Remarkably, the specific metabolic characteristics of G0 cells revealed metabolic functions like fatty acid β‐oxidation that are dispensable during proliferation but become a vulnerability in quiescence, potentially offering new and selective therapeutic targets in nondividing cells (Fendt et al, 2020).
Fatty acid beta‐oxidation has so far mostly been studied in specific cell types with a focus on its role in energy generation (Schafer et al, 2009; Ito et al, 2012; Knobloch et al, 2017; Shyh‐Chang & Ng, 2017) or redox homeostasis (Kalucka et al, 2018). Our results shed light on the multiple implications of fatty acid degradation functionality for cellular homeostasis and in mediating the reversible transition between proliferation and quiescence. Here, we show that the approved drug trimetazidine, inhibitor of FAO‐enzyme 3‐keto acyl‐CoA thiolase, whilst showing no activity against rapidly proliferating cells, is able to induce apoptosis in quiescence‐induced cells. Our metabolome‐based analysis suggests that interfering with fatty acid β‐oxidation using agents like trimetazidine can lead to the formation of bioactive signaling species such as apoptosis‐inducing ceramides, and ultimately cell death. We also observed increased levels of phospholipids containing long‐chain fatty acyls, and of phosphatidic acid, a central precursor of major classes of membrane phospholipids. While these types of phospholipids exert no known key signaling function, it is plausible that when FAO is impaired, long‐chain fatty acids are redirected for incorporation into phospholipids by de novo synthesis and/or remodeling of membrane phospholipids to avoid lipotoxicity induced by free or activated fatty acids (e.g., fatty acyl‐CoAs) (Ostrander et al, 2001; Penzo et al, 2002; Listenberger et al, 2003; Artwohl et al, 2009; Piccolis et al, 2019). Interfering with FAO using trimetazidine also impairs the ability of quiescence‐induced cells to reverse growth arrest, suggesting that following cell fate after treatment can offer new mechanistic insights and uncover modulators of cell state transitions.
While verification in in vivo models is needed to explore a potential therapeutic use of our findings, genome‐based investigations have demonstrated that metabolic shifts like enhanced FAO can be decisive for cell fate and proliferation in vivo (Echeverria et al, 2019; Oren et al, 2021). It is plausible that metabolic processes mediating homeostasis or cellular stress responses could similarly be key to the ability of quiescent cells to tolerate and resist treatments (Ramirez et al, 2016; Brown et al, 2017). Our approach, by uncovering common metabolic adaptations in cancer cell quiescence, offers new perspectives on the conventional search for chemotherapies based on the growth inhibitory activity against rapidly dividing cancer cells, leading to new strategies for the discovery of therapeutic agents against difficult‐to‐target nondividing cancer cell subpopulations. Obviously, it is crucial that agents interfering with essential metabolic processes in quiescence preserve healthy human quiescent cells such as immune, stem, or endothelial cells. Nevertheless, the presented findings unraveled the potential of exploring whether general medications with no significant adverse effects, like the anti‐ischemic therapeutic agent trimetazidine (Fragasso et al, 2003; Napoli et al, 2005), could be repurposed to selectively target quiescent cancer cells and potentially resensitize them to classical chemotherapeutic agents. Together with conventional anticancer agents, combination therapies (e.g., with trimetazidine) could simultaneously target highly proliferating and quiescent cancer cells, and thereby reduce the risk of cancer recurrence. Understanding the mechanisms that govern the ability to switch between proliferation and quiescence can shed light on fundamental aspects of tissue homeostasis, immune cell maintenance, and activation and have implications in largely diverse applicative fields, from tissue engineering to pharmacology.
Materials and Methods
Cell lines and cell cultivation
Six human‐derived cell lines were used in this study, four cancer cell lines A549, HCT116, MCF7, and SKOV3 (obtained as part of the NCI‐60 panel from the National Cancer Institute, Bethesda, MD, USA), and two nontransformed fibroblast cell lines CCD1070Sk and HFL1 (purchased from ATCC). The standard growth medium for all cell lines was RPMI‐1640 (cat. no. 01‐101‐1A, Biological Industries, Israel or cat. no. 21870076, Thermo Fisher Scientific) supplemented with 2 g/l glucose (as necessary, cat. no. G8644, Sigma Aldrich, Buchs, Switzerland), 2 mM glutamine (cat. no. 25030024, Thermo Fisher Scientific), 1% penicillin–streptomycin (P/S, cat. no. 15140122, Thermo Fisher Scientific) and 5% dialyzed fetal bovine serum (dFBS, cat. no. F0392, Sigma Aldrich, Buchs, Switzerland). Cultures were routinely tested for Mycoplasma contamination and were found contamination‐free.
Quiescence induction
For serum starvation and glutamine limitation, cells were seeded below confluence in normal growth medium (RPMI‐1640 with 2 g/l glucose, 2 mM glutamine, 1% P/S, and 5% dFBS) and allowed to attach overnight. To induce quiescence via serum starvation, the medium was then changed to RPMI‐1640 with 2 mM glutamine and 2 g/l glucose but without serum supplementation for 96 h. For glutamine limitation, the medium was changed to RPMI‐1640 with 2 g/l glucose and 5% dialyzed FBS but without glutamine supplementation, for 96 h. For contact inhibition, cells were seeded already close to confluence and allowed to attach overnight. The medium was then renewed once (RPMI‐1640, 2 g/l glucose, 2 mM glutamine, and 5% dFBS). All quiescence‐induced cell cultures were incubated for 96 h at 37°C in 5% CO2 atmosphere.
Continuous cell growth monitoring
To monitor cell numbers and growth in proliferating, quiescence‐induced (serum starvation or glutamine limitation), or quiescence‐exiting cells in situ in 96‐well plates, we used automated time‐lapse microscopy imaging in a plate reader to measure cell confluence, i.e., the area of the well bottom covered by cells. Using a TECAN Spark 10 M plate reader, we acquired bright‐field microscopy images of each well in 1.5‐h intervals in standard cell culture conditions (5% CO2 and 37°C). Images were analyzed and confluence estimated online in SparkControl software (TECAN, Männedorf, Switzerland). Confluence data during quiescence induction and subsequent regrowth are provided in Dataset EV2.
Estimation of growth rates and lag times
To estimate dynamic growth rates in each growth phase (e.g., between quiescence induction and stimulation), we used a moving window approach following an exponential growth model. First, we log‐transformed cell confluence data and performed linear regression analysis for 24‐h time windows (i.e., 16 consecutive data points) to determine the slope, representative of the log10 change in confluence per unit of time, i.e., growth rate with the unit h−1. Next, we shifted the time window by 8 h and repeated the analysis, thus iteratively scanning the entire growth curve and recording instantaneous growth rates (Dataset EV2). To estimate lag times, i.e., the duration between stimulation until the onset of growth with maximal rate, we calculated the time‐point at which the tangent to the growth curve at the maximum growth rate intersects with the initial confluence, using the slope and intercept determined by linear regression of log‐transformed confluence data in the time window where the highest growth rate is observed (Dataset EV2).
Cell cycle analysis using flow cytometry
To determine cell cycle distributions and G0 fractions in cell cultures exposed to quiescence stimuli, we used a well‐established flow cytometry assay (Kim & Sederstrom, 2001; Lemons et al, 2010; Hu et al, 2011) based on the quantification of single‐cell DNA and RNA contents. In brief, live cell cultures growing adherently in T75 flasks were detached using trypsin, resuspended in warm PBS (pH 7.4), and centrifuged at 400 g for 5 min. After discarding the supernatant, the cell pellets were resuspended in 1 ml PBS and fixed by drop‐wise addition of the cell suspension into 10 ml of a 70% ethanol/30% deionized water mixture (precooled to −20°C) in a 50 ml conical tube while vortexing. Samples were stored at 4°C until further processing. Immediately prior to flow cytometry analysis, the fixed cell suspension was centrifuged at 1,200 g for 15 min at 8°C. The supernatant was carefully aspirated, and the cell pellet was resuspended in 5 ml cold PBS and centrifuged again at 1,200 g for 15 min. The cell pellet was then resuspended in 500 μl cold PBS and mixed with a freshly prepared staining solution containing 4 μg/ml Hoechst 33342 (stains DNA) and 4 μg/ml pyronin Y (stains RNA) in PBS. Samples were incubated in the dark on ice for at least 15 min until flow cytometry analysis. The stained cell samples were analyzed using a BD LSRFortessa flow cytometry analyzer, using 405 and 561 nm lasers for excitation, and 450/40 and 586/15 emission filters for Hoechst 33342 and pyronin Y, respectively. At least 10.000 events were recorded in each sample with a flow rate of 12 μl/min. The measured data (Dataset EV1) were visually inspected in the instrument software and exported to fcs 3.0 file format. For further analysis, flow cytometry data were imported in Matlab using the function fca_readfcs (https://www.mathworks.com/matlabcentral/fileexchange/9608‐fca_readfcs). Cell cycle distributions and G0 fractions were determined using a custom script as follows (see also Appendix Fig S1). Samples collected at 8 h after quiescence induction (containing cells in all cell cycle phases) were used to define the gates separating the cell cycle phases in each cell line (Fig 1 and Appendix Fig S1). G1 and G2/M peaks (2n and 4n DNA contents, respectively) were picked based on DNA content measurements (Hoechst 33342 intensity) using the Matlab function findpeaks. Cells with DNA contents between G1 and G2/M phases were classified as S‐phase cells (Appendix Fig S1). Cells with 2n DNA content and an RNA content below S and G2/M phases are classified as G0 (Kim & Sederstrom, 2001) (Fig 1, Dataset EV1).
Metabolome analysis after trypsin‐mediated cell detachment
To assess the metabolic impact of enzymatic cell detachment (e.g., during flow cytometry workflows), we generated cell extracts using two different methods (see schematic overview in Appendix Fig S2), i.e., with or without prior trypsin treatment to digest extracellular matrix components that mediate the attachment of cells to the culture dish. To that end, we seeded four different cell lines, i.e., A549, IGROV1, OVCAR8, and UO31 cancer cell lines, in 6‐well plates to achieve approximately 50% confluence after 24 h (1.32e5, 1.80e5, 1.32e5 and 1.26e5 cells/well, respectively). Approximately 24 h after seeding, cells in three replicate cultures (i.e., containing identical cell numbers) of each cell line were extracted with or without prior cell detachment as follows. For cell detachment, the culture medium was aspirated, and cells were briefly rinsed with 2 ml warm phosphate‐buffered saline solution (PBS, pH 7.4, 37°C, cat. no. 10010023, Thermo Fisher Scientific). After removing the wash solution, 500 μl trypsin solution (0.25%, cat. no. 25200056, Thermo Fisher Scientific) was added to each well, and the cultures were incubated at 37°C in 5% CO2 atmosphere until cells were detached (approximately 5 min). Detached cells were subsequently resuspended in 2 ml cell culture medium containing 5% serum to inactivate trypsin, transferred to separate sample tubes, and immediately centrifuged at 400 g for 5 min at room temperature. Cell pellets were washed once with 2 ml warm 75 mM ammonium carbonate solution (pH 7.4, 37°C) and centrifuged as before. Finally, the wash solvent was discarded, and cells were extracted by adding 400 μl precooled extraction solvent (40% acetonitrile, 40% methanol, 20% water, with 25 μM phenyl hydrazine) to each tube. The samples were incubated for 1 h at −20°C, and subsequently stored at −80°C until MS analysis. In parallel, three replicate cultures of each cell line were extracted by in situ metabolite extraction as described previously (Dubuis et al, 2018; Ortmayr et al, 2019), i.e., culture media were removed, each well briefly washed with 2 ml prewarmed 75 mM ammonium carbonate solution, and the still attached cells were then directly extracted by addition of 400 μl of cold extraction solvent (40% acetonitrile, 40% methanol, 20% water, with 25 μM phenyl hydrazine). Plates were sealed with aluminum adhesive foil (cat. no AB0626, Thermo Fisher Scientific), incubated for 1 h at −20°C, and subsequently stored at −80°C. Immediately before MS analysis, the bottom of each well was scraped with a cell culture scraper, and the extract with cell debris was quantitatively transferred to a fresh sample tube. Together with the samples obtained from trypsin‐mediated cell detachment, all extracts were centrifuged to separate cell debris (5 min, 14,000 rpm). Cell‐free extracts were then transferred to fresh 96‐well plates with a conical bottom for MS injection. MS analysis and metabolite annotation was carried out as described below (section “Sample mixing and MS analysis”). MS intensity data are provided in Dataset EV3. To compare metabolic profiles between trypsin‐mediated cell detachment and in situ extraction, measured ion intensities were transformed to Z‐scores and analyzed by principal component analysis. In addition, to account for potential systematic differences in effectively extracted cell numbers (e.g., due to loss of detached cells during centrifugation steps prior to extraction), we repeated the analysis after centering metabolite intensities to the mean for each extraction method separately (Appendix Fig S2, Dataset EV3).
Evaluation of linearity of MS measurements
To evaluate the linearity of MS signals measured in cell extract samples, we supplemented cell extract samples with increasing concentrations of endogenous metabolites and measured MS signal intensities using FIA‐TOFMS (Fuhrer et al, 2011). To that end, we generated cell extracts of three different cell lines (i.e., A549, IGROV1, and MDAMB468 cancer cells), representing three potentially different sample matrices, and, for each cell line separately, mixed 25 μl extract with increasing amounts of 105 metabolites (equimolar mixture prepared from pure standards) ranging from 3 pmol to 3 nmol in a fixed volume of 5 μl. In parallel, metabolites were spiked at the same concentrations into cell‐free extraction solvent. All spiked samples were prepared in triplicates and immediately measured by FIA‐TOFMS.
Following metabolite annotation based on exact mass (3 mDa mass tolerance, 83 unique ions), we first determined the saturation limit for each annotated ion, i.e., the ion abundance above which a further increase in metabolite concentration no longer yields an increase in measured ion abundance (examples in Appendix Fig S3), due to ion suppression effects and/or saturation of the MS detector. Ions whose abundance was close to or above the saturation limit already in the unspiked cell extract samples were excluded from further analysis (13 ions). For all remaining spiked metabolites (75 unique ions, Appendix Fig S3), we evaluated the linearity of MS signals in each of the four sample matrices (i.e., three cell lines or cell‐free extract) as follows.
First, we asked whether the increase in MS ion intensity was linear with respect to the spiked metabolite concentration. To that end, for each sample matrix separately, we performed linear regression analysis on measured ion intensities to establish a base model that determines the slope of the linear relationship between ion intensity and the spiked metabolite concentration, and the intercept relating to the basal abundance of the metabolite in the cell extract (Dataset EV3). Measurements above the saturation limit were excluded from the analysis, allowing the fitting of a linear model across at least two orders of magnitude of ion intensity beyond the ion intensity in the unspiked cell extract for each metabolite (Appendix Fig S3, Dataset EV3).
In the second step, to test whether the same model also fits measured ion intensities in different sample matrices, we compared the predicted ion intensities in the base model to the measured ion intensity in all other sample matrices. Because 31 metabolites exhibited a cell‐type‐specific abundance in the unspiked extracts (1‐way ANOVA, adjusted P‐value <0.05, Benjamini–Hochberg multiple testing correction, Appendix Fig S3), we adjusted the intercept parameter to each sample matrix, while the slope parameter was fixed to the value determined in the base model. We then calculated R 2 values to quantify the deviation of model predictions from the actual MS measurements in each sample matrix (goodness of fit, Appendix Fig S3, Dataset EV3), i.e., the ratio of variance explained by the model (i.e., deviation from the model prediction) and the total variance (i.e., deviation from the mean). R 2 values close to 1 indicate an excellent fit, i.e., that the linear model explains most of the variance observed in the measured data. We repeated this linearity comparison for each sample matrix acting as the base model and applied each base model to all three other sample matrices (Appendix Fig S3 and Dataset EV3).
Sample generation for metabolome profiling in G0 cells
Cell extracts of quiescence‐induced cultures at 8 and 96 h exposure to the quiescence stimulus were generated in 6‐well plates to increase the sample volume for later preparation of mixed samples. Five 6‐well plates were prepared in each experiment, with 2 cell lines in three replicates each. At 8 and 96 h after induction of quiescence, an aliquot of the culture supernatant was removed and stored at −80°C, and the remainder was aspirated. Each well was subsequently washed once with fresh 75 mM ammonium carbonate (wash solvent, 37°C, pH 7.4), and metabolites were extracted from adherent cells in situ with 400 μl cold extraction solvent (40:40:20 acetonitrile:methanol:water with 25 μM phenyl hydrazine for the stabilization of α‐keto acids (Zimmermann et al, 2014)). The plates were sealed with aluminum adhesive foil, kept at −20°C for 1 h, and then stored at −80°C until further processing. A second plate was used to determine the cell number per well for later normalization. In each well, the medium was aspirated, cells were washed once with warm wash solvent and detached with 250 μl trypsin (0.25%, cat. no. 25200056, Thermo Fisher Scientific). Immediately after resuspending cells in 750 μl warm PBS, equal volumes of cell suspension and trypan blue solution (0.4%, Invitrogen) were mixed, and the cell concentration, average cell size, and viability were determined using a Countess II Automated Cell Counter (Invitrogen, Thermo Fisher Scientific).
Of note, for contact‐inhibited cultures, the samples at 8 h (i.e., the reference sample containing mostly proliferating cells in G1, S, or G2/M phases) were collected from subconfluent cultures incubated with spent medium from a fully confluent culture for 8 h, to mimic the acute exposure to low‐nutrient conditions.
In addition, we generated metabolite extracts for each cell line grown in normal growth conditions (i.e., subconfluent culture, standard growth medium with both dFBS and glutamine) at several time‐points between 20 and 80% cell confluence. These samples were used for the selection of ions of likely biological origin in our data analysis and deconvolution procedure (see below).
Sample mixing and MS
Immediately prior to MS analysis, the 6‐well plates holding cell extracts were briefly thawed on ice, and cells were detached from the well bottom using cell scrapers (cat. no. 3010, Corning). All subsequent steps were carried out on ice. The extracts were collected in fresh microcentrifuge tubes (cat. no. 0030120086, Eppendorf), mixed, and centrifuged at maximum speed (13,000 rpm in an Eppendorf 5424 R microcentrifuge) to deposit cell debris. The supernatant, i.e., the cell‐free metabolite extracts, was used for subsequent sample mixing and MS measurements. In brief, for each cell line and quiescence stimulus, the triplicate extracts obtained at 8 (Extract 1) and 96 h (Extract 2) were adjusted to the same average cell concentration and mixed at eight defined ratios, i.e., 100, 85, 70, 55, 40, 25, 10, 0% of Extract 1 in Extract 2, in a total volume of 50 μl. The mix samples were prepared independently for the three replicates in 96‐well microtiter plates. The metabolite extracts generated from cell cultures in normal growth conditions at different levels of cell confluence were processed as described above, but no mixing was applied. Empty wells on each plate were filled with fresh (i.e., cell‐free) extraction solvent or quality control samples, then plates were sealed and stored at 4°C until injection.
MS measurements were performed as described previously (Fuhrer et al, 2011) by flow‐injection analysis time‐of‐flight mass spectrometry (FIA‐TOFMS) on an Agilent 6550 iFunnel Q‐TOF LC–MS system (Agilent Technologies, Santa Clara, CA, USA). Raw MS spectra were aligned and centroids picked using in‐house data processing environment in Matlab R2018b (The Mathworks, Natick), yielding MS intensities for typically more than 10,000 unique m/z features in each sample.
Metabolite annotation
The detected m/z features were putatively annotated to known metabolites by matching accurate masses to metabolites listed in the genome‐scale reconstruction of human metabolism (Brunk et al, 2018) (Recon3D, 5835 metabolites) and the human metabolome database (HMDBv4; Wishart et al, 2018). Here, we putatively annotated 2,099 measured ions with a mass tolerance of 0.003 m/z. Sum formulae were used to calculate reference masses for 5,835 and 7,038 metabolites listed in Recon3D and HMDBv4 (subset of endogenous metabolites in urine, serum, feces, excluding drugs), respectively. Because α‐keto acids were derivatized with phenyl hydrazine (Zimmermann et al, 2014) during extraction, sum formulae for the phenyl hydrazone derivatives (+C6H8N2‐H2O) of 30 α‐keto acid compounds (selected via KEGG SimComp search, http://www.genome.jp/tools/simcomp/) were added to the metabolite list for annotation (marked by the prefix “PHderiv_” in Dataset EV4 and by the suffix “[d]” in figure labels).
Regression‐based deconvolution
We designed a two‐step procedure to analyze and deconvolute the metabolic profiles of cells in G0 as compared to any other cell cycle phase. Of note, most cells in the non‐G0 fraction resided in G1 phase (Fig 1).
In the first step, we selected only ions where the measured ion intensity is linearly dependent on the number of cells extracted, i.e., that are likely of biological origin. To that end, we adapted an approach we previously described in Ortmayr et al, 2019 for the comparative metabolic profiling of widely different cancer cell lines. During steady‐state growth, the metabolite concentration in each cell is constant in time, and the measured ion intensity of intracellular metabolites scales with the number of cells extracted. Ion signals not following this relationship are likely artifacts not related to the intracellular metabolic content or represent metabolites yielding ion abundances below the detection limit. Following this criteria, for each putatively annotated metabolite, we analyzed the ion intensities obtained in metabolite extracts of each cell line grown in normal growth conditions at different confluence levels (i.e., different amounts of cells extracted, see above for sample generation) using a multiple linear regression scheme (Matlab fitlm function) as described in detail in (Ortmayr et al, 2019). For each cell line, we obtained the slope and significance (P‐value) of the linear fit, and one value for the intercept, estimated from the measured intensity in a sample where no cells were extracted, and hence representative of the MS background signal independent of the cell line. Only putatively annotated metabolites with a regression P‐value below 3.97e‐06 (Bonferroni‐adjusted threshold, adjusted by the number of metabolites and cell lines) in at least one cell line were retained after this step.
In the second step, we used a multilinear regression scheme to estimate the relative metabolite abundance in G0 and non‐G0 cells in each cell line and quiescence‐inducing condition based on the measured ion intensities in mixed cell extracts (see above). While this approach can be in principle applied to estimate relative metabolic differences across multiple cell subpopulations, here we describe the approach for cell populations consisting of two main subpopulations. Key to this approach is to prepare samples in which the two different subpopulations are present in different ratios. The total measured ion intensity across samples can be expressed as a linear combination of metabolite concentrations in the two subpopulations. Specifically, ion intensities measured in mixed cell extract samples, can be expressed as:
| (1) |
where is a constant term representing the ion‐specific MS measurement background, and are the number of cells in either subpopulation in the mixed sample, and and are the parameters fitted in the model, representing the actual metabolite abundance in each subpopulation. By comparing the vs we can quantify relative differences in intracellular metabolite abundances between the two subpopulations. and are the cell volume of cells in the respective subpopulation. Here, we considered the volumes of cells equal, because flow cytometry‐based estimates of cell volume forward‐scatter (Tzur et al, 2011) indicated a characteristic difference in cell diameter between G0 and non‐G0 cells in any given cell line and quiescence stimulus (Appendix Fig S1).
Here, we applied this general model to deconvolute the relative metabolite abundances in G0 and non‐G0 cells (i.e., G1, S, or G2/M phase, Fig 1) in six cell lines exposed to three different quiescence‐inducing stimuli. According to the above‐described mixing scheme, for each cell line and quiescence stimulus, we obtained triplicate ion intensity measurements in eight different mix samples. The total number of cells is constant in all mix samples, and the variable number of cells in G0 (N Q ) or any other cell cycle phase (NP) is given by the G0 fractions determined using flow cytometry (assay described above) at 8 and 96 h after exposure to the quiescence stimulus, respectively.
Here, for each putatively annotated metabolite retained in step 1, we solved the basic model described in Equation (1) across all cell lines and quiescence stimuli all at once using a multilinear regression scheme (Matlab lsqlin function with model coefficients constrained from 0 to Inf):
| (2) |
The ion intensity in the mixed sample, I mix , the metabolite‐specific MS background signal, β (i.e., the constant term in Equation (1)), and the number of cells in G0 or any other cell cycle phase, N Q and N P , respectively, are measured, while the α coefficients are fitted. The index cl indicates the cell line, st the quiescence stimulus, m the sample mix (1–8 with predefined mixing ratios, see above), and n the replicate (1–3). For each metabolite, the model coefficients α cl,st,P and α cl,st,Q represent the relative intracellular abundance of the given metabolite. To estimate the error for each coefficient, we used a bootstrap resampling approach, where we first calculated the model residuals (i.e., the deviation of the model prediction from the measured values) for each subpopulation, and then selected a random sample of the residuals with replacement and added it to the model prediction. Using linear regression analysis, we then obtained new coefficient values α cl,st,P and α cl,st,Q . After 100 repetitions of these steps, we calculated the errors of the model coefficients, and , as the standard deviation of the bootstrapped coefficients. Using this approach, we obtained estimates of the relative intracellular abundance (coefficients α) and their standard errors separately for G0 and non‐G0 cells in each cell line and quiescence stimulus (i.e., 2‐cell states × 6‐cell lines × 3 quiescence stimuli = 36 observations per metabolite), for 1,940 putatively annotated metabolites (Dataset EV4).
Method validation
To verify the ability of the deconvolution workflow to disentangle the metabolic signatures of two distinct cell subpopulations, we tested whether known differences in metabolite abundance between two cell lines can be recovered after applying the deconvolution strategy described above. To that end, we generated cell extract samples from individual cultures of five cell lines in standard growth conditions (RPMI‐1640 with 2 g/l glucose, 2 mM glutamine, 1% P/S, and 5% dFBS), and calculated the cell concentration in the extract samples. Using the mixing scheme described above, we prepared eight mixed samples for each possible pair of cell lines, and measured metabolite abundances using FIA‐TOFMS as described above. After annotation, we applied the deconvolution approach (Equation (1)). For each cell line, we determined one model coefficient α and its error for 2,713 putatively annotated metabolites (Dataset EV3). Next, we compared these estimates of relative metabolite abundances across the five cell lines with existing data. We previously reported comparative metabolic profiles under steady‐state conditions for the same 5 cell lines as part of a larger panel of 54 adherent cancer cell lines (Ortmayr et al, 2019) (NCI‐60 panel). In that dataset, 267 out of 2,181 putatively annotated metabolites were characteristically different between the five cell lines, i.e., showing a variation across cell lines greater than three times the typical error of the estimates for individual cell lines. Of these metabolites showing the most characteristic differences between the cell lines, 117 were also annotated in the herein‐generated dataset after deconvolution. To systematically assess the overlap of the relative metabolite abundances for these key metabolites, we calculated Spearman correlation coefficients (Fig 2C), confirming that characteristic differences in the metabolic profiles of the five cell lines were recovered.
Calculation of purified ion intensity profiles of G0 and non‐G0 cells
In addition to obtaining the model parameters quantifying the characteristic relative metabolite abundance in G0 vs. non‐G0 cells (see above, Regression‐based deconvolution), we also reconstructed ion intensity profiles in the original cell extracts at 8 and 96 h (corresponding to mostly non‐G0, and mostly G0 cells, respectively), similar to the approach used in a previous study (Wang et al, 2016). To that end, we used the previously determined slope parameters from the regression model together with the known subpopulation fractions to calculate and subtract for each annotated metabolite the ion intensity attributed to the minor subpopulation, hence obtaining a purified intensity profile corresponding to only one subpopulation. For example, in the sample taken at 96 h, enriched for cells in G0, we multiplied the slope value for non‐G0 cells () by the number of non‐G0 cells () and subtracted this intensity value from the measured ion intensity , such that:
| (3) |
Vice versa, the intensities measured in extracts obtained at 8 h, containing mostly non‐G0 cells, were corrected for the ion intensity predicted to originate from the small subpopulation of G0 cells.
| (4) |
Similar to the original model, the cell volumes and were assumed to be constant (see also above). Importantly, this approach to separate metabolic signatures of cell subpopulations does not correct for differences in cell numbers, hence we additionally normalized the purified ion intensity profiles (Dataset EV4) to the number of non‐G0 cells (for the 8‐h sample) or G0 cells (for the 96‐h sample). All calculations and the subsequent analysis by principal component analysis (PCA, Appendix Fig S3) were carried out in Matlab 2019b. Of note, because the parameters and are as per model definition invariant to cell numbers and are derived across multiple independent ion intensity measurements (i.e., 8 different mixing ratios) rather than individual measurements of end‐point samples, all other analyses presented in this paper are obtained based on and as measures of the characteristic relative abundances of intracellular metabolites in non‐G0 and G0 cells, respectively.
Differential analysis: effect size
To systematically compare the metabolite abundances between G0 and any other cell cycle phase, we calculated effect sizes d for each annotated metabolite i, i.e., the difference in relative metabolite abundances α in matching cell types cl and quiescence‐triggering conditions st standardized to the pooled standard deviation (SD) of metabolite abundances:
| (5) |
| (6) |
where and are the errors in the estimates of relative metabolite abundances determined above. A negative effect size indicates a lower abundance of a metabolite in quiescent cells, while positive values reflect an accumulation of metabolites in quiescent cells. The result of this analysis is differential metabolic profiles in quiescent vs. proliferating cells for 1,940 putatively annotated metabolites in six cell types and three quiescence trigger signals (Dataset EV4).
Analysis of common metabolic changes in G0 cells
To identify metabolites that show a consistent pattern of differences between G0 phase and any other cell cycle phase (i.e., effect sizes calculated as described above) we used an iterative thresholding approach. The basic principle behind the analysis is to assess how strongly and significantly any given metabolite is associated with G0 state, based on how consistently and similarly the metabolite abundance changes between G0 and non‐G0 cells across 6 cell lines and 3 quiescence‐inducing stimuli. To avoid selecting a single threshold value for all metabolites and for both increasing and decreasing metabolite abundances (i.e., positive and negative effect sizes), we assessed the association with G0 for different effect size thresholds between 3 and 13 (the mean of all absolute effect size values) in increments of 1.
For each metabolite and effect size threshold, we first counted separately the number of effect sizes that exceed the positive threshold value, and the number of effect sizes that are lower than the negative threshold value. The sign with the larger number of changes is then prioritized, i.e., the metabolite is assigned either a consistently accumulating or decreasing pattern at that threshold value. To assess the statistical significance of such a consistent pattern at each threshold value, we used a hypergeometric test. Here, we assessed the probability of drawing the same or higher number of effect sizes exceeding the threshold value (for accumulated metabolites) or falling below the threshold value (for metabolites with decreased abundance in G0 cells) when sampling at random from all changes in the dataset with matching sign. Thus, at each threshold value, we recorded the sign and fraction of changes passing the threshold (out of 18 in total, i.e., 6‐cell lines × 3 quiescence stimuli), and the statistical significance (P‐value) of a common pattern for each metabolite. To define an overall G0‐associated metabolic signature, for each metabolite we selected the threshold value where the most significant common pattern (i.e., lowest P‐value) was observed. The resulting profile of G0 associations and P‐values (Benjamini–Hochberg correction for multiple hypothesis testing) for 1940 putatively annotated metabolites are reported in Fig 2F and Dataset EV4.
Inhibition of fatty acid β‐oxidation
We used two different pharmacological inhibitors of fatty acid β‐oxidation (FAO), i.e., trimetazidine and etomoxir. While trimetazidine competitively inhibits 3‐keto acyl‐CoA thiolase, i.e., directly targets the last enzymatic step of FAO, etomoxir (in its active form etomoxiryl‐CoA) is an irreversible inhibitor of carnitine palmitoyl transferase (CPT1), thus inhibiting FAO indirectly by limiting the substrate access into mitochondria. To treat adherent cancer cells, the drugs were added directly into the supernatant, either individually or in combinations, as indicated in the main text. Trimetazidine solutions were prepared by dissolving trimetazidine (1‐(2,3,4‐Trimethoxybenzyl)piperazine dihydrochloride, cat. no. 653322, Sigma Aldrich, Buchs, Switzerland) in deionized water to a concentration of 50 mM. The pH of the solution was adjusted to pH 7.4, and the solution was sterile‐filtered prior to addition to the culture supernatant. To establish the dose‐dependent effect of trimetazidine on serum‐starved cancer cells, we prepared serial dilutions (10 μM up to 1 mM) of the drug in serum‐free RPMI‐1640 with 2 g/l glucose, 2 mM glutamine, and 1% P/S. Growth phenotypic and metabolic changes in response to trimetazidine exposure in full medium and quiescence‐inducing conditions are reported in Dataset EV5 and EV6.
Targeted analysis of trimetazidine‐induced metabolic changes by LC–MS/MS
HCT116 cells were seeded in two 6‐well plates and incubated overnight at 37°C in 5% CO2 atmosphere to allow cell attachment. On the next day, on one plate (i.e., six replicate cultures) the medium was exchanged for serum‐free medium, and trimetazidine was added to three wells at a final concentration of 1 mM. Similarly, on the second plate, the medium was removed and replaced by a fresh growth medium containing 5% dialyzed FBS, and 1 mM of trimetazidine was added to three wells. Serum‐starved cultures with or without trimetazidine were extracted at 72 h after treatment, while cultures in full growth medium were sampled before reaching confluence, at 48 h. Cell extracts were generated using in situ extraction (Dubuis et al, 2018; Ortmayr et al, 2019) as described above, and stored at −80°C until MS analysis. Immediately prior to MS analysis, 150 μl aliquots of all cell extracts were dried by vacuum centrifugation and resuspended in 30 μl (5‐fold concentration) LC–MS grade water.
LC–MS analysis was carried out on a Thermo TSQ Vantage triple quadrupole mass spectrometer, using a chromatographic method adapted from a previous publication (Lu et al, 2010), and MS/MS parameters established in Buescher et al (2010). Peak integration in LC–MS/MS data was carried out in Skyline, and statistical analysis was performed in Matlab 2019b (Dataset EV6).
Viability imaging assay and CellProfiler analysis
To assess cell viability in adherent cell cultures in situ, we used a fluorescence microscopy assay based on live cell staining with the DNA‐binding dyes Hoechst 33342 and propidium iodide (PI). Hoechst 33342 is cell‐permeable and stains all cells (i.e., live and dead cells), while propidium iodide cannot enter live cells and stains only dead cells with damaged cell membranes. Hoechst 33342 (2 μg/ml in H2O, Life technologies cat. no. H3570) and propidium iodide (2 μg/ml, cat. no. P4864, Sigma Aldrich) were added directly into the supernatant of cell cultures in 96‐well plates, and the cells were incubated for 30 min at 37°C in 5% CO2 atmosphere before imaging. Without any prior washing steps, the cultures were imaged in 96‐well plates using a TECAN SparkCyto plate reader for fluorescence microscopy, recording images in the bright‐field, blue (Ex. 381–400 nm, Em. 414–450 nm) and red channels (Ex. 543–566 nm, Em. 580–611 nm). In each channel, multiple images were acquired of each well with 4× magnification and tiled online into a single image covering the whole well in the vendor software (TECAN SparkControl). The fluorescence images were analyzed in a custom image analysis pipeline in CellProfiler 3.1.9 (McQuin et al, 2018). For each well, the blue‐ and red‐channel images were first cropped into a circular area to exclude areas close to (200‐pixel border offset) and outside the well border and converted from RGB to gray scale. Next, both images were independently segmented to identify all nuclei (blue channel) and PI‐positive cells (red channel), respectively, using the IdentifyPrimaryObjects module of CellProfiler, and a global threshold estimated using Otsu's method (two classes). To improve the robustness of the automated threshold estimation, we constrained the lower bound for the threshold value in red channel images, thus preventing false‐positive recognition of dead cells in images where no or only few dead cells are present. In the last step, we applied the MaskObjects module to apply the PI‐positive cell mask to the segmented nuclei, i.e., nuclei for which a red object is recorded in the same location are recognized, and labeled as dead cells. As a measure of cell viability, we then calculate for each well the fraction of dead cells as the ratio of the number of dead cells (i.e., blue and red positive) over the total number of nuclei (blue objects), in % (Dataset EV6).
Metabolite supplementation under trimetazidine treatment
To investigate the functional role of FAO in quiescence‐induced cells, we supplemented several small molecules together with trimetazidine, or during regrowth after trimetazidine treatment, i.e., citrate, etomoxir, and inosine (Dataset EV5). Citrate supplementation can bypass the reduced citrate production from FAO‐derived acetyl‐CoA upon FAO inhibition. Therefore, we supplemented citrate at a final concentration of 250 μM in cell culture media either at the same time as trimetazidine was added (0.25, 0.5, or 1 mM doses) or when regrowth was stimulated following 96 h serum starvation in presence of trimetazidine (0.25, 0.5, 0.75, or 1 mM doses). Citrate stocks were prepared from powder (citric acid monohydrate, cat. no. 1.00244.1000, Merck Millipore) at 50 mM in deionized water, and sterile‐filtered (0.25 μm pore size) prior to addition to cell culture media. We confirmed that at the final concentration of 200 μM, the pH of the cell culture medium (i.e., pH 7.4 under 5% CO2 atmosphere) was not affected by citrate addition.
Etomoxir is a small‐molecule inhibitor of carnitine palmitoyltransferase I (CPT1), and can thus limit the entry of fatty acyl chains into mitochondria and potentially divert fatty acid flux away from mitochondria, avoiding damage sustained by the accumulation of fatty acyls in mitochondria upon FAO inhibition. Etomoxir was prepared from powder ((+)‐Etomoxir sodium salt hydrate, cat. no. E1905, Sigma Aldrich, Buchs, Switzerland) as a 10 mM stock solution in DMSO. Because commonly used 40 μM doses have been associated with indirect effects (Divakaruni et al, 2018) rather than specific action on CPT1, we opted for a lower concentration, i.e., 10 μM.
Inosine is a purine metabolism intermediate and can serve as a source of inosine 5′‐monophosphate (IMP), adenosine 5′‐monophosphate (AMP), and guanosine 5′‐monophosphate (GMP). Here, inosine was used as a control condition to test the effect of a supplementation unrelated to FAO functions (in contrast to citrate, see above), and to test whether regrowth after serum starvation is generally metabolically limited by the production of key biosynthetic precursors like nucleotides (e.g., for nucleic acid synthesis). To that end, inosine was supplemented in fresh growth media when cells were stimulated to regrow after 96 h serum starvation with or without trimetazidine (0.25, 0.5, 0.75, or 1 mM doses). Inosine stock solutions were prepared from powder (cat. no. I4125, Sigma Aldrich, Buchs, Switzerland) at 10 mM in deionized water, and sterile‐filtered (0.25 μm pore size) prior to addition to cell culture media.
Dynamic metabolome profiling under trimetazidine treatment
Time‐dependent changes in the abundance of individual metabolites were determined as described previously (Dubuis et al, 2018; Ortmayr et al, 2019). Cells were seeded in 96‐well plates in full growth medium (RPMI‐1640, 5% dialyzed FBS, 2 g/l glucose, and 2 mM glutamine). After allowing cells to attach overnight, media were replaced by serum‐free RPMI‐1640 in all wells to induce quiescence by serum starvation, and treatments were applied as indicated, i.e., trimetazidine was added to final concentrations of 400 μM or 1 mM from 50 mM stocks in RPMI‐1640 (pH adjusted to 7.4), with or without the addition of etomoxir at a final concentration of 10 μM from a 10 mM stock in DMSO. In experiments with cells in full medium, RPMI‐1640 with 5% dialyzed FBS was supplied. Samples for metabolome analysis were taken at 24‐h intervals after drug addition. During sampling, as described previously (Dubuis et al, 2018; Ortmayr et al, 2019), cells were washed once with 75 mM ammonium carbonate (pH 7.4, 37°C) and then immediately extracted in situ by adding 100 μl prechilled extraction solvent (40% methanol, 40% acetonitrile, 20% deionized water, −20°C) to each well without prior cell detachment. To estimate the number of cells in each sample, a second plate was processed as described above, but the medium was added instead of extraction solvent, and the plate was immediately imaged and analyzed for cell confluence on a TECAN Spark 10 M plate reader for automated bright‐field microscopy imaging. Extracted cell samples were incubated at −20°C for 1 h after extraction, and subsequently stored at −80°C until MS analysis. The MS‐based measurement of metabolite abundances was carried out as described above using untargeted high‐throughput flow‐injection analysis (Fuhrer et al, 2011) on an Agilent 6550 time‐of‐flight mass spectrometer. Metabolites were putatively annotated as described above, i.e., against Recon 3D and HMDBv4. In addition, all ions were matched to SwissLipids entries (https://www.swisslipids.org) via HMDB ids to classify lipid‐related metabolites and obtain sum composition information for putatively annotated lipids (Fig 3F–H and Dataset EV6). Metabolome profiles were normalized as described previously (Dubuis et al, 2018; Ortmayr et al, 2019), using a linear regression model to estimate the relationship between metabolite abundance and cell confluence for each putatively annotated metabolite at a steady state (i.e., in full medium). We then estimated the deviation of each metabolite's abundance from the expected steady‐state abundance by calculating the ratio of the measured abundance and the steady‐state abundance at the matching cell confluence based on the linear regression coefficients, as described in detail previously (Dubuis et al, 2018). In addition, we calculated the statistical significance (P‐value) of each change using an unpaired t‐test against all unperturbed samples. The resulting dataset of log2 fold‐changes in metabolite abundance and corresponding P‐values, also corrected for multiple hypothesis testing using the Benjamini–Hochberg method, is provided in Dataset EV6. For the data representation as a Volcano plot in Fig 3F, for each metabolite we subtracted the log2 fold‐change measured in serum starvation alone from the log2 FC values of trimetazidine‐treated cells, to highlight metabolites whose abundance was specifically altered by the added trimetazidine treatment. The statistical significance (P‐value) is estimated against the fold‐changes in the untreated quiescence‐induced condition, additionally applying the Benjamini–Hochberg correction for multiple hypothesis testing. In Fig 3G and H, we summarized the time‐dependent changes in abundance for each ion by taking the log2FC with the highest statistical significance (P‐value, t‐test against steady‐state abundance in full medium), i.e., the minimum of P‐values against full medium across all time‐points.
Dynamic monitoring of apoptosis induction
We used a fluorescence imaging assay to assess the fraction of early and late apoptotic cells continuously in live cell cultures (Appendix Fig S8, Dataset EV6) under incubation conditions (37°C, 5% CO2) in a TECAN SparkCyto fluorescence imaging system. The assay included three different fluorescent probes, i.e., Hoechst 33342 (Life technologies cat. no. H3570) for staining the nuclei of live cells, ApoTracker Green (BioLegend, San Diego, CA, USA) to stain cells with phosphatidylserine (PS) residues exposed on the cell surface as a marker for early stages of apoptosis, and the live cell‐impermeable propidium iodide (Sigma Aldrich, cat. no. P4864) to stain cells with compromised cell membranes during late‐stage apoptosis or necrosis. Of note, in contrast to the related PS‐binding by Annexin V, binding by ApoTracker Green is calcium‐independent, allowing reliable staining also in calcium‐low cell culture media like RPMI‐1640. The concentration of Hoechst 33342 was optimized for each cell line (110 nM for A549, and 55 nM for HCT116) to minimize phototoxicity effects during long‐term live cell imaging. For ApoTracker Green and propidium iodide, the dye concentrations in the culture supernatant were 200 nM and 0.5 μg/ml, respectively.
For each experiment, cells were seeded as indicated in 96‐well plates (Nunclon™ Delta cell culture treated surface, Thermo Scientific, cat. no. 167008), and the three fluorescent probes were added to each well parallel to the treatments. The experiment plate was then immediately loaded into the TECAN SparkCyto for continuous incubation (37°C, 5% CO2) and automated fluorescence imaging. Images covering the entire well area (with automated stitching in the instrument software) were acquired for each well in a fully automatized manner every 3 h using a 4× objective and the kinetic cycle and multicolor analysis options of the TECAN SparkControl software. Fluorescence microscopy images were acquired consecutively with 60 ms exposure for blue fluorescence (Hoechst 33342, excitation 381–400 nm, emission 414–450 nm), 150 ms for green fluorescence (ApoTracker Green, ex. 461–487 nm, em. 500–530 nm) and 200 ms for red fluorescence (propidium iodide, ex. 543–566 nm, emission 580–611 nm). Image analysis was optimized with TECAN ImageAnalyzer software and key settings were transferred to TECAN SparkControl for real‐time image analysis. Individual cells were recognized based on nuclear staining (Hoechst 33342), and two secondary masks (for green and red fluorescence, respectively) were used to measure the green and red fluorescence signals associated with each cell. The secondary masks were defined based on the nuclear mask (using Voronoi mask) with a radius of 14 μm and an intensity threshold of 0.02 and 0.01 RFU (relative fluorescence units) for green and red fluorescence, respectively. Nuclei counts and fractions of cells in each bin (i.e., blue+/green+, blue+/red+ or blue+/green+/red+) at each time‐point were exported in Microsoft Excel format and are provided in Dataset EV6.
Author contributions
Karin Ortmayr: Conceptualization; resources; data curation; software; formal analysis; funding acquisition; validation; investigation; visualization; methodology; writing—original draft; project administration; writing—review and editing. Mattia Zampieri: Conceptualization; resources; supervision; funding acquisition; methodology; writing—original draft; project administration; writing—review and editing.
In addition to the CRediT author contributions listed above, the contributions in detail are:
KO conceived and designed the project with advice from MZ. KO and MZ developed the experimental‐computational methodology. KO carried out all experiments and analyzed the data. KO and MZ wrote the manuscript.
Disclosure statement and competing interests
The authors declare that they have no conflict of interest.
Supporting information
Appendix
Dataset EV1
Dataset EV2
Dataset EV3
Dataset EV4
Dataset EV5
Dataset EV6
Acknowledgements
We thank the National Cancer Institute (NCI) for providing the cancer cell lines, and TECAN Group Ltd for providing access to the TECAN Spark Cyto fluorescence microscopy plate reader. This work was supported by project funding by the Krebsliga Schweiz (KLS‐4124‐02‐2017), the Novartis Stiftung für Medizinisch‐Biologische Forschung (17A038), Worldwide Cancer Research (WCR‐15‐1058), and Schweizerischer Nationalfonds zur Förderung der wissenschaftlichen Forschung (SNF Sinergia grant CRSII5_189952 to Mattia Zampieri). We thank the team of the ETH flow cytometry core facility for initial support in setting up the flow cytometry assay, Christoph Gruber and Tomek Diederen for preparing multimetabolite standard mixtures, Peter Doubleday for assistance with LC–MS/MS measurements, and Uwe Sauer for supporting this work and providing laboratory facilities. We thank Alaa Othman and Karsten Weis for helpful feedback and discussion.
Mol Syst Biol. (2022) 18: e10716
Data availability
Generated data are included in the Appendix and EV Datasets. Raw MS ion intensity data can be downloaded from https://www.ebi.ac.uk/biostudies with the accession number S‐BSST894.
References
- Aguirre‐Ghiso JA (2007) Models, mechanisms and clinical evidence for cancer dormancy. Nat Rev Cancer 7: 834–846 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahn E, Kumar P, Mukha D, Tzur A, Shlomi T (2017) Temporal fluxomics reveals oscillations in TCA cycle flux throughout the mammalian cell cycle. Mol Syst Biol 13: 953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aldridge S, Teichmann SA (2020) Single cell transcriptomics comes of age. Nat Commun 11: 4307 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrade J, Shi C, Costa ASH, Choi J, Kim J, Doddaballapur A, Sugino T, Ong YT, Castro M, Zimmermann B et al (2021) Control of endothelial quiescence by FOXO‐regulated metabolites. Nat Cell Biol 23: 413–423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artwohl M, Lindenmair A, Roden M, Waldhäusl W‐K, Freudenthaler A, Klosner G, Ilhan A, Luger A, Baumgartner‐Parzer SM (2009) Fatty acids induce apoptosis in human smooth muscle cells depending on chain length, saturation, and duration of exposure. Atherosclerosis 202: 351–362 [DOI] [PubMed] [Google Scholar]
- Barth ND, Subiros‐Funosas R, Mendive‐Tapia L, Duffin R, Shields MA, Cartwright JA, Henriques ST, Sot J, Goñi FM, Lavilla R et al (2020) A fluorogenic cyclic peptide for imaging and quantification of drug‐induced apoptosis. Nat Commun 11: 4027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer DE, Hatzivassiliou G, Zhao F, Andreadis C, Thompson CB (2005) ATP citrate lyase is an important component of cell growth and transformation. Oncogene 24: 6314–6322 [DOI] [PubMed] [Google Scholar]
- Binek A, Rojo D, Godzien J, Rupérez FJ, Nuñez V, Jorge I, Ricote M, Vázquez J, Barbas C (2019) Flow cytometry has a significant impact on the cellular metabolome. J Proteome Res 18: 169–181 [DOI] [PubMed] [Google Scholar]
- Boroughs LK, DeBerardinis RJ (2015) Metabolic pathways promoting cancer cell survival and growth. Nat Cell Biol 17: 351–359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JA, Yonekubo Y, Hanson N, Sastre‐Perona A, Basin A, Rytlewski JA, Dolgalev I, Meehan S, Tsirigos A, Beronja S et al (2017) TGF‐β‐induced quiescence mediates chemoresistance of tumor‐propagating cells in squamous cell carcinoma. Cell Stem Cell 21: 650–664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunk E, Sahoo S, Zielinski DC, Altunkaya A, Dräger A, Mih N, Gatto F, Nilsson A, Preciat Gonzalez GA, Aurich MK et al (2018) Recon3D enables a three‐dimensional view of gene variation in human metabolism. Nat Biotechnol 36: 272–281 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buescher JM, Moco S, Sauer U, Zamboni N (2010) Ultrahigh performance liquid chromatography−tandem mass spectrometry method for fast and robust quantification of anionic and aromatic metabolites. Anal Chem 82: 4403–4412 [DOI] [PubMed] [Google Scholar]
- Carmona‐Fontaine C, Deforet M, Akkari L, Thompson CB, Joyce JA, Xavier JB (2017) Metabolic origins of spatial organization in the tumor microenvironment. Proc Natl Acad Sci U S A 114: 2934–2939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang K‐T, Anishkin A, Patwardhan GA, Beverly LJ, Siskind LJ, Colombini M (2015) Ceramide channels: destabilization by Bcl‐xL and role in apoptosis. Biochim Biophys Acta 1848: 2374–2384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapman NM, Boothby MR, Chi H (2020) Metabolic coordination of T cell quiescence and activation. Nat Rev Immunol 20: 55–70 [DOI] [PubMed] [Google Scholar]
- Chen J, Li Y, Yu T‐S, McKay RM, Burns DK, Kernie SG, Parada LF (2012) A restricted cell population propagates glioblastoma growth after chemotherapy. Nature 488: 522–526 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung TH, Rando TA (2013) Molecular regulation of stem cell quiescence. Nat Rev Mol Cell Biol 14: 329–340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho IJ, Lui PP, Obajdin J, Riccio F, Stroukov W, Willis TL, Spagnoli F, Watt FM (2019) Mechanisms, hallmarks, and implications of stem cell quiescence. Stem Cell Rep 12: 1190–1200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coller HA (2011) The essence of quiescence. Science 334: 1074–1075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coller HA, Sang L, Roberts JM (2006) A new description of cellular quiescence. PLoS Biol 4: e83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coloff JL, Murphy JP, Braun CR, Harris IS, Shelton LM, Kami K, Gygi SP, Selfors LM, Brugge JS (2016) Differential glutamate metabolism in proliferating and quiescent mammary epithelial cells. Cell Metab 23: 867–880 [DOI] [PubMed] [Google Scholar]
- Dadsena S, Bockelmann S, Mina JGM, Hassan DG, Korneev S, Razzera G, Jahn H, Niekamp P, Müller D, Schneider M et al (2019) Ceramides bind VDAC2 to trigger mitochondrial apoptosis. Nat Commun 10: 1832 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daye D, Wellen KE (2012) Metabolic reprogramming in cancer: Unraveling the role of glutamine in tumorigenesis. Semin Cell Dev Biol 23: 362–369 [DOI] [PubMed] [Google Scholar]
- DeBerardinis RJ, Chandel NS (2016) Fundamentals of cancer metabolism. Sci Adv 2: e1600200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeBerardinis RJ, Cheng T (2010) Q's next: the diverse functions of glutamine in metabolism, cell biology and cancer. Oncogene 29: 313–324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeBerardinis RJ, Mancuso A, Daikhin E, Nissim I, Yudkoff M, Wehrli S, Thompson CB (2007) Beyond aerobic glycolysis: transformed cells can engage in glutamine metabolism that exceeds the requirement for protein and nucleotide synthesis. Proc Natl Acad Sci U S A 104: 19345–19350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dembinski JL, Krauss S (2009) Characterization and functional analysis of a slow cycling stem cell‐like subpopulation in pancreas adenocarcinoma. Clin Exp Metastasis 26: 611–623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Divakaruni AS, Hsieh WY, Minarrieta L, Duong TN, Kim KKO, Desousa BR, Andreyev AY, Bowman CE, Caradonna K, Dranka BP et al (2018) Etomoxir inhibits macrophage polarization by disrupting CoA homeostasis. Cell Metab 28: 490–503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubuis S, Ortmayr K, Zampieri M (2018) A framework for large‐scale metabolome drug profiling links coenzyme a metabolism to the toxicity of anti‐cancer drug dichloroacetate. Commun Biol 1: 101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Echeverria GV, Ge Z, Seth S, Zhang X, Jeter‐Jones S, Zhou X, Cai S, Tu Y, McCoy A, Peoples M et al (2019) Resistance to neoadjuvant chemotherapy in triple‐negative breast cancer mediated by a reversible drug‐tolerant state. Sci Transl Med 11: eaav0936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fendt S‐M, Frezza C, Erez A (2020) Targeting metabolic plasticity and flexibility dynamics for cancer therapy. Cancer Discov 10: 1797–1807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fragasso G, Piatti MPM, Monti L, Palloshi A, Setola E, Puccetti P, Calori G, Lopaschuk GD, Margonato A (2003) Short‐ and long‐term beneficial effects of trimetazidine in patients with diabetes and ischemic cardiomyopathy. Am Heart J 146: 854 [DOI] [PubMed] [Google Scholar]
- Fuhrer T, Heer D, Begemann B, Zamboni N (2011) High‐throughput, accurate mass metabolome profiling of cellular extracts by flow injection–time‐of‐flight mass spectrometry. Anal Chem 83: 7074–7080 [DOI] [PubMed] [Google Scholar]
- Giancotti FG (2013) Mechanisms governing metastatic dormancy and reactivation. Cell 155: 750–764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanahan D, Weinberg RA (2011) Hallmarks of cancer: the next generation. Cell 144: 646–674 [DOI] [PubMed] [Google Scholar]
- Herr P, Boström J, Rullman E, Rudd SG, Vesterlund M, Lehtiö J, Helleday T, Maddalo G, Altun M (2020) Cell cycle profiling reveals protein oscillation, phosphorylation, and localization dynamics. Mol Cell Proteomics 19: 608–623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoogendijk AJ, Pourfarzad F, Aarts CEM, Tool ATJ, Hiemstra IH, Grassi L, Frontini M, Meijer AB, van den Biggelaar M, Kuijpers TW (2019) Dynamic transcriptome‐proteome correlation networks reveal human myeloid differentiation and neutrophil‐specific programming. Cell Rep 29: 2505–2519 [DOI] [PubMed] [Google Scholar]
- Houten SM, Violante S, Ventura FV, Wanders RJA (2016) The biochemistry and physiology of mitochondrial fatty acid β‐oxidation and its genetic disorders. Annu Rev Physiol 78: 23–44 [DOI] [PubMed] [Google Scholar]
- Hu J, Nakhla H, Friedman E (2011) Transient arrest in a quiescent state allows ovarian cancer cells to survive suboptimal growth conditions and is mediated by both mirk/dyrk1b and p130/Rb2. Int J Cancer 129: 307–318 [DOI] [PubMed] [Google Scholar]
- Hua X, Thompson CB (2001) Quiescent T cells: actively maintaining inactivity. Nat Immunol 2: 1097–1098 [DOI] [PubMed] [Google Scholar]
- Ikediobi ON, Davies H, Bignell G, Edkins S, Stevens C, O'Meara S, Santarius T, Avis T, Barthorpe S, Brackenbury L et al (2006) Mutation analysis of 24 known cancer genes in the NCI‐60 cell line set. Mol Cancer Ther 5: 2606–2612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito K, Carracedo A, Weiss D, Arai F, Ala U, Avigan DE, Schafer ZT, Evans RM, Suda T, Lee C‐H et al (2012) A PML–PPAR‐δ pathway for fatty acid oxidation regulates hematopoietic stem cell maintenance. Nat Med 18: 1350–1358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson RC (1989) The problem of the quiescent cancer cell. Adv Enzyme Regul 29: 27–46 [DOI] [PubMed] [Google Scholar]
- Kalucka J, Bierhansl L, Conchinha NV, Missiaen R, Elia I, Brüning U, Scheinok S, Treps L, Cantelmo AR, Dubois C et al (2018) Quiescent endothelial cells upregulate fatty acid β‐oxidation for Vasculoprotection via redox homeostasis. Cell Metab 28: 881–894 [DOI] [PubMed] [Google Scholar]
- Keibler MA, Wasylenko TM, Kelleher JK, Iliopoulos O, Vander Heiden MG, Stephanopoulos G (2016) Metabolic requirements for cancer cell proliferation. Cancer Metab 4: 16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim KH, Sederstrom JM (2001) Assaying cell cycle status using flow cytometry. Curr Protoc Mol Biol 111: 28.61.1–28.6.11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knobloch M, Pilz G‐A, Ghesquière B, Kovacs WJ, Wegleiter T, Moore DL, Hruzova M, Zamboni N, Carmeliet P, Jessberger S (2017) A fatty acid oxidation‐dependent metabolic shift regulates adult neural stem cell activity. Cell Rep 20: 2144–2155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S, Sharife H, Kreisel T, Mogilevsky M, Bar‐Lev L, Grunewald M, Aizenshtein E, Karni R, Paldor I, Shlomi T et al (2019) Intra‐tumoral metabolic zonation and resultant phenotypic diversification are dictated by blood vessel proximity. Cell Metab 30: 201–211 [DOI] [PubMed] [Google Scholar]
- Lee H‐J, Jedrychowski MP, Vinayagam A, Wu N, Shyh‐Chang N, Hu Y, Min‐Wen C, Moore JK, Asara JM, Lyssiotis CA et al (2017) Proteomic and metabolomic characterization of a mammalian cellular transition from quiescence to proliferation. Cell Rep 20: 721–736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemons JMS, Feng X‐J, Bennett BD, Legesse‐Miller A, Johnson EL, Raitman I, Pollina EA, Rabitz HA, Rabinowitz JD, Coller HA (2010) Quiescent fibroblasts exhibit high metabolic activity. PLoS Biol 8: e1000514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontieva OV, Demidenko ZN, Blagosklonny MV (2014) Contact inhibition and high cell density deactivate the mammalian target of rapamycin pathway, thus suppressing the senescence program. Proc Natl Acad Sci U S A 111: 8832–8837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L, Clevers H (2010) Coexistence of quiescent and active adult stem cells in mammals. Science 327: 542–545 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Link H, Fuhrer T, Gerosa L, Zamboni N, Sauer U (2015) Real‐time metabolome profiling of the metabolic switch between starvation and growth. Nat Methods 12: 1091–1097 [DOI] [PubMed] [Google Scholar]
- Listenberger LL, Han X, Lewis SE, Cases S, Farese RV, Ory DS, Schaffer JE (2003) Triglyceride accumulation protects against fatty acid‐induced lipotoxicity. Proc Natl Acad Sci U S A 100: 3077–3082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Adler AS, Segal E, Chang HY (2007) A transcriptional program mediating entry into cellular quiescence. PLoS Genet 3: e91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llufrio EM, Wang L, Naser FJ, Patti GJ (2018) Sorting cells alters their redox state and cellular metabolome. Redox Biol 16: 381–387 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopaschuk GD, Barr R, Thomas PD, Dyck JRB (2003) Beneficial effects of trimetazidine in ex vivo working ischemic hearts are due to a stimulation of glucose oxidation secondary to inhibition of long‐chain 3‐ketoacyl coenzyme a Thiolase. Circ Res 93: e33–e37 [DOI] [PubMed] [Google Scholar]
- Lu W, Clasquin MF, Melamud E, Amador‐Noguez D, Caudy AA, Rabinowitz JD (2010) Metabolomic analysis via reversed‐phase ion‐pairing liquid chromatography coupled to a stand alone orbitrap mass spectrometer. Anal Chem 82: 3212–3221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ly T, Whigham A, Clarke R, Brenes‐Murillo AJ, Estes B, Madhessian D, Lundberg E, Wadsworth P, Lamond AI (2017) Proteomic analysis of cell cycle progression in asynchronous cultures, including mitotic subphases, using PRIMMUS. eLife 6: e27574 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyssiotis CA, Kimmelman AC (2017) Metabolic interactions in the tumor microenvironment. Trends Cell Biol 27: 863–875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McInnes L, Healy J & Melville J (2018) UMAP: uniform manifold approximation and projection for dimension reduction. arXiv https://arxiv.org/abs/1802.03426 [PREPRINT]
- McQuin C, Goodman A, Chernyshev V, Kamentsky L, Cimini BA, Karhohs KW, Doan M, Ding L, Rafelski SM, Thirstrup D et al (2018) CellProfiler 3.0: next‐generation image processing for biology. PLoS Biol 16: e2005970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mellor HR, Ferguson DJP, Callaghan R (2005) A model of quiescent tumour microregions for evaluating multicellular resistance to chemotherapeutic drugs. Br J Cancer 93: 302–309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melone MAB, Valentino A, Margarucci S, Galderisi U, Giordano A, Peluso G (2018) The carnitine system and cancer metabolic plasticity. Cell Death Dis 9: 1–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra M, Ho LD, Coller HA (2018) An in vitro model of cellular quiescence in primary human dermal fibroblasts. In Cellular Quiescence, Lacorazza HD (ed), pp 27–47. New York, NY: Humana Press; [DOI] [PMC free article] [PubMed] [Google Scholar]
- Napoli PD, Taccardi AA, Barsotti A (2005) Long term cardioprotective action of trimetazidine and potential effect on the inflammatory process in patients with ischaemic dilated cardiomyopathy. Heart 91: 161–165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogretmen B (2018) Sphingolipid metabolism in cancer signalling and therapy. Nat Rev Cancer 18: 33–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oren Y, Tsabar M, Cuoco MS, Amir‐Zilberstein L, Cabanos HF, Hütter J‐C, Hu B, Thakore PI, Tabaka M, Fulco CP et al (2021) Cycling cancer persister cells arise from lineages with distinct programs. Nature 596: 576–582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortmayr K, Dubuis S, Zampieri M (2019) Metabolic profiling of cancer cells reveals genome‐wide crosstalk between transcriptional regulators and metabolism. Nat Commun 10: 1841 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostrander DB, Sparagna GC, Amoscato AA, McMillin JB, Dowhan W (2001) Decreased cardiolipin synthesis corresponds with Cytochromec release in palmitate‐induced cardiomyocyte apoptosis. J Biol Chem 276: 38061–38067 [DOI] [PubMed] [Google Scholar]
- Pavlova NN, Thompson CB (2016) The emerging hallmarks of cancer metabolism. Cell Metab 23: 27–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penzo D, Tagliapietra C, Colonna R, Petronilli V, Bernardi P (2002) Effects of fatty acids on mitochondria: implications for cell death. Biochim Biophys Acta 1555: 160–165 [DOI] [PubMed] [Google Scholar]
- Piccolis M, Bond LM, Kampmann M, Pulimeno P, Chitraju C, Jayson CBK, Vaites LP, Boland S, Lai ZW, Gabriel KR et al (2019) Probing the global cellular responses to lipotoxicity caused by saturated fatty acids. Mol Cell 74: 32–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pietras EM, Warr MR, Passegué E (2011) Cell cycle regulation in hematopoietic stem cells. J Cell Biol 195: 709–720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramirez M, Rajaram S, Steininger RJ, Osipchuk D, Roth MA, Morinishi LS, Evans L, Ji W, Hsu C‐H, Thurley K et al (2016) Diverse drug‐resistance mechanisms can emerge from drug‐tolerant cancer persister cells. Nat Commun 7: 10690 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudd AK, Devaraj NK (2018) Traceless synthesis of ceramides in living cells reveals saturation‐dependent apoptotic effects. Proc Natl Acad Sci U S A 115: 7485–7490 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatier P, Saei AA, Wang S, Zubarev RA (2018) Dynamic proteomics reveals high plasticity of cellular proteome: Growth‐related and drug‐induced changes in cancer cells are comparable. Proteomics 18: 1800118 [DOI] [PubMed] [Google Scholar]
- Schafer ZT, Grassian AR, Song L, Jiang Z, Gerhart‐Hines Z, Irie HY, Gao S, Puigserver P, Brugge JS (2009) Antioxidant and oncogene rescue of metabolic defects caused by loss of matrix attachment. Nature 461: 109–113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shyh‐Chang N, Ng H‐H (2017) The metabolic programming of stem cells. Genes Dev 31: 336–346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sosa MS, Bragado P, Aguirre‐Ghiso JA (2014) Mechanisms of disseminated cancer cell dormancy: an awakening field. Nat Rev Cancer 14: 611–622 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzur A, Moore JK, Jorgensen P, Shapiro HM, Kirschner MW (2011) Optimizing optical flow cytometry for cell volume‐based sorting and analysis. PLoS One 6: e16053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valcourt JR, Lemons JMS, Haley EM, Kojima M, Demuren OO, Coller HA (2012) Staying alive. Cell Cycle 11: 1680–1696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vander Heiden MG, Cantley LC, Thompson CB (2009) Understanding the Warburg effect: the metabolic requirements of cell proliferation. Science 324: 1029–1033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vander Heiden MG, DeBerardinis RJ (2017) Understanding the intersections between metabolism and cancer biology. Cell 168: 657–669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Violante S, Achetib N, van Roermund CWT, Hagen J, Dodatko T, Vaz FM, Waterham HR, Chen H, Baes M, Yu C et al (2019) Peroxisomes can oxidize medium‐ and long‐chain fatty acids through a pathway involving ABCD3 and HSD17B4. FASEB J 33: 4355–4364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Violante S, Ijlst L, te Brinke H, Koster J, Tavares de Almeida I, RJA W, Ventura FV, Houten SM (2013) Peroxisomes contribute to the acylcarnitine production when the carnitine shuttle is deficient. Biochim Biophys Acta 1831: 1467–1474 [DOI] [PubMed] [Google Scholar]
- Wang M, Di Poto C, Ferrarini A, Yu G, Ressom HW (2016) Metabolomic data deconvolution using probabilistic purification models. Shenzhen: IEEE; [Google Scholar]
- Wishart DS, Feunang YD, Marcu A, Guo AC, Liang K, Vázquez‐Fresno R, Sajed T, Johnson D, Li C, Karu N et al (2018) HMDB 4.0: the human metabolome database for 2018. Nucleic Acids Res 46: D608–D617 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang HW, Cappell SD, Jaimovich A, Liu C, Chung M, Daigh LH, Pack LR, Fan Y, Regot S, Covert M et al (2020) Stress‐mediated exit to quiescence restricted by increasing persistence in CDK4/6 activation. eLife 9: e44571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeuner A (2015) The secret life of quiescent cancer stem cells. Mol Cell Oncol 2: e968067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, de Milito A, Olofsson MH, Gullbo J, D'Arcy P, Linder S (2015) Targeting mitochondrial function to treat quiescent tumor cells in solid tumors. Int J Mol Sci 16: 27313–27326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmermann M, Sauer U, Zamboni N (2014) Quantification and mass Isotopomer profiling of α‐keto acids in central carbon metabolism. Anal Chem 86: 3232–3237 [DOI] [PubMed] [Google Scholar]


