Accuracy and repeatability of an inertial measurement unit system for field-based occupational studies

Abstract

The accuracy and repeatability of an inertial measurement unit (IMU) system for directly measuring trunk angular displacement and upper arm elevation were evaluated over eight hours (i) in comparison to a gold standard, optical motion capture (OMC) system in a laboratory setting, and (ii) during a field-based assessment of dairy parlour work. Sample-to-sample root mean square differences between the IMU and OMC system ranged from 4.1° to 6.6° for the trunk and 7.2°–12.1° for the upper arm depending on the processing method. Estimates of mean angular displacement and angular displacement variation (difference between the 90th and 10th percentiles of angular displacement) were observed to change <4.5° on average in the laboratory and <1.5° on average in the field per eight hours of data collection. Results suggest the IMU system may serve as an acceptable instrument for directly measuring trunk and upper arm postures in field-based occupational exposure assessment studies with long sampling durations.

Practitioner Summary:

Few studies have evaluated inertial measurement unit (IMU) systems in the field or over long sampling durations. Results of this study indicate that the IMU system evaluated has reasonably good accuracy and repeatability for use in a field setting over a long sampling duration.

1. Introduction

Characterisation of the association between non-neutral working postures and work-related musculoskeletal disorders (MSDs) requires accurate and precise posture measurement for optimal exposure assessment. Direct measurement methods are widely considered to provide the most precise and unbiased information content for estimating occupational exposure to physical risk factors for MSDs, in comparison to self-report or observation-based methods (Burdorf and Van Der Beek 1999; Li and Buckle 1999; David 2005; Teschke et al. 2009). Accelerometers and gyroscopes, for example, are two small and portable direct measurement instruments commonly used in field-based studies to assess exposure to non-neutral working postures of the lower back and shoulder (Paquet, Punnett, and Buchholz 2001; Teschke et al. 2009; Fethke, Gant, and Gerr 2011; Douphrate et al. 2012; Van Driel et al. 2013). Despite their common use, accelerometer-based estimates have been observed to suffer from poor accuracy when work tasks involve complex, dynamic motions (Hansson et al. 2001; Brodie, Walmsley, and Page 2008a; Amasay et al. 2009; Godwin, Agnew, and Stevenson 2009) and gyroscope-based estimates suffer from large integration errors that severely restrict the duration of accurate measurements (Luinge and Veltink 2005). These limitations have led investigators to seek alternative direct measurement technologies that may be better suited for field-based exposure assessment studies.

An inertial measurement unit (IMU) is a small and portable device that combines information obtained from multiple electromechanical sensors (e.g. accelerometers, gyroscopes, and magnetometers) to estimate the spatial orientation of an object through the use of recursive sensor fusion algorithms such as a Kalman filter or complementary weighting algorithm (Kalman 1960; Higgins 1975; Luinge, Veltink, and Baten 1999; Bachmann 2000; Gallagher et al. 2004; Luinge and Veltink 2005; Sabatini 2006; Yun and Bachmann 2006; Madgwick et al. 2011; Sabatini 2011, 2012; Ligorio and Sabatini 2013; Bergamini et al. 2014). IMUs are considered advantageous to individual electromechanical sensors as the strengths of each individual electromechanical sensor component may help compensate for the limitations of another. For example, accelerometer-based orientation estimates resulting from the constant acceleration of gravity may be used to correct the ‘drift’ error known to affect purely gyroscope-based estimates of displacement (Luinge 2002; Zhu and Zhou 2004; Favre et al. 2006; Zhou, Hu, and Tao 2006; Bachmann, Yun, and Brumfield 2007; Wong and Wong 2008; Bergamini et al. 2014).

Several IMU systems have been observed to accurately estimate joint kinematics of the upper arm/shoulder (Zhou, Hu, and Tao 2006; Zhou and Hu 2007, 2010; Cutti et al. 2008; Zhou et al. 2008; de Vries et al. 2010; El-Gohary and McNames 2012), the cervical spine (Jasiewicz et al. 2007; Theobald, Jones, and Williams 2012; Duc et al. 2014), the lower extremity (Favre et al. 2008; Picerno, Cereatti, and Cappozzo 2008; Ferrari et al. 2010; Fong and Chan 2010), the trunk (Lee, Laprade, and Fung 2003; Goodvin et al. 2006; Giansanti et al. 2007; Plamondon et al. 2007; Roetenberg, Slycke, and Veltink 2007; Kim and Nussbaum 2013) and the whole body (Brodie, Walmsley, and Page 2008b) in comparison to laboratory-based human motion analysis techniques such as optical motion capture (OMC) (Cuesta-Vargas, Galán-Mercant, and Williams 2010). Despite their agreement with OMC systems in a laboratory setting, most studies examining the accuracy of IMU-based measurements have not sufficiently evaluated the repeatability of those measurements over a substantial time period, such as over the course of a full work shift (Mieritz et al. 2012; Bergamini et al. 2014). Some studies such as Plamondon et al. (2007), Kim and Nussbaum (2013) and Wong and Wong (2008) have included dynamic, intermediate duration tasks (lasting 30, 20 and 120 min in length, respectively) performed in intervals or blocks (e.g. three 20-min blocks with 10 min of rest between blocks as in Kim and Nussbaum [2013]) in their performance evaluations of IMUs to address this limitation. Further testing under longer durations and in the field environment is necessary, however, to determine if IMUs are effective devices for estimating occupational exposure to non-neutral postures associated with the development of MSDs in field-based studies.

The aim of this study, therefore, was to evaluate the accuracy and repeatability of estimates of trunk angular displacement and upper arm elevation obtained with a commercially available IMU system over the course of an eight-hour work shift. The study was conducted in two phases: (1) a laboratory-based evaluation of the accuracy and repeatability of the IMU system in comparison to a gold standard, OMC system, and (2) a field-based assessment of the repeatability of the IMU system during full work shift dairy parlour work, an occupation associated with substantial exposure to non-neutral postures and musculoskeletal health outcomes (Douphrate, Nonnenmann, and Rosecrance 2009; Douphrate et al. 2012, 2014).

2. Methods

2.1. Laboratory data collection

A simulated milking cluster attachment task common to dairy parlour work was completed by six participants to evaluate the accuracy and repeatability of the IMU system in a laboratory setting. All participants were male (mean age = 29 years, SD = 9.5) and right-hand dominant. Participants had a median height of 1.8 m (range of 1.7–2.0 m), a median body mass of 92.7 kg (range of 65.8–108.9 kg), and a median body mass index of 26.9 kg/m² (range of 19.1–29.3 kg/m²). Trunk angular displacement angles in the flexion/extension and lateral bending motion planes and dominant upper arm elevation (defined as forward flexion or abduction of the upper arm) were simultaneously measured using two systems: (1) an eight-camera OMC system (Model: T10S, Vicon Systems, Centennial, CO, USA), and (2) a commercially available IMU system (I2 M Motion Tracking, Series SXT, Nexgen Ergonomics, Inc., Pointe Claire, Quebec, CAN). The simulated cluster attachment task imitated a cyclic work task commonly performed by dairy parlour workers in their real work environment. In the field, workers bend forward to grasp a milking cluster (hanging at waist height) with both hands and then lift and secure the cluster to the teats of a cow before repeating the task on the next cow in line (Figure 1).

Figure 1.

Dairy workers performing milking cluster attachment task.

One ‘block’ consisting of ten, simulated milking cluster attachment cycles was completed at the beginning of every hour for eight hours. The first block was considered a baseline measurement and was referred to as ‘Block 0’. Each block began with the participants standing in an upright stance, with the arms hanging relaxed, and the feet shoulder-width apart. At the start of each hour, participants attached one milking cluster to a simulated cow teat (Figure 2). After the participants attached the milking cluster to the teat, they would briefly return to the resting position while a trained observer returned the milking cluster to its original starting location. Once the milking cluster was back in the starting position, the participants repeated the attachment task until the entire block of 10 cycles had been completed. At the end of each block, the participants were allowed to rest in a chair while a trained investigator monitored marker and IMU placement to minimise the potential for marker or IMU movement errors.

Figure 2.

Participant performing the simulated milking cluster attachment task.

The OMC reference system used single, passive reflective markers placed over the sternal notch, spinous process of the seventh cervical spine (C7), xiphoid process, acromion process, medial/lateral humeral epicondyle, anterior arm, radial/ulnar styloid process on the dominant limb, and on bilateral anterior superior iliac spine. Additionally, clusters of three markers were placed over the spinous process of the 8th thoracic spine (T8), sacrum, and over the 3rd metacarpal head on the dominant limb. The marker locations were selected based on the recommendation from the International Society of Biomechanics (ISB) (Wu et al. 2002, 2005). Marker data were initially digitised at 80 Hz and then down sampled to 20 Hz using linear interpolation to match trunk angular displacement and upper arm elevation information obtained with the IMU system.

Angular displacements of the trunk in the flexion/extension and lateral bending motion planes and dominant upper arm elevation (defined as forward flexion or abduction of the shoulder) with respect to gravity were estimated using three IMUs. Each IMU was a small (48.5 × 36 × 12 mm) wireless, battery-powered unit that measured and stored raw acceleration (triaxial, ±6 g), angular velocity (triaxial, ±2000° s⁻¹), magnetic field strength (triaxial, ±6 Gauss) and local sensor spatial orientation information in the form of quaternions. One IMU was secured to the anterior torso at the sternal notch, one IMU sensor was secured to the posterior pelvis at the L5/S1 vertebrae, and one IMU was secured to the lateral aspect of the dominant upper arm approximately one-half the distance between the lateral epicondyle and the acromion. Specifically, the IMUs were placed into small, custom pockets that were sewn into a nylon and spandex triathlon suit the participant wore during data collection. Compression wrap was used to minimise potential IMU movement on the skin. The IMU data streams were wirelessly sampled at 20 Hz and stored to on-board flash memory. Study procedures were approved by the University of Texas at San Antonio Human Subjects Institutional Review Board and written informed consent was obtained prior to participation.

2.2. Field data collection

Field-based data were collected in milking parlours of three large-herd dairy operations during the summer months of 2014. These dairies were located in Colorado, New Mexico and Texas. Among these three dairies were one parallel parlour, one herringbone parlour, and one rotary parlour. Ten dairy workers who each performed a full, eight-hour work shift were recruited for this study. All participants were male (mean age = 24 years, SD = 1.8) and right-hand dominant. Participants had a median height of 1.6 m (range of 1.6–1.8 m), a median body mass of 69.9 kg (range of 63.5–81.6 kg) and a median body mass index of 27.2 kg/m² (range of 25.6–30.0 kg/m²). Approximately, 45 min prior to starting work, each participant was fitted with three IMUs as described for the laboratory-based data collection procedure and a fourth IMU was placed on the non-dominant upper arm. Study procedures were approved by the University of Texas Health Science Center at Houston Committee for the Protection of Human Subjects Institutional Review Board and written informed consent was obtained prior to participation.

2.3. Instrumentation and data processing

Raw three-dimensional coordinate data obtained with the OMC system (sampled at 80 Hz) were low-pass filtered (zero-phase, 4th-order Butterworth; 10 Hz cut-off frequency) prior to down sampling to 20 Hz (Yu and Hay 1995). The filtered and down sampled data were then used to calculate estimates of trunk angular displacement and upper arm elevation relative to the global coordinate system (OMC_Global) for the laboratory-based component of this study. An OMC-based estimate of trunk angular displacement relative to the pelvis (OMC_Pelvis) and an estimate of upper arm elevation relative to the torso (OMC_Torso) were also calculated for comparison to analogous IMU-based measures of trunk and shoulder motion, respectively. The anatomic coordinate systems of the pelvis, upper torso and the shoulder joints were defined as recommended by the ISB (Wu et al. 2002, 2005). The shoulder joint centre was defined as described by Rab, Petuskey, and Bagley (2002) and shoulder angles were calculated using an Euler–Cardan angle method with rotation orders as recommended by the ISB (Wu et al. 2005). The upper torso orientation in the global reference frame was calculated using an Euler–Cardan angle method with a rotation order of flexion/extension, lateral bending and axial rotation.

Four IMU processing methods were used to estimate trunk angular displacement in the flexion/extension and lateral bending motion planes for both the laboratory- and field-based components of this study. The four methods included (1) a low passed (zero-phase, 2nd-order Butterworth; 3 Hz cut-off frequency) accelerometer-based estimate from the IMU secured to the sternum only (Accel-1); (2) a complementary weighting algorithm-based estimate incorporating accelerometer and gyroscope measurements from the IMU secured to the sternum only (Comp-1); (3) a low passed (zero-phase, 2nd-order Butterworth; 3 Hz cut-off frequency) accelerometer-based estimate calculated as the difference of the estimates provided from the IMUs secured to the sternum and L5/S1 body segments (Accel-2); and (4) a complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates from the IMUs secured to the sternum and L5/S1 body segments (Comp-2) (Schall et al. 2015). Estimates of trunk angular displacement in the axial rotation motion plane were not analysed as ferromagnetic disturbances in both the laboratory and field environments (determined through visual inspection of the angular displacement waveforms during analysis) prevented use of the magnetometer measurements in a Kalman-based estimate.

Three IMU processing methods were used to obtain estimates of dominant upper arm elevation for the laboratory-based component and bilateral upper arm elevation for the field-based component of this study. The three methods included (1) a low passed (zero-phase, 2nd-order Butterworth; 3 Hz cut-off frequency) accelerometer-based estimate from the IMU secured to the arm only (Accel-1); (2) a complementary weighting algorithm-based estimate incorporating accelerometer and gyroscope measurements from the IMU secured to the arm only (Comp-1); and (3) a complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates from the IMUs secured to the sternum and the arm (ART – ‘Arm Relative to Torso’).

Accelerometer-based inclination angle estimates for the trunk were calculated with respect to the gravity vector. Specifically, inclination angle estimates in the flexion/extension motion plane were calculated as ${\tan }^{-1}(\text{Az}/\text{Ax})$ and inclination angle estimates in the lateral bending plane were calculated as ${\tan }^{-1}(\text{Ay}/\text{Ax})$. Trunk estimates were calculated in this manner so that they could be paired directly with gyroscope measurements in the corresponding axis of rotation.

Accelerometer-based inclination angle estimates from the IMU secured to the arm were calculated as ${\cos }^{-1}\left(\text{Ax}/\sqrt{\text{A}{\text{x}}^2+\text{A}{\text{y}}^2+\text{A}{\text{z}}^2}\right)$

Complementary weighting algorithm-based estimates were derived as described in previous studies (Schall et al. 2014, 2015) and adjusted accelerometer-based inclination angle estimates at each sample using angular velocity information from the IMU’s gyroscope according to Equation (1):

$${\theta }_n=(1-K)\left[{\theta }_{n-1}+\left({\omega }_n\times dt\right)\right]+K\left({\alpha }_n\right)$$ (1)

${\theta }_n$ represents the complementary inclination angle estimate at the current sample, ${\theta }_{n-1}$ is the complementary inclination angle estimate at the previous sample, ${\omega }_n$ is the angular velocity at the current sample, ${\alpha }_{n}i$ is the inclination angle at the current sample based solely on the orientation of the accelerometer with respect to gravity, and dt is the time between samples. A weighting coefficient (K) value of 0.06 was used to maintain the time constant of 0.77 s used in previous studies (Schall et al. 2014, 2015). This value provided a sufficient acceleration reference to compensate for the ‘drift’ error that occurs when a raw gyroscope signal is integrated.

2.4. Statistical analysis

Estimates of the minimum (maximum extension or left lateral bending), maximum (maximum flexion or right lateral bending), mean, selected percentiles (10th, 50th, 90th and 99th) from the amplitude probability distribution function (APDF) and the difference between the estimates of the 90th and 10th percentiles of the APDF (referred to as the angular displacement variation) were calculated from the angular displacement waveforms obtained from each IMU processing method and the OMC reference system for each block of the cluster attachment task for the laboratory-based analysis. The 90th percentile, 10th percentile and the angular displacement variation (90th–10th percentiles) are summary metrics commonly used in field-based occupational exposure assessment studies (Kazmierczak et al. 2005; Hansson et al. 2010; Wahlstrom et al. 2010; Jonker et al. 2011; Moriguchi et al. 2013) for estimating ‘peak’, ‘static’, and variation in exposure, respectively. The estimates were summarised using means and standard deviations across all blocks and all participants.

Sample-to-sample root mean square differences (RMSD) for each block of cluster attachments were estimated by comparing the waveform of each IMU processing method to the waveform obtained with the OMC reference system for each participant using Equation (2), where θ is the estimate from an IMU processing method, θ′ is the estimate from the OMC reference system, n is the number of samples across the block of ten cluster attachment cycles and i is the sample number. Then, the arithmetic mean of the RMSDs for each block of cluster attachments and for each inter-method comparison across all participants was calculated.

$$\text{RMSD}=\sqrt{\sum _{i=1}^n{\left({\theta }_i-{\theta }_i^{\prime }\right)}^2/n}$$

The repeatability of the IMU measurements in both the laboratory and field-based analyses was assessed using a linear mixed model regression with the postural summary measure as the dependent variable and a fixed effect of time as the independent variable. The model also included random coefficient effects (i.e. intercepts and slopes) to account for between-subject variability (Littell et al. 2006). The regression coefficient associated with the fixed effect of time was scaled to represent the change in the postural summary measure per eight hours of sampling time. Postural summary measures included mean angular displacement and angular displacement variation of (i) the trunk in the flexion/extension and lateral bending motion planes and (ii) dominant upper arm elevation. A separate linear regression model was constructed for each postural summary measure. The slope of each regression line depicts the overall change in the postural summary measures over the entire sampling duration. A slope of zero indicates no change in the range of values, a positive slope indicates an increase in the range of values and a negative slope indicates a decrease in the range of values. All statistical procedures were performed using SAS (version 9.3, The SAS Institute, Cary, NC).

3. Results

3.1. Laboratory-based assessment of accuracy

The OMC reference system and each of the IMU measurement methods produced waveforms of trunk angular displacement and upper arm elevation with relatively similar characteristics (Figure 3). Descriptive statistics of the angular displacement and RMSD estimates between the OMC system and the IMU measurement methods for the trunk and the upper arm are provided in Tables 1 and 2, respectively.

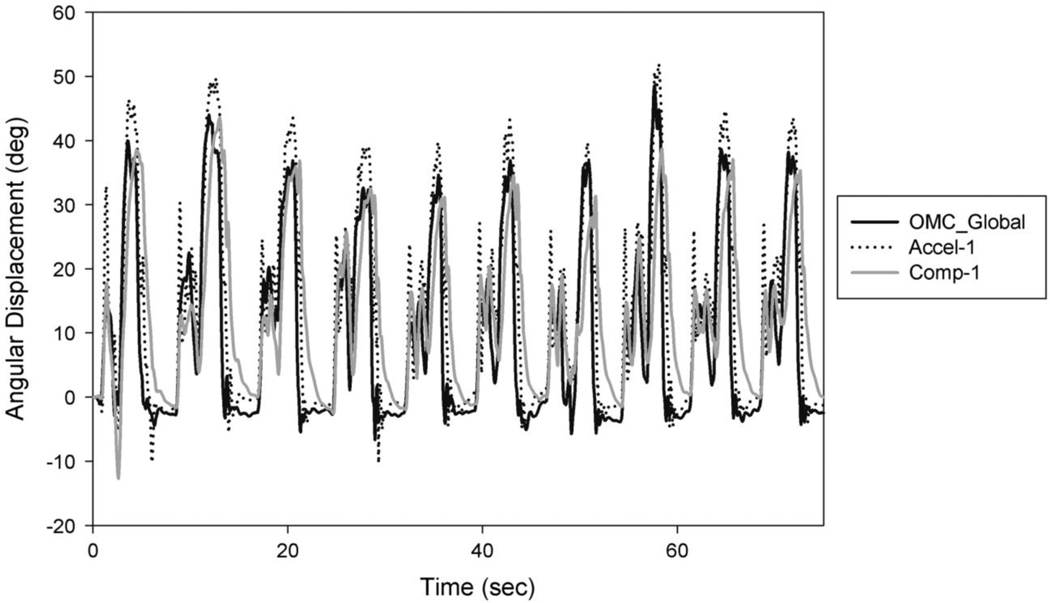
Figure 3.

Upper arm elevation waveform obtained with the OMC system and two IMU measurement processing methods for one block of the cluster attachment task.

Table 1.

Mean (SD) of trunk angular displacement estimates by measurement method.

Summary measure	OMC_Global	Accel-1	Comp-1	OMC_Pelvis	Accel-2	Comp-2
Flexion/Extension
Maximum extension (°)	−4.8 (3.5)	−5.5 (2.4)	−4.1 (2.4)	−5.6 (4.0)	−8.3 (5.1)	−5.8 (4.5)
Mean (°)	10.2 (4.8)	8.5 (4.8)	8.5 (4.8)	8.7 (4.0)	6.8 (3.1)	6.7 (3.0)
Maximum flexion (°)	45.6 (12.1)	44.3 (13.1)	39.4 (12.2)	34.9 (10.3)	30.1 (7.6)	26.4 (7.0)
10th percentile (°)	−0.6 (2.6)	−0.7 (1.4)	−0.4 (1.3)	−0.5 (2.7)	−1.1 (2.6)	−0.8 (2.4)
50th percentile (°)	6.0 (5.5)	4.4 (5.1)	4.9 (5.1)	5.8 (5.4)	4.3 (4.2)	4.5 (4.2)
90th percentile (°)	27.2 (11.5)	23.7 (12.0)	22.6 (11.5)	21.7 (8.5)	17.5 (6.2)	16.6 (5.7)
99th percentile (°)	39.0 (13.2)	37.2 (14.3)	33.7 (13.4)	29.8 (9.8)	25.3 (7.3)	23.0 (6.5)
Sample-to-sample RMSD (°)	-- Ref --	6.5 (2.3)	5.4 (2.6)	-- Ref --	6.6 (2.9)	6.2 (3.0)
Lateral bending
Maximum to the left (°)	−10.1 (6.0)	−14.8 (5.3)	−13.4 (5.9)	−8.4 (4.8)	−11.0 (3.9)	−11.7 (3.8)
Mean (°)	0.7 (1.8)	0.7 (2.7)	0.9 (2.6)	1.3 (2.1)	1.3 (2.5)	1.1 (2.4)
Maximum to the right (°)	12.5 (8.1)	18.9 (11.5)	15.7 (12.0)	12.9 (7.2)	19.0 (9.8)	15.2 (9.5)
10th percentile (°)	−2.2 (2.5)	−3.7 (2.3)	−2.9 (2.0)	−1.8 (2.1)	−2.3 (1.7)	−2.7 (1.9)
50th percentile (°)	0.4 (1.1)	0.2 (1.1)	0.4 (1.2)	0.9 (1.7)	0.5 (1.3)	0.6 (1.3)
90th percentile (°)	4.0 (3.7)	6.1 (7.7)	5.5 (7.4)	5.0 (4.8)	5.8 (6.4)	5.5 (5.9)
99th percentile (°)	8.5 (6.3)	12.8 (10.5)	11.2 (10.4)	9.3 (6.4)	11.9 (8.3)	10.7 (7.9)
Sample-to-sample RMSD (°)	-- Ref --	4.5 (2.4)	5.8 (2.9)	-- Ref --	4.1 (1.3)	5.0 (2.1)

Notes: OMC_Global = Low passed (zero-phase, 4th-order Butterworth, 10 Hz cut-off) OMC-based estimate relative to the global coordinate system; Accel-1 = Low passed (zero-phase, 2nd-order Butterworth, 3 Hz cut-off) accelerometer-based estimate from the IMU secured to the sternum only; Comp-1 = Complementary weighting algorithm-based estimate using accelerometer and gyroscope measurements from the IMU secured to the sternum only; OMC_Pelvis = Low passed (zero-phase, 4th-order Butterworth, 10 Hz cut-off) OMC-based estimate relative to the pelvis; Accel-2 = Low passed (zero-phase, 2nd-order Butterworth, 3 Hz cut-off) accelerometer-based estimate calculated as the difference of the estimates provided from the IMU secured to the sternum and L5/S1 body segments; Comp-2 = Complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates provided from the IMUs secured to the sternum and L5/S1 body segments.

Table 2.

Mean (SD) of the dominant (right) upper arm elevation estimates by measurement method.

Summary measure	OMC_Global	Accel-1	Comp-1	OMC_Torso	ART
Mean (°)	13.5 (7.0)	13.4 (7.4)	13.2 (7.8)	20.7 (9.9)	21.3 (11.5)
Maximum elevation (°)	50.0 (7.9)	51.5 (8.6)	46.1 (10.0)	67.8 (11.9)	65.2 (17.8)
10th percentile (°)a	−0.8 (2.1)	−0.9 (2.0)	0.1 (2.7)	0.0 (1.9)	2.3 (3.9)
50th percentile (°)	8.4 (10.7)	8.6 (10.6)	10.0 (10.6)	15.3 (17.3)	18.2 (17.4)
90th percentile (°)	35.9 (8.8)	35.2 (10.8)	31.6 (10.6)	49.2 (12.7)	44.0 (14.4)
99th percentile (°)	45.1 (7.5)	44.4 (9.2)	40.0 (9.7)	59.9 (12.0)	55.5 (16.1)
Sample-to-sample RMSD (°)	-- Ref --	7.2 (2.9)	8.5 (2.4)	-- Ref --	12.1 (3.2)

Notes: OMC_Global = Low passed (zero-phase, 4th-order Butterworth, 10 Hz cut-off) OMC-based estimate relative to the global coordinate system; Accel-1 = Low passed (zero-phase, 2nd-order Butterworth, 3 Hz cut-off) accelerometer-based estimate from the IMU secured to the sternum only; Comp-1 = Complementary weighting algorithm-based estimate using accelerometer and gyroscope measurements from the IMU secured to the sternum only; OMC_Torso = Low passed (zero-phase, 4th-order Butterworth, 10 Hz cut-off) OMC-based estimate relative to the torso; ART = a complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates from the IMUs secured to the sternum and upper arm (shoulder relative to the torso).

^aNegative values denote extension behind the body.

RMSD orientation error estimates between 4.1° and 6.6° were observed for all IMU processing methods in the flexion/extension and lateral bending trunk motion planes. In general, RMSD estimates were similar (within 1.5°) across methods obtained using only the IMU secured to the sternum and across methods obtained using both the IMUs secured to the sternum and L5/S1 body segment. RMSD estimates indicated that the complementary weighting algorithm-based approaches (Comp-1 and Comp-2) that incorporated accelerometer and gyroscope measurements were more comparable to the OMC system than solely accelerometer-based estimates (Accel-1 and Accel-2) in the flexion/extension motion plane. Conversely, RMSD estimates indicated that the solely accelerometer-based approaches (Accel-1 and Accel-2) were more comparable to the OMC system than the complementary weighting algorithm-based estimates (Comp-1 and Comp-2) for the lateral bending motion plane.

For the upper arm, RMSD orientation error estimates ranged from 7.2° for the accelerometer-based estimate from the IMU secured to the arm only (Accel-1) to 12.1° for the complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates from the IMUs secured to the sternum and upper arm (ART). The solely accelerometer-based estimate obtained from the IMU secured to the upper arm (Accel-1) had a smaller RMSD orientation error estimate in comparison to the OMC system than the complementary weighting algorithm-based estimate incorporating accelerometer and gyroscope measurements from the IMU secured to the upper arm only (Comp-1).

3.2. Laboratory-based assessment of repeatability

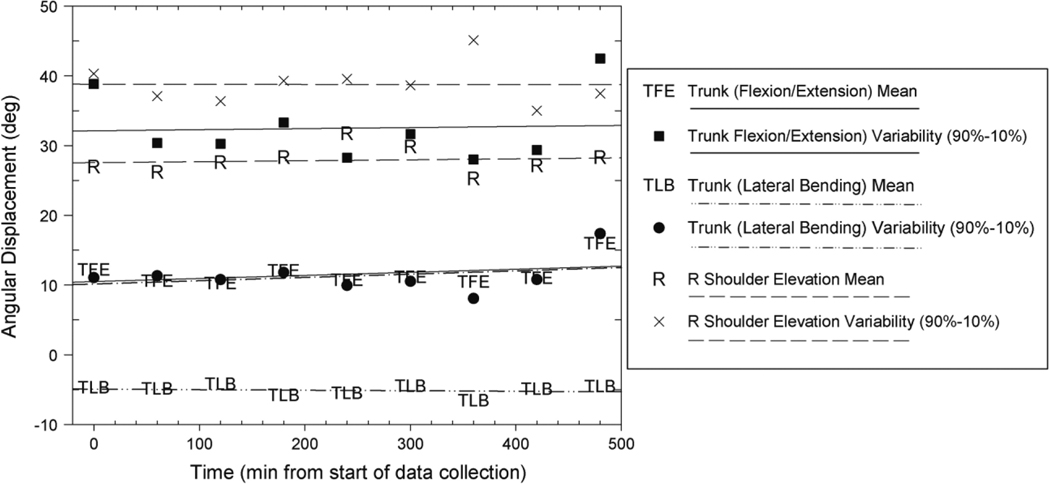
The IMU system produced reasonably stable mean angular displacement and mean angular displacement variation (90th–10th percentile) estimates of trunk posture and dominant upper arm elevation (Tables 3 and 4; Figure 4). On average, the IMU estimates were observed to change <4.5° over the eight-hour sampling duration. With the exception of the dominant (right) upper arm angular displacement variation slope estimates for the complementary weighting algorithm-based approaches (Comp-1 and ART), all trunk angular displacement and upper arm elevation slope estimates were statistically insignificant and suggested changes of <7.5° in mean angular displacement and mean angular displacement variation per eight hours of data collection. Trunk angular displacements in the flexion/extension plane were the most stable, changing <2.5° over the eight hours. The statistically significant complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates from the IMUs secured to the sternum and the right arm (ART) was observed to have the least stability and averaged roughly 9.5° of change in mean angular displacement and 8.5° of mean angular displacement variation per eight hours of data collection.

Table 3.

Laboratory-based and field-based slope estimates and associated 95% confidence intervals (CI) for the trunk (calculated as the ratio of the change in degrees of trunk angular displacement per eight hours) of the mean and angular displacement variation for each IMU processing method.^a

Summary measure	OMC_Global		Accel-1		Comp-1		OMC_Pelvis		Accel-2		Comp-2
	Slope	CI	Slope	CI	Slope	CI	Slope	CI	Slope	CI	Slope	CI
Laboratory-based
Trunk flexion/extension
Mean	−4.13	(−10.86–2.60)	−2.05	(−5.84–1.74)	−2.19	(−5.91–1.54)	−3.64	(−10.08–2.80)	−0.60	(−5.43–4.22)	−0.74	(−5.44–3.95)
Variation (90th–10th %)	−7.24	(−21.82–7.33)	−5.77	(−13.11–1.57)	−5.66	(−12.67–1.34)	−4.05	(−20.11–12.0)	−1.17	(−6.82–4.49)	−1.23	(−6.36–3.91)
Trunk lateral bending
Mean	−1.34	(−4.43–1.75)	−2.29	(−8.47–3.89)	2.08	(−8.06–2.64)	−1.83	(−5.29–1.62)	−2.64	(−7.40–2.13)	−2.68	(−6.61–1.26)
Variation (90th–10th %)	−0.94	(−6.49–4.61)	−7.38	(−21.96–7.20)	−6.49	(−20.28–7.30)	−2.26	(−10.79–6.26)	−6.29	(−18.51–5.92)	−5.04	(−15.66–5.58)
Field-based
Trunk flexion/extension
Mean	--	--	−2.24	(−6.76–2.27)	−2.43	(−7.14–2.28)	--	--	0.09	(−4.76–4.94)	−0.17	(−5.33–4.98)
Variation (90th–10th %)	--	--	−1.44	(−8.34–5.47)	0.05	(−4.92–5.02)	--	--	−2.33	(−6.74–2.08)	−0.88	(−5.59–3.83)
Trunk lateral bending
Mean	--	--	−0.53	(−5.14–4.08)	−0.67	(−5.11–3.77)	--	--	−1.22	(−3.73–1.29)	−1.38	(−4.00–1.24)
Variation (90th–10th %)	--	--	0.10	(−5.03–5.23)	0.31	(−4.70–5.32)	--	--	0.49	(−3.00–3.97)	−0.02	(−3.98–3.94)

^aColumn headers are defined in Tables 1 and 2.

Table 4.

Laboratory-based and field-based slope estimates and associated 95% confidence intervals (CI) for the upper arm (calculated as the ratio of the change in degrees upper arm elevation per eight hours) of the mean and angular displacement variation for each IMU processing method.^a

Summary measure	OMC_Global		Accel-1		Comp-1		OMC_Torso		ART
	Slope	CI	Slope	CI	Slope	CI	Slope	CI	Slope	CI
Laboratory-based
Right shoulder
Mean	−6.05	(−13.85–1.75)	−6.18	(−13.42 – 1.06)	−6.59	(−13.44–0.25)	−7.65	(−15.93–0.63)	−9.38	(−17.76–−1.00)*
Variation (90th–10th %)	−5.61	(−12.74–1.53)	−5.27	(−12.76–2.23)	−4.64	(−9.27–0.00)*	−7.67	(−15.22–−0.12)*	−8.49	(−14.46–−2.51)*
Field-based
Right shoulder
Mean	--	--	4.19	(−1.35–9.73)	4.87	(−0.36–10.10)	--	--	2.46	(−5.79–10.71)
Variation (90th–10th %)	--	--	−2.10	(−9.50–5.29)	−3.24	(−11.83–5.34)	--	--	−6.80	(−15.52–1.93)
Left shoulder
Mean	--	--	−0.52	(−3.34–2.31)	−0.61	(−3.08–1.85)	--	--	−2.14	(−7.08–2.80)
Variation (90th–10th %)	--	--	0.55	(−3.49–4.60)	0.48	(−5.25–6.21)	--	--	−1.45	(−10.10–7.19)

^aColumn headers are defined in Tables 1 and 2.

^*p ≤ 0.05.

Figure 4.

Trunk and dominant upper arm mean angular displacement and angular displacement variation (the difference between the 90th and 10th percentiles of angular displacement) estimates for the Accel-1 measurement method for one participant.

3.3. Field-based assessment of repeatability

Mean angular displacement and mean angular displacement variation (90th–10th percentile) estimates of trunk posture and bilateral upper arm elevation in the field were observed to be more stable than in the laboratory setting. On average, the IMU estimates were observed to change <1.5° over the eight-hour sampling duration. With the exception of the angular displacement variation slope estimate for the complementary weighting algorithm-based approaches for the right upper arm, almost all trunk angular displacement and bilateral upper arm elevation slope estimates were observed to exhibit <2.5° of change in mean angular displacement and mean angular displacement variation per eight hours of data collection (Tables 3 and 4). Similar to the laboratory-based assessment, the complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates from the IMUs secured to the sternum and the right arm (ART) was observed to have the least stability and averaged roughly 2.5° of change in mean angular displacement and 6.5° of mean angular displacement variation per eight hours of data collection, respectively. No statistically significant effects were observed for the field-based assessment.

4. Discussion

Although not directly comparable, the angular displacement RMSD estimates observed in the laboratory-based component of this study were reasonably similar to those reported in several other laboratory-based studies comparing trunk posture and upper arm elevation orientation error estimates obtained with IMU-based instrumentation systems to estimates obtained with an OMC system (Luinge, Veltink, and Baten 2007; Wong and Wong 2008; Godwin, Agnew, and Stevenson 2009; Martin-Schepers, Roetenberg, and Veltink 2010; de Vries et al. 2010; El-Gohary and McNames 2012; Kim and Nussbaum 2013). In particular, the mean RMSD estimates between 4.1° and 6.6° that were observed for all IMU processing methods in the flexion/extension and lateral bending trunk motion planes compare reasonably well to previous studies that have evaluated the accuracy of IMUs for measuring trunk posture during dynamic, manual work tasks of intermediate durations (Plamondon et al. 2007; Wong and Wong 2008; Kim and Nussbaum 2013). The results suggest that the IMU system examined in this study may serve as an acceptable instrument for directly measuring trunk angular displacement and upper arm elevation in field-based occupational exposure assessment studies.

The IMU system examined in this study generally exhibited strong stability to complement its reasonably good accuracy. Estimates of mean angular displacement and angular displacement variation were observed to change <4.5° on average in the laboratory and <1.5° on average in the field over eight hours of data collection. Comparable mean angular displacement and angular displacement variation estimates were observed for the OMC system. It is expected that the larger average changes in the laboratory setting were the result of greater variance in the stature of the participants and limited experience conducting the cluster attachment task. While we are aware of no empirical evidence suggesting acceptable amounts of IMU error, this amount seems relatively minor and suggests that the IMU system is capable of providing stable estimates of posture over long sampling durations (e.g. full work shift data collection) in a field setting. While these results are encouraging, investigators should be aware that these error estimates are an average and that errors larger than 3–5° may occur on an individual basis. Error estimates may also depend on the range of motion of the body segment or motion plane of interest for a particular task. For example, error estimates for the OMC system in the lateral bending motion plane were smaller than the error estimates for the flexion/extension motion plane of the trunk in this study. The estimates were likely smaller due to the smaller range of motion required by the cluster attachment task for the lateral bending motion plane.

An important observation from this study was that the accuracy of RMSD orientation error estimates between the IMU system and the OMC system did not appear to be directly associated with the comparability of estimates of commonly reported summary metrics such as percentiles of the APDF. IMU processing methods observed to have larger RMSD orientation errors in comparison to the ‘gold standard’ OMC system were, at times, observed to have more accurate estimates of common summary metrics in comparison to the OMC system. Estimates of ‘peak’ exposure (90th and 99th percentile) for the solely accelerometer-based approaches (Accel-1 and Accel-2), for example, were generally observed to be more comparable to the OMC system than the complementary weighting algorithm-based approaches (Comp-1 and Comp-2) for the flexion/extension plane despite a larger RMSD. At other times, when larger RMSD orientation errors were observed between a processing method and the OMC system, estimates of ‘peak’ exposure were observed to be more comparable. For example, the complementary weighting algorithm-based approaches (Comp-1 and Comp-2) for the lateral bending plane were generally observed to be more comparable to the OMC system than estimates obtained from the solely accelerometer-based approaches (Accel-1 and Accel-2). The results indicate that RMSD orientation error estimates may not be sufficient for evaluating the accuracy of an instrument in comparison to a ‘gold standard’. Comparisons of the summary metrics planned for analysis are necessary and may be more important for health outcomes research. Additionally, these results highlight the potential trade-off of adjusting the complementary weighting-algorithm. By increasing the proposed weighting coefficient (K) and including more accelerometer-based measurements, more accurate estimates of exposure in one motion plane may be attained while negatively affecting estimates in another. Further research exploring the sensitivity of the complementary weighting algorithm under different applications is needed.

Overall, this study represents the first effort we are aware of to evaluate the accuracy and repeatability of estimates of trunk angular displacement and upper arm elevation obtained with a commercially available IMU system over the course of an eight-hour work shift in both a laboratory and a field setting. The results contribute to the growing body of empirical evidence suggesting that IMUs may be useful instruments for use in field-based epidemiological studies seeking to accurately assess exposure to occupational physical risk factors associated with musculoskeletal health outcomes.

The results of this study must be interpreted in the context of several limitations. First, while we intended on using the full complement of IMU sensors (accelerometer, gyroscope and magnetometer) to analyse trunk angular displacements in the axial rotation motion plane and to separate upper arm elevation estimates into varying degrees of motion in the scapular plane, ferromagnetic disturbances in both the laboratory and field environments prohibited use of our magnetometer measurements. While the predominant theoretical strength of IMU technology is the ability to measure human motion in three-dimensional space using magnetometer measurements to compensate for the ‘drift’ of the gyroscope during motion about the gravity vector (Roetenberg et al. 2005), most field-based settings involve some ferromagnetic and/or electromagnetic sources that diminish the quality of magnetometer measurements. Modern dairy operations, in particular, are becoming larger and more mechanised (Douphrate et al. 2013). The introduction of new technologies such as automatic feeding systems and cow separation systems increases the presence of ferromagnetic materials in close proximity to the workers. Consequently, until standard guidelines and methods for defining, identifying and obtaining reasonable magnetometer measurements are developed, IMU-based measurement of motion that occurs about the gravity vector will continue to be severely flawed or unattainable.

Both the laboratory-based and field-based components of this study involved the analysis of a single cyclic work task performed by few participants (n = 6 for laboratory component; n = 10 for field component). The use of a single work task and few participants substantially limits the generalisability of the results to work tasks with comparable movement characteristics. Furthermore, while it was assumed that all participants performed the work task similarly in comparison to other participants and over time within a work shift, individual differences between study participants and uncontrolled factors such as fatigue and dairy parlour configuration likely affected the manner in which the work task was performed. These individual differences may partially explain changes in mean angular displacement and mean angular displacement variation (90th–10th percentile) estimates of trunk motion and upper arm elevation over time that may be interpreted as IMU measurement error.

While job specialisation is common to many occupations, including dairy work (Douphrate et al. 2012, 2013), task-based estimates of job exposures are not comprehensive and may be less correct than estimates based on the mean exposure of an occupational group (Mathiassen et al. 2005; Svendsen, Mathiassen, and Bonde 2005). Additional research employing direct measurement methods over long sampling durations are needed to sufficiently characterise biomechanical exposures to develop and evaluate maximally effective engineering and administrative controls (such as job rotation).

Variable time between cluster attachment blocks and an inconsistent number of blocks performed by participants in the field-based component of this study may also have contributed to errors in the estimates of repeatability of trunk motion and upper arm elevation over time. For example, while most participants in the field-based component of this study performed between eight and ten blocks of the cluster attachment task during the course of their work day, participants working at the dairy parlour with a rotary style configuration were observed to perform only three to four cluster attachment blocks. Rotary style configurations generally employ a job rotation strategy that limits the number of cluster attachment blocks performed by any single worker (Douphrate et al. 2012). The limited number of cluster attachment blocks may have created a situation in which some participants had a larger slope than what might be reasonably expected had more blocks been performed.

Finally, it is unknown how additional work activities normally performed during dairy parlour work may have affected IMU accuracy in comparison to the OMC system. The participants in the laboratory-based component of this study were instructed to rest in a chair between blocks to preserve the location of OMC markers and IMU placement to prevent errors due to marker or IMU movement. While it is possible that IMU movement on the skin did occur, the use of compression suits to minimise sensor movement appeared to work well and prevent gross changes in sensor placement. In a real work setting, additional work activities or sensor movement may contribute to increased errors in the accuracy of trunk motion and upper arm elevation estimates. Future work examining the performance of the IMU system during the completion of multiple work tasks with different kinematic characteristics (e.g. speeds and ranges of motion) is necessary. Additionally, further research on methods and strategies to improve the accuracy and precision of the individual sensors that comprise an IMU would be of value.