Efficient and relevant stepwise covariate model building for pharmacometrics

Abstract

Covariate modeling is an important opportunity for pharmacometrics to influence decision making in drug development. The stepwise covariate model (SCM) building procedure is the most common method for covariate model development. Despite its advantages, the traditional SCM method is known to have long runtimes and the suboptimal ability to select relevant covariates, especially in more complex phase III settings. In this work, two alternative approaches are presented: SCM+, which introduces the “adaptive scope reduction” and changes to general estimation settings, and “stage‐wise filtering,” which groups covariates into categories based on their importance (mechanistic, structural, and exploratory). The three methods (SCM, SCM+, and SCM+ with stage‐wise filtering) are applied to data from a simulated phase III population pharmacokinetic study and are compared in terms of efficiency and relevance. The two SCM+ methods were considerably more efficient than the traditional SCM: the number of function evaluations was reduced by 70% for SCM+ and by 76% for SCM+ with stage‐wise filtering compared to SCM; the corresponding number of executed models was reduced by 44% for SCM+ and 70% for SCM+ with stage‐wise filtering. In addition, among the three methods, SCM+ with stage‐wise filtering selected the highest number of relevant covariates. Given the improved efficiency and ability to select relevant covariates shown in this work, the use of SCM+ and stage‐wise filtering can greatly increase the efficiency of covariate modeling in drug development, which will ultimately facilitate more timely support for decision making.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Covariate modeling is an important opportunity for pharmacometrics to influence decision making in drug development. To this aim, the identified covariates need to be delivered on time and be considered relevant. Covariate modeling is often carried out using stepwise procedures (e.g., stepwise covariate model [SCM]). The standard SCM workflow is time‐inefficient with suboptimal ability to select relevant covariates.

• WHAT QUESTION DID THIS STUDY ADDRESS?

Can SCM be improved in terms of efficiency and ability to select relevant covariates?

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

SCM+ is introduced and shown to be more efficient than SCM, with similar ability to select relevant covariates. Stage‐wise filtering is a grouping principle that involves grouping covariates into categories (mechanistic, structural, and exploratory) and test them in order of importance. Stage‐wise filtering improved the ability to select relevant covariates.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

Given the improved efficiency and ability to select relevant covariates, the use of SCM+ and stage‐wise filtering can increase the influence that covariate modeling has on drug development decision making.

INTRODUCTION

Covariate model development is a key component of pharmacometrics, population pharmacokinetics (PKs), and PK/pharmacodynamic (PK/PD) model development. ¹ The covariate model may have meaningful influence on drug development decisions and can, for example, justify changes in dosing strategies, and identify patient subpopulations with specific characteristics of drug absorption or metabolism.

A comprehensive review of the methods used for covariate selection in pharmacometric analysis was published by Hutmacher and Kowalski in 2014. ¹ In the context of pharmacometric covariate model development, stepwise covariate model building procedures are the most commonly used. ¹ Among other advantages, these procedures are simple to implement, easy to understand, and generally accepted by regulatory authorities. On the other hand, an obvious drawback is that they may be time‐consuming, especially with complex models and/or with many potential parameter–covariate relations to consider. This is particularly relevant for the phase III setting, where focus is often set on identifying, or ruling out, the presence of patient subpopulations that may require alternative dosing schedules. In addition, stepwise variable selection models have been criticized for their sensitivity to high correlations between covariates, which may result in implausible selection of predictors and inclusion of excess noise variables ¹ , ² and may thus lead to models with poor predictive capabilities. However, as concluded by Ribbing and Jonsson, ³ selection bias and its impact on predictive performance is mainly an issue for covariates with a low power to be selected (i.e., typically weak covariates in small datasets).

Clinical drug development proceeds in phases, going from small studies in healthy volunteers aimed at establishing safe dose ranges (phase I), proof‐of‐concept and identification of candidate dosing regimen studies (phase II), to large clinical trials that focus on establishing therapeutic benefit in wider patient populations (phase III). The sequential nature of most drug development programs entails that once the program reaches phase III, considerable knowledge has been accumulated on the studied condition and the characteristics of the drug. This implies that before starting any covariate modeling work on the phase III data, the clinical development team often has reasonable expectations on candidates for relevant parameter–covariate relations. However, this knowledge is often not used (see Svensson et al. illustrating an exception ⁴ ) and covariate screening is performed with an exploratory mindset, where all covariates are treated in the same way, regardless of the prior knowledge accumulated.

In this work, we illustrate an alternative concept to the common framework for pharmacometric covariate model development using stepwise approaches. It is based on the implementation of stepwise covariate searches in Perl‐speaks‐NONMEM (i.e., the stepwise covariate model [SCM] tool in PsN. ⁵ , ⁶ This concept has two components: the first is SCM+, which is a development of the traditional stepwise algorithm used in SCM. ⁶ SCM+ introduces “adaptive scope reduction” (ASR) ⁷ and a number of changes to general estimation settings; SCM+ aims at improving the overall efficiency of the stepwise covariate search. The second component is “stage‐wise filtering,” which groups covariates into categories based on their importance (mechanistic > structural > exploratory covariates) and aims at improving the ability to select relevant covariates. Although the implementation of the SCM and SCM+ is NONMEM‐specific, ⁸ the general concepts explored in this paper can be adapted and used in other applications.

To characterize the benefits of this alternative approach over the traditional SCM approach, we applied the different methods to data from simulated phase III population PK studies and compared their efficiency and ability to select relevant covariates. Specifically, (a) the efficiency, in terms of total number of function evaluations and executed models, as well as (b) the ability to select relevant covariates were compared among SCM, SCM+, and SCM+ with stage‐wise filtering.

METHODS

Overview

A simulated phase III example study was used in this analysis. The simulation was designed to include some of the challenges often encountered in a phase III setting, for example, an analysis dataset including both smaller healthy‐volunteer studies and larger patient studies with different formulations, food effects, multiple dose levels (denoted low, middle, and high dose), and realistic covariate distributions (non‐normal correlations of varying magnitude). To add further complexity, the simulation model was different from the estimation model. This is partly because the simulation model is not identifiable from an estimation perspective and because of parameterization differences.

Simulated data

The example was setup to mimic an orally administered drug in a phase III setting: the PKs of the drug has been characterized using a pooled dataset consisting of two phase I studies and one phase III study. The characteristics of the studies closely resemble three real studies used in the analysis published by Smania and Jonsson ⁹ and are briefly described below. Altogether, 100 pooled analysis datasets were simulated and each of them was subjected to the SCM procedures investigated in this paper.

The studies

The first phase I study was a single high dose, cross‐over, food‐effect study and included 30 richly sampled (0–48 h postdose, 11 samples per subject) healthy volunteers.

The second phase I study included 30 healthy volunteers that were either poor or normal cytochrome P450 2D6 (CYP2D6) metabolizers. Fasting subjects were administered the low, middle, or high dose daily for 14 days. Rich sampling was carried out between 0 and 24 h after the first and last doses (19 samples per subject).

The phase III study included 500 patients with daily dosing of the low, middle, or high dose for 4 weeks. The sampling was sparse with one predose sample and one postdose sample (2–4 h after dosing) at 4 weeks. All subjects were assumed to be in the fed state at dosing and were assigned one of two different oral formulations.

Patient characteristics

Covariate data were simulated using conditional distribution (CD) modeling ⁹ based on the observed covariate distribution from the three real studies used as templates. This method retains the original multivariate distribution of the covariates without reducing the number of unique covariate vectors (per simulated dataset) like a bootstrap approach would. Eleven covariates were considered: age, alanine aminotransferase (ALT), aspartate aminotransferase (AST), bilirubin, creatinine clearance (CRCL), CYP2D6 genotype, ethnicity, National Cancer Institute (NCI) liver function classification, race, sex, and body weight (WT). The same age and sex values were used across the simulated datasets to “seed” the simulations. ⁹ Only baseline values were considered for these covariates. CRCL was calculated from the baseline serum creatinine using the Cockcroft–Gault formula ¹⁰ capping CRCL at 150 ml/min. The NCI liver function classification was based on bilirubin and ALT levels. ¹¹

In addition, food intake and formulation were considered as covariates and their values were given by the designs of the studies. Altogether, each subject was associated with 13 covariates. It was assumed that there were no missing covariates.

Simulation model for PK data

Plasma PK samples were simulated in NONMEM from a one‐compartment model with linear elimination and sequential zero and first‐order absorption. Elimination was simulated by including both hepatic and renal components. The renal contribution to elimination was regulated by the parameter f _e , set to 0.4 for the typical subjects.

A mixture of categorical and continuous covariate–parameter relations of various strengths were used. This process was assisted by visually comparing the simulated changes in parameters, given (a) the size of the coefficient and (b) the range or frequencies of the covariate (Figure S1). The parameterizations and coefficients used for simulation are available as supplementary material (Model code S1).

Regarding the covariate–parameter relationships considered, WT was included on hepatic clearance (CL) and volume of distribution (V) with allometric constants of, respectively, 0.75 and 1. Diet was a strong covariate on absorption, affecting the first‐order absorption rate constant, zero‐order absorption duration, and relative bioavailability (F _rel). CYP2D6 and NCI were intermediate covariates on hepatic CL and F _rel. The effect size of CYP2D6 genotype was set so that CYP2D6 was responsible for 50% of the hepatic CL (assuming hepatic extraction ratio of 0.35); coefficients were calibrated to achieve changes in apparent hepatic CL in line with values reported for an example CYP2D6 substrate. ¹² Formulation was a weak‐intermediate covariate on F _rel, whereas CRCL was a weak covariate on renal CL. Continuous covariate effects were implemented using an exponential parametrization, except for WT on CL and V, which were included using power relationships.

Interindividual variabilities (IIVs) were generally included using log‐normal distributions on all parameters, and weak correlations between these IIVs were included in the simulations. Finally, IIV was also included on f _e (additive on the logit scale), and the exponential residual error had an associated exponential IIV.

Estimation model

The estimation model had a different and simpler structure than the simulation model and is included in the supplementary material (Model code S1). The base estimation model was a one‐compartment model with linear elimination. In contrast to the simulation model, only total CL was modeled. The sequential zero and first‐order absorption was parameterized in terms of mean absorption time (MAT). The MAT was estimated as two fractions: one for the zero‐order absorption (Equation 1) and one for the first‐order absorption (Equation 2).

$${\mathrm{Dur}}_{0–\text{orderabs}}=\mathrm{MAT}·f_{0–\text{orderabs}}$$ (1)

$$k_a=\frac{1}{\left(\mathrm{MAT}·\left(1-f_{0-\text{orderabs}}\right)\right)}$$ (2)

where Dur_0–orderabs is the duration of the zero‐order absorption and f _0–orderabs is the fraction of MAT that reflects the zero‐order absorption and is an estimated parameter of the model.

CL, V, MAT, F _rel, and the residual error were associated with log‐normal IIVs without correlations.

Concentration measurements below an assumed lower limit of quantification were excluded from the estimation.

Stepwise covariate model building procedures

SCM and SCM+

The SCM approach proceeds in two stepwise phases: a forward inclusion phase and a backward elimination phase (Figure 1, green shapes). In each step of the forward phase, the covariate–parameter relationships in the defined search scope are tested one at a time. Among the statistically significant relationships, the most significant one (with the lowest p value) is included. This proceeds until no more relations are significant. The model obtained in this forward step is then subjected to a stepwise backward phase where, at each step, the least significant covariate–parameter relationship (with the highest p value), is removed from the model. This is repeated until no more relations can be removed, at which point the model is considered final. ⁵ , ⁶

FIGURE 1.

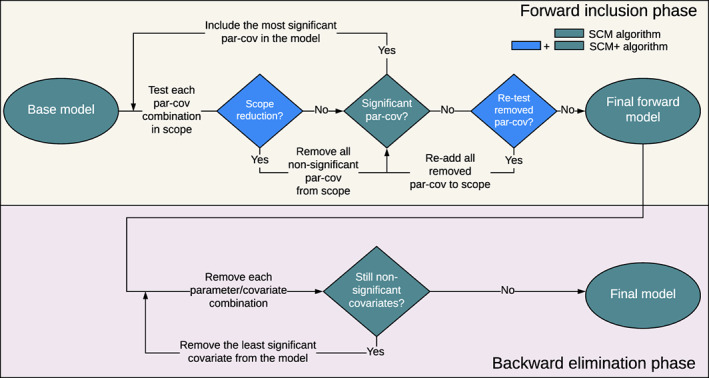
Overview of the stepwise covariate model (SCM) and SCM+ algorithms.

For the SCM+ approach, ⁷ ASR is added to the default SCM algorithm. ASR reduces the defined search scope during the forward search based on the performance of each covariate–parameter relation in the previous steps (Figure 1, blue shapes). Although the first forward step is identical to the SCM (Figure 1), when moving on to the next forward step the number of parameter–covariate relations to be tested is reduced. By using the ASR, any covariate–parameter relation that is not significant according to the forward inclusion criteria is removed from the search scope (until the additional forward step, see below). This process is repeated for each subsequent forward step until no additional covariate–parameter relation remains to be tested. After this, in an additional forward step, SCM+ retests all relationships that were excluded by the ASR. Should one of the removed covariates be significant in the retesting, the remaining removed covariates will be tested again until none of them is significant. Then, the backward elimination proceeds as described for the SCM.

To improve efficiency, SCM+ also uses different estimation settings than SCM. The default NONMEM termination criterion is changed to CTYPE = 4, which only considers changes in objective function value between iterations instead of the more complex criteria used by default. ⁷ The maximum number of function evaluations allowed (i.e., MAXEVAL in NONMEM) is also restricted in SCM+ and is set dynamically based on the number of function evaluations used by the base model. ⁷

Stage‐wise filtering

With stage‐wise filtering, the analyst categorizes covariates into three groups: mechanistic, structural, and exploratory. Mechanistic covariates are those known to have an impact on one or more parameters of the model and are included in the base model without being tested (e.g., often WT on elimination and disposition, based on the reasonable assumption that these processes are related to body size). Coefficients for mechanistic covariates can be fixed or estimated. Structural covariates are those that have a strong rationale to impact one or more model parameters; these are often specific to the study design (e.g., formulation or diet status). Structural covariates are tested prior to exploratory covariates. Exploratory covariates are those that are not mechanistic or structural and are explored for hypothesis‐generating reasons.

Stage‐wise filtering proceeds in three phases: (a) addition of mechanistic covariates to the base model and no testing is involved; (b) stepwise inclusion of structural covariates; and (c) stepwise inclusion of exploratory covariates. The stepwise inclusion phases can be done using either SCM or SCM+: in this paper, only SCM+ is used for the inclusion. The three covariate categories are hierarchical, meaning that a structural covariate cannot replace a mechanistic covariate, and an exploratory covariate cannot replace a structural or mechanistic covariate.

Covariate analysis

Additional settings were used for this analysis: covariate categories with 10 or fewer subjects were merged with the most common category (for unordered categorical variables) or nearest category (for ordered categorical variables). Categorical covariates were binarized so that each level became a yes/no covariate (“one‐hot encoding”). In the SCM and SCM+ analysis, covariate pairs that had an absolute correlation >0.6 were reduced so that only one of the covariates was used in the analysis. With stage‐wise filtering, the correlation filter was only used for the exploratory covariates.

The covariates tested with the SCM, SCM+, and SCM+ with stage‐wise filtering are listed in Table 1 according to their classification; the specific settings used for the comparison of the three approaches are listed in Table 2.

TABLE 1.

Covariates tested in the traditional SCM, SCM+, and SCM+ with stage‐wise filtering

Category	Parameter	SCM and SCM+	Stage‐wise filtering
Mechanistic	CL	None	WT, a genotype
	V		WT a
Structural	CL	None	CRCL
	MAT		Diet, formulation, genotype
	F rel		Diet, formulation, genotype
Exploratory	CL	CRCL, age, AST, ALT, BILI, sex, race, ethnicity, NCI, CYP2D6 genotype, WT	Age, AST, ALT, BILI, sex, race, ethnicity, NCI
	V	Age, AST, ALT, BILI, sex, race, ethnicity, NCI, WT	Age, AST, ALT, BILI, sex, race, ethnicity, NCI
	MAT	Age, AST, ALT, BILI, diet, sex, race, ethnicity, NCI, genotype, formulation	Age, AST, ALT, BILI, sex, race, ethnicity, NCI
	F rel	Age, AST, ALT, BILI, diet, sex, race, ethnicity, NCI, genotype, formulation	Age, AST, ALT, BILI, sex, race, ethnicity, NCI

Abbreviations: ALT, alanine aminotransferase; AST, aspartate aminotransferase; BILI, bilirubin; CL, clearance; CRCL, creatinine clearance; F _rel relative bioavailability; MAT, mean absorption time; NCI, National Cancer Institute – in reference to liver function classification; SCM, stepwise covariate model; V, volume of distribution; WT, body weight.

^a Fixed to the standard allometric exponents.

TABLE 2.

Settings and handling of covariates adopted, in each simulated dataset, for the three SCM approaches compared

	SCM (n = 100) a	SCM+ (n = 100) a	SCM+ with stage‐wise filtering (n = 100) a
Covariate–parameter relationships in base model	None	None	Weight on CL and V, with fixed allometric exponents (respectively 0.75 and 1); CYP2D6 genotype on CL
Stage‐wise filtering	No	No	Yes
Inclusion of covariates with absolute correlation coefficient >0.6	Only one of the covariates is included	Only one of the covariates is included	If mechanistic or structural covariates: both covariates are tested; if exploratory covariates: one of the covariates is omitted
The p value forward selection	0.01	0.01	0.01
The p value backward elimination	0.001	0.001	0.001
Adaptive scope reduction applied to all forward steps (threshold p value)	No	Yes (0.01)	Yes (0.01)
Retesting of all stashed relationships	No	Yes	Yes
General estimation settings applied	Those of the base model	CTYPE = 4 criterion b ; maximum number of function evaluations (MAXEVAL in NONMEM) set to 3.1 times the function evaluations used by the base model	CTYPE = 4 criterion b ; maximum number of function evaluations (MAXEVAL in NONMEM) set to 3.1 times the function evaluations used by the base model

Abbreviations: CL, clearance; SCM, stepwise covariate model; V, volume of distribution.

^a Number of simulated datasets.

^b The CTYPE = 4 criterion restricts the termination check to only consider the objective function value (OFV). ¹³

Evaluation of the stepwise procedures

The stepwise procedures were compared in terms of efficiency as well as in terms of ability to identify relevant covariate–parameter relations.

Efficiency was quantified in two ways: the total number of function evaluations and the number of executed NONMEM models. The number of function evaluations is an indicator of computational burden and should be less dependent on hardware differences and CPU load than actual runtime, whereas the number of executed NONMEM runs is independent of which underlying load balancing strategies are used.

Efficiency is presented as relative difference (in percentage) between the alternative approach and the SCM approach. Percentages are calculated using the formula (here, they are shown for the number of function evaluations, which is then adapted to consider the number of models):

$$\%=\frac{{\text{nEvals}}_{\mathrm{SCM}}-{\text{nEvals}}_{\mathrm{SCM}+}}{{\text{nEvals}}_{\mathrm{SCM}}}\times 100$$

The relevance of each method was evaluated as the number of identified covariate–parameter relations. Because the multilevel covariate CYP2D6 was binarized (see above), the relevance was evaluated both as the number of covariate coefficients as well as the number of covariates regardless of the number of coefficients identified. For the sake of simplicity, both statistics will be referred to as covariate–parameter relations until the actual results are presented. The identified covariate–parameter relations were divided into three groups: true, related, and unrelated. The group “true” includes all covariate–parameter relations present in the simulation model. “Related” indicates that the covariate has an absolute correlation of ≥0.5 with covariates included in the covariate–parameter relations in the simulation model. The group “unrelated” includes the remaining covariates. The frequency of covariate relations in each group gives a measure of relevance. In total, there were 14 true covariate coefficients in the simulation model (counting each of the three binarized CYP2D6 categories separately on both CL and F _rel) and 10 true possible covariate–parameter relations. When the covariate relations are considered in terms of being “related” or “unrelated,” their number varied among simulated datasets based on the correlations between covariates.

Software and hardware

The population PK analyses were performed in the nonlinear mixed effect modeling software NONMEM version 7.4.4 ⁸ using the first‐order conditional estimation method with interaction (FOCEI). SCM is implemented in PsN, ⁵ , ¹³ , ¹⁴ and the work in this paper, including SCM+, was done using PsN version 4.9.0. SCM+ is integrated in PsN versions from 5.2.6 and on. The software R version 3.5.3 ¹⁵ was used for the data management and postprocessing.

RESULTS

Description of the simulated covariate data

The simulated covariate data available for testing was summarized across all 100 datasets (Table 3) and their distribution was explored graphically for abnormalities (data not shown). The correlation structure between the covariates across all 100 simulated datasets is visualized in Figure S2 and the frequency of datasets with covariate pairs with absolute correlation of at least 0.5 or 0.6 is shown in Table 3. An absolute correlation coefficient higher than 0.6 (e.g., between ALT and AST) in a specific simulated dataset determined the exclusion of one of the covariates from the corresponding SCM and SCM+ analysis according to the settings described in Table 2.

TABLE 3.

Baseline characteristics across the 100 simulated datasets, including the percentage of the simulated datasets with absolute correlation greater or equal to 0.5 or 0.6

Covariate	Mean [min, max] a	Correlations b
Age, year	49.1 [49.1, 49.1] c	CRCL (49%/0%)
ALT (U/L)	30.5 [28.6, 32.9]	AST (100%/100%), NCI (97%/40%)
AST (U/L)	26.8 [25, 28.5]	ALT (100%/100%), NCI (3%/0%)
Bilirubin	9.05 [8.5, 9.7]	NCI (15%/0%)
CRCL (ml/min)	119 [116, 122]	Age (49%/0%), WT (100%/89%)
CYP2D6 genotype
EM	83% [79%, 88%]	None
IM	7.3% [5.2%, 11%]
PM	5.7% [2.5%, 7.7%]
UM	4% [2.1%, 5.9%]
Diet
Both	5.4% [5.4%, 5.4%]	None
Fasted	5.4% [5.4%, 5.4%]
Fed	89% [89%, 89%]
Ethnicity
Hispanic or Latino	43% [35%, 49%]	None
Not Hispanic nor Latino	57% [51%, 65%]
Formulation
Formulation 1	35% [35%, 35%]	None
Formulation 2	65% [65%, 65%]
NCI
Mild impairment	14% [11%, 17%]	ALT (97%/40%), AST (3%/0%), BILI (15%/0%)
Moderate impairment	1.1% [0.18%, 2.7%]
Normal function	85% [81%, 89%]
Race
American Indian or Alaska Native	0.88% [0.18%, 2.7%]	None
Asian	3.4% [1.8%, 6.2%]
Black or African American	15% [11%, 19%]
Native Hawaiian/Pacific Islander	1.2% [0.18%, 2.5%]
White	80% [76%, 85%]
Sex
Female	44% [44%, 44%] c	None
Male	56% [56%, 56%]
Weight (kg)	90.9 [88.6, 94.3]	CRCL (100%/89%)

Abbreviations: ALT, alanine aminotransferase; AST, aspartate aminotransferase; BILI, bilirubin; CRCL, creatinine clearance; EM, extensive metabolizer; IM, intermediate metabolizer; NCI, National Cancer Institute – in reference to liver function classification; PM, poor metabolizer; UM, ultrarapid metabolizer; WT, body weight.

^a For the continuous covariates, the mean is the mean of the means across the simulated datasets (and similarly for the min and max). For the categorical variables, the mean is the mean of the covariate category frequency across the simulated datasets (and similarly for the min and max).

^b The percentages in parentheses report the frequency of datasets with correlations between two covariates and refer to an absolute correlation greater or equal to, respectively, 0.5 and 0.6. For example, for the covariate CRCL with WT, the correlations “100%/89%” indicate that in 100% and 89% of the simulated data sets the absolute correlation exceeded respectively 0.5 and 0.6. Covariate pairs with absolute correlation below 0.5 in all simulated datasets are marked as “None” in the Correlation column.

^c The same age and sex values were used across the simulated datasets to “seed” the simulations (see Smania and Jonsson ⁸ for details).

Efficiency

Figure 2 shows the comparison of efficiency among the three methods. The two SCM+ methods were considerably more efficient than the SCM: the reduction in the number of function evaluations compared to the SCM was 70% for SCM+ and 76% for SCM+ with stage‐wise filtering. The corresponding reduction in the number of executed models was 44% for SCM+ and 70% for SCM+ with stage‐wise filtering.

FIGURE 2.

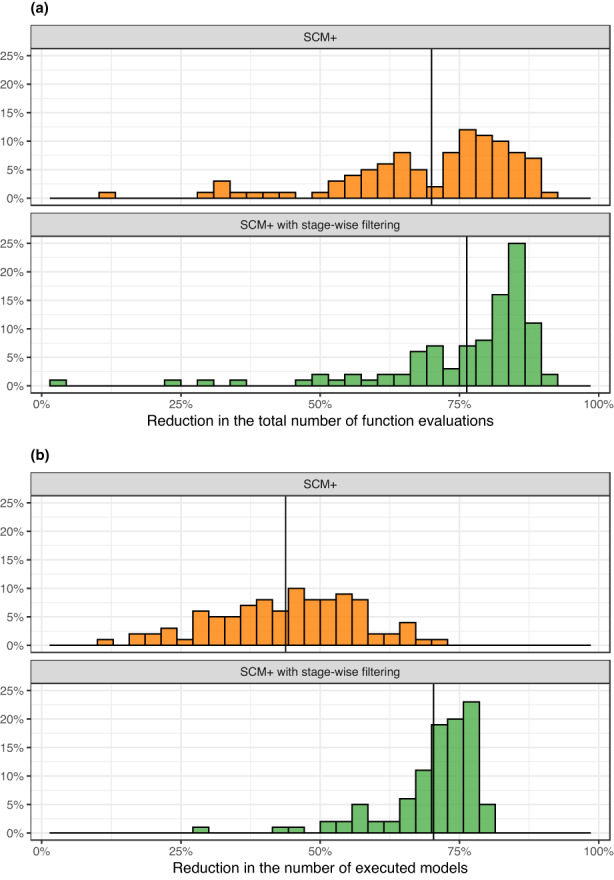
Comparison of efficiency between the stepwise covariate model (SCM) and either SCM+ or SCM+ with stage‐wise filtering. (a) Reduction in the number of function evaluations for SCM+ or SCM+ with stage‐wise filtering versus SCM. (b) Reduction in the number of executed models for SCM+ or SCM+ with stage‐wise filtering versus SCM. For both panels, the gain in efficiency is shown as the percentage reduction (higher value = more efficient) in total number of function evaluations or total number of models executed. The solid vertical line represents the median value within each panel. The plot is based on data from 100 simulated datasets.

Relevance

Table 4 provides a summary of the number of covariate–parameter relationships, stratified by true, related, and unrelated, for each of the three methods. SCM+ with stage‐wise filtering selected the highest number of true covariate coefficients (8.0 on average) compared to the SCM (5.1) and SCM+ (5.1) approaches. The SCM and SCM+ were in all aspects comparable. All approaches had low selection frequencies of related and unrelated covariate–parameter relationships.

TABLE 4.

Number of included covariate coefficients and covariate–parameter relationships for each SCM approach

	(n = 100)	Mean number of covariate coefficients [min, max]	Mean number of covariate–parameter relations [min, max]
Total	SCM	5.51 [3, 9]	5.45 [3, 9]
	SCM+	5.61 [3 ,9]	5.54 [3, 9]
	SCM+ with stage‐wise filtering	8.63 [8, 11]	6.63 [6, 9]
True a	SCM	5.06 [2, 8]	5 [2, 8]
	SCM+	5.11 [2, 8]	5.04 [2, 8]
	SCM+ with stage‐wise filtering	8.03 [7, 10]	6.03 [5, 8]
Related	SCM	0.32 [0, 1]	0.32 [0, 1]
	SCM+	0.28 [0, 2]	0.28 [0, 2]
	SCM+ with stage‐wise filtering	0.41 [0, 1]	0.41 [0, 1]
Unrelated	SCM	0.13 [0, 1]	0.13 [0, 1]
	SCM+	0.22 [0, 3]	0.22 [0, 3]
	SCM+ with stage‐wise filtering	0.19 [0, 2]	0.19 [0, 2]

Abbreviation: SCM, stepwise covariate model.

^a The total number of true covariate coefficients is 14 and of true covariate–parameter relations is 10.

Figure 3 visualizes the inclusion frequencies by parameter and type of covariate relations. Compared to the other two methods, SCM+ with stage‐wise filtering included more frequently the covariates CYP2D6 genotype, WT on CL, and WT on V, as these were considered mechanistic covariate–parameter relationships for stage‐wise filtering and were therefore included in the base model. Overall, the SCM and SCM+ approaches gave comparable selections of covariate–parameter relationships across parameters.

FIGURE 3.

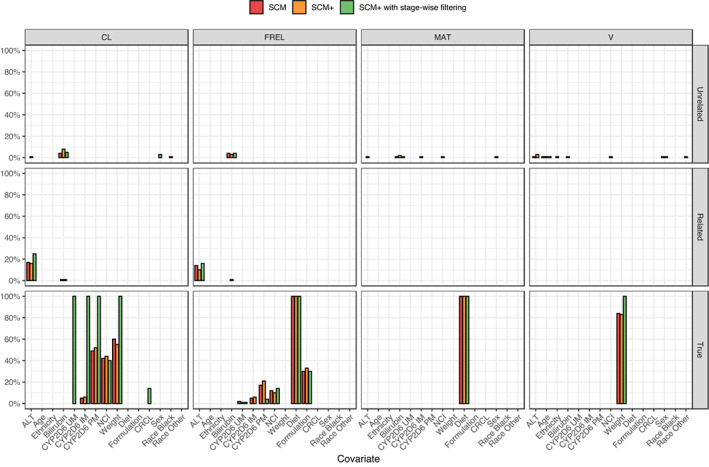
Frequency of included covariates stratified by relevance of the covariate–parameter relationship. Only covariates that were selected in at least one iteration are shown. The plot is based on data from 100 simulated datasets.

When frequency of inclusion was visualized stratifying by the covariates’ groups (mechanistic, structural, and exploratory), the mean number of mechanistic covariate coefficients selected by SCM and SCM+ was 2.0, whereas it was 5.0 for the stage‐wise filtering approach (Table S1). In addition, all three approaches had comparable means of included structural (about 2.2) and exploratory (about 1.3) covariate coefficients. The frequency of inclusion of structural and exploratory covariates did not differ among the three methods.

DISCUSSION

This analysis used simulated data to compare SCM, SCM+, and SCM+ with stage‐wise filtering in terms of efficiency and the ability to identify relevant covariates. SCM+ and SCM+ with stage‐wise filtering showed a considerably increased efficiency compared to the SCM (Figure 2), whereas SCM+ with stage‐wise filtering improved the ability to select relevant covariates compared to SCM or SCM+ (Table 4).

The work described in this paper required extensive computations and would not have been possible without using a large computational cluster. To generalize the results across different CPU speeds, cluster workload, and parallelization options, the total number of function evaluations was used as a proxy for overall runtime. Efficiency was also assessed as overall computational burden. Depending on the load balancing strategy used (i.e., how the parallel execution of multiple NONMEM runs is organized), the overall runtime may be reduced, but the overall computational burden will remain the same. This is an important aspect in a finite computational environment where the computational resources are shared with many users. In this work, the number of executed NONMEM models was used as a measure of overall computational burden.

Compared to SCM, SCM+ includes two main changes: the introduction of ASR and the use of more efficient estimation settings (CTYPE = 4 and a limit on MAXEVAL). The ASR reduces the number of models to estimate (44% reduction with SCM+; Figure 2b). The more efficient estimation settings will increase the efficiency per model but not the number of models. Together, these changes resulted in a 70% reduction in the total number of function evaluations for SCM+ versus SCM (Figure 2a).

SCM+ with stage‐wise filtering also showed a considerable reduction in the number of executed models compared to SCM (70%) and SCM+. The reason for this is that stage‐wise filtering already included WT on CL, WT on V, and CYP2D6 genotype on CL in the base model and no covariate testing was performed on these before inclusion. Despite the reduction in the required number of models compared to SCM+, SCM+ with stage‐wise filtering had a similar overall gain in efficiency (Figure 2a). The reason for this is that the base model for stage‐wise filtering is more complex and with more parameters to estimate, which in turn requires more function evaluations per model execution. In this work, the reduction in number of models and the overall increase in number of function evaluations per model balanced each other out so that the overall efficiency of SCM+ with stage‐wise filtering was comparable to that of SCM+.

Regarding the ability to identify relevant covariates, SCM and SCM+ showed comparable results, both in terms of the number of covariate coefficients and the number of covariate–parameter relationships included (Table 4). This is an important finding because the reduced search scope and fewer function evaluations per model in SCM+ may introduce a risk of not identifying important covariates. However, the comparable selection of relevant covariates by SCM and SCM+ suggests that using SCM+ does not lead to an apparent risk of selecting different covariates than the SCM. On the other hand, because the SCM and SCM+ are different search algorithms they may select slightly different covariates on a dataset‐by‐dataset basis, particularly for weak covariate relations.

Among the three approaches, SCM+ with stage‐wise filtering had the highest frequency of inclusion of relevant covariates, both in terms of the number of covariate coefficients and the number of covariate–parameter relationships (Table 4, Figure 3). This is mainly due to the inclusion of mechanistic covariates in the base model, and it demonstrates the benefits of including prior knowledge in the model development. Specifically, the difference between the number of covariate coefficients and covariate–parameter relationships was 2 (8.63 vs. 6.63), which matches the two additional coefficients included by considering CYP2D6 as mechanistic covariate. Mechanistic covariates are included in the model without testing, which is motivated by the fact that these covariates are classified as “mechanistic covariates.” Only covariates that are known to have an impact on model parameters (based on prior knowledge and/or mechanistic understanding) may fall into this category. Importantly, all involved stakeholders should agree on this classification (e.g., in a drug‐development setting the full team needs to accept this classification). Once the model is finalized, changes in the definition of mechanistic covariates will require a complete model re‐development. Therefore, if a complete agreement about these covariates is lacking, a better setup is to categorize them as structural covariates so that they are tested against the data.

A related question is what happens if the prior knowledge (i.e., the classification of a covariate as mechanistic and its inclusion in the model without testing), is incorrect. This depends on what “incorrect” means. If the mechanistic underpinning of the covariate categorization turns out to be wrong (e.g., if the drug is actually not a CYP2D6 substrate and previous study results were somehow artifacts), then, using CYP2D6 genotype as a mechanistic covariate can be claimed to be objectively incorrect. In this case, provided the coefficients for this covariate are estimated, the estimated impact of the covariate should approach zero with very wide confidence intervals. This does not impact the predictive abilities of the model and it should be clear to the analyst that there is no support for the covariate in the data. If the covariate coefficients were fixed in the model, the covariate will have to be removed from the scope and the model will have to be re‐developed. On the other hand, if the data does not support the estimation of a true covariate effect (e.g., the impact of smoking if there are no smokers in the dataset), then the estimated impact of the covariate will also approach zero with wide confidence intervals. The only way to separate this situation from the previous one is that there is a mechanistic underpinning for including smoking, whereas in the CYP2D6 case there is not. However, the fact that the data does not support the estimation of a covariate effect does not mean that the covariate is incorrect. In the end, to understand the covariate modeling results it is necessary to know why a certain covariate is in the model and what properties the current dataset has.

In ASR, the covariate categorization is made to reflect the current state of knowledge about the drug and is driven by the properties of the drug and not by generic and drug‐independent properties of the covariates. For example, CYP2D6 genotype may be a mechanistic covariate for a drug that is mainly eliminated via the CYP2D6 pathway but may be an exploratory covariate for a drug for which the elimination pathways are still to be elucidated. The categorization of a covariate may also change as more information about the drug is collected. In early drug development, it is likely that most covariates will be regarded as exploratory ones whereas in later phases, based on the accumulated knowledge, one or more covariates will probably be categorized as mechanistic for one or more parameters.

In this example, WT was regarded as a mechanistic covariate on CL and V, in line with the reasonable assumption that both drug elimination and disposition are related to body size. In addition, the simulated drug was assumed to be a CYP2D6‐substrate, a property that should be known when a drug reaches phase III; therefore, CYP2D6 genotype was regarded as a mechanistic covariate on CL. On the other hand, had the example been set in a phase I or II setting, it may have been more reasonable to consider CYP2D6 to be an exploratory covariate. As mentioned above, we strongly recommend that the categorizing of covariates is discussed and agreed on upfront with all involved stakeholders (subject matter experts, medical members of the team, etc.).

The stage‐wise filtering approach has the additional advantage that more plausible covariates are added (if they are mechanistic) or get a chance to be included in the model (if they are structural) before the more exploratory covariates are considered; in line with this, less plausible covariates cannot replace covariates that are already included in the model. This will help reducing discussions about why certain covariates were included in the model and if they potentially take the place of other covariates. Similarly, if exploratory covariates are identified without a plausible explanation, or if the involved stakeholders feel doubtful about their relevance, it is still possible to use the model with only mechanistic and structural covariates (for which there should be a clear rationale) for further analysis e.g., in PK/PD modeling.

The unrelated covariates, which can be considered as false covariates, were only selected with low frequency by the three approaches (Figure 3). This indicates that the settings used, and especially the p values, prevent the selection of false positive covariates. SCM+, and more so SCM+ with stage‐wise filtering, may be expected to include fewer false positive covariates than SCM because they require fewer models (Figure 2b), which in turn should result in lower type I errors.

An additional method in the context of shortening runtimes is model linearization. This method has been shown to increase the efficiency of stepwise covariate model development ¹⁶ even to a greater extent than what was found for SCM+ in this work. However, to our knowledge, the linearization approach has not been widely used for covariate modeling within drug development. On the other hand, nothing prevents model linearization from being used together with SCM+ for further efficiency gains.

In this work, the simulation setup used was more complicated than that usually seen in methodological studies. The covariate distributions in each simulated dataset were generated using CD modeling ⁹ : this approach retains the distributional properties of the real covariate data that was used as a template while still not resorting to random selection of complete individual covariate vectors. The combination of phase I studies with specific objectives (assessment of food effects and impact of CYP2D6 genotype) and large (phase III) patient studies mimic the common situation for which the SCM+, and particularly stage‐wise filtering, was designed for. With a simpler and, to some extent, less realistic analysis dataset structure, the practical benefits of SCM+ with and without stage‐wise filtering would have been less obvious. Another aspect that can be regarded as a concession to realism is that the simulation model is different from the estimation model. This will always be the case in a real situation, although in much more complex ways. The current example illustrates the difficulty in knowing what a true covariate is or how a covariate should be included “mechanistically” in a model. This explains also why the “related” covariate category was used in the assessment of the results. Selection of a “false” but correlated covariate, instead of the “true” covariate, does not mean that the selection is incorrect. Instead, it may mean that in a specific data sample the signal to which the two covariates are correlated is better described by the “false” rather than the “true” covariate.

The alternative covariate model building strategies implemented in this work build on the SCM tool as implemented in PsN and are therefore, by nature, NONMEM‐centric. However, the general concepts of ASR and stage‐wise filtering can be used in other applications and implementations. The additional NONMEM and FOCEI‐specific settings (adjusting MAXEVAL and changing the termination criteria to CTYPE = 4) may be harder to directly translate to other software; however, there may be settings of the same nature that can be tweaked to adjust the parameter estimation to suit what is needed in stepwise covariate searches. For example, if the Importance Sampling algorithm in NONMEM is used instead of FOCEI, CTYPE = 4 would still be applicable but the adjustments to MAXEVAL can be substituted with adjustments to the NITTER and ISAMPLE settings.

In summary, SCM+ and SCM+ with stage‐wise filtering are novel stepwise covariate model building strategies that are more efficient and with a greater ability to identify relevant covariates than the traditional SCM approach. Within the drug development setting this means that modeling results can be delivered within shorter time and with larger impact compared to methods that are less efficient and relevant.

AUTHOR CONTRIBUTIONS

R.J.E. and E.N.J. wrote the manuscript, designed the research, performed the research, and analyzed the data.

CONFLICT OF INTEREST

E.N.J. is a current Pharmetheus AB employee. R.J.S. was a Pharmetheus AB employee at the time this work was performed.

Supporting information

Appendix S1

Figure S1

Figure S2

Table S1

Svensson RJ, Jonsson EN. Efficient and relevant stepwise covariate model building for pharmacometrics. CPT Pharmacometrics Syst Pharmacol. 2022;11:1210‐1222. doi: 10.1002/psp4.12838