Do the green bonds overreact to the COVID-19 pandemic?

Abstract

This paper explores the impacts of the COVID-19 pandemic on the global green bond and conventional assets, including commodity, treasury, stock and clean energy markets, using Diebold and Yilmaz (2012) and Baruník and Křehlík, 2018b spillover framework. The results show that spillover transmitted from COVID-19 is relatively strong over a medium- and long-term horizon, and the spillover effects sharply increased when the pandemic became severe. Furthermore, green bonds are most affected by the COVID-19 pandemic, followed by the treasury, while the other conventional assets are only slightly affected. Additionally, our findings also contain a low-risk portfolio during COVID-19 pandemic.

1. Introduction

The COVID-19 pandemic has spread to over 200 countries and has damaged global public health and economy since it outbroke in December 2019. Studies show that COVID-19 pandemic significantly affects the stability of financial markets (Adekoya and Oliyide, 2021; So et al., 2021; Zhang et al., 2020), making them strongly volatile and unpredictable. Specifically, according to Moody's, the pandemic made the total amount of green bond decrease by 32% compared with 2019. Meanwhile, the return of American treasury set the new lowest record in history (0.318%), and the price of global commodity market decreased by 10% (as reported in China Foreign Exchange Trade System), which illustrates the importance of exploring the performance of different financial markets under the pandemic. This paper aims to complete related studies by comparing the different impacts of COVID-19 on green bond market and conventional financial markets.

The two most related studies are Naeem et al. (2021) and Arif et al. (2021). Specifically, Naeem et al. (2021) use asymmetric multifractal analysis to investigate the comparative efficiency of green bond and conventional asset markets pre-and during the COVID-19 pandemic. However, this paper only focuses on the time domain, lacking information on the frequency domain. Arif et al. (2021) explored the dynamics of connectedness between conventional and green investments in fixed income, equity, and energy markets in the time-frequency domain to fill this gap. However, the study focused on connectedness, not to further explore the impact of COVID-19 on green bond and conventional assets and make comparative analysis.

To fill the gap, this paper analyzes the different impacts of the COVID-19 pandemic on the green bond market and conventional financial markets through the spillover frameworks proposed by Diebold and Yilmaz (2012), Diebold and Yılmaz (2014) (hereafter, DY) and Baruník and Křehlík (2018a) (hereafter, BK). In addition, portfolio analysis is conducted to work out an investment strategy during COVID-19.

We contribute to the existing literature in three ways. First, this study conducts comparative analysis of the different reactions of the green bond market and conventional markets to the COVID-19 pandemic in time-frequency domain. Second, we apply portfolio analysis and work out a good investment strategy during the COVID-19 period. Third, to our knowledge, this is probably the first paper to take a comprehensive consideration of time-frequency return spillovers and portfolio analysis in a single study for evidence of impacts brought by the pandemic.

2. Methodology and data

2.1. Framework of spillover effects in the time domain

In order to investigate the connectedness among ID-EMV index, Green bond market and conventional bond markets in the time domain, we apply the methodology of Diebold and Yilmaz (2012), the DY method, which mainly uses the variance decomposition of the VAR model. The DY method first builds a VAR(p) model below:

$$X_t=\Phi \left(L\right)X_t+{\epsilon }_t=\sum _{h=1}^p{\Phi }_h{L}^h{X}_t+{\epsilon }_t$$ (1)

in which X(t) = (X _1t,X _2t,…, X_nt) stands for a variable vector at time t, Φ(L) is a pth lag order matrix measuring the autoregressive coefficients, L is the lag operator, Φ_h is the moving average coefficient matrix with the hth lag order, ε_t stands for a white noise vector with zero mean, whose covariance matrix is Σ.

The moving average form can be presented as

$$X_t=\Psi \left(L\right){\epsilon }_t=\sum _{i=1}^{\infty }{\Psi }_i{\epsilon }_{t-i}+{\epsilon }_t,$$ (2)

in which Ψ(L) stands for the moving average coefficients.

In the DY method, the generalized forecast error variance decomposition, i.e., GFEVD, at forecast horizon H is shown as

$${\theta }_{jk}\left(H\right)=\frac{{\sigma }_{kk}^{-1}{\sum }_{h=0}^H{\left({\left({\Psi }_h\Sigma \right)}_{jk}\right)}^2}{{\sum }_{h=0}^H{\left({\Psi }_h{\Sigma \Psi }_h^{{}^{\prime }}\right)}_{jj}}$$ (3)

in which σ_kk is the diagonal element matrix Σ. In addition, we can also standardize θ_jk(H) as

$${\tilde{\theta }}_{jk}\left(H\right)=\frac{{\theta }_{jk}\left(H\right)}{{\sum }_{k=1}^n{\theta }_{jk}\left(H\right)}$$ (4)

${\tilde{\theta }}_{jk}\left(H\right)$ stands for the directional spillover from variable k to j at forecast horizon H.

The overall spillover is represented as follows:

$$C_H=100\times \frac{{\sum }_{j,k=1,j\ne k}^n{\tilde{\theta }}_{jk}\left(H\right)}{{\sum }_{j,k=1}^n{\tilde{\theta }}_{jk}\left(H\right)},$$ (5)

The TO spillover is to measure the directional spillover from variable j to all other indices in the system:

$${\left(C_H\right)}_{·\leftarrow j}=100\times \frac{{\sum }_{k=1,k\ne j}^n{\tilde{\theta }}_{kj}\left(H\right)}{{\sum }_{j,k=1}^n{\tilde{\theta }}_{kj}\left(H\right)}$$ (6)

The FROM spillover is defined as follows:

$${\left(C_H\right)}_{j\leftarrow ·}=100\times \frac{{\sum }_{k=1,k\ne j}^n{\tilde{\theta }}_{jk}\left(H\right)}{{\sum }_{j,k=1}^n{\tilde{\theta }}_{jk}\left(H\right)}.$$ (7)

The net directional spillover of variable j is:

$${\left(C_H\right)}_j={\left(C_H\right)}_{·\leftarrow j}-{\left(C_H\right)}_{j\leftarrow ·}.$$ (8)

At last, the net pairwise spillover between index j and k is computed as follows:

$${\left(C_H\right)}_{jk}=100\times \frac{{\tilde{\theta }}_{kj}\left(H\right)-{\tilde{\theta }}_{jk}\left(H\right)}{n}$$ (9)

2.2. Framework of spillover effects in the frequency domain

Based on the DY model, Baruník and Křehlík (2018a) worked out a new method to measure the connectedness among several indices in the frequency domain. The proportion of index j’s information transmitted from index k at frequency ω can be defined as:

$${\theta }_{jk}\left(\omega \right)=\frac{{\sigma }_{kk}^{-1}{\left|{\left(\Psi \left(e^{-i\omega }\right)\Sigma \right)}_{jk}\right|}^2}{{\sum }_{h=1}^H{\left(\Psi \left(e^{-i\omega }\right)\Sigma {\Psi }^{-1}\left(e^{i\omega }\right)\right)}_{jj}}.$$ (10)

The standardized θ_jk(ω) is described as:

$${\tilde{\theta }}_{jk}\left(\omega \right)=\frac{{\theta }_{jk}\left(\omega \right)}{{\sum }_{k=1}^n{\theta }_{jk}\left(\omega \right)}.$$ (11)

In addition, we can furtherly extend frequency ω to a frequency band as d = (a, b); thus, the directional spillover at frequency band d is

$${\tilde{\theta }}_{jk}\left(d\right)=\underset{a}{\overset{b}{\int }}{\tilde{\theta }}_{jk}\left(\omega \right)d\omega .$$ (12)

In a similar way, we can calculate the directional spillover and net spillover in the same way indicated in (5), (6), (7), (8), (9).

We construct a multivariate (6 factors) model that includes ID-EMV index (I_t), the price indices of green bond (G_t), commodity (C_t), treasury (T_t), stock (S_t) and clean energy bond (E_t) as endogenous variables. The order of the 6 factors is as follows.

$$X_t=\left[I_t,G_t,C_t,T_t,S_t,E_t\right]$$ (13)

2.3. Data

To measure the extent of the COVID-19 pandemic, this paper introduces Infectious Disease Equity Market Volatility Tracker (ID-EMV) constructed by Baker et al. (2020). For Green bonds, we use the S&P Green Bond Index to describe the global green bond's price changes. As to the conventional financial markets, S&P GSCI Commodity Index, Barclays Bloomberg Global Treasury Index, S&P 500 Composite Index and S&P Clean Energy Index are chosen to reflect the circumstances in commodity, treasury, stock and clean energy markets. The data that is used to describe financial markets is collected from DataStream. In this paper, the returns are calculated as the first difference of the natural logarithms of the original prices. Our study considers the daily data ranging from January 1, 2020, to September 4, 2020 (totally 179 observations), covering the very beginning and severe periods of COVID-19 pandemic. All series are global indices, except for the S&P 500 Composite Index. The S&P 500 Composite Index is used as a proxy for global stock market because of its high weight (about 65%) in the MSCI World Index (Nguyen et al., 2021).

Table 1 presents the descriptive statistics of the data we use. The augmented Dickey-Fuller (ADF) test and Phillips-Perron (PP) test tell us that the original return series are not stationary. The ADF, PP and Kwiatkowski-Phillips-Schmidt-Shin (KPSS) tests further confirm the first difference of the natural logarithms of the original prices are stationary, which indicates the series are DS processes (Dickey and Fuller, 1979; Kwiatkowski et al., 1992; Laurent and Shi, 2020, 2022; Phillips and Perron, 1988).

Table 1.

Descriptive statistics of the series.

	In level
	ID-EMV	Green bond	Commodity	Treasury	Stock	Clean energy
Mean	20.6453	143.5026	1819.717	651.817	6296.015	1070.341
Std. Dev.	15.2113	4.7526	370.4905	14.2482	581.5979	179.4944
Maximum	68.37	152.3595	2642.496	679.6429	7358.49	1495.519
Minimum	0	133.1446	1249.251	621.684	4559.5	707.074
Skewness	0.7649	0.2193	0.8079	0.3597	−0.7927	0.4417
Kurtosis	3.3579	2.383	2.4288	2.1506	3.0691	2.7045
Jarque-Bera	18.3063	4.2502	21.785	9.1889	18.6753	6.4352
ADF	0.1068	0.7928	0.1928	0.3722	0.7135	0.9287
PP	0.0057	0.8109	0.2171	0.4224	0.7041	0.9007
KPSS	0.2742	0.934	0.8663	1.3927	0.4526	0.8333
	In 1st difference
	ID-EMV	Green bond	Commodity	Treasury	Stock	Clean energy
Mean	0.0118	0.0004	−0.0024	0.0003	0.0002	0.0018
Std. Dev.	0.5052	0.0047	0.0241	0.0046	0.0249	0.0275
Maximum	1.8293	0.0201	0.0712	0.0176	0.0898	0.1103
Minimum	−1.8294	−0.0242	−0.1252	−0.0201	−0.1276	−0.125
Skewness	0.1634	−1.3815	−1.4838	−0.7728	−0.7637	−1.2952
Kurtosis	2.1453	9.1229	7.8396	6.267	6.6735	6.3202
Jarque-Bera	32.203	638.3844	494.1319	291.4114	327.8927	327.8043
ADF	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
PP	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
KPSS	0.1806	0.1837	0.39	0.0237	0.174	0.1954

Notes: The Jarque-Bera statistics tests the null hypothesis of the normality of the sample return distribution. ADF and PP are the statistics of the unit root test based on the least AIC criterion, respectively. Kwiatkowski-Phillips-Schmidt-Shin is a test of the null hypothesis of stationary. The values in ADF and PP tests are p-values. KPSS is a test of the null hypothesis of stationary.

3. Empirical analysis

In this section, we present the empirical results from DY, BK methods, and portfolio analysis, based on our price indices and ID-EMV index samples during COVID-19 pandemic, with a focus on the comparative study of green bond and conventional markets.

3.1. Dynamic net return spillovers

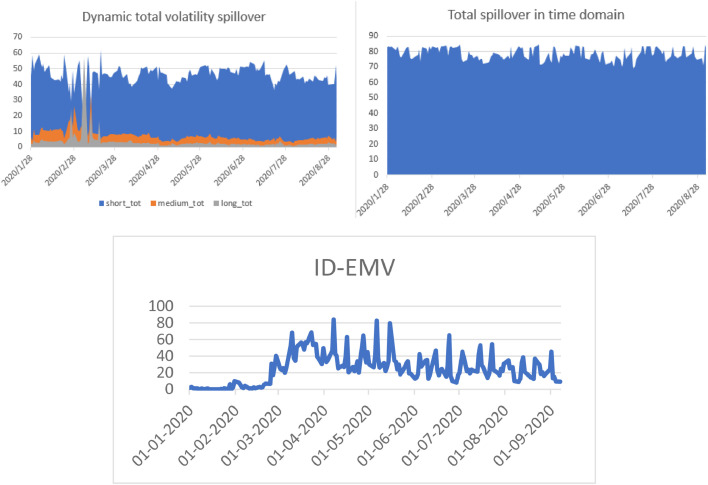
Fig. 1 shows the dynamic total spillovers between ID-EMV and the five analyzed markets in time and frequency domains, and the line chart of ID-EMV index as a reference. As to the time domain, the total return spillover is around 75% at most times, reaching the peak of nearly 85% in some cases, indicating that the internal relationship between ID-EMV, green bond and conventional bond markets during the period of COVID-19 is significantly strong (Altig et al., 2020), the reason of which may be that COVID-19 drives stronger fear in financial markets than the period before (Adekoya and Oliyide, 2022).

Fig. 1.

Time-varying total spillovers in time and frequency domains.

Note: The data presented in Fig. 1 is daily data ranging from January 1, 2020, to September 4, 2020 (totally 179 observations).

As to the frequency domain, which contains three different scales, the level of total spillovers is significantly higher in the short term than in the medium and long term in most time, consistent with the findings of Bai et al. (2021). However, the situation is opposite when ID-EMV index experienced a sudden surge, because the COVID-19 pandemic always exploded out of a sudden and is hard to control over a medium or long term, as described by WHO.

3.2. Dynamic directional pairwise return spillover

The empirical results of the DY spillover test are reported in Table 2 . These results show that the proportion of the spillover effect caused by the ID-EMV index differs dramatically across the five asset markets analyzed during the COVID-19, especially between green bonds and conventional bonds. The highest contribution of the ID-EMV index appears from its returns to the returns of the green bond price index, followed by treasury market (2.057%, 1.779%, respectively). It indicates that the green bond market is most affected by COVID-19, consistent with the circumstance in China (Yi et al., 2021), which can be explained that green bond, as a newly-rising bond first proposed formally in 2014, still lacks stability through crisis. The directional return spillovers from all markets to one specific market show that the green bond market is the most affected of all, especially by treasury and clean energy market, further confirming our analysis above. Also, it proves that the relationship between green bonds and conventional bonds is sensitive to external changes (Broadstock and Cheng, 2019).

Table 2.

Return spillover results.

DY spillover results
		ID-EMV		Green bond		Commodity	Treasury		Stock		Clean energy			from
ID-EMV		85.365		2.979		3.379	2.027		2.955		3.295			2.439
Green bond		2.057		38.064		7.839	23.557		11.441		17.042			10.323
Commodity		0.182		2.029		62.463	1.707		15.186		18.434			6.256
Treasury		1.779		30.184		4.700	43.399		8.655		11.382			9.433
Stock		0.272		7.379		9.661	2.419		46.223		34.045			8.963
Clean energy		0.115		4.952		13.852	0.667		34.024		46.391			8.935
To		0.734		7.920		6.572	5.063		12.043		14.016			46.349
Net		−1.705		−2.402		0.316	−4.371		3.081		5.081
BK spillover results
Frequency 1
	ID-EMV		Green bond		Commodity			Treasury		Stock		Clean energy	from
ID-EMV	81.948		2.862		3.120			1.829		2.445		2.955	2.202
Green bond	1.480		27.943		3.973			18.102		4.975		7.299	5.972
Commodity	0.149		2.023		53.061			1.262		13.088		15.774	5.383
Treasury	1.365		23.118		3.795			35.651		6.624		7.442	7.057
Stock	0.268		7.071		7.539			2.362		41.008		29.125	7.728
Clean energy	0.094		4.582		10.184			0.587		27.626		37.576	7.179
To	0.599		6.609		4.769			4.024		9.126		10.432	35.520
net	−1.642		0.638		−0.614			−3.034		1.399		3.254
Frequency 2
	ID-EMV		Green bond		Commodity			Treasury		Stock		Clean energy	from
ID-EMV	2.658		0.099		0.190			0.157		0.377		0.250	0.179
Green bond	0.432		7.579		2.840			4.152		4.727		7.139	3.215
Commodity	0.025		0.005		7.207			0.339		1.597		2.026	0.665
Treasury	0.313		5.328		0.684			5.943		1.529		2.865	1.787
Stock	0.004		0.223		1.558			0.050		3.840		3.599	0.906
Clean energy	0.015		0.266		2.728			0.065		4.748		6.543	1.304
To	0.132		0.987		1.333			0.794		2.163		2.646	8.055
net	−0.047		−2.228		0.668			−0.993		1.257		1.343
Frequency 3
	ID-EMV		Green bond		Commodity			Treasury		Stock		Clean energy	from
ID-EMV	0.759		0.018		0.069			0.040		0.133		0.090	0.058
Green bond	0.144		2.542		1.026			1.304		1.739		2.604	1.136
Commodity	0.008		0.000		2.195			0.106		0.501		0.635	0.208
Treasury	0.101		1.737		0.221			1.805		0.502		0.975	0.589
Stock	0.000		0.085		0.564			0.007		1.375		1.321	0.330
Clean energy	0.006		0.104		0.940			0.015		1.650		2.271	0.453
To	0.043		0.324		0.470			0.245		0.754		0.937	2.774
net	−0.015		−0.812		0.262			−0.344		0.425		0.485

Notes: Return spillovers following Diebold and Yilmaz (2012). The index in the lower right corner is the total connectedness index. The “from” column, “To” row and “net” refer to the from connectedness “To” connectedness and net connectedness. The jkth value is the directional connectedness from variable k to variable j. The results are expressed as percentages.

Note: Return spillover, the frequency domain connectedness following Baruník and Křehlík (2018a).

To get a deeper insight into the direction and size of return spillovers, we decompose the time series into different frequencies and work out the net pairwise spillovers. Generally speaking, the return spillover from the ID-EMV index to green bond and treasury price index stay relatively strong in the short, medium and long term. In contrast, the spillover effects from ID-EMV to other markets are mostly around 0.01%, which means our application of the DY-BK method reveals more information we cannot find out in time domain.

Table 3 represents the net pairwise spillover results. The green bond index plays the role of a net spillover receiver from all the analyzed markets, while similarly, the treasury market serves as another main net spillover receiver. Additionally, the ID-EMV index serves as a net spillover transmitter in the frequency domain, because the influence of the burst of the COVID-19 pandemic may be more robust in the short run (Zhang and Wang, 2021).

Table 3.

Net pairwise returns spillover results.

DY	ID-EMV			Green bond	Commodity		Treasury	Stock			Clean energy
ID-EMV	0			0.154	0.533		0.041	0.447			0.530
Green bond				0	0.968		−1.104	0.677			2.015
Commodity					0		−0.499	0.921			0.764
Treasury							0	1.039			1.769
Stock								0			0.004
Clean energy											0
BK1		ID-EMV	Green bond		Commodity	Treasury			Stock	Clean energy
ID-EMV		0	0.222		0.500	0.073			0.373	0.483
Green bond			0		0.403	−0.868			−0.228	0.641
Commodity					0	−0.433			0.933	0.917
Treasury						0			0.755	1.225
Stock									0	0.209
Clean energy										0
BK2		ID-EMV	Green bond		Commodity	Treasury			Stock	Clean energy
ID-EMV		0	-0.052		0.026	-0.025			0.057	0.036
Green bond			0		0.439	-0.183			0.701	1.066
Commodity					0	-0.052			-0.004	-0.115
Treasury						0			0.223	0.426
Stock										-0.166
Clean energy										0
BK3		ID-EMV	Green bond		Commodity	Treasury			Stock	Clean energy
ID-EMV		0	−0.016		0.008	−0.008			0.016	0.010
Green bond			0		0.126	−0.053			0.204	0.308
Commodity					0	−0.014			−0.008	−0.038
Treasury						0			0.061	0.118
Stock									0	−0.040
Clean energy										0

Note: Net pairwise return spillover, following Diebold and Yilmaz (2012). The meanings of the indices are the same as those in Table 2.

Note: Net pairwise return spillover, the frequency domain connectedness following Baruník and Křehlík (2018a).

To reveal the influence of the COVID-19 pandemic on the markets analyzed, we should pay more attention to the results in the frequency domain. From the results, in short, medium, and long terms, it is apparent to tell that the shock from ID-EMV to the green bond market is generally stronger than that to conventional bond markets, except treasury market. It may be because the treasury is mainly managed by governments, thus revealing the influence of the COVID-19 pandemic when governments globally were induced to shutter major parts of their economies in order to deal with the outbreak of pandemic .

3.3. Return spillover network

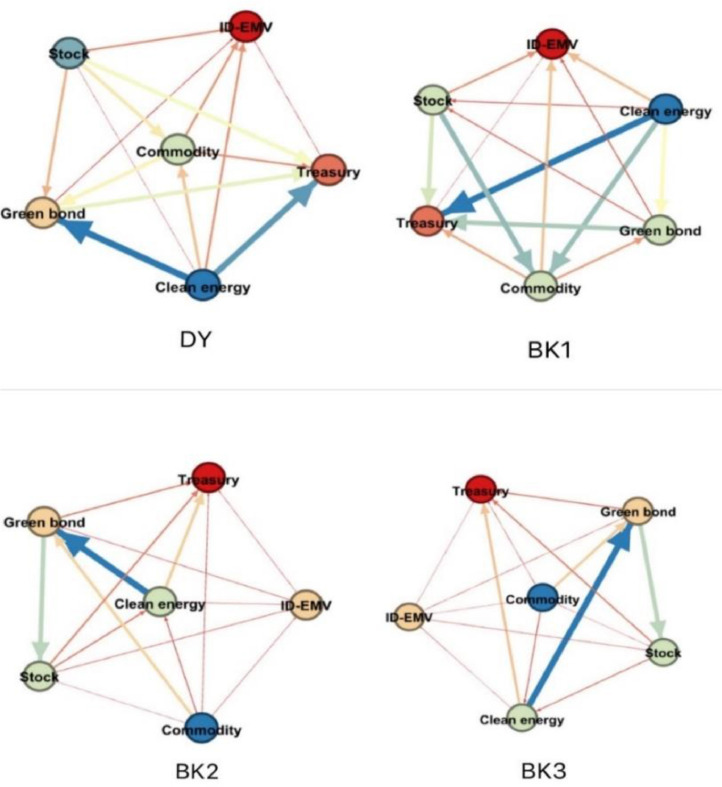
In this section, the information transmitted through the whole system is investigated. The spillover return connectedness network in Fig. 2 shows the net directional connectedness between the six indices in our study.

Fig. 2.

Network analysis of pairwise net spillovers.

Note: Each node represents a subject analyzed. The colours of the nodes represent the role this subject plays in the system. For example, red nodes represent net spillover receivers, while blue nodes represent net spillover contributors. Also, the closer to blue the color is, the more significant proportion the subject takes in this system. The edges between the two nodes reveal the spillover relationship between the two issues. The arrows represent the direction of information transmission. Furthermore, the thicker the line, the stronger the spillover effect is between these two subjects. All the results can be referred to in Table 3.

It is apparent from the DY graphs that the spillover between clean energy and green bond, between clean energy and treasury play the leading role in this connectedness network.

The results of the BK graphs significantly differ from those of the DY graphs. To specify, the ID-EMV index contributes more in low frequency than in high frequency, which further confirms our opinion that the influence of COVID-19 pandemic is more robust in short run because of its uncontrolled feature. Another noticeable change takes place in the green bond where the direction of return spillover from ID-EMV to green bond changes in medium and high frequencies. It can be interpreted that the poor stability of green bond mainly appears in medium- and short-term when exposed to crisis.

Additionally, the change of the role of ID-EMV in DY and BK graphs further confirms our findings in the last section that the impact of the COVID-19 pandemic is mainly reflected in the frequency domain than in the time domain.

3.4. Portfolio analysis

The empirical results provide the conditions of the return spillovers across the green bond and conventional financial markets analyzed. The results are meaningful for investors to decide on diversified portfolios and risk management efficiently. To manage the portfolio, we use the estimated results of the multivariate DCC-GARCH model, which helps investors make optimal portfolio allocation decisions by constructing dynamic risk-minimizing hedge ratios.

First, we assume that an investor holds a set of commodity assets and seeks to hedge their position against unfavorable effects using green bond assets. Specifically, we follow Kroner and Ng (1998) to compute the portfolio weight of the green bond asset holdings as:

$$\begin{array}{c}\hfill w^G=\frac{h_t^C-h_t^{G,C}}{h_t^G-2h_t^{G,C}+h_t^C},\text{with}{w}_t^G=\{\begin{array}{c}0w_t^G<0\\ w_t^{G}0\le w_t^G\le 1\\ 1w_t^G>1\end{array}\end{array}$$ (14)

Following Kroner and Sultan (1993), we quantify the beta hedge to minimize the risk of this commodity-green bond portfolio. The hedging ratio ${\beta }_t^G$(HR) can be calculated as follows:

$${\beta }_t^G=\frac{h_t^{G,C}}{h_t^G}$$ (15)

The hedging effectiveness (HE) of the constructed portfolios can be assessed by comparing the realized hedging errors (Ku et al., 2007) computed as:

$$HE=1-\frac{Va{r}_{hedged}}{Va{r}_{unhedged}}$$ (16)

Table 4 shows the optimal portfolios’ weights, hedge ratios (HR) and hedge effectiveness (HE) of portfolio pairs analyzed. The optimal weight of green bonds in almost all the portfolio pairs is higher than 0.9, which implies that the investment of green bond should take up a larger part in portfolio pairs including green bond, indicating that the hedging characteristic of green bond in normal time (Glomsrød and Wei, 2018; Jin et al., 2020; Kanamura, 2020) does not decay under COVID-19 pandemic.

Table 4.

Optimal portfolios' weights, hedge ratios, and hedging effectiveness of all the portfolio pairs analyzed.

Portfolio pairs	$w_t^G$	${\beta }_t^G$	HE(%)
Commodity/Green bond	0.908	0.366	96.24
Treasury/Green bond	0.309	0.765	5.42
Stock/Green bond	0.938	−0.011	96.21
Clean energy/Green bond	0.986	0.511	97.07
Treasury/Commodity	0.061	−0.024	8.33
Stock/Commodity	0.436	−0.124	26.92
Clean energy/Commodity	0.661	0.492	33.94
Stock/Treasury	0.916	−0.839	96.90
Clean energy/Treasury	0.954	−0.929	97.34
Clean energy/Stock	0.808	1.020	19.86

To compare the effectiveness of each portfolio pair, we introduced hedge effectiveness (HE). It is noticeable that the HE ranges from a maximum of 97.34% in clean energy-treasury pair to a minimum of 5.42% in treasury-green bond pair. It is also remarkable that the hedge effectiveness of almost every portfolio pair that includes green bonds is over 90%, except the treasury-green bond pair. It infers that an effective investment strategy could consist of one kind of traditional assets and green bond. Furthermore, the HE of stock-treasury and clean energy-treasury pair is over 95%, proving the similarity of green bond and treasury markets that they are both good hedging investments during COVID-19. However, the effectiveness of treasury-green bonds is only 5.42%, the reason of which may be that the characters of treasury and green bonds are so similar that they cannot reach a complementation.

4. Conclusion

This paper aims to investigate the different impacts of the COVID-19 pandemic on the green bond market and conventional financial markets, including commodity, treasury, stock, clean energy markets, in time-frequency domain.

The empirical findings can be listed as follows. First, according to the return spillovers between the ID-EMV index and asset markets, the findings show that the influence of COVID-19 on the green bond is greatly more substantial than that to conventional bond markets. Second, we find that COVID-19 has a medium-term and long-term impact on the asset markets from the angle of the frequency domain. Third, during every little burst of the COVID-19 pandemic, the price indices of markets analyzed fluctuate significantly along with the ID-EMV index. Fourth, the findings also show that green bond and treasury markets have similar characteristics. Finally, for international investors and portfolio managers, our portfolio analysis finds that a good investment strategy during the COVID-19 pandemic should include one kind of conventional asset and one kind of green bond, thus minimizing the risk.

CRediT authorship contribution statement

Tianxiang Cui: Supervision, Formal analysis, Visualization, Writing – original draft. Muhammad Tahir Suleman: Conceptualization, Methodology, Writing – review & editing. Hongwei Zhang: Data curation, Methodology, Writing – original draft.