Abstract
In the post-COVID-19 epidemic era (PCEE), the supply of empty containers will face stronger uncertainty. Estimating the amount of self-owned and leased empty containers that need to be allocated to each inland freight station in a specific area becomes a critical issue for liner companies in PCEE. However, owing to the high degree of unpredictability of the demand and the limited flexibility of empty container relocation, the abovementioned issue has not been fully addressed. This paper provides a model for empty container allocation without knowing the probability distribution function of empty container demand in advance. The abovementioned model can jointly optimize the quantities of self-owned empty containers and leased containers allocated to each inland freight station. To solve the model, a largest-debt-first policy is adopted to simplify the complicated model, and a differential evolutionary (DE) algorithm is developed to solve the simplified model. Compared with some commonly used algorithms, DE has advantages considering the ability to explore the optimal solution. In addition, the utility of the largest-debt-first policy proposed in this paper is compared with that of the traditional method. Experimental results show that in the case of high demand fluctuations, the proposed policy is better in controlling the operational and management costs. Overall, the theory and method proposed in this paper can effectively help the carrier set a reasonable regional empty container stock level and determine the number of self-owned and leased empty containers.
Keywords: Empty container allocation, Stochastic demand, Empty container management, Differential evolution, COVID-19
1. Introduction
Although the COVID-19 epidemic has been gradually controlled, the ‘sequelae’ in the container shipping industry caused by the pandemic still show no sign of abating. As the epidemic has seriously affected the efficiency of port and inland operational systems, the task of empty container replenishment at inland container freight stations is facing a series of thorny challenges. On the one hand, affected by the fluctuation of market capacity, the worldwide container transportation demand shows great fluctuation. This leads to fluctuations in the empty container demand at relevant inland freight stations. On the other hand, because the total amount of empty containers transported cannot meet the actual demands of inland container freight stations, carriers have to find a variety of ways to make up for the gap so that the supply structure of empty containers has become increasingly diversified. At present, the supply structure of empty containers has gradually changed from traditional self-owned containers to a combination of self-owned containers, leased containers and newly built containers. Considering the two changes mentioned above, the traditional empty container management methods and decision-making models have exposed many deficiencies, which may lead to the excessive setting of safety stock levels at inland freight stations. In addition, the existing theories pay less attention to the optimization of the empty container supply structure.
Motivated by this realistic background, our paper focuses on an inventory and transport problem in the inland empty container storage and transshipment system (IETS). An IETS (Fig. 1 ) is typically developed and operated by a liner company and consists of a container yard near a port and multiple inland freight stations. The role of a container yard is to store and transship empty containers. Inland freight stations are used to provide containerizing and unpacking services to shippers. IETS can be classified into two groups based on their functional characteristics: output type and input type. The former category includes the IETS required to export empty containers for an extended period, such as those in North America or Western Europe, while the latter category includes the IETS required to import empty containers for an extended period, such as those in China or Southeast Asia. In this paper, we focus on input type IETS to carry out specific research.
Fig. 1.
A typical inland empty container storage and transshipment system.
One of the key features of the input IETS is the necessity to have a certain number of empty containers on stock to deal with the uncertainty demand of empty containers. This storage is required to improve transit reliability, but it comes with significant storage and administrative costs (Griffiths et al., 2020; Shintani et al., 2019). As a result, determining the optimal quantity of empty containers to store in container yards has become a critical concern for liner companies. In practice, a solution to this problem has long been available. In a container yard, liner companies regularly overstock empty containers, which means that liner companies will store excess empty containers to fully meet demand. Although overstocking is a simple and straightforward process, it results in increased expenditures due to excess storage. As a result, an increasing number of liner companies are partnering with container rental companies (or other liner companies, the same below). Their partnership spawns another operation strategy known as the combination of storage and renting (Braga et al., 2020; Wang et al., 2008; Yu and Li, 2020). Under this strategy, liner companies can rent empty containers for temporary use in addition to storing and transporting their own empty containers (Lin, 2020; Yun et al., 2011b), and rental companies deliver empty containers to demand nodes in line with liner company specifications.
Clearly, there are several advantages of this strategy, including assisting liner companies in reducing the stock level of empty containers, compressing empty container administrative and transportation costs, and enhancing liner companies’ ability to deal with fluctuations in empty container demand. However, it may also result in hefty rental bills. This compels liner companies to consider the following two operational decisions carefully and simultaneously: 1) How can the empty container stock level in the container yard be determined according to the fluctuation of demand? 2) How can the number of empty containers be determined to be leased? In this paper, we address this combined optimization problem of self-owned empty container storage and leased container utilization (ECIP).
ECIP is not straightforward and easy. There are two challenges inherent in the decision-making process. First, if the overstocking strategy is to be abandoned, a more precise estimate of empty container storage is necessary. However, random fluctuations in empty container demand have increased in recent years, which could be attributed to the increased frequency of noncyclical adjustment of container shipping networks, the increasing prevalence of shippers returning empty containers interregionally, and the rapid growth of intercontinental rail container transportation. It has proven challenging to quantify the stochastic nature of empty container demand using a definite probability distribution function. In such circumstances, when the demand probability distribution function is virtually unknown, determining the appropriate amount of empty container storage is a difficult challenge. Second, the cost of transporting for self-owned containers and leased containers may vary greatly by area. For instance, an inland freight station may be closer to the rental company's container yard than to the liner company's container yard, resulting in a reduced operational cost when renting containers. This creates a mutually reinforcing and interdependent link between self-owned container volume and leased container volume. Due to the complexity of this connection, optimizing the empty container inventory becomes a difficult task. To the best of our knowledge, previous research has not been able to provide optimal answers to the abovementioned two challenges.
Therefore, in this paper, we propose a model for solving ECIP considering stochastic empty container demand based on inventory control theory to fill the abovementioned research gap. In the model, we allow liner companies to use leased empty containers at any time and fully consider the difference in transportation costs of different types of containers. Three major contributions are made by this paper.
-
(1)
A novel model for container inventory management is developed. We loosen the requirement that the probability distribution function of empty container demand should be known in this model and do not employ the traditional overstock inventory optimization principle, allowing liner companies to utilize leased containers more frequently to reduce operational costs.
-
(2)
A new resource allocation approach for empty containers is proposed, dubbed the largest-debt-first policy. On the one hand, this policy is straightforward and simple to apply for liner companies; on the other hand, it has the potential to cut liner companies' operational expenses while still optimizing their use of self-owned and leased containers.
-
(3)
Numerical experiments demonstrate that our proposed method can accomplish collaborative optimization of self-owned container inventory control and leased container utilization when a variety of practical factors are considered.
The remainder of this paper is organized as follows. Section 2 reviews the literature related to IETS. Our ECIP is then described in two phases in Section 3. We begin by defining the operation mode of the inland empty container storage and transshipment system. Then, we describe the assumptions and notations used in ECIP. Section 4 develops a stochastic decision model for ECIP. Although this model is difficult to solve directly, it can be transformed equivalently by implementing the largest-debt-first policy. After the transformation, the new model can be solved using a heuristic algorithm. We present this algorithm in detail in Section 5. In Section 6, numerical experiments are conducted to evaluate the effectiveness of the model and algorithm. Finally, Section 7 summarizes the paper and makes several recommendations for further research.
2. Literature review
In essence, ECIP can be viewed as a problem combining container transportation with inventory management. Representative studies can be found in Shintani et al. (2007), Deidda et al. (2008), Song and Dong (2015) and Abdelshafie et al. (2022). According to existing research, this section conducts a literature review from two aspects: the empty container allocation problem (Section 2.1) and the empty container inventory management problem (Section 2.2).
2.1. Research on the empty container allocation problem
Research related to the empty container allocation problem can be further divided into two major categories: deterministic and stochastic. In the context of deterministic studies, Wang and Jing (2020) considered container transshipments. They assumed that empty containers could be delivered to hubs first and then dispersed to inland freight stations, which significantly reduces transportation costs by taking advantage of the economies of scale of centralized transportation. Similarly, Vojdani et al. (2013), Bell et al. (2013), Ambrosino and Sciomachen (2014), and Yu et al. (2018) performed in-depth studies on ECIP in a port's hinterland. Meanwhile, other scholars conduct deterministic research on ECIP in conjunction with other aspects of shipping management. For example, Jeong et al. (2018) designed a shipping line network considering empty container management, and an empty container management strategy for bilateral trade was proposed. Dong et al. (2020) addressed a composite problem of ECIP and marine fleet deployment in the context of roll-on/roll-off shipping. The authors created large-scale linear programming by converting ECIP to numerous inventory management constraints. Du et al. (2021) discussed a composite problem combining the schedule of vessels, cargo routing and ECIP. The above problem aimed to minimize the total cost (including transportation cost, inventory holding cost, container leasing cost, and container repositioning cost) under the alliance cooperation situation. Hu et al. (2021) considered the balance between repositioning empty containers and leasing containers and constructed a two-stage model. The first stage of the model implemented the allocation of empty containers. In the second stage, inverse optimization theory was introduced to determine the rental guide price.
As Kamal (2021) pointed out, the structural trade imbalance has an impact on the fluctuation of demand in ECIP. Thus, it is not surprising that a growing number of scholars have focused on the unpredictability of empty container demand and have attempted to address stochastic ECIP in recent decades. For example, Song (2007) investigated a shuttle service system with unpredictable demand and limited repositioning capacity. Chou et al. (2010) considered the uncertainties of empty container demand, transportation costs, operational costs, and other factors when evaluating empty container relocation between several ports. They highlighted that the changing patterns of these factors are difficult to grasp and characterize. As a result, the authors applied fuzzy decision theory to conduct the uncertainty analysis of the problem, and a two-stage fuzzy optimization framework was developed. Lu et al. (2020) investigated simultaneous pricing and ECIP decisions considering stochastic demand in two-depot shipping services. They solved the problem by developing a large-scale dynamic programming model. The authors analyzed several complicated elements in the model, including price, empty container storage, empty container leasing, and empty container transportation. Lee and Moon (2020) proposed a robust optimization model to deal with an ECIP with foldable containers. To solve the model, a tractable approximation method was introduced to reformulate the multistage stochastic programming model. Since empty container requirements are random, limited information about the distribution function of demand was still needed.
2.2. Research on the empty container inventory management problem
Most of the literature related to the empty container allocation problem makes use of a mathematical programming methodology. However, mathematical programming models are inevitably sophisticated and computationally intensive, making them difficult to execute in practice because their underlying logic is concealed from the liner company (Du and Hall, 1997). To remedy this shortcoming, a school of researchers has attempted to investigate the container inventory management problem using classic inventory management theory.
A stream of research is the use of lean management ideas. Lean management is an important theory in supply chain management. In recent years, many scholars have carried out studies on the furniture industry (Chebet and Kitheka, 2019), manufacturing firms (Opoku et al., 2020), and small business warehouses (Maldonado Román, 2022). There are also many empirical studies to prove the validity of the above theory (e.g., Ramos et al. (2020), Odhiambo and Kihara (2018) and Khan (2020)). In the shipping field, Praharsi et al. (2021) applied the lean six sigma theory to the maritime industry during the era of the COVID-19 pandemic and developed a suitable continuous improvement method for the industry. Frontoni et al. (2020) took an Italian shipping company as an example to conduct a case study and introduced its method of combining lean thinking principles with the concept of Industry 4.0 to achieve cargo safety improvement and container inventory implementation status detection. The above concepts and methods help to avoid various wastes in the process of container inventory management and reduce management costs.
The second stream of research aims to help carriers develop an inventory management model. Some scholars are committed to designing a straightforward policy for empty container management. Typically, such a policy includes an upper and lower bound for the empty container inventory. When an empty container yard's inventory falls below the lower bound, empty containers should be shipped in. Conversely, when the inventory exceeds the upper restriction, empty containers must be transported out. As a result, this policy is typically referred to as an X-threshold policy. For example, Yun et al. (2011a) discussed the decision-making problem of a two-threshold policy in the hinterland of ports. Although the authors considered the time-varying characteristics of transportation demand, they did not present a quantitative optimization decision-making method but employed simulation for analysis. Li et al. (2004) proposed a two-threshold policy for the issue of single-port empty container shipping. Song and Carter (2008) developed a three-phase threshold policy for empty container repositioning. Zhang et al. (2014) investigated the repositioning problem of empty containers in a stochastic and dynamic environment characterized by lost sales to determine an optimal two-threshold policy. From a mathematical standpoint, their approach is novel in that it was the first to incorporate stochasticity, dynamics, and lost sales into an optimal control problem. The authors validated the existence of the optimal policy and created a model of dynamic stochastic programming to find it. Other scholars directly develop inventory management models to determine optimal inventory levels and inventory cycles. For example, Rajeswari et al. (2021) discussed an ECIP with a non-vessel operating common carrier considering the leasing option and fuzzy environment. A fuzzy inventory model that optimizes the empty container repositioning scheme and the leasing scheme was established to minimize the expected total cost. In Cai et al. (2022), two different inventory control strategies (i.e., the quantitative and periodic inventory control strategies) are applied to solve a multiperiod empty container repositioning problem between public hinterlands and ports.
2.3. Research gap
Based on a review of the above literature, we find that the preceding studies conducted extensive studies on ECIP under stochastic demand from a variety of perspectives, yielding several significant conclusions. However, most of the abovementioned deterministic studies assume that the transportation demand for empty containers is known and constant, making the approaches provided in our paper inapplicable to the ECIP. For stochastic studies, the authors assumed that if self-owned containers are not accessible, rental companies can always provide infinite empty containers to fulfill demand (see the assumptions in Li et al. (2007) and Song and Zhang (2010), Didenkulova (2020)). This further motived the authors share the same assumption: the probability distribution function of empty container demand is certain and known. As previously indicated, this assumption no longer meets the actual requirements for empty container management. Therefore, our paper fills the abovementioned research gap by deviating from this assumption and proposing a new method that combines storage and renting strategies for optimizing empty container management policies without knowing the probability distribution function of empty container demand in advance.
3. Problem description
To adequately explain the ECIP addressed in this paper, a more complete explanation of the input IETS operation mode is required (see Fig. 2 ). A liner company is the decision maker of the system, and it can use both self-owned containers and leased containers to meet shippers’ demand. Among them, leased containers are provided by rental companies, while self-owned containers have two sources. One is steady supply, i.e., empty containers are carried into the container yard on a regular basis and in a predefined number by the liner company. The second source is containers that the consignee returns after usage. Because the return time and quantity of these empty containers are difficult to predict accurately, this supply source is referred to as random supply.
Fig. 2.
The process of the container export and import scenario.
When empty containers are required for an export operation (as illustrated in Fig. 2(a)), the shipper must first make an application to the liner company for the reservation of shipping slots. The liner company then decides where to obtain empty containers based on available stock and related costs. If the liner company uses self-owned containers, then it is responsible for transporting the empty containers from the container yard to the inland freight station, as well as for transportation costs. When leased containers are used, the liner company rents empty containers from the rental company, which carries them to the inland freight station. Then, the consigner loads cargoes into empty containers and transports them to the container yard. The container import procedure is depicted in Fig. 2(b). After unloading from a ship, laden containers are delivered to the consignee's designated location. The steady supply of empty containers arrives at the port periodically and is transported to the container yard. The consignee then unloads the containers and delivers the empty containers to the liner company's appointed destination.
Based on the above discussions, the ECIP is described as follows. Under the premise that the empty container demand should be fully satisfied, the decision maker must optimize the following issues throughout a decision period to minimize the expected operational cost: the quantity of self-owned empty containers from the steady supply source and the utilization rate of self-owned empty containers at each inland freight station. The random supply probability information, the empty container leasing fee, and the freight rate of empty container transportation are known, but the probability distribution function of random demand for empty containers is unknown.
To facilitate the modeling, we introduce the following assumptions for the abovementioned operation mode (see Fig. 3 ).
Assumption 1
Only inland freight stations are used to load containers. In other words, we consider inland freight stations to be demand nodes for empty containers in this paper. We assume that the demand for empty containers at each inland freight station is independently and normally distributed. It should be noted that the loading operation is not allowed at the container yard in our model. This assumption is used to simplify the model. To allow the loading operation at the container yard, we can set a dummy inland freight station in the yard and set the transportation cost as zero between the yard and freight station. Note that we do not require the probability information of demand.
Assumption 2
Only the container yard has the capacity to keep empty containers. The container yard's operational cost is a strictly monotonic function of the total number of empty containers stored in the yard. This assumption is also introduced to simplify the problem.
In practice, inland freight stations usually have some capacity to store empty containers. However, this capacity is usually very limited. In addition, these empty containers are usually used immediately or transported to the designated yard for inspection, cleaning or maintenance in practice. In view of this, we assume that only the container yard near the port can be used to store empty containers to simplify the problem.
In addition, we assume that the container yard's operational cost is a strictly monotonic function of the total number of empty containers stored in the yard. This is because, in practice, the larger the empty container storage inventory in a region, the related expenses that a carrier usually needs to pay (for example, operational expenses, empty container depreciation and management costs) will also rise.
Assumption 3
The whole demand for empty containers must be met. For each inland freight station, the liner company must determine the proportion (called the ‘utilization rate’) of self-owned empty containers to the total supply of empty containers. The utilization rate is also the basis for determining the number of leased containers.
This assumption derives from operational practices. In practice, all empty container demands are generated based on the fact that the carrier has accepted the booking. To implement the transportation contract, the carrier has no choice but to ensure that the cargo owner can obtain the necessary empty containers.
Assumption 4
The liner company is responsible for transporting self-owned empty containers from the container yard to the freight station. Accordingly, the liner company is liable for the transportation costs connected with this. In addition, if self-owned empty containers are utilized, the consignee is responsible for returning the emptied containers to the container yard, including all the related transportation costs. In practice, the carrier will make an agreement with the consignee on the place of returning empty containers. When calculating the corresponding fees, the carrier will usually charge the consignee for the maintenance, cleaning and transfer of empty containers. For this reason, we introduce the above assumption.
Assumption 5
Shippers can obtain leased empty containers from the freight station, and consignees must return the leased empty container to the freight station. The utilization of leased empty containers incurs no transportation costs; nonetheless, leasing fees are incurred, which are paid by the liner company. This assumption still comes from operational practice. In practice, carriers are the main customers of a container renting company, which can use leased empty containers to deal with temporary shortages of empty containers. This method is usually referred to as temporary short-term container leasing in the industry. The extra cost due to leasing containers is usually borne by the carrier. For this reason, the cost of this method can also be regarded as the shortage cost of empty container resources. Of course, in practice, there is also a wide range of long-term empty container leases. Empty containers obtained by carriers in this way can be regarded as empty containers owned by the carrier, so we will not discuss this situation in depth.
Assumption 6
We presume that the probability distribution information for the random supply is known. For steady supply, we assume that the liner company can use this supply once in a time interval to replenish the empty containers in the container yard. Both the random and the steady supply determine the periodically empty container stock of the container yard together. Based on operational practice, random supply is usually stable and predictable. This is because the consignee needs to inform the carrier of the specific time of returning empty containers.
For the convenience of the reader, the arrangements for subsequent sections and notations frequently used in this paper are shown in Fig. 4 and Table 1 , respectively.
Fig. 3.
Suppliers and consumers of empty containers in the input IETS.
Fig. 4.
Arrangements for subsequent sections.
Table 1.
Parameters and variables.
| Parameters | |
|---|---|
| Number of inland freight stations | |
| Length of observed period (number of weeks), | |
| No. of inland freight stations, | |
| Adjustment coefficient for the operational cost at the container yard | |
| Empty container demand at inland freight station , the stochastic variable about | |
| Empty container demand at inland freight station , regardless of time interval | |
| Random supply, the stochastic variable about | |
| Random supply of empty containers, regardless of time interval | |
| Function for calculating the storage operational cost at the container yard (RMB/TEU) | |
| Transportation cost per TEU from container yard to inland freight station (RMB/TEU) | |
|
|
Rental fee per TEU at inland freight station (RMB/TEU) |
|
Variables | |
| The amount of steady supply obtained at the container yard in each interval | |
| The utilization rate of self-owned empty containers to the total supply at inland freight station | |
| The quantity of self-owned containers provided by the liner company at inland freight station in interval , where | |
| The quantity of leased containers at inland freight station in interval , where | |
4. Model development
4.1. Proposal of the model
In this section, a nonlinear stochastic programming empty container restoration model (ECRM) is constructed with the objective of minimizing the sum of the expected storage operational cost of self-owned containers, the expected transportation cost of self-owned containers and the expected rental cost of leased containers. The model can realize the synchronous optimization of the steady supply quantity (), the utilization rate (), and the self-owned containers supplied to each inland freight station in each interval (). The proposed ECRM is as follows.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Equation (1) is the objective function of the proposed ECRM. The first item is the expected value of the storage operational cost of the container yard, which is determined jointly by the expected values of steady supply S and random supply Y. The second item represents the cost incurred by the liner company to cope with the fluctuation of random supply. In reality, the number of empty containers returned by the consignee is random. This characteristic requires the liner company to take special measures to handle the randomness (for example, reserve some containers and temporary rental containers for such situations). These measures increase the operational cost at the container yard. The resulting influence is characterized by . The third item represents the expected sum of the transportation cost of self-owned containers and the rental cost of leased containers. Notably, since it is impossible to determine whether the limit exists at this time, we use the supremum in the function. The left part of inequality (2) represents the ratio of self-owned containers supplied by the liner company to the total empty container supply at inland freight station i. This ratio is almost surely not less than . Equation (3) indicates that for any time interval , the empty container demand of inland freight station i must be met. Equation (4) indicates that the total quantity of self-owned containers supplied by the liner company to all inland freight stations in any time interval shall not exceed the sum of steady supply and random supply obtained in that time interval.
The conventional way to handle stochastic variables in a stochastic programming model is to replace them with the mathematical expression of the expected value. However, even if we obtain the expression of , it is unreasonable to write at the right end of the equation because IETS requires to be equal to , not . Thus, if is replaced with , a gap will exist between the actual empty container transportation volume and the real demand. This is different from the original intention of our research and the requirements of IETS operation. Therefore, how to describe and characterize becomes key to solving ECRM. We may circumvent this issue by learning from the research on X-threshold policy settings.
The common practice in research on X-threshold policy settings is to introduce a policy for i to convert the formation process of into a stochastic process connected to and thereby simplify the model. In general, such a generation policy should meet the following two criteria: 1) convenience, i.e., the strategy should make it simple for decision makers to generate random variable samples; in other words, the logic for generating random variable samples should be simple and straightforward to apply in practice; 2) feasibility, i.e., the random variable samples generated by the strategy should satisfy the model's constraints. To create , we employ the largest-debt-first policy. This strategy enables us to convert the ECRM model to a more manageable stochastic programming model.
4.2. Largest-debt-first policy
The largest-debt-first policy allocates self-owned containers based on the gap between past demand for empty containers and historical replenishment. Specifically, we let the vector represent the cumulative shortage of self-owned containers at all inland freight stations in time interval t, that is, the cumulative ‘debt’. Therein, represents the shortage of self-owned containers of inland freight station i at time interval t, and the calculation method is shown in formula (7). equals the accumulation of the difference between the number of required self-owned empty containers () and the actual cumulative number of supplied containers () before time interval t.
| (7) |
Notably, when all values are known, equation (7) depicts only the theoretical value of the cumulative shortage of inland freight station i from interval 1 to t-1. We assume that once a shortage occurs in an inland freight station, we will use leased containers to compensate for the shortage; therefore, there is no actual shortage at any inland freight station in any interval. According to the accumulated debt of each inland freight station in interval t (), we determine the priority of empty container allocation of each inland freight station in descending order. An inland freight station with larger accumulated debt will have priority to obtain self-owned containers from the liner company. Specifically, we assume that the allocation order at time interval t () is , where represents the supply order of inland freight station i at time interval t. If , the requirement of inland freight station 1 should be satisfied prior to that of inland freight station 2. Based on the above symbols, the method for allocating empty containers can be written as equation (8).
| (8) |
According to Equation (8), empty containers available at the container yard are allocated to the inland freight station with the largest accumulated debt () at present. After the demands are satisfied, if there are still self-owned containers left, they will be allocated to the inland freight station with the second largest accumulated debt, and so on. In interval t, if the liner company allocates all self-owned empty containers according to the above principles and the empty container demands of the inland freight stations are still not met, additional empty containers are leased. The implementation process can be summarized as follows.
Step 1: Set the time interval as , and sort all inland freight stations in descending order according to the container demand at . Thus, we can obtain .
Step 2: Based on , the liner company determines the quantity of self-owned containers supplied to each inland freight station according to Equation (8), and the insufficient part is supplemented by leased containers.
Step 3: Set , and update the accumulated debt values () according to Equation (7) and the available quantity of self-owned containers.
Step 4: Update based on the accumulated debt values of all the inland freight stations.
Step 5: Return to Step 2 until .
4.3. Model transformation
According to Theorem 1 in Zhong et al. (2018), for a given , the ECRM can be equivalently transformed into model ECRM-1.
ECRM-1:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Based on the analysis of ECRM-1, we find that when is known, under the influence of the largest-debt-first policy, the steady supply S at the container yard in each interval satisfies Constraints (10)–(11) if and only if Constraints (4)–(5) are satisfied. More importantly, according to the proof process of the theorem, when observed period T approaches infinity, the quantities of self-owned containers and leased containers obtained by each inland freight station in each interval should satisfy Equations (12), (13). In other words, by using the largest-debt-first policy, the quantities of self-owned containers and leased containers obtained by each inland freight station in each interval converge to times and times the expected value of the actual demand at inland freight station i in the long run. This conclusion is interesting; it means that we can eliminate variables and from the model. Based on this idea, we substitute Constraints (12) and (13) into objective function (9); then, the ECRM can be further simplified to ECRM-2.
ECRM-2:
| (14) |
| s.t. (10), (11) |
Due to the presence of constraint (10), ECRM-2 is still difficult to solve directly. However, when is known, objective function (14) increases in a strict monotonic manner with respect to . As a result, if is known, the minimum satisfying constraints (10) and (11) is the optimal solution to ECRM-2. Thus, we can obtain with high efficiency through binary search and simulation. Based on this feature, we design an effective heuristic algorithm for ECRM-2 in Section 5.
5. Algorithm design
In Section 4, we obtain a concise ECRM-2 based on model transformation. However, due to constraint (10), ECRM-2 cannot yet be solved directly at this time. This is because both Y and in Equation (10) are stochastic variables, and S is essentially the stochastic variable determined by Y and . Equation (10) is equivalent to the following Equation (15) after transformation.
| (15) |
We find that the right side of the above inequality consists of the estimated value of decision variable S of demand and . In traditional research, one can still handle this inequality because the distribution situation of is assumed to be known. However, that is not applicable in this paper, as we do not know the distribution situation of . This leads to the fact that we cannot obtain the estimated analytic function of the related variables, making analysis rather difficult.
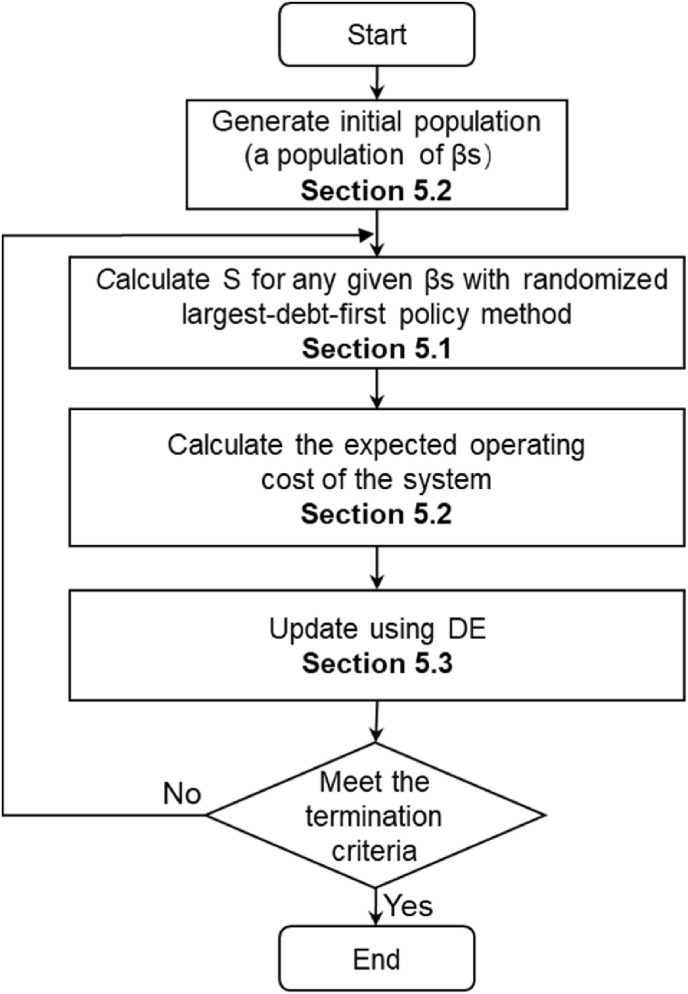
As a result, we have to devise heuristics based on the differential evolution (DE) framework to solve ECRM-2. DE is a population-based adaptive global optimization algorithm that is characterized by a simple structure, easy implementation and fast convergence (Fleetwood, 2004; Price, 2013). However, different from the traditional DE algorithm, we incorporate the inventory optimization method originating from Zhong et al. (2018). The basic flowchart of the proposed algorithm is shown in Fig. 5 . It shows that the solution of the decision variables is divided into two parts. First, is coded (details in Section 5.2), and S can be obtained by the largest-debt-first policy (details in Section 5.1). Afterwards, the fitness value of every individual is calculated according to and S (details in Section 5.2). Finally, a differential operation is adopted according to the fitness value (details in Section 5.3).
Fig. 5.
Basic flowchart of the proposed algorithm for solving ECRM-2.
5.1. Determination of empty container stock level based on binary search
Based on the research by Zhong et al. (2018), under the premise of a known , the ideal stock level can be calculated. The largest-debt-first policy can ensure that all inland freight stations receive the required empty containers. The execution logic of the method is as follows. First, we set an upper and lower bound of the stock level. Then, the binary search is used to gradually explore the minimum inventory that can satisfy the demands. Repeat the binary search.
In the above process, the most critical one is to judge whether the inventory obtained by the binary search satisfies the demands. To solve this problem, the proposed process for the judgment can be described as follows. First, for a given stock level (N), randomly generate the empty container demands of every inland freight station (D(t)). Then, use the proposed largest-debt-first policy to supply for D(t). The priority to supply for D(t) is recorded as P(t). Finally, a priority list is randomly selected from with equal probability, and is calculated. If is obviously lower than the predetermined target, it means that N cannot satisfy the demands; otherwise, N is acceptable. The detailed process for the method is as follows.
Step 1: According to Equation (16), calculate the upper and lower bounds of the optimal empty container stock . Therein, M is a very large positive value.
| (16) |
- Step 2: Adopt binary search. Take the midpoint of the upper and lower bounds obtained in the previous step as the stock level required for the simulation operation process and perform the following steps:
- Step 2.1: Randomly generate the empty container demand of every inland freight station in all T intervals. Based on the largest-debt-first policy, the priority of each interval t () is generated, the self-owned empty containers available are allocated to each inland freight station in each interval according to the priority list , and the inland freight stations that do not have their demands fully satisfied are allocated an appropriate quantity of leased containers.
- Step 2.2: Randomly select a priority list from with equal probability. Based on the selected priority list, calculate the utilization rate of self-owned containers obtained by each inland freight station i ().
Step 3: If for all , are no less than , the algorithm terminates; otherwise, set the value of the midpoint as the upper bound in the next iteration process, and return to Step 2.
5.2. Coding design and fitness calculation
In this section, we use the real number coding method to characterize , as shown in Fig. 6 . The coding of each individual is composed of several genes, and the length of the genes is equal to the number of inland freight stations. For example, if the number of inland freight stations is 20, then the length of the individual is 20. The value of each gene indicates the utilization rate of self-owned containers at inland freight station i (where i is the location value of the gene number), and the range of the value is . For example, the first gene in an individual represents the utilization rate of allocated self-owned empty containers at the container yard to inland freight station No. 1. The fitness calculation includes two steps. First, according to (determined by the code), the algorithm in Section 5.1 is used to obtain the optimal value of S. Then, S and are substituted into equation (14) to obtain the fitness value.
Fig. 6.
Individual coding.
5.3. Differential operator
The basic idea of the difference operator is as follows. First, in a randomly generated initial population, two individuals are arbitrarily selected (A and B), and their vector difference is multiplied by a decimal in the range of (we call this decimal the ‘differential mutation factor’) and added to another individual vector (C) to generate a new individual (D). Second, the crossover operation is performed on individuals D and A to generate child individual (E). Third, the fitness values of individuals E and A are compared. If the fitness value of individual E is better than that of individual A, individual E replaces individual A in the next generation; otherwise, individual A is retained. Through continuous iteration, the search results approach the optimal solution. The operation flow of the differential operator is shown in Fig. 7 (Price et al., 2006).
Fig. 7.
Flowchart of the differential operator.
Taking Fig. 8 as an example, we further illustrate the individual generation process based on the differential evolution operation (except the crossover and selection operations). First, the values of each gene in parents A and B are subtracted to obtain differential individual 1, which is multiplied by the mutation factor to obtain differential individual 2. Then, differential individual 2 is added to parent C to obtain new individual A after the differential operation. Notably, during the operation shown in Fig. 7, the gene value of the last gene point in new individual A is 1.38, which exceeded the upper limit. In this case, we randomly generate an effective value within the limits to replace the original gene value.
Fig. 8.
Generation method of a new individual.
Then, the new individual A and the parent individual A are subjected to the traditional crossover operation, and part of the genes of the new individual A are randomly replaced with genes at the corresponding gene points of parent A according to the crossover probability (as shown in Fig. 9 ).
Fig. 9.
The crossover operation.
6. Numerical experiments
To verify the advantages of the proposed model in its effectiveness and application value in the post-COVID-19 epidemic era, three experiments are designed in this section. In Experiment 1, we focus on testing the computational efficiency of the method proposed in this paper and verifying the effectiveness of this method compared with other traditional methods. In Experiment 2, some special phenomena in the container shipping market influenced by the outbreak of COVID-19 are analyzed. We carry out sensitivity analysis on different proportions of self-owned containers and temporary leased containers. In Experiment 3, the influence of the fluctuation degree of transportation demand on the results is discussed in detail. The remainder of this section is organized as follows. Section 6.1 introduces the data and relevant settings used in the experiment, and sections 6.2-6.4 discuss the specific steps and calculation results of experiments 1–3, respectively, in detail.
6.1. Experimental parameter setting
To simplify and analyze the investigated problem, we consider the stochastic container demands of 20 inland freight stations in the hinterland and analyze the changes in related indicators, such as the expected total cost of the liner company and the empty container stock level at the container yard.
Regarding the empty container demands of every inland freight station, we use the same setting rules unless special explanations are provided. Specifically, we assume that the container demand of each inland freight station is independent and follows a normal distribution. The expected values of the demands are shown in Table 2 , and the variance is a parameter that needs discussion in the sensitivity analysis. In addition, the random empty container supply Y (empty containers that the consignee returns after usage) also obeys the normal distribution, and the expected value and variance of Y are 30% of the total number at each freight station.
Table 2.
Demands and related costs for each inland freight station.
| No. of inland freight station | Average demand (TEU/interval) | Rental rate (RMB/TEU) | Transportation rate (RMB/TEU) | No. of inland freight station | Average demand (TEU/interval) | Rental rate (RMB/TEU) | Transportation rate (RMB/TEU) |
|---|---|---|---|---|---|---|---|
| 1 | 62 | 500 | 381 | 11 | 35 | 480 | 165 |
| 2 | 27 | 340 | 150 | 12 | 57 | 380 | 541 |
| 3 | 18 | 360 | 113 | 13 | 39 | 450 | 300 |
| 4 | 65 | 300 | 102 | 14 | 75 | 340 | 225 |
| 5 | 77 | 480 | 260 | 15 | 52 | 420 | 468 |
| 6 | 66 | 460 | 265 | 16 | 57 | 460 | 273 |
| 7 | 59 | 380 | 282 | 17 | 64 | 360 | 450 |
| 8 | 44 | 400 | 272 | 18 | 33 | 440 | 201 |
| 9 | 16 | 460 | 159 | 19 | 40 | 400 | 241 |
| 10 | 44 | 420 | 247 | 20 | 73 | 440 | 506 |
Regarding the empty container storage operational cost, the mathematical expression of the cost function is defined as follows, where , , and .
Regarding the empty container transportation cost and rental cost, we require that each inland freight station has a varied location, as well as a different time for cargo owners to use empty containers. Therefore, the unit empty container rental fees paid by the liner company vary depending on different inland freight stations. Thus, we can obtain the average demand of each inland freight station in each interval, the unit empty container rental cost of the liner company in each inland freight station and the unit empty container transportation costs from the container yard to each inland freight station, as shown in Table 2.
6.2. Experiment 1: efficiency analysis of the proposed method
Experiment 1 includes two stages. In the first stage, we focus on the effectiveness of the algorithm proposed in this paper. Specifically, based on the parameters given in Table 2, we use the genetic algorithm (GA), particle swarm optimization (PSO) and differential evolution algorithm (DE) proposed in this paper to carry out the comparative experiment. Due to the pretest for the parameter setting, the mutation factor F and crossover probability are set as 0.1 and 0.9, respectively, to obtain the optimal convergence characteristics. To avoid the randomness of the experimental results, we use the three algorithms to carry out the experiments with five different observed periods (T = 60, 90, 120, 150, 180). At the same time, the average of the fitness values obtained with different observed periods in every iteration are used to measure the advantages and disadvantages of the algorithm. During the calculation process, we assume that empty containers are allocated based on the principle of maximum debt priority proposed in this paper at all freight stations. In this experiment, the demand variance is set to 20% of the expected value of each inland freight station.
The calculation results are shown in Fig. 10 . It can be seen from the figure that the performance of PSO in solving ECRM is far inferior to that of GA and DE. It has no advantage in convergence speed. In addition, there is a large gap between the expected total costs from PSO and those from the other two algorithms. GA is superior to DE in computational convergence speed but slightly inferior to DE in computational quality. In summary, the DE proposed in this paper has a certain degree of improvement in the calculation quality compared with the traditional GA and PSO and can solve ECRM more effectively.
Fig. 10.
Comparison of the convergence characteristics of the proposed DE with GA and PSO.
In the second stage, we compare the results of the proposed method in solving ECRM with the solutions of the traditional inventory management method (, we call it the classic method afterwards) to verify the effectiveness of our proposed method. According to the expected value and variance data of the demand of each inland freight station, we use formula (17) to calculate the container inventory level at the container yard.
| (17) |
There are two points that need to be emphasized: 1) in this stage of the experiment, is still a decision variable that needs to be optimized. In (17), is the only decision variable, and and are the mean and variance of the demand samples for empty containers at inland freight station i. 2) In the traditional method, empty containers are allocated by the traditional principle of maximum comprehensive cost (that is, the sum of transportation cost and container rental cost), instead of the largest-debt-first policy proposed in this paper. In other words, empty containers will be preferentially allocated to inland freight stations with higher comprehensive costs. Since leasing empty containers is allowed, we can ensure that each inland freight station receives the necessary empty container resources. At this time, the cost of renting empty containers at each station can be regarded as the shortage cost.
Similar to the process in the first-stage experiment, we also set five observed periods (T = 60, 90, 120, 150, 180) to carry out experiments to analyze the effect of the largest-debt-first policy on medium- and long-term empty container inventory control. The calculation results of the two methods are shown in Fig. 11 . It can be found that the method proposed in this paper is significantly better than the traditional method in controlling operational cost with different observed periods.
Fig. 11.
Expected costs with changes in the observed period for Experiment 1.
To further investigate the effectiveness of the proposed ECRM, we carry out a simulation test based on the above calculation results. The test process is as follows: 1) based on the problem hypothesis, we generate a group of empty container demand sample sequences at all inland freight stations; 2) obtain the optimal S by solving the ECRM and allocate empty containers by the largest-debt-first policy; 3) according to the sample and allocation policy, calculate the average self-owned empty container utilization rate of each inland freight station () during the observed period.
Table 3 shows the optimal results of (the optimized value of the decision variable) compared with when the observed period T is 180. Table 3 shows that and are quite similar. This means that the largest-debt-first policy can help decision-makers easily achieve the optimization target.
Table 3.
Values of and for each inland freight station (T = 180).
| No. of inland freight station | No. of inland freight station | ||||
|---|---|---|---|---|---|
| 1 | 0.93 | 0.93 | 11 | 0.96 | 0.97 |
| 2 | 0.97 | 0.96 | 12 | 0 | 0.02 |
| 3 | 0.98 | 0.99 | 13 | 0.96 | 0.97 |
| 4 | 0.93 | 0.91 | 14 | 0 | 0.02 |
| 5 | 0.92 | 0.91 | 15 | 0 | 0.02 |
| 6 | 0.93 | 0.94 | 16 | 0.94 | 0.95 |
| 7 | 0 | 0.02 | 17 | 0 | 0.02 |
| 8 | 0.95 | 0.95 | 18 | 0.97 | 0.99 |
| 9 | 0.98 | 0.97 | 19 | 0.96 | 0.98 |
| 10 | 0.95 | 0.95 | 20 | 0 | 0.02 |
Of course, the difference between and is closely related to the length of the observed period. Thus, we show the difference (root mean square error, RMSE) between and under ECRM with different observed periods in Fig. 10. The results show that RMSE decreases with the increase in the length of the observed period. Therefore, for the scheme given by ECRM, the longer the observed period is, the closer the value of , and the utilization rate of self-owned containers can be.
6.3. Experiment 2: sensitivity analysis in the post COVID-19 epidemic era
In experiment 2, we focus on the characteristics of the container shipping market in the context of the post-COVID-19 epidemic. This experiment consists of two scenarios.
-
1)
In scenario 1, each inland freight station only uses its own containers for replenishment, and leasing containers cannot be obtained. This scenario corresponds to the container shipping market before the outbreak of COVID-19. , and S is the only decision variable. Liner companies allocate empty containers based on the largest-debt-first policy.
-
2)
In scenario 2, we consider the circumstance that only leased empty containers can be obtained while a self-owned container is not available. This scenario corresponds to the situation that in the post-COVID-19 epidemic era, liner companies have to obtain empty containers through other ways because the return of self-owned empty containers is rather difficult. In this scenario, , S = 0.
By comparing the optimal solution obtained by solving ECRM in Section 6.2 with those from scenarios 1 and 2, Fig. 12 can be obtained.
Fig. 12.
Expected costs with changes in the observed period for Experiment 2.
Similar to the previous subsection, we also carry out several tests for different observation periods (T = 60, 90, 120, 150 and 180). The results show that the cost given by ECRM is lower than that of scenario 1 with any observed period. This means that there are deficiencies in completely using self-owned empty containers to meet market demand. Reasonably optimizing and controlling the empty container stock level S can obviously reduce empty container storage and management costs.
In addition, it should be noted that although there is little difference in expected costs between scenarios 1 and 2, the result is of no practical significance. This is because the results are closely related to the setting of empty container rental fees. If we increase the empty container rental fee to simulate the carrier's behavior of manufacturing new empty containers to meet the demand for empty containers in practice, the expected costs will inevitably rise significantly.
On the other hand, the expected cost of the solution given by ECRM is significantly lower than that of scenario 2, which has some managerial implications. This means that within the range of normal operating cost parameters, it is impractical to completely use leased containers instead of self-owned containers. Liner companies must reasonably consider the utilization rate of self-owned empty containers and leased empty containers to control their own costs.
6.4. Experiment 3: sensitivity analysis of variance of the demands for inland freight stations
In experiment 3, we test the influence of a change in variance in inland freight stations' demand on the liner company's expected total cost with the observed period . For comparison, we take the ratio of the variance-to-mean of empty container demand () as the parameter of the sensitivity analysis. This parameter describes the fluctuation situation of empty container demand of inland freight stations. The greater this value is, the greater the volatility of demand. Table 4 and Fig. 13 show the results under the four scenarios.
Table 4.
Influence on the expected total cost with different values of the variance-to-mean ratio of demand.
| ECRM result (10000 RMB) | classic method (10000 RMB) | Scenario 1 (10000 RMB) | Scenario 2 (10000 RMB) | |
|---|---|---|---|---|
| 0 | 24.43 | 26.20 | 29.11 | 31.91 |
| 1/5 | 24.73 | 31.07 | 31.29 | 31.91 |
| 1/4 | 24.81 | 32.75 | 32.59 | 31.91 |
| 1/3 | 24.95 | 36.48 | 35.56 | 31.92 |
| 1/2 | 25.24 | 44.86 | 45.39 | 31.93 |
Fig. 13.
Influence on the expected cost with different values of the variance-to-mean ratio of container demand.
When the variance-to-mean ratio increases, the expected total costs of the classic method and scenario 1 show a significant upward trend because the liner company must prepare more empty containers to avoid a possible shortage of empty containers due to an increase in demand fluctuation. In contrast, the expected total costs of the ECRM result and scenario 2 are almost unaffected. The results of scenario 2 are in line with our expectations, as the expected total cost of scenario 2 is related to only the expected value of empty container demand. However, for ECRM, the results are surprising. The ECRM model, based on the largest-debt-first policy, can not only effectively reduce the safe empty container stock level but also effectively handle the adverse impact of the increase in demand fluctuation.
To explain the reason for this stability under ECRM, we further analyze the difference in empty container stock levels between ECRM and the classic method with different variance-to-mean ratios, as shown in Fig. 14 .
Fig. 14.
Optimized empty container stock with different variance-to-mean ratios.
With the classic method, to cope with the increasing fluctuation of empty container demand, the liner company must increase the empty container stock (even if has been optimized). This action directly leads to a significant increase in empty container storage operational costs in the classic method. In ECRM, because the largest-debt-first policy is adopted to allocate empty containers, the liner company can take advantage of the offset effect of demand fluctuation to effectively address the impact caused by the increase in demand fluctuation. Therefore, we can ensure that the empty container stock at the container yard is always maintained at a stable level and does not increase significantly with an increase in the variance-to-mean ratio, so the expected total cost does not change significantly. In addition, as the fluctuation range of empty container demand increases, the expected cost of ECRM is always lower than that of the other schemes. The above results again confirm that our proposed allocation policy is significantly better than the traditional policy.
7. Concluding remarks
To address the new combination of storage and rent container management modes, this paper considers the empty container allocation optimization problem for inland freight stations under the background of stochastic demands. By constructing a stochastic programming model with the minimum expected total cost of the liner company as the goal, the collaborative optimization of (1) the allocation of empty containers at container yards; (2) the transportation scheme of self-owned empty containers from container yards to every inland freight station; and (3) the proportion of self-owned containers to the total demands in each inland freight station can be realized. We also offer the largest-debt-first policy, which takes into account the model's complexity. From the standpoint of the long-term supply of empty containers, the liner company can attain the lowest expected total cost under this policy. The contribution of this paper can be summarized into two aspects, theoretically and practically.
Theoretically, in the traditional empty container inventory optimization problem, the distribution information of empty containers is usually assumed to be known. Our proposed empty container inventory optimization model does not need the empty container demand distribution information, which means that our model is more applicable. In addition, we discuss the optimization of the supply structure of empty containers for the first time. To the best of our knowledge, this paper is the first to discuss the collaborative optimization of the above two types of problems. Therefore, the model and method we propose have certain value for enriching the theory and methods of container management.
Practically, the model and approach proposed in this paper can significantly reduce the operational costs of liner companies. On the other hand, it is essentially an online inventory control management method. In the daily operation of liner companies, the model and approach proposed in this paper can be used repeatedly based on data accumulation to maintain the optimal empty container inventory level and empty container supply structure. This is of great practical significance to deal with the uncertainty of empty container demand and to improve the efficiency of liner route network operation.
In addition, by analyzing the calculation results, we can also obtain the following important managerial implications. First, the traditional empty container resource inventory management method based on the overstocking strategy has great limitations. For that reason, liner companies believe that in the face of volatile demand for empty containers, the stock level of empty containers is bound to increase. However, our experimental results show that with the offset effect of multi node demand fluctuations, liner companies only need low empty container storage to meet their demands. The fluctuation of demand at a node is not the only factor affecting the scale of empty container inventory.
The follow-up research directions of this paper include the following three aspects. First, we consider only the storage, transportation and rental costs of empty containers. However, the composition of empty container management costs is usually complicated in practice. How to fully consider the actual operational factors and include appropriate cost elements in the model framework is a future research direction. Second, we assume that each inland freight station's empty container demand is independent and identically distributed, ignoring the correlation of the empty container demands of inland freight stations. Therefore, the correlation of empty container demands of different inland freight stations should be considered in future research. Third, we use a differential evolution algorithm to solve the model. The algorithm can only obtain a satisfactory solution of the model. Improving the precision of the solution is also a fascinating study topic.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors would like to express their gratitude for the support provided by the National Natural Science Foundation of China [grant numbers 72071025, 72072097, 72001120, 72101129 and 71861006], the Science and Technology Plan Project of Guangxi Zhuang Autonomous Region [grant number 2021AC19334], the School-level Scientific Research Project of Beijing Wuzi University [grant number 2021XJKY10], the Social Science Planning Foundation of Liaoning [grant number L19BGL005], the Natural Science Foundation of Liaoning Province [grant number 2020-HYLH-39] and the Special Foundation for Basic Scientific Research of the Central Colleges of China [grant number 3132022271].
Data availability
The data that has been used is confidential.
References
- Abdelshafie A., Salah M., Kramberger T., Dragan D. Repositioning and optimal Re-allocation of empty containers: a review of methods, models, and applications. Sustainability. 2022;14(11):6655. [Google Scholar]
- Ambrosino D., Sciomachen A. Location of mid-range dry ports in multimodal logistic network. Procedia Soc. Behav. Sci. 2014;108:118–128. [Google Scholar]
- Bell M.G.H., Liu X., Rioult J., Angeloudis P. A cost-based maritime container assignment model. Transp. Res. Part B Methodol. 2013;58:58–70. [Google Scholar]
- Braga H.O., Pereira M.J., Musiello-Fernandes J., Morgado F., Soares A.M., Azeiteiro U.M. The role of local ecological knowledge for the conservation and sustainable fisheries of the sea lamprey (Petromyzon marinus Linnaeus, 1758) in the Iberian Peninsula. Ocean Coast Manag. 2020;198 [Google Scholar]
- Cai J., Li Y., Yin Y., Wang X., Lalith E., Jin Z. Optimization on the multi-period empty container repositioning problem in regional port cluster based upon inventory control strategies. Soft Comput. 2022:1–24. [Google Scholar]
- Chebet E., Kitheka S. Effects of inventory management system on firm performance–an empirical study. Int. J. Innovat. Sci. Res. Technol. 2019;4(9):34–242. [Google Scholar]
- Chou C.C., Gou R., Tsai C.-L., Tsou M.-C., Wong C.-P., Yu H.-L. Application of a mixed fuzzy decision making and optimization programming model to the empty container allocation. Appl. Soft Comput. 2010;10:1071–1079. [Google Scholar]
- Deidda L.G., Di Francesco M., Olivo A., Zuddas P. Implementing the street-turn strategy by an optimization model. Marit. Pol. Manag. 2008;35:503–516. [Google Scholar]
- Didenkulova E. Catalogue of rogue waves occurred in the World Ocean from 2011 to 2018 reported by mass media sources. Ocean Coast Manag. 2020;188 [Google Scholar]
- Dong B., Christiansen M., Fagerholt K., Bektaş T. Combined maritime fleet deployment and inventory management with port visit flexibility in roll-on roll-off shipping. Transport. Res. E Logist. Transport. Rev. 2020;140 [Google Scholar]
- Du B., Hu H., Zhang J., Meng M. A multi-stage approach for empty container repositioning under coordination among liner carriers. Transport. Res. Rec. 2021;2675(7):424–437. [Google Scholar]
- Du Y., Hall R. Fleet sizing and empty equipment redistribution for center-terminal transportation networks. Manag. Sci. 1997;43(2):145–157. [Google Scholar]
- Fleetwood K. Proceedings of Mathematics and Statistics of Complex Systems (MASCOS) One Day Symposium. 26th November. 2004. An introduction to differential evolution. Brisbane, Australia. [Google Scholar]
- Frontoni E., Rosetti R., Paolanti M., Alves A.C. HATS project for lean and smart global logistic: a shipping company case study. Manuf. lett. 2020;23:71–74. [Google Scholar]
- Griffiths L.L., Connolly R.M., Brown C.J. Critical gaps in seagrass protection reveal the need to address multiple pressures and cumulative impacts. Ocean Coast Manag. 2020;183 [Google Scholar]
- Hu H., Du B., Bernardo M. Leasing or repositioning empty containers? Determining the time-varying guide leasing prices for decision making. Marit. Pol. Manag. 2021;48(6):829–845. [Google Scholar]
- Jeong Y., Saha S., Chatterjee D., Moon I. Direct shipping service routes with an empty container management strategy. Transport. Res. E Logist. Transport. Rev. 2018;118:123–142. [Google Scholar]
- Kamal B. The use of fuzzy-bayes approach on the causal factors of empty container repositioning. Mar. Technol. Soc. J. 2021;55(5):20–38. [Google Scholar]
- Khan M.S.R. The effects of inventory management capability on performance of the firm-business strategies as a mediating role. Asian Finance & Bank Rev. 2020;4(2):1–7. [Google Scholar]
- Lee S., Moon I. Robust empty container repositioning considering foldable containers. Eur. J. Oper. Res. 2020;280(3):909–925. [Google Scholar]
- Li J.-A., Leung S.C., Wu Y., Liu K. Allocation of empty containers between multi-ports. Eur. J. Oper. Res. 2007;182(1):400–412. [Google Scholar]
- Li J.-A., Liu K., Leung S.C., Lai K.K. Empty container management in a port with long-run average criterion. Math. Comput. Model. 2004;40(1–2):85–100. [Google Scholar]
- Lin Y. Coupling analysis of marine ecology and economy: case study of Shanghai, China. Ocean Coast Manag. 2020;195 [Google Scholar]
- Lu T., Lee C.-Y., Lee L.H. Coordinating pricing and empty container repositioning in two-depot shipping systems. Transport. Sci. 2020;54:1697–1713. [Google Scholar]
- Maldonado Román S. Manufacturing Engineering; 2022. Lean Six Sigma Implementation in a Small Business Warehouse Inventory Management Redesign. [Google Scholar]
- Odhiambo M.O., Kihara A.N. Effect of inventory management practices on supply chain performance of government health facilities in Kisumu county in Kenya. J. Int. Buss. Innovat. Strat. Manag. 2018;2(2):145–166. [Google Scholar]
- Opoku R.K., Fiati H.M., Kaku G., Ankomah J., Opoku-Agyemang F. Inventory management practices and operational performance of manufacturing firms in Ghana. Adv. Res. 2020;21(10):1–18. [Google Scholar]
- Praharsi Y., Jami’in M.A., Suhardjito G., Wee H.M. The application of Lean Six Sigma and supply chain resilience in maritime industry during the era of COVID-19. Int. J. Lean Six Sigma. 2021;12(4):800–834. [Google Scholar]
- Price K., Storn R.M., Lampinen J.A. Springer Science & Business Media; 2006. Differential Evolution: a Practical Approach to Global Optimization. [Google Scholar]
- Price K.V. Handbook of Optimization. Springer; 2013. Differential evolution; pp. 187–214. [Google Scholar]
- Rajeswari S., Sugapriya C., Nagarajan D. Fuzzy inventory model for NVOCC's returnable containers under empty container repositioning with leasing option. Complex. Intel. Sys. 2021;7(2):753–764. [Google Scholar]
- Ramos E., Pettit T.J., Flanigan M., Romero L., Huayta K. Inventory management model based on lean supply chain to increase the service level in a distributor of automotive sector. Int. J. Supply Chain Manag. 2020;9(2):113–131. [Google Scholar]
- Shintani K., Imai A., Nishimura E., Papadimitriou S. The container shipping network design problem with empty container repositioning. Transport. Res. E Logist. Transport. Rev. 2007;43:39–59. [Google Scholar]
- Shintani K., Konings R., Imai A. Combinable containers: a container innovation to save container fleet and empty container repositioning costs. Transport. Res. E Logist. Transport. Rev. 2019;130:248–272. [Google Scholar]
- Song D.-P. Characterizing optimal empty container reposition policy in periodic-review shuttle service systems. J. Oper. Res. Soc. 2007;58(1):122–133. [Google Scholar]
- Song D.-P., Dong J.-X. In: Handbook of Ocean Container Transport Logistics: Making Global Supply Chains Effective. Lee C.-Y., Meng Q., editors. Springer International Publishing; 2015. Empty container repositioning; pp. 163–208. [DOI] [Google Scholar]
- Song D.-P., Zhang Q. A fluid flow model for empty container repositioning policy with a single port and stochastic demand. SIAM J. Control Optim. 2010;48(5):3623–3642. [Google Scholar]
- Song D.P., Carter J. Optimal empty vehicle redistribution for hub‐and‐spoke transportation systems. Nav. Res. Logist. 2008;55(2):156–171. [Google Scholar]
- Vojdani N., Lootz F., Rösner R. Optimizing empty container logistics based on a collaborative network approach. Marit. Econ. Logist. 2013;15:467–493. [Google Scholar]
- Wang R., Zhao X., Yu W., Zou W. IEEE International Conference on Industrial Engineering and Engineering Management. 2008. The study on empty containers allocation in the container transportation. 2008. [Google Scholar]
- Wang X., Jing Y. Research on optimization of port container inland collection and distribution network. E3S Web Conf. 2020;165 doi: 10.1051/e3sconf/202016506024. [DOI] [Google Scholar]
- Yu J.-K., Li Y.-H. Evolution of marine spatial planning policies for mariculture in China: overview, experience and prospects. Ocean Coast Manag. 2020;196 [Google Scholar]
- Yu M., Fransoo J.J., Lee C.-Y. Detention decisions for empty containers in the hinterland transportation system. Transp. Res. Part B Methodol. 2018;110:188–208. [Google Scholar]
- Yun W.Y., Lee Y.M., Choi Y.-S. Optimal inventory control of empty containers in inland transportation system. Int. J. Prod. Econ. 2011;133:451–457. [Google Scholar]
- Yun W.Y., Lee Y.M., Choi Y.S. Optimal inventory control of empty containers in inland transportation system. Int. J. Prod. Econ. 2011;133(1):451–457. [Google Scholar]
- Zhang B., Ng C.T., Cheng T.C.E. Multi-period empty container repositioning with stochastic demand and lost sales. J. Oper. Res. Soc. 2014;65:302–319. [Google Scholar]
- Zhong Y., Zheng Z., Chou M.C., Teo C.-P. Resource pooling and allocation policies to deliver differentiated service. Manag. Sci. 2018;64(4):1555–1573. doi: 10.1287/mnsc.2016.2674. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that has been used is confidential.