Stability matters, too – the thermodynamics of amyloid fibril formation

Abstract

Amyloid fibrils are supramolecular homopolymers of proteins that play important roles in biological functions and disease. These objects have received an exponential increase in attention during the last few decades, due to their role in the aetiology of a range of severe disorders, most notably some of a neurodegenerative nature. While an overwhelming number of experimental studies exist that investigate how, and how fast, amyloid fibrils form and how their formation can be inhibited, a much more limited body of experimental work attempts to answer the question as to why these types of structures form (i.e. the thermodynamic driving force) and how stable they actually are. In this review, I attempt to give an overview of the types of experiments that have been performed to-date to answer these questions, and to summarise our current understanding of amyloid thermodynamics.

The thermodynamics of amyloid formation has largely been neglected compared to kinetic studies. In this review, the current state of the experimental exploration of amyloid thermodynamics is presented and important open questions are highlighted.

Introduction

The polymerisation of proteins to form supramolecular fibrillar structures is of great biological significance. Protein polymers can provide mechanical stability to the cell and act as scaffolds and tracks that confine the movement of molecular motors. Furthermore, the polymerisation dynamics of proteins and the associated force generation are exploited in processes such as cellular movement and chromosome segregation. In many cases, biological polymers are formed from protein building blocks that adopt a very similar structure in the polymer to that in isolation, exemplified by the cytoskeletal proteins actin and tubulin, or bacterial flagellin. A different class of protein polymers is amyloid fibrils, the formation of which is usually associated with a substantial structural change that the individual polypeptide unit undergoes. Amyloid fibrils have been prominent objects of research in the last two decades because of their formation being the hallmark of a range of severe disorders, such as Alzheimer's disease or amyotrophic lateral sclerosis (ALS).¹ However, amyloid fibrils are also found to fulfill functional roles in biology (e.g. as storage forms for human hormones² or in bacterial biofilms³). Furthermore, many proteins can be induced to form amyloid fibrils in vitro under appropriate, often non-native conditions.⁴

In this work, I adopt the definition of amyloid fibrils generally accepted in biophysical studies, which is less stringent than the medical definition,⁵ and comprises all classes of protein filaments with certain common structural motifs. In amyloid fibrils, individual protein molecules are held together by intermolecular β-sheet formation, with the β-strands being oriented perpendicular to the long fibril axis (cross-β structure⁶). This is true whether or not the individual protein building blocks contain any β-sheet structure in solution. In many cases, amyloid fibrils are formed by proteins that are intrinsically disordered in solution, but also globular proteins with much α-helical structure are observed to form amyloid fibrils under some conditions.⁷ The requirement for a significant rearrangement of the building block explains why solution conditions that destabilise the native state (extremes of temperature, pH, and denaturant) of a protein are often highly conducive to the formation of amyloid fibrils.^4,8 This general observation in turn immediately suggests that the amyloid state itself is less susceptible to destabilisation under those conditions that destabilise the native state; otherwise the conversion reaction would not be facilitated. These findings have given rise to the notion of the amyloid fibril being in general a highly thermodynamically stable structure that is not easily reversible and the absolute stability of which is difficult to quantify. This assessment, together with the view that amyloid fibril formation is essentially a ‘kinetic problem’ (i.e. kinetic factors are decisive for the in vivo and in vitro behavior), has led to the thermodynamics of amyloid fibril formation being much less studied than its kinetics. The aim of this review article is to highlight these experimental studies that have addressed the thermodynamics of amyloid fibril formation and to point out the important open questions in this space to be addressed in the years to come.

The thermodynamics of protein folding

Energetics

Before I start with a survey of the available data on amyloid fibril thermodynamics, I will recall some of the main features of protein folding thermodynamics, in order to provide an appropriate context. Protein aggregation into amyloid fibrils is also often referred to as ‘misfolding’, reflecting the fact that the protein molecules adopt a specific structure when incorporating into amyloid fibrils. Even if this structural fold is not the native one, it is stabilised by the same types of fundamental inter- and intra-molecular interactions as the native state. Excellent reviews have been written on the energetics of protein folding;^9,10 therefore I will restrict the discussion to some essential aspects. For those readers who would like to refresh their knowledge on basic thermodynamics, Appendix 1 contains a short summary of the key ideas required for an understanding of protein folding and misfolding thermodynamics. The folding of even small proteins is a very complex process, involving the breaking and formation of hundreds of individual interactions that cancel each other out to a large extent. It is therefore not surprising that even after decades of work in this area, it is still very difficult to predict absolute thermodynamic stabilities of folded proteins, even if high resolution structures are available. The main types of interactions involved in protein folding are covalent bonds (disulfide links), hydrogen bonding, ionic interactions (e.g. salt bridges between positively and negatively charged amino acid side chains), and van der Waals and other non-covalent interactions. Most of these interactions make a net favourable contribution to the stability of the native state. However, there are also entropic factors that contribute significantly to protein folding, mostly the hydrophobic effect and the entropy of the polypeptide chain. The hydrophobic effect is related to the solvent (i.e. water) entropy that is reduced when small hydrophobes (substances incapable of engaging in hydrogen bonds with water) are solvated.¹¹ The assembly of small hydrophobes into clusters is driven by the associated increase in the solvent entropy. The single largest entropic factor that opposes protein folding is the conformational entropy of the polypeptide chain that is severely restricted when the protein transitions from a disordered chain to a well-defined three-dimensional shape. Overall, these different interactions cancel in large parts, both overall as well as in their respective enthalpic and entropic contributions (enthalpy-entropy compensation¹²), leading to moderate stabilities of the folded state of the order of a few tens of kJ mol⁻¹.⁹ This is equivalent to the net formation of 1–2 hydrogen bonds while hundreds of such bonds and other interactions are broken and formed in the process. This delicate balance of energies rationalises how in many cases a single amino acid change (‘point mutation’) can significantly destabilise a folded state of a protein to an extent that under physiological conditions a measurable concentration of (partly) unfolded protein exists, posing an increased risk for aggregation.¹³ A significant fraction of proteins are not able to adopt a stable fold in isolation and are known as intrinsically disordered proteins.¹⁴ They require a binding partner to do so, as only this interaction lowers the free energy of folding sufficiently.¹⁵ Folded proteins usually have a well-defined stability optimum (free energy minimum) at intermediate temperatures (∼30–50 °C) and become destabilised at hot and cold temperatures. For proteins from extremophile organisms, the temperatures of optimal stability may be shifted to higher or lower temperatures.¹⁶ At high temperatures proteins unfold because of the increasing contribution of chain entropy and at low temperatures because of the weakening of the hydrophobic effect, caused by the increased order in bulk water. The temperature-dependence of the free energy of protein folding can be quantified by the heat capacity of the folding reaction (i.e. the difference of the heat capacities of the unfolded and folded states), which is usually large and negative, and has been found to correlate with both the protein size and buried hydrophobic surface area (which are also strongly correlated with each other).¹⁷ Under conditions where the native state is stable with respect to the unfolded state, it is usually considered to represent the global minimum of the free energy.¹⁸ However, this applies only in (infinitely) dilute solution, as aggregated states (e.g. amyloid fibrils) become accessible at finite concentration and their stability is strongly concentration dependent (Fig. 1a). If one focuses on the stability of the native fold itself, a relatively weak, but finite concentration-dependence can be observed, e.g. in thermal unfolding experiments. Increasing the protein concentration can lead to both a higher (through molecular crowding¹⁹) or lower (through intermolecular interactions/aggregation²⁰) thermal stability.

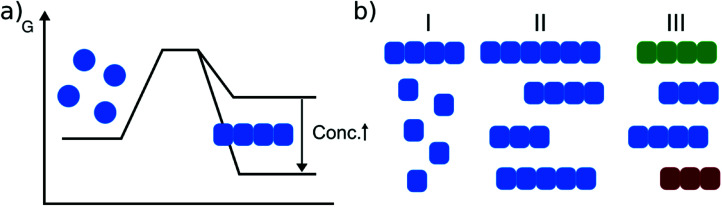
Fig. 1. Amyloid thermodynamics. (a) The position of the equilibrium between the soluble and fibrillar state depends strongly on the total protein concentration. (b) Amyloid fibril equilibria need to be defined with respect to I: free monomer concentration, II: fibril length distribution and III: populations of different fibrillar polymorphs (illustrated in different colors).

Probing and modulating protein stability

The conceptually simplest way to quantify the stability of a folded state of a protein is to determine the population of the unfolded state(s). However, in most cases this is not easily possible, because even a modest stability of the folded state of only 20 kJ mol⁻¹ translates into a ratio of the populations of the unfolded to folded state of 0.0003. Sophisticated fluorescence²¹ and NMR²² experiments can determine the populations of higher energy states in the few percent range, but this becomes very challenging for populations significantly smaller than this order of magnitude. Therefore, various methods have been established to increase the populations of the unfolded state by applying conventional or generalised thermodynamic forces. Proteins can be most literally unfolded by mechanical force, using an atomic force microscope (AFM²³) or optical tweezers.²⁴ In such experiments, most commonly one end of the protein is attached to a surface and the other end to the AFM cantilever or a bead in an optical trap, which allows us to acquire force-distance curves. Such experiments however, while allowing a relatively detailed characterisation of the free energy landscape,²⁵ are difficult to perform and analyse. More common is the application of generalised thermodynamic forces in the form of changes in temperature, pressure and chemical potential (see Appendix 1). High temperature and very high pressure are both found to efficiently destabilise proteins, even though organisms living at high temperatures and hydrostatic pressures have proteins that are adapted to these conditions.¹⁶ The observation that most folded proteins are sensitive to very high pressure⁹ suggests that the partial molar volume of the unfolded state is smaller than that of the folded state, which contains nanoscopic cavities. A change in chemical potential amounts in practice to a change in the solution composition and a wide range of changes in solution conditions have been shown to destabilise the folded state of the protein, such as organic solvents (modulation of the hydrophobic effect and electrostatic interactions),²⁶ chemical denaturants²⁷ (competition with intramolecular H-bonds) and extremes of pH (ref. 28) (intramolecular electrostatic repulsion). The most commonly employed method of chemical protein unfolding is by denaturants, such as urea or guanidinium chloride (GndHCl). It has been found empirically that the free energy of folding is to a good approximation a linear function of the denaturant concentration in many cases and this linear relationship can be used to determine the free energy of folding by extrapolation to zero denaturant.²⁹ It has to be noted that all types of protein unfolding experiments yield very different results if any covalent bonds, notably disulfide bonds, are broken prior to the experiment³⁰ because none of the denaturation methods described above is, as such, able to break covalent bonds.

The thermodynamics of some non-amyloid protein filament formation

Filamentous protein assemblies are ubiquitous in nature, and fulfil a range of important functions, for example for the cytoskeleton (actin- and tubulin-like proteins) or for cellular motility (flagellin). Even though an increasing number of biologically functional amyloid fibrils are being discovered, many of the functional protein filaments found in biology do not fulfil the structural definitions of amyloid fibrils. In fact, the systematic biophysical study of non-amyloid protein filaments significantly pre-dates that of amyloid fibrils. The time period from the 1950s to the 1970s was particularly active in this respect; notably the early work by Fumio Oosawa and co-workers should to be mentioned in this context.³¹ The reason why I bring up these non-amyloid protein polymers here is that they form a natural link between protein folding thermodynamics and amyloid thermodynamics, in that these types of polymers are formed from pre-folded building blocks that change their structure only marginally, if at all, when incorporated into a fibrillar polymer. In agreement with this basic feature, the functional protein polymers listed above, as well as sickle hemoglobin fibrils, which are also formed from essentially native building blocks, often display a well-defined stability optimum as a function of temperature.^32,33 The rapid loss in polymer stability already at moderate temperatures just above the physiological range can often be directly linked to a loss in stability of its building blocks. Other than temperature, the stability of functional polymers is also a function of chemical composition, particularly often also the concentration of divalent ions and of the energy currency ATP (or GTP). This feature can be explained by these polymerisation reactions being under tight cellular control and the expenditure of ATP allows the reversal of a spontaneous process. The solubilities, i.e. equilibrium monomer concentrations of polymers, such as actin and tubulin are of the order of hundreds of nM to a few μM.^33,34 Notably, the polymerisation of these proteins is able to generate a force,³⁵ and hence perform useful work for the cell, if the concentration of the growth-competent/activated monomer is maintained above the equilibrium concentration.

The thermodynamics of amyloid fibril formation

Amyloid fibril formation, particularly from disordered pre-cursors (‘misfolding’), can be considered a combination of protein folding and functional polymerisation. A key difference between folding and misfolding is the loss of translational and rotational entropy of the monomer upon addition to a fibril end. Historically, it has been surprisingly difficult to provide a good estimate for the translational entropy of a molecule in solution.³⁶ The main approach has been to apply the Sackur–Tetrode equation for the translational entropy of a gas molecule that depends logarithmically on the volume of the container in which the molecule is confined. In the case of a molecule in solution, very different relevant volumes have been proposed, ranging from the volume of the cage of water molecules around the solute all the way to the volume of the respective reaction vessel (e.g. test tube, plate well etc.), the latter leading to the same translational entropy of a molecule in solution as a molecule in the gas phase.^36,37 It is however generally recognised that the unmodified Sackur–Tetrode equation overestimates the translational entropy of a molecule in solution.^36,37 Rotational entropy of molecules in solution, on the other hand, is thought to be relatively well described by the corresponding expression for the gas phase.³⁷ Independent of the exact magnitude of the volume available to a freely diffusing protein molecule, the loss of translational entropy it experiences upon binding to another molecule depends on the overall concentration of the solution. The more dilute the solution, the greater the cost in translational entropy associated with binding and hence the less favourable the binding interaction, i.e. the less favourable the formation of an amyloid fibril (Fig. 1a). This factor is added to the loss in rotational and conformational entropy of the peptide chain that most amyloid proteins will experience upon binding to another monomer or a fibril end and adopting the conformation of the fibrillar state. These combined losses in translational, rotational and conformational entropy may in part be offset by an increase in solvent entropy upon binding, due to the burial of hydrophobic sequence regions. Independent of the exact magnitude by which the entropy of a protein molecule decreases upon binding to an amyloid fibril, this decrease is ultimately responsible for why amyloid fibrils (indeed, all non-covalently-bound molecular complexes) become unstable below a certain critical concentration, where the loss in entropy can no longer be compensated by the favourable intermolecular interactions. At the typical concentrations used in in vitro experiments, which can be more than two orders of magnitude above the solubility, this concentration dependence is often difficult to detect. Furthermore, the dissociation kinetics of amyloid fibrils upon dilution can be so slow that they may appear stable at low concentration, but are in reality only metastable. Indeed, the question whether or not a given system of amyloid proteins has reached equilibrium or not is important for an accurate characterisation of its thermodynamics.

Equilibrium experiments

Relatively early in the systematic study of amyloid fibrils it has been proposed that the amyloid state could be the true equilibrium state of polypeptides, the free energy minimum, at finite concentrations.³⁸ But what exactly does it mean for a solution of amyloid-forming protein molecules to have reached equilibrium? There are three main aspects to consider: free monomer concentration, length distribution and polymorph populations (Fig. 1b). All molecular systems that are capable of forming multimers, from micelles over virus capsids to amyloid fibrils, have a well-defined equilibrium solubility, i.e. the concentration of free soluble building blocks converges against a constant value, c_crit (the ‘critical concentration’), as the total concentration tends towards large values³⁹ (Fig. 2a). For highly cooperative structures that are defined by geometrical constraints of the building blocks, such as micelles and virus capsids, there is an abrupt transition between a linear increase in monomer concentration below c_crit and a constant monomer concentration above c_crit. Amyloid fibrils are linear polymers and it appears that only their width but not their length is subject to geometrical constraints, in that only certain well-defined widths, but a continuum of lengths, are normally observed. Therefore, amyloid systems can be expected to reach a constant free monomer concentration as a function of total concentration more gradually than micellar systems (Fig. 2a). However, at total concentrations 1–2 orders of magnitude above the limiting c_crit, the concentration of free monomer converges towards a constant value, c_crit. Considering the length distribution of fibrils, true equilibrium corresponds to a state in which it no longer changes. Nucleation, growth and fragmentation of fibrils are all processes that influence the evolution of the length distribution. The simplest model of a linear polymerisation equilibrium (no explicit time dependence) is the isodesmic model^39–41 with a single equilibrium constant for monomer addition to all species, which produces an exponentially decreasing length distribution. This also corresponds to the long term solution of nucleated polymerisation models, with explicit time dependence.⁴² In general, the free energy of the system depends only weakly on the shape of the length distribution for a given degree of polymerisation (i.e. free monomer concentration), which means that the driving force towards optimisation of the length distribution is weak, once c_crit has been reached. It is a common feature of amyloid systems that different molecular species can co-exist. For example oligomeric structures can co-exist with fibrils⁴³ and different types of fibrils (‘polymorphs’) can be found in the same sample.⁴⁴ Furthermore, for short peptides, a coexistence and competition between amyloid fibrils and microcrystals can be observed in some cases, e.g. for GNNQQNY.⁴⁵ The latter scenario corresponds to a competition between favourable crystal contacts and torsional energy caused by forcing the peptide molecules into a periodic crystal against their natural tendency to twist.⁴⁶ If the different types of aggregates have different stabilities, equilibrium corresponds to a state in which the populations of these species reflect their relative stabilities: the most stable structure will be the dominant one at equilibrium, according to the Boltzmann distribution. What makes amyloid thermodynamics so challenging to study is the fact that all three factors mentioned above are difficult to quantify accurately, even though much progress has been made in the identification of polymorph populations by high resolution imaging methods, particularly cryo-electron microscopy⁴⁴ and atomic force microscopy.⁴⁷ Furthermore the three relevant features with respect to which equilibrium can be defined are subject to kinetic factors that makes it difficult to ensure that equilibrium has actually been reached. In particular the nucleation rate, i.e. the rate of formation of new fibrils, is a critical factor in the establishment of equilibrium with respect to monomer concentration and length and polymorph distribution. If all rate constants are low, the equilibrium monomer concentration is only slowly approached. For initial monomer concentrations very close to c_crit, the system can in some cases remain almost indefinitely in a metastable state with c_sol > c_crit due to high nucleation barriers⁴⁸ (Fig. 2b). A system with a combination of low nucleation and fragmentation rate constants with a high growth rate constant can reach c_crit rapidly but leads to a skewed length distribution with few but very long fibrils. Furthermore, if a less stable fibril form has a much faster nucleation rate than a more stable one (which Ostwald's rule of stages predicts to often be the case⁴⁹), it may dominate the system for a very long time. Indeed, both the length distribution and the polymorph distribution are so strongly defined by kinetic factors that they may almost never reach equilibrium values in realistic settings, particularly in vivo. It is, however, possible to significantly accelerate the approach to the equilibrium of the fibril length distribution in in vitro experiments through mechanical action, which has been shown to act differently on different types of amyloid systems.⁵⁰

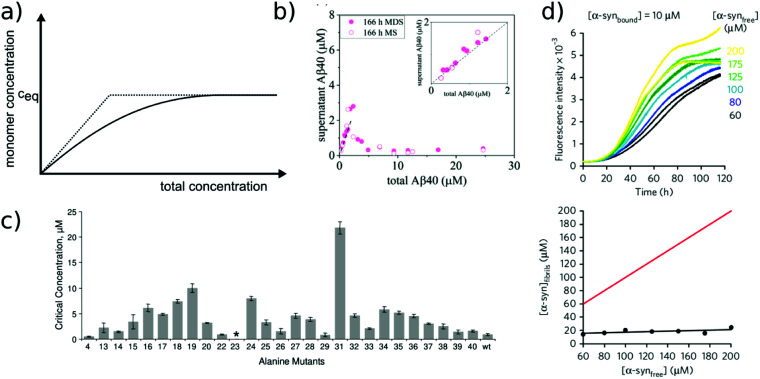
Fig. 2. Free monomer concentration as a measure of amyloid fibril stability. (a) Depending on the degree of cooperativity of a self-assembling system, a constant monomer concentration as a function of total concentration is reached very abruptly (dotted line, highly cooperative, micellar systems) or more gradually (solid line, e.g. linear polymers, such as amyloid fibrils). (b) In real amyloid systems (here Aβ (1–40)), the free monomer concentration can remain almost indefinitely in a metastable state due to high nucleation barriers preventing the formation of fibrils at concentrations right above c_crit. Reproduced from ref. 48 with permission from Elsevier, copyright 2021. (c) If the solubilities of systematically designed point mutations of an amyloid peptide (Aβ (1–40)) are measured, residue-specific information can be obtained about the importance of different sequence regions for the stability of the fibrillar fold. Reproduced from ref. 54 with permission from Elsevier, copyright 2006. (d) In some scenarios (here α-synuclein in the presence of DMPS liposomes), kinetically trapped states can be reached at which the concentration of amyloid fibrils does not depend on the initially added monomer concentration, but is limited by the lipid concentration (bottom, the red line indicates the concentration of fibrils that would be expected if all the initially added monomer was converted). In this case the free monomer concentration at the plateau of the kinetic experiment followed by thioflavin-T fluorescence (top) is not a measure of the stability of the amyloid fibrils. Reproduced from ref. 56 with permission from Springer Nature, copyright 2015.

Despite the recent advances in the quantification of polymorph populations and length distributions, we will nevertheless in the following focus on the (pseudo-)equilibrium with respect to the free monomer concentration, which is the most accessible, as well as the most informative thermodynamic parameter. It should however be noted that the three characteristics with respect to which equilibrium can be defined are not fully decoupled. For example, different fibril strains/morphologies may feature different equilibrium solubilities. Furthermore, for very short fibrils, the equilibrium monomer concentration may depend on the actual length distribution, due to finite end effects.³⁹

The free monomer concentration as a measure of amyloid fibril stability

The free monomer concentration at the end of an amyloid fibril formation reaction is often routinely quantified in order to probe the degree of conversion into fibrils. Such measurements have also, albeit less frequently, been used for the quantification of the thermodynamic stability of the fibrils.^48,51–53 A benchmark in this context is an extensive study of the solubilities of a large number of sequence variants of the Aβ peptide by the group of Ronald Wetzel⁵⁴ (Fig. 2c). Such experiments are usually performed by physically separating the aggregates from the monomer, e.g. by centrifugation, followed by quantification of the concentration in the supernatant. Whether or not all species except monomers are spun down in such experiments is determined by the applied centrifugation force. Ultracentrifugation at several tens of thousands of g is usually sufficient to ensure that most aggregated species are no longer found in the supernatant. When such experiments are performed with samples of amyloid proteins that, based on their kinetic profiles, appear to have reached equilibrium, the soluble concentrations of the monomer can vary dramatically, from tens of micromolar to virtually undetectable by classical means, i.e. nM or below. A key question in such scenarios is whether or not a given sample has actually reached equilibrium with respect to the free monomer concentration, something that is not always easy to establish. The most reliable way to ensure that equilibrium has in fact been reached is to demonstrate that the same free monomer concentration is reached, whether one starts with an excess of fibrils or an excess of monomer.⁵¹ When very high free monomer concentrations of tens of micromolar or higher are detected in cases where amyloid fibrils are formed by full length proteins, equilibrium should always be verified because such equilibrium free monomer concentrations would correspond to amyloid fibrils of an unusually low thermodynamic stability. However, for short peptide systems, the overall stabilities are generally lower and equilibrium concentrations in the hundreds of μM to mM range are not unusual.⁵⁵

At least in some cases, it has been demonstrated that amyloid systems can be kinetically trapped in states with monomer concentrations significantly above the equilibrium concentration, e.g. in the case of lipid-induced aggregation of α-synuclein⁵⁶ (Fig. 2d). In such cases, mechanical perturbation of the sample by sonication or vigorous stirring assists the approach to equilibrium, as it released fresh growth competent fibril ends. If it can be established that equilibrium has indeed been reached, then the free monomer concentration, i.e. the solubility, is a direct measure of the thermodynamic stability of the fibrils. If the total protein concentration is significantly higher than the measured free monomer concentration [m], the free energy difference between the monomer and fibril state, ΔG⁰, can be directly quantified from 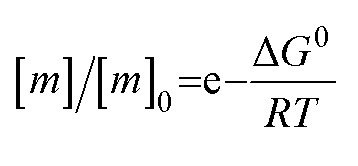, where [m]₀ is a reference concentration, chosen to be 1 M for convenience. For a given amyloid system, the free monomer concentration at equilibrium depends on a variety of factors, such as ionic strength, pH and temperature.⁵⁷ In particular electrostatic interactions have been found to be very important for amyloid fibril stability,^41,58–61 as is to be expected from a homopolymerisation reaction that leads to the formation of parallel in register intermolecular β-sheet structures in most cases.⁶² This structural arrangement can lead to stacks of equal charges along the entire fibril, a highly electrostatically unfavourable arrangement. Indeed, there is strong evidence from multiple types of experiments, such as calorimetry,⁶³ electrophoretic mobility⁶⁴ and direct pH change measurements,⁶⁵ that amyloid fibrils have a significantly lower net charge than expected from the net charge of the isolated monomeric building blocks in solution. The decrease in net charge upon incorporation into an amyloid fibril can be explained through shifts in the pK_a value or counterion condensation, the driving force for which is provided by the (non-electrostatic) favourable interactions that stabilise the fibril. In some amyloid and related systems (e.g. short aromatic peptide assembly), it has been shown that the free monomer concentration decreases in steps, rather than in a continuous manner, during the assembly process.⁶⁶ Importantly, this type of behaviour often requires direct quantification of the residual free monomer over the aggregation time course, as it can be masked if for example only Thioflavin-T (ThT) fluorescence is used to follow the progress of the reaction.⁶⁷ This can be interpreted within the context of Ostwald's rule of stages,⁴⁹ in that the system undergoes a series of transitions between distinct states, in which different molecular species are populated. The step-wise decrease in the free monomer concentration corresponds to a step-wise decrease in free energy, from less stable to more stable structures. A successive population of different types of aggregated species with increasing stability, e.g. oligomers, protofilaments and finally mature fibrils, is observed in many amyloid systems,^68–72 and it is often challenging to study the species with intermediate stability, due to their transient nature.⁶⁸ The transition from less stable to more stable assemblies has recently started to receive increased attention in the context of the maturation of dense condensate droplets formed by proteins that undergo liquid–liquid phase separation (LLPS). While LLPS is fully reversible in many cases, some proteins that can undergo LLPS are found to also subsequently transition from reversible droplets into irreversible aggregates over time.⁷³ This conversion is often defined by the associated decrease in diffusional dynamics of the protein molecules inside the evolving droplet, e.g. through fluorescence recovery after photobleaching (FRAP) experiments. A new experimental method, CapFlex, has recently been presented in this context that allows to follow directly this conversion reaction by monitoring the time evolution of the free monomer concentration.⁷⁴ We close this section with the general remark that amyloid fibril formation is expected to only occur to a very small (but nevertheless non-zero) extent at concentrations below the solubility, i.e. below the equilibrium monomer concentration, as defined by the limit of free monomer as the total concentration tends towards infinity⁴⁰ (Fig. 2a). This leads to the question how amyloid fibrils can form in vivo from protein species that are present at exceedingly low concentrations, below the solubility established in in vitro experiments, such as the amyloid β peptide (present overall at pM concentrations⁷⁵). While this is a topic that requires additional investigation, a possible explanation is that local up-concentration in vesicles⁷⁶ or on surfaces, particularly lipid bilayers, can lead to increased local concentrations that can reach values above the solubility, enabling amyloid fibril formation.^77,78 Molecular crowding by the high concentrations of other macromolecules is likely to also play an important role in rendering the thermodynamics of amyloid fibril formation more favourable at low concentrations. However, crowding effects on amyloid thermodynamics also require more detailed experimental study, given that most studies of crowding effects so far have focused on kinetics.⁷⁹

Chemical depolymerisation

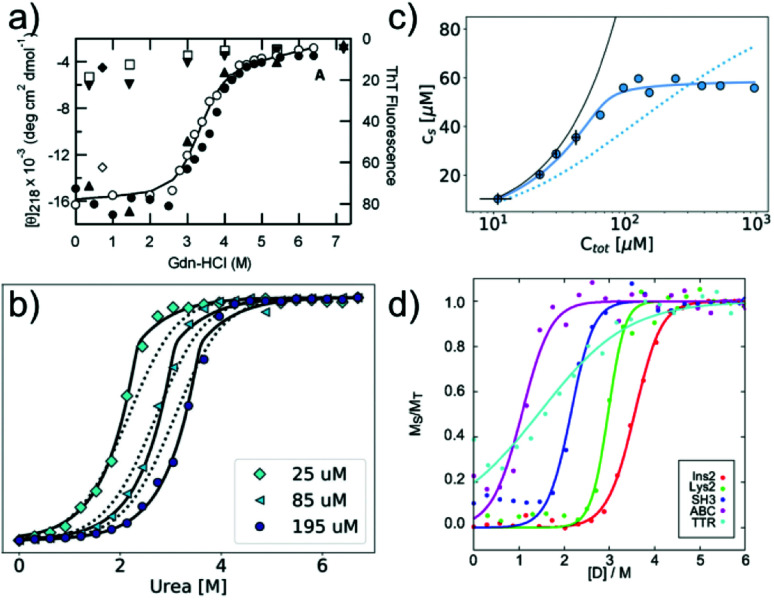
In many cases, the free monomer concentration at equilibrium is too low to be reliably measured. This corresponds to the equivalent situation in protein folding where the population of the unfolded monomer is too low to be detected under native conditions. The solution found for protein folding, i.e. chemical denaturation, can also be applied for amyloid fibrils, and this has been pioneered by Yuji Goto's group⁸⁰ (Fig. 3a). In such experiments, the soluble concentration of protein is plotted as a function of denaturant concentration, leading to a sigmoidal curve. The soluble concentration can be determined by direct measurement after centrifugation,⁸¹ or else spectroscopically, using circular dichroism, intrinsic fluorescence or thioflavin-T fluorescence.⁸⁰ Spectroscopic determination of the soluble protein population has the advantage that physical separation between aggregates and monomer is not necessary. In these types of experiments, the same denaturants are being used as in conventional protein denaturation, e.g. urea, GndHCl or GndSCN.⁸¹ While the relative strength of denaturants is similar to the case of protein unfolding, in that e.g. GndSCN is stronger than GndHCl,⁸¹ it has also been found that in some cases urea can be a stronger denaturant than GndHCl for amyloid fibrils.⁴¹ This is not usually observed for folded proteins and highlights very clearly the different importance of unfavourable electrostatic interactions in amyloid fibril formation vs. protein folding. In the former, the nature of GndHCl as a salt stabilises the fibrils at moderate concentrations relative to urea that has a purely destabilising effect. Chemical denaturation of amyloid fibrils and related aggregates can be used in a qualitative manner,⁸²e.g. to assess the stabilities of different fibril strains^83,84 or the effect of sequence changes,^85,86 by comparing the denaturation mid-points. However, it is also possible to perform a more quantitative analysis. Such an analysis needs to be based on the nature of amyloid fibril formation as a polymerisation process. The simplest model of equilibrium polymerisation is the so-called isodesmic linear polymerisation model, which assumes a single equilibrium constant for all monomer addition reactions, from dimer formation to n-mer formation with n reaching infinity.⁴⁰ Using the same linear free energy dependence on denaturants as is customary in protein unfolding, it is possible to derive an equation for the analysis of amyloid depolymerisation curves and fit the depolymerisation data^41,80,81 (Fig. 3a).

Fig. 3. Chemical depolymerisation of amyloid fibrils. (a) One of the earliest such data sets, in which β2-microglobulin amyloid fibrils have been destabilised by GndHCl and the depolymerisation has been followed by CD spectroscopy and ThT fluorescence. Reproduced from ref. 80 with permission from Elsevier, copyright 2004. (b) Global fit of chemical depolymerisation (by urea) of glucagon amyloid fibrils, followed by intrinsic fluorescence. It can be seen that a better fit is achieved with the cooperative linear polymerisation model (solid line) than with the simpler isodesmic linear polymerisation model (dotted line). (c) The dependence of the soluble concentration on the total concentration of glucagon amyloid fibrils is measured at 3 M urea (compare with panel b). In this type of experiment, the isodesmic model does not describe the data. (b) and (c) Reproduced from ref. 41 with permission from the RSC, copyright 2019. (d) Chemical depolymerisation analysis of different amyloid peptides and proteins revealed that the per-residue stability of amyloid fibrils is the highest for short sequences. Reproduced from ref. 81 with permission from the ACS, copyright 2019.

An important difference between the mathematical expression to be used for protein unfolding vs. depolymerisation experiments is that the latter explicitly contains the total protein concentration. This means that amyloid fibril depolymerisation curves are protein concentration-dependent. Individual depolymerisation curves can be very well fitted to the isodesmic model. In this context, it should be kept in mind that it has been well-established, particularly also in the amyloid field, that fitting individual sigmoidal data sets (e.g. kinetic time courses) to a sigmoidal mathematical expression is not a very stringent test of the given mechanistic model, and that global fits are usually needed.⁸⁷ The overall validity of the model is therefore not automatically established by the ability to fit amyloid fibril depolymerisation data to the isodesmic linear polymerisation model. Nevertheless, this model has been applied in a landmark study where depolymerisation curves of a range of proteins were analysed and some general principles of amyloid fibril stability were discovered⁸¹ (Fig. 3d). It was found that amyloid stability depends on the sequence length, and the stability per amino acid is the highest for short sequences, presumably due to less probability of frustrated interactions in short sequences. Also it was proposed that many amino acid sequences occur in vivo at concentrations that correspond to a metastable state with respect to their solubility. In other words, the formation of amyloid fibrils would correspond to a thermodynamically favourable reaction at these concentrations.⁸⁸ In a recent study, the validity of the isodesmic model has been more thoroughly tested by performing chemical depolymerisation experiments at different total protein concentrations.⁴¹ It was found that depolymerisation curves are indeed strongly concentration dependent, and that the isodesmic model cannot reproduce all the features of the data set if it is globally fitted (Fig. 3b). The extension of the model to include a different equilibrium constant for the initial association reactions (cooperative linear polymerisation model⁴⁰) improves the fits, which is also to be expected simply due to the introduction of additional free parameters. However, it was also found that in a variation of the conventional chemical depolymerisation experiments (protein concentration kept constant, denaturant concentration varied), where the denaturant concentration was kept constant at an intermediate value and the total protein concentration was varied, the isodesmic model was qualitatively unable to model the data⁴¹ (Fig. 3c). This finding provides evidence that the isodesmic model is an oversimplification and that depolymerisation experiments at different protein concentrations reveal its shortcomings.⁴¹ In the same study, it was also shown that urea is the denaturant of choice if electrostatic interactions in amyloid fibrils are to be probed, due to its neutral nature that does not screen electrostatics. By measuring the magnitude of electrostatic interactions that destabilise amyloid fibrils, far-reaching conclusions could be drawn. Notably, it was shown that the fibrillar state features similar albeit slightly stronger repulsive electrostatic interactions as the transition state for fibril growth.⁴¹ This finding provides evidence for the transition state of amyloid fibril growth being product like. Chemical depolymerisation of amyloid fibrils as a means to probe their thermodynamic stability is applicable in many cases, but it has also been reported that some types of amyloid fibrils resist even the most powerful denaturants, e.g. bacterial functional amyloid involved in biofilm formation. Even for such systems, solution conditions can be found that ultimately dissolve the fibrils, such as formic acid.⁸⁹ However, in such cases, the free energy of fibril formation is probably not well approximated as a linear function of the dissociating compound, and hence meaningful thermodynamic parameters are more difficult to extract. Similar to the case when the free monomer concentration is measured, it needs to be ensured in depolymerisation experiments that equilibrium has indeed been reached in all samples. Equilibration times can vary from hours to days, depending on the denaturant concentrations.^41,81 Verification that equilibrium has been reached can be achieved by approaching it from different sides, and by perturbing the system and observing its relaxation back to the equilibrium state.⁸¹ It has been reported that the age of the fibrils can have a significant effect on their susceptibility to denaturant.⁸⁴ This effect could be due to a bona fide ageing/maturation process of the fibrils, which may also involve increased higher order assembly.⁹⁰ It has, however, also been shown that intermolecular cross-links between the monomers inside a fibril can render them significantly more resistant towards chemical depolymerisation.⁹¹ Such covalent interactions (dityrosine links) were artificially introduced by UV radiation in this particular study,⁹¹ but similar effects could also arise naturally, e.g. through disulfide bond shuffling, oxidation etc. In such cases, the measured stability against chemical depolymerisation no longer corresponds to a well-defined thermodynamic property.

Non-equilibrium experiments

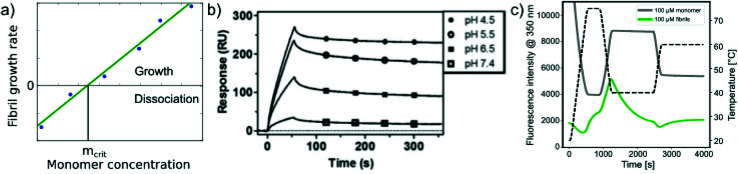
In addition to measuring the position of the equilibrium between the free monomer and the available fibrils (in the presence or absence of denaturants), the thermodynamics of the fibril growth reaction as the main driver of fibril thermodynamics can also be defined from measurements of growth and dissociation rates.^57,60,92 Growth rates can be measured by a range of different techniques, mostly in scenarios where seed fibrils are added, e.g. by ThT fluorescence or surface-based biosensing.⁹³ Fibril dissociation is less straightforward to measure because it is very slow under most conditions. A particularly suitable experimental platform is provided by biosensors, such as surface plasmon resonance (SPR) sensors^60,92 or the quartz crystal microbalance (QCM).⁵⁷ Using these platforms, a given constant ensemble of seed fibrils can be exposed to different monomer concentrations, and also rinsed with pure buffer. If the growth rate is measured systematically at decreasing monomer concentrations, the equilibrium solubility can be defined as the monomer concentration at which neither net growth nor net dissociation of fibrils is observed⁵⁷ (Fig. 4a). Such experiments were for example used to demonstrate a strong dependence of the stability of amyloid-β fibrils on solution pH (ref. 60) (Fig. 4b). An advantage of such measurements compared to direct determination of c_crit is that it is easier to prepare a protein solution at a given (low) concentration, and to measure the growth rate with a sensitive biosensor, than to accurately determine very low, unknown concentrations. An additional benefit in such biosensing experiments is that the affinity of the monomer for the surface of amyloid fibrils can be measured. The attachment of the monomer to the fibril surface is the first step in the secondary nucleation process, whereby new fibrils form on the surface of the existing ones. Such surface affinity measurements have been performed for the amyloid β peptide (1–40 (ref. 94) and 1–42 (ref. 95)) and it was found that the affinity of the monomer for the fibril surface is approximately two orders of magnitude lower than that for the fibril ends. Fibril growth and dissociation can also be studied by differential scanning fluorimetry (DSF), using intrinsic Trp fluorescence, e.g. by subjecting amyloid fibrils to sudden temperature jumps or to continuous temperature ramps⁵⁷ (Fig. 4c). The degree of dissociation of the fibrils in temperature ramps at any given temperature depends on the temperature scan rate and this can be used to determine the dissociation rate, as well as their temperature dependence.⁵⁷ It was found that the thermodynamic stabilities determined through these non-equilibrium DSF experiments agreed well with the results from equilibrium depolymerisation, confirming that both types of experiments essentially probe the interaction between fibril ends and monomers.⁵⁷

Fig. 4. Non-equilibrium experiments of growth and dissociation to assess amyloid fibril stability. (a) The monomer concentration at which amyloid fibrils are observed neither to grow nor to dissociate corresponds to their equilibrium solubility, c_eq. (b) The growth and dissociation rates of Aβ (1–40) amyloid fibrils attached to an SPR sensor surface were measured at different pH values. It was found that the growth rate, and ultimately the thermodynamic stability of the fibrils greatly increased as the pH was lowered. Reproduced from ref. 60 with permission from the ACS, copyright 2014. (c) Differential scanning fluorimetry experiments to probe amyloid fibril growth and dissociation rates. A temperature variation scheme is shown that includes a brief period at 75 °C, followed by equilibration at 40 °C (lower temperature) and a rapid change to 65 °C (upper temperature), where the dissociation is monitored. Fluorescence emission measured at 350 nm is shown for fibril (F) and monomeric reference (M) samples. The interrupted line indicates the measurement of the initial slope. If the upper temperature is systematically varied, the dissociation rates can be determined at these different temperatures.⁵⁷ Reproduced from ref. 57 with permission from Elsevier, copyright 2021.

Amyloid fibrils can generate force through their growth and the quantification of this force represents another handle on amyloid thermodynamics, similarly as is the case for functional protein polymers, such as actin and tubulin.³⁵ Such experiments were realised by trapping amyloid spherulites (gel-like particles with radially arranged amyloid fibrils⁹⁶) in microfluidic devices and measuring the bending of PDMS pillars against which the growing amyloid fibrils are pushing.⁹⁷ It was found that amyloid fibril growth can generate similar forces to the growth of functional protein polymers, which is consistent with the comparable stabilities of these types of structures. It has also been attempted to measure the force that is necessary to remove a monomer from a fibril end or from inside a fibril, by force spectroscopy with AFM⁹⁸ or optical traps.⁹⁹ Such experiments are, however, extremely difficult to perform in a highly controlled manner and therefore only little quantitative insight into amyloid thermodynamics has been obtained from atomic force spectroscopy to-date. Lastly, another scenario should be mentioned in which the non-equilibrium behaviour of amyloid fibrils allows insight to be generated into their thermodynamics. In addition to the fact that different numbers of individual amyloid protofilaments can assemble in various ways into ‘mature’ fibrils, these fibrils can themselves undergo higher order assembly into larger clusters. This corresponds to the flocculation process of unstable colloidal suspensions.³⁹ Such higher order assembly is particularly influenced by solution pH and ionic strength,^100,101 and can be followed e.g. by microscopy¹⁰⁰ or scattering techniques.¹⁰¹ The finding that a fibrillar suspension undergoes such higher order assembly spontaneously under some conditions indicates that individual suspended fibrils represent an unstable state. The fact that amyloid fibrils are mostly found in dense deposits in vivo, such as plaques, tangles and Lewy bodies, can presumably be partly explained by this tendency of fibrils to cluster.¹⁰²

Thermodynamic signatures of amyloid fibrils

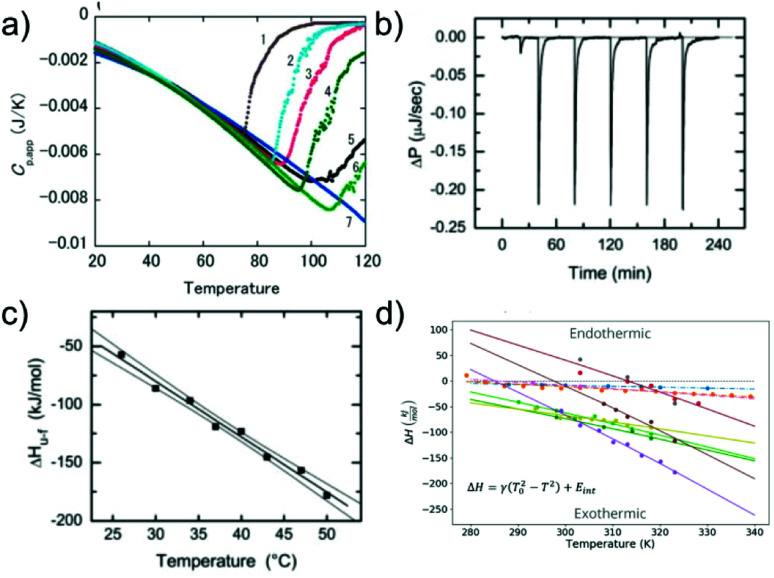
Similar to the case of protein folding, it is also of interest to investigate the thermodynamic signatures, i.e. the enthalpy-entropy balance of amyloid fibril formation. Calorimetry is the method of choice to obtain this type of experimental insight. Both protein folding and misfolding can be studied by differential scanning calorimetry, in which the temperature is scanned and the difference in heat absorption between a sample and reference cell is observed. Such experiments in general reveal a significantly higher thermal stability of amyloid fibrils than the corresponding native state of the building block (if it is folded under some conditions).^58,103 The thermal ‘unfolding’ or rather depolymerisation of amyloid fibrils is also generally found to be endothermic^58,104 (Fig. 5a) and strongly dependent on the scan-rate⁵⁷ and the protein concentration.⁵⁸ In contrast to protein folding, which is often very fast and not easily amenable to isothermal titration calorimetry (ITC), the much slower nature of seeded fibril growth makes it possible to be characterised by ITC. ITC allows us to probe the enthalpic signature of fibril growth at different temperatures and therefore also the associated heat capacity. It is generally found in most such experiments that amyloid fibril growth, similar to protein folding, is exothermic and associated with a significant negative heat capacity^61,105–109 (Fig. 5b and c). This means that fibril growth at higher temperature releases more heat than at lower temperature. Negative heat capacities in protein folding and association reactions are often attributed to the hydrophobic effect, even though it has also been proposed that other types of weak non-covalent interactions can lead to the same signature.¹² In selected cases, most notably α-synuclein, it has even been observed at moderate to lower temperatures that amyloid fibril growth can become endothermic.^61,108 Non-zero heat capacities of amyloid fibril growth automatically imply a parabolic stability profile of the fibrils, with a maximum in stability at intermediate temperatures, predicting a significant destabilisation of fibrils at low temperatures. α-Synuclein amyloid fibrils are notable as one of the very few amyloid systems in which the equivalent of protein cold denaturation, i.e. cold depolymerisation, was observed.^61,108,110 Overall, α-synuclein amyloid fibrils are consistently found in multiple studies to have only moderate stability under physiological conditions. This probably explains why they can be sufficiently destabilised by lower temperatures to lead to measurable dissociation. Similar to folded proteins, many amyloid fibrils may be slightly destabilised by cold temperatures, but if this change in stability does not translate into a measurable increase in the monomer concentration, it is difficult to detect. As an example, if a given amyloid fibril becomes destabilised from −50 kJ mol⁻¹ to −45 kJ mol⁻¹, its solubility changes from about 2 nM to 15 nM, whereas if it is destabilised by the same absolute magnitude, but from −30 to −25 kJ mol⁻¹, the solubility changes from 6 μM to 45 μM (using k_BT ≈ 2.5 kJ mol⁻¹). Scenario 1 is much more difficult to detect experimentally than scenario 2.

Fig. 5. The enthalpic signatures of amyloid fibril formation and dissociation. (a) Differential scanning calorimetry (DSC) experiments of β2-microglobulin amyloid fibrils at different NaCl concentrations, from lowest (1) to highest (7). The data show a strong dependence of amyloid thermal stability on salt concentration, as well as a strongly endothermic signature upon dissociation. Reproduced from ref. 58 with permission from Elsevier, copyright 2005. (b) Raw data of isothermal titration calorimetry (ITC) of β2-microglobulin amyloid fibril growth. Small portions of monomer solution are repeatedly injected into a suspension of fibrils. (c) If experiments such as the one shown in (b) are performed at different temperatures, the enthalpies of fibril growth can be determined at these different temperatures, and hence also the heat capacity ΔC_p of the elongation reaction. (b) and (c) Reproduced from ref. 106 with permission from the ASBMB, copyright 2004. (d) When the heat capacities of the elongation reaction of several different amyloid systems are quantified, it is found that they are negative in all cases, i.e. that the enthalpy of the reaction becomes more negative at higher temperatures.⁶¹ Further analysis shows that the magnitude of the heat capacity correlates with the buried hydrophobic surface area upon fibril growth. Reproduced from ref. 61 with permission from the PLoS, copyright 2020.

Similar to the case of protein folding, based on calorimetric data it has also been proposed for amyloid fibril growth that the magnitude of the heat capacity depends on the buried hydrophobic surface area upon addition of the monomer to the fibril end⁶¹ (Fig. 5d). Temperature as a generalised thermodynamic force to probe a given molecular system has the advantage of being easily controllable. The significant heat capacity in biomolecular interactions reflects the fact that most relevant interactions have a strong temperature dependence, rendering the interpretation of calorimetric or van't Hoff experiments often non-trivial. It has long been recognised that pressure is a conceptually simpler generalised force, and pressure effects can be straightforwardly interpreted as changes in the partial molar volume upon reaction. Inspired by pressure-induced protein unfolding, it has been shown in a range of studies that amyloid fibrils can be dissociated by the application of high hydrostatic pressures.^111–113 This finding confirms that while the amyloid state is on the whole a compact state of the polypeptide chain, it nevertheless also contains voids that render it susceptible towards high pressure. However, the changes in the partial molar volume upon amyloid fibril formation are so small that very high hydrostatic pressures (hundreds of atmospheres) are required to observe pressure-induced amyloid fibril depolymerisation. This leads to the requirement for complex high pressure equipment that is not widely available, explaining the relative scarcity of such studies.

How can amyloid fibril formation be reverted?

The main relevance of a discussion of amyloid thermodynamics, other than to obtain a better fundamental understanding of these fascinating self-assembled structures, is provided by the question of the long term fate and reversibility of amyloid fibrils in a biological context. The notion that amyloid fibrils are very stable structures and essentially irreversible stems from the long lived nature of disease-related amyloid depots, as well as the requirement for strong denaturants to dissolve amyloid fibrils in vitro. However, these features do not seem to be inextricably linked to the amyloid state as such. In a range of cases it was found that a sudden change in solution conditions (e.g. pH, protein concentration) can lead to rapid dissolution of amyloid fibrils, e.g. in the case of peptide hormones stored as amyloid fibrils,² or α-synuclein¹¹⁴ or β2-microglobulin¹¹⁵ fibrils that shed oligomers upon change in solution pH. Such sensitivity towards solution conditions is likely to have evolved by natural selection in the case of functional amyloid. Disease-related amyloid protein sequences often lead to disorders after the end of the reproductive life of the affected organism and hence are less subject to natural selection for reversibility of their associated amyloid fibrils. In these cases the dependence of stability on solution conditions may be accidental.

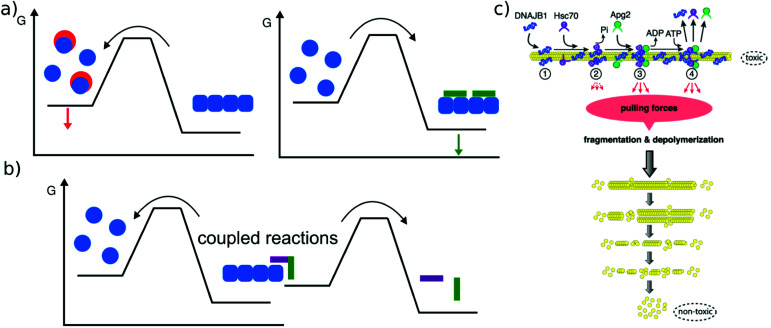
In addition to solvent conditions (pH, ionic strength, and co-solvents¹¹⁷) a wide range of different compounds has been reported to influence amyloid fibril stability, and they can be roughly divided into two classes, passive and active compounds. The former exert their effects through binding interactions (Fig. 6a), whereas the latter through energy expenditure (Fig. 6b), e.g. ATP hydrolysis. Before discussing some such compounds in more detail, it is worth considering the basic requirements of a passive compound able to destabilise amyloid fibrils. Based on fundamental physico-chemical reasoning, direct interaction between the compound and the amyloid fibril is neither sufficient nor even required to achieve destabilisation. The law of mass action states that if a given system is at equilibrium and we introduce an additional species that selectively interacts with one component of the equilibrium, this component will be stabilised. In other words, if an external compound binds selectively to amyloid fibrils in their most stable form, it will stabilise these fibrils further, rather than destabilise them (Fig. 6a). The only way in which a binding interaction can destabilise an amyloid fibril is if the compound interacts more strongly with any other state, e.g. an amorphous, oligomeric or monomeric state. In cases where the fibrillar ground state is in dynamic equilibrium with a less stable fibrillar conformation, this equilibrium could also be shifted towards the less stable state if the external compound preferentially interacts with it. Within this conceptual framework, the most straightforward manner by which fibril formation can be reverted is by providing a strong binding interaction with the monomeric state (Fig. 6a). Given the affinity of the monomer for the fibril end, a monomer binder needs to have an affinity at least of the order of μM, and in most cases of the order of nM to be able to out-compete fibril growth to a significant extent. Indeed, fibril dissolution, or significant shifts of the aggregation equilibrium towards the monomeric state, has been demonstrated by incubation with high affinity monomer binders, such as antibodies,¹¹⁸ affibodies,¹¹⁹ or lipid vesicles.⁵⁶ In cases where fibril dissolution is directly observed, its kinetics is limited by the rate of dissociation of the monomer from the fibril end, which can be very slow.¹²⁰ If no dissociation of pre-formed fibrils is observed in the presence of a high affinity monomer binder, this can therefore have two possible explanations: a very stable fibril structure or a very slow rate of dissociation. These two possibilities can be distinguished in principle by varying the concentration of the monomer binder; if the limiting factor is the fibril dissociation rate, this will have no effect. Similar to cases when monomer binding species are employed to inhibit amyloid fibril formation, fibril dissolution also requires stoichiometric amounts of binding species. Indeed, stoichiometric sequestration of monomers is the only available strategy to fully reverse fibril formation. It is therefore interesting to ask whether other strategies exist that would change the amyloid fibrils in such a way as to significantly alter their biological effects, without dissociating them into monomers. In this context, the concept of fibril ‘remodeling’ has been proposed, with the green tea compound epigallocatechin gallate (EGCG) being a prominent candidate for such effects,¹²¹ but other compounds have also been reported to act in similar ways.¹²² Overall the picture shows that such effects may indeed be possible, but significantly more quantitative and mechanistic research is needed in this area. Aspects that have so far not received enough attention are (1) quantitative evaluation of the effect of the compound on fibrils, particularly through the use of the latter as seeds,¹²³ rather than mostly basing the assessment on imaging of the fibrils; in the latter case results may be confounded by the compound itself. (2) Consideration of chemical reactions that compounds such as EGCG can undergo both by itself and with the protein.^124,125 (3) Detailed kinetic and thermodynamic analysis to assess the plausibility and mechanism of a given proposed effect. We end this section with a short discussion on cases where active compounds, such as biomolecular machines, achieve processing of amyloid fibrils with energy expenditure, i.e. by coupling a spontaneous reaction to the energy consuming process of fibril dissolution (Fig. 6b). This has been demonstrated for a range of chaperones (Hsp104 and¹²⁶ Hsp70,¹¹⁶Fig. 6c), as well as the proteasome.¹²⁷ Ever since living systems have started to use polypeptides as universal tools for almost all biological functions, they had to deal with the intrinsically low solubility, i.e. the fact that aggregated states have a high tendency to form.⁸⁸ Given that the cellular proteostasis machinery evolved in the presence of this fundamental physical constraint, it is not very surprising that various clearance mechanisms have been developed, and that the energetic uphill nature of aggregate reversal necessarily comes with an energetic cost. It is, however, remarkable that it has been possible in recent years to reconstitute some of this functionality in vitro. Such reconstituted systems allow a detailed study of their mechanisms and energy balance. It has for example recently been demonstrated that amyloid fibrils are dissociated from the ends by a chaperone.¹²⁸

Fig. 6. Reversal of amyloid fibril formation. (a) Passive compounds. Binding to monomers (left, red compounds) stabilises the soluble state and shifts the equilibrium towards the monomer, leading to fibril dissociation. Binding to fibrils (right, green compound) stabilises the fibrils and shifts the equilibrium towards the fibrillar state. (b) Active compounds are able to destabilise fibrils despite their affinity for the fibrillar state, by undergoing a spontaneous reaction, such as ATP hydrolysis that is coupled with the fibril dissociation reaction. (c) Example of an active compound, a chaperone, dissociating α-synuclein amyloid fibrils. This reaction requires energy in the form of ATP and various co-factors. Reproduced from ref. 116 with permission from CellPress, copyright 2015.

Summary

The experimental studies summarised in this review paint a clear picture of amyloid fibril formation (‘protein misfolding’) being equally amenable to detailed and quantitative thermodynamic analysis as protein folding. Very similar methods to those employed in protein folding studies can be applied to amyloid fibrils to modulate their free energy landscape and subsequently quantify the populations of soluble vs. aggregated states, as well as probe the thermodynamic signatures of the misfolding reaction. Difficulties specific to amyloid fibrils can arise from the potential heterogeneity of aggregated species in some cases, as well as the high resistance towards chemical and thermal denaturation of some amyloid systems. However, the view of the amyloid fibril as an ultra-stable, effectively irreversible state of a protein does not reflect the reality of many in vitro experiments. The stability of the amyloid state depends very strongly on the protein concentration and solution conditions and can therefore be often modulated to an extent that renders the direct quantification possible through determination of the relative populations of soluble and aggregated states at equilibrium. The stabilities of the native state of proteins and the amyloid state are defined by the same types of interactions, but their relative balance is different. Electrostatic interactions are mostly unfavourable in amyloid fibrils. The relative importance of hydrogen bonding and the hydrophobic effect are probably shifted towards hydrogen bonding in the case of amyloid,¹²⁹ even though the enthalpic and heat capacity signatures of amyloid fibril growth still appear to be dominated by the hydrophobic effect.⁶¹ Amyloid fibrils are on the whole less susceptible to unfolding by low and high temperatures than native states of proteins, reflecting a lower temperature dependence of the free energy of amyloid fibril formation, but both cold and heat-denaturation have been observed for amyloid fibrils. The latter often requires temperatures comparable to those at which hyperthermophilic proteins unfold. Kinetic effects play a very important role in amyloid fibril formation as well as dissociation, and have a strong potential to confound thermodynamic experiments. Therefore, special care needs to be taken that equilibrium has indeed been reached with respect to the process under study.

Open questions

My hope is that this overview stimulates much further experimental research in the area of amyloid fibril thermodynamics, which has been largely neglected compared to kinetic experiments. Large scale exploration of amyloid thermodynamics has been attempted by purely computational means,^130,131 but it mostly lacks quantitative experimental validation to-date. More quantitative experimental data on the thermodynamics of amyloid fibril assembly, combined with the recent revolution in structural biology (cryo-EM⁴⁴ and AlphaFold¹³²), have the potential to address the following important questions in the coming years:

- What is the role of amyloid thermodynamics in the biological effects of these structures and their resilience towards natural clearance mechanisms?

- How can amyloid fibrils form under the often very dilute concentrations in vivo, where they would not form in vitro?

- How do posttranslational modifications (truncation, phosphorylation, ubiquitination etc.) affect fibril stability?

- What changes in interactions drive the transition from reversible liquid droplets towards irreversible fibrillar aggregates?

- What are the mechanisms of fibril remodeling and dissolution by active and passive external compounds?

- What are the thermodynamic driving forces for novel types of fibrillar architectures, such as cross-α fibrils¹³³ or fibrillar structures of amino acids¹³⁴ and metabolites¹³⁵?

Answering these questions has the potential to enable us to develop targeted strategies to remove amyloid in scenarios when it is deleterious (pathologies and biofilms) and to enhance its resilience or engineer its reversibility for different types of applications related to materials science.

Appendix 1: Some basic notions of thermodynamics

If we are to discuss the thermodynamics and driving forces behind the formation of amyloid fibrils, it is useful to recall a few basic concepts of thermodynamics.

Classical thermodynamics deals with systems at equilibrium, i.e. the state of matter where all microscopic exchanges and fluxes balance and no measurable net change occurs in any macroscopic system parameter. In order to describe a system at equilibrium, we need to specify the values of the so-called state variables, also known as state functions, such as the temperature, the pressure, the entropy or the internal energy. If any of these state functions takes on a different value, then the system will be in a different equilibrium state. If a transition from one equilibrium state to another occurs infinitely slowly (without a net driving force, something that clearly never happens in practice) then the transition is said to be reversible (no associated increase in entropy). However, in the presence of a net driving force, transitions are usually irreversible and their description is the realm of non-equilibrium thermodynamics.

In analogy to mechanical systems, where work is given by the (scalar) product of a force times a displacement, W = F⃑·x⃑, in thermodynamics generalised forces and displacements can be defined, the product of which corresponds to energy. The change in internal energy of a system can be written in terms of differentials of these so-called conjugated pairs of generalised forces and displacements as:

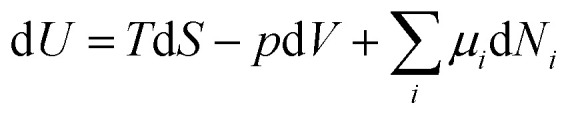1

where temperature T, pressure p and chemical potential μ correspond to the generalised forces, and the changes in entropy dS, in volume dV and in particle number (of species i) dN_i correspond to the generalised displacements. Gradients, or changes, in the generalised forces usually lead to changes in the system composition and the way how a given system responds to such external stimuli can reveal a lot of detailed information about the fundamental physico-chemical characteristics of the system. As can be seen throughout the present article, this approach has been, and is the methodology of choice to learn about the fundamental driving forces and origins of protein aggregation. Various experimental approaches merely differ by which generalised force is varied (temperature, pressure or chemical potential), and whether the external perturbation is applied slowly enough for the system to remain (approximately) at equilibrium throughout the transition or whether the transition corresponds to a non-equilibrium process. One might argue that in order to probe a biological system, the only generalised force that is appropriate to be used is the chemical potential, as this is the only handle that biology itself has in order to modify a system, whereas temperature and pressure are not under active biological control. However, a (bio)physicist will reply to this objection that it really does not matter which of the generalised forces one uses, as the powerful framework of thermodynamics allows us to freely interconvert the various forces and displacements, and that one should use whichever generalised force is most convenient in practical terms.

We need to introduce a few more basic concepts, most notably the Gibbs free energy G = H − TS, where H is the enthalpy, the heat exchanged at constant pressure. Closed systems (heat exchange, but no particle exchange with the surroundings) tend towards a state of minimal free energy (ΔG ≤ 0, with ΔG = 0 for reversible processes and ΔG < 0 for spontaneous processes), a statement that is equivalent to the maximisation of entropy of the system and the surroundings. 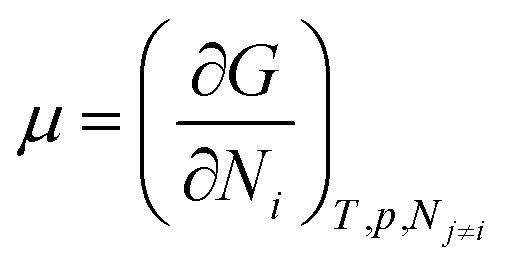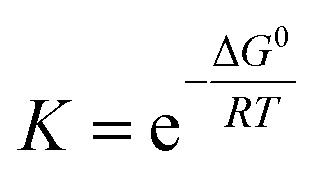Both the chemical potential μ and the equilibrium constant of a chemical reaction can be derived from the Gibbs free energy, according to and , with the superscript 0 referring to the free energy difference at some standard state of the reactants, for example 1 mol l⁻¹.

The last idea that we need in order to understand some of the discussions in the article is the link between the macroscopic definition of entropy, 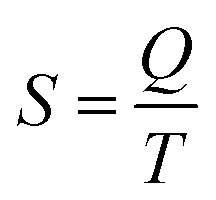, where Q is the heat that is exchanged at temperature T and the microscopic definition S = k_Blog(Ω) where k_B is the Boltzmann constant and Ω is the number of microstates, i.e. the number of microscopic arrangements of the components of a system that are compatible with its macroscopic state. This can be understood in such a way that any given macroscopic state has a large entropy when many possible microscopic arrangements of its component particles exist, as well as many ways to distribute the available energy. In order to increase the temperature of a molecular system, a certain amount of heat energy needs to be provided, which depends on the temperature difference intended and on the nature of the system. A system with many internal degrees of freedom, i.e. many vibrational modes over which energy can be distributed, as well as many interactions, will require more heat to increase its temperature. This idea can be quantified through the concept of the heat capacity, which is defined as 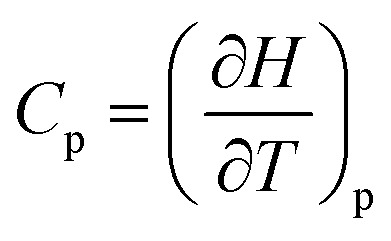, where the subscript p denotes constant pressure. If the heat capacity changes during a reaction, this indicates that the nature of the interactions that characterise the reactants and products differ.

Author contributions

AKB conceived the study and wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Biography

Alexander K. Buell.

Alexander K. Buell is a Professor of Protein Biophysics at the Technical University of Denmark, DTU. After studies of general and physical chemistry in Tübingen, Paris and Sydney, he went to the University of Cambridge, where he did his PhD and later stayed on as a research fellow at Magdalene College. From 2015–2019, Alexander was an assistant professor at the University of Düsseldorf before joining DTU. Alexander is interested in the physical chemistry of biomolecular self-assembly, and is the recipient of the 2016 Young Investigator Award of the German Society for Biophysics and the Biochemical Society 2017 Early Career Research Award for Biotechnology.