Ion slippage through Li⁺-centered G-quadruplex

Abstract

Single-ion conductors have garnered attention in energy storage systems as a promising alternative to currently widespread electrolytes that allow migration of cations and anions. However, ion transport phenomena of most single-ion conductors are affected by strong ion (e.g., Li⁺)–ion (immobilized anionic domains) interactions and tortuous paths, which pose an obstacle to achieving performance breakthroughs. Here, we present a Li⁺-centered G-quadruplex (LiGQ) as a class of single-ion conductor based on directional Li⁺ slippage at the microscopic level. A guanine derivative with liquid crystalline moieties is self-assembled to form a hexagonal ordered columnar structure in the LiGQ, thereby yielding one-dimensional central channels that provide weak ion-dipole interaction and straightforward ionic pathways. The LiGQ exhibits weak Li⁺ binding energy and low activation energy for ion conduction, verifying its viability as a new electrolyte design.

Li⁺-centered G-quadruplex enables directional Li⁺ slippage through its 1D central channels based on weak ion-dipole interaction.

INTRODUCTION

Ion transport in electrochemical systems, along with electron transport, plays a crucial role in determining their reaction kinetics (1–4). This issue has spurred the pursuit of advanced ion conductors, which have become more prevalent in energy storage systems represented by rechargeable lithium (Li)–ion batteries (5, 6).

Ideal ion transport can be achieved by complete ion dissociation and short tortuosity. The most common approach in Li-ion battery electrolytes is mixing solvents, e.g., carbonates, ethers (liquids), and polyethylene oxides (polymers) with Li salts (7, 8). However, the accompanying migration of counter anions tends to cause inhomogeneous ion flux and unwanted side reactions with electrode materials, resulting in performance degradation and safety failure of batteries (9, 10).

Substantial effort has been made to resolve these problems, with particular attention to the development of single Li⁺ conductors. Adding electrophiles (e.g., dielectric nanoparticles (11, 12), anion-trapping macrocycles (13, 14), and porous frameworks (15, 16)) to electrolytes was effective in suppressing anion mobility, thereby improving the Li⁺ transference numbers (t_Li+, 0.5 < t_Li+ < 0.7). A similar level of t_Li+ was reported for high-concentration liquid electrolytes, which could coordinate anions with solvation shells (17, 18). Recently, immobilized anionic domains such as inorganic lattices (oxides and sulfides) and polyanions have been extensively investigated as a solid-state single-ion conducting strategies (19–21). However, their intrinsically anionic moieties tightly hold Li⁺ via intermolecular ion-ion attraction. Furthermore, these electrolytes often have random and reticulated pathways for ion conduction (22, 23). Their ion transport behavior is conceptually illustrated and compared with that of an ideal single-ion conductor in Fig. 1A.

Fig. 1. LiGQ.

(A) Schematic comparison of ion transport phenomena in various ion conductors: traditional conductors versus an ideal conductor. (B) Theoretically simulated chemical structure of the single-strand LiGQ and its self-assembly procedure. The dotted line represents the ion-dipole interaction between Li⁺ and G-quartet. The close stacking of the G-quartets in the vertical direction leads to the formation of 1D central channels allowing straightforward Li⁺ conduction pathways in the LiGQ. To represent the LiGQ clearly, its hydrocarbons and bithiophenes are blurred.

Here, we demonstrate a Li⁺-centered G-quadruplex (LiGQ) as a new single-ion conduction strategy based on ion-dipole interaction. In sharp contrast to the above-described traditional single-ion conductors with strong ion-ion interactions and long tortuosity, ion transport of the LiGQ is enabled by directional Li⁺ slippage through its one-dimensional (1D) central channels at the microscopic level, which allow (i) weak ion (Li⁺)–dipole (originating from the cyclic tetramer, G-quartet) interaction and (ii) short and straightforward ionic pathways (Fig. 1B). This unusual Li⁺ slippage behavior of the LiGQ and its self-assembled crystalline structure were elucidated by in-depth experimental and theoretical investigations.

A GQ, which is known as a noncanonical nucleic acid secondary structure, is created by vertically stacking G-quartets (24–26). To achieve stable liquid-state G-quartets, a metal ion of suitable charge density that can enable ion-dipole interaction with oxygen (O) atoms of carbonyl groups on guanines rather than being solvated is needed. In most previously reported G-quartets that are hydrated in aqueous systems, potassium ions (K⁺) are commonly used to meet this requirement, while hydrated Li⁺ fails to form stable G-quartets (24, 25). Meanwhile, in the solid-state G-quartet systems that are not hydrated, G-quartet formation is expected to predominantly rely on ion-dipole interaction between central cations and guanines. We note that despite the highest charge density of Li⁺ in alkali metal cations, there have been no studies on the formation of solid-state Li⁺-centered G-quartets. To address this challenge, we introduce an oligothiophene-substituted guanine derivative bearing liquid-crystalline moieties (27). It can form GQs with Li⁺-conducting 1D channels through a combination of π-π stacking and Li⁺-dipole interaction. In addition, we exploit a nonsolvent diffusion–driven self-assembly to facilitate the formation of highly crystalline LiGQ with hexagonal columnar ordering.

RESULTS

The self-assembly procedure of the LiGQ, along with its chemical structure, is illustrated in Fig. 1B. The monomer was synthesized according to a previously reported method (27). The reaction details and characterizations of the monomer are described in the “Monomer synthesis” section in the Supplementary Materials (figs. S1 to S3). The bulky pan-shaped bithiophene on the C8 position of guanine, which is composed of π-conjugated aromatic rings and long lipophilic chains, induces a strong intra-/interquartet π-π stacking and lamellar stacking (27). Furthermore, the octyl side chain on the N9 position hinders unwanted hydrogen bonding at the N3 position (28), which could help form the LiGQ instead of ribbon-like polymorphs.

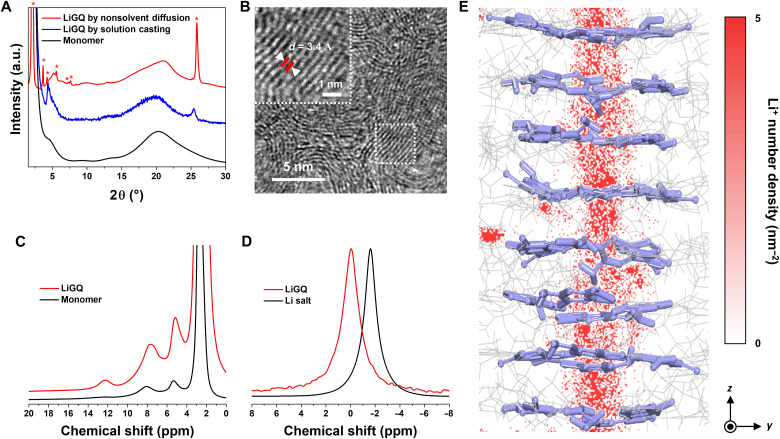
To prepare the highly crystalline LiGQ, we exploited a nonsolvent diffusion–driven self-assembly that can facilitate rearrangement of the monomer (26). Details on types of Li salts and their effect on the self-assembly are described in the “Self-assembly of the LiGQ” section in the Supplementary Materials (figs. S4 to S8 and tables S1 and S2). The obtained LiGQ showed no substantial weight loss up to approximately 300°C along with a melting peak temperature of 240°C (fig. S6), respectively, indicating its thermal stability. The synchrotron wide-angle x-ray diffraction (WAXD) pattern of the LiGQ showed clear diffraction peaks at 2.11° (100), 3.67° (110), 4.23° (200), and 25.9° (001) with a reciprocal d-spacing ratio of 1:√3:2 and high values of crystalline coherence length calculated by the Scherrer equation, demonstrating the superiority of this nonsolvent diffusion technique over a conventional casting one (Fig. 2A and table S1). In addition, this diffraction pattern verified the hexagonal columnar ordering of the LiGQ (27). The crystalline structure of the LiGQ was further elucidated by transmission electron microscopy (TEM; Fig. 2B). A well-aligned lattice was observed at a distance of ~3.4 Å, which was matched with the π-π stacking of LiGQ. These structural features exhibited the close stacking of G-quartets in the vertical direction, resulting in the formation of 1D central channels that allow short and straightforward Li⁺ migration pathways.

Fig. 2. Structural characterizations of the LiGQ.

(A) Synchrotron WAXD patterns of the LiGQs obtained by two different fabrication methods (nonsolvent diffusion and solution casting) and their monomer. The self-assembled LiGQ fabricated by the nonsolvent diffusion method shows a hexagonal columnar ordering with the distinct (001) peak. (B) TEM image of the LiGQ. The crystal lattice shows a π-π stacking distance of ~3.4 Å. Magic angle spinning (MAS) (C) ¹H and (D) ⁷Li nuclear magnetic resonance (NMR) spectra of the LiGQ. A characteristic ¹H NMR peak at 12 parts per million (ppm) exhibits the Hoogsteen hydrogen bond of G-quartet assembly. The deshielded singlet ⁷Li NMR peak at −0.044 ppm reveals the isolation of Li⁺ from its counter anion. (E) Contour plot of Li⁺ number density of the LiGQ under an electric field. Red bar indicates the 2D number density of Li⁺ projected to the yz plane.

The LiGQ showed a magic angle spinning ¹H nuclear magnetic resonance (MAS ¹H NMR) peak at 12 parts per million (ppm; Fig. 2C), which is assigned to the characteristic Hoogsteen hydrogen bond of G-quartet assembly (29). To further verify the formation of the LiGQ, a control sample was prepared by incorporating urea that destabilizes intermolecular hydrogen bonding (30). In comparison to the LiGQ, the control sample showed a decrease in the intensity of the characteristic (110) and (001) peaks in WAXD patterns and the peak at 12 ppm in the MAS ¹H NMR spectra (fig. S7). This result is an indirect evidence to verify the self-assembly of the LiGQ presented herein. In addition, the MAS ⁷Li NMR spectrum of LiGQ exhibited a deshielded singlet at −0.044 ppm relative to that of Li salt (Fig. 2D), revealing the isolation of Li⁺ from its counter anion. The ion-dipole interaction between Li⁺ and G-quartet was further verified by Fourier transform infrared spectroscopy (fig. S8), which showed red-shifted amine peaks (3293 and 3143 cm⁻¹), a blue-shifted carbonyl peak (1687 cm⁻¹), and a red-shifted sulfate peak (1030 cm⁻¹) (15, 27). Meanwhile, the composition ratio of the LiGQ was experimentally estimated by elemental analysis and it well-matched with the theoretical prediction (table S2). To the best of our knowledge, this is the first report on the successful self-assembly of a solid-state LiGQ.

We theoretically investigated the structural uniqueness of the LiGQ and its Li⁺ slippage behavior (“Computational demonstration of the LiGQ structure” section in the Supplementary Materials; figs. S9 to S13). Figure 2E shows the theoretically simulated crystal structure of the LiGQ and contour plot of its Li⁺ number density upon exposure to an electric field. The LiGQ features continuous Li⁺ arrays in the center of vertically stacked G-quartets, in which counter anions are trapped by guanines outside the Li⁺-centered channels. Notably, the contour plot of the Li⁺ number density showed a uniform Li⁺ distribution along the z axis, demonstrating the presence of 1D conduction conduits. Recent studies on porous-crystalline-framework–based ion conductors have focused on the ionic tortuosity confinement through their ordered structures, highlighting the importance of directional ion transport phenomena (15, 31). The Li⁺ conduction through the 1D central channels of the LiGQ was further identified by molecular dynamics (MD) calculations. Analyzing the mean square displacement of Li⁺ showed Li⁺ migration preferentially along the z axis rather than in other directions (fig. S13). In addition, a high t_Li+ (~0.91) was theoretically calculated, demonstrating that the movement of Li⁺ was faster than that of the counter anion.

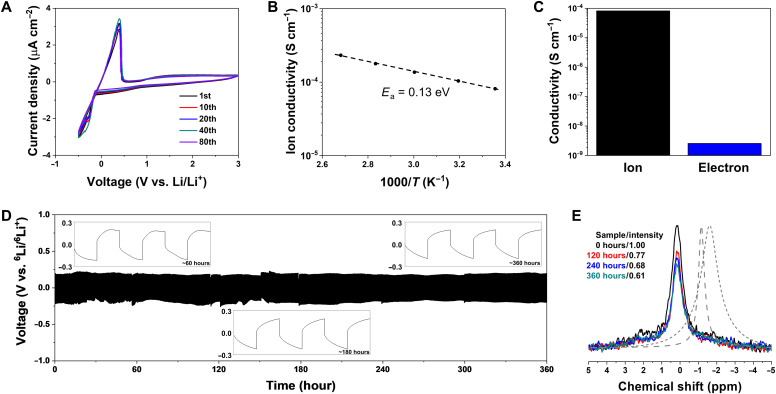
On the basis of the structural understanding of the LiGQ described above, we explored its feasibility as a single-ion conductor for potential use in Li batteries. The self-standing LiGQ pellet was prepared to conduct electrochemical characterization. The obtained pellet was pretreated with a very trace amount [~3.1 volume % (~5.1 weight %)] of fluoroethylene carbonate (FEC) solvent without any Li salts, in which FEC contributed to mitigating grain boundary resistance of LiGQ domains that could be generated during the pellet fabrication. As another promising approach to address the grain boundary resistance issue, LiGQ-customized mechanical pressing will be investigated in future studies. The cyclic voltammogram showed stable and reversible Li plating and stripping through the LiGQ without severe decomposition reactions (Fig. 3A). The anodic scan of linear sweep voltammogram exhibited an electrochemical stability window of 7.45 V (fig. S14). The Arrhenius plot shows a proportional increase in the logarithmic ionic conductivity with temperature, yielding an activation energy (E_a) of 0.13 eV along with a room temperature ionic conductivity (σ) of 8.1 × 10⁻⁵ S cm⁻¹ (Fig. 3B and fig. S15). From a potentiostatic polarization analysis, the t_Li⁺ of the LiGQ was estimated to be 0.87 (fig. S16), exhibiting the predominant contribution of Li⁺ to the ion conductivity. This ion conduction behavior of the LiGQ was compared with those of previously reported single-ion conductors, such as polyanions, inorganic conductors, covalent organic frameworks, and metal organic frameworks (table S3). Our particular attention is given to the substantially low E_a of the LiGQ, which indicates facile ion conduction with short tortuosity (15, 31). We note that these values of E_a and t_Li+ are difficult to achieve with typical liquid electrolytes, verifying the single-ion conducting capability of the LiGQ. Meanwhile, the LiGQ showed the disruption of its crystalline structure after exposure to thermal shock (200°C/1 hour), and consequently lost its ion-conducting capability (fig. S17), indicating that the ion conduction through the amorphous LiGQ was not allowed. We may assume that during the disruption of the crystalline LiGQ, Li⁺ in the LiGQ could be released and dissolved into the coexisting FEC, resulting in formation of Li⁺-containing FEC (i.e., a kind of liquid electrolyte) in the amorphous LiGQ. However, the resulting amorphous LiGQ failed to show appreciable ionic conductivity, demonstrating that the ordered 1D central channels of the LiGQ play a viable role in enabling the ion conduction.

Fig. 3. Electrochemical characteristics of the LiGQ.

(A) Cyclic voltammogram of the SUS|LiGQ|Li asymmetric cell at a sweep rate of 1 mV s⁻¹ in a voltage range of −0.5 to 3.0 V (versus Li/Li⁺), showing the stable and reversible Li plating and stripping through the LiGQ. (B) Arrhenius plot for the ion conductivity, yielding an E_a of 0.13 eV. (C) Comparison in the conductivities (ion versus electron) of the LiGQ, yielding an ion transference number of 0.99997. (D) Galvanostatic Li stripping and plating profile of the ⁶Li|LiGQ|⁶Li symmetric cell under a current density of 5 μA cm⁻² for 5 min per cycle at room temperature. (E) Ex situ MAS ⁷Li NMR spectra during the cycle test. The gradual decrease in the singlet peak intensity with the cycling time verified the Li⁺ conduction through the LiGQ. The spectra of Li salt (short-dashed line) and solvated Li⁺ (FEC was chosen as a solvent, long-dashed line) were provided as a reference.

We investigated chronoamperometry (CA) profiles of cells containing the LiGQ at a DC polarization of 100 mV (fig. S18). In a blocking symmetric cell (SUS|LiGQ|SUS), a steady-state current was ascribed to electronic leakage, resulting in an electron conductivity of 2.5 × 10⁻⁹ S cm⁻¹. By comparing the electron and ion conductivities (Fig. 3C), the ionic transference number of the LiGQ [=σ_ion/(σ_e + σ_ion)] (32) was estimated to be 0.99997. This result demonstrates that the LiGQ is ionically conductive and electronically insulating, which fulfills a requirement for a reliable ion conductor.

We synthesized a sodium ion (Na⁺)–centered GQ (NaGQ) using the same technique used for the preparation of the LiGQ to explore the feasibility of the GQ as a versatile ion-conducting medium (fig. S19). The synthesized NaGQ showed a Hoogsteen hydrogen bond and hexagonal ordering similar to those of the LiGQ. The Arrhenius plot of the NaGQ showed σ of 4.3 × 10⁻⁶ S cm⁻¹ at room temperature and an E_a of 0.15 eV, indicating the potential use of the GQ in the Na⁺ conductors similar to the Li⁺ conductors. Note that the ion conduction via the NaGQ is more sluggish than that of the LiGQ due to the higher affinity of Na⁺ for the G-quartet. More details on effects of cations on GQ formation and ion transport phenomena will be investigated in our future studies.

These unusual Li⁺ transport phenomena of the LiGQ were investigated in more detail. As a model study, we prepared a ⁶Li|LiGQ|⁶Li symmetric cell and monitored its galvanostatic Li plating and stripping behavior. The symmetric cell showed stable cycle performance over 360 hours without unstable and irreversible voltage fluctuations (Fig. 3D), demonstrating the reliable Li⁺ conduction through the LiGQ. This result was further evidenced by MAS ⁷Li-/¹H-NMR (33) and synchrotron WAXD analysis. In the ex situ MAS ⁷Li NMR spectra of the cycled LiGQ (Fig. 3E), the gradual decrease in the singlet peak intensity with the elapsed time verified the exchange between ⁷Li (LiGQ) and ⁶Li (Li electrode). Furthermore, the singlet peaks of the LiGQ did not undergo chemical shift during the cycling test, demonstrating that local environment of Li⁺ in the LiGQ remained intact. In contrast, a liquid electrolyte [lithium trifluoromethanesulfonate (LiOtf)–dissolved FEC] that was prepared as a control sample showed chemical shift of singlet peak upon solvation (see the spectra of solvated Li⁺ (long-dashed gray line) and Li salt [short-dashed gray one) in Fig. 3E]. This distinct difference between the LiGQ and Li salt–dissolved FEC indicates that Li⁺ in the LiGQ may be difficult to be released and dissolved in the FEC. This result is good evidence to prove the Li⁺ conduction through the LiGQ. In addition, the Hoogsteen hydrogen bond and hexagonal columnar ordering of the LiGQ remained almost unchanged (fig. S20), exhibiting its structural durability during the cycle test.

Meanwhile, the Li metal electrode after the cycle test showed a clean and smooth surface without dendritic Li growth (fig. S21). The surface of the cycled Li metal electrode was further analyzed using x-ray photoelectron spectroscopy (XPS) spectroscopy (fig. S22). The characteristic N1s peaks (assigned to amine and pyridine) and S2p peaks (corresponding to thiophene) were observed, revealing that the solid-electrolyte interphase layer formed on the Li metal electrode is related to the LiGQ. Moreover, peaks of C-F and S-O species, which may originate from counter anion (Otf⁻), were not detected, indicating that decomposition of counter anions in the LiGQ was suppressed. This result reveals that the single-ion conducting LiGQ enables the suppression of anion migration (causing unwanted interfacial side reactions with Li metals) and the uniform Li⁺ flux during the cycle test. These advantageous effects of the LiGQ, along with its high cationic transference number (t_Li+ = 0.87) that can increase Sand’s time [regarded as the starting time of Li dendrite growth (34)], allowed the homogeneous nucleation and growth of Li without random and irregular deposition that is commonly observed in typical liquid electrolytes that allow conduction of cations and anions (35, 36).

DISCUSSION

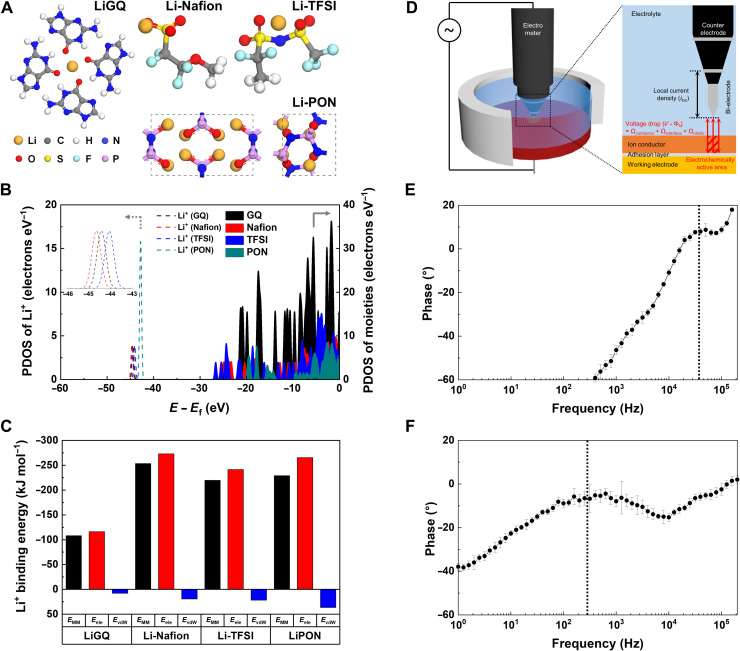
Considering that the ion-dipole interaction is weaker than the ion-ion interaction (37, 38), we expect that the intermolecular interaction of Li⁺ (ion) with G-quartet (dipole) in the LiGQ could be weaker than those of traditional single-ion conductors bearing negatively charged moieties (Nafion with sulfonates, garnet with oxygen sublattices, and others), eventually facilitating the transport kinetics of Li⁺. We theoretically investigated the interactions between Li⁺ and various ion-conducting moieties using a density functional theory (DFT) method. Along with the G-quartet, some representative ion-conducting moieties (6)—such as sulfonate (−SO₃⁻) of Nafion, bis(trifluoromethane)sulfonimide (−TFSI⁻) of polyanions and phosphorus oxynitride (−PON) of LiPON—were chosen as control systems. Their chemical structures and Li⁺ binding states are schematically depicted in Fig. 4A. The partial density of state (PDOS) for the Li⁺-bound ion-conducting moieties showed that the PDOS of Li⁺ was distributed at the range between −45 and −42 eV, but that of GQ, Nafion, TFSI, and PON were distributed above −28 eV energy levels (Fig. 4B). The PDOS of Li⁺ and ion-conducting moieties do not overlap in the bonding region below the Fermi level. Moreover, the atomic charges of Li⁺ and ion-conducting moieties remained almost unchanged after Li⁺ binding (table S4), indicating that chemical bonds between them may not be formed (39–42).

Fig. 4. Theoretical and experimental elucidations of the Li⁺ slippage phenomena in the LiGQ.

(A) Schematic representation of the chemical structures and Li⁺ binding states of the LiGQ and conventional single-ion conductors. (B) PDOS of the ion-conducting moieties and Li⁺. Colored and uncolored areas represent PDOS of ion conducting moieties and Li⁺, respectively. (C) Li⁺ binding energy (expressed as E_MM, E_ele, and E_vdW) calculated using AMBER force field. The binding energy is normalized by the number of oxygen atoms coordinating with Li⁺. (D) Schematic illustration showing the LEIS experiment. LEIS Bode plots of (E) LiGQ and (F) Li-Nafion. The profiles were measured 10 times to ensure reliability and are depicted in averaged values with error bars. The vertical dotted line represents the characteristic frequency for ion relaxation time.

On the basis of the aforementioned understanding of the physical bonding feature, we calculated the binding energies of Li⁺ with ion-conducting moieties using the molecular mechanics scheme with the assisted model building with energy refinement (AMBER) force field. The binding energies (E_MM) were deconvoluted into electrostatic (E_ele) and van der Waals (E_vdW) energies. These binding energies were normalized by the number of oxygen atoms that coordinate with Li⁺ because they can seriously affect the ion-ion or ion-dipole interaction between Li⁺ and ion-conducting moieties. Figure 4C shows that E_MM strongly depends on E_ele in all ion-conducting moieties examined here. The E_MM of the LiGQ was lower than those of the other ion-conducting moieties by a substantial gap of 100 to 150 kJ mol⁻¹. Furthermore, the LiGQ showed a longer binding distance and smaller average partial charge of oxygen atoms, demonstrating the weak binding of Li⁺ to the G-quartet via ion-dipole interaction (table S5).

According to the bond strength–coordination number fluctuation (BSCNF) model (43, 44), the mean residence time of an ion placed in a potential well is proportional to the product of ion binding energy and ion coordination number. We assume that Li⁺ in the LiGQ may have a lower mean residence time than those of other single-ion conductors owing to its weak binding strength with G-quartets. To experimentally verify this BSCNF model–based ion transport behavior of the LiGQ, we conducted a local electrochemical impedance spectroscopy (LEIS) analysis (Fig. 4D)—for details, see the “Local electrochemical impedance spectroscopy” section in the Supplementary Materials. The LEIS Bode plot (Fig. 4, E and F) of the LiGQ showed a notably higher peak frequency (3 × 10⁴ Hz) than that of the lithiated Nafion (4 × 10² Hz) chosen as a control sample. Considering that the characteristic frequency (f) of the ion migration is given by the reciprocal of ion relaxation time (τ, τ⁻¹ = 2πf) (45, 46), the LEIS result shows that the Li⁺ conduction through the LiGQ is driven by the faster Li⁺ relaxation, which is consistent with the lower binding energy of Li⁺ in the LiGQ discussed in the theoretical investigation. This result verifies that the weak ion-dipole interaction between Li⁺ and G-quartets plays a viable role in facilitating the Li⁺ transport via the LiGQ.

In summary, we have demonstrated a LiGQ as a class of single-ion conductor based on Li⁺ slippage. The directional Li⁺ slippage of the LiGQ was enabled through its 1D central channels that allowed weak ion (Li⁺)–dipole (G-quartet) interaction and short and straightforward ionic pathways at the microscopic level. The hexagonally ordered columnar structure of the LiGQ was formed by the nonsolvent diffusion–driven self-assembly of a guanine derivative with liquid crystalline moieties, eventually producing the Li⁺-conducting 1D central channels. The structural uniqueness of the self-assembled crystalline LiGQ and its Li⁺ slippage behavior were elucidated by experimental and theoretical investigations. In sharp contrast to traditional single-ion conductors with strong ion-ion interactions and long tortuosity, the LiGQ exhibited an exceptionally low E_a for ion conduction and weak Li⁺ binding energy, confirming its unusual Li⁺ slippage–driven conduction through the 1D central channels. This study demonstrated a promising new electrolyte design strategy based on the ion slippage-driven conduction mechanism. Future works will be devoted to exploring the physicochemical compatibility of the LiGQ with battery electrodes, along with continued efforts to improve its ionic conductivity and other electrolyte properties further by fine-tuning the dipole intensity of G-quartets and long-range ordered self-assembly.

MATERIALS AND METHODS

Two-dimensional–grazing incidence x-ray diffraction (2D-GIXD) measurements were performed at PLS-II 3C SAXS I and PLS-II 9A U-SAXS beamline of Pohang Accelerator Laboratory in Korea. The x-rays coming from the in-vacuum undulator (IVU) were monochromated (E_k = 9.81 keV and λ = 1.26 Å for 3C beamlines and E_k = 11.02 keV and λ = 1.13 Å for 9A beamlines) using a Si (111) double crystal monochromator. The incidence angle of x-rays for 2D-GIXD was adjusted in the range of 0.12°, which was close to the critical angle of samples. The 2D-GIXD patterns were recorded by a 2D charge-coupled device (CCD) detector (SX165, Rayonix, USA). The raw data were processed and analyzed using Igor-Pro software package.

Synchrotron WAXD measurements were conducted at PLS-II 6D UNIST-PAL beamline of Pohang Accelerator Laboratory in Korea. The x-rays coming from the IVU were monochromated (E_k = 11.6 keV and λ = 1.069 Å). The WAXD patterns were recorded by a 2D CCD detector (SX165, Rayonix, USA). The raw data were processed and analyzed using Igor-Pro software package.

MAS ¹H and ⁷Li NMR experiments were performed with an Agilent VNMRS 600-MHz narrow NMR spectrometer and 1.6-mm HXY Fast MAS T3 probe. The ¹H NMR spectra were recorded using one-pulse [or direct polarization (DP)] with recycle delay of 5 s, 90° pulse width of 6 μs, acquisition time of 0.0344 s, and 4096 complex points under 35-kHz spinning rate to the resonance frequency of 599.83 MHz. The total number of transients was 16. ⁷Li NMR spectra were recorded using one-pulse (or DP) with recycle delay of 45 s, 90° pulse width of 2 μs, acquisition time of 0.3539 s, and 16,384 complex points under 35-kHz spinning rate to the resonance frequency of 233.12 MHz. The total number of transients was 512. The chemical shift is referenced to a hexamethylbenzene at ¹H (2.2 ppm) and 1.0 M aqueous LiCl solution at ⁷Li (0 ppm). For the ex situ MAS ⁷Li NMR experiments, acquisition parameters (acquisition time = 353.894 ms, spectral width = 46,296.3 Hz, complex point = 16,384, receiver gain = 10, recycle delay = 45 s, number of scans = 512, 15° pulse for ⁷Li = 0.425 s, spinning rate = 35 kHz, and two-pulse phase-modulated decoupling = 2000) and processing parameters (Mnova 10.0.2, exponential = 10 Hz, zeo-filling = 65,536, and baseline correction = polynomial 3) as well as the quantity of the loaded sample are controlled for the quantitative comparison.

TEM and scanning electron microscopy (SEM) measurements were conducted using a JEOL JEM-2100F TEM at the acceleration voltage of 200 kV and a Hitachi S-4800 field-emission SEM at the acceleration voltage of 10 kV, respectively. For the TEM sampling, LiGQ was dispersed in FEC by mild sonication using a bath-type sonicator. Then, the suspension solutions were drop-casted on holey carbon–supported copper grids (300 mesh), followed by vacuum drying. Last, the sample grid was loaded on a single tilt holder.

XPS analysis was conducted using a Thermo Fisher Scientific K-alpha. For the XPS sampling, a cycled ⁶Li-metal anode was gently rinsed by anhydrous tetrahydrofuran and dried over 24 hours in Ar-filled glove box.

Cyclic voltammetry and linear scan voltammetry were conducted with a stainless steel (SUS)|LiGQ|Li asymmetric cell operated at room temperature using a Biologic VSP classic potentiostat under a sweep rate of 1 mV s⁻¹ in a voltage range of −0.5 to 3.0 V and 3.0 to 8.0 V (versus Li/Li⁺), respectively. The LiGQ self-standing pellet was prepared using a cold-pressing method in a glove box. The obtained pellet was pretreated with a very trace amount of FEC solvent without any Li salts before the electrochemical characterization, in which FEC contributed to mitigating grain boundary resistance of LiGQ domains that could be generated during the pellet fabrication. The FEC content in the pellet was 3.1 volume %, estimated by Thermogravimetric analysis analysis. CA was carried out at 100-mV bias using blocking (SUS|LiGQ|SUS) and nonblocking (Li|LiGQ|Li) cells.

Ion conductivity (σ) was recorded with a SUS|LiGQ|SUS symmetric cell based on an electrochemical impedance spectroscopy analysis at a frequency range 10⁻² to 10⁶ Hz with an applied amplitude of 10 mV. The σ was determined by following equation

$$\mathrm{\sigma }=\frac{l}{\mathit{RA}}$$

where l is the pellet thickness, R is the resistance, and A is the area in contact with the electrodes. The E_a was determined from the slope of the T-σ plot (Arrhenius plot).

Li⁺ transference number (t_Li+) was evaluated using a potentiostatic polarization method. The DC current flowing through the Li|LiGQ|Li symmetric cell under a 10-mV bias and the AC impedance (EIS) at a frequency range 10⁻² to 10⁶ Hz with an applied amplitude of 10 mV of the cell before and after polarization were measured to determine the t_Li+ value of LiGQ according to following equation

$$t_{\text{Li}+}=\frac{I_{\text{ss}}(∆V-I_{\mathrm{o}}{R}_{\mathrm{o}})}{I_0(∆V-I_{\text{ss}}{R}_{\text{ss}})}$$

where I_SS is the steady-state current, I_o is the initial current, ∆V is the applied potential, and R_o and R_SS are the interfacial resistances before and after the polarization, respectively.

⁶Li symmetric cell test was conducted with the ⁶Li|LiGQ|⁶Li symmetric cell under a current density of 5 μA cm⁻² for 5 min per cycle at room temperature. ⁶Li chunk was purchased from Sigma-Aldrich and used after cutting out the oxidized shell.

All-atom molecular mechanic (MM) and MD simulations were carried out using the GROningen MAchine for Chemical Simulations (GROMACS) 5.0.6 program (47). AMBER force field was used to describe the interaction between atoms constituting Li⁺, trifluoromethanesulfonate (−Otf⁻), G-quartet, sulfonate (−SO₃⁻), −TFSI⁻, and PON (48). Specifically, in case of G-quartet, −SO₃⁻, −TFSI⁻, and −Otf⁻, the antechamber program was used to generate parameters that are compatible with the AMBER force field (49). The short-range nonbonding interactions were calculated within the cutoff distance of 12 Å, and the particle mesh Ewald summation was used to calculate electrostatic interactions. Bonded interactions with the hydrogen atoms were constrained with the LINCS algorithm to secure larger timestep and improve the speed of simulation (50).

To calculate Li⁺ binding energy toward single-ion conducting moieties, adequate Li⁺ binding site was first investigated through Grand canonical monte carlo (GCMC) simulations using Sorption program (51). The GCMC simulations were performed with 10⁵ equilibration steps and 10⁶ production steps to obtain thermodynamically equilibrated binding sites of Li⁺ on G-quartet, −SO₃⁻, −TFSI⁻, and −Otf⁻ moieties. In case of PON, the structure obtained from crystallographic information file is used as initial structure (52). After finding proper binding site, Li⁺ binding structures were optimized and normalized binding energy between Li⁺ and binding moieties (E_MM) were calculated, applying the following equation

$$E_{\text{MM}}=(E_{{\text{Li}}^{+}+\text{moiety}}-E_{{\text{Li}}^{+}}-E_{\text{moiety}})/n$$

where E_Li⁺+moiety is nonbonding energy of Li bound single-ion conducting moiety, E_Li⁺ is nonbonding energy of Li⁺ ion, E_moiety is nonbonding energy of optimized structure of single-ion conducting moiety, and n is the number of oxygen atoms that participates to Li⁺ coordination in each binding moieties.

To investigate structural stability and explore Li⁺ conduction behavior of solid-sate LiGQ structure, the initial size and shape of bulk LiGQ unit cell were decided following the information of experiment XRD. Eight Li⁺-centered G-quartets were stacked into 48.04 Å–by–48.04 Å–by–30.4 Å sized hexagonal unit cell, maintaining the most stable stacking sequence. To relax the LiGQ structure, geometry optimization was carried out until the convergence criteria (1000 kJ·nm mol⁻¹ for the maximum energy change) were satisfied. Subsequently, the MD simulation under canonical ensemble were performed to anneal the alkyl chain moieties, with position restraints (applying harmonic spring constant k = 100 kJ mol⁻¹) on G-quartet atoms. The temperature of each system was maintained to 298 K for 1 ns with 1-fs time step. After the annealing, equilibration of the LiGQ was performed under the isothermal-isobaric ensemble, at 1 bar and 298 K with 1-fs time step until the unit cell length was converged. Production run was performed under the isothermal-isobaric ensemble at 1 bar and 298 K for 500 ps. In all MD simulations, the temperature and the pressure of each system were controlled by the Berendsen thermostat and barostat (53), respectively. During the equilibration and production run, the trajectories were analyzed every 1 ps.

DFT calculations were conducted using the Cambridge Serial Total Energy Package to investigate the PDOS of Li⁺ and single-ion conducting moieties (54). The spin-polarized calculations were performed using a generalized gradient approximation with Perdew-Burke-Ernzerhof functional (55). The interactions between the core and the valence electrons were described using the on-the-fly generation ultrasoft pseudopotential (55, 56); the energy cutoff was set to 517 eV. The Tkatchenko-Scheffler method for dispersion-corrected density functional theory correction was used to describe the van der Waals interaction (57). The Broyden-Fletcher-Goldfarb-Shanno algorithm was applied to the geometry optimization (58). The convergence threshold for the geometry optimization and self-consistent field density convergence were 1 × 10⁻⁵ and 1 × 10⁻⁶ eV atom⁻¹, respectively. The convergence precision of the geometry optimization for the maximum force, stress, and displacement was set to 0.03 eV Å⁻¹, 0.05 GPa, and 0.001 Å, respectively. The Monkhorst-Pack k-point grid was set to 3 × 3 × 3 (59).

Supplementary Materials

This PDF file includes:

Monomer synthesis

Self-assembly of the LiGQ

Computational demonstration of the LiGQ structure

Single Li⁺ conduction behavior of the LiGQ

Application to Na⁺ conductor

Postmortem analysis after the cycle test

Supplementary physical parameters for Li⁺ binding energy calculation

Local electrochemical impedance spectroscopy

Figs. S1 to S22

Tables S1 to S5

References