IBPred: A sequence-based predictor for identifying ion binding protein in phage

Graphical abstract

Abstract

Ion binding proteins (IBPs) can selectively and non-covalently interact with ions. IBPs in phages also play an important role in biological processes. Therefore, accurate identification of IBPs is necessary for understanding their biological functions and molecular mechanisms that involve binding to ions. Since molecular biology experimental methods are still labor-intensive and cost-ineffective in identifying IBPs, it is helpful to develop computational methods to identify IBPs quickly and efficiently. In this work, a random forest (RF)-based model was constructed to quickly identify IBPs. Based on the protein sequence information and residues’ physicochemical properties, the dipeptide composition combined with the physicochemical correlation between two residues were proposed for the extraction of features. A feature selection technique called analysis of variance (ANOVA) was used to exclude redundant information. By comparing with other classified methods, we demonstrated that our method could identify IBPs accurately. Based on the model, a Python package named IBPred was built with the source code which can be accessed at https://github.com/ShishiYuan/IBPred.

1. Introduction

Ion binding proteins (IBPs) are proteins that selectively and non-covalently interact with ions, charged atoms, or groups of atoms. Usually, most ion binding proteins bind to metal ions, and a small portion of the proteins can bind non-metal ions. Of course, there are also existing proteins that can bind to both. These ions can directly or allosterically regulate the catalysis and maintain the structural stability of proteins, thereby enriching and diversifying proteins’ structures and functions [1]. For example, the zinc finger proteins, which always bind DNA in several processes, bind to Zn²⁺ to form more stable space structures [2]. In phages, these IBPs can control and regulate a wide variety of biological processes, such as viral entry into host cell [3], viral tail assembly [3], cytolysis [4], DNA synthesis [5], RNA synthesis [6], and even neurotransmitter secretion [7]. IBPs have been studied for a long time and can be used to develop treatments for diseases caused by drug-resistant bacteria due to their important role in biological processes [8], [9]. Therefore, the identification of IBPs in phages can be helpful for drug development.

Although biochemical experiments are an effective approach for accurately identifying IBPs, they are slightly inferior in terms of time, labor, and material consumption. Owing to the convenience and high efficiency, computational methods are a good choice for identifying IBPs. Many machine learning algorithms, such as support vector machine (SVM) [10], [11], [12], deep learning (DL) [13], [14], [15], [16], [17], [18], [19], extreme boosting algorithm (XGBoost) [20], [21], [22], [23], [24], and stacking ensemble models [25], [26], [27], [28], [29], [30], etc., have been developed for protein function, structure, subcellular localization, and even other biological processes. Different feature descriptors such as amino acid composition (AAC) [31], [32], [33], reduced amino acid composition [34], [35], [36], g-gap dipeptide composition [37], [38], and secondary structure features [39], etc., were adopted to represent protein sequences. While there is still no computational method to identify IBPs in phages, this study aims to design a novel model for IBP prediction.

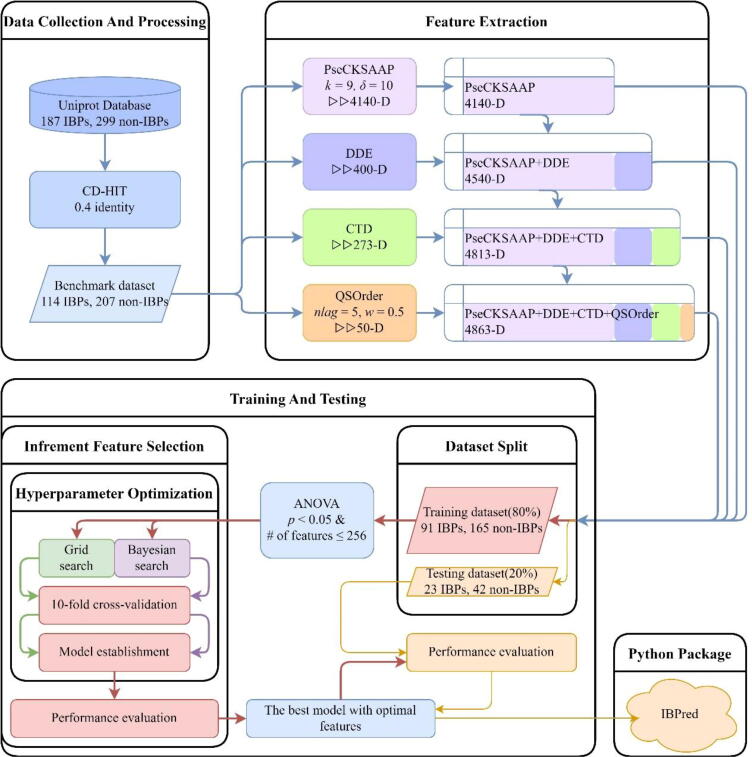
The following five steps were completed in this work to establish a Python package for the identification of IBPs. Firstly, the sequences of IBPs were collected to construct an objective benchmark dataset to train and test the model. Secondly, several feature extraction techniques were used for obtaining sample features. Thirdly, the ANOVA-based technique was applied in feature selection [40]. Fourthly, the RF [41] was selected to construct prediction models. Finally, based on the proposed model, a free and easy-to-use Python package called IBPred was established for the identification of IBPs. The workflow chart is shown in Fig. 1. Notably, the IBPred tool is only suitable for identifying IBPs from phages. Although IBPred can give probabilities of IBPs for protein sequences from other species, it lacks such accurate discrimination capacity as in phage.

Fig. 1.

The flow of the model building.

2. Material and methods

2.1. Benchmark dataset and independent dataset

We collected the proteins that meet our search results in the Universal Protein Resource (UniProt) [42], to establish prediction models. Manually annotated and reviewed sequences were chosen with query keywords “phage” in the Organism and “binding [0005488]” in the Gene Ontology (GO) [43]. Protein sequences that contain ambiguous residues, such as “B”, “J”, “O”, “U”, “X”, and “Z”, should be excluded. The raw data were divided into 187 IBPs and 299 non-IBPs according to the ion binding proteins tagged with the annotation term “ion binding [0043167]” in GO. Subsequently, the CD-HIT program [44] with a sequence identity threshold of 40 % was utilized to remove redundant sequences. 114 IBPs and 207 non-IBPs were retained as the benchmark dataset. To make the prediction more reliable, stratified sampling was used to split the benchmark dataset into the training set and testing set (8:2). Eventually, 91 IBPs and 165 non-IBPs were used for training, and 23 IBPs and 42 non-IBPs were used for independent testing.

2.2. Feature extraction

To extract characteristics of target proteins, transforming target protein sequences into numeric vectors is the key procedure in machine learning modeling. A protein P sequence with L amino acid residues can be expressed as follows:

$$P=R_1{R}_2{R}_3\cdots R_{L-1}{R}_L$$

where R_i (i = 1, 2, …, L) represents the i-th amino acid residue of the protein sequence. By using feature extraction methods, P can be converted to numeric vectors. Here, four types of feature extraction methods were utilized to describe protein sequences.

2.2.1. Pseudo composition of k-spaced amino acid pairs (PseCKSAAP)

The pseudo amino acid composition (PseAAC) [45], [46] is a feature extraction method that computes AAC and their physicochemical properties correlation. The composition of k-spaced amino acid pairs (CKSAAP) [47] is another feature descriptor calculating frequencies of dipeptides separated by various amino acid residues. By replacing AAC features with CKSAAP features, we developed a novel method called PseCKSAAP for sequence features extraction. Details of PseCKSAAP are described as follows.

The PseCKSAAP describes a feature vector with 400(k + 1) + nδ dimension which can be formulated as:

$$D={\left[f_1,f_2,\cdots ,f_{400(k+1)},f_{400(k+1)+1},\cdots ,f_{400(k+1)+n\delta }\right]}^T$$

where T is the transposition of the vector; k denotes the number of spaced residues between the paired residues; δ represents the rank of correlation, and is numerically shown as the position difference value between paired residues (theoretically δ < L); n is the rank value of physicochemical properties; f_i can be represented as:

$$f_i=\left\{\begin{array}{cc}{\phi }_i,& 1\le i\le 400(k+1)\\ {\epsilon }_i,& 400(k+1)<i\le 400(k+1)+n\delta \end{array}\right)$$

where φ_i denotes the frequency of the j-th dipeptide $n_j^k$ (j = 1, 2, …, 400) separated by k residues and formulated as:

$$\left\{\begin{array}{c}{\phi }_1=\frac{n_1^0}{L-1}\\ {\phi }_2=\frac{n_2^0}{L-1}\\ ⋮\\ {\phi }_{400}=\frac{n_{400}^0}{L-1}\\ {\phi }_{400+1}=\frac{n_1^1}{L-2}\\ {\phi }_{400+2}=\frac{n_2^1}{L-2}\\ ⋮\\ {\phi }_{400+400}=\frac{n_{400}^1}{L-2}\\ ⋮\\ {\phi }_{400k+j}=\frac{n_j^k}{L-k-1}\end{array}\right)(k<L-1)$$

The symbol ε_i in Eq. (3) is the δ-tier sequence correlation factor calculated by the following formulas:

$$\left\{\begin{array}{c}{\epsilon }_{400\left(k+1\right)+1}=\frac{1}{L-1}{\sum }_{t=1}^{L-1}{\theta }_{t,t+1}^1\\ {\epsilon }_{400\left(k+1\right)+2}=\frac{1}{L-1}{\sum }_{t=1}^{L-1}{\theta }_{t,t+1}^2\\ ⋮\\ {\epsilon }_{400\left(k+1\right)+n}=\frac{1}{L-1}{\sum }_{t=1}^{L-1}{\theta }_{t,t+1}^n\\ {\epsilon }_{400\left(k+1\right)+n+1}=\frac{1}{L-2}{\sum }_{t=1}^{L-2}{\theta }_{t,t+2}^1\\ {\epsilon }_{400\left(k+1\right)+n+2}=\frac{1}{L-2}{\sum }_{t=1}^{L-2}{\theta }_{t,t+2}^2\\ ⋮\\ {\epsilon }_{400\left(k+1\right)+n+n}=\frac{1}{L-2}{\sum }_{t=1}^{L-2}{\theta }_{t,t+2}^n\\ ⋮\\ {\epsilon }_{400\left(k+1\right)+n\delta }=\frac{1}{L-\delta }{\sum }_{t=1}^{L-\delta }{\theta }_{t,t+\delta }^n\end{array}\right)(\delta <L)$$

where ${\theta }_{x,y}^n$ is the correlation function of physicochemical properties between two residues R_x and R_y, it can be calculated by the following formula:

$${\theta }_{x,y}^n={\rho }^n\left(R_x\right)\times {\rho }^n\left(R_y\right)$$

where ρⁿ(R_x) and ρⁿ(R_y) denote the n-th kind physicochemical property value of R_x and R_y. To obtain a high-quality feature set, all physicochemical properties were subjected to a standard conversion as below:

$${\rho }^n\left(R_x\right)=\frac{{\rho }_0^n\left(R_x\right)-{\sum }_{k=1}^{20}{\rho }_0^n\left(R_k\right)/20}{\sqrt{{\sum }_t^{20}{\left({\rho }_0^n\left(R_t\right)-{\sum }_{k=1}^{20}{\rho }_0^n\left(R_k\right)/20\right)}^2/20}}$$

where ${\rho }_0^n\left(R_x\right)$ is the n-th kind physicochemical property original value of residue R_x. The values of the 14 types of physicochemical properties used in this work are listed in Table S1 [48], [49].

Due to the time-consuming of searching parameters and the consideration of the length of protein sequences, we set k = 9 and δ = 10. According to the parameters, the dimension of the extracted feature vector is 400 × (9 + 1) + 14 × 10 = 4140.

2.2.2. Dipeptide deviation from expected mean (DDE)

DDE is a feature descriptor about the fixed composition of dipeptides, which considers the coding diversity of codons [50]. Since amino acids can be determined by combinations of 3 bases, the occurrence frequencies of dipeptides in sequences are innated varied. For a given sequence, we can get the DDE values by standardization (or called z-score normalization) of directly calculated dipeptide composition.

DC_i (i = 1, 2, …, 400) describes the dipeptide composition and is given by:

$$D{C}_i=\frac{n_i}{L-1}$$

where n_i stands for the number of the i-th dipeptide in protein P. TM_i denotes the theoretical mean, and can be calculated by:

$$T{M}_i=\frac{C_r}{C_N}\times \frac{C_s}{C_N}$$

where $C_r$ is the number of codons that code for the first amino acid residue and $C_s$ is the number of codons that code for the second amino acid residue in the given dipeptide “rs”; $C_N$=61, is the total number of possible codons, excluding the three stop codons. TV_i, the theoretical variance of the dipeptide “rs”, is given by:

$$T{V}_i=\frac{T{M}_i(1-T{M}_i)}{L-1}$$

Finally, the DDE feature vector can be calculated by the following formula:

$$\mathit{DD}{E}_i=\frac{D{C}_i-T{M}_i}{\sqrt{T{V}_i}}$$

2.2.3. Composition transition distribution (CTD)

The CTD is a feature extraction method that was first proposed for protein folding class prediction [51]. In the CTD, 13 types of physicochemical properties were further breakdown into 3 subgroups: polar, neutral, and hydrophobic to generate features (Table S2) [52]. Thus, amino acids were divided into a total of 13 × 3 = 39 groups. The “Composition” (called CTDC) of the CTD method represents the composition percentage of each group in sequence and can produce three features per physicochemical property, which is given by:

$$C_{i,j}=\frac{n_{i,j}}{L}$$

where n_i,j is the number of residues in the i-th group of the j-th physicochemical property. The “Transition” (called CTDT) of the CTD method denotes the transition probability between two neighboring amino acid residues belonging to two different groups, and can be calculated by:

$$T_{i,j}=\frac{n_{\mathit{rs}}+n_{\mathit{sr}}}{L-1}$$

where n_rs and n_sr are the numbers of dipeptides “rs” and “sr” respectively, while “r” and “s” are amino acids in the i-th group and not. The “Distribution” (called CTDD) of the CTD method means the relative location in one sequence-represented distribution of residues of given groups. We can use $n_{i,j}^p$ denoting the number of residues of p% (p = 0, 25, 50, 75, 100) of the total number of residues in the i-th group of the j-th physicochemical property, and it can be calculated by:

$$n_{i,j}^p=\lfloor \frac{p}{100}\times n_{i,j}\rfloor$$

and if $n_{i,j}^p$ < 1, it will be equaled to 1. Then, the feature vector of CTDD can be represented as:

$$D_{i,j}^p=\frac{loc\left(n_{i,j}^p\right)}{L}\times 100$$

where $loc\left(n_{i,j}^p\right)$ denote the location at the sequence that the occurrence number of residues of a given group reaches $n_{i,j}^p$. Finally, we can get a 39 × (2 + 5) = 273 dimension of feature vector by concatenating $C_{i,j}$, $T_{i,j}$ and $D_{i,j}^p$ in CTD.

2.2.4. Quasi-sequence-order (QSOrder)

The quasi-sequence-order descriptor [53] can be defined as:

$$X_i=\left\{\begin{array}{cc}{X}_r=\frac{f_r}{{\sum }_{r=1}^{20}{f}_r+w{\sum }_{q=1}^{\mathit{nlag}}{\tau }_q},& 1\le i=r\le 20\\ X_{q+20}=\frac{w{\tau }_q}{{\sum }_{r=1}^{20}{f}_r+w{\sum }_{q=1}^{\mathit{nlag}}{\tau }_q},& 21\le i=q+20\le nlag+20\end{array}\right)$$

where f_r is the normalized occurrence of amino acid type r; w is a weighting factor; nlag denotes the maximum value of the lag, which is a parameter decided by the user; τ_q represents the q-th rank sequence-order-coupling number, and can be calculated as follows:

$${\tau }_q=\sum _{p=1}^{L-q}{(d_{p,p+q})}^2$$

where d_p,p+q denotes the item in a given distance matrix that describes the distance between two amino acids at position p and p + q of the protein. Both the Schneider-Wrede physicochemical distance matrix used by Chou [53] and the chemical distance matrix used by Grantham [54] are used to calculate the features. Here, a moderate setting of nlag = 5 and w = 0.5 was adopted. Therefore, (20 + 5) × 2 = 50 dimension of feature vector can be accessed from the QSOrder descriptor.

2.3. Feature selection

Generally, features contribute unequally to the prediction model. Some features make key contributions, some make minor contributions, and some might even reduce the performance of the model [55], [56], [57], [58], [59]. Therefore, feature selection is a vital step to improve classification performance.

To evaluate the classification contribution of each feature, ANOVA [40], [60] was used to score features in this work. The F-score for each feature is defined as follows:

$$F\left(i\right)=\frac{S_B^2\left(i\right)}{S_W^2\left(i\right)}$$

where F(i) is the F-score of the i-th feature; $S_B^2\left(i\right)$ and $S_W^2\left(i\right)$ denote the sample variance between groups (means square between, MSB) and the sample variable within groups (means square within, MSW), respectively. They can be expressed as:

$$\left\{\begin{array}{c}{S}_B^2\left(i\right)=\frac{{\sum }_{j=1}^K{m}_j{\left(\frac{{\sum }_{s=1}^{m_j}{f}_{s,j}\left(i\right)}{m_j}-\frac{{\sum }_{j=1}^K{\sum }_{s=1}^{m_j}{f}_{s,j}\left(i\right)}{{\sum }_{j=1}^K{m}_j}\right)}^2}{K-1}\\ S_W^2\left(i\right)=\frac{{\sum }_{j=1}^K{\sum }_{s=1}^{m_j}{\left(f_{s,j}\left(i\right)-\frac{{\sum }_{s=1}^{m_j}{f}_{s,j}\left(i\right)}{m_j}\right)}^2}{{\sum }_{j=1}^K{m}_j-K}\end{array}\right)$$

where K = 2, represents the number of groups; f_s,j(i) denotes the feature value of the i-th feature of the s-th sample in the j-th group; m_j is the number of samples in the j-th group.

It is obvious that the larger the F(i) value, the greater contribution of the i-th feature has. To eliminate the redundant features, all features were ranked according to their F-scores from high to low. Subsequently, incremental feature selection (IFS) was used to determine the optimal number of features. At the beginning, the performance of the first feature subset—which contains only the feature with the largest F-score, was examined. Then, the second feature subset that contains the top two features was evaluated. The process was repeated until all candidate features were added. The RF was used to evaluate the performance of each feature subset. The feature subset with the maximum AUC (the Area Under the receiver operating characteristic (ROC) Curve) was considered to be the optimal feature subset that does not contain redundant features. It should be noted that overfitting may occur when the dimension of the features is greater than the samples size. To avoid this problem, the top 256 feature subsets were used in this work.

2.4. Random forest and cross-validation

The RF is a classification algorithm for supervised machine learning [41], [61], [62], [63], [64]. As an ensemble method, the RF has good interpretability and a prominent advantage on small datasets. The forest consists of many decision trees, and each tree is built by the bootstrap sampling from the training dataset [65]. Additionally, the features are also randomly chosen during the tree construction. By averaging the predicted probabilities of the decision trees, the RF can achieve lower variance and more stable predictions. In this work, the scikit-learn (v1.0.1) package in Python (v3.9.7) was used to implement in RF [66].

In cross-validation methods, n-fold cross-validation, jackknife cross-validation, and independent data test are often used to measure the performance of prediction models [67], [68], [69], [70], [71]. Although jackknife cross-validation can produce a unique outcome, the time-consuming problem can be more serious. For the reliability of results, 10-fold cross-validation and independent test were adopted to evaluate the model performance.

2.5. Grid search and Bayesian search

Grid search (from scikit-learn) and Bayesian search (from scikit-optimize v0.9.0) methods were applied for hyperparameter optimization [72]. The search space of parameters and the number of parameter combinations in the two search methods are listed in Table 1.

Table 1.

The search spaces of search methods and the number of attempts.

Parameters	Grid Search	Bayesian Search
“criterion”	Gini, Entropy	Gini, Entropy
“max_depth”	5, 40, 75, 110, 145	5, 6, …, 150
“min_samples_split”	2, 7, 12, 17, 22, 27	2, 3, …, 30
“n_estimators”	10, 25, 63, 158, 398, 1000	10x, x∈[1], [3]
“min_samples_leaf”	5	1, 2, …, 10
“max_leaf_nodes”	100	50, 51, …, 150
“ccp_alpha”	0.001	10x, x ∈ [-10, 0]
# of attempts	360	64 (Our setting)

The search spaces of the two search strategies are quite different. The grid search tries all combinations of parameters, while its counterpart tries a given number of parameter settings. Here, “min_samples_leaf”, “max_leaf_nodes”, and “ccp_alpha” are not very important parameters and can be set as constant values. Since there are 2–6 options for each other parameters, the grid search method would try 360 times to find the best model. By using the Gaussian process model to approximate the result function, Bayesian search reduces the uncertainty of a given type (category, real number, integer, or in log-scale) and ranges of parameters. A total of 64 trials were conducted to reduce time consumption.

2.6. Performance evaluation

Six assessment criteria were used to evaluate the performance of the prediction models[73], [74], [75]: 1) sensitivity (Sn) and 2) specificity (Sp), were used to evaluate a model’s ability to correctly predict positive and negative samples, respectively; 3) Mathew’s correlation coefficient (MCC), was used to evaluate the reliability of the algorithm; 4) average accuracy (AA), was a combination of the prediction accuracy of positive and negative samples; 5) overall accuracy (OA), reflected the probability of the correct predicted samples in the entire dataset; and 6) area under the receiver operating characteristic (ROC) curve (AUC), was the embodiment of comprehensive performance of the model. The first five metrics are defined as:

$$\mathit{Sn}=\frac{\mathit{TP}}{\mathit{TP}+FN}$$

$$\mathit{Sp}=\frac{\mathit{TN}}{\mathit{TN}+FP}$$

$$\mathit{MCC}=\frac{\mathit{TP}\times TN-FP\times FN}{\sqrt{\left(TP+FP\right)\times \left(TN+FN\right)\times \left(TP+FN\right)\times \left(TN+FP\right)}}$$

$$\mathit{AA}=\frac{1}{2}\times \left(\frac{\mathit{TP}}{\mathit{TP}+FN}+\frac{\mathit{TN}}{\mathit{TN}+FP}\right)$$

$$\mathit{OA}=\frac{\mathit{TP}+TN}{\mathit{TP}+TN+FP+FN}$$

where TP and TN are the numbers of IBPs and non-IBPs that were correctly predicted, respectively; FP denotes the number of non-IBPs that were predicted as IBPs, while FN denotes the number of IBPs that were predicted as non-IBPs. The ROC curve is a type of comprehensive index that is drawn from the continuous variable of (1 – Sp) and Sn, which are the abscissa and the ordinate, respectively. The AUC could quantitatively evaluate the performance of the model. The greater the AUC, the better the performance of the prediction models is.

3. Results and discussion

3.1. Performance evaluation based on 10-fold cross-validation test and the independent data test

To find an appropriate way to represent the protein sequences, we investigated the performances of four feature extraction strategies: PseCKSAAP, PseCKSAAP + DDE, PseCKSAAP + DDE + CTD, and PseCKSAAP + DDE + CTD + QSOrder. The ANOVA combined with the IFS technique was used to evaluate and select the optimal features. Since there are four feature extraction strategies and two search methods (grid search and Bayesian search) for hyperparameter optimization, the IFS process was run eight times and eight models were constructed. The AUC of each feature subset was investigated using RF with 10-fold cross-validation on the training dataset. The feature subset that could produce the maximum AUC on the training dataset was regarded as the best features and was used to construct the model. After that, the performance of the models was examined on the testing dataset.

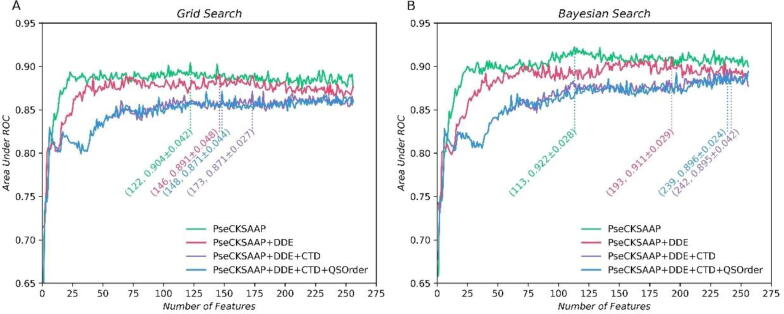
In the IFS curves using grid search (Fig. 2A), with the number of features increasing, the average AUCs rapidly rise to above 0.8 and then stabilize between 0.8 and 0.9. The curve of PseCKSAAP rises to the platform fastest in the first 25 features, and PseCKSAAP + DDE is slightly worse. The other two curves are very similar to each other. Before about 40 features, their AUCs fluctuate about 0.8 and rise rapidly to about 0.85. However, they are lower than the curve of PseCKSAAP + DDE. In the IFS curves using Bayesian search (Fig. 2B), the average AUCs also rapidly rise to more than 0.8. For PseCKSAAP, its AUCs slowly stabilize at about 0.9, and other AUCs of other strategies stabilize between 0.85 and 0.9. These IFS curves are in a similar tendency to the same feature extraction strategy in Fig. 2A.

Fig. 2.

The IFS curves of different search methods and feature extraction strategies on the 10-fold cross-validation test on the training dataset. The data in brackets are the best results of IFS curves that reached the highest average AUCs. (A) Grid search. (B) Bayesian search.

The results in Fig. 2 also showed that the IFS curves of PseCKSAAP are higher than other curves obtained from other features on the training dataset. By comparing the Bayesian search with the grid search, we found that PseCKSAAP achieves the maximum AUC of 0.922 when the feature dimension is 113 by using Bayesian search (Fig. 2B), whereas the maximum AUC of 0.904 when the feature dimension is 122 by using grid search (Fig. 2A). It indicates the Bayesian method can search for more feasible parameter settings and gain better performance. The result is not surprising because the Bayesian search method can explore wider spaces in a shorter time and gain better returns with some probability.

To further examine the robustness of the 8 optimal models obtained by different combinations and optimized by the two search methods, independent data was used. Results were recorded in Table 2. The ROC curves can demonstrate the predictive capability of the proposed method across the entire range of decision values. Thus, the ROC curves of eight models were plotted in Fig. S1.

Table 2.

The performance comparison of models on the training dataset and testing dataset using different search methods and feature extraction strategies.

Search Method	Features	AUCtraining	AUCtest	OA(%)	MCC	Sn(%)	Sp(%)	AA(%)
Grid	PseCKSAAP (122D)	0.904 ± 0.042	0.757	70.77	0.430	78.26	66.67	72.46
	PseCKSAAP + DDE (146D)	0.891 ± 0.048	0.808	75.38	0.517	82.61	71.43	77.02
	PseCKSAAP + DDE + CTD (173D)	0.871 ± 0.027	0.836	81.54	0.596	73.91	85.71	79.81
	PseCKSAAP + DDE + CTD + QSOrder (148D)	0.871 ± 0.044	0.804	78.46	0.515	60.87	88.10	74.48
Bayesian	PseCKSAAP (112D)	0.922 ± 0.028	0.751	73.85	0.558	95.65	61.90	78.78
	PseCKSAAP + DDE (193D)	0.911 ± 0.029	0.865	76.92	0.578	91.30	69.05	80.18
	PseCKSAAP + DDE + CTD (242D)	0.895 ± 0.042	0.774	67.69	0.480	95.65	52.38	74.02
	PseCKSAAP + DDE + CTD + QSOrder (239D)	0.899 ± 0.038	0.805	75.38	0.486	73.91	76.19	75.05

Note: Values are expressed as mean ± standard deviation in AUC_training metric that indicates the results on the training dataset. The values highlighted in bold denote the best performance value for each metric across search methods and feature extraction strategies.

From Table 2, we noticed that 193 optimal features obtained from PseCKSAAP + DDE by Bayesian search displays the best performance (AUC = 0.865) on the test dataset suggesting that the model has the best generalization ability, though optimal features from PseCKSAAP has the better result on the training dataset. By comparing the AUCs on independent data with it on the training dataset, we could notice a wide disparity, implying an overfitting problem. Since RF is a kind of ensemble method, it weakens the effects of some abnormal trees and strengthens the stability of the forest. Otherwise, the problem would be worse. In addition, due to the small sample size, it is not ideal to split the benchmark dataset into three datasets for training, validation, and independent test. It is possible to adjust the model and avoid overfitting by reducing the error rate on the validation dataset. However, the independent data test could provide enough information to examine models’ performance. Thus, we considered the model based on the selected 193 features as the best model for predicting ion binding protein.

We thought that if features of the model included CTD features and QSOrder features, the performance of the model would be improved. But surprisingly, the addition of these features reduces the prediction performance of the model. This may be because the dataset has some abnormal samples that are difficult to distinguish, or the training dataset is not enough to provide sufficient samples, resulting in insufficient learning and the ability of the model to distinguish between IBPs and non-IBPs worse. This demonstrates that it is not true that the more features, the better the performance of the model.

3.2. Performance comparison of different algorithms

The comparison with other algorithms could provide more information and confidence for developing better models. Because of the best results based on PseCKSAAP + DDE as shown in Table 2, these features were inputted into various algorithms. However, due to the high time cost of the grid search, we only used Bayesian search. Here, we only investigated the prediction performance of random forest (RF), support vector machine (SVM), decision tree (DT), Naïve Bayes (NB), and AdaBoost (AB), which were listed in Table 3.

Table 3.

The performance comparison of different algorithms on the training dataset and testing dataset using Bayesian search and PseCKSAAP + DDE for feature extraction.

Algorithm	AUCtraining	AUCtest	OA(%)	MCC	Sn(%)	Sp(%)	AA(%)
SVM (229D)	0.962 ± 0.028	0.769	69.23	0.500	95.65	54.76	75.21
DT (11D)	0.775 ± 0.059	0.698	60.00	0.386	95.65	40.84	68.06
NB (243D)	0.950 ± 0.033	0.693	63.08	0.458	100.00	42.86	71.43
RF (193D)	0.911 ± 0.029	0.865	76.92	0.578	91.30	69.05	80.18
AB (254D)	0.926 ± 0.041	0.671	60.00	0.386	95.65	40.48	68.06

Note: Values are expressed as mean ± standard deviation in AUC_training metric that indicates the results on the training dataset. The values highlighted in bold denote the best performance value for each metric across search methods and feature extraction strategies.

According to Table 3, the RF model is the best since it has the highest AUC on test data. Although the SVM, NB, and AB models can achieve relatively high AUCs on the training dataset, their AUC_test are lower than that of the RF model, suggesting that there are overfitting problems in these models. The ROCs of these models on test data were plotted in Fig. S2, and the results also demonstrate that the RF model outperforms other models. In the IBPred package, the optimum RF model with 193 features was set as the default predictor. Users can also manually select other models, including those recorded in Table 2.

3.3. Feature analysis

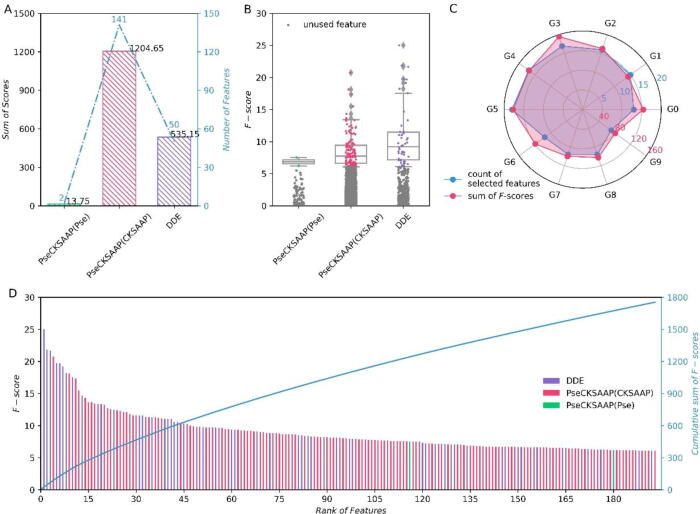
In the IFS process, the ANOVA was utilized to assess the significance of features. The F-scores can explain why the model has such a performance. Fig. 3 depicts basic statistical information about the 193 features with F-scores that are involved in building the optimal RF model.

Fig. 3.

The basic statistical information about the features of the optimal model. The PseCKSAAP(Pse) means the features extracted from the physicochemical properties in PseCKSAAP and the PseCKSAAP(CKSAAP) represents the features extracted from the CKSAAP part. (A) The sum of F-scores and the total number of features. (B) The F-scores of features are colored to indicate that they were applied in the optimal model. With a line at the median, the box stretches from the first quartile (Q1) to the third quartile (Q3) of F-scores. And the whiskers extend from the box by 1.5 times the inter-quartile range (IQR), which equals Q3 - Q1. The grey dots represent the features that were not involved in the optimal model construction (that is, were not contained in the optimal feature subset). (C) The counts of selected features and their sum of F-scores based on different gaps. “G0” to “G9” denote the 0–9 gap dipeptides, respectively. (D) The ranked features and their F-scores, as well as the cumulative sum of F-scores from 0 to all features used in the optimal model sequentially.

Among all the features involved in the construction of the optimal model, the physicochemical features are the least, the CKSAAP features are the most, and the DDE features are in the middle (Fig. 3A). Physicochemical features are not only rare, but also have low F-scores (Fig. 3B, D). Therefore, it should try more methods and strategies to extract useful physicochemical features that enhance the physicochemical property representation of proteins. The DDE method is the most efficient since 12.50 % of the original features (50 / 400) were applied to build the optimal model. In comparison, around 1.43 % and 3.53 % of features were selected from properties and CKSAAP, respectively. Most of the top-15 features (Fig. 3D) are DDE features (Fig. 3B), which further demonstrates that the DDE method is the most efficient.

The sum of F-scores of each “gap feature” suggests that their average contributions to the model’s discriminability are close (Fig. 3C). “G3” has the maximum sum of F-scores, whereas “G9” has the least. “G0”, “G3”, and “G6” features provide hints that their graphic points of sums of F-scores exceed the points of counts further than their counterparts. It is easy to infer that the composition of 0, 3, or 6-gap dipeptides in IBPs is significantly different from those in non-IBPs. One possibility is that amino acids attract or repel each other, and the local sequence forms a fragile structure. The different compositions of 0, 3, and 6-gap dipeptides between IBPs and non-IBPs lead to the disparity formation of specific structures for the acceptance of ions. However, amino acids can also attract or repel ions by their structure and physicochemical properties, thus affecting the structure formation. Therefore, it is necessary to further confirm the effect of these gap dipeptides.

Since both CKSAAP and DDE are dipeptide-based methods, the intersection of dipeptide features is most noteworthy. The heatmaps of F-scores of CKSAAP and DDE features extracted from the training dataset have been plotted in Fig. S3. All significant dipeptide features (p ≤ 0.001) of MAX_CKSAAP (a series of maximum scores of dipeptide features across the range of 0–9 gaps, Fig. S3) and DDE in the training dataset are recorded in Table 4.

Table 4.

Significant dipeptide features (p ≤ 0.001) in MAX_CKSAAP and DDE of training dataset.

MAX_CKSAAP	Intersection	DDE
NI, ND, DI, VF, QA, SD, CD, RK, IN, CN, AH, GM, NL, VW, CT, IS, GI, DW, CV	EC, II, YD	RL, VR, SR, ID, YD, RS, PP, PR, KF, FM, RV, KN

The dipeptides “EC”, “II”, and “YD” are in the intersection (Table 4), and their corresponding dipeptide features’ F-scores rank among the top few of all features. These dipeptide features deserve further research. Most significant CKSAAP features contain cysteine (C), aspartic acid (D), isoleucine (I), and asparagine (N), while DDE features contain more arginine (R) (Table 4). Additionally, The MAX_CKSAAP (Fig. S3) gathers strong signals at the C cluster, D cluster, I cluster, and N cluster (the clusters mean the dipeptides starting with C, D, I, or N), while the DDE has an obvious R cluster. Because the composition of dipeptides is related to the theoretical composition level that is fixed by codon numbers, the R becomes more significant in DDE features.

Glutamate (E), D and R are hydrophilic negatively charged amino acids, while R has a relatively long group. I and tyrosine (Y) are hydrophobic neutral amino acids, while Y has an aromatic ring. C and N are hydrophilic neutral amino acids, while C has sulfur to form disulfide bonds and fold protein sequences. “EC”, “II”, and “YD” (Table 4) corresponding significant features are “EC.0”, “II.0”, “II.6”, and “YD.0”. We believe that C and D in “EC.0” and “YD.0” can attract positively charged ions. However, we do not know the significance of I in “II.0”, “II.6”. One possible answer is that “II.0” and “II.6” have higher composition in non-IBPs. For E, D, R, I, Y, C, and N, their structure and physicochemical properties contribute to the binding of ions. By manually checking the known ion-binding sites of IBPs in the benchmark dataset, C, D, and histidine (H) are the most ion-binding residues. There is a possible relationship between two amino acid distributions. However, the relatively high frequency of H that bind ions was not captured by CKSAAP and DDE.

3.4. Performance on the extra dataset and limitation of IBPred

The benchmark dataset used for the construction of IBPred are all collected from phages. Thus, the model is specific to identifying IBPs in phages. To investigate whether IBPred can be used to identify IBPs in other species, such as human, mouse, etc, we collected IBPs and non-IBPs from other species with similar conditions to the benchmark dataset. There are two points different from the condition of benchmark dataset collection: 1) “NOT” query keywords “phage” in Organism; 2) The Protein Existence is “Evidence at protein level” to reduce the number of proteins. The CD-HIT [44], with an identity threshold of 40 %, was also utilized to remove redundant sequences. Finally, 14,101 IBPs and 12,924 non-IBPs were retained as the extra independent dataset. The dataset is much larger than benchmark dataset. Then, we tested several models from the IBPred package on the extra dataset (Table 5).

Table 5.

The performance of different models on extra dataset.

Search Method	Model	AUC	OA(%)	MCC	Sn(%)	Sp(%)	AA(%)
Grid	RF-P (122D)	0.548	52.46	0.033	99.35	1.29	50.32
	RF-PD (146D)	0.617	59.15	0.179	74.56	42.33	58.45
	RF-PDC (173D)	0.543	52.32	0.016	97.22	3.33	50.28
	RF-PDCQ (148D)	0.448	46.88	−0.072	56.00	36.94	46.47
Bayesian	RF-P (112D)	0.576	52.33	0.028	99.82	0.51	50.16
	RF-PD (193D)	0.604	57.74	0.149	69.58	44.82	57.20
	RF-PDC (242D)	0.499	52.18	0.000	100.00	0.00	50.00
	RF-PDCQ (239D)	0.488	51.67	−0.017	95.77	3.56	49.66
Bayesian	SVM-PD (229D)	0.633	60.82	0.214	75.21	45.11	60.16
	DT-PD (11D)	0.542	53.71	0.068	93.21	10.62	51.91
	NB-PD (243D)	0.597	58.89	0.180	82.63	32.99	57.81
	ABC-PD (254D)	0.624	58.13	0.179	89.48	23.93	56.70

Note: “P” is PseCKSAAP, “PD” is PseCKSAAP + DDE, “PDC” is PseCKSAAP + DDE + CTD, “PDCQ” is PseCKSAAP + DDE + CTD + QSOrder. The values highlighted in bold denote the best performance value for each metric across models.

The results in Table 5 show that SVM-PD (229D) has the best performance (AUC = 0.633) on extra dataset, while RF-PD (193D), the optimal model on test dataset from phage, is not satisfactory. It is surprising but reasonable that these models do not have good performances on the extra dataset as the test dataset. This indicates that the protein sequences in other species are quite different from those in phages. Since our features are extracted from phage proteins, these features could not well represent IBPs of other species. Additionally, the extra dataset is much larger than benchmark dataset. If we used the extra dataset as a new benchmark dataset to train models, the performance would be better. However, it is not this work’s theme. For a larger dataset, we need to consider neural networks, and the training time would be much longer.

Therefore, our proposed model cannot predict IBP in other species well. We recommend that users only use IBPred to identify IBPs in phages. If users want to identify IBPs in human, mouse, or other species, please try more models, such as SVM-PD (229D), ABC-PD (254D), etc., and consider the results comprehensively. In the future, we may try larger benchmark datasets, including more species and more methods in feature processing.

4. Conclusion

A random forest-based model was constructed for the accurate prediction of IBPs in phages. In this model, PseCKSAAP, DDE, CTD, and QSOrder were adopted to extract features. During the feature selection, the ANOVA was used to rank the importance of features, and then IFS was employed to determine the optimal feature subset. The RF model with the best performance was set as the default predictor. High AUCs indicated that the proposed method was an effective tool for predicting ion binding proteins. Based on the proposed method, a free and easy-to-use Python package has been built and is accessible at GitHub: https://github.com/ShishiYuan/IBPred, where the source code was also submitted.

Funding

This work has been supported by the grant from National Natural Science Foundation of China (62102067) and the Natural Science Foundation of the Inner Mongolia Autonomous Region (2018BS03021).

CRediT authorship contribution statement

Shi-Shi Yuan: Methodology, Software, Validation, Formal analysis, Data curation, Writing – original draft, Project administration. Dong Gao: Formal analysis, Investigation, Visualization. Xue-Qin Xie: Formal analysis, Investigation, Visualization. Cai-Yi Ma: Formal analysis, Investigation, Visualization. Wei Su: Writing – review & editing. Zhao-Yue Zhang: Writing – review & editing, Funding acquisition. Yan Zheng: Resources, Writing – review & editing, Funding acquisition. Hui Ding: Conceptualization, Methodology, Resources, Writing – review & editing, Supervision, Project administration, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: