Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2023 Sep 1.
Published in final edited form as: J Neuroimaging. 2022 Apr 17;32(5):968–976. doi: 10.1111/jon.12997

Bayesian Deep Learning Outperforms Clinical Trial Estimators of Intracerebral and Intraventricular Hemorrhage Volume

Matthew F Sharrock 1, W Andrew Mould 2, Meghan Hildreth 2, E Paul Ryu 2, Nathan Walborn 2, Issam A Awad 3, Daniel F Hanley 2, John Muschelli 4
PMCID: PMC9474710  NIHMSID: NIHMS1793888  PMID: 35434846

Abstract

Background and Purpose:

Intracerebral hemorrhage (ICH) and intraventricular hemorrhage (IVH) clinical trials rely on manual linear and semi-quantitative (LSQ) estimators like the ABC/2, modified Graeb and IVH scores for timely volumetric estimation from CT. Deep learning (DL) volumetrics of ICH have recently approached the accuracy of gold-standard planimetry. However, DL and LSQ strategies have been limited by unquantified uncertainty, in particular when ICH and IVH estimates intersect. Bayesian deep learning methods can be used to approximate uncertainty, presenting an opportunity to improve quality assurance in clinical trials.

Methods:

A DL model was trained to simultaneously segment ICH and IVH using diagnostic CT data from the Minimally Invasive Surgery Plus Alteplase for ICH Evacuation (MISTIE) III and Clot Lysis: Evaluating Accelerated Resolution of IVH (CLEAR) III clinical trials. Bayesian uncertainty approximation was performed using Monte-Carlo dropout. We compared the performance of our model with estimators used in the CLEAR IVH and MISTIE II trials. The reliability of planimetry, DL and LSQ volumetrics in the setting of high ICH and IVH intersection is quantified using consensus estimates.

Results:

Our DL model volume correlations and median Dice scores of 0.994 and 0.946 for ICH in MISTIE II, and 0.980 and 0.863 for IVH in CLEAR IVH respectively, outperforming LSQ estimates from the clinical trials. We found significant linear relationships between ICH uncertainty, Dice scores (r=−0.849) and relative volume difference (r=0.735).

Conclusion:

In our validation clinical trial dataset, DL models with Bayesian uncertainty approximation provided superior volumetric estimates to LSQ methods with real-time estimates of model uncertainty.

Keywords: Intracerebral Hemorrhage, Neuroimaging, Clinical Trials, Neural Networks

Introduction

Patients with intracerebral hemorrhage (ICH) are at risk of significant morbidity and mortality with the volume and location of the hematoma and the presence and volume of intraventricular hemorrhage (IVH) being well established predictors of outcome.1–6 On presentation, approximately 40% of ICH patients will have IVH, and during the natural course of the disease, a further 15% will develop it in a delayed fashion.7,8 Volumetric thresholds for the prediction of poor functional outcome have been reported as an ICH volume of greater than 30ml or an IVH volume of greater than 5ml.6,9,10 Reduction of ICH or IVH volume has been a therapeutic target in recent and ongoing randomized controlled trials.11–14

In order to support expedient screening and enrollment, trial investigators at clinical sites have utilized linear and semi-quantitative estimates (LSQ) of ICH and IVH volume to assess eligibility and provide primary or secondary outcome measures.7,14–16 Previously described and validated metrics include the linear ABC/2 formula to estimate ICH volume, and for IVH, semi-quantitative scoring systems such as the modified Graeb Score (mGS) and the IVH score (IVHS).2,16,17 LSQ estimates have been shown to be predictive of functional outcome and are considered to have sufficient inter-rater reliability (IRR) for clinical trial use.9,11,18 However, there are known limitations. The ABC/2 formula is less accurate when estimating the volume of lobar, complex hemorrhages and those with a volume of greater than 30ml.19–21 The mGS has reduced accuracy for IVH volumes of > 40ml and does not have a validated volumetric conversion formula17,22 The IVHS provides an internally validated exponential conversion of eIVHS/5 for IVH volume in ml.18,23,24

Deep neural network (DNN) models have recently been utilized for 2D segmentation and volumetric estimation of ICH25,26 Despite the large percentage of patients with co-occurring ICH and IVH, multi-class models of separate ICH and IVH have only recently been reported for hemorrhagic traumatic brain injury (TBI) lesions and primary ICH with small IVH volumes.27

Bayesian statistical methods provide a formalism for understanding and quantifying uncertainty associated with predictions by DNNs.28–30 Bayesian deep learning methods create probabilistic segmentations and uncertainty by sampling variations of the DNN itself in order to obtain a distribution of model parameters.31,32 This approach has been used to perform probabilistic segmentation with uncertainty estimation of anatomic structures, brain tumors, multiple sclerosis and ischemic stroke lesions.31,33–38

We utilised data from the Minimally Invasive Surgery Plus Alteplase for ICH Evacuation (MISTIE) and Clot Lysis: Evaluating Accelerated Resolution of IVH (CLEAR) clinical trials precise core lab segmentations of ICH and IVH volumes11–13,16,39 We will refer to the phase III trials as MISTIE III and CLEAR III and the phase II trials as MISTIE II and CLEAR IVH as this is how they are reported in the literature.

We tested three hypotheses: First, that the volume of ICH can be estimated reliably by human raters and DNN methods in the setting of significant intersection between ICH and IVH. Second, that DNN multi-class segmentation of ICH and IVH trained with combined data from the phase III CLEAR and MISTIE studies could outperform LSQ estimators in independent data from the phase II studies. Third, that Bayesian uncertainty approximation is correlated with ICH segmentation quality.

Methods

Data

Data in this study was from the phase II and phase III MISTIE and the phase II and phase III CLEAR multi-center randomized controlled trials. The use of CT imaging data from the MISTIE and CLEAR trials for DNN model training was approved by the Johns Hopkins Medicine institutional review board.

All images used were non-contrast CT images produced with a soft-tissue convolutional kernel, commonly sampled along the axial plane at 5mm intervals. All data was prior to randomization. Basic demographics and imaging information are in Table 1. Ground truth ICH and IVH planimetry volumes were manually segmented using Osirix imaging software (v10.0, Pixmeo, Geneva, CH) by expert raters formally trained in volumetric assessment and quantification of ICH and IVH of CT scans in accordance with the CLEAR and MISTIE protocols. All ICH and IVH estimations were verified by a board certified neurologist and board certified neurointensivist both with extensive clinical trial neuroimaging experience.

Table 1.

Demographics and imaging metrics for the MISTIE and CLEAR clinical trials.

Trial CLEAR IVH MISTIE II CLEAR III MISTIE III
Subjects (n) 51 135 500 499
Age (years) 56 (48, 64) 61 (54, 72) 59 (51, 67) 62 (52, 71)
Female (n(%)) 17 (33.3%) 44 (32.6%) 223 (44.6%) 194 (38.9%)
Race/Ethnicity (n (%))
African American 24 (47.1%) 40 (29.6%) 170 (34%) 87 (17.4%)
Hispanic 1(1.9%) 13(9.6%) 60 (12.0%) 68 (13.6%)
Asian 5 (9.8%) 5 (3.7%) 1 (0.2%) 2 (0.4%)
Caucasian 16 (31.4%) 77 (57.1%) 305 (61.0%) 374 (74.9%)
Other/Unknown 5 (9.8%) 0 (0.0%) 0 (0.0%) 0 (0.0%)
ICH Volume (ml) 5.6 (1.38,15.1) 34.8 (23.3, 50.7) 8.01 (3.0, 13.8) 41.8 (30.8, 54.5)
IVH Volume (ml) 37.8 (17.6, 57.2) 0 (0, 2.34) 24.5 (14.2, 39.8) 0 (0, 1.9)
Ictus to 1st CT (hrs) 1.00 (0.48, 1.85) 2.11 (1.18, 4.61) 0.96 (0.56, 2.03) 2.01 (1.20,5.10)
Open in a new tab

Metrics and demographics are listed by total number (n), hours (hrs), percentage (%) or median and interquartile range.

Image Processing

CT imaging data and hemorrhage masks were converted to the Neuroimaging Informatics Technology Initiative format using dcm2niix (v1.0.2, www.github.com/rordenlab/dcm2niix) Measures to ensure the accuracy of 3D volumetric data included gantry tilt correction and normalization of data with unequal slice thickness using our previously published, publicly available preprocessing pipeline including brain extraction and template registration.26

Intersection Estimation and Volume

The IRR of volumetric estimates where there is significant interface between ICH and IVH is unknown. ICH and IVH surface polygon meshes were constructed from planimetry estimates using the marching cube algorithm,41 and the surfaces of ICH, IVH and their intersection were computed using boolean operations in Blender (v.3.0.1, Blender Foundation, Amsterdam, NL, 2018, www.blender.org)(Figure 1). We denoted the ICH ventricular intersection area (VIA) and the ratio of the VIA to total ICH surface area, we called the ventricular intersection ratio (VIR). We a priori determined that a VIR > 0.25 would qualify for an evaluation with multiple raters (n = 3) using the same protocol. In order to create a consensus segmentation, the expectation-maximization algorithm for simultaneous truth and performance level estimation (STAPLE), a robust estimator of underlying ground truth from multiple raters was utilized.42,43 Deviation from the consensus by each rater was evaluated by rater-STAPLE Dice coefficient, volume correlation and absolute volume difference.

Figure 1.

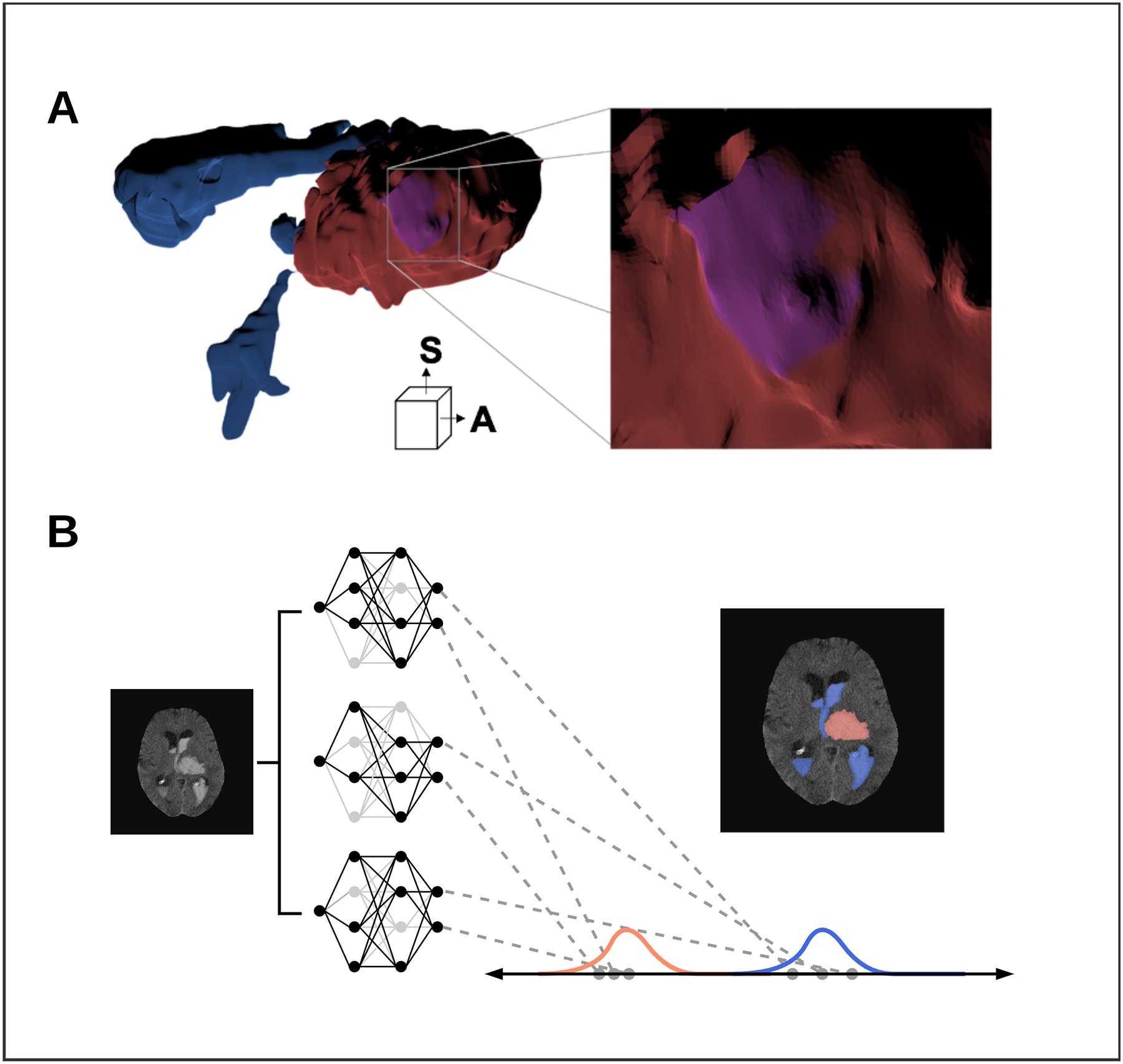
Figure 1.

Open in a new tab

Advanced imaging techniques including, ventricular intersection area (VIA) mesh construction and Bayesian deep learning uncertainty approximation.

A) 3D inner-surface renderings of ICH (Red), IVH (Blue) and the VIA (Purple) generated by a single rater. Anterior (A) and superior (S) directions are displayed Right: zoomed portion of the VIA along the inner ICH surface. B) Bayesian approximation in a deep neural network by Monte-Carlo dropout. Networks are loaded with different nodes stochastically ‘dropped out’ (light-grey) to create a group of related networks. Each segmentation is a distribution of ICH (red) and IVH (blue) segmentations.

Deep Neural Networks

We trained two networks: V-Net, an established DNN designed to segment 3D volumetric medical imaging data and a customized DNN we call our Intracerebral intraVentricular Network (IV-Net) (Figure 2).44 Our models were developed and validated using Tensorflow (version 2.3.0, Google, Mountainview, CA, www.tensorflow.org). IV-Net utilizes the encoder-decoder framework of V-Net but with the addition of architectural changes with two main goals: contextual propagation and uncertainty estimation. We employed two validated strategies: dilated convolutions, that forward contextual information through the encoder and multiclass attention-gating which helps focus learning on important context in the decoder.45–47 We utilized a 1ml threshold for the existence of ICH and IVH in our model output based on prior work.48 We trained the model for 200 epochs on the combined phase III MISTIE and CLEAR diagnostic scan datasets leaving out a ratio of 0.1 randomly for testing.

Figure 2.

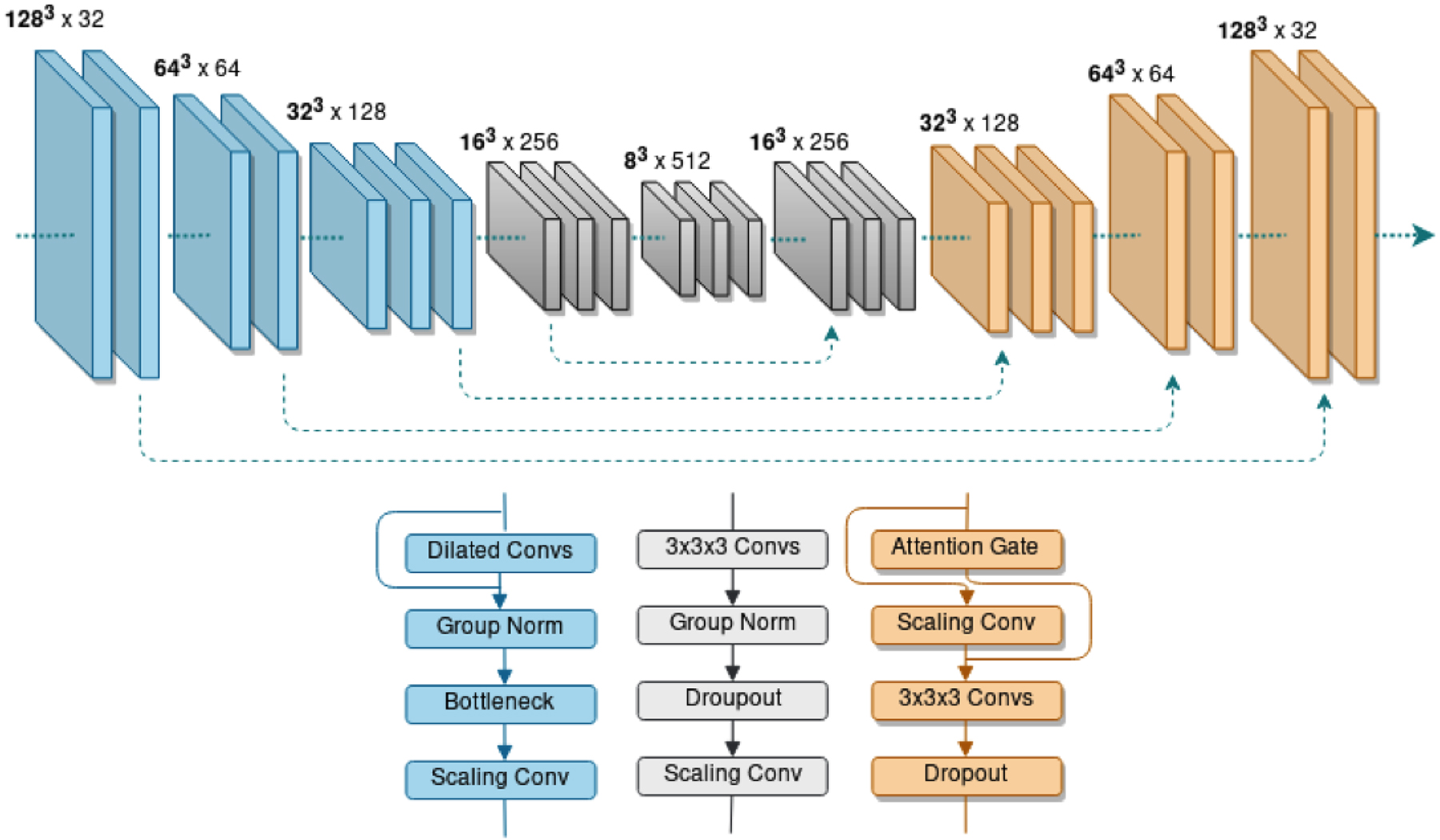
Figure 2.

Open in a new tab

IV-Net our Deep Neural Network automated method is a 5-layer network (Top) with 3 different architectural blocks (Bottom). In the encoder layers (Blue) densely connected dilated convolutions (Dilated Convs) are combined with Group Normalization (Group Norm), a Bottleneck layer and a scaling convolution (Scaling Conv). In the central layers (Grey) convolutions (3×3×3 Convs) are combined with Group Norm and a dropout layer (Dropout) before a Scaling Conv. The decoder layers (Orange) include Attention Gates. Skip connections (dashed arrows) span the network.

Bayesian Uncertainty Approximation

Uncertainty was estimated using Monte-Carlo Bernoulli dropout sampling, a theoretically and experimentally validated Bayesian uncertainty approximation.31 We added dropout to each layer of our neural network and therefore obtain different variations of the network during each stochastic forward pass (Figure 1). Based on prior work in multiclass anatomic brain segmentation, we utilized 10 stochastic samples.33 Our uncertainty metric is derived from the percentage of uncertain voxels that do not appear in the majority voting estimate.31

Volume and Uncertainty Analysis

Comparing predictions from our two models and ground truth segmentations of ICH from MISTIE II and IVH for CLEAR-IVH, we report the Dice score between predicted and ground truth segmentations,49 volume Pearson correlation coefficients and RMSE. The higher performing model was then evaluated on ICH, IVH and ICH + IVH from both trials as well as absolute volume difference < 5ml as 5ml is the clot stability threshold in the MISTIE and CLEAR trial protocols. To evaluate our uncertainty metric, we combined data from the phase II trials. Comparisons of Dice scores and volume metrics used the Kruskal-Wallis test between groups and then Wilcoxon signed rank test with Bonferroni correction,50 and p <.05 was considered statistically significant. 95% confidence intervals (95% CI) are provided for correlation coefficients. Analyses were conducted in R, (version 3.5.3, R Foundation for Statistical Computing, www.r-project.org)

Results

Linear and Semi-Quantitative Manual Estimators

LSQ estimator performance is summarized in Table 2. ICH volume ABC/2 estimates in the MISTIE II and CLEAR IVH trial were consistent with previous results at clinical trial sites and trial reading center, showing excellent correlation with planimetry volumes. However the percentage of scans below a threshold of < 5ml absolute volume difference was overall low.

Table 2.

Performance metrics for LSQ estimators at clinical sites and trial reading center.

Clinical Trial Subtype Estimator Volume Correlation (95% CI) RMSE (ml) Abs. Vol Diff. (ml) % < 5ml
MISTIE II ICH
(n=135)		 Site ABC/2 0.815
(0.75, 0.86)		 11.63 8.23
(3.67, 13.7)		 64.1%
RC ABC/2 0.916
(0.88, 0.94)		 12.38 5.38
(2.01, 10.0)		 48.1%
IVH
(n=48)		 eIVHS/5 0.759
(0.61, 0.86)		 7.13 1.34
(0.67, 5.43)		 68.9%
Site mGraeb 0.756
(0.60, 0.86)		 - - -
CLEAR IVH ICH
(n=40)		 RC ABC/2 0.826
(0.69, 0.90)		 5.62 1.64
(0.619, 5.61)		 57.6%
IVH
(n=51)		 eIVHS/5 0.690
(0.51, 0.81)		 22.34 12.24
(5.41, 25.0)		 21.2%
Site mGraeb 0.306
(0.03, 0.53)		 - - -
Open in a new tab

Performance metrics are listed for the for ABC/2, modified Grab Score (mGraeb) and from the clinical sites and ABC/2 and IVH Score volume estimates (eIVHS/5) from the centralized reading center (RC). Total subjects (n) are shown for each estimator. Volume Correlation is the Pearson correlation coefficient between the estimator and planimetry volumes with 95% confidence interval (95% CI). RMSE is the root mean squared error. Abs. Vol. Diff. is the absolute volume difference. % < 5ml is the percentage of predictions that were within 5ml.

IVH estimates showed a reduce correlation compared with ABC/2, in particular the site mGraeb score had a low correlation with IVH volume. LSQ estimates show an overall bias towards overestimating ICH and underestimating IVH (Figure 3).

Figure 3.

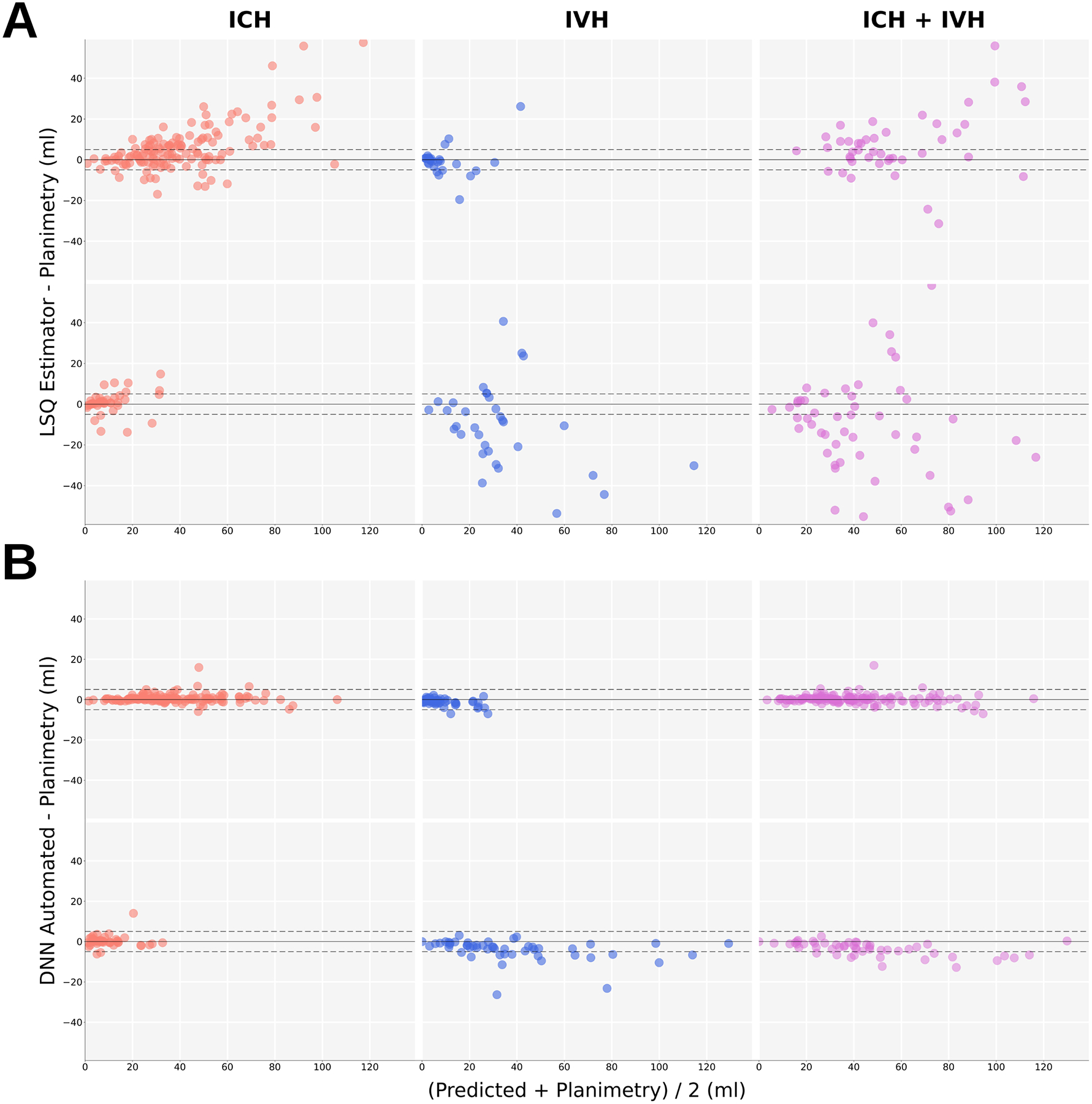
Figure 3.

Open in a new tab

Bland-Altman (BA) plots of linear and semi-quantitative (LSQ) estimates and Deep neural network (DNN) automated segmentation vs semi-automated planimetry. The dashed lines show −5ml and +5ml boundaries. A) BA plots of LSQ estimators vs planimetry. ABC/2 estimates of ICH (red), IVH Score estimates (blue) and combined ABC/2 and IVH Score volume estimates of ICH + IVH (purple) from MISTIE II (top row) and CLEAR IVH (bottom row) trials. B) DNN Automated segmentation vs planimetry volumes of ICH (red), IVH (blue) and combined ICH + IVH (purple) from CLEAR-IVH (top row) and MISTIE II trials (bottom row).

Ventricular Intersection and ICH Volume Estimation

Ventricular intersection metrics indicated that 12/51 (23.5%) in CLEAR-IVH and 0/135 (0%) in MISTIE II had a VIR > 0.25. An inter-rater analysis compared with the STAPLE consensus showed a mean Dice of 0.803, absolute volume difference of 1.47 ± 2.03 ml and volume correlation of 0.744 (95% CI [0.30, 0.92]). Kruskal-Wallace testing indicated there was no statistically significant difference across raters from STAPLE estimates by absolute volume difference (χ2 = 1.31, p = 0.52), but there was a significant difference for Dice (χ2 = 8.45, p = 0.02). Wilcoxon testing showed rater 1 did not have a significant relationship by Dice (W = 113, p = 0.151).

Deep Neural Networks with Bayesian Uncertainty Approximation

VNet and IV-Net performances on ICH segmentation were compared by Dice scores (0.904 vs 0.946), volume correlation (0.977 vs 0.994) and RMSE (4.21 vs 2.15). IVH segmentations similarly showed a trend toward accuracy in IV-Net by Dice scores (0.773 vs 0.863), volume correlations (0.960 vs 0.985) and RMSE (11.97 vs 6.67). These results favored IV-Net but were not statistically significant between the two models.

Additional analysis of IV-Net, now our DNN automated method was performed on ICH from CLEAR-IVH and IVH from MISTIE II, see Table 3. DNN automated estimates of IVH from MISTIE II maintained a volume correlation of 0.980 (95% CI [0.96, 0.99]). In CLEAR IVH, IVH results were favorable compared with LSQ estimators, with volume correlation of 0.985 (95% CI [0.97, 0.99]) and absolute volume difference showing a significant difterence from LSQ estimators (χ2 = 77, p < .001) and the strongest relationship with planimetry (W = 1214, p < .001). ICH predictions in CLEAR IVH showed slightly lower Dice coefficient of 0.881, volume correlation of 0.931 (95% CI [0.87, 0.96]) and a RMSE of 2.95. Median performance scans are shown in Figure 4A.

Table 3.

Performance metrics for DNN segmentation of ICH and IVH versus semi-automated planimetry.

Clinical Trial Subtype Dice Volume Correlation (95% CI) RMSE (ml) Abs. Vol Diff. (ml) < 5ml
MISTIE II ICH
(n=135)		 0.946 0.994
(0.99, 0.996)		 2.15 0.566
(0.264, 1.43)		 96.3%
IVH
(n=48)		 0.776 0.980
(0.96, 0.99)		 2.02 1.08
(0.463, 1.698)		 96.1%
ICH + IVH
(n=135)		 0.940 0.995
(0.99, 0.996)		 2.22 0.655
(0.339, 1.69)		 95.6%
CLEAR IVH ICH
(n=40)		 0.881 0.931
(0.87, 0.96)		 2.95 0.857
(0.388, 1.94)		 92.6%
IVH
(n=51)		 0.863 0.985
(0.97, 0.99)		 6.67 2.91
(1.52, 6.27)		 72.0%
ICH + IVH
(n=51)		 0.905 0.995
(0.99, 0.997)		 4.93 2.74
(1.19,5.80)		 70.0%
Open in a new tab

Total subjects (n) are listed for each study, then Dice score and volume correlation with 95% confidence interval (95% CI). RMSE is the root mean squared error in ml. Abs. Vol. Diff. is the absolute volume difference in ml by median and interquartile range.. %< 5ml is the percentage of predictions that were within 5ml.

Figure 4.

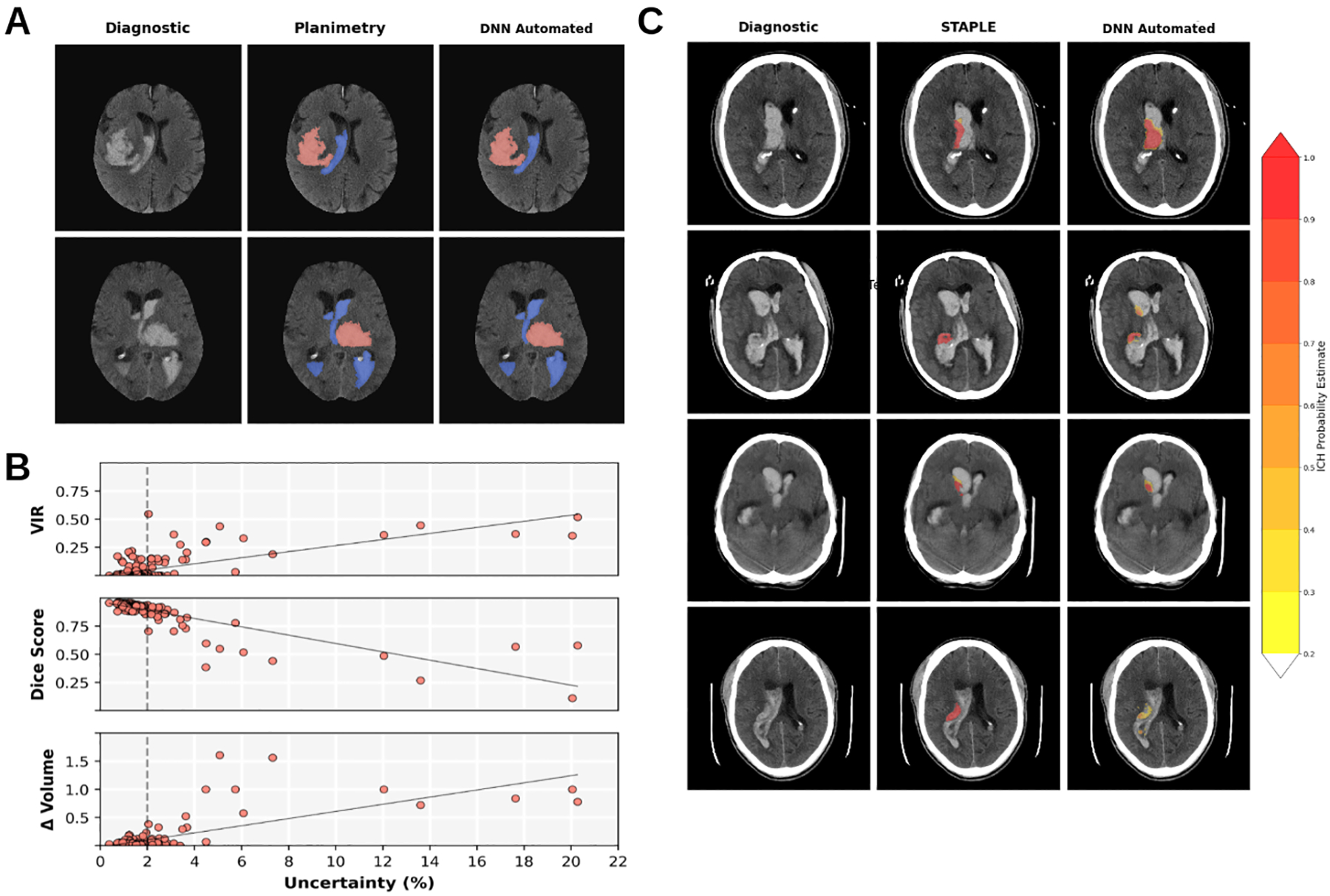
Figure 4.

Open in a new tab

Bayesian Deep Neural Network (DNN) segmentation images and uncertainty vs segmentation quality analysis. A) Median Dice score DNN automated segmentation images from MISTIE II (first row) and CLEAR IVH (second row) with ICH (red) and IVH (blue). B) Segmentation quality metrics vs Uncertainty (%) for majority voting ICH segmentations by from MISTIE II and CLEAR IVH. Top: Ventricular intersection ratio (VIR) vs Uncertainty (r= 0.699). Middle: Dice Scores vs Uncertainty (r=− 0.849). Bottom: The relative volume difference (Δ Volume) vs Uncertainty. For values beyond 2% (dashed lines) we see deviations from the linear relationships. C) Simultaneous truth and performance level estimation (STAPLE) and DNN Automated probability estimates of four patients with VIR > 0.25. On the left is the diagnostic scan, the center is overlayed with the planimetry STAPLE consensus estimate and right the DNN probabilistic output. Far right is a probability estimate colormap.

Figure 4B shows relationships between uncertainty and Dice scores with a correlation of −0.849 (95% CI [0.80, 0.89]), then relative volume difference with a positive correlation of 0.735 (95% CI [0.66, 0.79]) and then VIR showing a correlation of 0.699 (95% CI [0.62, 0.76]). with our uncertainty metric. We observed that both Dice scores and volume differences diverge from a linear relationship at > 2% uncertainty, and all scans with a VIR > 0.25 had > 2% uncertainty.

In the 12 patients with high VIR, ICH segmentation showed a mean Dice of 0.586 and volume correlation of 0.932 (95% CI [0.77, 0.98]) and absolute volume difference of 2.31 ± 4.02 ml. STAPLE and ICH probability estimates for four of these subjects are shown in Figure 4C, where lower probability outputs (yellow) may over or underestimate ICH compared with human raters, but high probability areas (red) agree volumetrically, even if overlap is reduced.

Discussion

Recent investigations of DNN segmentation of ICH and IVH have been reported in the literature for patients with TBI and primary ICH,27,48 but come with limitations as they only include small IVH volumes and do not quantify the degree of intersection or model uncertainty. In this study, we show that firstly despite significant ICH and IVH overlap, volumetric assessments by multiple raters are not significantly different, even though overlap metrics like Dice may significantly vary. We then showed that DNN volumetric estimates of ICH and IVH show improvent in image quality metrics over LSQ estimates in regards to volume correlation, absolute volume difference, RMSE and percentage of scans within 5ml volume. We found that Bayesian DNN uncertainty significantly correlates with lower Dice scores, higher relative volume difference and instances of high IVH/ICH intersection.

Uncertainty thresholds such as the 2% threshold in our paper, allow the selection of scans for additional review. In these cases, probability maps can be inspected and further interpreted by investigators examining the location, perihematomal density changes or clot textural features to help determine the location of ICH when admixed with IVH. In cases of model errors, the attention gates included in our model can be inspected by the trial imaging center as they add additional interpretability to the saliency maps in deep learning models.45

A limitation of this study is that it is biased towards patients with larger volumes of ICH or IVH and patients with tumors or vascular malformations were excluded from the trials. Our model was not designed as a screening tool for general CT scans to capture occurrences of ICH and IVH, but instead a volume quantification tool for patients pre-screened to have ICH and or IVH in multi-center clinical trials.

This study shows that automated methods can outperform LSQ methods where time constraints, human error and biases can potentially lead to inaccurate results, especially in patients with large ICH or IVH most at risk of a poor outcome and in need of intervention. We think that DNN methods of volume estimation still require human supervision and could take on a greater role in the clinical trial and clinical practice ecosystems once validated in prospective studies.

Acknowledgements and Disclosures

DFH reports personal fees from BrainScope, Neurotrope, Op2Lysis, Portola Pharmaceuticals, and medico-legal consulting, outside the submitted work. The other authors have no conflicts of interest to report.

Funding:

This work was supported primarily with grants from the National Institutes of Health (NIH), National Institute of Neurological Disorders and Stroke (NINDS), namely MISTIE III: 5U01NS08082405, CLEAR III: 5U01NS06285105, and MISTIE II: R01NS046309. Funding from the CLEAR IVH trial was given from the FDA: FDR00169306.

References

  • 1.Bhattathiri PS, Gregson B, Prasad KSM, Mendelow AD. Intraventricular hemorrhage and hydrocephalus after spontaneous intracerebral hemorrhage: results from the STICH trial. In: Brain Edema XIII Springer; 2006:65–8. [DOI] [PubMed] [Google Scholar]
  • 2.Broderick JP, Brott TG, Duldner JE, Tomsick T, Huster G. Volume of intracerebral hemorrhage: A powerful and easy-to-use predictor of 30-day mortality. Stroke 1993;24:987–93. [DOI] [PubMed] [Google Scholar]
  • 3.Gates PC, Barnett HJM, Vinters HV, Simonsen RL, Siu K. Primary intraventricular hemorrhage in adults. Stroke 1986;17:872–7. [DOI] [PubMed] [Google Scholar]
  • 4.Hemphill JC, Bonovich DC, Besmertis L, Manley GT, Johnston SC. The ICH Score. Stroke 2001;32:891–6. [DOI] [PubMed] [Google Scholar]
  • 5.Tuhrim S, Dambrosia JM, Price TR, et al. Intracerebral hemorrhage: External validation and extension of a model for prediction of 30-day survival. Ann Neurol 1991;29:658–63. [DOI] [PubMed] [Google Scholar]
  • 6.Tuhrim S, Horowitz DR, Sacher M, Godbold JH. Volume of ventricular blood is an important determinant of outcome in supratentorial intracerebral hemorrhage. Crit Care Med 1999;27:617–21. [DOI] [PubMed] [Google Scholar]
  • 7.Anderson CS, Huang Y, Wang JG, et al. Intensive blood pressure reduction in acute cerebral haemorrhage trial (INTERACT): a randomised pilot trial. Lancet Neurol 2008;7:391–9. [DOI] [PubMed] [Google Scholar]
  • 8.Dowlatshahi D, Demchuk AM, Flaherty ML, Ali M, Lyden PL, Smith EE. Defining hematoma expansion in intracerebral hemorrhage: Relationship with patient outcomes. Neurology 2011;76:1238–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Hwang BY, Bruce SS, Appelboom G, et al. Evaluation of intraventricular hemorrhage assessment methods for predicting outcome following intracerebral hemorrhage: Clinical article. Neurosurgery 2012;116:185–92. [DOI] [PubMed] [Google Scholar]
  • 10.Young WB, Lee KP, Pessin MS, Kwan ES, Rand WM, Caplan LR. Prognostic significance of ventricular blood in supratentorial hemorrhage: A volumetric study. Neurology 1990;40:616–9. [DOI] [PubMed] [Google Scholar]
  • 11.Hanley DF, Thompson RE, Muschelli J, et al. Safety and efficacy of minimally invasive surgery plus alteplase in intracerebral haemorrhage evacuation (MISTIE): a randomised, controlled, open-label, phase 2 trial. Lancet Neurol 2016;15:1228–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Hanley DF, Lane K, McBee N, et al. Thrombolytic removal of intraventricular haemorrhage in treatment of severe stroke: results of the randomised, multicentre, multiregion, placebo-controlled CLEAR III trial. Lancet 2017;389:603–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Hanley DF, Thompson RE, Rosenblum M, et al. Efficacy and safety of minimally invasive surgery with thrombolysis in intracerebral haemorrhage evacuation (MISTIE III): a randomised, controlled, open-label, blinded endpoint phase 3 trial. Lancet 2019;393:1021–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Labib MA, Shah M, Kassam AB, et al. The safety and feasibility of image-guided brainpath-mediated transsulcul hematoma evacuation: A multicenter study. Neurosurgery 2017;80:515–24. [DOI] [PubMed] [Google Scholar]
  • 15.Mayer SA, Brun NC, Begtrup K, et al. Efficacy and safety of recombinant activated factor VII for acute intracerebral hemorrhage. New Engl J Med 2008;358:2127–37. [DOI] [PubMed] [Google Scholar]
  • 16.Morgan T, Awad I, Keyl P, Lane K, Hanley D. Preliminary report of the clot lysis evaluating accelerated resolution of intraventricular hemorrhage (CLEAR-IVH) clinical trial. Acta Neurochir Suppl 2008;105:217–20. [DOI] [PubMed] [Google Scholar]
  • 17.Graeb DA, Robertson WD, Lapointe JS, Nugent RA, Harrison PB. Computed tomographic diagnosis of intraventricular hemorrhage. Etiology and prognosis. Radiology 1982;143:91–6. [DOI] [PubMed] [Google Scholar]
  • 18.Hwang BY, Appelboom G, Bruce SS, et al. Prospective validation of the IVH Score as a useful bedside tool for estimating intraventricular hemorrhage volume. Stroke 2011;42:e305. [Google Scholar]
  • 19.Kothari RU, Brott T, Broderick JP, et al. The ABCs of measuring intracerebral hemorrhage volumes. Stroke 1996;27:1304–5. [DOI] [PubMed] [Google Scholar]
  • 20.Wang CW, Juan CJ, Liu YJ, et al. Volume-dependent overestimation of spontaneous intracerebral hematoma volume by the abc/2 formula. Acta Radiologica 2009;50:306–11. [DOI] [PubMed] [Google Scholar]
  • 21.Webb AJS, Ullman NL, Morgan TC, et al. Accuracy of the ABC/2 Score for Intracerebral Hemorrhage: Systematic Review and Analysis of MISTIE, CLEAR-IVH, and CLEAR III. Stroke 2015;46:2470–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Morgan TC, Dawson J, Spengler D, et al. The modified graeb score: An enhanced tool for intraventricular hemorrhage measurement and prediction of functional outcome. Stroke 2013;44:635–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Hallevi H, Dar NS, Barreto AD, et al. The IVH Score: A novel tool for estimating intraventricular hemorrhage volume: Clinical and research implications. Crit Care Med 2009;37:969–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Duprey J, Dziodzio J, Palminteri J, Rughani A, Seder D. Failure to validate the IVH score as better than the ICH score alone to predict neurological outcome in intracerebral hemorrhage. Presented at the 41st Critical Care Congress; February 4–8, 2012; Houston [Google Scholar]
  • 25.Ironside N, Chen CJ, Mutasa S, et al. Fully automated segmentation algorithm for hematoma volumetric analysis in spontaneous intracerebral hemorrhage. Stroke 2019;50:3416–23. [DOI] [PubMed] [Google Scholar]
  • 26.Sharrock MF, Mould WA, Ali H, et al. 3D Deep neural network segmentation of intracerebral hemorrhage: Development and validation for clinical trials. Neuroinformatics 2021;19:403–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Zhao X, Chen K, Wu G, et al. Deep learning shows good reliability for automatic segmentation and volume measurement of brain hemorrhage, intraventricular extension, and peripheral edema. Eur Radiol 2021;31:5012–20. [DOI] [PubMed] [Google Scholar]
  • 28.Lampinen J, Vehtari A. Bayesian approach for neural networks - Review and case studies. Neural Netw 2001;14:257–74. [DOI] [PubMed] [Google Scholar]
  • 29.Hao W, Yeung DY. Towards Bayesian deep learning: A framework and some existing methods. IEEE Trans Knowl Data Eng 2016;28:3395–408. [Google Scholar]
  • 30.Weiss M, Tonella P. Fail-safe execution of deep learning based systems through uncertainty monitoring. IEEE ICST 2021:24–35. [Google Scholar]
  • 31.Gal Y, Ghahramani Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. ICML 2016;2016:1050–9. [Google Scholar]
  • 32.Camarasa R, Bos D, Hendrikse J, et al. Quantitative comparison of Monte-Carlo dropout uncertainty measures for multi-class segmentation. LNCS 2020;12443:32–41. [Google Scholar]
  • 33.Li W, Wang G, Fidon L, Ourselin S, Cardoso MJ, Vercauteren T. On the compactness, efficiency, and representation of 3D convolutional networks: Brain parcellation as a pretext task. Inf Process Med Imaging 2017;10265:348–60. [Google Scholar]
  • 34.Kwon Y, Won JH, Kim BJ, Paik MC. Uncertainty quantification using Bayesian neural networks in classification: Application to biomedical image segmentation. Comput Stat Data Anal 2020;142:106–16. [Google Scholar]
  • 35.Nair T, Precup D, Arnold DL, Arbel T. Exploring uncertainty measures in deep networks for Multiple sclerosis lesion detection and segmentation. Med Image Anal 2020;59:101557. [DOI] [PubMed] [Google Scholar]
  • 36.Jungo A, Balsiger F, Reyes M. Analyzing the quality and challenges of uncertainty estimations for brain tumor segmentation. Front Neurosci 2020;14:282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Zhao G, Liu F, Oler JA, Meyerand ME, Kalin NH, Birn RM. Bayesian convolutional neural network based MRI brain extraction on nonhuman primates. Neuroimage 2018;175:32–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Wang G, Li W, Aertsen M, Deprest J, Ourselin S, Vercauteren T. Aleatoric uncertainty estimation with test-time augmentation for medical image segmentation with convolutional neural networks. Neurocomputing 2019;338:34–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Dey M, Stadnik A, Awad IA. Spontaneous intracerebral and intraventricular hemorrhage: Advances in minimally invasive surgery and thrombolytic evacuation, and lessons learned in recent trials. Neurosurgery 2014;74:S142–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Lewiner T, Lopes H, Vieira AW, Tavares G. Efficient implementation of Marching Cubes’ cases with topological guarantees. J Graph Tools 2003;8:1–15. [Google Scholar]
  • 42.Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation. IEEE Trans Med Imaging 2004;23:903–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Carass A, Roy S, Gherman A, et al. Evaluating white matter lesion segmentations with refined Sørensen-Dice analysis. Sci Rep 2020;10:1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Milletari F, Navab N, Ahmadi SA. V-Net: Fully convolutional neural networks for volumetric medical image segmentation. Presented at 4th 4th International Conference on 3D Vision; October 25–28, 2016; Stanford [Google Scholar]
  • 45.Schlemper J, Oktay O, Schaap M, et al. Attention gated networks: Learning to leverage salient regions in medical images. Med Image Anal 2019;53:197–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions. Presented at the 4th International Conference on Learning Representations, ICLR; May 2–4, 2016; San Juan [Google Scholar]
  • 47.Zhu H, Shi F, Wang L, et al. Dilated dense U-net for infant hippocampus subfield segmentation. Front Neuroinform 2019;13:30. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Monteiro M, Newcombe VFJ, Mathieu F, et al. Multiclass semantic segmentation and quantification of traumatic brain injury lesions on head CT using deep learning: an algorithm development and multicentre validation study. Lancet Digit Health 2020;2:e314–22. [DOI] [PubMed] [Google Scholar]
  • 49.Dice LR. Measures of the amount of ecologic association between species. Ecology 1945;26:297–302. [Google Scholar]
  • 50.Muschelli J, Sweeney EM, Ullman NL, Vespa P, Hanley DF, Crainiceanu CM. PItcHPERFeCT: Primary intracranial hemorrhage probability estimation using random forests on CT. Neuroimage Clin 2017;14:379–90. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES