Accounting for Deformation in Deep Brain Stimulation Surgery with Models: Comparison To Interventional Magnetic Resonance Imaging

Abstract

The efficacy of deep brain stimulation (DBS) depends on electrode placement accuracy, which can be jeopardized by brain shift due to burr hole and dura opening during surgery. Brain shift violates assumed rigid alignment between preoperative image and intraoperative anatomy, negatively impacting therapy.

Objective:

This study presents a deformation-atlas biomechanical model-based approach to address shift.

Methods:

Six patients, who underwent interventional magnetic resonance (iMR) image-guided DBS burr hole surgery, were studied. A patient-specific model was employed under varying surgical conditions, generating a collection of possible intraoperative shift estimations or a ‘deformation atlas.’ An inverse problem was driven by sparse measurements derived from iMR to determine an optimal fit of solutions of the atlas. This fit was then used to obtain a volumetric deformation field, which was utilized to update preoperative MR and estimate shift at surgical target region localized on iMR. Model performance was examined by quantitatively comparing intraoperative subsurface measurements to their model-predicted counterparts, and qualitatively comparing iMR, preoperative MR, and model updated MR. A nonrigid image registration was introduced as a comparator.

Results:

Model-based approach reduced general parenchyma shift from 8.2±2.2 to 2.7±1.1 mm (~66.8% correction), and produced updated MR with better agreement to iMR than that of preoperative MR. The average model estimated shift at target region was 1.2 mm.

Conclusions:

This study demonstrates the feasibility of a model-based shift correction strategy in DBS surgery with only sparse data.

Significance:

The developed strategy has the potential to complement and/or enhance current clinical approaches in addressing shift.

I. Introduction

The quality of deep brain stimulation (DBS) therapy is highly dependent on the accurate placement of electrode contacts into the region of interest, e.g. subthalamic nucleus (STN), a common target structure for Parkinson’s disease (PD). This task is particularly challenging considering the size of DBS target structure (e.g. the STN is ~6×4×5 mm) and the dimensions of the DBS electrodes (e.g. length and diameter of electrode contacts of Medtronic 3389 (Medtronic Inc., Minneapolis, MN, USA) are 1.5 and 1.27 mm respectively) [1, 2]. Accurate placement of electrodes is critical in achieving effective therapy: Balachandran et al. indicated that modulation treatment may be rendered ineffective due to misplacement of electrodes by 3–4 mm; Anderson et al. and McClelland et al. similarly argued that mistargeting of greater than 3 mm would significantly and negatively impact the clinical efficacy of DBS therapy [2–4]. While Ivan et al. further suggested misplacement by as little as 2 mm can cause inadequate treatment and poor outcome; similarly in Kremer et al., where intraoperative CT (iCT) was utilized for the verification of DBS electrode position, lead repositioning was performed if a deviation of greater than 2 mm from intended target was detected [5, 6]. Moreover, accurate targeting can aid and facilitate achieving optimal postoperative programming to minimize side effects and prolong battery life (e.g. reducing the need for higher current to compensate for suboptimal lead placement), potentially reducing the frequency of battery replacement surgery [2, 3].

Compounding the challenge of accurate electrode placement is brain shift, which is introduced by burr hole (small craniotomy ~14-mm in size) and dura opening during surgery [5]. Brain shift compromises the spatial alignment between the preoperative imaging data, which are used for surgical planning, targeting and navigation, and intraoperative patient anatomy. Previously groups have observed brain shift in DBS burr hole surgery: Winkler et al. reported brain shift of 2 mm in the STN (n=1) [7]; Khan et al. observed average displacement of 1.8 and 1.6 mm at anterior commissure (AC) and posterior commissure (PC), respectively, and up to 4 mm in deep brain structures (n=25) [8]; Elias et al. found 7.6% of patients with AC shift over 2 mm and 13.6% with AC shift over 1.5 mm (n=66) [9]. Most of the above and similar studies used preop- and postop-magnetic resonance (MR) images to estimate shift of critical deep brain structures. Intraoperative shift estimation was achieved in a comprehensive study by Ivan et al. via interventional MR (iMR) [5]. The study found shift ranging 0.0–10.1 mm (n=44) with the greatest shift in the frontal lobe; the study also found 9% of patients with shift over 2 mm in deep brain structures and 20% with shift 1–2 mm [5]. An additional finding shared among these studies was that the majority of shift was in the direction of gravity.

The potential detrimental impact of brain shift is typically confronted clinically by two approaches, namely microelectrode recording (MER)-assistance or iMR-guidance. Awake-MER assisted procedure is a widely used technique and is considered the gold standard. However, MER requires: (i) prior to surgery, patients must be off medication, which negatively affects their ability to tolerate the procedure; (ii) during surgery, patient participation is required, thus limiting treatment availability to those who cannot tolerate such distress [10, 11]; (iii) MER can involve multiple electrode passes to optimize lead placement, and an increased number of passes has shown to increase the risk of intracranial hemorrhage and other complications [10–12]. These deficiencies of MER are addressed in iMR-guided procedures where direct target visualization and brain shift monitoring are possible with patients under general anesthesia [10, 13]. However, burdens associated with cost, training and workflow posed by iMR must be considered.

An alternative approach, albeit less explored, to address brain shift in DBS burr hole surgery is to employ a biomechanical model-based method. Model-based approaches that leverage sparse data obtained via low-cost and convenient intraoperative instrumentation to account for deforming neuroanatomy, if accurate, could complement and/or reduce the reliance on current clinical approaches (e.g. for centers without iMR-guidance systems) while overcoming the above deficiencies without disrupting existing clinical infrastructure or workflow.

Efforts to employ model-based brain shift correction strategy in DBS are limited. Early work was reported by Bilger et al., where brain shift due to cerebrospinal fluid (CSF) loss was simulated [14]. The later work of Bilger et al. was then further developed in Hamze et al. for DBS trajectory planning with a linear stress and strain description of the brain [15, 16]. Independently from the group above, model-based approach proposed by Bennion et al. attempted to consider different material models for different structures such as dural septa and ventricles [14–17]. However, these studies suffered from the same limitation: the lack of realistic in vivo patient data for validation, as they largely focused on the feasibility of forward model solution, or preliminary validation with limited synthetic/simulated data [14–17]. Recent work using preoperative MR and iMR in [18], and preop- and postop-computed tomography (CT) in [19], both used model-based approaches in a single patient to investigate shift compensation in DBS. The results provided in both studies showed promise for a model-based approach. It should be noted the former in [18] is a preliminary version of this work with one patient presented at SPIE Medical Imaging 2018.

Here we further developed and examined a model-based shift correction strategy in 6 patients who underwent iMR-guided DBS surgery. These patients were considered as having experienced significant asymmetric shift, both observed clinically and measured by high fidelity iMR data. While the construction of the finite element model in the proposed approach relies solely on the preoperative MR without the dependency of iMR, the aforementioned iMR imaging data afforded the comparison between iMR measured shift (considered gold standard measurements) and corresponding model predicted shift, specifically here, model performance was retrospectively examined: (i) quantitatively by comparing intraoperative subsurface general parenchyma shift measurements to their model-predicted counterparts, and (ii) qualitatively by comparing iMR, preoperative MR, and model updated MR.

The objective of this study is to demonstrate the feasibility of a model-based shift correction strategy for DBS surgery using only sparse data, which would enable possible intraoperative deployment of the method, and provide a model updated MR that more accurately represents the intraoperative patient anatomy to aid surgical navigation and targeting, as well as direct visualization.

II. Methodology

A. Data

Six patients who underwent iMR-guided DBS burr hole surgery at University of California, San Francisco (UCSF) and experienced significant asymmetric brain shift were studied. Preoperative and iMR imaging volumes were acquired with patient consent and IRB approval. The specifications of the imaging data are shown in Table I. The details of the surgical procedure may be found in [5].

Table I.

Preoperative MR and iMR Imaging Data Information

	Preoperative MR		iMR
Case #	Dimension	Spacing (mm)	Dimension	Spacing (mm)
1	240×240×85	1.00×1.00×2.00	256×256×107	1.02×1.02×1.50
2	240×240×80	1.00×1.00×2.00	256×256×107	1.02×1.02×1.50
3	256×256×75	1.02×1.02×2.00	256×256×120	1.02×1.02×1.50
4	256×256×120	1.02×1.02×1.50	256×256×120	1.02×1.02×1.50
5	240×240×85	1.00×1.00×2.00	256×256×107	1.02×1.02×1.50
6	240×240×85	1.00×1.00×2.00	256×256×107	1.02×1.02×1.50

Here case 1 was a unilateral implantation while the remaining five cases were bilateral. It should also be noted here that preoperative MR and iMR imaging data were acquired with the patient’s head immobilized in a head frame and with no patient or table movement between image acquisitions.

An example of the acquired data is shown in Fig. 1, where significant asymmetric shift is readily observable. Moreover, the corresponding crosshairs indicate subsurface deformation occurring at the lateral ventricle. Midline shift is also observed. Here it should be noted that the insertion path of the electrode leads and resultant imaging artifacts are visible (red arrows) on the iMR imaging volume.

Fig. 1.

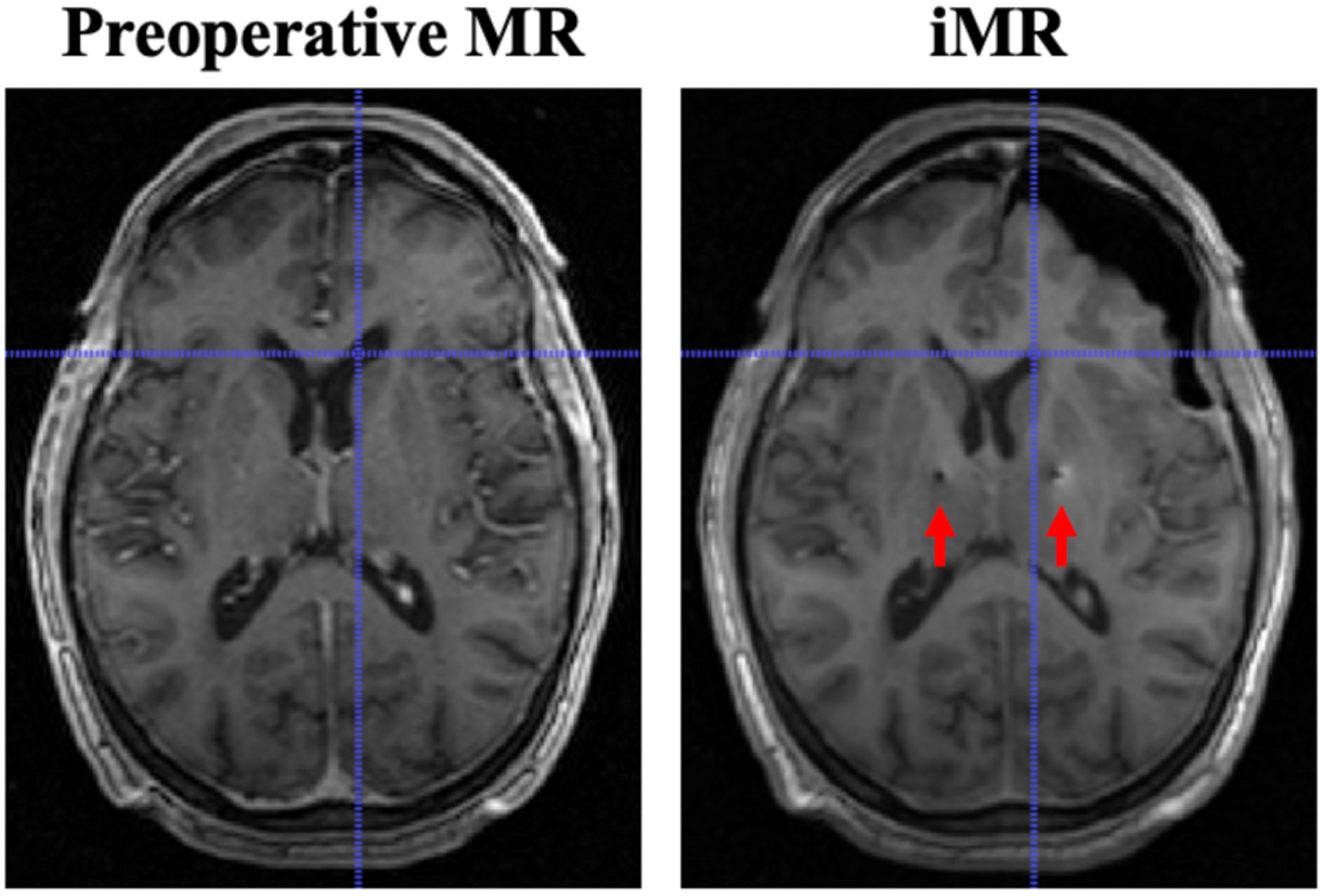
Comparison of preoperative MR and iMR imaging data on a corresponding slice. Significant asymmetric shift can be observed. Subsurface shift, e.g. at the lateral ventricle, is indicated by the crosshairs. Midline shift is also observed. The insertion path of the electrode leads and resultant imaging artifacts can be observed (red arrows) on iMR imaging data.

B. Biomechanical Model-based Deformation Atlas

Fundamental to the developed deformation-atlas model-based approach is the construction of patient-specific finite element (FE) biomechanical model and the appropriate boundary condition assignment that reflects the understanding of the physics of shift phenomenon in DBS burr hole surgery.

To construct the biomechanical model, patient brain volume was manually segmented from the preoperative MR image. A surface was then extracted from the segmented brain via a marching cubes algorithm. The surface mesh was provided to a custom-build mesh generator to obtain a volumetric tetrahedral mesh [20]. An atlas brain volume was rigidly and nonrigidly registered to the patient image [21]. Subsequently the rigid and nonrigid transformations were applied to the brain stem, falx and tentorium segmented from the atlas image to obtain patient specific representations of these structures, shown in Fig. 2(a) [21–24]. Once patient specific FE mesh was obtained, displacement and pressure boundary conditions were assigned based on an algorithm developed and tested in previous work for tumor surgery but significantly modified to the unique nature of shift in DBS herein [18, 24–27].

Fig. 2.

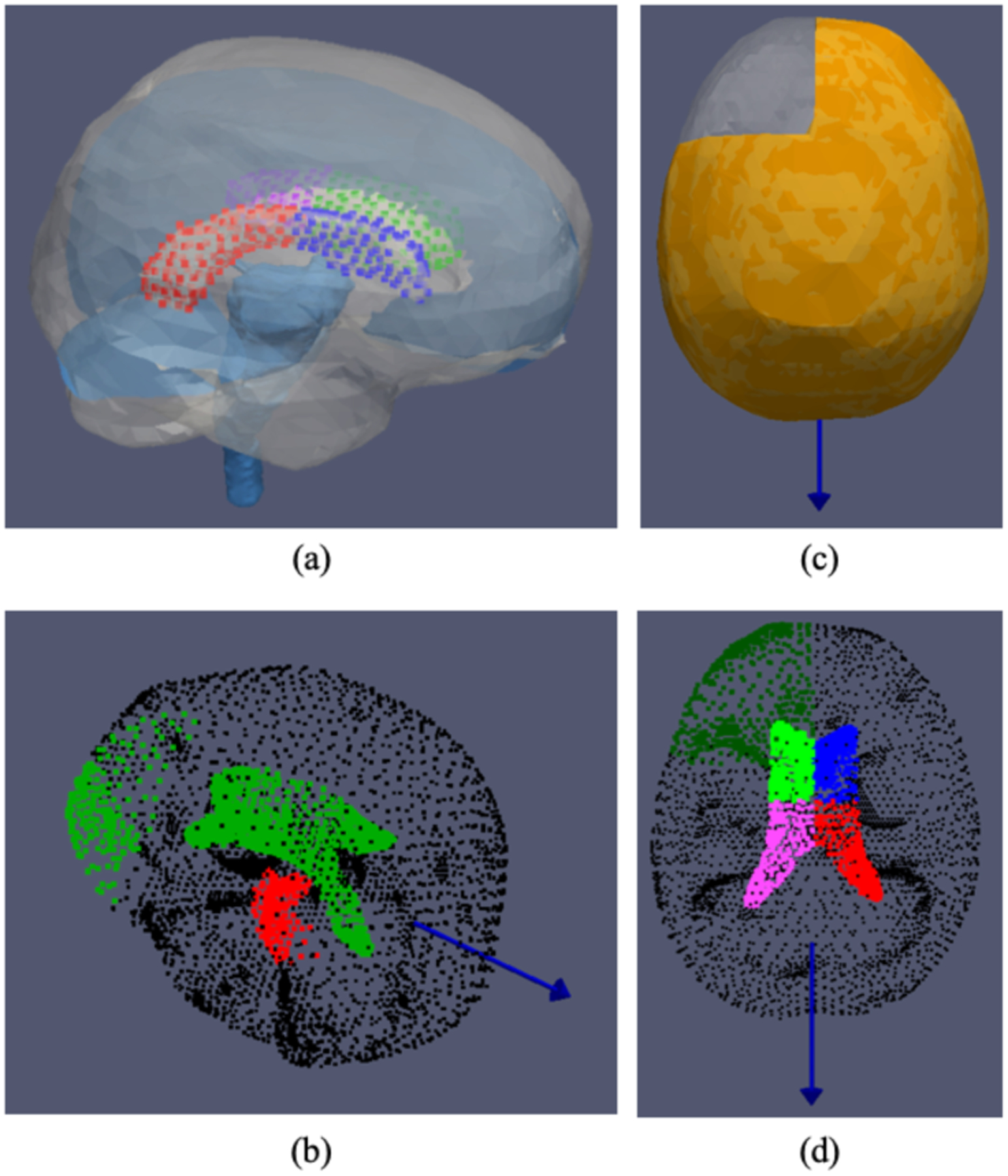
(a) Computational domain of the patient specific biomechanical model. Patient specific falx, tentorium and brain stem structures determined via an automated process using rigid and nonrigid image registration between patient imaging data and an atlas image. The lateral ventricle is further partitioned into four segments (illustrated with different colors) for additional boundary condition considerations. (b)-(d) An example of boundary conditions considered, where the blue vector represents the direction of gravity with the patient in supine position. (b) Displacement condition: green is stress free nodes, black is slip condition nodes, red or brain stem region is for fixed displacement. (c) Fluid condition: asymmetric drainage simulated in the model where orange represents the tissue submerged in CSF. (d) Pressure condition: dark green is Dirichlet reference pressure, black is no drainage condition and four segments of the ventricle (different colors of neon green, blue, pink and red) are given additional Dirichlet pressure considerations to simulate the effect of pneumocephalus.

Specifically, previous reports have observed and hypothesized that contributing factors to brain shift in DBS, in particular asymmetric shift, are gravity, CSF loss and intracranial air invasion or pneumocephalus [5, 8, 28–32]. In the model-based approach reported here, displacement and pressure boundary conditions were designated: (i) brain surface above a preset level was stress free (i.e. freely deforming); (ii) brain stem region was fixed in displacement; (iii) the rest of brain surface and tentorium were given slip conditions (tangential movement allowed but no normal motion); (iv) nodes above a fluid drainage level had a defined pressure reference value and below had a Neumann condition, i.e. no drainage allowed. Material properties used in the model may be found in [24].

To accommodate the unique shift phenomenon in DBS, the following conditions were also prescribed: (i) to simulate asymmetric shift, CSF loss was also modeled in an asymmetric manner, i.e. one hemisphere was fully saturated. Furthermore, in the biphasic biomechanical model employed here [33], CSF loss precipitates brain tissue sag, i.e. CSF loss decreases buoyancy, thus causing the brain tissue to sag due to gravity. (ii) With the observation of ventricular shape change (e.g. in Fig. 1, specifically hemispheric asymmetric deformation), additional boundary descriptions were given to the ventricle. The lateral ventricle was segmented from preoperative MR and modeled as a void and further divided into four segments spatially, shown in different colors in Fig 2. Different assigned Dirichlet pressure conditions (direct pressure values that are specified) [34] were considered for these segments in order to describe an apparent presence of a pressure gradient due to pneumocephalus. (iii) Based on previous studies, it has been suggested that material properties near/of the lateral ventricle warrant additional consideration, therefore the elements surrounding the structure of the lateral ventricle in the FE mesh were determined and given a stiffer material property [17, 35]. (iv) While our previous protocol had assigned slip displacement boundary condition to falx [18, 24], such assignment would prevent movement in the normal direction, thus disabling the model to recover midline shift such as observed in Fig. 1. However entirely removing this constraint is also unreasonable due to the natural structural integrity presented by the falx [26]. To reconcile, elements surrounding the patient-specific falx representation were determined and given stiffer material property, thus allowing normal motion yet offering resistance due to falx structure similar to [36]. To supplement the descriptions of the above steps in boundary condition generation, a sample of the boundary conditions deployed is shown in Fig. 2(b)–(d), where Fig. 2 (b) depicts displacement boundary condition: green represents stress free condition, black represents slip condition and red or brain stem region has fixed displacement. Fig. 2(c) describes fluid drainage, specifically asymmetric drainage simulated in the model where orange represents the tissue submerged in CSF. Fig. 2(d) depicts pressure boundary condition, where dark green represents the reference pressure, black represents no drainage condition, lastly four segments of the ventricle (illustrated in different colors of neon green, pink, blue and red corresponding to Fig. 2(a)) are given additional Dirichlet pressure considerations described previously.

With the aforementioned modifications, a DBS-specific model-based approach that accounts for neuroanatomical constraints, gravity, asymmetric CSF loss, and pneumocephalus interaction was realized. The deformation-atlas approach calls for a collection of possible intraoperative shift solutions reflecting systematically varying surgical conditions. Thus here, 3 different CSF drainage levels and 21 CSF fluid configurations, as well as 5 modestly varied head configurations relative to gravity were created assuming the patient was in supine position (i.e. direction of gravity shown as the blue vector in Fig. 2) [5]. Additionally, for the ipsilateral ventricle associated with asymmetric shift, the ventricle was separated into two segments. Each segmental partition was assigned a Dirichlet pressure condition with 3 different possible nonzero pressure levels considered. Given the combinations available, this provided a total of 9 pressure configurations in the solution distribution. With respect to the two segments associated with the contralateral ventricle, both were given pressure value of zero. To some degree, the absolute pressure values are secondary to the proposed established gradient due to the pneumocephalus. The prescribed gradients however reflected ranges within 7.5 mmHg.

Finally, with conditions reflecting the aforementioned configurations defined, specifically a total of 2835 biophysical driving states, a biphasic biomechanical model was driven to resolve the volumetric displacement field for each configuration; collectively the solutions form the deformation atlas. While the duration of this pre-computing phase (i.e. deformation atlas construction) varies based on numerous factors such as mesh size, on average the time to generate such deformation atlas was ~ 4 hours.

C. Inverse Problem Approach

An inverse problem approach was employed to estimate intraoperative brain shift. Specifically in (1), the objective function is designed to minimize the difference between the sparse intraoperative shift measurement and the optimized model prediction (i.e. a linear combination of the deformation atlas obtained above) in a least-squared manner [37]:min

$$\text{min}\Vert \text{Mw}-\text{u}{\Vert }^2\exists {\text{w}}_{\mathrm{i}}\ge 0\text{ and }{\sum }_{\text{i}=1}^{\text{n}}{\text{w}}_{\mathrm{i}}\le 1$$ (1)

where M is an m×n deformation atlas (m represents the number of measurement points, and n is the total number of solutions in the deformation atlas), w are the combinatory coefficients, and u are the measured intraoperative displacements. Here constraints on the coefficients safeguard reasonable prediction and prevent extrapolation outside of the represented atlas.

In this study, the sparse intraoperative measurement used to drive the inverse problem was derived from iMR data, i.e. homologous surface and subsurface points were designated on preoperative and iMR images (e.g. in Fig 3) in a process similar to [27, 38]. In particular, corresponding discernible subsurface features in Fig. 3(a) and (b) were found in the anterior frontal lobe on the ipsilateral side at various depths on preoperative MR and iMR. An example of the distribution of designated subsurface points is shown as red points in Fig. 3(c). Fig. 3(c) also illustrates the spatial relations of these points to the approximated surgical target region, i.e. electrode implant, shown as the blue point, localized via iMR and a process explained in details later.

Fig. 3.

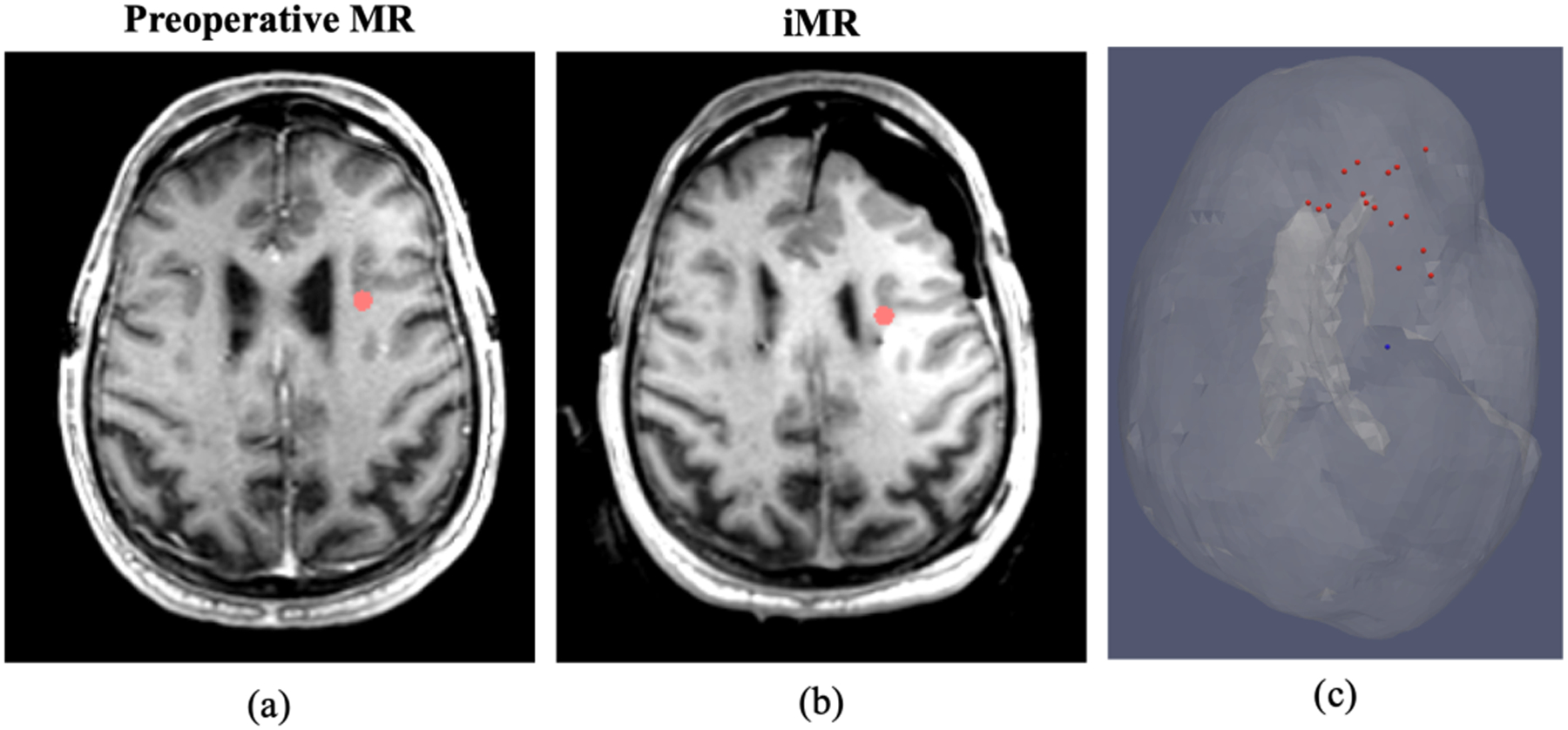
(a) and (b) Homologous subsurface point designation (red dots) on preoperative MR and iMR, respectively. (c) Distribution of designated subsurface points (red) and its spatial relation to approximated surgical target region (blue) in translucent brain mesh with the incorporation of the lateral ventricle also shown.

The number of designated surface and subsurface points used for this study is summarized in Table II.

Table II.

Summary of Homologous Points

Case #	Total points	Surface points	Subsurface points
1	27	12	15
2	19	11	8
3	27	11	16
4	29	14	15
5	27	12	15
6	31	15	16
Overall	160	75	85

The rationale for the use of surface and subsurface sparse data, instead of the whole iMR dataset, is twofold: (i) while we have previously demonstrated the ability to collect inverse problem driving data without significantly disrupting workflow [24, 39, 40], it is always desirable to reduce the quantity of data needed to drive the model in order to minimize workflow-related burdens posed by the model-based approach; and (ii) the small size of burr hole impedes the ability to use surface data in the operating room (OR), an input source that most model-based methods rely on, therefore subsurface input was also used here in anticipation of a data acquisition approach that would provide subsurface information without presenting the cost and workflow burdens of iMR, i.e. a transcranial or burr hole ultrasound (US) driven approach.

The utilization of subsurface data however required modification to the inverse problem approach used previously, which was driven exclusively by surface data [24, 27, 39]. Specifically, in the fitting process of previous work, the optimization constructed the M matrix in (1) based on the mesh nodes closest to the measurement points. If such approach were used for subsurface measurement points, the model’s predictive accuracy would be impacted by the mesh resolution. The magnitude and trajectory of measured shift could be affected in the process of finding the closest mesh node to a measurement point. Thus, a new implementation of the inverse problem to accommodate input data of both surface and subsurface measurements was created. This new approach centers around constructing the M matrix in (1) at the measurement point instead of the closest mesh node. To achieve: (i) for a subsurface measurement point, the mesh element containing this point and thus the four nodes forming this tetrahedral element were determined. The barycentric coordinate coefficients of this local tetrahedron were computed and displacement solutions at the four vertices in the deformation atlas could then be interpolated and mapped to the measurement point via weighted combination; and (ii) for a surface measurement point, the surface triangle closest to the point based on projection distance was found and the three nodes forming this triangle were determined. Similar to the treatment of subsurface data, local barycentric coordinate coefficients were computed based on the measurement point projected onto the triangle and displacement solutions at the projected point were subsequently obtained. Another advantage provided by this new approach is that with the specification of surface and subsurface input, the inverse problem can be driven solely with surface data, or solely with subsurface data, or a mixture of the two.

Finally, once the optimal coefficients for the linear combination of the deformation atlas were found in (1), these coefficients were used to obtain a whole brain displacement field prediction. Subsequently this displacement field was used to (i) deform the designated preoperative points to facilitate comparisons of model predicted updated positions and their intraoperative measured counterparts; and (ii) deform the preoperative MR in obtaining a model updated MR reflecting model predicted presentation of patient intraoperative anatomy.

D. Model Performance Assessment

Quantitative and qualitative assessments were conducted to examine the model’s performance of brain shift compensation. Quantitatively, since a particular interest of the study is to assess the model’s ability to correct intraoperative subsurface shift, subsurface points in the previous section were used to gauge model shift correction performance. An additional consideration of utilizing and evaluating these subsurface points is that a comparison study was conducted between model-based approach and a nonrigid image registration technique where registration of preoperative MR and iMR was performed. In that study described later, since the nonrigid image registration would enjoy the information provided by whole image volumes (both preoperative MR and iMR), to facilitate a comparable and fairer comparison, the model-based approach was afforded both the sparse surface and subsurface data. Specifically, for points of interest, the difference between preoperative and intraoperative feature points represented a displacement measurement. Upon reconstruction with (1), this measurement could be compared to the model-derived counterpart. We also note that this is a fitting process from a finite representation of deformations. Here, the differences between intraoperative and model-predicted positions represent the residual error of the model-based approach. An additional quantitative metric employed is percent correction in (2), which relates the residual error to the measured shift:

$$\text{Percent correction }=\left(1-\frac{‖{\overrightarrow{\text{u}}}_{\text{predicted}}-{\overrightarrow{\text{u}}}_{\text{measured}}‖}{‖{\overrightarrow{\text{u}}}_{\text{measured}}‖}\right)\times 100\%$$ (2)

where vector, $\overrightarrow{u}$ is the displacement vector, subscript predicted represents the reconstructed model predicted vector, measured represents the expert measured vector, and ||·|| is the L2 norm of the vector or the Euclidean distance.

Qualitatively, model updated MR was compared to iMR in conjunction with preoperative MR, where misalignment between iMR and preoperative MR would indicate brain shift, and agreement between iMR and model updated MR would illustrate the recovery of said shift by the model-based approach. These comparisons represent qualitative evaluations of image-based anatomical feature alignments.

E. Estimation of Brain Shift at Surgical Target Region

The estimation of brain shift at surgical target region, i.e. region of interest where electrode implants would exert therapeutic impact, is challenging since such target region is not designated in the preoperative space in this study. Here to estimate shift at target region, we leveraged the localization of the tip of electrode leads on iMR imaging data. Briefly, given the insertion path of the electrode leads was visible on iMR (shown in Fig. 1), the tip was localized with the assumption that it would be the most distal end of the insertion path. The target region was then defined as the region within a capture radius of 1.5 mm of the localized tip (i.e. within a 3-mm diameter sphere). This region-based definition of target via the localized tip was selected for analysis as that within a given brain target, the ideal electrode placement is within a region roughly 3 mm in diameter. Yet, placement outside of this ideal region may lead to suboptimal clinic benefit with stimulation and/or bothersome side effects from stimulation of structures immediately adjacent to the target. It should also be noted however that the model estimation of target region shift here aims to provide an understanding of bulk tissue movement in deep brain structure, instead of shift experienced by an individual electrode contact. With target region defined in the iMR space, predicted displacement field was used to determine its counterpart in the preoperative space. Subsequently the tissue displacement trajectories that result in the co-location of these corresponding target regions in the undeformed and deformed spaces can be computed. Similarly, the nonrigid image registration methodology adopted in the following section can provide shift estimation at target region via the same process.

F. Comparison to Nonrigid Image Registration

As alluded to in the above sections, with iMR data available, it was also possible to estimate a displacement map via nonrigid image registration of preoperative MR and iMR. While this nonrigid image registration process is not required to generate a predicted shift profile for the proposed model-based approach, here the purpose of this independent comparator is twofold: (i) the performance of the nonrigid image registration at designated subsurface points would inform the fidelity of the measurements, i.e. better performance would indicate that the measurement derived from expert designated points is in agreement with the predicted movement through nonrigid image registration; and (ii) the displacement at target region predicted by the image registration technique could serve as a comparator to the model-based approach as discussed in the previous section.

To achieve, the Advanced Normalization Tools (ANTs) was used to nonrigidly register preoperative MR and iMR data [41]. Additional care was taken to address image artifacts introduced by the electrode leads (e.g. shown in Fig. 1). Specifically, regions impacted by image artifacts were manually segmented and an inpainting technique was used to limit the impact due to electrode lead presence to the registration, in particular with respect to surgical target region [42, 43]. With that, once nonrigid image registration was complete, (i) preoperative points could be deformed based on displacement map predicted by ANTs, and the deformed positions could be compared to measured intraoperative positions; and (ii) trajectory of surgical target region could be obtained and compared as discussed previously.

III. Result

A. Shift Correction Performance on Parenchymal Targets

The impact of model-based correction strategy can be observed by comparing the surface meshes generated from preoperative MR (white) and iMR (red), with model deformed preoperative MR mesh (blue) shown in Fig. 4 (a) and (b).

Fig. 4.

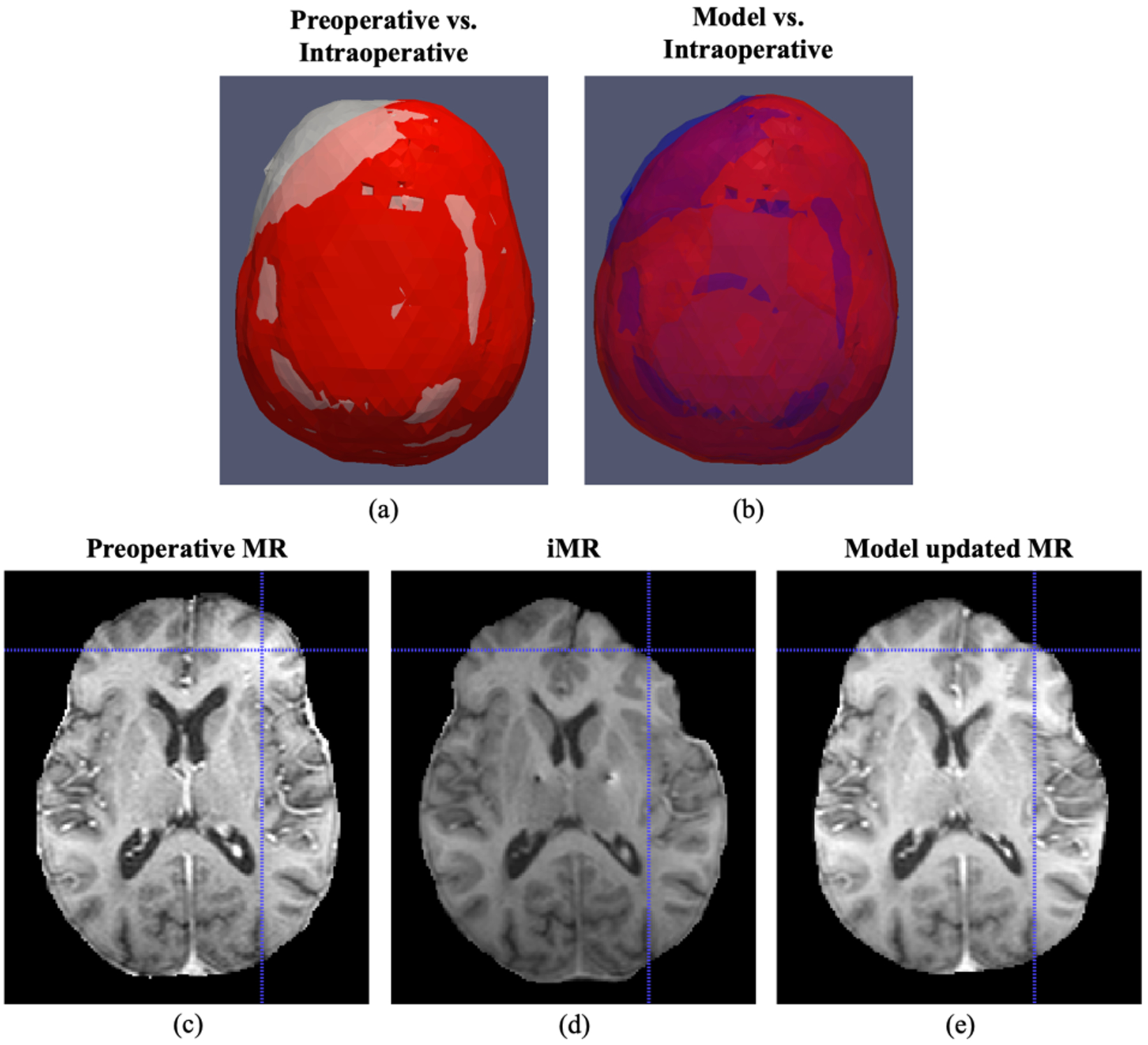
(a)-(b) Comparison of surface meshes generated from preoperative MR (white), model updated MR (blue) and iMR (red), where brain shift experienced is illustrated in the comparison between preoperative (white) and intraoperative (red) meshes, and the recovery of shift is demonstrated by comparing model (blue) and intraoperative (red) meshes. (c)-(e) Comparison of preoperative MR, iMR and model updated MR with corresponding crosshairs on the surface indicating better surface recovery by the model.

Here it is worth noting better agreement between model deformed mesh and iMR mesh (blue and red), as well as asymmetric shift predicted by the model, demonstrating the recovery of brain shift by the model-based approach on the brain surface. This observation was further supported by comparing preoperative MR, iMR and model updated MR in Fig. 4(c)–(e) where the corresponding crosshairs indicate the surface shift experienced by the patient from preoperative state to intraoperative state, and this shift was better recovered on the model updated MR.

Quantitively, a total of 85 subsurface points were examined. Individual case and overall performances are summarized in Table III. Briefly, the model reduced misalignment due to brain shift from 8.2±2.2 to 2.7±1.1 mm when comparing the 2^nd and 3^rd columns for percent correction of ~66.8±13.2% seen in the 4^th column. Furthermore, when breaking down into components of x (medial-lateral), y (anterior-posterior) and z (inferior-superior), we found the model reduced measured shift of 2.4 (medial-lateral shift, 8.5% of overall measured shift), 6.6 (anterior-posterior, 67.4%) and 4.0 (inferior-superior, 24.1%) mm to 1.6, 1.4 and 1.2 mm for ~31.9%, 79.6% and 69.3% correction. Here it also should be noted that majority of the shift is in the direction of gravity (anterior-posterior), which is consistent with previous reports.

Table III.

Correction Performance Summary

Case #	Measured shift (mm) [# of points]	Model residual error (mm)	Model percent correction (%)	ANTs residual error (mm)	ANTs percent correction (%)
1	9.1±2.4 [15]	3.4±0.7	62.8±7.50	1.7±1.0	80.5±11.5
2	5.7±0.9 [8]	2.3±0.7	59.0±13.0	1.4±0.8	76.0±14.5
3	6.7±1.9 [16]	1.9±0.7	71.8±10.1	1.5±0.7	78.2±10.7
4	8.9±1.6 [15]	2.5±1.0	72.0±11.1	1.3±0.7	85.6±8.4
5	9.2±2.3 [15]	3.5±1.4	61.5±14.8	1.8±1.0	80.0±11.3
6	8.6±1.4 [16]	2.6±0.9	69.5±10.8	1.3±0.5	85.0±6.0
Overall	8.2±2.2 [85]	2.7±1.1	66.8±13.2	1.5±0.8	81.6±10.2

Moreover, Table III 5^th and 6^th columns represents the counterpart results of residual error and percent correction provided by ANTs for the same 85 targets. The residual error due to ANTs displacement field was 1.5±0.8 mm (~81.6±10.1% correction). This provides some sense of the fidelity of shift correction possible to discern.

Qualitatively, preoperative MR, iMR and model updated MR were compared, different examples shown in Fig. 5. Model updated MR exhibits better feature agreements (particularly in the frontal lobe) using only sparse measurements with iMR data as compared to preoperative MR. Crosshairs in Fig. 5 indicate better shift recovery at lateral ventricle by the model updated MR. While not exact, it was pleasing to see midline shift was recovered to a good degree by the model-based approach.

Fig. 5.

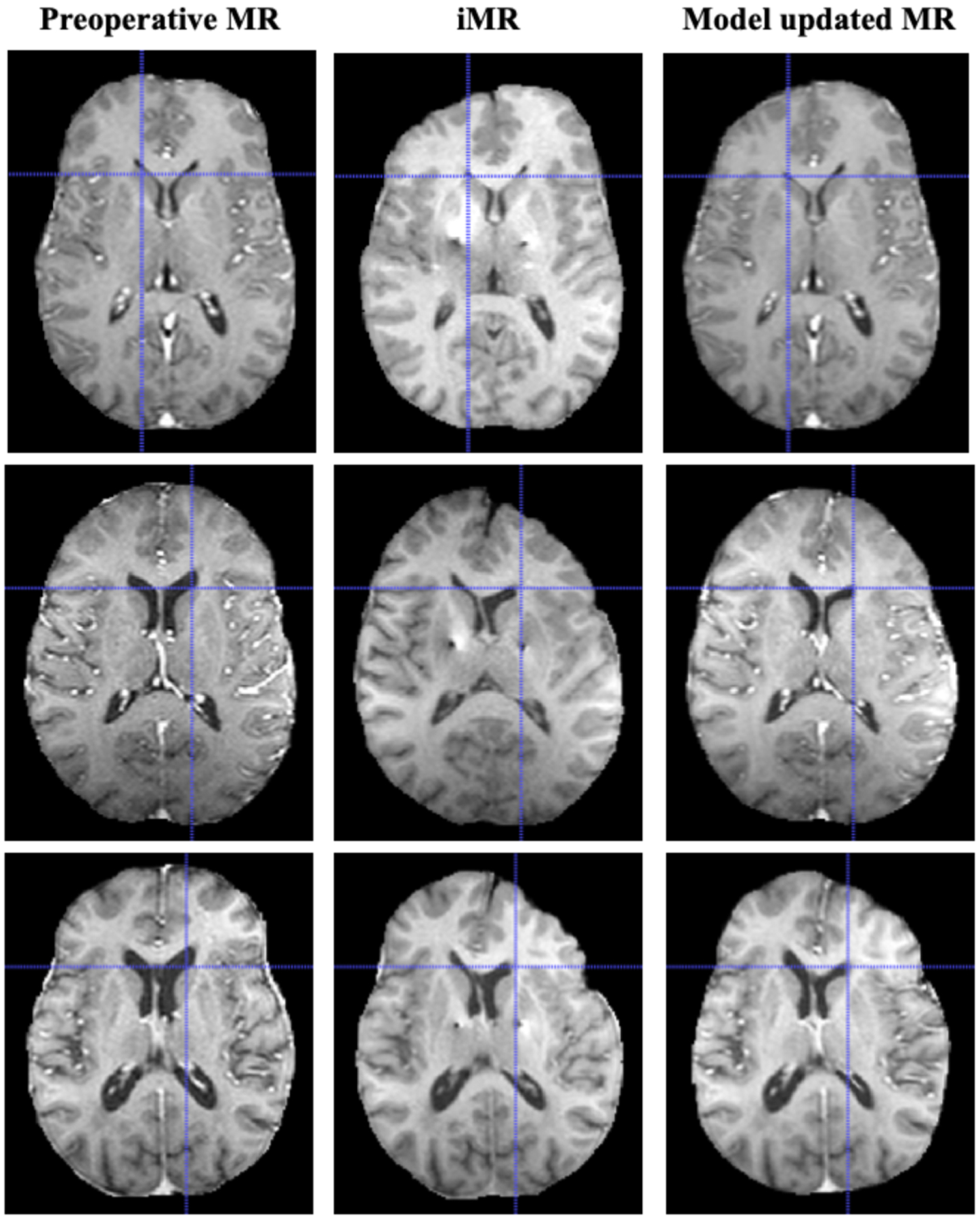
Comparison of preoperative MR, iMR and model updated MR. For each case, better feature agreement was observed between model updated MR and iMR vs. preoperative MR, particularly in the frontal lobe. Crosshairs indicate better subsurface recovery at the lateral ventricle by the model. The model was also able to recover the observed midline shift to some extent.

Lastly, to speak to performance, the computational speed of the model-based approach (specifically intraoperative components that would be executed in surgery to obtain a full volumetric shift prediction profile) was analyzed across 6 cases averaged from 3 trials. The mean duration of computing barycentric coordinate coefficients (the number of input points varied from 19–31 with an average of 26.7, see Table II) is 0.7 seconds, subsequently the average time of computing a whole brain displacement is 27.1 s, and the average time of updating preoperative MR is 5.0 s. Overall the duration from sparse data input to model updated MR is 32.9 s using a standard desktop computer running Windows 7 with 8GB RAM and Intel Core i7 CPU at 3.60GHz.

B. Shift Estimation at Surgical Target Region

By localizing the tip of electrode leads and applying the inverse predicted displacement field (both model and ANTs), shift experienced by surgical target region can be computed. The predicted shifts by the model-based approach and ANTs for each case is summarized in Table IV across the 2^nd and 3^rd column for the right and left implants respectively. The angular differences between the displacement solution provided by the model and ANTs is provided in the 4^th and 5^th column for the two implants. The positional difference between the predicted target locations between model and ANTs is shown in the 6^th and 7^th column.

Table IV.

Compare Shift Estimation at Surgical Target Region Model-based Approach vs. ANTs

	Shift Magnitude: Model/ANTs (mm)		Angular difference: Model vs. ANTs (deg)		Positional difference: Model vs. ANTs (mm)
Case #	Right	Left	Right	Left	Right	Left
1	3.2/2.5	—	6.4	—	0.7	—
2	0.4/0.5	2.0/1.2	73.8	43.8	0.6	1.4
3	1.1/1.1	0.3/1.4	59.0	58.4	1.1	1.2
4	0.2/0.6	1.6/2.7	97.8	25.5	0.7	1.5
5	1.8/1.3	0.5/1.0	62.3	111.8	1.7	1.3
6	0.5/1.2	1.8/1.6	86.1	84.2	1.3	2.3
Average	1.2 ± 1.1/1.2 ± 0.7	1.2 ± 0.8/1.6 ± 0.7	62.2 ± 31.8	64.7 ± 34.0	1.0 ± 0.4	1.5 ± 0.4
Overall	1.2 ± 0.9/1.4 ± 0.7		64.5 ± 31.1		1.2 ± 0.5

IV. Discussion

A biomechanical model-based brain shift correction strategy tailored for DBS burr hole surgery has been developed, and subsequently evaluated using high fidelity iMR data in 6 patients. The model-based approach, built to account for physical events hypothesized to introduce asymmetric brain shift in DBS, namely gravity, asymmetric CSF loss and pneumocephalus, was able to reduce misalignment due to brain shift from 8.2±2.2 to 2.7±1.1 mm for ~66.8±13.2% correction across 6 cases analyzed with sparse input (surface and subsurface) data for general parenchymal targets. Furthermore, model updated MR image demonstrated better agreement with iMR compare to preoperative MR, which suggests that as a complementary technology to existing clinical approaches, model-based method may aid and enable better direct visualization, as well as enhanced surgical navigation and targeting. When displacement at surgical target region, i.e. at/near critical deep brain structure, was examined via the model-based approach and a separate independent nonrigid image registration technique serving as a comparator, while some differences in magnitude and direction were observed and will be discussed later, results indicated an average bulk tissue shift between 1–2 mm at the surgical target region of interest. These shift magnitude observations are consistent with previous literatures and illustrate the existence and thus the need to correct for intraoperative brain shift for deep brain structure in DBS surgery. Another encouraging aspect of this study is the examination of model’s ability to use both surface and subsurface data to estimate volumetric brain shift in a time efficient manner that would not impede clinical workflow, enhancing its potential for intraoperative deployment. It should also be noted that while the pre-computing phase (prior to surgery and only needing preoperative MR imaging data) of deformation atlas construction of ~4 hours is quite workflow-friendly, future improvements of our method, such as the utilization of semi-automated approach in brain segmentation demonstrated in [23, 24], can further facilitate and expedite this pre-computing phase. Despite these promising outcomes, there are several aspects of this study that can be improved and should be discussed.

First, the designation of surface and subsurface targets is a subjective process and intra- and inter- operator error should be assessed. We have previously examined the intra-operator error [27], where the same point set in the preoperative space was presented to the same operator, its intraoperative corresponding point set was then designated three different times with sufficient time in between selections to prevent bias. We found the intra-operator error to be approximately 0.8 mm. As for inter-operator error, we believe the result from ANTs, whose registration leverages the information of the entire preoperative MR and iMR imaging volumes, demonstrate the fidelity of point designation. Specifically, when presented with preoperative designation of points and blinded to intraoperative designations, the error between deformed point position based on registration outputs (virtually as a second operator) and intraoperative designation was merely 1.5 mm on average, shown in Table III, especially considering the axial spacing of the preoperative MR and iMR ranges from 1.5 to 2.0 mm in Table I. Additionally, considering the imperfect nature of nonrigid registration as well as the aforementioned potential intra-operator error, the residual error of ANTs with respect to the subsurface points suggests the fidelity and validity of the point designation. While we considered examining the model-based approach at the AC and PC, the localization error due to image resolution (image spacing varying from 1.00 mm to 2.00 mm shown in Table I), coupled with potential intra-operator error described above, would complicate the assessment at these points whose movement is believed to be on the order of 1–2 voxels. Furthermore, a study by Pallavaram et al. found significant variability in designating AC and PC even among trained neurosurgeons [44]. When 43 neurosurgeons (38 attendings and 5 residents or fellows) were presented with 2 high resolution MR volumes and asked to designate the AC and PC, the study found the average inter-surgeon variability (pairwise deviation) to be 1.92±1.96 and 2.27±3.92 mm for AC and PC, respectively, for the first image volume; and 1.44±1.05 and 2.05±3.46 mm for the second image volume. Such variability even among experienced neurosurgeons suggests potential challenges in using these points for the purpose of model validation here. Moreover, numerous previous studies relied on AC and PC as surrogates for shift measurement due to (i) poor soft tissue contrast of the imaging modality used (e.g. CT) to extract additional features for analysis; and (ii) the ambiguity in localizing the clinical therapeutic target region. Here the utilization of feature- and data- rich iMR imaging data addresses (i) and the identification and extraction of the tip of the electrode leads on iMR offer an improvement in (ii), especially considering the introduction of a secondary comparator, namely ANTs, which uses a different principle of re-aligning the preoperative and intraoperative information than the biophysics-based model.

In addition to surgical targeting, a less discussed yet potentially important topic is surgical navigation. Studies have suggested that the penetration of the lateral ventricle can increase the risk of intracranial hemorrhage and negatively impact the quality of DBS therapy, yet it can be readily observed that brain shift significantly impacts the structure of the lateral ventricle (Fig. 1 and Fig. 5), illustrating the potential usefulness of the model-based approach in updating the preoperative MR volume to better align imaging data with intraoperative state of the patient [8, 45, 46].

The methodology presented here represents our current understanding of shift phenomenon in DBS and its modeling, in achieving, several interesting biomechanical events unique to DBS burr hole surgery have been potentially discovered and implemented accordingly: (i) a major improvement in this work compared to our previous one patient proof-of-concept work [18] is in the shift recovery in the medial-lateral direction via a different implementation for pneumocephalus. Moreover, as the understanding and implementation of the biophysics contributing to shift are advanced, corresponding refinement of the model and subsequently better correction results are possible. (ii) Changes in our falx description, originated from the observation of midline shift in iMR data, also provided better shift prediction when modeled as herein. (iii) The observation of the falx behavior could also lead to additional considerations of compartmentalization, such as the partition of the falx structure (anterior vs. posterior) to allow different degree of rigidity [26]. (iv) Related to (iii), the stiffness assigned to the elements associated with falx and ventricle in this study could be further investigated through a possible parametric sweep to determine optimality and to compare to a wide range of material properties of brain components previously reported [47]. (v) With respect to compartmentalization, in the current implementation, the left and right lateral ventricles were treated as one entity, however from Fig. 1 and Fig. 5, it appears the septum pellucidum, which separates left and right lateral ventricle, is also impacted by brain shift and its incorporation may further improve model performance. Nevertheless, the methodology presented here provides the following contribution to the field: (i) the study here incorporates multiple biophysical events such as CSF drainage, gravity, pneumocephalus-induced pressure phenomenon, material stiffness consideration to different components of the brain, into one comprehensive modeling approach to account for factors believed to introduce shift in DBS; (ii) to our knowledge, the consideration of ventricle, in particular in a segmental fashion, to simulate pneumocephalus-induced pressure phenomenon, is a novel approach and potentially provides insight on the underlying physics of shift in DBS; (iii) compare to previous studies in Introduction, considerable efforts are made in this study to ensure the intraoperative deployability of the methodology and its potential clinical appeal via the pre-computed deformation atlas as well as efficient intraoperative execution; (iv) also compare to previous studies, validation effort with 6 patients with high fidelity iMR data, which is considered the gold standard measurement tool, is a significant improvement, especially considering iMR measured shift is not subject to the potential drawback of postoperative shift recovery if shift were to be measured between preop- and postop- image volumes [48]; (v) the technical details employed here to enable subsurface data to be used in the inverse problem framework, specifically the interpolative method at sparse data points extracted from the deformation atlas, have not been previously reported.

With respect to shift estimated at the target region, the accuracy of this estimation is inferred from the correction results (Table III) of identified features (points shown in Fig. 3) that can be localized within the imaging data with high confidence (considering imaging resolution in Table I). In this feasibility study, approaching validation via targets of high soft tissue contrast in regions with considerable deformation is a logical first step in evaluating the modeling framework. With that understanding, although satisfying to observe that the bulk tissue movement at deep brain target predicted by both model-based approach and ANTs is similar and within the range of literature findings summarized in Introduction, the difference in magnitude and direction between model-based approach and ANTs warrants closer examination of the shortcomings of each approach. For model-based approach, it is apparent from the residual error and percent correction result that further improvements are needed to better account for the physics of shift, and the introduction of increasingly sophisticated modeling may help resolve the differences. For ANTs, while great care was taken to minimize the impact of image artifacts introduced by electrode leads, it is likely that image artifacts degraded the quality of registration and prediction, especially at surgical target region. Moreover, ANTs registration may be impacted by the manual identification of image artifacts for inpainting, manual segmentations of preoperative and intraoperative brains for image registration, as well as sensitivity to tunable parameters in both registration and inpainting. For example, in parameterization experiments not reported in detail here, ANTs registration parameters were varied over a realistic range yielding acceptable nonrigid image registration results. Within these experiments, parenchymal target shift correction (e.g. Table III) was observed to vary on the order of 0.2 mm on average with respect to residual error, and on the order of 0.3 mm when intra-operator target noise was introduced for added scrutiny (i.e. half of the intra-operator error described previously was analyzed with respect to true target location). Within the backdrop of this variability in expert-defined parenchymal target error with respect to realistic parameter prescription with ANTs, it is important to estimate the impact of that variability regarding shift at therapeutic target region. With respect to results in Table IV and allowing for realistic driving parameters for ANTs, the variation in average positional difference of predicted positions was 0.4±0.2 mm with respect to the centroid over the parameter space, and the average angular difference between these individual predictions was 32.5±23.3 deg. These variations showed that while the comparison between model and ANTs is informative and interesting, in particular with respect to the evaluation of bulk tissue movement, the differences in Table IV should not be regarded as a ground truth error per se but rather as a comparator method with a limited understanding of ground truth. It would be appropriate however to state that ANTs registration performance utilizing the entirety of 3D imaging data outperformed the sparse-data driven model at expert-defined parenchymal target shifts. It is difficult to assert however that an analogous performance increase is present at therapeutic target region given that features that drive registration are less rich in the target area, and an added inpainting image alteration has been performed to handle the electrode artifact. Furthermore, when angular difference was examined for the subsurface points, the difference between intraoperative measured vector and ANTs predicted vector was found to be 9.3 deg, intraoperative measured vector and model predicted vector was 17.4 deg, and model and ANTs vectors was 17.3 deg. While this was not surprising, as indicated by the residual error result (ANTs 1.5 mm vs. model 2.7 mm), the directional difference of 17.3 deg between ANTs and model may partly explain the directional difference at surgical target as well. However, it also should be noted the nonrigid image registration via ANTs requires full image volumes of preoperative MR and iMR with computation time > 1 hour, while the computation time to generate a whole brain displacement field for the model-based approach was ~30 seconds with only sparse input data needed. In addition, it must also be recognized that parenchymal shift prediction by ANTs using the entirety of the data did still have on average of ~18% residual error remaining.

Considering the shortcomings or deficiencies of each method discussed above, the ultimate arbiter of the angular difference between the two methods could be the functional impact—a future study could retrospectively examine and relate shift estimation at surgical target region provided by the two methods to therapy outcome via electrophysiological mapping and monitoring such as MER, or postoperative programming optimization, e.g. electrode contact selection and subsequent adjustment needed with corresponding patient response. Nevertheless, with data currently available and limited in this study (preoperative and iMRs), the average bulk tissue movement predicted by both methods at deep brain structure is similar (model 1.2 mm and ANTs 1.4 mm overall). This general agreement between two methods, as well as with previous reports in the literature, indicates that brain shift and its correction must be considered in a non-negligible portion of patients undergoing DBS burr hole surgery to optimize treatment outcome. To better understand the impact of brain shift on functional outcome with the potential of consequently optimizing therapy, we have worked towards establishing an integrated framework of biomechanical and bioelectric models where both brain shift and volume of tissue activation (VTA), subsequently tractography, due to neuromodulation may be accounted for in [49]. Preliminary results using this multi-physics framework in 2 patients further illustrate and reinforce the need to account for brain shift in DBS as shift impacts the extent, number, and volume of neuronal pathways affected [49].

Lastly, although the objective of this study is to examine the feasibility and to establish potential accuracy metrics for a model-based approach to confront brain shift in DBS under an experimental design compatible with the data sparsity expected in surgery, to ensure the clinical translatability of the method, it is important to assess and consider the potential challenges associated with the deployablity and usability of the proposed approach in the OR, especially with respect to obtaining sparse intraoperative measurements needed to drive the inverse problem via OR-compatible and -friendly means, as it likely will be the rate limiting step of the proposed approach. While we have previously demonstrated abilities to acquire intraoperative surface data in the OR via laser range scanning [39], stereovision [50], or optically tracked stylus [51], it is recognized that the extent of surface data used in this study may not be available in the OR. However there exist several OR-compatible approaches to acquire and augment sources of data that are needed to drive the inverse problem. (i) One possibility to address this problem is the use of iCT. The use of iCT in DBS burr hole surgery has been demonstrated by groups such as Burchiel et al. [32], and the potential use of CT data (via preop- and postop- CTs) in providing input surface data to a model-based approach is illustrated by Li et al. [19, 52]. However, a potential shortcoming of iCT should be noted here: the soft tissue discrimination of CT is such that the brain target being implanted is not directly visible. The iCT image set must therefore be co-registered with a preoperative MR image set, which introduces the potential for error associated with the image registration and fusion process, particularly if pneumocephalus is present on iCT images. For the model-based approach proposed here, iCT will likely offer intraoperative surface deformation information to drive the inverse problem; however, again the poor soft tissue contrast of iCT would limit finding corresponding features. (ii) Another alternative route is the use of subsurface data via US (transcranial or burr hole). A difficulty associated with this approach is finding corresponding features as model input. However in one recent study conducted, a SIFT Rank algorithm was employed to detect and track corresponding features from multiple ultrasound acquisitions [53] and validated in [54], subsequently the model was able to provide fairly good brain shift reduction when driven solely with subsurface features and validated with independently designated subsurface targets in 15 patients and 24 individual surgical scenarios [55, 56]. This framework may be utilized here to provide an input data stream to the inverse problem.

V. Conclusion

A biomechanical model-based brain shift correction strategy for DBS burr hole surgery was developed, where volumetric shift estimation was achieved by leveraging sparse intraoperative measurement in an inverse problem approach framework. The established method was evaluated in six patients with high fidelity iMR data. The model-based approach was able to account for shift appreciably at subsurface points as well as provide updated MR image that presents better agreement with iMR compared to preoperative MR, illustrating its potential as a complementary technology to existing clinical methods in addressing brain shift to enhance surgical navigation and targeting, as well as enable direct visualization. The model-based approach was also able to estimate shift experienced at critical deep brain structure, and its estimated average bulk tissue movement at surgical target region is comparable to results produced by a sophisticated nonrigid image registration algorithm given access to complete volumetric pre- and post- intervention data. Furthermore, the model-based approach is able to provide shift prediction with a mixture of surface and/or subsurface data, enabling the flexibility of the possible utilization of iCT and/or iUS, and in an efficient execution manner that presents minimal disruption to existing clinical infrastructure and workflow. While demonstrating its potential, further validation with a larger patient population with iMR, an increased sophistication of modeling to better account and understand the physics of shift phenomenon in DBS, as well as the incorporation of iCT and/or US into the proposed brain shift correction framework, are desired.