Deep learning for tipping points: Preprocessing matters

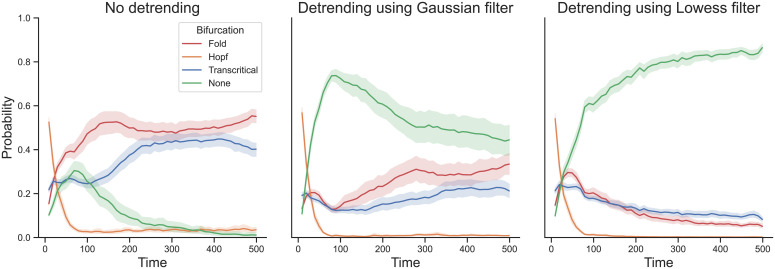
Bury et al. (1) present a powerful approach to anticipating tipping points based on deep learning that not only substantially outperforms traditional early warning indicators but also classifies the type of bifurcation that may lie ahead. Deep learning methods are notorious for sometimes exhibiting unintended behavior, and we show that this is also the case here. We simulated $n=500$ observations from an AR(1) process with lag-1 autocorrelation $\rho =0.50$ and standard Gaussian noise term and applied the deep learning method. Fig. 1, Left shows the probability of a fold (red), Hopf (orange), transcritical (blue), and no (green) bifurcation. The method incorrectly suggests that the process is approaching a fold/transcritical bifurcation. Fig. 1, Middle shows that detrending with a Gaussian filter with bandwidth 0.20 improves performance, but substantial uncertainty remains. Fig. 1, Right shows that, after detrending using a Lowess filter with span 0.20, as performed by Bury et al. (1), the method is able to correctly classify the system as not approaching a bifurcation.*

Fig. 1.

Deep learning classification for a stationary AR(1) process without detrending (Left) and with detrending using a Gaussian (Middle) and Lowess (Right) filter with bandwidth/span of 0.20. Solid lines show averages, and shaded regions show SDs over 100 iterations.

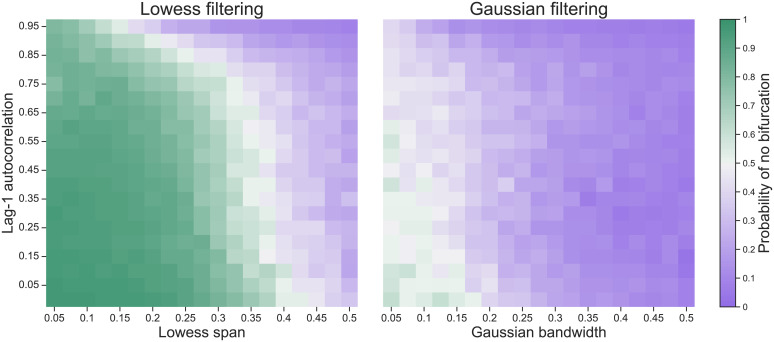
We conducted the same analysis for a range of lag-1 autocorrelations $\rho \in [0,0.05,\dots ,0.95]$ and Lowess spans/Gaussian bandwidths $b\in [0.05,0.075,\dots ,0.50]$. Fig. 2, Left shows the probability of correctly classifying the time series as approaching no bifurcation after observing all $n=500$ data points. Classification becomes more challenging as the lag-1 autocorrelation approaches one. In general, the deep learning method performs better the smaller the Lowess span. Performance drops substantially when using Gaussian filtering, as Fig. 2, Right shows.

Fig. 2.

Probability of correctly inferring that no bifurcation lies ahead after observing $n=500$ data points from a stationary AR(1) process across different lag-1 autocorrelations and Lowess spans (Left) or Gaussian bandwidths (Right), averaged over 100 iterations.

Bury et al. (1) trained the deep learning method only on time series that have been detrended using a Lowess filter with span 0.20. While the authors show that the method exhibits excellent performance in several empirical and model systems, we find that it does not extract features generic enough to classify stationary AR(1) processes that have not been detrended (or have been detrended using a Gaussian filter) as approaching no bifurcation. This sensitivity to different types of detrending suggests that the method may have learned features specific to a Lowess filter rather than (only) generic features of a system approaching a bifurcation. Interestingly, detrending takes on a different purpose in this context: For traditional early warning indicators, adequate detrending helps avoid biased estimates (e.g., ref. 2), while for the deep learning method developed by Bury et al. (1) a particular type of detrending is necessary because all training examples were detrended using it. Bury et al. (1) and Lapeyrolerie and Boettiger (3) note that the training set would have to be expanded substantially to include richer dynamical behavior than fold, transcritical, and Hopf bifurcations. With this note, we suggest that other aspects of the training, including preprocessing, also need careful consideration.