Gull dynamic pitch stability is controlled by wing morphing

Significance

While flying, birds manipulate their wing joints to adapt to atmospheric disturbances or perform extraordinary maneuvers. Yet, little is known about how these disturbances affect birds’ speed and orientation. Here, we fused traditional aeronautical methods with biological insights to develop a theoretical model of avian gliding flight, which allowed us to quantify a gliding gull’s response to disturbances while holding different wing postures. Our model reveals that a gull can manipulate its wing joints to adjust between a completely stable and unstable trimmed flight position and to control the fluctuations in its speed and orientation caused by a gust. These results enhance our fundamental understanding of bird flight and highlight that morphing wing joints may replicate avian-like maneuverability in aircraft.

Abstract

Birds perform astounding aerial maneuvers by actuating their shoulder, elbow, and wrist joints to morph their wing shape. This maneuverability is desirable for similar-sized uncrewed aerial vehicles (UAVs) and can be analyzed through the lens of dynamic flight stability. Quantifying avian dynamic stability is challenging as it is dictated by aerodynamics and inertia, which must both account for birds’ complex and variable morphology. To date, avian dynamic stability across flight conditions remains largely unknown. Here, we fill this gap by quantifying how a gull can use wing morphing to adjust its longitudinal dynamic response. We found that it was necessary to adjust the shoulder angle to achieve trimmed flight and that most trimmed configurations were longitudinally stable except for configurations with high wrist angles. Our results showed that as flight speed increases, the gull could fold or sweep its wings backward to trim. Further, a trimmed gull can use its wing joints to control the frequencies and damping ratios of the longitudinal oscillatory modes. We found a more damped phugoid mode than similar-sized UAVs, possibly reducing speed sensitivity to perturbations, such as gusts. Although most configurations had controllable short-period flying qualities, the heavily damped phugoid mode indicates a sluggish response to control inputs, which may be overcome while maneuvering by morphing into an unstable flight configuration. Our study shows that gulls use their shoulder, wrist, and elbow joints to negotiate trade-offs in stability and control and points the way forward for designing UAVs with avian-like maneuverability.

Imagine uncrewed aerial vehicles (UAVs) performing social aerial aerobatics like ravens (1), rapidly diving like gannets (2), and skillfully maintaining their position under high wind and gusty conditions like kestrels and gulls (3, 4). These nature documentary–worthy feats often exceed the maneuverability of modern comparable UAVs, especially nonrotary designs (5). The ability for UAVs to effectively maneuver is becoming increasingly important, as UAVs more often operate close to or within crowded environments, such as urban centers (6, 7).

To determine how to best improve UAV maneuverability based on insights from birds, we must first quantify maneuverability. Maneuverability is broadly defined as the ability to change the magnitude and/or direction of a flyer’s velocity vector (8, 9). Although, there are multiple ways to evaluate flight maneuverability, many traditional methods quantify an aircraft’s stability and control characteristics across relevant flight conditions (10, 11). This is often done by linearizing the governing equations of motion about an equilibrium condition (also known as a trim state) and solving the resultant eigenvalue problem to extract information about the aircraft’s response to small perturbations (11, 12). For complete stability, the flyer must be both statically and dynamically stable. A flyer is statically stable if after a perturbation the flyer’s initial tendency is to return toward its trim state (time invariant), while a flyer is dynamically stable if it eventually returns to its trim state after a perturbation (time variant). Static stability is a necessary but insufficient condition for dynamic stability. In the longitudinal plane (x–z plane; Fig. 1), the dynamic response is commonly characterized by two superimposed oscillatory modes: the short period and phugoid. For traditional aircraft, the short-period mode is usually a heavily damped, high-frequency oscillation in the angle of attack and pitch rate (Fig. 1A), while the phugoid mode is a lightly damped, lower-frequency oscillation in the flight speed and pitch angle (Fig. 1B) (11). The associated damping ratio and natural frequency of these modes dictate how “sluggish” or “sensitive” an aircraft is to control inputs and thus are often used to define an aircraft’s flying qualities (12–17).

Fig. 1.

Gulls can morph their wings to adjust key flight parameters. (A) The short-period mode largely affects the angle of attack ($\alpha$) and pitch rate (q) and is visualized by the oscillation of the center line (dotted gray line) about the fixed velocity vector (solid green line). (B) The phugoid mode largely affects the flight speed (u) and pitch angle ($\theta$) and is visualized by the oscillation of the center line (dotted gray line) about the fixed horizon (solid black line). (C) Front view of a gull, visualizing the shoulder dihedral angle where a positive angle is an upwards deflected wing. (D) Dorsal view of a gull, visualizing the shoulder sweep angle where positive is a backward swept wing. Elbow and wrist angles are always positive with higher angles as the wing extends. (E) Side view of a gull with key flight parameters illustrated.

This stability-based approach to quantifying maneuverability requires knowledge of the aerodynamic and inertial characteristics across all flight conditions and configurations. Obtaining these data for birds is challenging because of their complex and variable geometries. As a result, there are few studies that have quantified the dynamic flight response of gliding birds throughout wing morphing. Instead, studies of gliding maneuverability often leverage observations of live birds by tracking and analyzing their morphology and flight path (18–20). For example, in their thesis, Durston (18) used live birds, three-dimensional printing techniques, and X-ray computed tomography scanning to show that three species of raptors are dynamically unstable in the longitudinal axis while gliding toward their handler. Although this work provides a detailed investigation of avian dynamic stability, the results are limited to the wing shapes and behaviors that the birds used during the recorded flights.

Here, we investigated a gull’s longitudinal dynamic stability across the range of elbow and wrist flexion and extension known to be used in gliding flight (21). Our dynamic analyses were informed by previous studies on hybrid glaucous-winged (Larus glaucescens) $\times$ western (Larus occidentalis) gulls. The aerodynamic results were obtained with an open-source numerical lifting line method (MachUpX) (22), and the inertial characteristics were obtained with an open-source method that models birds as a composite of simple objects (AvInertia) (23). As the previous aerodynamic investigation found that gull-wing–body configurations were unable to trim at a fixed shoulder angle with no sweep or dihedral (22), we incorporated a furled (unspread; Fig. 1D) tail and two additional degrees of freedom: shoulder dihedral (Fig. 1C) and sweep angle (Fig. 1D). By coupling these extended aerodynamic and inertial results with a traditional stability-based dynamic analysis framework, we derived the small perturbation equations of motion across the in vivo range of motion of the elbow and wrist for a gliding gull (21). Next, we investigated the oscillatory response of the gull with its wings in each morphed configuration, which allowed us to extract the natural frequencies and damping ratios of the system. Finally, to visualize the effect of wing morphing on the gull’s time response, we investigated two types of simplified gusts: 1) a simplified transverse gust modeled by an initial offset in the angle of attack and 2) a simplified streamwise gust modeled by an increase in the forward speed with a 1-cosine profile (13).

Results and Discussion

Trim States.

We solved for the trim angle of attack (${\alpha }_0$), trim speed ($U_0$), and trim glide angle (${\gamma }_0$) for wing configurations that spanned the in vivo range (Fig. 2A). If the calculated trim glide angle was less than −45°, the trim angle of attack was greater than 5°, or there was no trim solution, we did not include these results (Methods). For the configurations within these bounds (n = 1,457), we found that the trim speed ranged from 11.8 to 29.8 m/s, and the shallowest trim glide angle was −12.2° (Fig. 2B and C). In-flight measurements of gulls gliding past an urban environment by Shepard et al. (24) showed an airspeed range from 8.1 to 19.9 m/s, which includes approximately half of our configurations (n = 768). This previous study investigated gulls in transient flight and did not include behaviors with high glide angles, such as those used in landing flight. As such, we expect that gulls have the capability to trim at the higher speeds as predicted by our model. Note that due to the constraints on our aerodynamic estimates (Methods), it is likely and probable that gulls can also trim at lower speeds and shallower glide angles by using different wing joint configurations paired with spreading and/or pitching their tail downward. Future work should expand these aerodynamic methods and incorporate a morphing tail to investigate these additional configurations. However, our identified trim states permit an initial evaluation of dynamic stability in gull gliding flight.

Fig. 2.

Wing morphing allows gulls to switch between statically stable and unstable configurations. (A) The gull can fold its wrist to trim as speeds increase. (B and C) The configurations capable of trimmed flight (n = 1,457) include multiple forward sweep angles. (D) Gull-wing morphing allows a substantial static margin shift largely due to a neutral point shift as the center of gravity shift remains relatively small. (E) The gliding gull is unstable if the neutral point is in front of the center of gravity and stable if it is behind. (F) Adjusting the forward sweep angle ensures that the majority of elbow and wrist configurations at a 20° dihedral angle can trim, but most configurations with high wrist angles become statically unstable (hollow squares).

To determine how varying the three different wing joints affects the trim state, we fit linear models, which revealed strong interactive effects between the elbow, wrist, and sweep angles on the trim speed and glide angle. Folding the wrist increased the trim glide speed for over 80% of tested configurations, and folding the elbow increased the trim glide speed for 60% of tested configurations. Because there is evidence that many bird species, including gulls, fold their wing joints as wind speeds increase (21, 25–32), our results suggest that this wing-morphing behavior allows gliding birds to adjust their trim condition to adapt to different flight conditions. In addition, we found that reducing the forward sweep at the shoulder joint caused the trim glide speed to increase (and the glide angle to steepen) for each tested configuration, as expected from traditional aeronautical results (5). Yet, there is little documented evidence of birds sweeping their wings backward at the shoulder joint in response to increased wind speeds. Therefore, it is possible that to trim, birds preferentially fold their wings rather than adjusting their shoulder joint sweep angle. One benefit to folding the elbow and wrist over sweeping the entire wing would be that folding the wing both reduces the total wing lifting area and moves the wings closer to the body. These two effects would reduce the wing-bending moment, whereas adjusting the shoulder sweep angle would not change the wing area and only marginally move the wings closer to the body. A directed study is required to determine if and how birds balance trade-offs between structural constraints and aerodynamic loading in trimmed flight.

Static Stability about the Trim State.

With the known trim state for each configuration, we next investigated the static stability. We quantified static stability with the static margin, a measure of the distance between the center of gravity and the neutral point. The neutral point is the location where the distributed forces and moments can be modeled as point loads. It differs from the center of pressure because the pitching moment about the neutral point is independent of the angle of attack. If the neutral point is behind the center of gravity, the configuration has a positive static margin and is statically stable (Fig. 2E) (22).

We found that the majority of trimmed elbow, wrist, and shoulder combinations for the gull were statically stable (solid squares, n = 1,331; Fig. 2F), but there was a set of configurations with extended wrist angles that were unstable (hollow squares, n = 126; Fig. 2F). This result agrees with Durston’s finding that raptors gliding toward their trainers with fully extended wing configurations were statically unstable (18). However, our results expand on this understanding to reveal that a gull can fold its wrist to achieve a stabilized configuration, allowing a shift between stable and unstable flight conditions. The continuous progression toward instability was largely driven by a shift in the neutral point rather than the center of gravity as expected, since wing morphing has only a marginal effect on shifting the center of gravity (Fig. 2D for a constant 15° forward sweep angle) (23).

This capacity to adjust stability characteristics with wing morphing agrees with a previous finding that most species can shift between stable and unstable flight (23). However, that previous study was limited to 0° shoulder sweep and dihedral angles and found that gulls were entirely stable (21–23). Here, we expanded on these results to show that including the shoulder joint further enhances birds’ ability to transition between statically stable and unstable flight. It is important to highlight that there are limited data on the true shoulder angles used in bird flight. However, gulls are often observed flying with swept forward wings held at a positive dihedral angle (33); therefore, this stability shift is likely used by live gliding gulls.

Dynamic Stability about the Trim State.

Static stability is a necessary but insufficient condition for full flight stability. To determine if a gull is completely stable, we next calculated the dynamic characteristics by solving for the eigenvalues of the rigid gull modeled as a fourth-order system (Methods). We found that all the statically stable configurations had eigenvalues with negative real values for both oscillatory modes (solid points, n = 1,331; Fig. 3 A and B), leading the gull to be dynamically, and thus completely, stable in the longitudinal axis. Only statically unstable configurations had dynamically unstable responses and exhibited a nonoscillatory divergent response, which was characterized by eigenvalues with only real parts, similar to Durston’s results (18). This indicates that the gull was only completely stable or unstable, and there were no configurations that exhibited static stability and dynamic instability. Of note, we found that the phugoid mode remained stable even for the statically unstable configurations (Fig. 3B), and thus the dynamic instability was entirely due to the unstable short-period response, which is driven by the static instability.

Fig. 3.

The short-period and phugoid mode characteristics are significantly affected by the wing positioning. (A and B) The poles of the fourth-order system are displayed for a forward sweep angle of 5° (triangles) and 15° (circles). (C and E) Within the in vivo range (above a 90° elbow angle), wrist extension tends to decrease the short-period natural frequency (C) and increase the damping ratio (E). (D and F) The effect of wrist extension on the phugoid natural frequency (D) and damping ratio (F) depends on the elbow angle.

With the complex and real components of the eigenvalues, we calculated the damping ratio (ζ) and natural frequency (ω) associated with the two oscillatory modes for all the stable configurations. The first mode that we considered had a high-frequency, highly damped response (Fig. 3 C and E) independent of the speed (demonstrated by the low magnitude of the teal dots in Fig. 4A), which is characteristic of the short-period mode (Fig. 1A). The short-period frequency ranged from 8.9 to 41.0 rad/s, which is approximately half to more than double the frequency of a similar-sized UAV (Fig. 3C) (16). Previous studies have shown that small UAVs will have higher short-period frequencies than large aircraft due to scaling alone (16, 17). The gull’s variable frequency response is because wing morphing allows a substantial shift in the static margin, and thus the static stability, compared with values used in traditional UAV designs (11, 12). To this end, wing morphing has a strong effect on the short-period characteristics for gulls. Furthermore, we found significant interactive effects between the elbow, wrist, and sweep angles (visualized in Fig. 3 C and E). Despite these interactive effects, general trends in the short-period characteristics are apparent within our investigated joint ranges. For example, wrist extension decreased the short-period natural frequency (Fig. 3C) and increased the damping ratio (Fig. 3E) when the elbow angle was above 90°.

Fig. 4.

Short-period and phugoid modes were identified from the magnitude of the eigenvectors. All magnitudes and phases were normalized to the pitch rate (maroon dot) to facilitate comparison. (A) The short period was characterized by the high-magnitude response in the pitch rate (maroon dots) and a small-magnitude response in the speed (dark teal dots). (B) The phugoid mode was characterized by a high-magnitude response in the speed (dark teal dots) and pitch angle (orange dots) with a small-magnitude response in the angle of attack (pale blue dots).

Next, the second identified mode had a substantially lower frequency response (Fig. 3D) and was independent of the angle of attack (demonstrated by the low magnitude of the light blue dots in Fig. 4B), which is characteristic of the phugoid mode (Fig. 1B). The phugoid mode had a similar or slightly lower frequency than a similar-sized UAV ranging from 0.45 to 1.10 rad/s (Fig. 3D). However, we found that the phugoid mode was heavily damped, with a damping ratio on the same order of magnitude as the short-period mode (Fig. 3F). This is unlike most comparable UAVs or large-scale aircraft (11, 16, 17), although a flight test on a smaller morphing gull-wing UAV found a similar heavily damped phugoid mode (6). We expect that the high damping is because we investigated gliding flight rather than steady, level cruise and because our configurations were limited to angles of attack below 5°, which excludes the most aerodynamically efficient results for these wing configurations. Per Pamadi’s phugoid approximation, these combined effects decrease the phugoid frequency and increase the damping ratio (11). Therefore, it remains possible that at more efficient trim conditions, a gull configuration could be statically stable but dynamically unstable due to reduced phugoid damping. Like the short-period mode, we found significant interactive effects between the elbow, wrist, and sweep angles (visualized in Fig. 3 D and F). Unlike the relatively consistent wing-morphing trends for the short period, the effect of wrist extension on the phugoid frequency (Fig. 3D) and damping (Fig. 3F) reverses signs within our investigated ranges. For example, the damping ratio tends to increase with wrist extension at low elbow angles but tends to decrease with wrist extension at high elbow angles.

Flying Qualities.

To better understand the dynamic response characteristics, we compared the estimated flying qualities of the gull to known aircraft specifications. We evaluated the flying qualities as established by the US Department of Defense’s MIL-F-8785C specification (13). This specification defines three levels of flying qualities: level 1 flying qualities are clearly adequate for the given flight phase, level 2 necessitates a higher pilot workload and/or degradation of mission effectiveness, and level 3 results in an excessive workload or inadequate mission effectiveness. We considered only qualities associated with flight phases that include nonterminal flight maneuvers, such as a gliding descent (category B per MIL-F-8785C).

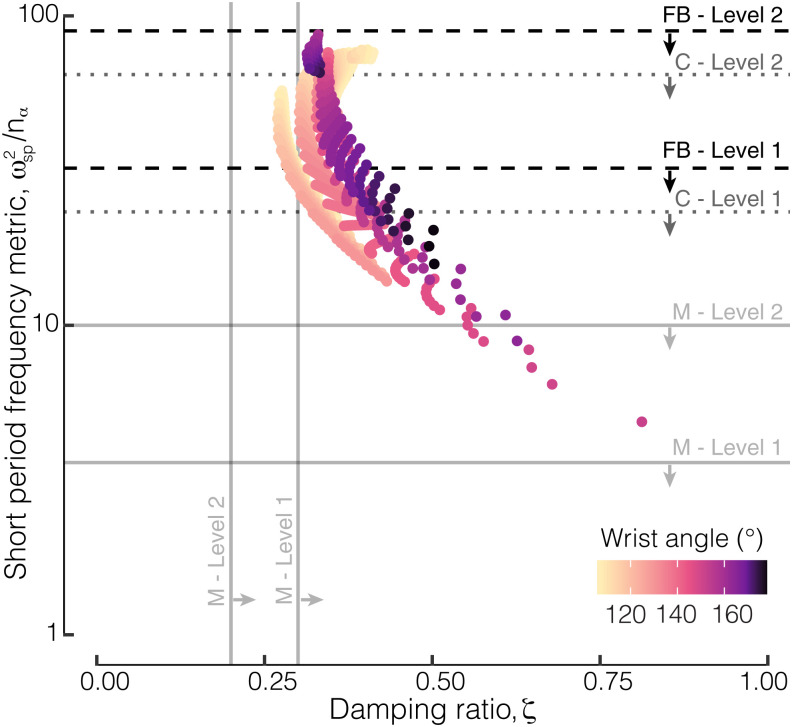
MIL-F-8785C defines desirable short-period characteristics by the damping ratio (ζ) and a short-period frequency metric, which is the ratio of the natural frequency squared (ω_sp²) to the load factor per angle of attack (n_α) (y axis, Fig. 5). Considering the damping ratio limits, we found that most configurations (n = 1,232) satisfied the level 1 requirements; however, some configurations (n = 99) with a 20° forward sweep angle only satisfied the level 2 requirements (Fig. 5, M, solid vertical lines). Considering the frequency metric requirements, we found that only seven configurations satisfied level 2 requirements (Fig. 5, M, solid horizontal lines). Although interactive effects were again significant, we found that sweeping the wing forward, extending the wrist, or folding the elbow angle tended to reduce the short-period frequency metric, thus improving the flight quality (P values < 0.001, R² = 0.9083; Fig. 5). All stable configurations exhibited at least level 3 qualities in the damping ratio and frequency limits, but this is indicative of a flyer that would be difficult to control (13).

Fig. 5.

Most gull configurations satisfied level 2 short-period requirements for human pilots per adjusted UAV guidelines. For the damping ratio, all configurations satisfy at least level 2 MIL-F-8785C (M, solid vertical lines). For the frequency metric, no configurations satisfied the level 1 MIL-F-8785C requirements (M, solid horizontal lines). Adjusting for two previously published UAV metrics revealed that 185 configurations satisfied Capello et al.’s level 1 upper limits (C, gray dotted lines), and 457 configurations satisfied Foster and Bowman’s level 1 upper limits (FB, black dashed lines). All configurations satisfied Foster and Bowman’s level 2 upper limits.

However, studies on small UAVs have shown that the MIL-F-8785C short-period frequency metric guidelines do not accurately capture the flying qualities of small UAVs (14–17). As a result, previous studies have proposed new scaling parameters. Incorporating Foster and Bowman’s (17) scaling, we found that all of our stable, trimmed gull configurations (n = 1,331) would have at least level 2 flying qualities, and 457 configurations would have level 1 flying qualities (Fig. 5, FB, dashed lines). Incorporating Capello et al.’s scaling (16), we found that 1,167 configurations would have level 2 flying qualities, and 185 would have level 1 (Fig. 5, C, dotted lines). Note that we used a Cessna 172 as the comparable large-scale aircraft to calculate the scaling constant (16, 34). Thus, by accounting for known differences between large-scale aircraft and small UAVs, our results suggest that a gull-like UAV design with wings swept forward less than 20° would be flyable albeit with a higher pilot workload for many configurations.

Unlike the short-period mode, MIL-F-8785C only provides a minimum criterion on the phugoid damping ratio, and UAV-focused studies tend to agree with the effectiveness of this parameter (16, 17). Our results show that the gull was substantially above the level 1 minimum damping ratio of 0.04 (Fig. 3E) and had nearly an order of magnitude higher damping ratio than comparable UAVs. As discussed previously, this is due both to our gliding analysis and the lower aerodynamic efficiency in the tested configurations. Future work is required to determine if these values exhibited by gliding gulls are too heavily damped for effective implementation in a gliding UAV. A higher damped phugoid mode may be beneficial, as this mode is notorious for pilot-induced oscillations; but the high damping also suggests that there is a slow response to control inputs for the flight speed and pitch angle. This sluggish response to elevator inputs was observed for a small gull-wing morphing UAV (6).

These differences in the phugoid modes between gulls and UAVs are intriguing because they may play a role in avian gust response, which tends to outperform comparable fixed-wing UAVs. Small perturbations in the forward velocity of a trimmed gliding gull would be quickly damped out according to our model. However, the gull would need to use larger control inputs to maneuver away from the equilibrium condition. These results reveal a reason that gulls may elect to adjust from a stable to an unstable configuration. Gulls could use a stable configuration to passively reject undesired perturbations from their local environment while in transit or foraging for food. Then, gulls could extend their wrists to morph into an unstable configuration to gain a more sensitive reaction to control inputs, which would support rapid maneuvering.

However, although the discussed flight qualities are a useful comparative tool, the MIL-F-8785C and the adjusted UAV guidelines are dictated by conversations with pilots (13, 16, 17). These flying qualities do not necessarily translate to avian flying qualities, which are unlikely to be directly comparable to human metrics. Future work is required to explore and identify the flying qualities that are desirable for the avian neurological control system.

Simplified Gust Response.

Because the heavily damped phugoid mode pointed to possible gust-related benefits, we explored the time response of the gull to transverse and streamwise gusts (Methods). Note that a bird’s gust response affects their foraging and landing capabilities (35–37). Intriguingly, a study of live gulls in a wind tunnel found that increased turbulence intensity (a measure of variation in the freestream velocity) had no effect on the overall metabolism of the bird and thus no effect on their energetic requirements (38). Since we found that both the phugoid and short-period modes are heavily damped, it is possible that a gliding gull in a stabilized configuration does not require active control to return quickly to an equilibrium condition, which may reduce energetic costs.

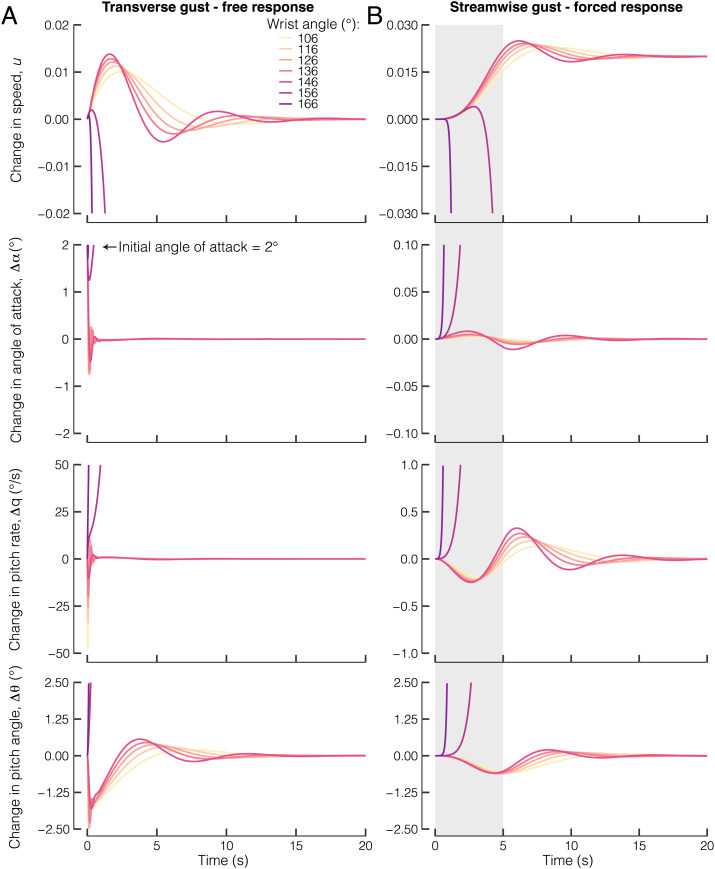
To visualize the effect of small environmental fluctuations, we calculated the dynamic responses to disturbances modeled with either a 2° step change in the angle of attack or a 2% increase in the forward speed (Methods). We investigated configurations with a fixed elbow angle (130°) and fixed shoulder sweep angle (15°) but a variable wrist angle (Fig. 6). This range allowed us to explore both stable and unstable configurations across a broad range of wrist angles. Each wing configuration was at a different trim state. The wrist angle of 156° had a trim glide angle (γ₀) of −61° and was excluded from the previous analyses as it is steeper than our imposed limit of −45° (Methods). We included it in this analysis for completeness.

Fig. 6.

By morphing its wrist, a gull gains substantial control over its gust response. (A) A simplified transverse gust modeled as an initial offset of a 2° angle of attack. (B) A discrete 1-cosine streamwise gust modeled as an increase of 2% of the initial trim speed ($U_0$) over 5 s (gray box). Only configurations with an elbow angle of 130° and a forward sweep angle of 15° are shown.

The time responses of these configurations captured the quickly diverging dynamics associated with higher wrist angles and showed that small perturbations in the angle of attack (Fig. 6A) or speed (Fig. 6B) would be quickly damped out for lower wrist angles. For stable configurations with lower wrist angles, the time to half the amplitude varied between 2.22 and 2.52 s for the phugoid mode and 0.05 and 0.12 s for the short-period mode. For the unstable configurations with higher wrist angles, time to double the amplitude varied from 0.80 to 1.69 s for the phugoid mode and 0.03 to 0.04 s for the short-period mode. All these dynamic responses are slower than the amount of time that it takes a particle to pass over the wing root chord, which ranged from 0.01 to 0.02 s, although the short-period mode responses are roughly on the same order of magnitude. In all, these results show that gulls gain substantial control over their dynamic characteristics through solely adjusting their wrist joints. It is important to again highlight that the strong interactive effects between the elbow, wrist, and shoulder joints means that the effect of each morphing joint depends on the other joint positions, and these evaluated configurations are only a representative sample. These interactive effects indicate that a complex control system would be required to effectively pilot a gull-like UAV.

Conclusions

Gulls regularly morph their wings in flight, which has been hypothesized to permit enhanced maneuverability and control. Our work incorporated existing studies on the aerodynamic and inertial properties of a gliding gull to provide a detailed investigation of dynamic stability characteristics throughout wing morphing. Our results suggest that the gull could fold its wing joints or sweep its wings backward to remain in a trimmed state as wind speeds increase. Further, we showed that most gull-wing configurations have a short-period mode that satisfies the minimum controllability requirements for level 2 human-piloted aircraft as well as a heavily damped phugoid mode. We suggested that the high phugoid damping acts to reduce the gull’s sensitivity to small perturbations in the localized environment. However, this reduced sensitivity suggests that the gull would have a sluggish response to control inputs needed to effectively maneuver. Thus, we hypothesized that gulls initiate sudden maneuvers by morphing into unstable configurations and morph back into a stabilized configuration to reject nondesirable perturbations to their flight path.

It is important to highlight the limitations and simplifications used throughout this work. Predominately, this approach uses a quasi-steady aerodynamic analysis of a rigid gull undergoing small perturbations in symmetric flight. Additional work is required to extend this analysis to include a lateral analysis, nonlinear and unsteady flight conditions, and larger-scale atmospheric gusts. In addition, feather flexibility will affect the aerodynamic characteristics; however, this effect is expected to be minor at the Reynold’s numbers that are relevant for bird flight (39). We assumed that the tail was furled for this analysis, but future work should also investigate the role of a morphing tail. Further, we used a single gull specimen to focus our study, but there will be individual differences as well as species-specific differences in the dynamic characteristics of bird flight. To extend this study, further work should improve the aerodynamic prediction capabilities at higher angles of attack to allow an investigation of the most aerodynamically efficient configurations, which would shed light on the interaction between performance and stability characteristics. Finally, the flying qualities section is most relevant for a UAV designed to mimic gull flight. Connecting our results with information about the avian neurological control system will be a necessary next step to understand avian flight control methodologies.

In all, our study confirms that gulls can negotiate trade-offs in stability and maneuverability by morphing their wings between dynamically stable and unstable configurations and provides a mechanism for how birds exhibit both stable flight and sudden, rapid maneuvers. Our results encourage additional engineering investigations into morphing wing UAVs that can substantially shift their static margin. With this capability, we will be able to identify whether the ability to shift stability modes is necessary to achieve avian-like maneuverability and if this approach can be harnessed to advance the maneuverability of future UAVs.

Methods

We developed the governing equations of motion for a gliding gull in the longitudinal plane. We assumed a rigid, nonporous, symmetric gull undergoing small perturbations in a quasi-steady state. These assumptions allowed us to evaluate longitudinal (i.e., pitch) characteristics separate from the lateral (i.e., roll and yaw) characteristics and to obtain a state-space representation of the longitudinal governing equations.

Determining the Trim States.

Our previous aerodynamic study on gulls found that wing–body configurations were unable to trim when the wings were held at a shoulder angle with 0° dihedral and 0° sweep (22) (Fig. 1 C and D). These configurations could not trim because they generated a negative zero-lift pitching moment and a negative pitch stability derivative; thus, there was no angle of attack that generated positive lift while the pitching moment was zero, which is necessary to trim (22).

However, the existence of a trim state is necessary for most stability analyses. To address this issue, we first adjusted the model to include a furled, static tail (Fig. 1D). The tail was modeled as a flat, thin, rectangular wing behind the body with a NACA 0006 airfoil and dimensions based on previously obtained furled tail measurements from the same gull species (23). We found that the tail had a minor stabilizing effect but alone was not sufficient to trim. We expect that the tail will have a larger impact when spread and/or if it is rotated at an incidence angle relative to the body, like an aircraft’s elevator.

As gulls are capable of gliding with their tail furled, we next included two additional degrees of freedom: the sweep and dihedral angle at the shoulder joint (Fig. 1 C and D). We investigated setting the shoulder dihedral angle at 0°, 10°, and 20° and the shoulder sweep angle at −20°, −10°, 0°, 10°, and 20°. Because these additional parameters required 15-fold more configurations to be tested, we subsampled the elbow and wrist configurations that we ran in MachUpX to 200, down from 1,031 in the previous aerodynamic study (22). We ensured that the configurations were equally distributed by binning in increments of 5° of elbow angle and by 5° of wrist angle and randomly selecting one configuration from each bin. In addition, to increase the convergence speed for these complex wing shapes, we implemented a custom line search that leverages an inverse parabolic interpolation (40) to calculate the optimal relaxation factor for each iteration of MachUpX’s Newton method (41, 42). We verified that this update returned the same converged result as MachUpX’s fixed relaxation factor. In addition to the updated aerodynamic results, we used outputs from our previous inertia study (23) to recompute the center of gravity and moment of inertia of each wing configuration, allowing for the additional degrees of shoulder motion (SI Appendix).

With the aerodynamic and inertial results, we fit linear models to the coefficient of lift ($C_{\text{L}}$), coefficient of pitching moment ($C_{\text{m}}$), and moment of inertia about the pitching axis ($I_{\text{yy}}$) as the dependent variables (SI Appendix). The origin of the coefficient of pitching moment and moment of inertia was set at each configuration’s center of gravity. We could not use MachUpX’s results to predict the coefficient of drag ($C_{\text{D}}$) because the numerical results differed substantially from experimental wind tunnel data for gull wings that had more folded wrist angles (22). Instead, we fit a low-order linear model to the experimental data and used this model to predict the drag of all configurations (22). This approach did not account for changes in the drag due to shoulder sweep and dihedral angle or due to the added tail. For this reason, we kept the sweep and dihedral angle below 20°. We expect only minor effects of the furled tail on the drag at the low angles of attack investigated in this work. Future work is required to account for the changes in drag due to the furled tail and shoulder sweep and dihedral angle. Finally, we calculated the pitch rate (q) derivatives by running the nine wind tunnel configurations in MachUpX with pitch rates varying from −0.5 to 0.5 rad/s and fitting a linear model to the outputs. In all, fitting these linear models allowed us to establish a general method to predict the aerodynamic and inertial characteristics for any wing configuration.

Next, to calculate the trim position of each configuration, we iterated through combinations of the elbow, wrist, and shoulder angle in the in vivo gull gliding range to calculate the trim position of each configuration (21). The elbow angle was varied from 86° to 164° (Δ2°), the wrist angle from 106° to 178° (Δ2°), the sweep angle from −20° to 20° (Δ5°), and the dihedral angle from 10° to 20° (Δ5°). For each configuration, we calculated the trim angle of attack (${\alpha }_0$), trim speed ($U_0$), and trim glide angle (${\gamma }_0$) from the following system of equations (Fig. 1E):

$$\begin{array}{l}-(1/2)\rho U_0{}^{2}S{C}_{\text{D}}-W\text{sin}\left({\gamma }_0\right)=0\\ -(1/2)\rho U_0{}^{2}S{C}_{\text{L}}+W\text{cos}({\gamma }_0)=0\\ (1/2)\rho U_0{}^{2}Sc{C}_{\text{m}}=0.\end{array}$$

Here, $\rho$ is the air density, $S$ is the maximum wing–body area across all morphed configurations, $c$ is the maximum wing root chord across all morphed configurations, and $W$ is the weight. To ensure compatibility across all metrics, the reference area, chord, and weight are all from one gull specimen with 0° shoulder sweep and dihedral angle that was investigated in our previous inertial study (23). We limited our results to configurations that could trim at ${\alpha }_0$ < 5° because MachUpX best matched the experimental data at low angles of attack (22). If a configuration with a given combination of joint angles could not trim within our set parameter space, it was not included in the analysis.

We found that increasing the shoulder dihedral angle and sweeping the wings forward allowed more wing configurations to trim due to an increased zero-lift pitching moment. Because we found that the majority of elbow and wrist configurations could trim at 20° dihedral with forward swept wings, we limited our results to these shoulder angle parameters for the remainder of the study. Note that higher dihedral angles would allow all combinations of elbow and wrist angles to trim, but we limited our analysis to 20° to minimize the effects on drag estimation. Even with these limitations, some of the configurations required extremely steep trim glide angles (${\gamma }_0$), likely closer to terminal velocity than true gliding flight. Therefore, we limited our results to configurations that had ${\gamma }_0$ > −45°. In total, 1,457 configurations both satisfied our imposed limitations and were able to trim (Fig. 2F).

Formulation of the Governing Equations.

We formulated the equations of motion following procedures similar to those outlined in aeronautical texts (11, 12). Any deviations from these texts are due to assumptions on the aerodynamic derivatives and are detailed in the SI Appendix. Although we modeled the bird as a rigid body, we accounted for a change in the aerodynamic and inertial characteristics between each different wing configuration. This approach of solving the dynamic response for each fixed configuration independently is similar to the approach used to establish the operating parameters for aircraft across different flight conditions independently (12). We can write the final small perturbation state-space representation of each bird configuration as

$$\dot{X}=AX+BU$$

$$X=\left[\begin{array}{c}u\\ \mathrm{\Delta }\alpha \\ \mathrm{\Delta }q\\ \mathrm{\Delta }\theta \end{array}\right]$$

$$A=\left[\begin{array}{cccc}-2\tilde{m}{C}_{\text{D}}& \tilde{m}\left(C_{\text{L}}-\frac{\partial C_{\text{D}}}{\partial \alpha }\right)& 0& -\frac{g}{U_0}\text{cos}\left({\gamma }_0\right)\\ -2\tilde{m}{C}_{\text{L}}& \tilde{m}\left(-C_{\text{D}}-\frac{\partial C_{\text{L}}}{\partial \alpha }\right)& 1-\tilde{m}\frac{\partial C_{\text{L}}}{\partial q}& -\frac{g}{U_0}\text{sin}\left({\gamma }_0\right)\\ 0& \widetilde{I_{\text{yy}}}\frac{\partial C_{\text{m}}}{\partial \alpha }& \widetilde{I_{\text{yy}}}\frac{\partial C_{\text{m}}}{\partial q}& 0\\ 0& 0& 1& 0\end{array}\right]$$

where

$$\tilde{m}=\frac{\mathrm{\rho }{U}_{0}S}{2m} \widetilde{I_{\text{yy}}}=\frac{\mathrm{\rho }{U}_0^{2}Sc}{2I_{\text{yy}}}.$$

$X$ is the state vector and includes perturbations in the speed ($u$, normalized by the trim speed), angle of attack ($\mathrm{\Delta }\alpha$), pitch rate ($\mathrm{\Delta }q$), and pitch angle ($\mathrm{\Delta }\theta$). These equations model the longitudinal dynamics of the fixed-wing gull as a fourth-order system under the simplifications outlined above and within the SI Appendix.

To quantify the free response of the system, we solved for the eigenvalues and eigenvectors of $A$ at all trimmed configurations using a custom Python script. With these outputs, we calculated the damping ratio and frequency of the short-period and phugoid modes of each configuration (11) as

$$\omega =\sqrt{R{e}^2+ I{m}^2}$$

$$\zeta =\frac{-Re}{\omega },$$

where Re and Im represent the real and imaginary parts of each eigenvalue, respectively.

Next, we used the Python Control Systems Library (43) to solve for the time response of the gull for two simplified gusts. First, to model a simplified transverse gust, we solved the free response of the system with an initial angle of attack of 2°. This is mathematically equivalent to an impulse in the angle of attack. Due to the rigid body assumption, we did not model the joints as independent controls, and thus the input vector ($U$) is zero for this case. Second, to model a streamwise gust, we solved for the forced response of a discrete gust model as implemented within MIL-F-8785C, which uses a 1-cosine velocity profile (13). This model assumes an increase of 2% in the streamwise velocity over a period of 5 s and then for the velocity to remain fixed at this increased value (SI Appendix). Solving the state space equations under these conditions returned the time response of each of the four variables within the state vector X.

Data, Materials, and Software Availability

All data reported in this paper have been deposited in the public repository https://doi.org/10.6084/m9.figshare.c.5895032 (44). Custom codes reported in this paper have been deposited in the public repository https://github.com/charvey23/AvianDynStab (45). All other data are included in the manuscript and/or SI Appendix.