Abstract
Motivation
Cancer is a genetic disease in which accumulated mutations of driver genes induce a functional reorganization of the cell by reprogramming cellular pathways. Current approaches identify cancer pathways as those most internally perturbed by gene expression changes. However, driver genes characteristically perform hub roles between pathways. Therefore, we hypothesize that cancer pathways should be identified by changes in their pathway–pathway relationships.
Results
To learn an embedding space that captures the relationships between pathways in a healthy cell, we propose pathway-driven non-negative matrix tri-factorization. In this space, we determine condition-specific (i.e. diseased and healthy) embeddings of pathways and genes. Based on these embeddings, we define our ‘NMTF centrality’ to measure a pathway’s or gene’s functional importance, and our ‘moving distance’, to measure the change in its functional relationships. We combine both measures to predict 15 genes and pathways involved in four major cancers, predicting 60 gene–cancer associations in total, covering 28 unique genes. To further exploit driver genes’ tendency to perform hub roles, we model our network data using graphlet adjacency, which considers nodes adjacent if their interaction patterns form specific shapes (e.g. paths or triangles). We find that the predicted genes rewire pathway–pathway interactions in the immune system and provide literary evidence that many are druggable (15/28) and implicated in the associated cancers (47/60). We predict six druggable cancer-specific drug targets.
Availability and implementation
The code and data are available at: https://gitlab.bsc.es/swindels/pathway_driven_nmtf
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Cancer is a genetic disease in which the accumulation of genetic mutations leads to the uncontrolled proliferation of tumor cells (Vogelstein et al., 2013). Specifically, mutations to cancer driver genes lead to the reprogramming of cellular pathways: functional subnetworks within the cell that once activated lead to a certain product, or a change within the cell (DeBerardinis and Chandel, 2016). This causes the cell to gain and lose functions that enable tumor growth and metastatic dissemination, such as gaining the ability to sustain proliferative signaling and resisting cell death, whilst losing the ability to respond to growth suppressors (Hanahan and Weinberg, 2011). To gain insight into the mechanisms underlying cancer, often pathway-based methods are considered, as they provide functional context to the observed gene mutations. This, in turn, helps to generate testable hypotheses, to identify drug targets and to determine tumor subtypes (Creixell et al., 2015). Furthermore, pathway-based approaches offer a higher level point of view to uncover functional changes in cancer than the gene level. For instance, clinically similar cancer patients could have different sets of mutated genes, but have similar perturbed pathways (Vogelstein et al., 2013). As such, pathway-based approaches are often applied to provide insight into disease mechanisms, in cancer and other diseases. For instance, they are applied to study the differences between clonal subtypes in triple-negative breast cancer (Kim et al., 2018), to study the replication mechanisms of SARS-CoV-2 (Han et al., 2021) and to uncover risk factors in Alzheimer’s disease (Zhao et al., 2020).
1.1 Current pathway-based approaches to study cancer
Currently, there are two major classes of pathway-based approaches for studying cancer in biological networks, each of which can be sub-divided into two sub-classes. Gene set enrichment (GSE) approaches identify predefined pathways (e.g. from curated databases such as Reactome; Jassal et al., 2019) that are enriched in genes that have their expression altered. For a given pair of case and control gene expression samples, Over-Representation Analysis (ORA) identifies those pathways that contain more differentially expressed genes than expected by chance, typically determined using Fisher’s exact test. Popular implementations include g:Profiler (Raudvere et al., 2019) and WebGestalt (Liao et al., 2019). However, as ORA approaches consider genes to be either differentially expressed or not, they ignore the magnitude of gene expression changes. To counter this issue, Function Class Scoring (FCS) approaches identify disease pathways based on the aggregate of their gene expression values being higher or lower than expected. Concretely, FCS methods take multiple gene expression data matrices that correspond to case and control samples as an input. First, genes are sorted in ascending order according to their ability to predict the case phenotype. Then, pathways are prioritized if they are enriched in top-ranking genes. FCS methods include GSEA (Subramanian et al., 2005), GSVA (Hänzelmann et al., 2013) and many variations thereof. As GSE approaches consider pathways as gene sets, they ignore the interactions between the genes within and across pathways.
Network-based approaches consider pathways not as gene sets, but as networks, where nodes represent genes and edges represent interactions or associations. Usually, protein–protein interaction (PPI) networks are considered, in which edges represent physical interactions between the protein gene products. Within this class of approaches, pathway-topology-based (PTB) approaches extend FCS methods to account for the topological importance or centrality of the genes in a pathway. Intuitively, if a gene has many interactions in the pathway (i.e. is topologically important), it is assumed to be important to the pathway’s functioning. So, changes in gene’s expression should have a larger or lesser impact on a pathway’s perturbation score dependent on its topological importance. For instance, in Signalling Pathway Impact Analysis (SPIA) (Tarca et al., 2009), the perturbation score of a given gene is based on its own log-fold change in gene expression and that of its neighbors. As SPIA diffuses gene expression changes as signals through the pathway, the (aggregated) pathway perturbation score gets amplified if the most strongly perturbed genes are also those central to the pathway (i.e. have many neighbors that are also highly connected). However, as PTB methods consider pathways in isolation, i.e. gene perturbations outside the pathway do not affect its score, and current pathway annotation data are very incomplete, they are prone to producing many false negatives (Ogris et al., 2017). Crosstalk enrichment (CE) methods acknowledge that pathways are part of a larger network. Given a large-scale network, CE methods prioritize pathways based on their association, i.e. crosstalk, with a set of differentially expressed genes. For instance, EnrichNet performs random walks on a large-scale network, starting the walks from nodes corresponding to differentially expressed genes. Pathways are prioritized as cancer pathways based on their overlap with the random walks (Glaab et al., 2012). Alternatively, ANUBIX first considers the subnetwork induced by a set of differentially expressed genes on the large-scale network. A pathway is scored by comparing its edge-overlap with this subnetwork against the overlap expected by chance (Castresana-Aguirre and Sonnhammer, 2020).
1.2 Shortcomings of current pathway-focused approaches
Current pathway-based approaches to study cancer have a few shortcomings. First, in spirit, current pathway-based approaches identify cancer implicated pathways as those most (internally) perturbed by cancer-driven gene expression changes. However, in previous work, we observed that known cancer driver genes are central in the communication between pathways, as they are statistically significantly frequently found as hub nodes between pathways (Windels et al., 2022). Moreover, this observation has also been made for diseases outside cancer. For instance, genes implicated in cryptorchidism, a congenital disease characterized by the absence of at least one testy from the scrotum, have also been shown to occur as hub nodes between disease implicated pathways (Cannistraci et al., 2013). These findings imply that to identify pathways implicated in cancer, and potentially many other diseases, we should not focus on pathways that are significantly perturbed internally, but instead prioritize pathways whose interactions and functional relationships with other pathways change substantially in disease. This conclusion is in line with prevailing literature, where it is recognized that to fully understand cancer disease mechanisms, it is essential to consider the tangled networks into which pathways are integrated (Vogelstein et al., 2000).
Additionally, current pathway-focused network-based methods only consider standard adjacency: two nodes are connected by an edge if they (directly) interact. To go beyond such simple connectivity patterns and include information about the higher-order molecular organization of a network (e.g. pathways or protein complexes), we recently introduced graphlet adjacency, which considers two nodes adjacent if they participate in a network pattern of a pre-specified shape, for instance, a triangle or a square (Windels et al., 2019). In particular, graphlet adjacencies based on paths and claws have been shown to capture topologically different hub roles of genes between pathways (Windels et al., 2022). In network biology, it is assumed that highly interconnected nodes in a network, i.e. nodes that cluster, contribute to the same biological function. Through cluster enrichment analysis of molecular networks, we illustrated that graphlet adjacencies based on different ‘small network shapes’ (i.e. graphlets) capture complementary views of the networks’ global connectivity and hence of its functional organization (Windels et al., 2019). We also illustrated this topology–function relationship at the node (gene) level, by showing that the functional importance of some genes in pathways is only reflected in their topological importance when measured using a particular graphlet adjacency (Windels et al., 2022). Therefore, by only considering standard adjacency, current methods ignore the opportunity to potentially better capture the reorganization of pathway relationships in cancer and the hub-roles of cancer genes.
1.3 Taking ideas from Natural Language Processing
Learning relationships between entities is a key part of Natural Language Processing (NLP). Semantic analysis, which tries to determine the meaning of a word or sentence, starts by learning a semantic space: a dense, low dimensional space that captures the semantic similarity between words or sentences. In this space, words and sentences are represented by embeddings, d-dimensional vector representations, where words or sentences of similar meaning have similar embeddings (i.e. are embedded nearby in space) (Mikolov et al., 2013). This semantic space can be queried through analogies: simple linear operations on the word or sentence embeddings. For instance, in a semantic space trained by Glove, based on their word embeddings King—Man + Woman Queen (Pennington et al., 2014).
A more recent trend is the embedding of biological networks, finding applications in protein function prediction, drug repurposing and patient stratification (Su et al., 2020). Analogous to NLP’s semantic space, the goal of network embedding is to find a low dimensional space that captures the global connectivity of the network, i.e. nodes are embedded nearby in this space if they tend to connect to the same nodes (i.e. if they cluster) in the network. Non-negative matrix tri-factorization (NMTF), a machine learning method originally proposed for co-clustering and dimensionality reduction (Wang et al., 2008), is a popular network embedding method because of its interpretability and flexibility as a data integration algorithm.
1.4 Contribution
In this study, we aim to prioritize cancer-implicated pathways whilst simultaneously providing insight into the key genes involved, in four cancers: lung and colorectal cancer, respectively the deadliest cancer, and prostate and ovarian cancer, the most prevailing gender-specific cancers (Sung et al., 2021). To do so, we define a two-step approach: we first identify pathways implicated in cancer and then predict genes implicated in cancer in those pathways. We predict pathways or genes not based on their (internal) perturbation, but based on their functional importance and the change in their functional relationships in cancer.
For a given cancer, we create a case and control PPI network, representing a cancerous and a healthy cell, by overlaying a generic PPI network with cancerous and healthy gene expression data. To learn the functional organization of a healthy cell, we propose pathway-driven non-negative matrix tri-factorization model (PNMTF), which simultaneously decomposes ‘healthy’ curated pathways, encoded as induced subgraphs of the control PPI network. In this space, we define pathway and gene embeddings, based on the pathways in a healthy and diseased state (represented by the subgraphs induced by curated pathways on the case and control PPI network). Based on these embeddings, we define ‘NMTF centrality’, which measures the functional importance of a pathway or gene as the norm of its healthy embedding and ‘moving distance’, which measures the disruption of a pathway’s or gene’s functional relationships as the distance between its healthy and cancerous embedding.
We validate that PNMTF captures the functional organization of pathways in the cell: embedding all pathways in the shared space, we find that their embeddings form well-separated and functionally coherent clusters. Then, we show that pathways or genes with high centralities and moving distances are likely to be cancer related, effectively identifying cancer-related pathways and genes not based on their (internal) perturbation but their functional relationships in the cell. Additionally, we show that higher-order topologies based on graphlets that encode different hubness properties allow us to exploit cancer drivers tending to perform hub roles between pathways to improve our prediction accuracy. Finally, we focus on the top 15 predicted genes for each of the four cancers, which cover 28 unique genes in total. We find that they rewire pathway–pathway interactions in the immune system for three of the four cancers. We validate 47/60 (78%) of the gene–cancer associations in the literature and show that the genes of the 13 unvalidated gene–cancer associations are implicated in other cancers. Moreover, 15/28 (54%) of the prioritized genes are known drug targets. As 6 of the 13 unvalidated cancer–genes associations involve druggable genes, we suggest them as cancer-specific drug targets.
2 Materials and methods
To allow us to consider the higher-order topology of networks to better capture different types of roles of nodes, we first recall the formal definition of graphlet adjacency (see Section 2.1). Next, to capture the higher-order organization encoded by graphlet adjacencies in a lower-dimensional space, we define our baseline model Global-NMTF (see Section 2.2.1). Then, we extend our NMTF model to Pathway-driven NMTF to benefit from the known functional organization of pathways in Reactome (see Section 2.2.2). Finally, to identify pathways and genes implicated in cancer, we define our embedding-based centrality and moving distance measures, which respectively measure the (topological) importance of a pathway or gene and how much the their functional relationships change between a healthy to a diseased state (see Sections 2.3.1 and 2.3.2).
2.1 Graphlet adjacency
Graphlets are small, connected, non-isomorphic, induced subgraphs of a large network (Pržulj et al., 2004). All graphlets with up to four nodes are depicted in Figure 1A. Nodes u and v of a network H are considered graphlet adjacent w.r.t. a given graphlet, Gi, if they simultaneously touch Gi (Windels et al., 2019). In the network presented in Figure 1B, we find that nodes a and b are adjacent with respect to graphlet G1 (a three-node path) twice, as G1 can be induced on the example network twice including both nodes a and b: along paths a-b-c and a-b-e. Given this extended definition of adjacency, the graphlet adjacency matrix is defined as:
| (1) |
where is the number of times the nodes u and v are graphlet adjacent w.r.t. graphlet . Note that , is equivalent to the standard adjacency matrix. Analogously, the graphlet degree generalizes the node degree as the number of times node u touches graphlet . The Graphlet Degree matrix for graphlet Gi, , is defined as:
| (2) |
where is the number of times node u touches graphlet Gi. The symmetrically normalized graphlet adjacency matrix is defined as:
| (3) |
where is a scalar equal to the node count of graphlet Gi minus 1. This scaling factor is applied so that the entries in fall in the range. For more details, see Windels et al. (2019).
Fig. 1.
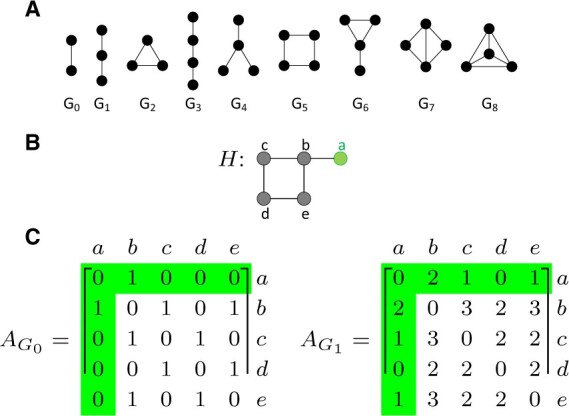
An illustration of graphlets and graphlet adjacencies. Node a is highlighted throughout. (A) All graphlets with up to four nodes, labeled G0 to G8. (B) Example network H. (C) The graphlet adjacency matrices and for graphlets G0 and G1 of the example network H, shown in panel (B). The off-diagonal elements correspond to the number of times two nodes touch a given graphlet together. , as a and b form G0 once. , as a and b form G1 twice, via paths a-b-c and a-b-e. This figure is adapted from Fig. 1 in Windels et al. (2019)
2.2 NMTF models
To capture the functional organization of the cell as an embedding space, we define our baseline NMTF model called Global NMTF (GNMTF) (see Section 2.2.1). Then, we extend our NMTF model to benefit from the known functional organization of pathways (see Section 2.2.2). The solvers for both models are presented in Supplementary Section S2.
2.2.1 Global NMTF model: a basic approach to learning the organization of the healthy cell
GNMTF aims to learn a d-dimensional embedding space that captures a healthy cell’s higher-order connectivity as described by a given graphlet adjacency. We represent the n-node PPI network of a healthy cell by graphlet adjacency matrix , and decompose as the product of three non-negative matrix factors, : . This corresponds to solving the following optimization problem:
| (4) |
where F denotes the Frobenius norm. We determine the numbers of dimensions d using the rule of thumb: (Kodinariya and Makwana, 2013). We interpret V as an orthogonal basis that captures the functional organization of the cell as captured by , and E = US as embedding all genes in common space V. Each row of E corresponds to the embedding of a gene, which we denote , in the space spanned by V. Then, analogous to NLP, where sentences can be represented by the average embedding of their constituent words (Le and Mikolov, 2014), we define the embedding of a pathway, which we denote , as the average embedding of its genes: , where mp is the set of gene embeddings for genes in a given pathway p.
2.2.2 Pathway-driven NMTF model: improved learning of the organization of the healthy cell
We extend our model to benefit from the known functional organization of pathways in Reactome. With PNMTF, we learn a latent representation for each pathway and an embedding space that organizes these discrete latent representations. Specifically, we encode how each pathway p interacts within the healthy cell by taking the rectangular submatrix, , induced by the genes in the pathway and n genes in the cell on . Then, we simultaneously decompose the Hp-matrices for all of the r pathways in Reactome into r pairs of non-negative latent matrices and one orthogonal non-negative latent matrix : for all . This corresponds to solving the following optimization problem:
| (5) |
Analogous to d, we determine the numbers of dimensions dp using the rule of thumb: (Kodinariya and Makwana, 2013). We interpret as embedding the genes of pathway p in the orthogonal space spanned by V. Each row of Ep corresponds to the embedding of a gene in the (functional) context of a given pathway p, which we denote by . Analogous to our GNTMF model, we define the embedding of a pathway p as the average embedding of its genes: , where mp is the set of gene embeddings for genes in pathway p.
2.2.3 Extending PNMTF: learning representations for cancer-affected pathways
To enable us to identify pathways whose functional relationships change the most in cancer (see Section 2.3.2), we aim to learn how cancer-affected pathways change their interactions with other pathways. To do so, we fix the common space V learned in Equation (5) based on the control PPI network, and solve PNMTF based on the case (cancer) PPI network to learn a second latent representation for each pathway, this time in a diseased state.
2.3 NMTF scores for cancer predictions
To identify pathways and genes implicated in cancer, we define three heuristics based on our PNMTF pathway and gene embeddings.
2.3.1 NMTF centrality
Here we define how we measure the topological importance of a pathway or gene based on its embedding. To do so, we take inspiration from the eigencentrality, which considers a node important if it is highly connected to other highly connected nodes, i.e. if it is part of a cluster of nodes in the network. It is computed as the eigenvector corresponding to the highest eigenvalue of the adjacency matrix:
| (6) |
where λ is the highest eigenvalue of A and is the corresponding eigenvector. By replacing A with the normalized graphlet-adjacency matrix, we defined graphlet eigencentrality in Windels et al. (2022).
In NMTF, the left and right latent matrices’ rows can also be interpreted as cluster-indicator vectors, where the entity corresponding to the row is assigned to the cluster corresponding to the column containing the highest valued entry. Therefore, following the proposition that an entity is considered central if it is part of one or more clusters, we measure the centrality of a pathway or gene by the Euclidean norm of its embedding:
| (7) |
where is the embedding of a healthy pathway (i.e. ) or gene (i.e. ) (see Section 2.2.2).
2.3.2 Moving distance
Here we define our moving distance, which measures how a pathway’s or gene’s functional relationships change when moving from a healthy to a diseased state. To do so, we take the Manhattan distance between a pathway’s or gene’s embedding in a healthy and diseased state (see Sections 2.2.2 and 2.2.3):
| (8) |
where and are the embeddings of a pathway or gene in a healthy and cancerous state, respectively (see Sections 2.2.2 and 2.2.3).
2.3.3 Hybrid score
We use the geometric mean to combine our centrality and moving distance:
| (9) |
where and are the embeddings of a pathway or gene in a healthy and cancerous state, respectively (see Sections 2.2.2 and 2.2.3).
2.4 Data
2.4.1 Case and control protein–protein interaction networks
We create four pairs of case and control PPI networks (i.e. cancerous and healthy), one pair for each of the four cancers considered. First, we create a generic PPI network by combining the experimentally validated PPI, only those captured using Two-hybrid or Affinity Capture-based methods, from BioGRID version 4.4.197 (Stark et al., 2006) and the PPI from Reactome (Jassal et al., 2019). Then, we overlay the RNA-SEQ gene expression data for four cancer cell lines and their corresponding control tissue from the Human Protein Atlas, on the generic PPI network (Uhlén et al., 2015). We consider prostate cancer (cell line PC-3), lung cancer (cell line A549), colon cancer (cell line CACO-2) and ovarian cancer (cell line EFO-21). Basic network statistics are presented in Supplementary Tables S1 and S2.
2.4.2 The Reactome Pathway Ontology
The Reactome Ontology is a collection of 23 directed acyclic graphs (DAGs), encoding the relationships between 2516 pathway annotations from the most generic to the most specific (Jassal et al., 2019). For each of our four pairs of case and control networks, we determine the set of pathways that induce a subnetwork of at least 10 and up to 100 nodes on either of the networks. The number of pathways per pair of networks (case and control) is presented in Supplementary Table S3.
2.4.3 Cancer annotation data
For the pathways and genes considered for each cancer (see Sections 2.4.2 and 2.4.1), we collect cancer annotation data. At the pathway level, we collect ‘cancer pathway’-annotations from Reactome, which indicate if a given pathway is considered to be a cancer pathway. At the gene level, we collect driver genes from the COSMIC database (Tate et al., 2019). We consider a gene to be a cancer driver if it is a known cancer driver in at least one cancer, with strong evidence (i.e. ‘Tier 1’) in the literature. Also, we collect a set of tissue-specific prognostic genes from the Pathology Atlas (Uhlen et al., 2017). The number of cancer pathways, driver genes and prognostic genes per cancer are presented in Supplementary Table S4.
3 Results and discussion
We apply our method to uncover novel pathways and genes involved in lung, colorectal, prostate and ovarian cancer. Specifically, for a given cancer type, we construct a case and a control network, representing a cancerous and a healthy cell (see Section 2.4.1). For the case and control networks, we compute all graphlet adjacency matrices for graphlets up to four nodes (see Section 2.1). Then, for a given graphlet adjacency, we learn the higher order functional organization of the healthy cell as an embedding space using our PNMTF model, in which we embed pathways and genes (see Section 2.2.2). Next, in this same space, we also compute embeddings for pathways and genes of a cancer affected cell, by fixing the basis trained for the control cell and solving PNMTF for the case PPI network (see Section 2.2.3). Finally, having computed a pair of embeddings for each pathway and gene based on the cell’s healthy and cancerous state, we apply our NMTF-scores: NMTF centrality, moving distance and hybrid score (see Section 2.3) to predict their cancer relatedness.
In our analysis, we first validate that PNMTF captures the functional organization of pathways in the cell (Section 3.1). Then we show that using our NMTF scores we can prioritize pathways and genes implicated in cancer (Sections 3.2 and 3.3). Finally, for each of our four cancers, we validate our top 15 predicted cancer genes and pathways involved in the literature (i.e. predicting 60 cancer-specific gene-pathway pairs in total, see Section 3.4). Due to different cancers sharing disease mechanisms, there is some overlap between our predictions at both the pathway and gene level, which we quantify in Supplementary Sections S3.4 and S3.7, respectively.
3.1 PNMTF captures the functional organization of the cell described by the Reactome pathway ontology
First, we validate that PNMTF best captures the functional organization of pathways in the healthy (control) cell, compared to GNMTF (essentially a standard NMTF model). To do so, for a given control network and graphlet adjacency, we train PNMTF and GNMTF (see Sections 2.2.1 and 2.2.2), embed all pathways in the shared space V and apply agglomerative hierarchical clustering on their pairwise Euclidean distances. Then, we confirm that pathway embeddings based on PNMTF form better separable and more functionally coherent clusters than those based on GNMTF.
We present the results for lung cancer based on graphlet adjacency in Figure 2. We observe that the agglomerative clustering uncovers a better separable clustering when applying PNMTF than GNMTF (cophenetic correlation 86.5% versus 66%). To measure how well both methods group functionally related pathways, we extract 65 clusters from both hierarchical clusterings (we determine this is the optimal number of clusters applying an elbow method in Supplementary Section S3.1.2), and check their enrichment in pathway ancestors, less specific pathways higher up in the Reactome ontology (see Supplementary Section S3.1.3). We observe that clusters of pathways based on PNMTF are more functionally coherent than those based on GNMTF (95% of the 65 clusters are enriched versus 75%). We provide similar results for all four control networks (representing four healthy cells) and graphlet adjacencies in Supplementary Section S3.1.
Fig. 2.
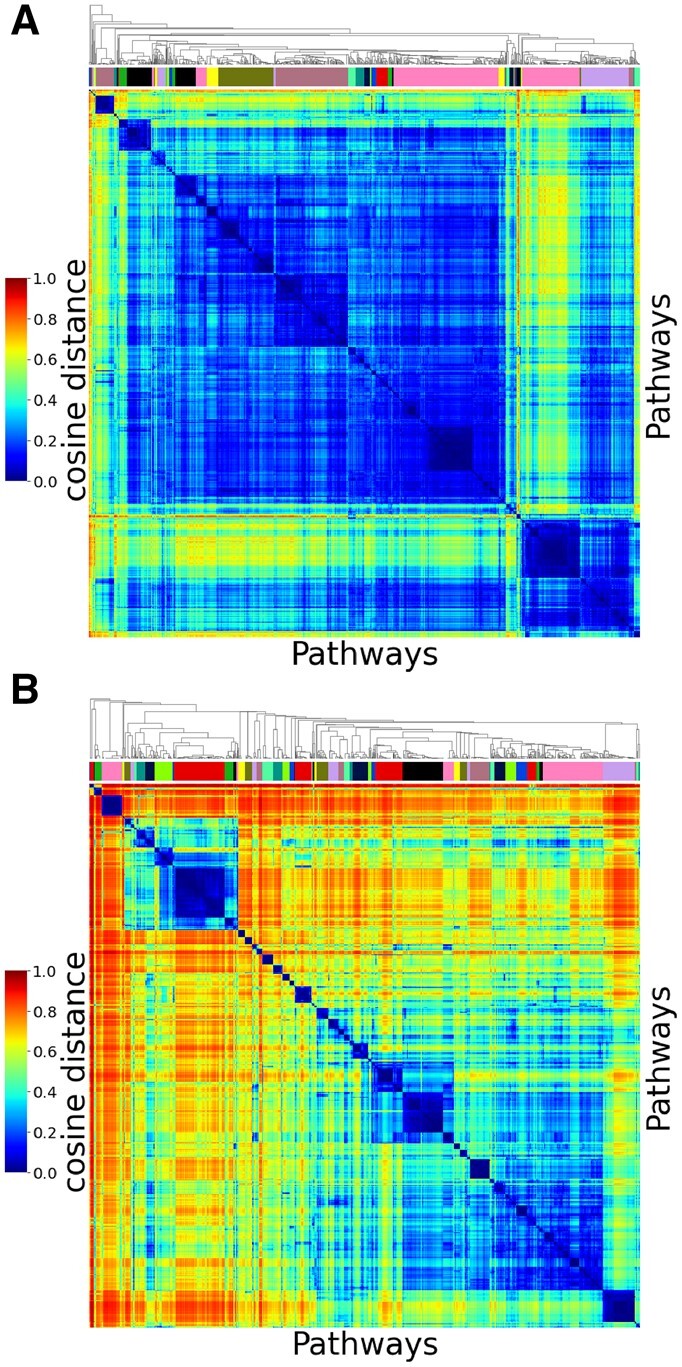
PNMTF best captures the functional organization of pathways in the healthy lung cell. (A) and (B) show a clustered heat map of the pairwise cosine distances between all pathway embeddings in the shared space V learned based on graphlet adjacency by GNMTF and PNMTF, respectively. For each heat map, the color bar under the hierarchical tree on the top indicates the 65 pathway clusters
In conclusion, compared to GNMTF, PNMTF-based pathway embeddings form clusters that are better separable (indicated by the high cophenetic correlation coefficient) and more functionally coherent (indicated by the high percentage of ancestor-enriched clusters), hence we conclude that PNMTF better captures the functional organization of pathways in the (healthy) cell than the standard GNMTF model.
3.2 PNMTF identifies pathways implicated in cancer
Having validated that PNMTF captures the functional organization of pathways in the healthy cell, we assess if our three NMTF scores: centrality, moving distance and hybrid score (defined in Sections 2.3.1–2.3.3) can be used to prioritize pathways implicated in cancer. Specifically, for a given NMTF score, cancer and graphlet adjacency, we measure the Matthews Correlation Coefficient (MCC) using the set of known cancer pathways in Reactome as a gold standard and a set of top-scoring pathways for each method as predictions for pathways implicated in cancer (see Supplementary Section S2.4). To determine the set of top-scoring pathways for each cancer, graphlet adjacency and NMTF score, we apply an elbow method. The results are presented in Supplementary Figure S4. As all three NMTF scores plateau beyond 100 pathways, regardless of the cancer and graphlet adjacency, we consider the top 100 highest scoring pathways as our prediction set for pathways implicated in cancer. Applying a hypergeometric test, we find that this set of pathways is enriched in Reactome cancer pathways (least significant P-value 4.67e−08). Additionally, we acknowledge that many pathways not labeled as cancer pathways in Reactome might overlap with cancer-mechanisms. For that reason, we also consider the ratio of driver genes in a pathway as an indication of its engagement in cancer. Then, to evaluate a given pathway prediction method, we measure the Spearman rank correlation between this ratio and a pathway’s score.
We compare the results for all different graphlet adjacencies, averaged over the four cell types, in Supplementary Figure S5. We observe the highest MCC and rank correlations when applying PNMTF based on . Here, we compare the results based on these top-scoring graphlet adjacencies and those based on pathway prediction methods ‘ORA’ (which despite its simplicity is still widely used) and ‘ANUBIX’ (a state of the art CE method), see Figure 3. Note that the three methods share the same input data: the set of genes expressed in a healthy and diseased sample, the assignment of genes to pathways and, for ANUBIX and PNMTF, PPI data. As such, all three methods are unsupervised, i.e. do not rely on any prior knowledge on pathway–cancer association when making their predictions. We cannot compare against FCS and PTB methods as they require multiple case and control samples for a given cancer.
Fig. 3.
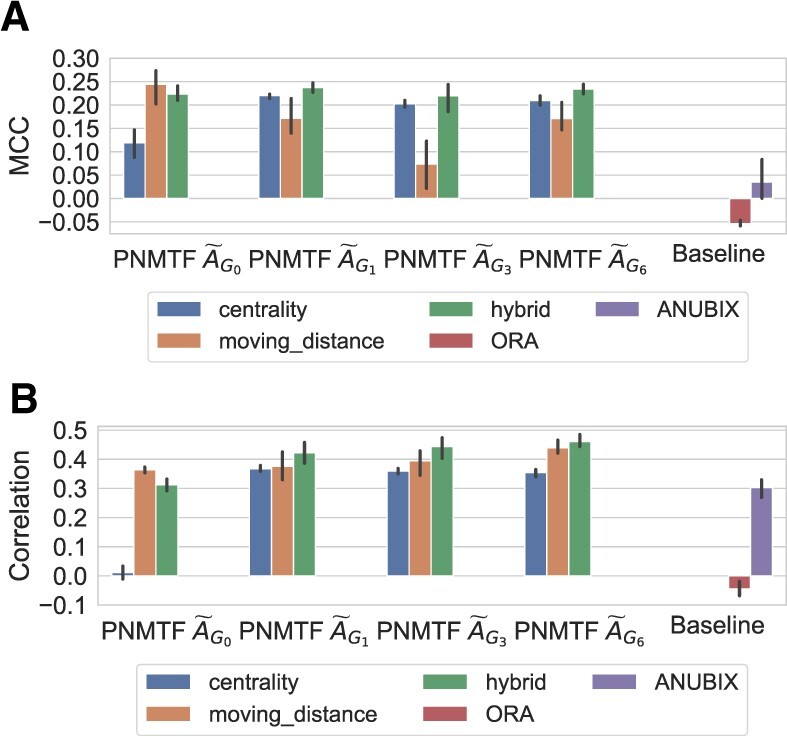
PNMTF identifies pathways implicated in cancer. Sub-plots (A) and (B) show the MCC and rank-correlation scores for predicting Reactome cancer pathways, respectively. From left to right, we present the results for PNMTF based on different graphlet adjacencies (x-axis) and different NMTF-scores (legend), against the state-of-the-art (far right)
First, we observe that in terms of MCC (see Fig. 3A), the best performance is achieved using our moving distance and regular adjacency (0.244), just outperforming our hybrid score with graphlet adjacencies (0.237, 0.220 and 0.233, respectively). All of the variations of our method mentioned above outperform ORA (−0.054) and ANUBIX (0.032). This renders our PNMTF scores more practical for further downstream analysis than ORA and ANUBIX, as our top ranked pathways are more likely to be cancer related. Looking at our correlation results (see Fig. 3B), we find that our hybrid score with graphlet adjacencies greatly outperform the moving distance with regular adjacency (0.42, 0.443 and 0.461, compared to 0.363). We also observe ANUBIX scores drastically better in terms of correlation (0.302) than in terms of MMC, which indicates that ANUBIX is able to rank pathways according to their likely involvement in cancer in general, although the set of top 100 highest ranked pathways is not particularly enriched in cancer pathways. We consider our hybrid score based on graphlet adjacency as the best approach, as it is only marginally behind our moving distance with , the best method in terms of MMC, but greatly outperforms this method in terms of rank correlation. Finally, we note that the highest scoring graphlet adjacencies, happen to be based on graphlets capturing betweenness and hubness, suggesting that cancer-related pathways tend to have hub roles. This is in line with our previous results, where we observed that cancer driver genes occur in statistically significantly more pathways than non-driver genes (Windels et al., 2022).
To further validate that our method captures cancer-implicated pathways, we investigate the top 10 highest scoring pathways in lung cancer (see Supplementary Table S5). We observe that 5/10 pathways are cancer pathways. All top 10 pathways are related to the RAS-MAPK pathway, which transduces extracellular signals to the cell nucleus, regulating cell growth, division and repair. The RAS-MAPK pathway is frequently associated with oncogenesis, tumor progression and drug resistance, and is a frequent subject of therapeutic studies (Braicu et al., 2019).
3.3 PNMTF identifies genes implicated in cancer
Having shown that our method can identify pathways implicated in cancer, we move on to find cancer-related genes within our set of 100 top-scoring pathways for each cancer. To identify a set of top scoring genes, we apply an elbow method to our three NMTF -scores: centrality, moving distance and hybrid score (defined Sections 2.3.1–2.3.3). The results are presented in Supplementary Figure S7. We observe that our gene scores plateau beyond the top 100 scoring genes, hence we choose to focus on the top 100 highest scoring genes in our previously identified set of top 100 highest scoring pathways (see Section 3.2). Then, we measure the MCC score using our set of top-scoring genes as a prediction and the driver genes in COSMIC as the gold standard (see Section 2.4.3). We compare PNMTF for graphlet adjacency against: PNMTF with regular adjacency, graphlet eigencentrality for (which predicts cancer genes based on their topological importance, see Section 2.3.1) and network diffusion for (which predicts genes as cancer related if they are in the network neighborhood of differentially expressed genes, see Supplementary Section S2.5. We tune diffusing parameter α to 1.9, which leads to the highest MCC scores when ranging α from 0.1 to 2.0 in increments of 0.1). The results are presented in Figure 4.
Fig. 4.
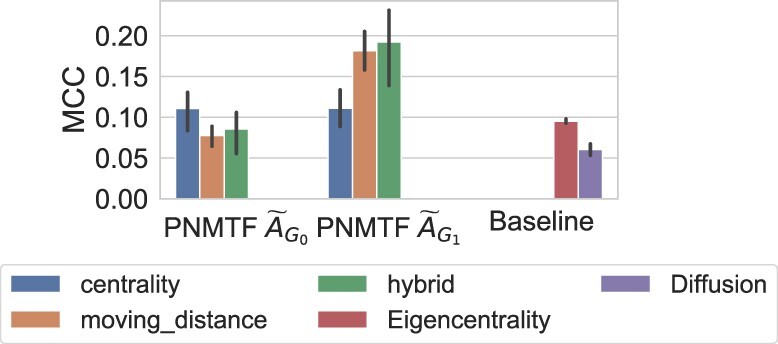
PNMTF identifies genes implicated in cancer. From left to right, we present the MCC scores for predicting cancer-related genes using PNMTF based on graphlet adjacencies and (x-axis) using different NMTF-scores (color coded, see legend), and compare against the state of the art (far right)
We observe that by using PNMTF based on and by using our hybrid heuristic, we achieve the highest score (average MCC of 0.18). This implies that cancer-related genes are best predicted when they are simultaneously of high importance in the control (healthy) networks (i.e. have a high centrality) and have a large shift in functional relations between case and control (i.e. have a high moving distance). Additionally, we observe that by considering the higher-order topology of pathways, as captured by , to take advantage of cancer drivers performing hub roles between pathways, we manage to increase the performance of our method compared to regular adjacency by 40% (average MCC with hybrid heuristic of 0.12). Lastly, we observe that our method outperforms graphlet eigencentrality and diffusion (average MCC of 0.09 and 0.10). Given that our method greatly outperforms our baseline methods, we conclude that PNMTF allows us to predict cancer-related genes with high accuracy, whilst indicating the pathways involved. In the next section, we investigate our results more in detail and perform literature validation.
3.4 Case study: identifying cancer-implicated genes in lung cancer and the pathways involved
We showed that by applying our PNMTF scores consecutively at the pathway and gene level, we can predict cancer-implicated pathways and cancer-implicated genes within those pathways (see Sections 3.2 and 3.3). In other words, our method allows us to predict cancer-implicated genes, whilst predicting for each gene the main pathway involved. Next, we validate in the literature the top 15 predicted genes in Section 3.3 based on our hybrid PNMTF scores with graphlet adjacency for each cancer (lung, colon, prostate, ovarian), and discuss the potential cancer relatedness of the prioritized pathways associated with those 15 gene predictions. Here, we discuss the results for lung adenocarcinoma (see Supplementary Table S9). For the other cancers, see Supplementary Tables S10–S12.
We first validate that our method prioritizes genes with hub roles between pathways. We apply a Mann–Whitney U (MWU) test to confirm that our prioritized genes, i.e. the top 15 genes based on our hybrid score (see Supplementary Table S9, column 2), participate more frequently in our prioritized pathways (see Supplementary Table S9, column 3) compared to the remaining, non-prioritized genes in those pathways. The MWU test yields a significant result (the prioritized genes participate on average in 2.0 of the prioritized pathways compared to 1.4 for the remaining, non-prioritized genes, P-value 2.22e−04). Therefore, as our prioritized genes occur more frequently in the prioritized pathways, they are the genes connecting those pathways, validating our method. We do not find this when applying our method on regular adjacency, highlighting that graphlet adjacency G1 enables us to capture the hub roles of potential cancer drivers. Further, we validate in the literature that 11/15 (73%) of the prioritized genes are implicated in lung cancer (see Supplementary Table S9, column 4). For our four unvalidated genes: CSK, HSP90AA1, HNRNPH1 and GNG2, we find strong web-lab evidence in the literature that they are involved in other cancers (see Supplementary Table S9, column 6). We find that HSP90AA1 is a known cancer driver in non-Hodgkins lymphoma (COSMIC), HNRNPH1 supports cancer-cell proliferation in rhabdomyosarcoma (Li et al., 2018) and CKS and GNG2 have tumor suppressing roles in colon cancer and melanoma, respectively (Nakagawa et al., 2000; Yajima et al., 2014). Moreover, we find that 11/15 (73%) of the prioritized genes are known drug targets, including CSK, HSP90AA1 and HNRNPH1 (see Supplementary Table S9, column 7).
Next, we focus on the associated prioritized pathways, which serve as a functional contexts to our gene predictions (see Supplementary Table S9, column 3). From the network perspective, we observe that the union of the prioritized pathways induces on both the case and control PPI network a connected sub-network that is denser than expected by chance (both P-values 1.00e−4, based on bootstrapping, obtained by sampling 10 000 sets of pathways that are of size within the range of those in our prioritized pathway list). This indicates that our prioritized pathways are likely functionally related (as they are overlapping in the PPI network) and that our method is capturing an underlying disease-related signal (as the pathways are more intertwined than expected by chance). Further, we validate that our method prioritizes pathways based their altered pathway–pathway interactions rather than their internal perturbation. To do so, we assess if our prioritized pathways have significantly more edges rewired (i.e. added or deleted) that connect them to the other prioritized pathways compared to the number of edges they have rewired within them, by applying a hypergeometric test. We find that edges between pathways are 12 times more rewired (P-value 3.40e−19), validating our method.
From a functional perspective, we find that our prioritized pathways are enriched in Reactome ‘Immune System’ pathways (pathways ranked 2, 3, 4, 8 and 15 in Supplementary Table S9, P-value 2.31e−2). Furthermore, the remaining pathways can easily be related to the immune system. For instance, pathways 9 and 14 are downstream of GCPR signaling, which regulates T-cell immunity (Wang, 2018). Pathway 12, ‘Receptors for oestrogens signalling’, regulates immune system pathways, as well as immune cell development (Kovats, 2015). These results are in line with the cancer literature, as immune system rewiring is necessary for cancer cells to evade immunological response and to enable them to abuse inflammatory responses as a source for bioactive molecules (e.g. growth factors) (Hanahan and Weinberg, 2011). Combined with our results at the gene level, we conclude that our method uncovers a cancer-induced rewiring of the proteins linking immune system pathways in lung cancer.
We obtain similar results across all four cancers, see Supplementary Section S3.7. Considering the top 15 predicted genes for the four cancers collectively, we validate 47/60 (78%) of these gene–cancer associations in the literature. We show that the genes involved in the 13 unvalidated gene–cancer associations are implicated in other cancers. As the top 15 predicted genes across the four cancers overlap, which is expected as cancers can share the same disease mechanisms, we predict 28 unique genes in total. Of these genes, 15/28 (54%) are known drug targets (see Supplementary Tables S9–S12, column 7). As 6 of the 13 unvalidated gene–cancer associations that involve druggable genes, we suggest them as cancer-specific drug targets: CSK, HSP90AA1 and HNRNPH1 for lung cancer, HSP90AA1 for colon cancer and prostate cancer, and HNRNPH1 for ovarian cancer. At the pathway level, find that our method uncovers a cancer-induced rewiring of the proteins connecting pathways involved in the immune system in colon and prostate cancer. As cancer immunotherapy is becoming a pillar in cancer treatment (Esfahani et al., 2020), this gives further interest to our predictions.
4 Conclusion
In this study, we suggest our PNMTF model, which learns an embedding space that captures the functional organization of pathways in a cell. In this embedding space, we define two heuristics: NMTF centrality and moving distance, which measure the importance and disruption of functional relationships of a pathway or gene in cancer, respectively. We apply these heuristics to predict cancer-implicated pathways and genes in four cancers. Additionally, we exploit cancer genes tending to perform hub roles between pathway interactions by considering graphlet-based higher-order topologies that encode hub roles. We find that our method uncovers a cancer-induced rewiring of the genes linking pathways involved in the immune system for three out of the four cancers. This is in line with the literature, where the immune system’s rewiring is considered a hallmark of cancer. Finally, we provide literary evidence indicating our top predicted genes are likely involved in cancer and find many are known drug targets, allowing us to predict six druggable cancer-specific drug targets.
Further, our analysis opens up multiple research questions:
To uncover emerging (disappearing) functional relationships in cancer and thus give insight into cancer development, it could be interesting to see what pathways become (less) central and form new (no longer form) dense clusters in cancer.
To extend PNMTF’s applicability, additional data could be integrated. For instance, to give insight into drugs affecting pathways, gene–drug data could be added. To study pathway relationships at different omics levels, more omics data could be added (e.g. Durán et al., 2021).
PNMTF could be applied to diseases outside cancer, particularly as disease genes perform hub roles between pathways in other diseases.
Lastly, PNMTF can be applied outside of biology, when the input data are a network and domain knowledge categorizing the nodes. For instance, PNMTF could be applied on trade networks, where nodes are countries and edges are the value of the trade between them, while trade agreements form a prior grouping of the nodes.
Funding
This work was supported by the European Research Council (ERC) Consolidator Grant 770827 and the Spanish State Research Agency AEI 10.13039/501100011033 [grant number PID2019-105500GB-I00].
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Sam F L Windels, Department of Computer Science, University College London, London WC1E 6BT, UK; Barcelona Supercomputing Center, 08034 Barcelona, Spain.
Noël Malod-Dognin, Department of Computer Science, University College London, London WC1E 6BT, UK; Barcelona Supercomputing Center, 08034 Barcelona, Spain.
Nataša Pržulj, Department of Computer Science, University College London, London WC1E 6BT, UK; Barcelona Supercomputing Center, 08034 Barcelona, Spain; ICREA, 08010 Barcelona, Spain.
References
- Braicu C. et al. (2019) A comprehensive review on MAPK: a promising therapeutic target in cancer. Cancers, 11, 1618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannistraci C.V. et al. (2013) Pivotal role of the muscle-contraction pathway in cryptorchidism and evidence for genomic connections with cardiomyopathy pathways in RASopathies. BMC Med. Genomics, 6, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castresana-Aguirre M., Sonnhammer E.L.L. (2020) Pathway-specific model estimation for improved pathway annotation by network crosstalk. Sci. Rep., 10, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Creixell P. et al. (2015) Pathway and network analysis of cancer genomes. Nat. Methods, 12, 615–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeBerardinis R.J., Chandel N.S. (2016) Fundamentals of cancer metabolism. Sci. Adv., 2, e1600200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durán C. et al. (2021) Nonlinear machine learning pattern recognition and bacteria-metabolite multilayer network analysis of perturbed gastric microbiome. Nat. Commun., 12, Article number: 1926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esfahani K. et al. (2020) A review of cancer immunotherapy: from the past, to the present, to the future. Curr. Oncol., 27, 87–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaab E. et al. (2012) EnrichNet: network-based gene set enrichment analysis. Bioinformatics, 28, i451–i457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han N. et al. (2021) Identification of SARS-CoV-2–induced pathways reveals drug repurposing strategies. Sci. Adv., 7, eabh3032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanahan D., Weinberg R.A. (2011) Hallmarks of cancer: the next generation. Cell, 144, 646–674. [DOI] [PubMed] [Google Scholar]
- Hänzelmann S. et al. (2013) GSVA: gene set variation analysis for microarray and RNA-seq data. BMC Bioinformatics, 14, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jassal B. et al. (2019) The reactome pathway knowledgebase. Nucleic Acids Res., 48, 498–503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim C. et al. (2018) Chemoresistance evolution in triple-negative breast cancer delineated by single-cell sequencing. Cell, 173, 879–893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kodinariya T.M., Makwana P.R. (2013) Review on determining number of cluster in k-means clustering. Int. J. Adv. Res. Comput. Sci. Manage. Stud., 1, 90–95. [Google Scholar]
- Kovats S. (2015) Estrogen receptors regulate innate immune cells and signaling pathways. Cell. Immunol., 294, 63–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Q., Mikolov T. (2014) Distributed representations of sentences and documents. In: International Conference on Machine Learning, pp. 1188–1196.
- Li Y. et al. (2018) HNRNPH1 is required for rhabdomyosarcoma cell growth and survival. Oncogenesis, 7, 9–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao Y. et al. (2019) WebGestalt 2019: gene set analysis toolkit with revamped UIs and APIs. Nucleic Acids Res., 47, W199–W205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikolov T. et al. (2013). Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781.
- Nakagawa T. et al. (2000) Overexpression of the csk gene suppresses tumor metastasis in vivo. Int. J. Cancer, 88, 384–391. [PubMed] [Google Scholar]
- Ogris C. et al. (2017) A novel method for crosstalk analysis of biological networks: improving accuracy of pathway annotation. Nucleic Acids Res., 45, e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennington J. et al. (2014) Glove: Global vectors for word representation. In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Stroudsburg, Pennsylvania, pp. 1532–1543. 10.3115/v1/D14-1162. [DOI]
- Pržulj N. et al. (2004) Modeling interactome: scale-free or geometric? Bioinformatics, 20, 3508–3515. [DOI] [PubMed] [Google Scholar]
- Raudvere U. et al. (2019) g:Profiler: a web server for functional enrichment analysis and conversions of gene lists (2019 update). Nucleic Acids Res., 47, W191–W198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark C. et al. (2006) BioGRID: a general repository for interaction datasets. Nucleic Acids Res., 34, D535–D539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su C. et al. (2020) Network embedding in biomedical data science. Brief. Bioinformatics, 21, 182–197. [DOI] [PubMed] [Google Scholar]
- Subramanian A. et al. (2005) Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA, 102, 15545–15550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sung H. et al. (2021) Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin., 71, 209–249. [DOI] [PubMed] [Google Scholar]
- Tarca A.L. et al. (2009) A novel signaling pathway impact analysis. Bioinformatics, 25, 75–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tate J.G. et al. (2019) COSMIC: the catalogue of somatic mutations in cancer. Nucleic Acids Res., 47, D941–D947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhlén M. et al. (2015) Tissue-based map of the human proteome. Science, 347, 1260419. [DOI] [PubMed] [Google Scholar]
- Uhlen M. et al. (2017) A pathology atlas of the human cancer transcriptome. Science, 357, eaan2507. [DOI] [PubMed] [Google Scholar]
- Vogelstein B. et al. (2000) Surfing the p53 network. Nature, 408, 307–310. [DOI] [PubMed] [Google Scholar]
- Vogelstein B. et al. (2013) Cancer genome landscapes. Science, 339, 1546–1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang D. (2018) The essential role of G protein-coupled receptor (GPCR) signaling in regulating T cell immunity. Immunopharmacol. Immunotoxicol., 40, 187–192. [DOI] [PubMed] [Google Scholar]
- Wang F. et al. (2008) Semi-supervised clustering via matrix factorization. In: Proceedings of the 2008 SIAM International Conference on Data Mining, SIAM, Philadelphia, PA, pp. 1–12.
- Windels S.F.L. et al. (2019) Graphlet laplacians for topology-function and topology-disease relationships. Bioinformatics, 35, 5226–5234. [DOI] [PubMed] [Google Scholar]
- Windels S.F.L. et al. (2022) Graphlet eigencentralities capture novel Central roles of genes in pathways. PLoS One., 17, e0261676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yajima I. et al. (2014) GNG2 inhibits invasion of human malignant melanoma cells with decreased FAK activity. Am. J. Cancer Res., 4, 182–188. [PMC free article] [PubMed] [Google Scholar]
- Zhao N. et al. (2020) Alzheimer’s risk factors age, APOE genotype, and sex drive distinct molecular pathways. Neuron, 106, 727–742.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


