Abstract
The search for disease modifying therapies in Alzheimers disease (AD) has recently led to promising results but also revealed design issues in clinical trials themselves. Of particular importance is the potential statistical challenges that can arise when dosages change after an interim analysis, which is not uncommon in contemporary AD trials. Following the recent Aducanumab trials, we sought to study the implications of dose changes on the statistical power of an AD trial. We conducted extensive simulations to calculate statistical power when the relationship between treatment effect size and time is linear or non-linear, and the investigated drug has delayed treatment effect or not. Statistical power depends on many design factors including the dose change time, correlation, population homogeneity, and treatment effect time. We recommend that researchers conduct simulation studies at the interim analysis to justify the modified sample size and/or follow-up time modification meanwhile the type I and II error rates are controlled.
Keywords: Aducanumab trial, Alzheimer’s disease, Dose change, Statistical power
1. Introduction
Clinical trial designs for disease modifying therapies (DMTs) for Alzheimer’s disease (AD) have become increasingly complex. Several clinical trial programs including those involving gantenerumab [1], solanezumab (A4 study) and aducanumab (EMERGE and ENGAGE studies) have incorporated mid-trial dose adjustments [2], [3], [4]. The Dominantly Inherited Alzheimer Network-Trials Unit (DIAN-TU) reported their first trial for patients with dominantly inherited Alzheimer’s disease (DIAD) treated with gantenerumab or solanezumab (two anti-amyloid monoclonal antibodies) [1]. During that trial, the doses of both drugs were escalated. Interim analysis or new information has led to alterations in drug dosing during the study that were not part of the initial trial design [5], [6]. Given the time frame needed to show disease modification in AD clinical trials (usually a minimum of 18 months), and the expenses associated with such large-scale and complicated studies, interim analyses [7] are often done for a number of reasons including to: (1) gauge the likelihood of success of the agent and (2) modify the trial if needed, including dose adjustment. Reasons for changing the dose within a given study vary, but the rates of adverse events and differences in rates of target engagement to biomarker effects are often cited as rationale [8]. Equally important as the methodological changes, particular attention must also be paid to the potential impact of dose changes on the originally formulated statistical plans. Failure to properly account for the effects of dose changes, as was seen in EMERGE/ENGAGE trials [2], [3], [4], can have far reaching effects on study outcomes.
The Emerge and Engage phase III trials in particular point out the difficulties with instituting dose changes during a clinical trial [4], [9], [10]. In the aducanumab trial, there initially were a total of three groups: placebo, low dose, and high dose. Based on the information gathered during the study, the low dose group had their dose increased to the high dose. However, one of the statistical challenges raised from the aducanumab trial was that the trial duration for participants with the dose change remained the same as did the timing of an interim futility analysis. While the trail was subsequently stopped for futility the final analysis which included additional follow up showed a positive result for the primary outcome measure in one of the two trials [11], [12].
As more potential AD DMTs go into clinical trials, and often earlier in the disease process, it is critical to develop statistical methods that are able to adapt to the data that is collected and analyzed during the study itself and prospectively integrate these methods at the outset. We propose a means to calculate how the sample size or duration of a trial could be modified in response to changes made in dosing during a clinical trial. The purpose of this paper is to examine the effects of dose changes on study design and power analyses and to describe methodology for modeling dose changes. Finally, we apply our approach to the experience of the EMERGE/ENGAGE studies [2], [3], [4] to demonstrate the importance of correctly modeling dose changes.
2. Methods
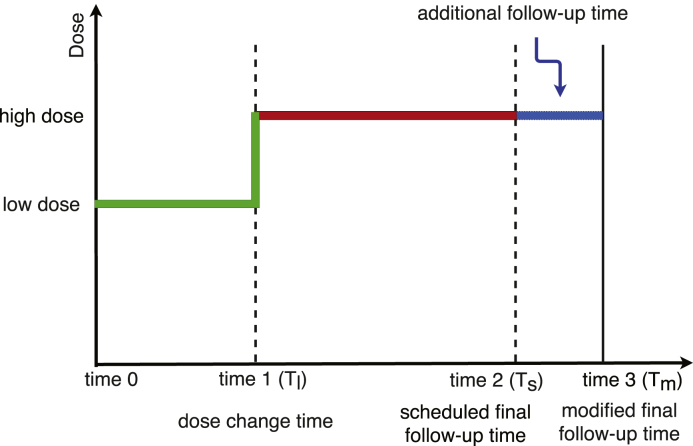
In this section we propose a method for modeling the effects of dose change on clinical trial designs. Suppose is the originally planned total follow up time, and is the time when a patient is switched from low dose to high dose, see Fig. 1. The time on high dose is . Over the course of the trial, the accumulated total doses for patient switched from low dose to high dose, are less than the total doses for patients from the original high dose group because of the lower dose from (baseline) to . The total dose difference between these two subpopulations depends on the time of dose change . When is close to baseline, their difference becomes very small. Otherwise, is close to , and a big difference would be expected. When dose change is scheduled to occur during an on-going trial based on the results from an interim analysis, it is critical to understand how this dose modification would affect the statistical power.
Fig. 1.
Dose change flow chart.
In reality, participants with dose changes are often included in the high dose group because their final dose at the time of is high dose [1], [2], [3], [6], [13]. However, including these participants in analyses and treating them the same as those originally randomized to the high dose group, without accounting for the lower accumulated dose, may ultimately decrease the overall treatment effect for the high dose group. If enough patients are changed from a low to a high dose in a trial, the overall impact would increase the likelihood of reducing the treatment effect and lead to the failure of an investigational new drug. In addition, some drugs might have delayed treatment effects on improving symptoms, delaying the onset, and slowing the progression. Then, the treatment effect at time for patients with dose change could be smaller than that for patients who are always on high dose. Therefore, it is important to adjust the follow-up time for patients with dose change in a study when the planned dose has been changed. This effect may be even more pronounced for drugs that might have a delayed treatment effect, which could further mask the disease modifying effects of treatment.
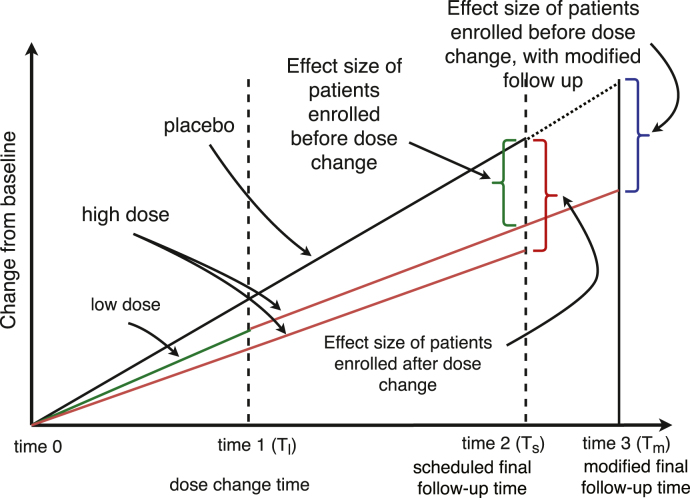
In accounting for mid trial dosage changes we propose extending the follow-up time from to with additional time on high dose, as illustrated in Fig. 1. As mentioned above if participants who are switched are only analyzed at their cumulative treatment exposure is lower than those on high dose the duration of the trial and thus not comparable. The additional time would thus be added for participants who have undergone a dose change to increase their dose exposure at time (blue in Fig. 2), where would account for the time on lower dose and match cumulative dose exposure to those who were started at the higher doses at baseline (red in Fig. 2).
Fig. 2.
Treatment effect sizes for a study with or without dose change.
Multiple other factors contribute to the estimation of treatment effect at for patients always on high dose, and that at for patients with dose change. Suppose the parameter of interest is the change of the primary outcome from to in designing clinical trials. The estimated difference between groups is the primary factor, . Correlation between outcome at and that at , , is another important factor. Correlation affects the sample size calculation in a before–after study [14]. In addition, variances of outcome at baseline and the end are another two factors in power analysis. The estimated values from these four parameters are traditionally used in sample size calculation. Suppose and are the outcomes at and . The sample size calculation based on the score change [15], which is presented as
where is the variance of , and is the th quantile of the standard normal distribution.
Other factors could affect the statistical power, including the relationship between treatment effect and time: linear or non-linear for a drug with delayed treatment effect, and the ratio of patients who are always on high dose and those with dose change. Finally, the modified time for patients with dose change is another factor to consider. These factors are studied in the following section in the power analysis.
3. Numerical results
Suppose we conduct a hypothetical study with a dose change incorporated during the conduct of the study. In this study there are three arms: a low dose group, a high dose group, and a placebo group. Suppose it is a randomized balanced clinical trial with sample size of per group.
3.1. Model for linear relationship
The estimated mean value of the primary outcome at baseline for the three groups is assume to be the same as . For purposes of illustration, higher scores indicate worse performance (e.g., Alzheimer’s Disease Assessment Scale–Cognitive subscale (ADAS-Cog)). Let the scheduled follow-up time be months. After 24 months, suppose the placebo group declines by 6 points (), the low dose group by 4 points (), and the high dose group by 2 points ().
At baseline, patients are more likely to be similar across the groups. Standard deviation (SD) at baseline is assumed to be the same for the three group: . In the placebo group, the SD is assumed to be constant over the trial. In the treatment groups, however, variance in the primary outcome could increase as time goes on. The SD value at is in the low dose group, and in the high dose group. Six correlation coefficients between and are studied: , 0.10, 0.15, 0.20, 0.35, and 0.55.
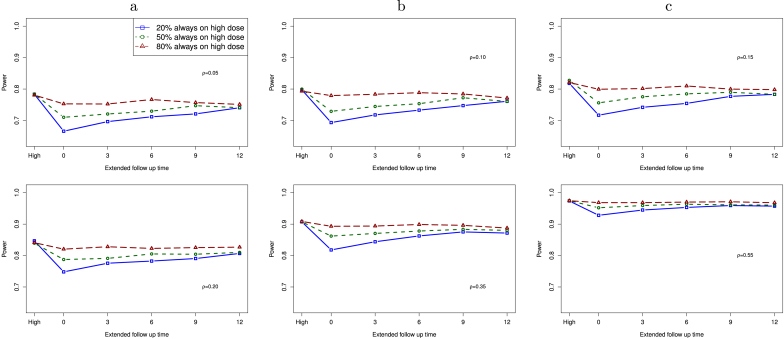
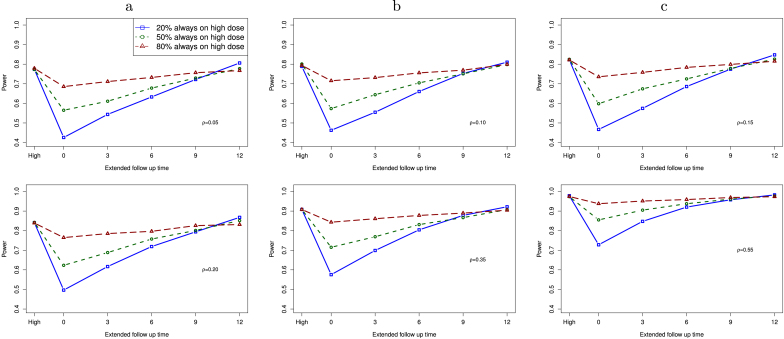
In Fig. 3, we present the computed statistical power for a study with dose change as a function of the modified follow-up time under the assumption of linear treatment effect within each group. The outcome at time is . For patients with dose change, we assume that the change time for these patients is uniformly distributed from baseline to . We compute power for a study with 3 different proportions of patients who are always on high dose: 60 (20%), 150 (50%), and 240 (80%). When 80% patients are always on high dose, the remaining 20% patients have dose change from a low dose to a high dose during the study. The far left value (“High” in the x-axis) is the statistical power for comparing the placebo group with the high dose group. In this configuration, all patients in the high dose group received the high dose at baseline.
Fig. 3.
Power of a study with dose change as a function of additional follow-up time under the assumption of linear treatment effect, when the proportion of high dose patients is 20%, 50%, and 80%. Six correlation values are studied: , 0.10, 0.15, 0.20, 0.35, and 0.55. “High” on the far left is for the case that all patients are in the high dose group without any dose change.
When the extended follow-up time is 0, this is a study that conducts the interim analysis as originally planned. As a result, patients with dose change do not expose to the same total dosing as those always on high dose. We expect that the observed treatment effect size could be smaller from patients with dose change, as compared to the original high dose group. As the extended follow-up time increases in the dose change group, the statistical power increases when the proportion of patients always on high dose is not too large (e.g., 20%, 50%), and it is close to that for a study without dose change when additional months are added in the follow up. Within each plot, we observe that power of a study goes up when more patients are from the high dose group without dose change. Between these plots, statistical power increases as correlation goes up.
3.2. Model for delayed treatment effect
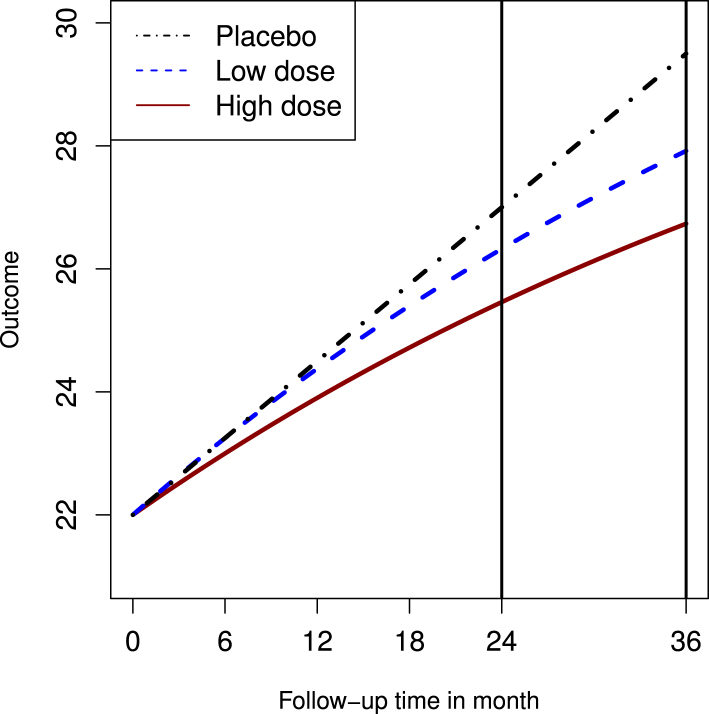
Many agents for neurodegenerative diseases may have delayed treatment effects. This is important to account for that effect when modeling dose changes. For this model we assumed a non-linear relationship in the treatment group (but not in the placebo) with the baseline value of in this subsection. In the placebo group, a linear treatment effect is assumed with from 22 at baseline. While in the two treatment groups, we assume the treatment effect follows an exponential distribution with the rate parameter , with the relationship between the outcome and time as: , where is time by month, is a scale parameter, and is the cumulative distribution function of an exponential distribution. The scale parameter can be determined by solving the following equation: for the low dose group having , and 25.46 for the high dose group with . The three curves are presented in Fig. 4.
Fig. 4.
Non linear curve.
In Fig. 5, we present the statistical power under the assumption of a non-linear treatment effect [1] given the proportion of patients who are always on high dose as 60 (20%), 150 (50%), and 240 (80%). Six correlation values from the linear treatment effect configurations are also studied here. It can be seen from the figure that power increases as the modified follow-up time goes up, and a study with a higher correlation often has a higher statistical power. When the extended time is long enough (e.g., 12 months), power of a study with a low correlation could have a slight higher power than studies with higher correlations.
Fig. 5.
Power of a study with dose change as a function of additional follow-up time under the assumption of non-linear treatment effect, when the proportion of high dose patients is 20%, 50%, and 80%. Six correlation values are studied: , 0.10, 0.15, 0.20, 0.35, and 0.55. “High” on the far left is for the case that all patients are in the high dose group without any dose change.
3.3. Studies with different variances
Neurodegenerative diseases are multifactorial diseases that may be effected by unaccounted for factors such as genetics, medical comorbidities, pharmacokinetics/dynamics likely resulting in differential response rates to treatment. In Fig. 6, we set the estimated mean value of the primary outcome at baseline for the three groups as . After 24 months, suppose the placebo group declines by 6 points (), the low dose group by 5 points (), and the high dose group by 4 points ().
Fig. 6.
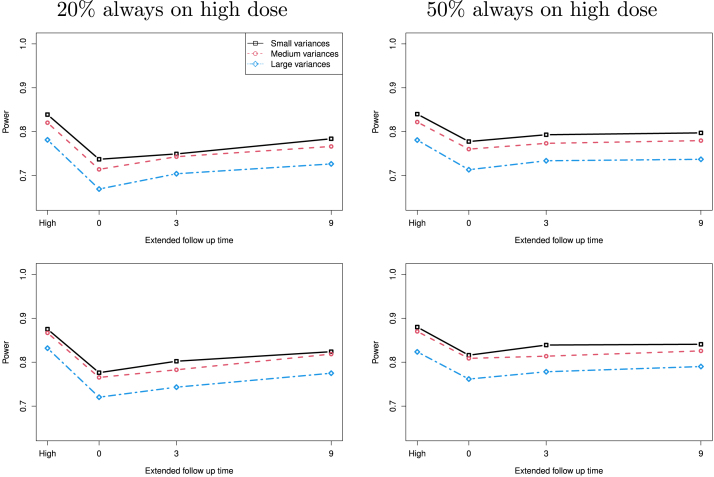
Power of a study with dose change as a function of additional follow-up time under the assumption of linear treatment effect when on the first row and 0.2 on the second row, for for small variances, (6.0, 6.6, 7.2) for medium variances, and (6.0, 7.8, 8.4) for large variances. “High” on the far left is for the case that all patients are in the high dose group without any dose change.
In Fig. 6, we present the statistical power as a function of the extended follow-up time for studies with different variances: for small variances, (6.0, 6.6, 7.2) for medium variances, and (6.0, 7.8, 8.4) for large variances. As we expected, studies with larger variances, both for the low and high dose groups, have smaller statistical power. When the extended time increase the estimated statistical power increases. Given the proportion of participants on high dose, a larger correlation is often associated with higher power. When more participants on the high dose (e.g. 50% on the right plots) additional follow up time after 3 months only slightly increases the statistical power. As the proportion of participants on high dose increases its statistical power is much higher when Tm is short, and its advantage goes away when the extended follow up time goes longer.
3.4. Example
If we apply the methodology we describe in the previous sections we can begin to get a clearer picture of how the EMERGE and ENGAGE studies [2], [3], [4] failed their futility analysis. The trials were designed with a total of three arms: a high dose treatment arm, a low dose treatment arm, and a placebo group. The primary outcome of the studies was the change in Clinical Dementia Rating Scale-Sum of Boxes (CDR-SOB) at week 78 from baseline. The CDR-SOB is a composite index summed from six cognitive and functional domains: memory, orientation, judgment and problem-solving, community affairs, home and hobbies and personal care. The range of CDR-SOB is 0–18 with higher scores indicating greater impairment.
For these studies the expected increase in of the CDR-SOB score was 2 in the placebo group. The assumed baseline value was 2.45 all groups. Based on data from earlier Phase Ib studies, an increase of 1.74 was expected in the low dose treatment arm and 1.5 in the high dose treatment arm. The improvement of 0.5 in the high dose group represents a 25% reduction in the primary outcome (e.g. clinical worsening or slowed rate of decline).
In our model we apply several assumptions: variances in CDR-SOB at baseline of 1.50 in all groups; at 78 weeks variances of 1.50 in the placebo group, 1.55 in the low dose group, and 1.60 in the high dose group. Correlation of CDR-SOB at baseline at week 78 is assumed to be the same across the groups, we study four correlation coefficients: 0.05, 0.1, 0.2, 0.30, and 0.40. Suppose in the high dose group, only 60% of participants (240 out of 400 for a study with 400 per arm) were actually exposed to high dose from baseline to week 78.
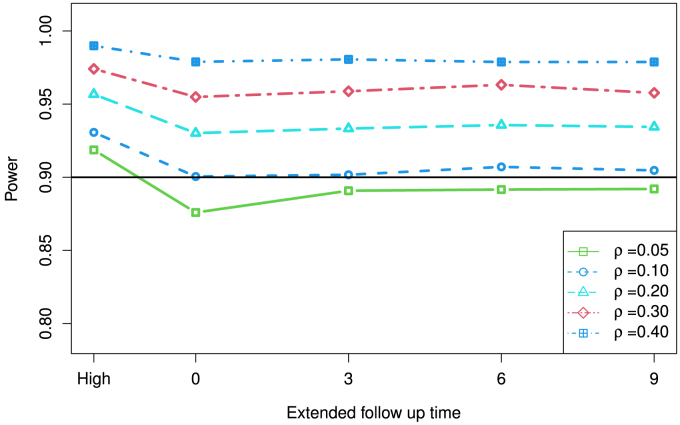
Using a sample size of 400 per group to calculate the statistical power in Fig. 7 with or without dose change the computed statistical power increases as the extended follow-up time goes up. For this particular example, power is similar to each when the extended follow up time is 3 months or more for each configuration. Power for a study with the extended time of 9 months is slightly below the study with participants only on the high dose. When the correlation is 10% or above, a study with 3 months extended time has a power above 90%. For a study with a low correlation (e.g. 0.05) the estimated power for a study with a dose change could be below 90% even with an extended follow up.
Fig. 7.
Example from the aducanumab trial using the CDR-SB score. “High” on the far left is for the case that all patients are in the high dose group without any dose change.
4. Discussion
In this article, we evaluate the statistical power in a study with dose increasing for one group. It is also possible in trials that the assigned dose for one group could be changed to a lower level due to the concerns from the trial (e.g., side effects). In general, a lower dose is often associated with a lower rate of incidences. For a study with more than 2 treatment groups, dose changes could happen in multiple groups based on the results from interim analysis to increase the success rate of the on-going trial [16], [17], [18]. We would recommend researchers conduct sufficient enough simulation studies to justify the sample size and/or follow-up time modification meanwhile the type I and II error rates are controlled.
EMERGE and ENGAGE were identical Phase III studies looking at the potential disease modifying effects of the monoclonal antibody aducanumab in individuals with early AD [2], [3], [4], [19], [20]. The trials were designed with a total of three arms: a high dose treatment arm, a low dose treatment arm, and a placebo group. Within each treatment arm there were a total of two possible doses—6 mg/kg or 10 mg/kg in the high dose and 4 mg or 6 mg in the low dose treatment arm [21]. To avoid a common dose-related side effect known more frequently seen in individuals with the APOE E4 genotype, the dose in the high dose treatment group was initially limited to 6 mg/kg in E4 carriers. When it became clear that the incidence of symptomatic ARIA remained low, a protocol amendment allowed for all high dose participants to be titrated to 10 mg/kg. Despite this dose adjustment, no changes were made to the follow up time and the interim analysis plan remained unchanged. At the scheduled interim analysis, both trials appeared headed for failure and stopped for futility [22], [23].
Clinical trials of disease modifying agents in AD often span over a number of years due to the time it takes to enroll study participants and the duration of these studies [24], [25], [26]. During that time, new information and data may become available to the study investigators which would influence the decision on optimum drug dosing or sample size in the study. However, introducing protocol changes during the study that were not pre-planned raise the possibility of ending up with a type II error and discarding a potentially useful treatment.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors are very grateful to the Editor, Associate Editor, and reviewers for their insightful comments that help improve the manuscript. Shan’s research is partially supported by grants from the National Institutes of Health, United States of America : R01AG070849 and R03CA248006.
References
- 1.Salloway S., Farlow M., McDade E., Clifford D.B., Wang G., Llibre-Guerra J.J., et al. A trial of gantenerumab or solanezumab in dominantly inherited Alzheimer’s disease. Nat. Med. 2021;27(7):1187–1196. doi: 10.1038/s41591-021-01369-8. Available from: https://www.nature.com/articles/s41591-021-01369-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sperling R.A., Aisen P.S., Beckett L.A., Bennett D.A., Craft S., Fagan A.M., et al. Toward defining the preclinical stages of Alzheimer’s disease: Recommendations from the national institute on aging-Alzheimer’s association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimer’s Dementia. 2011;7(3):280–292. doi: 10.1016/j.jalz.2011.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sevigny J., Chiao P., Bussière T., Weinreb P.H., Williams L., Maier M., et al. The antibody aducanumab reduces A plaques in Alzheimer’s disease. Nature. 2016;537(7618):50–56. doi: 10.1038/nature19323. [DOI] [PubMed] [Google Scholar]
- 4.Fillit H., Green A. Aducanumab and the FDA — where are we now? Nat. Rev. Neurol. 2021;17(3):129–130. doi: 10.1038/s41582-020-00454-9. Available from: https://pubmed.ncbi.nlm.nih.gov/33442064/ [DOI] [PubMed] [Google Scholar]
- 5.Schneider L. A resurrection of aducanumab for Alzheimer’s disease. Lancet Neurol. 2020;19(2):111–112. doi: 10.1016/S1474-4422(19)30480-6. Available from: https://pubmed.ncbi.nlm.nih.gov/31978357/ [DOI] [PubMed] [Google Scholar]
- 6.Cummings J., Aisen P., Lemere C., Atri A., Sabbagh M., Salloway S. Aducanumab produced a clinically meaningful benefit in association with amyloid lowering. Alzheimer’s Res. Therapy. 2021;13(1):1–3. doi: 10.1186/s13195-021-00838-z. Available from: https://link.springer.com/article/10.1186/s13195-021-00838-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Whitehead J., Todd S., Whitehead A., Stallard N. Interim analyses in clinical trials. Br. J. Clin. Pharmacol. 2001;51(5):393. doi: 10.1046/j.1365-2125.2001.01382.x. Available from: /pmc/articles/PMC2014469/ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2014469/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Le Tourneau C., Lee J.J., Siu L.L. Dose escalation methods in phase i cancer clinical trials. J. Natl. Cancer Inst. 2009;101(10):708–720. doi: 10.1093/jnci/djp079. Available from: /pmc/articles/PMC2684552/ /pmc/articles/PMC2684552/?report=abstract https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2684552/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sabbagh M.N., Cummings J. Open peer commentary to “failure to demonstrate efficacy of aducanumab: An analysis of the EMRGE and ENGAGE trials as reported by biogen December 2019”. Alzheimer’s Dementia. 2020 doi: 10.1002/alz.12235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shan G., Banks S., Miller J.B., Ritter A., Bernick C., Lombardo J., Cummings J.L. Statistical advances in clinical trials and clinical research. Alzheimer’s Dementia: Transl. Res. Clin. Interv. 2018;4:366–371. doi: 10.1016/j.trci.2018.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shan G., Zhang H., Jiang T. Adaptive two-stage optimal designs for phase II clinical studies that allow early futility stopping. Sequential Anal. 2019;38(2):199–213. [Google Scholar]
- 12.Shan G. Optimal two-stage designs based on restricted mean survival time for a single-arm study. Contem. Clin. Trials Commun. 2021;21 doi: 10.1016/j.conctc.2021.100732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cummings J., Salloway S. Aducanumab: Appropriate use recommendations. Alzheimer’s Dementia. 2021 doi: 10.1002/alz.12444. Available from: https://alz-journals.onlinelibrary.wiley.com/doi/10.1002/alz.12444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lakens D. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Front. Psychol. 2013;4(NOV):863. doi: 10.3389/fpsyg.2013.00863. Available from: http://journal.frontiersin.org/article/10.3389/fpsyg.2013.00863/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Clifton L., Birks J., Clifton D.A. Comparing different ways of calculating sample size for two independent means: A worked example. Contemp. Clin. Trials Commun. 2019;13 doi: 10.1016/j.conctc.2018.100309. Available from: /pmc/articles/PMC6297128/ /pmc/articles/PMC6297128/?report=abstract https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6297128/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Miller J.B., Shan G., Lombardo J., Jimenez-Maggoria G. Biomedical informatics applications for precision management of neurodegenerative diseases. Alzheimer’s Dementia: Transl. Res. Clin. Interv. 2018;4:357–365. doi: 10.1016/j.trci.2018.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shan G., Zhang H. Two-stage optimal designs with survival endpoint when the follow-up time is restricted. BMC Med. Res. Methodol. 2019;19(1) doi: 10.1186/s12874-019-0696-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shan G. Sample size calculation for agreement between two raters with binary endpoints using exact tests. Stat. Methods Med. Res. 2018;27(7):2132–2141. doi: 10.1177/0962280216676854. Available from: http://view.ncbi.nlm.nih.gov/pubmed/27856958. [DOI] [PubMed] [Google Scholar]
- 19.Wilding G.E., Shan G., Hutson A.D. Exact two-stage designs for phase II activity trials with rank-based endpoints. Contemp. Clin. Trials. 2012;33(2):332–341. doi: 10.1016/j.cct.2011.10.008. [DOI] [PubMed] [Google Scholar]
- 20.Wilding G.E., Consiglio J.D., Shan G. Exact approaches for testing hypotheses based on the intra-class kappa coefficient. Stat. Med. 2014;33(17):2998–3012. doi: 10.1002/sim.6135. [DOI] [PubMed] [Google Scholar]
- 21.Cummings J., Lee G., Ritter A., Sabbagh M., Zhong K. Alzheimer’s disease drug development pipeline: 2019. Alzheimer’s Dementia: Transl. Res. Clin. Interv. 2019;5:272–293. doi: 10.1016/j.trci.2019.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bernick C., Cummings J., Raman R., Sun X., Aisen P. Age and rate of cognitive decline in Alzheimer disease: Implications for clinical trials. Arch. Neurol. 2012;69(7):901–905. doi: 10.1001/archneurol.2011.3758. [DOI] [PubMed] [Google Scholar]
- 23.Shan G., Moonie S., Shen J. Sample size calculation based on efficient unconditional tests for clinical trials with historical controls. J. Biopharm. Statist. 2016;26(2):240–249. doi: 10.1080/10543406.2014.1000545. Available from: http://view.ncbi.nlm.nih.gov/pubmed/25551261. [DOI] [PubMed] [Google Scholar]
- 24.Ritter A., Cummings J., Nance C., Miller J.B. Neuroscience learning from longitudinal cohort studies of Alzheimer’s disease: Lessons for disease-modifying drug programs and an introduction to the center for neurodegeneration and translational neuroscience. Alzheimer’s Dementia: Transl. Res. Clin. Interv. 2018;4:350–356. doi: 10.1016/j.trci.2018.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shan G., Wang W. Advanced statistical methods and designs for clinical trials for COVID-19. Int. J. Antimicrob. Ag. 2021;57(1) doi: 10.1016/j.ijantimicag.2020.106167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shan G., Gerstenberger S. Fisher’s exact approach for post hoc analysis of a chi-squared test. PLoS One. 2017;12(12) doi: 10.1371/journal.pone.0188709. [DOI] [PMC free article] [PubMed] [Google Scholar]