Inferring the initiation and development of myeloproliferative neoplasms

Significance

Myeloproliferative neoplasm (MPN) blood cancers are often detected at an advanced age, after complications such as thrombosis and cardiovascular events. Understanding the MPN disease dynamics (initiation and development) could help set up early screening strategies, and more broadly, provide insight into the developmental history of blood cancer. For that purpose, we developed a mathematical approach combining modeling and statistical inference and apply it to the two most prevalent mutations in MPNs. We evidence differences in the clonal expansion of the CALR^m mutation compared to JAK2^V617F, suggesting different types of mechanisms for the driver mutation acquisition.

Abstract

The developmental history of blood cancer begins with mutation acquisition and the resulting malignant clone expansion. The two most prevalent driver mutations found in myeloproliferative neoplasms—JAK2^V617F and CALR^m—occur in hematopoietic stem cells, which are highly complex to observe in vivo. To circumvent this difficulty, we propose a method relying on mathematical modeling and statistical inference to determine disease initiation and dynamics. Our findings suggest that CALR^m mutations tend to occur later in life than JAK2^V617F. Our results confirm the higher proliferative advantage of the CALR^m malignant clone compared to JAK2^V617F. Furthermore, we illustrate how mathematical modeling and Bayesian inference can be used for setting up early screening strategies.

Myeloproliferative neoplasm (MPN) blood cancers are characterized by abnormal proliferation of myeloid hematological cells. These pathologies result from gain-of-function somatic mutations of specific genes occurring in hematopoietic stem cells (HSCs). Two main driver mutations of the MPN disease affect genes encoding proteins playing a crucial role in cell signaling: JAK2 (JAK2^V617F) and calreticulin (exon 9 mutations, CALR^m) (1–6). However, their precise role in the development of clonal hematopoiesis and in the disease dynamics remains poorly understood. Of particular debate is the expansion kinetics of a malignant clone emanating from a single mutated cell. While JAK2^V617F was reported to be acquired decades before disease onset and even during fetal life (7–10), there is no such result for the CALR^m mutation. MPNs are generally detected at advanced ages when the malignant clone is present at significant Variant allele frequency (VAF) in peripheral blood. Late detection, often after complications such as thrombosis and cardiovascular events, or more rarely at the leukemic stage, further increases the death rate. Methods to understand disease initiation and clonal expansion of mutated HSCs are thus crucial to develop adequate screening strategies and to avoid delayed medical care.

A major difficulty for this task comes from the fact that human HSCs are difficult to access and in vivo expansion of mutated HSCs cannot be observed. We therefore propose a mathematical model to infer the dynamics of the disease, from the acquisition of the driver mutation to the appearance of the symptoms. Stochastic models, such as the Wright-Fisher model used in population genetics (11) or branching processes (12), are appropriate choices to describe the expansion of a clone from a unique mutated cell. However, their calibration from real observations remains challenging and requires setting up an extensive optimization procedure to achieve convergence of the algorithms in a realistic time.

To understand how JAK2^V617F and CALR^m malignant clones might expand over time, we propose a model relying on a continuous-time Markov chain (CTMC) process. When a certain number of mutated HSCs is reached, we show numerically that a deterministic law can approximate the process. This approximation further facilitates the calibration of the model that otherwise would not be computationally feasible. We estimate the model parameters using an approximate Bayesian computation method based on sequential Monte Carlo (ABC-SMC) (13, 14), with data from recently diagnosed JAK2^V617F and CALR^m patients. To achieve a faster convergence, we use an optimal affectation procedure based on the Hungarian algorithm (15, 16). We apply this mathematical approach—combining modeling and statistical inference—to investigate potential differences in the disease dynamics of CALR^m vs. JAK2^V617F MPN patients.

Results

CALR^m Mutations Appear to be Acquired Later than JAK2^V617F.

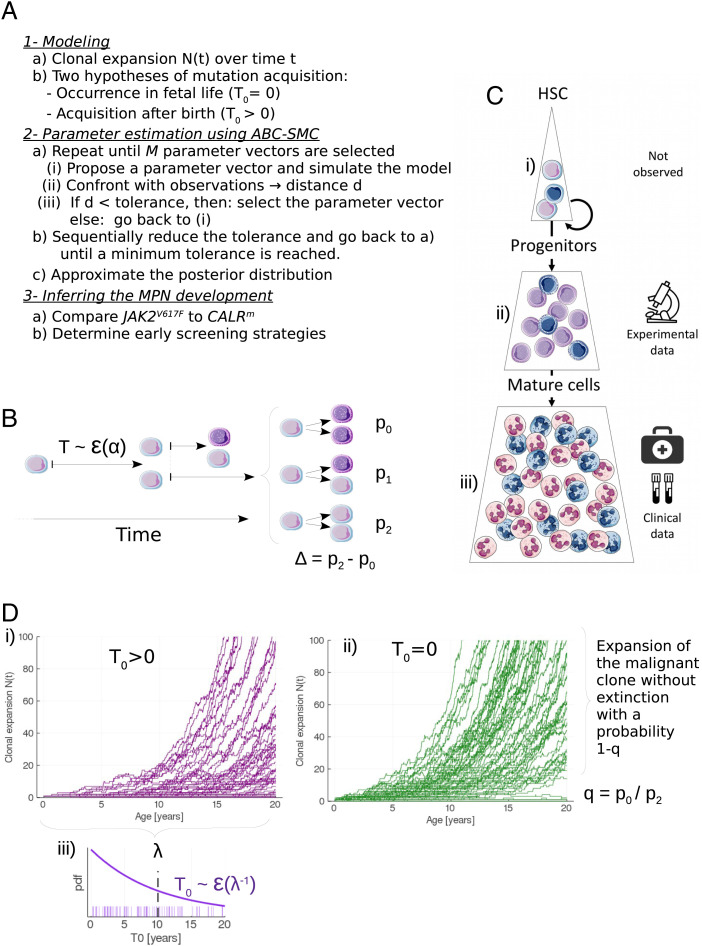
To analyze the initiation and dynamics in MPN disease and compare the expansion kinetics of CALR^m vs. JAK2^V617F malignant clones, we propose an approach based on mathematical modeling (Fig. 1A) focusing on the proliferation dynamics of mutated HSCs (see Materials and Methods). In brief, we assume that a given mutated HSC divides at a rate α into 0, 1, or 2 mutated HSCs, depending on whether the division is differentiated, asymmetric, or symmetric, with probabilities p₀, p₁, and p₂, respectively (Fig. 1B). Daughter cells, if not HSCs, are progenitor cells that will further proliferate to give rise to mature cells (Fig. 1C). We denote by N(t) the number of mutated HSCs that have expanded from a single mutated cell at age t > T₀, with T₀ satisfying N(T₀) = 1 (Fig. 1D). We further assume that the acquisition time T₀ follows an exponential distribution of mean λ > 0 (Fig. 1 D, iii). T₀ > 0 corresponds to an occurrence of the mutation after birth. Since Williams et al. (8) reported that JAK2^V617F might be acquired in fetal life, we also verify if our data could be in agreement with the hypothesis of mutation acquisition in utero (T₀ = 0) for all individuals, corresponding to the limit case λ = 0 (Fig. 1 D, ii).

Fig. 1.

Method and model for inferring the development of MPNs. (A) Overview of the method. (B) Modeling the stem cell proliferation dynamics: a given mutated HSC divides after a random time T that follows an exponential law ε(α) of rate α. After dividing, the mutated HSC gives birth to 0, 1, or 2 mutated HSC with probabilities p₀, p₁, or p₂, respectively. Daughter cells, if not HSCs, are progenitor cells (represented in a darker color). On this example, the first division is symmetric, and the division of one of the daughter cells (on the top) is asymmetric. (C) The hematopoietic dynamics can be modeled with three compartments: i) the stem cell pool consisting of a limited number of HSCs that can self-renew and thus drive the long-term clonal expansion; ii) the progenitor cells (CD34⁺) that arise from HSCs. Our model of MPN expansion is calibrated from measured CF of those cells; iii) a pool of mature cells, whose measure of the VAF in clinical routine can allow the early detection of the mutation. Blue cells are mutated. (D) Modeling the stochastic expansion of the malignant clone from a single mutated cell, where N(t) is the number of mutated HSCs over time t. Two hypotheses are compared for the modeling of the mutation acquisition: either i) after birth (T₀ > 0) or ii) during fetal life (T₀ = 0). In the former case, T₀ follows an exponential law ε(1/λ), of rate 1/λ (where λ > 0 corresponds to the mean acquisition time), whose probability density function (pdf) is represented in (iii). For each scenario 100 simulations are computed, with α = 1/30, Δ = 0.02, q = 1/3, and λ = 10 (for (i) only).

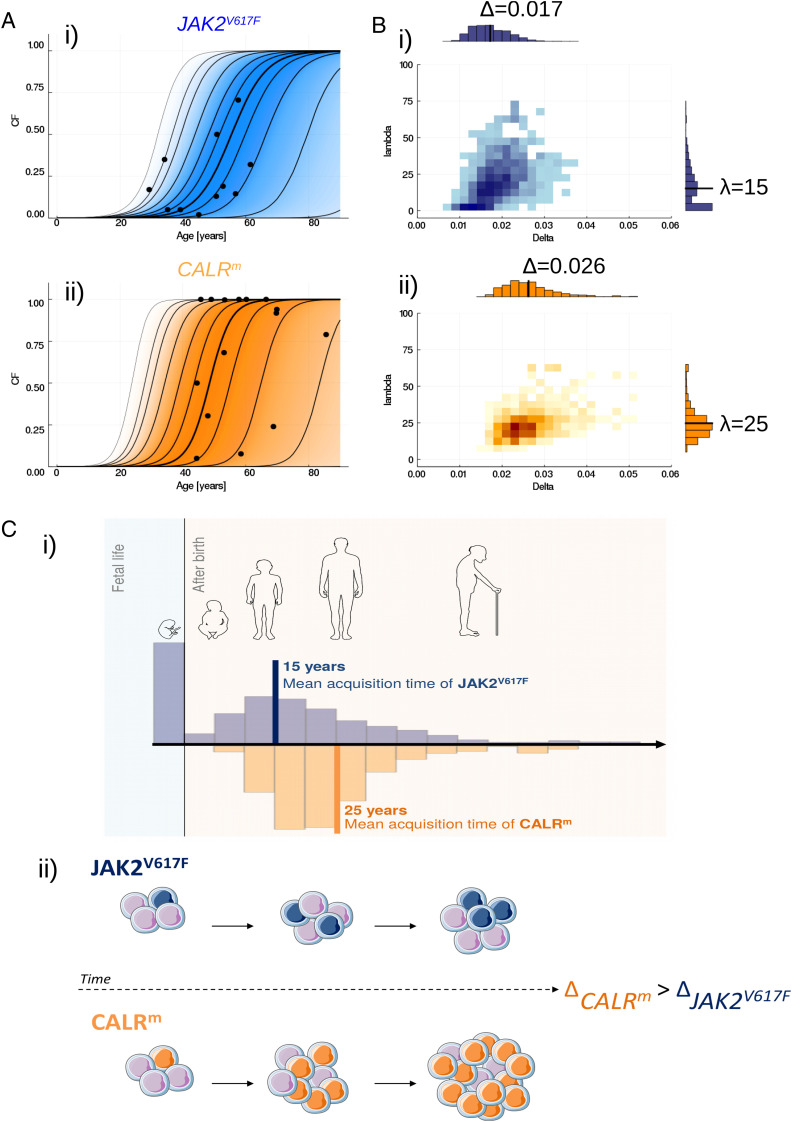
Parameter values are estimated from single observations of 26 patients diagnosed with JAK2^V617F or CALR^m MPNs using a likelihood-free estimation procedure, namely ABC-SMC (17). Data (D), previously reported by Mosca et al. (18) and El-Khoury et al. (19), consist of clonal fractions (CF) for progenitor cells (see Materials and Methods and Fig. 2A). We estimate the model parameters separately for JAK2^V617F and CALR^m patient populations. The mean mutation acquisition time of the JAK2^V617F mutation E[λ] is estimated at ∼15 y (Fig. 2 B, i). Furthermore, concerning the hypothesis that mutation occurs in fetal life for the population of JAK2^V617F patients, we estimate its probability p [λ = 0 |D] to be equal to 0.24. These findings are consistent with the values reported by Van Egeren et al. (7) and Williams et al. (8) (SI Appendix, section E.1). Interestingly, for the CALR^m patient population, we infer that almost surely λ > 0, that is, the hypothesis of a mutation acquisition during fetal life for all CALR^m patients is unlikely. We also estimate a higher expected mean acquisition time (E[λ]∼25 y) than for JAK2^V617F (Fig. 2 B, ii and C, i).

Fig. 2.

Inferring the MPN development. (A) Confronting JAK2^V617F (i) or CALR^m (ii) patient observations (black points) to the inferred evolution of the CF among progenitor cells. The dynamics of clonal expansion over time are obtained from 10,000 simulations of the model, sampling the parameters from the estimated posterior distributions. The bold line represents the median CF, computed over 10,000 simulated trajectories at each age, when the lines on both sides materialize 25, 50, 75, 90, 95 and 99% credibility intervals. The gradient of color indicates where the trajectories can be found; the darker, the higher probability. (B) Estimated joint posterior distributions of parameters Δ and λ, for JAK2^V617F (i) or CALR^m (ii). Black solid lines in the one-dimensional histograms correspond to the mean values. The darkest regions on the two-dimensional histograms correspond to those of higher probability density. (C) Schematic representation of the MPN development for JAK2^V617F and CALR^m malignant clones. i) JAK2^V617F mutation is found to be acquired earlier on average than CALR^m mutation (15 vs. 25 y old), and potentially during fetal life (with probability p[λ = 0 |D] = 0.24 when the same probability is estimated at zero for CALR^m). The histograms represent the distribution of parameter λ. ii) CALR^m is found to have a higher proliferative advantage at the stem cell level than JAK2^V617F. CALR^m malignant clone (in orange) will expand over time in a pool of WT HSCs (purple cells) at a higher rate than JAK2^V617F (in blue).

Higher Proliferative Advantage Inferred for the CALR^m Malignant Clone.

In the proposed model, the proliferative advantage of the mutated cells is described thanks to parameter Δ = p₂ − p₀, which represents the unbalance between symmetric and differentiated divisions that drives the clonal expansion of the mutation when Δ > 0. The higher its value, the faster the malignant clone will expand. We estimate Δ for CALR^m and JAK2^V617F malignant clones separately and infer that the proliferative advantage of the CALR^m malignant clone at the stem cell level is higher than that of JAK2^V617F (Fig. 2B), with mean values of Δ respectively equal to 0.026 and 0.017. The propensity of CALR^m HSCs for symmetric divisions and thus for the invasion of the stem cell pool is higher than that of JAK2^V617F HSCs (Fig. 2 C, ii). This observation explains that, even if the CALR^m mutation is acquired later in life, the malignant clone can generally reach high CF more quickly (Fig. 2A). Our estimate of Δ for JAK2^V617F is bigger than the one found by Watson et al. (9), since we estimate Δ from observations of individuals having an MPN while Watson et al. (9) studied clonal hematopoiesis of healthy donors (SI Appendix, section E.2). In addition, we estimate a high probability of stochastic extinction (q = p₀/p₂) for JAK2^V617F and CALR^m malignant clones, with mean values of q = 0.94 and 0.87, respectively, meaning that the acquisition of the mutation would lead to a clonal expansion—and then potentially a disease onset—in only ∼10% of the cases (SI Appendix, section D.2).

Early Screening Might be a Viable Clinical Option to Detect JAK2^V617F Mutations.

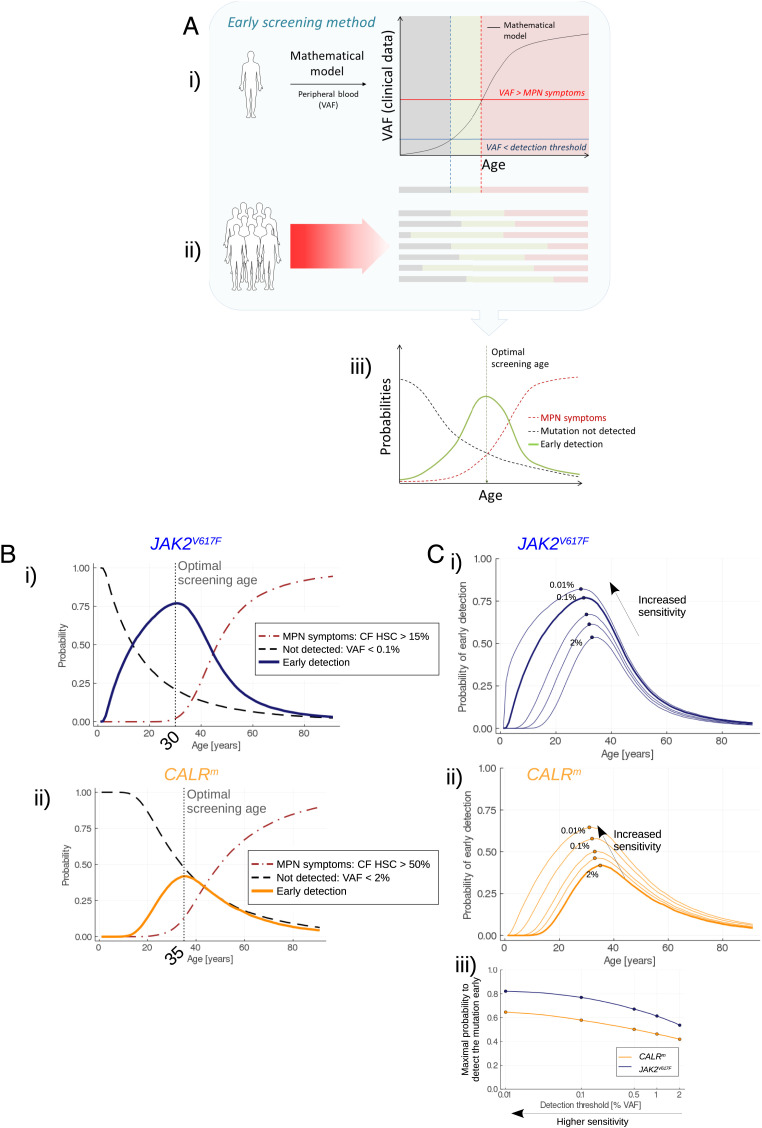
Having estimated the mean parameter values of the model and their probability distributions, we can infer the MPN development and deduce early screening strategies (see Materials and Methods and Fig. 3A). The goal is to detect the mutation of interest in an individual as early as possible, i.e., before the onset of the disease. Early screening requires collecting blood samples from individuals and performing analysis of the gene of interest to measure the VAF in the peripheral blood (note that we always associate the term VAF with mature cells). The usual techniques in clinical practice can detect CALR^m mutations at a VAF above 2% with CALR sizing and at around 0.1% for JAK2^V617F (0.01 to 1% using allele-specific PCR). We consider that the detection is too late if the CF in HSCs is above 50% for CALR^m (19) and above 15% for JAK2^V617F (20), corresponding to the thresholds above which there is a high risk of MPN development and potential thrombosis. Our approach leverages the posterior distribution of the model’s parameters to compute the probability of detecting the mutation at different ages and thus it can help determine the best timing for screening. The optimal age for screening is found at 30 for the JAK2^V617F mutation (Fig. 3 B, i), and at 35 for the CALR^m mutation (Fig. 3 B, ii).

Fig. 3.

Early screening. (A) Overview of the method for determining the optimal screening age. i) One trajectory of the stochastic model (after its calibration from actual observations) corresponds to the disease expansion in an arbitrary (randomly sampled) patient. From the model, we obtain the progression of the VAF in mature cells over the years. Three periods in the patient’s life can be considered. First, the VAF is lower than a detection threshold (gray area); the malignant clone has already begun expanding but is still undetectable. Then (green area), the mutation becomes detectable still with a sufficiently low CF so that there is a low risk of MPN symptoms. Theoretically, it would be the appropriate period for the early screening of this particular patient. Eventually, the malignant clone continues to expand; the VAF exceeds a threshold above which there is a risk of MPN symptoms (red area): screening would be too late. ii) Because of the heterogeneity between patients, the three previously defined periods [mutation not detected (gray); early detection (green); and MPN symptoms (red)] are different between individuals. iii) Considering a high number of MPN patients, we obtain as functions of age the frequencies (or probabilities) of early screening (green line), to not detect the mutation (dashed gray line), or to have MPN symptoms (red dashed line). The probability of early screening reaches a maximum at the optimal screening age, that is, the age at which it would be optimal to test the population for the considered mutation. The value reached at the optimal screening age corresponds to the highest proportion of patients that would be detected early enough (according to our mathematical model and its calibration). The higher this value, the more efficient the screening. (B) Evolution of the probability of early detection (solid line, blue for JAK2^V617F (i) and orange for CALR^m (ii)), false negative rate (dashed line), and too late detection (dash-dotted line) when testing the population for the JAK2^V617F (i) or CALR^m (ii) mutation at different ages. Here, we consider that CALR^m mutation is detected in mature cells for a VAF higher than 2% (sizing CALR) and that JAK2^V617F is detected for a VAF higher than 0.1% (allele-specific PCR). (C) Impact of the sensitivity of the techniques for detecting JAK2^V617F (i) or CALR^m (ii) mutations. As expected, higher sensitivities increase the probability to detect the mutations, at earlier ages. In (iii), we compute the maximal probability to detect the mutation (at the corresponding optimal screening age) for different VAF thresholds ranging from 2 to 0.01% (x-axis in log scale).

At this optimal age of detection, there are three possibilities for individuals having the mutation: the detection is too late because they already suffered from symptoms of the disease, we manage to detect the mutation early (true positive), or we do not (false negative). For CALR^m patients, the probability of early detection computed at the optimal screening age remains low (42%), leaving 46% of the individuals who would later develop the disease undetected, and 12% for whom the detection would be too late. In contrast, early screening might be a viable clinical option to detect JAK2^V617F mutations, with 79% of the individuals being detected early at the optimal screening age of 30.

In addition, we study how the sensitivity of the screening techniques influences the previous results. We compare different sensitivities with detection thresholds (corresponding to the VAF in mature cells) ranging from 0.01 to 2% (Fig. 3C). Both for CALR^m and JAK2^V617F malignant clones, higher sensitivities increase the probability of detecting the mutation at lower ages. However, still at ultra-sensitive levels (detection threshold as low as 0.01%), the probability of early detection at the optimal screening age is below 65% for CALR^m, which is lower than the value obtained for JAK2^V617F with a VAF threshold of 0.5% (Fig. 3 C, iii).

Discussion

We developed a mathematical approach combining modeling and statistical inference to help infer the disease dynamics (initiation and development) and set up early screening strategies in MPNs, specifically JAK2^V617F and CALR^m MPNs. Both driver mutations occur in HSCs, making it difficult to study this disease experimentally in humans and justifies the use of mathematical models. These are necessarily simplifications of reality and are based on several assumptions, without which it would not be possible to make statistical inferences from data. We assumed that model parameters only depend on the type of the main driver mutation (JAK2^V617F vs. CALR^m) and not on the patients. Thus, heterogeneity between patients was only considered to result from stochastic effects. To refine our results and explore the influence of additional genetic factors, we would need to increase the number of patients included in our cohort to split them into subgroups of sufficient size. In particular, it would be relevant to increase the number of CALR^m patients to account for differences between CALR^m T1 and T2 mutations, which are clinically distinct (21). A limitation of our work is that we only include patients without homozygous subclones. Yet, homozygous mutated cells are supposed to have an increased proliferative advantage that might accelerate the disease development (8). Thus, an extension of our work would be to complexify the model by integrating the homozygous subclones dynamics. Such an extended model could also describe the expansion of subclones with additional MPN mutations (TET2, DNMT3A, etc.). The proliferative advantage of malignant clones, modeled by Δ, was also considered constant over life. However, more accurate models should probably take into account threshold effects, possibly justified by regulatory mechanisms, to avoid the possibility of unrealistic high clonal expansion. Wild-type (WT) HSCs are also likely to acquire mutations that increase their proliferative advantage, reducing the relative selective advantage of JAK2^V617F or CALR^m clones, while these latter could also acquire associated mutations, increasing their proliferative advantage. Parameter Δ should be thus considered an averaged value that embeds different effects occurring over life. Besides, we implicitly considered that the evolution of MPN blood cancers is driven by natural selection by assuming Δ > 0 and proliferation of the malignant clone occurring in a large and constant pool of WT HSCs. As discussed in Lyne et al. (22), a proper estimation of the number of WT HSCs would be essential to distinguish natural selection from neutral evolution, but also in our case, to quantify more precisely parameter Δ. Furthermore, the fact that aged HSCs might encounter more symmetric divisions, as discussed in Florian et al. (23), would imply that the number of WT HSCs increases over age and does not stay constant. More complex models could be developed, but they would require longitudinal observations and larger datasets for their calibration. Our model has the advantage that it can be used to study other mutations occurring in various blood cancers and that its calibration only needs measures of CF among progenitor cells. Applied to the JAK2^V617F mutation, we found a mean acquisition time consistent with other studies (7, 8). Our estimate of parameter Δ is bigger than that obtained by Watson et al., who studied clonal hematopoiesis of normal individuals (9); the aggressiveness of MPNs appears compatible with a higher proliferative advantage of the mutant clones compared to general clonal hematopoiesis (24–26). Furthermore, by applying the same approach to CALR^m patients, we could evidence differences between the clonal expansion of the two main driver mutations in MPNs. These different effects of JAK2^V617F and CALR^m have also been observed in mouse models through competitive engraftment of bone marrow cells at limiting dilution of HSCs in which the CALR^m HSCs outcompete WT cells more rapidly than JAK2^V617F HSCs to induce the disease (27–29). In agreement with our data, it has been shown in early progenitors from essential thrombocythemia patients that JAK2^V617F gave a lower clonal dominance than CALR^m (7, 19, 20, 30). Moreover, our results suggest that the CALR^m mutation is unlikely acquired during fetal life, but on average 25 y after birth, in contrast to the JAK2^V617F mutation. It is consistent with observations that young MPN patients with inaugural Budd-Chiari syndrome (mean age of 35 y) harbor more JAK2^V617F than CALR^m (90% versus 2%) (31). Yet, recent findings have also evidenced a possible acquisition of CALR^m mutation in utero (32). Different types of mechanisms seem to exist for the driver mutation acquisition. A possible explanation is that a difference in the type of mutation, i.e., a point mutation for JAK2^V617F and deletions/insertions with +1 frameshift for CALR mutations, could result in two distinct types of deficient DNA repair mechanisms (leading to G->T transversion and to deletion/insertion), and that these defects might occur at different life ages. An interesting observation from Cordua et al. (33) is that even if JAK2^V617F is more frequent than CALR^m mutation in the general healthy population, the proportion of diseased patients in CALR^m individuals is much higher than in JAK2^V617F individuals. It suggests that the latency of the disease is shorter with the CALR^m mutation and that the CALR^m clone expands faster than JAK2^V617F, in keeping with our results. Moreover, even if the JAK2^V617F mutation occurs before CALR^m, the faster expansion for CALR^m can explain that the CALR^m disease starts 10 y in average before the JAK2^V617F disease (34, 35).

Finally, our inference method relies on a Bayesian framework providing the parameter probability distributions, and thus a proper assessment of parameter uncertainty. Such an approach is computationally expensive and relies on efficient numerical methods to obtain convergence of the algorithms in a realistic time. We set up an optimization procedure to make this study possible, deriving a deterministic approximation of our stochastic model, and using an optimal assignment algorithm. Then, from the posterior distributions of the parameters, we were able to infer more precisely the dynamics of the clonal expansion and explore strategies for early screening. We found that almost half of CALR^m patients would not be detected at the optimal screening age. Therefore, testing for the CALR mutation is not recommended unless the individuals are examined several times in their lives. In contrast, we found that early detection might be a viable clinical option to detect JAK2^V617F mutation, with an optimal age for measuring VAF in peripheral blood of around 30 y. Since this mutation is present in a substantial number of cases with unexplained splanchnic and cerebral thromboses for patients that exhibit a nondiagnosed MPN with low JAK2^V617F VAF, early detection may prevent thrombotic events.

To conclude, our method, applied to the two most prevalent driver mutations for MPNs, illustrates the potential of mathematical modeling to help infer the timing of blood cancer initiation, better understand its development, and design early detection strategies tailored to the type of mutation. In the future, it may be possible to test for many malignant mutations through NGS simultaneously instead of considering each of them separately. Such a large-scale screening effort would result in a more complex optimization problem; yet, the flexibility of our modeling framework makes its extension to a panel of genes feasible. In the future, generalizing the application of our mathematical approach could yield pragmatic and efficient prevention strategies against blood cancers.

Materials and Methods

Model and Parameters.

To model the MPN disease dynamics, we consider a clonal expansion in a stem cell pool whose number N_WT of WT cells is assumed constant and equal to 100,000 (36). The expansion from a single mutated HSC begins at age T₀. N(t) is the number of mutated cells at age t. The invasion of the stem cell pool is modeled by considering an unbalance between symmetric (occurring with probability p₂) and differentiated divisions (occurring with probability p₀). Δ = p₂−p₀, is the parameter that describes the proliferative advantage of the malignant clone, as introduced by Mosca et al. (18). Considering that the mutation confers a proliferative advantage at the stem cell level, we have Δ > 0. We further assume that a given mutated HSC divides at a rate α. Mathematically, this expansion process is described as a CTMC, where the probability of extinction q of the mutant cell population is equal to q = p₀/p₂. Throughout all the article, we focus on trajectories without extinction. During the expansion process, mutated HSCs also give rise to progenitor cells. Although these latter arise from HSCs, their CF is not a proxy for the CF among HSCs. However, by model identification and notably estimating parameter Δ, we can infer the CF in the progenitor compartment at age t, denoted by η(t):

$$\eta \left(t\right)=\frac{\left(1-\mathrm{\Delta }\right)N\left(t\right)}{\left(1-\mathrm{\Delta }\right)N\left(t\right)+N_{WT}}$$ [1]

Progenitor cells then give rise to mature cells. In clinical routine, the VAF measured in peripheral blood provides insight into the disease progression (note that we only consider heterozygous mutated cells: therefore, the percentage of mutated cells is twice that of mutated alleles). JAK2^V617F but also, to a lesser extent, CALR^m progenitor cells proliferate more than WT cells during the latest stages of hematopoiesis. Extending Eq. [1], the VAF in peripheral blood at time t is equal to:

$$\text{VAF}\left(t\right)=0.5\frac{\left(1-\mathrm{\Delta }\right)k_{m}N\left(t\right)}{\left(1-\mathrm{\Delta }\right)k_{m}N\left(t\right)+N_{WT}}$$ [2]

where k_m models the proliferative advantage of mutated cells, from progenitors to mature cells, compared to WT cells.

We consider an acquisition time T₀ that follows an exponential distribution. Without prior knowledge, the exponential law is an appropriate and convenient choice that introduces only one additional parameter to estimate, namely the mean of the exponential distribution denoted by λ > 0. T₀ = 0 corresponds in our model to an acquisition in fetal life; it is not a punctual event but rather a period of about 0.75 y during which the WT stem cell pool quickly expands. Williams et al. (8) reported that JAK2^V617F mutation could be acquired during this period. Therefore, we study two hypotheses: either the mutation occurs (for all patients of one of our two populations of interest, i.e., with CALR^m or with JAK2^V617F) in fetal life, that is, T₀ = 0, or later after birth, T₀ > 0. We consider that the latter corresponds to λ > 0 when the former corresponds to the limit case λ = 0, the problem of model selection (selection between both hypotheses) is thus reduced to a question of parameter estimation. We consider a priori that λ = 0 with a nonzero probability, such that its posterior could be a zero-inflated distribution. p [λ = 0 | D] will correspond to the probability of mutation acquisition in fetal life (SI Appendix, section B.4).

More details about the model, its assumptions, and the prior distributions of the parameters are given in SI Appendix, section A.

Data.

Parameter values are estimated from the observations of 15 patients diagnosed with CALR^m MPNs (19), and 11 patients diagnosed with JAK2^V617F MPNs (18). Data were obtained by determining the clonal architecture of the CD34⁺ progenitors purified from blood samples (SI Appendix, Tables D1 and D2). Thus, we get for each MPN patient i the CF of progenitor cells η(t_i) at time t_i that can be confronted with the theoretical value given by Eq. [1]. We only consider patients with heterozygous clones. Some patients have associated mutations with clonal hematopoiesis, so the patients of our cohort can be regarded as representative of the MPN population. Our model does not directly account for differences between patients, except for the main driver mutation (CALR^m or JAK2^V617F).

More details are given in SI Appendix, section D.1.

Likelihood-Free Estimation Procedure.

We consider a Bayesian framework and estimate the parameter vector’s posterior distribution given the observed data D: p[θ|D] ∝ p[D|θ]p[θ] (where θ is the parameter vector).

For CTMC, the expression of the likelihood for pointwise observations is generally intractable. We therefore use a likelihood-free estimation procedure, namely ABC-SMC (17). With this method, the posterior distribution is obtained by iterative rejection sampling, using a decreasing sequence of tolerances (SI Appendix, section B.1). In brief, the posterior distribution will be approximated based on M particles (we chose M = 2,000), that is, M parameter vectors. For a given particle, a parameter vector is sampled (initially from the prior distribution), the model is simulated, and generates as many dynamics as we have observations. The quadratic error (distance d) between data and simulations is computed. If d is below the considered tolerance (at the current stage of the algorithm), the parameter vector is assigned to the particle. If not, the previous steps are repeated. When each particle is associated with a parameter value, the method is repeated with a lower tolerance until the algorithm has converged, that is, until the estimation of the posterior distribution no longer changes when decreasing the tolerance (SI Appendix, Figs. B1–B3).

ABC-SMC relies on extensive model simulations and their confrontation to experimental observations in our patients’ populations (first JAK2^V617F, then CALR^m). To achieve computation within a reasonable time (less than 6 h when running the computations in parallel using 250 processors of an HPC cluster), we optimized the procedure. First, we derived a hybrid model, considering that only the early invasion of the stem cell pool by the malignant clone is driven by stochastic effects and then switching to a deterministic expansion when we reach a sufficient number of mutated HSCs N_c = 2,000 (i.e., a CF approximately equal to 2%). The deterministic expansion is an approximation valid for N_c large. The choice of N_c, determined through a numerical calibration procedure, is a compromise between reducing the approximation error and increasing the computation speed, that impacts the quality of the inference (SI Appendix, section B.2 and Figs. B4–B6). Second, we use an optimal assignment procedure for ABC-SMC, the Hungarian algorithm (15, 16) when comparing the simulations of all individuals to the patients’ observations (SI Appendix, section B.3).

Using synthetic datasets, we check that the number of patient observations is sufficient to draw robust conclusions from the proposed parameter estimation procedure (SI Appendix, sections C.1 and C.2 and Table C1). We study how different model assumptions impact the estimation of parameter Δ (SI Appendix, section C.3). We then run these computations on the actual dataset, and evaluate the model fit quality through a leave-one-out analysis (SI Appendix, section D). Finally, we assess to what extent our results for JAK2^V617F were consistent with other reports (SI Appendix, section E).

Optimal Strategies for Early Screening.

Having estimated the parameter posterior distributions, we can infer the dynamics of the clonal expansion and thus deduce optimal strategies for early screening. We face an optimization problem. If too early, the screening will come with an essential risk of false-negative results; a high proportion of people would develop the disease but not be identified. On the other hand, if too late, people might be detected when their stem cell pool is already invaded. With the proposed model, we can then solve this optimization problem numerically since we infer the dynamics of the malignant clone initiation and expansion. We consider that the detection is too late when the CF among HSCs is above a threshold CF_late:

$$N\left(t\right)/\left(N\left(t\right)+N_{WT}\right)>C{F}_{\mathit{\text{late}}}$$ [3]

with CF_late = 50% for CALR^m (19) and equal to 15% for JAK2^V617F (20), corresponding to the thresholds above which there is a risk of MPN onset and potential thrombosis.

In clinical routine, only the VAF in peripheral blood is measured. However, the VAF measure is not a good proxy for the CF among progenitors, let alone stem cells. In our model, VAF(t) at time t is given by Eq. [2]. We consider that an existing mutation is not detected (false negative) when VAF(t) < VAF_detection where VAF_detection = 0.1% for JAK2^V617F and VAF_detection = 2% for CALR^m.

Finally, the optimization problem to solve is to find the age at which the probability of early screening in the population is as high as possible:

$$T^{*}=\underset{t}{\max }\hspace{0.17em}\mathbb{P}\left[\text{VAF}\left(t\right)>{\text{VAF}}_{\mathit{\text{detection}}};N\left(t\right)/(N\left(t\right)+N_{WT})<C{F}_{\mathit{\text{late}}}|\mathcal{D}\right]$$ [4]

We solve this problem numerically for JAK2^V617F and CALR^m separately, evaluating the probability of early detection at age t by sampling parameters from the estimated posterior distribution. We simulate 20,000 trajectories this way and represent in Fig. 3B the probability of early screening as well as the rate of false-negative results and the probability of a too late detection (MPN symptoms), from which we can deduce the optimal age for screening.

Then, we study the effect of the sensitivity of the techniques that detect the mutation on these results (Fig. 3C).

Data, Materials, and Software Availability

Data were previously reported by Mosca et al. (18) and El-Khoury et al. (19) (SI Appendix, Tables D1 and D2).

The ABC-SMC framework used to calibrate the model was implemented using the programming language Julia and made available on GitLab: https://gitlab-research.centralesupelec.fr/2017bentrioum/markovprocesses.jl (37).

As well as the model implementation: https://gitlab-research.centralesupelec.fr/2012hermangeg/mpn-development (38).

All study data are included in the article and/or supporting information.