Electron Diffraction of 3D Molecular Crystals

Abstract

Electron crystallography has a storied history which rivals that of its more established X-ray-enabled counterpart. Recent advances in data collection and analysis have sparked a renaissance in the field, opening a new chapter for this venerable technique. Burgeoning interest in electron crystallography has spawned innovative methods described by various interchangeable labels (3D ED, MicroED, cRED, etc.). This Review covers concepts and findings relevant to the practicing crystallographer, with an emphasis on experiments aimed at using electron diffraction to elucidate the atomic structure of three-dimensional molecular crystals.

1. Introduction and Historical Background

In 1927, Davisson and Germer conducted one of the most consequential experiments of the twentieth century.¹⁻³ Using a heated tungsten filament as a thermionic gun, they fired a collimated beam of slow-moving electrons (accelerated by a potential of ∼60 V) at a polished chunk of crystalline nickel. As a makeshift detector, they installed a galvanometer enclosed within a Faraday box capable of rotating along a 135° arc. To their astonishment, Davisson and Germer observed that the reflected electrons displayed a discrete distribution of scattering angles, precisely analogous to diffraction of X-ray photons. Invoking Bragg’s law, Davisson and Germer then found very good agreement between their putative electron wavelength and the theoretical value predicted by the de Broglie relation , which de Broglie had proposed only three years earlier.⁴ Their discovery, widely recognized as the first demonstration of electron diffraction (ED), provided powerful experimental evidence that electrons conformed to wave-particle duality, an idea still nascent at the time. Several months later, Davisson and Germer’s results were echoed by Thomson and Reid, who bombarded a thin film of polycrystalline celluloid using a beam of higher-energy electrons propagated through a greater potential drop (∼13 kilovolts).⁵ On a photographic plate, Thomson and Reid observed a series of concentric rings evocative of X-ray powder diffraction. In subsequent studies, Thomson went on to disclose similar ring-like patterns formed upon irradiation of metallic films composed of polycrystalline platinum, aluminum, and gold.^6,7 Thomson’s calculations, just like Davisson and Germer’s, showed excellent agreement between the theoretical de Broglie wavelength and the experimental electron wavelength back-calculated from Bragg’s law. Naturally, he concluded that such diffraction patterns could only have originated if the scattered electrons had behaved as waves. Merely a decade after the publication of these seminal papers, Davisson and Thomson received the 1937 Nobel Prize in Physics for “their experimental discovery of the diffraction of electrons by crystals.” Their pioneering work created the field of electron crystallography.

Davisson and Thomson’s results prompted a flurry of activity during the interwar period. In 1933, Laschkarew and Usyskin disclosed a painstaking electron-diffraction analysis of Debye lines generated by polycrystalline ammonium chloride (NH₄Cl), through which they managed to estimate the N—H covalent bond length with remarkable accuracy (0.95 ± 0.07 Å).⁸ Although very sporadically cited, Laschkarew and Usyskin’s work represents the first (albeit indirect) detection and localization of hydrogen atoms by electron diffraction, a feat which was subsequently reinvestigated many times in later decades.⁹⁻¹¹ This early report explicitly underscored a key distinction between ED and conventional X-ray diffraction, where observation of H atoms is comparatively more difficult. Three years later, Rigamonti conducted an ED study of several straight-chain n-alkane crystals.¹² Intriguingly, Rigamonti’s work paired quantitative experimental intensities alongside theoretical structure-factor amplitudes, foreshadowing later attempts at reconstruction by Fourier synthesis. Subsequently, Charlesby et al. carried out a detailed single-crystal investigation of anthracene, complete with photocopied electron diffraction patterns meticulously indexed by hand.¹³ Their results largely confirmed unit cell vectors and angles previously measured by X-ray diffraction, providing a compelling validation of ED as a capable standalone method for crystallographic analysis. Taken in tandem, these three reports paint a portrait of early electron crystallography as a vibrant field of study already producing impactful discoveries only a few short years after its birth in 1927.

In the postwar years, however, progress in the field began to decelerate considerably. ED never quite came into its own as a widely used means of structure determination. Instead, it was rapidly eclipsed by single-crystal X-ray diffraction, which by the mid-twentieth century had become well-established as the gold standard for crystallographic analysis. This remarkable shift in trajectory, which initially appears perplexing given the impressive heights scaled by ED in the 1930s, was spurred by increasingly strident fears over multiple scattering, a physical phenomenon intrinsic to ED.¹⁴ These concerns were buttressed by historical constraints (such as low operating voltages), which amplified the probability of observing multiple scattering artifacts, ultimately inhibiting ED’s development as an independent experimental technique. For decades, ED was relegated to a niche method championed mostly by Vainshtein and co-workers, who developed a specialized electron diffractometer capable of collecting so-called texture patterns from 3D crystallites. An excellent summary of their work is available in Vainshtein’s 1964 monograph Structure Analysis by Electron Diffraction, which details >30 3D structures, ranging from inorganic salts to organic small molecules, methodically solved by electron diffraction.¹⁵ Nevertheless, it was not until Dorset’s retroactive validation of Vainshtein’s work in the 1990s that the stigma surrounding multiple scattering began to dissipate.¹⁶ ED then experienced a belated resurgence in activity in the mid-2010s, driven by methodological and hardware-based advances which enabled collection of diffraction patterns minimizing the deleterious influence of multiple scattering.¹⁷ Nearly a century after Davisson and Germer, ED now appears poised to reclaim its mantle as one of the most promising techniques for structure elucidation of 3D molecular crystals.

2. Theoretical Foundations

2.1. Differences Between X-ray and Electron Scattering

In real space, X-ray photons scatter solely off the periodic charge density distribution ρ(r⃗), which emanates from the electron clouds encapsulating atoms within the crystal lattice. In chemistry parlance, ρ(r⃗) is often referred to simply as “electron density.” Following Fourier synthesis, X-ray diffraction (XRD) ultimately recapitulates a real-space map of ρ(r⃗). As uncharged, massless quanta, however, incident X-rays interact with matter quite weakly. Practically, in a routine XRD experiment conducted on an in-house diffractometer, a macroscopic crystal at least ∼10⁵ μm³ in volume is desired to generate enough signal for structure determination. High-flux microfocus beamlines at third-generation synchrotron facilities can push this lower-size threshold down to ∼10³ μm³; these highly brilliant X-ray sources have enabled viable diffraction from crystals with dimensions as small as 1–10 μm on one side.¹⁸ Below this 1 μm limit, crystals quickly become smaller than the wavelength of visible light, rendering them invisible to optical microscopy. At this submicrometric scale, only the exceptionally intense pulses produced by X-ray free-electron lasers (XFELs) can extract diffraction from slurries of submicrometer-sized crystals. Nevertheless, XFELs currently do not present a widely accessible or convenient means for routine structure elucidation.

In this context, electron diffraction, typically conducted in a transmission electron microscope (TEM), provides a powerful alternative which empowers us to interrogate nanocrystals inaccessible to conventional XRD. Disparities in intrinsic physical properties cause X-rays and electrons to interact with atoms differently. Because of their nonzero mass and inherent negative charge, incident electrons experience electrostatic attraction toward protons in atomic nuclei in addition to repulsion from ρ(r⃗). As a direct consequence of this remarkably strong Coulombic interaction, incident electrons can produce tractable diffraction from minuscule crystals many orders of magnitude smaller in volume (∼10^–2 μm³) than those needed for conventional XRD. Unlike X-ray scattering, elastic electron scattering is dictated by electrostatic potential (ESP), or V(r⃗). V(r⃗) amalgamates contributions from both ρ(r⃗) and nuclear charge density δ(r⃗), which is usually expressed as a point charge weighted by atomic number. The key relation between atomic charge density and ESP is given by Poisson’s equation:

where ∇² is the Laplace operator, Z is the atomic number, δ(r⃗) is a Dirac delta function representing nuclear charge density, e is the elementary charge, and ϵ₀ is the permittivity of free space.¹⁹

A central pillar of crystallography is the notion that every diffraction pattern encodes critical information about the Fourier transform of the periodic real-space density distribution which produced it. In Fourier space, the atomic scattering factor or form factor f(s) describes the scattering amplitude of an isolated, stationary atom by an incident wave, where . Formally, f(s) is defined as the probability amplitude of the exit spherical wave relative to the incoming plane wave. Informally, f(s) simply provides us with a way to quantify the scattering power of different atoms in reciprocal space. It follows that f(s) is highly dependent on the identity of the impinging quanta. Mathematically, f(s) is derived via Fourier transform of its corresponding real-space counterpart: ρ(r⃗) for X-rays and V(r⃗) for electrons. To convert between X-ray and electron scattering factors, we invoke the Mott–Bethe formula, which functionally provides a reciprocal-space equivalent to Poisson’s equation:

where m₀ is the electron rest mass, ℏ is the reduced Planck constant, and we denote X-ray scattering factors as f_x(s) and electron scattering factors as f_e(s).²⁰

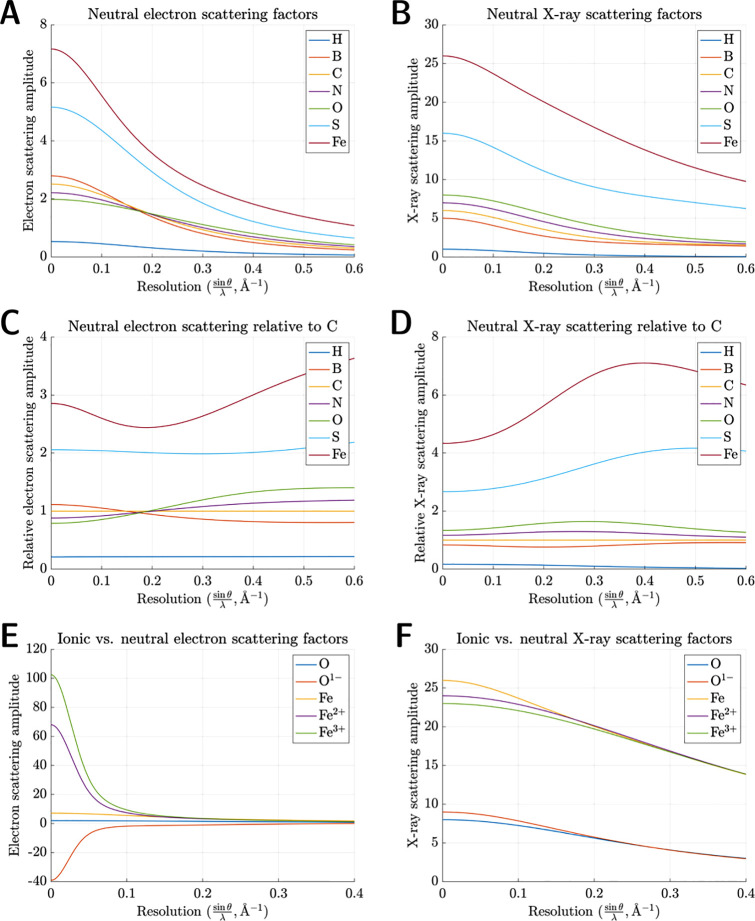
Inspection of these equations unveils several key distinctions between X-ray and electron scattering factors. First, the Mott–Bethe formula indicates no simple, monotonic relationship between f_x(s) and f_e(s). Instead, we observe a nonlinear scaling factor of s^–2. Second, unlike their X-ray counterparts, electron scattering amplitudes do not always scale linearly with Z. f_e(s) is directly proportional to atomic number only at high spatial frequencies, where electron scattering is dominated by Z-weighted nuclear charge density. At low spatial frequencies, electron scattering is influenced by repulsion from outer-shell valence electrons, which causes f_x(s) and f_e(s) to exhibit disparate behavior in the limit as s → 0. For instance, following a shared inflection point at ∼0.16 Å^–1 (∼3 Å), boron becomes a stronger electron scatterer than carbon, nitrogen, and oxygen at low resolution despite its smaller atomic mass. This order is reversed at scattering angles corresponding to high resolution (Figure 1A). Conversely, all X-ray scattering factors obey the constraint

where Z₀ is the number of electrons associated with each atom. A straightforward consequence of this limit is that heavier atoms always scatter X-rays more strongly than lighter atoms, regardless of resolution (Figure 1B). Furthermore, X-ray scattering amplitudes for adjacent neutral elements never converge to a shared point (apart from collectively dwindling to zero as s → ∞), whereas this behavior is permissible for electron scattering amplitudes. As a result, in ED, certain elements become physically indistinguishable at specific scattering angles (Figure 1C). Broadly, relative differences between elements shrink in ED; at 0.2 Å^–1 (2.5 Å), for example, iron scatters electrons merely 2.4× more strongly than carbon. This ratio grows to approximately 6× for X-rays, which is much more commensurate with the discrepancy in atomic mass between C and Fe. By the same token, however, lighter elements contribute a greater fraction of scattering signal in ED relative to XRD. This property empowers ED to detect and localize atoms such as hydrogen, which typically scatter X-rays very weakly. Finally, arguably the most drastic disparity between electron and X-ray scattering factors lies in electrons’ ability to visualize charged states.²¹V(r⃗) contains an explicit contribution from nuclear charge density δ(r⃗), which renders its Fourier transform f_e(s) innately sensitive to the excess nuclear charge intrinsic to ionized atoms. Consequently, electron scattering amplitudes for neutral atoms diverge strikingly from those of their ionic counterparts, especially at low spatial frequencies. As s → 0, f_e(s) skyrockets toward ∞ for cations and plummets toward −∞ for anions (Figure 1E). These differences materialize much more subtly in X-ray scattering, which remains comparatively uninfluenced by nuclear charge density (Figure 1F).

Figure 1.

(A) Neutral electron scattering factors for seven representative elements. All neutral scattering factors were parametrized into five Gaussians and plotted within the range [0 < < 0.6 Å^–1], equivalent to [∞ < d < 0.83 Å]. (To convert between 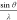and d, recall Bragg’s law: .) (B) Neutral X-ray scattering factors. (C) Neutral electron scattering relative to carbon. Relative scattering amplitudes were calculated by dividing each scattering factor by f(s) for neutral carbon. (D) Neutral X-ray scattering relative to carbon. (E) Ionic vs neutral electron scattering factors for O and Fe. To avoid physically unrealistic values in the limit as 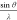tends to zero, O^1– was truncated at 0.02 Å^–1 before parametrization into five Gaussians, while Fe²⁺ and Fe³⁺ were truncated at 0.05 Å^–1. (F) Ionic vs neutral X-ray scattering factors.

2.2. Differences Between X-ray and Electron Wavelengths

Conventional TEMs accelerate electrons to a significant fraction of the speed of light, exploiting voltage differences to produce a high-energy beam (i.e., 100–300 keV) in which each constituent electron is forcibly propagated through a potential drop. At these energies, an accurate calculation of the de Broglie electron wavelength must incorporate relativistic contraction, as follows:

where h is Planck’s constant, c is the speed of light in a vacuum, m₀ is the rest mass of the electron, and E is the kinetic energy (in keV) imparted by the accelerating voltage (in kV). Discrepancies between the nonrelativistic (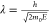) and relativistic calculations widen significantly as E rises (Figure 2). At 300 keV, for instance, the error grows to approximately 13.7%; these two wavelengths would generate distinct Ewald spheres with markedly different radii, underscoring the importance of using the relativistically corrected value.

Figure 2.

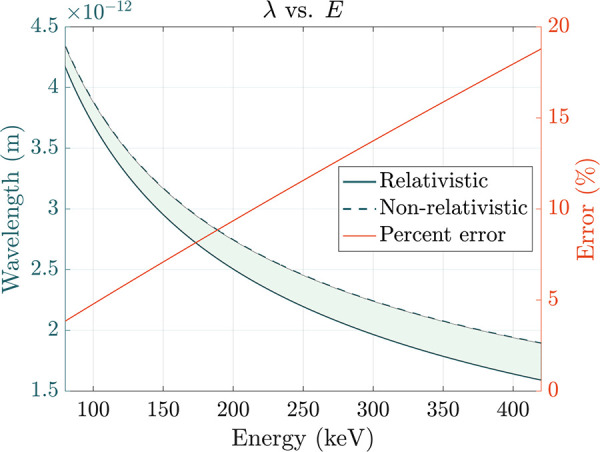
Relativistic (solid blue line) and nonrelativistic (dashed blue line) electron wavelengths plotted as a function of incident energy (E) at a range of accelerating voltages accessible to TEM. Percent error between the two calculations is plotted in orange; characteristic values include ∼4.7% at 100 keV, ∼9.3% at 200 keV, ∼13.7% at 300 keV, and ∼17.9% at 400 keV.

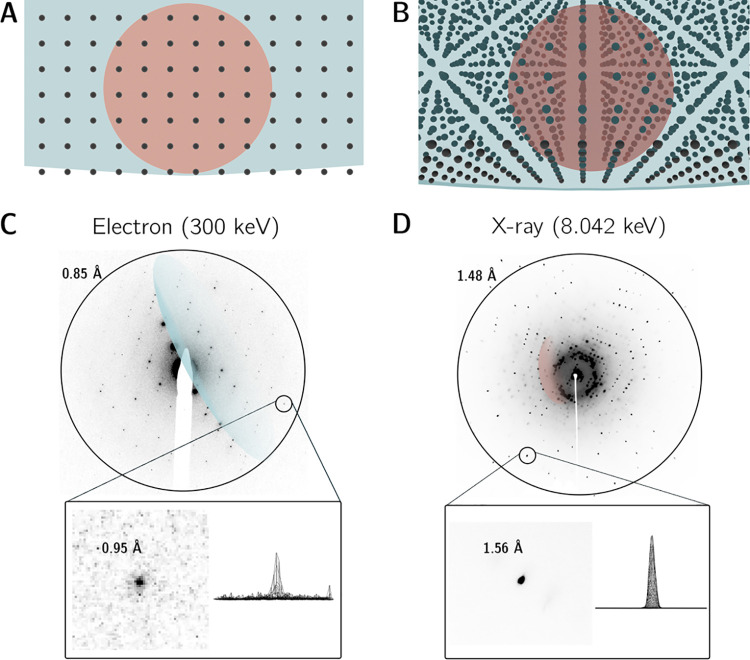
For additional perspective, a systematic comparison of typical X-ray and electron wavelengths is given in Table 1. These numbers indicate that 100–300 keV electrons exhibit relativistic wavelengths roughly 50–100× shorter than their X-ray counterparts, which leads to an array of experimental consequences. Because the radius λ^–1 of the Ewald sphere scales inversely with the wavelength of the impinging quanta, electrons at these energies divulge expansive Ewald spheres which intercept the reciprocal lattice along gently sloping arcs (Figure 3A). This geometry stands in stark contrast to X-ray diffraction, where inherently longer wavelengths produce smaller Ewald spheres featuring distinct surface curvature (Figure 3B). As a result, the cascades of circular lunes seen in X-ray diffraction patterns give way to nearly planar slices in electron diffraction patterns, which resemble canonical precession photographs (Figure 3C).

Table 1. Systematic Comparison of X-ray and Electron Wavelengths at a Range of Relevant Energies.

energy (keV)	quanta	β (v/c)	wavelength (Å)	radius of Ewald sphere (Å–1)
8.042	X-rays (Cu Kα)	1.0	1.5418	0.6485
12.65	X-rays (Se K)	1.0	0.9795	1.0209
17.44	X-rays (Mo Kα)	1.0	0.7107	1.4070
100	electrons	0.548	0.0370	27.027
200	electrons	0.695	0.0251	39.840
300	electrons	0.776	0.0197	50.761

Figure 3.

X-ray vs electron Ewald spheres and experimental diffraction patterns. Superimposed X-ray (rendered in blood orange, E = 8.042 keV, λ = 1.541 Å, radius = 0.6485 Å^–1, volume = 1.142 Å^–3) and electron (rendered in blue, E = 300 keV, λ = 0.0197 Å, radius = 50.76 Å^–1, volume = 5.478 × 10⁵ Å^–3) Ewald spheres are drawn intersecting a cubic reciprocal lattice. The X-ray Ewald sphere is comfortably dwarfed by its much more voluminous electron counterpart. (A) 2D orthographic projection viewed normal to an arbitrary reciprocal lattice vector. (B) Alternate view revealing the three-dimensionality of the reciprocal lattice. (C) Electron diffraction pattern acquired using an accelerating voltage of 300 kV. Inset shows a close-up view and somewhat noisy 3D peak profile of a 0.95 Å resolution Bragg reflection. (D) X-ray diffraction pattern acquired on an in-house diffractometer equipped with a Cu Kα anode (8.042 keV). Inset shows a close-up view and strong 3D peak profile of a 1.56 Å Bragg reflection.

Each sampled Bragg peak represents an intersection between a reciprocal lattice vector and the surface of the Ewald sphere. A wider, flattened Ewald sphere causes ED patterns to accommodate different groups of reflections per scattering angle relative to XRD. For instance, observation of several Friedel mates within a singular diffraction pattern is commonplace in ED, whereas the curvature of the X-ray Ewald sphere curtails this in XRD. Furthermore, because of planarity, a singular ED pattern generally only permits deduction of two unit cell vectors at once (exceptions include strongly diffracting samples in materials science, where higher-order Laue zone reflections can reveal three-dimensionality in the reciprocal lattice²²). Conversely, a lone XRD pattern typically samples all three dimensions of the reciprocal lattice simultaneously. In practice, to reliably determine all three unit cell parameters, indexing requires comparatively more consecutive frames in ED (often covering a ∼15–25° angular wedge of reciprocal space) than it does in XRD, where one or two can theoretically suffice. Finally, the set of permissible scattering angles in ED (i.e., values of θ which satisfy the Bragg condition) encompasses a much smaller numerical range versus XRD, a direct consequence of substituting shorter wavelengths into Bragg’s law. To compensate for this, ED requires a significantly longer detector distance than XRD to discriminate between Bragg peaks, often in the vicinity of ∼1 m. Another key distinction is that adjustments to detector distance in XRD involve physically moving a piece of hardware. Conversely, in a transmission electron microscope, the physical distance between the sample and the detector is fixed. ED performed in TEMs utilizes a system of postspecimen electromagnetic lenses to generate virtual camera lengths, effectively either magnifying or demagnifying the reciprocal lattice projected onto the detector.

2.3. Multiple Scattering

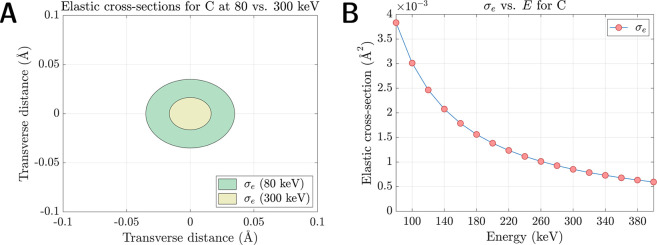
As another consequence of their augmented cross-sections relative to X-rays, incident electrons have a higher relative likelihood of undergoing multiple scattering events while traversing an illuminated crystal.²³⁻²⁷ This phenomenon, frequently referred to as “dynamical” scattering, a term which specifically encompasses multiple elastic events, was for decades considered a daunting bulwark against accurate structure determination by electron crystallography. Broadly, the probability of detecting multiple scattering is chiefly influenced by three factors: (a) the incident electron energy, (b) the irradiated crystal’s density and thickness, and (c) its geometric orientation relative to the impinging beam. Within an energy range germane to TEM (i.e., accelerating voltages between 80–300 kV), electron cross-sections for all neutral elements vary as a monotonic function of kinetic energy E (Figure 4B). As E becomes progressively larger (i.e., as the relativistic electron velocity asymptotically approaches c), the likelihood of any singular scattering event, and, by extension, the likelihood of multiple scattering, becomes progressively lower. For instance, the elastic cross-section of carbon at 300 keV is ∼4× smaller than its counterpart at 80 keV (Figure 4A). In principle, the probability of multiple scattering is therefore diminished at higher incident energies and maximized at lower incident energies.

Figure 4.

(A) Elastic cross-sections for neutral carbon at 80 keV (green) and 300 keV (yellow); cross-sectional areas expressed as concentric circles. (B) Elastic cross-section for neutral carbon decreasing as a monotonic function of incident energy, plotted at a range of accelerating voltages relevant to TEM.

Furthermore, substrate-specific attributes such as crystal density determine the incident electrons’ elastic and inelastic mean free paths (MFPs). MFPs provide a statistical estimate of the average distance traveled between each respective scattering event. Assuming a randomly distributed set of point scatterers, the MFP is defined as

where N is the number of atoms per unit cell volume and σ is a weighted mean cross-section which represents an “average atom” within the unit cell. Clearly, MFPs scale inversely with N and σ, indicating that the probability of multiple scattering is amplified if the incident electrons must penetrate (a) dense, tightly packed lattices or (b) unit cells containing strong scatterers such as heavy metals, whose cross-sections eclipse those of lighter elements. These scenarios lead to shorter MFPs. Theoretically, if the crystal under interrogation is several MFPs thick, multiple scattering becomes a statistical inevitability.

Finally, geometric orientations where the incident beam illuminates major zone axes can cause excitation of many Bragg reflections all at once. If an incident electron undergoes exclusively multiple elastic scattering, its ultimate fate likely lies within a Bragg peak regardless of how many scattering events it experiences. Thus, because zone-axis diffraction patterns feature simultaneous excitation of a wide range of Bragg peaks, they effectively open many more avenues through which multibeam interference could potentially occur. This effect is intensified by low mosaicity. In sum, ED studies which report severe multiple scattering typically feature some combination of low accelerating voltages, near-perfect or minimally mosaic crystals, alignment at major zone-axis orientations, or thick and dense samples. All these experimental conditions maximize the occurrence of dynamical effects.

If singular elastic or “kinematical” scattering holds, the integrated intensity of each Bragg peak is proportional to the squared modulus of its corresponding structure factor:

In conventional X-ray crystallography, this relationship is almost universally observed. In ED, however, multiple elastic scattering stochastically redistributes some fraction of the diffracted intensities, a process mathematically described by self-convolution of I_hkl.²⁸ Such self-convolution breaks a key tenet of kinematical scattering, where the intensity of any random Bragg reflection is decoupled from that of its neighbor. Conversely, dynamical scattering imbues the intensities of compromised reflections with some degree of dependence on the intensities of their simultaneously excited counterparts. Two diagnostic markers of this effect include (a) violation of Friedel’s law²⁹⁻³¹ and (b) appearance of symmetry-forbidden Bragg peaks at reciprocal lattice points where glide planes, screw axes, or nonprimitive lattices would normally mandate systematic extinctions.^14,32−39 In space groups which contain these symmetry operators, a useful metric to quantify the extent of multiple scattering is the ratio between average intensities of symmetry-forbidden versus symmetry-allowed reflections within a particular zone axis.^35,37,38 If the recorded diffraction pattern is sufficiently marred by these artifacts, the fundamental link between I_hkl and |F_hkl|² becomes increasingly tenuous, undermining the validity of the measured intensities. In milder cases, multiple elastic scattering would simply intensify weaker reflections and attenuate stronger reflections. In severe cases, multiple scattering would theoretically sever this link altogether, producing a pseudouniform distribution of intensities which ablates distinctions between ideally independent reflections.³⁹ This homogenization of relative differences between Bragg peaks would render any structure-factor amplitudes derived from such intensities meaningless.

For many years, these concerns led to a self-imposed moratorium on structure elucidation by electron diffraction, as ED intensities were considered too corrupted to yield reliable atomic coordinates.⁴⁰ Such sentiments were succinctly expressed in The Determination of Crystal Structures, the classic 1966 textbook by Lipson and Cochran.⁴¹ Following a perfunctory summary of Vainshtein’s work, the authors concluded that electron diffraction was “inferior to the other two diffraction techniques [X-ray and neutron] because of the many difficulties which stand in the way of making accurate intensity measurements.” In some laboratories, this belief rapidly ossified into dogma, and the steady stream of small-molecule ED structures solved by Vainshtein and co-workers in the Soviet Union was treated with suspicion. In 1968, Cowley¹⁴ felt compelled to write that it was “perhaps significant that the first work on structure analysis by electron diffraction, and most of the subsequent work, was done in the USSR and Australia, countries well removed [emphasis added] from the leading pre-war experimental electron diffraction groups in England and the groups in Japan which had the most complete knowledge of dynamical theory.”

A key breakthrough was provided by Hauptman and Karle’s development of direct methods, which supplied an objective means of phase retrieval from integrated intensities.⁴²⁻⁴⁵ Because direct methods leverage statistical relationships between accurately sampled structure-factor amplitudes, untethering I_hkl and |F_hkl|² should have nullified any possibility of ab initio phasing. Dynamically corrupted intensities would have led direct methods to formulate incorrect phase relationships between structure-factor amplitudes, ultimately generating a nonsense structure. However, in a seminal 1976 study, Dorset and Hauptman deployed ab initio phasing to successfully decipher the subcell structures of two organic compounds, n-hexatriacontane and racemic 1,2-dipalmitoyl-glycerophosphoethanolamine, via electron diffraction.⁴⁶ This work provided robust experimental evidence that structure elucidation using the kinematical approximation was plausible despite the countervailing influence of multiple scattering. Specifically, Dorset and Hauptman found that the utility of the triplet and quartet phase invariants (as well as the centrosymmetric phase restriction ϕ_hkl = 0 or π) emerged unscathed, notwithstanding usage of amplitudes presumably distorted by multiple scattering. Dorset and Hauptman’s results were especially compelling given their relatively low operating voltages of 80–100 kV (i.e., energies at which the probability of multiple scattering was already amplified). In a steadily increasing number of counterexamples, ominous predictions about multiple scattering have generally failed to hold true outside specific extenuating circumstances, and dynamical effects have not impeded structure solution by direct methods (Table 3). In sum, multiple elastic scattering rarely distorts intensities with enough severity to generate an experimental Patterson map out of sync with the autocorrelation function of the genuine structure.⁴⁷

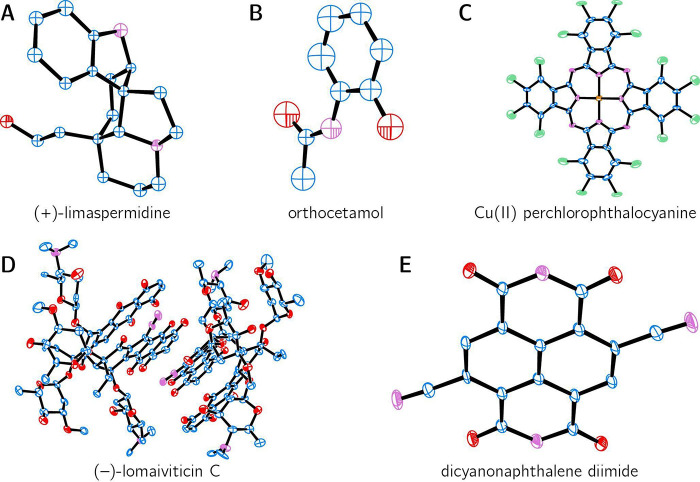
Table 3. List of Small-Molecule 3D ED Structures Deposited in the CSD as of October 2021, Excluding Duplicates^a,^b.

compound name	empirical formula	CSD accession code	year	resolution (Å)	space group	R1	ref
biotin	C10H16N2O3S	BIOTIN13	2018	0.9	P212121	17.81	(200)
carbamazepine	C15H12N2O	CBMZPN28	2016	0.8	P21/n	25.45	(225)
epicorazine A	C18H16N2O6S2	BISGAO	2019	0.83	P212121	15.43	(144)
dehydrocurvularin	C16H18O5	IRELOH01	2019	0.82	P212121	14.95	(144)
(+)-limaspermidine	C19H26N2O	CAHKUU01	2018	0.77	P212121	18.22	(200)
cimetidine	C10H16N6S	CIMETD06	2019	1.0	C2/c	19.69	(227)
cinchonine	C19H22N2O	CINCHO11	2018	1.0	P21	17.80	(200)
paracetamol (monoclinic polymorph)	C8H9NO2	COTZAN07	2018	0.86	P21/n	26.46	(199)
Schwartz’s reagent	C24H34Cl2Zr2	DIZZUK	2019	1.15	Pnnm	14.95	(163)
Pd(II) ethylene insertion product	C36H40B18O2P2Cl18Pd2	DOBBEE	2019	0.9	P1̅	18.22	(163)
Pd(dba)(PHOX)	C43H43NO2PPd	DOBCAB	2019	1.0	P212121	14.32	(163)
polyamylose–propanol complex	(C42H70O35)n, (C3H8O)4n, (H2O)6n	GUTGAF	2015	3.03	P212121	34.19	(275)
paracetamol (orthorhombic polymorph)	C8H9NO2	HXACAN41	2018	0.8	Pcab	8.89a	(143)
ibuprofen	C13H18O2	IBPRAC20	2018	0.9	P21/c	25.41	(200)
Ni(dppf)Cl2	C34H28Cl2FeNiP2	KADXES02	2019	1.0	Pna21	11.25	(163)
methylene blue derivative (MBBF4)	(C30H31N7S) 2+,2(C30H30N7S)+,4(BF4)−	LIMZAL01	2018	0.9	C2/c	25.83	(199)
brucine	C23N2O4	MAJRIZ02	2018	0.9	P21	18.29	(200)
[Co(ddpd)2](BF4)2	(C34H34N10Co)2+,2(BF4)−	MOTNUG	2015	1.2	P21/c	28.81	(276)
nicotinic acid	C6H5NO2	NICOAC05	2016	0.75	P21/c	30.26	(225)
ethisterone	C21H28O2	POSJAI01	2018	0.9	P21	22.21	(200)
Grubbs’ catalyst (1st generation)	C43H72Cl2P2Ru	IKORIK03	2019	0.85	P21/n	15.95	(163)
progesterone	C21H30O2	PROGST15	2018	0.9	P212121	17.65	(200)
HKL-I-029	C19H17NO5	QILJUT	2018	1.0	P21/n	22.23	(200)
n-tritriacontane	C33H68	QQQFVD03	1999	N/Ab	A21am	21.00	(277)
HRh(CO) (PPh3)3	C55H46OP3Rh	RCOHPH04	2019	1.0	P21/n	13.24	(163)
Fe(acac)3	C15H21FeO6	XAQVIX01	2019	0.9	Pbca	16.07	(163)
C68-warped nanographene	C68H28	AQETUO	2021	0.85	P42	16.47	(218)
loratadine	C22H23N2O2Cl	BEQGIN08	2020	1.2	C2/c	57.58	(125)
(−)-lomaiviticin C	C68H82N4O24	ERUHEH	2021	1.05	P21	12.06	(207)
sofosbuvir/l-proline cocrystal	C22H29FN3 O9P, C5H9N O2	EYIQEL	2019	1.0	P212121	9.62a	(175)
polycyclic indole-derived ester	C19H14N4O2	FABTIP	2020	0.83	R3̅	15.77	(217)
remdesivir	C27H35N6O8P	IQIMAZ02	2021	0.9	P21	16.09	(232)
glycine (α-polymorph)	C2H5NO2	KUFDIB	2020	0.703	P21/n	21.88	(278)
glycine (β-polymorph)	C2H5NO2	KUFDOH	2020	0.751	P21	12.76	(278)
glycine (γ-polymorph)	C2H5NO2	KUFDUN	2020	0.7	P31	30.64	(278)
dipyrrolidine perylene diimide	C32H24N4O4	LACPAJ01	2020	0.6	Cc	19.91	(54)
dicyano naphthalene diimide	C16H4N4O4	TUKVON	2020	0.57	P21/c	13.76	(54)
diketopyrrolopyrrole	C54H70N8O6S2	TUKVUT	2020	0.9	P21/n	23.5	(54)
l-histidine	C6H9N3O2	LHISTD15	2019	0.88	P212121	19.81	(227)
nickel carbene complex	C27H31N3O2Ni	LUZZUE	2020	0.85	Pca21	24.63	(279)
[Fe(bpy)3](PF6)2	(C30H24FeN6)2+, 2(PF6)−	NUZKOI13	2020	N/A	P3̅c1	N/Ab	(279)
[11]helicene	C88H92O10	QADMUH	2020	1.0	P212121	11.73	(216)
[11]helicene monoquinone	C86H86O10	QADNAO	2020	1.1	Iba2	17.04	(216)
[11]helicene diquinone	C84H80O10	QADNES	2020	1.0	P1̅	17.16	(216)
[11]helicene diquinoxaline	C96H88N4O6	QADNIW	2020	1.0	I4̅c2	15.41	(216)
[11]helicene monoquinoxaline	C92H90N2O8	QADNOC	2020	1.0	Iba2	18.80	(216)
B/N-doped p-arylenevinylene chromophore	C102H114B2N2	SADGEN	2020	0.95	P1̅	24.29	(281)
spiroconjugated carbon-bridged p-phenylenevinylene	C42H26O	SUVJOL	2020	0.95	P1̅	24.29	(282)
copper(II) perchlorophthalocyanine	C32N8Cl16Cu	UZEMIY	2021	0.8	C2/m	27.85	(205)
olanzapine/ phenol cocrystal	C17H20N4S, C6H6O	WACDEN	2020	1.0	P1̅	31.40	(229)
tryptophan-derived oxindole	C12H14N2O3	YOYXAO	2019	0.9	P21/c	17.77	(213)
tryptophan-derived indanone	C13H15NO3	YOYYOD	2019	0.9	P212121	17.07	(213)
glucopyranosyl uric acid derivative	C11H14N4O8	YURNIL	2020	1.0	P1	14.01	(215)
metaxalone	C12H15NO3	ZUQXIV	2020	0.78	P212121	38.95	(230)
orthocetamol	C8H9NO2	WOFXEX	2019	0.9	C2/c	32.70	(204)
bismuth subgallate	C7H5BiO6	JAXSUZ	2017	0.7	Pmna	11.80	(226)
teniposide	C32H32O13S	KUXJUL	2021	0.9	P212121	9.76	(231)
thiophene-fused cyclooctatetraene	C36H36O12NS4	AQECOR	2021	0.8	P1̅	23.96	(223)

^aCases applying dynamical refinement.

^bCIF files for entries NUZKOI03 and QQQFVD03 do not contain any structure-factor amplitudes or phases, simply atomic coordinates. Abbreviations used: acac = acetylacetonate, bpy = 2,2′-bipyridine, dppf = 1,1′-bis(diphenylphosphino)ferrocene, dba = dibenzylideneacetone, ddpd = N,N′-dimethyl-N,N′-dipyridine-2-yl-pyridine-2,6-diamine. If any discrepancies were found between the R-factors reported in the CSD vs the R-factors quoted in the associated publications, we cited those listed in the CSD.

An impactful portion of this dogma-busting work was conducted by Dorset, who embarked on a quest to apply direct methods to electron-diffraction amplitudes originally recorded at ∼50 kV by Vainshtein, Zvyagin, and other pioneering electron crystallographers in the 1950s.⁴⁸⁻⁵² Because these ED data were collected prior to the advent of ab initio phasing, Vainshtein and co-workers usually relied on pairing experimental ED amplitudes with phases borrowed from corresponding X-ray structures. Naturally, this approach invited concerns regarding phase bias. Nevertheless, armed with the objectivity of direct methods, Dorset was able to replicate Vainshtein’s structures of diketopiperazine, urea, and thiourea, all using a simple kinematical approximation. This resounding vindication of Vainshtein’s early work, nearly three-and-a-half decades after it was first published, dispelled much of the stigma projected by dynamical scattering. In 2010, Dorset concluded the diketopiperazine saga with another reevaluation of Vainshtein’s results, this time equipped with contemporary crystallographic software.⁵³ A full-matrix least-squares refinement of 60-year-old data in SHELXL proved remarkably successful, yielding an R1 residual comparable to recent ED structures obtained using modern instrumentation.

3. Experimental Setup

3.1. Sample Preparation

Sample preparation for 3D electron crystallography involves dispersing a micro- or nanocrystalline powder onto an EM grid 3.05 mm in diameter. For a wide range of small molecules, this procedure is quite simple; it merely entails inserting an EM grid into a scintillation vial containing a few milligrams of substrate and vigorously shaking for ∼10 s (Figure 5B). If this “shake-n-bake” method produces an unduly sparse distribution of crystals, an alternative strategy involves immersing a small quantity of powder in a volatile solvent (ideally one in which the substrate is completely insoluble), drop-casting 2–3 μL of the resultant slurry directly onto the grid using a micropipette, and allowing it to air-dry at RT. Alternatively, crystals suitable for ED can be grown or annealed directly on EM grids by drop-casting a dilute solution of analyte and letting it evaporate, prompting in situ nucleation and crystallization.^54,55 Optionally, excess solvent can be wicked away using filter paper or drained under reduced pressure by a vacuum pump.⁵⁶ Because the amorphous carbon surface of many grids is somewhat hydrophobic, it generally interferes with adherence of aqueous solvents. This mismatch can prevent the drop-casted suspension from spreading uniformly across the film. A highly uneven distribution of crystallites can lead to a few overly congested grid squares, prohibiting isolation of a single crystal within the selected area aperture. To combat this, the surface of the grid can be rendered hydrophilic by glow-discharging before use.

Figure 5.

(A–C) Optical microscopy of several crystalline compounds suitable for 3D electron crystallography. (A,C) Formally recrystallized material (an organic small molecule suspended in glycerol in A, an oligopeptide suspended in a hanging drop in C) requiring additional pulverization before ED due to their macroscopic size. (B) An inherently microcrystalline powder amenable to a direct “shake-n-bake” approach with a standard 3.05 mm lacey carbon EM grid, encircled in blue. (D–F) Transmission electron microscopy reveals micro- and nanocrystalline specimens with a range of morphologies, all suitable for ED analysis.

An added layer of complexity is presented by crystals which contain disordered channels of volatile solvent, such as proteins.⁵⁷⁻⁵⁹ These species can undergo swift lattice collapse when subjected to the high vacuum (typically <10^–4 Pa) of the TEM. Therefore, as a prophylactic measure, electron diffraction of solvated crystals is generally recorded under cryogenic (−175 °C) conditions facilitated by liquid nitrogen. Common practice involves implementing well-established cryo-preservation techniques borrowed from single-particle cryo-EM.⁶⁰⁻⁶³ Encasing susceptible crystals within a thin layer of vitreous ice shields them from the TEM vacuum and preserves the lattice in a frozen-hydrated state. Cryogenic temperatures also delay the onset and progression of radiation damage, which is frequently quite severe for macromolecular crystals at RT. For proteins and oligopeptides, several step-by-step protocols detailing cryo-preservation procedures have been published.^64,65 A glow-discharged EM grid is first loaded with 2–3 μL of an aqueous suspension of protein crystals (usually immersed in mother liquor from a successful crystallization trial, such as the hanging drop in Figure 5C). Subsequently, the grid is blotted and rapidly plunged into a small reservoir (∼4 mL) of liquid ethane. Ethane’s high specific heat capacity allows it to function as a ruthlessly efficient cryogen, ensuring complete vitrification of residual water without cocrystallization of adventitious ice. Because pure ethane solidifies upon prolonged exposure to liquid nitrogen, eutectic mixtures of ethane and propane have also been proposed as alternatives with depressed freezing points.⁶⁶ This step is typically carried out at high speed by automated vitrification robots, although manual plunge-freezing is also an option. Frozen grids can then be immediately cryo-transferred to the TEM or indefinitely stored in liquid nitrogen for future use. Finally, for substrates such as beam-sensitive, unsolvated small molecules, vitrification is generally unnecessary. Nonetheless, these crystals may still benefit considerably from the reduced radiation damage engendered by cryogenic conditions. A typical tactic therefore involves skipping vitrification and simply slow-cooling the sample within a cryo-holder following insertion into the TEM.

Atomic-resolution ED data have been routinely recorded from crystals hundreds of nanometers thick. Nevertheless, as crystal thicknesses approach the 1 μm mark, data quality rapidly deteriorates, largely due to prohibitive amounts of inelastic scattering overwhelming productive signal from Bragg peaks.⁶⁷ Thus, sonicating the microcrystalline slurry (or vortexing with acid-washed glass beads) is often necessary to shatter crystals into smaller, thinner shards amenable to ED. In cases where a suitably inert drop-casting solvent is unavailable, simply grinding dry powder between two glass coverslips can achieve an analogous effect via shear force. Alternatively, focused ion-beam (FIB) milling can shave excessively thick crystals down to thin electron-transparent lamellae with precision.⁶⁸⁻⁷¹ Although quite powerful, FIB milling requires usage of specialized ancillary equipment (a scanning electron microscope), as well as multiple cumbersome cryo-transfer steps if dealing with vitrified samples.

3.2. 3D ED Data Collection Procedures

Historically, electron diffraction patterns were recorded after tilting the crystal to a low-index zone-axis orientation.¹³ In principle, in-zone diffraction patterns near-perfectly coincide with sets of parallel Bragg planes within the reciprocal lattice (Figure 6A). As a result, these slices of the Ewald sphere contain an especially high density of simultaneously excited reflections. Such circumstances present a double-edged sword. On one hand, a well-defined zone-axis geometry facilitates indexing and simplifies determination of unit cell parameters. By the same token, however, this method is blind to reflections located between zone axes, leaving interstitial corridors of reciprocal space undersampled. Furthermore, zone-axis orientations maximize the probability of observing multiple elastic scattering, impeding accurate integration of quasi-kinematical intensities needed for structure solution. To compound matters, merging intensities recorded solely from disparate still-frame in-zone patterns is often quite difficult. Excitation error can cause even small angular deviations to produce prohibitive variations in intensities recorded slightly outside their exact Bragg condition. As the relatively small handful of successful examples attests,⁷²⁻⁷⁴ab initio structure determination from oriented zone-axis patterns was never widely adopted as a robust means of solving 3D structures.

Figure 6.

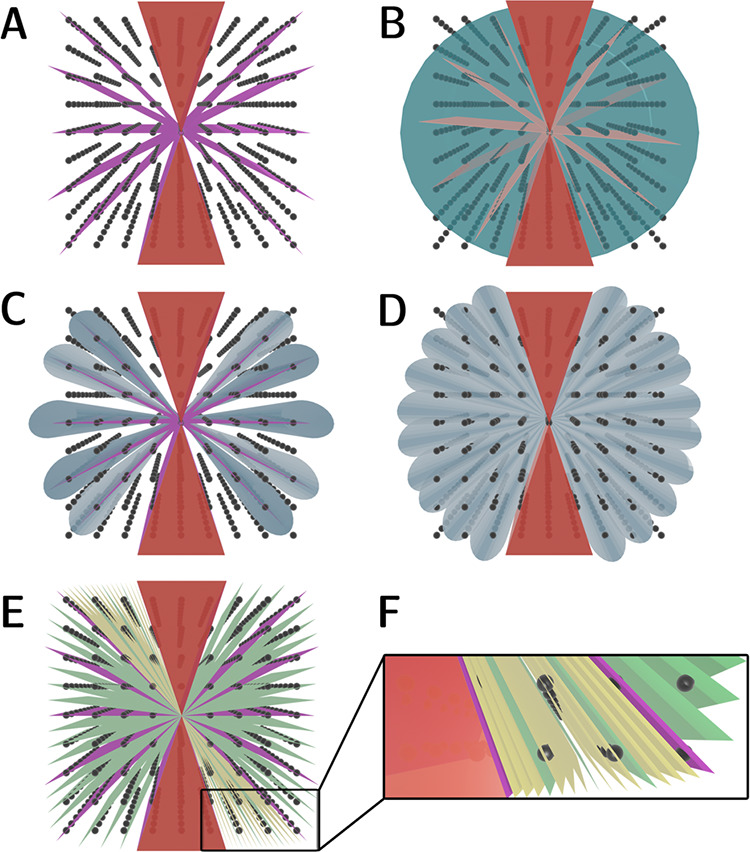
Different modalities of 3D ED data collection. In all schematics, the hourglass-shaped missing wedge intrinsic to the TEM goniometer is depicted in red. (A) Zone-axis orientations (purple planes) accessed via stepwise angular tilts. This approach maximizes the density of Bragg reflections per diffraction pattern, streamlining deduction of unit cell parameters. It also leaves several corridors of reciprocal space between zone axes (white) unsampled, hampering completeness. (B) Continuous-rotation electron diffraction. Blue wedges correspond to regions of reciprocal space sampled during the exposure time, whereas red planes represent gaps left unsampled while the TEM stage continues to rotate during the detector readout time; these become negligibly small with modern active-pixel sensors. (C) Zone-axis precession electron diffraction (PED). Thanks to the gyrating motion of the incident beam (blue cones), this method intercepts several off-zone reflections neglected in (A). (D) Precession-assisted electron diffraction tomography (PEDT). This technique combines beam precession with rotation about the goniometer axis, further enhancing coverage of reciprocal space. (E) Automated diffraction tomography (ADT). Stepwise tilts about the goniometer axis ensure that most diffraction patterns (green planes) represent off-zone orientations. (F) Rotation electron diffraction (RED). Exploitation of electron beam tilt enables finer sampling of reciprocal space (closely spaced yellow planes) than relying on the mechanical precision of the TEM goniometer alone (green planes).

In 1994, Vincent and Midgley pioneered precession electron diffraction (PED), a novel means of data collection that mitigated some of these issues.⁷⁵ In their method, the incident electron beam is effectively precessed within a fixed, hollow cone whose vertex is coincident with the plane of the illuminated crystal.⁷⁶ The resultant diffraction patterns contain signal averaged over elongated conical sections of the Ewald sphere rather than planar slices through zone axes (Figure 6C). These cones encompass both in-zone reflections and several previously neglected off-zone reflections. Critically, because the gyrating beam captures most off-zone reflections sequentially and not all at once, they generally do not undergo simultaneous excitation. Consequently, PED reduces the number of plausible multibeam pathways for dynamical scattering. Furthermore, accurate measurement of PED intensities is facilitated by integration over a more complete snapshot of the Bragg condition for each observed reflection. As an ensemble, these intensities largely behave quasi-kinematically.⁷⁷⁻⁷⁹ A straightforward tactic to further minimize dynamical effects involves widening the angle of precession,⁷⁷ which has been shown to systematically diminish the intensities of symmetry-forbidden reflections.³⁵ PED also expands coverage of reciprocal space relative to sampling exclusively in-zone reflections. Nevertheless, this technique still favors locating zone-axis orientations and adds only a subset of off-zone reflections (i.e., those proximal to their in-zone counterparts). As a result, ab initio structures solved by zone-axis PED often relied on high-symmetry centrosymmetric space groups to simplify phasing and bolster completeness.^80,81

A crucial step forward was taken by Kolb et al. in 2007; these researchers proposed collecting a tomographic series of diffraction patterns, using the TEM goniometer to tilt the substrate in a sequence of discrete angular steps (Figure 6E).^82,83 Because the axis of the TEM goniometer is geometrically arbitrary with respect to the orientation of the crystal, ED data collected in this way represent slices of the Ewald sphere which overlap “only accidentally” with crystallographic zone axes.⁸² Therefore, this approach, originally termed automated diffraction tomography (ADT), banished the persistent specter of zone-axis orientations amplifying multiple scattering. Indeed, ADT deliberately ensured that most diffraction patterns were collected off-zone, providing ideal conditions for observing quasi-kinematical scattering.^84,85

ADT’s most salient limitation was its tendency to leave unsampled gaps in reciprocal space between angular tilts: essentially a less severe version of the large swaths overlooked by zone-axis diffraction. Several subsequent strategies were developed to address this. ADT was swiftly combined with beam precession by Mugnaioli et al., who developed a hybrid technique coined precession-assisted electron diffraction tomography (PEDT; Figure 6D).⁸⁶ PEDT represented the first ED technique to gain some level of traction as a generally applicable method for structure elucidation despite the necessity of specialized external hardware to implement beam precession.⁸⁷ Alternatively, Hovmöller, Zou, and co-workers devised a means of slicing reciprocal space more finely by supplementing coarse mechanical tilts with electron beam tilts (Figure 6F).⁸⁸ This approach was dubbed rotation electron diffraction (RED); it utilized custom software to enable data collection in very granular angular steps (Δη < 0.1°), which eclipsed the precision of the TEM goniometer.

These developments paved the way for arguably the most impactful methodological advance in 3D electron crystallography: continuous rotation, which was formulated nearly in parallel by Nederlof et al. and Nannenga et al. in 2013 and 2014, respectively.^89,90 Unlike PEDT or RED, no ancillary hardware or software is strictly required to implement continuous-rotation ED; most commercially available TEMs can collect continuous-rotation data with little to no reconfiguration. In this technique, reciprocal space is regularly sampled in periodic intervals, while the irradiated crystal is unidirectionally rotated about the TEM goniometer axis (Figure 6B). Each diffraction pattern thus represents signal averaged over an oscillation range whose thickness in reciprocal space is given by

where ω_rot is the rotational velocity of the goniometer (typically expressed in degrees per second) and τ_exp is the exposure time (for instance, 2–3 s).⁹¹ In practice, because no detector operates instantaneously, Δη is modified by adding a hardware-specific parameter τ_dead, which represents the readout time needed to store the data collected during τ_exp:

Especially in older systems containing slow-scan charge-coupled device (CCD) detectors, τ_dead can become significant. In such cases, each consecutive diffraction pattern is separated by a missing wedge (Δη_dead = ω_rotτ_dead) corresponding to the angular range left unsampled during the readout period. A viable tactic to minimize dead time entails spatial subsampling or binning each recorded frame, although this may ultimately compromise maximum achievable resolution. Nannenga et al. circumvented this issue by using a complementary metal–oxide–semiconductor (CMOS) detector in rolling-shutter mode, which provided a readout speed sufficiently high that τ_dead was rendered negligible relative to τ_exp. This breakthrough allowed continuous-rotation ED to fully sample all regions of reciprocal space accessible to the TEM goniometer. By integrating signal over an angular wedge, continuous-rotation ED also evaded all the canonical problems associated with multiple elastic scattering and partially recorded reflections. Nannenga et al. demonstrated this by using molecular replacement to solve a 2.5 Å ED structure of hen egg white lysozyme (HEWL), a protein frequently used as a standard in X-ray crystallography. HEWL crystallizes in the primitive tetragonal space group P4₃2₁2, which features several sets of systematic absences orchestrated by the 4₃ and 2₁ screw axes. Critically, Nannenga et al. hunted for symmetry-forbidden reflections and found that their intensities were quite weak, contributing only ∼2.5% of observed signal relative to their symmetry-allowed counterparts (vs ∼5% for a previous ED investigation³⁷ of HEWL using still frames collected at discrete tilts).

These results sparked a renaissance in the field. In recent years, continuous rotation has clearly emerged as the method of choice for ED data collection. This has been accompanied by a variety of acronyms, including microcrystal electron diffraction (MicroED),⁹⁰ integrated electron diffraction tomography (IEDT),⁹¹ and continuous-rotation electron diffraction (cRED).⁹² Ultimately, these all describe the same technique. We find Gemmi et al.’s adoption of the umbrella term 3D electron diffraction (3D ED)¹⁷ a useful construct and follow this convention throughout.

3.3. Serial Electron Diffraction

To maximize sampling of reciprocal space, diffraction experiments have often relied on merging data sets collected from multiple crystals. Serial X-ray crystallography stretches this idea to its limit, exploiting X-ray free-electron lasers to collect and combine one-shot diffraction patterns extricated from hundreds of thousands of randomly oriented specimens.⁹³ Almost instantly after producing diffraction, these exceptionally brilliant lasers leave a bleak obliteration zone in their wake, vaporizing every crystal they touch. Ironically, XFELs come closest to generating diffraction patterns undistorted by radiation damage because each successive crystal is exposed to a femtosecond-scale X-ray pulse only once before it is annihilated (as encapsulated in the mantra “diffraction before destruction”).⁹⁴ Ever-faster detectors at synchrotron facilities have driven serial X-ray crystallography’s proliferation to many beamlines. Likewise, growing digitization and improved hardware have also enabled more ambitious, automated data collection strategies in ED.⁹⁵⁻⁹⁷ Recent studies have exploited the automation capabilities of modern TEMs to collect data from thousands of crystals per hour. This approach, termed serial electron diffraction (serial ED),⁹⁸ generally relies on merging snapshots recorded from disparate crystals at distinct orientations, foregoing conventional sampling of a lone crystal at multiple angles. As with serial XRD, this technique exploits single exposures in an attempt to outrun radiation damage. With plenty of real estate on a typical EM grid, an experimentalist (or algorithm) can easily find dozens or possibly thousands of well-diffracting crystals during a routine search. Although many publications only report the number of crystals merged to produce a structure solution, hundreds more are typically probed and then belatedly abandoned.

Serial ED has successfully determined a small handful of structures, including HEWL, granulovirus occlusion bodies, and several highly symmetric zeolites.^98,99 Elucidation of entirely novel structures remains a challenge, as it would require ab initio indexing, merging, and phasing. Nevertheless, serial ED has rapidly emerged as a potent microscopic alternative to the much larger-scale experiments conducted at synchrotrons or X-ray free-electron laser facilities. In addition to greater accessibility, the TEM unlocks another crucial advantage over conventional XFEL experiments: the power of real-space imaging. Indeed, the ability to visualize target crystals greatly streamlines the hunt for well-diffracting specimens, which for nanocrystals can be a blind and comparatively inefficient process in serial X-ray crystallography.

In this context, 4D scanning transmission electron microscopy (4DSTEM) also merits discussion because it too harmoniously combines real-space screening with reciprocal-space sampling.¹⁰⁰ This method leverages a scanning nanobeam to record ED patterns at an array of real-space points defined by a 2D raster scan across a user-selected region of a crystalline specimen.^101,102 For instance, within an illuminated area of 500 nm², individual diffraction patterns can be collected every 20 nanometers. Conceptually, therefore, 4DSTEM provides an inherently serial approach to diffraction, simply localized with nanoscale precision onto the canvas of a single crystal. In principle, 4DSTEM’s ability to digitally pinpoint a specific nanoscale volume for data collection is quite powerful; for instance, it could allow facile deconvolution of signal from twinned, metamict, or otherwise imperfect regions present within an already submicrometer-sized crystal. 4DSTEM analysis can reveal complex mosaic substructures even in crystals anticipated to contain monolithic lattices.¹⁰¹ A conventional selected-area aperture is far too large to permit such granular spatial subsampling. Thanks to cryogenic conditions, 4DSTEM has also proved compatible with a range of beam-sensitive materials,¹⁰³ and stepwise rotation of the TEM stage has allowed for tomographic data collection amenable to 3D structure determination. In sum, this approach permits ex post facto extraction and summation of diffraction signal from arbitrary regions of a 4DSTEM scan. These slices can subsequently be assembled into a more conventional tilt series comprehensible to standard data processing pipelines.

4. Data Processing

4.1. Data Reduction

Prior to the widespread adoption of continuous rotation, 3D ED data processing was nontrivial and somewhat opaque to the nonspecialist; it was typically handled by a suite of dedicated programs^104−107 developed by a coterie of seasoned electron crystallographers. Continuous-rotation 3D ED, however, is directly analogous to rotation of a mounted crystal on an X-ray diffractometer equipped with a single-axis goniometer. As a result, 3D ED data collected in this way can undergo indexing, integration, merging, and scaling routines implemented in several software packages originally written for X-ray crystallography. With minimal modification, well-established programs such as iMosflm,¹⁰⁸ DIALS,¹⁰⁹ and XDS¹¹⁰ have all been successfully applied to continuous-rotation 3D ED data reduction. Detailed tutorials (such as for DIALS¹¹¹ and XDS⁶⁵) easily comprehensible to any practicing X-ray crystallographer have subsequently appeared in the literature. Likewise, current processing pipelines for serial diffraction (such as crystFEL¹¹²) have also been ported to ED data.¹¹³ Indexed lists of integrated intensities generated by these programs can directly serve as input for phasing algorithms.

4.2. Phasing by Direct Methods

It is a truth universally acknowledged that any diffraction experiment must overcome the phase problem, and ED is no exception. Since its initial demonstration by Dorset and Hauptman in 1976,⁴⁶ab initio phasing has been successfully deployed on virtually all small-molecule substrates solved by 3D ED. If Sheldrick’s criterion^114,115 is met (i.e., if the illuminated crystal diffracts to at least ∼1.2 Å resolution and completeness in the outermost 1.2–1.1 Å shell exceeds 50%) or exceeded, direct methods (DM) has proved a robust and reliable means of phasing ED data. As in X-ray diffraction, the presence of (a) centrosymmetry, (b) sparsely populated unit cells, and (c) heavy atoms often permits some relaxation of Sheldrick’s criterion (which is simply a conservative empirical estimate). Prior to the advent of automated software, venerable statistical approaches such as the Sayre equation and the tangent formula were applied manually, phase-by-phase. Today, widely used programs such as SHELXT¹¹⁶ and SHELXD¹¹⁷ have also found routine utility in ED data processing.

As currently implemented, DM algorithms generally hinge on two key constraints: atomicity and positivity. Because X-ray scattering amplitudes for all atoms remain non-negative regardless of resolution, positivity is a clearly justified postulate in X-ray crystallography. Indeed, the periodic electron density function recapitulated from X-ray diffraction is universally positive. An intriguing phenomenon intrinsic to ED, however, is that electron scattering amplitudes for negatively charged ions dip well below zero at low resolution, analogous to the negative scattering lengths exhibited by elements like H or Li in neutron diffraction. Consequently, in ED, anionic species can legally contribute negative density to electrostatic potential maps, a nuance to which ab initio phasing intended for X-ray diffraction is currently blind. As discussed in detail by Altomare et al., violation of the positivity postulate is expected to alter the triplet phase invariant relationships traditionally exploited by direct methods.¹¹⁸ Evidence from difference Fourier maps indicates that this limitation may have contributed to erroneous assignment of charged moieties (such as deprotonated carboxylates) as neutral atoms.^119−121

Nevertheless, ab initio phasing by DM remains the gold standard in 3D ED, and the diverse array of structures determined by this approach has played a pivotal role in dispelling doomsday predictions about multiple scattering. Ab initio phasing has proved remarkably successful even on 3D ED data recorded from crystals hundreds of nanometers thick, despite multislice simulations¹²² suggesting a much lower thickness threshold for purportedly irreversible dynamical corruption. This yawning chasm between theory and experiment is fueled by many factors, such as complex mosaicity at the nanoscale,¹⁰¹ unmodeled inelastic scattering,¹²³ and the now-widespread usage of off-zone data collection. DM continues to face a stiff, often insurmountable challenge from macromolecular crystals containing >50% disordered solvent, which generally fail to diffract to atomic resolution. For lower-quality diffraction data extracted from small molecules, phasing by simulated annealing¹²⁴ has also proved a useful approach in 3D ED, often in conjunction with DM.^125,126

4.3. Phasing by Molecular Replacement

Intrinsic disorder often prevents macromolecular crystals from diffracting to a resolution sufficiently high for direct methods. In such cases, if a search model with adequate sequence homology (generally at least 25%) is available, molecular replacement (MR) is a tried-and-tested means of phasing 3D ED data. Programs such as Phaser¹²⁷ and MOLREP¹²⁸ have been applied relatively seamlessly to ED; almost all protein structures solved by 3D ED have been phased via MR using an existing X-ray structure as a template. A substantial fraction originates from studies demonstrating new methodological approaches to 3D ED; this has resulted in well-studied proteins typically used as standards in X-ray crystallography (especially proteinase K, lysozyme, and catalase), accounting for over 40% of macromolecular ED structures deposited in the PDB. Comparatively few de novo structures have been determined by MR; currently, these remain limited to a handful of oligopeptides (with a maximum sequence length of 11 residues; see Table 2) and a single novel protein, R2lox¹²⁹ (which was later supplanted by a higher-quality X-ray structure¹³⁰).

Table 2. List of Amyloid or Amyloid-adjacent 3D ED Structures Deposited in the PDB as of October 2021, Excluding Duplicates^a.

parent protein	amino acid sequence	PDBaccession code	phasing method	resolution (Å)	space group	Rwork/Rfree	ref
α-synuclein (68–78)	GAVVTGVTAVA	4RIL	MR	1.4	C2	0.248/0.275	(186)
α-synuclein (47–56)	GVVHGVTTVA	4ZNN	MR	1.4	P21	0.235/0.282	(186)
human islet amyloid polypeptide (19–29, S20G)	SGNNFGAILSS	5KNZ	MR	1.9	P212121	0.228/0.275	(188)
human islet amyloid polypeptide (15–25)	FLVHSSNNFGA	5KO0	MR	1.4	P1	0.225/0.259	(188)
Sup35 (8–13)	Zn-NNQQNY	5K2E	DM	1.0	P21	0.152/0.194	(187)
Sup35 (8–13)	Cd-NNQQNY	5K2F	DM	1.0	P21	0.220/0.241	(187)
Sup35 (7–13)	GNNQQNY	5K2G	DM	1.1	P21	0.187/0.224	(187)
Sup35 (7–13)	GNNQQNY	5K2H	DM	1.05	P212121	0.177/0.186	(187)
Tau (306–311)	VQIVYK	5K7N	DM	1.1	C2	0.210/0.223	(64)
Tau (591–600)	KVQIINKKLD	5V5B	MR	1.5	P21	0.190/0.213	(189)
Tau (592–597)	VQIINK	5V5C	MR	1.25	P21212	0.219/0.266	(189)
Tau (305–310)	SVQIVY	6ODG	DM	1.0	P21	0.245/0.266	(190)
TDP-43 (333–343)	SWGMMGMLASQ	6CFH	MR	1.5	P1	0.280/0.313	(192)
TDP-43 (312–317, A315pT)	NFGpTFS	6CF4	DM	0.75	P212121	0.232/0.251	(192)
TDP-43 (312–317, A315E)	NFGEFS	5WKB	DM	1.0	P21212	0.220/0.270	(192)
TDP-43 (247–257)	DLIIKGISVHI	5W52	MR	1.4	P1	0.262/0.306	(191)
bank vole prion protein (168–176)	QYNNQNNFV	6AXZ	DM	0.75	P1	0.242/0.246	(165)
human prion protein (169–175)	GSNQNNF	6CLC	DM	1.01	P1	0.159/0.178	(261)
InaZ (707–712)	rac-GSTSTA	6M9J	DM	0.9	P21/c	0.233/0.252	(193)
InaZ (707–712)	GSTSTA	6M9I	DM	0.9	P212121	0.217/0.232	(193)
Nup98 (116–123)	GFGNFGTS	6BZM	DM	0.9	P1	0.226/0.264	(183)
amyloid-β (20–34, D23iD)	FAEiDVGSNKGAIIGL	6NB9	DM	1.05	P21	0.198/0.246	(195)
amyloid-β (20–34)	FAEDVGSNKGAIIGL	6OIZ	DM	1.1	P21	0.194/0.213	(195)
amyloid-β (24–34)	VGSNKGAIIGL	5VOS	MR	1.42	P21	0.234/0.292	(273)
heterogeneous nuclear ribonucleoprotein A1 (209–217)	GFGGNDNFG	6J60	DM	0.96	P212121	0.233/0.248	(196)
fused in sarcoma (77–82)	STGGYG	6BZP	DM	1.1	P212121	0.219/0.255	(183)
fused in sarcoma (37–42)	SYSGYS	5XSG	DM	0.73	P21	0.261/0.289	(197)
fused in sarcoma (37–42)	SYSGYS	6KJ1	DM	0.65	P21	0.229/0.240	(198)
fused in sarcoma (37–42)	SYSGYS	6KJ3	DM	0.6	P21	0.307/0.326	(198)
Tau (591–599)	KVQIINKKL	6NK4	MR	1.99	P61	0.260/0.299	(274)
amyloid-β (16–26, D23N)	KLVFFAENVGS	6O4J	MR	1.4	P21	0.237/0.283	(194)
OsPYL/RCAR5 (24–29)	AVAAGA	6UOR	DM	0.9	P212121	0.206/0.240	(102)

^aAbbreviations used: MR = molecular replacement, DM = direct methods, pT = phosphorylated l-threonine, rac = racemic, iD = l-isoaspartic acid.

If existing models prove insufficient for MR and >1.2 Å resolution nullifies DM, fragment-based phasing (FBP) has emerged as a potential alternative enabling structure determination. As implemented in the ARCIMBOLDO suite of programs, this approach mines focused fragment libraries derived from distant homologues or idealized elements of secondary structure (such as polyalanine α-helices). Iterative omission or placement of these fragments into a nascent structure solution allows for assessment of their respective phasing power. Ultimately, structures phased by this method fall conceptually closer to MR than to DM, although not quite as phase-biased as MR from a unitary model. Originally demonstrated on a variety of X-ray data sets by Usón and co-workers,^131,132 FBP has recently been extended to a few ED cases where MR and DM had collectively proved ineffective,^102,133 in addition to a proof-of-concept FBP structure of proteinase K.¹³⁴ Interestingly, FBP appears uniquely suited to probe smaller species with less predictable folds, including polymorphic amyloid oligopeptides.¹³³ Like MR, FBP is also theoretically compatible with fragments harvested from computationally generated models (i.e., AlphaFold¹³⁵ or RoseTTAFold¹³⁶ for proteins, or DFT for small molecules), removing the need for an experimentally determined template.

5. Structure Refinement

5.1. Theoretical Background

3D ED recapitulates a three-dimensional map of electrostatic potential derived from interaction between the incident electron beam and the substrate under interrogation. Refinement of ESP maps is carried out by programs such as Phenix,¹³⁷ REFMAC,¹³⁸ and SHELXL,¹³⁹ which attempt to iteratively minimize the discrepancy between theoretically calculated (F_calc) and experimentally observed (F_obs) structure factors in reciprocal space. Ultimately, the agreement between F_calc and F_obs is encapsulated in a residual or R-factor, which is defined as

and is generally reported as a universal validation metric to assess map quality. Computation of F_calc hinges on approximations of constituent atoms in terms of their parametrized electron scattering factors:

where f_j(s) is the individual electron scattering factor for the j^th atom, h, k, and l correspond to the Miller indices, and x, y, and z give the fractional coordinates of the jth atom in real space. Just like XRD, each atomic scattering factor is treated as a sum of Gaussians, given the computational tractability of calculating Fourier transforms on Gaussian functions. These take the general form

where j = 4 or 5 and a_j and b_j represent arbitrary fitting coefficients. Some approximations also add a scalar constant

which can augment the accuracy of the Gaussian fit. Specifically for ionic electron scattering factors, a divergent charge-correction term is historically used

where ΔZ = Z – Z₀ and therefore represents excess nuclear charge.²⁰ The above equation yields a very accurate fit for ionic electron scattering factors. Unfortunately, because of the resultant singularity at s = 0, inclusion of a divergent charge-correction term is incompatible with widely used refinement programs, rendering such parametrizations unusable for routine analysis of continuous-rotation 3D ED data. This dearth has forced groups interested in the process of refining charged species to compute their own parametrizations.¹⁴⁰ As a resource for the community, we have developed a publicly accessible web server, factors of atomic electron scattering (FAES, https://srv.mbi.ucla.edu/faes), which returns refinement-friendly parametrizations of all electron scattering factors currently tabulated in the International Tables for Crystallography, as well as fractionally charged scattering factors computed via linearly weighted combinations of integer parents. We also harness FAES’ 5 Gaussian parametrization to derive elastic and estimated inelastic cross-sections for all neutral elements.

A survey of published 3D ED structures, encompassing oligopeptides (Table 2), small molecules (Table 3), and proteins (Table 4) reveals average refinement residuals in the ∼20–30% range, markedly greater than values typically observed in XRD (Figure 7). To a certain extent, however, this gap is cosmetic. In many cases, structures generated by 3D ED have yielded stubbornly inflated refinement R-factors despite featuring no errors in atomic assignment or placement. Additional validation of these ESP maps is provided by all-atom RMSD analyses relative to known X-ray structures, which often compare very favorably. Especially if initial data reduction statistics (such as R_meas, ⟨I/σ(I)⟩, and CC_1/2) appear well-behaved, elevated refinement R-factors may partially reflect systematic inaccuracies in computation of F_calc rather than deficiencies in the atomic model itself. For instance, although 3D ED modalities such as continuous rotation and precession minimize the effects of multiple elastic scattering, dynamical diffraction can still distort structure-factor amplitudes. Conventional refinement procedures (in programs originally written for X-ray diffraction) neglect this and simply assume singular elastic scattering. To rectify this oversight, a series of studies by Palatinus and co-workers has formulated a refinement approach which incorporates dynamical diffraction theory into calculation of model structure factors.^107,141,142 As implemented in Jana2006, this procedure has diminished refinement R-factors for 3D ED data and seemingly enhanced the ability to detect granular details such as H atoms in Fourier difference maps.¹⁴³ Nevertheless, dynamical refinement is not yet a routine procedure, partially because its computational expense renders it currently unsuitable for larger systems like macromolecules. Alternative approaches involve application of various correction factors to measured intensities,^140,144 including off-label use of a primary extinction parameter originally intended for X-ray diffraction.¹⁴⁵ These methods may help compensate for lingering dynamical effects.

Table 4. List of Macromolecular 3D ED Structures Deposited in the PDB as of October 2021^a.

protein	sequence length	PDB accession code	phasing method	resolution (Å)	space group	Rwork/Rfree	ref
HEWL (tetragonal polymorph)	129	3J4G	MR	2.9	P43212	0.255/0.278	(37)
HEWL (tetragonal polymorph)	129	3J6K	MR	2.5	P43212	0.220/0.255	(38)
catalase	527	3J7B	MR	3.2	P212121	0.262/0.308	(90)
calcium ATPase	994	3J7T	MR	3.4	C2	0.277/0.315	(157)
HEWL (orthorhombic polymorph)	129	5A3E	MR	2.5	P212121	0.213/0.253	(38)
catalase	527	5GKN	MR	3.2	P212121	0.251/0.304	(158)
proteinase K	279	5I9S	MR	1.75	P43212	0.217/0.266	(283)
HEWL (tetragonal polymorph)	129	5K7O	MR	1.8	P43212	0.239/0.284	(64)
xylanase	190	5K7P	MR	2.3	P212121	0.230/0.267	(64)
thaumatin	207	5K7Q	MR	2.5	P41212	0.251/0.294	(64)
trypsin	223	5K7R	MR	1.7	P212121	0.248/0.281	(64)
proteinase K	279	5K7S	MR	1.6	P43212	0.224/0.255	(64)
thermolysin	316	5K7T	MR	2.5	P6122	0.290/0.310	(64)
HEWL (orthorhombic polymorph)	129	5O4W	MR	2.11	P21212	0.335/0.350	(284)
HEWL (orthorhombic polymorph)	129	5OCV	MR	2.2	P21212	0.236/0.270	(285)
TGF-β/TGF-β receptor 2 complex	103/97	5TY4	MR	2.9	P212121	0.292/0.328	(64)
proteinase K	279	6CL7	MR	1.71	P43212	0.221/0.253	(261)
NaK ion channel	96	6CPV	MR	2.5	I4	0.218/0.263	(286)
HEWL (tetragonal polymorph)	129	6H3V	MR	1.9	P43212	0.291/0.283	(68)
HEWL (monoclinic polymorph)	129	6HU5	MR	2.8	P21	0.297/0.339	(287)
catalase (energy-filtered)	527	6JNT	MR	3.0	P212121	0.251/0.283	(170)
catalase (energy-filtered)	527	6JNU	MR	3.0	P212121	0.207/0.251	(170)
thiostrepton	19	6MXF	MR	1.91	P43212	0.190/0.218	(200)
CTD-SP1 fragment of HIV-1 Gag	110	6N3J	MR	3.0	C2	0.254/0.292	(250)
proteinase K (FIB-milled)	279	6N4U	MR	2.75	P43212	0.238/0.263	(70)
R2-like ligand-binding oxidase (R2lox)	328	6QRZ	MR	3.0	P21212	0.318/0.335	(129)
proteinase K	279	6V8R	FBP	1.6	P43212	0.195/0.232	(134)
acetazolamide-bound human carbonic anhydrase II	260	6YMA	MR	2.5	P21	0.224/0.255	(249)
human carbonic anhydrase II	260	6YMB	MR	2.5	P21	0.249/0.276	(249)
granulovirus occlusion body	248	6S2O	MR	1.55	I23	0.171/0.197	(99)
HEWL (tetragonal polymorph)	129	6S2N	MR	1.8	P43212	0.272/0.316	(99)
catalase	527	7DI8	MR	3.2	P212121	0.309/0.348	(288)
thermolysin	316	6ZHJ	MR	3.26	P6122	0.210/0.292	(140)
thaumatin	207	6ZHN	MR	2.76	P41212	0.280/0.321	(140)
voltage-dependent anion-selective channel protein 1	295	7KUH	MR	3.12	C2	0.257/0.287	(289)
bovine insulin	21/30	6ZHB	MR	3.25	H3	0.181/0.319	(140)
myeloid differentiation primary response 88	151	7BEQ	MR	3.0	C2	0.223/0.280	(290)
proteinase K (LCP)	279	6PQ0	MR	2.0	P43212	0.217/0.267	(291)
proteinase K (LCP)	279	6PQ4	MR	2.0	P43212	0.244/0.282	(291)
CypA	165	6U5G	MR	2.5	P212121	0.185/0.224	(292)
human adenosine receptor	447	7RM5	MR	2.79	C2221	0.248/0.288	(248)
vancomycin (triclinic polymorph)	7	7C4V	MR	1.05	P1	0.232/0.268	(293)
vancomycin (orthorhombic polymorph)	7	7C4U	MR	1.2	P22121	0.202/0.216	(293)
granulovirus occlusion body	248	6YNG	MR	2.83	I23	0.184/0.226	(99)
proteinase K	279	6ZEV	MR	2.4	P43212	0.200/0.243	(295)
proteinase K	279	6ZET	MR	2.7	P43212	0.225/0.268	(295)
proteinase K	279	6ZEU	MR	2.0	P43212	0.199/0.234	(295)

^aVancomycin and thiostrepton, although more akin to small molecules, are categorized here because of their presence in the PDB.

Figure 7.

Circles represent the mean resolution and refinement R-factor (R1 for small molecules, R_work for peptides and proteins) for each category of substrate, whereas error bars signify one standard deviation in each direction. Data were taken from Tables 2, 3, and 4.

Another potential source of error lies in f_e(s) itself. Inverse Fourier transforms of conventional electron scattering factors ultimately yield spherical, isotropic distributions capable of accommodating a Gaussian model. This is emblematic of electrostatic potential projected by an isolated atom. In real systems, however, ESP almost always experiences perturbations due to environmental effects. Specifically, low-angle scattering is especially sensitive to the redistribution of valence electrons which accompanies ionization or chemical bonding. Isolated scattering factors disregard these effects. Chang et al. analyzed this issue by conducting Hartree–Fock molecular orbital calculations at the 6-31G* level of theory, which they then transformed into substrate-specific molecular electron scattering factors.¹⁴⁶ Yamashita and Kidera developed a similar treatment using the hybrid functional B3LYP, decomposing output from DFT into parametrized, atom-specific contributions.¹⁴⁷ Both investigations concluded that ESP is represented more accurately by aspherical, anisotropic scattering factors, particularly at low spatial frequencies. However, neither of these approaches has since been applied in a generalizable or user-friendly fashion to experimental 3D ED data sets. More recent work by Dominiak and co-workers^148,149 has focused on refining 3D ED data against aspherical ESP produced by applying the Mott–Bethe formula to multipolar electron density distributions tabulated in databases such as ELMAM2.¹⁵⁰ Nonetheless, this method ultimately led only to an incremental (1–2%) improvement in refinement R-factors, suggesting that the isolated atom model (although imperfect) is fairly accurate for neutral atoms, particularly at high resolution. For charged species, however, isolated electron scattering factors’ sharp divergence to infinity is likely a significant exaggeration of ionic ESP in crystal structures, where excess charge is either balanced by the presence of proximal counterions or diluted by noncovalent interactions such as hydrogen bonding. To indirectly account for this, it is helpful to introduce fractionally charged scattering factors, which can provide a proxy for modeling effective, partial, or delocalized charge.

5.2. Charged Species

Historically, several 2D electron crystallographic studies had already demonstrated that ionic electron scattering factors’ divergent behavior as s → 0 renders ED uniquely capable of differentiating neutral atoms and ionized states. Grigorieff et al. observed effects consistent with negative charge in their 3.5 Å 2D ED structure of bacteriorhodopsin, where they visualized weakly resolved electrostatic potential enveloping the carboxylate termini of aspartate and glutamate side chains.¹⁵¹ Similar findings were reported by Fujiyoshi and co-workers, who recorded systematically absent ESP for several putatively deprotonated aspartate and glutamate residues in bacteriorhodopsin at 3.0 Å.¹⁵² These artifacts materialized most prominently in low-resolution shells, where ionic electron scattering amplitudes diverge strikingly from their neutral counterparts. Kimura et al. provided a compelling validation of theory by calculating experimental ESP maps omitting low-resolution reflections, which regenerated positive density around ionized carboxylates.¹⁵³ Intriguingly, Fujiyoshi and co-workers also visualized negative peaks on backbone carbonyl O atoms in Fourier difference maps computed assuming neutral electron scattering factors, suggesting experimentally observable partial charge even on formally neutral moieties. Indeed, Fujiyoshi and co-workers obtained slightly diminished refinement R-factors by assigning fractional charges of +0.5 and −0.5 to carbonyl C and O atoms, respectively. Later work by Hirai et al. further validated a range of these observations via computational simulations of charged states.¹⁵⁴ In addition to these extensive studies on proteins, ionic ESP has also been analyzed quantitatively in inorganic salts, where bonding features far less covalent character.^155,156

A string of investigations by Yonekura and co-workers has propelled the study of ionized states into 3D ED territory.^157−159 Their results have largely reproduced the effects previously observed by their 2D predecessors: anions contribute negative density to ESP maps, whereas cations lead to modest enhancements in scattering power. In parallel, Wang has catalogued a variety of artifacts in ESP maps which may indicate the presence of deprotonated carboxylates incorrectly modeled as neutral oxygen atoms.¹¹⁹ Specifically, several experimental 3D ED structures feature (a) strong negative peaks localized on carboxylate O atoms in Fourier difference maps calculated presuming neutral electron scattering factors, (b) weak or nonexistent density enveloping these O atoms in experimental ESP maps, and (c) aberrantly high, physically absurd B-factors associated with the offending atoms. Ions mistreated in this way would also increase refinement R-factors. Yonekura and co-workers managed to mitigate this via implementation of fractionally charged scattering factors.¹⁵⁸ Collectively, these studies underscore the necessity of integrating treatment of charged states as a routine facet of 3D ED analysis. Although this has been thwarted by the nonexistence of appropriately parametrized scattering factors, we hope tools like FAES and the ScatCurve package¹⁵⁸ developed by Yonekura and Maki-Yonekura clear a path toward refinement of ionic species in 3D ED data.

Finally, a currently underexplored strategy to unequivocally validate differences resulting from charge is joint refinement¹⁶⁰ of 3D ED structures alongside corroborating X-ray diffraction data. Because electron density in X-ray structures is universally positive and comparatively insensitive to charge, ESP from 3D ED could potentially convey complementary information about ionized states. Furthermore, 3D ED usually suffers from relatively low completeness; this is easily rectified by addition of X-ray data, which is typically highly redundant and much more complete. More uncharted territory is also provided by the prospect of joint refinement with neutron diffraction, which could serve as a useful cross-validation metric for localization of hydrogen atoms.^161,162 For instance, 3D ED has already demonstrated its potential to elucidate structures of transition-metal hydrides,¹⁶³ a family of organometallic complexes which has historically relied on single-crystal neutron diffraction for solid-state detection of H atoms.¹⁶⁴ Although the hydride ligand carries a formal negative charge, many species classified as “hydrides” nevertheless display acidic properties. 3D ED offers the tantalizing possibility of evaluating hydridic character via analysis of ionic ESP, whereas neutron diffraction can easily corroborate spatial positions of H atoms. Interestingly, however, bond lengths involving H atoms will likely prove slightly inconsistent between ED, XRD, and neutron diffraction, as these three forms of incident quanta all interact with hydrogen in appreciably different ways. Incident electrons experience perturbation due to both positively charged nuclei and atomic charge density projected by the electron cloud, placing them in between the two extremes of X-rays (which interact solely with the cloud) and neutrons (which interact solely with atomic nuclei). Such variability has already been noted in a 0.75 Å ED structure of a prion protofibril,¹⁶⁵ as well as a 1.22 Å single-particle cryo-EM structure of apoferritin.¹⁶⁶ In both of these cases, individual H atoms in Fourier difference maps appeared consistently different from their putative X-ray positions, indicating observable deviation from the idealized geometry of the riding model. Joint refinement would allow for a detailed analysis of such discrepancies.

5.3. Energy Filtration

Every practical aspect of crystallography is substantially influenced by the energy of the incident quanta. Thanks to the energy–time uncertainty principle, a perfectly coherent beam is forbidden by quantum mechanics, and the incident energy of the impinging electrons is properly described as a statistical distribution (with a full-width half-maximum of ΔE) in lieu of a discrete value E.¹⁶⁷ Typical TEM instruments suitable for 3D ED employ either field-emission guns (FEGs) or thermionic cathodes (containing tungsten hairpin filaments or lanthanum hexaboride crystals) as electron sources, all of which feature their own characteristic ΔE ranges. FEGs generate an especially coherent beam, with an energy spread ΔE of < 0.7 eV; W filaments and LaB₆ crystals exhibit less monochromatic ΔE values of 1.5–3 and 1–2 eV, respectively.¹⁶⁷ Nevertheless, 3D ED structures have been routinely solved using instruments employing all three sources, which compare favorably to the monochromaticity obtained using an in-house X-ray diffractometer. In HRTEM imaging, ΔE has direct experimental repercussions; in reciprocal space, its influence on phase contrast is captured by a damped envelope function which delineates the maximum achievable resolution for an image. Such chromatic aberration (resulting from inherent fluctuations in energy within the incident beam) is also reflected in measured diffraction patterns, albeit more indirectly; it effectively causes the surface of the Ewald sphere to thicken. However, its influence on diffraction is not quite as consequential as its impact on imaging. Indeed, ΔE is quite small compared to the energy dispersion induced by the complex set of elastic and inelastic scattering events arising from the beam impinging upon an illuminated crystal.

In this context, postspecimen energy filtration (achieved, for example, via installation of a postcolumn filter) is an impactful and currently underutilized strategy in 3D ED. Energy filtration allows selective exclusion of any scattered electrons which suffered some degree of energy loss (resolved, for instance, within fixed-width windows of 10, 50, or 100 eV). Theoretically, diffraction signal is contributed largely by elastically scattered quanta residing within or very near the zero-loss peak, whereas inelastically scattered electrons mostly generate diffuse noise. Zero-loss energy filtration purges any evidence of inelastic scattering events polluting regions of reciprocal space proximal to Bragg reflections. Consequently, it significantly augments the accuracy of integrated intensities.¹⁶⁸

This phenomenon is especially well-illustrated by filtration of diffraction recorded from thick, frozen-hydrated specimens. In these systems, a substantial fraction of scattering signal is contributed by amorphous solvent and vitreous ice. For instance, in protein crystals, unfiltered ED patterns often feature a dense halo of low-frequency noise protruding radially from the central beam. By using an in-column energy filter, Yonekura and co-workers demonstrated that much of this detrimental noise is easily eliminated; energy filtration (with a slit width of 10 eV relative to the zero-loss peak) resulted in a pronounced enhancement in signal-to-noise for all reflections.^168−170 Furthermore, removal of inelastically scattered electrons disinterred a range of low-resolution reflections previously occluded by the diffuse penumbra emanating from the central beam (a dramatic illustration is provided by Figure 4 in ref (170)). Because Bragg peaks at mid-to-low spatial frequencies encipher crucial information about scattering differences between elements (as well as distinctions between neutral atoms and charged states), unveiling these reflections could have deeper consequences beyond more accurate integration of intensities. For instance, in addition to enabling proper refinement of ionized species, accentuation of scattering differences could potentially facilitate experimental phasing by multiple isomorphous replacement (MIR). Because discrepancies between elements become comparatively muted in ED versus XRD, MIR has been proposed¹⁷¹ but never convincingly demonstrated in ED. Presumably the likelihood of reliably detecting these discrepancies would grow if energy filtration enabled facile detection and integration of low-resolution reflections. Similar logic also applies to radiation-induced phasing.¹⁷²

Intriguingly, inelastically scattered electrons which undergo relatively small energy losses can also end up within the vicinity of Bragg peaks. In fact, unfiltered Bragg reflections really represent a coalescence of signal from singular and multiple elastic scattering in tandem with a non-negligible fraction of inelastic scattering events. By removing any contributions from inelastic collisions, zero-loss energy filtration would in principle provide a more accurate measurement of multiple elastic scattering.¹²³ Dynamical refinement would presumably profit considerably from this. Although dynamical refinement explicitly seeks to treat effects arising from multiple elastic scattering, it is currently challenged by the prospect of accurately accounting for inelastically scattered electrons also contributing to individual integrated intensities. Finally, despite yielding cleaner diffraction patterns, energy filtration’s extraction of inelastically scattered signal comes at the expense of attenuating the intensities of weak, high-resolution reflections. This tradeoff indicates that the net impact of energy filtration on 3D ED is likely to be nuanced, and future investigations would benefit from a systematic comparison of data reduction and refinement statistics against filter slit width.

5.4. Absolute Structure and Absolute Configuration

An especially impactful aspect of X-ray crystallography is its ability to routinely determine the absolute configuration of individual stereocenters in chiral molecules.¹⁷³ X-ray diffraction’s sensitivity to chirality is conferred by anomalous dispersion, a resonant scattering effect which leads to enantiospecific violation of Friedel’s law.¹⁷⁴ Analogously, in electron diffraction, a similar breakdown of Friedel symmetry is caused by multiple elastic scattering.^29,30 Recent work by Brázda et al. has shown that this discrepancy is detectable using dynamical refinement, which permits discrimination between enantiomers via an R-factor comparison against the inverted structure.¹⁷⁵ This approach derives its sensitivity to chirality from an incorporation of dynamical effects into computation of F_calc (distinguishing it from a standard kinematical refinement, where enantiomorphic crystals would yield identical distributions of calculated structure factors and therefore identical R-values). Initially, however, this type of procedure may appear somewhat counterintuitive, as methodological developments in 3D ED have followed a trajectory specifically intended to diminish the effects of multiple scattering. For instance, electron diffraction patterns collected via continuous rotation have proven generally devoid of dramatic dynamical artifacts. Today’s status quo is a far cry from historical work, where aberrations such as violation of systematic absences were both very strong and routinely observed.¹⁴ To quote Dorset,¹⁷⁶ “certainly the existence of higher voltage sources than used in pioneering work allows the quasi-kinematical approximation to be satisfied for samples that would have caused problems” in the past. In this context, it remains somewhat unclear exactly how much dynamical diffraction is (a) quantifiably present in 3D ED patterns and (b) strictly necessary to reliably detect disruption of Friedel symmetry and confidently assign absolute structure.

To further develop the analogy to conventional X-ray crystallography, XRD’s capacity to detect absolute chirality is directly tethered to the strength of the observed anomalous signal. As a result, X-ray methods did not always yield a reliable readout of absolute chirality in systems where resonant scattering was inherently weak, such as organic compounds composed entirely of lighter atoms. These cases necessitated the development of alternative statistical approaches with heightened sensitivity to differences in Bijvoet pair intensity, such as the Bayesian methods outlined by Hooft and co-workers.¹⁷⁷ In 3D ED, a rigorous examination of dynamical scattering’s sensitivity to several similarly intertwined variables is currently lacking. For instance, parameters such as accelerating voltage, elemental composition, defects or imperfections in lattice structure, and variable thicknesses across data sets merged from several crystals would all systematically alter the probability of multiple elastic scattering. In cases where nanocrystals have been milled to thicknesses at or below the elastic mean free path of the material, dynamical scattering is expected to be weak or unobservable. Nevertheless, the outlook for 3D ED appears promising, as recent work by Klar et al. has extended the scope of dynamical refinement to a wide range of data sets collected using continuous rotation.¹⁷⁸ An encouraging experiment reported by Klar et al. involves a double-blind comparison against analogous X-ray data collected on a chiral zeolite. In this case, dynamical refinement on 3D ED data returned internally consistent results with an independent assessment of absolute structure made via the Flack parameter. Remaining challenges include implementation in a realistic case where absolute chirality is genuinely unknown, such as a crystalline sample obtained from a synthetic mixture with poor enantiomeric excess. Intriguingly, simulations by Spence and Donatelli have suggested that retrieval of chirality via exploitation of dynamical effects is thwarted both by very low thicknesses and by very high thicknesses.¹⁷⁹ A detailed experimental investigation of the conditions under which this approach is expected to falter is still required. Regardless, in the absence of appreciable dynamical signal, 3D ED remains perfectly capable of inferring stereochemistry relative to an internal chiral reference, such as another stereocenter whose absolute configuration is known a priori. One viable strategy to achieve this involves cocrystallization with enantiopure additives.¹⁸⁰

6. Applications

6.1. Amyloids and LARKS

Continuous-rotation 3D ED has emerged as a highly useful tool for studying the atomic structure of amyloid-forming peptides. A wide range of proteins can access the amyloid state, which is marked by dense fibrillar aggregates of interdigitated β-sheets cross-linked by hydrogen bonds.^181,182 Accumulation of these aggregates is implicated in several fatal diseases, such as transmissible spongiform encephalopathy, Alzheimer’s disease, Parkinson’s disease, and Huntington’s chorea. Amyloid fibrils exhibit a characteristic left-handed helical twist arising from their cross-β-sheet architecture. This makes it difficult for amyloidogenic proteins to crystallize in the fibrillar state because the translational symmetry imposed by the Bravais lattice forcibly restricts their ability to twist.¹⁸² Usually, the ensuing buildup of lattice strain prohibits the growth of X-ray-scale crystals. An analogous set of circumstances is presented by intrinsically disordered proteins (IDPs) containing low-complexity aromatic-rich kinked segments (LARKS), which often congeal into semisolid hydrogels.¹⁸³ These species also exhibit amyloid-like cross-β-sheet morphology, although fibrils formed by LARKS appear more susceptible to chemically induced denaturation than their amyloid counterparts.

In 2001, Eisenberg and co-workers discovered that short oligopeptide fragments (4–7 residues) of amyloidogenic proteins do form microcrystals amenable to synchrotron X-ray diffraction at microfocus beamlines.^184,185 Nevertheless, these peptides’ propensity to crystallize tended to diminish with increasing sequence length, and a number of species continued to stubbornly resist X-ray-scale crystallization. These circumstances prompted a prescient attempt at electron diffraction of nanocrystalline GNNQQNY, a seven-residue peptide from the yeast prion protein Sup35.³⁴ Remarkably, GNNQQNY nanocrystals divulged clear Bragg peaks at comfortably subangstrom (∼0.7 Å) resolution, and the corresponding diffraction patterns permitted indexing of reasonable orthorhombic unit cell parameters. Despite their ultrahigh resolution, these 3D ED data were recorded as a discrete tilt series of still frames, which apparently thwarted reliable integration of diffracted intensities. In addition to prohibitively partial sampling of Bragg reflections, Diaz-Avalos et al. observed weak violations of 2₁ systematic absences, suggesting some degree of distortion by multiple scattering.

Although this initial foray into electron diffraction did not allow full structure elucidation, this study clearly foreshadowed future success, which arrived 12 years later. For nearly a decade, the 11-residue core of the amyloidogenic protein α-synuclein (termed NACore), a key component of Lewy bodies in Parkinson’s disease, had yielded only submicrometer-sized crystals invisible to optical microscopy. Despite years of extensive attempts at X-ray-scale crystallization, this species exclusively formed nanocrystals with dimensions smaller than the wavelength of visible light. In 2015, Rodriguez et al. subjected frozen-hydrated NACore nanocrystals to ED using continuous rotation, which facilitated accurate integration of intensities out to a resolution of 1.4 Å.¹⁸⁶ These data were successfully phased via molecular replacement to yield the first novel solid-state structure solved by continuous-rotation ED. Subsequent reinvestigation of GNNQQNY by Sawaya et al. once again yielded high-resolution diffraction (∼1.0–1.1 Å), this time amenable to successful structure determination via direct methods.¹⁸⁷ Notably, continuous rotation greatly minimized the presence of dynamical scattering artifacts, which failed to impede ab initio phasing.

Since these proof-of-concept studies, a slew of amyloidogenic peptide fragments, as well as a smaller subset of LARKS, has been investigated by continuous-rotation 3D ED (Table 2). These include segments derived from human islet amyloid polypeptide,¹⁸⁸ several isoforms of tau,^64,189,190 TAR DNA-binding protein 43,^191,192 bank vole prion protein,¹⁶⁵ the ice-nucleation protein InaZ,¹⁹³ amyloid-β,^194,195 heterogeneous nuclear ribonucleoprotein A1,¹⁹⁶ fused in sarcoma (FUS),^183,197,198 and nuclear pore complex protein 98.¹⁸³ Several of these reports exploited the atomic-resolution information provided by 3D ED to design small-molecule or peptide inhibitors of amyloid fibril aggregation, highlighting 3D ED’s potential to elucidate key structural details relevant to drug discovery.^188−190 Many of these amyloidogenic peptide structures ultimately tell a similar story: in addition to collectively displaying canonical amyloid-like features such as steric zippers, several refused to yield X-ray-scale crystals despite considerable effort. A fairly typical example is Guenther et al.’s 1.0 Å structure of NFGEFS (Figure 8A), which features face-to-back packing of parallel in-register sheets.¹⁹² Additionally, Gallagher-Jones et al.’s 0.75 Å structure of QYNNQNNFV unveiled a unique structural motif termed a polar clasp (Figure 8B),¹⁶⁵ whereas Warmack et al.’s 1.1 Å structure of the 15-residue peptide FAEiDVGSNKGAIIGL extended the scope of direct methods to the lengthiest sequence yet (Figure 8C).¹⁹⁵ Finally, Zhou et al.’s 0.6 Å structure of SYSGYS,¹⁹⁸ a hexapeptide derived from the low-complexity domain of FUS, is noteworthy for its unusually granular resolution, although this species has also been solved at 1.1 Å via synchrotron X-ray diffraction.¹⁸³

Figure 8.

Ab initio atomic-resolution 3D ED structures of three novel oligopeptide fragments derived from pathologically relevant proteins. Carbon atoms and the peptide backbone are rendered in blue, oxygen atoms in orange, and nitrogen atoms in purple. (A) 1.0 Å resolution structure of ³¹²NFGEFS³¹⁷ (PDB 5WKB), a hexapeptide segment from the low-complexity domain of the A315E familial mutant of TAR DNA-binding protein 43. (B) 0.75 Å resolution structure of ¹⁶⁸QYNNQNNFV¹⁷⁶ (PDB 6AXZ), a nonapeptide segment from the β2−α2 loop of the bank vole prion protein. (C) 1.1 Å resolution structure of ²⁰FAEiDVGSNKGAIIGL³⁴ (PDB 6OIZ), a 15-residue segment from wild-type amyloid-β.

6.2. Small Molecules

In 2018, the near-simultaneous release of two papers by Gruene et al.(199) and Jones et al.(200) generated an abrupt resurgence of interest in applying continuous-rotation ED techniques to small molecules.^201−203 By this point, a considerable number of small-molecule structures had already been deciphered by 3D electron crystallography (by Dorset, Abrahams, Hovmöller, Kolb, and others, in addition to an extensive body of historical work by Vainshtein). Nevertheless, these two reports transformed the landscape of 3D electron crystallography by re-exposing its potential to a nonspecialist audience. Synthetic chemists, for instance, frequently produce small quantities of seemingly amorphous powders recalcitrant to X-ray-scale crystallization. In this context, ED’s ability to extract atomic-resolution diffraction from nanocrystals is potentially liberating.

For instance, Jones et al. solved a 0.77 Å structure of synthetic (+)-limaspermidine from a few milligrams of solid residue obtained after in vacuo evaporation of eluent from flash column chromatography (Figure 9A).²⁰⁰ Furthermore, Jones et al. went on to determine four independent structures of biotin, acetaminophen, cinchonine, and brucine from a heterogeneous mixture of powders deposited on a single grid. At the bulk scale, overlapping signals from different components in this mixture would likely have prohibited clear disambiguation via X-ray powder diffraction or NMR spectroscopy. These results demonstrated how ED could function as a powerful addition to the synthetic chemist’s toolbox. Not only does ED slot conveniently into established purification workflows, often obviating any need for formal recrystallization, it also offers elusive solid-state structural information potentially inaccessible via conventional methods.

Figure 9.

ORTEP diagrams of five ab initio small-molecule 3D ED structures, with H atoms omitted. Carbon atoms are rendered in blue, nitrogen atoms in lilac, oxygen atoms in red, chlorine atoms in sea green, and copper atoms in orange. All thermal ellipsoids are drawn at 50% probability, except for compound D, which is depicted at 15% for clarity. (A) 0.77 Å resolution structure of synthetic (+)-limaspermidine (CSD: CAHKUU01), a monoterpene indole alkaloid featuring a cis-fused azadecalin core. Suitable microcrystals were obtained directly from flash column chromatography, without any formal recrystallization. (This compound did not undergo B-factor refinement, so its thermal ellipsoids do not carry any physical meaning.) (B) 0.9 Å resolution structure of the analgesic orthocetamol (CSD: WOFXEX), refined isotropically. (C) 0.8 Å resolution structure of the viridian pigment copper(II) perchlorophthalocyanine (CSD: UZEMIY), refined anisotropically. (D) 1.05 Å resolution structure of the genotoxic natural product (−)-lomaiviticin C (CSD: ERUHEH), featuring two independent molecules in the asymmetric unit. (E) 0.57 Å resolution structure of the organic semiconductor dicyanonaphthalene diimide (CSD: TUKVON), refined anisotropically. This entry represents one of the highest-resolution small-molecule structures currently solved by 3D ED.

A handful of small-molecule studies have rapidly delivered on this promise; two illustrative examples are highlighted here. Andrusenko et al. elucidated a 0.9 Å 3D ED structure of orthocetamol, a regioisomer of the antipyretic paracetamol (Figure 9B).²⁰⁴ This simple compound exhibits a bizarre morphology in which assemblies of nanocrystals coalesce into flat quadrilateral platelets up to ∼300 μm in length. To further complicate matters, these tetragonal conglomerates display high susceptibility to pseudomerohedral twinning. These characteristics had thwarted structure determination of orthocetamol by X-ray crystallography for over a century. Andrusenko et al.’s ED structure supplied an unambiguous solution to this perennial problem.

In a similar vein, Gorelik et al. solved a 0.8 Å 3D ED structure of copper(II) perchlorophthalocyanine (also known as phthalo green or viridian), a widely used synthetic pigment (Figure 9C).²⁰⁵ Phthalo green is stubbornly insoluble in a remarkably wide range of solvents, which effectively precludes X-ray-scale recrystallization. Thanks to prior investigations by Uyeda et al.(206) and Dorset,⁴⁸ ED had already established a partially complete structure of this compound. Although several subtleties remained unclear, this organometallic species had nonetheless become something of a poster child for ED, appearing on the cover of Dorset’s 1995 textbook Structural Electron Crystallography.¹⁷⁶ Gorelik et al.’s data capped off the copper(II) perchlorophthalocyanine saga by confirming earlier results with a complete 3D structure. These cases demonstrated 3D ED’s ability to resolve two longstanding quandaries in conventional X-ray crystallography with ease.

In these examples, however, the atomic connectivity of both compounds was already well-established; 3D ED simply contributed a solid-state structure that reinforced what was previously known. In this context, Kim et al.’s 1.05 Å structure of (−)-lomaiviticin C provides a compelling case where ED data spurred reevaluation of an existing structural assignment (Figure 9D).²⁰⁷ (−)-Lomaiviticin C is a genotoxic bacterial metabolite which has evaded 20 years of efforts aimed at total synthesis and X-ray-scale crystallization. Intriguingly, this natural product (NP) contains an unusual monomeric aglycon moiety in which only 6 out of 19 carbon atoms feature bonds to hydrogen. This dearth of proton-attached carbons, in tandem with a high degree of unsaturation, rendered inference of connectivity quite challenging based on NMR spectroscopy alone. Ultimately, Kim et al.’s ED structure, alongside high-field (800 MHz) NMR spectroscopic studies and DFT calculations which further substantiated the ED assignment, corrected several errors originally caused by misinterpretation of fortuitously misleading HMBC coupling constants.²⁰⁸ This study underscores ED’s vast potential to make impactful contributions to elucidation of NPs, many of which feature some combination of forbidding structural complexity, scarcely available source material, and potentially inconclusive NMR data. In a field continually grappling with the myriad pitfalls²⁰⁹ associated with analysis of complex 2D NMR spectra, the clarity provided by a corroborating crystal structure seems almost cathartic. Furthermore, when applied in tandem with comparative genomics or metabolomics (to mine relevant biosynthetic gene clusters) and synthetic biology (to express those genes in model organisms), 3D ED could also significantly accelerate the rate of NP discovery.^210−212 More broadly, 3D ED is rapidly finding a complementary niche within the wider context of synthetic chemistry; a growing number of reports now feature 3D ED structures of relevant synthetic targets or intermediates which proved unsuitable for single-crystal XRD.^213−224 These structures include two noncanonical amino acids bearing all-carbon quaternary stereocenters,²¹³ a trio of organic semiconductors solved at ultrahigh resolution (one of which is depicted in Figure 9E),⁵⁴ a family of electron-deficient expanded helicenes,²¹⁶ a pentacyclic indole-derived ester,²¹⁷ and a synthetic mimic of the cuboidal subunit in the oxygen-evolving complex of photosystem II.²²⁰

Finally, 3D ED has also tackled a bevy of small-molecule active pharmaceutical ingredients (APIs), including carbamazepine,^200,225 niacin (nicotinic acid),²²⁵ bismuth subgallate,²²⁶ ibuprofen,²⁰⁰ ethisterone,²⁰⁰ progesterone,²⁰⁰ biotin,²⁰⁰ paracetamol (acetaminophen),^143,199,200 cimetidine,²²⁷ loratadine,¹²⁵ sofosbuvir,¹⁴³ ramelteon,²²⁸ tolvaptan,²²⁸ olanzapine,²²⁹ epicorazine A,¹⁴⁴ dehydrocurvularin,¹⁴⁴ metaxalone,²³⁰ teniposide,²³¹ remdesivir,²³² and indomethacin.¹²⁶ Because many APIs exist natively as microcrystalline powders, 3D ED could potentially revolutionize solid-state structure determination in the pharmaceutical industry,^231,233 where size-limited single-crystal XRD is currently the gold standard. Specifically, 3D ED’s sensitivity to variable polymorphism at the nanoscale could provide crucial insights into API stability and solubility, as different polymorphs of the same drug can often display drastically disparate pharmacokinetic profiles.^234−237 For instance, in orally administered drugs, an API’s immediate bioavailability is controlled partially by its rate of dissolution in the gastrointestinal tract, which can vary considerably as a function of altered lattice packing. Ultimately, structural information supplied by 3D ED could play a pivotal role in guiding crystal engineering efforts²³⁸ aimed at designing solvates, cocrystals, or polymorphs of APIs with optimized pharmacokinetic properties.

Undoubtedly, 3D ED has plenty of potential in this area. Despite the considerable hype,^201−203 however, the interested synthetic chemist is confronted with several issues that warrant caution. First, electrostatic potential maps cannot always distinguish between disparate elements as unambiguously as atomic charge density maps derived from X-ray diffraction. Unlike their X-ray counterparts, elastic electron scattering factors do not scale linearly or monotonically with Z. As a result, relative differences between elements become diminished, as discussed earlier. Therefore, electrostatic potential alone does not always provide a self-sufficient means of differentiating neutral C, N, and O, particularly if the diffraction data set samples heavily within the vicinity of 3 Å resolution. Indeed, ab initio phasing algorithms frequently assign these atoms interchangeably,^199,207 particularly because they typically presume X-ray-scale scattering differences between elements. In these cases, even at the refinement stage, elemental identity can be arduous or impossible to deduce based solely on experimental difference Fourier maps. Given these limitations, if attempting to solve a challenging novel structure such as a complex natural product (generally replete with heteroatoms such as O and N) via 3D ED, rigorous corroboration with external data from NMR spectroscopy and mass spectrometry remains essential.^207,212

Second, 3D ED always requires well-formed single crystals. Serendipitously, many compounds may inhabit a specific “Goldilocks zone” where they refuse to form X-ray-scale crystals yet grudgingly aggregate into crystalline assemblies at the nanoscale. ED is well-equipped to solve structures which fit this profile. Nevertheless, ED is not a panacea; it cannot salvage genuinely amorphous substrates. Species which systematically failed to form macroscopic crystals, especially if such reluctance reflects thermodynamic instability in the crystalline state, could just as easily fail at the microscopic level. Before attempting 3D ED on seemingly amorphous material, X-ray powder diffraction (XRPD) is strongly recommended as a simple, effective test to screen for the presence of microcrystalline domains. If XRPD fails to yield clear, well-resolved rings, structure determination by ED is unlikely to succeed.

Third, ceteris paribus, current 3D ED data quality is often inferior to X-ray data quality by a range of metrics (R_meas, ⟨I/σ(I)⟩, CC_1/2), although this gap is beginning to contract quickly for small molecules. An especially relevant statistic is completeness because ED’s coverage of reciprocal space is inherently limited by the restricted tilt range available to the TEM goniometer. The resultant “missing wedge” becomes particularly problematic if the space group symmetry of the crystal is low or if orientation bias is severe. X-ray diffractometers can easily collect 360° of data, unlocking regions of the reciprocal lattice potentially inaccessible by continuous-rotation ED. Moreover, some fraction of small molecules deemed “impossible” to solve by XRD may simply indicate a lack of rigorous screening. In macromolecular crystallography, screening thousands of crystallization conditions via high-throughput hanging-drop vapor diffusion is routine. Similar methods have not yet percolated widely into small-molecule work, where venerable techniques such as slow evaporation of layered solvents usually reign supreme. Thus, molecules seemingly “uncrystallizable” for XRD may benefit considerably from a broader, more systematic exploration of crystallization conditions.²³⁹ Although ED’s lower size constraint confers a distinct advantage over XRD, high-flux microfocus beamlines can now produce tractable X-ray diffraction from microcrystals with dimensions as small as 1–10 μm.¹⁸ Whenever possible, XRD remains the technique of choice for small-molecule structure determination.²⁴⁰ Nevertheless, if X-ray-scale crystals prove impossible to obtain despite rigorous effort, ED is a powerful alternative which can match or surpass the resolution achieved by XRD. As the technique continues to mature, the development of specialized hardware engineered exclusively for ED will undoubtedly alleviate many current issues with data quality.²⁴¹

6.3. Proteins

Continuous-rotation electron diffraction was originally developed specifically for the purpose of interrogating three-dimensional macromolecular crystals.^37,89 This work traces its origins to a venerable tradition of two-dimensional electron crystallography, where amplitudes derived from 2D diffraction patterns were historically paired with phases obtained via direct Fourier transform of real-space images.^242−244 Key milestones in this field include Henderson et al.’s 3.5 Å structure of bacteriorhodopsin²⁴⁵ and Gonen et al.’s 1.9 Å structure of aquaporin,²⁴⁶ two intermembrane proteins whose biological roles naturally predispose formation of 2D crystals. In this context, continuous rotation emerged as a method to analyze proteins not innately suited to aggregating into 2D arrays. Shi et al.’s 2.9 Å structure of HEWL³⁷ represented the first protein successfully solved by 3D electron crystallography; it was rapidly followed by a suite of canonical soluble proteins well-studied by conventional X-ray methods.⁶⁴ Since these pioneering studies, however, 3D ED of proteins appears to have progressed more slowly than expected, especially when juxtaposed against the explosion of interest in small molecules. This is largely because sample preparation in macromolecular electron crystallography is typically much more laborious, and most major advances have therefore focused on methodological development in lieu of elucidating novel structures. For instance, a series of reports by Gonen and co-workers have demonstrated that continuous-rotation ED is procedurally compatible with focused ion-beam milling and in meso crystallogenesis within lipidic cubic phases (LCPs).^70,247,248 These techniques were applied in tandem to solve a 1.9 Å structure of the human A_2A adenosine receptor, marking a significant breakthrough for ED given the inherent difficulty of working with lipophilic membrane proteins.²⁴⁸ Another emphasis has been placed on soaking protein nanocrystals with solutions of pharmacologically relevant ligands to visualize their substrate-binding pockets. These efforts have culminated in a 2.5 Å structure of human carbonic anhydrase bound to the sulfonamide inhibitor acetazolamide,²⁴⁹ as well as a 3.0 Å structure of an HIV-1 Gag polyprotein fragment bound to the steroidal inhibitor bevirimat.²⁵⁰

Interestingly, when contrasted with analogous structures solved by single-crystal XRD, macromolecular crystals have historically diffracted to worse resolution by 3D ED, typically by a factor of 1.5–2. For instance, despite the considerable number of proteinase K ED structures currently deposited in the PDB, none have surpassed a resolution finer than 1.5 Å. Nevertheless, the PDB is replete with just over 100 sub-1.5 Å X-ray structures of proteinase K, including several determined to subangstrom resolution. No such discrepancy has been observed with small molecules, which routinely diffract to subangstrom resolution by both 3D ED and XRD. In fact, the average resolution of structures catalogued in Table 4 is only 2.5 Å (cf. 0.95 Å in Table 3); 2.5 Å is ultimately an underwhelming number, especially given the overrepresentation of well-diffracting crystallographic standards within the sample size. Relative to small molecules, protein crystals suffer from a couple of unique disadvantages in addition to innately higher disorder. Although signal-to-noise in ED is boosted by a greater number of repeating units, protein crystals’ larger unit cells provide an inherently lower bound on the maximum thickness permissible before inelastic scattering overpowers Bragg peaks. Furthermore, vitrification and frozen hydration remain experimental necessities, and insulating layers of amorphous ice will always contribute noise.

An illustrative example is provided by Xu et al.’s multipart investigation of an R2-like ligand-binding oxidase (a metalloenzyme originally isolated from Sulfolobus acidocaldarius).^129,130 In 2018, Xu et al. disclosed a 3.0 Å 3D ED structure of R2lox, phased by molecular replacement using a homologous X-ray structure with 35% shared sequence identity as a template. Although novel at the time, this structure nevertheless exhibited less-than-ideal completeness (62.8%, despite merging data from 21 crystals, suggesting stark orientation bias) and unusually high R_meas (56.1% overall) statistics. A subsequent reinvestigation of this species by synchrotron X-ray diffraction yielded a higher-quality 2.1 Å X-ray structure (featuring 99.4% completeness and 16.6% overall R_meas), which corrected several deficiencies in the 3D ED model. Specifically, 3D ED had omitted the presence of a fatty acid ligand bound to the enzyme’s active site, as well as an 11-residue stretch between amino acids 249 and 261. While most general aspects of the 3D ED structure proved consistent with XRD, middling resolution and low completeness conspired to limit its utility in modeling biologically relevant details. Xu et al.’s commendable decision to pursue a corroborating X-ray structure in these circumstances reflects ED’s current challenge in consistently matching XRD data quality in macromolecular crystallography.

A promising step forward has recently been contributed by Gonen and co-workers’ 0.87 Å structure of triclinic HEWL.²⁵¹ This report exploited the heightened sensitivity of a direct electron detector operating in counting mode to break the subangstrom resolution barrier for 3D electron crystallography of proteins, albeit on a well-diffracting standard. In addition to this study, a potential blueprint for macromolecular electron crystallography to overcome its current limitations is also provided by Yonekura and co-workers’ development of energy-filtered 3D ED,¹⁷⁰ as well as Bücker et al.’s serial approach to data collection.⁹⁹ These tactics could work in tandem to mitigate radiation damage and boost diffraction data quality, allowing 3D ED to deliver novel macromolecular structures on par with XRD.

6.4. Radioactive Minerals and Inorganic Compounds

Although slightly esoteric to chemists, mineralogy is a field replete with ideal samples for investigation by 3D ED. In fact, mineralogy has historically functioned as a key impetus behind research in 3D electron crystallography, dating back to Zvyagin’s studies of celadonite and muscovite.⁵¹ A detailed discussion on applications of 3D ED to mineralogy has been provided by Mugnaioli and Gemmi.³⁹ Here we would like to specifically highlight radioactive metamict minerals, which comprise a fascinating and seemingly tailor-made class of substrates for 3D ED.²⁵² Metamict systems feature an intricate lattice structure punctuated by trace impurities of radioactive elements like uranium or thorium.²⁵³ Over geologic timescales, these interstitial radionuclides undergo alpha decay, selectively destroying certain regions of the lattice from within. This process, known as metamictization, gradually results in total amorphization of crystalline order. In a compelling study, Capitani et al. used the presence of Bragg peaks in ED patterns to spatially map metamict domains in the mineral samarskite at the nanoscale.²⁵² After targeting specific submicrometer-sized zones where crystallinity seemed best preserved, Capitani et al. collected a tomographic series of still-frame ED patterns. These 0.8 Å ED data successfully yielded a solution via direct methods, providing an elusive 3D structure of metamict samarskite. Critically, at the single-crystal X-ray scale, alpha decay had rendered the bulk sample mostly amorphous, carving a unique niche for ED. In many ways, this work also echoes the more general blueprint formulated by Baybarz and co-workers at Oak Ridge National Laboratory in the 1970s.^254−256 These researchers worked primarily with inorganic salts formed by fully anthropogenic, superheavy elements like einsteinium, californium, or fermium. Synthetic Es and Fm typically decay so rapidly and destructively that formation of high-quality X-ray-scale crystals is a nonstarter; self-irradiation would likely cause lattices containing Es or Fm to collapse well before growing to X-ray size. Furthermore, synthesis of transplutonium elements is exceptionally arduous, often divulging only nanogram-scale quantities of material (which then immediately begins to decay!). Undeterred, Baybarz and co-workers exploited ED’s ability to interrogate submicrometer-sized crystals and deduced the unit cell parameters of several Es and Cf oxides from polycrystalline ED patterns recorded at 80 kV. Following a long hiatus, their torch has recently been lifted by Minor, Abergel, and co-workers.²⁵⁷ Given contemporary advances in data collection and analysis, ED appears uniquely poised to deliver 3D structures of inorganic systems containing either superheavy or primordial radionuclides, an exciting prospect.

6.5. Radiation Damage

As with any diffraction experiment, the maximum achievable signal-to-noise in 3D ED is ultimately constrained by radiation damage, which begins as soon as the crystal of interest is exposed to the impinging beam. ED leverages information about structure-factor amplitudes encoded in Bragg peaks, which result from elastic scattering of incident electrons. Because the low-angle elastic collisions contributing to Bragg peaks involve negligible (<1 eV) energy loss,²⁵⁸ they leave the crystal lattice completely intact. (At higher incident energies, elastic scattering can destructively dislocate atoms via knock-on displacement, but the likelihood of these events relative to radiolysis is negligible at TEM accelerating voltages.²⁵⁹) Conversely, inelastic scattering causes impinging electrons to deposit a significant fraction (10–100 eV) of their incident energy within the sample, damaging the structural integrity of the lattice. Second-row elements such as carbon, nitrogen, and oxygen possess inelastic electron cross-sections roughly 3× greater than their elastic counterparts (Figure 10). On a per electron basis, therefore, any crystal composed primarily of C, N, and O atoms is 3× more likely to undergo unproductive inelastic scattering.²⁶⁰ Although seemingly inauspicious, this ratio is actually superior to the corresponding fraction for X-ray diffraction; incident X-rays can inflict up to 3 orders of magnitude more collateral damage per useful elastic scattering event. (In principle, this advantage is attenuated somewhat by electrons’ propensity for multiple scattering because they interact with the substrate more frequently than X-rays.)

Figure 10.

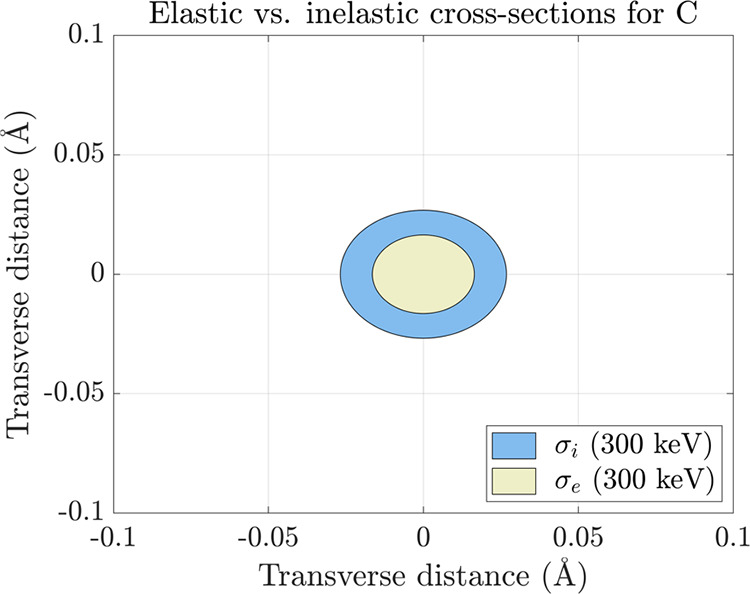
Elastic vs inelastic cross-sections for neutral carbon at 300 keV, expressed as concentric circles.

High-resolution information is especially sensitive to degradation of lattice structure. Therefore, in reciprocal space, radiation damage begins by consuming high-resolution reflections, causing Bragg peaks at the periphery of the detector to diminish in intensity until they become indistinguishable from noise. Ultimately, as crystalline order is totally destroyed, low-resolution reflections also recede into the void space of the noise floor. Statistically, this manifests as a monotonic decrease in ⟨I/σ(I)⟩ which starts in the outermost resolution shell and spreads gradually inward. In real space, radiation damage results in two major global consequences: a uniform increase in B-factors and an expansion of unit cell volume.²⁶¹ Bloated B-factors represent growing uncertainty in atomic positions, whereas unit cell volume is thought to expand due to radiolytic generation of hydrogen gas within the lattice.²⁶² A systematic study by Hattne et al. found that site-specific radiation damage inflicted upon particular functional groups largely mirrors the progression observed in X-ray diffraction.^263,264 In frozen-hydrated proteinase K, Hattne et al. observed perturbation of metal cations, elongation and lysis of disulfide bonds, and radiolytic decarboxylation of aspartate and glutamate side chains, all in quick succession. Loss of near-atomic resolution (∼2 Å) information generally occurred after a total accumulated exposure of 3 e^– Å^–2. By collecting 3D ED data at an ultralow flux density (<0.01 e^– Å^–2 s^–1), staying well below this threshold is quite feasible. Furthermore, this cutoff is substrate-specific. For instance, organometallic complexes, which frequently exhibit denser packing and lattices free of solvent channels, could potentially tolerate equivalent levels of fluence quite easily, even at ambient temperatures.¹⁶³ Nevertheless, in virtually all cases, radiation damage is significantly abated by cryogenic temperatures, which presumably stall the thermal diffusion of destructive free radicals generated by radiolysis.^265−267 Another bulwark against radical-induced decay is the presence of highly conjugated polyaromatic systems, which could facilitate delocalization of errant secondary electrons via resonance.^268−270 This effectively provides a thermodynamic sink for radicals which would otherwise propagate freely throughout the crystal lattice.

Finally, some clarification on nomenclature is warranted (Table 5). Formally, dose refers to energy absorbed per unit mass²⁷¹ (measured in units of MGy, or 10⁶ J kg^–1), whereas fluence corresponds to particles delivered per unit area (measured in units of e^– Å^–2 for electrons, or γ μm^–2 for X-ray photons). Regrettably, these two terms have become thoroughly muddled in the cryo-EM literature, where they are frequently used interchangeably. For instance, a substantial fraction of ED structures deposited in the PDB currently reports a “dose” tabulated in units of e^– Å^–2. This value is really a misrepresentation of total accumulated fluence. Although often strongly correlated, dose and fluence do not represent fungible observables, making their conflation incorrect and potentially misleading. The key distinction is that dose is a quantity specific to the substrate under interrogation. Conversely, fluence is a property of the incident beam, which is completely decoupled from the identity of the substrate. To illustrate this point, consider two identical, isomorphous protein crystals exposed to a fixed fluence: (a) one native and (b) one derivative intercalated with heavy metal cations. Because heavy metals feature significantly higher elastic-to-inelastic cross-section ratios than lighter elements such as C, N, and O, crystal B could experience a smaller proportion of inelastic scattering events than crystal A. In that case, crystal B would experience a lower dose than crystal A, notwithstanding being illuminated with the same fluence. In other words, despite being exposed to the same number of particles per unit area, crystal A’s elevated susceptibility to inelastic scattering would cause it to absorb more energy per unit mass than crystal B. In sum, different specimens exposed to an identical fluence can accumulate variable quantities of dose based on their chemical composition. Dose is a more suitable metric for assessing radiation damage than total accumulated fluence because it situates electron exposure within the specific context of the substrate itself.²⁷²

Table 5. Definitions and Typical Units for Several Terms in Dosimetry.

observable	unit (electrons)	unit (X-rays)	description
dose	MGy (106 J kg–1)	MGy (106 J kg–1)	energy absorbed per unit mass
fluence	e– Å–2	γ μm–2	particles delivered per unit area
flux	e– s–1	γ s–1	particles delivered per unit time
flux density	e– Å–2 s–1	γ μm–2 s–1	fluence delivered per unit time

7. Conclusion and Outlook

As a science born in the quantum age, crystallographic analysis has been intimately shaped by our increasingly sophisticated understanding of incident quanta. Modern transmission electron microscopy is a powerful tool capable of generating highly coherent, atomically precise beams of electrons which would have been inconceivable to pioneering researchers like Davisson and Germer. Our ability to probe the atomic structure of 3D molecular nanocrystals at subangstrom resolution is a testament to electron diffraction’s burgeoning relevance and vast potential. This Review has focused on pivotal concepts and experiments which have underpinned 3D electron crystallography’s ongoing transformation from a somewhat esoteric subfield to an area of swiftly growing importance. We conclude with forward-looking recommendations organized around two central themes: increasing transparency and expanding access.

7.1. Increasing Transparency

It has become standard operating procedure to deposit fully refined structures to databases like the CSD or the PDB, although these resources have yet to flag 3D ED data in an easily identifiable or searchable way. To ensure maximum transparency, we also recommend concurrent deposition of raw, unprocessed data (i.e., a tilt series of diffraction patterns in a file format compatible with data reduction software) on public repositories such as Zenodo. Furthermore, automated validation routines, such as those embedded in checkCIF, typically raise an array of objections when presented with 3D ED structures, some of which reflect intrinsic disparities between 3D ED and XRD rather than genuine deficiencies in the deposited models. Moving forward, establishment of ED-specific validation criteria cognizant of the various differences between 3D ED and XRD would provide a more accurate record of the quality of 3D ED structures reported in the literature.

7.2. Expanding Access

Although ED is en route to becoming a more mainstream technique, its current practitioners remain limited to a relatively small (albeit growing) handful of specialists. Transmission electron microscopy presents a steeper economic barrier to entry than X-ray crystallography; a mid- to high-end TEM optimally equipped for ED carries a hefty six-digit price tag, whereas a standard X-ray diffractometer is usually up to an order of magnitude cheaper. Retrofitting used or refurbished TEMs for ED is usually a more viable option, although still expensive. Sadly, lack of widespread access to the appropriate instrumentation can thwart researchers otherwise interested in incorporating ED into their work. Furthermore, TEM maintenance is typically carried out by trained engineers or facility managers whom many institutions may not have the financial bandwidth to hire. Systemic inequities aside, however, the conceptual learning curve for ED is comparatively gentle, especially thanks to the advent of continuous rotation. Any practicing X-ray crystallographer has already attained the requisite skillset to start solving structures from continuous-rotation 3D ED data, leaving lack of access as the main bottleneck. To rectify this, investment in a subsidized infrastructure for ED data collection at dedicated user facilities, analogous to the now well-established network of synchrotron beamlines across the globe, will prove especially critical. ED will reach its considerable potential only when the technique proliferates to more users outside its current niche.

Glossary

Abbreviations

ED

electron diffraction

3D ED

three-dimensional electron diffraction

cryo-EM

cryogenic electron microscopy

TEM

transmission electron microscopy

XRD

X-ray diffraction

XRPD

X-ray powder diffraction

ESP

electrostatic potential

MFP

mean free path

DM

direct methods

MR

molecular replacement

FBP

fragment-based phasing

FIB

focused ion beam

PED

precession electron diffraction

PEDT

precession-assisted electron diffraction tomography

ADT

automated diffraction tomography

RED

rotation electron diffraction

CCD

charge-coupled device

CMOS

complementary metal oxide semiconductor

MicroED

microcrystal electron diffraction

IEDT

integrated electron diffraction tomography

cRED

continuous-rotation electron diffraction

4DSTEM

four-dimensional scanning transmission electron microscopy

nanoEDT

nanobeam electron diffraction tomography

HRTEM

high-resolution transmission electron microscopy

MIR

multiple isomorphous replacement

DFT

density functional theory

IDP

intrinsically disordered protein

LARKS

low-complexity aromatic-rich kinked segments

HEWL

hen egg white lysozyme

FUS

fused in sarcoma

API

active pharmaceutical ingredient

LCP

lipidic cubic phase

MGy

megagrays

Biographies

Ambarneil Saha was born in Starkville, Mississippi, in 1996. After spending his more impressionable years growing up in Cupertino, California, he earned an A.B. in Chemistry from Cornell University in 2018, where he worked on electrochemical difunctionalization of alkenes with Professor Song Lin. He is currently a Ph.D. candidate and NSF fellow in the Rodríguez laboratory at UCLA.

Shervin S. Nia was born in Los Angeles, California, in 1999. He earned his B.S. in Biochemistry from UCLA in 2021. During his undergraduate career, he studied eye tracking and reaction times in virtual reality with Professor Katsushi Arisaka before joining the Rodríguez group. Currently, Shervin performs computational work creating reconstructions of cryoEM datasets to characterize elusive crystal structures.

José A. Rodríguez was born in Aguascalientes, Mexico, in 1985. He emigrated to and spent his formative years in Los Angeles, California, before earning a B.S. in Biophysics from UCLA in 2007. He has remained at UCLA ever since, subsequently obtaining a Ph.D. in Molecular Biology and postdoctoral training in bioimaging, crystallography, and biological chemistry. He is currently an associate professor of chemistry and biochemistry at UCLA (http://rodriguez.chem.ucla.edu/).

The authors declare the following competing financial interest(s): J.A.R. is a founder and equity stake holder of MEDSTRUC INC.