Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Aug 23;22(17):7049–7056. doi: 10.1021/acs.nanolett.2c01943

Small Charging Energies and g-Factor Anisotropy in PbTe Quantum Dots

Sofieke C ten Kate †,‡, Markus F Ritter †, Andreas Fuhrer †, Jason Jung §, Sander G Schellingerhout §, Erik P A M Bakkers §, Heike Riel †, Fabrizio Nichele †,*
PMCID: PMC9479220  PMID: 35998346

Abstract

graphic file with name nl2c01943_0005.jpg

PbTe is a semiconductor with promising properties for topological quantum computing applications. Here, we characterize electron quantum dots in PbTe nanowires selectively grown on InP. Charge stability diagrams at zero magnetic field reveal large even–odd spacing between Coulomb blockade peaks, charging energies below 140 μeV and Kondo peaks in odd Coulomb diamonds. We attribute the large even–odd spacing to the large dielectric constant and small effective electron mass of PbTe. By studying the Zeeman-induced level and Kondo splitting in finite magnetic fields, we extract the electron g-factor as a function of magnetic field direction. We find the g-factor tensor to be highly anisotropic with principal g-factors ranging from 0.9 to 22.4 and to depend on the electronic configuration of the devices. These results indicate strong Rashba spin–orbit interaction in our PbTe quantum dots.

Keywords: PbTe, selective-area growth, quantum dot, charging energy, g-factor, spin−orbit interaction

The quest for realizing topological superconductivity in trivial semiconductors, with accompanying Majorana zero modes, would benefit from materials with strong spin–orbit interaction and large Landé g-factors.1−5 In this context, PbTe may offer advantages compared to more established platforms such as InSb and InAs. Work on PbTe reported large and anisotropic g-factors, with absolute values up to 586 and strong spin–orbit interaction (SOI);7 both advantageous properties for the realization of sizable topological gaps at moderate magnetic fields.8,9 PbTe, which is a well-known thermoelectric material,10,11 also exhibits a direct band gap Eg = 190 meV,12 electron effective masses of 0.024me – 0.24me,13 and a large dielectric constant ϵr ∼ 1350 at low temperatures12 (compared to ϵr ∼ 14 for InAs and InSb14), which is expected to result in efficient screening of impurities and, consequently, high electron mobilities.15 Recent work demonstrated the possibility to grow high-quality PbTe nanowires, either with vapor–liquid–solid epitaxy16 or the selective-area-growth (SAG) technique.15 Electrical characterization also demonstrated ambipolar characteristics, small charging energies and large g-factors.17

Here, we investigate electron quantum dots in PbTe nanowires selectively grown on insulating InP substrates. We find that charging energies are typically smaller than single-particle excitation energies, producing a pronounced even–odd spacing between Coulomb blockade peaks that is lifted by applying modest magnetic fields. Such even–odd spacing is consistent with the strong screening expected from the PbTe material. Studying the evolution of spin excited state level splittings and Kondo peaks in a magnetic field, we extract the three-dimensional effective g-factor tensor, that is the electronic g-factor as a function of magnetic field direction.

Our results indicate that the effective g-factor tensor is highly anisotropic, moreover it varies from device to device and depends on the gate configuration of each device. In the stable gate configurations we investigated, the principal g-factors varied from 0.9 to 22.4, with smaller values obtained for magnetic fields parallel to the substrate. No relation between effective g-factor tensor and crystal direction was found.

Figure 1 shows false-colored scanning electron micrographs of the two quantum dot devices used in this study, together with the measurement configurations. The PbTe nanowires are colored red, the Ti/Au contacts yellow, and the Ti/Au gates orange. Nanowires were grown in an MBE on a (111)A InP substrate along a ⟨110⟩ (Device 1) and a ⟨112⟩ (Device 2) crystal direction. The lithographic distance between the source and drain contacts of both quantum dot devices is 720 nm and the width is 80 and 100 nm for Device 1 and 2, respectively. Schematics of the device cross sections in Figure 1c,d shows the InP substrate, SiNx growth mask, PbTe nanowire with terminating facets and Ti/Au side gates. The nanowire cross-section, obtained by TEM imaging of similar nanowires, is a consequence of the crystal direction of the growth mask relative to the substrate and will be discussed in more detail in a separate work.

Figure 1.

Figure 1

Open in a new tab

Two quantum dot devices in SAG PbTe nanowires on (111)A InP. (a,b) False-colored SEM micrographs of devices with crystal and magnetic field directions indicated. The nanowires are red, the Ti/Au contacts are yellow, and the Ti/Au gates are orange. For Device 2, VR was grounded. (c,d) Schematic cross sections as indicated in (a,b) by blue dashed lines. The terminating facets of the nanowires differ due to their different crystal directions.

Measurements were carried out in a dilution refrigerator equipped with a vector magnet at a mixing chamber base temperature below 20 mK. A variable DC voltage bias ±VSD/2 was applied to source and drain contacts, respectively, superimposed on an AC voltage bias of 3 μV. The resulting AC current and voltage drop were measured with lock-in amplifiers to determine the differential conductance G of the devices. Both devices were tuned with side gate voltages VL, VPG, and VR, applied pairwise to opposite facing gate electrodes. For Device 2, the gray gate pair in Figure 1b showed leakage to the nanowire for VR < −600 mV and was grounded throughout the measurements. In this case, the quantum dot was formed by setting VL and VPG to negative voltages. Both quantum dots showed gate instabilities over their entire gate voltage space, resulting in frequent charge rearrangements, some of which are visible in the Figures below. The gate configurations characterized in this paper were selected to limit the occurrence of such events.

Our key measurement results are shown in Figures 2, 3, and 4, which we will analyze and discuss below. Figure 2a–d depicts Coulomb blockade measurements as a function of gates VL and VR for Device 1 in a perpendicular magnetic field. Charge stability diagrams at zero and finite magnetic field are shown in Figure 2e,f, respectively, with VPG = −1.25 V and VL = −2.4 V. The average gate lever arm of gate VR was αR = 0.0092. The low value of αR is consistent with large source and drain lever arms, accounting for most of the quantum dot capacitance. A discussion of the lever arms can be found in the Supporting Information.

Figure 2.

Figure 2

Open in a new tab

Electrical characterization of quantum dot Device 1 at zero and finite magnetic fields. (a–d) Evolution of even–odd spacing between Coulomb blockade peaks as a function of magnetic field. VPG = −1.4 V is applied to the lower plunger gate in Figure 1a. Note that the rapid changes in slope at VR = −1.9 V are due to fast gate resetting after each horizontal scan. (e,f) Charge stability diagrams showing Kondo peaks, which split in a finite magnetic field. VPG = −1.25 V and VL = −2.4 V. The onset of inelastic cotunneling, which coincides with an excited state, is marked in (e) with an orange arrow and the level splitting is marked in (f) with a yellow double-arrow.

Figure 3.

Figure 3

Open in a new tab

Electrical characterization of quantum dot Device 2 at zero and finite magnetic field. (a) Charge stability diagram at zero magnetic field and VL = −3.825 V, showing Kondo peaks in odd Coulomb diamonds and inelastic cotunneling in even diamonds. (b,c) Zoom-ins of the Coulomb diamond indicated with an arrow in (a), depicting the (split) Kondo peak at zero and finite magnetic field. (d) Evolution of the Kondo peak splitting as a function of magnetic field. The dashed line is a guide for the eye, which shows that the splitting is linear. For (a–c), VL = −3.825 V. For (d), VL = −3.825 V and VPG = −2.344 V.

Figure 4.

Figure 4

Open in a new tab

g-factor anisotropy of all investigated quantum dot gate configurations. (a–c) In-plane g-factors extracted from energy level and Kondo peak splittings (red) and fits of the effective g-factor tensors (blue). The magnetic field was rotated in steps of 15°. The nanowires are displayed in each polar plot. (d–f) 3D plots of the g-factors extracted from three magnetic field rotations (red, purple, green lines) and the fits of the effective g-factor tensors (surface plots and black lines). The nanowire devices (orange), substrate planes (gray), and the magnetic field coordinate system are depicted.

The Coulomb peak spacing in Figure 2a follows a pronounced even–odd pattern, with the boundaries of even-occupied states (indicated with green squares) much more separated in gate space than those of odd-occupied states (indicated with blue circles). This observation indicates that the charging energy of the quantum dot is much smaller than the orbital energy. At increasing magnetic fields, the closely spaced Coulomb blockade peaks move further apart, consistent with two electrons of opposite spin filling the same orbital level. From Figure 2a–d, we verified that the splitting is linear up to 200 mT, at least.

The large difference between the charging energy and single-particle excitation energy is evident in Figure 2e,f. The charge stability diagrams of Device 1 show alternating Coulomb diamond sizes, consistent with the large even–odd spacing in Figure 2a,d. From the height of the odd Coulomb diamonds in Figure 2e, we extracted an average charging energy of EC ≈ 110 μeV using Eadd = EC,18 where Eadd is the addition energy. From the height of the central even Coulomb diamond, we extracted a single-particle excitation energy of Δ ≈ 500 μeV using Eadd = EC + Δ.18 Inelastic cotunneling19 is observed near the tips of the even Coulomb diamond and, for the lower tip, the onset of cotunneling coincides with a faint excited state of an odd Coulomb diamond [see the orange arrow in Figure 2e]. In addition, conductance peaks at zero bias voltage are observed in odd Coulomb diamonds, which split in a finite magnetic field perpendicular to the substrate, as seen in Figure 2f. Therefore, we conclude that the peaks are manifestations of the spin-1/2 Kondo effect.20−23 We investigated a second stable gate configuration for Device 1, where the charge occupation is similar to gate configuration 1, but VL ≥ VR, opposite to gate configuration 1. Charge stability diagrams obtained in gate configuration 2 are presented in Supporting Information Figure S1 and show similar results.

A charge stability diagram of Device 2 is shown in Figure 3a. As for Device 1, odd Coulomb diamonds are smaller than even Coulomb diamonds. From the two leftmost odd Coulomb diamonds, we extracted an average charging energy of EC ≈ 130 μeV, and a lever arm with respect to gate VPG of αPG = 0.021, similar to that of Device 1. From the height of the leftmost even Coulomb diamond we extracted a single-particle excitation energy of Δ ≈ 170 μeV, which is significantly lower than the value found for Device 1. All odd Coulomb diamonds in Figure 3a feature Kondo peaks and all even Coulomb diamonds feature inelastic cotunneling. Zoom-ins of the Coulomb diamond marked in Figure 3a at zero and finite magnetic field are depicted in Figure 3b,c, respectively, and show that the Kondo peak splits in a finite magnetic field. Figure 3d shows that the Kondo splitting at VPG = −2.344 V is indeed linear up to 100 mT.

In the following, we use two distinct signatures of the Zeeman splitting at finite magnetic field to determine the g-factor, namely Kondo splitting and level splitting between ground and excited state of an unpaired spin at odd electron filling [see the yellow double-arrow in Figure 2f]. Both of these energy splittings have been widely used for the extraction of g-factors in quantum dots.23−31 For the Kondo splitting, the effective g-factor was extracted as20−23

graphic file with name nl2c01943_m001.jpg 1

where μB is the Bohr magneton and ΔVSD is the separation of the two maxima in G(VSD). For the excited state level splitting, which measures variations of energy levels with respect to only one lead of the device, a prefactor (1 ± δα) needs to be included in eq 1.27 The quantity δα = αS – αD is the difference in source and drain lever arm and accounts for the asymmetric coupling to source and drain. For further details on this see the Supporting Information.

The g-factor extracted from the Kondo splitting in Figure 3c is 3.8. Repeating the analysis for all the Kondo peaks in Figure 3a yields g-factors between 0 and 4.8. These results are shown in Supporting Information Figure S2 and they indicate that the g-factor strongly varies with gate voltage. Here, we focus on the state marked with a white arrow in Figure 3a and investigate its g-factor for different magnetic field orientations. To this end, a magnetic field with a fixed magnitude of 100 mT was rotated by 360° in steps of 15° along three orthogonal planes. Charge stability diagrams such as Figure 3c were obtained for all magnetic field orientations and the g-factor was extracted from Kondo splittings, because level splittings could not be resolved at all magnetic field orientations. A similar analysis was carried out for both gate configurations of Device 1, where the out-of-plane rotations were perpendicular and parallel to the nanowire axis. For the latter device, a magnetic field magnitude of 200 mT was used and the g-factor was extracted from the level splittings. Schematics of the magnetic field rotations are depicted in Figure S3g,h for Device 1 and 2, respectively, together with definitions of the azimuthal angle ϕ and polar angle θ, which were used to define the rotations. The set of g-factors of each gate configuration was fit with an effective g-factor tensor, which describes the g-factor as a function of magnetic field direction

graphic file with name nl2c01943_m002.jpg 2

where gi are the principal g-factors, pointing along the principal axes of the effective g-factor tensor, and Bi are the magnetic field components along the principal axes.26,32

The results of this analysis are shown in Figure 4 with g-factors extracted from energy level splittings (Device 1, two gate configurations) and Kondo splittings (Device 2). Figure 4a–c depicts polar plots of the g-factors extracted for the in-plane rotations of the magnetic field (red) and the fits of the tensor 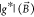Inline graphic (blue). The nanowires are shown schematically in each polar plot. The polar plots showing the g-factors for the out-of-plane magnetic field rotations are presented in Supporting Information Figure S3a–f. Figure 4d–f shows the extracted g-factors for all magnetic field rotations (red, purple, green lines) and the fits of eq 2 with the principal g-factors from Table 1 (surface plots) for each gate configuration. The principal g-factors are depicted as black lines. The values of the principal g-factors, as well as their polar and azimuthal angles, are displayed in Table 1.The g-factor is anisotropic for all investigated stable gate configurations in Figure 4. The values of the principal g-factors vary between 0.9 and 22.4, depending on the magnetic field orientation. Moreover, the in-plane g-factors are typically smaller than the out-of-plane g-factors.

Table 1. Principal g-Factors of the Effective g-Factor Tensor from Equation 2 for All Investigated Quantum Dot Gate Configurations.

  g1 g2 g3
Device 1, gate configuration 1
Value 9.3 14.1 0.9
ϕ 276.5° 40.8° 159.0°
θ 53.4° 52.8° 58.1°
Device 1, gate configuration 2
Value 7.0 22.4 3.3
ϕ 144.3° 149.8° 54.7°
θ 104.9° 14.9° 88.6°
Device 2
Value 5.1 11.2 2.3
ϕ 187.7° 142.9° 95.7°
θ 100.8° 15.0° 100.3°
Open in a new tab

The experimental results have been presented and will be discussed in the remainder of this paper. PbTe is expected to have an extremely large dielectric constant ϵr ∼ 1350 at low temperatures.12 It is therefore crucial to understand how this value impacts the physics of our quantum dots. We consistently found small charging energies, which might be due to the large dielectric constant of PbTe. Our results are similar to the observation of vanishingly small charging energies in vertically grown PbTe nanowires,17 which were also interpreted as consequences of the large dielectric constant of PbTe. However, unlike ref.,17 our devices always show finite, albeit small, charging energies. Differences in the properties of the PbTe nanowires and in the quantum dot sizes and geometries could explain these dissimilarities.

Due to the expected large dielectric constant, understanding the impact of side gates is not trivial. The expansion of field lines at the interface between a material with small ϵr (vacuum, SiNx or InP) and one with large ϵr (PbTe) might result in a side gate affecting the chemical potential of the nanowire over a length much larger than the gate width. In this scenario, due to the extraordinarily high dielectric constant of PbTe, the quantum dots would not be defined by the side gates, but by the length of the entire nanowire (2 μm). The gate lever arms measured in all gate configurations were similar and approximately equal to 0.01, indicating that the center of the quantum dot coincides with the center of the nanowire. Since all gate lever arms of a quantum dot need to sum to unity,33 we deduce that αS and αD are substantially larger than the gate lever arms. This is confirmed by the more quantitative analysis presented in the Supporting Information, from which we find that the source and drain tunnel barriers are most likely induced by the side gates and formed inside the nanowire. Moreover, the length L of the quantum dot can be estimated from the level spacing Δ. We omit the smallest dimension (height) for simplicity and consider the quantum dot as an ellipse with an aspect ratio of 1:10, thus conserving the aspect ratio of the nanowire region between the contacts. Using 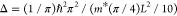Inline graphic,34 where m* is the effective electron mass m* = 0.024me – 0.24me13 and Δ = 170–500 μeV, we find L ∼ 160–860 nm. This result implies that the quantum dots are likely defined by the side gates, and therefore the electric field distribution along the nanowire length is not uniform, which could indicate that the dielectric constant of the nanowires is somewhat lower than the expected bulk dielectric constant of PbTe. The presence of charge fluctuations does not differentiate between these situations, since even with perfect screening, charge rearrangements on the surface of the nanowire or in the air gap between the gates and the nanowire may affect the potential in the nanowire globally, and this cannot be differentiated from a local change in potential. Thus, our findings imply that although the dielectric constant of the PbTe nanowires is large, its value is likely reduced with respect to the bulk dielectric constant. A reduction of the dielectric constant with decreasing nanowire diameter was already found for ZnO nanowires.35 Future investigations of nonlocal gating and dielectric constant reduction can give more insight into quantum dot formation in PbTe nanowires.

The single-particle excitation energy for Device 1, 500 μeV, was significantly larger than that of Device 2, 170 μeV, which we attribute to either the different nanowire thicknesses, resulting in a stronger confinement and thus a larger single-particle excitation energy for Device 1, or to different effective masses in the devices. For instance, a large dependence of the electron effective mass on nanowire crystal direction was predicted.36 A more systematic study of nanowire geometry and crystal orientation is needed to exclude device to device variability as the root cause of the observed different single-particle excitation energies.

Using two distinct methods to extract the g-factor, namely Kondo splitting and level splitting, we found strong g-factor anisotropies for all investigated stable gate configurations. By comparing the level splitting to the Kondo splitting for several magnetic field rotations, we found that the Kondo splitting underestimates extracted g-factors by about 20% compared to the level splitting. This is in qualitative agreement with expectations from theory.37 Thus, whenever the excited state level splitting can be resolved, this method should be preferred over Kondo splitting for extracting g-factors. The principal axes of the effective g-factor tensors 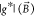Inline graphic for the different gate configurations are neither aligned, nor perpendicular to the nanowire axes. Moreover, the g-factor anisotropy did not present any correlation to the nanowire crystal directions. The g-factor anisotropy varied for the two devices and for different gate configurations within Device 1. These observations point to strong Rashba spin–orbit interaction and asymmetric confinement potentials in the PbTe quantum dots.26 This is consistent with predicted small Dresselhaus SOI in PbTe due to its inversion-symmetric rocksalt crystalline structure38 and large Rashba SOI, as measured in PbTe quantum wells.7 Moreover, g-factor anisotropy was predicted for [100] and [111] PbTe quantum wells,13 where the authors included the contributions of wave function barrier penetration, confinement energy shift, and interface SO interaction in their calculations of the quantum well g-factors. Furthermore, they found that a confining mesoscopic potential renormalizes the g-factor through Rashba SOI.

Besides the g-factor anisotropy, we observed that the g-factor varies for neighboring electronic states in Device 2, similar to results on quantum dots in InAs nanowires,39 where the authors attributed this g-factor variation to random fluctuations in the confinement potential, as well as strong Rashba SOI. Additionally, the g-factors that we found are typically lower than the g-factors of bulk PbTe. It is known that the g-factor is reduced in low dimensions due to quantum confinement, which leads to quenching of the orbital angular momentum, as observed for quantum dots in InAs nanowires.25

In conclusion, we characterized quantum dot devices in zero and finite magnetic fields. The SAG approach allowed investigation of quantum dots in nanowires with different crystal directions. Despite SAG of PbTe was only recently achieved,15 we could identify gate configurations with electronic stability that allowed extensive characterization. Charging energies and single-particle excitation energies were extracted from charge stability diagrams. From the energy level and Kondo peak splitting at finite magnetic fields, we extracted the electron g-factor as a function of magnetic field direction. The anisotropy of the g-factor was attributed to strong Rashba SOI and quantum confinement. Therefore, PbTe in combination with a superconductor is a promising platform for studying topological superconductivity. The large g-factor anisotropy and the fact that small g-factors are observed for in-plane magnetic fields should be considered in device design.

Methods

Device Fabrication

Nanowires were selected by imaging with scanning electron microscopy. A double resist layer, consisting of PMMA AR-P 669.04 and PMMA AR-P 672.02, was spun onto the chip and patterned with e-beam lithography. After developing the resist with MIBK/IPA (1:2), an Ar reactive ion etch was performed to remove native oxide on the PbTe nanowires.40 Immediately after the Ar etch, the chip was loaded into an e-beam evaporator where 5 nm Ti and 50 nm Au were deposited. Then, lift-off was carried out in acetone. Four quantum dot devices were fabricated and all had well-defined lithographic features. One of these devices was insulating irrespective of applied gate voltage. Inspection with SEM after warming up the chip revealed damages due to electrostatic discharges during wire bonding and/or loading. A second device was conducting, but too unstable to be tuned to the Coulomb blockade regime. The two remaining devices are presented here.

g-Factor Fitting

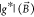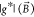By fitting the complete set of g-factors extracted for all magnetic field orientations with eq 2, we determined the principal g-factors and the principal axes of the effective g-factor tensor Inline graphic. The magnetic field components Bx, By, Bz and the measured g-factors formed the set of input parameters for the fit. The fit parameters were the principal g-factors g1, g2, g3 and the Euler angles of rotation ϕ, θ, ψ.41 With these angles, the magnetic field components were transformed from the Cartesian coordinate system to the coordinate system of the principal axes of Inline graphic. This fitting procedure was repeated for two stable gate configurations of Device 1 and for one stable gate configuration of Device 2. Subsequently, with the Euler angles of rotation found by the fits, we transformed the principal g-factors to spherical coordinates to determine the orientation of each principal g-factor.

Acknowledgments

We thank W. Riess, G. Salis, E. G. Kelly, F. J. Schupp, and the Cleanroom Operations Team of the Binnig and Rohrer Nanotechnology Center (BRNC) for their help and support. A. Fuhrer acknowledges support from NCCR SPIN, funded by the SNSF under Grant 51NF40-180604. The work in Eindhoven is supported by the European Research Council (ERC TOCINA 834290). F. Nichele acknowledges support from the European Research Council, grant number 804273, and the Swiss National Science Foundation, Grant 200021_201082.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.2c01943.

  • Additional charge stability diagrams and a gate overview scan of Device 1; additional charge stability diagrams of Device 2; polar plots of the g-factor anisotropy for out-of-plane magnetic field rotations (PDF)

Author Contributions

∥ S.C.t.K and M.F.R. contributed equally to this paper.

The authors declare no competing financial interest.

Notes

Data supporting this study are openly available from Zenodo at DOI: 10.5281/zenodo.7014602.

Supplementary Material

nl2c01943_si_001.pdf (2.1MB, pdf)

References

  1. Prada E.; San-Jose P.; de Moor M. W. A.; Geresdi A.; Lee E. J. H.; Klinovaja J.; Loss D.; Nygård J.; Aguado R.; Kouwenhoven L. P. From Andreev to Majorana bound states in hybrid superconductor–semiconductor nanowires. Nature Reviews Physics 2020, 2, 575–594. 10.1038/s42254-020-0228-y. [DOI] [Google Scholar]
  2. Lutchyn R. M.; Bakkers E. P. A. M.; Kouwenhoven L. P.; Krogstrup P.; Marcus C. M.; Oreg Y. Majorana zero modes in superconductor–semiconductor heterostructures. Nature Reviews Materials 2018, 3, 52–68. 10.1038/s41578-018-0003-1. [DOI] [Google Scholar]
  3. Kanne T.; Marnauza M.; Olsteins D.; Carrad D. J.; Sestoft J. E.; de Bruijckere J.; Zeng L.; Johnson E.; Olsson E.; Grove-Rasmussen K.; Nygård J. Epitaxial Pb on InAs nanowires for quantum devices. Nat. Nanotechnol. 2021, 16, 776–781. 10.1038/s41565-021-00900-9. [DOI] [PubMed] [Google Scholar]
  4. Pendharkar M.; et al. Parity-preserving and magnetic field–resilient superconductivity in InSb nanowires with Sn shells. Science 2021, 372, 508–511. 10.1126/science.aba5211. [DOI] [PubMed] [Google Scholar]
  5. Op het Veld R. L. M.; Xu D.; Schaller V.; Verheijen M. A.; Peters S. M. E.; Jung J.; Tong C.; Wang Q.; de Moor M. W. A.; Hesselmann B.; Vermeulen K.; Bommer J. D. S.; Sue Lee J.; Sarikov A.; Pendharkar M.; Marzegalli A.; Koelling S.; Kouwenhoven L. P.; Miglio L.; Palmstrøm C. J.; Zhang H.; Bakkers E. P. A. M. In-plane selective area InSb–Al nanowire quantum networks. Communications Physics 2020, 3, 59. [Google Scholar]
  6. Patel C. K. N.; Slusher R. E. Electron Spin-Flip Raman Scattering in PbTe. Phys. Rev. 1969, 177, 1200–1202. 10.1103/PhysRev.177.1200. [DOI] [Google Scholar]
  7. Peres M.L.; Chitta V.A.; Maude D.K.; Oliveira N.F.; Rappl P.H.O.; Ueta A.Y.; Abramof E. Spin-orbit coupling in n-type PbTe/PbEuTe quantum wells. Acta Phys. Polym., A 2011, 119, 602–605. 10.12693/APhysPolA.119.602. [DOI] [Google Scholar]
  8. Lutchyn R. M.; Sau J. D.; Das Sarma S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. 10.1103/PhysRevLett.105.077001. [DOI] [PubMed] [Google Scholar]
  9. Oreg Y.; Refael G.; von Oppen F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. 10.1103/PhysRevLett.105.177002. [DOI] [PubMed] [Google Scholar]
  10. Ravich Y. I.; Efimova B. A.; Smirnov I. A.. Semiconducting Lead Chalcogenides; Springer: New York, 1970. [Google Scholar]
  11. LaLonde A. D.; Pei Y.; Wang H.; Jeffrey Snyder G. Lead telluride alloy thermoelectrics. Mater. Today 2011, 14, 526–532. 10.1016/S1369-7021(11)70278-4. [DOI] [Google Scholar]
  12. Bauer G.; Springholz G. In Encyclopedia of Modern Optics; Guenther R. D., Ed.; Elsevier: Oxford, 2005; pp 385–392. [Google Scholar]
  13. Ridolfi E.; Silva E. A. d. A. e.; La Rocca G. C. Effective g-factor tensor for carriers in IV-VI semiconductor quantum wells. Phys. Rev. B 2015, 91, 085313. 10.1103/PhysRevB.91.085313. [DOI] [Google Scholar]
  14. Rodilla H.; González T.; Pardo D.; Mateos J. High-mobility heterostructures based on InAs and InSb: A Monte Carlo study. J. Appl. Phys. 2009, 105, 113705. 10.1063/1.3132863. [DOI] [Google Scholar]
  15. Jiang Y.; et al. Selective area epitaxy of PbTe-Pb hybrid nanowires on a lattice-matched substrate. Phys. Rev. Materials 2022, 6, 034205. 10.1103/PhysRevMaterials.6.034205. [DOI] [Google Scholar]
  16. Schellingerhout S. G.; de Jong E. J.; Gomanko M.; Guan X.; Jiang Y.; Hoskam M. S. M.; Jung J.; Koelling S.; Moutanabbir O.; Verheijen M. A.; Frolov S. M.; Bakkers E. P. A. M. Growth of PbTe nanowires by molecular beam epitaxy. Materials for Quantum Technology 2022, 2, 015001. 10.1088/2633-4356/ac4fba. [DOI] [Google Scholar]
  17. Gomanko M.; de Jong E. J.; Jiang Y.; Schellingerhout S. G.; Bakkers E. P. A. M.; Frolov S. M.. Spin and Orbital Spectroscopy in the Absence of Coulomb Blockade in Lead Telluride Nanowire Quantum Dots. 2021; arXiv:2111.13242. arXiv. https://arxiv.org/abs/2111.13242 (accessed July 12, 2022).
  18. Björk M. T.; Thelander C.; Hansen A. E.; Jensen L. E.; Larsson M. W.; Wallenberg L. R.; Samuelson L. Few-Electron Quantum Dots in Nanowires. Nano Lett. 2004, 4, 1621–1625. 10.1021/nl049230s. [DOI] [Google Scholar]
  19. De Franceschi S.; Sasaki S.; Elzerman J. M.; van der Wiel W. G.; Tarucha S.; Kouwenhoven L. P. Electron Cotunneling in a Semiconductor Quantum Dot. Phys. Rev. Lett. 2001, 86, 878–881. 10.1103/PhysRevLett.86.878. [DOI] [PubMed] [Google Scholar]
  20. Goldhaber-Gordon D.; Shtrikman H.; Mahalu D.; Abusch-Magder D.; Meirav U.; Kastner M. A. Kondo effect in a single-electron transistor. Nature 1998, 391, 156–159. 10.1038/34373. [DOI] [Google Scholar]
  21. Cronenwett S. M.; Oosterkamp T. H.; Kouwenhoven L. P. A Tunable Kondo Effect in Quantum Dots. Science 1998, 281, 540–544. 10.1126/science.281.5376.540. [DOI] [PubMed] [Google Scholar]
  22. Inoshita T. Kondo Effect in Quantum Dots. Science 1998, 281, 526–527. 10.1126/science.281.5376.526. [DOI] [Google Scholar]
  23. Jespersen T. S.; Aagesen M.; Sørensen C.; Lindelof P. E.; Nygård J. Kondo physics in tunable semiconductor nanowire quantum dots. Phys. Rev. B 2006, 74, 233304. 10.1103/PhysRevB.74.233304. [DOI] [Google Scholar]
  24. Nilsson H. A.; Caroff P.; Thelander C.; Larsson M.; Wagner J. B.; Wernersson L.-E.; Samuelson L.; Xu H. Q. Giant, Level-Dependent g Factors in InSb Nanowire Quantum Dots. Nano Lett. 2009, 9, 3151–3156. 10.1021/nl901333a. [DOI] [PubMed] [Google Scholar]
  25. d’Hollosy S.; Fábián G.; Baumgartner A.; Nygård J.; Schönenberger C. g-factor anisotropy in nanowire-based InAs quantum dots. AIP Conf. Proc. 2013, 1566, 359. [Google Scholar]
  26. Mu J.; Huang S.; Wang J.-Y.; Huang G.-Y.; Wang X.; Xu H. Q. Measurements of anisotropic g-factors for electrons in InSb nanowire quantum dots. Nanotechnology 2021, 32, 020002. 10.1088/1361-6528/abbc24. [DOI] [PubMed] [Google Scholar]
  27. Fasth C.; Fuhrer A.; Samuelson L.; Golovach V. N.; Loss D. Direct Measurement of the Spin-Orbit Interaction in a Two-Electron InAs Nanowire Quantum Dot. Phys. Rev. Lett. 2007, 98, 266801. 10.1103/PhysRevLett.98.266801. [DOI] [PubMed] [Google Scholar]
  28. Björk M. T.; Fuhrer A.; Hansen A. E.; Larsson M. W.; Fröberg L. E.; Samuelson L. Tunable effective g factor in InAs nanowire quantum dots. Phys. Rev. B 2005, 72, 201307. 10.1103/PhysRevB.72.201307. [DOI] [Google Scholar]
  29. Hanson R.; Witkamp B.; Vandersypen L. M. K.; van Beveren L. H. W.; Elzerman J. M.; Kouwenhoven L. P. Zeeman Energy and Spin Relaxation in a One-Electron Quantum Dot. Phys. Rev. Lett. 2003, 91, 196802. 10.1103/PhysRevLett.91.196802. [DOI] [PubMed] [Google Scholar]
  30. Escott C. C.; Zwanenburg F. A.; Morello A. Resonant tunnelling features in quantum dots. Nanotechnology 2010, 21, 274018. 10.1088/0957-4484/21/27/274018. [DOI] [PubMed] [Google Scholar]
  31. Hanson R.; Kouwenhoven L. P.; Petta J. R.; Tarucha S.; Vandersypen L. M. K. Spins in few-electron quantum dots. Rev. Mod. Phys. 2007, 79, 1217–1265. 10.1103/RevModPhys.79.1217. [DOI] [Google Scholar]
  32. Brouwer P. W.; Waintal X.; Halperin B. I. Fluctuating Spin g-Tensor in Small Metal Grains. Phys. Rev. Lett. 2000, 85, 369–372. 10.1103/PhysRevLett.85.369. [DOI] [PubMed] [Google Scholar]
  33. Ihn T.Semiconductor Nanostructures; Oxford University Press, 2010. [Google Scholar]
  34. Kouwenhoven L. P.; Marcus C. M.; McEuen P. L.; Tarucha S.; Westervelt R. M.; Wingreen N. S. In Mesoscopic Electron Transport; Sohn L. L., Kouwenhoven L. P., Schön G., Eds.; Springer Netherlands: Dordrecht, 1997; pp 105–214. [Google Scholar]
  35. Yang Y.; Guo W.; Wang X.; Wang Z.; Qi J.; Zhang Y. Size Dependence of Dielectric Constant in a Single Pencil-Like ZnO Nanowire. Nano Lett. 2012, 12, 1919–1922. 10.1021/nl204353t. [DOI] [PubMed] [Google Scholar]
  36. Cao Z.; Liu D. E.; He W.-X.; Liu X.; He K.; Zhang H. Numerical study of PbTe-Pb hybrid nanowires for engineering Majorana zero modes. Phys. Rev. B 2022, 105, 085424. 10.1103/PhysRevB.105.085424. [DOI] [Google Scholar]
  37. Moore J. E.; Wen X.-G. Anomalous Magnetic Splitting of the Kondo Resonance. Phys. Rev. Lett. 2000, 85, 1722–1725. 10.1103/PhysRevLett.85.1722. [DOI] [PubMed] [Google Scholar]
  38. Peres M.L.; Chitta V.A.; Maude D.K.; Oliveira N.F.; Rappl P.H.O.; Ueta A.Y.; Abramof E. Spin-orbit coupling in n-type PbTe/PbEuTe quantum wells. Acta Phys. Polym., A 2011, 119, 602–605. 10.12693/APhysPolA.119.602. [DOI] [Google Scholar]
  39. Csonka S.; Hofstetter L.; Freitag F.; Oberholzer S.; Schönenberger C.; Jespersen T. S.; Aagesen M.; Nygård J. Giant Fluctuations and Gate Control of the g-Factor in InAs Nanowire Quantum Dots. Nano Lett. 2008, 8, 3932–3935. 10.1021/nl802418w. [DOI] [PubMed] [Google Scholar]
  40. Yang Y.; Kung S. C.; Taggart D. K.; Xiang C.; Yang F.; Brown M. A.; Kruse T. J.; Hemminger J. C.; Penner R. M. Synthesis of PbTe Nanowire Arrays using Lithographically Patterned Nanowire Electrodeposition. Nano Lett. 2008, 8, 2447–2451. 10.1021/nl801442c. [DOI] [PubMed] [Google Scholar]
  41. Liles S. D.; Martins F.; Miserev D. S.; Kiselev A. A.; Thorvaldson I. D.; Rendell M. J.; Jin I. K.; Hudson F. E.; Veldhorst M.; Itoh K. M.; Sushkov O. P.; Ladd T. D.; Dzurak A. S.; Hamilton A. R. Electrical control of the g tensor of the first hole in a silicon MOS quantum dot. Phys. Rev. B 2021, 104, 235303. 10.1103/PhysRevB.104.235303. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl2c01943_si_001.pdf (2.1MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES