Abstract
Polyelectrolyte complexes formed from nucleic acids and synthetic polycations have been studied because of their potential in gene delivery. Coarse-grained molecular dynamics simulations are performed to examine the impact of chain length and polyanion stiffness on polyplex formation and aggregation. Polyplexes containing single polyanion chain fall into three structural regimes depending on polyanion stiffness: flexible polyanions form collapsed complexes, semiflexible polyanions form various morphologies including toroids and hairpins, and stiff polyanions form rod-like structures. Polyplex size generally decreases as polycation length increases. Aggregation (i.e., formation of complexes containing multiple polyanions) is observed in some simulations containing multiple polyanions and an excess of short polycations. Aggregation is observed to only occur for semiflexible and stiff polyanions and is promoted by shorter polycation lengths. Simulations of short, stiff polyanions condensed by long polycations are used as a model for siRNA gene delivery complexes. These simulations show multiple polyanions are spaced out along the polycation with polyanion-polyanion interactions, usually limited to overlapping chain ends. These structures differ from aggregates of longer polyanions in which the polyanions are packed together in parallel, forming bundles.
Keywords: Polyplex, coarse-grained, gene delivery
Graphical Abstract
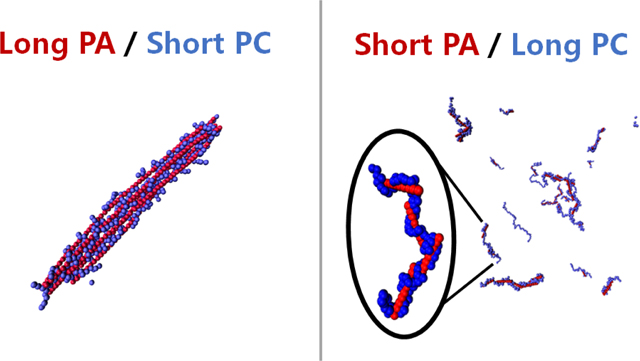
Coarse-grained molecular dynamic simulations are performed to shed light on polyplex structures formed in polymer based gene delivery. Long stiff polyanions (PA) condensed by short flexible polycations (PC), mimicking delivery of plasmid DNA, formed bundles, whereas short stiff polyanions condensed by long flexible polycations, mimicking delivery of siRNA, did not form bundles.
1. Introduction
Polyelectrolyte complexes have great importance in a variety of biological and industrial applications, including drug delivery, layer-by-layer assembly, and packaging of genetic materials.[1–3] One highly studied application of polyelectrolyte complexes has been non-viral gene delivery systems containing polyanionic nucleic acids (usually plasmid DNA or siRNA) and synthetic polycations, such as polyethyleneimine (PEI) or poly-L-lysine (PLL).[2–4] Packaging therapeutic nucleic acids into polyelectrolye complexes protects them from degradation and enhances their uptake into cells. These polyplexes can be further enhanced by linking the polycation to hydrophilic polymers to increase stability and/or to ligands that target specific cell types.[2,5] However, polycation-based gene delivery treatments remain under development and would benefit greatly from improved understanding of the relationship between the properties of the polyelectrolytes, the resulting structure of the polyelectrolyte complex and the efficacy/safety of the complex as a gene delivery vector.[2,3]
One common focus of studies of polyelectrolyte complex structure has been determining the composition of the polyplexes (i.e. the numbers of polycations and nucleic acid chains in the polyplex) and, more specifically, if the polyplexes are aggregates, where we use the term aggregate to refer to a polyplex containing multiple polyanion chains.[6–15] For example, examination of polyplexes consisting of PEI and plasmid DNA has shown that polyplexes can be aggregates containing dozens of DNA plasmids and PEI molecules,[6] and that aggregation depends on DNA concentration, the length and type (e.g. linear or branched) of the PEI, and the ratio of PEI amine groups to DNA phosphates (a property referred to as the N/P ratio).[7] The systems in these studies were typical of many potential gene delivery preparations, as they involve long, comparatively stiff polyanions (plasmid DNA which is typically thousands of basepairs long) interacting with an excess of shorter, more flexible polycations. However, not all gene therapy polyplexes fit this paradigm, as the lengths and rigidities of the polyelectrolytes in gene delivery complexes vary. Significantly, gene delivery based on either siRNA, which is ~20 nucleotides long, or single-stranded oligonucleotides, which are much more flexible than their double-stranded counterparts, has also been investigated. Thus, there have been several experimental investigations of how polyelectrolyte length and rigidity impact complex structure.[8–15] Hayashi et al. examined complexation between a ~+40 charged PLL-PEG block copolymer and a 21-mer of either double-stranded siRNA or single-stranded RNA. They found that, at sufficient RNA concentrations, complexes formed from single-stranded RNA chains formed aggregates containing many RNA chains, while double-stranded siRNA did not aggregate.[8] Lueckheide et al. examined a similar PLL-PEG block copolymer system but used DNA, instead of RNA, as the polyanion and found different results.[9] In this study, single-stranded DNA complexes were spheroidal micelles while double-stranded DNA complexes were cylindrical structures with the DNA helices hexagonally packed in parallel.
Despite the advancements provided by these experimental results, their interpretation is challenging, as it can be difficult to determine if differences in complex structures are due to differences in polyelectrolyte chain lengths, polyelectrolyte flexibilities or other factors such as the molecular level details of the chains. For example, experiments have indicated that differences in the charge density, and not the flexibility, of single- and double-stranded polyanions are the cause of the differences in the structures of polyplexes composed of PLL homopolymers and either single-stranded or double-stranded DNA.[10] Coarse-grained simulations, which offer precise control over the specific properties that are varied, are, therefore, useful in investigating the impact of variation in polyelectrolyte chain length and flexibility on polyplex structure and interpreting experimental results. Some relevant coarse-grained studies have been performed previously,[16,17,26–28,18–25] and, notably, there have been a few recent investigations of the formation of aggregates.[29–34] These coarse-grained studies of aggregate formation have had two main areas of focus. First, there have been studies that focused on the aggregation of double-stranded DNA or siRNA, specifically, using a coarse-grained model that was parameterized for DNA/siRNA[32,33] or an atomistic model for siRNA.[34,35] A second group of simulations focused on the aggregation of polyanions in the presence of small cations and investigated how the flexibility of the polyanions, the charge density of the polyanions and the valency of the cations impacted aggregation.[29–31]
Here, we use coarse-grained molecular dynamics simulations to examine the impact of variation in polyelectrolyte chain length and flexibility on the structures of complexes formed from oppositely charged polyelectrolyte chains. The polyelectrolytes in the simulations are simple models, in which the beads of the polyanion and polycation chains have opposite unit charges but are identical in terms of mass and size. Thus, we isolate how changes in chain length and flexibility impact complex structure without complications from the molecular level details of the polyelectrolyte chains. In the first section, we examine the structure of complexes formed in simulations containing a single polyanion chain with charge −50 whose flexibility is varied in the presence of several shorter flexible polycation chains whose chain lengths and numbers are varied. In the second section, we perform simulations containing several polyanion chains and investigate how polyanion flexibility and the lengths of the oppositely charged polycations impact the formation of polyplex aggregates.
2. Methods
2.1. Chain Models
The polyelectrolytes were modeled using a bead-spring model that has been extensively used in previous studies.[18,28,36–38] All parameters in the system are given in terms of the basic unit of energy , the basic unit of length σ and the basic unit of mass m. The basic units of time and temperature T are given by and , where is the Boltzmann constant. Bonded beads interact through an attractive finite extensive, nonlinear elastic (FENE) potential given by
| (1) |
with spring constant and maximum bond distance , producing an average bond length of 1.1 σ. The stiffness of the polyanion chain was varied through the angle flexibility term,
| (2) |
where is the angle stiffness term and is the bond angle in degrees. The equilibrium bond angle in these simulations was always set to 180°. The polyanions were modeled with a wide range of angle stiffness terms with , taking values between 0 and 300 /deg2. The exact values used for the polyanions are specified in the Results section and Table S1. In all simulations, the polycations are assumed to be fully flexible with .
The beads in the simulations also interact through two non-bonded interactions: a purely repulsive Lennard Jones (LJ) potential and a Coulomb potential. The shifted LJ potential is given by
| (3) |
such that the LJ interaction becomes zero at , placing the chains in a good solvent. The Coulomb potential is given by
| (4) |
where is the valence of particle i, and is Bjerrum length, which is the distance at which the interaction energy between two unit charges would be equal to . In water at 300 K, . The charge-to-charge distance along the phosphate backbone in DNA is ~3.4 Å, resulting in a Coulomb strength parameter for ssDNA and dsDNA, where is the average distance between charges along the chain. In the coarse-grained model used here, all beads carry a single charge and are separated by a bond with average length 1.1 σ. We set , giving a Coulomb strength parameter for the coarse-grained polyelectrolytes, a value between those of ssDNA and dsDNA. This value was not varied in these simulations.
The simulations were performed using the LAMMPS molecular dynamics software package.[39] A Langevin thermostat with damping constant was used to maintain a constant temperature . Long-range electrostatic interactions were included using the P3M mesh-Ewald method. The initial configurations of the systems were generated randomly. Chains were built as random walks with the requirement that the minimum next nearest neighbor distance between chain beads was 2 σ, producing starting conformations that were extended. Counterions were added to the simulation boxes when necessary to produce systems with a net charge of 0. The counterion beads had the same parameters as the monomers.
Every simulation began with an initial equilibration period using a short time step, , that was gradually increased from 10−5 to 0.005 to allow for relaxation of high LJ energies resulting from initial configurations with overlapping beads. All production runs used a time step and were performed for at least 0.75 × 106 . Simulations with multiple polyanion chains were performed for longer, ranging from 1.5 × 106 to 30 × 106 . All simulations were performed in cubic boxes with edge lengths between 75 and 100 σ. The details for all simulations, including production lengths and box sizes, are given in Table S1. The trajectories were visualized using VMD.[40]
2.2. Monitoring Conformation of Chains
The conformational properties of the chains were monitored by determining the radius of gyration tensor which was then diagonalized to obtain the three principal components, , and (Equation 5), where is the largest component and is the smallest component. The relative shape anisotropy (RSA or ) is calculated from these principal components as shown in Equation 6. RSA can range between zero when the shape of the polyanion is spherical and 1 when all its monomers lie in a straight line (i.e. a rigid rod). and RSA are reported as averages, and , over the last 0.45 × 106 of the trajectories.
| (5) |
| (6) |
Preliminary simulations of a single 50mer polyanion in the presence of only counterions were performed to examine how , and persistence length change in response to alone (Figure S1). As expected, both and gradually increase with . Furthermore, the maximum was determined to be ~16 σ. The morphologies of the polyanions can be roughly characterized using this maximum and . Rods have maximum and values of ~16 σ and ~1.0 while collapsed structures have significantly lower values. Hairpins have roughly equal to half of the maximum (~8 σ in this case) and a relatively high of ~0.8 due to their linear-like shape. On the other hand, toroids have and values less than the half maximums ( < 8 σ and < 0.5). The gradually increases with in a linear fashion as shown in Figure S1. However, the stiffness of the polyanion will be denoted by , not , in the remainder of the study.
3. Monitoring Conformation of Chains
3.1. A Single Polyanion Condensed by Multiple Polycations
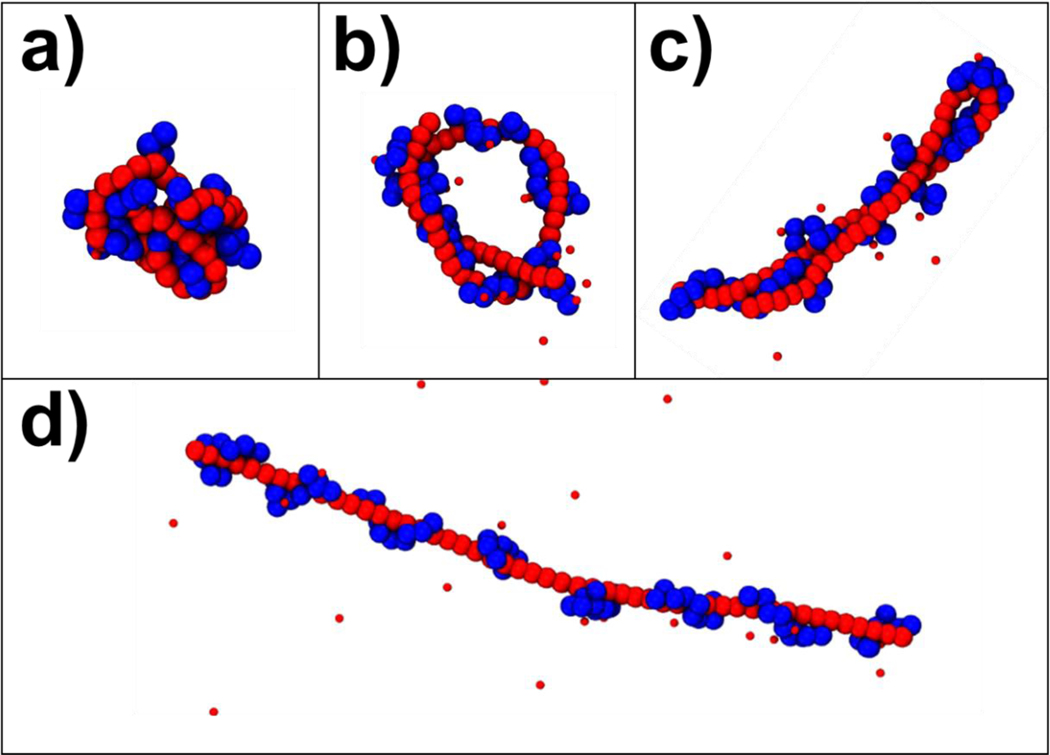
We first examine polyplexes formed in simulations containing a single polyanion chain, whose flexibility was varied through the angle bending stiffness in the chain, and multiple flexible polycations. The single polyanion chain had length 50, giving a total polyanion charge of −50, while the average polycation length and the total charge of the polycations were varied. Polycations of slightly different lengths were used to maintain consistent values of ; for example, simulations with could include two polycations of length 9 and four of length 8, giving , or two polycations of length 12 and two of length 13, giving . For more details, Table S2 contains the explicit number and length of the polycation chains for each respective value. The polyelectrolyte complexes had a wide variety of structures in these simulations, depending on the flexibility of the polyanion chain (Figure 1), ranging from collapsed globules that were typical for flexible polyanions (Figure 1a) to toroids and hairpins for polyanions with intermediate flexibilities (Figure 1b and c) to rod-like shapes for stiffer polyanions (Figure 1d).
Figure 1.
Snapshots of polyplexes formed from single polyanions with varying stiffnesses and multiple, short polycations with varying lengths. Polyanions chains are shown in red, while polycation chains are shown in blue. The small red beads are neutralizing counterions. The panels show complexes of (a) a polyanion with and , (b) a polyanion with and , (c) a polyanion and and (d) a polyanion with and .
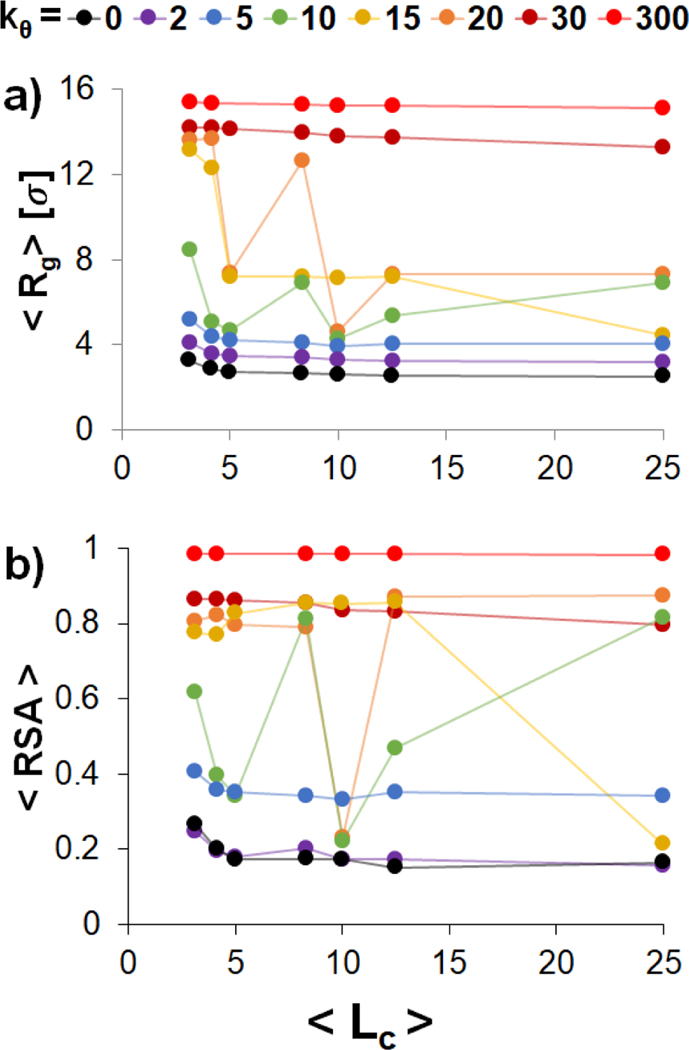
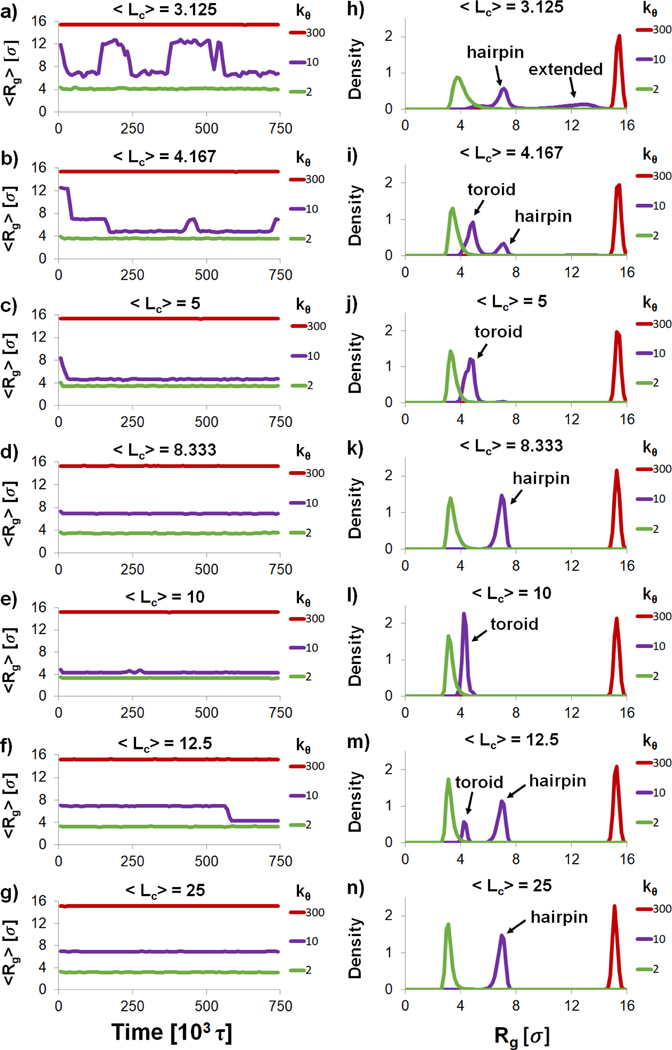
To quantify the impact of varying and on polyplex structure, we calculated and of the polyanion as a function of with (Figure 2). In agreement with previous results[21], there are three structural regimes based on the flexibility of the polyanion. First, for flexible polyanions , is small and continuously decreases as increases. ranges between 0.4 and 0.2 in this regime, indicating that the polyanion adopts a globular form. Second, for stiff polyanions , and maintain values of approximately 16 σ and 1.0, respectively, for all , indicating that stiff polyanions remain in rod-like conformations. Third, for semiflexible polyanions (), and fluctuate wildly as increases; these fluctuations are due to the formation of toroids , hairpins , and other morphologies similar to those shown in Fig. 1 panels (b) and (c), and slow transitions between one morphology to the other. To better quantify the structural changes in the three regime, we present the moving average of over the length of the trajectory and histograms of for every and in Figure 3. It can be clearly seen that the flexible polyanion forms a globular complex and the rigid polyanion remains rodlike . On the other, the semiflexible polyanion can vary between toroids (with that are slightly greater than 4 σ) and hairpins (with that are slightly less than 8 σ). Obtaining converged values in semiflexible regime is therefore challenging and would require more sampling beyond the scope of this study.
Figure 2.
(a) and (b) of a 50-bead polyanion with varying flexibility condensed by multiple polycation chains as a function of , the average length of the polycation chains in the system. The flexibility of the polyanion was varied by changing the value of shown in the figure legend) by fixing total polycation-to-polyanion charge ratio at 1. Table S2 contains the explicit number and length of the polycation chains for each respective value. The and were calculated from the last 0.3 × 106 of the trajectory.
Figure 3.
(a-g) Moving averages of (taken over a ±7.5 × 103 τ window) over the length of the simulation and (h-n) histograms of for all of the listed values in Table S2. Only representative stiffnesses of for the flexible, semiflexible and stiff regime are shown for the sake of clarity.
The data in Figure 2 are obtained when (the total positive charge of the polycations equals the negative charge of the polyanion). However, there is great interest in other ratios, as experiments often study the condensation of polyanions while increasing the polycation concentration (i.e, increasing the N/P ratio). Thus, these experimental studies focus on when condensation of the polyanion is complete and whether added polycations associate with condensed polyanions or remain free in solution.[7,41–43] For example, one study of PEI-based gene delivery showed that, while DNA condensation was complete when N/P = 3, gene transfection efficiency improved significantly when N/P = 10, indicating that unbound PEI may facilitate gene transfection.[7,42,43] To investigate the impact of the total polycation charge on polyplex structure, we performed simulations for a total of three polycation/polyanion charge ratios ( and 2, in addition to ). The existence of three structural regimes based on the flexibility of the polyanion was also observed when and 2 (Figures S2 and S3). We note that direct comparisons between N/P and may be difficult in some cases, especially for polycations such as PEI where some amine nitrogens remain unprotonated.[44]
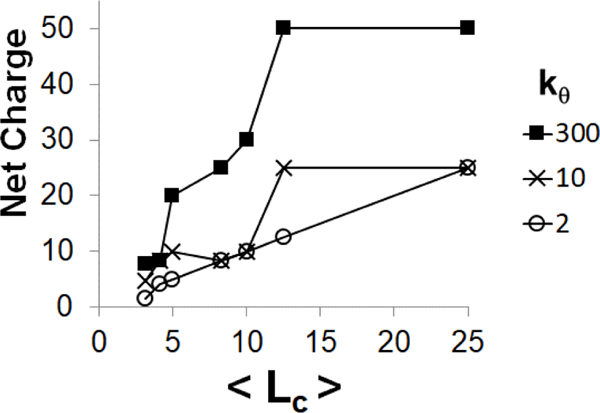
For undercharged () and neutral systems (), all of the polycations were found to bind to the polyanion chain for all and values, where polycation chains are classified as bound to the polyanion if any bead of the polycation chain was within 2 σ of any bead of the polyanion. However, this is only rarely observed in overcharged systems (); in these systems, the net charge of the polyplex (i.e., the sum of the charges of all polyelectrolyte chains in the polyplex) is positive, but, in most cases, one or more polycation chains remain free in solution. The magnitude of the net charge on the polyplex varies depending on the flexibility of the polycation and length of the polycation (Figure 4). The net charge was calculated by multiplying the number of polycation chains within 2 σ of the polyanion by the and subtracting the charge of the polyanion. In general, increased polyanion stiffness promoted the binding of additional polycations, resulting in polyplexes with stiff polyanions usually having higher net charges than corresponding polyplexes with more flexible polyanions. For example, all of the polycations in the simulation with bind to the stiff () polyanion, but do not do so when the polyanion is more flexible. Additionally, the net charge of the polyplex generally increases with polycation length, in agreement with previous results by Dias et al.[22] Thus, longer polycation chains are more likely to form overcharged polyplexes.
Figure 4.
Net charge of a complex formed from a single polyanion condensed by multiple polycation chains as a function of the average length of the polycation chains . Three different polyanions flexibilities were investigated: flexible (, empty circles), semiflexible (, crosses) and rigid (, filled squares). The total polycation-to-polyanion charge ratio is equal 2. The net charge of the complex was calculated by multiplying the number of polycations within 2 σ of the polyanion by and subtracting the charge of the polyanion.
We now examine how the condensation of the polyanion responds to variation in the charge ratio for each of the three structural regimes. In the flexible polyanion regime (), values of both and of the polyanion are larger in the system than in the corresponding neutral and overcharged systems for all values of (Figure 5). The charge of the polycations in the undercharged system does not neutralize the polyanion charge, resulting in intrachain repulsion and a relative expansion of the polyanion. For both the undercharged and neutral system, and gradually decrease as is increased. This behavior agrees with phenomena mentioned by Dias et al., in which complexes with longer polycations lengths lead to compaction for undercharged and neutral systems.[22] In contrast, there is an expansion of the polyanion in the overcharged system () for longer polycations (). This expansion is associated with an increase in the net charge within the polyplex, as shown previously (Figure 3).
Figure 5.
Variation of and of a single polyanion in the flexible regime () condensed by multiple polycation chains with (empty circles), 1 (crosses), and 2 (filled squares) as a function of .
The impact of variation in on polyplex structure in the semiflexible regime () is harder to interpret (Figure 6), as and change significantly when the polyanion adopts different morphologies, including extended structures , hairpins and toroids (Figure 6). However, many of the trends that were observed for the flexible polyanion are repeated, as the polyanion is typically smallest in the neutral system and is at a maximum in the presence of short polycations. Unless the polycations are very short, the polyanions in the undercharged system typically have and , indicating the formation of hairpins. Both toroid and hairpin structures are formed in the neutral and overcharged systems, with and , indicating the formation of a toroid when . The and of rigid polyanions () remain near their maximum values of 16 σ and 1.0 for all values of and (Figure 7), indicating that the chain remains in a rod-like conformation.
Figure 6.
Variation of (a) and (b) of a single polyanion in the semiflexible regime () condensed by multiple polycation chains with (empty circles), 1 (crosses) and 2 (filled squares) as a function of values.
Figure 7.
Variation of (a) and (b) of a single polyanion in the stiff regime condensed by multiple polycation chains with (empty circles), 1 (crosses) and 2 (filled squares) as a function of .
Many of the results presented here can be compared with previous coarse-grained simulations of polyelectrolyte complexation. Notably, Narambuena et al. also identified three distinct structural regimes and found that semiflexible chains form hairpins/toroids while stiffer polyanions maintain extended conformations.[21] Another coarse-grained study by Dias et al.[22] found that short polycations are only loosely bound to relatively long polyanions and that polyanions have more compact structures when condensed by longer polycations, a result that agrees with our observations of the behavior of flexible and semi-flexible polyanions (Fig. 2, 5, and 6). In contrast, Zhou et al.[25] found that varying polycation length had only a small impact on the Rg of the polyanion; however, this study used only a small range of polycation lengths. Finally, both Dias et al.[22] and Zhou et al.[25] found that the polyanion expands in the presence of an excess of polycations when the net charge of the polyplex becomes positive, in agreement with the results found here.
3.2. Multiple Long Polyanions Condensed by Multiple Polycations
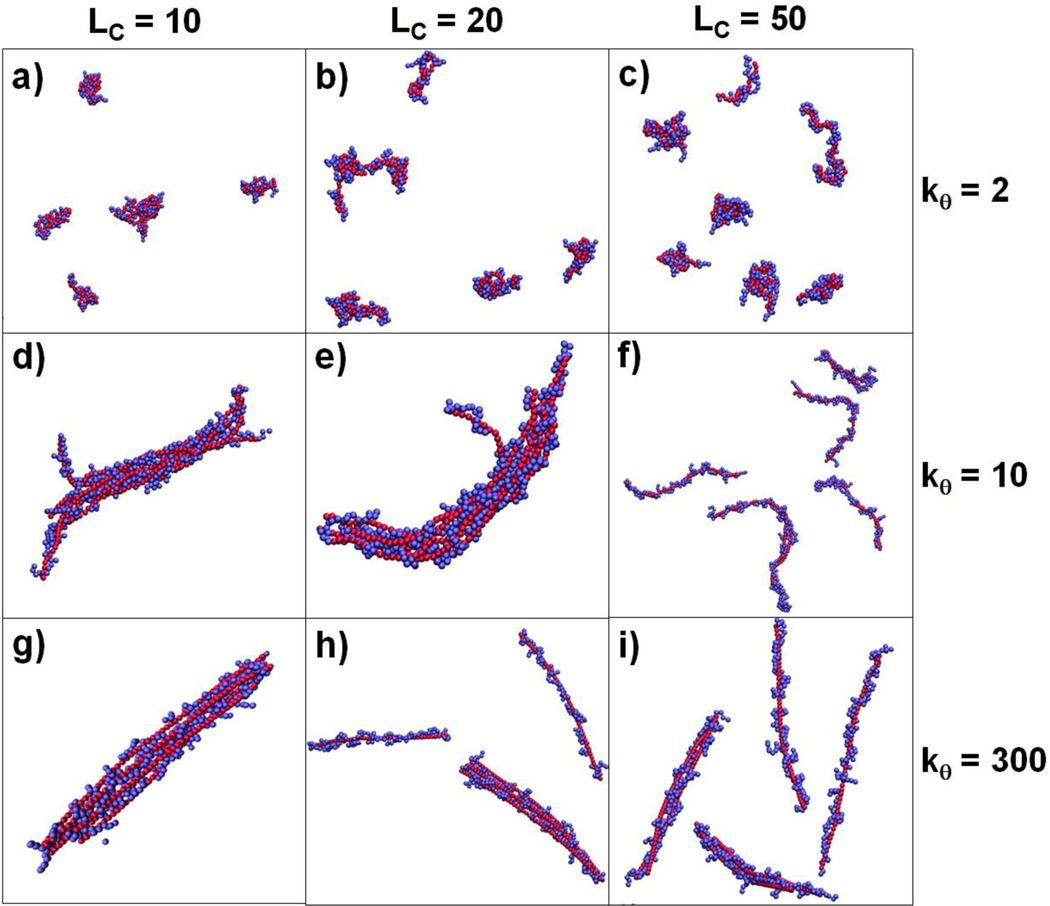
In this section, we present coarse-grained simulations of systems containing multiple polyanion chains and examine factors that lead to the formation of polyplex aggregates, where aggregation refers to the formation of a polyelectrolyte complex that contains multiple polyanion chains. Specifically, these simulations contained 6 polyanion chains of length of 50 () and multiple polycation chains whose charge totaled +1200, producing a system with . The flexibility of the polyanions and the lengths of the polycations were varied in nine different simulations, with and = 10, 20 & 50. The final configuration of each system is presented for each polyanion flexibility and polycation length in Figure 8. Large polyplex aggregates containing all or most of the polyanion chains are produced in some of these simulations. The polyanions in these aggregates are generally aligned parallel to each other, with polycation chains wrapped between and around the polyanions within the aggregate. Aggregate formation is influenced by both polyanion flexibility and polycation chain length. In particular, it seems some threshold of polyanion stiffness is required for the formation of stable aggregates, as both semiflexible () and stiff () polyanions formed large, long-lasting aggregates, while flexible polyanions () did not aggregate, but were, instead, individually condensed by the polycations. Aggregation was also enhanced when polycations were short. Both semiflexible and stiff polyanions formed a single, large aggregate with the shortest polycations (Figure 8, panels d and g) and did not form large aggregates in the presence of the longest polycations (Figure 8, panels f and i).
Figure 8.
Images from the final time step of multiple polyanion simulations for polycation lengths and polyanion stiffnesses . Polyanion beads are shown in red, while polycation beads are shown in blue. Only polycation beads within 4 σ of any polyanion are shown for clarity.
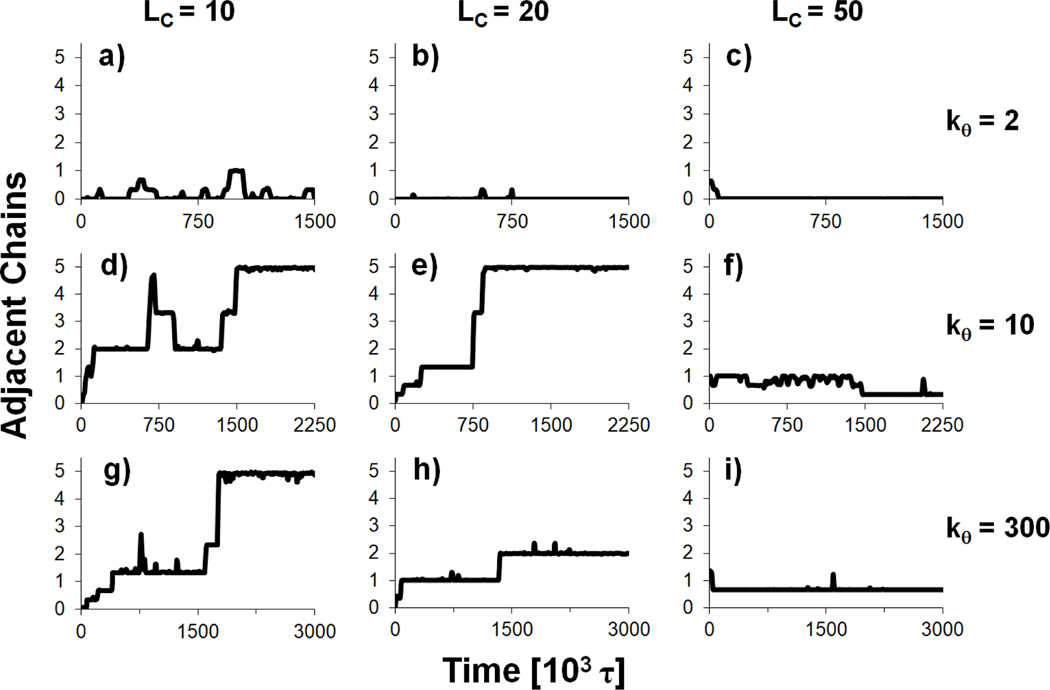
To quantify the formation and stability of the aggregates, we calculated the number of polyanion chains that were adjacent to each polyanion as a function of time, where polyanions were defined as being adjacent if any two beads of the chains were within 4σ (Figure 9). As these systems contained 6 polyanions, each polyanion could be adjacent to, at most, 5 other polyanions and the polyplex is fully aggregated if the number of adjacent chains is equal to 5. For flexible chains (), the average number of adjacent polyanions does not exceed 1, as there is little to no direct interaction between these very flexible polyanions. In contrast, the semiflexible and stiff polyanions formed a single, large aggregate when that remained stable throughout the remainder of the simulation. Based on the simulations performed here, it is difficult to make any conclusions about differences in the tendency to aggregate between semiflexible and stiff polyanions. When , the semiflexible polyanions form a single aggregate, while the stiff polyanions form a smaller aggregate containing only 4 of the polyanion chains (Figure 8h). However, this behavior may be the result of differences in the starting configuration or other kinetic effects, and the stiff polyanions may fully aggregate in the system if the simulation was continued. Thus, the simulations here only seem to indicate that there is a threshold value of between 2 and 10; polyanion chains must be stiffer than this threshold for significant aggregation to occur.
Figure 9.
The average number of polyanion chains adjacent to each polyanion for polycation lengths and polyanion stiffnesses . The number of adjacent chains is defined as the number of polyanions that have at least one bead within 4 σ of a given polyanion. The data are shown as moving averages over a ± 7.5 × 103 τ window.
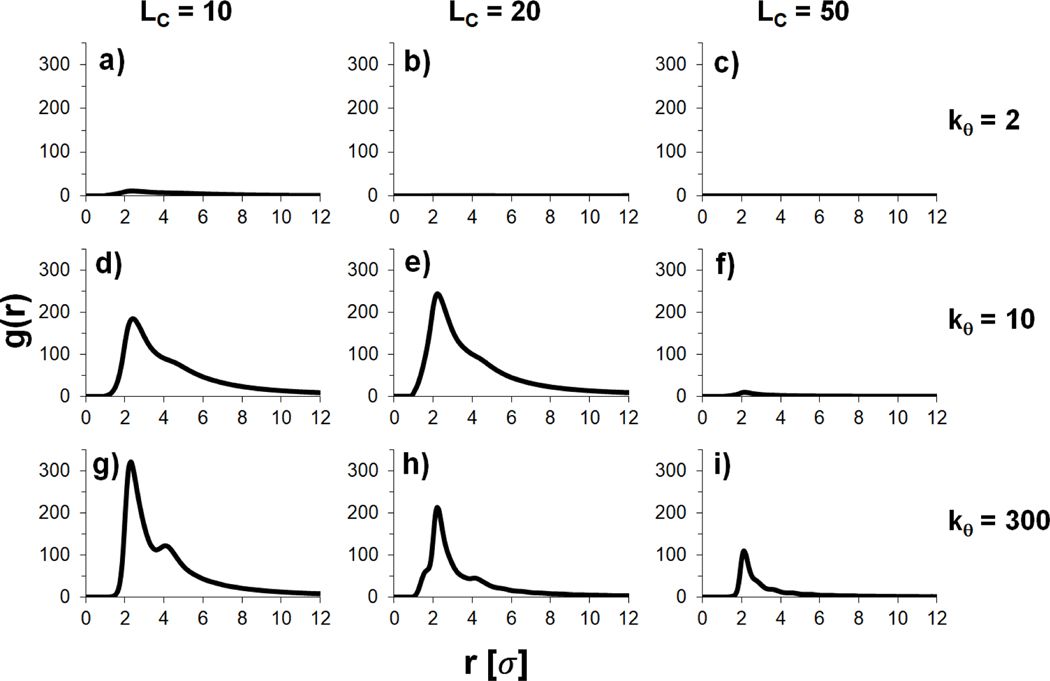
Although it cannot be definitively determined whether semiflexible or stiff polyanions aggregate more, there does appear to be a difference in the structures of their aggregates. To quantitatively characterize the structure of the aggregate, the radial distribution function (RDF) between polyanion beads of separate chains was plotted for each stiffness ( = 2, 10 & 300) and polycation length (, and 50) in Figure 10. The RDF of the fully aggregated stiff polyanion system (, ) is the most ordered with a clear first peak at 2.3 σ and a smaller second peak at 4.3 σ. The semiflexible polyanion RDF has a broader, single broad peak with a maximum at 2.4 σ for and at 2.6 σ for . An examination of of the polyanions in the aggregated polyplexes also indicates that polyanion flexibility influences the polyplex structure (Figure S4). While the semiflexible polyanions in the aggregates do not form toroids or hairpins as they did in the single polyanion simulations, values of the semiflexible polyanions in the aggregates are less than that of the stiff polyanions.
Figure 10.
Bead-to-bead radial distribution functions (RDFs) of separate polyanions from the last 450 × 103τ of multiple polyanion simulations for polycation lengths and polyanion stiffnesses
3.3. Multiple Short Polyanions Condensed by Multiple Long Polycations
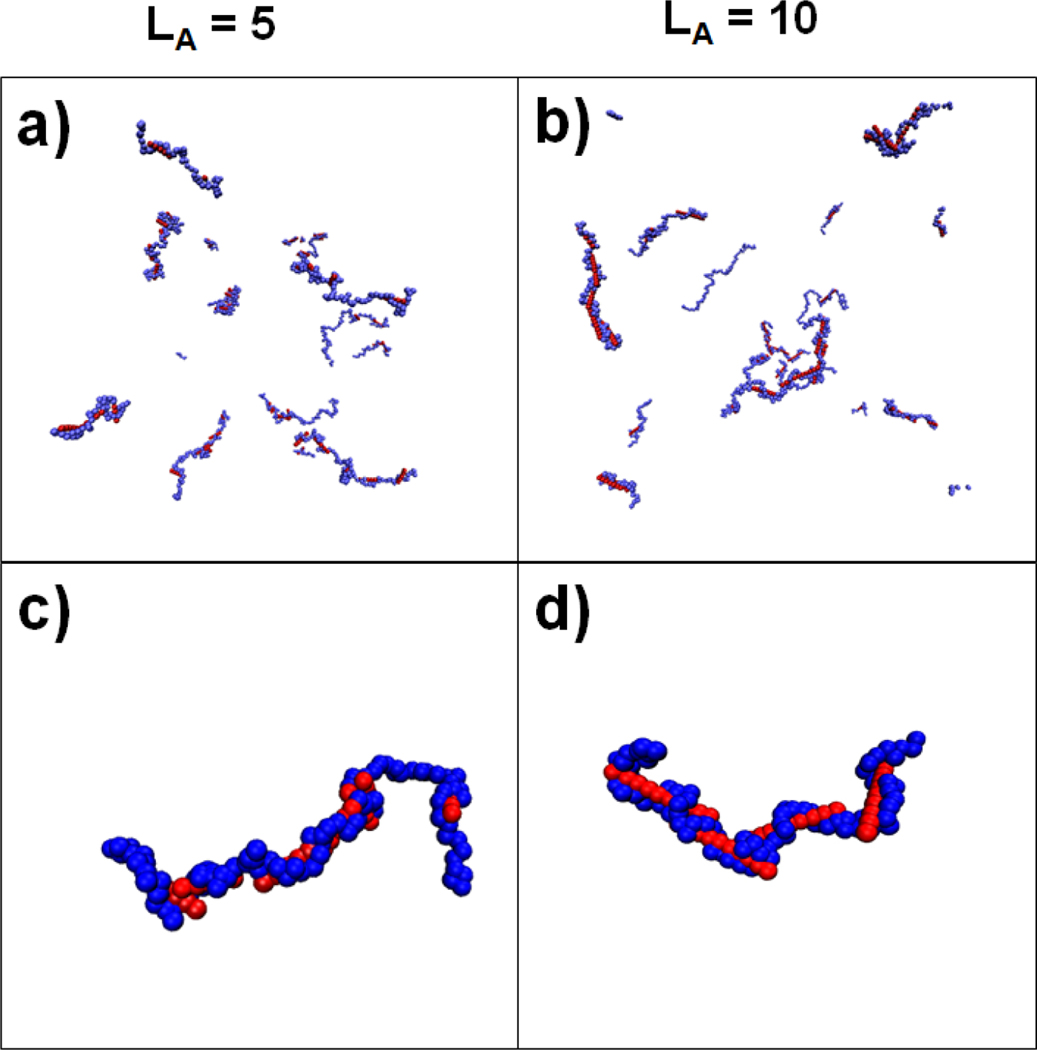
Polyplexes containing ~20 bp long siRNA have repeatedly been shown to be less stable than those containing their much longer plasmid DNA counterparts in experiments.[45,46] It has been commonly suggested that this difference in stability is the result of the large differences between the chain lengths (and charges) of the two nucleic acids. To investigate structures of siRNA-based polyplexes, we performed simulations of complexation between relatively short, stiff () polyanions and longer, flexible polycations. These simulations contained multiple stiff polyanions of length 5 or 10 to have a total charge of −250 (fixed) and 10 polycations of length 100, giving . The final steps of both simulations (Figure 11a and b) show that the polycation chains remain distinct and large complexes containing multiple polycations do not form. Furthermore, despite the polycations being extremely flexible (), they do not collapse, but remain extended to enable interactions with many of the short, stiff polyanions. This is unlike what is observed for both the single (Figure 5) and multiple flexible polyanion (Figure 8a, b, and c) simulations where complexes of long, flexible polyelectrolytes have globular configurations.
Figure 11.
Images of complexes formed from longer flexible polycations (shown in blue) and short, rigid polyanions (red). The images show either the entire system [panels (a) and (b)] or focus on a selected complex [panels (c) and (d)]. , the length of the polyanion chains, is 5 [panels (a) and (c)] or 10 [panels (b) and (d)]. The images are from the final snapshot of a 3 × 106 τ long simulation.
Additionally, images of selected polycation chains bound to several of the short polyanions show that the complex structures differ from the aggregates of longer, stiff polyanions that were shown previously (Figure 11c and d). When these short polyanions interact, they do not form the parallel, ordered bundles like those that were found for longer polyanions and, instead, typically interact by having overlapping ends. This is especially true for polyanions with as shown in snapshots of the last 50 timesteps of the trajectory (Figure S5). Additionally, the interactions between the polyanions with are relatively unstable, as the polyanions move along the polycation to which they are bound, only briefly interacting with other polyanions in the complex (Figure S6).
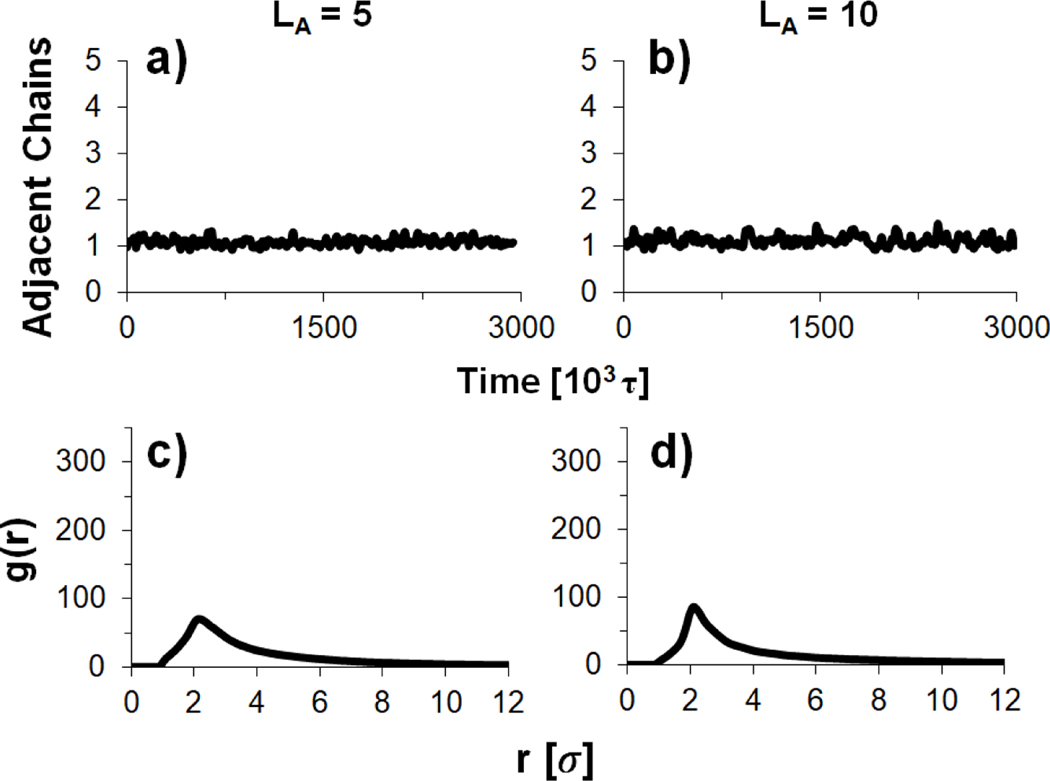
To quantitatively characterize interactions between short polyanions in these polyplexes, we calculated both the average number of adjacent polyanions and the bead-to-bead RDF of separate polyanions (Figure 12), as was done for simulations with longer polyanions (Figure 10). The average number of adjacent chains for both polyanion lengths ( and 10) fluctuates around 1 throughout the simulations, indicating that on average each polyanion would be overlapping end-to-end with one other polyanion. However, as discussed previously, these interactions are less stable than the long-lasting aggregates observed for longer polyanions simulations (Figures 8 and 9). The RDFs for the two short polyanion lengths are also similar and have magnitudes that are lower than what was observed in aggregates of long polyanion chains (Figure 10). Thus, they confirm that interactions between short, stiff polyanions are present, but less prevalent than in the aggregates of long, stiff polyanion complexes.
Figure 12.
Moving average number of polyanion chains adjacent to each polyanion [panels (a) and (b)] and bead-to-bead RDFs of polyanion chains [panels (c) and (d)] for systems containing short, stiff polyanions in the presence of longer, flexible polycations. The polyanion chain length, , was either 5 [panels (a) and (c)] or 10 [panels (b) and (d)].
4. Discussion and Conclusion
We performed coarse-grained simulations to examine the impact of varying polyanion chain stiffness and polycation chain length on the formation and structure of polyelectrolyte complexes and aggregates (i.e. complexes that contain multiple polyanion chains). In agreement with previous results,[21] our analysis of the complexation of single polyanion chains indicated that polyanions of different flexibilities could be separated into three categories based on the structures of their complexes. Flexible polyanions formed collapsed globules when condensed by polycation chains of any length, while stiff polyanions remained in rod-like conformations. Polyanions with intermediate flexibilities formed a variety of morphologies including extended structures, toroids, and hairpins when complexed with polycations of different lengths.
Based on these results, we selected a representative stiffness for each regime (bending constants ) to investigate the formation of polyplex aggregates. Complex aggregates containing all of the polyanion chains in the system were formed for some combinations of polyanion stiffness and polycation chain length. The polyanion chains in these aggregates were, roughly, in extended conformations and parallel to each other, with the flexible polycation chains wrapped between the stiffer polyanions. We identified two factors that promoted the formation of aggregates in these systems: (1) The polyanion chains had to have some amount of stiffness to form aggregates, as complexes containing very flexible polyanions did not aggregate. (2) The polycation chains should be relatively short, as the largest polyplex aggregates were formed when the polycation chain length was less than that of the polyanion.
The aggregation behavior observed here can be compared with previous simulations by a group investigating the aggregation of polyanion chains in the presence of small mono- or trivalent cations.[29–31] These simulations showed that bundled aggregate structures, similar to those shown in Figure 8 here, are produced in systems containing trivalent cations and polyanions with a charge density similar to that used here.[30] Interestingly, this group also showed that flexible polyanion chains could aggregate into large globular structures in the presence of trivalent cations if the Bjerrum length of the system was sufficiently short.[31] In our simulations, the Bjerrum length of the system was kept constant, and we did not investigate how varying the system Bjerrum length and, thus, the charge density of the polyelectrolyte chains impacts aggregation.
The simulations presented here can shed light on the structures of polyplexes created for use in gene delivery and related experimental results. First, the simulations confirm that polyplex aggregates with relatively stiff polyanion chains packed in parallel arrangements can be produced solely as a result of electrostatic interactions with flexible polycation chains. Thus, the similar structures that have been found in studies of gene delivery complexes[9,47] are not necessarily specific to the atomic level properties of nucleic acids, but may, instead, be understood in terms of general features of polyelectrolytes. Second, while polyelectrolyte charge density was not varied in the simulations here, the simulation results can be used to supplement the suggestion that differences in the aggregation of complexes formed from single-stranded and double-stranded nucleic acids may be due to differences in the charge density, and not the rigidity, of the nucleic acids.[8,9] Specifically, Hayashi et al. reported that more flexible single-stranded RNA was more likely to aggregate than stiffer siRNA when complexed with pLys-PEG.[8] As our simulations indicated that increased stiffness, in isolation, tended to increase aggregation, they suggest that factors other than flexibility, such as differences in charge density, are the reason for this experimental result.
Finally, our results may help explain why PEI/pDNA complexes have been consistently shown to be more stable than their PEI/siRNA counterparts.[45,46] Simulations of longer, stiff polyanions in the presence of shorter, flexible polycations (a system similar to pDNA/PEI) results in the formation of tight bundles of the polyanions, as discussed previously. In contrast, shorter, stiff polyanions bound to a longer, flexible polycation (a system similar to siRNA/PEI) do not interact as extensively. Thus, the short polyanions would be more exposed than longer, aggregated polyanions and the short polyanion/long polycation (siRNA/PEI-like) complexes would be more easily disrupted. We note that a recent study of the complexation of siRNA by block copolymers found complex structures that were similar to those found in our simulations, with multiple siRNAs bound to a single longer polycation chain.[34] The siRNA chains in these complexes remained spaced along the polycation and did not extensively interact with the other bound siRNAs, similar to behavior found here.
Lastly, we note that the simulations presented here focused on examining the impact of chain length and polyanion flexibility on polyplex formation and aggregation. Thus, other characteristics of polyelectrolyte chains, such as the relative hydrophobicity of the polymer and the distance between charges along the chain (i.e. Coulomb strength Γ), are likely to influence polyplex structures. The impact of these characteristics on polyplex formation and aggregation will be investigated in a future study.
Supplementary Material
Acknowledgements
Funding Sources
We acknowledge the partial financial support for this work from NIH/NIGMS,1R15GM106326-01A.
Footnotes
Supporting Information.
Simulation details for the systems examined, Table S1; Specific combinations of polycation chains for the reported , Table S2; Plots of and of a 50-bead polyanion as a function of its bending stiffness , Figure S1; Plots of and of the single 50-bead polyanion as a function of for and , Figures S2 and S3; Subplots of multiple 50-bead polyanions over time for polycation lengths and polyanion stiffnesses , Figure S4; Snapshots during the last 0.75 τ of a single complex within the short polyanion simulations ( & ), Figures S5 and S6.
References
- [1].Sing CE, Adv. Colloid Interface Sci 2017, 239, 2. [DOI] [PubMed] [Google Scholar]
- [2].Chen J, Wang K, Wu J, Tian H, Chen X, Bioconjug. Chem 2018, 30, 338. [DOI] [PubMed] [Google Scholar]
- [3].Schubert US, Traeger A, Bus T, J. Mater. Chem. B 2018, DOI 10.1039/C8TB00967H. [DOI] [PubMed]
- [4].Boussif O, Lezoualc’h F, Zanta MA, Mergny MD, Scherman D, Demeneix B, Behr JP, Proc. Natl. Acad. Sci 1995, 92, 7297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Jäger M, Schubert S, Ochrimenko S, Fischer D, Schubert US, Chem. Soc. Rev 2012, 41, 4755. [DOI] [PubMed] [Google Scholar]
- [6].Perevyazko IY, Bauer M, Pavlov GM, Hoeppener S, Schubert S, Fischer D, Schubert US, Langmuir 2012, 28, 16167. [DOI] [PubMed] [Google Scholar]
- [7].Dai Z, Wu C, Macromolecules 2012, 45, 4346. [Google Scholar]
- [8].Hayashi K, Chaya H, Fukushima S, Watanabe S, Takemoto H, Osada K, Nishiyama N, Miyata K, Kataoka K, Macromol. Rapid Commun 2016, 37, 486. [DOI] [PubMed] [Google Scholar]
- [9].Lueckheide M, Vieregg JR, Bologna AJ, Leon L, Tirrell MV, Nano Lett. 2018, 18, 7111. [DOI] [PubMed] [Google Scholar]
- [10].Vieregg JR, Lueckheide M, Marciel AB, Leon L, Bologna AJ, Rivera JR, Tirrell MV, J. Am. Chem. Soc 2018, 140, 1632. [DOI] [PubMed] [Google Scholar]
- [11].Elsayed M, Corrand V, Kolhatkar V, Xie Y, Kim NH, Kolhatkar R, Merkel OM, Biomacromolecules 2014, 15, 1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Jiang Y, Sprouse D, Laaser JE, Dhande Y, Reineke TM, Lodge TP, J. Phys. Chem. B 2017, 121, 6708. [DOI] [PubMed] [Google Scholar]
- [13].Jiang Y, Reineke TM, Lodge TP, Macromolecules 2018, 51, 1150. [Google Scholar]
- [14].Zheng C, Niu L, Yan J, Liu J, Luo Y, Liang D, Phys. Chem. Chem. Phys 2012, 14, 7352. [DOI] [PubMed] [Google Scholar]
- [15].Zheng C, Niu L, Pan W, Zhou J, Lv H, Cheng J, Liang D, Polymer (Guildf). 2014, 55, 2464. [Google Scholar]
- [16].Hayashi Y, Ullner M, Linse P, J. Chem. Phys 2002, 116, 6836. [Google Scholar]
- [17].Winkler RG, Steinhauser MO, Reineker P, Phys. Rev. E - Stat. Physics, Plasmas, Fluids, Relat. Interdiscip. Top 2002, 66, 1. [Google Scholar]
- [18].Crozier PS, Stevens MJ, J. Chem. Phys 2003, 118, 3855. [Google Scholar]
- [19].Hayashi Y, Ullner M, Linse P, J. Phys. Chem. B 2003, 107, 8198. [Google Scholar]
- [20].Hayashi Y, Ullner M, Linse P, J. Phys. Chem. B 2004, 108, 15266. [Google Scholar]
- [21].Narambuena CF, Leiva EPM, Chávez-Páez M, Pérez E, Polymer (Guildf). 2010, 51, 3293. [Google Scholar]
- [22].Dias RS, Linse P, Pais CAAC, J. Comput. Chem 2011, 32, 2697. [DOI] [PubMed] [Google Scholar]
- [23].Jorge AF, Dias RS, Pais AACC, Biomacromolecules 2012, 13, 3151. [DOI] [PubMed] [Google Scholar]
- [24].Lazutin AA, Semenov AN, Vasilevskaya VV, Macromol. Theory Simulations 2012, 21, 328. [Google Scholar]
- [25].Zhou J, Barz M, Schmid F, J. Chem. Phys 2016, 144, 0. [DOI] [PubMed] [Google Scholar]
- [26].Andreev M, Prabhu VM, Douglas JF, Tirrell M, De Pablo JJ, Macromolecules 2018, 51, 6717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Rathee VS, Sidky H, Sikora BJ, Whitmer JK, J. Am. Chem. Soc 2018, 140, 15319. [DOI] [PubMed] [Google Scholar]
- [28].Ziebarth J, Wang Y, J. Phys. Chem. B 2010, 114, 6225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Varghese A, Rajesh R, Vemparala S, J. Chem. Phys 2012, 137, DOI 10.1063/1.4771920. [DOI] [PubMed]
- [30].Tom AM, Rajesh R, Vemparala S, J. Chem. Phys 2016, 144, DOI 10.1063/1.4939870. [DOI] [PubMed]
- [31].Tom AM, Rajesh R, Vemparala S, J. Chem. Phys 2017, 147, DOI 10.1063/1.4993684. [DOI] [PubMed]
- [32].Kang H, Yoo J, Sohn BK, Lee SW, Lee HS, Ma W, Kee JM, Aksimentiev A, Kim H, Nucleic Acids Res. 2018, 46, 9401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Sun T, Mirzoev A, Minhas V, Korolev N, Lyubartsev AP, Nordenskiöld L, Nucleic Acids Res. 2019, 47, 5550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Tabujew I, Heidari M, Freidel C, Helm M, Tebbe L, Wolfrum U, Nagel-Wolfrum K, Koynov K, Biehl P, Schacher FH, Potestio R, Peneva K, Biomacromolecules 2019, DOI 10.1021/acs.biomac.9b01061. [DOI] [PubMed]
- [35].Kim M, Kim HR, Chae SY, Larson RG, Lee H, Park JC, J. Phys. Chem. B 2013, 117, 6917. [DOI] [PubMed] [Google Scholar]
- [36].Stevens MJ, Biophys. J 2001, 80, 130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Stevens MJ, Kremer K, J. Chem. Phys 1995, 103, 1669. [Google Scholar]
- [38].Stevens MJ, S. J. Plimpton, 1998, 2, 341. [Google Scholar]
- [39].Plimpton S, J. Comput. Phys 1995, 117, 1. [Google Scholar]
- [40].Humphrey W, Dalke A, Schulten K, J. Mol. Graph 1996, 14, 33. [DOI] [PubMed] [Google Scholar]
- [41].Boeckle S, von Gersdorff K, van der Piepen S, Culmsee C, Wagner E, Ogris M, J. Gene Med 2004, 6, 1102. [DOI] [PubMed] [Google Scholar]
- [42].Yue Y, Jin F, Deng R, Cai J, Chen Y, Lin MCM, Kung HF, Wu C, Control J. Release 2011, 155, 67. [DOI] [PubMed] [Google Scholar]
- [43].Yue Y, Jin F, Deng R, Cai J, Dai Z, Lin MCM, Kung HF, Mattebjerg MA, Andresen TL, Wu C, Control J. Release 2011, 152, 143. [DOI] [PubMed] [Google Scholar]
- [44].Gallops CE, Yu C, Ziebarth JD, Wang Y, ACS Omega 2019, 4, 7255. [Google Scholar]
- [45].Richards Grayson AC, Doody AM, Putnam D, Pharm. Res 2006, 23, 1868. [DOI] [PubMed] [Google Scholar]
- [46].Kwok A, Hart SL, Nanomedicine Nanotechnology, Biol. Med 2011, 7, 210. [DOI] [PubMed] [Google Scholar]
- [47].Hud NV, Downing KH, Proc. Natl. Acad. Sci. U. S. A 2001, 98, 14925. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.