Complementarities between Early Educational Intervention and Later Educational Quality? A Systematic Review of the Sustaining Environments Hypothesis

Abstract

The sustaining environments hypothesis refers to the popular idea, stemming from theories in developmental, cognitive, and educational psychology, that the long-term success of early educational interventions is contingent on the quality of the subsequent learning environment. Several studies have investigated whether specific kindergarten classroom and other elementary school factors account for patterns of persistence and fadeout of early educational interventions. These analyses focus on the statistical interaction between an early educational intervention – usually whether the child attended preschool – and several measures of the quality of the subsequent educational environment. The key prediction of the sustaining environments hypothesis is a positive interaction between these two variables. To quantify the strength of the evidence for such effects, we meta-analyze existing studies that have attempted to estimate interactions between preschool and later educational quality in the United States. We then attempt to establish the consistency of the direction and a plausible range of estimates of the interaction between preschool attendance and subsequent educational quality by using a specification curve analysis in a large, nationally representative dataset that has been used in several recent studies of the sustaining environments hypothesis. The meta-analysis yields small positive interaction estimates ranging from approximately .00 to .04, depending on the specification. The specification curve analyses yield interaction estimates of approximately 0. Results suggest that the current mix of methods used to test the sustaining environments hypothesis cannot reliably detect realistically sized effects. Our recommendations are to combine large sample sizes with strong causal identification strategies, and to study combinations of interventions that have a strong probability of showing large main effects.

Introduction and Background

“Preschool is not an inoculation against the next 12 years of a child’s life.” This is a common refrain amongst early childhood education researchers on the expected impacts of attending a quality preschool program on children’s developmental trajectories. Despite renowned studies like Perry and Abecedarian, in which disadvantaged children randomly assigned to receive high quality preschool and experienced beneficial long-run impacts on several measures of adult well-being (Barnett & Masse, 2007; Belfield, Nores, Barnett, & Schweinhart, 2006; Campbell et al., 2014; Campbell et al., 2012), and despite good evidence of short-run impacts from preschool programs operating at scale, little evidence exists to support intermediate- and long-run impacts of these modern programs (Phillips et al., 2017). The challenge of generating persistent effects on children’s academic skills is of great interest to researchers, policymakers, and practitioners working to understand how to get the most out of early childhood educational programs.

One of the central ideas in theories of the persistence of early childhood education impacts is that experiencing a school environment that fosters continued learning will prolong the persistence of preschool impacts. This possibility, articulated by Bailey, Duncan, Odgers, and Yu (2017) as the “sustaining environments hypothesis”, refers to the idea that long-term success of early interventions is contingent on the quality of the subsequent learning environment. A sustaining environment is, by definition, a subsequent environment that generates persistent treatment effects of the earlier intervention. Features of sustaining environments are often predicted on the basis of theories in cognitive, developmental, and educational psychology, and may include academic rigor, social support, curricular alignment with an early childhood academic intervention, or many peers who also received high quality early educational experiences (e.g., Bronfenbrenner & Morris, 2006; Stanovich, 1986;Vygotsky, 1978; ). This hypothesis is especially relevant for policy because children eligible for targeted preschool programs tend to come from low-income families, tend to live in low-income neighborhoods, and are more likely to enter schools with fewer resources; thus, children who participate in targeted preschool programs like Head Start experience schools that may be ill-equipped to build upon the skills children gained during preschool (Crosnoe & Cooper, 2010; Currie & Thomas, 2000; Lee & Loeb, 1995; Reynolds, Ou, & Topitzes, 2004; Zhai, Raver, & Jones, 2012).

Several studies have investigated whether specific kindergarten classroom and other elementary school factors account for patterns of persistence and fadeout. These analyses focus on the statistical interaction between some early educational intervention – usually whether the child attended preschool – and a measure of the subsequent educational environment. The key prediction of the sustaining environments hypothesis is clear: a positive interaction between these two variables. Yet recent studies in this area have produced mixed results (e.g., Ansari & Pianta, 2018; Bassok, Gibbs, & Latham, 2018; Jenkins et al., 2018).

History of the Sustaining Environments Hypothesis

The sustaining environments hypothesis has been engrained in the conventional wisdom in child development since the origins of U.S. federal involvement in early education—the Head Start program. In the 1960s, a consortium of researchers was formed at Cornell University to determine the effectiveness of Head start and other compensatory education programs. From this work Zigler (1978) concluded that the persistence of impacts from an early intervention depend upon the degree of parental involvement and, “whether or not the schools follow the pre-school program with further intervention to build upon initial gains” (pp. 73–74). The idea that an effective early educational intervention followed by a high-quality environment is preferable to a counterfactual of an effective early educational intervention followed by a low-quality environment is uncontroversial and nearly tautological. However, a slightly different possibility – that the benefits of an effective early childhood intervention will be amplified when children enter higher quality subsequent educational environments – would have important implications for research and policy. If true, the sustaining environments hypothesis might account for important heterogeneity in the medium- and long-term effects of early educational interventions. Also, more efficiently coordinating investments between early and later educational intervention might have large positive-sum benefits, even holding total funding constant. This idea has been commonly invoked as an insight for maintaining early benefits of preschool (Bogard & Takanishi, 2005; Phillips, 2017). A recent review by Brooks-Gunn, Markman-Pithers, and Rouse (2016) on the directions of future work in early education stated that “if quality is high in a pre-K program but not in the K–3 classrooms that a child later attends, it stands to reason that sustained achievement gains will likely be low” (p. 13). Thus, there is a widespread interest in the field to align the preschool curriculum with the kindergarten to third-grade curriculum to ensure a sustaining environment (Stipek, Clements, Coburn, Franke, & Farran, 2017).

Skill Building Theories and the Sustaining Environments Hypothesis

The sustaining environments hypothesis might function through a variety of mediating processes. However, the most straightforward and intuitive is the notion that “skills beget skills”, an idea called “dynamic complementarity” in the economics literature on early skill formation (Cunha & Heckman, 2007). This is also the basis of the popular concept in cognitive developmental psychology of a “Matthew Effect”, where the (cognitively) rich get richer, as their cognitive skills present them with compounding advantages (Stanovich, 1986). For example, because counting is used to bootstrap children’s learning of basic addition strategies (Baroody, 1987), and addition is often employed as a way to solve multiplication problems (Lemaire & Siegler, 1995), one could imagine an early counting intervention having compounding effects on children’s mathematics achievement, with children who received a counting intervention responding more strongly to subsequent instruction on addition and then multiplication.

However, the evidence for the sustaining environments hypothesis is equivocal. A straightforward implication of dynamic complementarity and the Matthew Effect is that children’s skill levels will diverge during development, as children who start with higher skill levels will accumulate the most benefits from subsequent environments. There is somewhat mixed evidence for this possibility: for example, on achievement tests that can be administered to children at different ages, scores often converge over time, consistent with the hypothesis that later instruction is, on average, a substitute for cognitive skills (i.e., there is a negative interaction between cumulative educational inputs and prior skill level). In contrast, in some datasets, race gaps are found to grow in the early school years, consistent with the possibility that schooling benefits advantaged children more.¹

Evidence for the sustaining environments hypothesis is also mixed in studies that estimate the benefits of investments for individuals with varying levels of prior knowledge or ability. In mostly correlational studies of the relative contributions of prior levels of practice and cognitive ability on skilled performance, findings show that these factors tend to be additive rather than multiplicative, suggesting they are neither complements nor substitutes (Hambrick & Meinz, 2011; Meinz & Hambrick, 2010). In a recent meta-analysis, Simonsmeier and colleagues (under review) estimated a null average correlation between children’s prior domain knowledge and their learning during subsequent instruction. However, they also reported evidence for complementarity (i.e., a positive interaction between prior knowledge and later instruction) when the subsequent instruction was cognitively demanding (i.e., when participants were required to use prior knowledge and/or cognitive processing to learn from the instruction), and for substitutability (i.e., a negative interaction between prior knowledge and later instruction) when later instruction had low cognitive demands. The implications of these findings for making predictions about sustaining environments are not clear. If cognitively demanding instruction implies teaching more advanced content to students in early elementary school, then this aligns strongly with psychological theories of sustaining environments; providing just the right amount of challenge to each student at the appropriate time for continual healthy development (Vygotsky, 1978) may sustain the advantages of early academic intervention. However, schooling likely includes a combination of high- and low-demand instruction; further, instruction about more advanced content may be presented in ways that place high or low demands on children’s cognitive resources.

Evidence from Real World Educational Settings

Prior studies, primarily using correlational data, provide mixed evidence of complementarities between early educational intervention and later educational quality. Several studies use the Early Childhood Longitudinal Studies of Kindergarten (ECLS-K) 1998 cohort panel data to test these interactions. Magnuson, Ruhm, and Waldfogel (2007) found, counter to theoretical predictions, that preschool advantages persisted into elementary school for children attending less enriching classes that were larger and had lower total instruction time. This was due to children with no preschool experience benefitting more from small, academically focused classes, allowing them to catch up; non-preschool attendees attending less academically-focused classes did not catch up, so the preschool advantage persisted.

Using the same data, Claessens, Engel, and Curran (2013) examined whether exposure to advanced math or language and literacy content in kindergarten instruction moderated the impact of preschool. They found that “advanced” reading and math content in kindergarten was beneficial for all students, not differentially beneficial—either as a complement or substitute—for preschool attendees. Bassok et al. (2018) tested moderation of preschool attendance by six different features f kindergarten classroom enrichment using both the 1998 and 2010 ECLS-K cohorts: full-day kindergarten, small class size, kindergarten school co-located with preschool, peer preschool attendance, use of kindergarten transition practices, time spent on reading in kindergarten. In line with Claessens et al. (2013), they found no significant interactions between preschool and subsequent experiences, and no differences in the pattern of null results between the 1998 and 2010 cohort analyses. However, Ansari and Pianta (2018b) analyzed the same data and found that math and language and literacy benefits of preschool attendance persisted for students who attended elementary schools with higher scores on a school quality index.

Despite using the same dataset, the studies vary substantially on other analytic features, including the choice of sustaining environments, their definitions of preschool attendance, sometimes including Head Start children, other times omitting them from all analyses, and their definitions of achievement, with some using growth in achievement and others using total achievement scores. It is not obvious which analytic decisions are most appropriate, which is why we will systematically test the sensitivity of the key interaction estimates to these analytic decisions in a specification curve analysis. Further, it is important to note that in all of these studies, children were not randomly assigned to their early educational intervention (e.g., center-based care) or subsequent educational environments, and are therefore likely subject to selection bias into both preschool interventions and subsequent environments.

More causally informative are quasi-experimental analyses of pairs of programs that are rolled out independently of one another. Perhaps the strongest evidence of complementarity between early and later educational investments comes from Johnson and Jackson’s (2017) analysis of the effects of changes in Head Start and K-12 funding on children’s later educational attainment. They find that the effects of Head Start funding on educational attainment are larger for children who lived in areas that also increased subsequent K-12 funding. Their analysis includes a large sample size and strong checks for threats to internal validity, but a limitation is that the causal mechanisms are not clear: Although an explanation based on complementary academic skills as described above is tempting, others have hypothesized that preschool programs’ impacts on long-term outcomes act through other pathways, such as changes to children’s personality (for a review, see Elango et al., 2015). Further, complementarity is not always found using these kinds of designs. For example, Rossin-Slater and Wüst (2017) found that a Danish preschool program and a nurse-home visiting program were substitutes for each other, with both showing estimated impacts on children’s later educational attainment only for children who were not receiving the other. This lends some evidence to the hypothesis that, at least in the Danish case, health might have been an important mediating pathway through which the preschool program affected much later child outcomes.

Given the strong theoretical reasons for thinking that academic interventions might complement each other, why might such conflicting results appear? One may be that school curricula are sufficiently redundant with effective early educational interventions that children who do not receive the early intervention learn the skills anyway, aided by the steeper learning curve at the beginning of knowledge acquisition (Campbell & Frey, 1970). Additionally, redundant curricula in the early school years may limit opportunities of preschool attendees to build on the knowledge they gained during an effective early educational intervention (Engel, Claessens, & Finch, 2013; Sarama & Clements, 2015). Based on the latter explanation, perhaps exposure to advanced instruction is a promising candidate for a sustaining environment following an early educational intervention.

On the other hand, complementarity may be limited because it is difficult for children to transfer knowledge learned in one context to another (Bailey, 2019; Kang et al., 2018). In combination with rapid learning among children who do not receive high quality educational interventions, both factors might limit the intervention children’s opportunities to transfer knowledge to content months or years later. If true, perhaps cognitive psychological theories may not inform predictions about sustaining environments in real world educational settings as well as they appear to.

Current Study

The purpose of the current study is to quantify evidence in favor of the sustaining environments hypothesis, as measured by positive interactions between early educational intervention and later educational quality on children’s later academic achievement. We begin by meta-analyzing existing studies that have attempted to estimate interactions between preschool and later educational quality. We then attempt to establish the direction and a plausible range of estimates of the interaction between preschool attendance and subsequent educational quality by using a specification curve analysis in a large, nationally representative dataset that has been used in several recent studies of the sustaining environments hypothesis. Specification curve analysis has been used in psychological research to test how analytical decisions affect the pattern of results (e.g., Rohrer, Egloff, & Schmukle, 2017).

The core theoretical prediction of the sustaining environments hypothesis is that the estimated causal effects of early educational interventions that raise children’s academic skills should be larger in higher quality subsequent educational environments. However, two additional auxiliary theories are needed to support this prediction: 1) the causal effects of preschool attendance and later educational quality can be estimated, and that 2) high-quality educational environments improve children’s academic skills. Assumption 1 warrants careful investigation, because data frequently come from studies using non-experimental designs, leaving estimates subject to selection bias. Violations of assumption 2 make tests of the sustaining environments hypothesis conceptually difficult: If a preschool program does not raise children’s elementary school achievement, on average, it is not clear that the sustaining environments hypothesis predicts complementarity between the preschool program and later educational quality. We attempt to address the key prediction and auxiliary assumptions of tests of the sustaining environments hypothesis by including the results of both experimental and non-experimental estimates in our meta-analysis and by generating estimates in the specification curve analysis based on a range of different statistical controls, definitions of preschool attendance, and measures of sustaining environmental factors.

Meta-Analytic Method

Data

We first conducted a literature search to identify all studies that reported a statistical interaction between a measure of early childhood educational quality and later childhood educational quality predicting to children’s later academic achievement. We searched the top three education and developmental research search engines, EBSCO host, ERIC, and PsycINFO for the terms shown in the supplementary materials, shown in Table S1, and sent out inquiries to researchers who had published in the area regarding relevant articles that we may have missed or have not been published. Our search terms were assessed through iterative inclusion and exclusion of terms that would appropriately capture studies addressing the interaction between a pre-K intervention and the quality of the subsequent environment utilizing different analytical strategies, datasets, and constructs. The criteria used to determine the most accurate search terms was to ensure that the following articles would be identified in each of the databases explored : Bailey, Duncan, Odgers, & Yu, (2017), Claessens, Engel, & Curran (2014), Jenkins et al (2018), and Magnuson, Ruhm, & Waldfogel (2007). . Only peer reviewed articles published in scholarly journals or working papers available from university websites, written in English, with a U.S. based sample, measuring early and later school quality, reporting achievement outcomes, and reporting an interaction between early and later school environment were included.

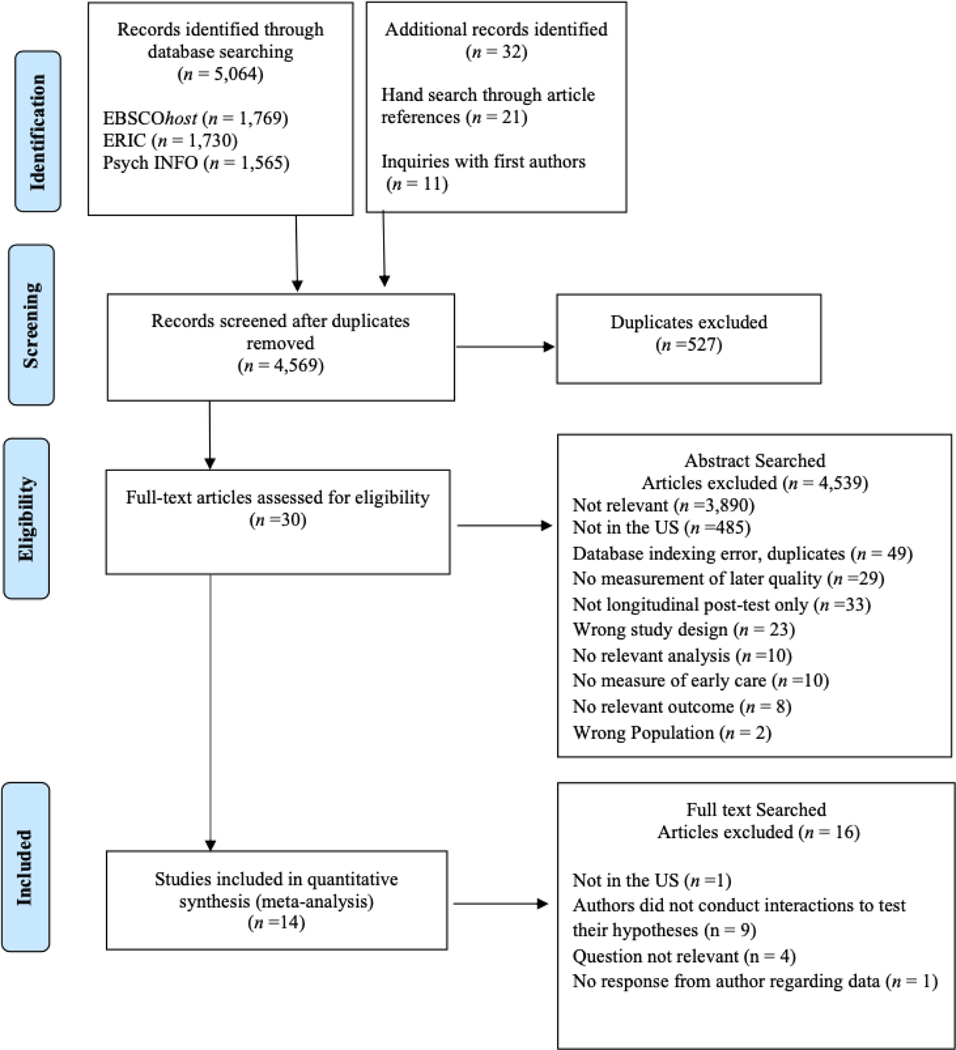
Database results were compiled and screened using the Rayyan website application (Ouzzani et al., 2016), then we hand searched the reference lists of the articles retained and reviewed Google Scholar for all the articles citing the articles identified. Fourteen articles were eligible for analysis; the process of article selection is shown on the PRISMA flowchart (Moher, Liberati, Tetzlaff, & Altman, 2009) in Figure 1. Article titles and abstracts were screened followed by a full text review of articles meeting the inclusion criteria. After the third author screened the article abstract to determine which ones were relevant to the research question, the eligible articles were co-reviewed by all the authors. Disagreements were resolved through group discussion. Five articles reported having run interactions that were not published in the paper; authors of four of the five responded to requests for these estimates. Data were initially entered by the first author, and all entries were checked by the third author. Discrepancies between entries were resolved by the first and third authors. The resulting sample consisted of 82 effect sizes from 16 studies from 14 papers, all with U.S. samples. The list of studies appears in Table 1. The meta-analytic database is available in the online supplementary materials, Appendix A. Notably, our literature search identified a large number of studies published in the two years preceding the search, indicating growing recent interest in this area.

Figure 1.

Flow of Publications Through the Different Stages of the Systematic Review

Table 1:

Studies and Study Characteristics in Meta-Analytic Sample

Reference Authors and Year	Dataset	Outcome Measures	Early Intervention Measures	Later Quality Measures	Early Quality Identification Strategy	Later Quality Identification Strategy
Magnuson, K. A., Ruhm, C., & Waldfogel, J. (2007).	ECLS-K (1998)	Reading and math achievement change from K-3	Preschool enrollment	Low instruction (reverse scored); large class (reverse scored)	OLS	OLS
Claessens, A., Engel, M., & Curran, F. C. (2014).	ECLS-K (1998)	Kindergarten reading and math achievement	Center-based care; Head Start	Minutes of advanced math and reading instruction	OLS	OLS
Swain, W. A., Springer, M. G., & Hofer, K. G. (2015).	Tennessee Pre-k	End of 1st grade Woodcock-Johnson composite scores	Tennessee Pre-k	First grade teacher quality	OLS	OLS
Ansari, A., & Pianta, R. C. (2018a).	NICHD Study of Early Child Care and Youth Development	9th grade math and reading achievement	Early Child Care Quality Composite	Elementary school classroom quality	OLS	OLS
Ansari, A., & Pianta, R. C. (2018b).	ECLS-K (1998)	5th grade achievement index	Preschool enrollment	Moderate and high scores on elementary school quality index	PSM and OLS	PSM and OLS
Bassok, D., Gibbs, C. R., & Latham, S. (2018).	ECLS-K (1998)	Spring Kindergarten math and literacy scores	Preschool enrollment	Full-day kindergarten, kindergarten transitions, advanced math and literacy instruction; small kindergarten class size	OLS	OLS
Bassok, D., Gibbs, C. R., & Latham, S. (2018).	ECLS-K (2010)	Spring Kindergarten math and literacy scores	Preschool enrollment	Full-day kindergarten, kindergarten transitions, advanced math and literacy instruction; small kindergarten class size	OLS	OLS
Jenkins, J. M., Watts, T. W., Magnuson, K., Gershoff, E. T., Clements, D. H., Sarama, J., & Duncan, G. J. (2018).	Head Start Impact Study	Kindergarten or 1st grade language and literacy composite	Head Start offer	Advanced literacy activities in kindergarten and grade 1; full-day kindergarten; kindergarten class size (reverse scored); classroom % FRPL (reverse scored); school % FRPL (reverse scored); school % reading and math proficient	Random Assignment	OLS
Jenkins, J. M., Watts, T. W., Magnuson, K., Gershoff, E. T., Clements, D. H., Sarama, J., & Duncan, G. J. (2018).	TRIAD study of Building Blocks Curriculum	1st grade math composite	Building Blocks math curriculum	Number of kindergarten and 1st grade math activities; mathematics teaching quality	Random Assignment	OLS
Ansari, A., Pianta, R. C., Whittaker, J. V., Vitiello, V. E, & Ruzek, E. A. (2019).	Large U.S. county	Spring pre-k language, literacy, and math achievement	Center-based care or preschool at age 3	Public or private preschool at age 4	PSM and OLS	PSM and OLS
Carr, R. C., Mokrova, I. L., Vernon-Feagans, L., & Burchinal, M. R. (2019).	NCEDL Multi-State Study of Pre-K	Spring Kindergarten language, literacy, and math achievement	Pre-k classroom emotional and instructional support	Kindergarten classroom emotional and instructional support	OLS	OLS
Han, J., O’Connor, E. E., & McCormick, M. P. (2019)	NICHD Study of Early Child Care and Youth Development	Grade 1, 3, and 5 math, reading, and vocabulary achievement	Pre-k classroom quality ratings	Elementary school emotional and instructional support ratings	HLM	HLM
Mashburn, A. J., & Yelverton, R. (2019).	Head Start Impact Study	Spring Kindergarten reading, vocabulary, and math achievement	Time on literacy and language or math activities in Head Start	Time on literacy and language or math activities in Kindergarten	OLS	OLS
Ou, S. R., Arteaga, I., & Reynolds, A. J. (2019).	Chicago Child-Parent Center Program	8th grade math and reading achievement	CPC pre-k intervention	CPC intervention for 1, 2, or 3 or more subsequent years	PSM and OLS	PSM and OLS
Pearman, F.A., Springer, M., Lipsey, M., Lachowicz, M., Swain, W., & Farran, D. (2019).	Tennessee Pre-k	3rd grade math and ELA achievement	Tennessee pre-k offer subsequent years	School quality and number of high quality teachers in grades K-3	Random Assignment	OLS
Carr, R. C., & Vernon-Feagans, L. (2019).	Family Life Project	Spring Kindergarten language, literacy, and math achievement	Head Start attendance	Instructional and emotional support and classroom organization in Kindergarten	PSM and OLS	OLS

Measures.

Outcomes.

In all cases, outcomes were standardized achievement test scores. When multiple outcomes were reported at the same wave (e.g., first grade math and reading achievement), both were entered into the meta-analytic database. When the same construct was used as an outcome at multiple waves (e.g., kindergarten and first grade math achievement), we entered results for only the most recent outcome measure. In 9 out of 16 studies, the outcomes were assessed at kindergarten or first grade, with the exceptions of Magnuson et al. (2007, who reported estimated effects on standardized growth in achievement from K-3), Ansari and Pianta (2018a; ninth grade math and reading achievement scores), Ansari and Pianta (2018b; fifth grade achievement composite), Ansari and colleagues (2019; spring pre-k math and reading achievement), Han and colleagues (2019; first, third, and fifth grade math and reading achievement included in the same longitudinal HLM), Ou and colleagues (2019; eighth grade math and reading achievement), and Pearman and colleagues (2019; third grade math and reading achievement).

Preschool Attendance and Early Childhood Intervention Quality.

In 11 out of 16 studies, preschool attendance was operationalized as some kind of business-as-usual preschool offer or enrollment, contrasted with no preschool offer or enrollment (i.e., a home-based care environment). Five of these studies used either the Early Childhood Longitudinal Study-Kindergarten (ECLS-K) data for either the 1998 (Ansari & Pianta, 2018b; Bassok et al., 2018; Claessens et al., 2014; Magnuson et al., 2007) or 2010 (Bassok et al., 2018) cohorts. Importantly, these studies varied in how they defined preschool: Magnuson and colleagues (2007) compared children who attended preschool to children who received parental care, Head Start, or other care. Claessens and colleagues (2014) separately compared children who attended preschool and children who attended Head Start to children who received home or other care. Bassok and colleagues (2018) omitted children who attended Head Start from their analysis, citing differences across the two ECLS-K cohorts in how Head Start participation was measured, including only students who attended preschool and those who attended neither preschool nor Head Start. Ansari and Pianta (2018b) also omitted Head Start attendees because Head Start is “widely regarded as different than standard center-based care or state-funded pre-K” (p. 121), such that the researchers were unable to find balance when matching Head Start children to children attending other preschools, and that Head Start in the ECLS-K does not appear to benefit children’s achievement scores beyond informal care. These studies included sample sizes ranging from 7,748 to 15,892, depending on the study’s inclusion criteria and the number of covariates used to statistically control for differences between these groups. The other studies used randomly-assigned access to an early mathematics intervention in preschool, compared with preschool-as-usual (Jenkins et al., 2018), a standardized composite score of early child care quality (Ansari & Pianta, 2018a; Han et al., 2019), measures of time on literacy and language activities during Head Start (Mashburn & Yelverton, 2019), and a set of continuous measures or preschool quality (Carr et al., 2019).

In 13 out of the 16 studies, neither early educational quality nor later sustaining environments was randomly assigned. In the 2 studies analyzed by Jenkins and colleagues (2018) and one by Pearman and colleagues (2019), the preschool treatment was randomly assigned. In these cases, the sustaining environments were not randomly assigned, but the authors reported that randomly assigned earlier treatments were not significantly related to subsequent high-quality elementary educational experiences. Thus, these studies had the highest internal validity.

Sustaining Environments.

Measures of elementary school sustaining environments were generally variables thought for strong empirical and/or theoretical reasons to impact learning in the early school years, and included minutes of advanced math or reading instruction, rated teacher or classroom quality, full-day kindergarten, the use of transition practices for children entering kindergarten, small class size, school or classroom level achievement and poverty rate, later preschool attendance (if the preschool measure was taken for 3-year olds), and classroom quality ratings.

One exception was a study of the Chicago Parent-Child Center (CPC) program, for which years of exposure to the program after preschool (0, 1, 2, or 3) was the sustaining environments measure (Ou et al., 2019). This is theoretically significant, because the program was designed to be coherent across years, which may provide more opportunities for complementarity. However, because children were not randomly assigned to remain in the program after preschool, selection is a major concern. Indeed, children who stayed in the program all 4 years were relatively more advantaged, with significantly lower levels of neighborhood poverty and mothers who did not complete high school relative to both students who attended the CPC program in only some years and children in the comparison group (Ou et al., 2019).

Analysis

Effect Size Calculation.

Each row in the meta-analytic database included a main effect of early childhood education intervention quality, a main effect of sustaining environments, and an interaction between these variables. However, the estimates were not all easily interpretable or comparable. Before the meta-analysis, we rescaled them to maximize both interpretability and comparability. We began by scaling all of the effects to correspond to effect sizes in outcome measure standard deviation (SD) units by dividing them by the SD of the outcome measure.

When early and later quality variables were both dichotomous (e.g., no preschool, coded as 0, or preschool, coded as 1; half- or full-day kindergarten, coded as 0 or 1), interpreting the resulting main effects and interaction is straightforward: The main effect of the early childhood intervention variable is the estimated effect of attending, generally, a preschool program compared with students who did not attend preschool.² The main effect of the sustaining environments variable is the estimated effect of moving from the theoretically lower quality level of that variable to the theoretically higher quality level of that variable in the reference group of the early childhood intervention variable—i.e., children who did not attend preschool. For example, Bassok and colleagues (2018) estimated that, for children who did not attend full-day kindergarten, attending preschool has an effect of .10 SD on children’s spring of kindergarten math achievement. For children who did not attend preschool, the estimated effect of attending full-day kindergarten was .18 SD. And the interaction estimate of .02 indicates that the effect of preschool was .10 + .02, or .12 SD for children who attended full-day kindergarten.

When early intervention and/or sustaining environments variables were continuous, we assessed the main effect of the other quality measure at the mean of the continuous measure and scaled continuous variables to have a mean of 0 and SD of 1. Therefore, the interpretation of the main effects of the continuous variables are estimated changes in children’s skills as a result of a 1 SD increase in these variables at the reference group (for dichotomous variables) or mean (for continuous variables) of the other quality variable. For example, Bassok and colleagues (2018) estimated that for children who received the mean number of weekly advanced kindergarten math activities (.23), attending preschool has an effect of .19 SD on children’s spring of kindergarten math achievement using data from the ECLS-K 1998 Cohort. The regression coefficient can be interpreted as… For children who did not attend preschool, the estimated regression coefficient on standardized math activities in kindergarten was .07, which, if taken as causally informative, can be interpreted as meaning that a 1 SD increase in kindergarten math activities will increase children’s spring of kindergarten math achievement by .07 SD. The interaction estimate of .04 indicates that the effect of preschool was .19 + .04, or .23 SD for children who received 1 SD more math instruction than their peers.

The standard errors from these models were not re-calculated, meaning that the main effects that were estimated in the original sources at a reference value outside the range of values in the data (e.g., Swain et al. (2015) reported the main effect of preschool enrollment at a teacher quality value of 0, but the teacher quality scale went from 1–5, and the lower values were rarely used; Jenkins et al. (2018) reported the main effect of receiving a Head Start offer for students in schools with 0% of students proficient in reading, but the sample mean was 66%) are reported with upwardly biased standard errors. However, the standard errors of the primary estimates of interest – the interactions between early educational intervention and later educational quality – are not affected by these scaling decisions.

Meta-Analytic Approach.

We used the metafor and robumeta packages in R (Fisher & Tipton, 2015; Viechtbauer, 2010) to conduct two sets of meta-analyses: a multilevel meta-analysis, with effect sizes nested in studies and studies nested in articles and a meta-analysis with standard errors adjusted using robust variance estimation with small sample correction. In our first model, we conducted a meta-analysis of the interactions between early educational intervention and later childhood quality, obtaining the average estimate.

Next, we tested whether this estimate was sensitive to a precision effect estimate of standard error (PEESE) adjustment (Stanley & Doucouliagos, 2014). The PEESE test tests whether estimates’ standard errors are associated with the estimates’ effect sizes, as would be predicted if estimates are selected on the basis of their statistical significance in a single direction. The intercept in the model that includes the standard error as a predictor can be interpreted as the estimate adjusted for publication bias, which in the case of publication bias will be smaller in magnitude than the unadjusted estimate.

Finally, we tested whether a pattern of effect size heterogeneity was predictable from the sustaining environments hypothesis by testing whether interactions are more positive in studies that showed positive main effects of both early and later educational quality. This is a reasonable prediction: The key prediction of the sustaining environments hypothesis is that subsequent educational quality magnifies the effects of prior educational quality, which are plausibly captured by the main effects.

Meta-Analytic Results

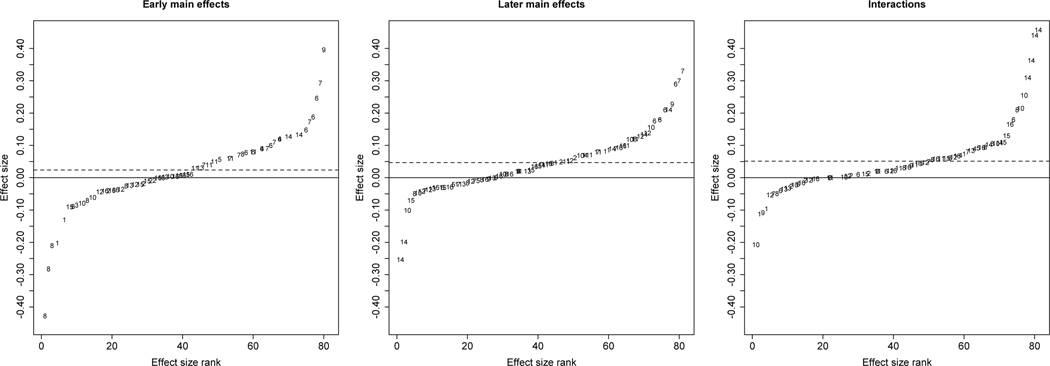
The estimated main effects of early educational intervention are sorted by magnitude and study in the left panel of Figure 2. As noted above, these can be interpreted as the estimated standardized effect of a one unit change in early educational intervention (e.g., from no preschool to preschool) when later educational quality is set to 0 (e.g., at the mean of weekly advanced kindergarten math activities, or for children who do not attend full-day kindergarten). The estimates range from approximately −.40 to approximately .40, with an unweighted mean of approximately .02. They appear to be clustered substantially by study. The most negative estimates come from Jenkins and colleagues’ (2018) analysis of the Head Start Impact Study and Magnuson and colleagues’ (2007) analysis of the ECLS-K 1998. Notably, the Magnuson et al. (2007) study used gain scores from kindergarten to grade 3 as an outcome measure; however, kindergarten scores are likely positively influenced by preschool attendance, and these estimates are difficult to interpret.

Figure 2:

Estimates Sorted by Magnitude

Note: Dashed lines are unweighted means. Numbers indicate the study from which the estimates were derived. Study numbers by first author and dataset are: 1 = Magnuson, ECLS-K (1998); 2 = Claessens, ECLS-K (1998); 3 = Swain, Tennessee Pre-k; 4 = Ansari, NICHD Study of Early Child Care and Youth Development; 5 = Ansari, ECLS-K (1998); 6 = Bassok, ECLS-K (1998); 7 = Bassok, ECLS-K (2010); 8 = Jenkins, Head Start Impact Study; 9 = Jenkins, TRIAD study of Building Blocks Curriculum; 10 = Ansari, large U.S. county; 11 = Carr, NCEDL Multi-State Study of Pre-K; 12 = Han, NICHD Study of Early Child Care and Youth Development; 13 = Mashburn, Head Start Impact Study; 14 = Ou, Chicago Child-Parent Center Program; 15 = Pearman, Tennessee Pre-K; 16 = Carr, Family Life Project.

The estimated main effects of later educational quality appear in the middle panel of Figure 2. As noted above, these can be interpreted as the estimated standardized effect of a one unit change in later educational quality (e.g., a 1 SD increase in the mean of weekly advanced kindergarten math activities, or attending full-day vs. not full-day kindergarten) when early educational intervention is set to 0 (e.g., not attending preschool). These estimates are more tightly bunched, with a similar mean around .05. The largest negative estimates come from Ou’s and colleagues’ (2019) analysis of CPC. As noted above, selection bias is a likely explanation, because years of exposure to the program after the end of pre-K was not randomly assigned and was thus endogenous to child level factors: children who left the program were more disadvantaged than children who stayed in for all four years.

The interaction estimates (Figure 2, right panel) have a similar unweighted mean of .05. The most positive estimates came from Ou and colleagues’ (2019) CPC analysis, again, potentially because of positive selection into sustaining environments for children who received the pre-k treatment. Aside from this study, interaction estimates generally fall within a narrow range of −.10 and .10.

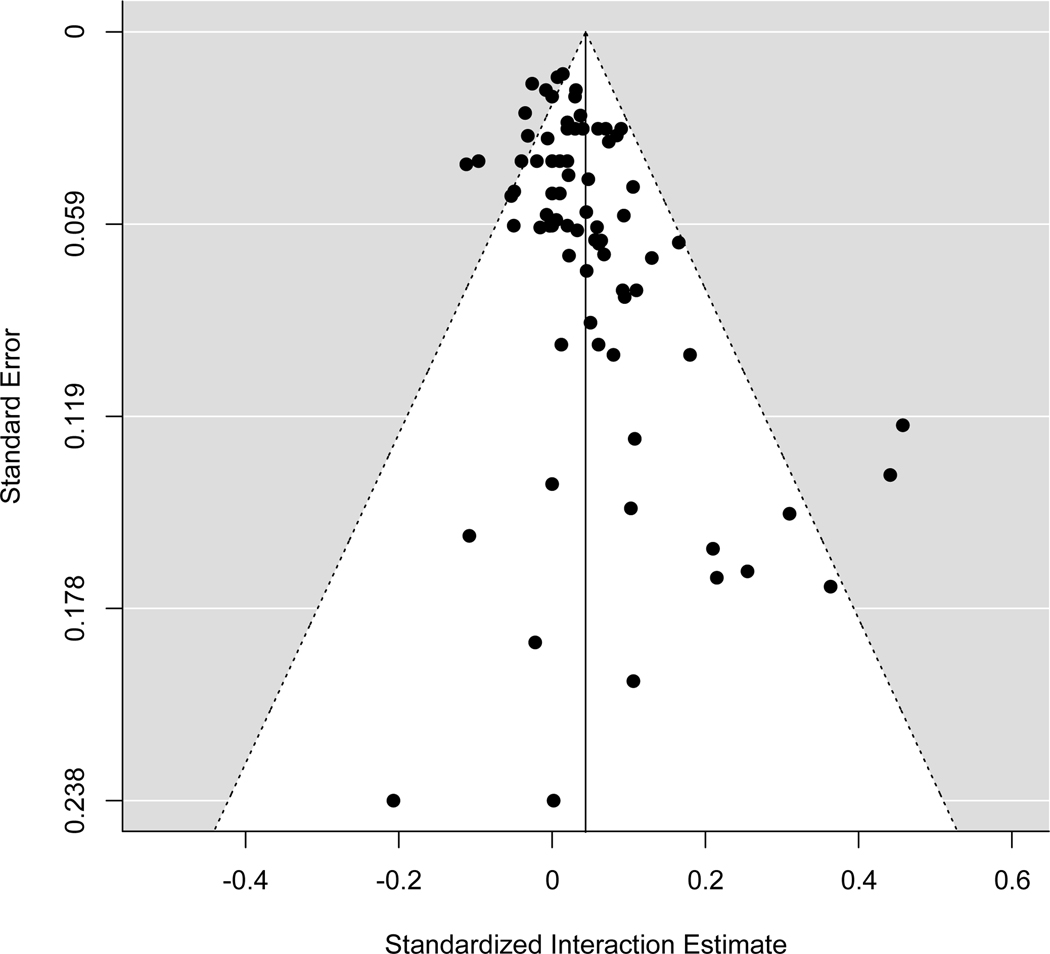
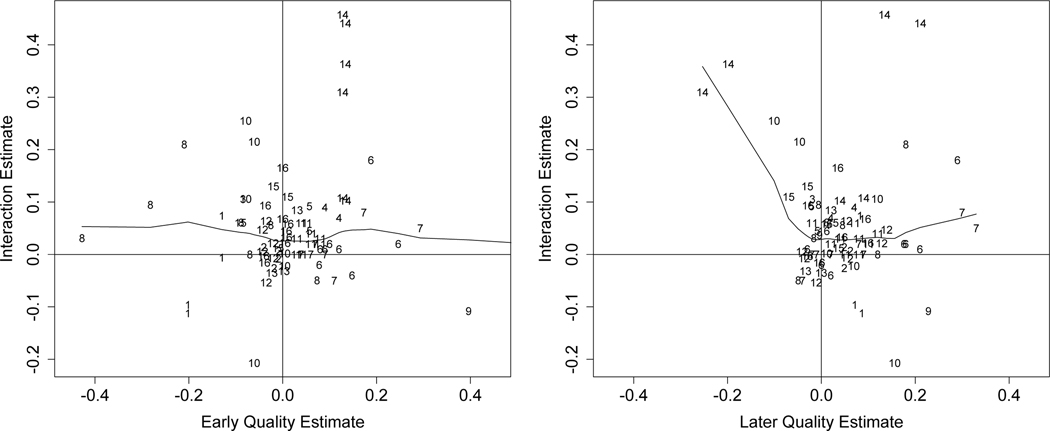
The meta-analytic model estimates are displayed in Table 2. In the unconditional models, the estimated interaction effects were .04 (SE = .02, p = .006) and .030 (SE = .01, p = .027) for the multilevel random and robust variance estimation models, respectively. There was a statistically significant level of heterogeneity across estimates (from the multilevel model, Q=128.91, p<.001; from the robust variance estimation model, I² = 53%), indicating moderate heterogeneity (i.e., that a single interaction estimate does not hold across this set of studies, which include children who varied in their early and subsequent educational experiences and selection therein, time and place, and other factors). In the PEESE models, the estimate’s standard error is included as a predictor of the effect size. The funnel plot (Figure 4) indicates some asymmetry, with the largest positive interactions coming from smaller studies, possibly indicating some publication bias. The PEESE predictor was significant in the multilevel model and had a similar magnitude but was nonsignificant in the robust variance estimation model, and in both cases the adjustment reduced the meta-analytic estimate of the interaction between early and later educational quality to almost exactly 0. Finally, we tested whether interactions were more positive when the main effects of early intervention and later quality were both positive than when at least one of them were negative. As Figure 1 indicates, a substantial number of cases yielded at least one main effect that was negative, and in such cases, it is not clear whether the quality of the early intervention of interest is more clearly conceptualized as positive or negative, relative to the reference group. Consistent with Figure 3, which indicates no clear relation between the estimated main effects of early and later quality and the corresponding interaction estimates, this indicator was not a significant moderator (Table 2, Model 3); in other words, early educational interventions and later educational experiences with estimated positive effects did not produce significantly larger statistical interactions than early educational interventions and later experiences for which at least one effects was estimated to be negative. The left panel of Figure 3 indicates that there was no clear relation between the estimated effect of early quality and the interaction coefficient. Although the upper right quadrant of this figure represents the classical formulation of the sustaining environments hypothesis, the upper right and lower left quadrants indicate that the interaction has the same sign as the main effect.

Table 2:

Meta-Analytic Estimates

	k	Random effects	Robust Variance Estimation
Interaction only	81
Interaction		.044** (.016)	.033* (.013)
PEESE adjustment	81
Interaction		−.001 (.019)	.003 (.023)
Moderator: Standard error of estimate		.808** (.264)	.668 (.463)
Moderator model	81
Interaction		.038* (.016)	.021 (.017)
Moderator:
Main effects are both positive		.017 (.015)	.032 (.024)

Note. Standard errors are in parentheses. Intercepts are estimate of the early quality by later quality interaction when moderators are set to 0. All models are estimated separately using random effects meta-analyses with studies nested within analyses nested within papers and robust variance estimation. The interaction only model includes no moderators; The PEESE adjustment model includes the interaction estimate standard error as a moderator to adjust for publication bias; The moderator model includes an interaction for whether both the estimated main effects of early and later quality were positive.

^*p<.05

^**p<.01

^***p<.001

Figure 4:

Funnel Plot of Interaction Estimates

Note: Plot of standardized interaction estimate by the standard error of each interaction included in the meta-analysis

Figure 3:

Relation between Interaction Estimates and Early and Later Quality Estimates across all Models

Note: Curves are Lowess curves. Numbers indicate the study from which the estimates were derived. Study numbers by first author and dataset are: 1 = Magnuson, ECLS-K (1998); 2 = Claessens, ECLS-K (1998); 3 = Swain, Tennessee Pre-k; 4 = Ansari, NICHD Study of Early Child Care and Youth Development; 5 = Ansari, ECLS-K (1998); 6 = Bassok, ECLS-K (1998); 7 = Bassok, ECLS-K (2010); 8 = Jenkins, Head Start Impact Study; 9 = Jenkins, TRIAD study of Building Blocks Curriculum; 10 = Ansari, large U.S. county; 11 = Carr, NCEDL Multi-State Study of Pre-K; 12 = Han, NICHD Study of Early Child Care and Youth Development; 13 = Mashburn, Head Start Impact Study; 14 = Ou, Chicago Child-Parent Center Program; 15 = Pearman, Tennessee Pre-K; 16 = Carr, Family Life Project.

Specification Curve Method

Data

Sample.

We use the publicly-available version of the Early Childhood Longitudinal Study – Kindergarten Cohort (ECLS-K) of 1998 for the Specification Curve phase of our study. We selected these data because they were used in 5 of the 16 studies reviewed, allowing a direct comparison to many of the estimates included in the meta-analysis.³ The ECLS-K is a nationally representative sample of 21,409 children entering Kindergarten in the Fall of 1998 conducted by the National Center for Education Statistics (NCES) that contains information on children’s families, classrooms, and schools from kindergarten entry through eighth grade (NCES, 2004). The data were collected using a complex survey sampling design. The full ECLS-K base-year sample includes 22,000 children who attended about 1,000 kindergarten programs during the 1998–99 school year. We use the data from the kindergarten year, which includes information gathered during parent interviews in the Fall, information from surveys from teachers and school administrators in the Fall, and direct assessments of children’s reading and math skills in the Spring. These data include population weights such that estimates can be considered nationally representative.

The data demands for our study (i.e., complete information on preschool and sustaining environments) impose some sample restrictions that are also standard in other studies using the ECLS-K (including but not limited to those reviewed here). To make transparent the reductions in sample size and changes in sample characteristics due to missingness on key covariates, we present descriptive statistics for the full ECLS-K sample and in two stages of our sample restrictions in Table 3. We first must exclude children who do not have outcome assessment scores at the end of kindergarten (N=3,787). This also excludes dual language learners who were not able to complete the reading assessments in English. We then exclude children who were not first-time kindergarteners (N=751). Our last restriction is for observations without complete information on all of the child and family covariates we use (N=3,969). The remaining 11,633 children comprise our final analysis sample.

Table 3:

Descriptive Statistics of ECLS-K First-Time Kindergarten Samples

	(1)		(2)		(3)
	Full ECLS-K sample		Sample with Spring assessments and 1st time K status		Complete case analysis sample with all covariates*
	count	mean	count	mean	count	mean
Child and Family Characteristics
Spring reading score (std.)	18937	−0.00	15602	0.02	11633	0.04
Spring math score (std.)	19649	−0.00	15588	0.06	11621	0.10
Child age at Spring assessment	19907	74.67	15602	74.47	11633	74.55
Male	21396	0.51	15602	0.50	11633	0.50
White	21409	0.55	15602	0.60	11633	0.63
Black	21409	0.15	15602	0.15	11633	0.14
Hispanic	21409	0.18	15602	0.14	11633	0.14
Asian	21409	0.06	15602	0.05	11633	0.04
Other race	21409	0.05	15602	0.06	11633	0.06
Home language non-English	21275	0.13	15575	0.09	11633	0.08
Mother’s education
High School or less	19810	0.45	15365	0.41	11633	0.40
Some college	19810	0.32	15365	0.33	11633	0.34
College +	19810	0.23	15365	0.25	11633	0.26
Mother’s education imputed (1=yes)	20141	0.02	15602	0.01	11633	0.01
Family income (thousands; imputed)	20141	52.04	15602	54.76	11633	55.79
Income imputed (1=yes)	20141	0.28	15602	0.26	11633	0.22
Below poverty level	21409	0.20	15602	0.18	11633	0.17
Urban	21260	0.41	15602	0.40	11633	0.40
Rural	21260	0.20	15602	0.21	11633	0.22
Northeast	21260	0.18	15602	0.19	11633	0.19
Midwest	21260	0.25	15602	0.26	11633	0.28
Southeast	21260	0.33	15602	0.32	11633	0.33
West	21260	0.23	15602	0.22	11633	0.20
Child birthweight	17591	6.92	15228	6.94	11633	6.95
Mother employed	17627	0.67	15224	0.69	11633	0.69
Num. children in household	18097	2.49	15602	2.45	11633	2.45
Num. books in home	17912	72.80	15443	76.82	11633	79.33
Read books at home (1–4)	18027	2.98	15561	2.99	11633	2.99
Mother felt depressed	18730	0.28	14832	0.28	11633	0.28
Mother age	17722	33.21	15293	33.36	11633	33.27
Kindergarten Teacher Characteristics
Teacher Master’s degree	16871	0.35	13457	0.36	11633	0.36
Teacher certification	18415	0.86	14612	0.86	11633	0.87
Years teaching Kindergarten	17895	8.95	14231	9.16	11633	9.20
Preschool
Full-time preschool attendance	15450	0.61	13421	0.63	10153	0.64
Public preschool	8683	0.30	7076	0.31	5125	0.29
Preschool attendance - exclude HS	18062	0.66	15585	0.69	11633	0.69
Head Start attendance	18097	0.49	15602	0.50	11633	0.51
Preschool attendance - any	21239	0.12	15473	0.13	11633	0.13
Sustaining Environments
Advanced literacy activities (per month; tot.)	21409	34.52	15602	36.80	11633	36.60
Advanced math activities (per month; tot.)	21409	22.24	15602	23.89	11633	23.67
Full-day K	19796	0.56	15602	0.55	11633	0.56
Small K class size	17355	0.54	13832	0.53	11261	0.54
K transition practices (1–6)	21409	2.72	15602	3.05	11633	3.15
School % at grade level in reading and math	12076	64.07	9208	65.06	7058	65.35

Note:

^*Analysis sample for specification-curve

The set of figures in the first super-column of Table 3 represent the total number of nonmissing observations and sample means for each of our analysis variables for the full ECLS-K sample. The figures in the second super-column show how the sample size and characteristics change when we restrict to an analysis sample with outcome assessment data in the Spring and to first-time kindergarteners. The figures in super-column 3 represent our analysis sample for each of the specifications we test with complete information on all covariates. The only exception to this analysis sample rule is for the school-level sustaining environment variable, percent of school performing at grade level or above in reading and math. (School-level variables come from the school administrator survey, which has high levels of missingness.) Note that the NCES-provided ECLS-K population weights were designed to also account for item-level missingness from the different surveys available, such that the restricted samples can maintain national representativeness.

Measures.

Child reading and math skills.

Our outcome variables are assessments of children’s reading and math skills during the Spring of kindergarten. These measures are criterion-referenced proficiency scores that describe a given child’s mastery of specific content derived from direct, one-on-one assessments. The kindergarten reading assessment captured information on children’s basic language and literacy skills, such as understanding the directionality of print, recognizing letters, identifying sounds, word reading, vocabulary, and reading comprehension (α= .93-.97; NCES, 2002) (National Center for Education Statistics, 2002) . The mathematics assessment measured children’s conceptual understanding of numbers, shapes, patterns, mathematical operations, and processes for problem solving (α=.92-.94; NCES, 2002). We use the standard score values of the assessments, which are transformations of latent ability scores into standardized t-scores that have a mean of 50 and standard deviation of 10 (based on the full sample distribution). To interpret our results as effect sizes, we then restandardized the assessment scores to have a mean of 0 and standard deviation of 1.

Preschool attendance.

Indicators of preschool attendance come from parent interviews during the Fall of kindergarten, when parents were asked whether in the year prior to kindergarten their child had been in: center-based child care, relative care, non-relative care, or Head Start. Parents were also asked about the number of hours of care during a typical week. We considered children as having attended any preschool if they participated in either center-based care or Head Start for at least five hours per week, in line with prior studies using these data (Bassok, Gibbs, & Latham, 2018). We also separated preschool status into Head Start and non-Head Start preschool. Children who did not attend preschool spent the year prior to kindergarten in home-based relative or non-relative care and serve as the comparison group for all analyses. Other preschool-related covariates we include in our analyses are indicators for full-time attendance and for public school-based preschool.

Sustaining environments.

We selected the following six measures of elementary school sustaining environments based on our meta-analytic review of studies: advanced reading activities and advanced mathematics activities in the kindergarten classroom, full-day kindergarten, small kindergarten class size, practicing kindergarten transition activities, and the elementary school-level percentage of students whose math and reading skills are at or above grade level.

Advanced reading activities.

We follow Claessens et al. (2013) in creating the advanced reading activities measure. This was created from nine items from the teacher survey regarding classroom content. The measures comprising the advanced activities are: matching letters to sounds, common prepositions, and using context cues for comprehension. Teachers reported on how often they taught particular content using a 6-point Likert scale that included the following categories: never, once a month or less, two or three times a month, once or twice a week, three or four times a week, or daily. Using the averages for each category, we follow Claessens et al. (2013) coding scheme by rescaling responses that indicate the number of days per month a teacher reported teaching that content in the following way: 0 (never), 1 (once a month or less), 2.5 (two or three times a month), 6 (once or twice a week), 14 (3 or 4 times a week), or 20 (daily) days per month. We summed these items to create the total advanced reading activities measure. So that our coefficients are comparable across measures of the sustaining environment, we then standardized this total score to have a mean of 0 and standard deviation of 1.

Advanced math activities.

We also follow Claessens et al. (2013) in creating the advanced math activities measure. This was created using eight items from the teacher survey that include place value, reading two-digit numbers, and adding single-digit numbers. We used the same coding scheme described for advanced reading activities to convert teacher responses into days per month, creating both a total advanced math activities measure and a standardized version for analysis.

Full-day kindergarten.

We generated an indicator for full-day kindergarten that equals 1 if the classroom met for five or more hours per day.

Small kindergarten class size.

Following Bassok et al. (2018) and Magnuson et al. (2007), we define a kindergarten class as small if there are 20 students or less.

Kindergarten transition activities.

Following Bassok et al. (2018), we generated a measure of the number of kindergarten transition activities used by the kindergarten teacher. In the Fall survey, teachers were asked whether they used each of the following six transition activities: sending information about kindergarten home to parents of preschoolers, visits to the kindergarten classroom for preschoolers, and visits to the classroom for children and their parents prior to the start of the school year, shortened school days at the beginning of the year, teacher visits to children’s homes at the beginning of the year, and parent orientation prior to the start of school. We generated the total number of transition practices for each teacher, ranging from zero to six.

School percentage at or above grade-level.

We include in our analysis a measure of school-level quality, defined as the average of two items from the Fall school administrator survey: the percentage of students at grade level or above in reading, and the percentage of students at grade level or above in math. To make this measure comparable across measures of the sustaining environments, we standardized the average to have a mean of 0 and standard deviation of 1.

Covariates.

We include a large set of child, family, and teacher covariates in our analyses, shown in Table 3. Child characteristics include: child age at the spring assessment, sex, race and ethnicity, and birthweight. Family characteristics include income, poverty status, maternal education, maternal age, the number of children in the household, whether English is the primary language spoken at home, parental employment, number of books in the home, whether the parent reads books with their child (1–4 Likert response), whether the mother experienced feelings of depression, region of the country of residence, and urbanicity. Both maternal education and income include imputed values generated by NCES, and we also include indicators for whether an observation was imputed. Teacher characteristics include indicators for having a master’s degree and for having the highest level of teaching certification, and the number of years of kindergarten teaching experience.

Analysis

Selection into preschool and sustaining environments.

To determine whether preschool and later school environments are complementary, we need to address the possibility that selection into either earlier or later treatments could generate biased outcomes. We use the rich covariates available in the ECLS-K to examine the extent to which observable characteristics of children and their families are correlated with both selection into preschool and into the six sustaining environmental factors we test. This involves simple bivariate regressions between each of the preschool and sustaining environment conditions and the full set of characteristics shown in Table 3. We apply the ECLS-K sample probability weights and cluster standard errors at the Primary Sampling Unit (PSU) to account for the complex survey sampling design using STATA 15 software.

Specification Curves.

We use the analytic approach designed by Simonsohn, Simmons, and Nelson (2015) of Specification-Curve Analysis. The purpose of this approach is to overcome bias in published research that stems from researcher discretion in data analysis. Researchers make important, necessary decisions at each stage of the data analysis process. Although these decisions are oftentimes defensible, they can also be arbitrary and subject to researcher bias (Leamer, 1983). Furthermore, researchers often disagree about whether a given specification is an appropriate test of the hypothesis of interest, or whether it is statistically valid for a given sample or treatment context. Simonsohn et al. (2015) developed specification-curve analysis to mitigate these issues and to better synthesize the implications of different decisions on analysis outcomes. The approach consists of reporting results for all “reasonable specifications,” defined as specifications that: are consistent with the underlying theory; are expected to be statistically valid; and are not redundant with other specifications tested. In so doing, specification-curve analysis aims to expand what gets reported from the few selective specifications researchers select in their papers to that of all similarly reasonable specifications.

There are three main steps to specification-curve analysis. We first define the set of reasonable specifications to estimate. This is depicted in Table 4, organized by each key element of a sustaining environments hypothesis specification: child outcome, sustaining environmental factor, set of control variables, and the definition of preschool. Each of the alternatives presented are tested in the studies listed in Table 1. For the control variables, we created four tiers in terms of the depth of covariate adjustment to parsimoniously test the sensitivity of results to additional controls. The first of these tiers is “No controls”, which we include to examine how selection bias may influence the main effects and interaction coefficients, in terms of magnitude and direction. Variations on each of the four specification elements gave us a total of 144 reasonable specifications.

Table 4:

Outline of all reasonable specifications tested using specification-curve analysis

Specification element	Alternative specifications tested
Outcome	Math skills Reading skills
Sustaining environmental factor	Advanced reading activities Advanced math activities Full-day kindergarten Small kindergarten class size Use of kindergarten transition activities School-level % at grade level in reading and math
Control variables	No controls Basic demographic controls   Child race, gender, age at assessment, home language not English, mother’s education, income, poverty status, urbanicity, region Full demographic controls   Basic + child birthweight, number of children in the household, number of books in the household, whether parent reads books with their child, whether parent experiences depressive symptoms, maternal age, preschool attendance full-time, preschool attendance at public school Full demographic + teacher controls   Full demographic + teacher has master’s degree, teacher has highest certification, number of years teaching kindergarten
Preschool treatment definition and comparison	Preschool attendance that excludes Head Start vs. home-based care Head Start vs. home-based care Preschool attendance that includes Head Start vs. home-based care

The second step is to estimate all specifications and report the results in what Simonsohn et al. (2015) call a “descriptive specification curve”. This involves displaying the range of estimates that are obtained through the alternative reasonable specifications and identifying the analytic decisions that are most consequential by displaying these decisions in conjunction with coefficient magnitude and significance. We estimate all 144 specifications using ordinary least squares regression weighted by the sample populations weights with standard errors clustered at the PSU. We create descriptive specification curves for our three coefficients of interest: preschool, sustaining environments, and the interaction of the two. We adapted the code provided by Simonsohn (2015) for generating all specifications and the specification curve graphs shown in Figure 5.

Figure 5a.

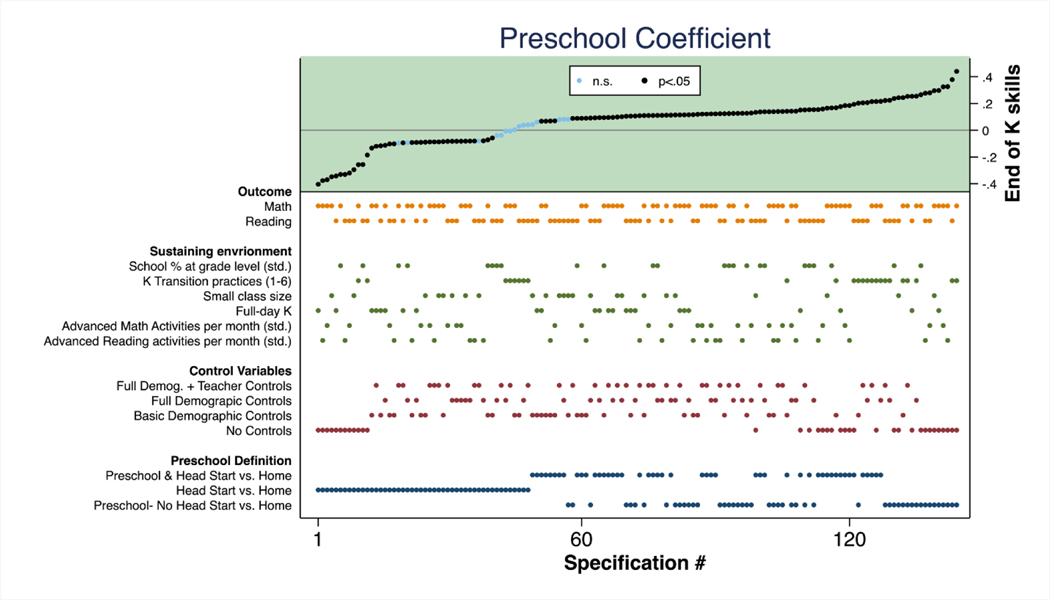
Specification Curve Results: Preschool Coefficient from all Model Specifications

The third step is to conduct joint statistical tests using what Simonsohn et al. (2015) define as an “inferential specification curve”. This involves permutation techniques whereby the key variables of interest are reshuffled within the dataset while maintaining other features of the original dataset (i.e., non-shuffled variables remain unaltered in each observation). This effectively removes the link between the variable(s) of interest and the outcome and covariates. One repeats this shuffling exercise many times, estimating each of the specifications on each of the shuffled datasets. The distribution of specification curves that result from these shuffled estimates is the expected distribution when the null hypothesis is true; that is, when there is no relation between the key variables and the outcomes. The results of this process are then displayed graphically in a specification curve, with both the specification curve from the observed (original) data and 95% confidence intervals overlaid. We adapted the code provided by Simonsohn for generating the specification curves from 500 shuffled datasets shown in Figure 6. Simonsohn et al. (2015) also propose three different test statistics to summarize the results shown in the graph. The first is the proportion of shuffled samples with a median effect size that is as large or larger than the median effect size of the coefficient of interest in the original data. That proportion generates a p-value from each of the 500 shuffled datasets (proportion of datasets with > median effect size). The second is the share of the results with the “dominant sign”, which in our study, would be positive, and third is the share of estimates that are of the dominant sign and are statistically significant (p < .05).

Figure 6.

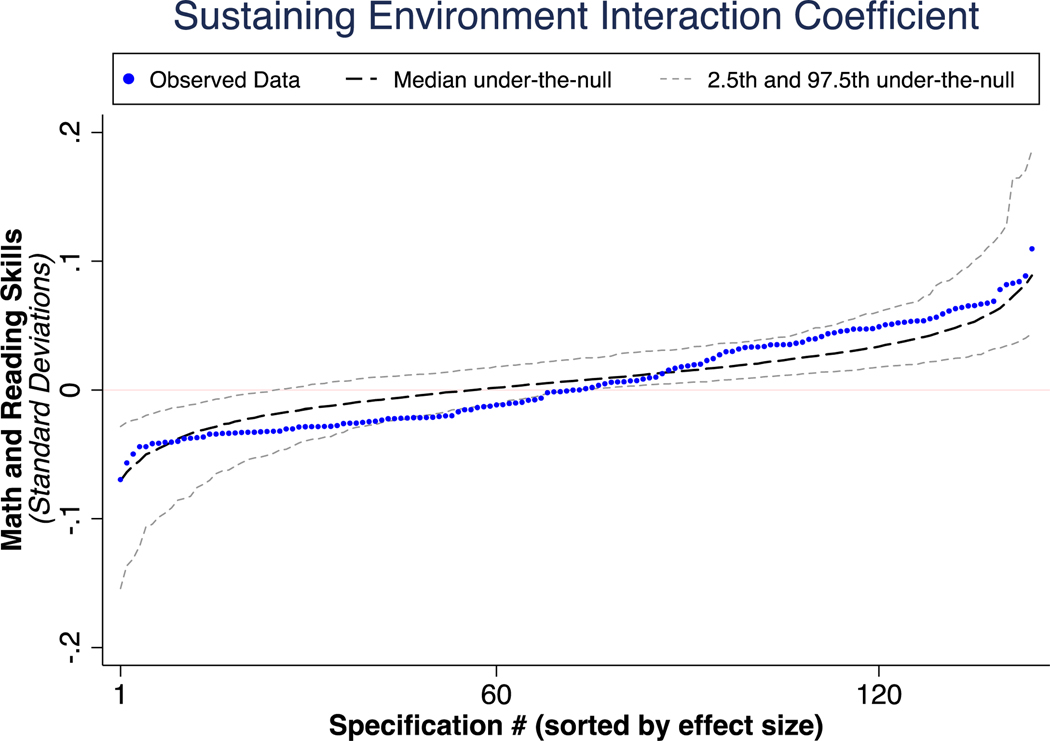
Inferential Specification Curve

Note. All specifications are estimated on each shuffled sample. The resulting estimates for each shuffled dataset are ranked from smallest to largest. The dashed lines depict the 2.5^th, 50^th, and 97.5^th percentiles for each of these ranked estimates. The blue dots are the specification curve for the observed data.

Specification Curve Results

Selection into Preschool and Sustaining Environments

We present the results from selection analyses in Table 5, where preschool selection results are shown in the top panel, sustaining environment results shown in the bottom panel, and each coefficient comes from a separate bivariate regression.

Table 5:

Selection into Preschool and Sustaining Environments from child and family−level characteristics

	Male	Black	Hispanic	Asian	Other race	Home lang. non− English	Some college	College +	Family income (1000s)	Below poverty level	Urban	Rural	Mom employed	Child birth− weight	Num. books in home	Read books at home (1–4)	Mom felt depressed	Mom age
Coefficients from separate bivariate regressions
Preschool Treatments
Head Start	−0.00 (0.01)	0.27* (0.05)	0.08* (0.02)	−0.00 (0.00)	0.03 (0.03)	0.04* (0.01)	−0.06* (0.02)	−0.23* (0.01)	−36.54* (2.02)	0.36* (0.03)	0.04 (0.04)	0.14* (0.03)	−0.05* (0.02)	−0.32* (0.06)	−36.42* (3.02)	0.07* (0.03)	0.12* (0.01)	−2.87* (0.21)
Preschool attendance - exclude HS	0.00 (0.01)	−0.07* (0.02)	−0.09* (0.02)	0.00 (0.00)	−0.02 (0.02)	−0.05* (0.01)	0.06* (0.01)	0.21* (0.01)	27.60* (1.03)	−0.19* (0.01)	−0.00 (0.03)	−0.11* (0.02)	0.15* (0.01)	0.15* (0.03)	23.91* (1.69)	−0.01 (0.01)	−0.08* (0.01)	2.08* (0.08)
Preschool attendance - any	0.00 (0.01)	0.06* (0.01)	−0.06* (0.01)	−0.00 (0.00)	−0.01* (0.00)	−0.04* (0.01)	0.04* (0.01)	0.12* (0.01)	11.54* (0.75)	−0.03* (0.01)	0.02 (0.01)	−0.05* (0.01)	0.14* (0.01)	−0.01 (0.03)	7.37* (0.89)	0.03* (0.01)	−0.02* (0.01)	0.80* (0.12)
Sustaining Environments
Advanced literacy activities (per month; std)	0.00 (0.00)	0.04* (0.01)	0.01 (0.01)	0.00* (0.00)	−0.00 (0.00)	0.00* (0.00)	−0.01* (0.00)	0.01* (0.00)	0.13 (1.36)	0.02* (0.01)	0.05* (0.02)	−0.03+ (0.01)	−0.00 (0.00)	−0.03* (0.01)	−2.38* (0.55)	0.05* (0.01)	−0.01* (0.00)	−0.05 (0.06)
Advanced math activities (per month; std)	−0.00 (0.00)	0.01 (0.01)	0.00 (0.01)	0.00 (0.00)	−0.00 (0.00)	−0.00 (0.00)	0.00 (0.01)	−0.00 (0.01)	0.69 (1.56)	0.00+ (0.00)	0.02 (0.02)	−0.01 (0.02)	0.00 (0.00)	0.00 (0.01)	−0.67 (0.87)	0.01 (0.01)	−0.00+ (0.00)	−0.03 (0.09)
Full−day K	−0.01 (0.01)	0.14* (0.02)	−0.03 (0.02)	−0.00 (0.00)	0.01 (0.01)	−0.01 (0.01)	−0.04* (0.01)	−0.03* (0.01)	−6.78* (2.02)	0.07* (0.02)	0.08* (0.03)	0.07* (0.01)	0.02 (0.02)	−0.17* (0.03)	−13.64* (1.64)	0.05* (0.02)	0.01 (0.01)	−0.45* (0.12)
Small K class size	0.01 (0.01)	−0.02 (0.04)	−0.01 (0.01)	−0.00 (0.00)	0.00 (0.00)	−0.00 (0.01)	−0.00 (0.01)	0.01 (0.02)	2.27 (1.98)	−0.00 (0.01)	−0.02 (0.01)	0.04* (0.01)	0.00 (0.01)	0.01 (0.03)	0.46 (1.74)	−0.02 (0.02)	0.01 (0.01)	0.09 (0.16)
K transition practices (1−6)	0.00 (0.00)	−0.05* (0.00)	−0.04* (0.01)	0.00 (0.00)	−0.01* (0.00)	−0.03* (0.01)	0.00 (0.01)	0.04* (0.01)	6.12* (1.13)	−0.04* (0.01)	−0.05* (0.02)	0.04* (0.02)	0.01* (0.00)	0.02* (0.01)	7.65* (1.19)	−0.01 (0.01)	−0.01* (0.00)	0.40* (0.12)
School % grade level in reading and math (avg.; std)	−0.01 (0.01)	−0.08* (0.00)	−0.03* (0.01)	0.00 (0.00)	−0.01* (0.01)	−0.02* (0.01)	−0.01 (0.01)	0.1 2* (0.01)	15.72* (1.81)	−0.08* (0.01)	−0.03 (0.02)	−0.03 (0.04)	−0.00 (0.01)	0.10* (0.02)	14.45* (1.50)	−0.00 (0.01)	−0.05* (0.00)	1.33* (0.10)

Standard errors in parentheses; std. indicates that the variable is standardized.

Comparing children who attended Head Start with all other children in the sample (i.e., other preschool and no preschool) demonstrates clearly that the families of Head Start children are more disadvantaged across nearly all characteristics: maternal education, native English speakers, family income and poverty status, parental employment, birthweight, books in the home, maternal depression and maternal age. This is not surprising, given that the Head Start program is available only to economically disadvantaged families. In contrast, children who attended a center-based preschool program other than Head Start were more advantaged across each of these characteristics. This demonstrates very clearly the importance of both the inclusion of robust control variables and examining different types of preschool exposures.

In the bottom panel of Table 5 we see selection into sustaining environments for three of the six factors we test, though the relations are not as strong as selection into preschool. We do not find differential selection into kindergarten classrooms with more advanced literacy or math activities, or with smaller class sizes (<20). Results do reveal that full-day kindergarten programs are more likely to be attended by socioeconomically disadvantaged students, while kindergarten transition practices are more common for socioeconomically advantaged students. Overall school performance—the percent of students performing at or above grade level in reading or math—is positively associated with family advantage (income, books in home, maternal age).

Overall, we find evidence of selection bias from observable characteristics into both preschool and subsequent sustaining kindergarten environments.

Specification Curve Results

Descriptive specification curve.

Descriptive specification curves for the main effect of preschool, the main effect of sustaining environment, and the sustaining environment*preschool interaction coefficient are presented in Figure 5a, b, and c, respectively. These figures present for each of the different specifications the resulting coefficient for that variable (e.g., preschool main effect), along with its statistical significance, which are displayed in rank order by coefficient magnitude.

The key benefit of specification curve analyses do not stem from any novel approach to model estimation, but rather from their illustrations of a range of plausible estimates and how model specification systematically affects conclusions. Starting with the preschool coefficient, the descriptive specification curve makes clear that preschool attendance is robustly significantly related to math and reading outcomes at the end of kindergarten. However, when the preschool treatment is defined as Head Start, this relationship is always significant and negative, regardless of the control variable set. In turn, preschool is most strongly and positively related to math and reading skills when Head Start attendees are omitted from the analysis. Most of the positive correlations between preschool and outcomes are in the range of 0.1–0.2 SD. The Head Start estimates are most negative, and the preschool estimates are most positive in the models with no covariates. These findings very clearly highlight the role of omitted variables and selection bias for these estimates. Importantly, although the models with full controls indicate effect sizes closer to 0, their magnitudes and even directions may be influenced by remaining selection bias (for a review, see Duncan & Gibson-Davis, 2006).

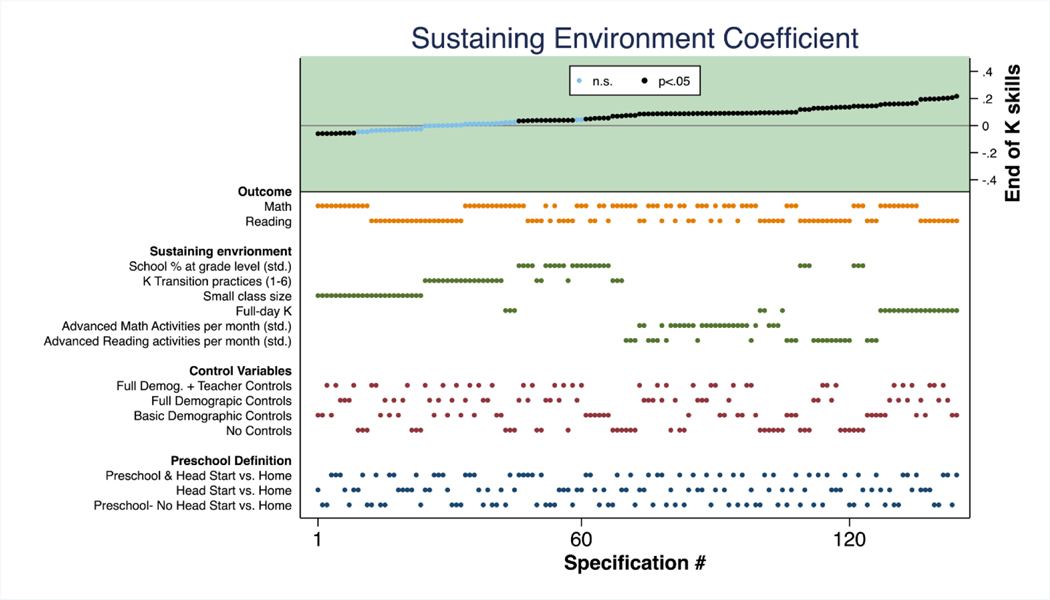
Turning to Figure 5b, we can see that the sustaining environment coefficient follows a similar pattern; many specifications result in a positive and significant relationship between kindergarten environments and reading and math outcomes, but a consistent set of specifications result in a negative coefficient. Small class size is either not significantly correlated with achievement or is negatively correlated. Kindergarten transition practices are not correlated with achievement based on both the significance and magnitude (near zero) for each of the specifications using this environmental measure. Full-day kindergarten was the most strongly correlated environmental measure, followed by advanced reading and math activities. School proportion of students performing at or above grade level in reading and math was positively correlated with outcomes, but these estimates come from the most restricted sample (n=7058 vs. 11633 for other specifications) because of item missingness. Positive correlations with child outcomes ranged from 0.01–0.2 SD.

Figure 5b.

Specification Curve Results: Sustaining Environment Coefficient from all Model Specifications

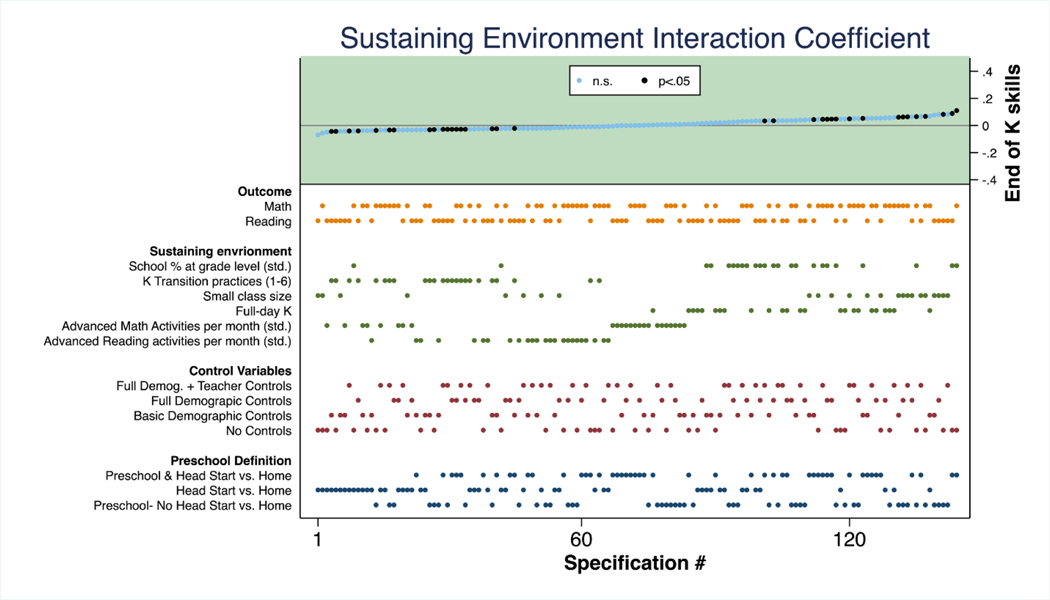
Figure 5c displays estimates for our primary coefficient of interest, the interaction between early childhood educational intervention and later educational quality. Again, the illustrative power of specification curve analyses make clear that there are a few select instances for which the sustaining environments hypothesis is supported. The most consistently positive interaction between preschool and the subsequent environment is for full-day kindergarten. Significant negative interaction effects come from specifications where kindergarten transition practices are interacted with all preschool definitions. The magnitude of coefficients range from 0.1 to −0.1, clustering mainly around 0. Overall, 35 out of the 144 specifications resulted in a significant interaction coefficient, and 17 out of 144 (12%) were significant and positive (nearly symmetrically, 18 out of the 144 – 13% - were significant and negative).

Figure 5c.

Specification Curve Results: Interaction Coefficient from all Model Specifications

Inferential specification curve.

We further assess the robustness of the sustaining environment interaction coefficient with the inferential specification curve shown in Figure 6. Here, we contrast the specification curves from 500 shuffled samples with that from the original, observed ECLS-K data. The observed curve from the real data is quite similar to that obtained from the shuffled datasets, and both curves fall within the 95% confidence interval of effect sizes obtained from the distribution of the 500 samples. This confirms that the results generated from the original data match that of data where the null hypothesis of no effect is true by construction (i.e. removing the relations between the environmental factors and preschool treatments with covariates and outcomes). This means that the specification curve analysis indicates the sustaining environments hypothesis is not supported in the ECLS-K sample.

The median effect size for the interaction term in the original data was extremely small, .0000116. Ninety-nine percent of the simulated datasets had median effect size of the interaction term that was at least this large such that the p-value of our first Simonsohn et al. (2015) specification curve test statistic is .99. In the original data, 72 of the observed interaction coefficients were positive, the expected sign, which is roughly half of the total specifications. This was also true in all of the shuffled data, meaning that the effect direction pattern follows that of data where the null hypothesis is true (p-value=.50). In the original ECLS-K analysis sample, 17 out of the 144 specifications are statistically significant with the expected positive sign. Among the 500 shuffled samples we generated, 185 have at least 17 specifications where the interaction term was positive and statistically significant. This gives us a test statistic p-value of .37 (185/500), further indication that we cannot reject the null hypothesis of no complementarities between preschool and later educational quality.

Discussion

The purpose of this study was to quantify evidence in favor of the sustaining environments hypothesis, as measured by positive interactions between early educational intervention and later educational quality on children’s later academic achievement. In a meta-analysis of studies that have estimated interactions between early childhood educational intervention and later educational quality and a specification curve analysis with the most frequently used dataset to test these interactions, we mostly found interactions very close to zero.

Possible Explanations

Results of the meta-analysis and specification curve analysis indicated precisely estimated near zero average interactions between early educational intervention and later educational quality on later assessments of children’s skills. The analysis suggests several possible reasons why, which we will review below: 1) the null hypothesis is true, 2) we did not have statistical power to detect interactions of a realistic magnitude, 3) model misspecification because of theoretical ambiguity or selection bias, and 4) heterogeneity of these interactions across treatments, contexts, and children.

1. The null hypothesis. One possibility is that there are not complementarities between early and later educational quality captured in children’s achievement scores. We found more evidence in favor of the hypothesis that subsequent educational quality is additive and not multiplicative. This would imply that later educational quality is not a complement to early educational interventions (i.e., a significant interaction between preschool and subsequent quality), but is beneficial for all students regardless of early experience. Perhaps the impacts of early educational intervention do not depend on the subsequent quality of the educational environment. Although lab studies and cognitive theory make this hypothesis difficult to accept in all cases, the null hypothesis may be seriously worth considering, at least for this limited set of treatments and outcomes. Substantively, perhaps this is because the markers of educational quality used by researchers in this domain are likely to benefit students, on average, throughout the achievement distribution.

2. A lack of power. In both the meta-analysis and specification curve analysis, the average magnitude of estimated main effects of early childhood educational intervention and later educational quality on children’s test scores were small. Under the reasonable assumption that interactions will be smaller in magnitude than these main effects, perhaps the existing literature is underpowered to detect complementarity between early childhood educational intervention and later educational quality. This assumption is supported by a recent large investigation of the sizes of interaction effects between broad psychological and contextual factors, which Sherman and Pashler (2019) conclude are often either Type I errors or otherwise quite small (in the range of r = 0.02). The minimum standard error of an interaction between early childhood educational intervention and later educational quality from our meta-analytic database (.013) and the median (.057) imply 80% power to detect interactions of .04 and .16, respectively. These values may seem like small detectable effects, but they are close to or larger than the average estimated main effect of early childhood educational intervention (.060) and the average estimated main effect of subsequent environmental quality (.065) of the ECLS-K in the specification curve analysis. Thus, lack of power is a major concern in this area. Studies with the median standard error in our meta-analytic sample are unlikely to detect interaction effects of realistic magnitudes; realistically sized interaction effects may even be too small to reliably detect in the large ECLS- K dataset.

3. Model misspecification because of theoretical ambiguity or selection bias. Both of our analyses suffered from an unanticipated problem in the link between theory and data as demonstrated by the inconsistent direction of the association between early childhood educational interventions and child assessment scores. Specifically, several of the meta-analytic and specification curve main effects of early childhood educational intervention were negative. In such cases, complementarity is difficult to define: Should one define educational quality based on the theoretical or empirical direction of the effect of the quality measures? An obvious cause of the negatively signed estimates (and some of the positively signed estimates) is omitted variable bias: In most of our analyses, children were not randomly assigned to receive an early educational intervention. Children in Head Start must be economically disadvantaged to be eligible for participation, which makes it difficult to statistically control for unobserved differences between Head Start attendees and other children. The direction of this bias is clear for the main effects of preschool statuses—our models with no controls were overrepresented at the opposite ends of the specification curve—but unclear for the interaction between early childhood educational intervention and later educational quality, when neither of which is randomly assigned. As noted in the results, the largest interactions come from an analysis of an evaluation of the CPC program, where children in the treatment group selected into sustaining environments, but children in the comparison group could not. Because children who received both the early and later treatments were more advantaged than either the comparison group or children in the treatment group who left the program, this design may be particularly prone to yielding positive interactions. Because the specification curve contains estimates without covariates, it is likely that the plausible range of estimates for main effects and perhaps also for the range of estimates for interactions are overstated in the specification curves.

4. Heterogeneity across treatments, contexts, and children. One possibility is that, although these interactions averaged out to approximately 0, some of them were reliably positive, consistent with complementarity between early educational intervention and later education quality, and others were reliably negative, consistent with substitutability. We find mixed evidence for this, with a statistically significant test for heterogeneity in the meta-analysis and more than 5% statistically significant estimates in the specification curve analysis, but an inferential specification curve consistent with a relatively homogenous effect of approximately 0. Importantly, this occurs despite our inclusion of a heterogeneous set of definitions of early childhood intervention and later educational quality in our analysis, methods that might reasonably be expected to increase the heterogeneity of estimates⁴. Additionally, although the meta-analysis indicated a moderate amount of heterogeneity in interaction estimates, the prediction we thought most directly followed from the sustaining environments hypothesis – namely, that interactions would only be positive when the main effects of early and later quality were positive – was not supported. Still, perhaps the most compelling argument for heterogeneity is that it is real but not well observed in these data, because we did not measure the “right” later educational moderators of early educational intervention effects. We will discuss this possibility below.

Recommendations for Future Work

Precision in the derivation chain.

We have described instances above in which the direction and magnitude of the predicted estimates in tests of the sustaining environments hypothesis are not clear. More precisely specifying the nature and predictions of the sustaining environments hypothesis may be necessary for us to be able to use it to generate useful knowledge (Meehl, 1990). We propose that a primary implication of these findings for future research on the sustaining environments hypothesis is that predictions about the circumstances under which such complementarities arise should be better informed by theory. The parsimonious and intuitive hypothesis that “quality complements quality” is probably far too simple. When making predictions about complementary factors that might contribute to children’s academic achievement, theories of children’s cognitive development, along with careful observations of what children are exposed to in classrooms, may prove useful. For example, to the extent that there is any redundancy at all between the content taught in an early educational intervention and in the subsequent educational environment, learning curves will be steeper for this knowledge in the no preschool group, and some degree of fadeout will be likely (Campbell & Frey, 1970). Additionally, some research suggests that a sustaining environment is not simply more whole-class advanced instruction, but the extent to which subsequent instruction is individualized or differentiated based on a child’s skill level. Some experimental research suggests that literacy instruction that explicitly differentiates classroom instruction and in-class group work by a child’s literacy skills promotes the greatest learning (Connor et al., 2009). Future studies of differentiated instructional strategies tailored to the skill level of preschool graduates may be a more precise operationalization of the sustaining environments hypothesis. A better understanding of the complementary skills or structures underlying the findings from Johnson and Jackson’s (2017) analysis of Head Start and K-12 funding – including a serious consideration of the possibility that factors proximal to academic achievement may not be the key mediators of the lasting effects of early childhood educational intervention – may also inform theories of sustaining environments.

To improve the clarity and precision of predictions about complementarity it will be necessary to identify educational constructs or treatments that can be well measured and for which there is a well-defined cognitive prediction about how they might interact with prior knowledge. For example, perhaps the impact of an effective algebra intervention will be more persistent for students who subsequently enroll in an algebra II course than for students who subsequently enroll in a geometry course. This approach might be useful in studies of older children, who are sometimes placed into mathematics courses with different titles (e.g., algebra II and geometry) and somewhat predictable content, despite being in the same grade in the same school. Although these predictions are more difficult to make for young children, experimental manipulation of specific types of educational content might allow for stronger tests of complementarity.

Studying larger effects.

Given the reasonable possibility that interactions are likely to be smaller than the main effects of educational interventions, explanations 1 and 2 above for our generally null results could be more strongly tested with data from early educational interventions and subsequent educational experiences with larger main effects. Studying educational interventions with large positive average treatment effects would also circumvent explanation 3. One possible strategy would be to select field interventions for follow-up on the basis of their end-of-treatment impacts. A problem with this plan is that it might lead to incentives for over-estimating these important impacts. Another possibility would be to provide funding for promising studies to add in a follow-up treatment condition that is fully crossed with assignment to the initial treatment. Some work has found that providing kindergarten and first grade teachers with professional development after the end of an effective preschool mathematics intervention improves children’s mathematics achievement (Clements et al., 2013). However, because there is no set of children randomly assigned to receive no early treatment and randomly assigned to receive the later treatment, these findings are consistent with either a main effect of the later teacher intervention or a positive interaction between earlier and later intervention.

Stronger causal identification.

In the absence of educational interventions that produce long-term effects substantially larger than estimated in the analyses included in the current study, causal identification of the main effects and interaction between early educational intervention and later educational quality is very important. The possible influence of selection bias on these estimates could be substantial, relative to their magnitudes: for example, the negative estimated effects of Head Start on children’s achievement in kindergarten (Figure 5) are plausibly wholly attributable to Head Start eligibility criteria. One can make reasonable speculations about the size and direction of selection bias on the estimated main effects of these variables, but it is much more difficult to intuit the direction (much less the magnitude) of selection bias on the interactions of interest. A possible approach that would provide strong causal identification and larger causal effects may be small field experiments in which children are randomly assigned to receive an intensive set of lessons or business as usual followed by a hypothesized complementary intervention or business as usual.

Although we suggest substantial changes in the design and analysis of studies on the sustaining environments hypothesis, there is at least one reason to be optimistic about progress in this area: This area of research appears to have positive norms pertaining to reporting of analyses. Authors in this field regularly publish null estimates, although there was some asymmetry in the funnel plot. Additionally, the location of the distribution of the published set of interaction estimates (Figure 2) appears to be similar to, although it is more variable than, the set of interaction estimates derived in our specification curve analysis (Figures 5 and 6).

Conclusion

Our study aimed to quantify evidence in favor of the sustaining environments hypothesis, as measured by positive interactions between early educational intervention and later educational quality on children’s later academic skills. Although we found little support for this hypothesis, we also highlighted key weaknesses in the available meta-analytic data as well as in the ECLS-K data used in the specification curve analyses, both in which mapping theory to predictions and selection bias are major concerns. For these reasons, our study does not falsify the sustaining environments hypothesis; rather, it suggests some ways of strengthening future tests of the sustaining environments hypothesis. In short, results suggest that the current mix of causal identification strategies, sample sizes, and measures used to test the sustaining environments hypothesis cannot reliably detect realistically sized effects. Our recommendations are to combine large sample sizes with strong causal identification strategies, and to study combinations of treatments that have a strong probability of showing large main effects.

The challenge of generating persistent effects of early educational on children’s academic skills is still of great interest to researchers, policymakers, and practitioners. We hope that our study helps to carefully guide future studies in this pursuit.

Highlights.

• We test interactions predicted by the sustaining environments hypothesis on achievement

• The key prediction is a positive interaction between early and later educational quality

• We conduct a meta-analysis of existing studies and specification curve analysis

• Both analyses yield very small interaction estimates

• We consider a range of plausible explanations and offer recommendations