Exploring Structural Flexibility and Stability of α-Synuclein by the Landau-Ginzburg-Wilson Approach

Abstract

α-Synuclein (αS) is the principal protein component of the Lewy body and Lewy neurite deposits that are found in the brains of the victims of one of the most prevalent neurodegenerative disorders, Parkinson’s disease. The αS can be qualified as a chameleon protein because of the large number of different conformations that it is able to adopt: it is disordered under physiological conditions in solution, in equilibrium with a minor α-helical tetrameric form in the cytoplasm, and is α-helical when bounded to a cell membrane. Also, in vitro, αS forms polymorphic amyloid fibrils with unique arrangements of cross-β-sheet motifs. Therefore, it is of interest to elucidate the origins of the structural flexibility of αS, and what makes αS stable in different conformations. We address these questions here by analyzing the experimental structures of the micelle-bound, tetrameric and fibrillar αS in terms of a kink (heteroclinic standing wave solution) of a generalized discrete nonlinear Schrödinger equation. It is illustrated that without molecular dynamics simulations the kinks are capable to identify the key residues causing structural flexibility of αS. Also, the stability of the experimental structures of αS is investigated by simulating heating/cooling trajectories using the Glauber algorithm. The findings are consistent with experiments.

Graphical Abstract

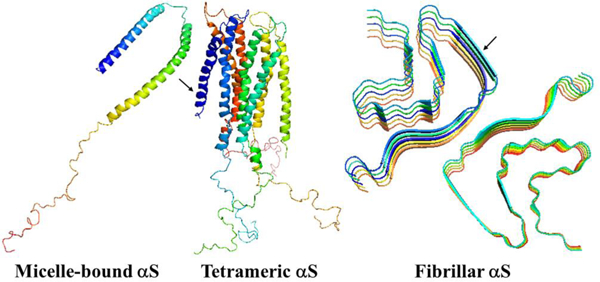
Introduction

α-Synuclein (αS) is a small (140 residue) intrinsically disordered protein (IDP) expressed in neurons and presynaptic nerve terminals.¹ It is abundant in the neuronal cytosol of a healthy brain, and its function is thought to be associated with axonal transport.^2,3 The assembly of monomeric αS into amyloid fibrils that form Lewy bodies (LBs) and Lewy neurites is a hallmark of Parkinson’s disease (PD),⁴ the second most common neurodegenerative disorder (after Alzheimer’s disease) nowadays with a significant rise in the number of affected patients and cost of care.⁵ αS is characterized by three domains: (i) an amphipathic N-terminal region dominated by four 11- residue repeats including the consensus sequence KTKEGV (residues 1−60); (ii) a central hydrophobic region, which includes the nonamyloid-β component (NAC) region and two additional repeats, involved in protein aggregation (residues 61−95); and (iii) a highly acidic and proline-rich region which has no distinct structural propensity (residues 96−140).

From a structural point of view, αS is a chameleon protein;^6,7 i.e., it is a disordered monomer in solution, which undergoes a large-scale disorder-to-helix transition upon binding to vesicles of different types,^8,9,10 and also can adopt a folded tetrameric state that has a relatively high helical content under physiological conditions.^11,12 When incubated under physiological conditions in vitro, αS aggregates into fibrils with polymorphic cross-β-sheet conformations, in which a core of β-strands is aligned perpendicular to the fibril axis forming extended regular β-sheets with different arrangements.^13,14,15,16 In addition to cylindrical fibrils, ribbon aggregates have also been observed.¹⁷ Therefore, it is of interest to know (i) what governs the structural flexibility of αS; (ii) the actual stability of these structures; (iii) what underlies the aforementioned structural stability.

It should be noted that αS has been the subject of not only extensive experimental^8–17 but also theoretical^{6,18,19,20,21} studies, in which molecular dynamics (MD) simulations were used to complement ensemble-averaged experiments. Although MD simulations have proven to be a very powerful tool for examining protein folding dynamics, the correctness of such simulations depends on the force field employed to describe physical interactions within and between peptide units. The present force fields, both all-atom and coarse-grained, are far from being accurate. Even small errors in the description of protein energy surfaces can accumulate over a polypeptide chain to distort the correct fold. The inaccuracy problem becomes more significant when the folding of weakly stable proteins is studied, in which barriers between folded and unfolded states are very low. Therefore, in order to answer the abovementioned question, in this study, we investigate the experimental structures of the micelle-bound,⁸ tetrameric,¹² and fibrillar¹⁴ αS from another, complementary point of view. In particular, instead of analyzing individual interactions that contribute to the formation of the folded structure, model-independent principles that are based on symmetry are explored. We suggest that all the physical forces, both strong and weak, combine together to give rise to a particular type of protein dynamics, expressed by a generalized version of the discrete nonlinear Schrödinger (DNLS) equation, and propose that various parametrizations of a kink, or heteroclinic standing wave solution, of a generalized version of the DNLS equation to be utilized as the basic modular building blocks of folded proteins.^{22,23,24,25,26,27,28,29,30,31,32} The DNLS equation is the paradigm nonlinear equation that describes kinks as soliton solutions. The specific form that we use, is selected as it is the simplest possible form that both supports kinks as stable soliton solutions and introduces chirality of the C^α backbone. The main limitation would come from the complexity of loop structure, when the loops become so long that it is no longer practical to decompose them in terms of individual kinks. But that is rarely the case of globular proteins, with regular secondary structures such as helices and strands between loops. Proteins are, of course, examples of linear polymers, but a generic polymer often does not have identifiable super-secondary structures, like globular proteins do in their collapsed phase. Thus, it can be more difficult to reliably identify the kink structures.

Note that, unlike some recent studies,^22–28,30 in which the epithet topological (dark) soliton was used, here we prefer to use kink. This choice highlights that the potential in the DNLS equation displays a spontaneous breakdown of a discrete symmetry, and the kink describes the ensuing domain wall;^{33,34,35,36,37} in the case of a folded protein, an individual kink corresponds to a supersecondary structure such as a helix−loop−helix or strand-loop-strand motif. Also, the kink considered here has no direct relationship with the concept of Davydov’s soliton.³⁸ The kink in a protein is a purely topological (geometric) structure, and the Davydov’s soliton, in turn, is associated with collective excitations traveling along a chain (perturbations of electron density). In the end, we should mention that proposed approach has been successfully used for studying the dynamics of IDPs, as well.^27,30,32

Methods

In this work, we are interested in describing the geometry of a protein backbone in terms of a piecewise linear polygonal framed chain, as seen from the point of view of an imaginary observer who traverses the backbone by moving between the C^α atoms. For this, we employ the purely geometrically determined discrete of the Frenet framing,^25,29 described in the Supporting Information. We emphasize that these frames depend only on the C^α backbone geometry, and neither the side-chain structure nor the individual peptide plane structure are involved in their definition.

Kink of the DNLS Equation.

According to Anfinsen’s dogma,³⁹ the protein in the native state locates at the global minimum of Helmholtz free energy

$$F=U-TS$$ (1)

where U is the internal energy, S is the entropy and T is the temperature. The angles κ_i and γ_i are adopted as the structural variables of the free energy because of their intrinsic connection with the coordinates of C^α atoms. Considering the ℤ₂ gauge symmetry shown in Eq. (S8), the Landau-Ginzburg-Wilson free energy F is naturally introduced to describe the backbone C^α chain of protein.²² When the deformations of protein around the energy minimum keep slow and small, the free energy can be expended as follows:

$$F=-{\sum }_{i=1}^{N-1}2{\kappa }_{i+1}{\kappa }_i+{\sum }_{i=1}^N\left\{2{\kappa }_i^2+\lambda {\left({\kappa }_i^2-m^2\right)}^2+\frac{q}{2}{\kappa }_i^2{\gamma }_i^2-p{\gamma }_i+\frac{r}{2}{\gamma }_i^2\right\}$$ (2)

where λ, q, p, r, and m are parameters. The detailed derivation of Eq. (2) can be found in Refs. [22,23,29]; here it suffices to state that this free energy can be shown to relate to the long-distance limit that describes the full microscopic energy of a folded protein in the universal sense of Refs. [40,41,42,43]. As such, it does not explain the details of the (sub)atomic level mechanisms that give rise to protein folding.

In order to determine the kink content of the backbones, at first, we should define positions of the inflection points (kink centers). We can find the inflection points by analyzing the three-dimensional structure (protein topology) and the experimental values of the angles (κ_i, γ_i). Inflection points correspond to the centers of kinks. Then, the angular spectrum should be reconstructed using the ℤ₂ transformation at the kink centers (it should be noted that the three-dimensional shape of the protein is invariant under ℤ₂ transformation). After that, for a given kink structure, we look for a minimum of global energy using a combination of simulated annealing and gradient descent methods. For this proposal a special toolkit for protein structure visualization and analysis was developed [https://protoin.ru/propro/index.php].⁴⁴

In short, the search for the minimum energy occurs in the following order. The virtual-bond angles κ are first extended to negative values, using the ℤ₂ gauge symmetry [Eq. (S8)]. The virtual-bond-dihedral angles γ are then expressed as functions of the virtual-bond angles κ

$${\gamma }_i\left[\kappa \right]=\frac{p}{r+q{\kappa }_i^2}\equiv \frac{u}{1+v{k}_i^2}$$ (3)

with u = p/r and v = q/r. By inserting Eq. (3) into Eq. (2), the virtual-bond-dihedral angles γ are eliminated and the following system of equations for the motion of the virtual-bond angles κ is obtained:

$${\kappa }_{i+1}=2{\kappa }_i-{\kappa }_{i-1}+\frac{dV\left[\kappa \right]}{d{\kappa }_i^2}{\kappa }_i\left(i=1,\dots ,N\right),$$ (4)

where ${\kappa }_0={\kappa }_{N+1}=0$ and

$$V\left[\kappa \right]=\frac{p}{r+q{\kappa }^2}+2\left(1-\lambda m^2\right){\kappa }^2+\lambda {\kappa }^4,$$ (5)

where the familiar structure of the generalized DNLS equation is recognized.^22–32,44 The kink solution to Eq. (4) can be constructed numerically by following the iterative procedure of Ref. [23]. But its explicit form has not so far been found in terms of elementary functions. However, an excellent approximation is obtained by naively discretizing the heteroclinic standing wave solution to the continuum nonlinear Schrödinger equation^22–32,44

$${\kappa }_i=\frac{b exp\left[{\sigma }_1\left(i-s\right)\right]+a exp\left[-{\sigma }_2\left(i-s\right)\right]}{exp\left[{\sigma }_1\left(i-s\right)\right]+exp\left[-{\sigma }_2\left(i-s\right)\right]}$$ (6)

and with γ_i[κ] evaluated from Eq. (3). Here, s is a parameter that determines the center of the kink. The a, b ∈ [0,π] mod(2π) are parameters which determine the amplitude of the variation of κ and the asymmetry of the inflection regions; they correspond to the minima of the potential energy contribution V [κ] in Eq. (5). The parameters σ₁ and σ₂ are related to the inverse of the range of the kink. It should be noted that, in the case of proteins, the values of a, b are determined entirely by the adjacent helices and strands. Far away from the center of the kink (see Figure 6 in Ref. [29])

$${\kappa }_i\to \left\{\begin{array}{c}b\hspace{1em}\hspace{1em}mod\left(2\pi \right) i>s\\ a\hspace{1em}\hspace{1em} mod\left(2\pi \right) i<s\end{array}\right.$$ (7)

and according to Eqs. (S9) and (S10), the asymptotic values

$${\kappa }_i\approx \pi /2 \hspace{1em}\text{or}\hspace{1em}-\pi /2\hspace{1em}\text{and}\hspace{1em}{\kappa }_i\approx 1\hspace{1em}\text{or}\hspace{1em}-1$$ (8)

correspond to the α-helix or β-strand, respectively. In order to satisfy the monotonic character of the profile of Eq. (6), the experimentally measured values of κ_i have to vary monotonically along the amino-acid sequence. Otherwise, a multiple of 2π is added to the experimental values. This does not affect the backbone geometry because κ_i^’s are defined mod (2π). The σ₁ and σ₂ are intrinsically specific parameters for a given loop. But they specify only the length of the loop, not its shape which is defined by the functional form of Eq. (6), and in the case of a and b, they are combinations of the parameters in Eq. (5).

In Eq. (3) for the virtual-torsion angles, γ_i, there are only two independent parameters u and v. As a consequence, the profile of γ_i is determined entirely by the profile of κ_i, and on the structure of the adjacent regular secondary structures.

Finally, we introduce the concept of folding index of a protein backbone. The formation, evolution and structure of a loop along a folding protein can be monitored in terms of topologically determined folding indices. Folding index^28,29 is defined by following equation:

$$In{d}_f=\left[\frac{\text{Γ}}{\pi }\right]$$ (9)

$$\text{Γ}=\sum _{i=n_1+2}^{n_2-2}\left\{\begin{array}{c}{\gamma }_{i,i+1}-{\gamma }_{i-1,i}-2\pi if {\gamma }_{i,i+1}-{\gamma }_{i-1,i}>\pi \\ {\gamma }_{i,i+1}-{\gamma }_{i-1,i}+2\pi if {\gamma }_{i,i+1}-{\gamma }_{i-1,i}<-\pi \\ {\gamma }_{i,i+1}-{\gamma }_{i-1,i}\hspace{0.5em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\end{array}\right.$$ (10)

where [x] denotes the integer part of x, and Γ is the total rotation angle (in radians) that the projections of the C^α atoms of the consecutive loop residues make around the north pole. The folding index is a positive integer when the rotation is counterclockwise, and a negative integer when the rotation is clockwise. The folding index classifies loop structures and entire folded proteins in terms of its values.

Results and Discussion

Scrutiny of the Experimental Structures of the Micelle-Bound, Tetrameric, and Fibrillar α-Synuclein in Terms of Kinks.

The study of kinks is more easily understood from a differential representation of the protein backbone. Assuming constant virtual bond distances between the C^α atoms, the free-energy of the polymer can be written in terms of (κ,γ) internal coordinates using a Landau-Ginzburg-Wilson free-energy model^22–32 [Eq. (2)]. Minimizing this free-energy relative to κ and γ lead to a nonlinear equation of motion for the curvature similar to a generalized DNLS which admits kinks as particular solutions.

In earlier studies,^22–32 the modular building blocks of folded proteins, i.e. super-secondary structure such as a helix-loop-helix or strand-loop-strand motif, have been described in terms of the kink of a generalized version of the DNLS equation. It was found that the formation of a kink is initiated by an abrupt change in the orientation of a pair of consecutive side chains in the loop region.²⁹ Moreover, kink analysis enabled us to realize the importance of local interactions, specifically the bimodal character of the potential of mean force in virtual-bond angles κ, as the driving force of folding.²⁹ It should be noted that the only long-range interaction present in the Landau-Ginzburg-Wilson Hamiltonian^22–32 is a step-wise Pauli exclusion that introduces self-avoidance and prevents chain crossing. The effects of the long-range Coulomb and Van der Waals interactions are accounted for by the global multi-kink profile resulting from the minimization of free energy.⁴⁵ The multi-kink structure describes both local and collective motions. Previously, it was shown that by using kink parameters that are derived from the experimental folded protein structure, its folding can be simulated,^{27,44,46,47,48} as well as without MD simulations the kinks are able (i) to capture the sites of the protein that govern the system to change the folding scenario³¹ and (ii) to identify the phosphorylated sites of protein, the key players in phosphorylation-induced folding.³² Also, phase diagram of protein with temperature (T) and acidity (pH) as the thermodynamic variables can be constructed as well.⁴⁶ Therefore, it is of interest to investigate whether a kink analysis of the experimental structures^8,12,14 can uncover the mechanisms of folding, misfolding and aggregation, as well as the reasons for the structural flexibility and stability of α-synuclein.

Kink structures of the micelle-bound, tetrameric and fibrillar α-synuclein.

In the present work, we have carried out a detailed analysis of experimental structures of the micelle-bound αS (PDB ID: 1XQ8),⁸ the first chain of tetrameric αS (a structure generously provided by Dr. Thomas Pochapsky),¹² and A-chain of fibrillar αS (PDB ID: 6CU7)¹⁴ in terms of kinks. It should be noted that, of the 140 residues present in the experimental structures of the micelle-bound and tetrameric αS, 95-residue fragments (Met1 – Val95) were selected (C terminal, which has no distinct structural propensity, was removed, because it is extremely difficult to select kinks that give meaningful results for this region of the system), whereas entire experimental structure (Leu38 – Lys97) was selected in the fibrillar αS. For the sake of simplicity below these truncated and in two cases incomplete (only one chain is examined) systems will be called as the micelle-bound, tetrameric and fibrillar αS. Using experimental values of the κ and γ angles, we started resolving the kink structures of these proteins. The multi-kink is a configuration that minimizes free energy [Eq. (2)], with an acceptable small deviation, the root-mean-square deviation (RMSD), from the three-dimensional experimental structure. Minimum energy, as well as RMSD fitting, is achieved using a combination of simulated annealing and gradient descent methods. Multi-kink structures that are combinations of 5, 8 and 9 individual kinks, differing in the arrangement along the protein chain, were obtained for the micelle-bound, tetrameric, and fibrillar α-synuclein, respectively. With RMSD < 1.0 Å, a total of 31 structures were initially obtained for the micelle-bound αS, 16 structures for the tetrameric αS, and 8 structures for the fibrillar αS. For each system, three representative structures were then selected for a detailed analysis. In particular, the structures with (i) RMSD = 0.79Å, 0.81Å, 0.87Å for the micelle-bound αS, (ii) RMSD = 0.94Å, 0.95Å, 0.96Å for the tetrameric αS, and (iii) RMSD = 0.76Å, 0.76Å, 0.78Å for the fibrillar αS. Figure 1 illustrates comparison of the κ and γ angles, experimental and calculated, along the chains of three selected structures of the micelle-bound, tetrameric, and fibrillar α-synuclein. In addition, for each protein, Figure 2 shows experimental values of the κ and γ angles in the first panels, and most representative kink structures in the three remaining panels. Data on this figure allow us to scrutinize the correlations between the location of kinks and folding/misfolding paths. [The experimental and three computed representative structures for the micelle-bound, tetrameric, and fibrillar αS are shown in Fig. S3 (Supporting Information)].

Figure 1.

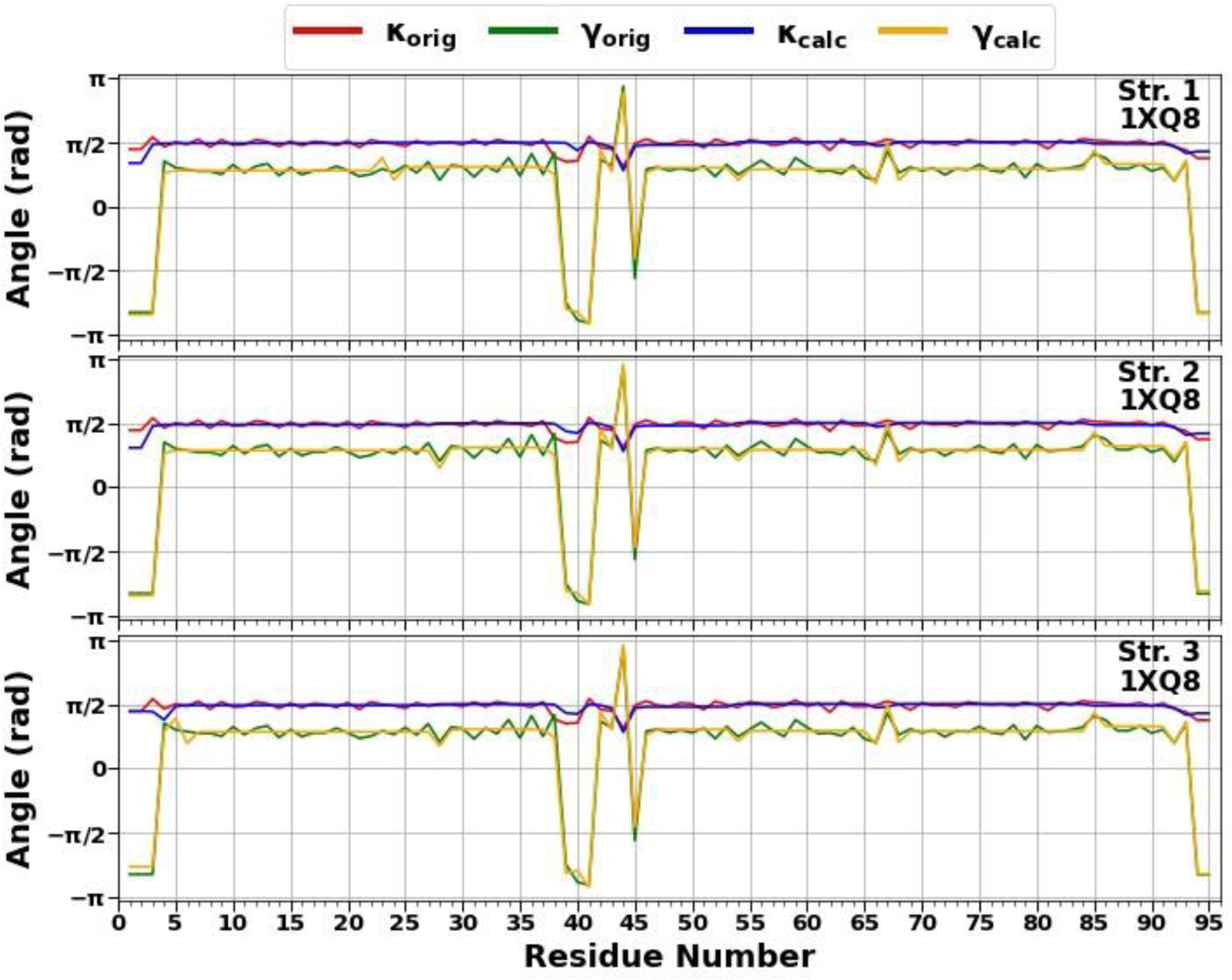
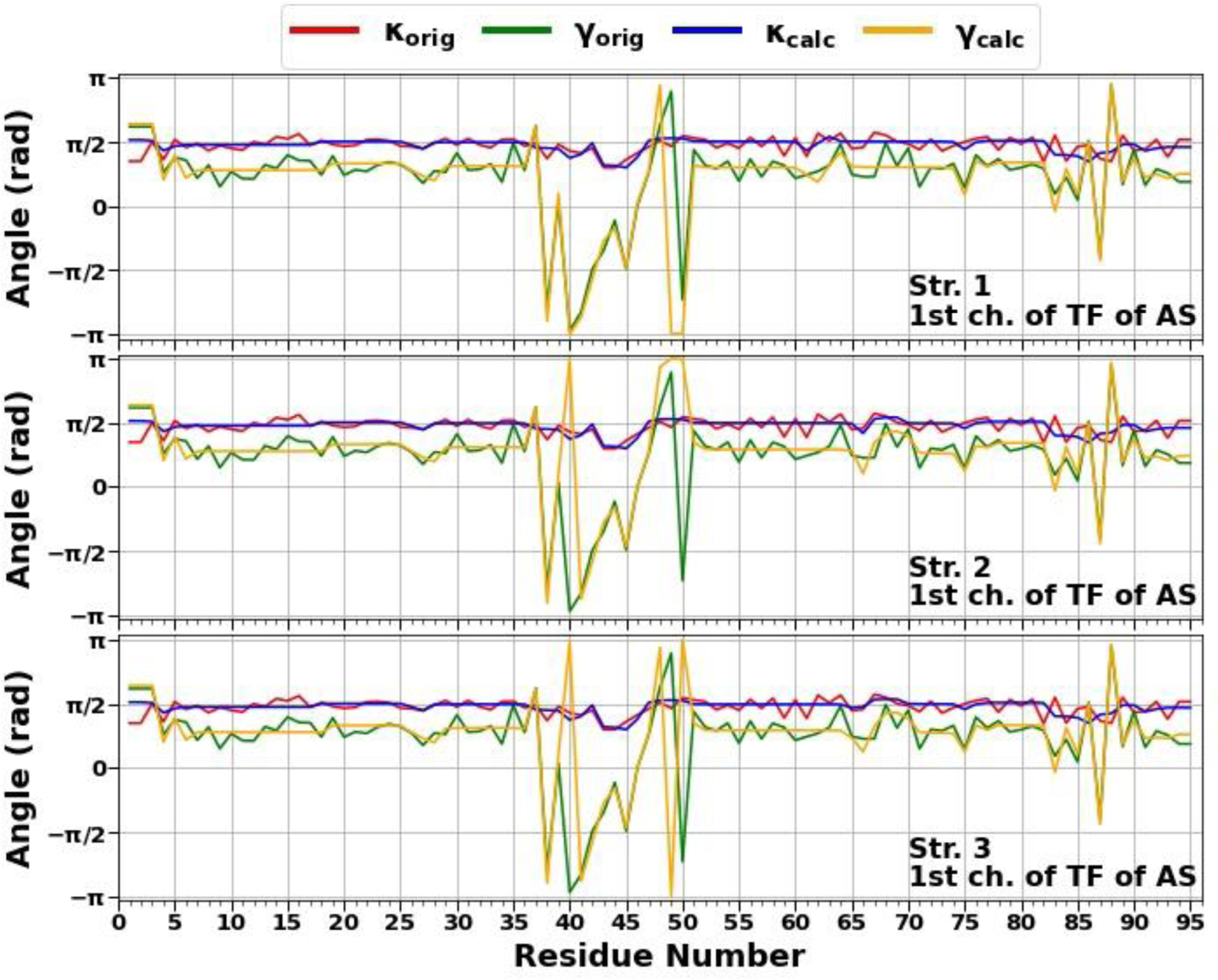
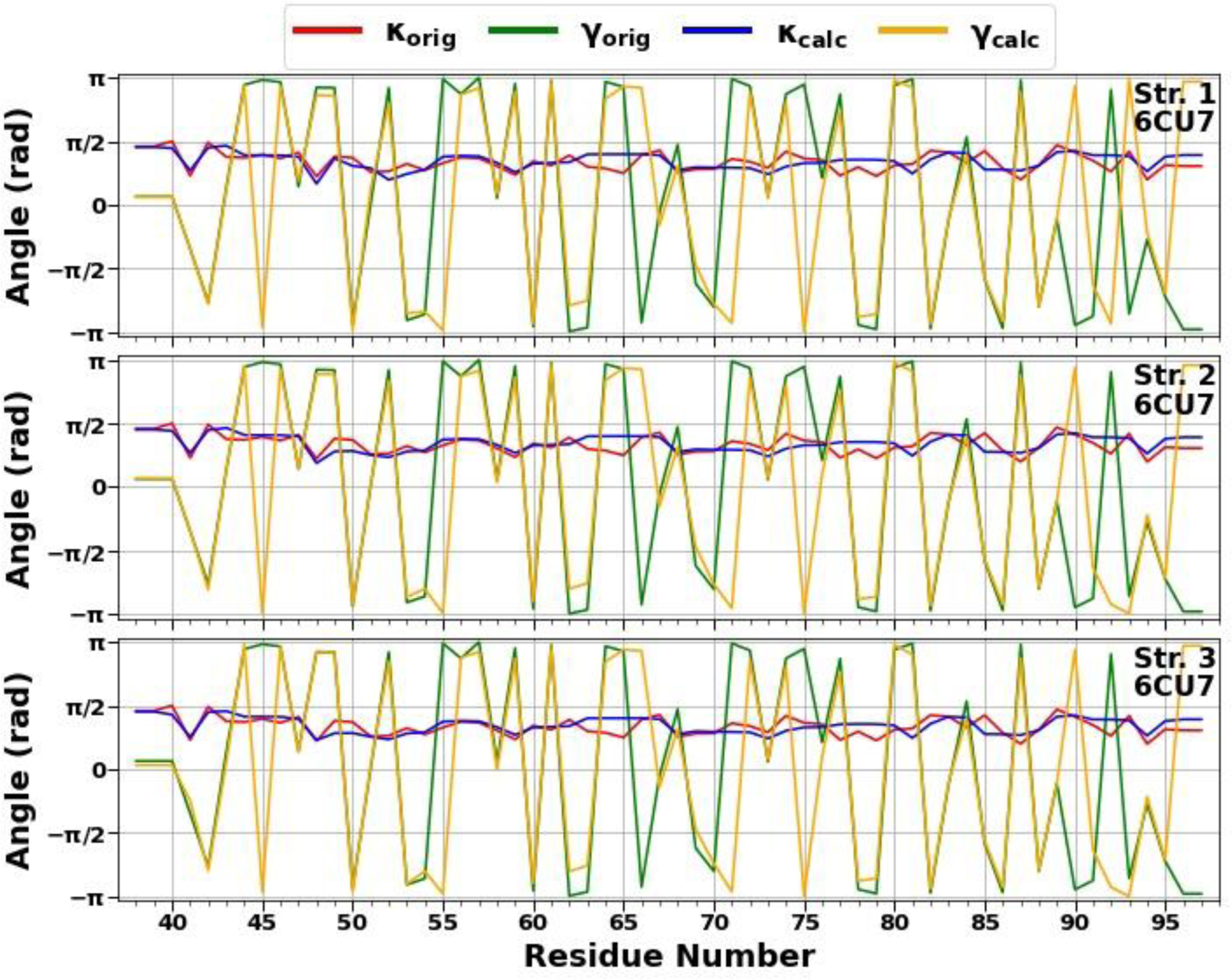
The comparison of experimental and calculated angle spectra of three selected structures for the micelle-bound (top 3 panels), tetrameric (middle 3 panels), and fibrillar (bottom 3 panels) αS in terms of virtual-bond κ_i (experimental-red, calculated-blue) and torsion γ_i (experimental-green, calculated-yellow) values.

Figure 2.

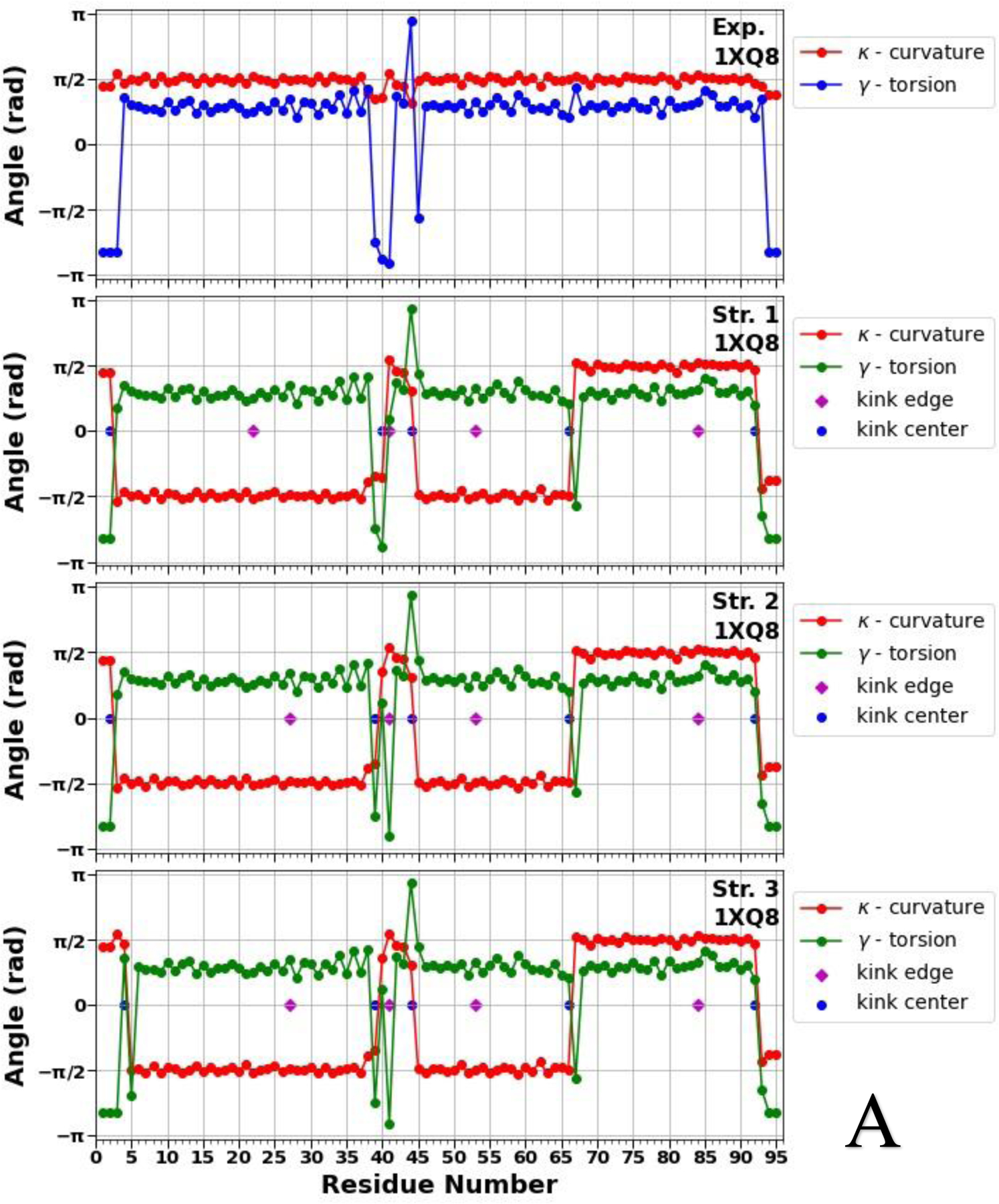
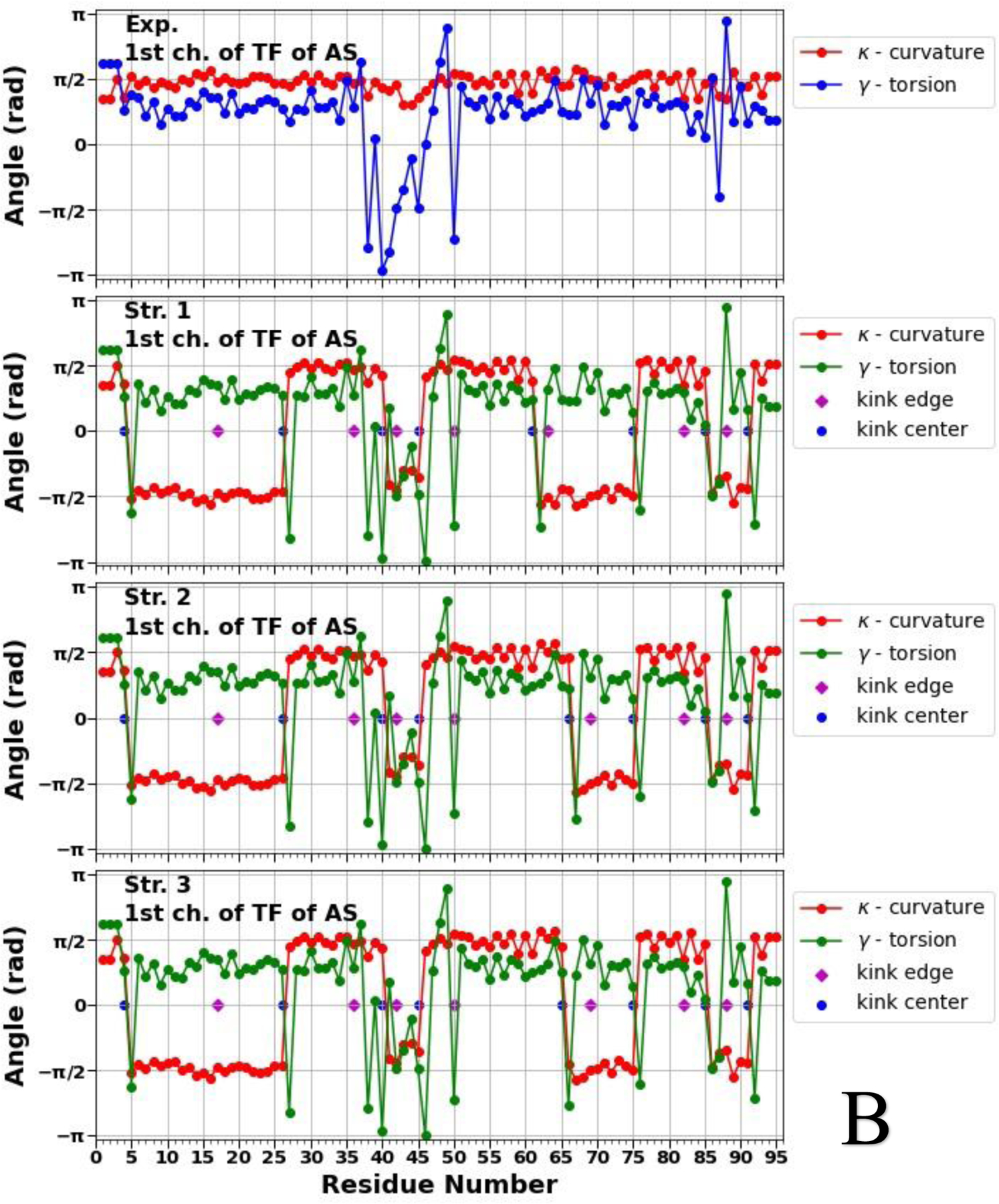
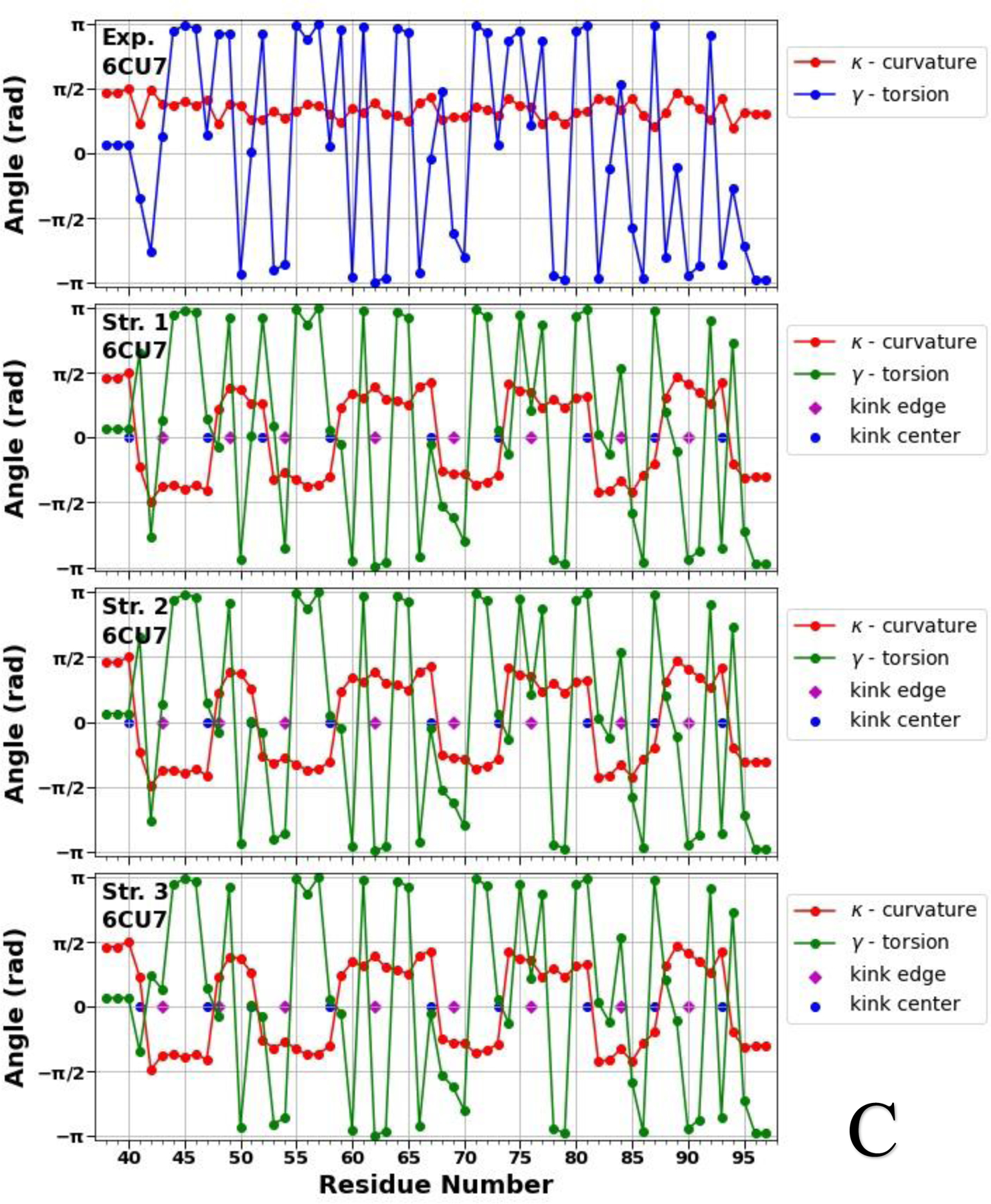
Top panels of A, B and C represent experimental values of the virtual-bond κ_i (red) and torsion γ_i (blue) angle spectra of the micelle-bound (panel A), tetrameric (panel B) and fibrillar (panel C) αS. Remaining three panels in A, B and C illustrate kink structures, i.e., the virtual-bond κ_i (red) and torsion γ_i (green) angle spectra for three selected structures of the micelle-bound (panel A), tetrameric (panel B) and fibrillar (panel C) αS, after ℤ₂ gauge transformation [Eq. (S8)] was made. Blue circles represent centers of kinks, purple rhombuses represent the right edges of left kinks.

Figure 2 illustrates that not only the number of the kinks, but also the kink locations along the sequences of the αS are changing, which indicate the structural flexibility and weak stability of the system. In our recent work,¹⁹ by analyzing the all-atom MD trajectories of the monomeric (including the micelle-bound αS) and tetrameric αS in terms of the local and global motions, correlations between the main-chain and the side-chain motions and steric parameters along the amino-acid sequence, we were able to elucidate a fundamental relationship between monomers and tetramers. It was found that the sites with high values of the correlation coefficient and with low values of the steric parameter are responsible for high-flexibility and disorder of the αS.¹⁹ The locations of the kink centers for the micelle-bound and tetrameric αS [see Fig. 2 (A, B)] coincide with the peaks on the correlation coefficient curves and with the minima on the steric parameter curves. These correlations indicate that each chain separately in the tetramer is more unstable than the micelle-bound monomer, which is more proof that the αS in the monomeric form is an IDP. Moreover, if we extrapolate these correlations on the fibrillar αS, then the here presented results (see Fig. 2 C) indicate an instability of each chain separately in the fibrillar αS, which is in harmony with experiment stating that fibrils are repositories of soluble intermediates and a source of harmful oligomers.⁴⁹ It should be noted that all 5 kinks obtained in the micelle-bound αS are present in the tetrameric and fibrillar αS with small shifts of the kink centers caused by different “environments”. The three (39/40, 44, 66), six (26, 40, 45, 61/65/66, 75, 85) and eight (40/41, 47, 51/52, 58, 67, 73, 81, 87) kink centers of the micelle-bound, tetrameric and fibrillar αS, respectively, pertain to seven imperfect 11-mer repeats; and one (44), four (26, 45, 61, 85) and three (47, 58, 81) kink centers of the micelle-bound, tetrameric and fibrillar αS, respectively, pertain to the conserved αS “KTKEGV” repeat motifs.⁵⁰ Also, the kinks are able to identify the important sites, within an accuracy of one residue, mutations of which (E46K and A53T) decrease tetramer/monomer ratios and αS solubility, and induce neurotoxicity.⁵¹ In particular, the center of the fourth kink (at 45^th residue) in the tetrameric αS and centers of the second and third kinks (at 47^th and 52^nd residues) in the fibrillar αS are shifted from these sites by one residue.

Folding index for the micelle-bound, tetrameric, and fibrillar αS.

Figure 3 illustrates the accumulation of the folding index^28,29 [Eqs. 9 and 10] along the trajectories for the micelle-bound (A), tetrameric (B), and fibrillar (C) αS, together with the folding index dependence on length of the protein (D).

Figure 3.

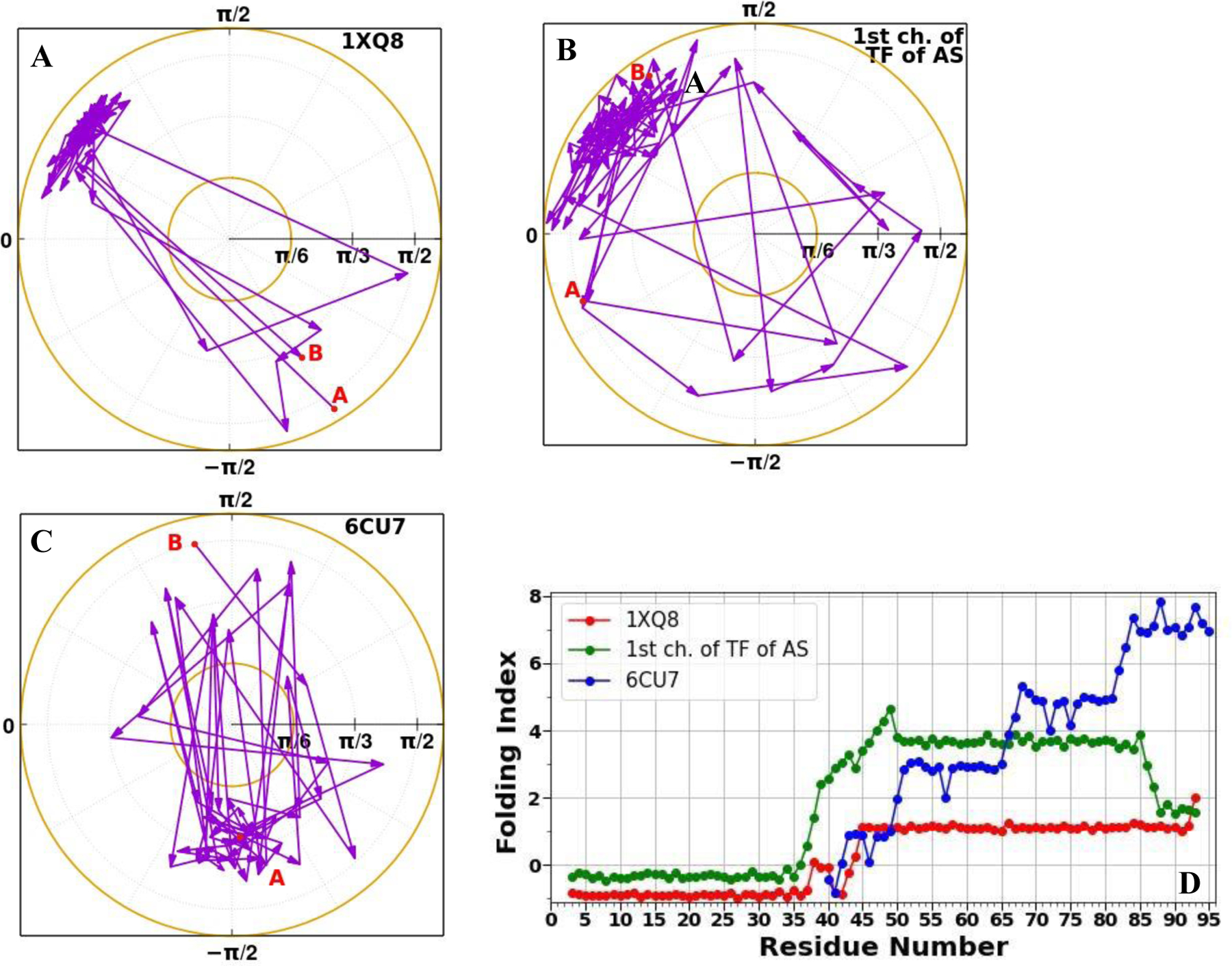
Folding index trajectories for the micelle-bound (A), tetrameric (B), and fibrillar (C) αS, and the folding index (D) for the micelle-bound (red), tetrameric (green), and fibrillar (blue) αS.

As was expected, two regions corresponding to the right-handed α (A, B) and β (C) structure were explored by the systems. The area explored by the tetrameric αS is larger than areas explored by the micelle-bound and fibrillar αS, which indicates on looseness of the tetrameric structure. Moreover, the “behavior” of the folding index vs residue number for the micelle-bound, tetrameric, and fibrillar αS differ from each other. In particular, one peak at the 38^th residue and one significant jump from −0.8 to 1.1 reaching maximum value at the 45^th residue can be observed in the folding index graph for the micelle-bound αS (red curve in panel D). In our recent study on dimers of wild type (WT) αS and its mutants,⁵² we found that the A53T and E46K mutants exhibit high propensities (the first and second highest peaks, respectively) to aggregate at residue L38. The second significant residue K45 is “a neighbor” of abovementioned important site E46. The shift by one residue might be due to the influence of micelle. One major peak at the 49^th residue can be seen in the folding index graph for the tetrameric αS (green curve in panel D), that is one residue away from the H50 residue, the mutation of which (H50Q) enhances the aggregation, secretion, and toxicity of αS.⁵³ It should be noted that there are some similarities in the behavior of these two folding indices. Three main regions can be picked out: the first and third regions exhibit plateaus with negative and positive values of the folding indices, respectively; the middle region is the most important, acting as a transition region, and contains residues playing a crucial role in the stability of the system. Since the fibrillar αS represents a misfolded structure, it is not surprising that the behavior of the folding index of the fibrillar αS significantly differs from the previous two folded structures of αS. In particular, the folding index of the fibrillar αS increases gradually along the sequence and exhibits several peaks, which are far from the dominant missense mutation sites. On the contrary, it exhibits a minimum at residue 46 with a zero value for the folding index (blue curve in panel D).

In order to explain the importance of these findings, we should mention that the peak at certain site in the folding index graph indicates that the site plays an essential role in the stability of the protein,^{29, 31,32} unless the folding index value at peak is zero. When the folding index vanishes (i.e. it obtains zero value) at a certain site, this is an indication of instability.²⁹ Based on this, we can conclude that the folding index captures successfully important sites of the system, which are responsible for the stability of αS. These findings are in agreement with previous experimental^50,51,53 and theoretical studies,⁵² in which the authors illustrated that the mutations of the sites identified by the folding index decrease the stability, and consequently enhance the aggregation and toxicity of the system. It is not surprising that the folding index value at the 38^th residue (one of the peaks in red curve in panel D) is almost zero (~ 0.1), because when αS folds the role of this site in aggregation vanishes. Also, zero value of the folding index at the 46^th residue in the fibrillar αS is a good manifestation of how aggregation and fibrillation can change the property of a site in the system.

Glauber algorithm for protein stability.

We examined the stability of the micelle-bound, tetrameric and fibrillar αS by simulating heating and cooling trajectories using the Glauber algorithm.⁴⁶ In other words, we combine the Landau-Ginzburg-Wilson approach with Glauber dynamics to study in detail, how these systems unfold and fold. Glauber dynamics is a Markov chain Monte Carlo method, that is widely used to describe near-equilibrium relaxation dynamics of a statistical system towards equilibrium Gibbs state. It should be noted that the Glauber algorithm manages the dynamics of simple spin chain systems coming close to the thermal equilibrium, which also obeys the Arrhenius law.⁵⁴ Since proteins can be regarded as spin chains, it is natural to simulate the protein folding in terms of Glauber algorithm.

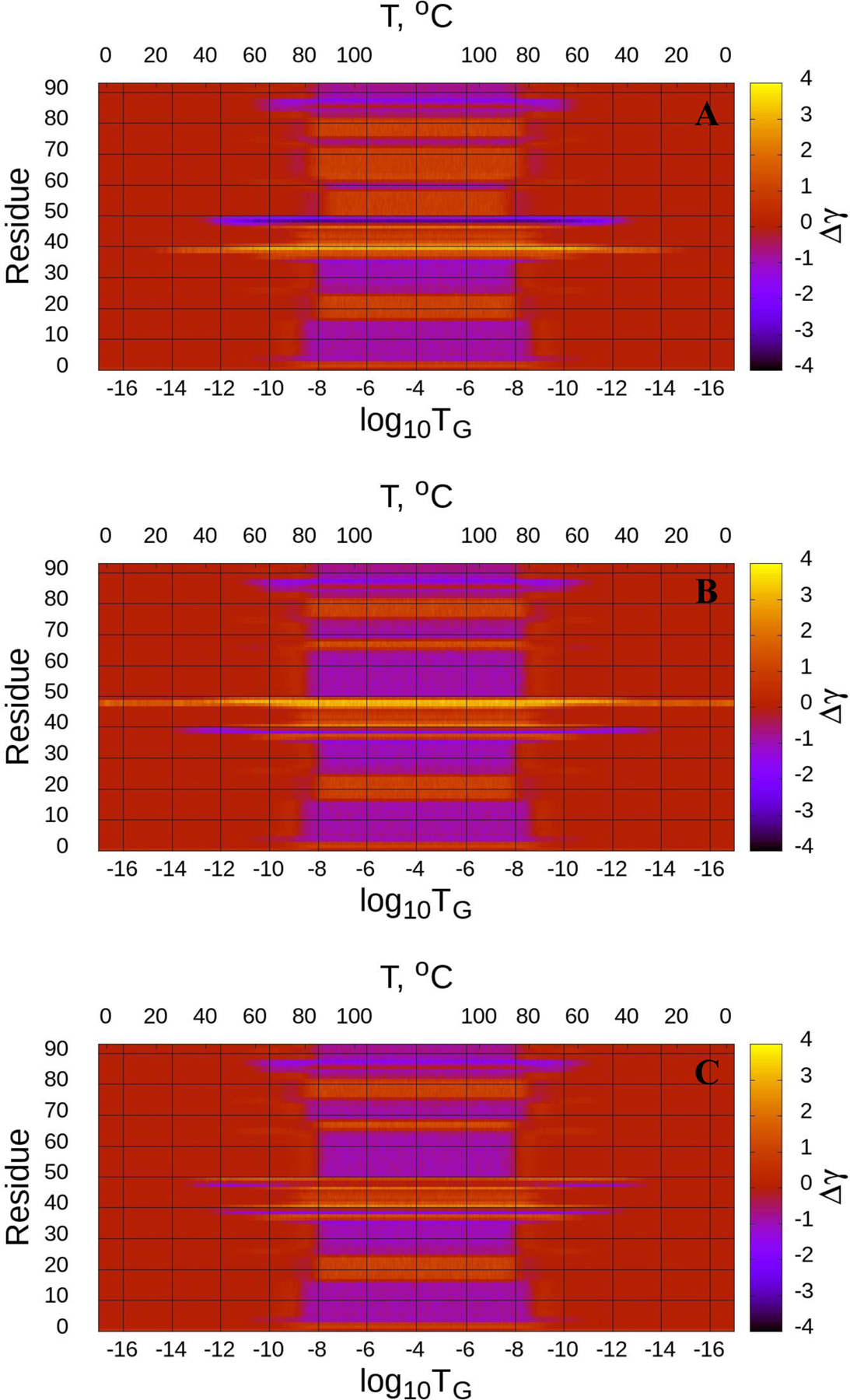
The Figures 4–6 (panels A-C) illustrate the heating/cooling maps for three calculated structures of the micelle-bound, tetrameric and fibrillar αS, respectively. In particular, they show the systems’ disordering/ordering during a heating and cooling simulation cycle as a function of temperature in terms of the average value of torsion angles γ. The first part of the maps (from the beginning up to log₁₀T_G ≈ - 8) corresponds to the thermal unfolding, the middle part of the maps (from log₁₀T_G ≈ −8 to log₁₀T_G ≈ - 8) is the random walk phase, and the last part of the maps (from log₁₀T_G ≈ - 8 to the end) corresponds to folding (misfolding for the fibrillar αS) due to protein cooling. The radius of gyrations (R_G), with representative structures of different temperatures, of three calculated structures as functions of Glauber temperature for the micelle-bound, tetrameric and fibrillar αS are plotted in panel D of Figures 4–6.

Figure 4.

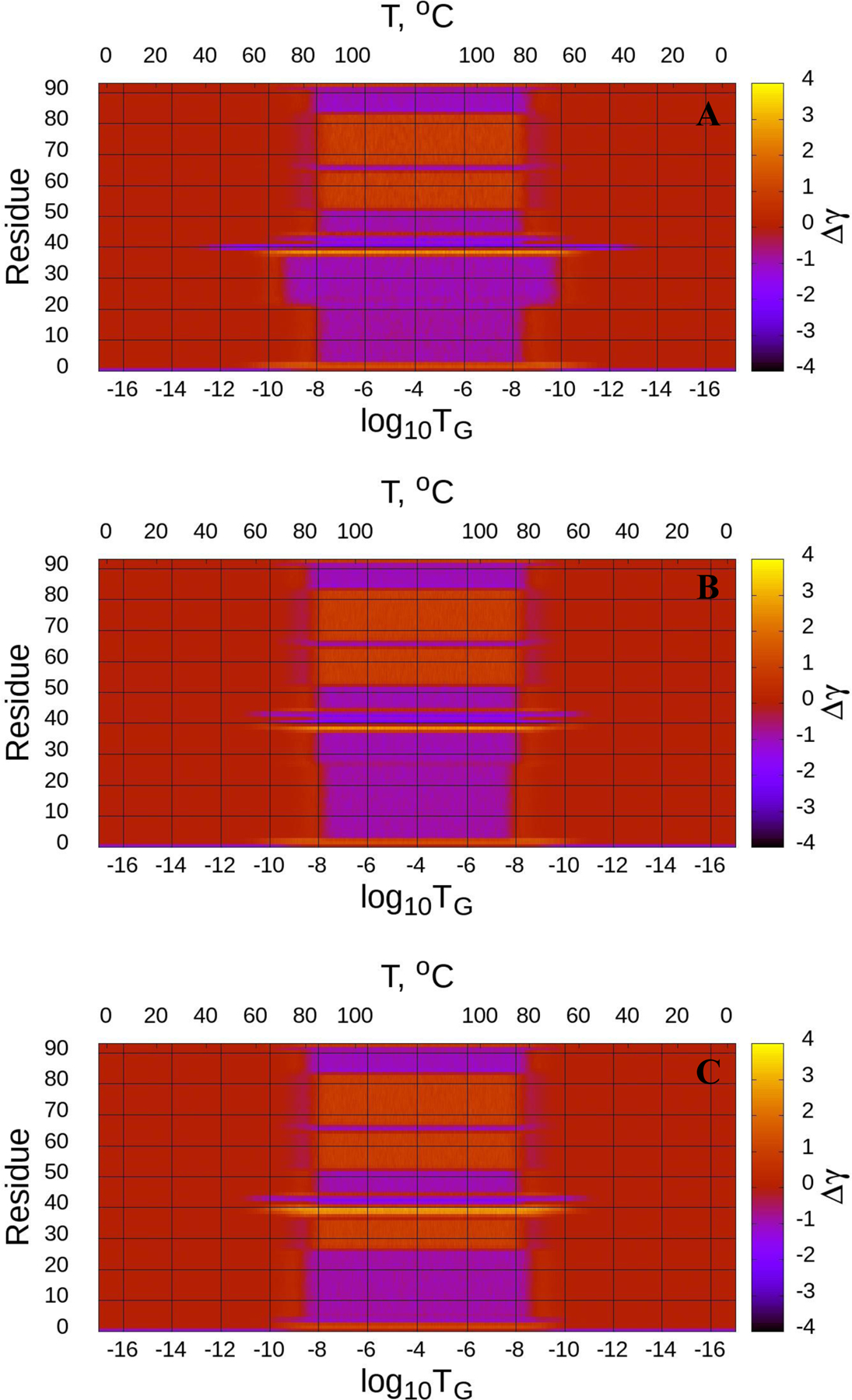
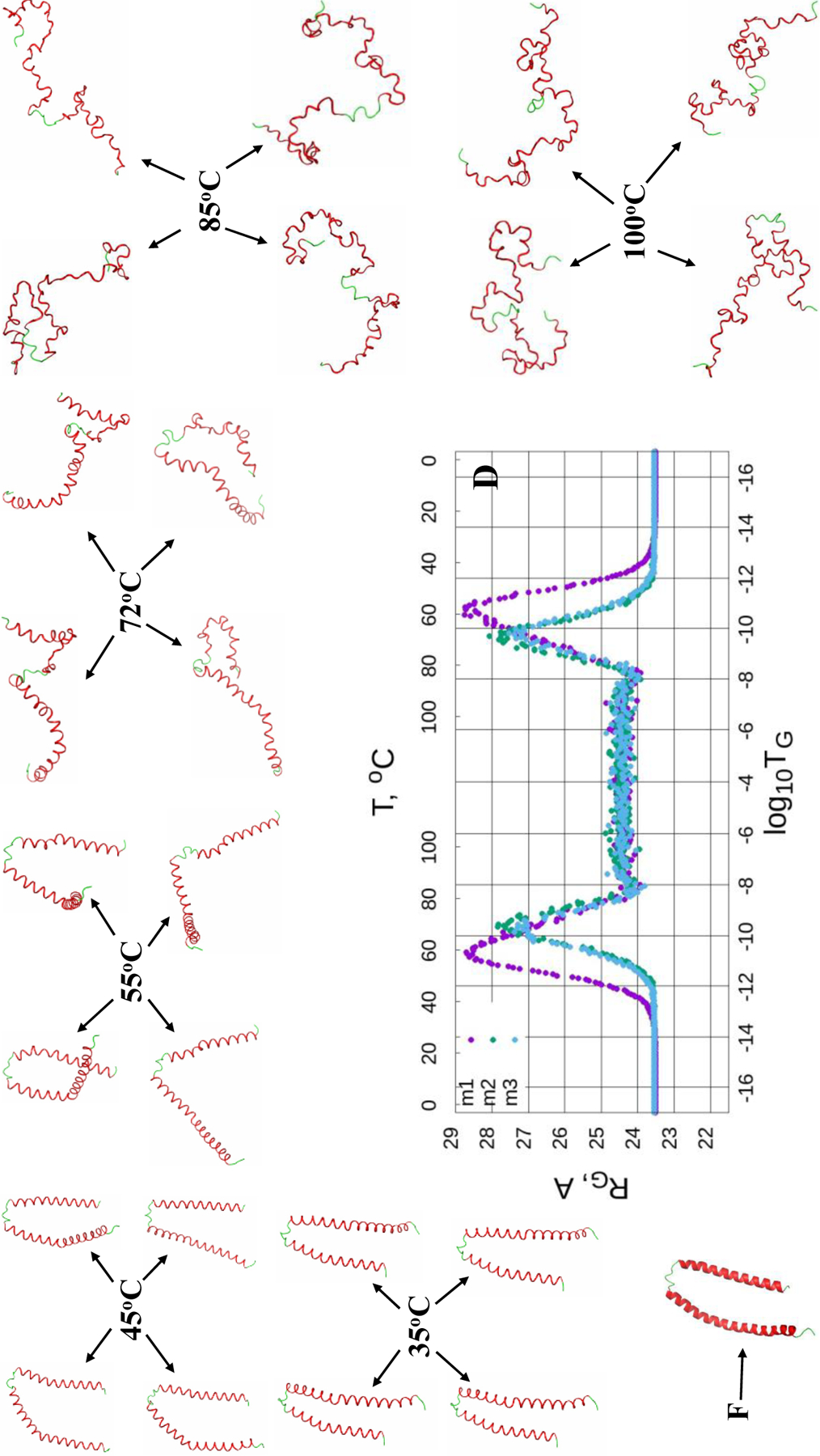
(Dis)ordering during a heating and cooling simulation cycle as a function of Glauber temperature (T_G) in terms of the average value of torsion angles γ for three selected structures of the micelle-bound αS (A-C), and the radius of gyrations (R_G) of three selected structures as functions of Glauber temperature (D). The representative structures at six different temperatures along with the folded (F) structure show the unfolding/folding pathways of the system (D).

Figure 6.

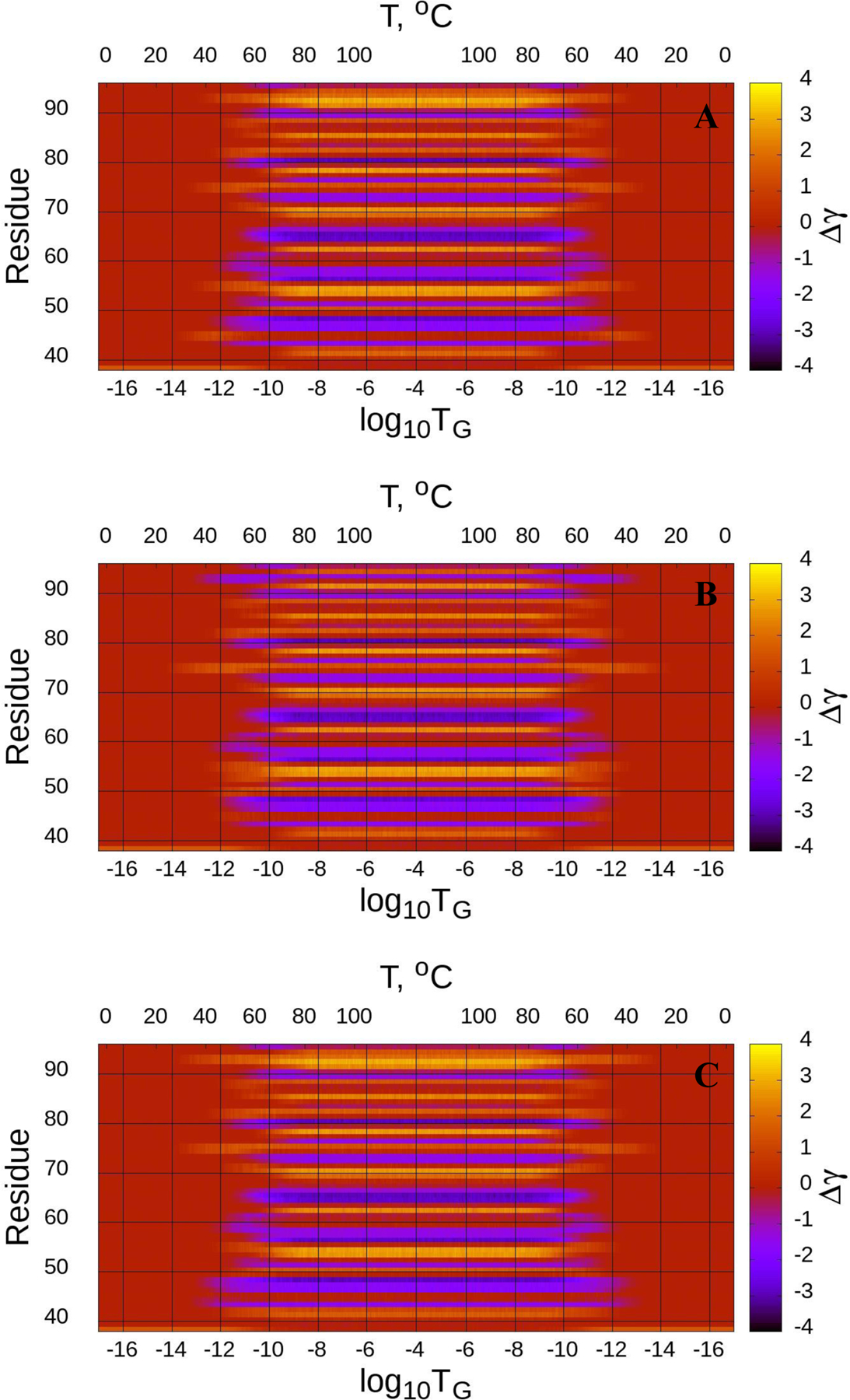
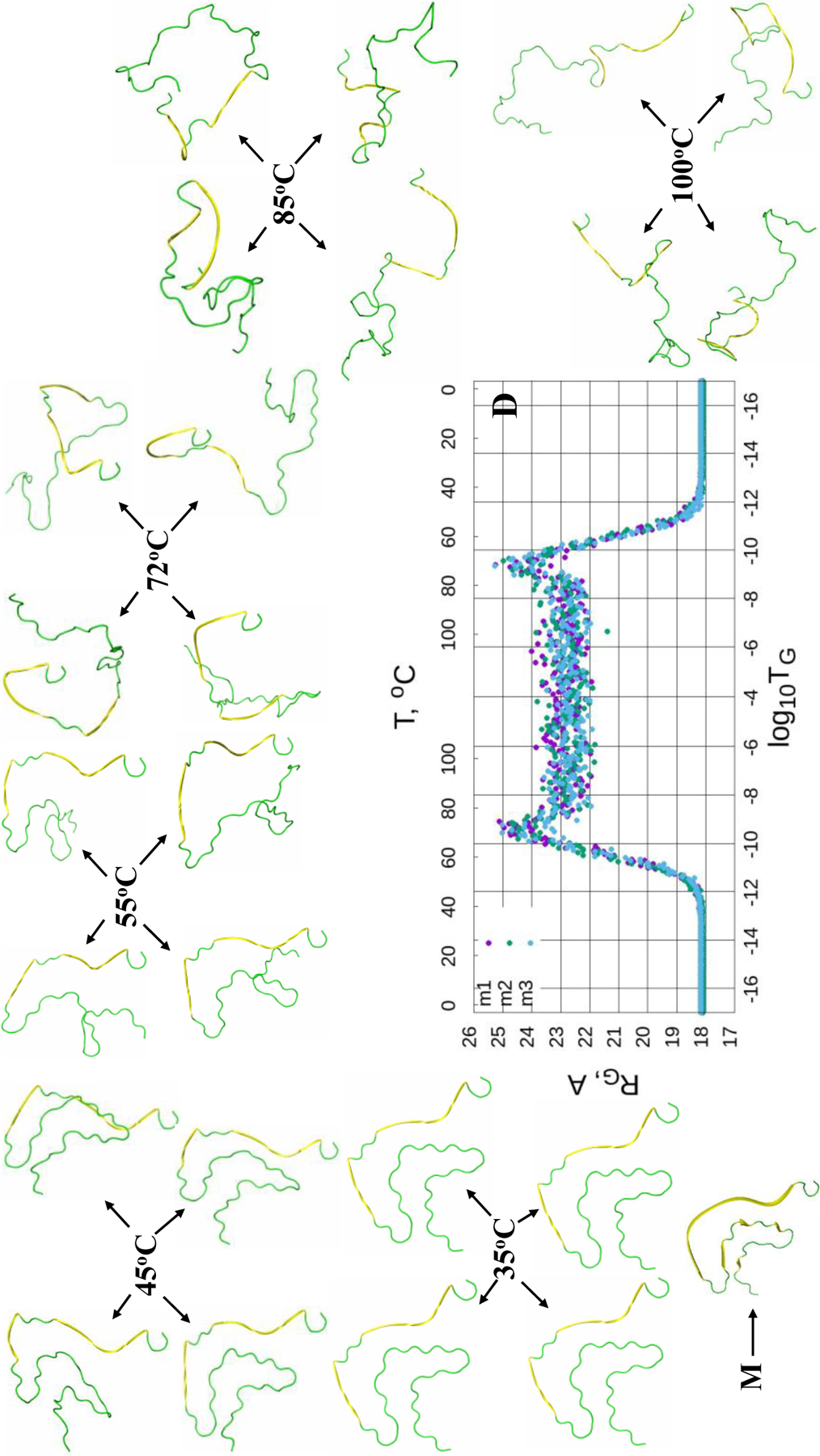
(Dis)ordering during a heating and cooling simulation cycle as a function of Glauber temperature (T_G) in terms of the average value of torsion angles γ for three selected structures of the fibrillar αS (A-C), and the radius of gyrations (R_G) of three selected structures as functions of Glauber temperature (D). The representative structures at six different temperatures along with the misfolded (M) structure show the unfolding/folding pathways of the system (D).

The maps of the micelle-bound αS [Fig. 4 (A-C)] show that all three calculated structures exhibit more or less similar behavior. Both helices of these three structures correctly react to the heating/cooling process, i.e., γ angles pertaining to α-helices change during thermal unfolding, remain stable in the random walk phase, and return to initial values with cooling. Among all helices the first helix of the first calculated structure is the most sensitive to the heating process by starting to unfold at log₁₀T_G ≈ - 9, while others start unfolding at log₁₀T_G ≈ - 8. Half of the γ angles pertaining to the loops have the same reaction to the heating/cooling process as α-helices, and the other half of the γ angles remain unchanged during the entire heating/cooling process. Only the loop of the first structure exhibits more sensitivity to the heating process by starting to unfold at log₁₀T_G ≈ - 12, while others start unfolding at log₁₀T_G ≈ - 10. The R_G vs Glauber temperature plots (panel D in Fig. 4) reflect the differences found in the heating/cooling maps. In particular, the first structure starts unfolding at log₁₀T_G ≈ −13 and remains unfolded until log₁₀T_G ≈ - 13, while the other two start unfolding at log₁₀T_G ≈ - 12 and remain unfolded until log₁₀T_G ≈ - 12; consequently, they are folded in the log₁₀T_G ≈ - 17 - log₁₀T_G ≈ - 13 and log₁₀T_G ≈ - 13 - log₁₀T_G ≈ - 17 temperature regions (first structure), and in the log₁₀T_G ≈ - 17 - log₁₀T_G ≈ - 12 and log₁₀T_G ≈ - 12 - log₁₀T_G ≈ - 17 temperature regions (second and third structures). The representative structures at six different temperatures illustrate the unfolding/folding pathways of the micelle-bound αS. We also computed helical contents (in %) as functions of temperature for three calculated structures of the micelle-bound αS (Fig. S4), which show how helicity changes with the increase/decrease of temperature.

A reaction of all three calculated structures of the tetrameric αS on the heating/cooling process is similar to the reaction by the micelle-bound αS, however, there are some differences. In particular, loops of all calculated structures of the tetrameric αS are more sensitive to the heating process by starting to unfold at lower temperatures log₁₀T_G ≈ - 14 (first structure), log₁₀T_G ≈ - 17 (second structure) and log₁₀T_G ≈ - 12 (third structure) [Fig. 5 (A-C)], whereas the behavior of α-helices remains almost the same, they start unfolding at log₁₀T_G ≈ - 8.5. The differences in sensitivity of loops on heating expressed in the heating/cooling maps are not reflected in the R_G vs Glauber temperature plots (panel D in Fig. 5). All three structures start unfolding at log₁₀T_G ≈ - 13 and remain unfolded until log₁₀T_G ≈ - 13; hence, they are folded in the log₁₀T_G ≈ - 17 - log₁₀T_G ≈ - 13 and log₁₀T_G ≈ - 13 - log₁₀T_G ≈ - 17 temperature regions. As in the micelle-bound αS, the representative structures at six different temperatures show the unfolding/folding pathways of the tetrameric αS (panel D in Fig. 5), and helical contents (in %) as functions of temperature for three calculated structures of the tetrameric αS (Fig. S5) illustrate how helicity changes with the increase/decrease of temperature.

Figure 5.

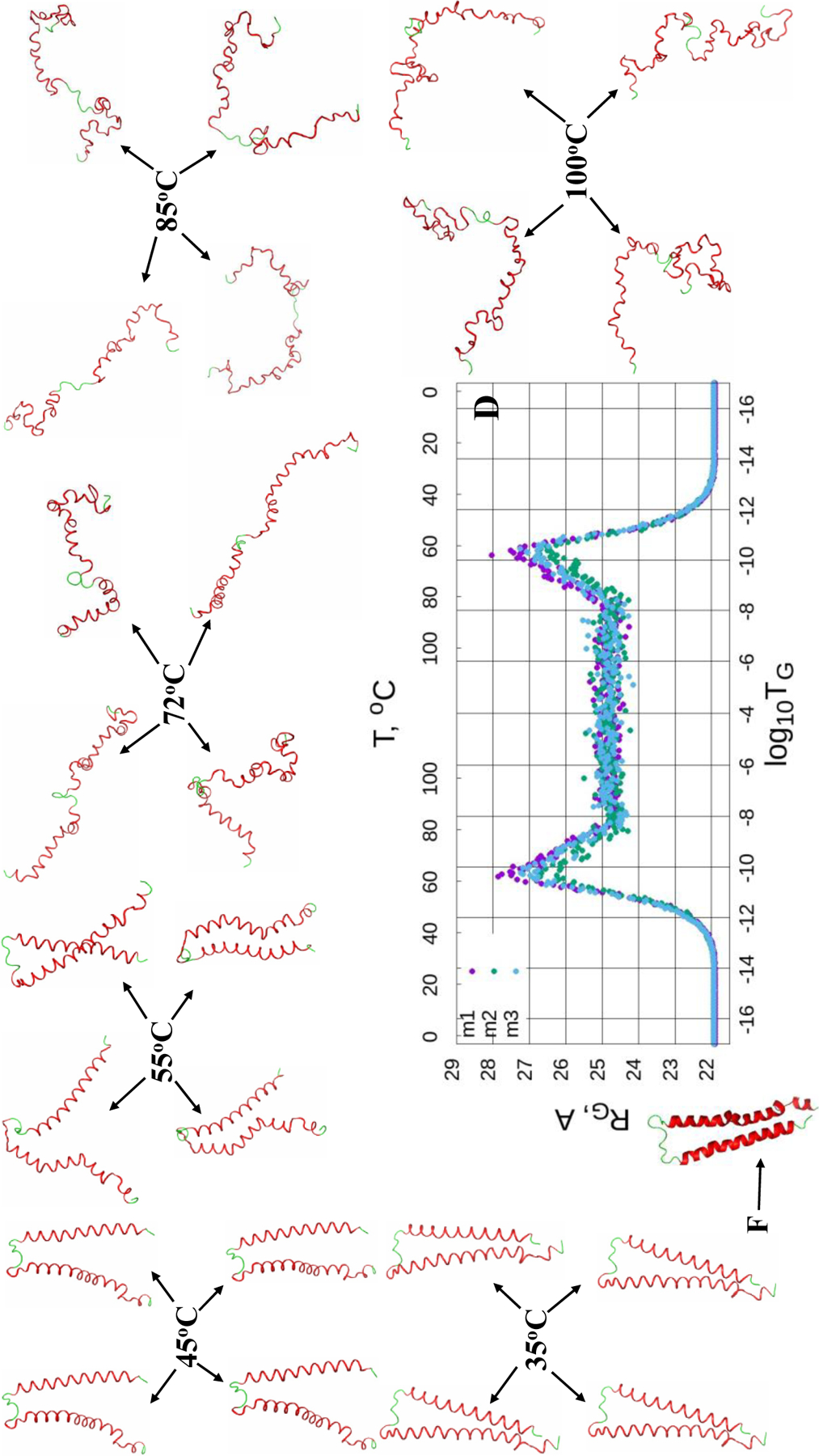
(Dis)ordering during a heating and cooling simulation cycle as a function of Glauber temperature (T_G) in terms of the average value of torsion angles γ for three selected structures of the tetrameric αS (A-C), and the radius of gyrations (R_G) of three selected structures as functions of Glauber temperature (D). The representative structures at six different temperatures along with the folded (F) structure show the unfolding/folding pathways of the system (D).

The heating/cooling maps for three calculated structures of the fibrillar αS [Fig. 6 (A-C)] are quite versatile compared to the micelle-bound and tetrameric αS. Unlike previous cases, in which helical contents almost disappear (~ 1%) in the random walk phase (Figs. S4 and S5), β-strands and loops in the fibrillar αS partially react to the heating/cooling process, i.e., only part of the γ angles pertaining to β-strands and loops change during thermal unfolding. Plus, these changes are not consistent, manifestation of which are the spectra representing different γ angles in these maps. The parts of β-strands and loops reacting to the heating process start unfolding at log₁₀T_G ≈ - 12. All three calculated structures exhibit quite similar behavior, which is reflected in the R_G vs Glauber temperature plots (panel D in Fig. 6). In particular, all three structures start unfolding at log₁₀T_G ≈ - 12 and remain unfolded until log₁₀T_G ≈ - 12; consequently, they are misfolded in the log₁₀T_G ≈ - 17 - log₁₀T_G ≈ - 12 and log₁₀T_G ≈ - 12 - log₁₀T_G ≈ - 17 temperature regions. The representative structures at six different temperatures show the unfolding/misfolding pathways of the fibrillar αS (panel D in Fig. 6), and β-strand contents (in %) as functions of temperature for three calculated structures of the fibrillar αS (Fig. S6) illustrate how β-strand content changes with the increase/decrease of temperature.

Based on the representative structures at different temperatures (panel D in Figs. 4–6), we can conclude that the unfolding/folding pathways and hence scenarios for the micelle-bound and tetrameric αS are more or less similar, but differ significantly from ones for the fibrillar αS. This is another manifestation of the flexibility of αS.

Two-dimensional (2-D) histograms of the micelle-bound, tetrameric and fibrillar αS.

To obtain more insight into the unfolding/(mis)folding kinetics of these systems, we analyzed the distribution of the conformational states in terms of 2-D histograms along the RMSD from the (mis)folded structures and the R_G as order parameters. Figures 7–9 illustrate 2-D histograms along the RMSD and R_G at six different temperatures for the micelle-bound, tetrameric and fibrillar αS, respectively. As was expected, the center of the distribution evolves with the increase of temperature in each system. The white dash line in each panel illustrates the trace of evolvement of the distribution centers of each system. Obtained results indicate on the phase transition, which can be an onset of the (mis)folding-unfolding transitions, at the temperature slightly higher than 45°C for the micelle-bound and tetrameric αS (Figs. 7 and 8), and at ~ 55°C for the fibrillar αS (Fig. 9).

Figure 7.

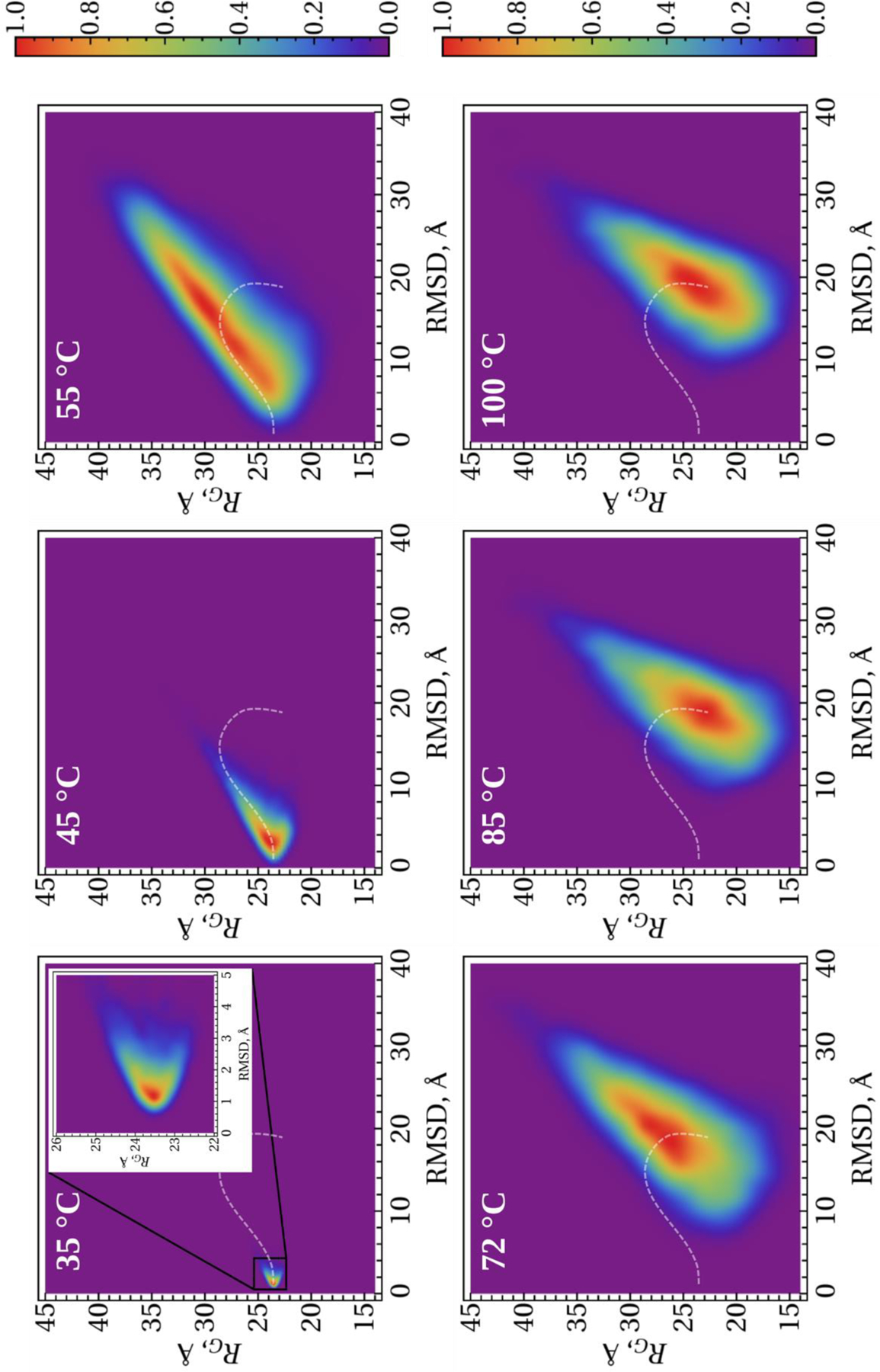
2-D histograms along the RMSD and R_G order parameters for the micelle-bound αS. The white dash lines show the trace of evolvement of the distribution centers with the temperature.

Figure 9.

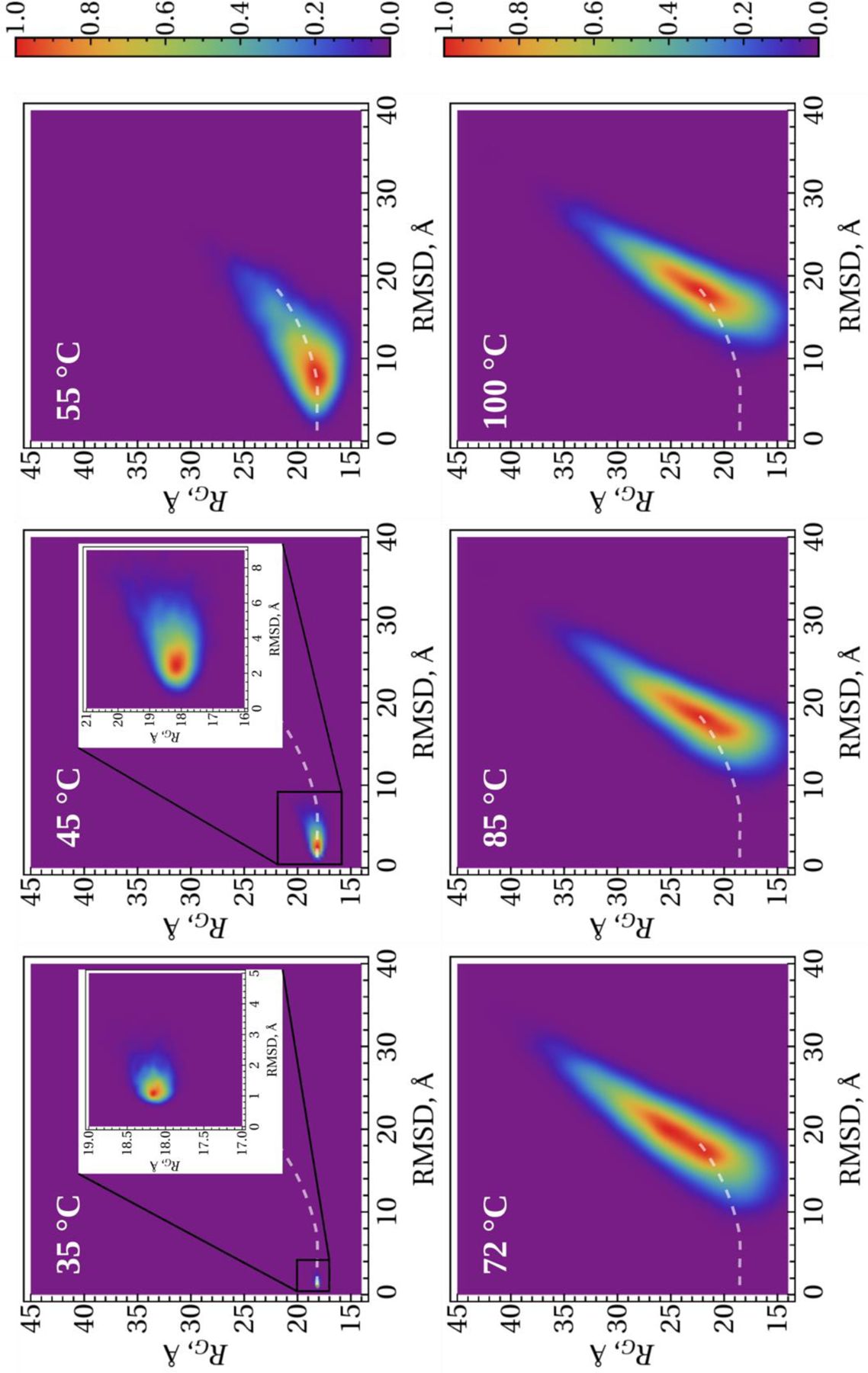
2-D histograms along the RMSD and R_G order parameters for the fibrillar αS. The white dash lines show the trace of evolvement of the distribution centers with the temperature.

Figure 8.

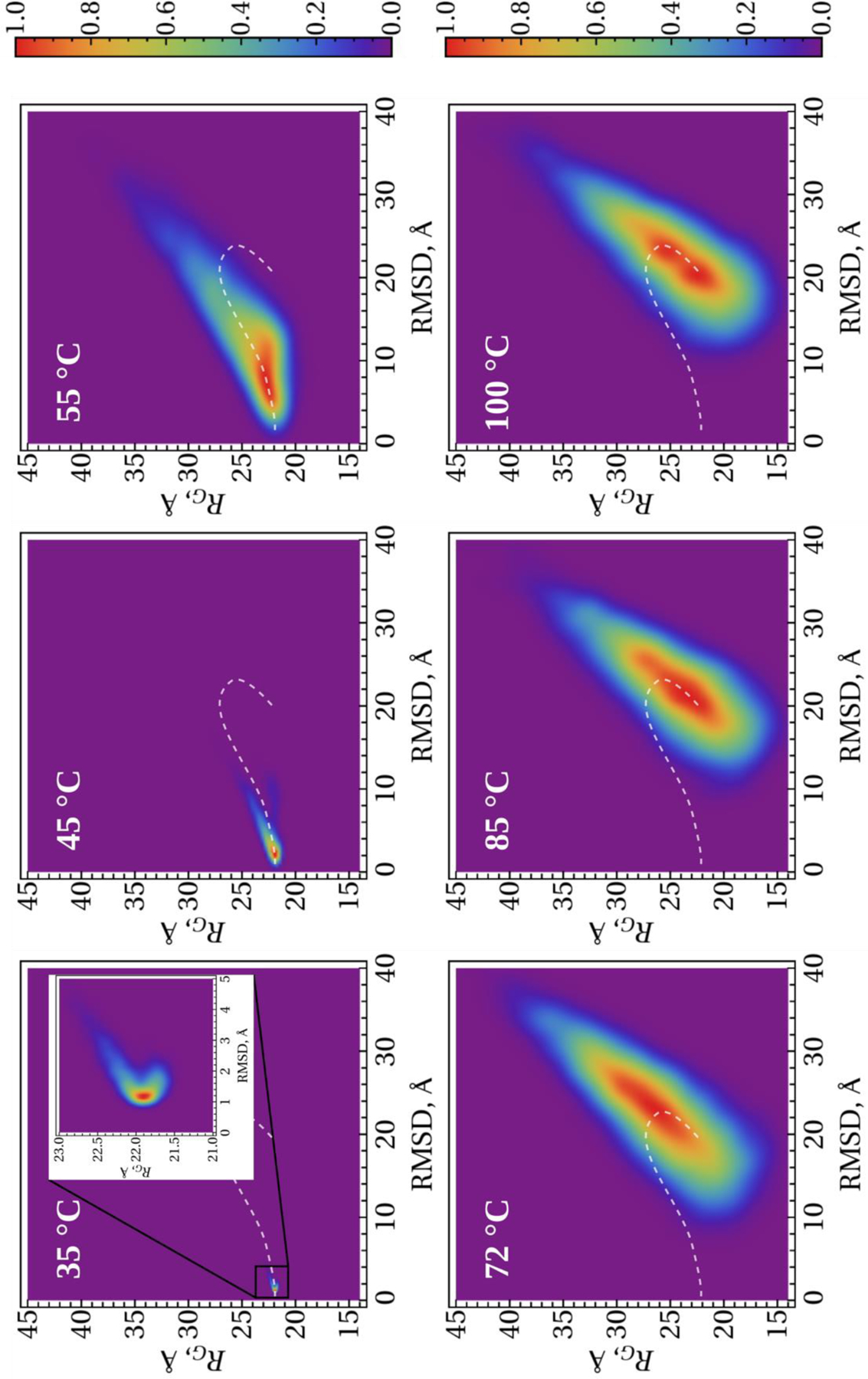
2-D histograms along the RMSD and R_G order parameters for the tetrameric αS. The white dash lines show the trace of evolvement of the distribution centers with the temperature.

Conclusions

The experimental structures of the micelle-bound, tetrameric and fibrillar αS have been analyzed in terms of kinks. Without MD simulations, kinks were able to capture the key residues playing a crucial role in structural flexibility of these three structures of αS, which makes kinks a very effective method for better understanding IDPs. Moreover, the stability of the micelle-bound, tetrameric and fibrillar αS was studied by simulating heating and cooling trajectories using the Glauber algorithm. The differences in stability of the experimental structures were shown; and the reasons for differences were explained.

Finally, it should be mentioned that kinks can provide (i) a conceptual advantage in addressing the formation of structure in protein collapse; and (ii) a simulation-free prediction of local collective motions, and can therefore be used to describe protein dynamics. This provides a new approach to the understanding of IDPs. This work is the first step in development of an innovative approach, that we are planning to do, to the elucidation of the oligomeric structures of the biomedically important IDPs from experimental fibril structures. In this approach each monomer will be modeled as a multi-kink, but interaction between different monomers will be modeled differently. A combination of electrostatic and Lennard-Jones potentials between side chains of monomers will be introduced. The side chains will be described as point-like. The evolution of the system will be monitored using Glauber dynamics by varying a temperature.