Diversity and function of the fused anuran radioulna

Abstract

In tetrapods, fusion between elements of the appendicular skeleton is thought to facilitate rapid movements during running, flying, and jumping. Although such fusion is widespread, frogs stand out because adults of all living species exhibit fusion of the zeugopod elements (radius and ulna, tibia and fibula), regardless of jumping ability or locomotor mode. To better understand what drives the maintenance of limb bone fusion in frogs, we use finite element modeling methods to assess the functional consequences of fusion in the anuran radioulna, the forearm bone of frogs that is important to both locomotion and mating behavior (amplexus). Using CT scans of museum specimens, measurement tools, and mesh‐editing software, we evaluated how different degrees of fusion between the radius and ulna affect the von Mises stress and bending resistance of the radioulna in three loading scenarios: landing, amplexus, and long‐axis loading conditions. We find that the semi‐fused state observed in the radioulna exhibits less von Mises stress and more resistance to bending than unfused or completely fused models in all three scenarios. Our results suggest that radioulna morphology is optimized to minimize von Mises stress across different loading regimes while also minimizing volume. We contextualize our findings in an evaluation of the diversity of anuran radioulnae, which reveals unique, permanent pronation of the radioulna in frogs and substantial variation in wall thickness. This work provides new insight into the functional consequences of limb bone fusion in anuran evolution.

Using finite element analysis, we find that the semi‐fused state of the frog forelimb bone experiences less von Mises stress than hypothetical fully fused or split conditions across multiple loading scenarios. The results support the idea that the semi‐fused state is an adaptation for saltation in frogs, and may be maintained by other forces such as amplexus. This work expands our understanding of the evolution of saltatory morphotypes in tetrapods.

1. INTRODUCTION

Many clades of vertebrates exhibit fusion between elements of the appendicular skeleton. Well‐known examples are found in the limbs of modern birds and mammals. These include the tibiotarsus, tarsometatarsus, and carpometacarpus bones in birds, the fused radius and ulna in bats, horses, and artiodactyls (Figure 1d), and the fused tibia and fibula in hedgehogs, sea‐lions, coneys, rodents, rabbits, armadillos, aardvarks, and tarsiers (Barnett & Napier, 1953; Sahd et al., 2019; Salami et al., 2011). In extant frogs, the tibia and fibula as well as the radius and ulna are always completely fused in adults (Duellman & Trueb, 1986) and the proximal tarsal bones are fused in some or all species in several families (Centrolenidae, Microhylidae, Pelodytidae; Duellman & Trueb, 1986; Fouquet et al., 2021).

FIGURE 1.

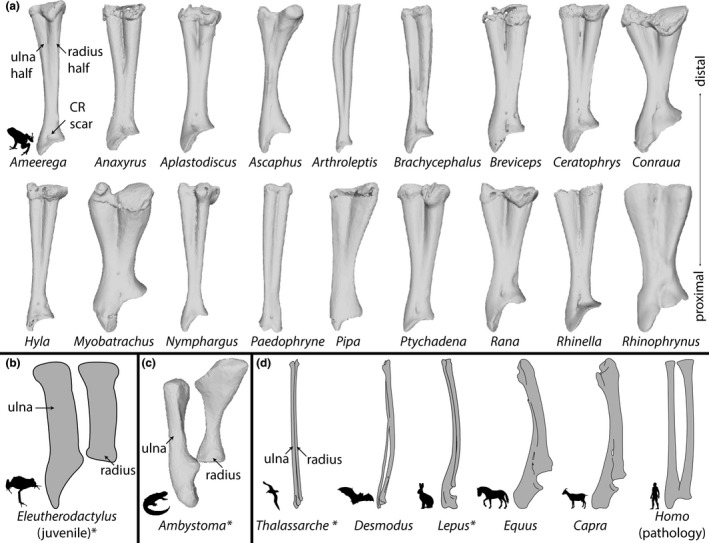
A sample of the morphological diversity of the radioulna, depicted via illustrations and 3D models derived from CT scans. (a) A sample of 18 radioulnae from frogs in our dataset, (b) a tracing of a juvenile frog radius and ulna before fusion of the radius and ulna in a direct‐developing frog (Hanken et al., 2001), (c) the zeugopod elements of a salamander, and (d) select zeugopod elements from various amniote groups. All zeugopod elements are from the right forelimb shown in the ventral view. Asterisks following names of genera indicate that the radius and ulna are unfused in that example. DOIs of CT scans and publications referenced are listed in Table S1. Organism silhouettes were reproduced from PhyloPic using the “RPHYLOPIC” package (Chamberlain, 2018). Abbreviations: CR = m. coracoradialis.

The function of limb bone fusion is often stated to increase the strength of the limb, reduce its weight, or facilitate rapid movements (Barnett & Napier, 1953; Bühler, 1992; Coombs Jr., 1978; Heers & Dial, 2012; Howell, 1944). This fusion most often occurs in the context of energetic locomotor modes like cursoriality, saltation, and flying. However, the fusion of limb bones is observed in vertebrates of a wide range of sizes and locomotor modes and the degree and manner of fusion varies widely (Figure 1). In those species that do not experience high locomotor stresses on the limb, what is the evolutionary advantage of limb bone fusion?

This question can be illustrated most clearly within frogs. Frogs exhibit a high degree of fusion among many bones, which is thought to be an adaptation for their saltatory locomotor style. Although the ancestral condition of frogs was likely saltatory (Jenkins Jr. & Shubin, 1998; Přikryl et al., 2009; Sigurdsen et al., 2012; Abdala et al., 2022; although see Reilly & Jorgensen, 2011), many extant frogs do not typically jump (Emerson, 1978) or do not use the forelimbs during landing (Essner et al., 2010, 2022; Reilly et al., 2016). All frogs have fused radioulnae (Figure 1a) and tibiofibula, regardless of saltation ability. Frogs span a wide range of locomotor types, including gliding, burrowing, swimming, jumping, climbing, and walking, and recent work highlights the close relationship between frog limb shape and microhabitat (Emerson & Koehl, 1990; Stepanova & Womack, 2020; Vidal‐García et al., 2014). The distal limb bones of frogs have been found to evolve at a higher rate and to be more morphologically variable than more proximal bones (Stepanova & Womack, 2020). This is possibly due to relaxed developmental constraints, as the distal limb bones often develop the latest in ontogeny. In spite of this variation, there are no exceptions to the fusion of the radioulna and tibiofibula in adult frogs.

The lack of transitional morphologies has historically made it impossible to test hypotheses about the role of bone fusion in anuran evolution. However, recent advancements in experimental methods have opened the door to new questions about this topic. Modeling hypothetical morphologies can be done physically with robotics (Lauder, 2022) and 3D printing, as well as with digital methods like finite element analysis (FEA). FEA is a popular tool for assessing the functional performance of bones in a non‐destructive manner (Brassey et al., 2013; Rayfield, 2007; Richmond et al., 2005). The method involves producing a 3D mesh, converting it into many small, independent elements connected via nodes, and assigning these certain mechanical properties. It is then possible to compute the performance of the 3D mesh under specified loading conditions. FEA is well established as a way to model biomechanical systems in vertebrate animals, including amphibians (Bates et al., 2021; Engelkes et al., 2020; Gilbert et al., 2016; Mielke & Nyakatura, 2019; Porro et al., 2013).

In this study, we used FEA to assess the functional consequences of fusion in the anuran radioulna. Since wide‐scale, detailed morphological analyses of the radioulna bone are lacking, we provided context for our investigation by first sampling and measuring CT scans of museum specimens across a variety of locomotor modes and body sizes. For one representative species, we used mesh‐editing software to adjust in silico the degree of fusion in the radioulna. We then used FEA to test the unedited and hypothetical models in identical loading scenarios and compared the differences in stress across the models. Following this, we cross‐referenced our findings by calculating the bending resistance across each of our models. Our goals were threefold: (1) to describe and assess variation in radioulna morphology in frogs, (2) to analyze with FEA the consequences of fusion on stress distribution in the radioulna, and (3) to discuss functional consequences of fusion in the context of anuran evolution.

2. MATERIAL AND METHODS

2.1. Taxon sampling and morphometrics

We first compiled a sample of 27 frog species across 17 families that span a range of body sizes and several microhabitat types (aquatic, semi‐aquatic, terrestrial, fossorial, and arboreal) and thus differ in locomotor modes. We also targeted several families (e.g., Centrolenidae and Pelodytidae) in which the tibiale and fibulare exhibit a range of fusion as an analog for fusion in the radioulna. For each taxon, we obtained CT scans from fluid‐preserved museum specimens based on scans available via MorphoSource (see Table S1 for DOIs), most of which were generated at the University of Florida's Nanoscale Research Facility as part of the openVertebrate (oVert) Thematic Collections Network. Visualizations and segmentation of skeletal elements were performed in Volume Graphics VGSTUDIO MAX v3.2. Segmentation involved setting a gray value threshold at the edge of bony elements for each individual CT volume and producing a single region of the full skeleton. Following this, the right radioulna was isolated with the polyline tool and the resulting segment was cleaned with the edge refinement and smoothing tools.

We took several measurements in VGSTUDIO MAX including snout–vent length (SVL), radioulna width (at the distal margin, proximal margin, and minimum), radioulna length, radioulna wall thickness, radioulna cavity diameter, position of m. coracoradialis (CR) scar, radioulna pronation angle, and angle between radius and ulna (Figure 2; Table S2). Articular cartilages were excluded from length and width measurements (Figure 2a). Wall thickness and cavity diameter were measured at the point of minimum diaphysis width (Figure 2b). Cavity diameter was taken at a 45° angle between the shortest and longest cavity diameter measures in cross‐sectional view and wall thickness was measured at a point of average cortical bone thickness in the same cross‐sectional view (Figure 2b). “Radioulna angle” and “pronation angle” were calculated using the same three landmarks: the CR scar as the vertex, with two rays passing through the center of the radius half at its distal margin and the center of the ulna half at its distal margin respectively (Figure 2b and c). Radioulna angle was measured with the radioulna in ventral view and pronation angle was calculated with the radioulna in lateral view (Figure 2b and c).

FIGURE 2.

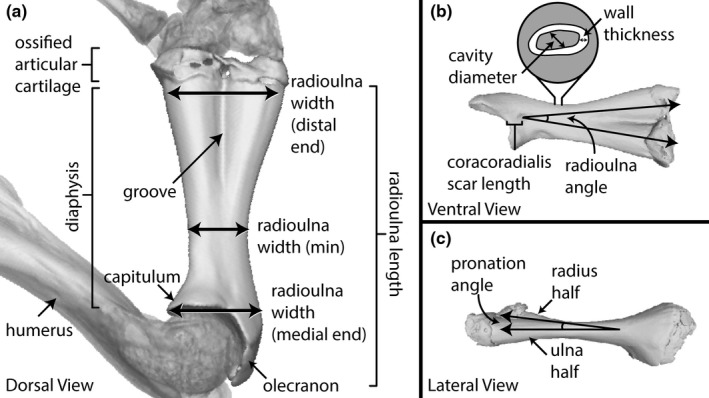
Illustrations of the measurements of the radioulna (see Table S2) and anatomical terminologies; (a) the right radioulna of R. catesbeiana in dorsal view, (b) ventral view, and (c) lateral view.

To estimate the second moment of area (I) for the cross‐section of the radioulna diaphysis, we used the formula for I of a hollow circle, as the radioulna is a hollow, tubular bone. The formula of a hollow circle is derived from the formula for the second moment of area for a circle, I = πd⁴/64, (Pilkey, 2005), where the I value of the inner circle is subtracted from that of the outer circle. In our case, the diameter of the internal cavity at the point of minimum diaphysis width was the diameter of the inner circle (d ₁ ), and the diameter of the outer circle (d) was d ₁ plus two times the wall thickness at that same cross‐section. This gives the following formula:

$$I=\frac{\pi d^4}{64}-\frac{{\mathit{\pi d}}_1^4}{64}$$ (1‐1)

We then scaled I by SVL for each species to obtain the proportional bending resistance (see Table S2).

We also estimated the mechanical advantage of the radioulna as a third‐order lever with respect to the insertion position of the tendon of the m. coracoradialis (the main retractor muscle of the radioulna) as effort force and the end of the radius half as the fulcrum position:

$$\mathit{MA}=L_i/L_o$$ (1‐2)

where MA = mechanical advantage, L _i  = in‐lever, and L _o  = out‐lever (Emerson, 1991).

Using our collected measurements, we ran eight linear models and Pearson's correlation tests in R Studio (R Core Team, 2021) among key variables which describe general trends in radioulna proportions (Table S3) and plotted the results using the package “ggplot” (Wickham, 2016) with points coded by locomotor mode (Figure 3). We defined outliers in our linear models as any data point that fell outside the bounds of the third quartile plus 1.5 times the interquartile range and the first quartile minus 1.5 times the interquartile range (Walfish, 2006).

FIGURE 3.

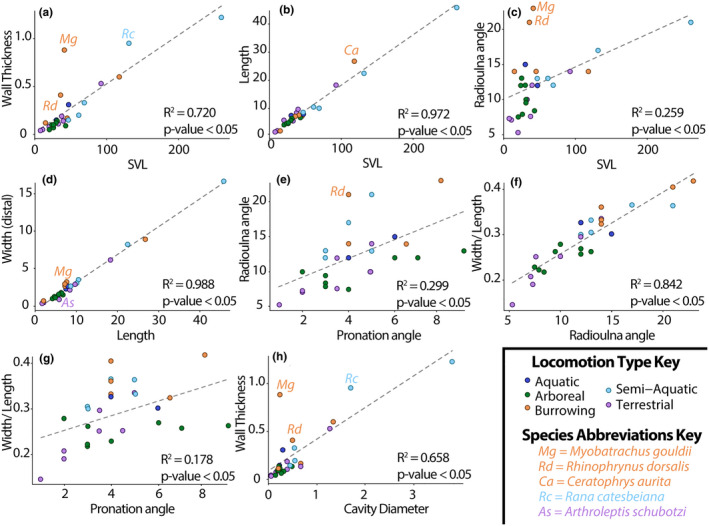
Plots (a–h) visualizing linear regressions of various meristic measurements taken from our sample (see Tables [Link], [Link]). Points are color‐coded by locomotor mode; regression lines are indicated with a dotted gray line. Outlier species are labeled, see legend. Abbreviation: SVL = snout–vent length.

2.2. Mesh preparation

We produced four models to test the effects of the degree of fusion. The STL model of the radioulna of Rana catesbeiana (UF‐Herp‐111243) was imported into the digital modeling software Blender v2.90 (Blender Online Community, 2018). In Blender, the mesh was smoothed and cleaned to remove floating elements and the distal articular cartilages. Rana catesbeiana was chosen because the species is saltatory, the CR scar is well defined, and there are clearly defined portions of the radioulna corresponding to the radius and ulna.

The cleaned mesh (Figure 4b) was then duplicated and edited to create three hypothetical morphologies with the same dimensions (i.e., length, width, height) as the original: one in which the radius and ulna are completely fused into a single element (Figure 4a), one in which the radius and ulna are reconstructed as separate bones (Figure 4d), and one in which the isolated radius and ulna are only partially fused, with an interosseus space between them (Figure 4c). The fully fused model (Figure 4a) lacked both the dividing wall inside the diaphysis that is normally present in anuran radioulnae and the groove between the radius and ulna (Figure 2a). The completely split model (Figure 4d) was sculpted from the portions of the radius and ulna of the original model using the morphology of juvenile frogs (Figure 1b; Púgener & Maglia, 1997; Maglia & Púgener, 1998; Hanken et al., 2001) and adult salamanders (Figure 1c) as a reference. The semi‐split model design was informed both by patterns of radioulna development in juvenile frogs (Engelkes et al., 2021; Hanken et al., 2001; Maglia & Púgener, 1998; Púgener & Maglia, 1997) and the fusion patterns we observed in the tibiale and fibulare of species in our sample.

FIGURE 4.

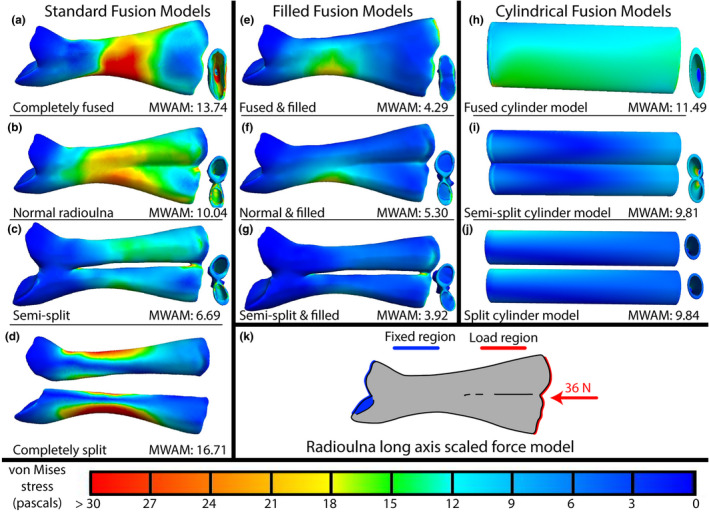
Results of our finite element analyses showing von Mises stresses of each of our models in the long‐axis loading condition (a–j), boundary conditions, and force vector (red arrow) are illustrated in schematic (k). Areas of red indicate regions experiencing the highest stresses, blues the lowest (see color legend at the bottom of the figure). The far‐left column depicts the four standard fusion models, modified from the normal morphology of the radioulna (b). The middle column depicts the filled versions of the models to their left. The right column depicts the three cylindrical, geometrically symmetrical models. Radioulnae models are shown in dorsal view, distal end on the right, proximal on the left. On their right, minimized, is a distal view of each model. MWAM values and model names are indicated at bottom of each cell (a–j). See main text and Table S4 for the exact angle of the force vector. Abbreviations: MWAM = mesh‐weighted arithmetic mean von Mises stress.

For three of these four models, we generated a solid version to assess the role of hollow cavities in the radioulna (Figure 4e–g). We additionally constructed three geometrically symmetrical models based on the dimensions of the lengths and wall thicknesses of the standard fusion models; one modeled after the hypothetical completely fused morphology (Figure 4h), one after the hypothetical partially fused morphology (Figure 4i), and one after the sculpted isolated radius (Figure 4j). These models were made to compare normal radioulna shape to a null model. Each model was then imported into Meshlab (Cignoni et al., 2008) where the models were further cleaned to ensure the mesh contained no holes or non‐manifold edges. Each mesh had a face count of 300,000 (except the three cylinder models, for which such high resolution was unnecessary). All models were oriented in the same way as the normal radioulna model. The normal radioulna was oriented so its centroid overlapped with the origin, its distal end pointed towards the negative x direction, proximal end toward the positive x direction, its dorsal surface to the positive y direction, and its ventral surface toward the negative y direction. Final models were exported as binary encoded STL files. In total, we produced 10 models.

2.3. Finite element analysis

We imported our models into FEBio Studio (v1.7.1; Maas et al., 2012) to prepare them for analysis. In FEBio, we converted each STL mesh into a 3D tetrahedral mesh (average element volume = 2.69E‐7 cm³). We modeled the material properties of the meshes based on previous work on amphibian finite element models: isotropic elastic material with a Young's modulus of 10 GPa and a Poisson's ratio of 0.35 (Engelkes et al., 2020). We tested three different loading conditions for each of our 10 models: long‐axis, landing (from a jump), and amplexus (a mating behavior in frogs in which males grasp a female's body with their forearms). These models allowed us to examine how the radioulna responds to stress in two important scenarios relating to locomotory and reproductive behaviors and compare those to a long‐axis loading condition of the bone.

The long‐axis loading direction for each bone is a compressive load applied to the distal end and directed down the middle of the long axis (Figure 4k). We calculated the direction of this vector in Blender using the long axis of the normal radioulna model (Figure 4b). For the sake of comparison, this vector direction was used for all models regardless of how their altered morphology may have slightly displaced their actual long axis from the original model (see Figure 4 and Figures [Link], [Link]). After establishing the direction of the vector, we then determined its magnitude. In our case, this was 36 N. The magnitude of the vector was chosen to represent a reasonable maximum loading force that our representative R. catesbeiana specimen may encounter in life. Ground reaction forces (GRFs) during jump take‐off are approximately 2 N for small ranid frogs (Astley & Roberts, 2014; Nauwelaerts & Aerts, 2006). Our specimen likely had a larger body mass than those used in previous studies: at 13.11 cm SVL, it would be ~341 g based on scaling values for ranids given in Santini et al. (2018). Based on the scaling for maximum jump takeoff force by body mass for Limnodynastes peronii (family Limnodynastidae) found by Wilson et al. (2000), a 341 g frog would experience nearly 11.5 N during takeoff, which we rounded to 12 N. Maximum landing forces are nearly three times higher than maximum takeoff forces for ranids (Nauwelaerts & Aerts, 2006), which gives ~36 N. This value is an overestimate and assumes only one arm is in contact with the ground on impact, but the magnitude of our vectors is unimportant as long as the same magnitude is used in all analyses being compared.

Within FEBio, we set the humerus‐articulating surface as a fixed boundary condition (selected nodes fixed in all degrees of freedom) and the distal‐most region of each model as the load area. Load areas were measured in FEBio and recorded for each model (Table S4). We checked for differences in load area sizes between models by re‐running our long‐axis loading models with 36 N divided by the area to which they were applied in each model (Figure S1). Because the major results of these scaled and non‐scaled tests were similar, we used non‐scaled forces in the other loading scenarios. In addition, for the isolated “radius” and “ulna” models, we halved the loading force for each analysis since, hypothetically, the two meshes would split the landing force between them. Using these boundary conditions, we applied a load of 36 N down the long axis of each of our 10 models and calculated the von Mises stress values for each element. Finally, we extracted the volume of each element and calculated the mesh‐weighted arithmetic mean (MWAM) for von Mises stresses (Marcé Nogué et al., 2016) in each model for comparison.

In addition to comparing the von Mises stress in each model in their long‐axis loading scenario, we also performed two further rounds of analyses that simulated the force vectors acting on the radioulna during landing (Figure S2k–l) and amplexus (Figure S3k–l). We retained the same vector magnitude (36 N) for all tests for the sake of comparison (although 36 N may not be an unreasonable estimate for amplexus forces in frogs; see Rueda‐Solano et al., 2022). For the direction of our landing vector, we generated a landing force vector based on angle measurements from previous work measuring the GRF of ranids (Nauwelaerts & Aerts, 2006; Reilly et al., 2016) as well as XROMM video data of R. catesbeiana jumping (R. Keeffe, unpublished data). The vector used is listed in Table S4 (which has a 36.90° angle with the x axis, 125.86° angle with the y axis, and an 82.46° angle with the z axis). It is important to note that the GRF during landing is variable among frogs (Griep et al., 2013; Reilly et al., 2016). For example, in the bufonid Rhinella marina the vertical component of the GRF is higher than the horizontal component (Gillis et al., 2014), but in the ranid Rana esculenta, the reverse is true (Nauwelaerts & Aerts, 2006). The angle of the radioulna itself also differs during maximum landing forces (8° from the horizontal axis in Rana compared to 36° in Rhinella).

To model the force exerted on the radioulna during amplexus, we focused on the major flexors of the forearm that adduct the radioulna toward the pectoral girdle. The main retractor muscle of the radioulna in frogs is the m. coracoradialis (Duellman & Trueb, 1986). In frogs, the m. coracoradialis originates broadly on the omosternum and epicoracoid cartilages and inserts as a thin tendon on the proximal end of the radioulna (see CR scar position in Figure 1a). As the scar from the m. coracoradialis is clear in R. catesbeiana, we used this indented region on the bone as the load area for our completely fused and normal radioulna models (Figure S3a,e,b,f). To determine the placement of this tendon in our semi‐split and completely split models (which lacked the CR scar due to our manipulations), we examined the homolog of this tendon in frogs' closest living relatives, salamanders. In salamanders, the m. coracoradialis (synonymous with m. sternoradialis) originates on the ventral surface of the coracoid and inserts as a thin tendon on both the proximal part of the humerus and the proximal part of the radius (Diogo & Tanaka, 2012). Thus, we estimated this position on our models which lacked an obvious CR scar (Figure S3c–d,g–j). We estimated the direction of the vector by referring to the position of the CR scar in our specimen and illustrations of the coracoradialis tendon from existing contrast‐enhanced CT datasets (Engelkes et al., 2021; Keeffe & Blackburn, 2020). The vector used is listed in Table S4 (which has a 56.19° angle with the x axis, 133.44° angle with the y axis, and a 62.20° angle with the z axis). We chose not to model an additional force on the distal part of the radioulna because the body of the female is not a rigid substrate and we also did not have enough information about that contact zone to accurately add to our models. This model simulates only a single load acting on the muscle scar region.

For each analysis, specific information regarding boundary condition areas, force vectors, and mesh‐weighted arithmetic means are recorded in Table S4.

2.4. Beam modeling

To corroborate our findings from the FEAs, we calculated the second moment of area (I) for the cross‐sections of each of the radioulna models. The I value measures how well a particular cross‐section of a beam resists bending, with higher values resisting more than lower values. The cross‐sectional area of our radioulna models is not consistent across the diaphysis, so some regions of the model will resist bending more than other regions. The I values calculated across the length of the diaphysis should generally corroborate the patterns produced in the FEAs.

We used the SegmentGeometry extension (Huie et al., 2022) for 3D Slicer (Kikinis et al., 2014) to calculate the I value of 100 cross‐sectional slices of each of our radioulna models (Table S5). We calculated the second moment of area for both the minor principal axis (I _minor) and major principal axis (I _major) of each model, as well as the second moment of area for the axes passing through the diaphysis laterally (i.e., I _{neutral axis}) and dorso‐ventrally (i.e., I _{loading axis}) when the radioulna is in ventral view (Figure 5; Table S5). For the completely split model (Figure 4d), we performed separate analyses for the “radius” and “ulna.” Additionally, we exported measurements of compactness for each cross‐sectional slice; compactness refers to slice area divided by total area including hollow spaces. Because the radioulna is a stout bone, the aspect ratio (the ratio of length to width) was less than 10 for all models, so the “no‐shear” assumption may have been violated in these tests.

FIGURE 5.

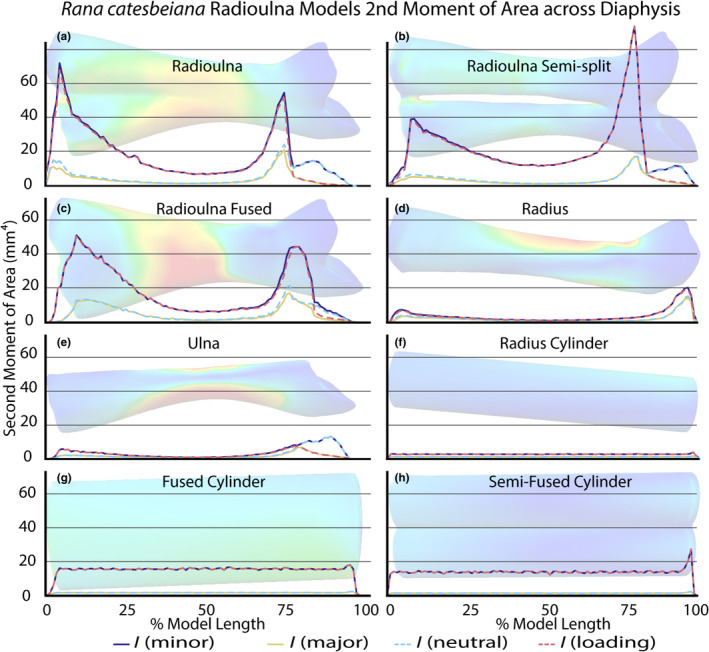
Measures of the second moment of the area along the length of the radioulna standard fusion (a–e) and cylindrical (f–h) models. The distal end of each model is on the left and proximal end on the right of each plot. Blue and pink dotted lines indicate the neutral and loading axes, respectively. The loading axis was manually set in SegmentGeometry perpendicular to the length of the diaphysis along the lateral plane. Purple and yellow solid lines indicate the minor and major principal axes, respectively. FEA results for each model (Figure 4) are transposed behind the plots to illustrate the x axis. See Table S5 for raw exported data from 3D Slicer.

3. RESULTS

3.1. Comparative morphology of the radioulna

We found considerable variation in morphological diversity among the radioulnae that we examined (Table S2; Figure 1a). Although length and width measurements are highly correlated (R ² = 0.99, Figure 3d; Tables [Link], [Link]), the proportions of radioulna width (proximal) versus length varies across our sample (minimum = 0.11, Arthroleptis schubotzi; maximum = 0.40, Myobatrachus gouldii). Stouter bones have a greater radioulna angle (R ² = 0.84, Figure 3f), as well as a greater pronation angle than those that are comparatively more slender (R ² = 0.18, Figure 3g). SVL predicts overall radioulna length (R ² = 0.97, Figure 3b) and weakly predicts radioulna angle (R ² = 0.26, Figure 3c). The average angle between the radius and ulna is 12.33 ± 0.87° (mean ± standard error) and the average pronation angle is 4.26 ± 0.36° (Table S2); these angles are positively correlated (R ² = 0.30, Figure 3e).

The wall thickness distance at the minimum diaphysis width positively correlates with SVL (R ² = 0.72, Figure 3a), but also varies (0.28 ± 0.06 mm) among our sample (Tables [Link], [Link]). Wall thickness positively correlates with cavity diameter (R ² = 0.66; Figure 3h), and that comparison yields several outliers (Myobatrachus gouldii, Rhinophrynus dorsalis, Rana catesbeiana; Figure 3h). The average ratio of wall thickness to cavity diameter is 0.60 ± 0.12 (Table S2). Given the wall thickness and cavity diameter, we estimated I of that cross‐section to be 2.82 ± 2.36 mm⁴ on average. This range varies notably across SVL (average = 0.01 ± 0.01 mm⁴; minimum = 2.30E‐6 mm⁴, Paedophryne amauensis; maximum = 0.25 mm⁴, Conraua goliath).

The position of the CR scar along the diaphysis varies (Figure 1a). This produced variable measures of mechanical advantage across our sample (CR scar length divided by radioulna length average = 0.08 ± 0.01; Table S2).

In addition to our quantitative findings, we qualitatively observed variation in the degree of fusion between the radius and ulna. The radius and ulna halves are always completely fused along the length of the bone. The depth and length of the groove between the two elements varies between species. In some species (especially several of the centrolenids; see Table S2 notes), the radioulna is nearly bifurcated distally, with only a thin wall of bone between the two elements. One individual of Espadarana prosoblepon nearly had a transverse hole in the left radioulna visible in the CT dataset, but manual dissection of another individual of the same species revealed no such hole in the radioulna; thus we do not consider this a genuine example of incomplete zeugopod fusion as it is likely a case of individual variation. In some species (especially those with stout radioulnae), the groove extends for over half the length of the diaphysis, but in others (with more slender radioulnae) the groove is much shorter. Uniquely, the radioulna of Ascaphus truei has a shallow groove, two lateral flanges at the midshaft of the diaphysis, and a nearly solid diaphysis with a narrow cavity diameter. Finally, the ossified articular cartilage of the distal epiphysis varies in both shape and degree of ossification.

3.2. Finite element analysis of radioulna fusion models

Among the four standard fusion models (Figure 4a–d), the semi‐split model (Figure 4c) experienced the lowest MWAM von Mises stresses (6.69 Pa) across all three loading scenarios that we tested (Table S4; Figure 4; Figures [Link], [Link]). The unedited, normal radioulna model experienced the second‐lowest (10.04 Pa), the fused model the third‐lowest (13.74 Pa), and the completely split model experienced the highest MWAM von Mises stresses (16.71 Pa). When the long axis force was scaled by loading area, the completely fused model experienced the highest von Mises stresses, the split model the second highest, but the semi‐split model still experienced lower MWAM von Mises stress than the normal radioulna model (Figure S1).

In all four fusion models, the stress distribution is highest around the middle of the diaphysis and lowest at the proximal epiphysis in the long‐axis loading scenario (Figure 4). In the split model (Figure 4d), the stress is highest on the edges of the diaphysis instead of the flat face of the diaphysis as in the other three models. The three cylindrical models (Figure 4h–j) experience slightly less MWAM von Mises stresses than their counterparts (Figure 4a,b,d, respectively), and the stress is more evenly distributed along the cylindrical models. The filled versions (Figure 4e–g) experience even lower MWAM von Mises stresses than the cylindrical and standard versions of the radioulna, but the stress distribution along the length of the bone is similar to the standard versions (Figure 4a,b,c respectively).

In the landing scenario, the MWAM von Mises stresses are much higher than in the above long‐axis models, but the overall pattern of highest to lowest stress among the models is the same as in the long‐axis loading scenario (Figure S2; Table S4). The semi‐split model again experiences the lowest stress (51.97 Pa) and the completely split model the highest (169.99 Pa). In all standard fusion models (Figure S2a–d) and filled models (Figure S2e–g), the stress distribution is localized to the proximal half of the diaphysis on the side of the diaphysis opposite the CR scar. Again, the cylinder models (Figure S2h–j) exhibit slightly less MWAM von Mises stresses than their standard counterparts (Figure S2a,b,d) and the filled versions (Figure S2e–g) even less than the cylinder models.

In the amplexus scenario, the MWAM von Mises stresses are much lower than in other scenarios for all models examined, but again the overall pattern of highest to lowest stress among the models is the same (Figure S3; Table S4). The semi‐split model experienced the lowest stress (0.55 Pa) and the completely split model the highest (1.04 Pa). The stress distribution in both the standard and filled models is localized to the loading area, although in the cylindrical models it is localized slightly proximal to the loading area. In this loading scenario, the cylindrical models (Figure S3h–j) experience more MWAM von Mises stresses than their standard counterparts (Figure S3a,b,d) and the filled versions (Figure S3e–g) less than their standard counterparts.

3.3. Bending resistance of the radioulna

Among our four standard fusion models, we found that bending resistance is greater at the epiphyses than along the diaphysis, with the least resistance at the narrowest part of the diaphysis (Figure 5a–e; Table S5). We recovered evidence of directional anisotropy across the entire length of the model for three of our models (Figure 5a–c), with I _minor larger than I _major, which is especially pronounced at the epiphyses of the models. There is less directional anisotropy in the two parts of the split model (Figure 5d–e), with only some at the epiphyses. The semi‐split model (Figure 5b) has the greatest I _minor values overall, with the unedited radioulna having the second greatest values (Figure 5a), the fused model with the third greatest (Figure 5c), and the completely split model the least (Figure 5d–e). The three cylinder models that we tested have uniform I values across the length of each model, with the fused cylinder having the greatest (Figure 5g), the semi‐fused cylinder the second greatest (Figure 5h), and the split cylinder the least (Figure 5f).

The compactness of the models is highest at the epiphyses and lowest at the narrowest part of the diaphysis. Average compactness is highest in the unedited radioulna model (0.80) and lowest in the semi‐fused cylindrical model (0.46); see Table S5 for full output files.

4. DISCUSSION

4.1. Functional consequences of fusion

In many frog species, the forelimb plays a key role both in takeoff and in shock absorption following a leap (Liem et al., 2001; Nauwelaerts & Aerts, 2006; Zug, 1972). It has been proposed that fused limb bones increase the strength of the limb and decrease its weight (Barnett & Napier, 1953; Coombs Jr., 1978; Howell, 1944), which are both considered adaptive for saltation. Our findings corroborate the idea that radioulna fusion is an adaptation for saltation by both strengthening and lightening the forelimb during landing.

Based on our results, the semi‐fused state of the radioulna is advantageous by lessening the von Mises stress of landing than in completely fused or split morphologies (Figure S2). Among our four standard models of potential fusion states, the two partially‐fused models always exhibited the least amount of von Mises stress and the highest resistance to bending compared to the split and fully‐fused models (Figures 4, 5; Figures [Link], [Link]). The split model (Figure 4d) may experience more stress because the radius and ulna are thinner bones and do not distribute stress as efficiently as the fused models. The fully‐fused model (Figure 4a) may experience more stress because removing the groove between the radius and ulna may weaken the structural integrity of the bone. These findings indicate that a partially‐fused morphology of the radioulna may be less likely to break under high loading forces such as those during jumping and therefore may increase performance in that scenario.

Additionally, we found that between the two semi‐fused models (Figure 4b and c), the simulated semi‐split model experienced less von Mises stress than the unedited radioulna morphology of R. catesbeiana. The main difference between these models is an interosseus space between the radius and ulna halves in the simulated model that is absent in the unedited model. Because all frog species lack an interosseus space between the radius and ulna in adults, there is likely some other evolutionary force that makes the observed state more advantageous, such as decreasing the weight of the bone to make jumping easier. Decreasing the volume, and thus mass, of the limb counterbalances the tendency to add mass to strengthen the limb (Hildebrand et al., 1985). While our standard fusion models varied little in volume (0.128 ± 0.013 cm³), they were not completely equivalent due to their morphological differences. The split and semi‐split models had the highest volume, the unedited model slightly less, and the completely fused model the least (Table S4). It may be that the slight decrease in bone volume (0.0162 cm³) saved by removing the interosseus space offsets the increased von Mises stress in the unedited morphology, and thus is the morphology invariably found in all modern anurans. Alternatively, the unedited morphology may reduce stress in other loading scenarios not tested in this study, such as torsional or asymmetrical loads.

Similarly, we found through testing of our filled fusion models (Figure 4e–g) that radioulna models with no internal cavities exhibit less von Mises stress than the standard models, which may indicate a tradeoff between volume and stress. Vertebrate bones are rarely solid due to the functional importance of decreasing bone volume and weight. There are diminishing returns of bending resistance as the wall thickness of a tube increases (Alexander, 1968). Although the filled models that we tested consistently experienced the least von Mises stress among all models in our three loading scenarios, the filled models also had much higher volumes than the standard models (160% more volume on average, Table S4). Given the variation we observed in radioulna wall thicknesses (Table S2) and the complete lack of interosseus space between the radius and ulna, it seems likely that bending resistance and weight tradeoffs are mediated by adjusting the wall thickness rather than the degree of fusion between the radius and ulna (see Vera et al., 2020 for the description of inter‐specific variation in wall thickness of the anuran femur and tibiofibula).

In this study, we also examined one simulation of amplexus forces on the radioulna, which favored fusion of the radius and ulna in terms of lessening von Mises stress, as well as the non‐cylindrical models compared to the cylindrical models (Figure S3). We found that one of the highest points of bending resistance in the diaphysis occurs in the same location that the m. coracoradialis inserts on the radioulna (Figure 5a). Bone is predicted to be the thickest in the region where the bending moment is highest (Alexander, 1968). It may be that the high second moment of area generated by the complete fusion of the radius and ulna at this part of the diaphysis is necessary for the radioulna to withstand the forces exerted there during amplexus (Figure S3l). Many frogs use their forelimbs in amplexus (Duellmann & Trueb, 1986) or in male–male combat (Duellman & Savitzky, 1976), and perhaps these selection pressures maintain fusion across frog diversity even when frogs do not rely on their forelimbs for landing.

4.2. Morphological diversity

Previous studies of radioulna morphology in frogs generally used length (occasionally width) measurements to describe shape variation (Citadini et al., 2018; Enriquez‐Urzelai et al., 2015; Fabrezi et al., 2017; Vidal‐García et al., 2014; Vidal‐García & Keogh, 2015), with more recent work using four 3D landmarks (Stepanova & Womack, 2020). Our study is the first to describe radioulna morphological diversity in further depth, describing variation in wall thickness, CR scar position, three width measurements, and two angle measurements (Table S2). In our sample of 17 frog families, we found that the radioulna is invariably fused along its entire length (except potentially in one case of individual variation, e.g., Espadarana prosoblepon), but the proportion of length to width, relative position of the minimum width of the diaphysis, the wall thickness of the diaphysis, and angles between the radius and ulna portions varied relative to body size (Figure 3). Three of the species identified as outliers are burrowing specialists, which may indicate that locomotor mode plays a role in radioulna morphological variation (Figure 3). We tested the impact of fusion on one individual from one species, R. catesbeiana, which in two of our measurements was an outlier (Figure 3). Given this morphological diversity (as well as the diversity of material properties of bone between species; see Wilson et al., 2009), it may be that changing the degree of fusion would affect other species and loading scenarios differently (i.e., Myobatrachus gouldii, a forward‐burrower).

We completed a cursory comparison of non‐anuran vertebrate radioulnae and found some notable differences. In other clades that exhibit fusion of the radius and ulna (e.g., bats, perissodactyls, and artiodactyls), there are typically interosseus spaces between the fused radius and ulna (Figure 1d). In lagomorphs and birds (in which the forelimb participates in energetic movements), the radius and ulna are closely associated but unfused (Figure 1d; Dial, 1992; Young et al., 2014). Additionally, in non‐anuran groups, radius and ulna fusion occurs most completely at the distal end of the zeugopod rather than the proximal end as it does in frogs (except in the case of human radioulnar synostosis, Rutkowski & Samora, 2021; Figure 1d). Besides frogs, only lagomorphs consistently land with the forelimb among terrestrial, saltatory vertebrates, and the radii and ulnae of lagomorphs are unfused (Figure 1d). Frogs differ from lagomorphs in many ways, but one relevant distinction is that frogs have a sprawling gait and lagomorphs an erect gait. The force vectors acting on the forelimb would therefore be different and may select for different zeugopod morphologies. The medial rotation of the carpals (and manus) is thought to be an adaptation related to saltation in frogs (Fabrezi et al., 2017). Yet this is not seen in saltatory mammals and therefore may be an adaptation to landing forelimb‐first with a sprawling gait. Indeed, other anuran locomotor modes, such as walking, may also benefit from such zeugopod morphologies. We found that all frog species in our study showed partial, permanent pronation of the radius and ulna (4.26 ± 0.36°; Table S2). This is likely related to maintaining this posture and may influence the unique fusion patterns found in the anuran zeugopod.

Other selection pressures, such as those related to amplexus behaviors, may be responsible for the unique, proximally‐dominated fusion pattern of the radius and ulna in frogs. This, however, requires a broader examination of frog diversity, including those that vary in the mode of amplexus (Carvajal‐Castro et al., 2020). Such future work would offer a unique perspective on the evolution of saltatory morphotypes in vertebrates and the potential tradeoffs between locomotory and other behaviors.

4.3. Future considerations

As mentioned, there are several avenues for future investigations stemming from this work that would help to develop a richer understanding of the radioulna diversity found in frogs and why it differs so markedly from other vertebrates. To start, our finite element models only examined the radioulna in isolation and did not incorporate the complex cushioning mechanisms of the hands (Abdala et al., 2022), pectoral girdle (Emerson, 1983; Nauwelaerts & Aerts, 2006), and other ventral elements (Essner et al., 2010) that may obscure the true loading conditions shaping the anuran radioulna morphology. For example, the MA measurement that we collected is one of three measurements of mechanical advantage in the forelimb that are relevant for forelimb‐involved amplexus (m. coracoradialis, pectoral muscles, forearm flexors; Emerson, 1991). Further investigation of this system, looking wholistically at the pectoral girdle, manus, and forelimb will be necessary to probe further into the relationship between radioulna fusion and reproductive and locomotor behavioral pressures.

Additionally, both amplexus (Carvajal‐Castro et al., 2020) and landing behaviors (Abdala et al., 2022; Bijma et al., 2016; Reilly et al., 2016) in frogs are diverse and thus there could be different loading optima in different clades. Many species do not use the forelimb during amplexus (e.g., Breviceps, Mantidactylus, Dendrobates; Duellman & Trueb, 1986; Carvajal‐Castro et al., 2020). The one species from our dataset that lacked forelimb‐involved amplexus (Breviceps poweri; Figure 1) did not differ greatly in terms of MA calculations (Table S2). Regarding saltation, many frogs that jump do not brace with the forelimb upon landing (Essner et al., 2010, 2022; Reilly et al., 2016) and yet the radius and ulna are always fused in modern frogs. In Ascaphus, the radius and ulna are fused (Figure 1a) despite Ascaphus actively avoiding using its forelimbs during landing behaviors (Essner et al., 2010). It may be that the “belly flop” landing of Ascaphus, Leiopelma, and others is a derived behavior (Sigurdsen et al., 2012) and that forelimb bracing was secondarily lost (although see Essner et al., 2010). It may be that complete fusion of the radius and ulna may not be as critical to saltation as previously thought. Or, potentially, the fusion of zeugopod elements may not be costly enough to select against fusion in frogs that do not jump. Previous work on bone adaptations in mammals found that the bending resistance of limb bones in hopping macropods and artiodactyls is similar across clades even when the forelimb is mostly unloaded (Doube et al., 2018). This suggests that low‐intensity loads might adequately maintain bone mass across lineages over evolutionary timescales. Perhaps in lineages of frogs that do not use the forelimb as a landing shock absorber, lesser loads like those of amplexus and other locomotor modes act to maintain radioulna fusion.

Last, frogs have a highly conserved body shape (Handrigan & Wassersug, 2007; Inger, 1967), perhaps due to strong developmental constraints that limit the evolution of certain morphologies. Fusion of the zeugopod elements has been present in the anuran lineage since at least the early Jurassic (e.g., Prosalirus bitis; Shubin & Jenkins, 1995). Anuran saltation is thought to have an origin in riparian ecosystems where frogs could escape from land into water (Essner et al., 2010; Gans & Parsons, 1966). In modern frogs, fusion of zeugopod elements begins early in development, prior to the end of digit differentiation (Fabrezi et al., 2017). Further investigation into the development and evolution of the radioulna would be valuable in addressing questions of why all frogs retain a fused zeugopod.

5. CONCLUSION

We found evidence that the semi‐fused condition of the anuran radioulna experiences less von Mises stress and has overall higher bending resistance than completely fused or completely split conditions across multiple loading scenarios. The addition of an interosseus space between the radius and ulna lessens von Mises stress and increases bending resistance, but also slightly increases the volume of the radioulna compared to the natural condition. This suggests that the natural condition of the radioulna is a tradeoff between strength and lightness. This supports the hypothesis that the fused radioulna is primarily an adaptation for landing following jumping in frogs.

Patterns of fusion and bending resistance in the radioulna may indicate that the anuran radioulna is reinforced to withstand loading forces during amplexus. The cross‐section of the radioulna associated with the CR scar has increased bending resistance compared to other parts of the diaphysis. The semi‐fused condition of the radioulna exhibited the least amount of von Mises stress in amplexus conditions compared to split, fused, and even geometrically cylindrical models. Amplexus may contribute to the unique morphology of the anuran radioulna, although one species that does not use the arms during amplexus showed similar radioulna morphology.

Radioulna morphology was more variable than previously described. New measurements were presented such as wall thickness, position of the CR scar, angle between the radius and ulna, and angle of pronation. The morphological variation found indicates that there is some effect of locomotor mode and body size on radioulna shape. Frogs are unique among vertebrates in the proximally‐oriented pattern of fusion of the radioulna. Wider‐scale analyses among anuran and vertebrate diversity would be useful for deepening our understanding of the evolution of saltatory morphotypes in vertebrates.

Supporting information

Figure S1

Figure S2

Figure S3

Table S1

Table S2

Table S3

Table S4

Table S5

Supporting Information

Keeffe, R. & Blackburn, D.C. (2022) Diversity and function of the fused anuran radioulna. Journal of Anatomy, 241, 1026–1038. Available from: 10.1111/joa.13737

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available via MorphoSource. A list of specimen numbers and MorphoSource DOIs for the data used in this study are listed in Table S1.